This is “Statistical Inferences About ?1”, section 10.5 from the book Beginning Statistics (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
10.5 Statistical Inferences About β1
Learning Objectives
- To learn how to construct a confidence interval for , the slope of the population regression line.
- To learn how to test hypotheses regarding
The parameter , the slope of the population regression line, is of primary importance in regression analysis because it gives the true rate of change in the mean in response to a unit increase in the predictor variable x. For every unit increase in x the mean of the response variable y changes by units, increasing if and decreasing if We wish to construct confidence intervals for and test hypotheses about it.
Confidence Intervals for β1
The slope of the least squares regression line is a point estimate of A confidence interval for is given by the following formula.
Confidence Interval for the Slope of the Population Regression Line
where and the number of degrees of freedom is
The assumptions listed in Section 10.3 "Modelling Linear Relationships with Randomness Present" must hold.
Definition
The statistic is called the sample standard deviation of errorsThe statistic .. It estimates the standard deviation σ of the errors in the population of y-values for each fixed value of x (see Figure 10.5 "The Simple Linear Model Concept" in Section 10.3 "Modelling Linear Relationships with Randomness Present").
Example 6
Construct the 95% confidence interval for the slope of the population regression line based on the five-point sample data set
Solution:
The point estimate of was computed in Note 10.18 "Example 2" in Section 10.4 "The Least Squares Regression Line" as In the same example was found to be The sum of the squared errors was computed in Note 10.23 "Example 4" in Section 10.4 "The Least Squares Regression Line" as Thus
Confidence level 95% means so From the row labeled in Figure 12.3 "Critical Values of " we obtain Therefore
which gives the interval We are 95% confident that the slope of the population regression line is between 0.1215 and 0.5661.
Example 7
Using the sample data in Table 10.3 "Data on Age and Value of Used Automobiles of a Specific Make and Model" construct a 90% confidence interval for the slope of the population regression line relating age and value of the automobiles of Note 10.19 "Example 3" in Section 10.4 "The Least Squares Regression Line". Interpret the result in the context of the problem.
Solution:
The point estimate of was computed in Note 10.19 "Example 3", as was Their values are and The sum of the squared errors was computed in Note 10.24 "Example 5" in Section 10.4 "The Least Squares Regression Line" as Thus
Confidence level 90% means so From the row labeled in Figure 12.3 "Critical Values of " we obtain Therefore
which gives the interval We are 90% confident that the slope of the population regression line is between −3.00 and −1.10. In the context of the problem this means that for vehicles of this make and model between two and six years old we are 90% confident that for each additional year of age the average value of such a vehicle decreases by between $1,100 and $3,000.
Testing Hypotheses About β1
Hypotheses regarding can be tested using the same five-step procedures, either the critical value approach or the p-value approach, that were introduced in Section 8.1 "The Elements of Hypothesis Testing" and Section 8.3 "The Observed Significance of a Test" of Chapter 8 "Testing Hypotheses". The null hypothesis always has the form where B0 is a number determined from the statement of the problem. The three forms of the alternative hypothesis, with the terminology for each case, are:
| Form of Ha | Terminology |
|---|---|
| Left-tailed | |
| Right-tailed | |
| Two-tailed |
The value zero for B0 is of particular importance since in that case the null hypothesis is , which corresponds to the situation in which x is not useful for predicting y. For if then the population regression line is horizontal, so the mean is the same for every value of x and we are just as well off in ignoring x completely and approximating y by its average value. Given two variables x and y, the burden of proof is that x is useful for predicting y, not that it is not. Thus the phrase “test whether x is useful for prediction of y,” or words to that effect, means to perform the test
Standardized Test Statistic for Hypothesis Tests Concerning the Slope of the Population Regression Line
The test statistic has Student’s t-distribution with degrees of freedom.
The assumptions listed in Section 10.3 "Modelling Linear Relationships with Randomness Present" must hold.
Example 8
Test, at the 2% level of significance, whether the variable x is useful for predicting y based on the information in the five-point data set
Solution:
We will perform the test using the critical value approach.
-
Step 1. Since x is useful for prediction of y precisely when the slope of the population regression line is nonzero, the relevant test is
-
Step 2. The test statistic is
and has Student’s t-distribution with degrees of freedom.
-
Step 3. From Note 10.18 "Example 2", and From Note 10.30 "Example 6", The value of the test statistic is therefore
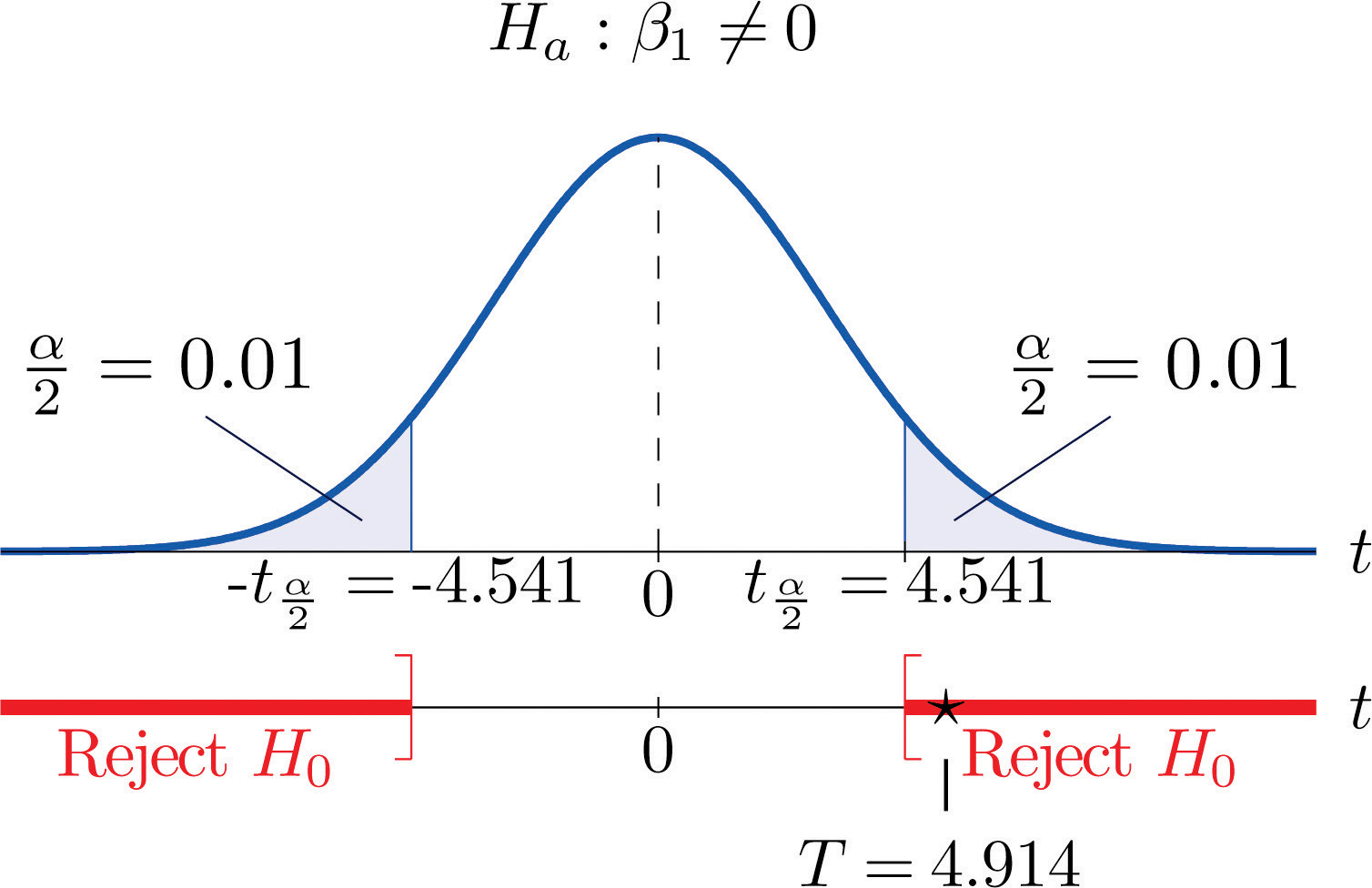
- Step 4. Since the symbol in Ha is “≠” this is a two-tailed test, so there are two critical values Reading from the line in Figure 12.3 "Critical Values of " labeled , The rejection region is
-
Step 5. As shown in Figure 10.9 "Rejection Region and Test Statistic for " the test statistic falls in the rejection region. The decision is to reject H0. In the context of the problem our conclusion is:
The data provide sufficient evidence, at the 2% level of significance, to conclude that the slope of the population regression line is nonzero, so that x is useful as a predictor of y.
Figure 10.9 Rejection Region and Test Statistic for Note 10.33 "Example 8"
Example 9
A car salesman claims that automobiles between two and six years old of the make and model discussed in Note 10.19 "Example 3" in Section 10.4 "The Least Squares Regression Line" lose more than $1,100 in value each year. Test this claim at the 5% level of significance.
Solution:
We will perform the test using the critical value approach.
-
Step 1. In terms of the variables x and y, the salesman’s claim is that if x is increased by 1 unit (one additional year in age), then y decreases by more than 1.1 units (more than $1,100). Thus his assertion is that the slope of the population regression line is negative, and that it is more negative than −1.1. In symbols, Since it contains an inequality, this has to be the alternative hypotheses. The null hypothesis has to be an equality and have the same number on the right hand side, so the relevant test is
-
Step 2. The test statistic is
and has Student’s t-distribution with 8 degrees of freedom.
-
Step 3. From Note 10.19 "Example 3", and From Note 10.31 "Example 7", The value of the test statistic is therefore
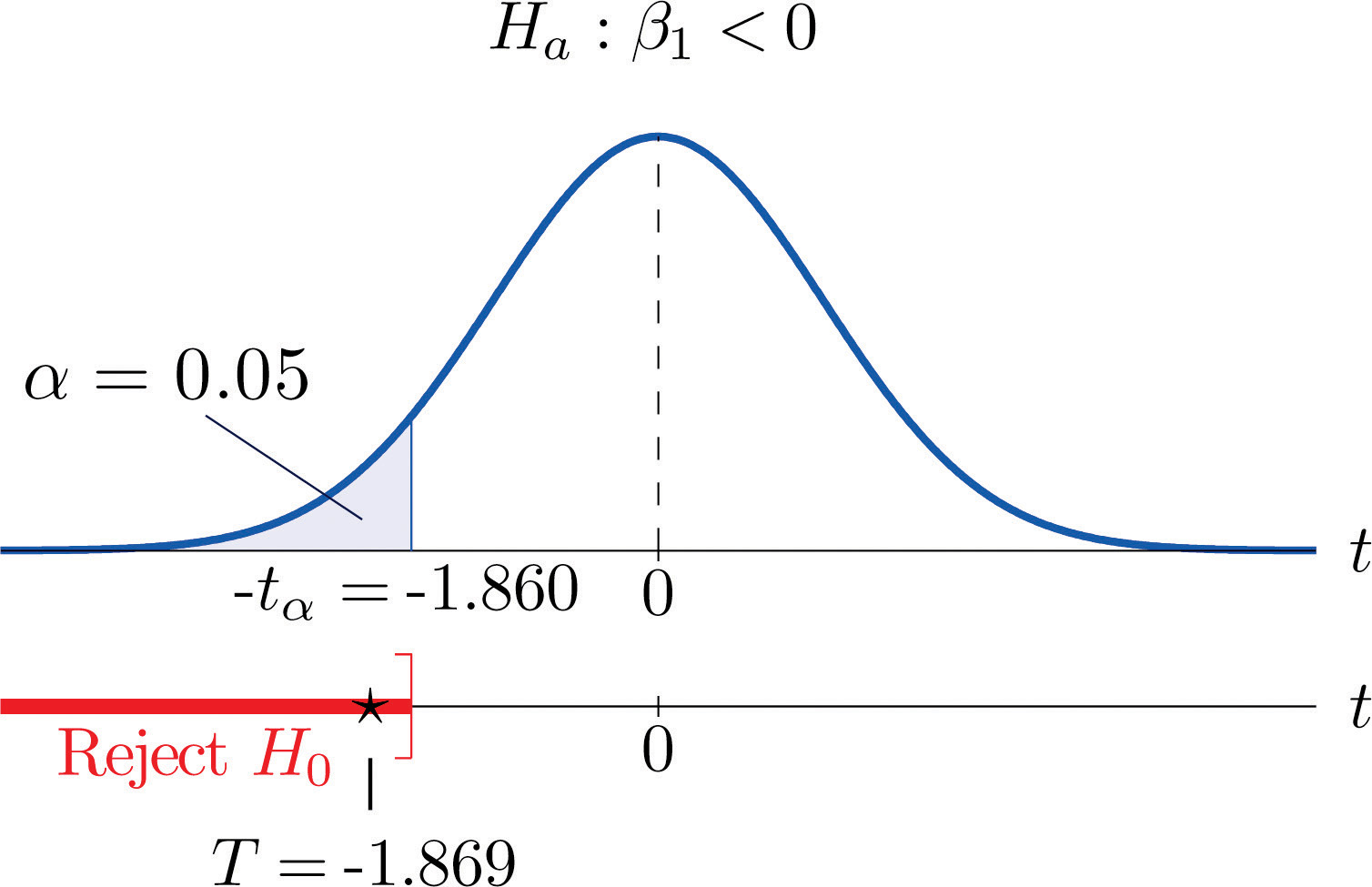
- Step 4. Since the symbol in Ha is “<” this is a left-tailed test, so there is a single critical value Reading from the line in Figure 12.3 "Critical Values of " labeled , The rejection region is
-
Step 5. As shown in Figure 10.10 "Rejection Region and Test Statistic for " the test statistic falls in the rejection region. The decision is to reject H0. In the context of the problem our conclusion is:
The data provide sufficient evidence, at the 5% level of significance, to conclude that vehicles of this make and model and in this age range lose more than $1,100 per year in value, on average.
Figure 10.10 Rejection Region and Test Statistic for Note 10.34 "Example 9"
Key Takeaways
- The parameter , the slope of the population regression line, is of primary interest because it describes the average change in y with respect to unit increase in x.
- The statistic , the slope of the least squares regression line, is a point estimate of Confidence intervals for can be computed using a formula.
- Hypotheses regarding are tested using the same five-step procedures introduced in Chapter 8 "Testing Hypotheses".
Exercises
-
Construct the 95% confidence interval for the slope of the population regression line based on the sample data set of Exercise 1 of Section 10.2 "The Linear Correlation Coefficient".
-
Construct the 90% confidence interval for the slope of the population regression line based on the sample data set of Exercise 2 of Section 10.2 "The Linear Correlation Coefficient".
-
Construct the 90% confidence interval for the slope of the population regression line based on the sample data set of Exercise 3 of Section 10.2 "The Linear Correlation Coefficient".
-
Construct the 99% confidence interval for the slope of the population regression Exercise 4 of Section 10.2 "The Linear Correlation Coefficient".
-
For the data in Exercise 5 of Section 10.2 "The Linear Correlation Coefficient" test, at the 10% level of significance, whether x is useful for predicting y (that is, whether ).
-
For the data in Exercise 6 of Section 10.2 "The Linear Correlation Coefficient" test, at the 5% level of significance, whether x is useful for predicting y (that is, whether ).
-
Construct the 90% confidence interval for the slope of the population regression line based on the sample data set of Exercise 7 of Section 10.2 "The Linear Correlation Coefficient".
-
Construct the 95% confidence interval for the slope of the population regression line based on the sample data set of Exercise 8 of Section 10.2 "The Linear Correlation Coefficient".
-
For the data in Exercise 9 of Section 10.2 "The Linear Correlation Coefficient" test, at the 1% level of significance, whether x is useful for predicting y (that is, whether ).
-
For the data in Exercise 10 of Section 10.2 "The Linear Correlation Coefficient" test, at the 1% level of significance, whether x is useful for predicting y (that is, whether ).
Basic
For the Basic and Application exercises in this section use the computations that were done for the exercises with the same number in Section 10.2 "The Linear Correlation Coefficient" and Section 10.4 "The Least Squares Regression Line".
-
For the data in Exercise 11 of Section 10.2 "The Linear Correlation Coefficient" construct a 90% confidence interval for the mean number of new words acquired per month by children between 13 and 18 months of age.
-
For the data in Exercise 12 of Section 10.2 "The Linear Correlation Coefficient" construct a 90% confidence interval for the mean increased braking distance for each additional 100 pounds of vehicle weight.
-
For the data in Exercise 13 of Section 10.2 "The Linear Correlation Coefficient" test, at the 10% level of significance, whether age is useful for predicting resting heart rate.
-
For the data in Exercise 14 of Section 10.2 "The Linear Correlation Coefficient" test, at the 10% level of significance, whether wind speed is useful for predicting wave height.
-
For the situation described in Exercise 15 of Section 10.2 "The Linear Correlation Coefficient"
- Construct the 95% confidence interval for the mean increase in revenue per additional thousand dollars spent on advertising.
- An advertising agency tells the business owner that for every additional thousand dollars spent on advertising, revenue will increase by over $25,000. Test this claim (which is the alternative hypothesis) at the 5% level of significance.
- Perform the test of part (b) at the 10% level of significance.
- Based on the results in (b) and (c), how believable is the ad agency’s claim? (This is a subjective judgement.)
-
For the situation described in Exercise 16 of Section 10.2 "The Linear Correlation Coefficient"
- Construct the 90% confidence interval for the mean increase in height per additional inch of length at age two.
- It is claimed that for girls each additional inch of length at age two means more than an additional inch of height at maturity. Test this claim (which is the alternative hypothesis) at the 10% level of significance.
-
For the data in Exercise 17 of Section 10.2 "The Linear Correlation Coefficient" test, at the 10% level of significance, whether course average before the final exam is useful for predicting the final exam grade.
-
For the situation described in Exercise 18 of Section 10.2 "The Linear Correlation Coefficient", an agronomist claims that each additional million acres planted results in more than 750,000 additional acres harvested. Test this claim at the 1% level of significance.
-
For the data in Exercise 19 of Section 10.2 "The Linear Correlation Coefficient" test, at the 1/10th of 1% level of significance, whether, ignoring all other facts such as age and body mass, the amount of the medication consumed is a useful predictor of blood concentration of the active ingredient.
-
For the data in Exercise 20 of Section 10.2 "The Linear Correlation Coefficient" test, at the 1% level of significance, whether for each additional inch of girth the age of the tree increases by at least two and one-half years.
-
For the data in Exercise 21 of Section 10.2 "The Linear Correlation Coefficient"
- Construct the 95% confidence interval for the mean increase in strength at 28 days for each additional hundred psi increase in strength at 3 days.
- Test, at the 1/10th of 1% level of significance, whether the 3-day strength is useful for predicting 28-day strength.
-
For the situation described in Exercise 22 of Section 10.2 "The Linear Correlation Coefficient"
- Construct the 99% confidence interval for the mean decrease in energy demand for each one-degree drop in temperature.
- An engineer with the power company believes that for each one-degree increase in temperature, daily energy demand will decrease by more than 3.6 million watt-hours. Test this claim at the 1% level of significance.
Applications
-
Large Data Set 1 lists the SAT scores and GPAs of 1,000 students.
http://www.flatworldknowledge.com/sites/all/files/data1.xls
- Compute the 90% confidence interval for the slope of the population regression line with SAT score as the independent variable (x) and GPA as the dependent variable (y).
- Test, at the 10% level of significance, the hypothesis that the slope of the population regression line is greater than 0.001, against the null hypothesis that it is exactly 0.001.
-
Large Data Set 12 lists the golf scores on one round of golf for 75 golfers first using their own original clubs, then using clubs of a new, experimental design (after two months of familiarization with the new clubs).
http://www.flatworldknowledge.com/sites/all/files/data12.xls
- Compute the 95% confidence interval for the slope of the population regression line with scores using the original clubs as the independent variable (x) and scores using the new clubs as the dependent variable (y).
- Test, at the 10% level of significance, the hypothesis that the slope of the population regression line is different from 1, against the null hypothesis that it is exactly 1.
-
Large Data Set 13 records the number of bidders and sales price of a particular type of antique grandfather clock at 60 auctions.
http://www.flatworldknowledge.com/sites/all/files/data13.xls
- Compute the 95% confidence interval for the slope of the population regression line with the number of bidders present at the auction as the independent variable (x) and sales price as the dependent variable (y).
- Test, at the 10% level of significance, the hypothesis that the average sales price increases by more than $90 for each additional bidder at an auction, against the default that it increases by exactly $90.
Large Data Set Exercises
Answers
-
-
-
-
-
, , do not reject H0
-
-
-
-
, , reject H0
-
-
words
-
-
, , reject H0
-
-
- thousand dollars,
- , , do not reject H0;
- , reject H0
-
-
, , reject H0
-
-
, , reject H0
-
-
- hundred psi,
- , , reject H0
-
-
- vs. Test Statistic: Rejection Region: Decision: Reject H0.
-
-
- vs. Test Statistic: Rejection Region: Decision: Reject H0.




