This is “Negative Exponents”, section 5.6 from the book Beginning Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
5.6 Negative Exponents
Learning Objectives
- Simplify expressions with negative integer exponents.
- Work with scientific notation.
Negative Exponents
In this section, we define what it means to have negative integer exponents. We begin with the following equivalent fractions:
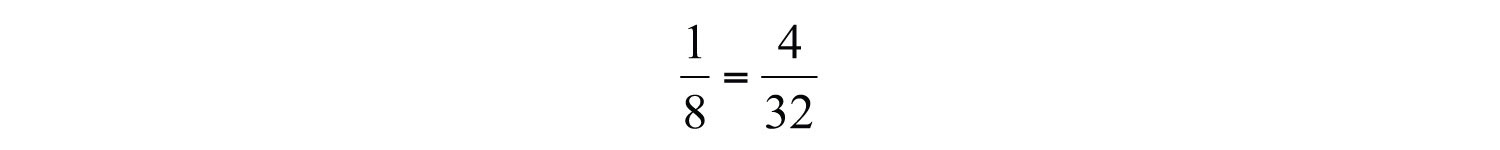
Notice that 4, 8, and 32 are all powers of 2. Hence we can write , , and .
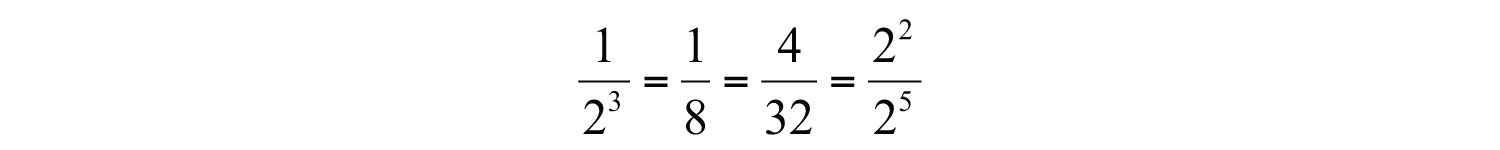
If the exponent of the term in the denominator is larger than the exponent of the term in the numerator, then the application of the quotient rule for exponents results in a negative exponent. In this case, we have the following:
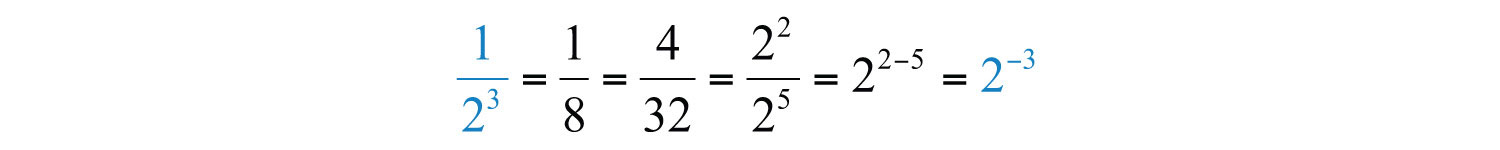
We conclude that . This is true in general and leads to the definition of negative exponents given any integer n, where x is nonzero.. Given any integer n and , then
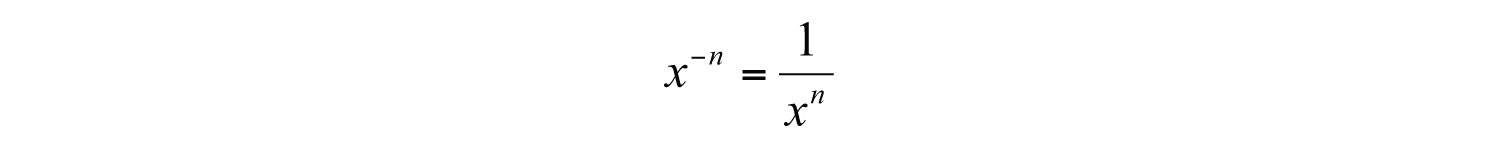
Here because is undefined. For clarity, in this section, assume all variables are nonzero.
Simplifying expressions with negative exponents requires that we rewrite the expression with positive exponents.
Example 1: Simplify: .
Solution:
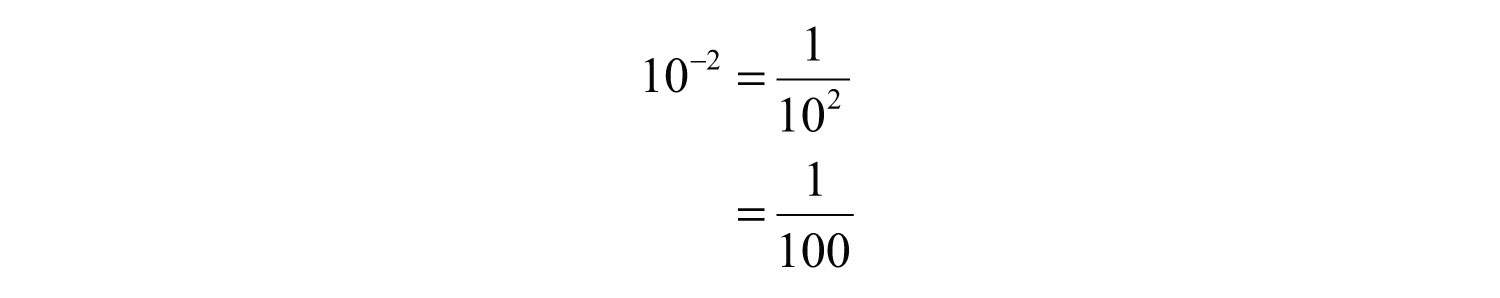
Answer:
Example 2: Simplify: .
Solution:
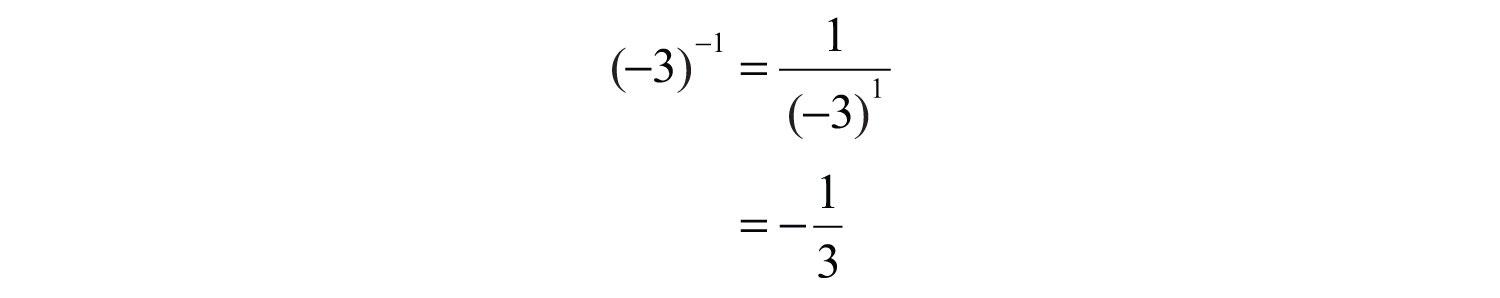
Answer:
Example 3: Simplify: .
Solution:
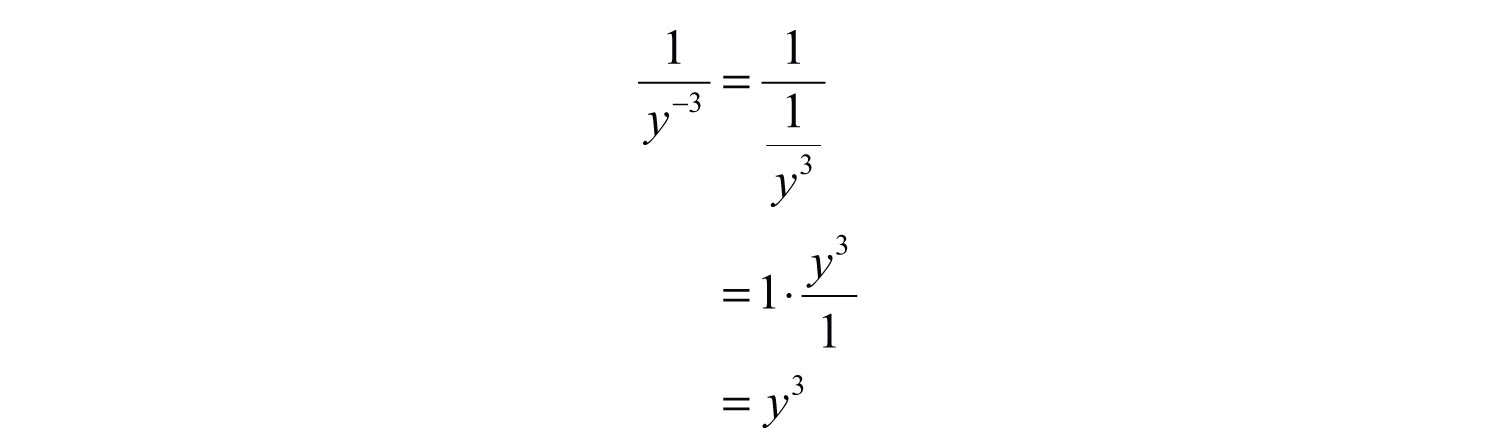
Answer:
At this point we highlight two very important examples,

If the grouped quantity is raised to a negative exponent, then apply the definition and write the entire grouped quantity in the denominator. If there is no grouping, then apply the definition only to the base preceding the exponent.
Example 4: Simplify: .
Solution: First, apply the definition of −3 as an exponent and then apply the power of a product rule.

Answer:
Example 5: Simplify: .
Solution:
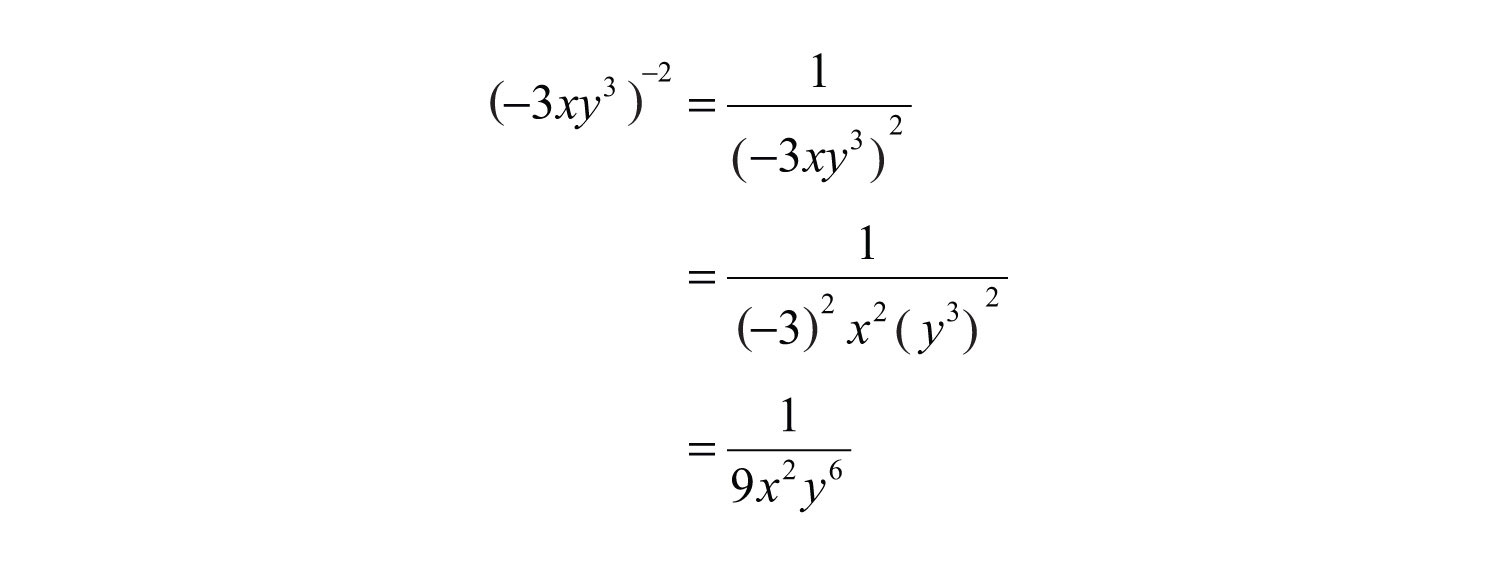
Answer:
Example 6: Simplify: .
Solution:
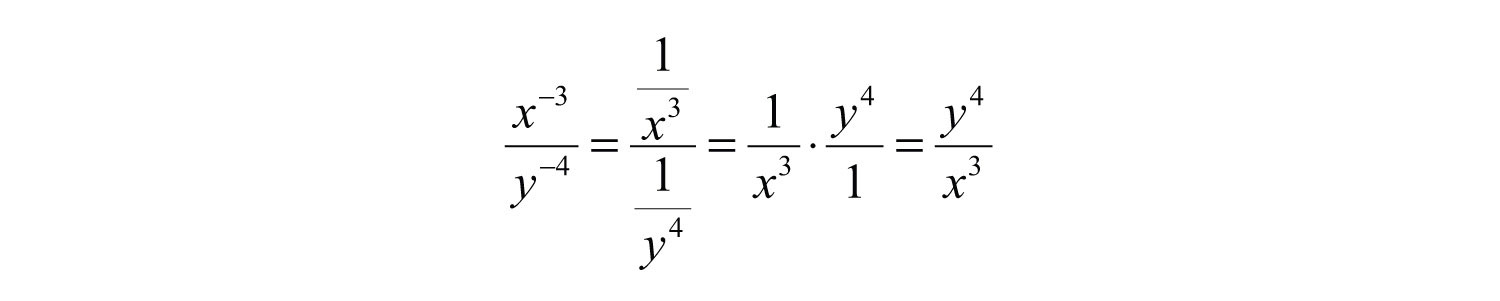
Answer:
The previous example suggests a property of quotients with negative exponents, given any integers m and n, where and .. If given any integers m and n, where and , then
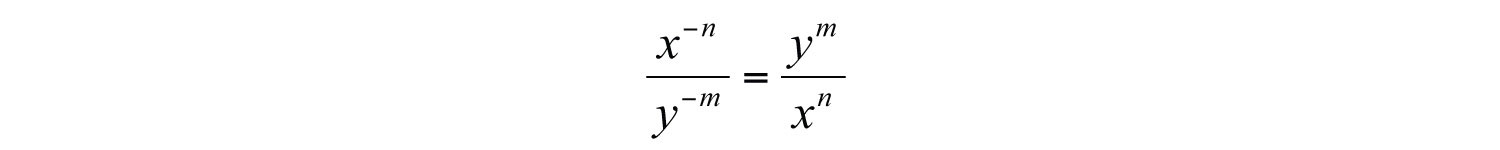
In other words, negative exponents in the numerator can be written as positive exponents in the denominator, and negative exponents in the denominator can be written as positive exponents in the numerator.
Example 7: Simplify: .
Solution: Take care with the coefficient −2; recognize that this is the base and that the exponent is actually +1: . Hence the rules of negative exponents do not apply to this coefficient; leave it in the numerator.
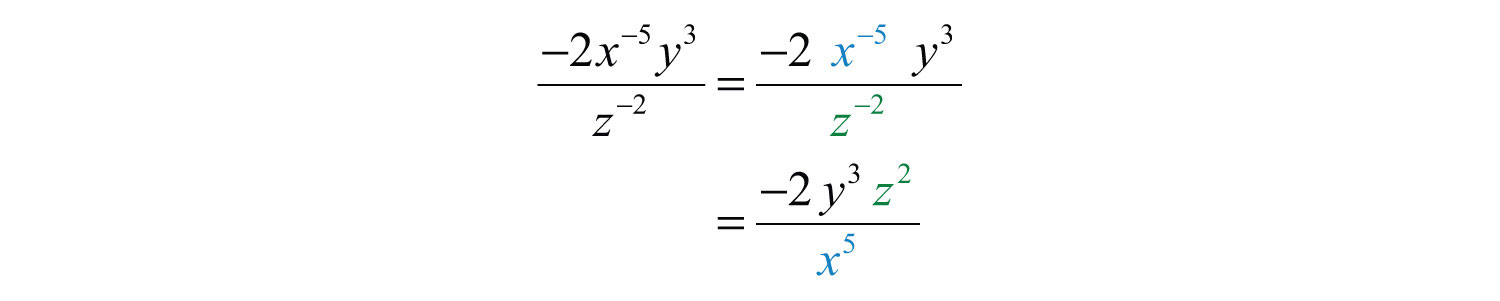
Answer:
Example 8: Simplify: .
Solution: Apply the power of a product rule before applying negative exponents.

Answer:
Example 9: Simplify: .
Solution:
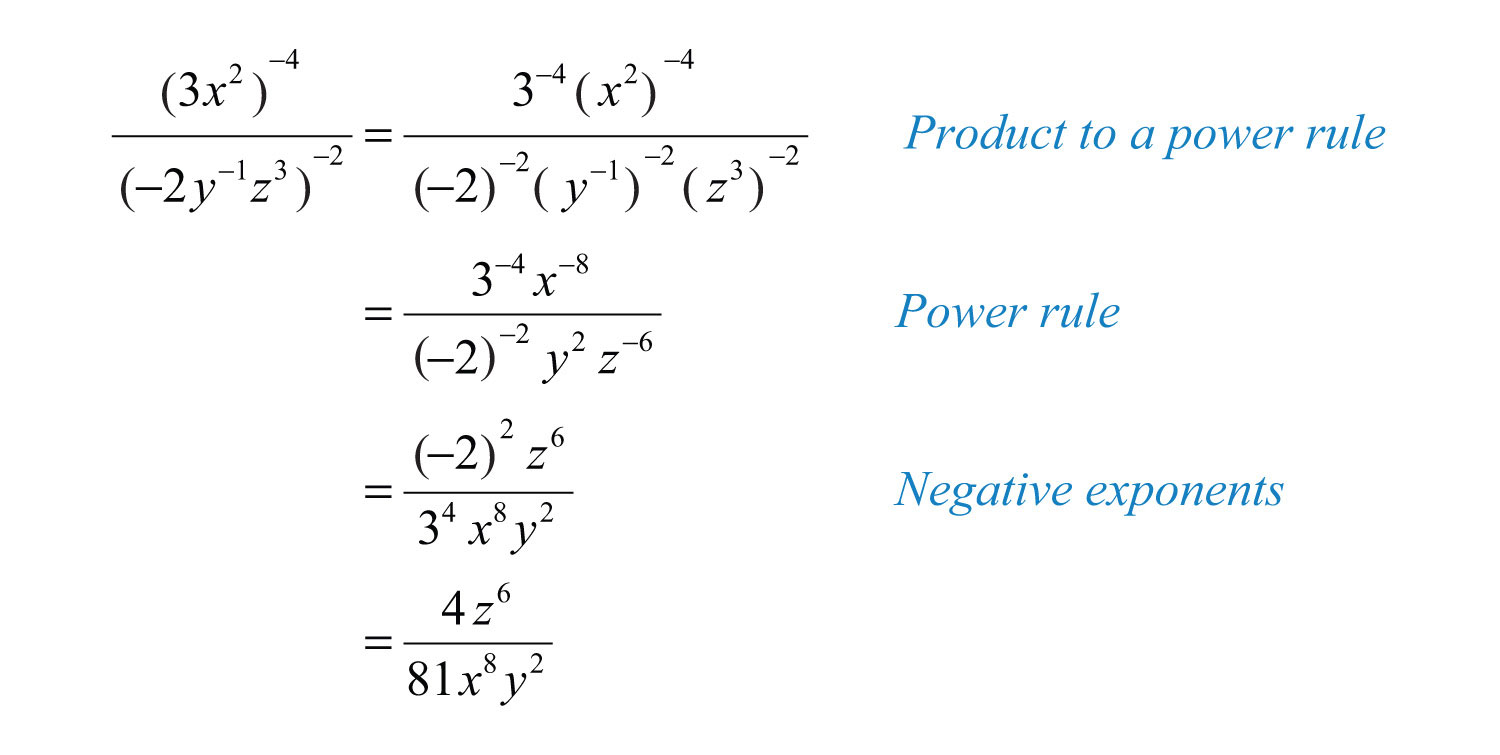
Answer:
Example 10: Simplify: .
Solution: First, apply the power of a product rule and then the quotient rule.
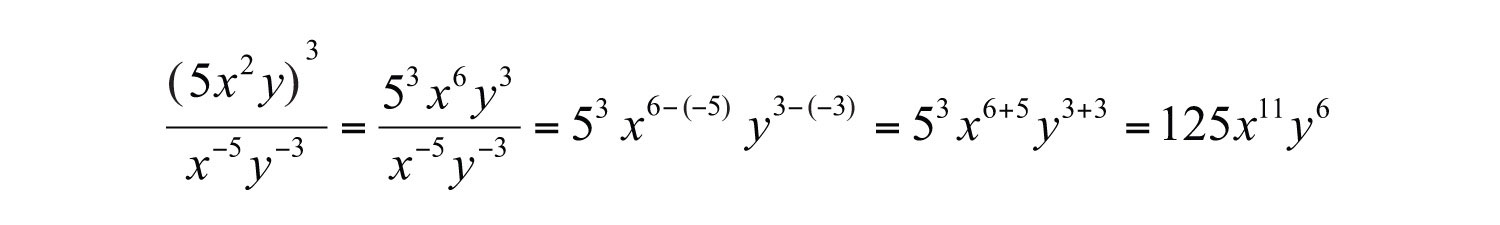
Answer:
To summarize, we have the following rules for negative integer exponents with nonzero bases:
| Negative exponents: | |
| Quotients with negative exponents: |
Try this! Simplify: .
Answer:
Video Solution
(click to see video)Scientific Notation
Real numbers expressed in scientific notationReal numbers expressed in the form , where n is an integer and . have the form
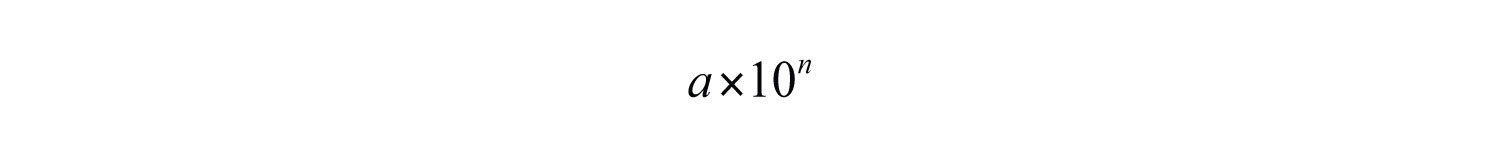
where n is an integer and . This form is particularly useful when the numbers are very large or very small. For example,
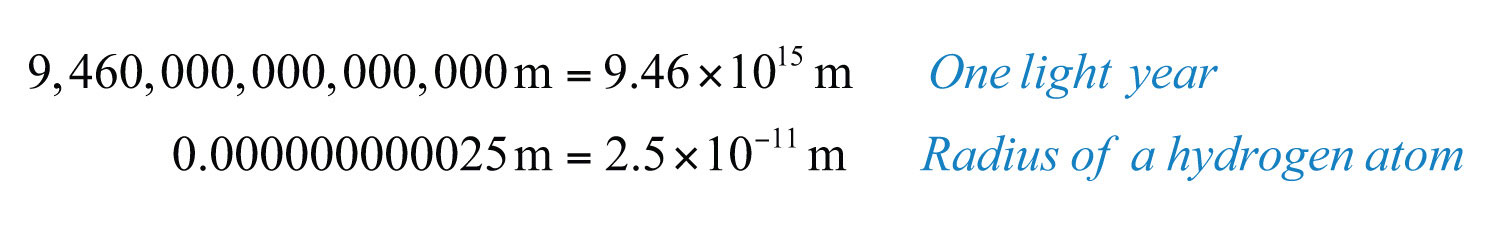
It is cumbersome to write all the zeros in both of these cases. Scientific notation is an alternative, compact representation of these numbers. The factor indicates the power of 10 to multiply the coefficient by to convert back to decimal form:
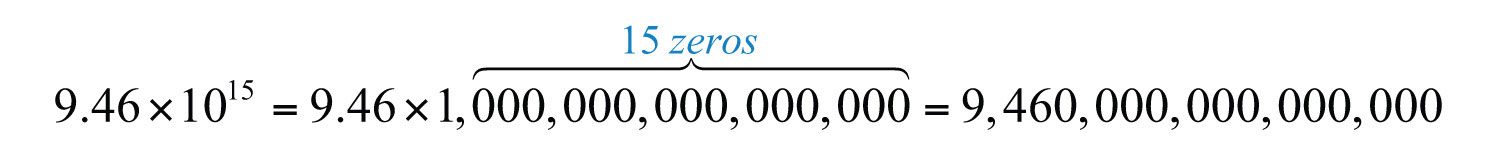
This is equivalent to moving the decimal in the coefficient fifteen places to the right. A negative exponent indicates that the number is very small:

This is equivalent to moving the decimal in the coefficient eleven places to the left.
Converting a decimal number to scientific notation involves moving the decimal as well. Consider all of the equivalent forms of with factors of 10 that follow:
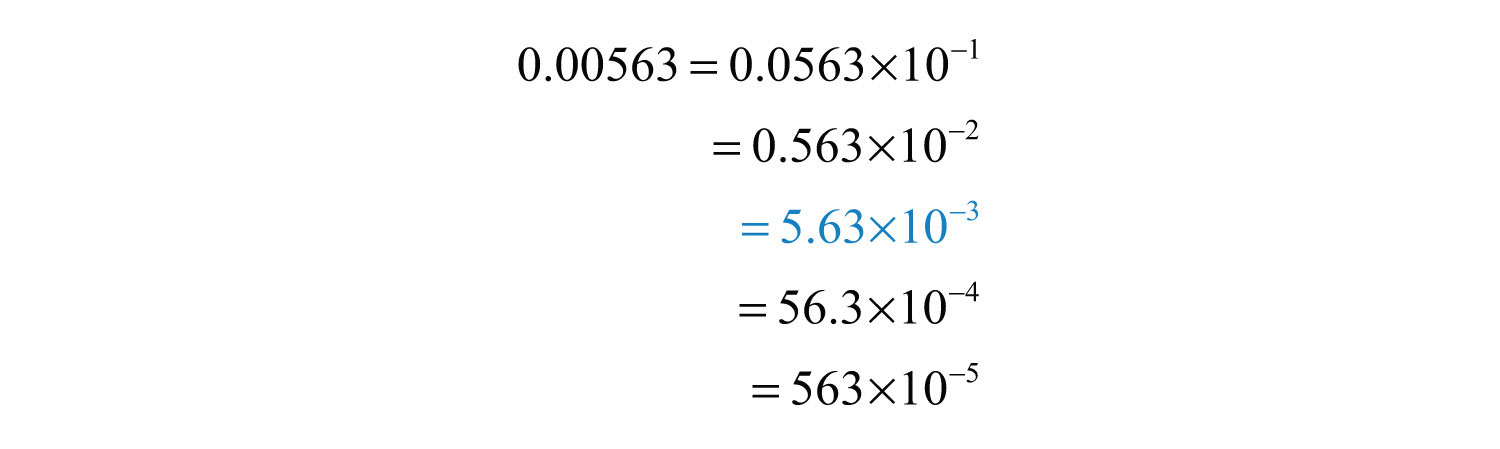
While all of these are equal, is the only form considered to be expressed in scientific notation. This is because the coefficient 5.63 is between 1 and 10 as required by the definition. Notice that we can convert back to decimal form, as a check, by moving the decimal to the left three places.
Example 11: Write using scientific notation.
Solution: Here we count twelve decimal places to the left of the decimal point to obtain the number 1.075.
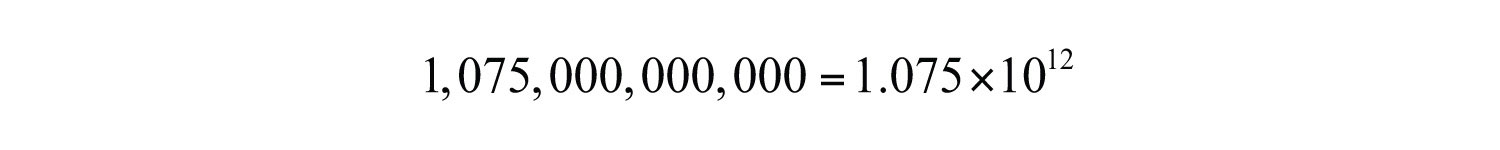
Answer:
Example 12: Write using scientific notation.
Solution: Here we count six decimal places to the right to obtain 3.045.
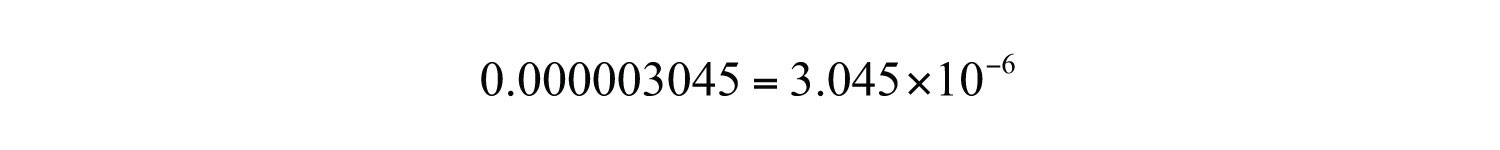
Answer:
Often we will need to perform operations when using numbers in scientific notation. All the rules of exponents developed so far also apply to numbers in scientific notation.
Example 13: Multiply: .
Solution: Use the fact that multiplication is commutative and apply the product rule for exponents.
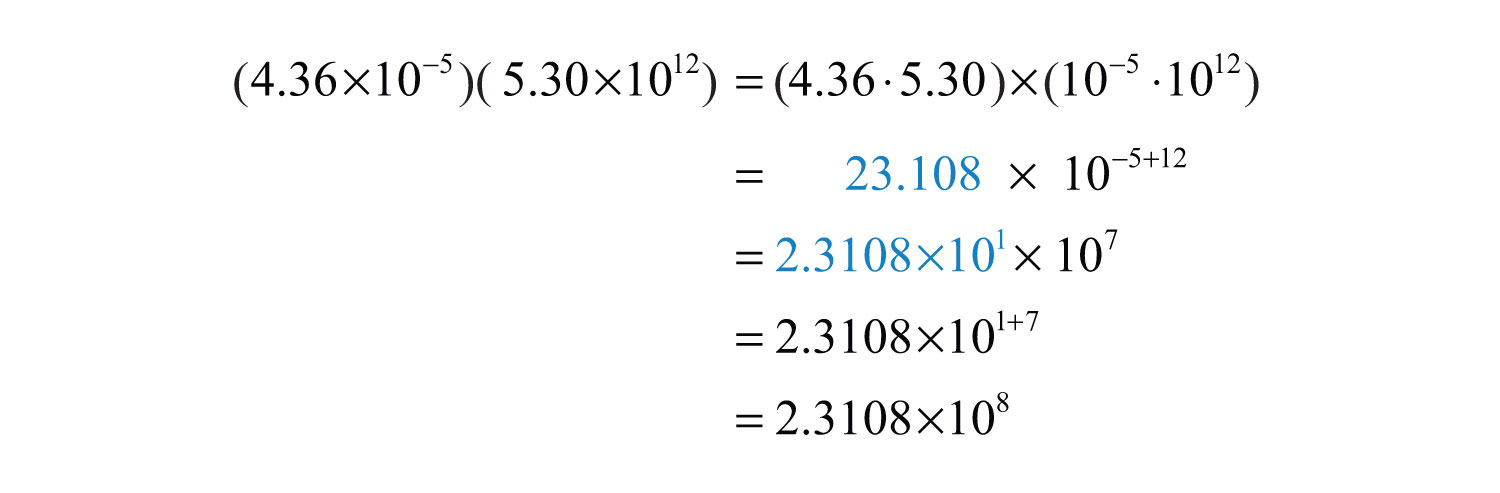
Answer:
Example 14: Divide: .
Solution:
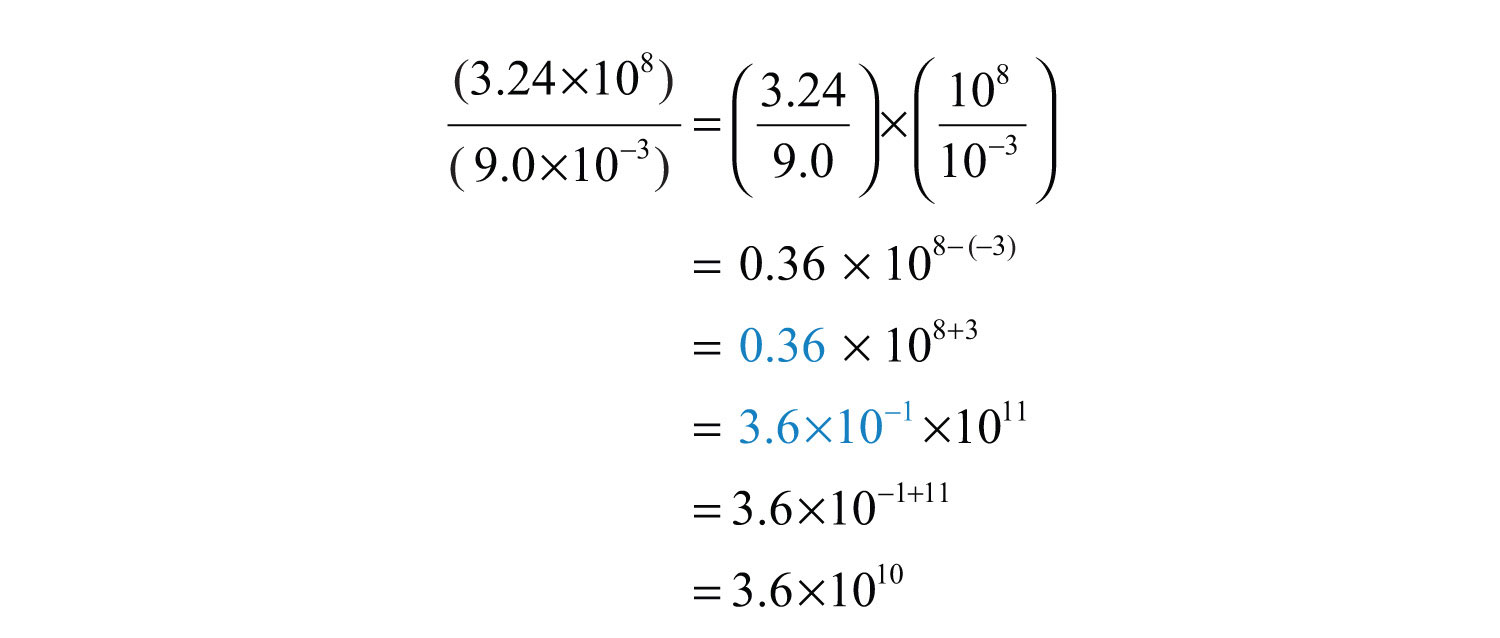
Answer:
Example 15: The speed of light is approximately miles per hour. Express this speed in miles per second.
Solution: A unit analysis indicates that we must divide the number by 3,600.

Answer: The speed of light is approximately miles per second.
Example 16: By what factor is the radius of the sun larger than the radius of earth?
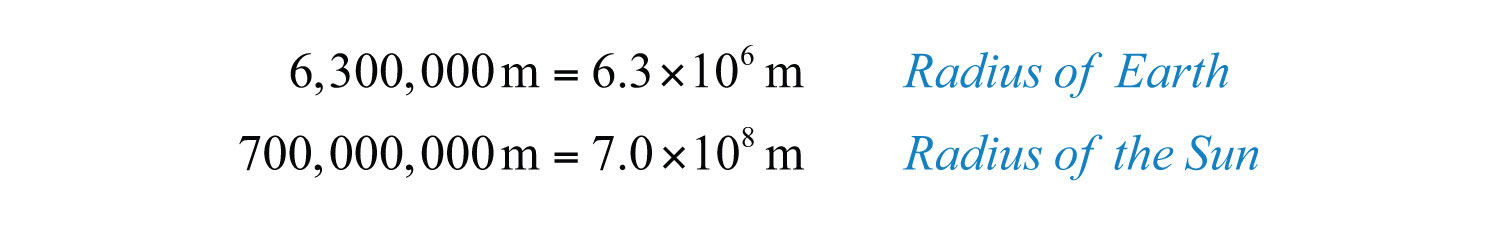
Solution: We want to find the number that when multiplied times the radius of earth equals the radius of the sun.

Source: NASA and European Space Agency, from http://solarsystem.nasa.gov/multimedia/display.cfm?IM_ID=188.
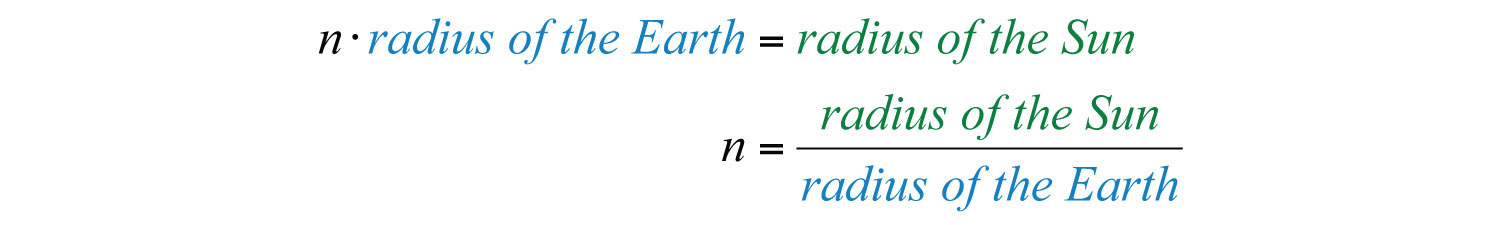
Therefore,
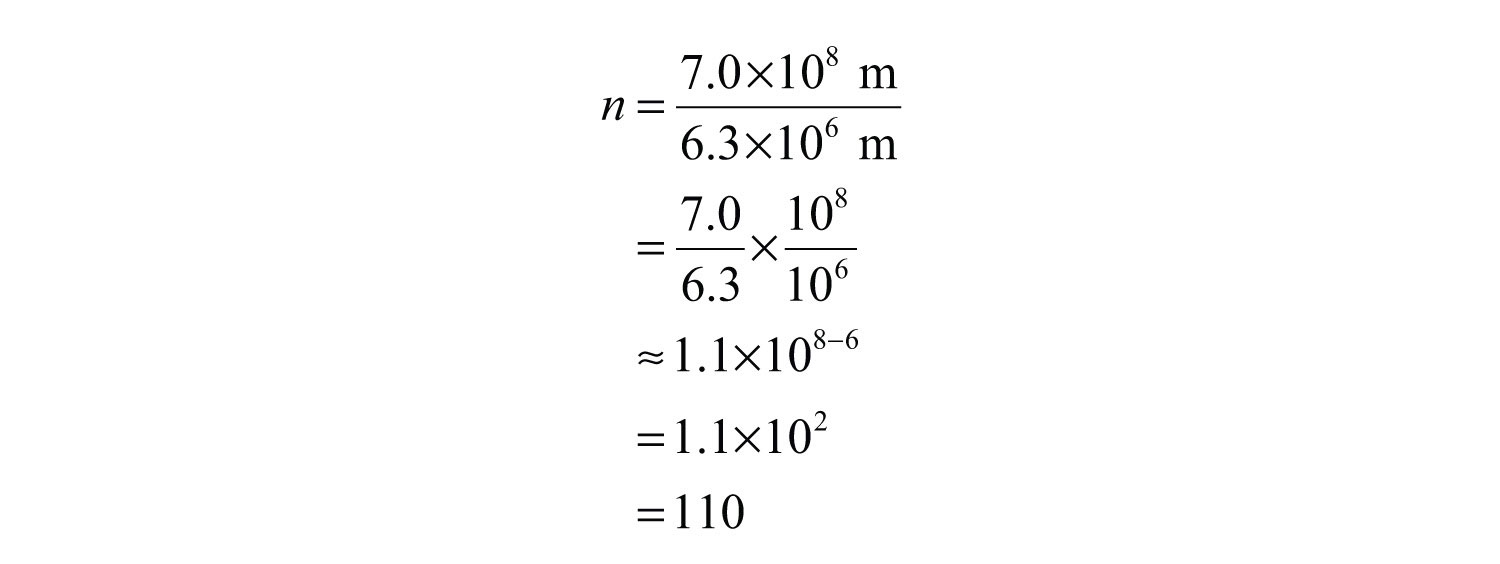
Answer: The radius of the sun is approximately 110 times that of earth.
Try this! Divide: .
Answer:
Video Solution
(click to see video)Key Takeaways
- Expressions with negative exponents in the numerator can be rewritten as expressions with positive exponents in the denominator.
- Expressions with negative exponents in the denominator can be rewritten as expressions with positive exponents in the numerator.
- Take care to distinguish negative coefficients from negative exponents.
- Scientific notation is particularly useful when working with numbers that are very large or very small.
Topic Exercises
Part A: Negative Exponents
Simplify. (Assume variables are nonzero.)
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
The value in dollars of a new MP3 player can be estimated by using the formula , where t is the number of years after purchase.
47. How much was the MP3 player worth new?
48. How much will the MP3 player be worth in 1 year?
49. How much will the MP3 player be worth in 4 years?
50. How much will the MP3 player be worth in 9 years?
51. How much will the MP3 player be worth in 99 years?
52. According to the formula, will the MP3 ever be worthless? Explain.
Part B: Scientific Notation
Convert to a decimal number.
53.
54.
55.
56.
57.
58.
59.
60.
Rewrite using scientific notation.
61. 500,000,000
62. 407,300,000,000,000
63. 9,740,000
64. 100,230
65. 0.0000123
66. 0.000012
67. 0.000000010034
68. 0.99071
Perform the indicated operations.
69.
70.
71.
72.
73.
74.
75.
76.
77. 59,000,000,000,000 × 0.000032
78. 0.0000000000432 × 0.0000000000673
79. 1,030,000,000,000,000,000 ÷ 2,000,000
80. 6,045,000,000,000,000 ÷ 0.00000005
81. The population density of earth refers to the number of people per square mile of land area. If the total land area on earth is square miles and the population in 2007 was estimated to be people, then calculate the population density of earth at that time.
82. In 2008 the population of New York City was estimated to be 8.364 million people. The total land area is 305 square miles. Calculate the population density of New York City.
83. The mass of earth is kilograms and the mass of the moon is kilograms. By what factor is the mass of earth greater than the mass of the moon?
84. The mass of the sun is kilograms and the mass of earth is kilograms. By what factor is the mass of the sun greater than the mass of earth? Express your answer in scientific notation.
85. The radius of the sun is miles and the average distance from earth to the moon is miles. By what factor is the radius of the sun larger than the average distance from earth to the moon?
86. One light year, meters, is the distance that light travels in a vacuum in one year. If the distance to the nearest star to our sun, Proxima Centauri, is estimated to be meters, then calculate the number of years it would take light to travel that distance.
87. It is estimated that there are about 1 million ants per person on the planet. If the world population was estimated to be 6.67 billion people in 2007, then estimate the world ant population at that time.
88. The sun moves around the center of the galaxy in a nearly circular orbit. The distance from the center of our galaxy to the sun is approximately 26,000 light years. What is the circumference of the orbit of the sun around the galaxy in meters?
89. Water weighs approximately 18 grams per mole. If one mole is about molecules, then approximate the weight of each molecule of water.
90. A gigabyte is bytes and a megabyte is bytes. If the average song in the MP3 format consumes about 4.5 megabytes of storage, then how many songs will fit on a 4-gigabyte memory card?
Answers
1:
3:
5:
7:
9:
11:
13:
15:
17:
19:
21:
23:
25:
27:
29:
31:
33:
35:
37:
39:
41:
43:
45:
47: $100
49: $20
51: $1
53: 9,300,000,000
55: 60,800,000,000
57: 0.000000401
59: 0.0099
61:
63:
65:
67:
69:
71:
73:
75:
77:
79:
81: About 116 people per square mile
83: 81.2
85: 1.807
87: ants
89: grams




