Dividing Polynomials

5.5 Dividing Polynomials

Learning Objectives

Divide by a monomial.
Divide by a polynomial using the division algorithm.
Divide polynomial functions.

Dividing by a Monomial

Recall the quotient rule for exponents: if x is nonzero and m and n are positive integers, then

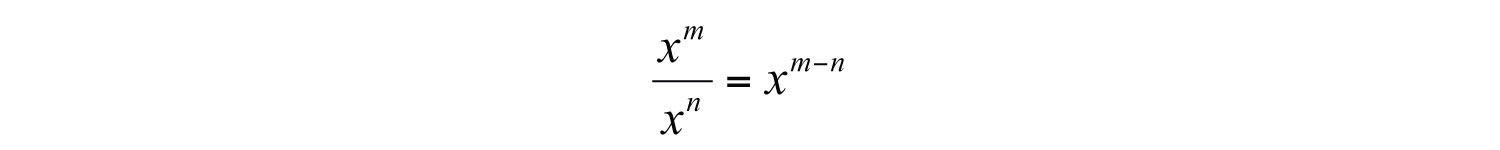
In other words, when dividing two expressions with the same base, subtract the exponents. This rule applies when dividing a monomial by a monomial. In this section, we will assume that all variables in the denominator are nonzero.

Example 1: Divide: $\frac{28 y^{3}}{7 y}$ .

Solution: Divide the coefficients and subtract the exponents of the variable y.

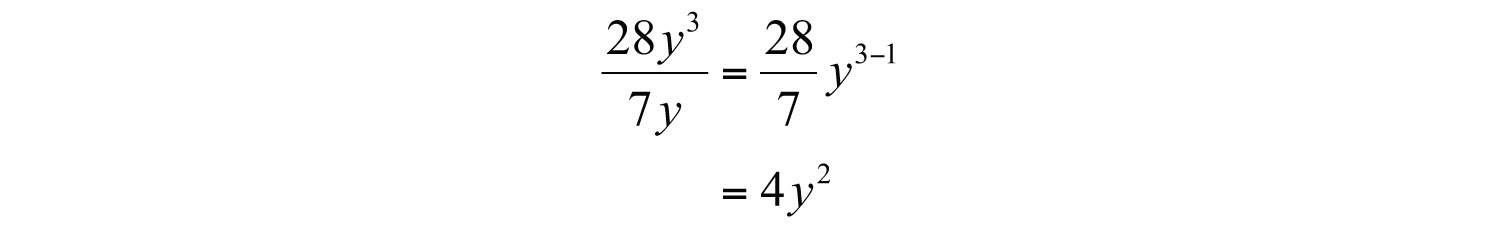
Answer: $4 y^{2}$

Example 2: Divide: $\frac{24 x^{7} y^{5}}{8 x^{3} y^{2}}$ .

Solution: Divide the coefficients and apply the quotient rule by subtracting the exponents of the like bases.

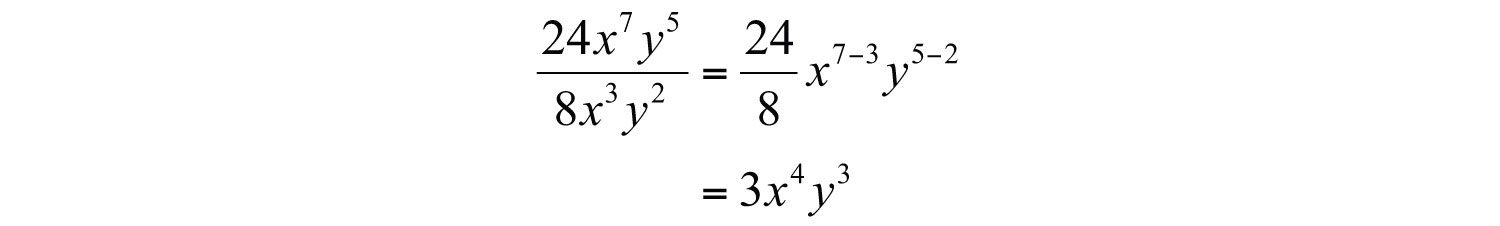
Answer: $3 x^{4} y^{3}$

When dividing a polynomial by a monomial, we may treat the monomial as a common denominator and break up the fraction using the following property:

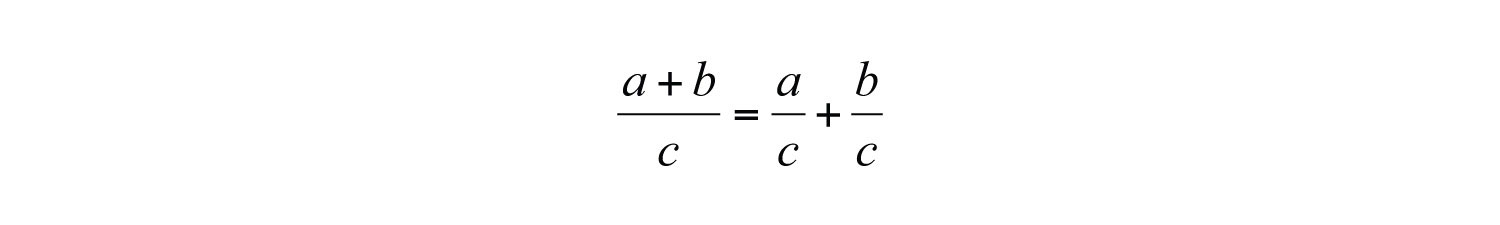
Applying this property results in terms that can be treated as quotients of monomials.

Example 3: Divide: $\frac{- 5 x^{4} + 25 x^{3} - 15 x^{2}}{5 x^{2}}$ .

Solution: Break up the fraction by dividing each term in the numerator by the monomial in the denominator and then simplify each term.

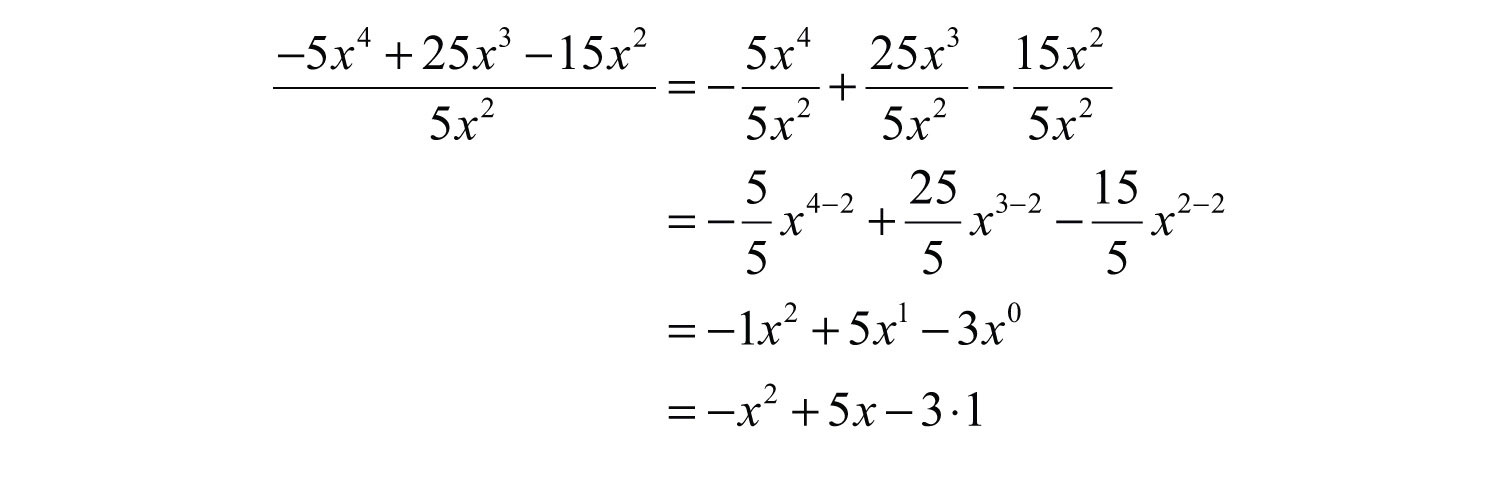
Answer: $- x^{2} + 5 x - 3$

Check your division by multiplying the answer, the quotientThe result after dividing., by the monomial in the denominator, the divisorThe denominator of a quotient., to see if you obtain the original numerator, the dividendThe numerator of a quotient..

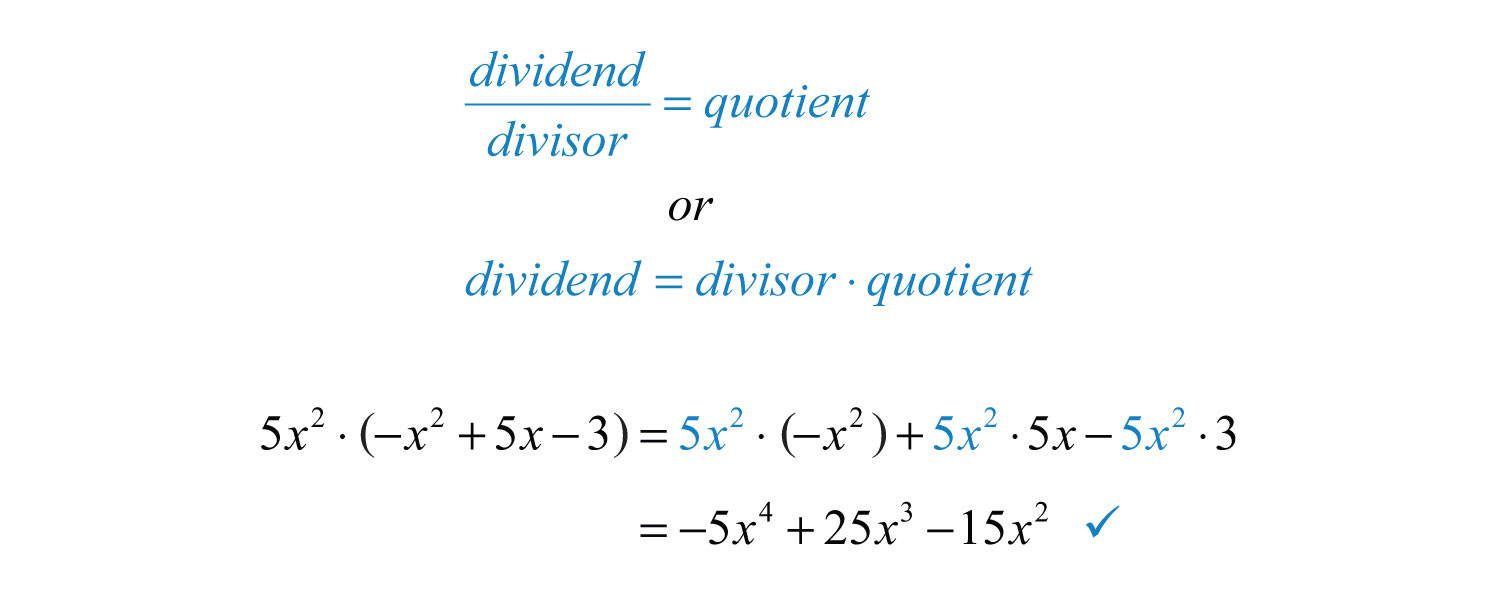
Example 4: Divide: $\frac{9 a^{4} b - 7 a^{3} b^{2} + 3 a^{2} b}{- 3 a^{2} b}$ .

Solution:

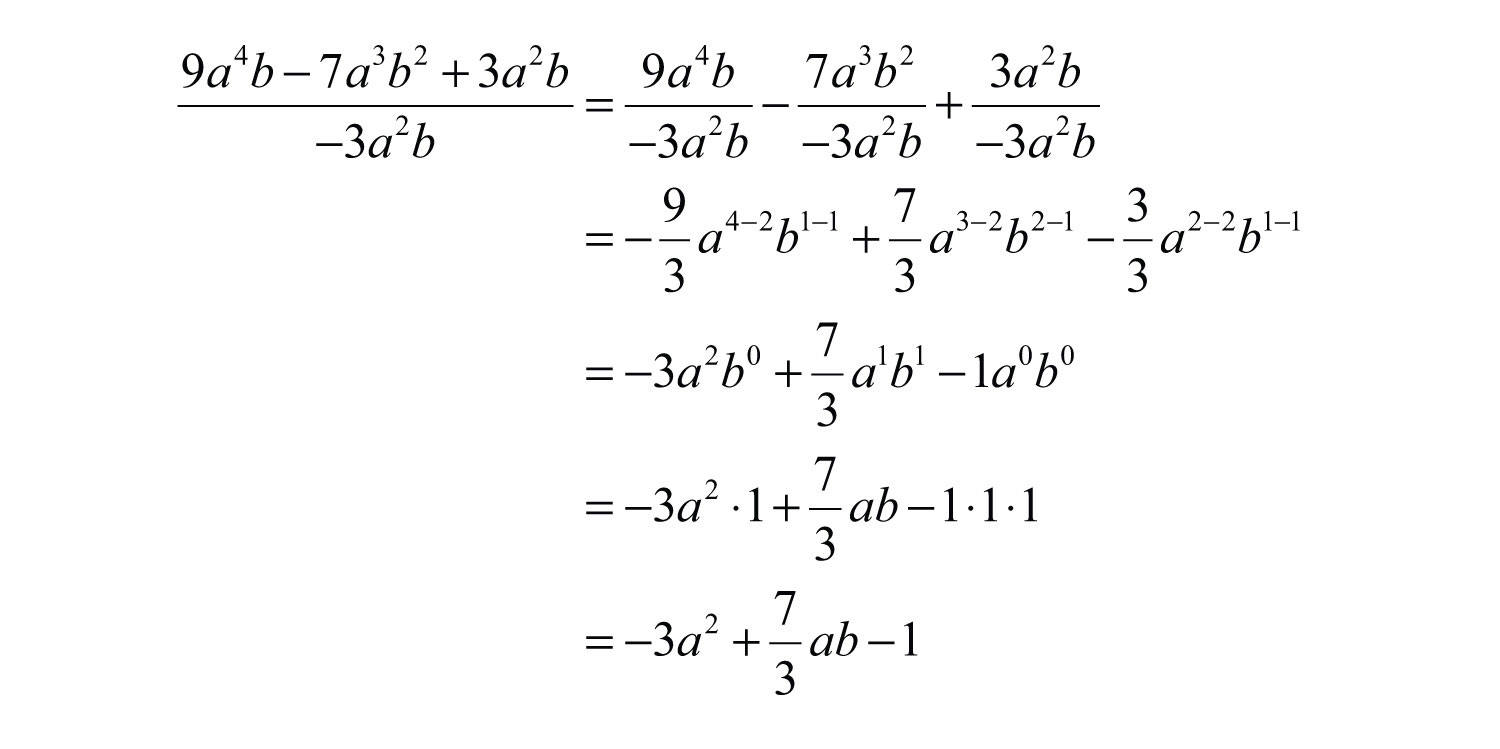
Answer: $- 3 a^{2} + \frac{7}{3} a b - 1$ . The check is optional and is left to the reader.

Try this! Divide: $(16 x^{5} - 8 x^{4} + 5 x^{3} + 2 x^{2}) \div (2 x^{2})$ .

Answer: $8 x^{3} - 4 x^{2} + \frac{5}{2} x + 1$

Video Solution

(click to see video)

Dividing by a Polynomial

The same technique outlined for dividing by a monomial does not work for polynomials with two or more terms in the denominator. In this section, we will outline a process called polynomial long divisionThe process of dividing two polynomials using the division algorithm., which is based on the division algorithm for real numbers. For the sake of clarity, we will assume that all expressions in the denominator are nonzero.

Example 5: Divide: $\frac{x^{3} + 3 x^{2} - 8 x - 4}{x - 2}$ .

Solution: Here $x - 2$ is the divisor and $x^{3} + 3 x^{2} - 8 x - 4$ is the dividend.

Step 1: To determine the first term of the quotient, divide the leading term of the dividend by the leading term of the divisor.

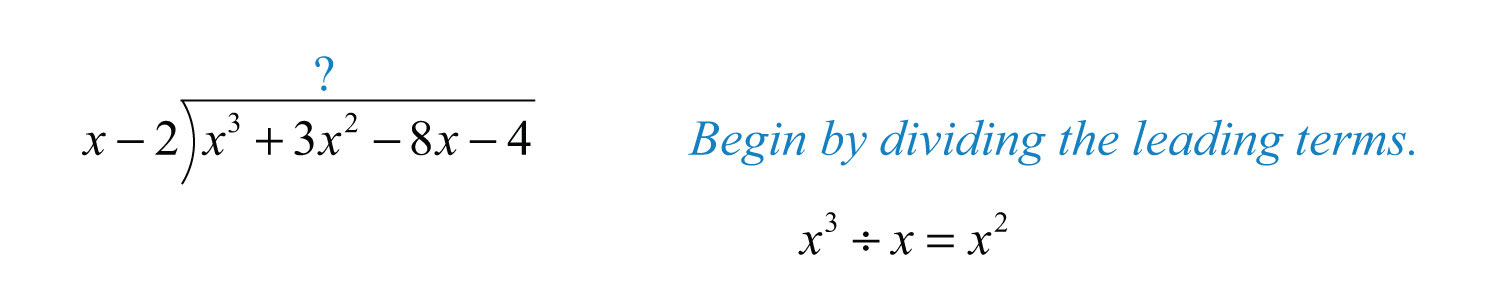
Step 2: Multiply the first term of the quotient by the divisor, remembering to distribute, and line up like terms with the dividend.

Step 3: Subtract the resulting quantity from the dividend. Take care to subtract both terms.

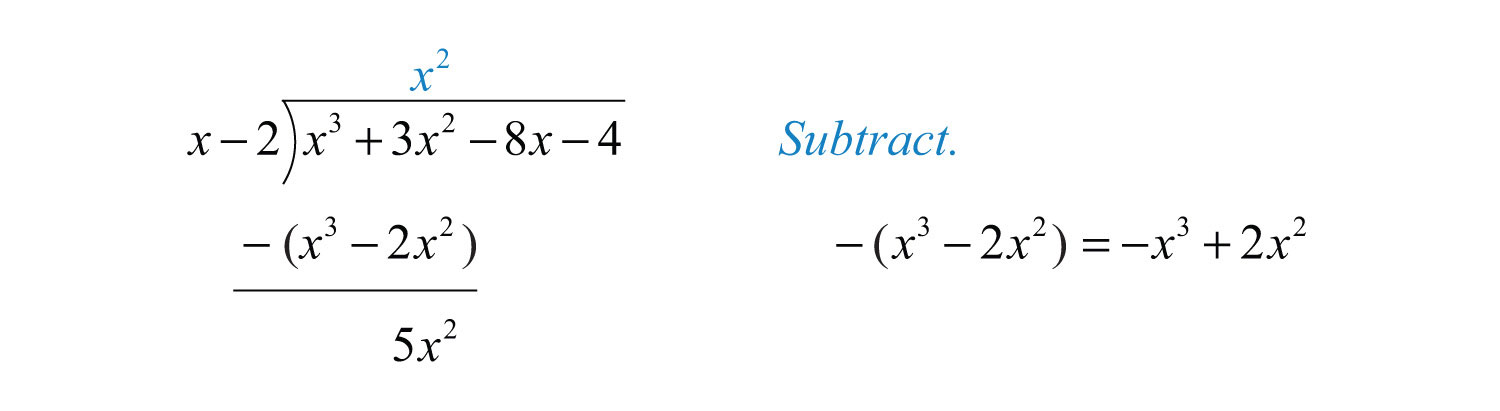
Step 4: Bring down the remaining terms and repeat the process from step 1.

Notice that the leading term is eliminated and that the result has a degree that is one less than the dividend. The complete process is illustrated below:

Polynomial long division ends when the degree of the remainderThe expression that is left after the division algorithm ends. is less than the degree of the divisor. Here the remainder is 0. Therefore, the binomial divides the polynomial evenly and the answer is the quotient shown above the division line.

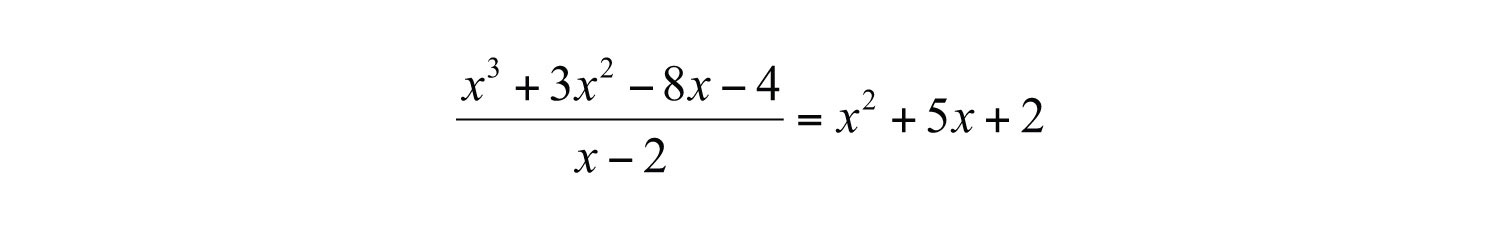
To check the answer, multiply the divisor by the quotient to see if you obtain the dividend:

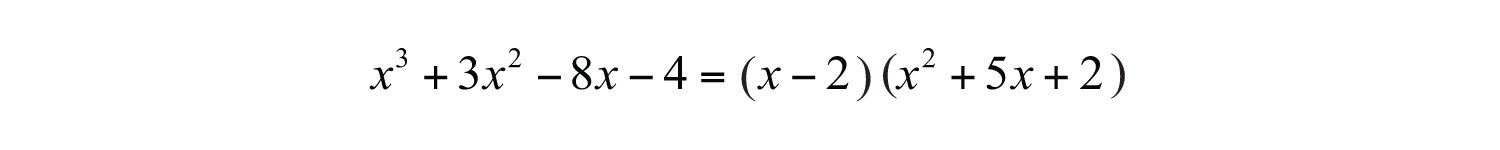
Answer: $x^{2} + 5 x + 2$

Next, we demonstrate the case where there is a nonzero remainder.

Just as with real numbers, the final answer adds the fraction where the remainder is the numerator and the divisor is the denominator to the quotient. In general, when dividing we have

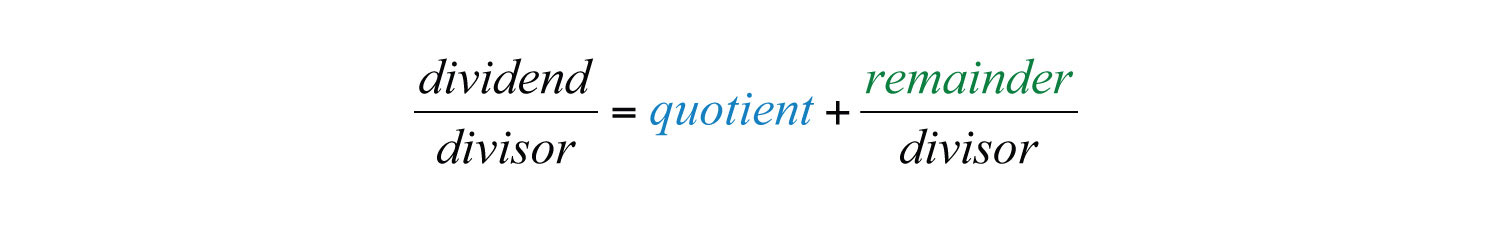
If we multiply both sides by the divisor we obtain

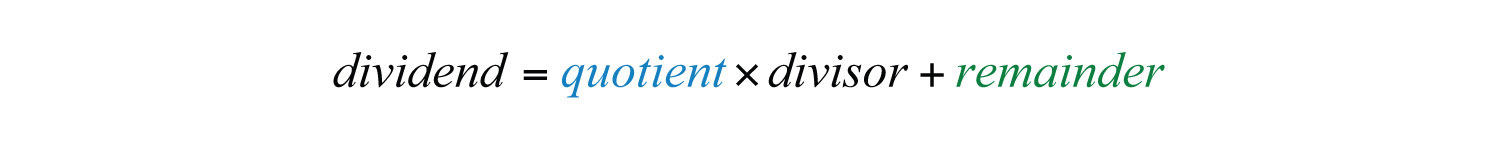
Example 6: Divide: $\frac{6 x^{2} - 5 x + 3}{2 x - 1}$ .

Solution: Since the denominator is a binomial, begin by setting up polynomial long division.

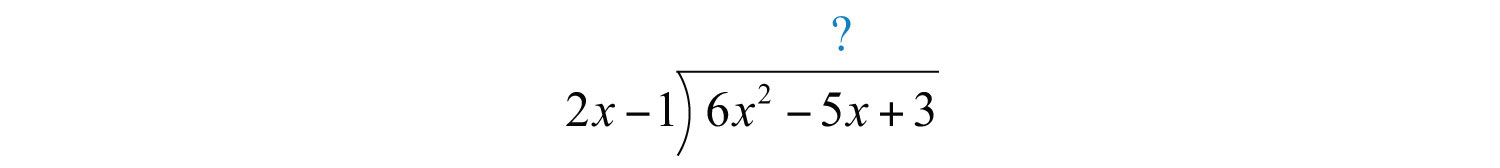
To start, determine what monomial times $2 x - 1$ results in a leading term $6 x^{2}$ . This is the quotient of the given leading terms: $(6 x^{2}) \div (2 x) = 3 x$ . Multiply $3 x$ times the divisor $2 x - 1$ and line up the result with like terms of the dividend.

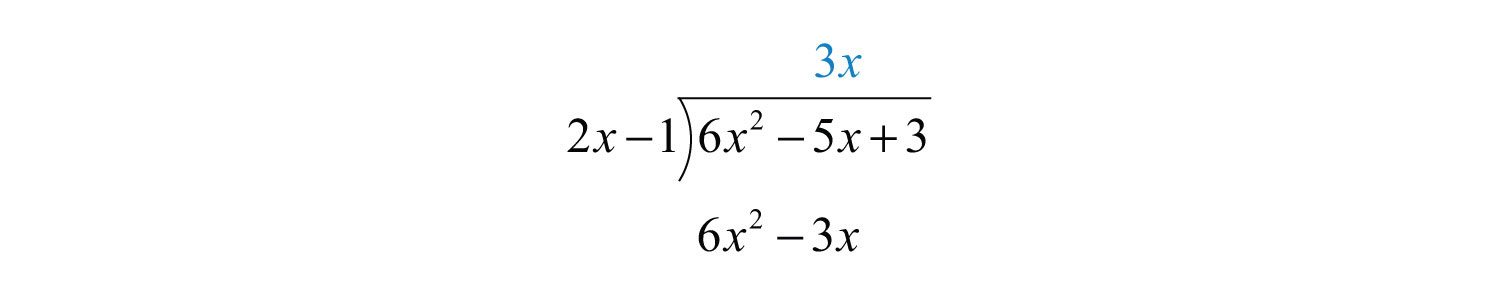
Subtract the result from the dividend and bring down the constant term +3.

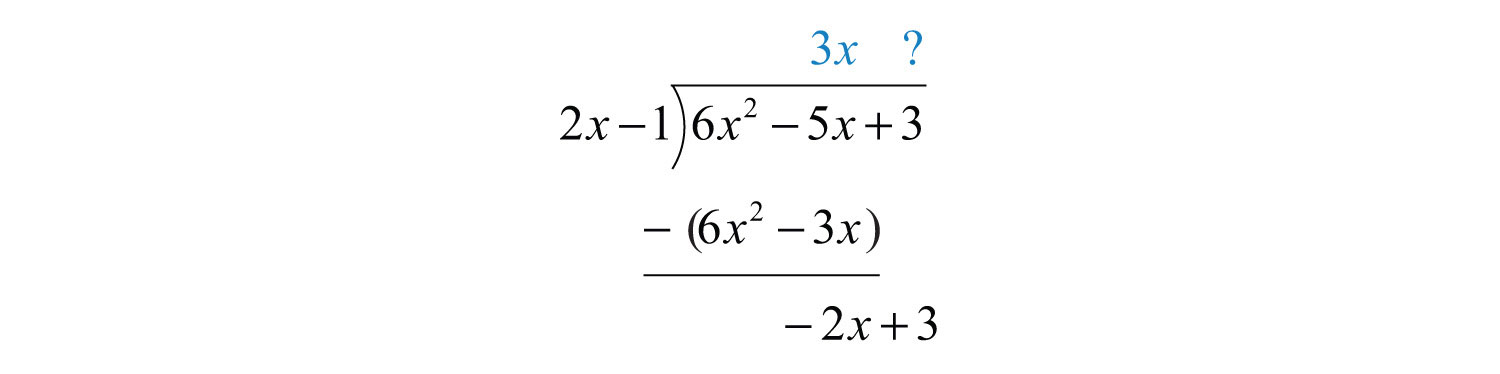
Subtracting eliminates the leading term and $- 5 x - (- 3 x) = - 5 x + 3 x = - 2 x$ . The quotient of $- 2 x$ and $2 x$ is −1. Multiply $2 x - 1$ by −1 and line up the result.

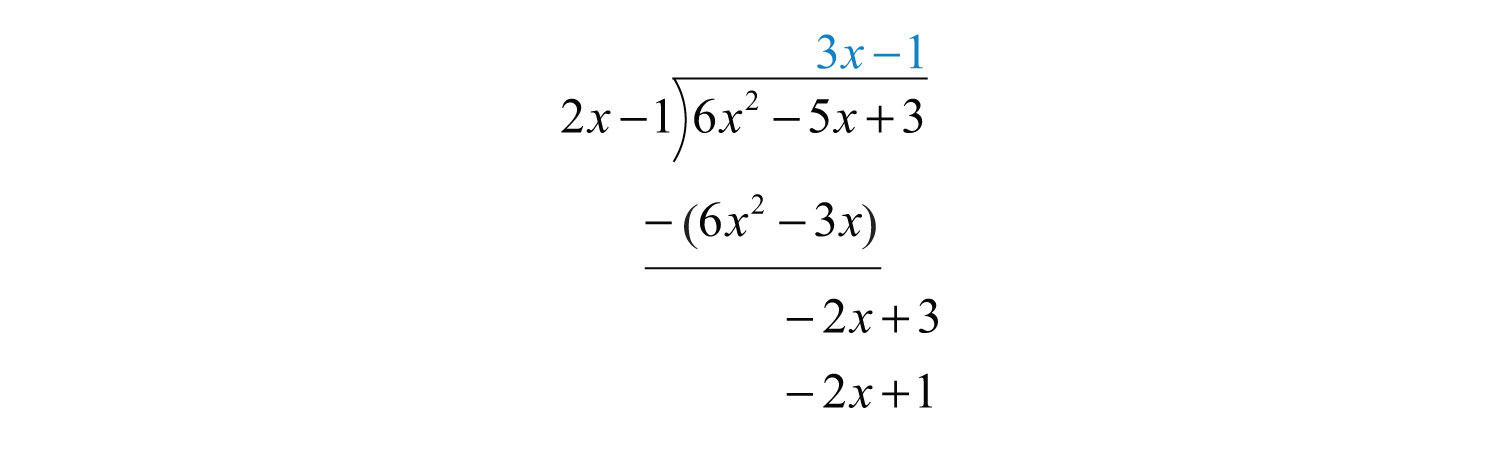
Subtract again and notice that we are left with a remainder.

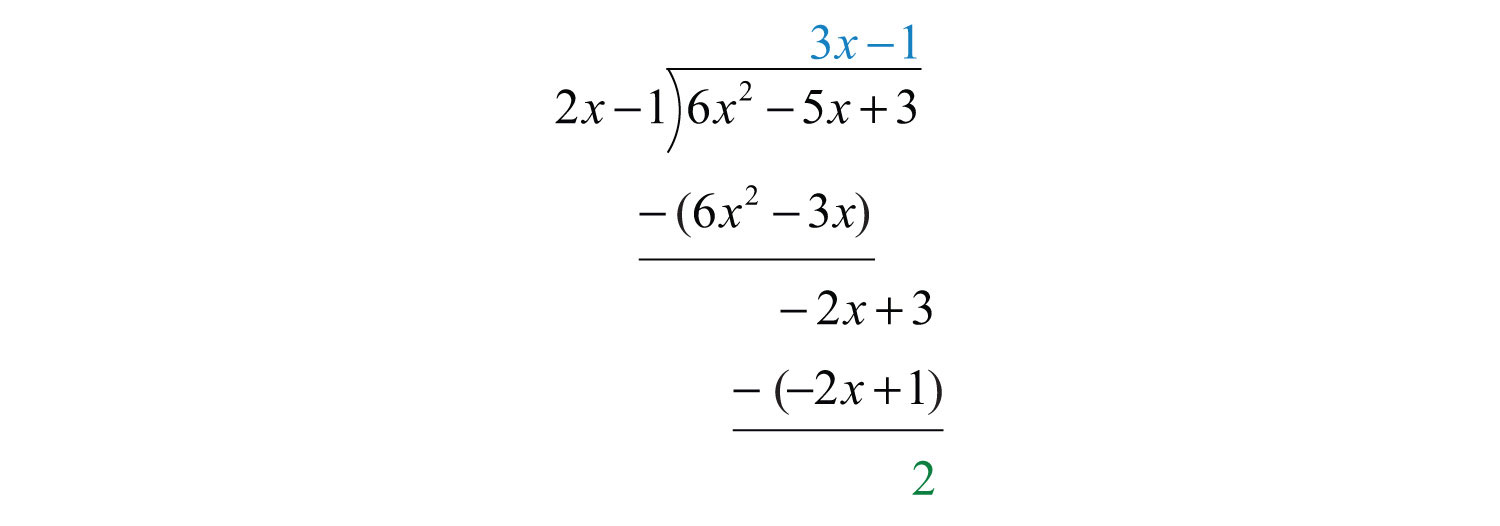
The constant term 2 has degree 0, and thus the division ends. We may write

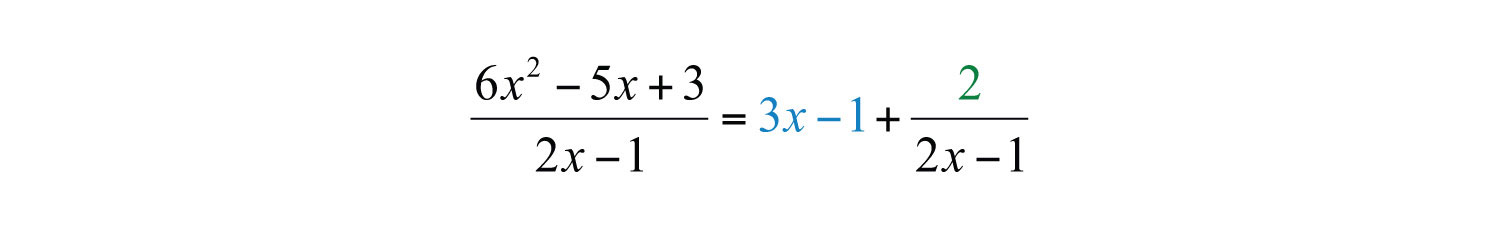
Answer: $3 x - 1 + \frac{2}{2 x - 1}$ . To check that this result is correct, we multiply as follows:

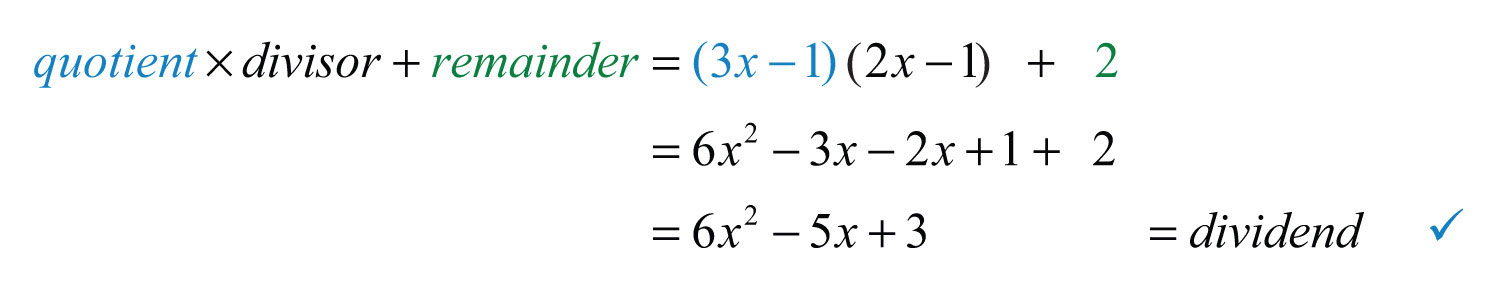
Occasionally, some of the powers of the variables appear to be missing within a polynomial. This can lead to errors when lining up like terms. Therefore, when first learning how to divide polynomials using long division, fill in the missing terms with zero coefficients, called placeholdersTerms with zero coefficients used to fill in all missing exponents within a polynomial..

Example 7: Divide: $\frac{27 x^{3} + 64}{3 x + 4}$ .

Solution: Notice that the binomial in the numerator does not have terms with degree 2 or 1. The division is simplified if we rewrite the expression with placeholders:

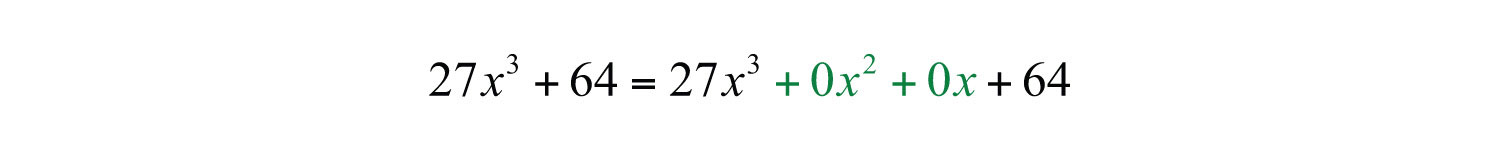
Set up polynomial long division:

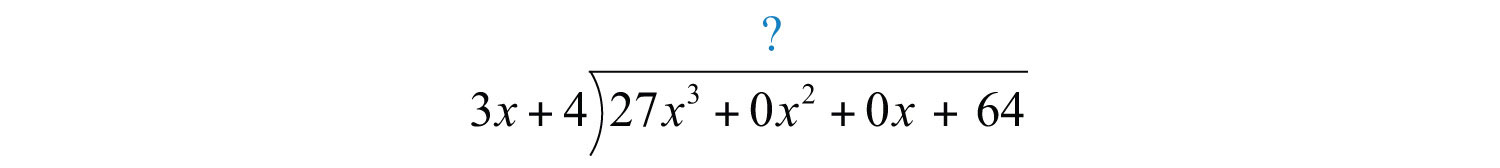
We begin with $27 x^{3} \div 3 x = 9 x^{2}$ and work the rest of the division algorithm.

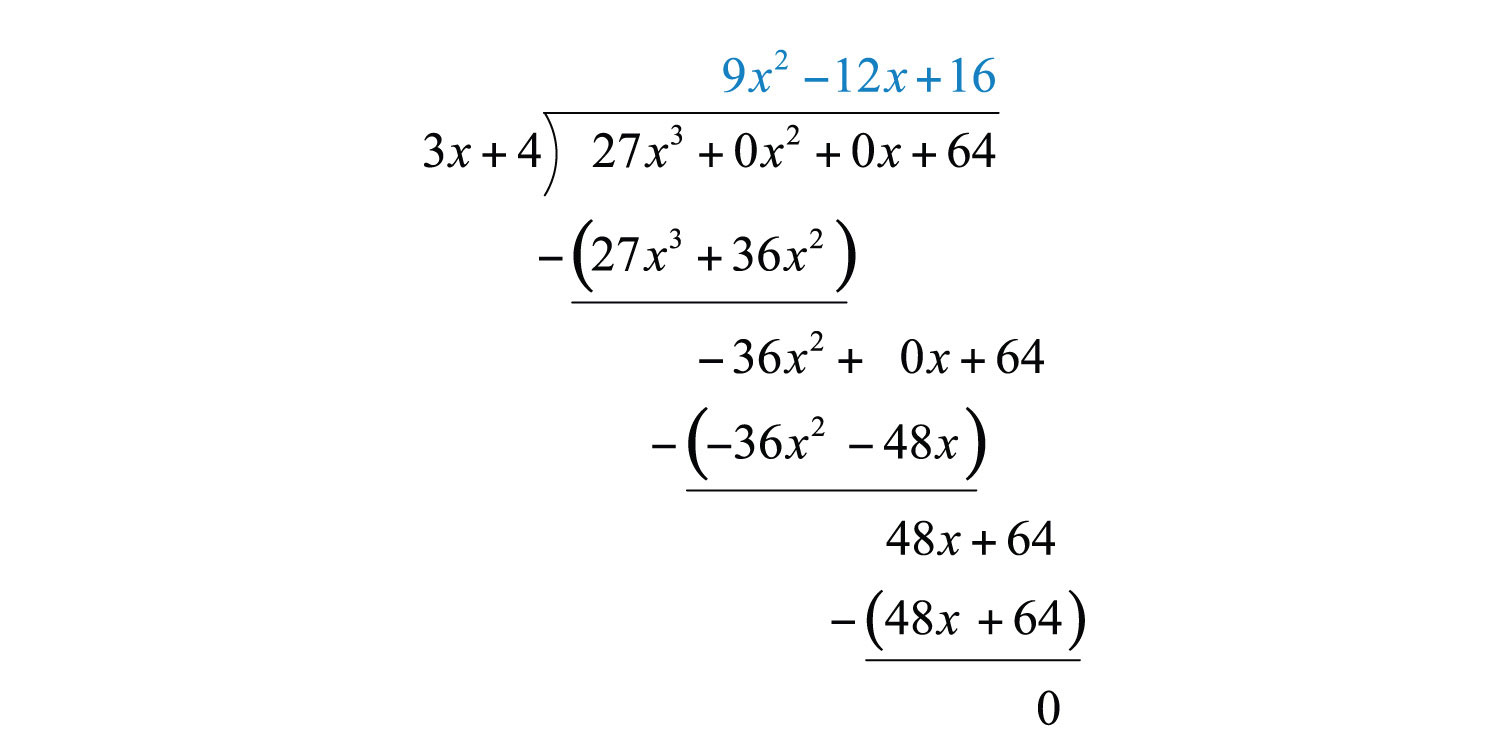
Answer: $9 x^{2} - 12 x + 16$

Example 8: Divide: $\frac{3 x^{4} - 2 x^{3} + 6 x^{2} + 23 x - 7}{x^{2} - 2 x + 5}$ .

Solution:

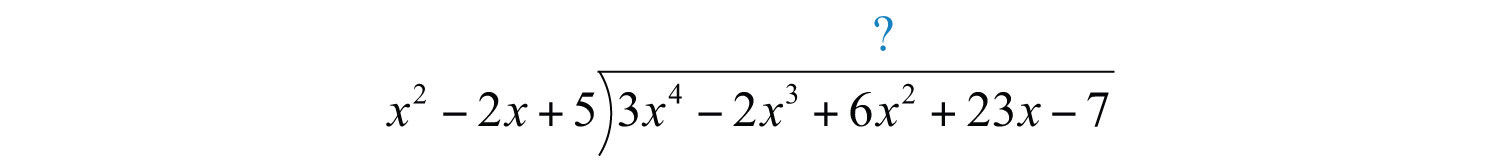
Begin the process by dividing the leading terms to determine the leading term of the quotient $3 x^{4} \div x^{2} = 3 x^{2}$ . Take care to distribute and line up the like terms. Continue the process until the remainder has a degree less than 2.

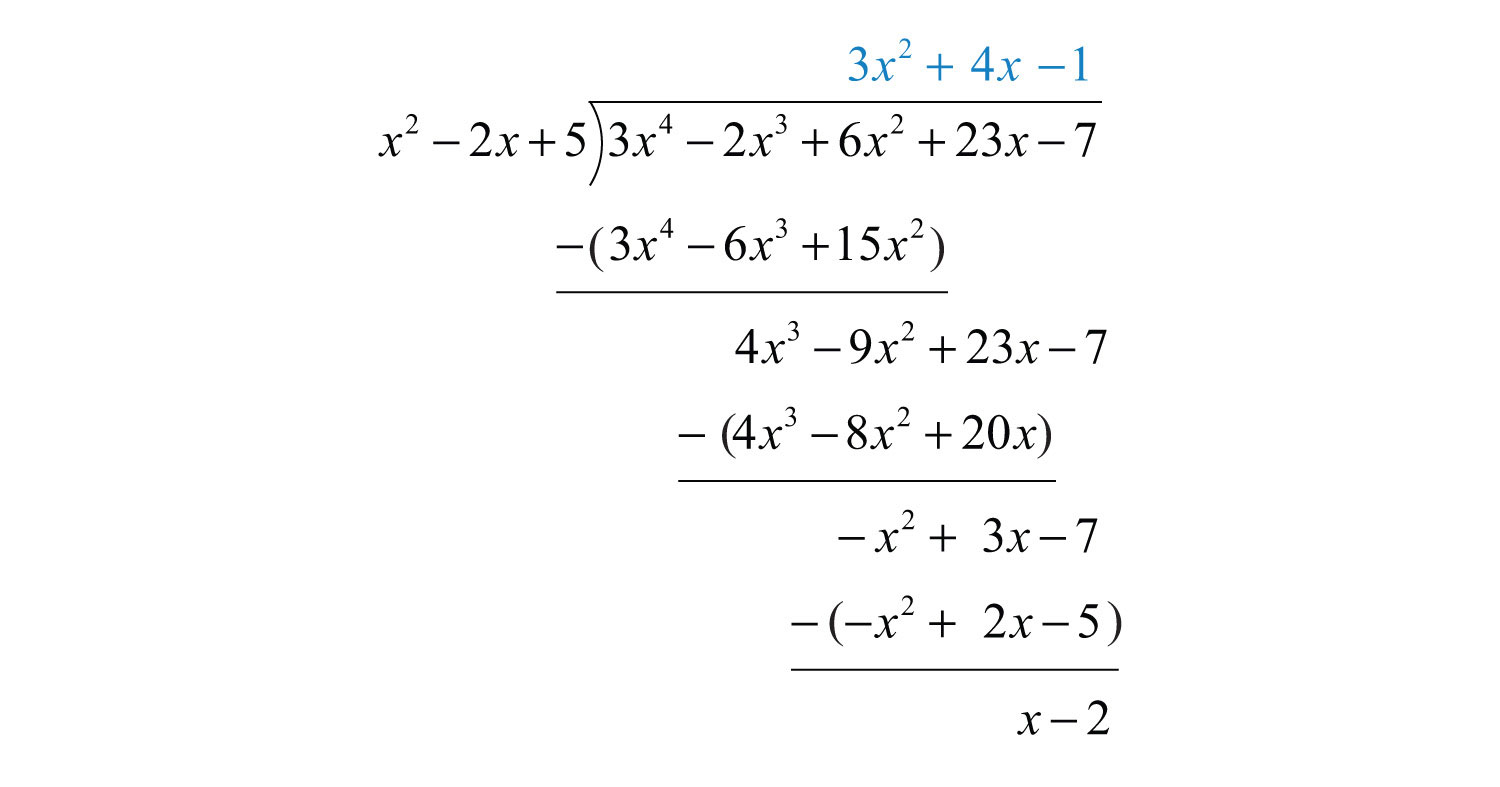
The remainder is $x - 2$ . Write the answer with the remainder:

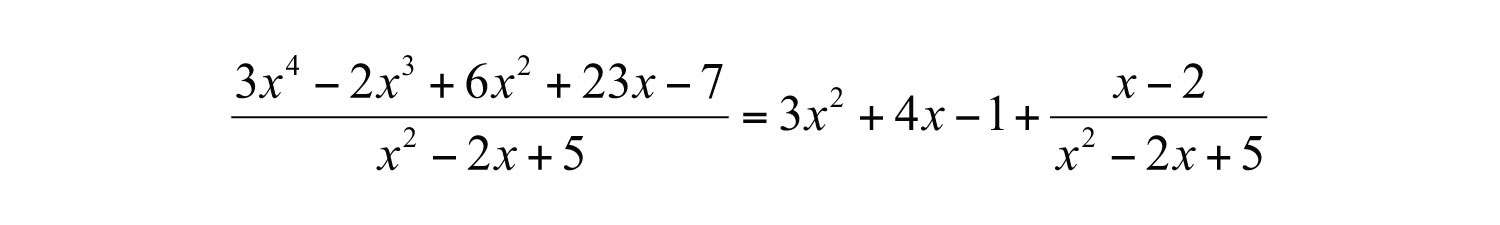
Answer: $3 x^{2} + 4 x - 1 + \frac{x - 2}{x^{2} - 2 x + 5}$

Polynomial long division takes time and practice to master. Work lots of problems and remember that you may check your answers by multiplying the quotient by the divisor (and adding the remainder if present) to obtain the dividend.

Try this! Divide: $\frac{20 x^{4} - 32 x^{3} + 7 x^{2} + 8 x - 10}{5 x - 3}$ .

Answer: $4 x^{3} - 4 x^{2} - x + 1 - \frac{7}{5 x - 3}$

Video Solution

(click to see video)

Dividing Polynomial Functions

We may use function notation to indicate division as follows:

Division of functions:

(f / g) (x) = \frac{f (x)}{g (x)}

The quotient of two polynomial functions does not necessarily have a domain of all real numbers. The values for x that make the function in the denominator 0 are restricted from the domain. This will be discussed in more detail at a later time. For now, assume all functions in the denominator are nonzero.

Example 9: Calculate: $(f / g) (x)$ given $f (x) = 6 x^{5} - 36 x^{4} + 12 x^{3} - 6 x^{2}$ and $g (x) = - 6 x^{2}$ .

Solution: The notation indicates that we should divide:

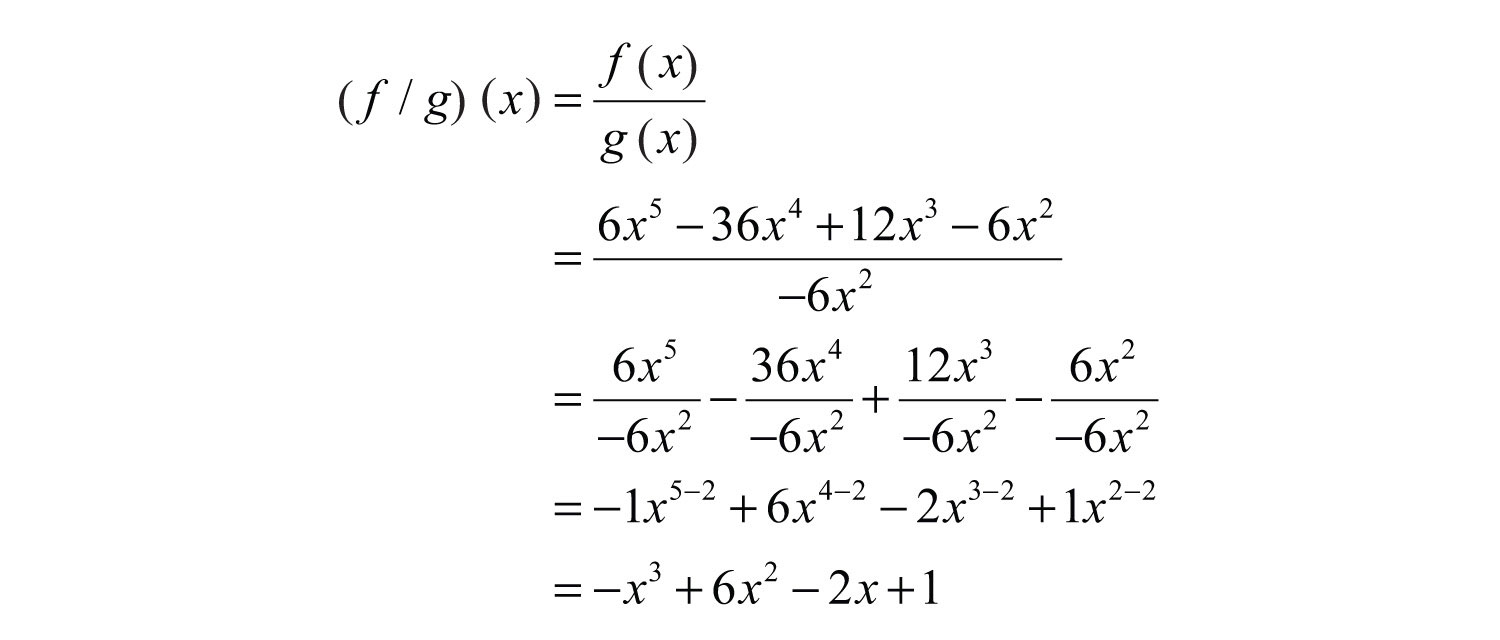
Answer: $(f / g) (x) = - x^{3} + 6 x^{2} - 2 x + 1$

Example 10: Calculate: $(f / g) (- 1)$ , given $f (x) = - 3 x^{3} + 7 x^{2} - 11 x - 1$ and $g (x) = 3 x - 1$ .

Solution: First, determine $(f / g) (x)$ .

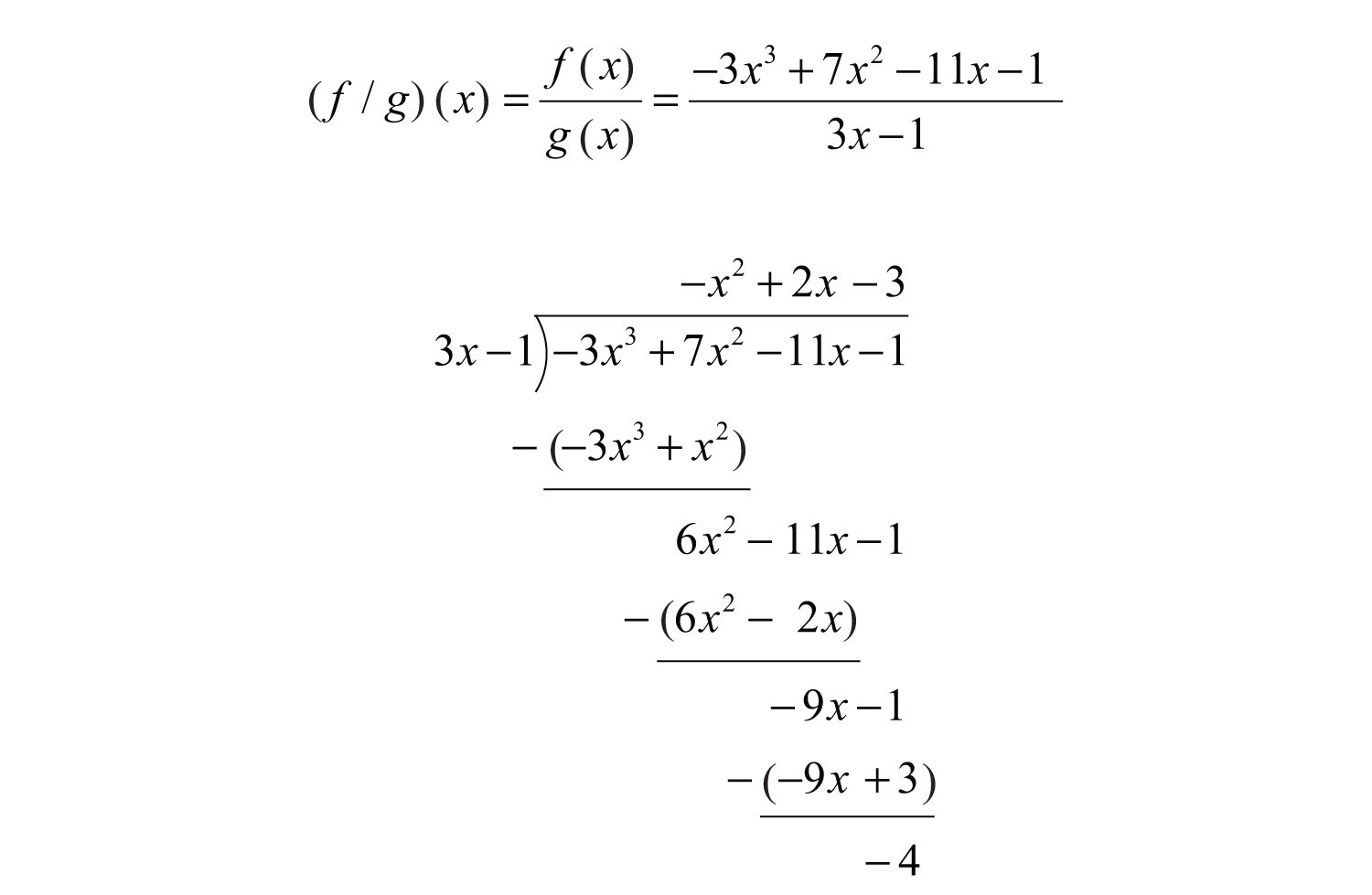
Therefore,

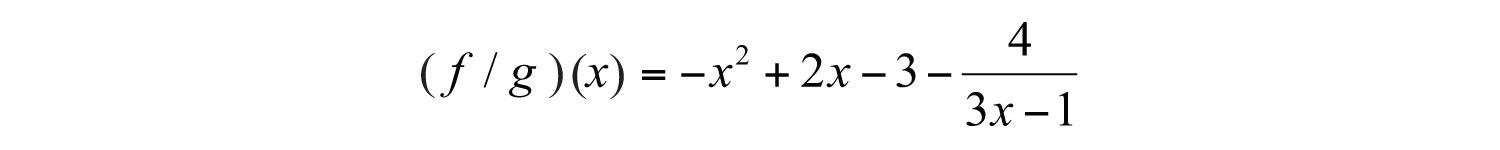
Substitute −1 for the variable $x$ .

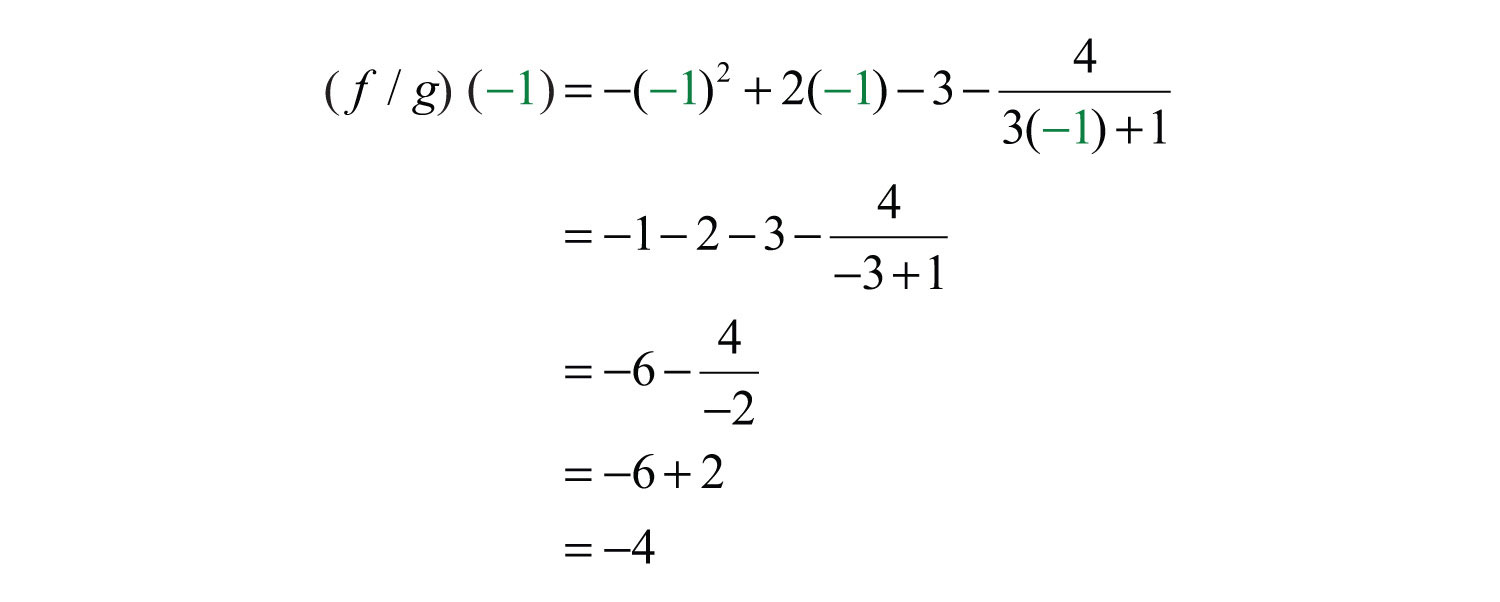
Answer: $(f / g) (- 1) = - 4$

Key Takeaways

When dividing by a monomial, divide all terms in the numerator by the monomial and then simplify each term. To simplify each term, divide the coefficients and apply the quotient rule for exponents.
When dividing a polynomial by another polynomial, apply the division algorithm.
To check the answer after dividing, multiply the divisor by the quotient and add the remainder (if necessary) to obtain the dividend.
It is a good practice to include placeholders when performing polynomial long division.

Topic Exercises

Part A: Dividing by a Monomial

Divide.

1. $\frac{81 y^{5}}{9 y^{2}}$

2. $\frac{36 y^{9}}{9 y^{3}}$

3. $\frac{52 x^{2} y}{4 x y}$

4. $\frac{24 x y^{5}}{2 x y^{4}}$

5. $\frac{25 x^{2} y^{5} z^{3}}{5 x y z}$

6. $- \frac{77 x^{4} y^{9} z}{22 x^{3} y^{3} z}$

7. $\frac{125 a^{3} b^{2} c}{- 10 a b c}$

8. $\frac{36 a^{2} b^{3} c^{5}}{- 6 a^{2} b^{2} c^{3}}$

9. $\frac{9 x^{2} + 27 x - 3}{3}$

10. $\frac{10 x^{3} - 5 x^{2} + 40 x - 15}{5}$

11. $\frac{20 x^{3} - 10 x^{2} + 30 x}{2 x}$

12. $\frac{10 x^{4} + 8 x^{2} - 6 x}{24 x}$

13. $\frac{- 6 x^{5} - 9 x^{3} + 3 x}{- 3 x}$

14. $\frac{36 a^{12} - 6 a^{9} + 12 a^{5}}{- 12 a^{5}}$

15. $\frac{- 12 x^{5} + 18 x^{3} - 6 x^{2}}{- 6 x^{2}}$

16. $\frac{- 49 a^{8} + 7 a^{5} - 21 a^{3}}{7 a^{3}}$

17. $\frac{9 x^{7} - 6 x^{4} + 12 x^{3} - x^{2}}{3 x^{2}}$

18. $\frac{8 x^{9} + 16 x^{7} - 24 x^{4} + 8 x^{3}}{- 8 x^{3}}$

19. $\frac{16 a^{7} - 32 a^{6} + 20 a^{5} - a^{4}}{4 a^{4}}$

20. $\frac{5 a^{6} + 2 a^{5} + 6 a^{3} - 12 a^{2}}{3 a^{2}}$

21. $\frac{- 4 x^{2} y^{3} + 16 x^{7} y^{8} - 8 x^{2} y^{5}}{- 4 x^{2} y^{3}}$

22. $\frac{100 a^{10} b^{30} c^{5} - 50 a^{20} b^{5} c^{40} + 20 a^{5} b^{20} c^{10}}{10 a^{5} b^{5} c^{5}}$

23. Find the quotient of $- 36 x^{9} y^{7}$ and $2 x^{8} y^{5}$ .

24. Find the quotient of $144 x^{3} y^{10} z^{2}$ and $- 12 x^{3} y^{5} z$ .

25. Find the quotient of $3 a^{4} - 18 a^{3} + 27 a^{2}$ and $3 a^{2}$ .

26. Find the quotient of $64 a^{2} b c^{3} - 16 a^{5} b c^{7}$ and $4 a^{2} b c^{3}$ .

Part B: Dividing by a Polynomial

Divide.

27. $(2 x^{2} - 5 x - 3) \div (x - 3)$

28. $(3 x^{2} + 5 x - 2) \div (x + 2)$

29. $(6 x^{2} + 11 x + 3) \div (3 x + 1)$

30. $(8 x^{2} - 14 x + 3) \div (2 x - 3)$

31. $\frac{x^{3} - x^{2} - 2 x - 12}{x - 3}$

32. $\frac{2 x^{3} + 11 x^{2} + 4 x - 5}{x + 5}$

33. $\frac{2 x^{3} - x^{2} - 4 x + 3}{2 x + 3}$

34. $\frac{- 15 x^{3} - 14 x^{2} + 23 x - 6}{5 x - 2}$

35. $\frac{14 x^{4} - 9 x^{3} + 22 x^{2} + 4 x - 1}{7 x - 1}$

36. $\frac{8 x^{5} + 16 x^{4} - 8 x^{3} - 5 x^{2} - 21 x + 10}{2 x + 5}$

37. $\frac{x^{2} + 8 x + 17}{x + 5}$

38. $\frac{2 x^{2} - 5 x + 5}{x - 2}$

39. $\frac{6 x^{2} - 13 x + 9}{- 2 x + 1}$

40. $\frac{- 12 x^{2} + x + 1}{3 x + 2}$

41. $\frac{x^{3} + 9 x^{2} + 19 x + 1}{x + 4}$

42. $\frac{2 x^{3} - 13 x^{2} + 17 x - 11}{x - 5}$

43. $\frac{9 x^{3} - 12 x^{2} + 16 x - 15}{3 x - 2}$

44. $\frac{3 x^{4} - 8 x^{3} + 5 x^{2} - 5 x + 9}{x - 2}$

45. $(6 x^{5} - 13 x^{4} + 4 x^{3} - 3 x^{2} + 13 x - 2) \div (3 x + 1)$

46. $(8 x^{5} - 22 x^{4} + 19 x^{3} - 20 x^{2} + 23 x - 3) \div (2 x - 3)$

47. $\frac{5 x^{5} + 12 x^{4} + 12 x^{3} - 7 x^{2} - 19 x + 3}{x^{2} + 2 x + 3}$

48. $\frac{6 x^{5} - 17 x^{4} + 5 x^{3} + 16 x^{2} - 7 x - 3}{2 x^{2} - 3 x - 1}$

49. $\frac{x^{5} + 7 x^{4} - x^{3} - 7 x^{2} - 49 x + 9}{x^{2} + 7 x - 1}$

50. $\frac{5 x^{6} - 6 x^{4} - 4 x^{2} + x + 2}{5 x^{2} - 1}$

51. $\frac{x^{3} - 27}{x - 3}$

52. $\frac{8 x^{3} + 125}{2 x + 5}$

53. $(15 x^{5} - 9 x^{4} - 20 x^{3} + 12 x^{2} + 15 x - 9) \div (5 x - 3)$

54. $(2 x^{6} - 5 x^{5} - 4 x^{4} + 10 x^{3} + 6 x^{2} - 17 x + 5) \div (2 x - 5)$

55. $\frac{x^{5} - 2 x^{3} + 3 x - 1}{x - 1}$

56. $\frac{x^{4} - 3 x^{2} + 5 x - 13}{x + 2}$

57. $\frac{a^{2} - 4}{a + 2}$

58. $\frac{a^{5} + 1}{a^{5} + 1}$

59. $\frac{a^{6} - 1}{a - 1}$

60. $\frac{x^{5} - 1}{x - 1}$

61. $\frac{x^{5} + x^{4} + 6 x^{3} + 12 x^{2} - 4}{x^{2} + x - 1}$

62. $\frac{50 x^{6} - 30 x^{5} - 5 x^{4} + 15 x^{3} - 5 x + 1}{5 x^{2} - 3 x + 2}$

63. $\frac{5 x^{5} - 15 x^{3} + 25 x^{2} - 5}{5 x}$

64. $\frac{- 36 x^{6} + 12 x^{4} - 6 x^{2}}{6 x^{2}}$

65. $\frac{150 x^{5} y^{2} z^{15} - 10 x^{3} y^{6} z^{5} + 4 x^{3} y^{2} z^{4}}{10 x^{3} y^{2} z^{5}}$

66. $\frac{27 m^{6} + 9 m^{4} - 81 m^{2} + 1}{9 m^{2}}$

67. Divide $3 x^{6} - 2 x^{5} + 27 x^{4} - 18 x^{3} - 6 x^{2} + 7 x - 10$ by $3 x - 2$ .

68. Divide $8 x^{6} + 4 x^{5} - 14 x^{4} - 5 x^{3} + x^{2} - 2 x - 3$ by $2 x + 1$ .

Part C: Dividing Polynomial Functions

Calculate $(f / g) (x)$ , given the functions.

69. $f (x) = 40 x^{8}$ and $g (x) = 10 x^{5}$

70. $f (x) = 54 x^{5}$ and $g (x) = 9 x^{3}$

71. $f (x) = 12 x^{2} + 24 x - 15$ and $g (x) = 2 x + 5$

72. $f (x) = - 8 x^{2} + 30 x - 7$ and $g (x) = 2 x - 7$

73. $f (x) = 18 x^{2} - 36 x + 5$ and $g (x) = 3 x - 5$

74. $f (x) = - 7 x^{2} + 29 x - 6$ and $g (x) = 7 x - 1$

75. $f (x) = 10 x^{3} - 9 x^{2} + 27 x - 10$ and $g (x) = 5 x - 2$

76. $f (x) = 15 x^{3} + 28 x^{2} - 11 x + 56$ and $g (x) = 3 x + 8$

77. $f (x) = 2 x^{4} + 5 x^{3} - 11 x^{2} - 19 x + 20$ and $g (x) = x^{2} + x - 5$

78. $f (x) = 4 x^{4} - 12 x^{3} - 20 x^{2} + 26 x - 3$ and $g (x) = 2 x^{2} + 2 x - 3$

Given $f (x) = 6 x^{3} + 4 x^{2} - 11 x + 3$ and $g (x) = 3 x - 1$ , find the following.

79. $(f / g) (x)$

80. $(f / g) (- 1)$

81. $(f / g) (0)$

82. $(f / g) (1)$

Given $f (x) = 5 x^{3} - 13 x^{2} + 7 x + 3$ and $g (x) = x - 2$ , find the following.

83. $(f / g) (x)$

84. $(f / g) (- 3)$

85. $(f / g) (0)$

86. $(f / g) (7)$

Part D: Discussion Board Topics

87. How do you use the distributive property when dividing a polynomial by a monomial?

88. Compare long division of real numbers with polynomial long division. Provide an example of each.

Answers

1: $9 y^{3}$

3: $13 x$

5: $5 x y^{4} z^{2}$

7: $- \frac{25}{2} a^{2} b$

9: $3 x^{2} + 9 x - 1$

11: $10 x^{2} - 5 x + 15$

13: $2 x^{4} + 3 x^{2} - 1$

15: $2 x^{3} - 3 x + 1$

17: $3 x^{5} - 2 x^{2} + 4 x - \frac{1}{3}$

19: $4 a^{3} - 8 a^{2} + 5 a - \frac{1}{4}$

21: $- 4 x^{5} y^{5} + 2 y^{2} + 1$

23: $- 18 x y^{2}$

25: $a^{2} - 6 a + 9$

27: $2 x + 1$

29: $2 x + 3$

31: $x^{2} + 2 x + 4$

33: $x^{2} - 2 x + 1$

35: $2 x^{3} - x^{2} + 3 x + 1$

37: $x + 3 + \frac{2}{x + 5}$

39: $- 3 x + 5 + \frac{4}{- 2 x + 1}$

41: $x^{2} + 5 x - 1 + \frac{5}{x + 4}$

43: $3 x^{2} - 2 x + 4 - \frac{7}{3 x - 2}$

45: $2 x^{4} - 5 x^{3} + 3 x^{2} - 2 x + 5 - \frac{7}{3 x + 1}$

47: $5 x^{3} + 2 x^{2} - 7 x + 1$

49: $x^{3} - 7 + \frac{2}{x^{2} + 7 x - 1}$

51: $x^{2} + 3 x + 9$

53: $3 x^{4} - 4 x^{2} + 3$

55: $x^{4} + x^{3} - x^{2} - x + 2 + \frac{1}{x - 1}$

57: $a - 2$

59: $a^{5} + a^{4} + a^{3} + a^{2} + a + 1$

61: $x^{3} + 7 x + 5 + \frac{2 x + 1}{x^{2} + x - 1}$

63: $x^{4} - 3 x^{2} + 5 x - \frac{1}{x}$

65: $15 x^{2} z^{10} - y^{4} + \frac{2}{5 z}$

67: $x^{5} + 9 x^{3} - 2 x + 1 - \frac{8}{3 x - 2}$

69: $(f / g) (x) = 4 x^{3}$

71: $(f / g) (x) = 6 x - 3$

73: $(f / g) (x) = 6 x - 2 - \frac{5}{3 x - 5}$

75: $(f / g) (x) = 2 x^{2} - x + 5$

77: $(f / g) (x) = 2 x^{2} + 3 x - 4$

79: $(f / g) (x) = 2 x^{2} + 2 x - 3$

81: $(f / g) (0) = - 3$

83: $(f / g) (x) = 5 x^{2} - 3 x + 1 + \frac{5}{x - 2}$

85: $(f / g) (0) = - \frac{3}{2}$