This is “Multiplying Polynomials”, section 5.4 from the book Beginning Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
5.4 Multiplying Polynomials
Learning Objectives
- Multiply a polynomial by a monomial.
- Multiply a polynomial by a binomial.
- Multiply a polynomial by any size polynomial.
- Recognize and calculate special products.
- Multiply polynomial functions.
Multiplying by a Monomial
Recall the product rule for exponents: if m and n are positive integers, then
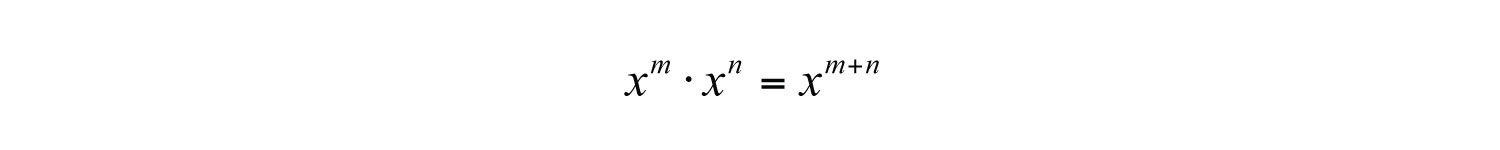
In other words, when multiplying two expressions with the same base, add the exponents. This rule applies when multiplying a monomial by a monomial. To find the product of monomials, multiply the coefficients and add the exponents of variable factors with the same base. For example,
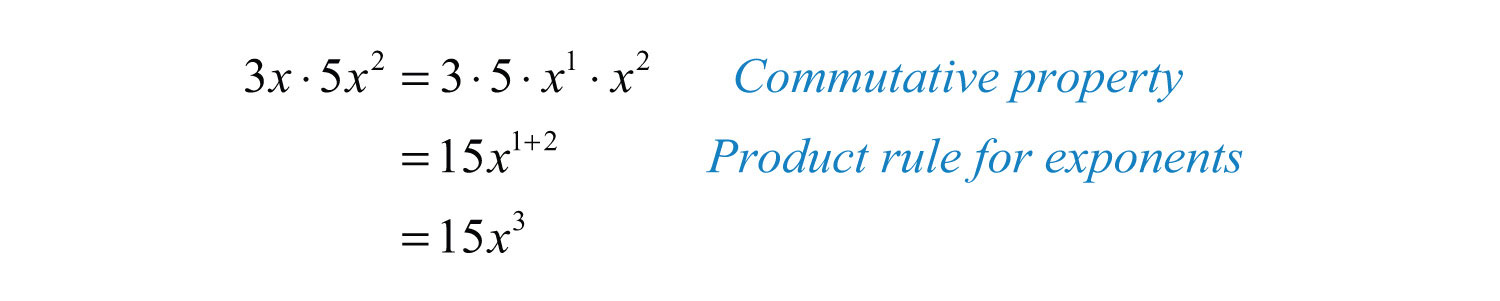
To multiply a polynomial by a monomial, apply the distributive property and then simplify each term.
Example 1: Multiply: .
Solution: In this case, multiply the monomial, , by the binomial, . Apply the distributive property and then simplify.
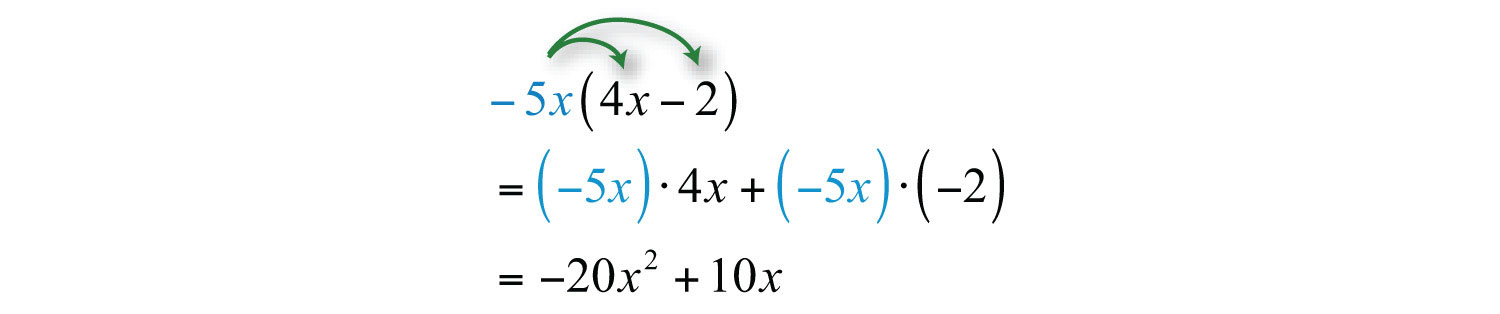
Answer:
Example 2: Multiply: .
Solution: Apply the distributive property and then simplify.
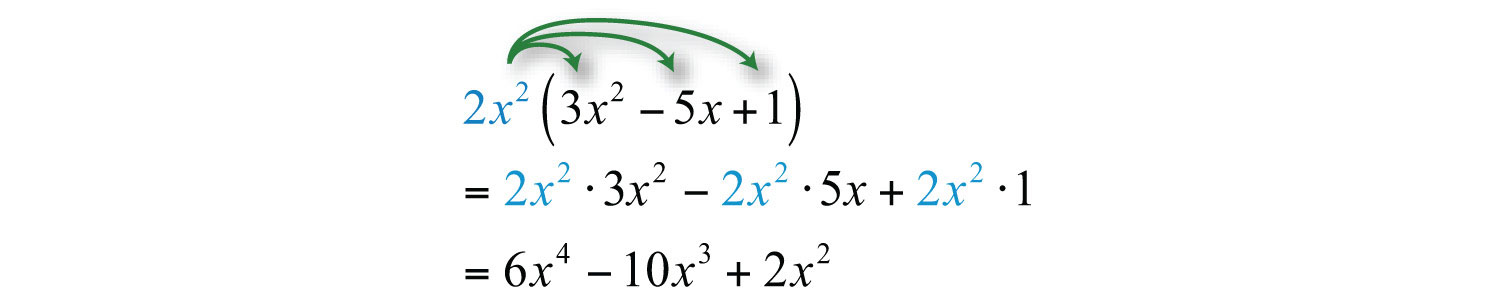
Answer:
Example 3: Multiply: .
Solution:
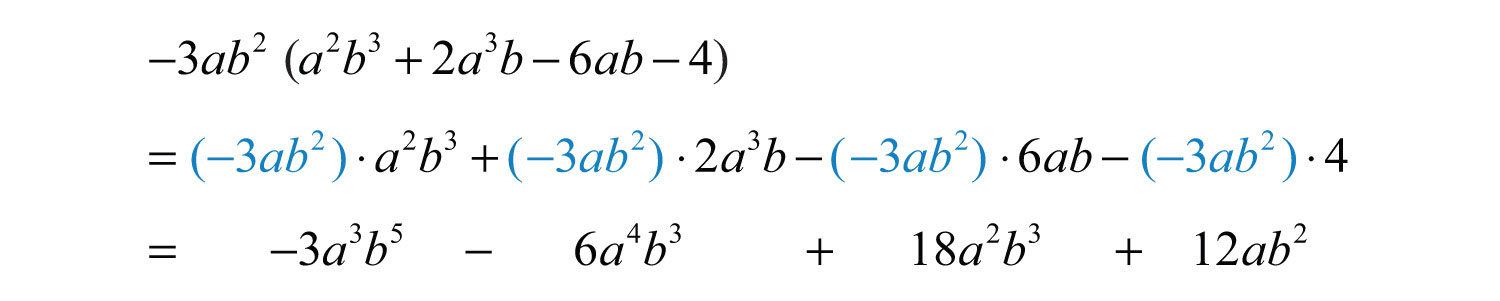
Answer:
To summarize, multiplying a polynomial by a monomial involves the distributive property and the product rule for exponents. Multiply all of the terms of the polynomial by the monomial. For each term, multiply the coefficients and add exponents of variables where the bases are the same.
Try this! Multiply: .
Answer:
Video Solution
(click to see video)Multiplying by a Binomial
In the same way that we used the distributive property to find the product of a monomial and a binomial, we will use it to to find the product of two binomials.
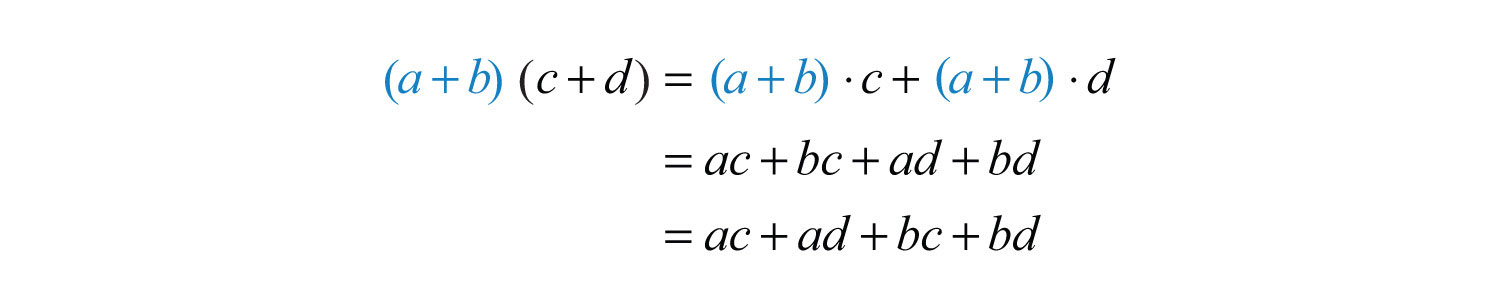
Here we apply the distributive property multiple times to produce the final result. This same result is obtained in one step if we apply the distributive property to a and b separately as follows:
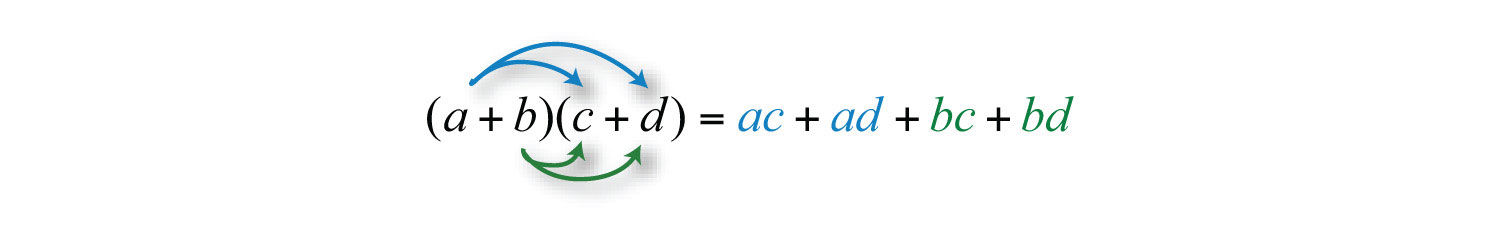
This is often called the FOILWhen multiplying binomials we apply the distributive property multiple times in such a way as to multiply the first terms, outer terms, inner terms, and last terms. method. We add the products of the first terms of each binomial ac, the outer terms ad, the inner terms bc, and finally the last terms bd. This mnemonic device only works for products of binomials; hence it is best to just remember that the distributive property applies.
Example 4: Multiply: .
Solution: Distribute and then distribute 3.
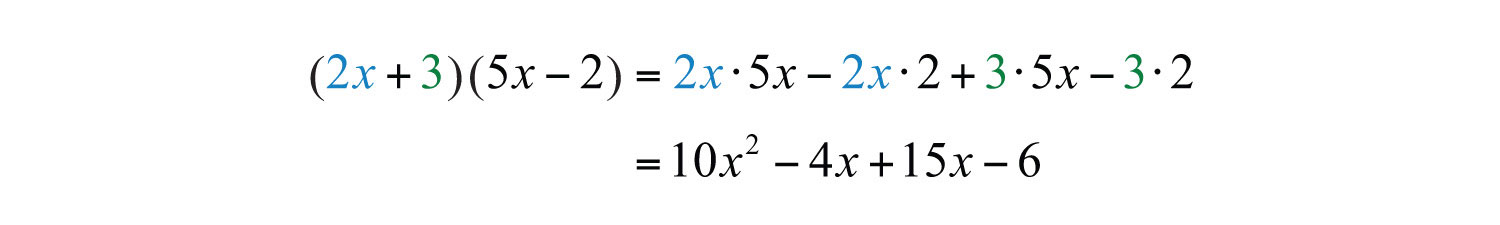
Simplify by combining like terms.
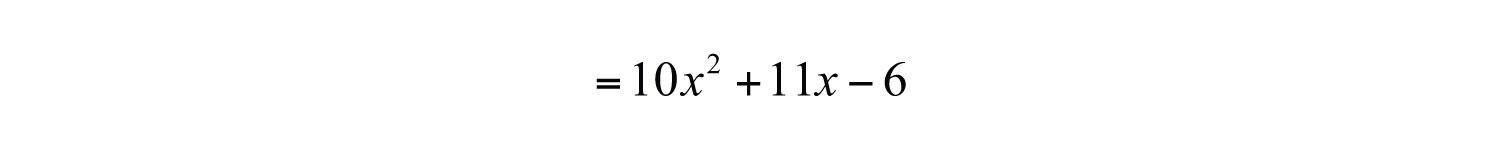
Answer:
Example 5: Multiply: .
Solution: Distribute and then distribute .
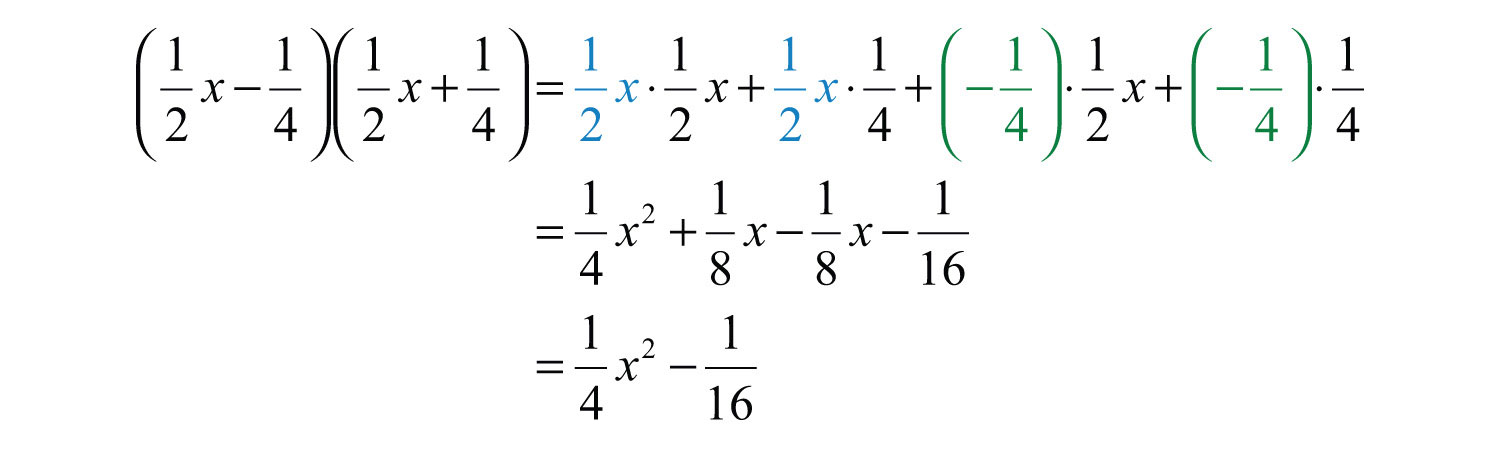
Answer:
Example 6: Multiply: .
Solution:
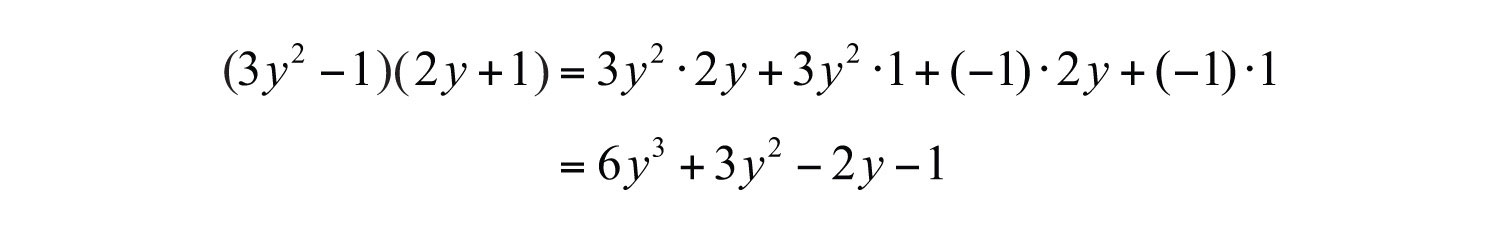
Answer:
After applying the distributive property, combine any like terms.
Example 7: Multiply: .
Solution: After multiplying each term of the trinomial by and , simplify.
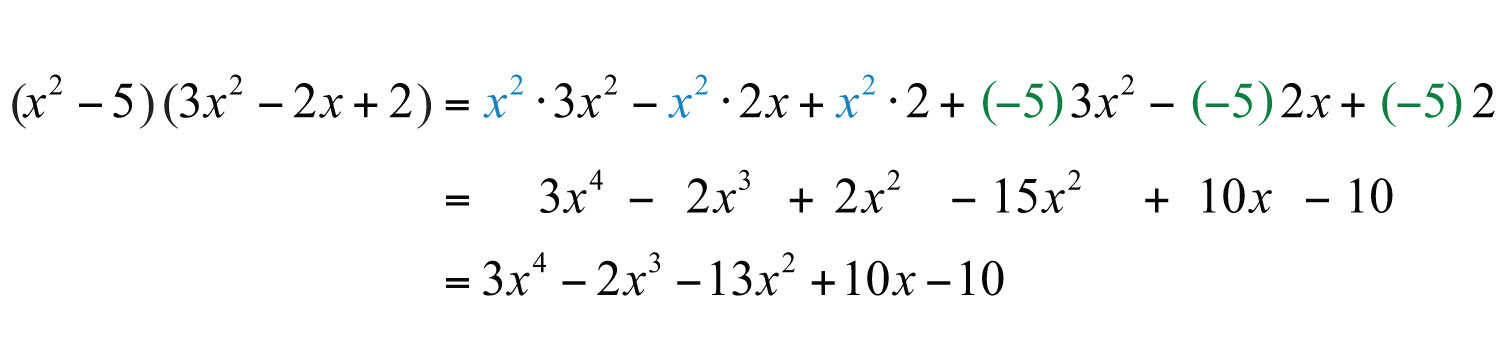
Answer:
Example 8: Multiply: .
Solution: Perform one product at a time.
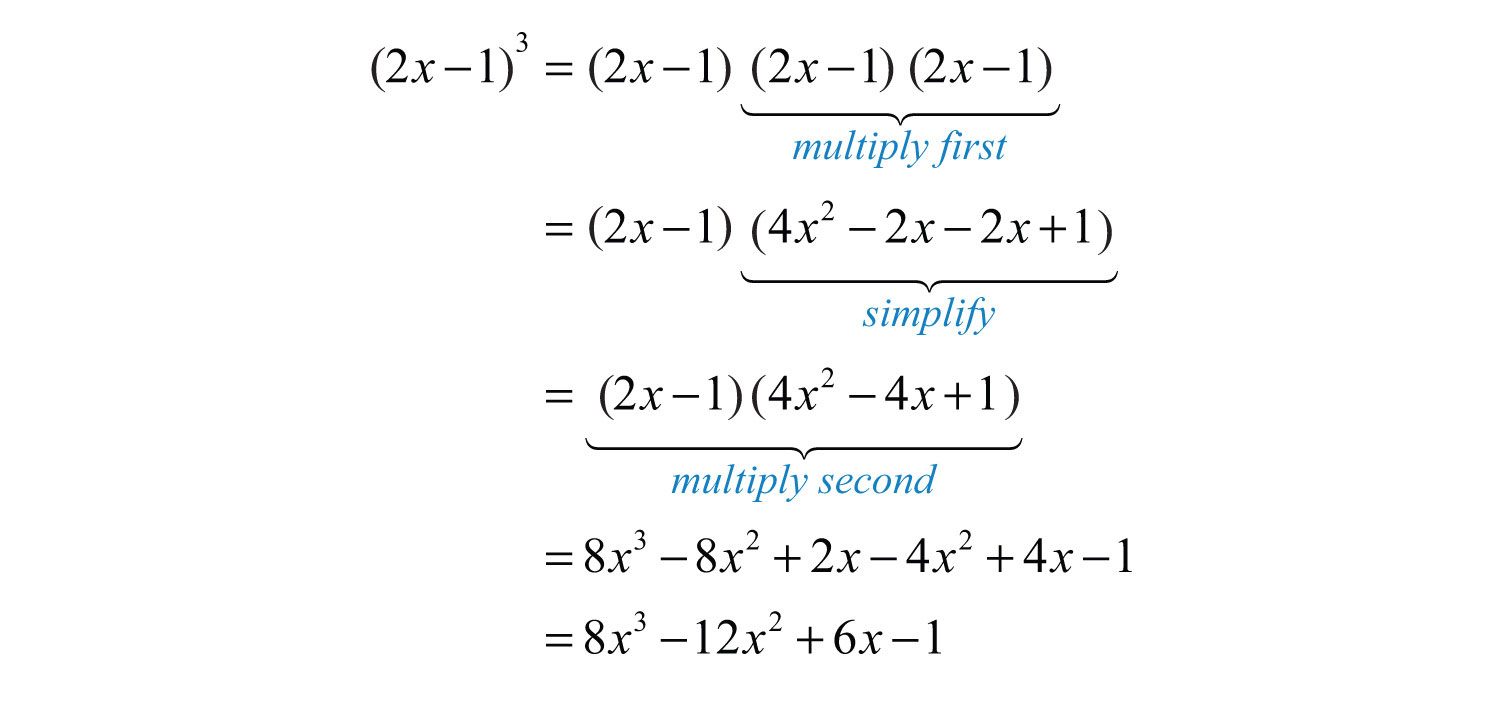
Answer:
At this point, it is worth pointing out a common mistake:
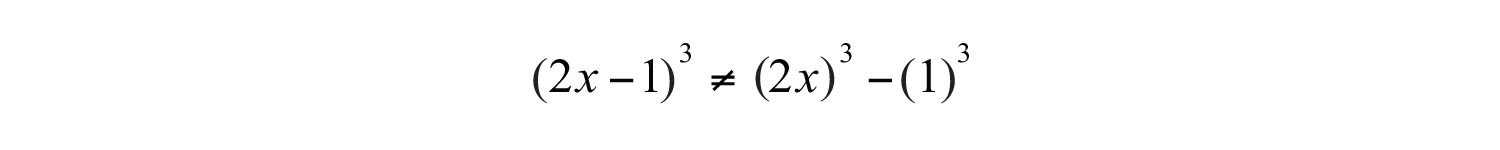
The confusion comes from the product to a power rule of exponents, where we apply the power to all factors. Since there are two terms within the parentheses, that rule does not apply. Care should be taken to understand what is different in the following two examples:
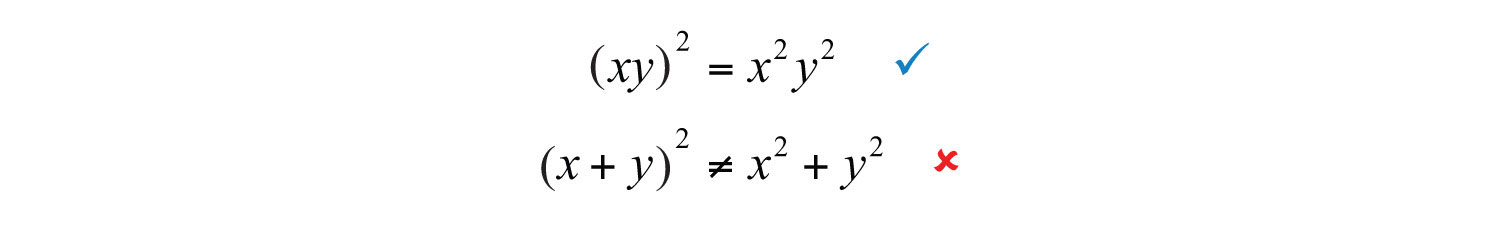
Try this! Multiply: .
Answer:
Video Solution
(click to see video)Product of Polynomials
When multiplying polynomials, we apply the distributive property many times. Multiply all of the terms of each polynomial and then combine like terms.
Example 9: Multiply: .
Solution: Multiply each term of the first trinomial by each term of the second trinomial and then combine like terms.
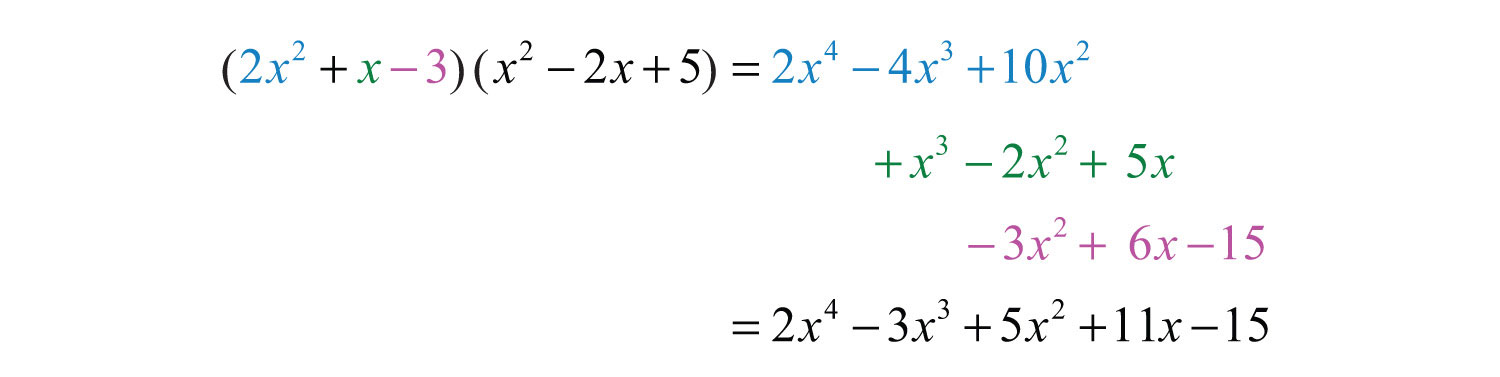
Aligning like terms in columns, as we have here, aids in the simplification process.
Answer:
Notice that when multiplying a trinomial by a trinomial, we obtain nine terms before simplifying. In fact, when multiplying an n-term polynomial by an m-term polynomial, we will obtain n × m terms.
In the previous example, we were asked to multiply and found that
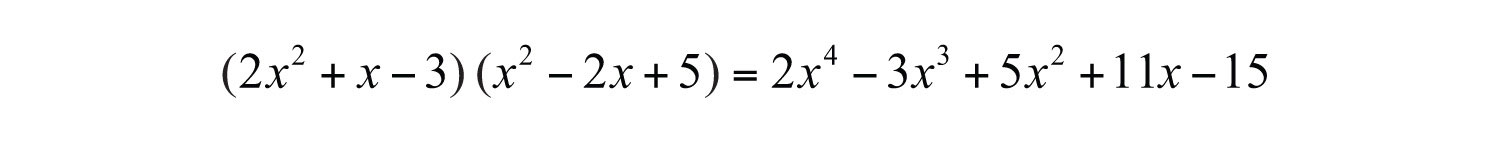
Because it is easy to make a small calculation error, it is a good practice to trace through the steps mentally to verify that the operations were performed correctly. Alternatively, we can check by evaluatingWe can be fairly certain that we have multiplied the polynomials correctly if we check that a few values evaluate to the same results in the original expression and in the answer. any value for x in both expressions to verify that the results are the same. Here we choose x = 2:
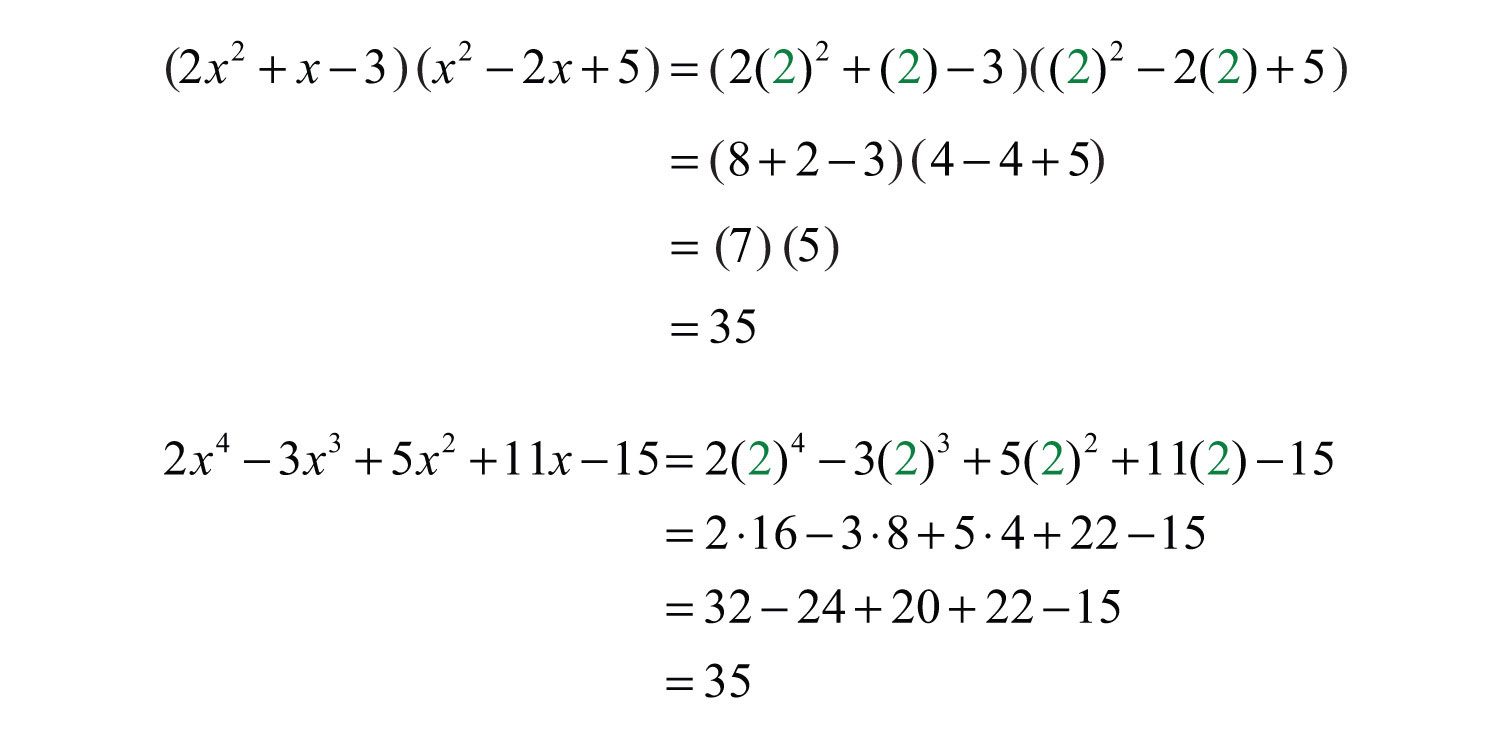
Because the results could coincidentally be the same, a check by evaluating does not necessarily prove that we have multiplied correctly. However, after verifying a few values, we can be fairly confident that the product is correct.
Try this! Multiply: .
Answer:
Video Solution
(click to see video)Special Products
In this section, the goal is to recognize certain special products that occur often in our study of algebra. We will develop three formulas that will be very useful as we move along. The three should be memorized. We begin by considering the following two calculations:
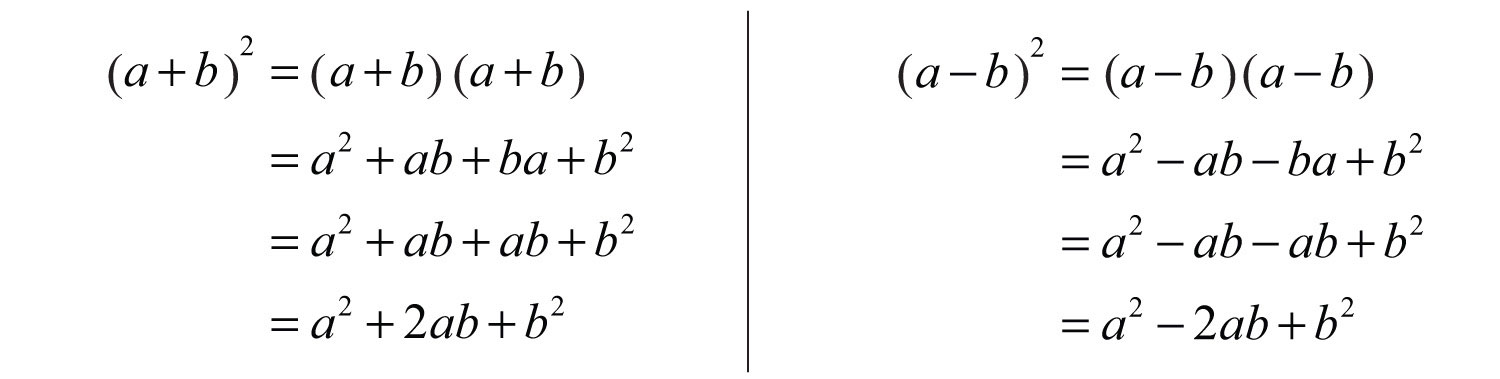
This leads us to two formulas that describe perfect square trinomialsThe trinomials obtained by squaring the binomials and :
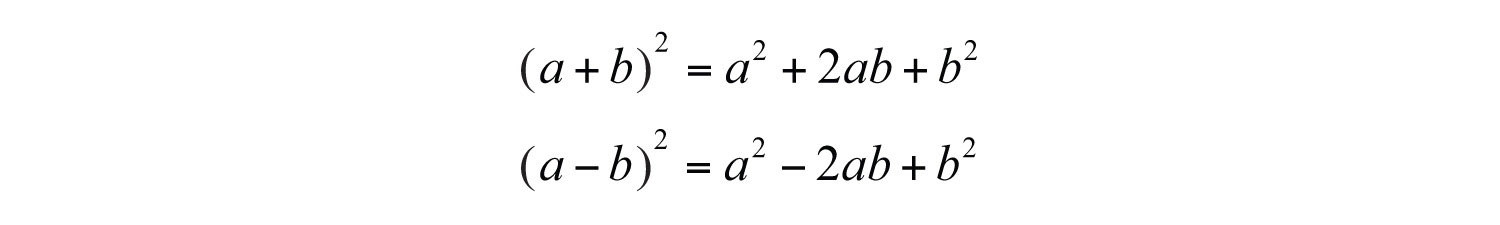
We can use these formulas to quickly square a binomial.
Example 10: Multiply: .
Solution: Here and . Apply the formula:
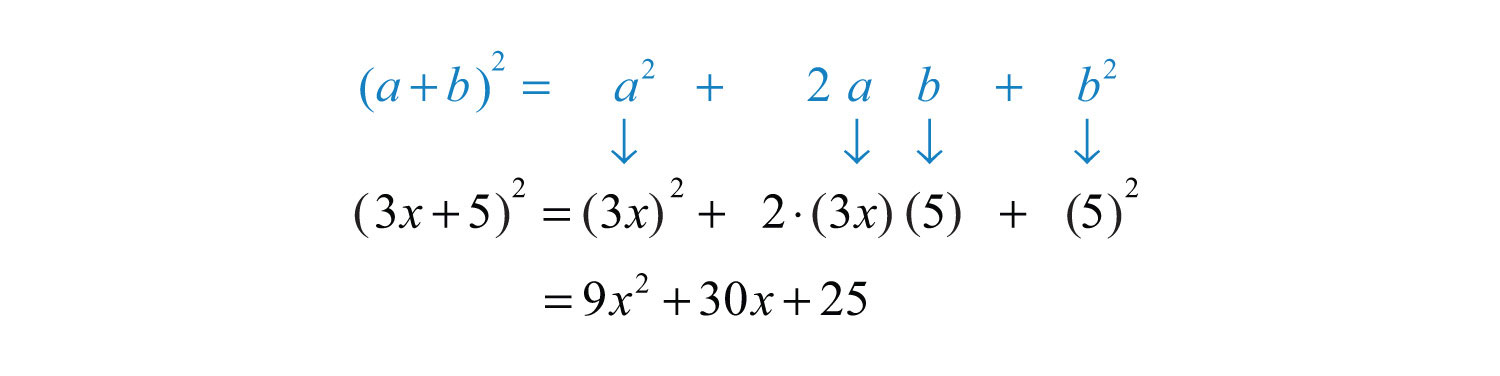
Answer:
This process should become routine enough to be performed mentally.
Example 11: Multiply: .
Solution: Here and . Apply the appropriate formula as follows:
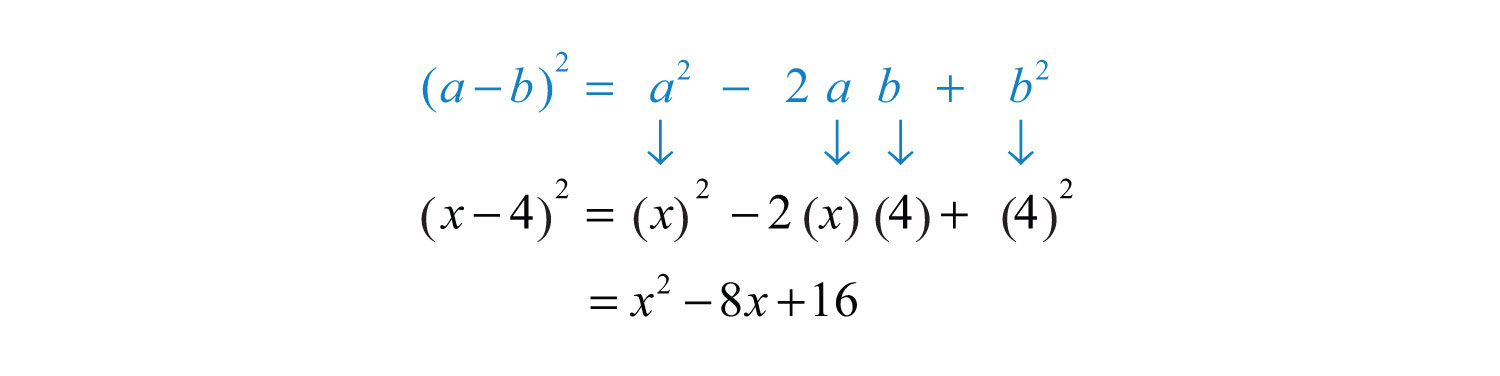
Answer:
Our third special product follows:
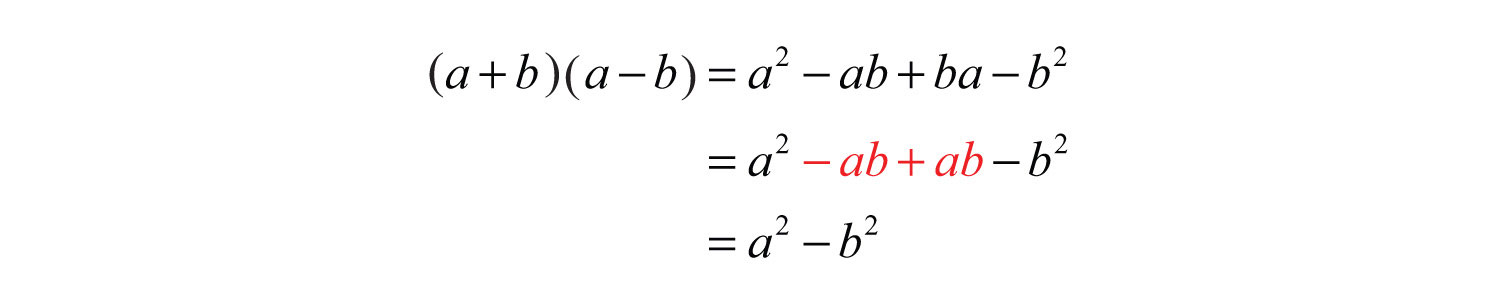
This product is called difference of squares where a and b represent algebraic expressions.:
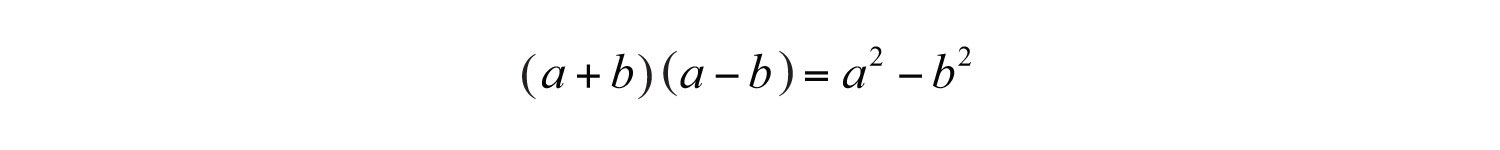
The binomials and are called conjugate binomialsThe binomials and .. Therefore, when conjugate binomials are multiplied, the middle term eliminates, and the product is itself a binomial.
Example 12: Multiply: .
Solution:
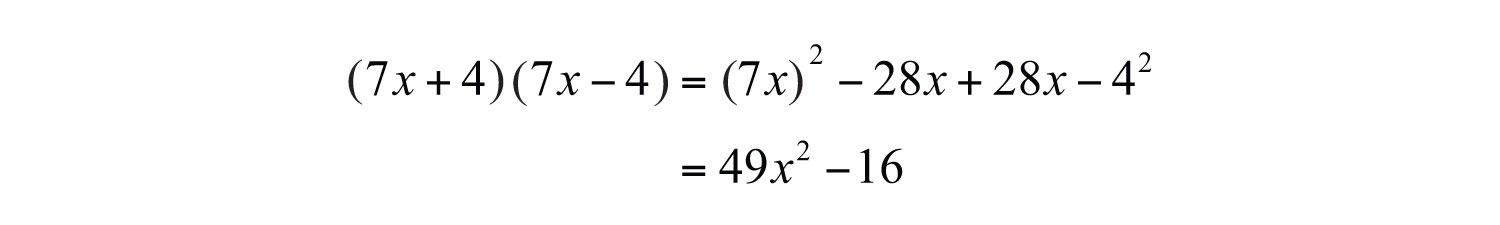
Answer:
Try this! Multiply: .
Answer:
Video Solution
(click to see video)Multiplying Polynomial Functions
We use function notation to indicate multiplication as follows:
| Multiplication of functions: |
Example 13: Calculate: , given and .
Solution: Multiply all terms of the trinomial by the monomial function .
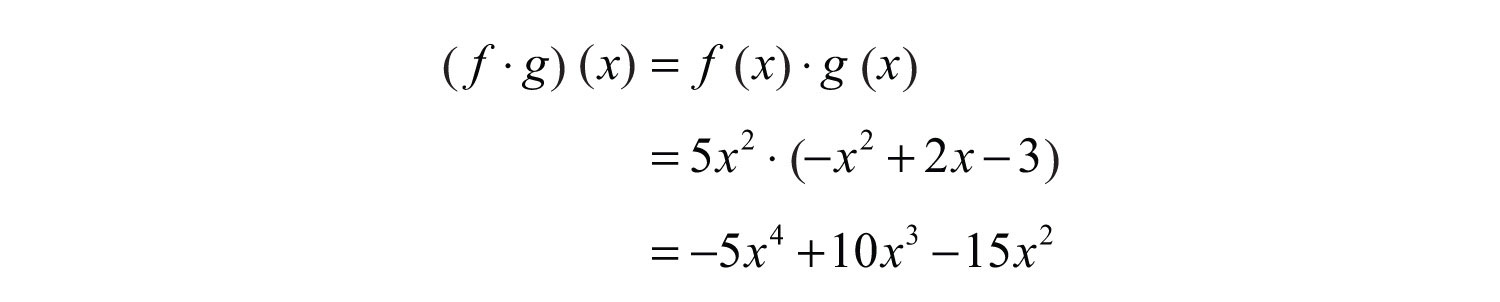
Answer:
Example 14: Calculate: , given and .
Solution: First, determine .
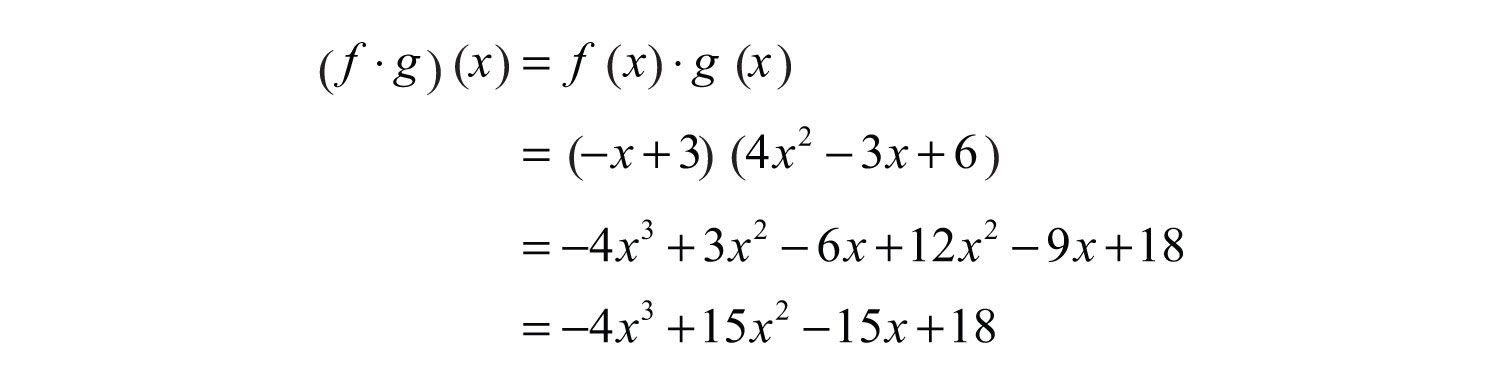
We have
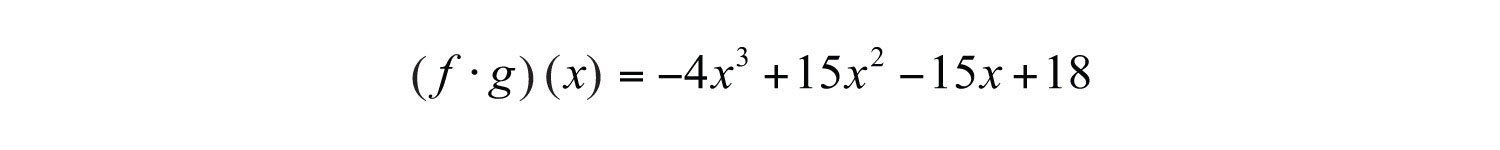
Next, substitute −1 for the variable x.
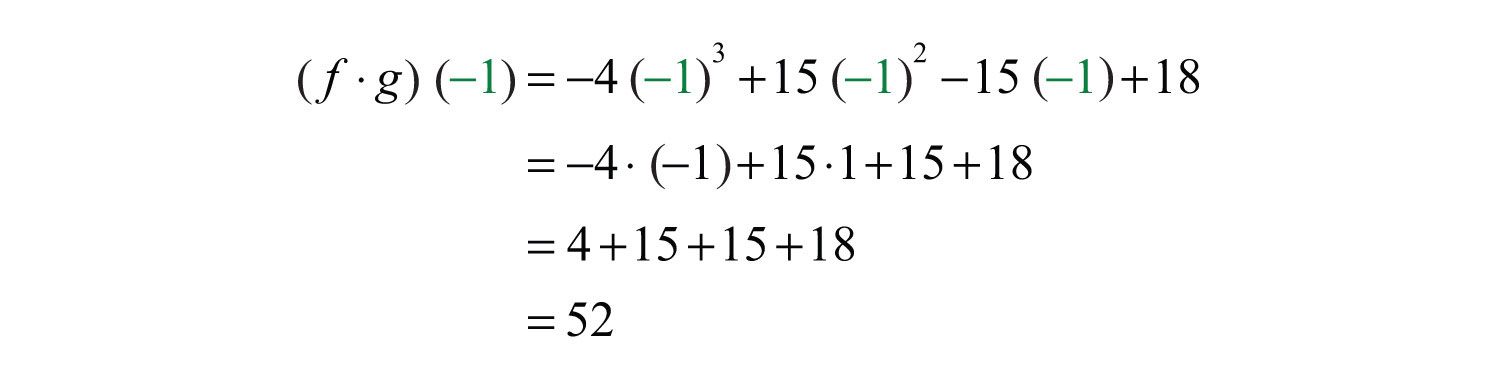
Answer:
Because , we could alternatively calculate and separately and then multiply the results (try this as an exercise). However, if we were asked to evaluate multiple values for the function , it would be best to first determine the general form, as we have in the previous example.
Key Takeaways
- To multiply a polynomial by a monomial, apply the distributive property and then simplify each of the resulting terms.
- To multiply polynomials, multiply each term in the first polynomial with each term in the second polynomial. Then combine like terms.
- The product of an n-term polynomial and an m-term polynomial results in an m × n term polynomial before like terms are combined.
- Check results by evaluating values in the original expression and in your answer to verify that the results are the same.
- Use the formulas for special products to quickly multiply binomials that occur often in algebra.
Topic Exercises
Part A: Product of a Monomial and a Polynomial
Multiply.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29. Find the product of and .
30. Find the product of and .
31. Find the product of and .
32. Find the product of and .
Part B: Product of a Binomial and a Polynomial
Multiply.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
Part C: Product of Polynomials
Multiply.
61.
62.
63.
64.
65.
66.
67.
68.
69. Find the volume of a rectangular solid with sides measuring , , and units.
70. Find the volume of a cube where each side measures units.
Part D: Special Products
Multiply.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
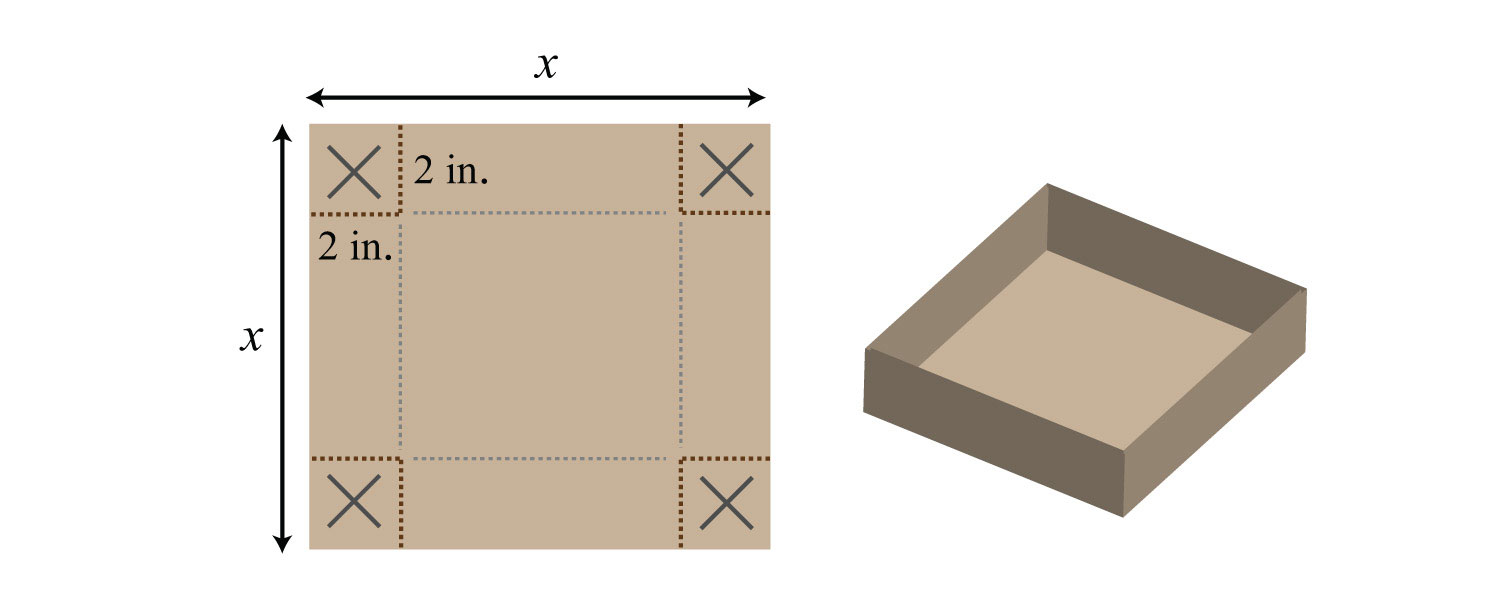
91. A box is made by cutting out the corners and folding up the edges of a square piece of cardboard. A template for a cardboard box with a height of 2 inches is given. Find a formula for the volume, if the initial piece of cardboard is a square with sides measuring x inches.
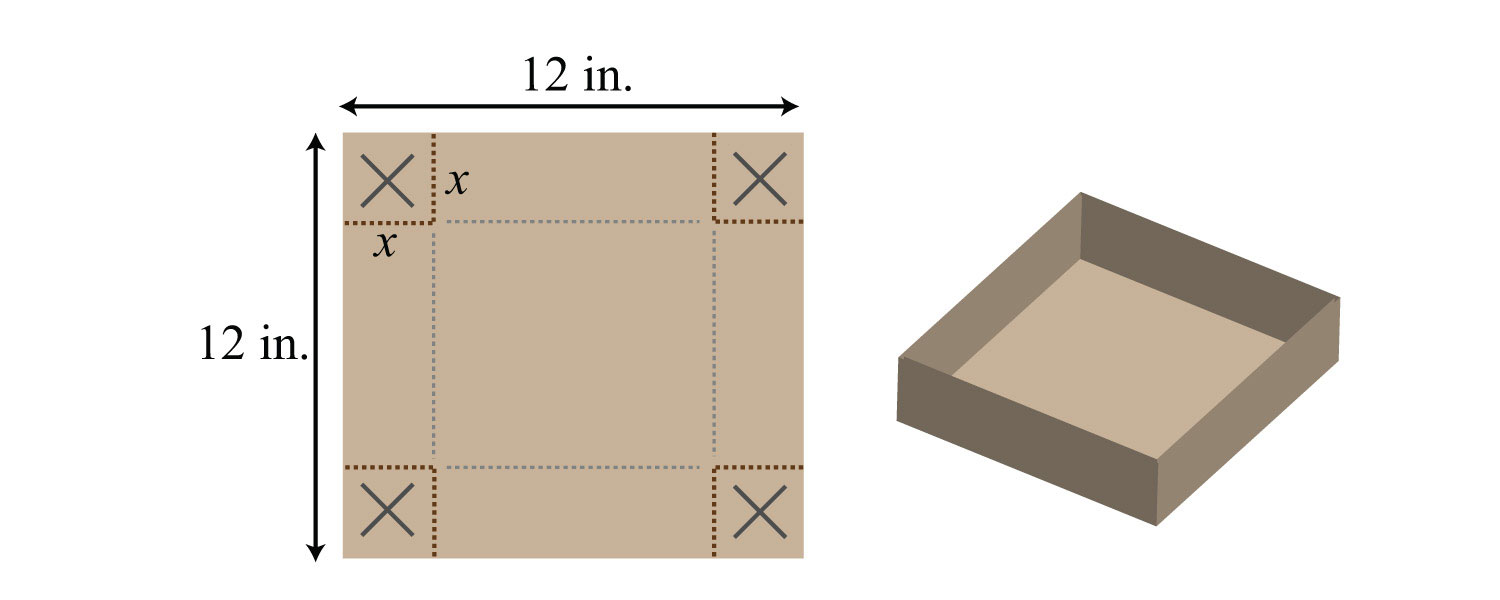
92. A template for a cardboard box with a height of x inches is given. Find a formula for the volume, if the initial piece of cardboard is a square with sides measuring 12 inches.
Part E: Multiplying Polynomial Functions
For each problem, calculate , given the functions.
93. and
94. and
95. and
96. and
97. and
98. and
Given and , find the following.
99.
100.
101.
102.
103.
104.
Given and , find the following.
105.
106.
107.
108.
109.
110.
111.
112.
Part F: Discussion Board Topics
113. Explain why .
114. Explain how to quickly multiply a binomial with its conjugate. Give an example.
115. What are the advantages and disadvantages of using the mnemonic device FOIL?
Answers
1:
3:
5:
7:
9:
11:
13:
15:
17:
19:
21:
23:
25:
27:
29:
31:
33:
35:
37:
39:
41:
43:
45:
47:
49:
51:
53:
55:
57:
59:
61:
63:
65:
67:
69:
71:
73:
75:
77:
79:
81:
83:
85:
87:
89:
91: cubic inches
93:
95:
97:
99:
101:
103:
105:
107:
109:
111:




