This is “Simplifying Algebraic Expressions”, section 2.2 from the book Beginning Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
2.2 Simplifying Algebraic Expressions
Learning Objectives
- Apply the distributive property to simplify an algebraic expression.
- Identify and combine like terms.
Distributive Property
The properties of real numbers are important in our study of algebra because a variable is simply a letter that represents a real number. In particular, the distributive propertyGiven any real numbers a, b, and c, or . states that given any real numbers a, b, and c,
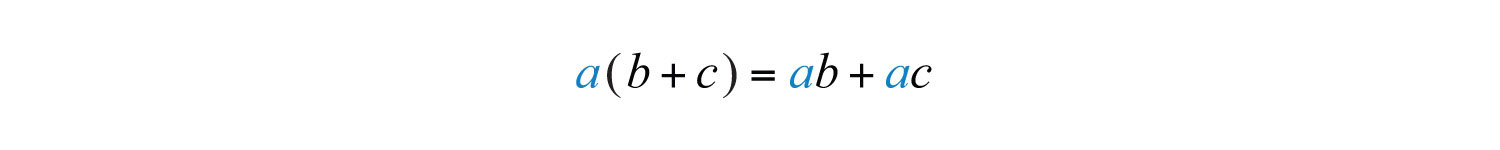
This property is applied when simplifying algebraic expressions. To demonstrate how it is used, we simplify in two ways, and observe the same correct result.

Certainly, if the contents of the parentheses can be simplified, do that first. On the other hand, when the contents of parentheses cannot be simplified, multiply every term within the parentheses by the factor outside of the parentheses using the distributive property. Applying the distributive property allows you to multiply and remove the parentheses.
Example 1: Simplify: .
Solution: Multiply 5 times each term inside the parentheses.
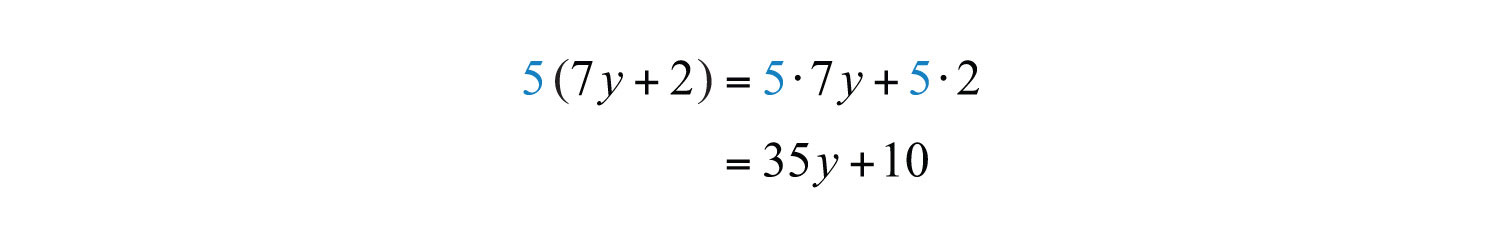
Answer:
Example 2: Simplify: .
Solution: Multiply −3 times each of the coefficients of the terms inside the parentheses.
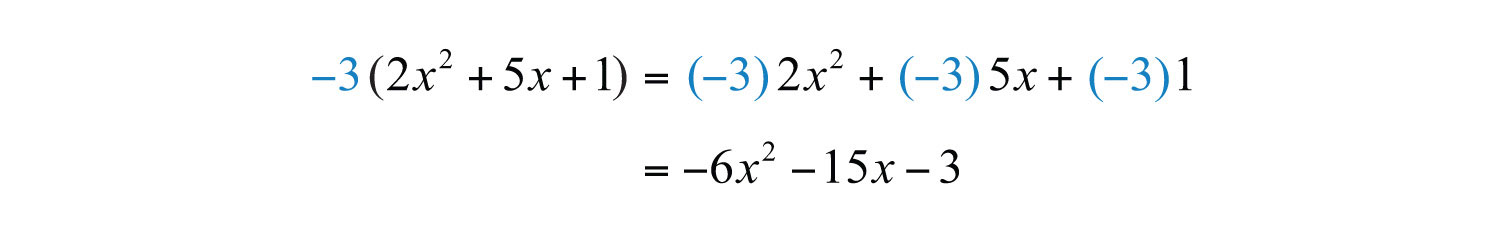
Answer:
Example 3: Simplify: .
Solution: Apply the distributive property by multiplying only the terms grouped within the parentheses by 5.
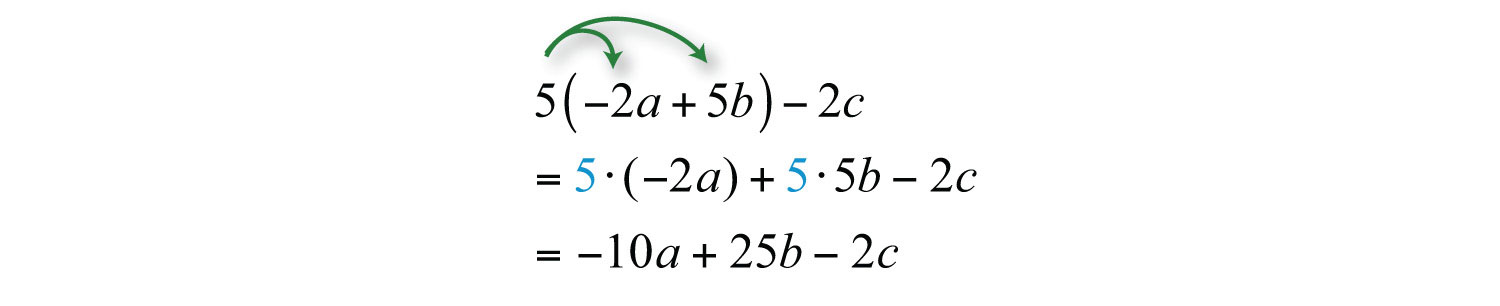
Answer:
Because multiplication is commutative, we can also write the distributive property in the following manner: .
Example 4: Simplify: .
Solution: Multiply each term within the parentheses by 3.
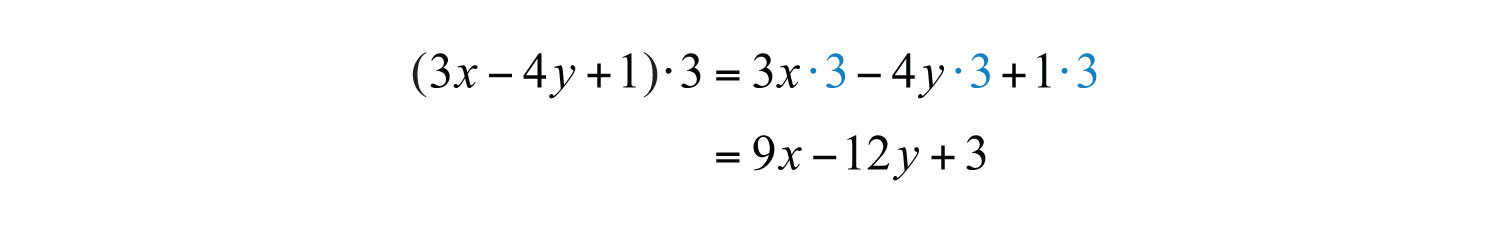
Answer:
Division in algebra is often indicated using the fraction bar rather than with the symbol (÷). And sometimes it is useful to rewrite expressions involving division as products:
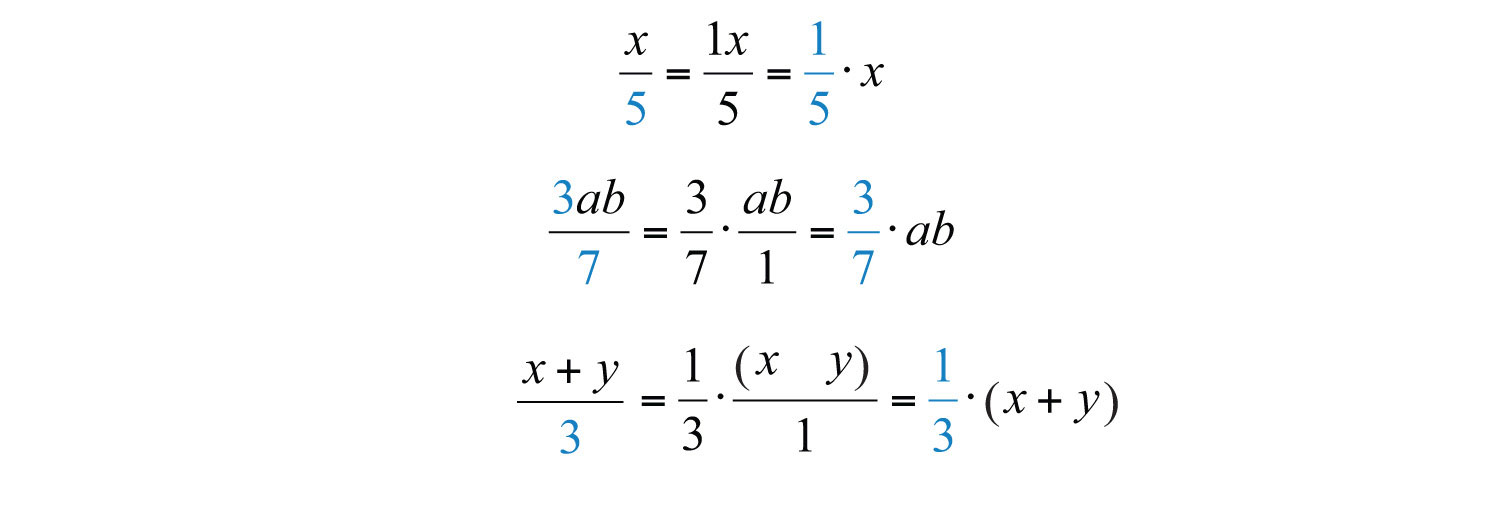
Rewriting algebraic expressions as products allows us to apply the distributive property.
Example 5: Divide: .
Solution: First, treat this as times the expression in the numerator and then distribute.
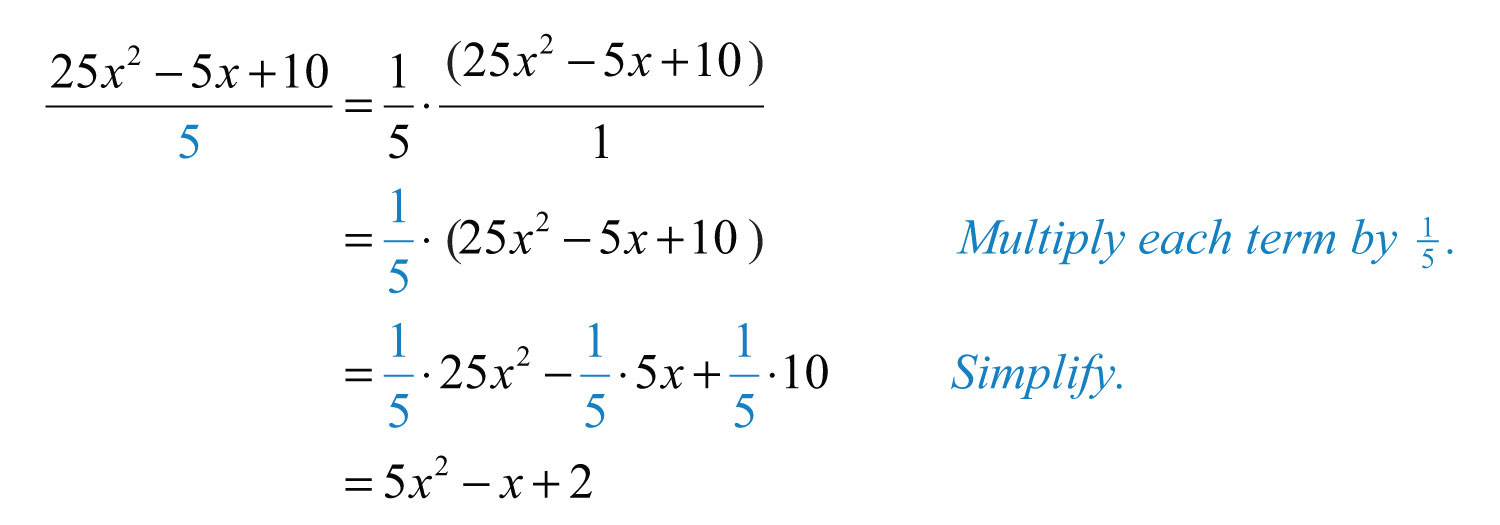
Alternate Solution: Think of 5 as a common denominator and divide each of the terms in the numerator by 5:
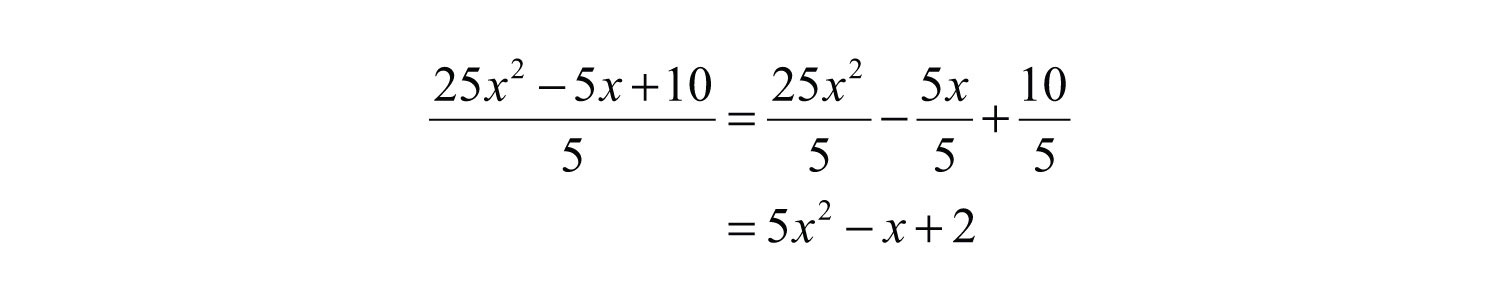
Answer:
We will discuss the division of algebraic expressions in more detail as we progress through the course.
Try this! Simplify: .
Answer:
Video Solution
(click to see video)Combining Like Terms
Terms with the same variable parts are called like termsConstant terms or terms with the same variable parts., or similar termsUsed when referring to like terms.. Furthermore, constant terms are considered to be like terms. If an algebraic expression contains like terms, apply the distributive property as follows:
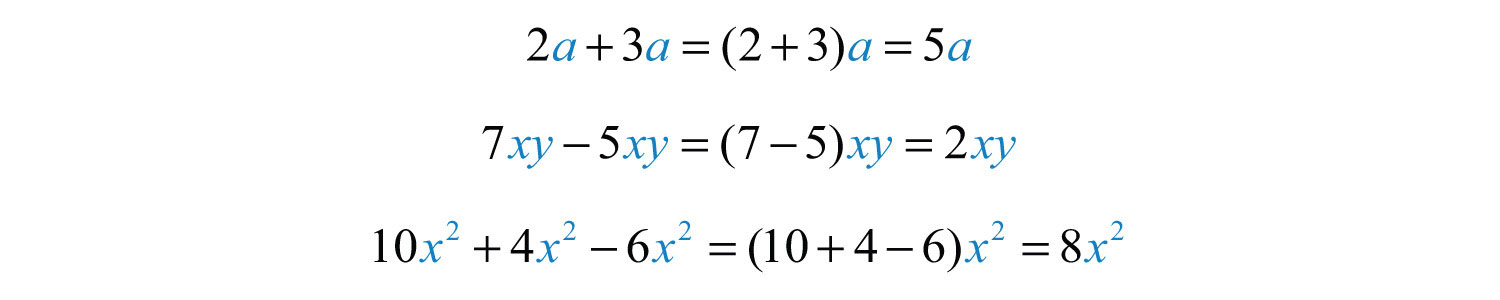
In other words, if the variable parts of terms are exactly the same, then we may add or subtract the coefficients to obtain the coefficient of a single term with the same variable part. This process is called combining like termsAdding or subtracting like terms within an algebraic expression to obtain a single term with the same variable part.. For example,
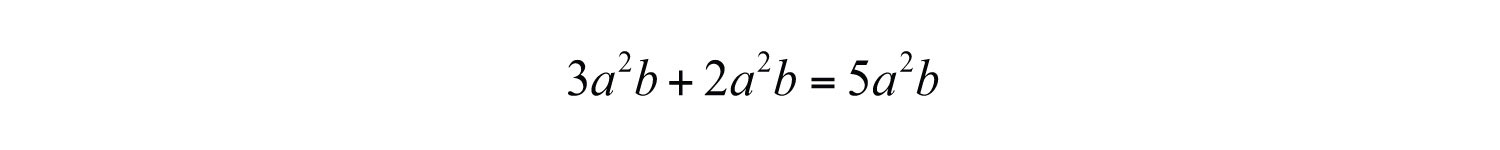
Notice that the variable factors and their exponents do not change. Combining like terms in this manner, so that the expression contains no other similar terms, is called simplifying the expressionThe process of combining like terms until the expression contains no more similar terms.. Use this idea to simplify algebraic expressions with multiple like terms.
Example 6: Simplify: .
Solution: Identify the like terms and combine them.
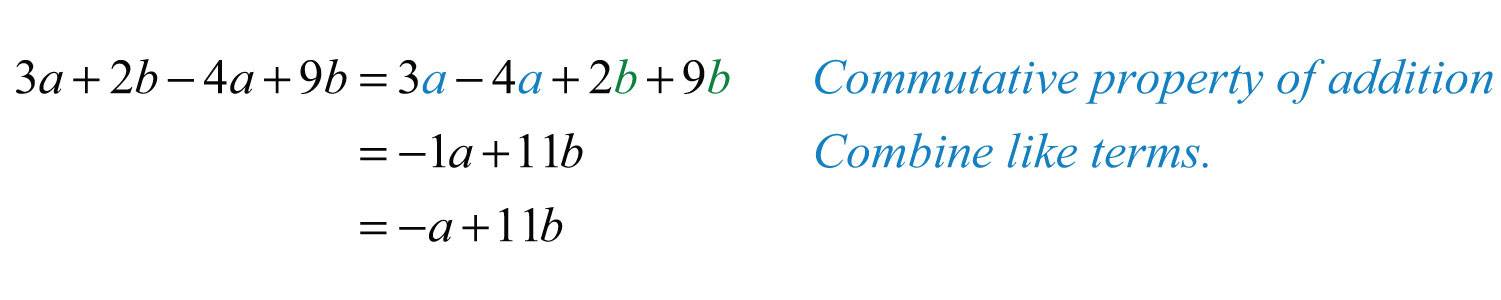
Answer:
In the previous example, rearranging the terms is typically performed mentally and is not shown in the presentation of the solution.
Example 7: Simplify: .
Solution: Identify the like terms and add the corresponding coefficients.
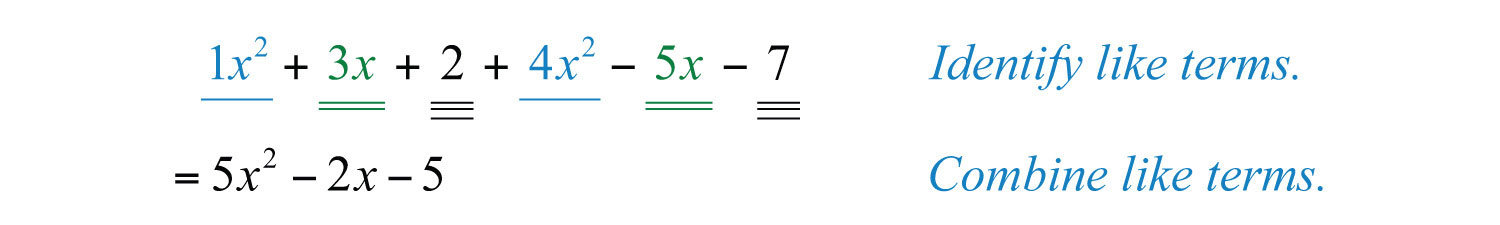
Answer:
Example 8: Simplify: .
Solution: Remember to leave the variable factors and their exponents unchanged in the resulting combined term.
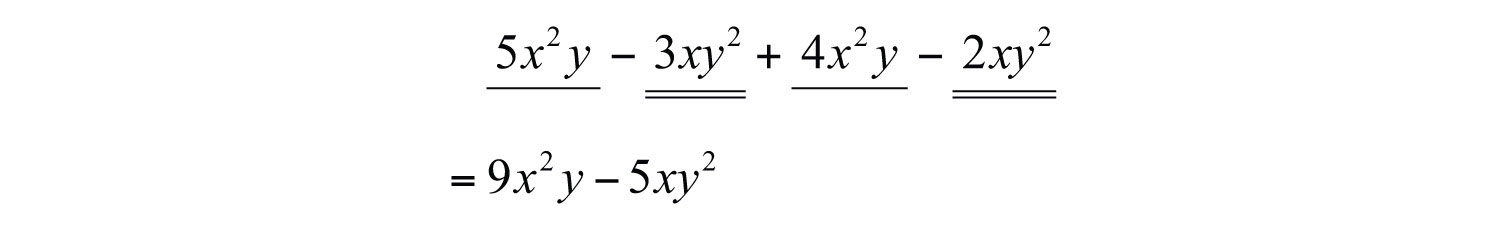
Answer:
Example 9: Simplify: .
Solution: To add the fractional coefficients, use equivalent coefficients with common denominators for each like term.
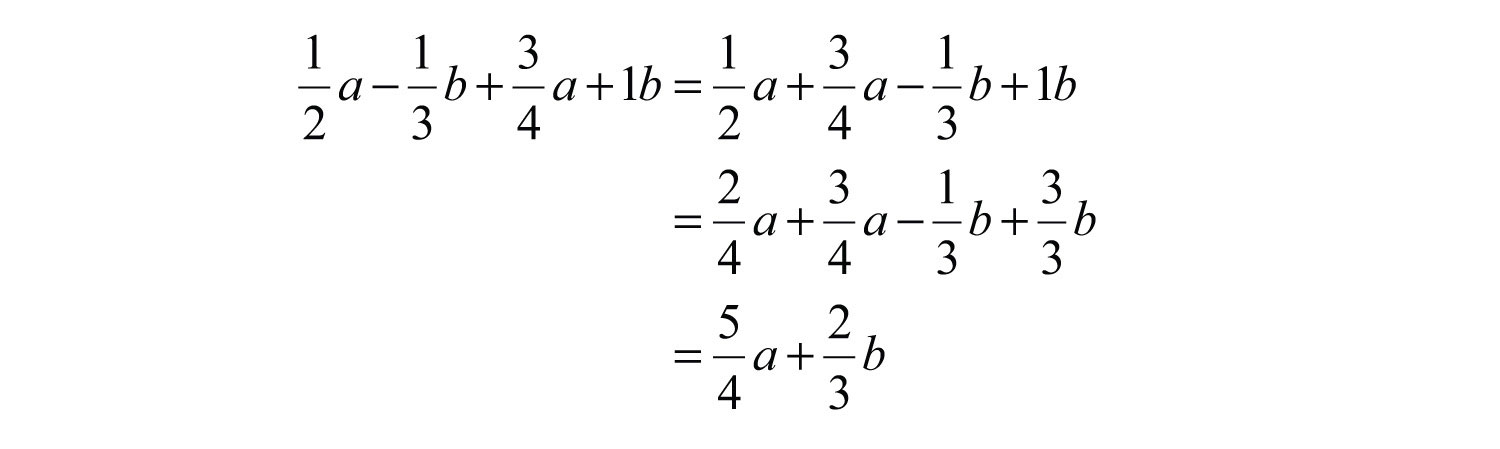
Answer:
Example 10: Simplify: .
Solution: Consider the variable part to be . Then this expression has two like terms with coefficients −12 and 26.
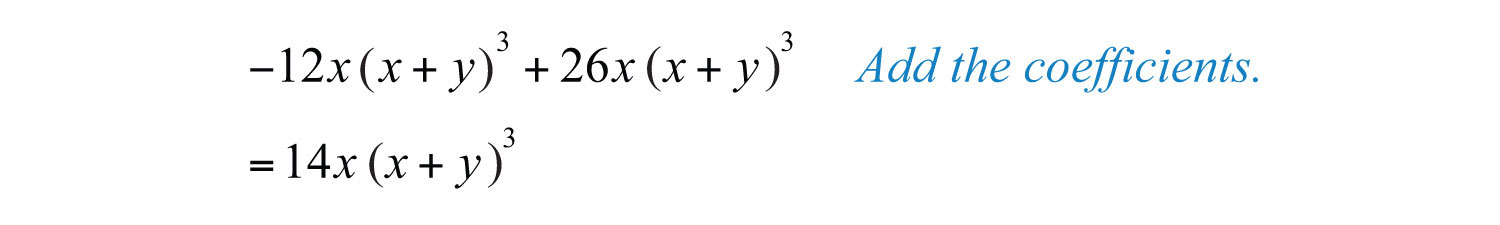
Answer:
Try this! Simplify: .
Answer:
Video Solution
(click to see video)Distributive Property and Like Terms
When simplifying, we will often have to combine like terms after we apply the distributive property. This step is consistent with the order of operations: multiplication before addition.
Example 11: Simplify: .
Solution: Distribute 2 and −7 and then combine like terms.
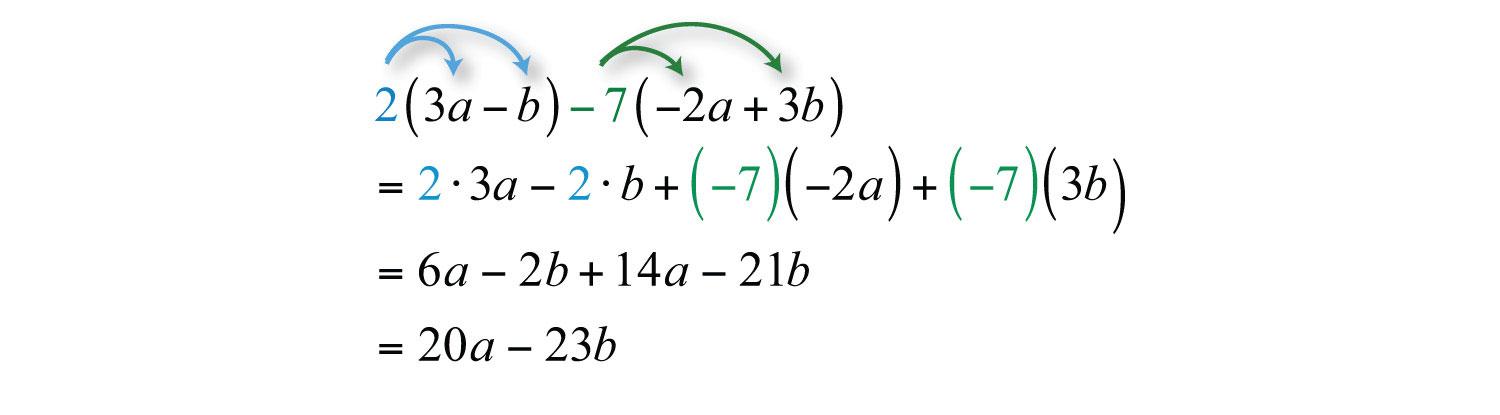
Answer:
In the example above, it is important to point out that you can remove the parentheses and collect like terms because you multiply the second quantity by −7, not just by 7. To correctly apply the distributive property, think of this as adding −7 times the given quantity, .
Try this! Simplify: .
Answer:
Video Solution
(click to see video)Often we will encounter algebraic expressions like or . As we have seen, the coefficients are actually implied to be +1 and −1, respectively, and therefore, the distributive property applies using +1 or –1 as the factor. Multiply each term within the parentheses by these factors:
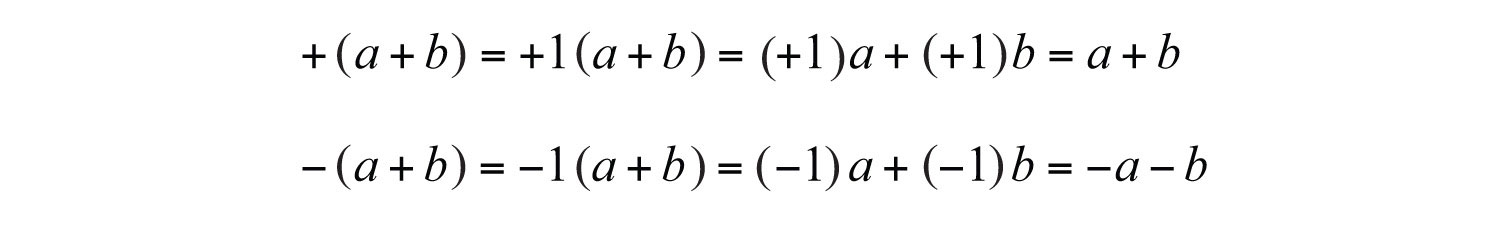
This leads to two useful properties,
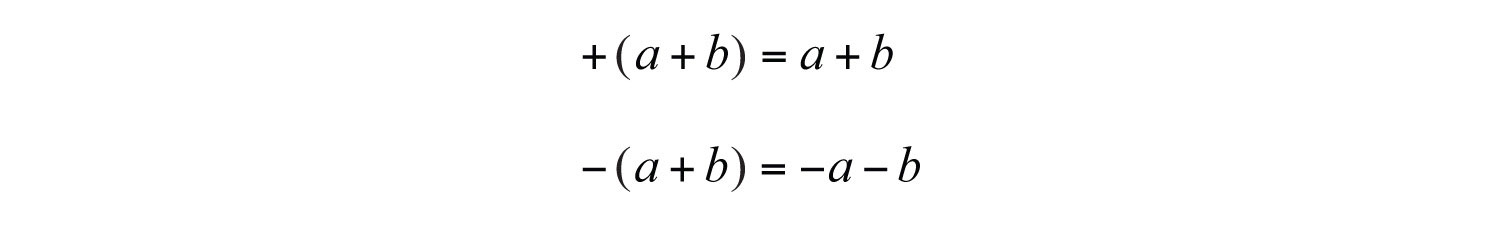
Example 12: Simplify: .
Solution: Multiply each term within the parentheses by −1 and then combine like terms.
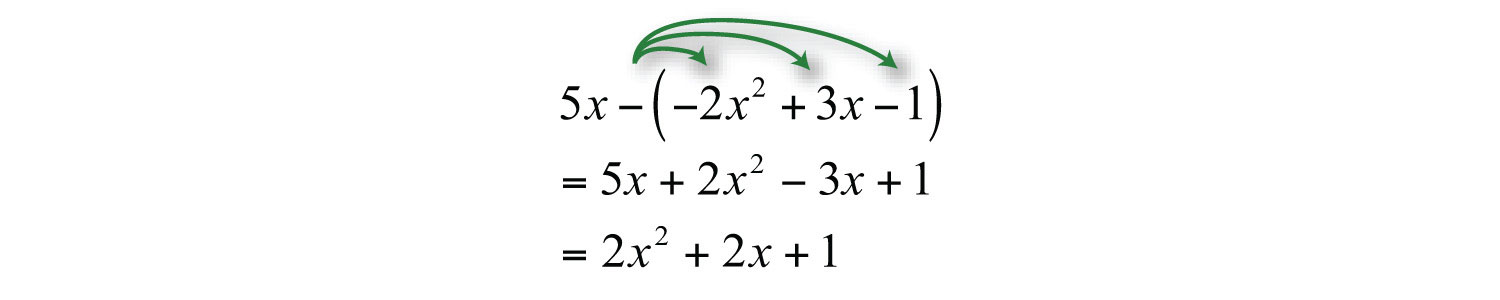
Answer:
When distributing a negative number, all of the signs within the parentheses will change. Note that in the example above is a separate term; hence the distributive property does not apply to it.
Example 13: Simplify: .
Solution: The order of operations requires that we multiply before subtracting. Therefore, distribute −2 and then combine the constant terms. Subtracting 5 − 2 first leads to an incorrect result, as illustrated below:
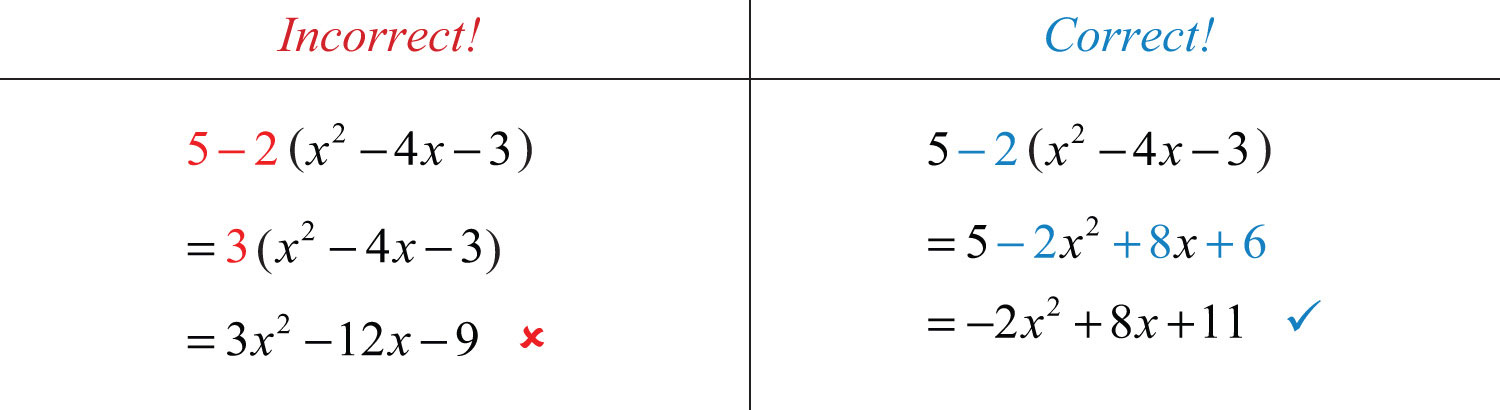
Answer: −2x2 + 8x + 11
Caution
It is worth repeating that you must follow the order of operations: multiply and divide before adding and subtracting!
Try this! Simplify: .
Answer:
Video Solution
(click to see video)
Example 14: Subtract from twice the quantity .
Solution: First, group each expression and treat each as a quantity:
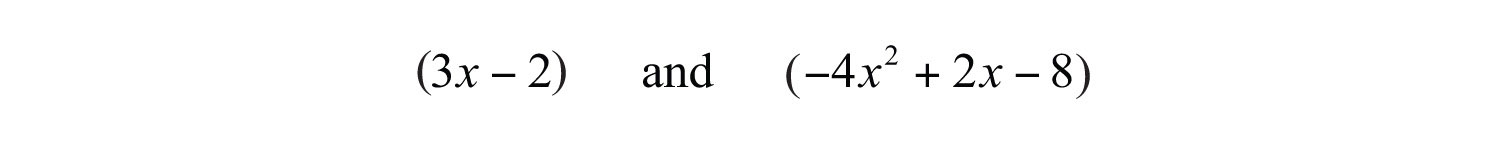
Next, identify the key words and translate them into a mathematical expression.
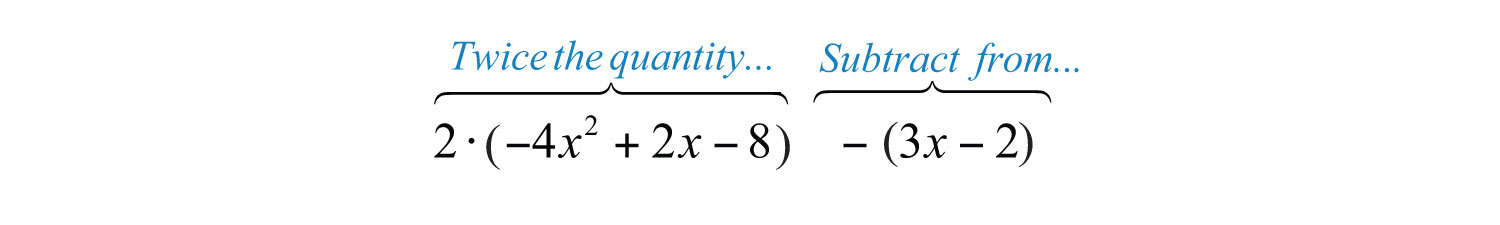
Finally, simplify the resulting expression.
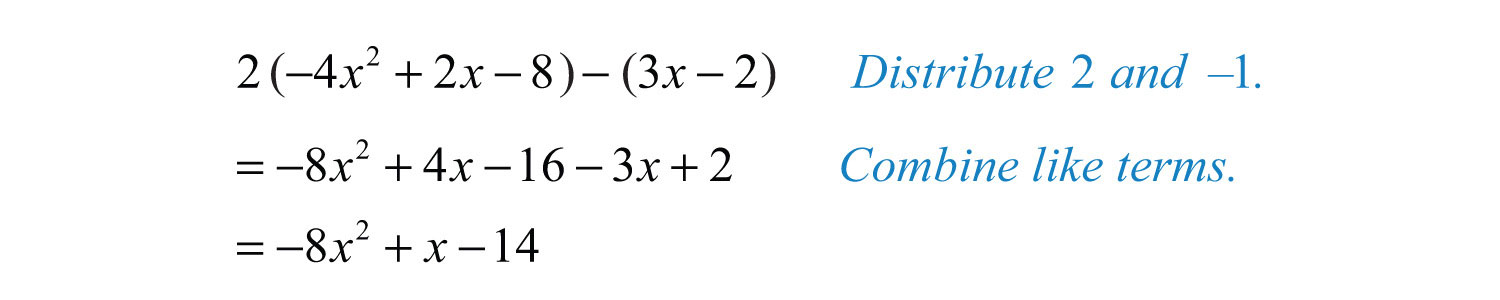
Answer:
Key Takeaways
- The properties of real numbers apply to algebraic expressions, because variables are simply representations of unknown real numbers.
- Combine like terms, or terms with the same variable part, to simplify expressions.
- Use the distributive property when multiplying grouped algebraic expressions, .
- It is a best practice to apply the distributive property only when the expression within the grouping is completely simplified.
- After applying the distributive property, eliminate the parentheses and then combine any like terms.
- Always use the order of operations when simplifying.
Topic Exercises
Part A: Distributive Property
Multiply.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
Translate the following sentences into algebraic expressions and then simplify.
31. Simplify two times the expression .
32. Simplify the opposite of the expression .
33. Simplify the product of 5 and .
34. Simplify the product of −3 and .
Part B: Combining Like Terms
Simplify.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
Part C: Mixed Practice
Simplify.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
Translate the following sentences into algebraic expressions and then simplify.
97. What is the difference of and ?
98. Subtract from .
99. Subtract from twice the quantity .
100. Subtract three times the quantity from .
Part D: Discussion Board Topics
101. Do we need a distributive property for division, ? Explain.
102. Do we need a separate distributive property for three terms, ? Explain.
103. Explain how to subtract one expression from another. Give some examples and demonstrate the importance of the order in which subtraction is performed.
104. Given the algebraic expression , explain why subtracting is not the first step.
105. Can you apply the distributive property to the expression ? Explain why or why not and give some examples.
106. How can you check to see if you have simplified an expression correctly? Give some examples.
Answers
1:
3:
5:
7:
9:
11:
13:
15:
17:
19:
21:
23:
25:
27:
29:
31:
33:
35:
37:
39:
41:
43:
45:
47:
49:
51:
53:
55:
57:
59:
61:
63:
65:
67:
69:
71:
73:
75:
77:
79:
81:
83:
85:
87:
89:
91:
93:
95:
97:
99:




