This is “Introduction to Algebra”, section 2.1 from the book Beginning Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
2.1 Introduction to Algebra
Learning Objectives
- Identify an algebraic expression and its parts.
- Evaluate algebraic expressions.
- Use formulas to solve problems in common applications.
Preliminary Definitions
In algebra, letters are used to represent numbers. The letters used to represent these numbers are called variablesLetters or symbols used in algebra to represent numbers.. Combinations of variables and numbers along with mathematical operations form algebraic expressionsCombinations of variables and numbers along with mathematical operations used to generalize specific arithmetic operations., or just expressions. The following are some examples of expressions with one variable, x:
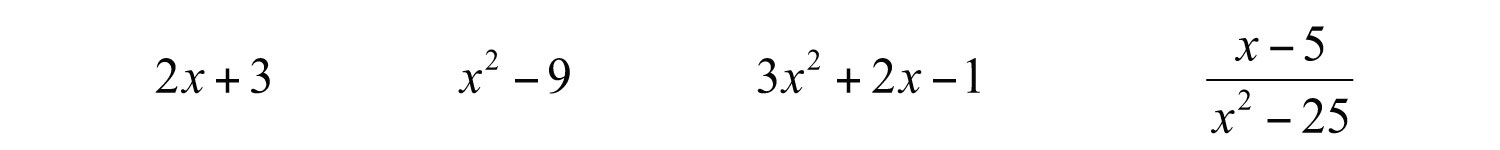
TermsComponents of an algebraic expression separated by addition operators. in an algebraic expression are separated by addition operators, and factorsAny of the numbers or expressions that form a product. are separated by multiplication operators. The numerical factor of a term is called the coefficientThe numerical factor of a term.. For example, the algebraic expression can be thought of as and has three terms. The first term, , represents the quantity , where 3 is the coefficient and x is the variable. All of the variable factors, with their exponents, form the variable part of a termAll the variable factors with their exponents.. If a term is written without a variable factor, then it is called a constant termA term written without a variable factor.. Consider the components of ,
| Terms | Coefficient | Variable Part |
|---|---|---|
| 3 | ||
| 2 | ||
| −1 | −1 |
The third term in this expression, −1, is a constant term because it is written without a variable factor. While a variable represents an unknown quantity and may change, the constant term does not change.
Example 1: List all coefficients and variable parts of each term: .
Solution: Think of the third term in this example, , as .
| Terms | Coefficient | Variable Part |
|---|---|---|
| 5 | ||
| −4 | ||
| −1 |
Answer: Coefficients: ; variable parts:
Some terms, such as and , appear not to have a coefficient. The multiplicative identity property states that 1 times anything is itself and occurs so often that it is customary to omit this factor and write
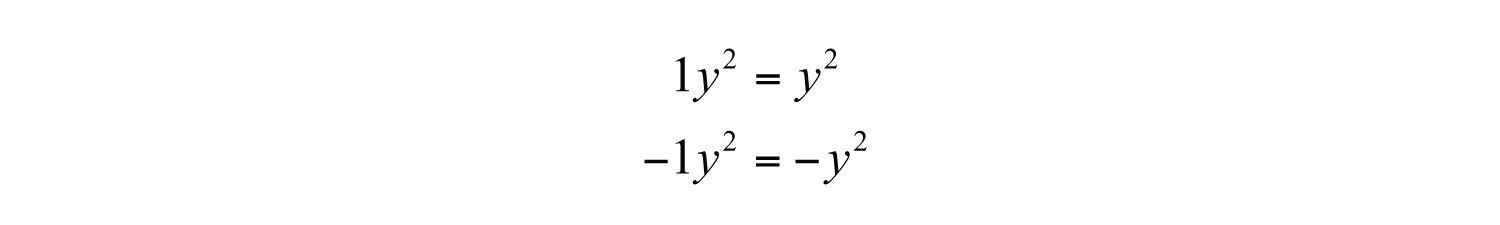
Therefore, the coefficient of is actually 1 and the coefficient of is −1. In addition, you will encounter terms that have variable parts composed of algebraic expressions as factors.
Example 2: List all coefficients and variable parts of each term: .
Solution: This is an expression with two terms:
| Terms | Coefficient | Variable Part |
|---|---|---|
| −3 | ||
| 1 |
Answer: Coefficients: ; variable parts:
In our study of algebra, we will encounter a wide variety of algebraic expressions. Typically, expressions use the two most common variables, x and y. However, expressions may use any letter (or symbol) for a variable, even Greek letters, such as alpha () and beta (). Some letters and symbols are reserved for constants, such as and . Since there is only a limited number of letters, you will also use subscripts, , to indicate different variables.
Try this! List all coefficients and variable parts of the expression: .
Answer: Coefficients: ; variable parts:
Video Solution
(click to see video)Evaluating Algebraic Expressions
Think of an algebraic expression as a generalization of particular arithmetic operations. Performing these operations after substituting given values for variables is called evaluatingThe process of performing the operations of an algebraic expression for given values of the variables.. In algebra, a variable represents an unknown value. However, if the problem specifically assigns a value to a variable, then you can replace that letter with the given number and evaluate using the order of operations.
Example 3: Evaluate:
a. , where
b. , where
Solution: To avoid common errors, it is a best practice to first replace all variables with parentheses and then replace, or substituteThe act of replacing a variable with an equivalent quantity., the given value.
a.
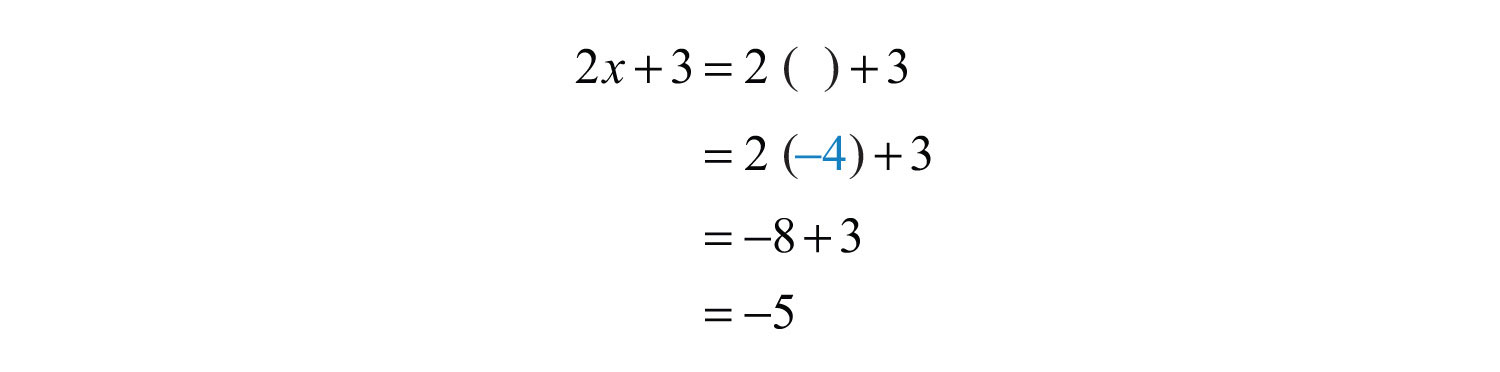
b.
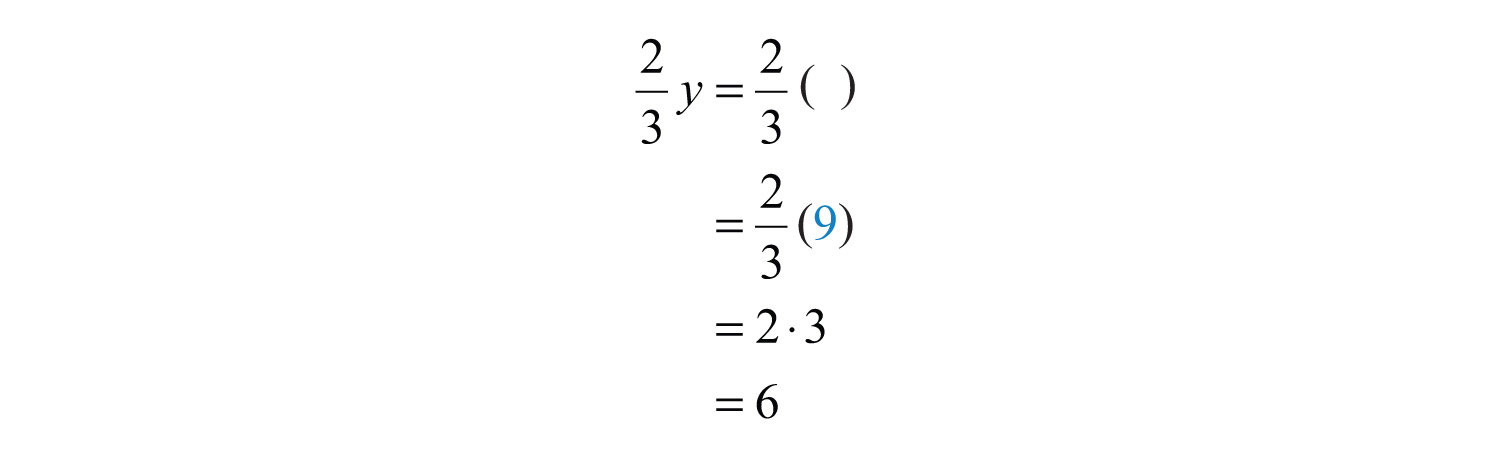
Answers: a. −5; b. 6
If parentheses are not used in part (a) of the previous example, the result is quite different: . Without parentheses, the first operation is subtraction, which leads to an incorrect result.
Example 4: Evaluate: , where and .
Solution: After substituting the given values for the variables, simplify using the order of operations.

Answer: 13
Example 5: Evaluate: , where and .
Solution:
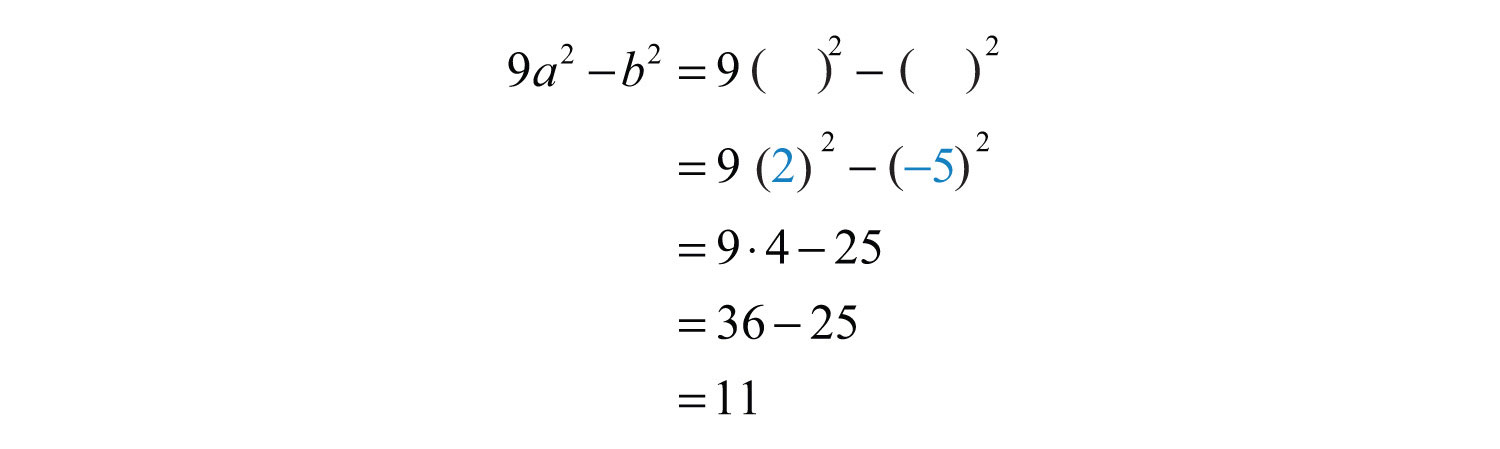
Answer: 11
Example 6: Evaluate: , where .
Solution:
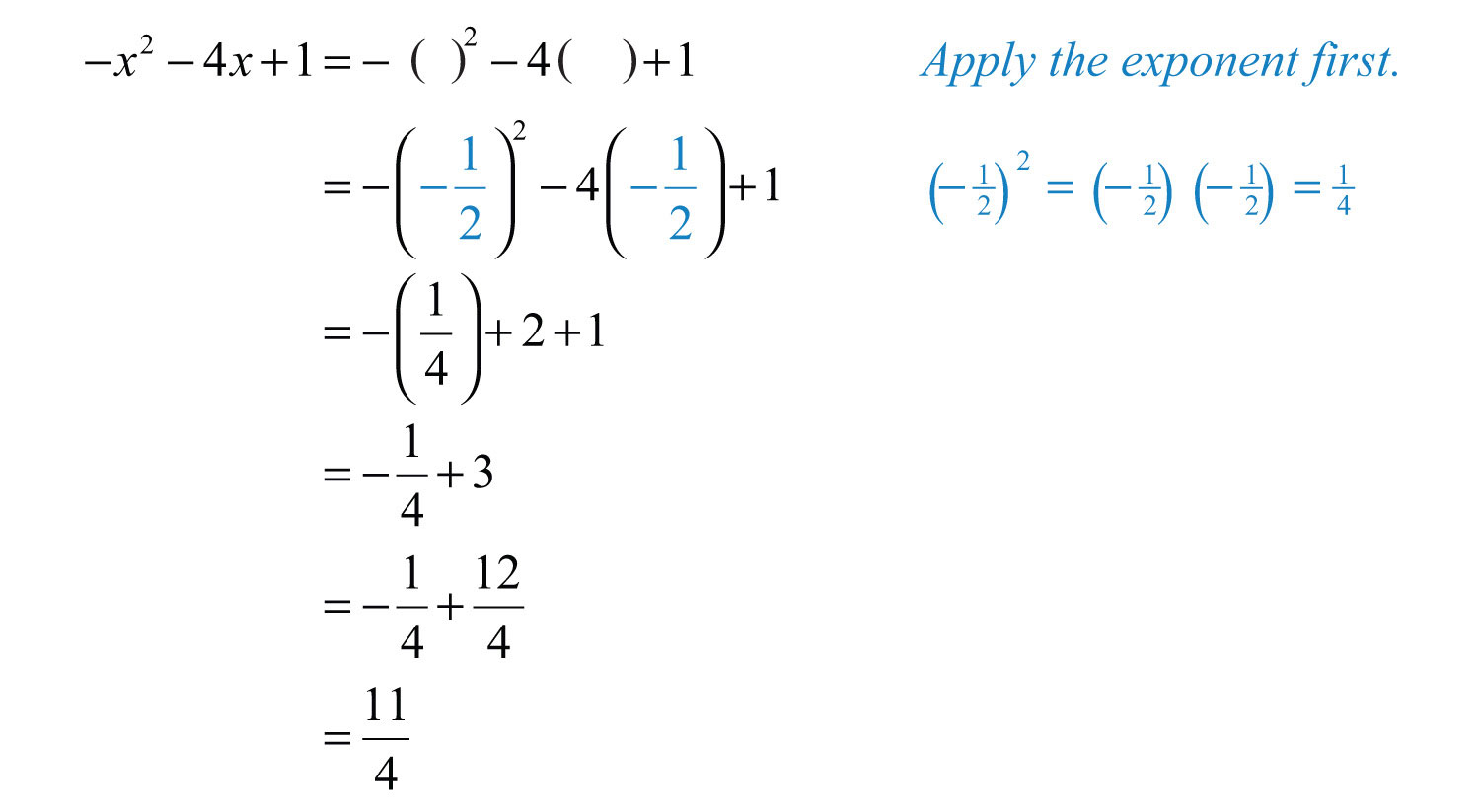
Answer: 11/4
The answer to the previous example is , which can be written as a mixed number . In algebra, improper fractions are generally preferred. Unless the original problem has mixed numbers in it, or it is an answer to a real-world application, solutions will be expressed as reduced improper fractions.
Example 7: Evaluate: , where .
Solution: The order of operations requires us to perform the operations within the parentheses first.
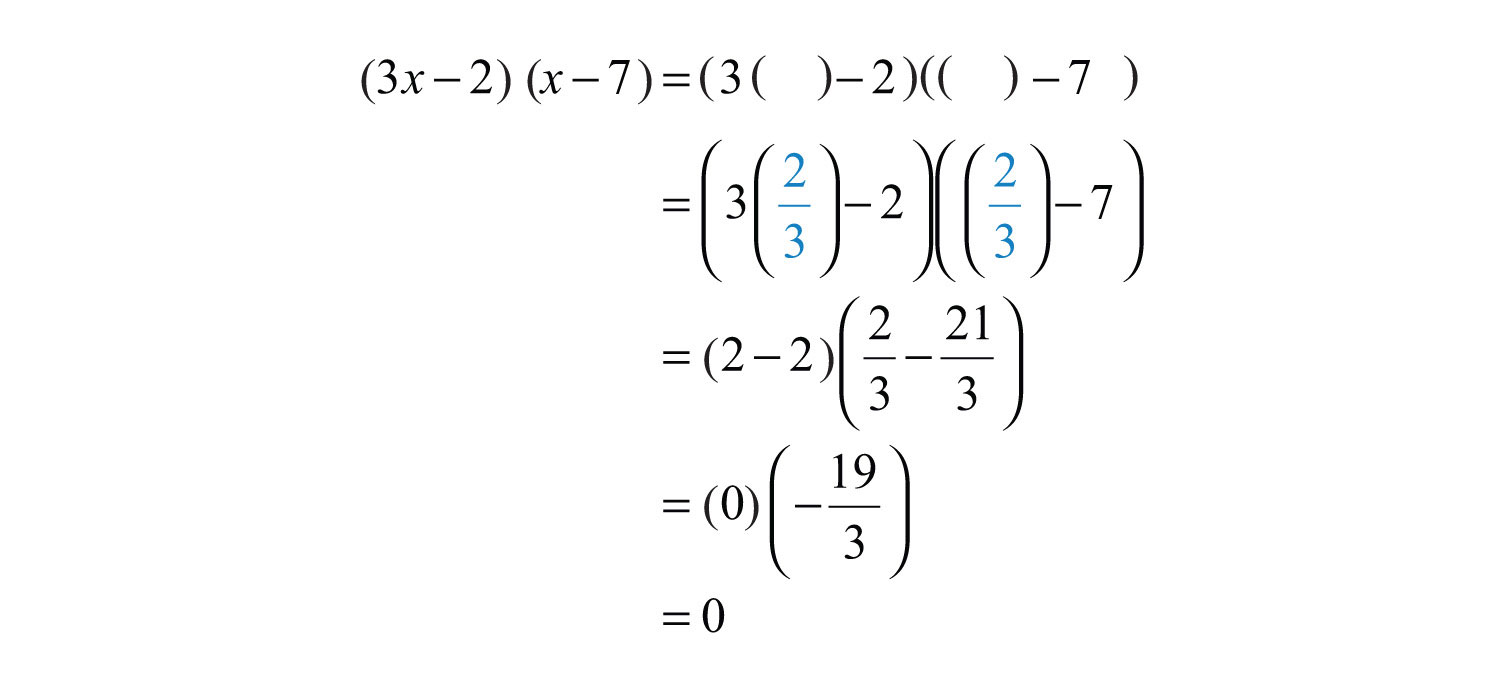
Answer: 0
Example 8: Evaluate: , where , , and .
Solution: The expression is called the discriminantThe algebraic expression .; it is an essential quantity seen later in our study of algebra.
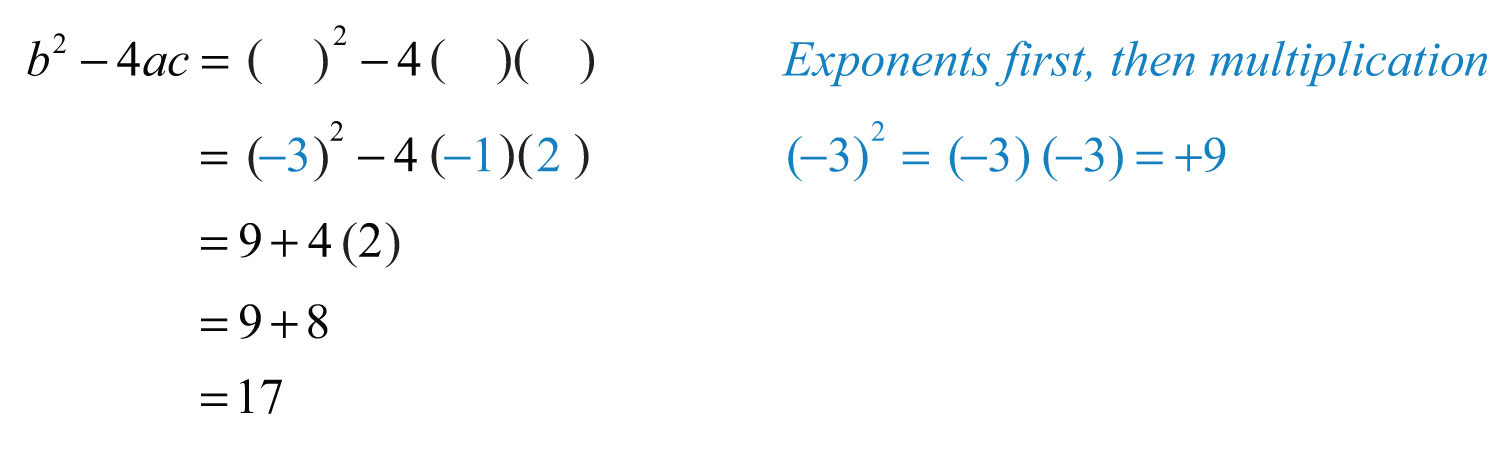
Answer: 17
Try this! Evaluate , where and .
Answer: 35
Video Solution
(click to see video)Using Formulas
The main difference between algebra and arithmetic is the organized use of variables. This idea leads to reusable formulasA reusable mathematical model using algebraic expressions to describe a common application., which are mathematical models using algebraic expressions to describe common applications. For example, the area of a rectangle is modeled by the formula:
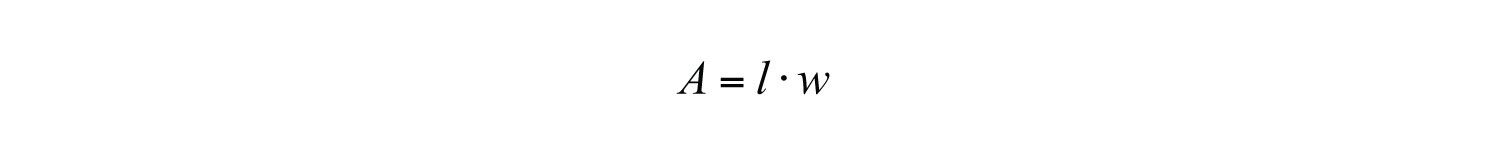
In this equation, variables are used to describe the relationship between the area of a rectangle and the length of its sides. The area is the product of the length and width of the rectangle. If the length of a rectangle measures 3 meters and the width measures 2 meters, then the area can be calculated using the formula as follows:

Example 9: The cost of a daily truck rental is $48.00 plus an additional $0.45 for every mile driven. This cost in dollars can be modeled by the formula , where x represents the number of miles driven in one day. Use this formula to calculate the cost to rent the truck for a day and drive it 120 miles.
Solution: Use the formula to find the cost when the number of miles .
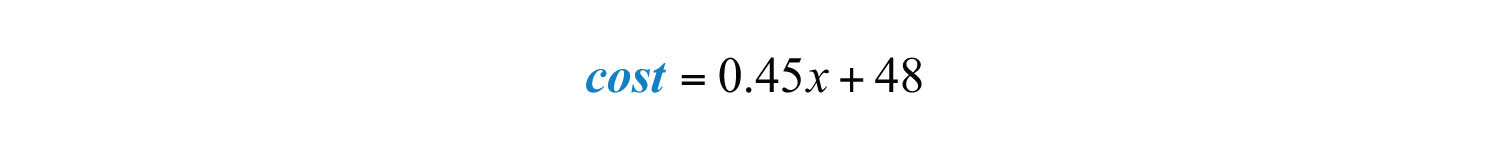
Substitute 120 into the given formula for x and then simplify.
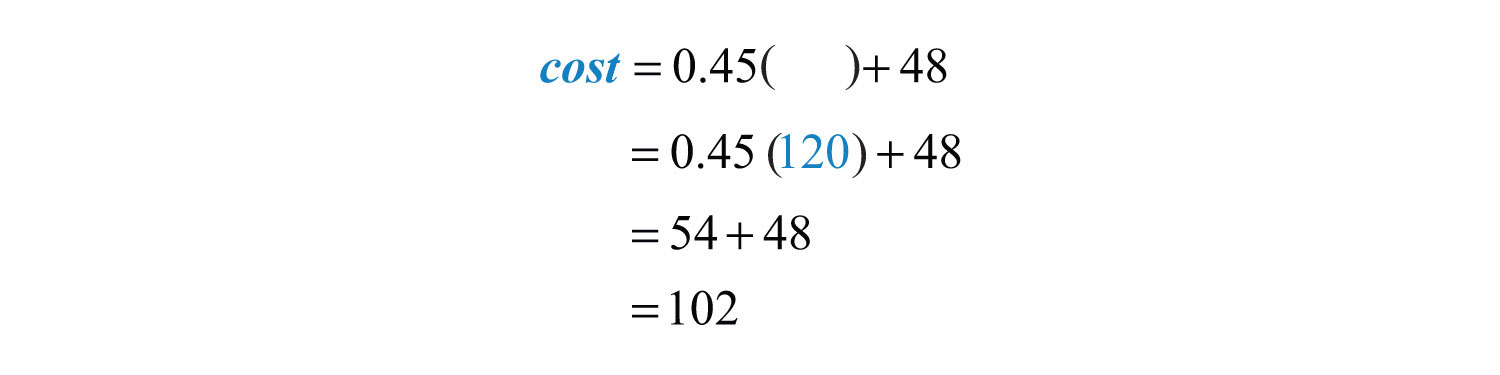
Answer: The rental costs $102.
Uniform motionDescribed by the formula , where the distance D is given as the product of the average rate r and the time t traveled at that rate. is modeled by the formula , which expresses distance D in terms of the average rate r, or speed, and the time t traveled at that rate. This formula, , is used often and is read “distance equals rate times time.”
Example 10: Jim’s road trip takes hours at an average speed of 66 miles per hour. How far does he travel?
Solution: Substitute the appropriate values into the formula and then simplify.
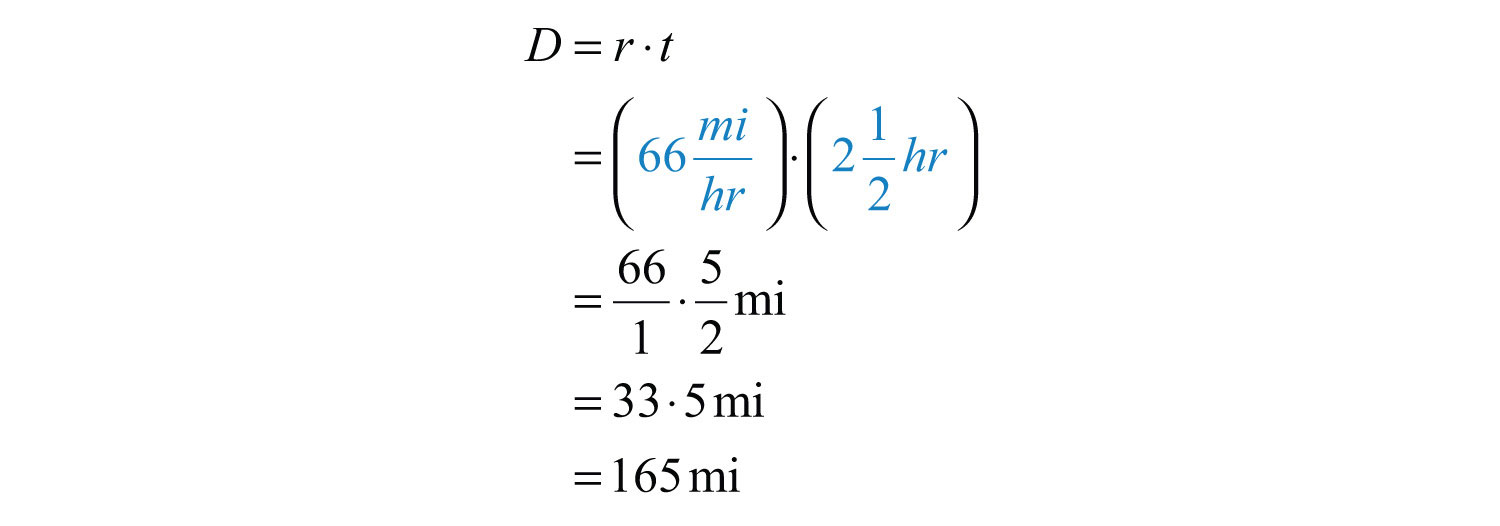
Answer: Jim travels 165 miles.
The volume in cubic units of a rectangular box is given by the formula , where l represents the length, w represents the width, and h represents the height.
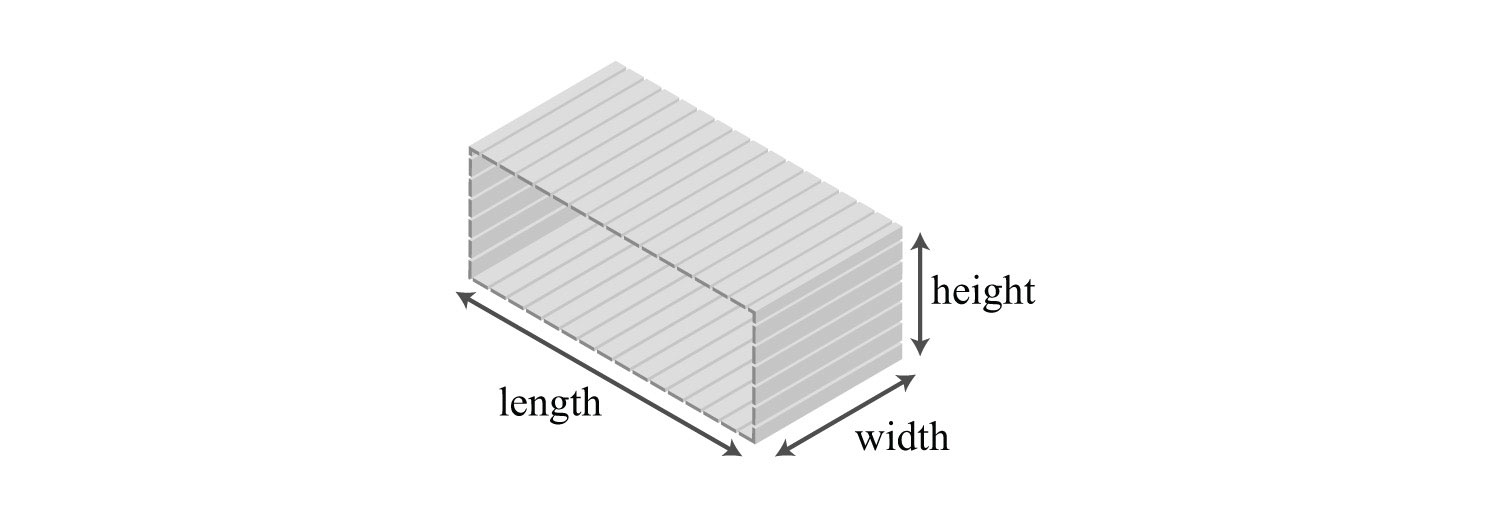
Example 11: A wooden box is 1 foot in length, 5 inches wide, and 6 inches high. Find the volume of the box in cubic inches.
Solution: Take care to ensure that all the units are consistent and use 12 inches for the length instead of 1 foot.

Answer: The volume of the box is 360 cubic inches.
Simple interestModeled by the formula , where p represents the principal amount invested at an annual interest rate r for t years. is given by the formula , where p represents the principal amount invested at an annual interest rate r for t years.
Example 12: Calculate the simple interest earned on a 2-year investment of $1,250 at an annual interest rate of .
Solution: Convert to a decimal number before using it in the formula.
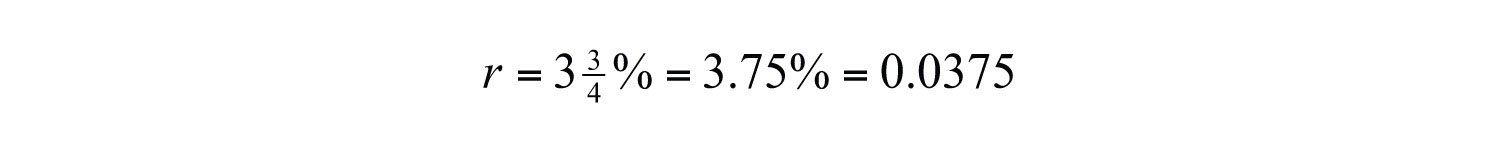
Use this value for r and the fact that p = $1,250 and t = 2 years to calculate the simple interest.

Answer: The simple interest earned is $93.75.
Try this! The perimeter of a rectangle is given by the formula , where l represents the length and w represents the width. Use the formula to calculate the perimeter of a rectangle with a length of 5 feet and a width of feet.
Answer: 15 feet
Video Solution
(click to see video)Key Takeaways
- Think of algebraic expressions as generalizations of common arithmetic operations that are formed by combining numbers, variables, and mathematical operations.
- It is customary to omit the coefficient if it is 1, as in .
- To avoid common errors when evaluating, it is a best practice to replace all variables with parentheses and then substitute the appropriate values.
- The use of algebraic expressions allows us to create useful and reusable formulas that model common applications.
Topic Exercises
Part A: Definitions
List all of the coefficients and variable parts of the following expressions.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Part B: Evaluating Algebraic Expressions
Evaluate.
11. , where
12. , where
13. , where
14. , where
15. , where
16. , where
17. , where
18. , where
19. , where
20. , where
21. , where
22. , where
For each problem below, evaluate , given the following values for a, b, and c.
23. , ,
24. , ,
25. , ,
26. , ,
27. , ,
28. , ,
Evaluate.
29. , where and
30. , where and
31. , where and .
32. , where and
33. , where and
34. , where
35. , where
36. , where
37. , where
38. , where
39. , where and
40. , where and
41. Evaluate , given and .
42. Evaluate , given and .
43. Evaluate , given and .
44. Evaluate , given and .
Part C: Using Formulas
Convert the following temperatures to degrees Celsius given , where F represents degrees Fahrenheit.
45. 86°F
46. 95°F
47. −13°F
48. 14°F
49. 32°F
50. 0°F
Given the base and height of a triangle, calculate the area. ()
51. centimeters and centimeters
52. inches and inches
53. foot and feet
54. inches and inches
55. A certain cellular phone plan charges $23.00 per month plus $0.09 for each minute of usage. The monthly charge is given by the formula , where x represents the number of minutes of usage per month. What is the charge for a month with 5 hours of usage?
56. A taxi service charges $3.75 plus $1.15 per mile given by the formula , where x represents the number of miles driven. What is the charge for a 17-mile ride?
57. If a calculator is sold for $14.95, then the revenue in dollars, R, generated by this item is given by the formula , where q represents the number of calculators sold. Use the formula to determine the revenue generated by this item if 35 calculators are sold.
58. Yearly subscriptions to a tutoring website can be sold for $49.95. The revenue in dollars, R, generated by subscription sales is given by the formula , where q represents the number of yearly subscriptions sold. Use the formula to calculate the revenue generated by selling 250 subscriptions.
59. The cost of producing pens with the company logo printed on them consists of a onetime setup fee of $175 plus $0.85 for each pen produced. This cost can be calculated using the formula , where q represents the number of pens produced. Use the formula to calculate the cost of producing 2,000 pens.
60. The cost of producing a subscription website consists of an initial programming and setup fee of $4,500 plus a monthly Web hosting fee of $29.95. The cost of creating and hosting the website can be calculated using the formula , where n represents the number of months the website is hosted. How much will it cost to set up and host the website for 1 year?
61. The perimeter of a rectangle is given by the formula , where l represents the length and w represents the width. What is the perimeter of a fenced-in rectangular yard measuring 70 feet by 100 feet?
62. Calculate the perimeter of an 8-by-10-inch picture.
63. Calculate the perimeter of a room that measures 12 feet by 18 feet.
64. A computer monitor measures 57.3 centimeters in length and 40.9 centimeters high. Calculate the perimeter.
65. The formula for the area of a rectangle in square units is given by , where l represents the length and w represents the width. Use this formula to calculate the area of a rectangle with length 12 centimeters and width 3 centimeters.
66. Calculate the area of an 8-by-12-inch picture.
67. Calculate the area of a room that measures 12 feet by 18 feet.
68. A computer monitor measures 57.3 centimeters in length and 40.9 centimeters in height. Calculate the total area of the screen.
69. A concrete slab is poured in the shape of a rectangle for a shed measuring 8 feet by 10 feet. Determine the area and perimeter of the slab.
70. Each side of a square deck measures 8 feet. Determine the area and perimeter of the deck.
71. The volume of a rectangular solid is given by , where l represents the length, w represents the width, and h is the height of the solid. Find the volume of a rectangular solid if the length is 2 inches, the width is 3 inches, and the height is 4 inches.
72. If a trunk measures 3 feet by 2 feet and is 2½ feet tall, then what is the volume of the trunk?
73. The interior of an industrial freezer measures 3 feet wide by 3 feet deep and 4 feet high. What is the volume of the freezer?
74. A laptop case measures 1 feet 2 inches by 10 inches by 2 inches. What is the volume of the case?
75. If the trip from Fresno to Sacramento can be made by car in 2½ hours at an average speed of 67 miles per hour, then how far is Sacramento from Fresno?
76. A high-speed train averages 170 miles per hour. How far can it travel in 1½ hours?
77. A jumbo jet can cruises at an average speed of 550 miles per hour. How far can it travel in 4 hours?
78. A fighter jet reaches a top speed of 1,316 miles per hour. How far will the jet travel if it can sustain this speed for 15 minutes?
79. The Hubble Space Telescope is in low earth orbit traveling at an average speed of 16,950 miles per hour. What distance does it travel in 1½ hours?
80. Earth orbits the sun a speed of about 66,600 miles per hour. How far does earth travel around the sun in 1 day?
81. Calculate the simple interest earned on a $2,500 investment at 3% annual interest rate for 4 years.
82. Calculate the simple interest earned on a $1,000 investment at 5% annual interest rate for 20 years.
83. How much simple interest is earned on a $3,200 investment at a 2.4% annual interest for 1 year?
84. How much simple interest is earned on a $500 investment at a 5.9% annual interest rate for 3 years?
85. Calculate the simple interest earned on a $10,500 investment at a annual interest rate for 4 years.
86. Calculate the simple interest earned on a $6,250 investment at a annual interest rate for 1 year.
Part D: Discussion Board Topics
87. Research and discuss the history of the symbols for addition (+) and subtraction (−).
88. What are mathematical models and why are they useful in everyday life?
89. Find and post a useful formula. Demonstrate its use with some values.
90. Discuss the history and importance of the variable. How can you denote a variable when you run out of letters?
91. Find and post a useful resource describing the Greek alphabet.
Answers
1: Coefficients: ; variable parts:
3: Coefficients: ; variable parts:
5: Coefficients: ; variable parts:
7: Coefficients: ; variable parts:
9: Coefficients: ; variable parts:
11: −1
13: 0
15: 24
17: 90
19: 5/3
21: 5/2
23: −8
25: −48
27: 19/12
29: 48
31: −5
33: 0
35: −6
37: 6
39: −17
41: 20.04
43: 1.32
45: 30°C
47: −25°C
49: 0°C
51: 125 square centimeters
53: 1/2 square feet
55: $50
57: $523.25
59: $1,875.00
61: 340 feet
63: 60 feet
65: 36 square centimeters
67: 216 square feet
69: Area: 80 square feet; Perimeter: 36 feet
71: 24 cubic inches
73: 36 cubic feet
75: 167.5 miles
77: 2,200 miles
79: 25,425 miles
81: $300
83: $76.80
85: $1,785




