This is “Solving Linear Equations: Part I”, section 2.3 from the book Beginning Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
2.3 Solving Linear Equations: Part I
Learning Objectives
- Identify linear equations with one variable and verify their solutions.
- Use the properties of equality to solve basic linear equations.
- Use multiple steps to solve linear equations by isolating the variable.
- Solve linear equations where the coefficients are fractions or decimals.
Linear Equations with One Variable and Their Solutions
Learning how to solve various algebraic equations is one of the main goals in algebra. This section introduces the basic techniques used for solving linear equations with one variable.
An equationStatement indicating that two algebraic expressions are equal. is a statement indicating that two algebraic expressions are equal. A linear equation with one variableAn equation that can be written in the general form , where a and b are real numbers and ., x, is an equation that can be written in the general form , where a and b are real numbers and . Here are some examples of linear equations, all of which are solved in this section:
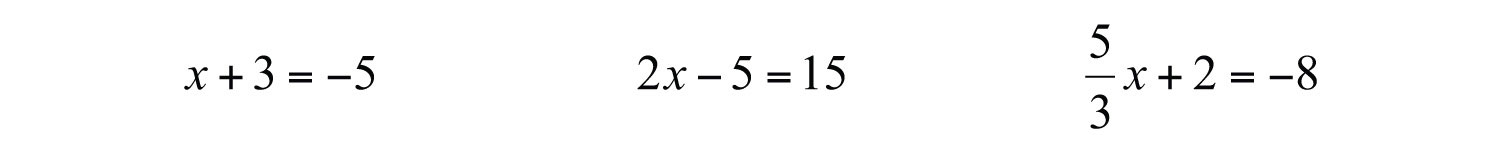
A solutionAny value that can replace the variable in an equation to produce a true statement. to a linear equation is any value that can replace the variable to produce a true statement. The variable in the linear equation is x, and the solution is . To verify this, substitute the value 5 for x and check that you obtain a true statement.

Alternatively, when an equation is equal to a constant, we can verify a solution by substituting the value for the variable and show that the result is equal to that constant. In this sense, we say that solutions satisfy the equationAfter replacing the variable with a solution and simplifying, it produces a true statement..
Example 1: Is a solution to ?
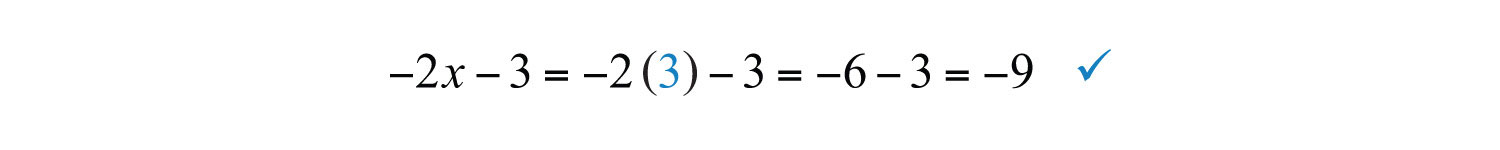
Answer: Yes, it is a solution, because satisfies the equation.
Example 2: Is a solution to ?
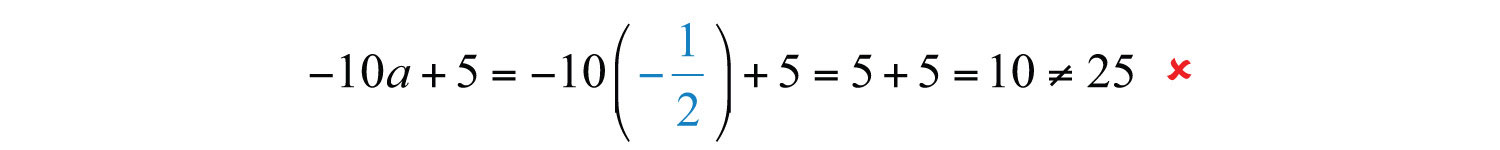
Answer: No, it is not a solution, because does not satisfy the equation.
Recall that when evaluating expressions, it is a good practice to first replace all variables with parentheses, then substitute the appropriate values. By making use of parentheses we avoid some common errors when working the order of operations.
Example 3: Is a solution to ?
Solution:

Answer: Yes, it is a solution, because produces a true statement.
Try this! Is a solution to ?
Answer: No
Video Solution
(click to see video)Solving Basic Linear Equations
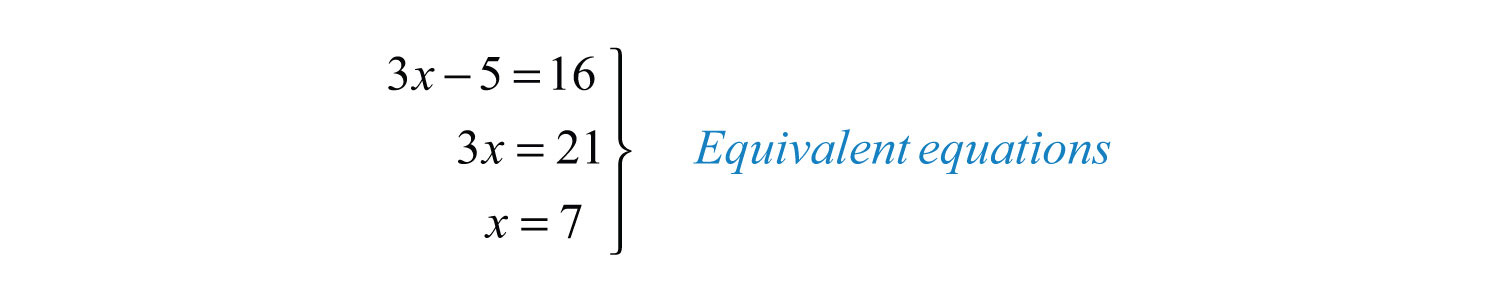
We begin by defining equivalent equationsEquations with the same solution set. as equations with the same solution set. Consider the following two linear equations and check to see if the solution is .

Here we can see that the two linear equations and are equivalent because they share the same solution set, namely, {7}. The goal is to develop a systematic process to find equivalent equations until the variable is isolated:
To do this, use the properties of equalityProperties that allow us to obtain equivalent equations by adding, subtracting, multiplying, and dividing both sides of an equation by nonzero real numbers.. Given algebraic expressions A and B, where c is a real number, we have the following:
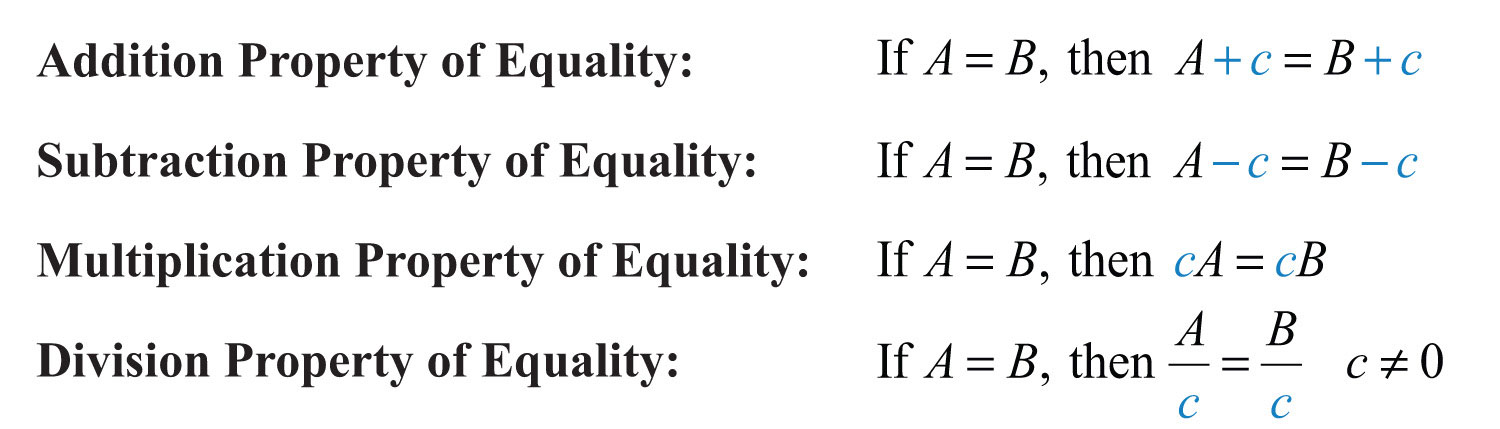
Note
Multiplying or dividing both sides of an equation by 0 is carefully avoided. Dividing by 0 is undefined and multiplying both sides by 0 results in the equation 0 = 0.

To summarize, equality is retained and you obtain an equivalent equation if you add, subtract, multiply, or divide both sides of an equation by any nonzero real number. The technique for solving linear equations involves applying these properties in order to isolate the variable on one side of the equation. If the linear equation has a constant term, then we add to or subtract it from both sides of the equation to obtain an equivalent equation where the variable term is isolated.
Example 4: Solve: .
Solution: To isolate the variable x on the left side, subtract 3 from both sides.

Answer: The solution is . To check that this is true, substitute −8 into the original equation and simplify to see that it is satisfied: ✓.
In the previous example, after subtracting 3 from both sides, you get . By the additive identity property of real numbers, this is equivalent to . This step is often left out in the presentation of the solution.
If the variable term of the equation (including the coefficient) is isolated, then apply the multiplication or division property of equality to obtain an equivalent equation with the variable isolated. In other words, our goal is to obtain an equivalent equation with x or 1x isolated on one side of the equal sign.
Example 5: Solve: .
Solution: The coefficient of x is –5, so divide both sides by −5.
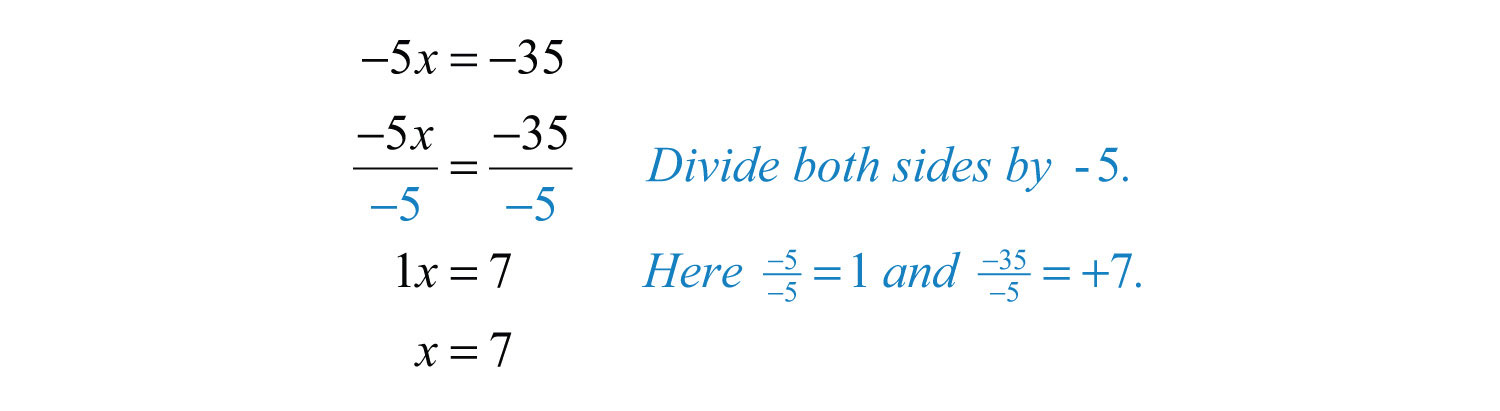
Answer: The solution is . Perform the check mentally by substituting 7 for x in the original equation.
In the previous example, after dividing both sides by −5, x is left with a coefficient of 1, because . In fact, when we say “isolate the variable,” we mean to change the coefficient of the variable to 1, because is equivalent to . This step is often left out of the instructional examples even though its omission is sometimes a source of confusion.
Another important property is the symmetric propertyAllows you to solve for the variable on either side of the equal sign, because is equivalent to .: for any algebraic expressions A and B,
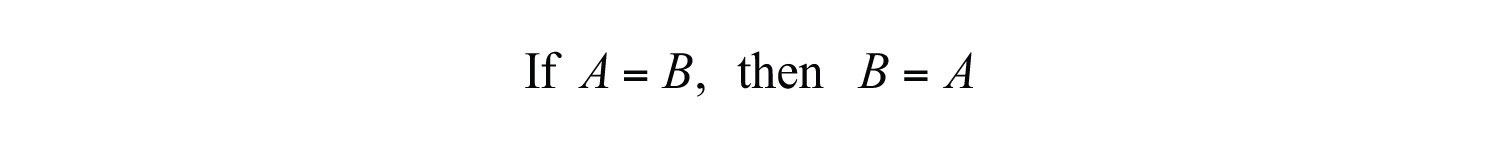
The equation is equivalent to . It does not matter on which side we choose to isolate the variable.
Example 6: Solve: .
Solution: Isolate the variable x by subtracting 5 from both sides of the equation.

Answer: The solution is −3, and checking the solution shows that 2 = 5 − 3.
Try this! Solve: .
Answer:
Video Solution
(click to see video)Isolating the Variable in Two Steps
A linear equation of the form takes two steps to solve. First, use the appropriate equality property of addition or subtraction to isolate the variable term. Next, isolate the variable using the equality property of multiplication or division. Checking solutions in the following examples is left to the reader.
Example 7: Solve: .
Solution:

Answer: The solution is 10.
Example 8: Solve: .
Solution:
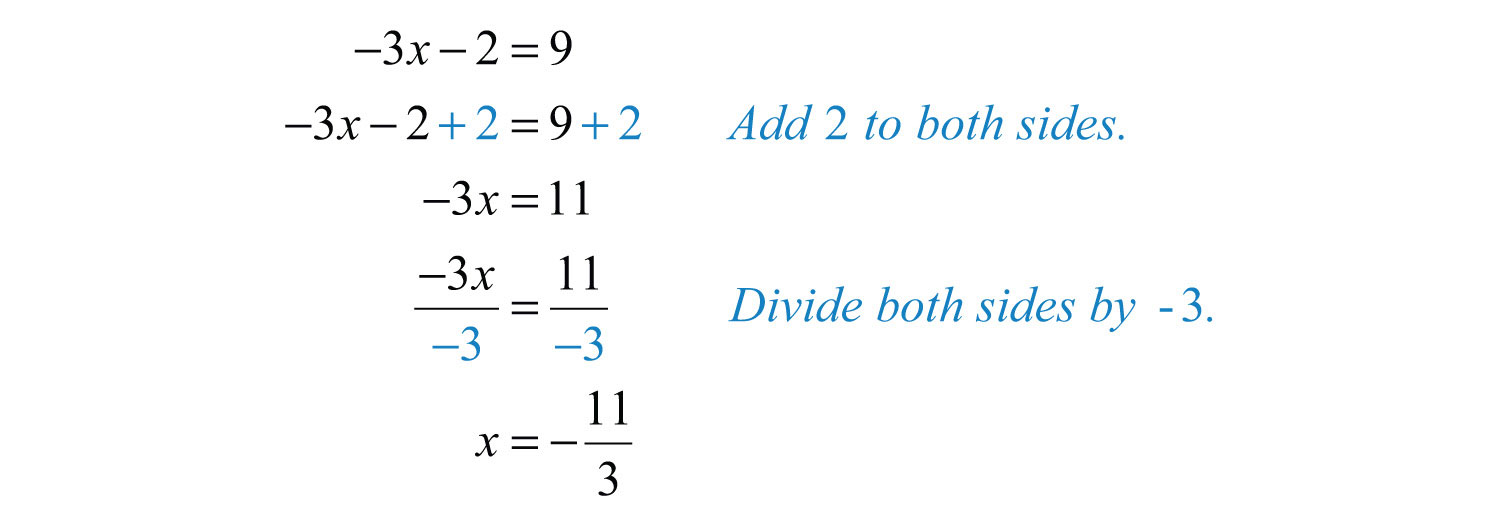
Answer: The solution is .
Example 9: Solve: .
Solution: When no sign precedes the term, it is understood to be positive. In other words, think of this as . Begin by subtracting 6 from both sides of the equal sign.

Answer: The solution is 4.
Example 10: Solve: .
Solution:

Answer: The solution is .
Example 11: Solve: .
Solution:
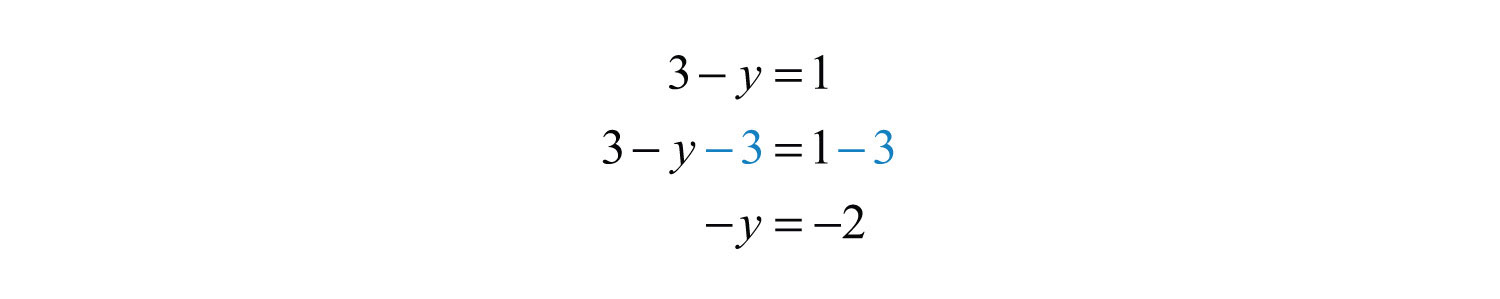
Recall that is equivalent to ; divide both sides of the equation by −1.
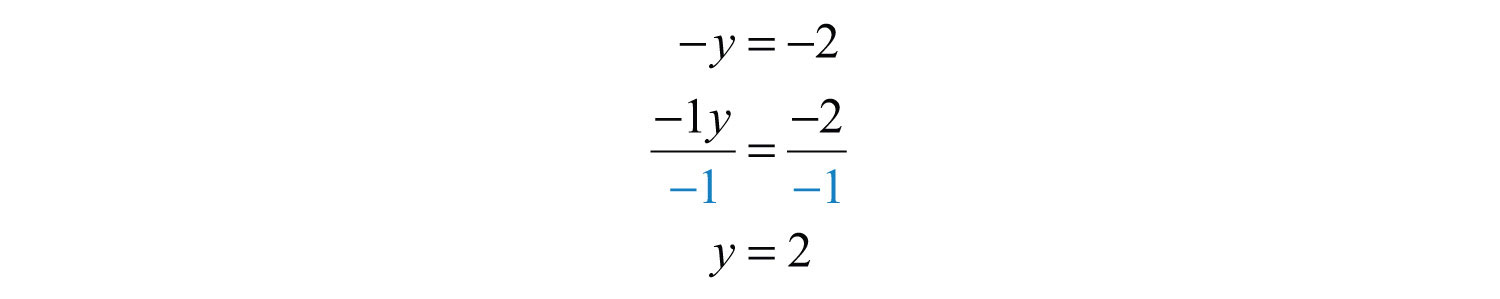
Alternatively, multiply both sides of by −1 and achieve the same result:
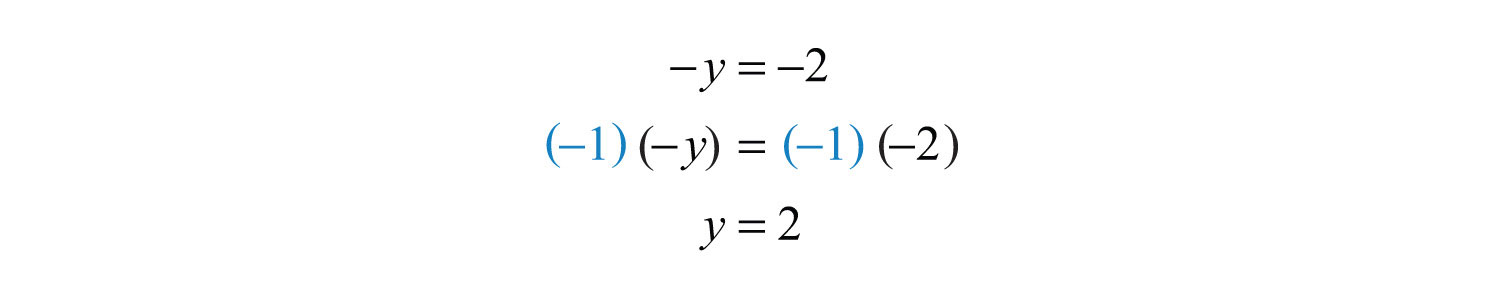
Answer: The solution is 2.
In summary, to retain equivalent equations, we must perform the same operation on both sides of the equation. First, apply the addition or subtraction property of equality to isolate the variable term and then apply the multiplication or division property of equality to isolate the variable on one side of the equation.
Try this! Solve: .
Answer:
Video Solution
(click to see video)Multiplying by the Reciprocal
To solve an equation like , we can isolate the variable by dividing both sides by the coefficient. For example,
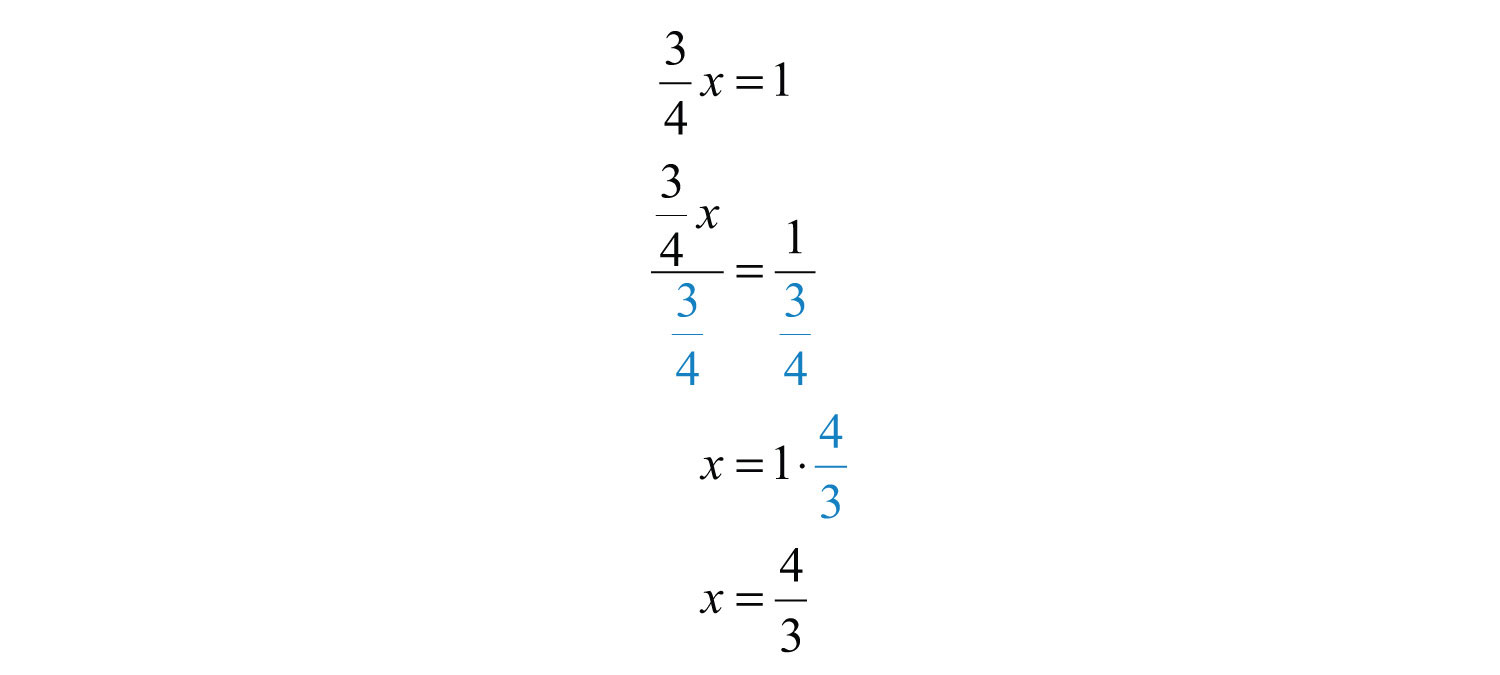
On the left side of the equal sign, the fraction cancels. On the right side, we have a complex fraction and multiply by the reciprocal of the coefficient. You can save a step by recognizing this and start by multiplying both sides of the equation by the reciprocal of the coefficient.
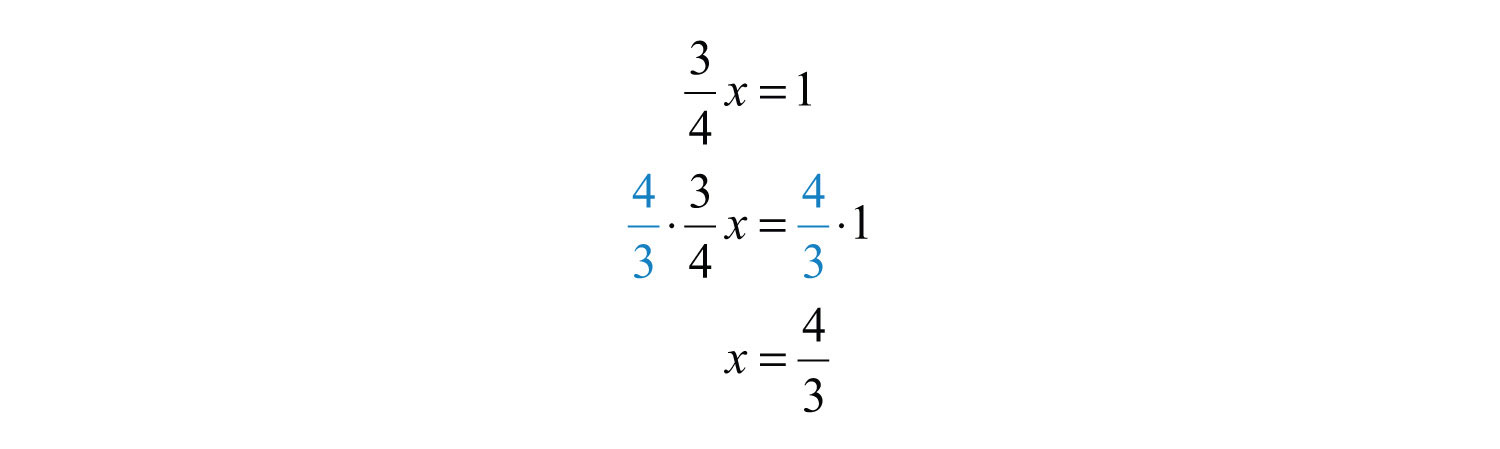
Recall that the product of reciprocals is 1, in this case , leaving the variable isolated.
Example 12: Solve: .
Solution: Isolate the variable term using the addition property of equality and then multiply both sides of the equation by the reciprocal of the coefficient .

Answer: The solution is −6.
Example 13: Solve: .
Solution:
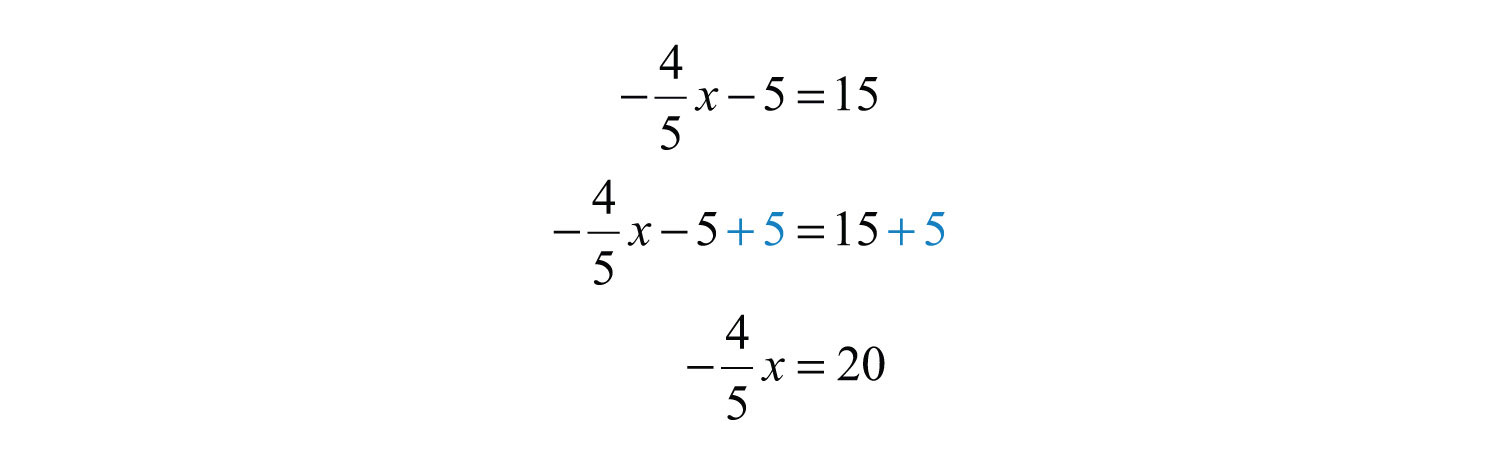
The reciprocal of is because . Therefore, to isolate the variable x, multiply both sides by .
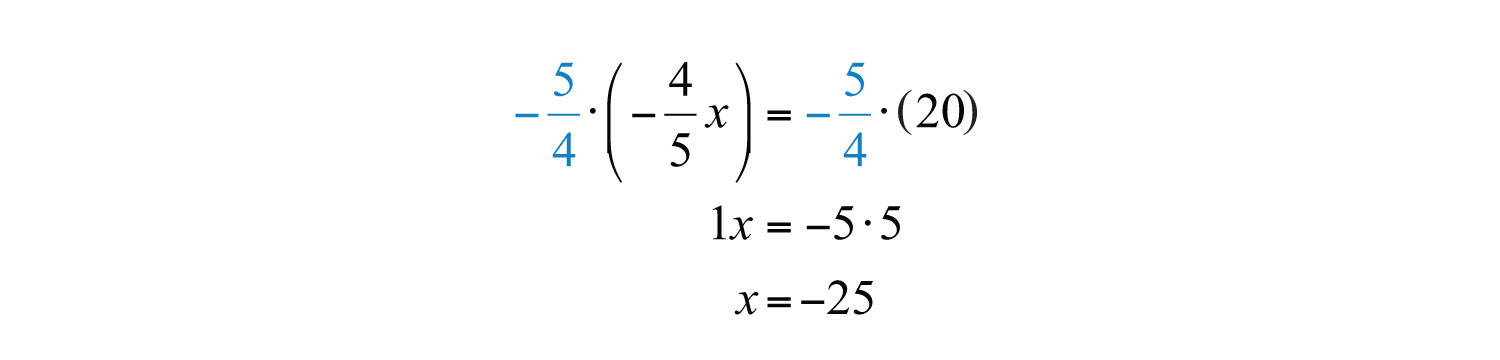
Answer: The solution is −25.
Try this! Solve: .
Answer:
Video Solution
(click to see video)Key Takeaways
- Linear equations with one variable can be written in the form , where a and b are real numbers and .
- To “solve a linear equation” means to find a numerical value that can replace the variable and produce a true statement.
- The properties of equality provide tools for isolating the variable and solving equations.
- To solve a linear equation, first isolate the variable term by adding the opposite of the constant term to both sides of the equation. Then isolate the variable by dividing both sides of the equation by its coefficient.
- After isolating a variable term with a fraction coefficient, solve by multiplying both sides by the reciprocal of the coefficient.
Topic Exercises
Part A: Solutions to Linear Equations
Is the given value a solution to the linear equation?
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13. ;
14. ;
Part B: Solving Basic Linear Equations
Solve.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
Part C: Solving Linear Equations
Solve.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
Translate the following sentences into linear equations and then solve.
73. The sum of 2x and 5 is equal to 15.
74. The sum of −3x and 7 is equal to 14.
75. The difference of 5x and 6 is equal to 4.
76. Twelve times x is equal to 36.
77. A number n divided by 8 is 5.
78. Six subtracted from two times a number x is 12.
79. Four added to three times a number n is 25.
80. Three-fourths of a number x is 9.
81. Negative two-thirds times a number x is equal to 20.
82. One-half of a number x plus 3 is equal to 10.
Find a linear equation of the form with the given solution, where a and b are integers. (Answers may vary.)
83.
84.
85.
86.
Part D: Discussion Board Topics
87. How many steps are needed to solve any equation of the form ? Explain.
88. Instead of dividing by 6 when , could you multiply by the reciprocal of 6? Does this always work?
Answers
1: Yes
3: No
5: Yes
7: Yes
9: Yes
11: Yes
13: Yes
15: 10
17: 18
19: 5/6
21: 5/6
23: −11
25: −13
27: 0
29: 3/2
31: −7
33: −3/2
35: −3/14
37: −3/2
39: 5
41: 10
43: 1/3
45: 1/5
47: 2
49: 14.2
51: 7
53: −5/2
55: 7/5
57: 1/8
59: 1/3
61: −9
63: −125
65: 6
67: −12
69: 5.3
71: 1/16
73: ;
75: ;
77: ;
79: ;
81: ;
83:
85:




