This is “Binomial Theorem”, section 9.4 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
9.4 Binomial Theorem
Learning Objectives
- Evaluate expressions involving factorials.
- Calculate binomial coefficients.
- Expand powers of binomials using the binomial theorem.
Factorials and the Binomial Coefficient
We begin by defining the factorialThe product of all natural numbers less than or equal to a given natural number, denoted n!. of a natural number n, denoted n!, as the product of all natural numbers less than or equal to n.
For example,
We define zero factorialThe factorial of zero is defined to be equal to 1; to be equal to 1,
The factorial of a negative number is not defined.
Note: On most modern calculators you will find a factorial function. Some calculators do not provide a button dedicated to it. However, it usually can be found in the menu system if one is provided.
The factorial can also be expressed using the following recurrence relation,
For example, the factorial of 8 can be expressed as the product of 8 and 7!:
When working with ratios involving factorials, it is often the case that many of the factors cancel.
Example 1
Evaluate: .
Solution:
Answer: 665,280
The binomial coefficientAn integer that is calculated using the formula: , denoted , is read “n choose k” and is given by the following formula:
This formula is very important in a branch of mathematics called combinatorics. It gives the number of ways k elements can be chosen from a set of n elements where order does not matter. In this section, we are concerned with the ability to calculate this quantity.
Example 2
Calculate: .
Solution:
Use the formula for the binomial coefficent,
where and After substituting, look for factors to cancel.
Answer: 35
Note: Check the menu system of your calculator for a function that calculates this quantity. Look for the notation in the probability subsection.
Consider the following binomial raised to the 3rd power in its expanded form:
Compare it to the following calculations,
Notice that there appears to be a connection between these calculations and the coefficients of the expanded binomial. This observation is generalized in the next section.
Binomial Theorem
Consider expanding :
One quickly realizes that this is a very tedious calculation involving multiple applications of the distributive property. The binomial theoremDescribes the algebraic expansion of binomials raised to powers: provides a method of expanding binomials raised to powers without directly multiplying each factor:
More compactly we can write,
Example 3
Expand using the binomial theorem:
Solution:
Use the binomial theorem where and
Sometimes it is helpful to identify the pattern that results from applying the binomial theorem. Notice that powers of the variable x start at 5 and decrease to zero. The powers of the constant term start at 0 and increase to 5. The binomial coefficents can be calculated off to the side and are left to the reader as an exercise.
Answer:
The binomial may have negative terms, in which case we will obtain an alternating series.
Example 4
Expand using the binomial theorem:
Solution:
Use the binomial theorem where , , and and then simplify each term.
Answer:
Next we study the coefficients of the expansions of starting with :
Write the coefficients in a triangular array and note that each number below is the sum of the two numbers above it, always leaving a 1 on either end.

This is Pascal’s triangleA triangular array of numbers that correspond to the binomial coefficients.; it provides a quick method for calculating the binomial coefficients. Use this in conjunction with the binomial theorem to streamline the process of expanding binomials raised to powers. For example, to expand we would need two more rows of Pascal’s triangle,
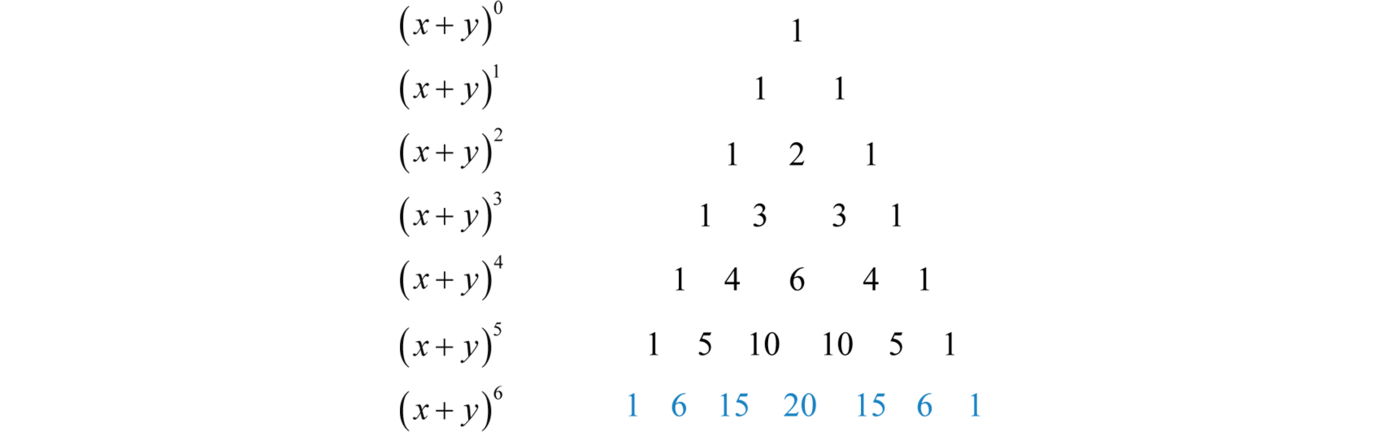
The binomial coefficients that we need are in blue. Use these numbers and the binomial theorem to quickly expand as follows:
Example 5
Expand using the binomial theorem and Pascal’s triangle:
Solution:
From Pascal’s triangle we can see that when the binomial coefficients are 1, 4, 6, 4, and 1. Use these numbers and the binomial theorem as follows:
Answer:
Key Takeaways
- To calculate the factorial of a natural number, multiply that number by all natural numbers less than it: Remember that we have defined
- The binomial coefficients are the integers calculated using the formula: .
- The binomial theorem provides a method for expanding binomials raised to powers without directly multiplying each factor: .
- Use Pascal’s triangle to quickly determine the binomial coefficients.
Topic Exercises
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
13
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Part A: Factorials and the Binomial Coefficient
Evaluate.
Rewrite using factorial notation.
Calculate the indicated binomial coefficient.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
,
-
,
-
-
-
-
-
-
Part B: Binomial Theorem
Expand using the binomial theorem.
-
Determine the factorials of the integers 5, 10, 15, 20, and 25. Which grows faster, the common exponential function or the factorial function ? Explain.
-
Research and discuss the history of the binomial theorem.
Part C: Discussion Board
Answers
-
720
-
-
3,628,800
-
-
120
-
-
17,160
-
-
15,840
-
-
-
-
- 30
- 5,040
-
-
-
-
-
-
-
-
-
-
15
-
-
21
-
-
1
-
-
1
-
-
-
-
45
-
-
1
-
-
-
-
Answer may vary
-




