This is “Geometric Sequences and Series”, section 9.3 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
9.3 Geometric Sequences and Series
Learning Objectives
- Identify the common ratio of a geometric sequence.
- Find a formula for the general term of a geometric sequence.
- Calculate the nth partial sum of a geometric sequence.
- Calculate the sum of an infinite geometric series when it exists.
Geometric Sequences
A geometric sequenceA sequence of numbers where each successive number is the product of the previous number and some constant r., or geometric progressionUsed when referring to a geometric sequence., is a sequence of numbers where each successive number is the product of the previous number and some constant r.
And because , the constant factor r is called the common ratioThe constant r that is obtained from dividing any two successive terms of a geometric sequence; . For example, the following is a geometric sequence,
Here and the ratio between any two successive terms is 3. We can construct the general term where,
In general, given the first term and the common ratio r of a geometric sequence we can write the following:
From this we see that any geometric sequence can be written in terms of its first element, its common ratio, and the index as follows:
In fact, any general term that is exponential in n is a geometric sequence.
Example 1
Find an equation for the general term of the given geometric sequence and use it to calculate its 10th term:
Solution:
Begin by finding the common ratio,
Note that the ratio between any two successive terms is 2. The sequence is indeed a geometric progression where and
Therefore, we can write the general term and the 10th term can be calculated as follows:
Answer: ;
The terms between given terms of a geometric sequence are called geometric meansThe terms between given terms of a geometric sequence..
Example 2
Find all terms between and of a geometric sequence. In other words, find all geometric means between the 1st and 4th terms.
Solution:
Begin by finding the common ratio r. In this case, we are given the first and fourth terms:
Substitute and into the above equation and then solve for r.
Next use the first term and the common ratio to find an equation for the nth term of the sequence.
Now we can use where n is a positive integer to determine the missing terms.
Answer: −15, −45,
The first term of a geometric sequence may not be given.
Example 3
Find the general term of a geometric sequence where and
Solution:
To determine a formula for the general term we need and A nonlinear system with these as variables can be formed using the given information and :
Solve for in the first equation,
Substitute into the second equation and solve for r.
Back substitute to find :
Therefore, and
Answer:
Try this! Find an equation for the general term of the given geometric sequence and use it to calculate its 6th term:
Answer: ;
Geometric Series
A geometric seriesThe sum of the terms of a geometric sequence. is the sum of the terms of a geometric sequence. For example, the sum of the first 5 terms of the geometric sequence defined by follows:
Adding 5 positive integers is managable. However, the task of adding a large number of terms is not. Therefore, we next develop a formula that can be used to calculate the sum of the first n terms of any geometric sequence. In general,
Multiplying both sides by r we can write,
Subtracting these two equations we then obtain,
Assuming dividing both sides by leads us to the formula for the nth partial sum of a geometric sequenceThe sum of the first n terms of a geometric sequence, given by the formula: , :
In other words, the nth partial sum of any geometric sequence can be calculated using the first term and the common ratio. For example, to calculate the sum of the first 15 terms of the geometric sequence defined by , use the formula with and
Example 4
Find the sum of the first 10 terms of the given sequence: 4, −8, 16, −32, 64,…
Solution:
Determine whether or not there is a common ratio between the given terms.
Note that the ratio between any two successive terms is −2; hence, the given sequence is a geometric sequence. Use and the fact that to calculate the sum of the first 10 terms,
Answer:
Example 5
Evaluate: .
Solution:
In this case, we are asked to find the sum of the first 6 terms of a geometric sequence with general term Use this to determine the 1st term and the common ratio r:
To show that there is a common ratio we can use successive terms in general as follows:
Use and to calculate the 6th partial sum.
Answer: 26,040
Try this! Find the sum of the first 9 terms of the given sequence: −2, 1, −1/2,…
Answer:
If the common ratio r of an infinite geometric sequence is a fraction where (that is ), then the factor found in the formula for the nth partial sum tends toward 1 as n increases. For example, if and we have,
Here we can see that this factor gets closer and closer to 1 for increasingly larger values of n. This illustrates the idea of a limit, an important concept used extensively in higher-level mathematics, which is expressed using the following notation:
This is read, “the limit of as n approaches infinity equals 1.” While this gives a preview of what is to come in your continuing study of mathematics, at this point we are concerned with developing a formula for special infinite geometric series. Consider the nth partial sum of any geometric sequence,
If then the limit of the partial sums as n approaches infinity exists and we can write,
Therefore, a convergent geometric seriesAn infinite geometric series where whose sum is given by the formula: is an infinite geometric series where ; its sum can be calculated using the formula:
Example 6
Find the sum of the infinite geometric series:
Solution:
Determine the common ratio,
Since the common ratio is a fraction between −1 and 1, this is a convergent geometric series. Use the first term and the common ratio to calculate its sum.
Answer:
Note: In the case of an infinite geometric series where , the series diverges and we say that there is no sum. For example, if then and we have
We can see that this sum grows without bound and has no sum.
A repeating decimal can be written as an infinite geometric series whose common ratio is a power of 1/10. Therefore, the formula for a convergent geometric series can be used to convert a repeating decimal into a fraction.
Example 7
Write as a fraction:
Solution:
Begin by identifying the repeating digits to the right of the decimal and rewrite it as a geometric progression.
In this form we can determine the common ratio,
Note that the ratio between any two successive terms is . Use this and the fact that to calculate the infinite sum:
Therefore, and we have,
Answer:
Example 8
A certain ball bounces back to two-thirds of the height it fell from. If this ball is initially dropped from 27 feet, approximate the total distance the ball travels.
Solution:
We can calculate the height of each successive bounce:
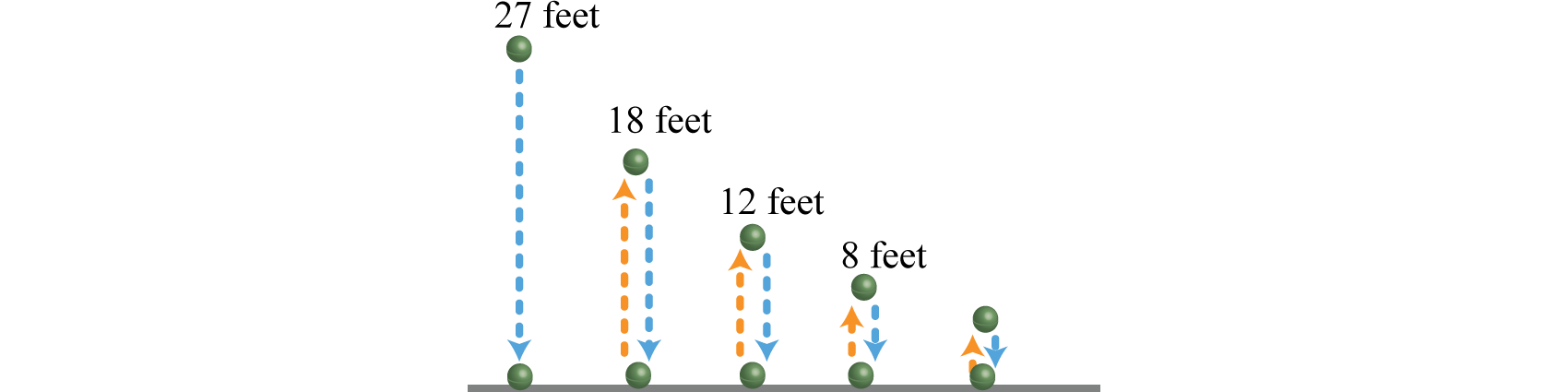
The total distance that the ball travels is the sum of the distances the ball is falling and the distances the ball is rising. The distances the ball falls forms a geometric series,
where and Because r is a fraction between −1 and 1, this sum can be calculated as follows:
Therefore, the ball is falling a total distance of 81 feet. The distances the ball rises forms a geometric series,
where and . Calculate this sum in a similar manner:
Therefore, the ball is rising a total distance of 54 feet. Approximate the total distance traveled by adding the total rising and falling distances:
Answer: 135 feet
Key Takeaways
- A geometric sequence is a sequence where the ratio r between successive terms is constant.
- The general term of a geometric sequence can be written in terms of its first term , common ratio r, and index n as follows:
- A geometric series is the sum of the terms of a geometric sequence.
- The nth partial sum of a geometric sequence can be calculated using the first term and common ratio r as follows:
- The infinite sum of a geometric sequence can be calculated if the common ratio is a fraction between −1 and 1 (that is ) as follows: If , then no sum exists.
Topic Exercises
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
7, 28, 112,…
-
−2, −10, −50,…
-
2, , ,…
-
1, , ,…
-
8, 4, 2,…
-
6, 2, ,…
-
−1, , ,…
-
2, , ,…
-
, −2, 12,…
-
, −2, 10,…
-
−3.6, −4.32, −5.184,…
-
0.8, −2.08, 5.408,…
-
Find the general term and use it to determine the 20th term in the sequence: ,…
-
Find the general term and use it to determine the 20th term in the sequence: ,…
-
The number of cells in a culture of a certain bacteria doubles every 4 hours. If 200 cells are initially present, write a sequence that shows the population of cells after every nth 4-hour period for one day. Write a formula that gives the number of cells after any 4-hour period.
-
A certain ball bounces back at one-half of the height it fell from. If this ball is initially dropped from 12 feet, find a formula that gives the height of the ball on the nth bounce and use it to find the height of the ball on the 6th bounce.
-
Given a geometric sequence defined by the recurrence relation where and , find an equation that gives the general term in terms of and the common ratio r.
-
Given the geometric sequence defined by the recurrence relation where and , find an equation that gives the general term in terms of and the common ratio r.
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
-
and
Part A: Geometric Sequences
Write the first 5 terms of the geometric sequence given its first term and common ratio. Find a formula for its general term.
Given the geometric sequence, find a formula for the general term and use it to determine the 5th term in the sequence.
Given the terms of a geometric sequence, find a formula for the general term.
Find all geometric means between the given terms.
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
-
-
-
-
-
-
-
-
;
-
;
-
;
-
;
-
;
-
;
-
-
-
-
-
-
-
1.222…
-
5.777 …
-
2.252525…
-
3.272727…
-
1.999…
-
1.090909…
-
Suppose you agreed to work for pennies a day for 30 days. You will earn 1 penny on the first day, 2 pennies the second day, 4 pennies the third day, and so on. How many total pennies will you have earned at the end of the 30 day period? What is the dollar amount?
-
An initial roulette wager of $100 is placed (on red) and lost. To make up the difference, the player doubles the bet and places a $200 wager and loses. Again, to make up the difference, the player doubles the wager to $400 and loses. If the player continues doubling his bet in this manner and loses 7 times in a row, how much will he have lost in total?
-
A certain ball bounces back to one-half of the height it fell from. If this ball is initially dropped from 12 feet, approximate the total distance the ball travels.
-
A golf ball bounces back off of a cement sidewalk three-quarters of the height it fell from. If the ball is initially dropped from 8 meters, approximate the total distance the ball travels.
-
A structured settlement yields an amount in dollars each year, represented by n, according to the formula What is the total amount gained from the settlement after 10 years?
-
Beginning with a square, where each side measures 1 unit, inscribe another square by connecting the midpoints of each side. Continue inscribing squares in this manner indefinitely, as pictured:

Find the sum of the area of all squares in the figure. (Hint: Begin by finding the sequence formed using the areas of each square.)
Part B: Geometric Series
Calculate the indicated sum.
Write as a mixed number.
-
-
-
-
-
-
-
-
-
-
-
-
-
1, −1, 1, −1,…
-
0, 0, 0,…
-
;
-
;
-
;
-
;
-
;
-
;
-
-
-
-
-
-
Part C: Sequences and Series
Categorize the sequence as arithmetic, geometric, or neither. Give the common difference or ratio, if it exists.
Categorize the sequence as arithmetic or geometric, and then calculate the indicated sum.
Calculate the indicated sum.
-
Use the techniques found in this section to explain why
-
Construct a geometric sequence where Explore the nth partial sum of such a sequence. What conclusions can we make?
Part D: Discussion Board
Answers
-
1, 5, 25, 125, 625;
-
-
2, 6, 18, 54, 162;
-
-
2, −6, 18, −54, 162;
-
-
3, 2, , , ;
-
-
1.2, 0.72, 0.432, 0.2592, 0.15552;
-
-
,
-
-
,
-
-
,
-
-
,
-
-
,
-
-
,
-
-
;
-
-
400 cells; 800 cells; 1,600 cells; 3,200 cells; 6,400 cells; 12,800 cells; cells
-
-
-
-
-
-
-
-
-
-
-
-
-
-
10, 50
-
-
−200; −2,000
-
-
16,380
-
-
-
-
305
-
-
-
-
3,905
-
-
4,092
-
-
−177,144
-
-
-
-
-
-
-
-
−1
-
-
3
-
-
No sum
-
-
-
-
-
-
-
-
2
-
-
1,073,741,823 pennies; $10,737,418.23
-
-
36 feet
-
-
$26,778.77
-
-
Geometric;
-
-
Arithmetic;
-
-
Neither
-
-
Arithmetic;
-
-
Neither
-
-
Geometric;
-
-
Geometric;
-
-
Geometric; 292,968
-
-
Arithmetic; 210
-
-
Geometric;
-
-
3,575
-
-
−1,365
-
-
200
-
-
Answer may vary
-




