This is “Interest Rates”, chapter 4 from the book Finance, Banking, and Money (v. 1.1). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
Chapter 4 Interest Rates
Chapter Objectives
By the end of this chapter, students should be able to:
- Define interest and explain its importance.
- Write and explain the present value formula.
- Write and explain the future value formula.
- Calculate present and future value for multiple periods with annual and more frequent compounding.
- Define and price major types of debt instruments including discount bonds, simple loans, fixed payment loans, and coupon bonds.
- Define yield to maturity and identify the types of financial instruments for which it is relatively easy to calculate.
- Explain why bond prices move inversely to market interest rates.
- Explain why some bond prices are more volatile than others.
- Define rate of return and explain how it differs from yield to maturity.
- Explain the difference between real and nominal interest rates.
4.1 The Interest of Interest
Learning Objective
- What is interest and why is it important?
InterestThe opportunity cost of money., the opportunity cost of money, is far from mysterious, but it warrants our careful consideration because of its importance. Interest ratesThe price of borrowed money., the price of borrowing money, are crucial determinants of the prices of assets, especially financial instruments like stocks and bonds, and general macroeconomic conditions, including economic growthReal per capita GDP.. In fact, ceteris paribusAll else equal. (like your grades!) the probability of you landing a job upon graduation will depend in large part on prevailing interest rates. If rates are low, businesses will be more likely to borrow money, expand production, and hire you. If rates are high, businesses will be less likely to expand or to hire you. Without a job, you’ll be forced to move back home. Best to pay attention then!
Interest can be thought of as the payment it takes to induce a lender to part with his, her, or its money for some period of time, be it a day, week, month, year, decade, or century. To make comparisons between those payments easier, interest is almost always expressed as an annual percentage rate, the number of dollars (or other currency)http://fx.sauder.ubc.ca/currency_table.html paid for the use of $100 per year. Several ways of measuring interest rates exist, but here you’ll learn only yield to maturityThe most economically accurate way of measuring interest rates., the method preferred by economists for its accuracy. The key is to learn to compare the value of money today, called present valueThe value of money today. (represented here by the variable PV and aka present discounted value or price), to the value of money tomorrow, called future valueThe value of money at some point in the future. (represented here by the variable FV).
Key Takeaways
- Interest is the opportunity cost of lending money or the price of borrowing it and can be thought of as the payment a borrower needs to induce him, her, or it to lend.
- Interest is important because it helps to determine the price of assets, especially financial assets, and to determine various macroeconomic variables, including aggregate output.
4.2 Present and Future Value
Learning Objective
- What are the formulas for present value and future value, and what types of questions do they help to answer?
A moment’s reflection should convince you that money today is alwaysCertain interest rates occasionally turn very slightly (−0.004%) negative. The phenomenon is so rare and minor that it need not detain us here.worth more than money tomorrow. If you don’t believe me, send me all of your money immediately. I’ll return every cent of it—scout’s honor—in exactly one year. I won’t hold my breath. You’d be foolish indeed to forgo food, clothes, housing, transportation, and entertainment for a year for no remuneration whatsoever. That’s why a dollar today is worth more than a dollar tomorrow. (Another reason that a dollar today is worth more than a dollar tomorrow is that, in modern economies, for reasons discussed in Chapter 17 "Monetary Policy Targets and Goals", prices tend to rise every year. So $100 tomorrow will buy fewer goods and services than $100 today will. We will discuss the impact of inflationA sustained increase in the price level or average prices. on interest rates more at the end of this chapter. For now, we consider only nominal interest ratesThe price of borrowing money as it is usually stated, unadjusted for inflation., not real interest ratesThe price of borrowing money adjusted for inflation..) But what if I told you that if you gave me $100 today, I’d give you $1,000 in a year? Most lenders would jump at that offer (provided they thought I would pay as promised and not default), but I wouldn’t offer it and neither would most borrowers. In fact, about $110 would be the most I’d be willing to give you in a year for $100 today. That’s an interest rate of 10 percent ($10/$100 = .1 or 10%), which, as comedian Adam Sandler might say, is “not too shabby.”www.tsrocks.com/a/adam_sandler_texts/the_chanukah_song.html If we let the loan ride, as they say, capitalizing the interest or, in other words, paying interest on the interest every year, called annually compoundingEarning interest on interest. interest, your $100 investment would grow in value, as shown in Figure 4.1 "The fate of $100 invested at 10%, compounded annually".
Figure 4.1 The fate of $100 invested at 10%, compounded annually
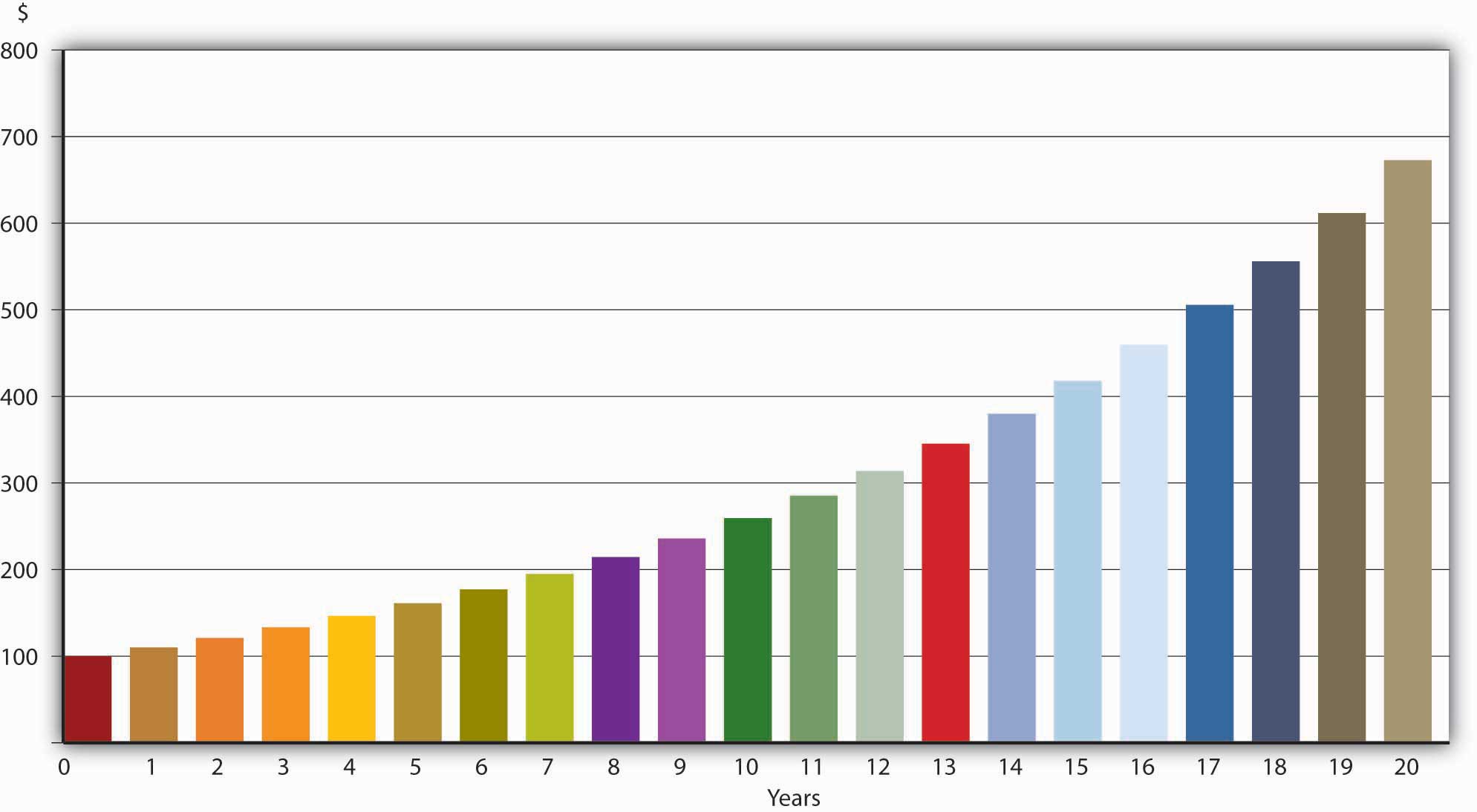
The figures in the table are easily calculated by multiplying the previous year’s value by 1.10, 1 representing the principal value and .10 representing the interest rate expressed as a decimal. So $100 today (year = 0) is, at 10 percent interest compounded annually, worth $110 in a year (100 × 1.1), $121 after two years (110 × 1.1), $131.10 after three years (121 × 1.1), and so forth. The quick way to calculate this for any year is to use the following formula:
FV = PV(1 + i)n
where
FV = the future value (the value of your investment in the future)
PV = the present value (the amount of your investment today)
(1 + i)n = the future value factor (aka the present value factor or discount factor in the equation below)
i = interest rate (decimalized, for example, 6% = .06; 25% = .25, 2.763% = .02763, etc.)
n = number of terms (here, years; elsewhere days, months, quarters)
For $100 borrowed today at 10 percent compounded annually, in 100 years I’d owe you $1,378,061 (FV = 100 × 1.1100). (Good luck collecting that one!)
What if someone offers to pay you, say, $1,000 in 5 years? How much would you be willing to pay today for that? Clearly, something less than $1,000. Instead of taking a PV and expanding it via multiplication to determine an FV, here you must do the opposite, or in other words, reduce or “discount” an FV to a PV. You do so by dividing, as in the following formula:
Obviously, we can’t solve this equation unless one of the two remaining variables is given. If the interest rate is given as 5 percent, you would pay $783.53 today for $1,000 payable in 5 years (PV = 1000/1.055). If it is 20 percent, you’d give only $401.88 (PV = 1000/1.25). If it is 1 percent, you would give $951.47 (PV = 1000/1.015). Notice that as the interest rate rises (falls), the price of the bond falls (rises). In other words, the price of some future payment (some FV; generically, a bond) and the rate of interest are inversely related. You can see this algebraically by noting that the i term is in the denominator, so as it gets larger, PV must get smaller (holding FV constant, of course). Economically this makes sense because a higher interest rate means a higher opportunity cost for money, so a sum payable in the future is worth less the more dear money is.
If payment of the bond described just above were to be made in ten years instead of five, at 1 percent interest per year, you’d pay $905.29 (PV = 1000/1.0110). Note here that, holding the interest rate (and all other factors) constant, you give less today for a payment further in the future ($905.29 < $951.47). That too makes good sense because you’re without your money longer and need to be compensated for it by paying a lower price for the bond/promise/IOU today.
Stop and Think Box
Congratulations, you just won the Powerball: $100 million payable in $5 million installments over 20 years! Did you really win $100 million? (Hint: Calculate the PV of the final payment with interest at 4 percent.)
No; 5 × 20 = 100, but the money payable next year and in subsequent years is not worth $5 million today if interest rates are above 0, and they almost always are. For example, the last payment, with interest rates at 4 percent compounded annually, has a PV of only 5,000,000/(1.04)20 = $2,281,934.73.
This is a great place to stop and drill until calculating present value and future value becomes second nature to you. Work through the following problems until it hurts. Then do them again, standing on your head or on one leg.
Exercises
For all questions in this set, interest compounds annually and there are no transaction fees, defaults, etc.
- On your seventieth birthday, you learn that your grandma, bless her soul, deposited $50.00 for you on the day of your birth in a savings account bearing 5 percent interest. How much is in the account?
- You won $1 million in the lottery but unfortunately the money is payable in a year and you want to start spending it right away. If interest is at 8 percent, how much can you receive today in exchange for that $1 million in year?
- As a college freshman, you hoped to save $2,500 to “pimp your ride” as a college graduation present to yourself. You put $2,012.98 from your high school graduation haul in the bank at 5 percent interest. Will you meet your goal?
- You’ve won a scholarship for your senior year worth $1,500, but it is payable only after graduation, a year hence. If interest is at 15 percent, how much is your scholarship worth today?
- You determine that you need $1,750,000 saved in order to retire comfortably. When you turn 25, you inherit $350,017. If you invest that sum immediately at 4.42 percent, can you retire at age 65 if you have no other savings?
- You own two bonds, each with a face, or payoff, value of $1,000. One falls due in exactly one year and the other in exactly three years. If interest is at 2.35 percent, how much are those bonds worth today? What if interest rates jump to 12.25 percent?
- To purchase a car, you borrowed $10,000 from your brother. You offered to pay him 8 percent interest and to repay the loan in exactly three years. How much will you owe your bro?
- As part of a lawsuit settlement, a major corporation offers you $100,000 today or $75,000 next year. Which do you choose if interest rates are 5 percent? If they are 13.47886 percent?
- Exactly 150 years ago, the U.S. government promised to pay a certain Indian tribe $3,500, or 7 percent interest until it did so. Somehow, the account was unpaid. How much does the government owe the tribe for this promise?
- As part of an insurance settlement, you are offered $100,000 today or $125,000 in five years. If the applicable interest rate is 1 percent, which option do you choose? What if the interest rate is 5 percent?
Key Takeaways
- The present value formula is PV = FV/(1 + i)n where PV = present value, FV = future value, i = decimalized interest rate, and n = number of periods. It answers questions like, How much would you pay today for $x at time y in the future, given an interest rate and a compounding periodThe amount of time that passes before interest begins to earn interest..
- The future value formula is FV = PVx(1 + i)n. It answers questions like, How much will $x invested today at some interest rate and compounding period be worth at time y?
4.3 Compounding Periods
Learning Objective
- If interest compounds other than annually, how does one calculate PV and FV?
Interest does not always compound annually, as assumed in the problems already presented in this chapter. Sometimes it compounds quarterly, monthly, daily, even continuously. The more frequent the compounding period, the more valuable the bond or other instrument, all else constant. The mathematics remains the same (though a little more difficult when compounding is continuous), but you must be careful about what you plug into the equation for i and n. For example, $1,000 invested at 12 percent for a year compounded annually would be worth $1,000 × (1.12)1 = $1,120.00. But that same sum invested for the same term at the same rate of interest but compounded monthly would grow to $1,000 × (1.01)12 = $1,126.83 because the interest paid each month is capitalized, earning interest at 12 percent. Note that we represent i as the interest paid per period (.12 interest/12 months in a year = .01) and n as the number of periods (12 in a year; 12 × 1 = 12), rather than the number of years. That same sum, and so forth with interest compounded quarterly (4 times a year) would grow to $1,000 × (1.03)4 = $1,125.51. The differences among annual, monthly, and quarterly compounding here is fairly trivial, amounting to less than $7 all told, but is important for bigger sums, higher interest rates, more frequent compounding periods, and longer terms. One million dollars at 4 percent for a year compounded annually comes to $1,000,000 × (1.04) = $1,040,000, while on the same terms compounded quarterly, it produces $1,000,000 × (1.01)4 = $1,040,604.01. (I’ll take the latter sum over the former any day and “invest” the surplus in a very nice dinner and concert tickets.) Likewise, $100 at 300 percent interest for 5 years compounded annually becomes 100 × (4)5 = $102,400. Compounded quarterly, that $100 grows to $100 × (1.75)20 = $7,257,064.34! A mere $1 at 6 percent compounded annually for 100 years will be worth $1 × (1.06)100 = $339.30. The same buck at the same interest compounded monthly swells in a century to $1 × (1.005)1200 = $397.44. This all makes good sense because interest is being received sooner than the end of the year and hence is more valuable because, as we know, money now is better than money later.
Do a few exercises now to make sure you get it.
Exercises
For all questions in this set, interest compounds quarterly (four times a year) and there are no transaction fees, defaults, etc.
- On your seventieth birthday, you learn that your grandma, bless her soul, deposited $50.00 for you on the day of your birth in a savings account bearing 5 percent interest. How much is in the account?
- You won $1 million in the lottery but unfortunately the money is payable in a year and you want to start spending it right away. If interest is at 8 percent, how much can you receive today in exchange for that $1 million in year?
- As a freshman, you hoped to save $2,500 to “pimp your ride” as a college graduation present to yourself. You put $2,012.98 from your high school graduation haul in the bank at 5 percent interest. Will you meet your goal if you graduate in four years?
- You’ve won a scholarship for your senior year worth $1,500, but it is payable only after graduation, a year hence. If interest is at 15 percent, how much is your scholarship worth today?
Key Takeaways
- Present and future value can be calculated for any compounding period using the same formulas presented in this chapter.
- Care must be taken, however, to ensure that the i and n terms are adjusted appropriately.
4.4 Pricing Debt Instruments
Learning Objective
- What are debt instruments and how are they priced?
Believe it or not, you are now equipped to calculate the price of any debt instrumentA bond, IOU, or other contract (like a discount bond, simple loan, fixed payment loan, or coupon bond) promising the payment of money in the future.or contract provided you know the rate of interest, compounding period, and the size and timing of the payments. Four major types of instruments that you are likely to encounter include discount coupon bonds, simple loans, fixed-payment loans, and coupon bonds. A discount bondA debt instrument that makes only one payment, its face value on its maturity or redemption date. Also known as a zero coupon bond. (aka a zero coupon bondSee discount bond. or simply a zeroSee discount bond.) makes only one payment, its face value on its maturity or redemption date, so its price is easily calculated using the present value formula. A simple loanA debt instrument where the borrower repays the principal and interest at the end of the loan. is the name for a loan where the borrower repays the principal and interest at the end of the loan. Use the future value formula to calculate the sum due upon maturity. A fixed-payment loanA debt instrument in which the borrower makes periodic repayments of principal and interest. (aka a fully amortized loan) is one in which the borrower periodically (for example, weekly, bimonthly, monthly, quarterly, annually, etc.) repays a portion of the principal along with the interest. With such loans, which include most auto loans and home mortgages, all payments are equal. There is no big balloon or principal payment at the end because the principal shrinks, slowly at first but more rapidly as the final payment grows nearer, as in Figure 4.2 "Sample thirty-year amortizing mortgage".
Principal borrowed: $500,000.00; Annual number of payments: 12; Total number of payments: 360; Annual interest rate: 6.00%; Regular monthly payment amount: $2,997.75
Figure 4.2 Sample thirty-year amortizing mortgage
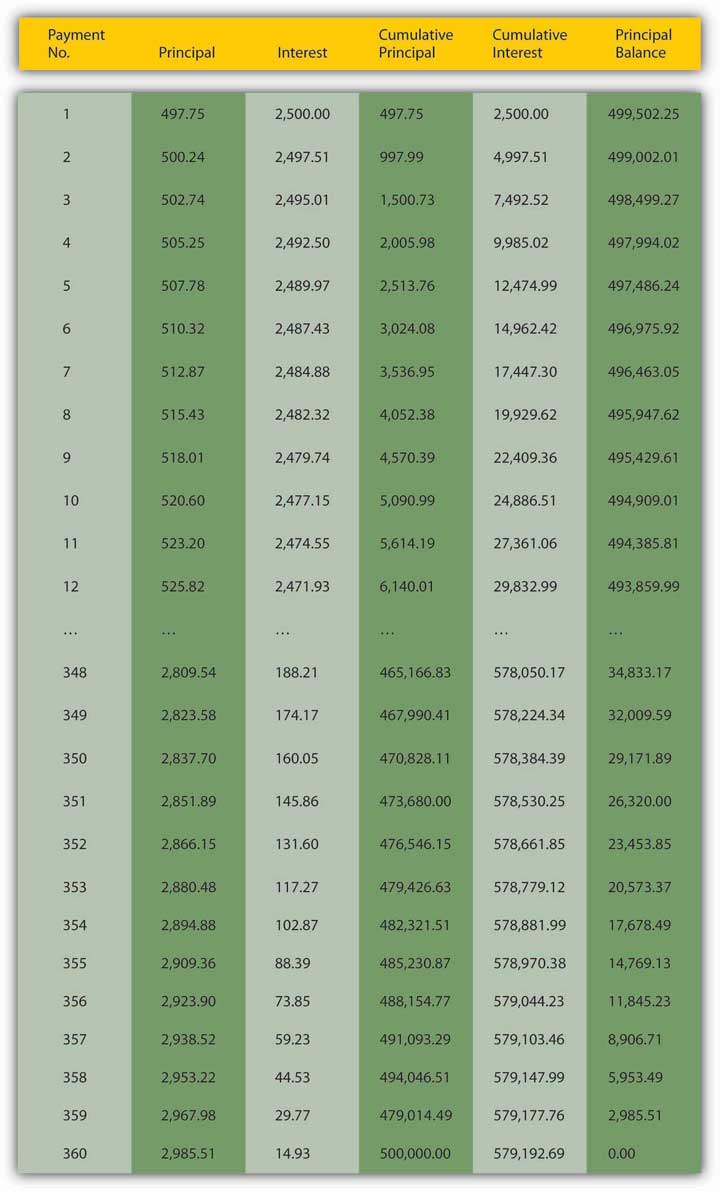
Today, such schedules are most easily created using specialized financial software, including Web sites like http://ray.met.fsu.edu/cgi-bin/amortize, http://www.yona.com/loan/, or http://realestate.yahoo.com/calculators/amortization.html. If you wanted to buy this mortgage (in other words, if you wanted to purchase the right to receive the monthly repayments of $2,997.75) from the original lender (there are still secondary markets for mortgages, though they are less active than they were before the financial crisis that began in 2007), you’d simply sum the present value of each of the remaining monthly payments. (Again, a computer is highly recommended here!)
Finally, a coupon bondA debt instrument that makes interest payments periodically until its maturity or redemption date, when the final interest payment and the principal are to be paid.is so-called because, in the past, owners of the bond received interest payments by clipping one of the coupons and remitting it to the borrower (or its paying agent, usually a bank). Figure 4.3 "Sample bond coupon, Malden & Melrose Railroad Co., 1860", for example, is a coupon paid (note the cancellation holes and stamp) to satisfy six months’ interest on bond number 21 of the Malden & Melrose Railroad Company of Boston, Massachusetts, sometime on or after April 1, 1863. Figure 4.4 "Michigan Central Railroad, 3.5 percent bearer gold bond with coupons attached, 1902" is a $1,000 par value coupon bond issued in 1932, with many of the coupons still attached (on the right side of the figure).
Figure 4.3 Sample bond coupon, Malden & Melrose Railroad Co., 1860

Courtesy of CelebrateBoston.com
Figure 4.4 Michigan Central Railroad, 3.5 percent bearer gold bond with coupons attached, 1902

Museum of American Finance
Even if it no longer uses a physical coupon like those illustrated in Figure 4.3 "Sample bond coupon, Malden & Melrose Railroad Co., 1860" and Figure 4.4 "Michigan Central Railroad, 3.5 percent bearer gold bond with coupons attached, 1902", a coupon bond makes one or more interest payments periodically (for example, monthly, quarterly, semiannually, annually, etc.) until its maturity or redemption date, when the final interest payment and all of the principal are paid. The sum of the present values of each future payment will give you the price. So we can calculate the price today of a $10,000 face or par value coupon bond that pays 5 percent interest annually until its face value is redeemed (its principal is repaid) in exactly five years if the market rate of interest is 6 percent, 4 percent, or any other percent for that matter, simply by summing the present value of each payment:
PV1 = $500/(1.06) = $471.70 (This is the interest payment after the first year. The $500 is the couponThe interest rate promised to the owner of a coupon bond. or interest payment, which is calculated by multiplying the bond’s face value, in this case, $10,000, by the bond’s contractual rate of interest or “coupon rate,” in this case, 5 percent. $10,000 × .05 = $500.)
That adds up to $9,578.77. If you are wondering why the bond is worth less than its face value, the key is the difference between the contractual interest or coupon rate it pays, 5 percent, and the market rate of interest, 6 percent. Because the bond pays at a rate lower than the going market, people are not willing to pay as much for it, so its price sinks below par. By the same reasoning, people should be willing to pay more than the face value for this bond if interest rates sink below its coupon rate of 5 percent. Indeed, when the market rate of interest is 4 percent, its price is $10,445.18 (give or take a few pennies, depending on rounding):
If the market interest rate is exactly equal to the coupon rate, the bond will sell at its par value, in this case, $10,000.00. Check it out:
Calculating the price of a bond that makes quarterly payments over thirty years can become quite tedious because, by the method shown above, that would entail calculating the PV of 120 (30 years times 4 payments a year) payments. Until not too long ago, people used special bond tables to help them make the calculations more quickly. Today, to speed things up and depending on their needs, most people use financial calculators, specialized financial software, and canned spreadsheet functions like Excel’s PRICEDISC or PRICEMAT, custom spreadsheet formulas, or Web-based calculators like http://www.calculatorweb.com/calculators/bondcalc.shtml or http://www.investinginbonds.com/calcs/tipscalculator/TipsCalcForm.aspx. It’s time once again to get a little practice. Don’t worry; these are easy enough to work out on your own.
Exercises
Assume no default risks or transaction costs.
- What is the price of a 10 percent coupon bond, payable annually, with a $100 face value that matures in 3 years if interest rates are 7 percent?
- If interest rates were 4 percent, how much would you give today for a loan with a $100,000 balloon principal payment due in a year and that will pay $16,000 in interest at the end of each quarter, including the final quarter when the principal falls due?
- What is the value today of a share of stock that you think will be worth $50 in a year and that throws off $1 in dividends each quarter until then, assuming the market interest rate is 10 percent?
- What is the value today of a share of stock that you think will be worth $50 in a year and that throws off $1 in dividends each quarter until then if the market interest rate is 1 percent?
Key Takeaways
- Debt instruments—like discount bonds, simple loans, fixed payment loans, and coupon bonds—are contracts that promise payment in the future.
- They are priced by calculating the sum of the present value of the promised payments.
4.5 What’s the Yield on That?
Learning Objective
- What is yield to maturity and for what types of financial instruments is the yield to maturity relatively easy to calculate?
Thus far, we have assumed or been given a market interest rate and then calculated the price (PV) of the instrument. Or, given the PV and an interest rate, we’ve calculated the FV. Sometimes it is useful to do the opposite, to calculate the interest rate or, yield to maturity, if given the PV and FV. Say that you know that someone paid $750 for a zero coupon bond with a face value of $1,000 that will mature in exactly a year and you want to know what interest rate he or she paid. You know that PV = FV/(1 + i). Solving for i:
You can check your work by reversing the problem—that is, asking how much you’d pay today for $1,000 in a year if interest was at 33.33 percent: PV = 1000/(1.3333333) = $750. Voilà!
Stop and Think Box
Suppose you have $1,000 to invest for a year and two ways of investing it (each equal in terms of risk and liquidity): a discount bond due in one year with a face value of $1,000 for $912 or a bank account at 6.35 percent compounded annually. Which should you take?
Choose the bond, which will yield 9.65 percent: (1000 − 912)/912 = .0965. To maximize your haul, invest the $88 left over from the purchase of the bond in the bank account.
Calculating the yield to maturity for a perpetual debt, one with no maturity or repayment date, like a ConsolA type of perpetual bond issued by the British government., ground rent, or perpetual interest-only mortgage, is also quite easy. The price or PV of a perpetuity is equal to the yearly payment divided by the going rate of interest:
So a $1,000 ground rent that pays $50 a year (a 5 percent coupon rate) would be worth $1,000 if interest rates were 5 percent, less if rates are higher, more if lower:
Calculating the yield to maturity of a perpetuity, if given the PV and FV, is easily done by taking the equation and solving for i:
So the yield to maturity of a ground rent that pays $60 per year and that currently sells for $600 would be 10 percent: i = 60/600 = .10 = 10%.
Stop and Think Box
A ground rent contract consummated in Philadelphia, Pennsylvania, in 1756 is still being paid today. Someone recently paid $455 for the $23.17 annual payment. What is the ground rent’s yield to maturity? If the interest rate rises to 10 percent, how much will the ground rent be worth? What if interest falls to 2 percent?
i = C/P so i = 23.17/455 = 0.05092 = 5.09%; PV = 23.17/.1 = $231.70; PV = 23.17/.02 = $1,158.50.
Calculating yield to maturity for coupon bonds and fixed-payment loans, however, is mathematically nasty business without a computer or bond table. In the past, people used to estimate the yield to maturity on such instruments by pretending they were perpetuities or engaging in trial-and-error interpolation. In the first method, you use the easy perpetuity equation above (i = FV/PV) to get a quick estimate called the current yieldA quick (i = FV/PV) but flawed method for calculating interest rates of nonperpetual debt.. Unfortunately, current yield can be wide of the mark, especially for bonds with maturities less than twenty years and bonds whose prices are far from their par value.Current yield is simply the yield to maturity of a perpetuity, so the more like a perpetuity a bond is, the better the current yield will approximate its yield to maturity. The shorter the maturity of a bond, the less like a Consol it is, so the less accurate the current yield formula will be. Similarly, the current yield works better the closer a bond’s price is to par because yield to maturity equals the coupon rate when the bond is at par. As the price deviates further from par, the less well the current yield can approximate the yield to maturity. In the second method, one backs into the yield to maturity by making successive guesses about i and plugging them into the PV formula. Not fun, but you’ll eventually get there. Most people today therefore use a financial calculator, spreadsheet, or Web-based utility rather than such erroneous (current yield) or laborious (interpolation) processes. You should be able to calculate the yield to maturity of one-year discount bonds or perpetuities by hand, or at worst with the aid of simple (nonfinancial) calculator. Here is a little practice.
Exercises
- A $100 bond payable in a year sells for $97.56. What is the yield to maturity?
- Sam promises to pay Joe $1,904 in a year if Joe gives him $1,498 today. What interest rate is Sam paying and what interest rate Joe is earning?
- Every year, the U.S. government pays a certain Indian tribe $10,000 and, by terms of its treaty with that tribe, must do so forever. Mr. Trump offered to purchase the right to receive that stream for a one-time payment of $143,500. What yield to maturity did Trump offer the Indians?
- What is the yield to maturity of a British Consol paying £400 per year that sold for £27,653?
Key Takeaways
- Yield to maturity is the most economically accurate way of measuring nominal interest rates.
- It is easily calculated for one-year discount bonds i = (FV–PV)/PV and perpetuities i = C/PV where C is the coupon or annual payment.
4.6 Calculating Returns
Learning Objective
- What is the rate of return and how does it differ from yield to maturity?
This is not all you need to know about bonds if you were to become a bond trader because the bond market, which in the United States is over 200 years old, has some odd conventions that do not make much economic sense. Most students will not become professional bond traders, so in the interest of sanity, yours and ours, we will not delve into the intricacies here. (If you do become a bond trader, you will quickly and easily pick up on the conventions anyway.) Our goal here is to understand the basics of PV, FV, yield to maturity (YTM), and, finally, rate of returnA measure of the profitability of an investment that takes into account changes in the value of the bond or other asset.. Students sometimes conflate the last two concepts. The yield to maturity is merely a measure of the interest rate. The rate of return is more a measure of how lucrative an investment is because it accounts for changes in the price of the bond (or other asset, financial or otherwise). More formally,
where:
R = return from holding the asset for some time period, t0 to t1
Pt0 = the price at time t0 (this can also be thought of as the purchase price)
Pt1 = the price at time t1 (this can also be thought of as the sale or going market price)
C = coupon (or other) payment
So imagine you purchased a 5 percent coupon bond with a $100 face value that matures in three years when the interest rate is 5 percent. As we learned above, the market price of such a bond would equal its face value, or $100. We also learned that bond prices and interest rates are inversely related. As the market interest rate increases, the PV of the bond’s future payments decreases and the bond becomes less valuable. As the rate decreases, the PV of future payments increases and the bond becomes more valuable. If the interest rate increased (decreased) to 6 (4) percent, the value of the bond would decrease (increase), so the returns you earned on the bond would not equal the yield to maturity. For example, suppose you purchased the bond for $100 but its price a year hence stood at $103 because interest rates decreased a little. Your return would be R = (5 + 3)/100 = .08, or 8%. But if in the next year, interest rates soared, driving the market price of the bond down to $65, your return (from purchase) would be R = (10 − 35)/100 = −.25 or negative 25%. Yes, negative. It is quite possible to lose wealth by investing in bonds or other fixed-rate financial instruments, even if there is no default (i.e., even if payments are punctually made as promised).
Stop and Think Box
As part of its effort to repay the large debts it accrued during the Revolutionary War, the U.S. federal government in the early 1790s issued three types of bonds: a coupon bond that paid 6 percent per year, a coupon bond that paid 3 percent per year, and a zero coupon bond that became a 6 percent coupon bond in 1801. For most of the 1790s and early 1800s, the price of the 6 percent bonds hovered around par. Given that information, what was the yield to maturity on government debt in that period? What, in general terms, were the prices of the 3 percent and zero coupon bonds?
The yield to maturity was about 6 percent because the 6 percent coupon bonds traded at around par. The price of the 3 percent coupon bonds must have been well below par because who would pay $100 to get $3 a year when she could pay $100 and get $6 a year? Finally, the zeroes must have appreciated toward the price of the 6 percent coupon bonds as the conversion date neared.
Note that the loss is not, repeat not, predicated on actually selling the bond. One way to think about this is that the rate of return formula merely calculates the return if the bond were to be sold. Another way to think about it is to realize that whether the bond is sold or not, its owner is still poorer by the amount of the loss because the value of his assets, and hence his net worth, has shrunk by that amount. The risk of such loss is known as interest rate riskThe risk that the market price of a bond or other debt instrument will decrease due to increases in the interest rate. to distinguish it from other types of risks, like default riskThe risk that a bond or other debt instrument will not make the promised payments. (the risk of nonpayment). Interest rate risk is higher the longer the maturity of a bond because more FVs are affected by increasing the interest rate, and the most distant ones are the most highly affected. Check this out: The PV of $1,000 in 10 years at 5% compounded annually is 1,000/(1.05)10 = $613.91. At 10% it is 1,000/(1.10)10 = $385.54, a loss of 37.2%. The PV of $1,000 in 30 years at 5% and 10% is 1,000/(1.05)30 = $231.38 and 1,000/(1.10)30 = $57.31, respectively, a loss of 75.23 percent. Duration is a technical measure of interest rate risk that we will not investigate here, where the main point is merely that rising interest rates hurt bond prices (and hence bondholders); falling interest rates help bond prices.
Key Takeaways
- The rate of return accounts for changes in the market price of a bond or other asset while the yield to maturity does not.
- Yield to maturity (YTM) is almost always positive but returns are often negative due to interest rate risk, the risk that interest rates will rise, depressing bond prices.
- When the market interest rate increases, bond prices decrease because the opportunity cost of lending money has increased, making bonds less attractive investments unless their price falls.
- Algebraically, PV = FV/(1 + i)n. The interest rate is in the denominator, so as i gets bigger, PV must get smaller.
- Bonds with longer periods to maturity have more volatile prices, ceteris paribus, because the PV of their distant FV shrinks more, to very small sums.
4.7 Inflation and Interest Rates
Learning Objective
- What is the difference between real and nominal interest rates and why is the distinction important?
You might well ask at this point, What factors change interest rates? One big factor is inflation. As the price level rises, so too do interest rates, or at least what economists call nominal interest rates, the type of rates we’ve discussed so far. If nominal rates do not increase (and they often don’t, or can’t), lenders might receive more nominal dollars than they lent but actually get back less purchasing power. Imagine, for example, that you lent $100 for one year at 6 percent interest when a loaf of bread, pack of chewing gum, and two-liter bottle of Mountain Dew each cost $1. At the end of the simple loan, you would get back $100 × 1.06 = $106 and be able to enjoy an extra $6 of goods, say, two loaves of bread, two packs of gum, and two bottles of the caffeine and sugar rush known as Doin’ the Dew. But what if prices doubled over that year? Instead of some combination of 106 goodies, you’d be able to buy only fifty-three. Your nominal return would be positive, but your real return, what you could actually buy with the $106, would be steeply negative.
A simple equation, the Fisher Equation, named after Irving Fisher, the early twentieth-century U.S. economist who articulated it,To be frank, Benjamin Franklin and other colonists in eighteenth-century America understood it well.helps us to understand the relationship between inflation and interest rates more precisely:
where
ir = the real interest rate
i = the nominal interest rate (the type of interest rate the first part of this chapter discussed exclusively)
1= inflation (or expected inflation)
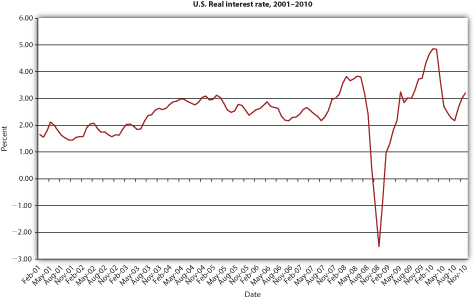
Figure 4.5 U.S. real interest rate, 2001–2010
In plain English, after the fact (ex postAfter the fact. in economists’ lingo), the nominal interest rate is equal to the real interest rate plus actual inflation. Before the fact (ex anteBefore the fact. in economists’ lingo), the nominal interest rate is equal to the real interest rate plus the expectation of inflation.
Stop and Think Box
In early 2007, a man had a wallet returned that he had lost over sixty years earlier in France, during World War II.ABC News video, “Wallet Returned, 60 Years Later, A World War II Veteran gets his wallet returned to him sixty years later” (1/9/2007). In addition to his original Social Security card and a picture of his parents, the man received an unspecified sum of cash. Was losing the wallet a good investment? Why or why not?
No, because the risk that it would never be returned was very high. Plus, the dollar lost a significant amount of its purchasing power over the period due to inflation and the money earned no interest. At just 3 percent compounded annually, $100 would have grown to 100 × (1.03)60 = $589.16 after 60 years. At 6 percent, $100 would have grown to 100 × (1.06)60 = $3,298.77.
Traditionally, inflation expectations were unobservable so real rates were known only ex post. However, relatively new and special types of bonds indexed to inflation, called Treasury Inflation Protection Securities (TIPS), provide real interest rate information, allowing market participants to observe ex ante inflation expectations. For example, if the yield to maturity on a regular, nonindexed ten-year Treasury bond is 5 percent, and the yield on the ten-year TIPS is 2 percent, the inflation expectation, via the Fisher Equation π = i − ir, is 5 −2 = 3 percent. Figure 4.5 "U.S. real interest rate, 2001–2010" shows how inflation expectations have waxed and waned since the introduction of TIPS in 1997.
Key Takeaways
- The difference between the real and the nominal interest rate is literally inflation or inflation expectations.
- According to the Fisher Equation, nominal interest equals real interest plus inflation (or inflation expectations), or real interest equals nominal interest minus inflation (expectations).
- If actual inflation exceeds inflation expectations, real ex post (inflation-adjusted, after the fact) returns on bonds can be negative.
4.8 Suggested Reading
Fisher, Irving. The Purchasing Power of Money: Its Determination and Relation to Credit Interest and Crises. New York: Cosimo Classics, 2006.
Strumeyer, Gary. Investing in Fixed Income Securities: Understanding the Bond Market. Hoboken, NJ: John Wiley and Sons, 2005.
Wild, Russell. Bond Investing for Dummies. Hoboken, NJ: John Wiley and Sons, 2007.




