This is “Probability Computations for General Normal Random Variables”, section 5.3 from the book Beginning Statistics (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
5.3 Probability Computations for General Normal Random Variables
Learning Objective
- To learn how to compute probabilities related to any normal random variable.
If X is any normally distributed normal random variable then Figure 12.2 "Cumulative Normal Probability" can also be used to compute a probability of the form by means of the following equality.
If X is a normally distributed random variable with mean μ and standard deviation σ, then
where Z denotes a standard normal random variable. a can be any decimal number or ; b can be any decimal number or
The new endpoints and are the z-scores of a and b as defined in Section 2.4.2 in Chapter 2 "Descriptive Statistics".
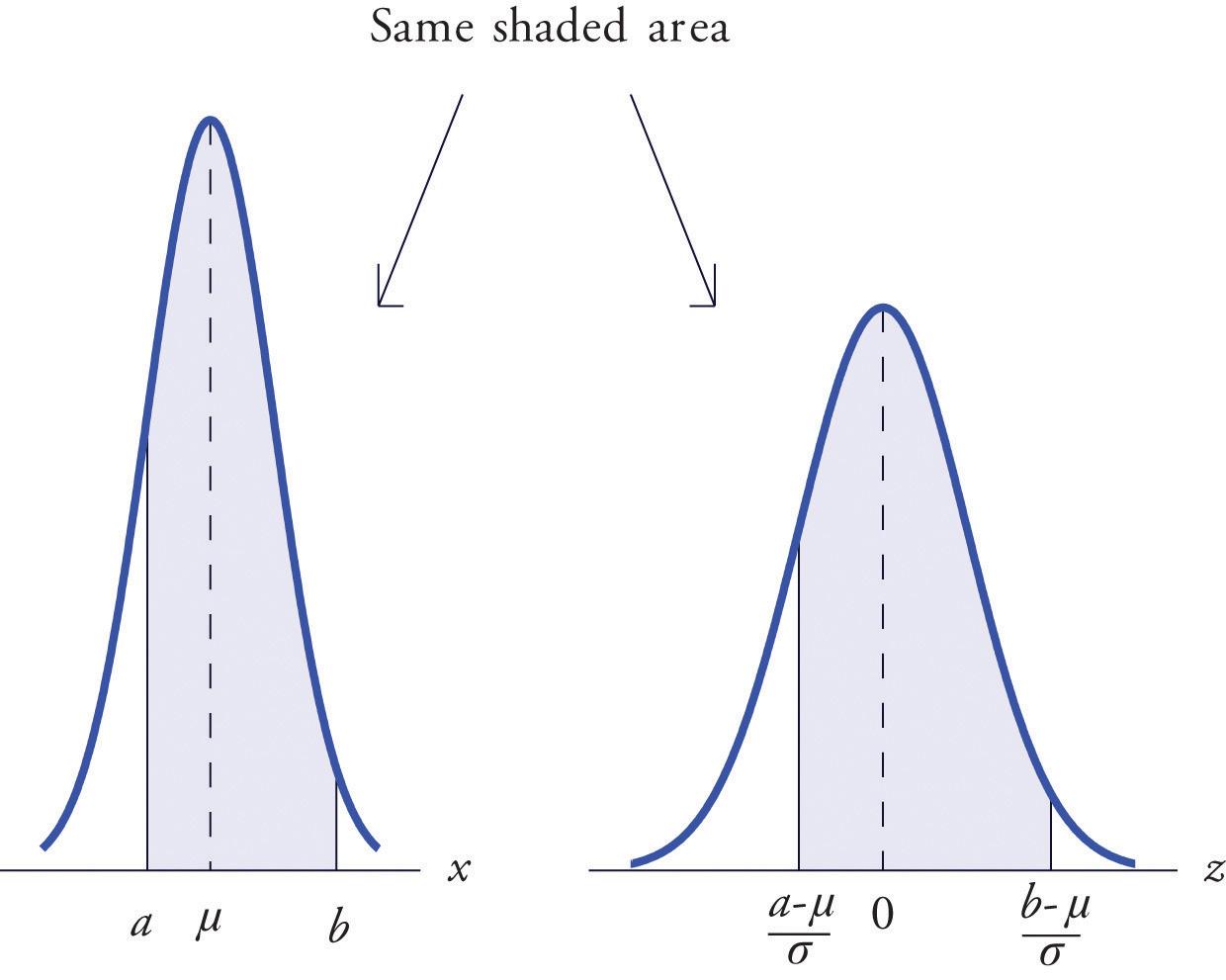
Figure 5.14 "Probability for an Interval of Finite Length" illustrates the meaning of the equality geometrically: the two shaded regions, one under the density curve for X and the other under the density curve for Z, have the same area. Instead of drawing both bell curves, though, we will always draw a single generic bell-shaped curve with both an x-axis and a z-axis below it.
Figure 5.14 Probability for an Interval of Finite Length
Example 9
Let X be a normal random variable with mean μ = 10 and standard deviation σ = 2.5. Compute the following probabilities.
- P(X < 14).
Solution:
Figure 5.15 Probability Computation for a General Normal Random Variable
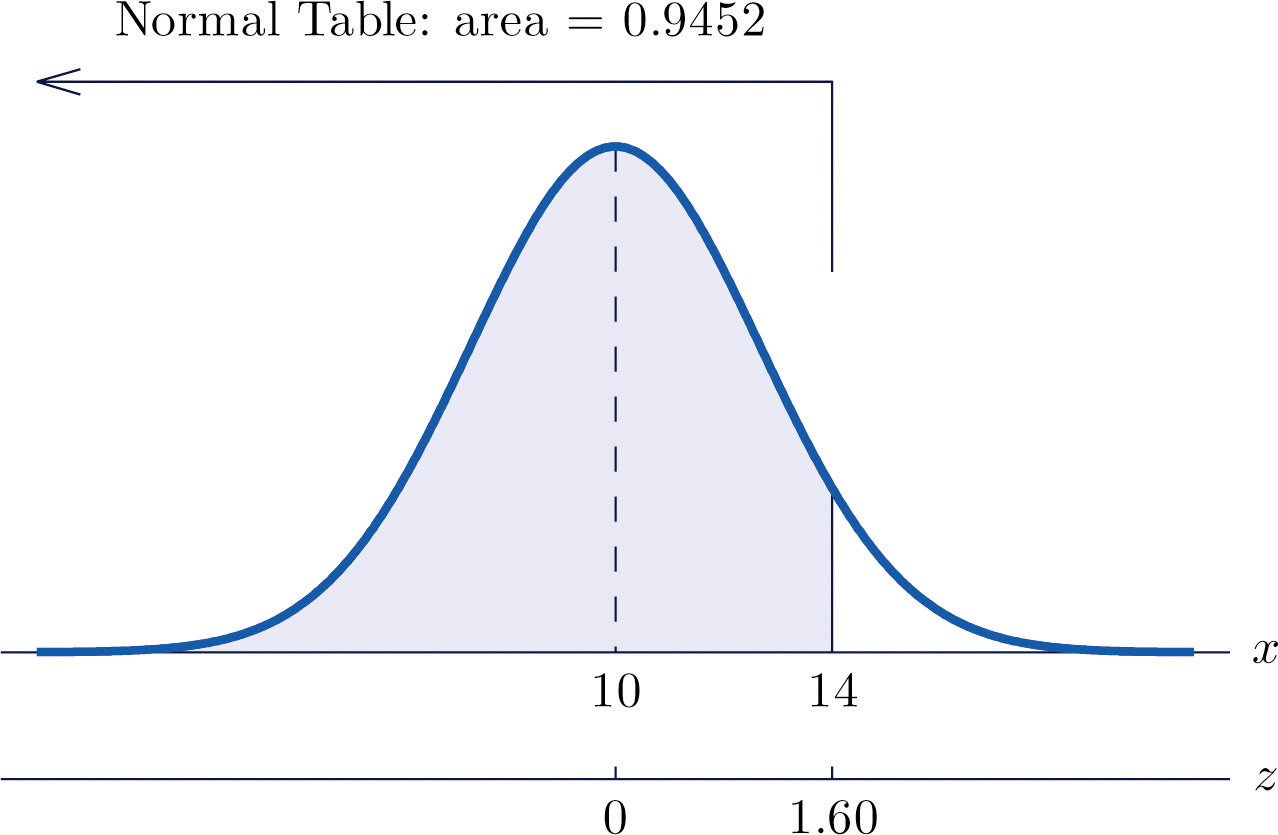
Figure 5.16 Probability Computation for a General Normal Random Variable
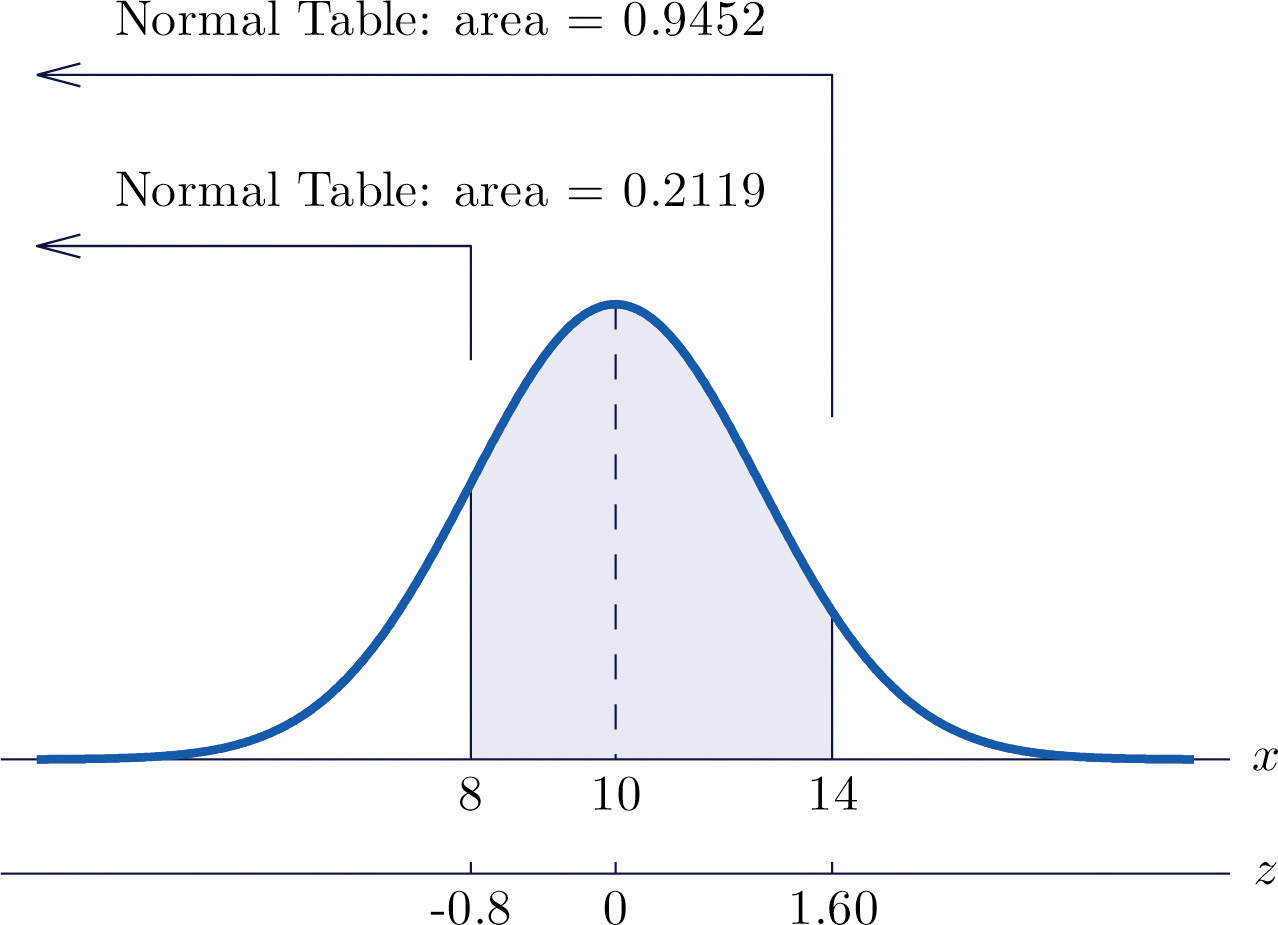
Example 10
The lifetimes of the tread of a certain automobile tire are normally distributed with mean 37,500 miles and standard deviation 4,500 miles. Find the probability that the tread life of a randomly selected tire will be between 30,000 and 40,000 miles.
Solution:
Let X denote the tread life of a randomly selected tire. To make the numbers easier to work with we will choose thousands of miles as the units. Thus μ = 37.5, σ = 4.5, and the problem is to compute Figure 5.17 "Probability Computation for Tire Tread Wear" illustrates the following computation:
Figure 5.17 Probability Computation for Tire Tread Wear
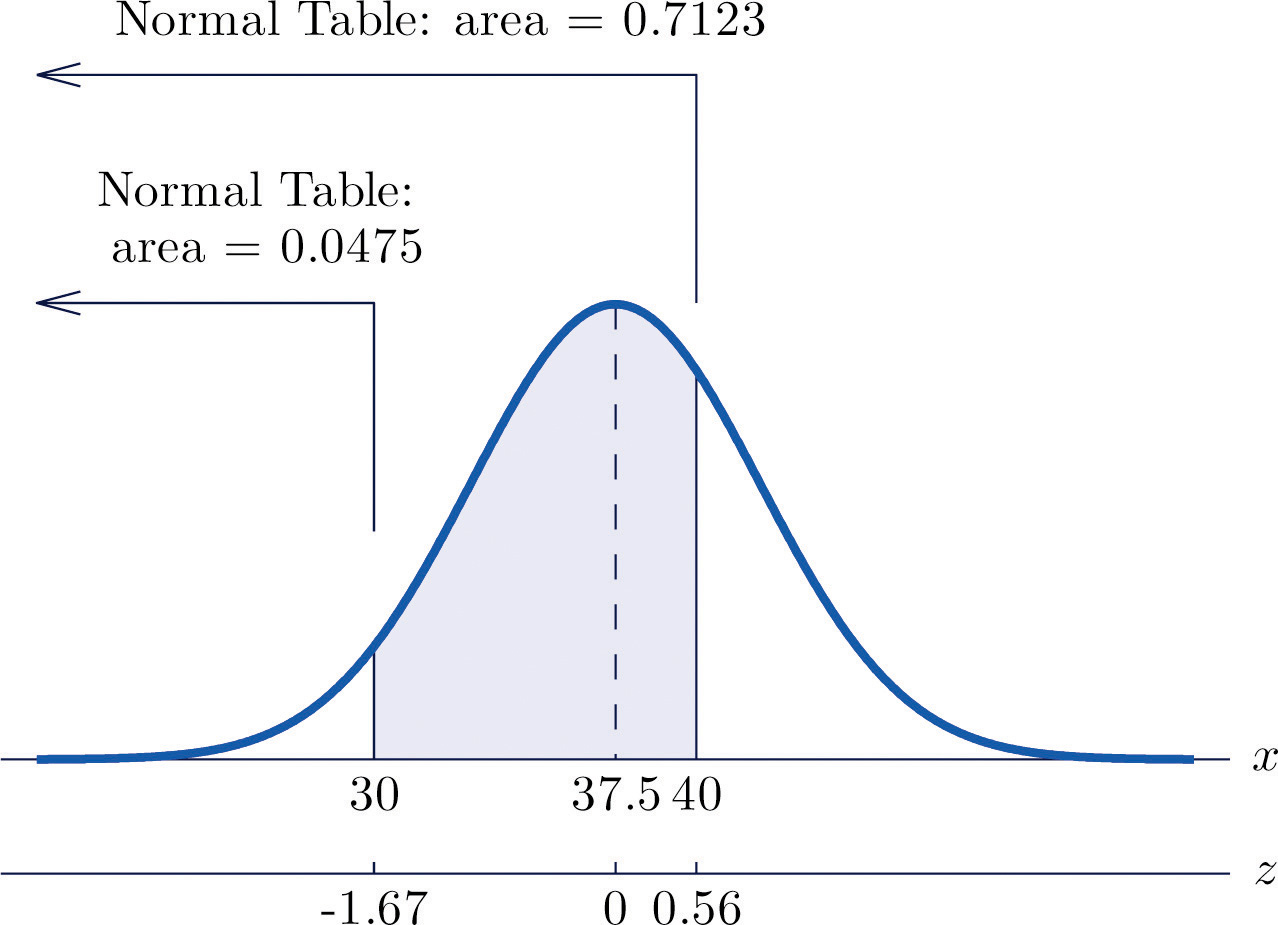
Note that the two z-scores were rounded to two decimal places in order to use Figure 12.2 "Cumulative Normal Probability".
Example 11
Scores on a standardized college entrance examination (CEE) are normally distributed with mean 510 and standard deviation 60. A selective university considers for admission only applicants with CEE scores over 650. Find percentage of all individuals who took the CEE who meet the university's CEE requirement for consideration for admission.
Solution:
Let X denote the score made on the CEE by a randomly selected individual. Then X is normally distributed with mean 510 and standard deviation 60. The probability that X lie in a particular interval is the same as the proportion of all exam scores that lie in that interval. Thus the solution to the problem is P(X > 650), expressed as a percentage. Figure 5.18 "Probability Computation for Exam Scores" illustrates the following computation:
Figure 5.18 Probability Computation for Exam Scores
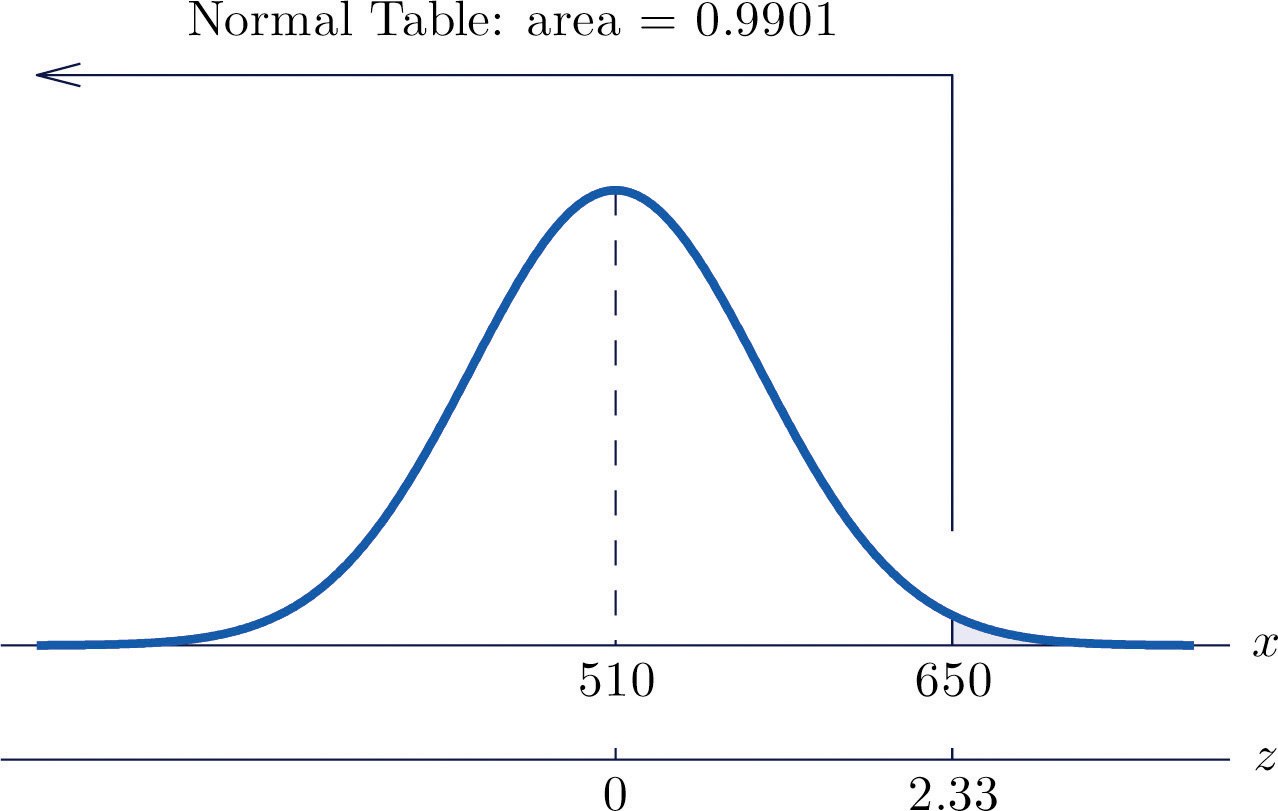
The proportion of all CEE scores that exceed 650 is 0.0099, hence 0.99% or about 1% do.
Key Takeaway
- Probabilities for a general normal random variable are computed using Figure 12.2 "Cumulative Normal Probability" after converting x-values to z-scores.
Exercises
-
X is a normally distributed random variable with mean 57 and standard deviation 6. Find the probability indicated.
- P(X < 59.5)
- P(X < 46.2)
- P(X > 52.2)
- P(X > 70)
-
X is a normally distributed random variable with mean −25 and standard deviation 4. Find the probability indicated.
- P(X < −27.2)
- P(X < −14.8)
- P(X > −33.1)
- P(X > −16.5)
-
X is a normally distributed random variable with mean 112 and standard deviation 15. Find the probability indicated.
-
X is a normally distributed random variable with mean 72 and standard deviation 22. Find the probability indicated.
-
X is a normally distributed random variable with mean 500 and standard deviation 25. Find the probability indicated.
- P(X < 400)
-
X is a normally distributed random variable with mean 0 and standard deviation 0.75. Find the probability indicated.
- P(−4.02 < X < 3.82)
- P(X > 4.11)
-
X is a normally distributed random variable with mean 15 and standard deviation 1. Use Figure 12.2 "Cumulative Normal Probability" to find the first probability listed. Find the second probability using the symmetry of the density curve. Sketch the density curve with relevant regions shaded to illustrate the computation.
- P(X < 12), P(X > 18)
- P(X < 14), P(X > 16)
- P(X < 11.25), P(X > 18.75)
- P(X < 12.67), P(X > 17.33)
-
X is a normally distributed random variable with mean 100 and standard deviation 10. Use Figure 12.2 "Cumulative Normal Probability" to find the first probability listed. Find the second probability using the symmetry of the density curve. Sketch the density curve with relevant regions shaded to illustrate the computation.
- P(X < 80), P(X > 120)
- P(X < 75), P(X > 125)
- P(X < 84.55), P(X > 115.45)
- P(X < 77.42), P(X > 122.58)
-
X is a normally distributed random variable with mean 67 and standard deviation 13. The probability that X takes a value in the union of intervals will be denoted Use Figure 12.2 "Cumulative Normal Probability" to find the following probabilities of this type. Sketch the density curve with relevant regions shaded to illustrate the computation. Because of the symmetry of the density curve you need to use Figure 12.2 "Cumulative Normal Probability" only one time for each part.
-
X is a normally distributed random variable with mean 288 and standard deviation 6. The probability that X takes a value in the union of intervals will be denoted Use Figure 12.2 "Cumulative Normal Probability" to find the following probabilities of this type. Sketch the density curve with relevant regions shaded to illustrate the computation. Because of the symmetry of the density curve you need to use Figure 12.2 "Cumulative Normal Probability" only one time for each part.
Basic
-
The amount X of beverage in a can labeled 12 ounces is normally distributed with mean 12.1 ounces and standard deviation 0.05 ounce. A can is selected at random.
- Find the probability that the can contains at least 12 ounces.
- Find the probability that the can contains between 11.9 and 12.1 ounces.
-
The length of gestation for swine is normally distributed with mean 114 days and standard deviation 0.75 day. Find the probability that a litter will be born within one day of the mean of 114.
-
The systolic blood pressure X of adults in a region is normally distributed with mean 112 mm Hg and standard deviation 15 mm Hg. A person is considered “prehypertensive” if his systolic blood pressure is between 120 and 130 mm Hg. Find the probability that the blood pressure of a randomly selected person is prehypertensive.
-
Heights X of adult women are normally distributed with mean 63.7 inches and standard deviation 2.71 inches. Romeo, who is 69.25 inches tall, wishes to date only women who are shorter than he but within 4 inches of his height. Find the probability that the next woman he meets will have such a height.
-
Heights X of adult men are normally distributed with mean 69.1 inches and standard deviation 2.92 inches. Juliet, who is 63.25 inches tall, wishes to date only men who are taller than she but within 6 inches of her height. Find the probability that the next man she meets will have such a height.
-
A regulation hockey puck must weigh between 5.5 and 6 ounces. The weights X of pucks made by a particular process are normally distributed with mean 5.75 ounces and standard deviation 0.11 ounce. Find the probability that a puck made by this process will meet the weight standard.
-
A regulation golf ball may not weigh more than 1.620 ounces. The weights X of golf balls made by a particular process are normally distributed with mean 1.361 ounces and standard deviation 0.09 ounce. Find the probability that a golf ball made by this process will meet the weight standard.
-
The length of time that the battery in Hippolyta's cell phone will hold enough charge to operate acceptably is normally distributed with mean 25.6 hours and standard deviation 0.32 hour. Hippolyta forgot to charge her phone yesterday, so that at the moment she first wishes to use it today it has been 26 hours 18 minutes since the phone was last fully charged. Find the probability that the phone will operate properly.
-
The amount of non-mortgage debt per household for households in a particular income bracket in one part of the country is normally distributed with mean $28,350 and standard deviation $3,425. Find the probability that a randomly selected such household has between $20,000 and $30,000 in non-mortgage debt.
-
Birth weights of full-term babies in a certain region are normally distributed with mean 7.125 lb and standard deviation 1.290 lb. Find the probability that a randomly selected newborn will weigh less than 5.5 lb, the historic definition of prematurity.
-
The distance from the seat back to the front of the knees of seated adult males is normally distributed with mean 23.8 inches and standard deviation 1.22 inches. The distance from the seat back to the back of the next seat forward in all seats on aircraft flown by a budget airline is 26 inches. Find the proportion of adult men flying with this airline whose knees will touch the back of the seat in front of them.
-
The distance from the seat to the top of the head of seated adult males is normally distributed with mean 36.5 inches and standard deviation 1.39 inches. The distance from the seat to the roof of a particular make and model car is 40.5 inches. Find the proportion of adult men who when sitting in this car will have at least one inch of headroom (distance from the top of the head to the roof).
Applications
-
The useful life of a particular make and type of automotive tire is normally distributed with mean 57,500 miles and standard deviation 950 miles.
- Find the probability that such a tire will have a useful life of between 57,000 and 58,000 miles.
- Hamlet buys four such tires. Assuming that their lifetimes are independent, find the probability that all four will last between 57,000 and 58,000 miles. (If so, the best tire will have no more than 1,000 miles left on it when the first tire fails.) Hint: There is a binomial random variable here, whose value of p comes from part (a).
-
A machine produces large fasteners whose length must be within 0.5 inch of 22 inches. The lengths are normally distributed with mean 22.0 inches and standard deviation 0.17 inch.
- Find the probability that a randomly selected fastener produced by the machine will have an acceptable length.
- The machine produces 20 fasteners per hour. The length of each one is inspected. Assuming lengths of fasteners are independent, find the probability that all 20 will have acceptable length. Hint: There is a binomial random variable here, whose value of p comes from part (a).
-
The lengths of time taken by students on an algebra proficiency exam (if not forced to stop before completing it) are normally distributed with mean 28 minutes and standard deviation 1.5 minutes.
- Find the proportion of students who will finish the exam if a 30-minute time limit is set.
- Six students are taking the exam today. Find the probability that all six will finish the exam within the 30-minute limit, assuming that times taken by students are independent. Hint: There is a binomial random variable here, whose value of p comes from part (a).
-
Heights of adult men between 18 and 34 years of age are normally distributed with mean 69.1 inches and standard deviation 2.92 inches. One requirement for enlistment in the military is that men must stand between 60 and 80 inches tall.
- Find the probability that a randomly elected man meets the height requirement for military service.
- Twenty-three men independently contact a recruiter this week. Find the probability that all of them meet the height requirement. Hint: There is a binomial random variable here, whose value of p comes from part (a).
-
A regulation hockey puck must weigh between 5.5 and 6 ounces. In an alternative manufacturing process the mean weight of pucks produced is 5.75 ounce. The weights of pucks have a normal distribution whose standard deviation can be decreased by increasingly stringent (and expensive) controls on the manufacturing process. Find the maximum allowable standard deviation so that at most 0.005 of all pucks will fail to meet the weight standard. (Hint: The distribution is symmetric and is centered at the middle of the interval of acceptable weights.)
-
The amount of gasoline X delivered by a metered pump when it registers 5 gallons is a normally distributed random variable. The standard deviation σ of X measures the precision of the pump; the smaller σ is the smaller the variation from delivery to delivery. A typical standard for pumps is that when they show that 5 gallons of fuel has been delivered the actual amount must be between 4.97 and 5.03 gallons (which corresponds to being off by at most about half a cup). Supposing that the mean of X is 5, find the largest that σ can be so that P(4.97 < X < 5.03) is 1.0000 to four decimal places when computed using Figure 12.2 "Cumulative Normal Probability", which means that the pump is sufficiently accurate. (Hint: The z-score of 5.03 will be the smallest value of Z so that Figure 12.2 "Cumulative Normal Probability" gives )
Additional Exercises
Answers
-
- 0.6628
- 0.7881
- 0.0359
- 0.0150
-
-
- 0.5959
- 0.2899
- 0.3439
-
-
- 0.0000
- 0.9131
-
-
- 0.0013, 0.0013
- 0.1587, 0.1587
- 0.0001, 0.0001
- 0.0099, 0.0099
-
-
- 0.4412
- 0.1236
- 0.1676
- 0.0208
-
-
- 0.9772
- 0.5000
-
-
0.1830
-
-
0.4971
-
-
0.9980
-
-
0.6771
-
-
0.0359
-
-
- 0.4038
- 0.0266
-
-
- 0.9082
- 0.5612
-
-
0.089
-




