This is “Factoring and Solving by Factoring”, chapter 6 from the book Beginning Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
Chapter 6 Factoring and Solving by Factoring
6.1 Introduction to Factoring
Learning Objectives
- Determine the greatest common factor (GCF) of natural numbers.
- Determine the GCF of monomials.
- Factor out the GCF of a polynomial.
- Factor a four-term polynomial by grouping.
GCF of Natural Numbers
The process of writing a number or expression as a product is called factoringThe process of writing a number or expression as a product.. If we write 60 = 5 ⋅ 12, we say that the product 5 ⋅ 12 is a factorizationAny combination of factors, multiplied together, resulting in the product. of 60 and that 5 and 12 are factorsAny of the numbers or expressions that form a product.. Typically, there are many ways to factor a number. For example,
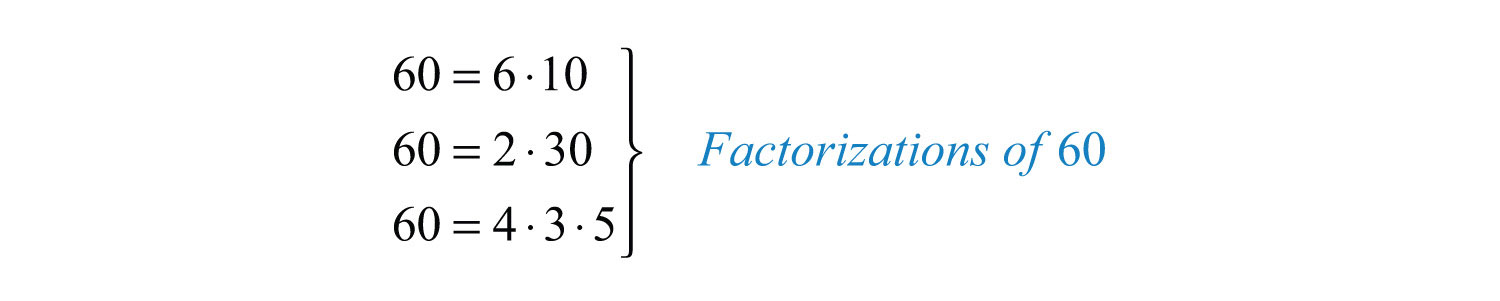
Recall that a prime number is defined as a natural number with exactly two natural number factors, 1 and itself. The first ten prime numbers follow:
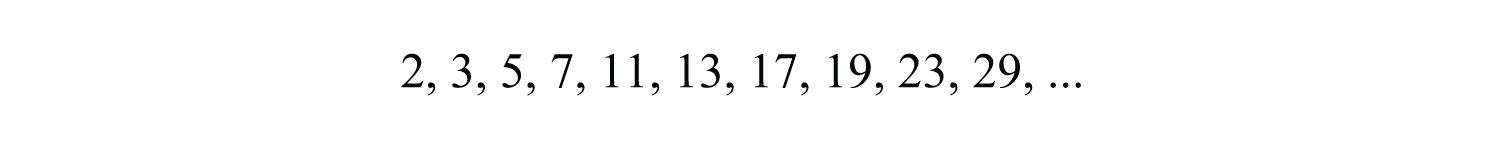
Any natural number greater than 1 can be uniquely written as a product of prime numbers. This product is called the prime factorizationThe unique factorization of a natural number written as a product of primes.. The prime factorization of 60 can be determined by continuing to factor until only a product of prime numbers remains.
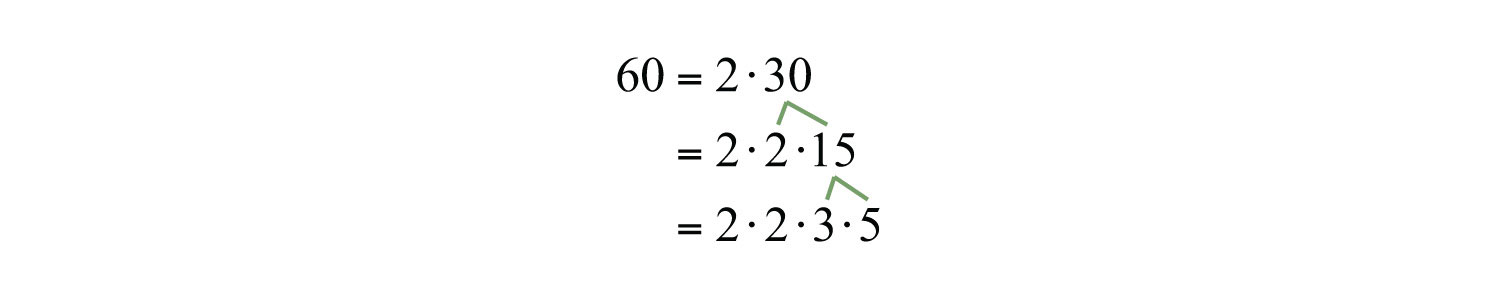
Since the prime factorization is unique, it does not matter how we choose to initially factor the number; the end result will be the same. The prime factorization of 60 follows:

Recall that the greatest common factor (GCF)The product of all the common prime factors. of any two natural numbers is the product of all the common prime factors.
Example 1: Find the GCF of 60 and 140.
Solution: First, determine the prime factorizations of both integers.

The product of the common prime factors is ; hence the . To see that it is the greatest common factor, we can write the following:
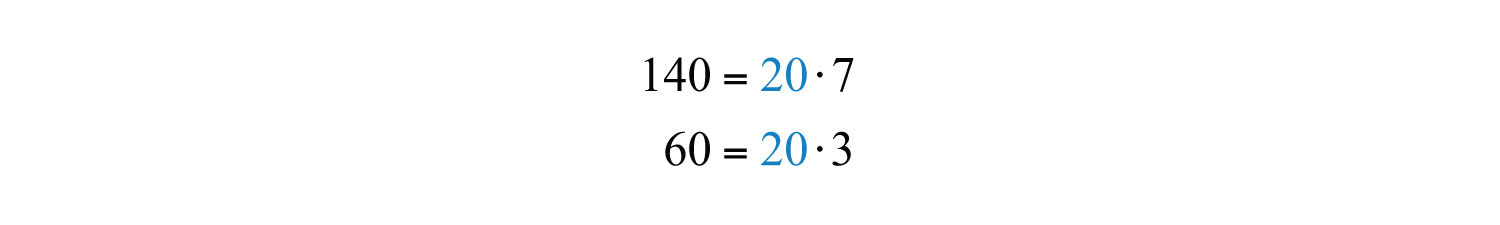
Answer: The greatest common factor of 60 and 140 is 20.
Example 2: Find the GCF of 504 and 1,080.
Solution: First, determine the prime factorizations of both integers.

The product of the common prime factors is . The . Note that we multiplied the common prime factors with the smallest exponent.
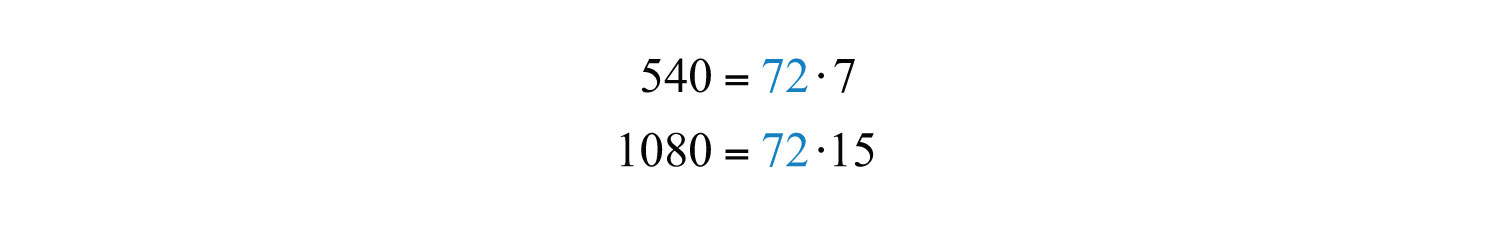
The numbers 7 and 15 share no common natural number factor other than 1; we say that they are relatively primeExpressions that share no common factors other than 1..
Answer: The greatest common factor of 504 and 1,080 is 72.
GCF of Monomials
We next consider factorizations of monomials. For example, and are factors of because . Typically, there are many ways to factor a monomial. Some factorizations of follow:
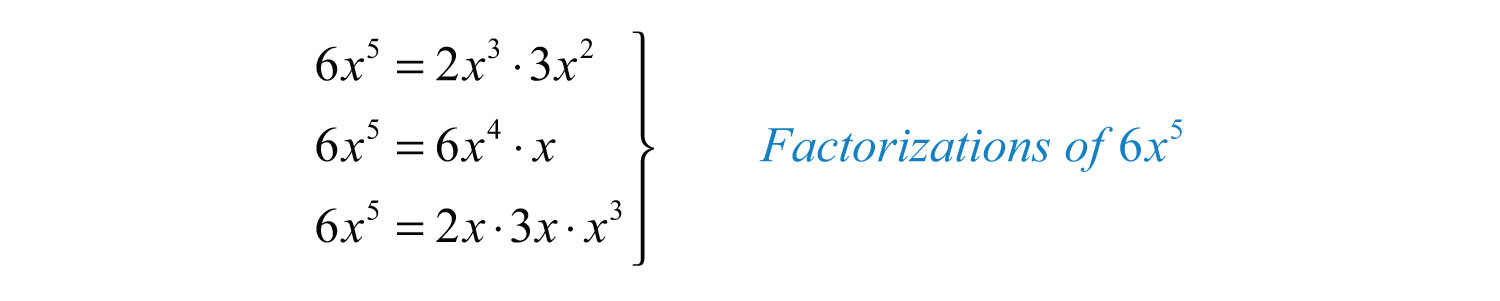
Given two or more monomials, it will be useful to find the greatest common monomial factor of each. For example, consider and . The variable part of these two monomials look very much like the prime factorization of natural numbers and, in fact, can be treated the same way. Steps for finding the GCF of monomialsThe product of the GCF of the coefficients and all common variable factors. are outlined in the following example.
Example 3: Find the GCF of and .
Solution:
Step 1: Find the GCF of the coefficients.
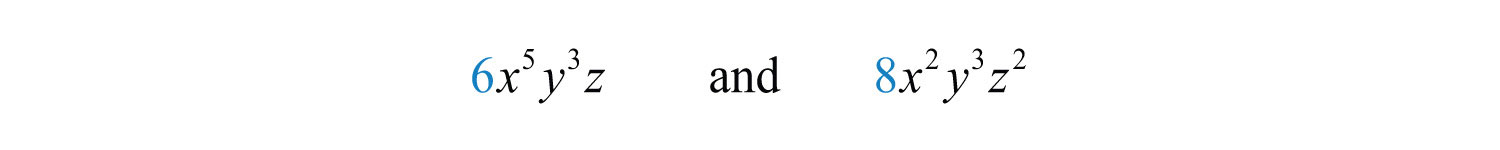
In this case, the .
Step 2: Determine the common variable factors with smallest exponents.
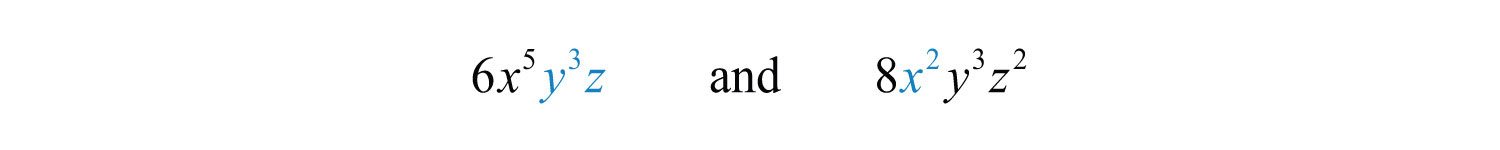
In this case, the common variables with the smallest exponents are , , and .
Step 3: The GCF of the monomials is the product of the common variable factors and the GCF of the coefficients. Therefore,
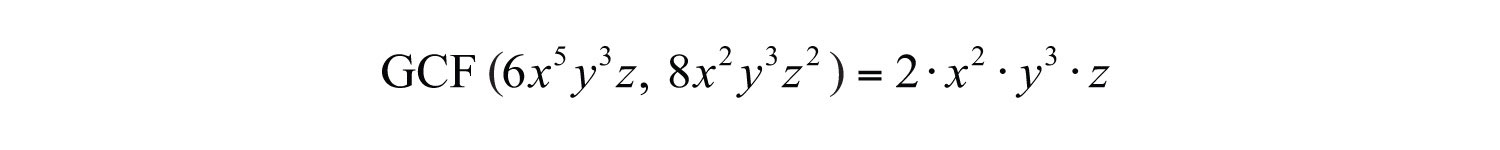
Answer:
It is worth pointing out that the GCF in the previous example divides both expressions evenly:
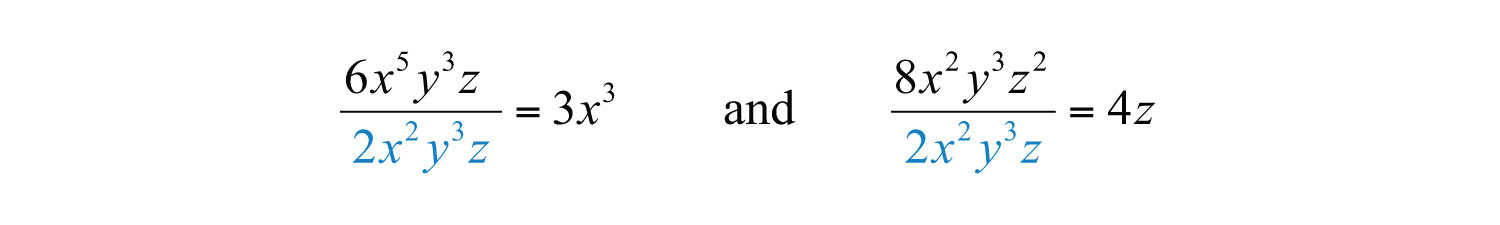
Furthermore, we can write the following:
The factors and share no common monomial factors other than 1; they are relatively prime.
Example 4: Determine the GCF of the following expressions: and .
Solution: The prime factorizations of the coefficients are
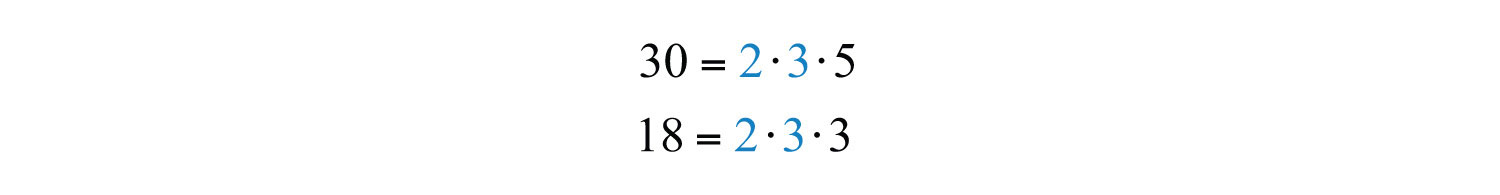
Thus the GCF(30, 18) = 2 ⋅ 3 = 6. Next, consider the variable part:
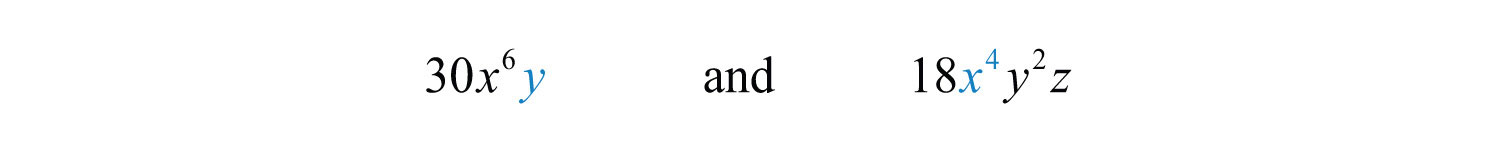
The variable factors in common are and y. The factor z is not in common and we have
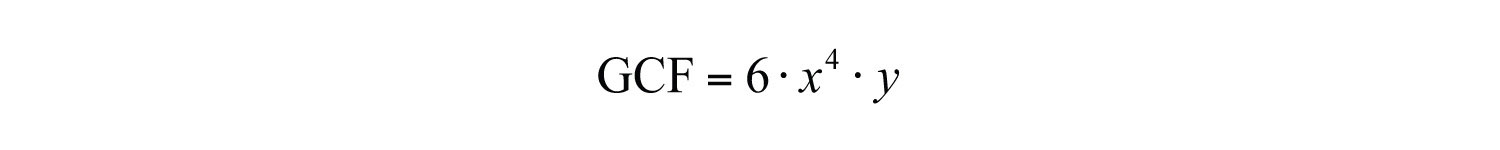
Answer:
Example 5: Determine the GCF of the following three expressions: , , and .
Solution: First, determine the GCF of the coefficients.
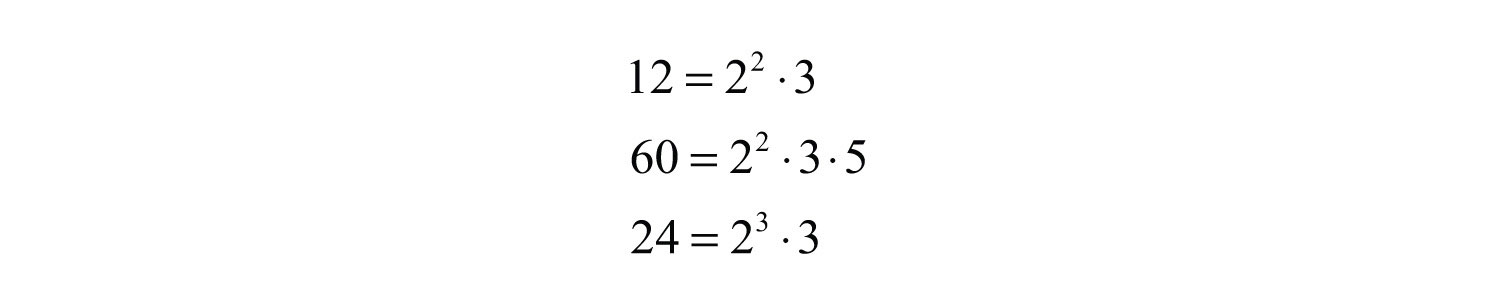
The . Next, determine the common factors of the variable part:
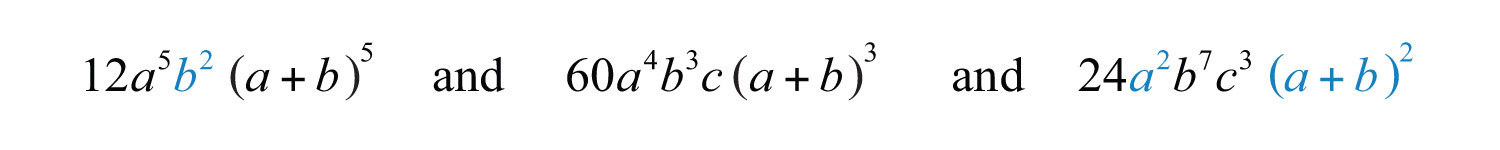
The variable factors in common are , , and . Therefore,
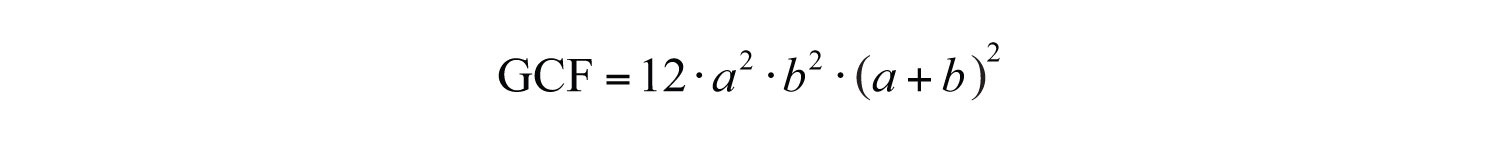
Answer: . Note that the variable c is not common to all three expressions and thus is not included in the GCF.
Try this! Determine the GCF of the following: , , and .
Answer:
Video Solution
(click to see video)Factoring out the GCF
We have seen that application of the distributive property is the key to multiplying polynomials. The process of factoring a polynomialThe process of rewriting a polynomial as a product of polynomial factors. involves using the distributive property in reverse to write each polynomial as a product of polynomial factors.
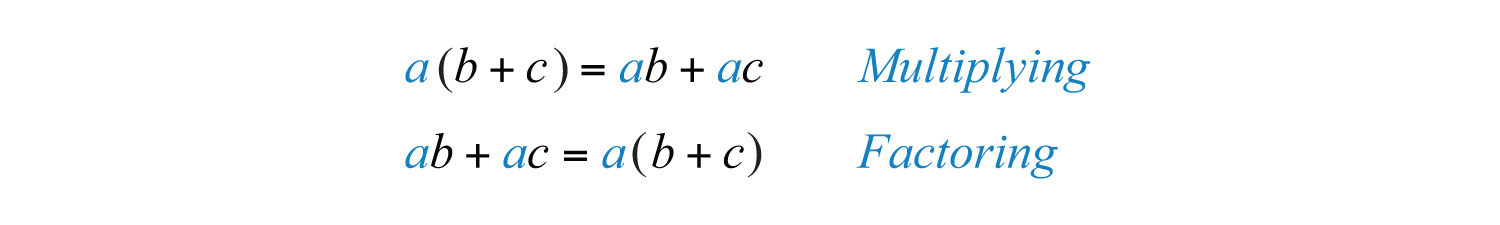
To demonstrate this idea, we multiply and factor side by side. Factoring utilizes the GCF of the terms.

In the previous example, we see that the distributive property allows us to write the polynomial as a product of the two factors and . Note that in this case, is the GCF of the terms of the polynomial:
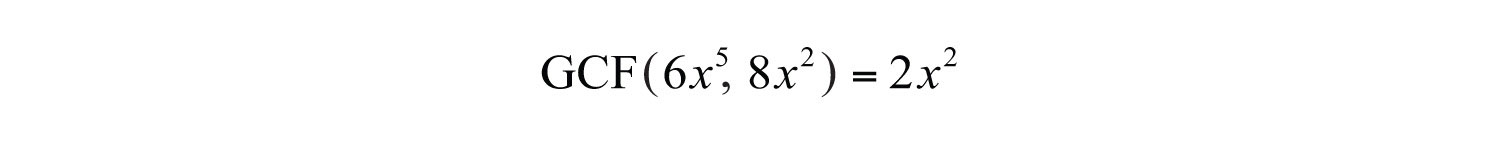
Factoring out the GCFThe process of rewriting a polynomial as a product using the GCF of all of its terms. involves rewriting a polynomial as a product where a factor is the GCF of all of its terms:
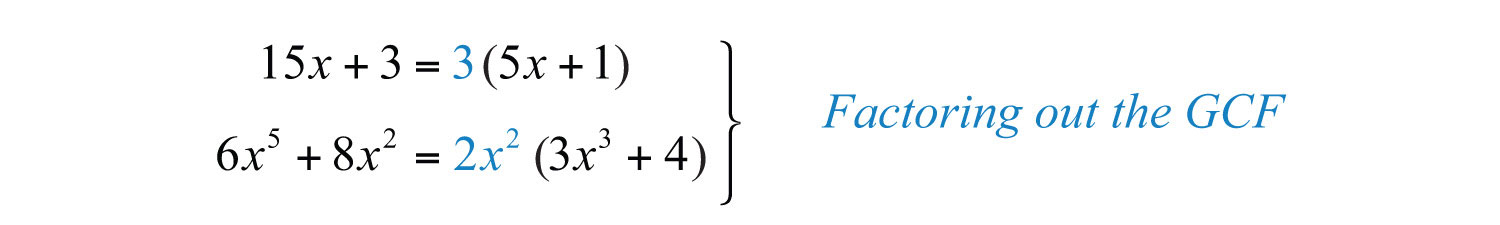
The steps for factoring out the GCF of a polynomialThe greatest common factor of all the terms of the polynomial. are outlined in the following example.
Example 6: Factor out the GCF: .
Solution:
Step 1: Identify the GCF of all the terms. In this case, the GCF(7, 21, 14) = 7, and the common variable factor with the smallest exponent is . The GCF of the polynomial is .
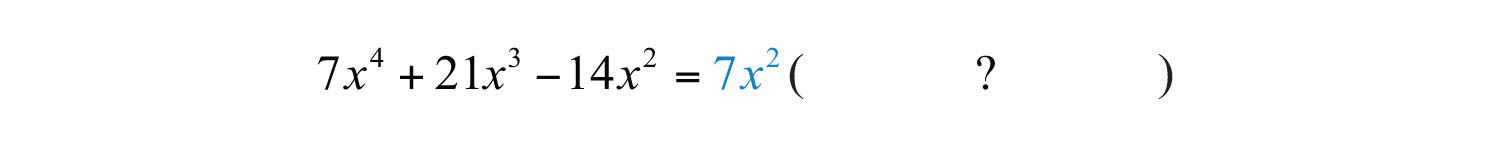
Step 2: Determine the terms of the missing factor by dividing each term of the original expression by the GCF. (This step is usually performed mentally.)
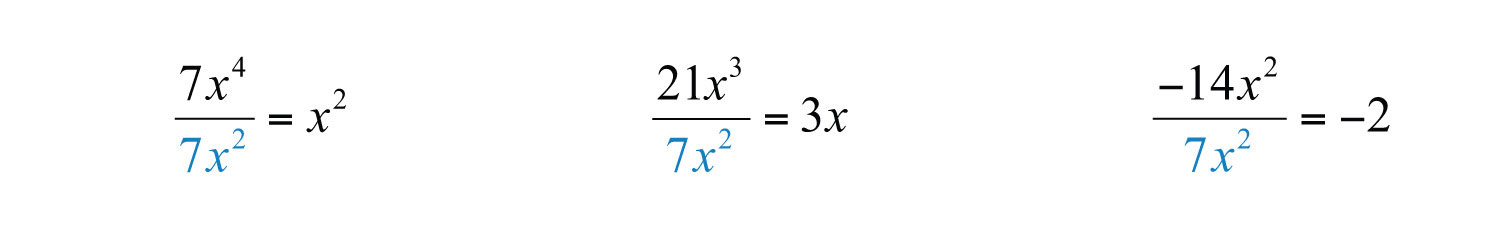
Step 3: Apply the distributive property (in reverse) using the terms found in the previous step.
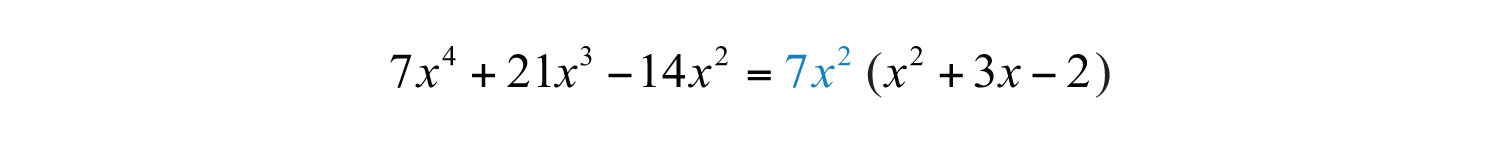
Step 4: As a check, multiply using the distributive property to verify that the product equals the original expression. (This step is optional and can be performed mentally.)
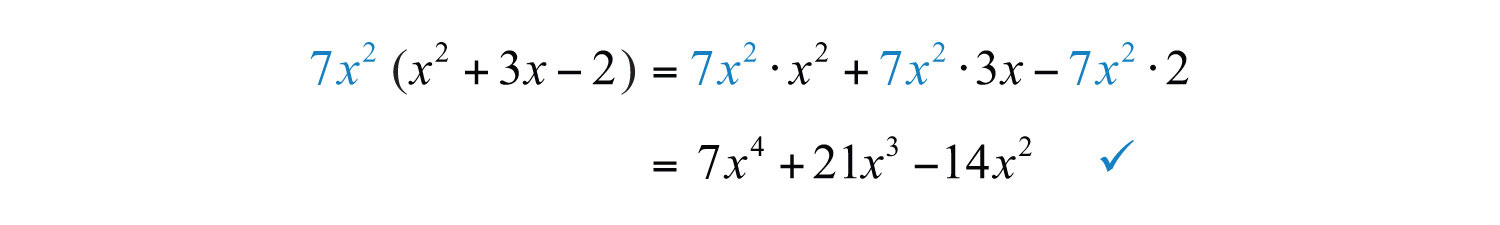
Answer:
Example 7: Factor out the GCF: .
Solution: There are no variable factors in common and the GCF(48, 16, 4) = 4.
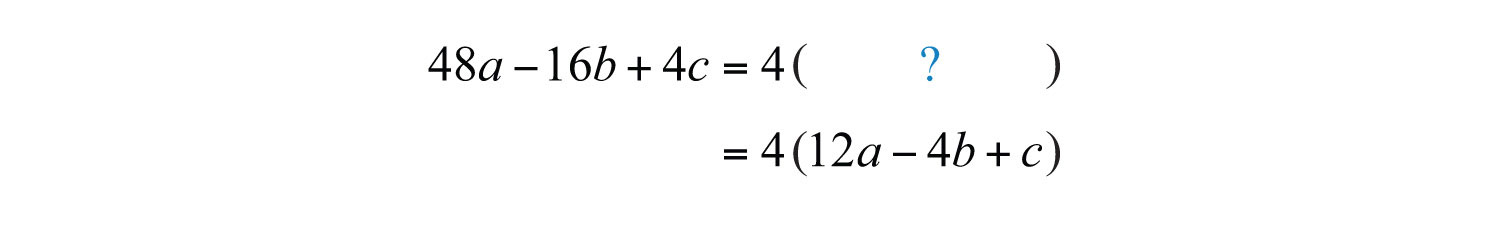
Answer:
Example 8: Factor out the GCF: .
Solution: The GCF(25, 15, 5) = 5, and the common variable factor with smallest exponents is . The GCF of all the terms is .
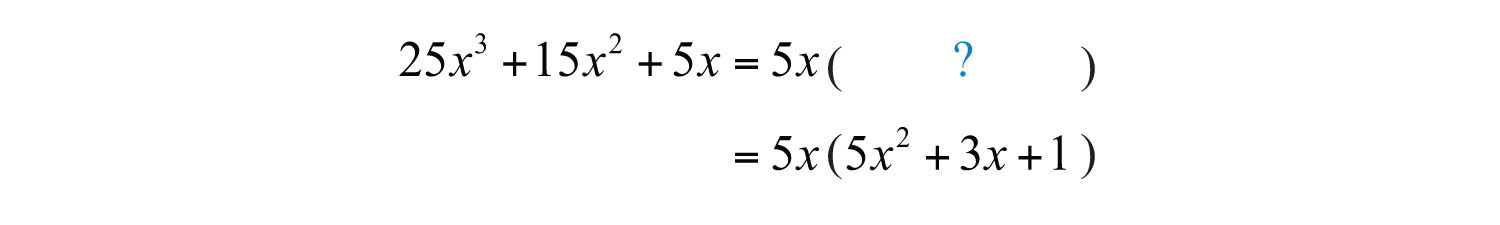
Answer:
If the GCF is the same as one of the terms, then, after the GCF is factored out, a constant term 1 will remain. In the previous example, we can see that . The importance of remembering the constant term becomes clear when performing the check using the distributive property:

The constant term 1 allows us to obtain the same original expression after we distribute.
Example 9: Factor out the GCF: .
Solution: The , and the common variables with smallest exponent are and . Therefore, the GCF of the terms is . The first term does not have a variable factor of and thus cannot be a part of the greatest common factor. If we divide each term by , we obtain
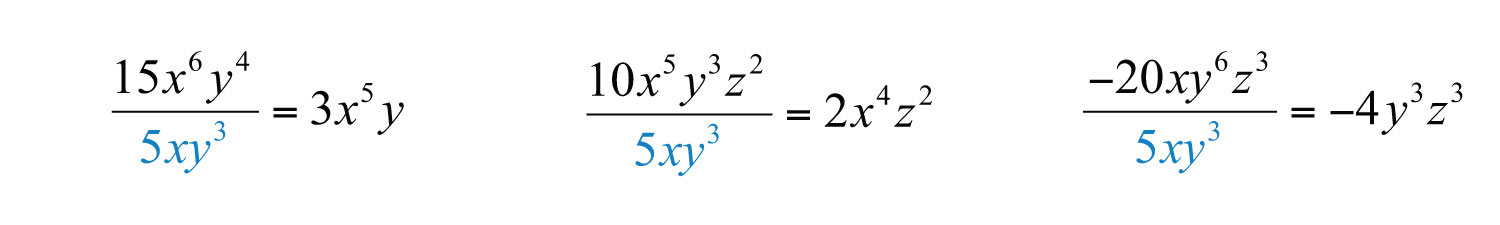
and can write
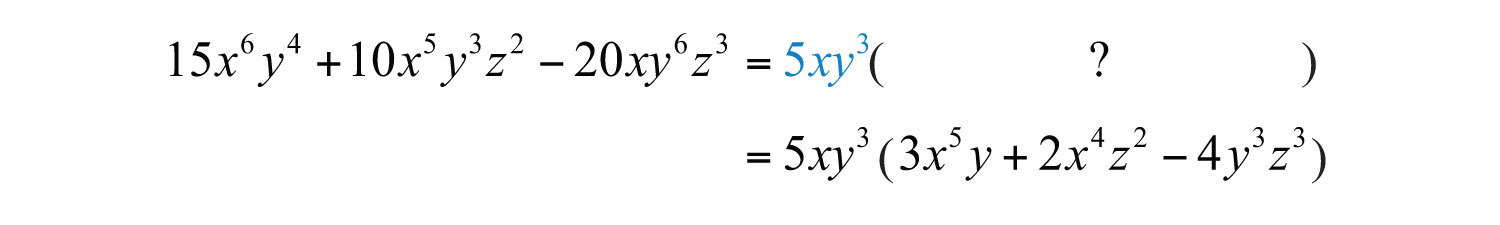
Answer:
Example 10: Factor out the GCF: .
Solution: The GCF(24, 8) = 8, and the variable factors with smallest exponents are , , and . Therefore, the GCF of all the terms is .
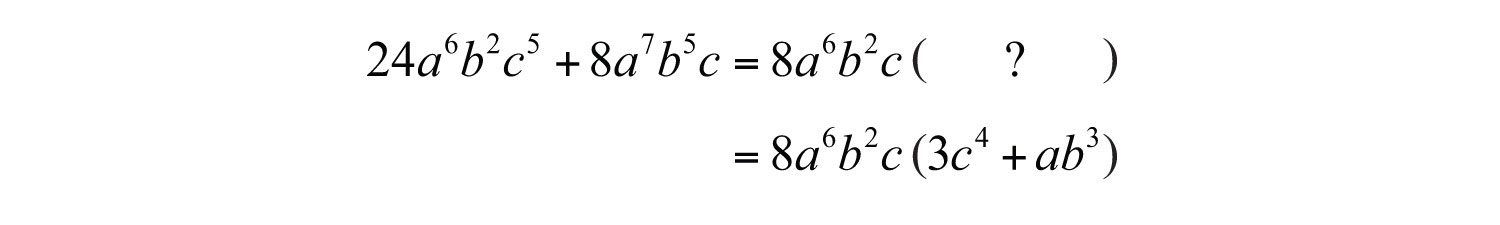
Answer:
Of course, not all polynomials with integer coefficients can be factored as a product of polynomials with integer coefficients other than 1 and itself. If this is the case, then we say that it is a prime polynomialA polynomial with integer coefficients that cannot be factored as a product of polynomials with integer coefficients other than 1 and itself..
Example 11: Factor: .
Solution: Prime: there are no polynomial factors other than 1 and itself.
Answer: Prime
Try this! Factor out the GCF: .
Answer:
Video Solution
(click to see video)Factor by Grouping
In this section, we outline a technique for factoring polynomials with four terms. First, review some preliminary examples where the terms have a common binomial factor.
Example 12: Factor: .
Solution: This expression is a binomial with terms and . In this case, is a common factor. Begin by factoring this common factor out:
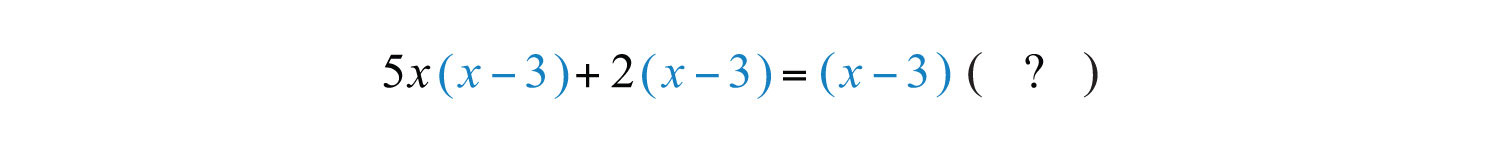
To determine the terms of the remaining factor, divide each term by :

This step is typically performed mentally. We have
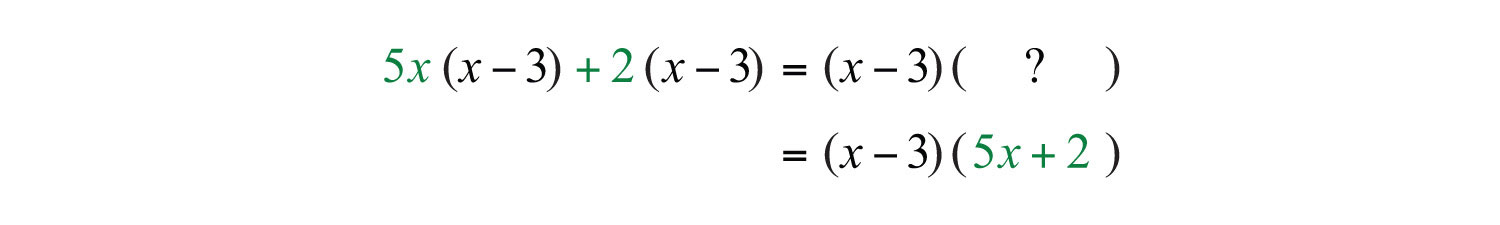
Answer:
Recall that 1 is always a common factor. If the GCF is the same as a term, then the factor 1 remains after we factor out that GCF.
Example 13: Factor: .
Solution: Rewrite the second term as and then factor out the common binomial factor .
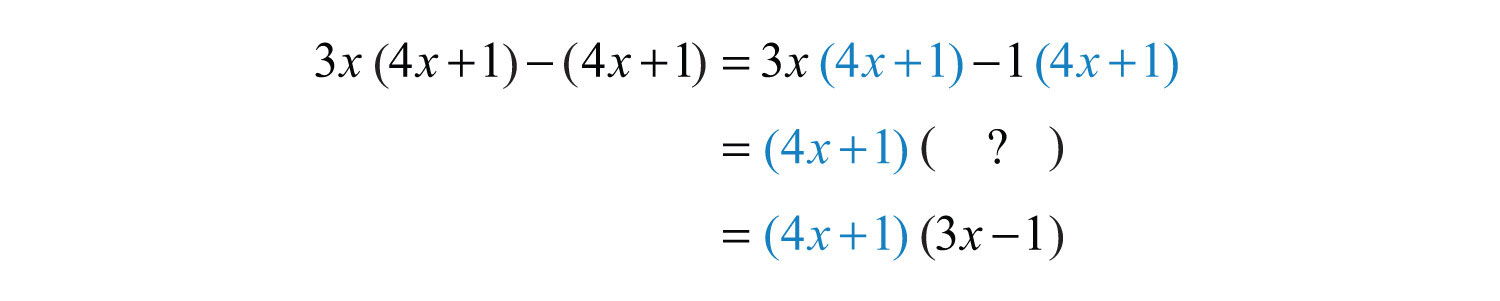
Answer:
Remember that the goal for this section is to develop a technique that enables us to factor polynomials with four terms into a product of binomials. The intermediate step of this process looks like the previous two examples. For example, we wish to factor
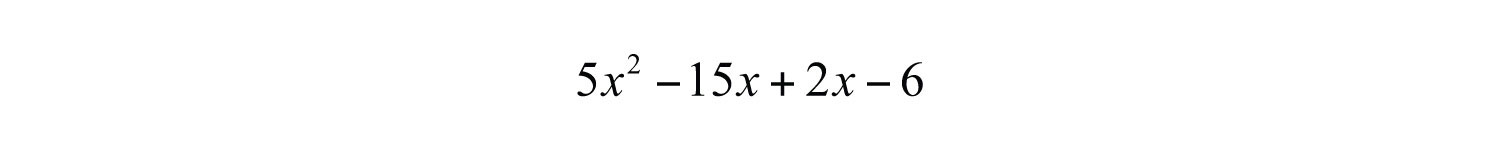
Begin by grouping the first two terms and the last two terms. Then factor out the GCF of each grouping:
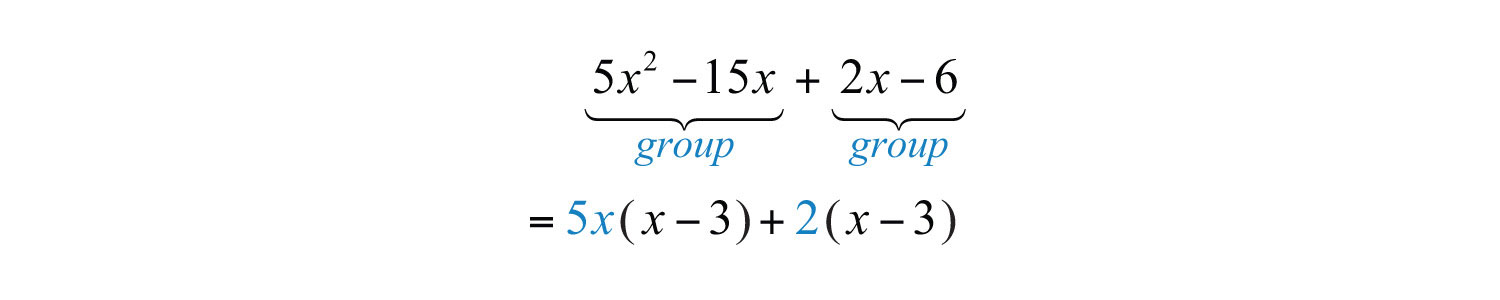
In this form, it is a binomial with a common binomial factor, .
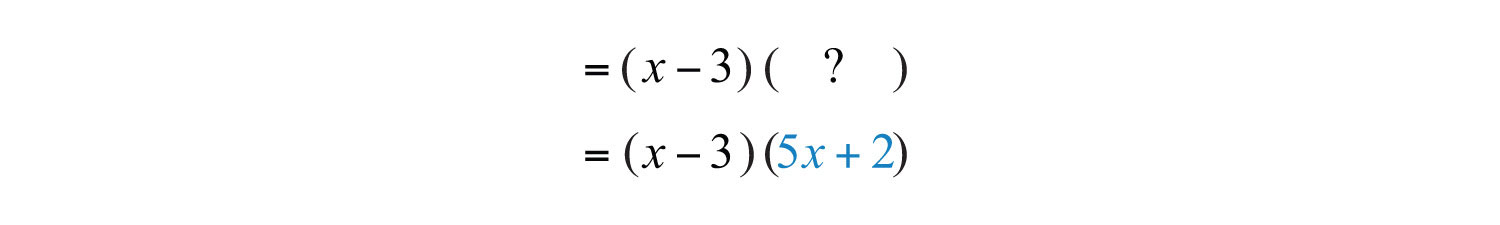
The steps that follow outline a technique for factoring four-term polynomials called factor by groupingA technique for factoring polynomials with four terms..
Example 14: Factor: .
Solution: Group terms in such a way as to obtain a binomial with common factors.
Step 1: Group the first two and last two terms and then factor out the GCF of each.
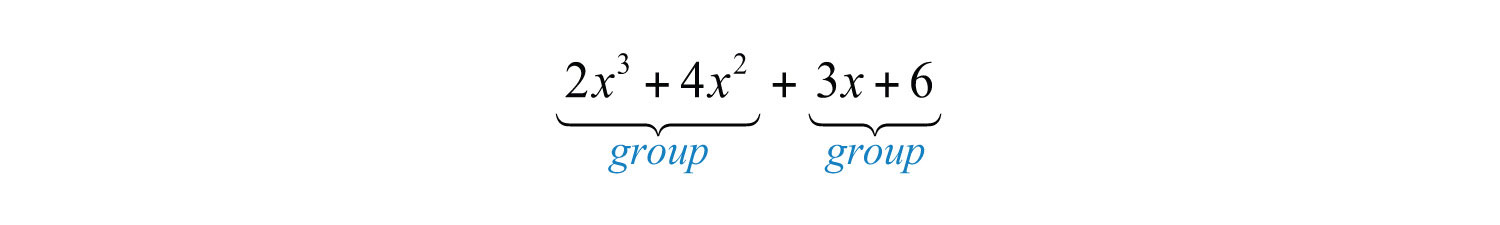
The GCF of the first two terms is , and the GCF of the second two terms is 3.
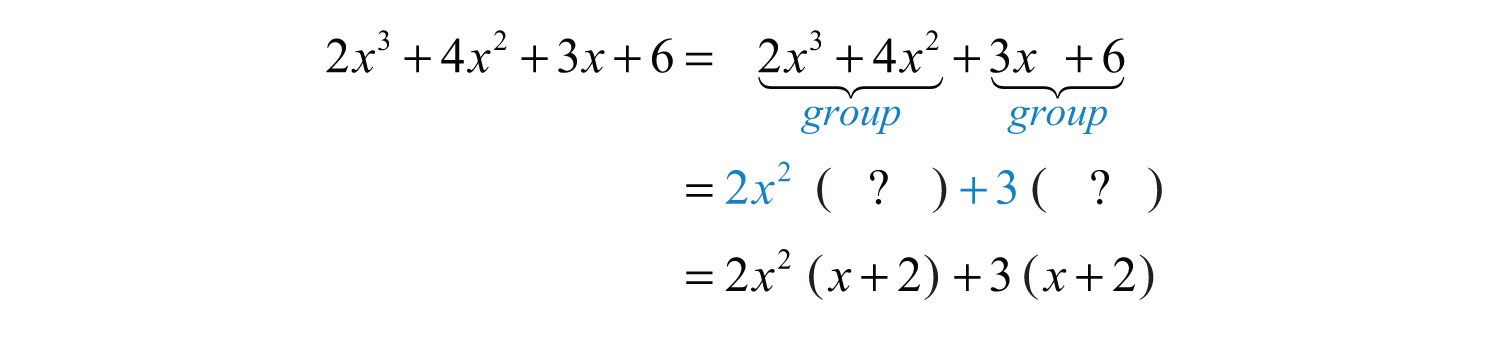
Step 2: At this point, the polynomial is a binomial. Factor out any factors common to both terms. Here is a common factor.
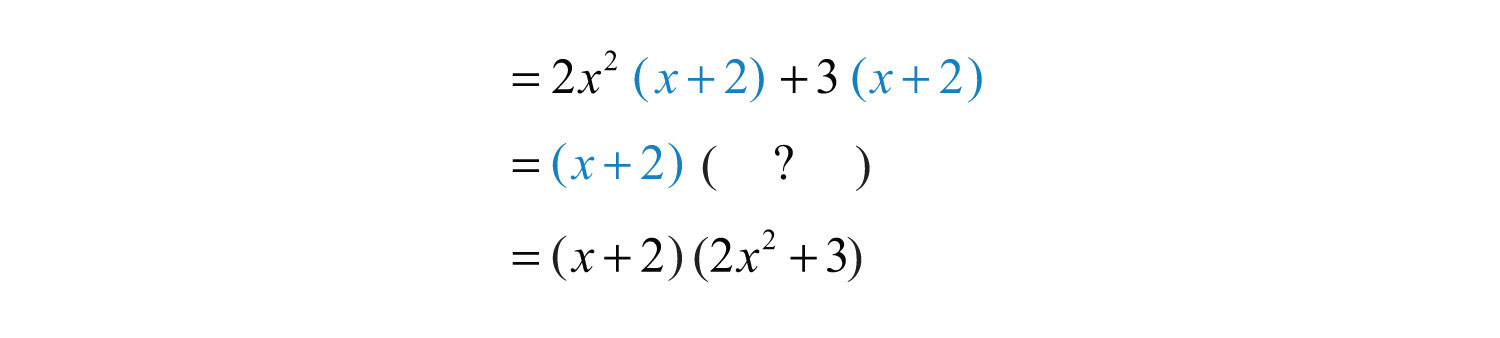
Step 3: Optional check: multiply to verify that we obtain the original expression.
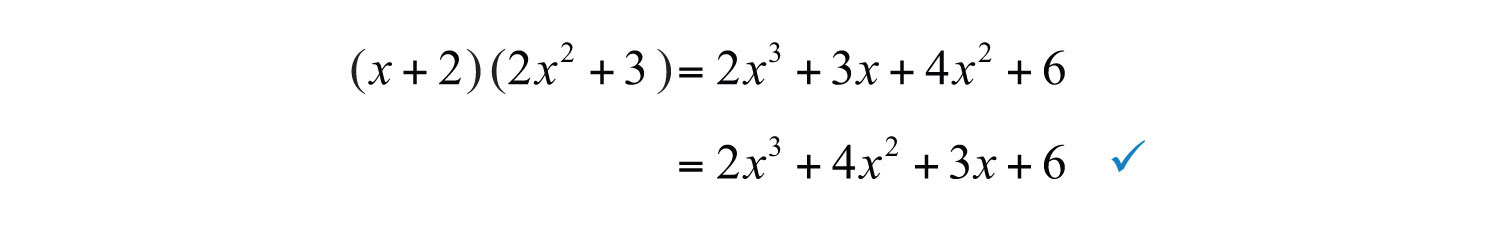
Answer:
Example 15: Factor: .
Solution: The GCF of the first two terms is and the GCF of the second two terms is 1.
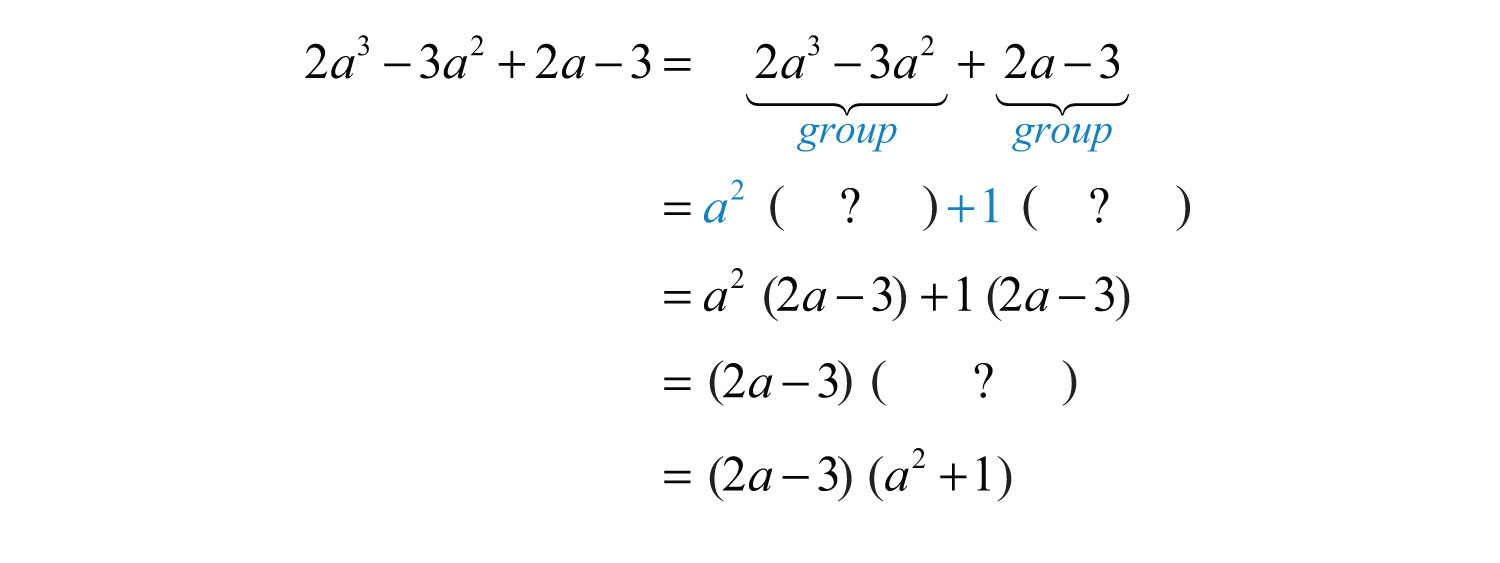
Answer: . The check is left to the reader.
Example 16: Factor: .
Solution: The GCF for the first group is . We have to choose 5 or −5 to factor out of the second group.
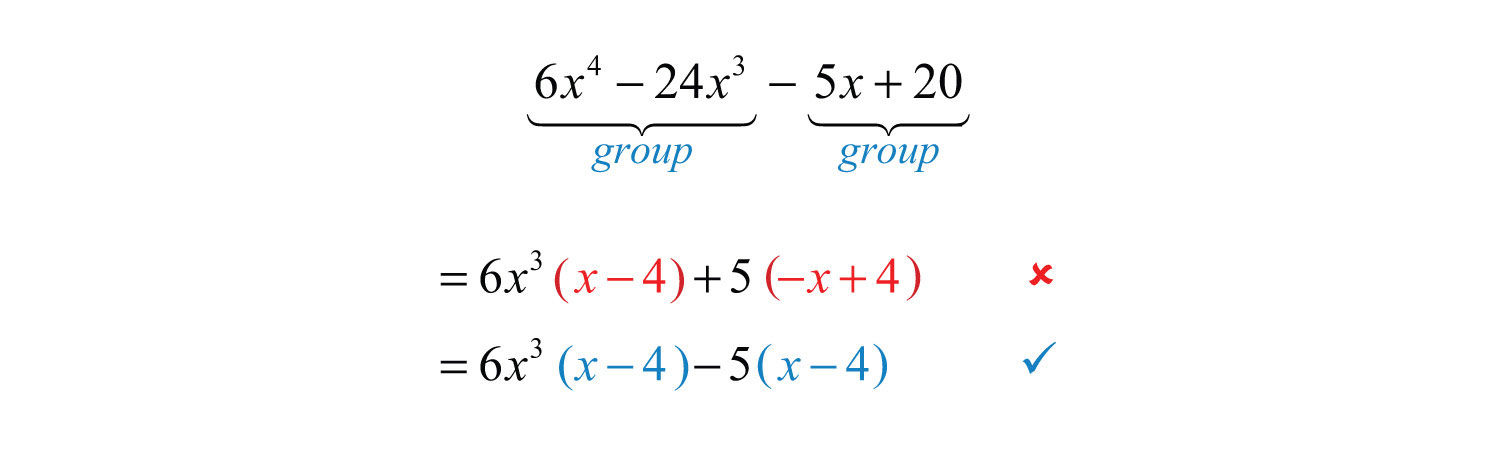
Factoring out a +5 does not result in a common binomial factor. If we choose to factor out −5, then we obtain a common binomial factor and can proceed. Note that when factoring out a negative number, we change the signs of the factored terms.

Answer: . The check is left to the reader.
Tip
The sign of the leading coefficient in the second grouping usually indicates whether or not to factor out a negative factor. If that coefficient is positive, factor out a positive factor. If it is negative, factor out a negative factor.
When all the terms of a polynomial have a GCF other than 1, it is a best practice to factor that out before factoring by grouping.
Example 17: Factor: .
Solution: Here we notice that the greatest common factor of all the terms is . Begin by factoring out the GCF and then factor the result by grouping.
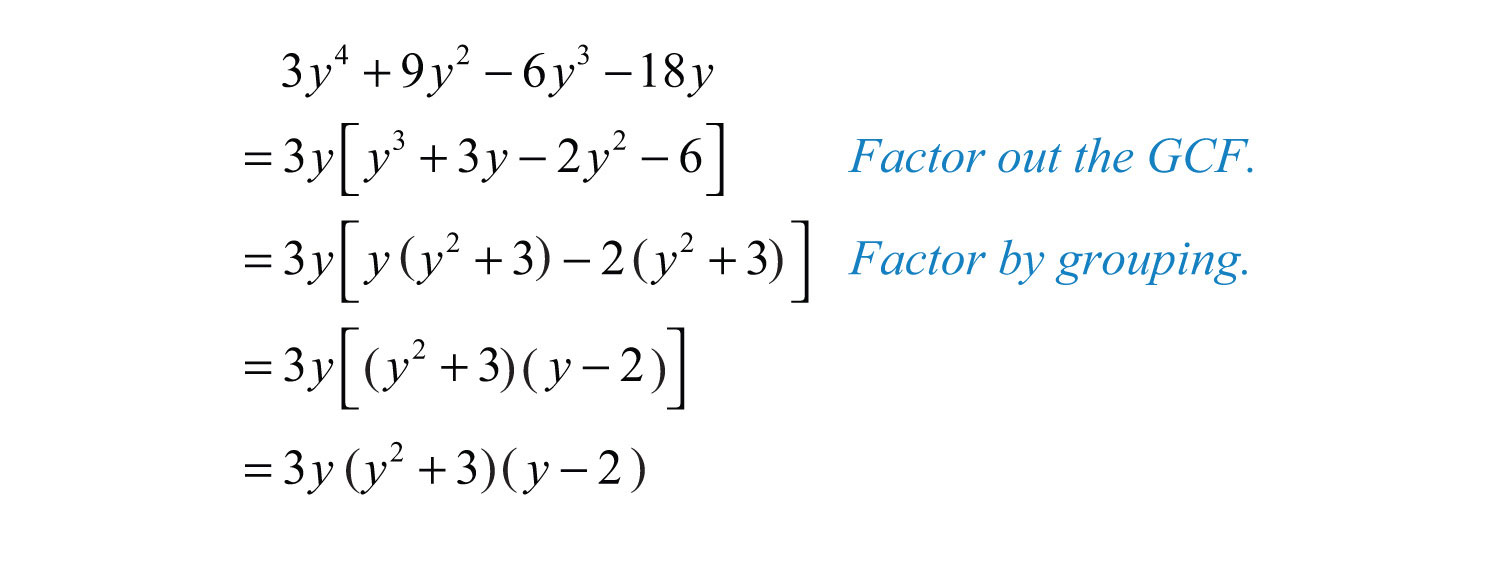
Answer:
Sometimes we must first rearrange the terms in order to obtain a common factor.
Example 18: Factor: .
Solution: Simply factoring the GCF out of the first group and last group does not yield a common binomial factor.
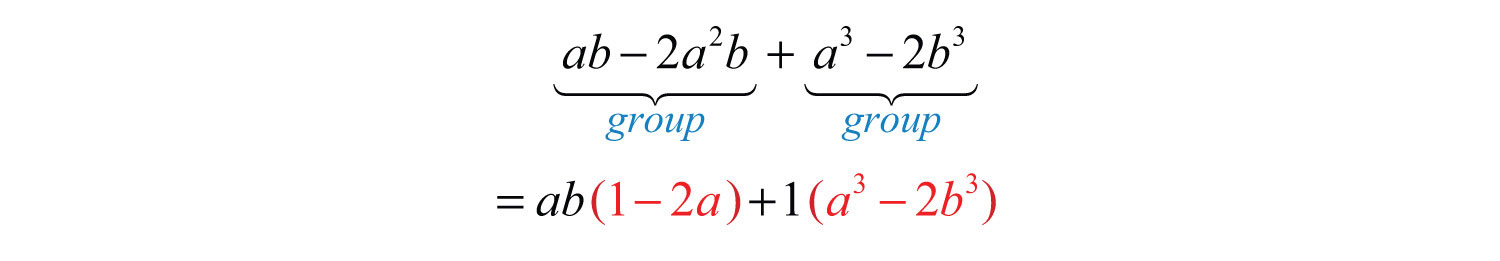
We must rearrange the terms, searching for a grouping that produces a common factor. In this example, we have a workable grouping if we switch the terms and .
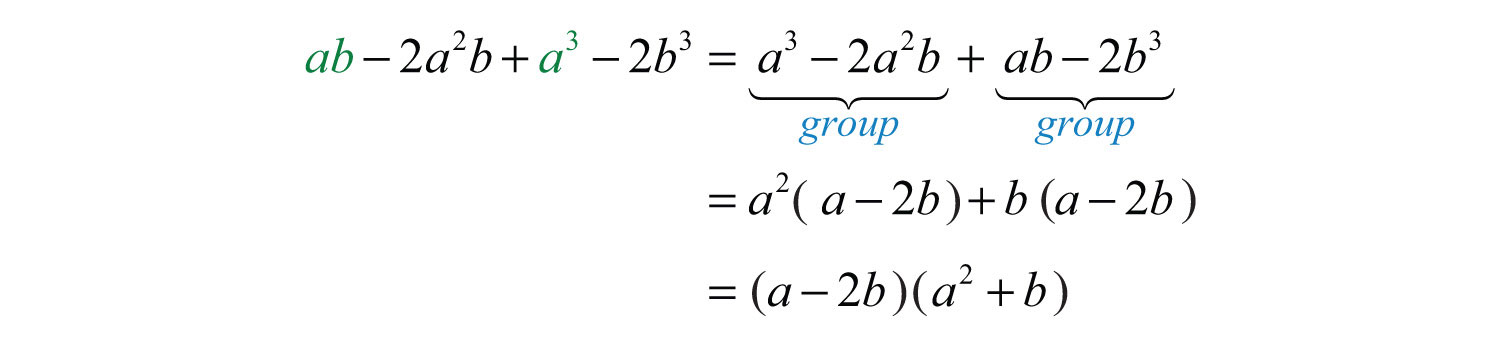
Answer:
Not all factorable four-term polynomials can be factored with this technique. For example,
This four-term polynomial cannot be grouped in any way as to produce a common binomial factor. Despite this, the polynomial is not prime and can be written as a product of polynomials. It can be factored as follows:
Factoring such polynomials is something that we will learn to do as we move further along in our study of algebra. For now, we will limit our attempt to factor four-term polynomials to using the factor by grouping technique.
Try this! Factor: .
Answer:
Video Solution
(click to see video)Key Takeaways
- To find the greatest common factor (GCF) of any collection of natural numbers, first find the prime factorization of each. The GCF is the product of all the common prime factors.
- The GCF of two or more monomials is the product of the GCF of the coefficients and the common variable factors with the smallest power.
- If the terms of a polynomial have a greatest common factor, then factor out that GCF using the distributive property. Divide each term of the polynomial by the GCF to determine the terms of the remaining factor.
- Some four-term polynomials can be factored by grouping the first two terms and the last two terms. Factor out the GCF of each group and then factor out the common binomial factor.
- When factoring by grouping, you sometimes have to rearrange the terms to find a common binomial factor. After factoring out the GCF, the remaining binomial factors must be the same for the technique to work.
- Not all polynomials can be factored as the product of polynomials with integer coefficients. In this case, we call it a prime polynomial.
Topic Exercises
Part A: GCF of Natural Numbers
Give the prime factorization of each number and determine the GCF.
1. 18, 24
2. 45, 75
3. 72, 60
4. 168, 175
5. 144, 245
6. 15, 50, 60
7. 14, 63, 70
8. 12, 48, 125
9. 60, 72, 900
10. 252, 336, 360
Part B: GCF of Variable Expressions
Determine the GCF of all the terms.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
Part C: Factoring out the GCF
Given the GCF, determine the missing factor.
23.
24.
25.
26.
27.
28.
Factor out the GCF.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
Are the following factored correctly? Check by multiplying.
65.
66.
67.
68.
69.
70.
Use polynomial long division to show that the given factor divides the polynomial evenly.
71. Show that is a factor of .
72. Show that is a factor of .
73. Show that is a factor of .
74. Show that is a factor of .
75. The height in feet of an object tossed into the air is given by the function , where t is the time in seconds after it is tossed. Write the function in factored form.
76. The height in feet of an object dropped from a 16‑foot ladder is given by the function , where t is the time in seconds after it is tossed. Write the function in factored form.
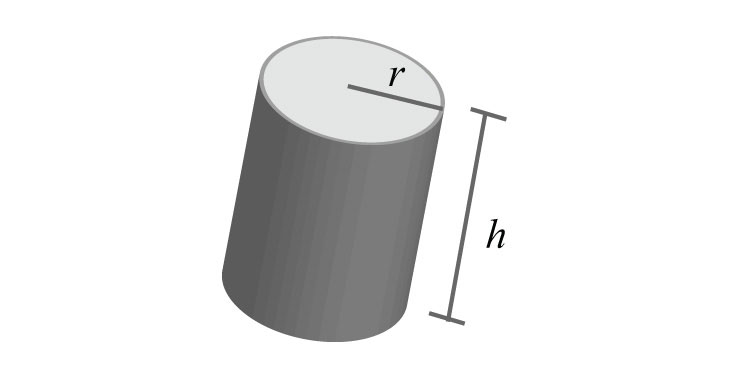
77. The surface area of a cylinder is given by the formula , where r represents the radius of the base and h is the height of the cylinder. Express this formula in factored form.
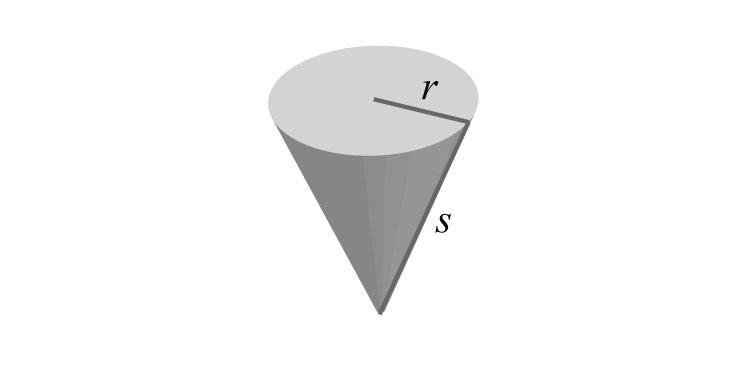
78. The surface area of a cone is given by the formula , where r represents the radius of the base and s represents the slant height. Express this formula in factored form.
Part D: Factor by Grouping
Factor by grouping.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
99.
100.
Factor out the GCF first and then factor by grouping.
101.
102.
103.
104.
105.
106.
107.
108.
109.
110.
Part E: Discussion Board Topics
111. Research the Euclidean algorithm for finding the GCF of two natural numbers. Give an example that illustrates the steps.
112. Research and discuss the contributions of Euclid of Alexandria.
113. Explain what factoring is and give an example.
114. Is fully factored? Explain.
115. Make up a factoring problem of your own and provide the answer. Post the problem and the solution on the discussion board.
Answers
1: , , GCF = 6
3: , , GCF = 12
5: , , GCF = 1
7: , , , GCF = 7
9: , , , GCF = 12
11: 15
13:
15:
17:
19:
21:
23:
25:
27:
29:
31:
33: Prime
35:
37:
39:
41:
43:
45:
47:
49:
51:
53:
55:
57:
59:
61:
63:
65: Yes
67: No
69: No
75:
77:
79:
81:
83:
85:
87:
89:
91:
93:
95:
97:
99:
101:
103:
105:
107:
109:
6.2 Factoring Trinomials of the Form x^2 + bx + c
Learning Objectives
- Factor trinomials of the form .
- Factor trinomials using the AC method.
Factoring Trinomials of the Form x^2 + bx + c
Some trinomials of the form can be factored as a product of binomials. For example,
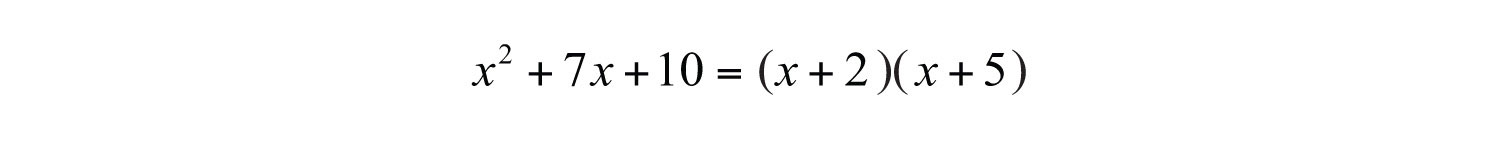
We can verify this factorization by multiplying:
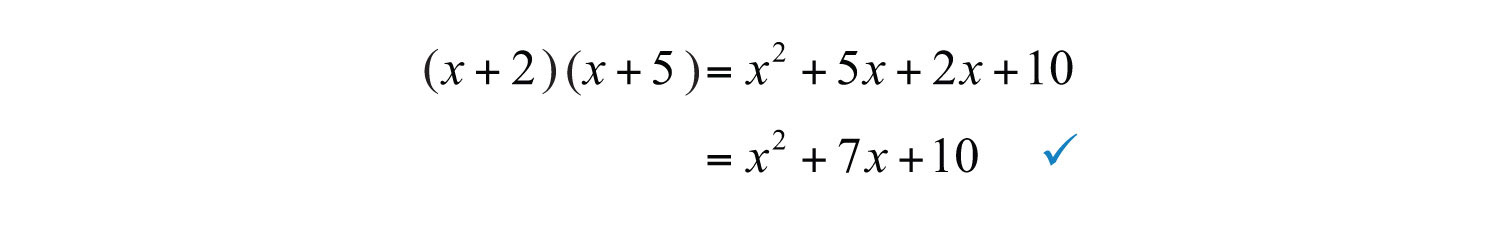
Factoring trinomials requires that we work the distributive process in reverse. Notice that the product of the first terms of each binomial is equal to the first term of the trinomial.
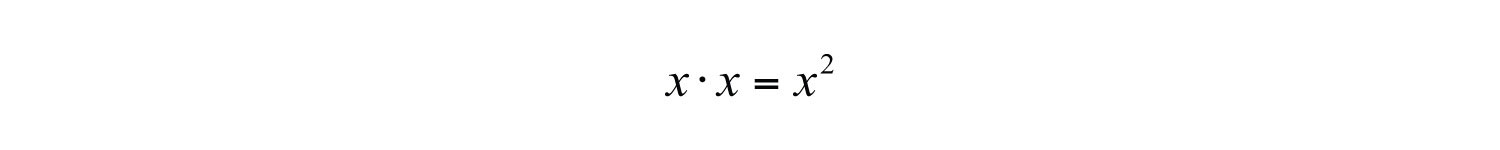
The middle term of the trinomial, 7x, is the sum of the products of the outer and inner terms of the binomials:
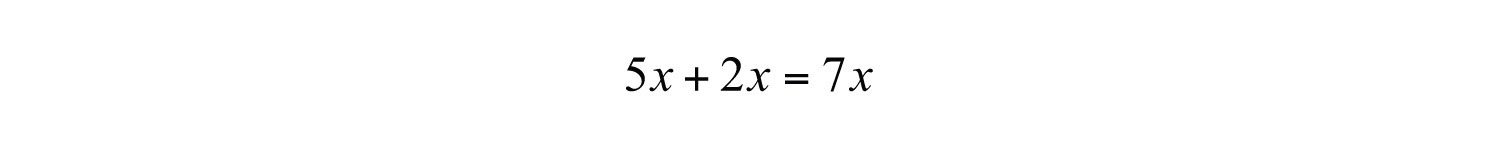
And the product of the last terms of each binomial is equal to the last term of the trinomial.
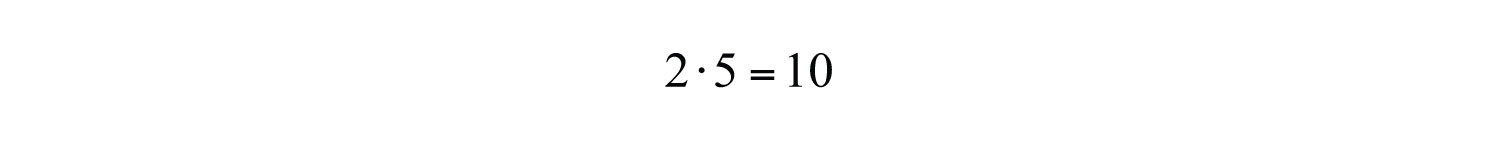
This can be visually interpreted as follows:

If a trinomial of this type factors, then these relationships will be true:

This gives us
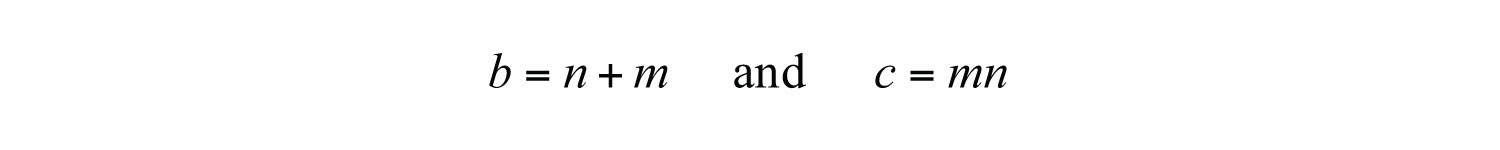
In short, if the leading coefficient of a factorable trinomial is one, then the factors of the last term must add up to the coefficient of the middle term. This observation is the key to factoring trinomials using the technique known as trial and errorDescribes the method of factoring a trinomial by systematically checking factors to see if their product is the original trinomial. (or guess and checkUsed when referring to the trial and error method for factoring trinomials.). The steps are outlined in the following example.
Example 1: Factor: .
Solution: Note that the polynomial to be factored has three terms; it is a trinomial with a leading coefficient of 1. Use trial and error to factor as follows:
Step 1: Write two sets of blank parentheses. If a trinomial of this form factors, then it will factor into two linear binomial factors.
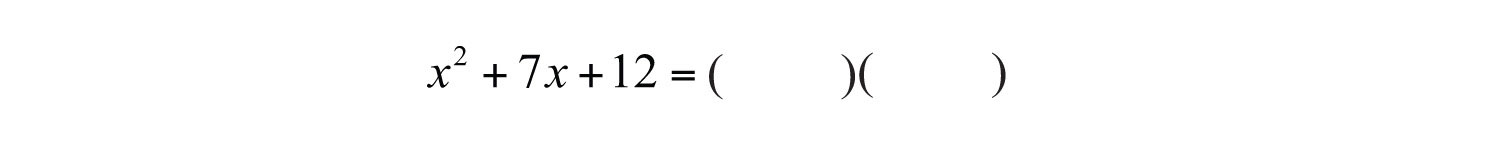
Step 2: Write the factors of the first term in the first space of each set of parentheses. In this case, factor .
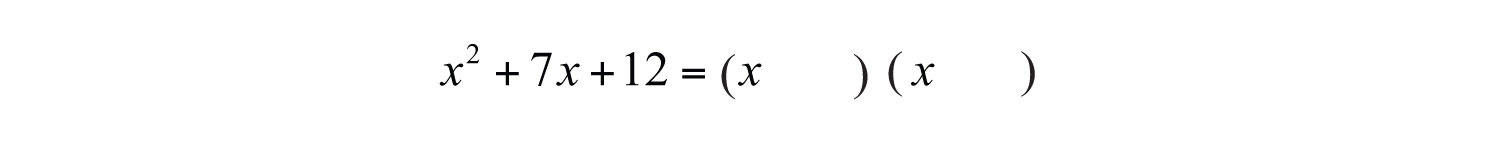
Step 3: Determine the factors of the last term whose sum equals the coefficient of the middle term. To do this, list all of the factorizations of 12 and search for factors whose sum equals the coefficient of the middle term, 7.
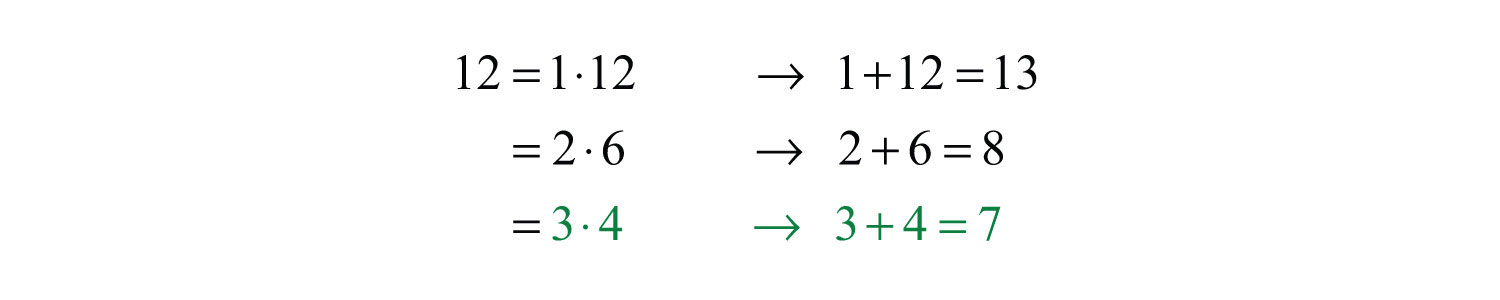
Choose 12 = 3 ⋅ 4 because 3 + 4 = 7.
Step 4: Write in the last term of each binomial using the factors determined in the previous step.
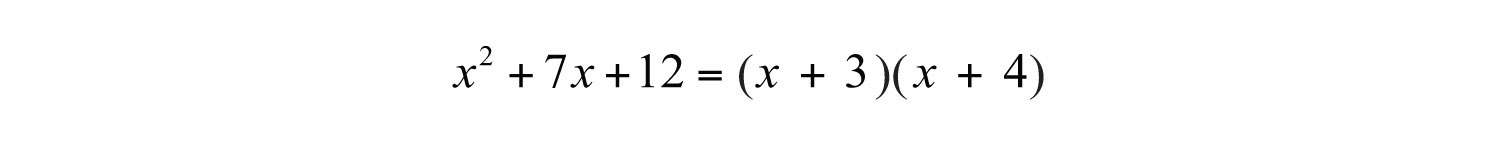
Step 5: Check by multiplying the two binomials.
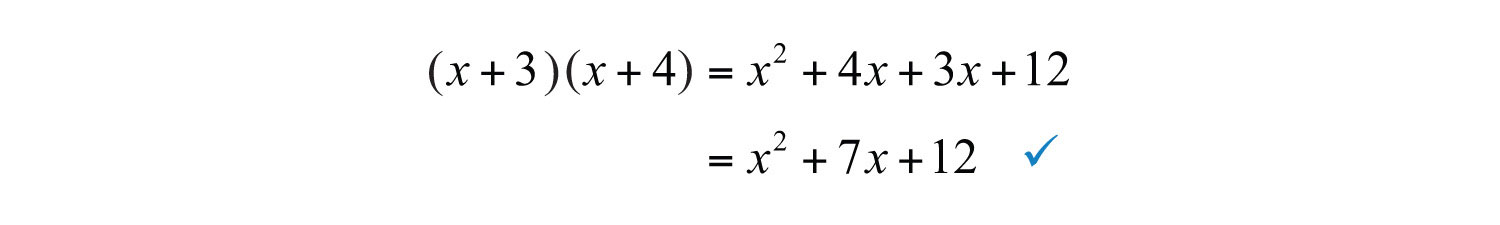
Answer:
Since multiplication is commutative, the order of the factors does not matter.
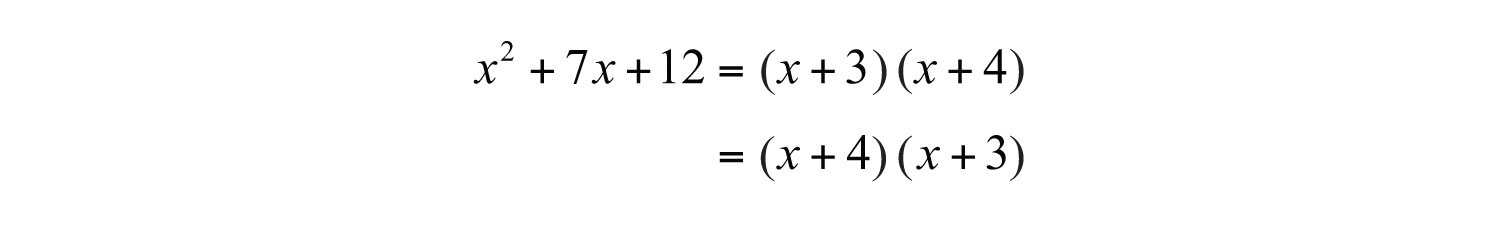
If the last term of the trinomial is positive, then either both of the constant factors must be negative or both must be positive. Therefore, when looking at the list of factorizations of the last term, we are searching for sums that are equal to the coefficient of the middle term.
Example 2: Factor: .
Solution: First, factor .
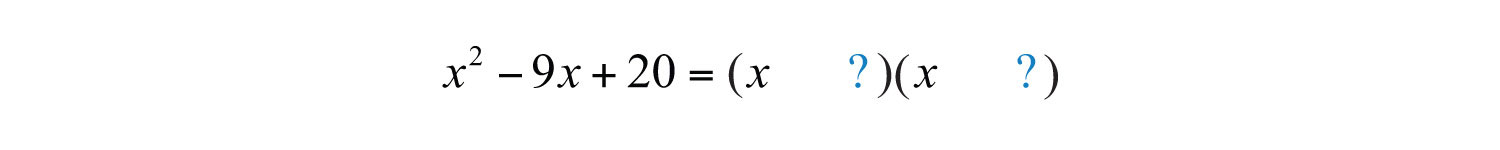
Next, determine which factors of 20 add up to −9:
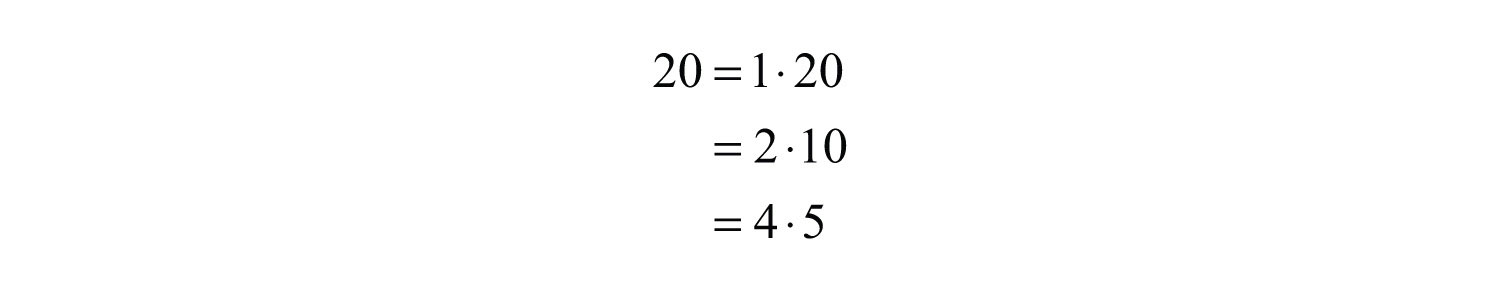
In this case, choose −4 and −5 because and .
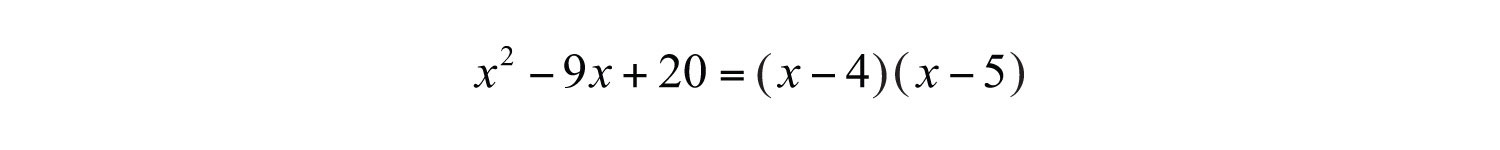
Check.
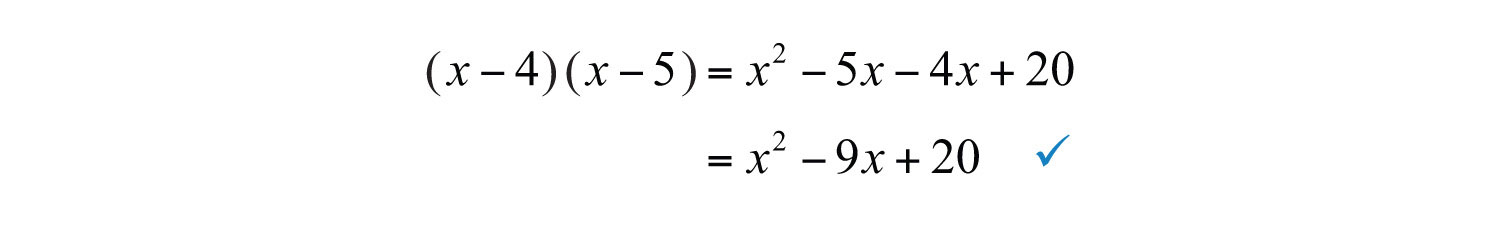
Answer:
If the last term of the trinomial is negative, then one of its factors must be negative. In this case, search the list of factorizations of the last term for differences that equal the coefficient of the middle term.
Example 3: Factor: .
Solution: Begin by factoring the first term .
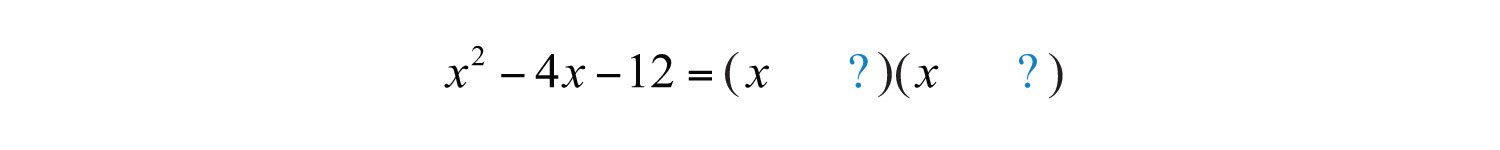
The factors of 12 are listed below. In this example, we are looking for factors whose difference is −4.
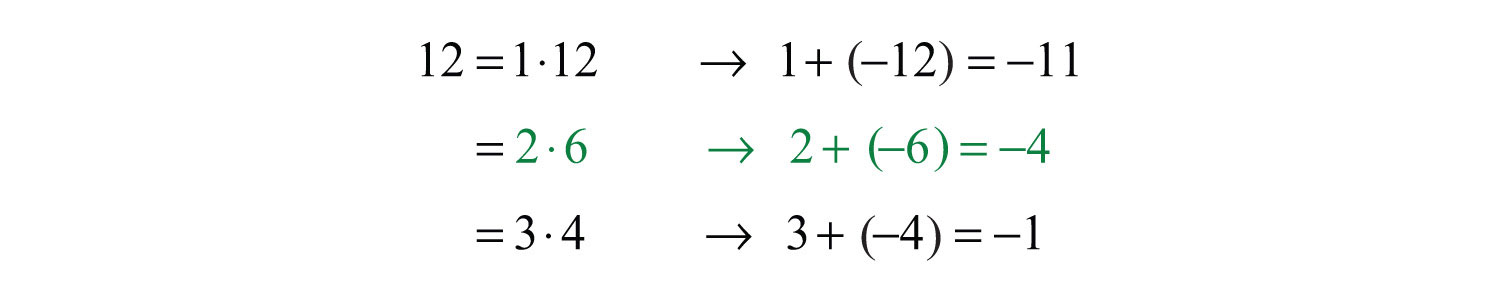
Here choose the factors 2 and −6 because the coefficient of the middle term, −4, is obtained if we add .
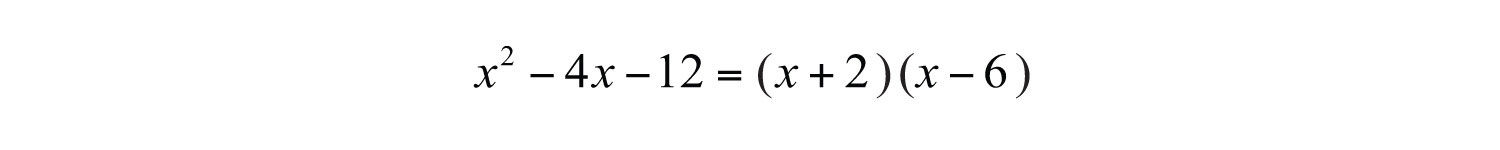
Multiply to check.
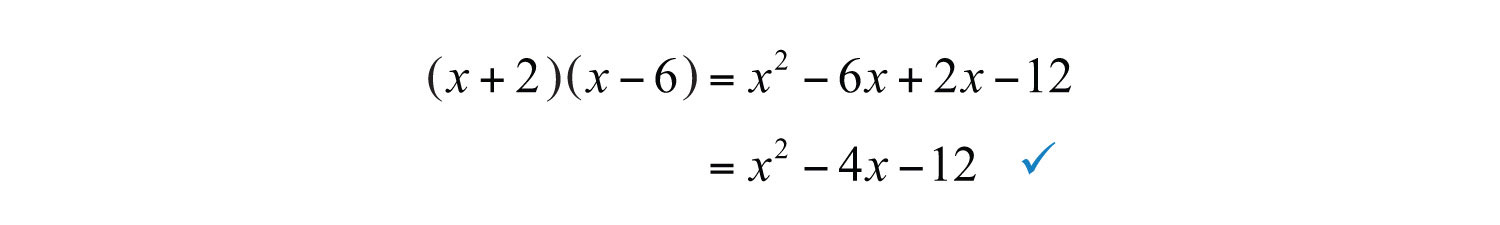
Answer:
Often our first guess will not produce a correct factorization. This process may require repeated trials. For this reason, the check is very important and is not optional.
Example 4: Factor: .
Solution: The first term of this trinomial factors as .
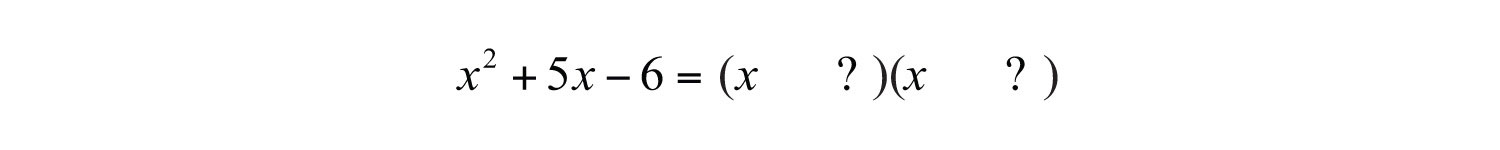
Consider the factors of 6:
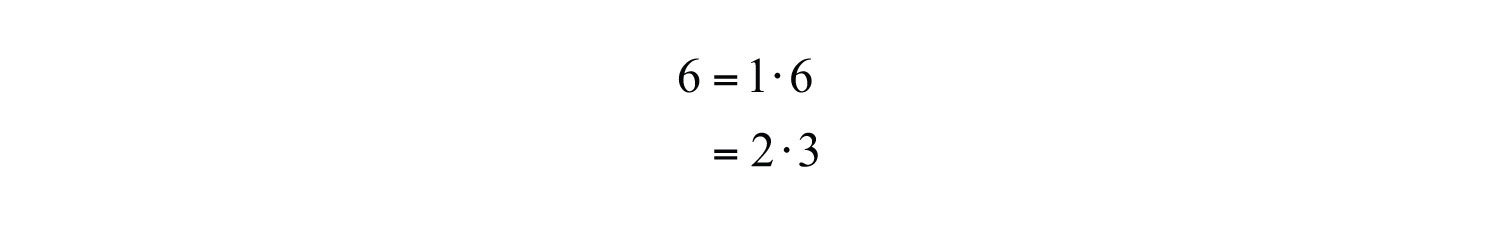
Suppose we choose the factors 2 and 3 because 2 + 3 = 5, the coefficient of the middle term. Then we have the following incorrect factorization:
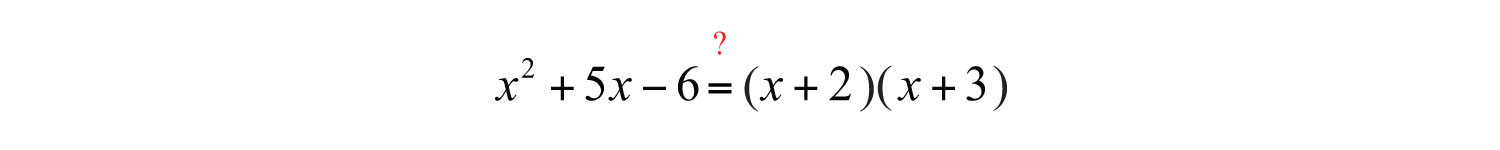
When we multiply to check, we find the error.

In this case, the middle term is correct but the last term is not. Since the last term in the original expression is negative, we need to choose factors that are opposite in sign. Therefore, we must try again. This time we choose the factors −1 and 6 because .
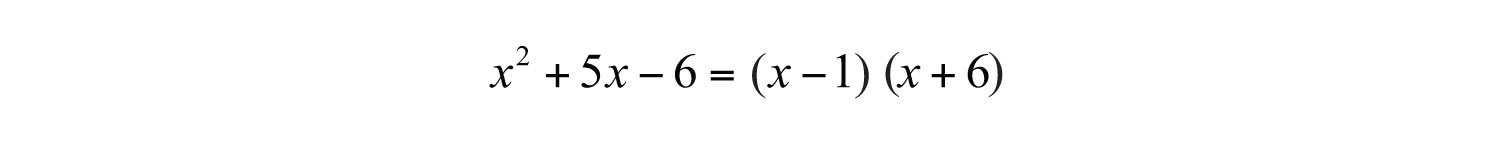
Now the check shows that this factorization is correct.
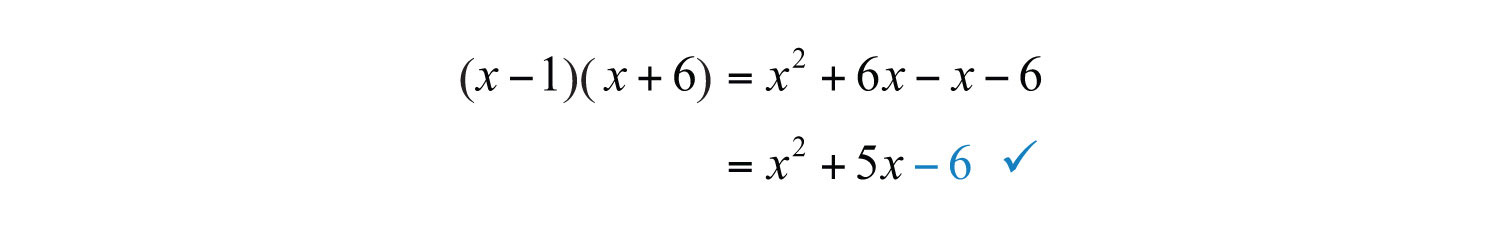
Answer:
If we choose the factors wisely, then we can reduce much of the guesswork in this process. However, if a guess is not correct, do not get discouraged; just try a different set of factors.
Example 5: Factor: .
Solution:
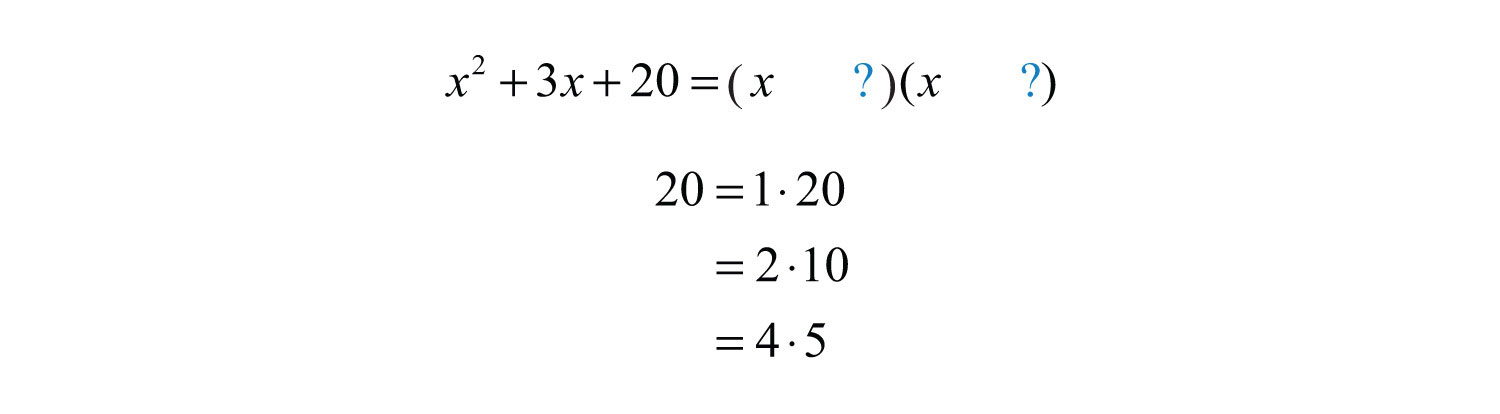
Here there are no factors of 20 whose sum is 3. Therefore, the original trinomial cannot be factored as a product of two binomials. This trinomial is prime.
Answer: Prime
Try this! Factor: .
Answer:
Video Solution
(click to see video)The techniques described can also be used to factor trinomials with more than one variable.
Example 6: Factor: .
Solution: The first term factors as .
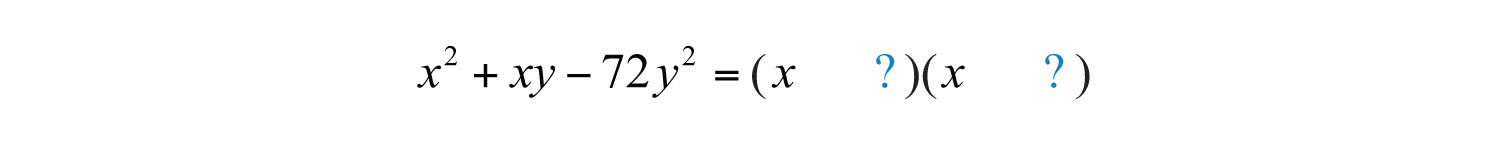
Next, look for factors of the coefficient of the last term, 72, whose sum is −14.

Therefore, the coefficient of the last term can be factored , where . Because the last term has a variable factor of , factor as and try the following factorization:
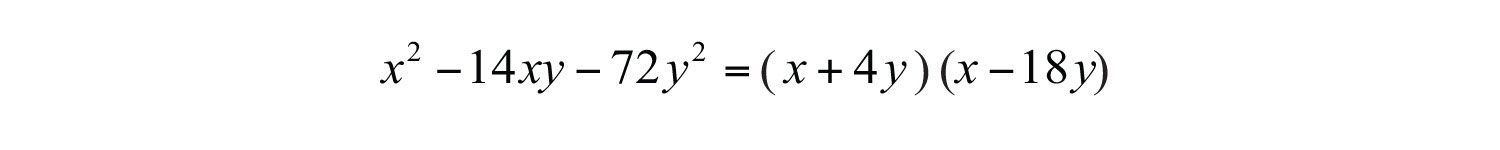
Multiply to check.
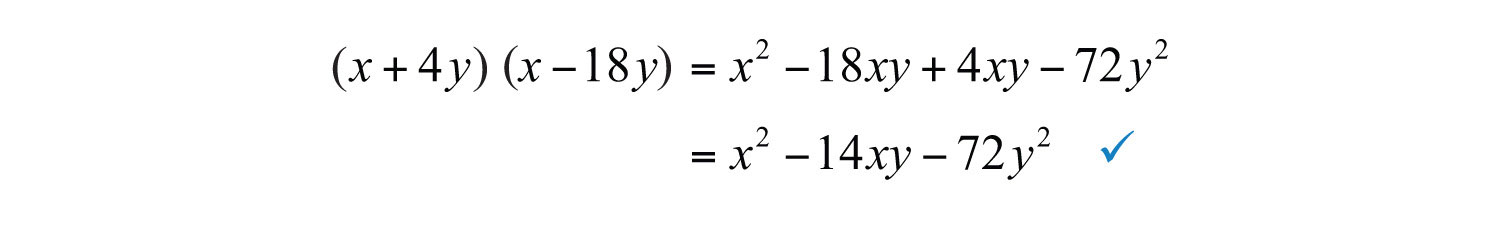
Visually, we have the following:

Answer:
Try this! Factor: .
Answer:
Video Solution
(click to see video)Factoring Using the AC Method
An alternate technique for factoring trinomials, called the AC methodMethod for factoring trinomials by replacing the middle term with two terms that allow us to factor the resulting four-term polynomial by grouping., makes use of the grouping method for factoring four-term polynomials. If a trinomial in the form can be factored, then the middle term, bx, can be replaced with two terms with coefficients whose sum is b and product ac. This substitution results in an equivalent expression with four terms that can be factored by grouping. The steps are outlined in the following example.
Example 7: Factor using the AC method: .
Solution: In this example a = 1, b = −1, and c = −30.
Step 1: Determine the product ac.

Step 2: Find factors of ac whose sum equals the coefficient of the middle term, b.

We can see that the sum of the factors 5 and −6 is equal to the coefficient of the middle term, −1.
Step 3: Use the factors as coefficients for the terms that replace the middle term. Here . Write
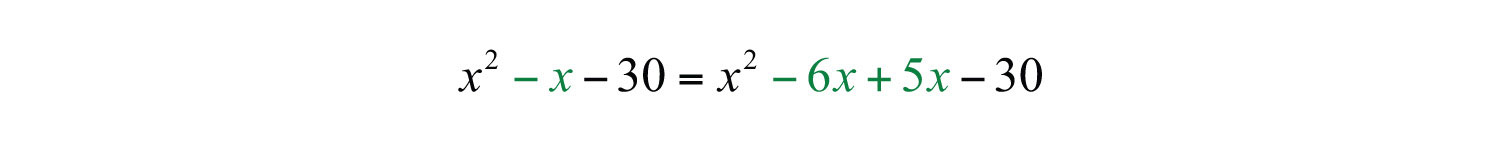
Step 4: Factor the equivalent expression by grouping.
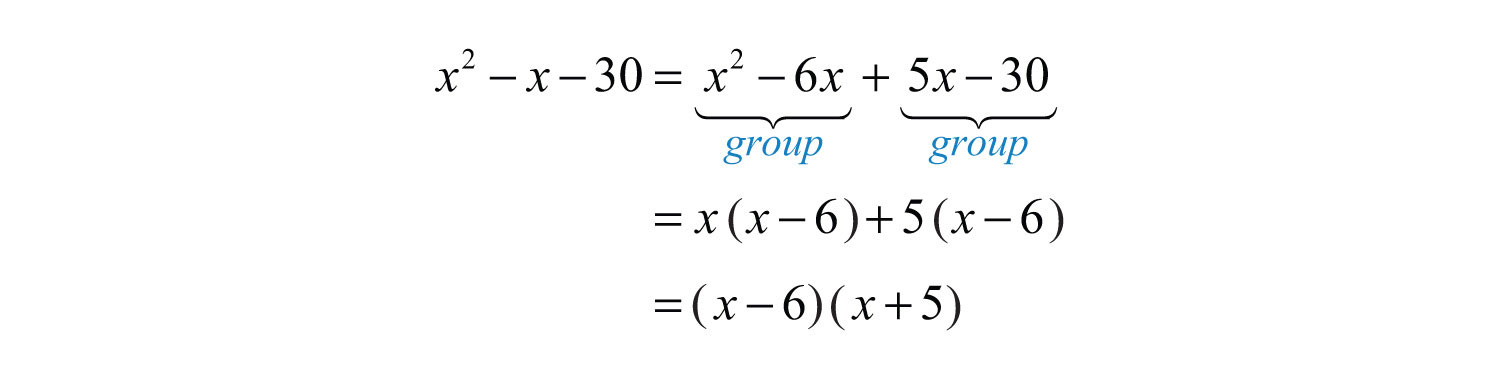
Answer:
Notice that the AC method is consistent with the trial and error method. Both methods require that , where . In the example above, and . The only difference between the methods, when the leading coefficient is 1, is in the process used to obtain the final factorization.
Example 8: Factor: .
Solution: Here ac = 48 and we search for factors whose sum is −14.
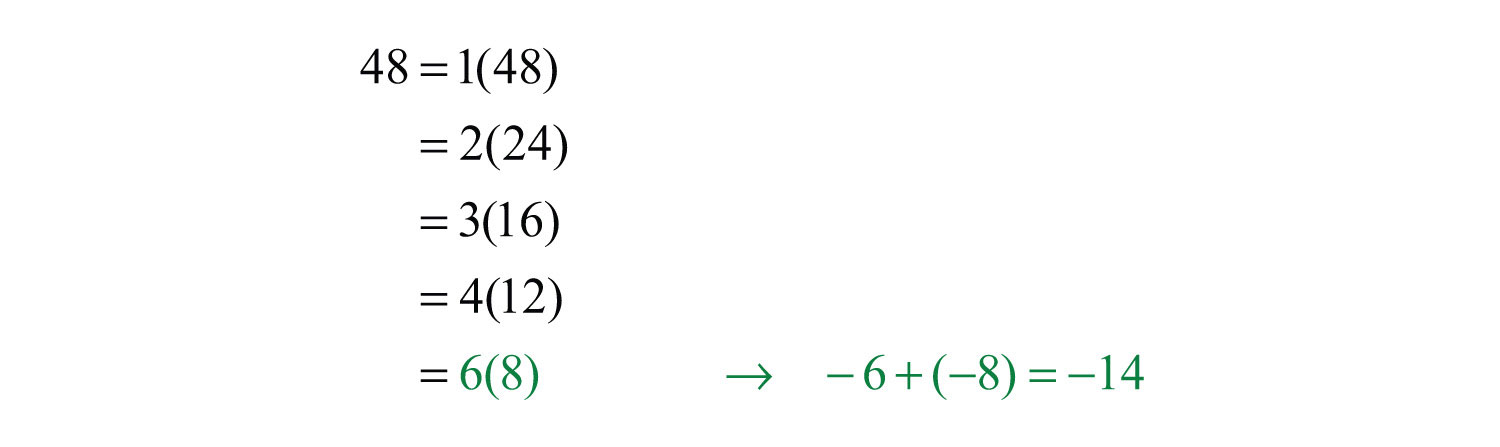
Therefore, . Substitute the new terms and factor by grouping.
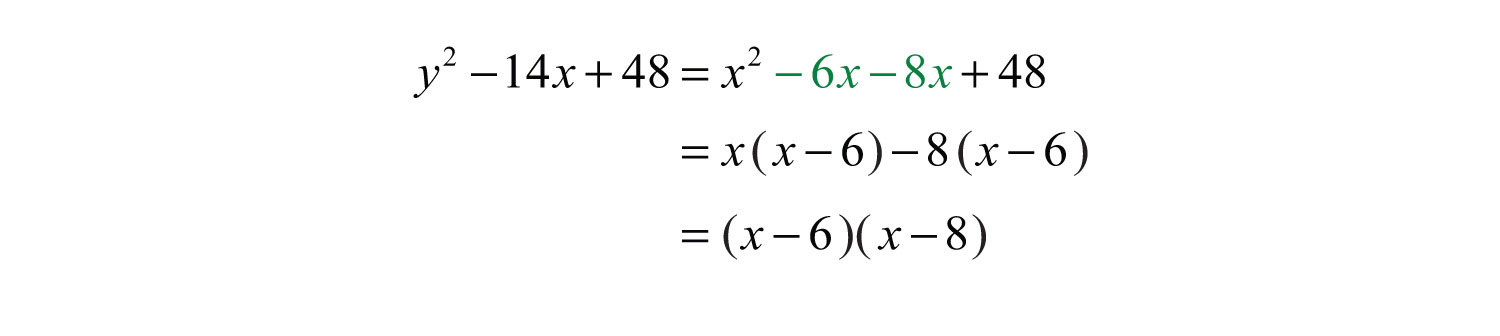
Answer: . The check is left to the reader.
At this point, it is recommended that the reader stop and factor as many trinomials of the form as time allows before moving on to the next section. Factoring trinomials is one of the more important skills that we learn in this course and should be mastered.
Key Takeaways
- Factor a trinomial by systematically guessing what factors give two binomials whose product is the original trinomial.
- If a trinomial of the form factors into the product of two binomials, then the coefficient of the middle term is the sum of factors of the last term.
- Not all trinomials can be factored as the product of binomials with integer coefficients. In this case, we call it a prime trinomial.
- Factoring is one of the more important skills required in algebra. For this reason, you should practice working as many problems as it takes to become proficient.
Topic Exercises
Part A: Factoring Trinomials with Leading Coefficient 1
Are the following factored correctly? Check by multiplying.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Factor.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57. The area of a square is given by the function , where x is measured in meters. Rewrite this function in factored form.
58. The area of a square is given by the function , where x is measured in meters. Rewrite this function in factored form.
Part B: Factor Using the AC Method
Factor using the AC method.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
Part C: Discussion Board Topics
71. Create your own trinomial of the form that factors. Share it along with the solution on the discussion board.
72. Write out your own list of steps for factoring a trinomial of the form and share your steps on the discussion board.
73. Create a trinomial that does not factor and share it along with an explanation of why it does not factor.
Answers
1: No
3: Yes
5: Yes
7: No
9: Yes
11:
13:
15:
17:
19:
21:
23: Prime
25:
27:
29: Prime
31:
33:
35:
37:
39: Prime
41:
43:
45:
47:
49:
51:
53:
55:
57:
59:
61:
63:
65:
67: Prime
69:
6.3 Factoring Trinomials of the Form ax^2 + bx + c
Learning Objectives
- Factor trinomials of the form .
- Factor trinomials with a common factor.
Factoring Trinomials of the Form ax^2 + bx + c
Factoring trinomials of the form can be challenging because the middle term is affected by the factors of both a and c. To illustrate this, consider the following factored trinomial:
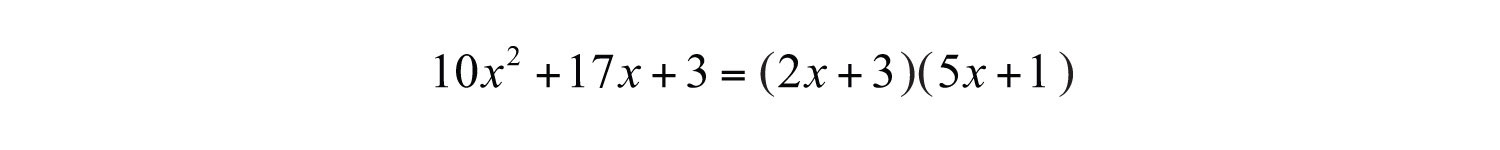
We can multiply to verify that this is the correct factorization.
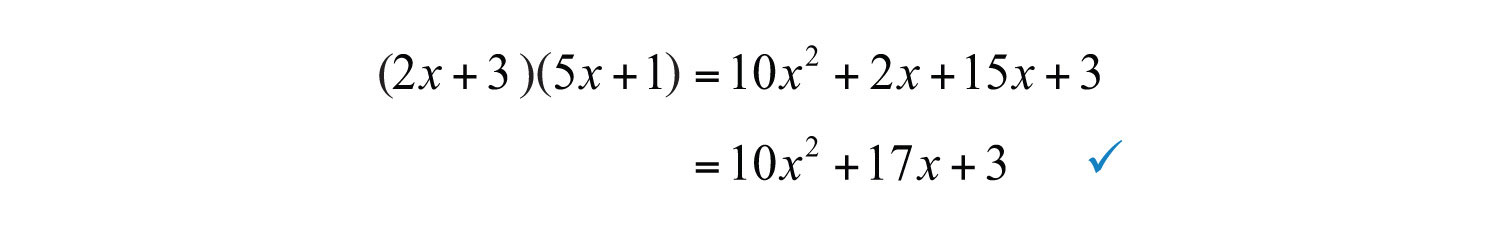
As we have seen before, the product of the first terms of each binomial is equal to the first term of the trinomial. The middle term of the trinomial is the sum of the products of the outer and inner terms of the binomials. The product of the last terms of each binomial is equal to the last term of the trinomial. Visually, we have the following:

In general,
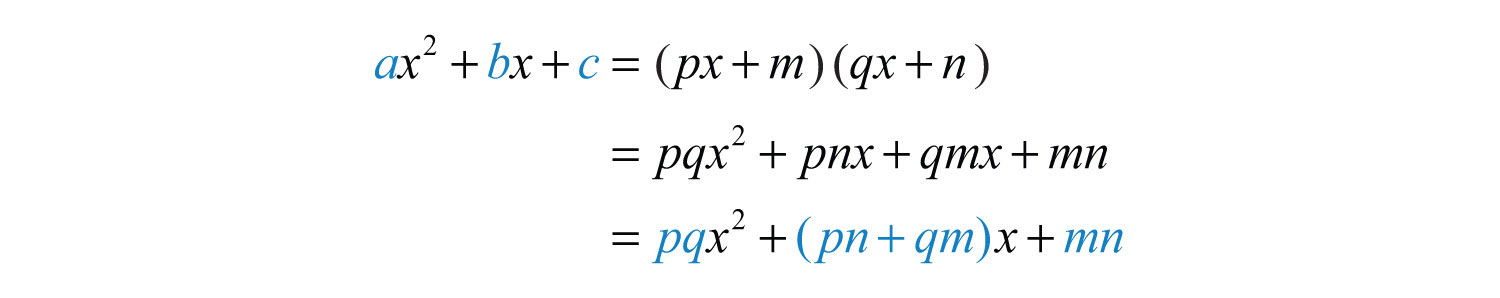
This gives us,
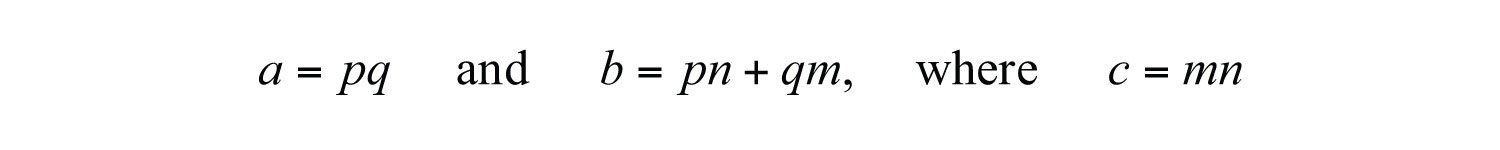
In short, when the leading coefficient of a trinomial is something other than 1, there will be more to consider when determining the factors using the trial and error method. The key lies in the understanding of how the middle term is obtained. Multiply and carefully follow the formation of the middle term.
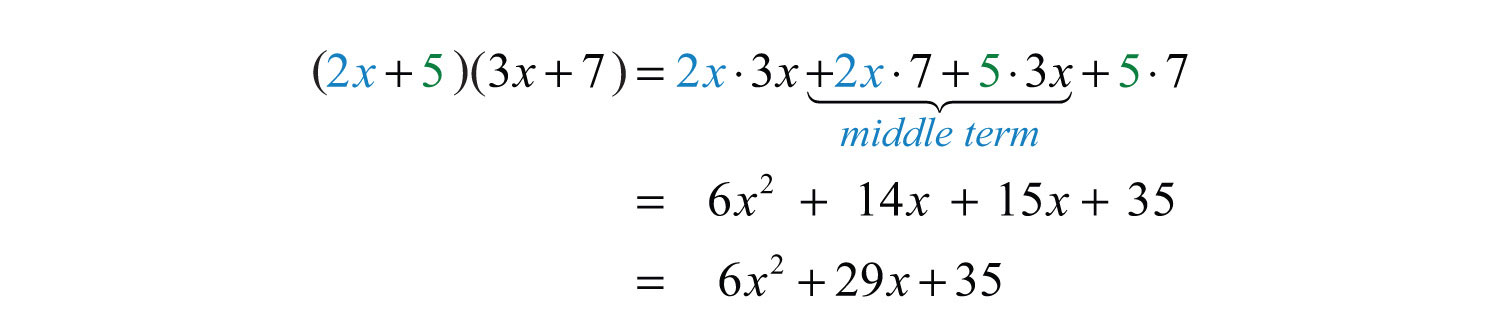
If we think of the FOIL method for multiplying binomials, then the middle term results from the sum of the inner product and the outer product. In this case, , as illustrated below:
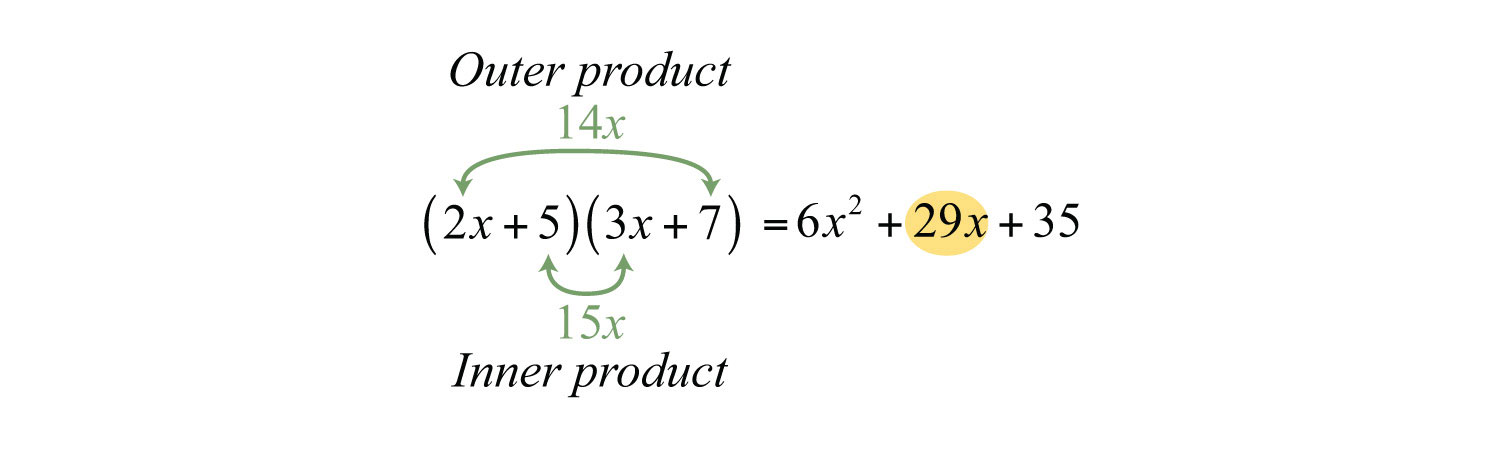
For this reason, we need to look for products of the factors of the first and last terms whose sum is equal to the coefficient of the middle term. For example, to factor , look at the factors of 6 and 35.

The combination that produces the coefficient of the middle term is . Make sure that the outer terms have coefficients 2 and 7, and that the inner terms have coefficients 5 and 3. Use this information to factor the trinomial:
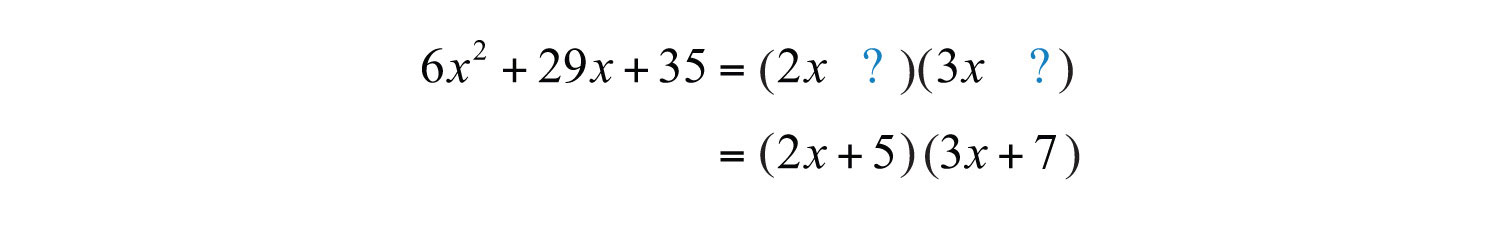
Example 1: Factor: .
Solution: Since the leading coefficient and the last term are both prime, there is only one way to factor each.
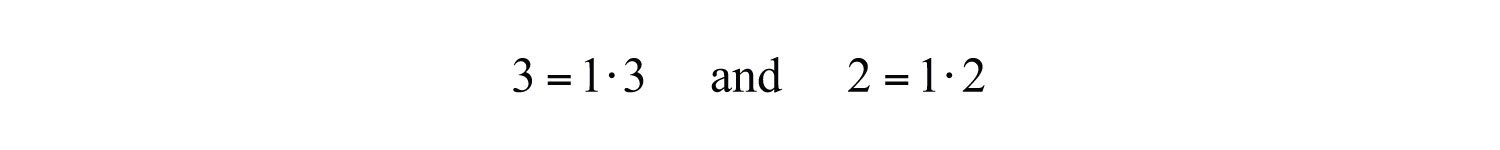
Begin by writing the factors of the first term, , as follows:
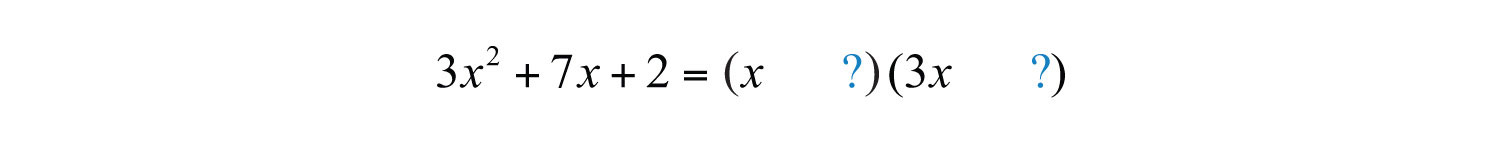
The middle and last term are both positive; therefore, the factors of 2 are chosen as positive numbers. In this case, the only choice is in which grouping to place these factors.
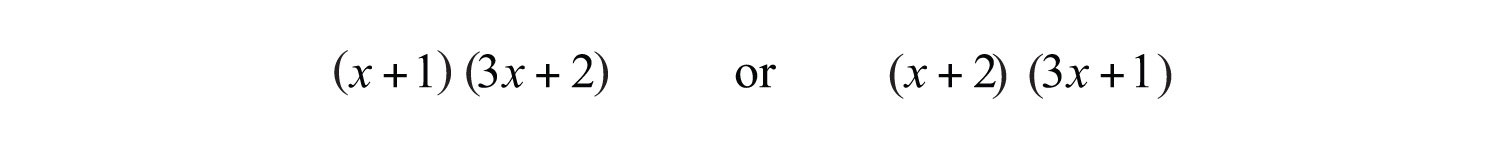
Determine which grouping is correct by multiplying each expression.
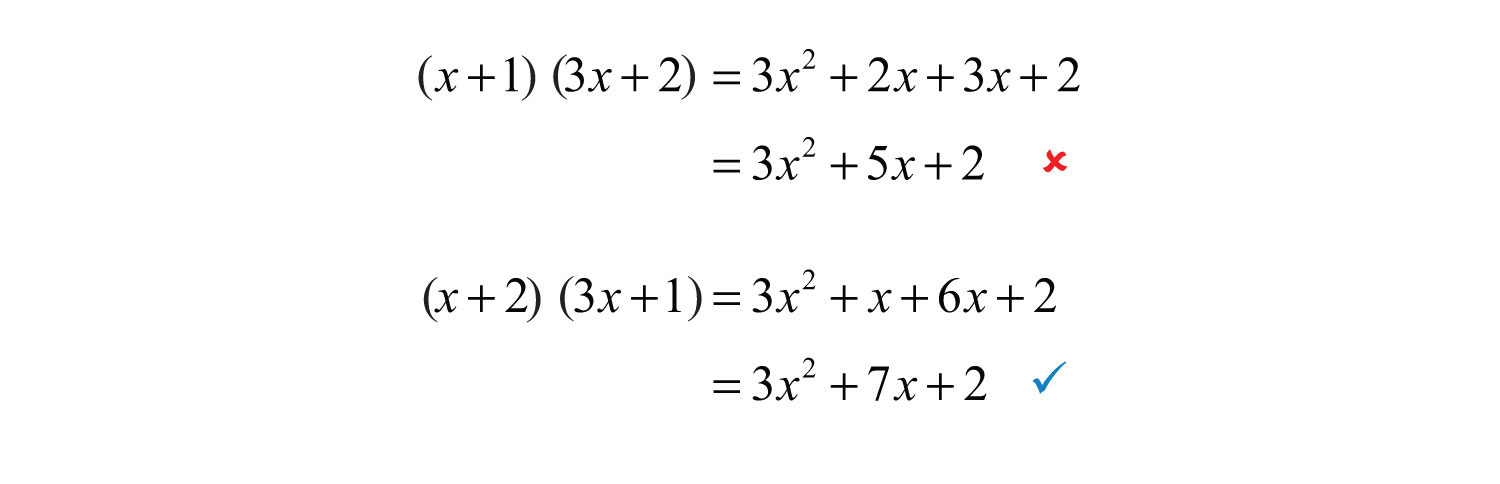
Notice that these products differ only in their middle terms. Also, notice that the middle term is the sum of the inner and outer product, as illustrated below:
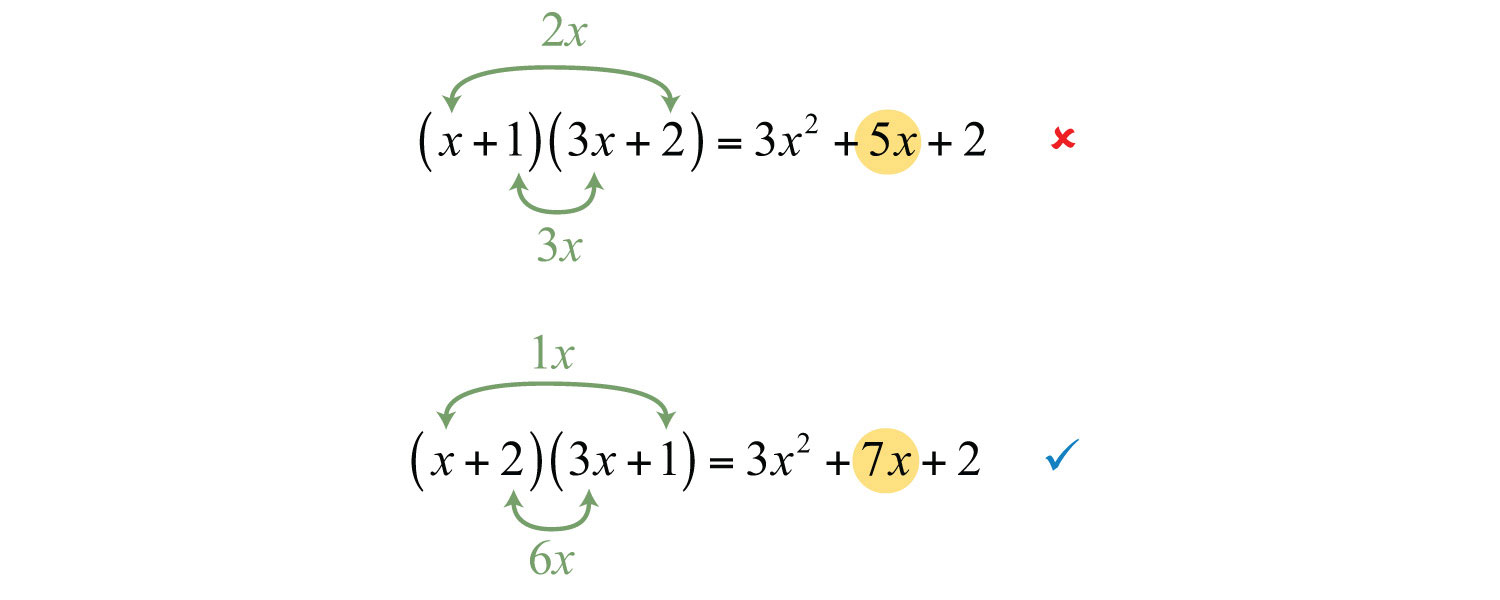
Answer:
Example 2: Factor: .
Solution: First, consider the factors of the first and last terms.

We search for products of factors whose sum equals the coefficient of the middle term, 38. For brevity, the thought process is illustrated starting with the factors 2 and 6. Factoring begins at this point with the first term.
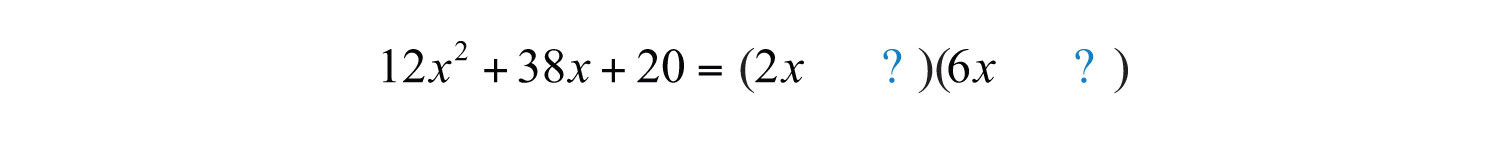
We search for factors of 20 that along with the factors of 12 produce a middle term of 38x.

Here the last combination produces a middle term of 38x.
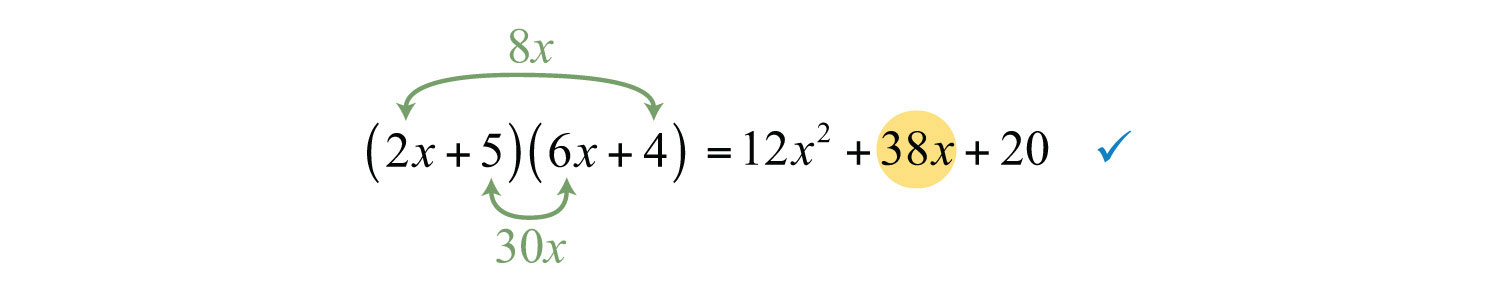
Answer:
Example 3: Factor: .
Solution: First, consider the factors of the first and last terms.

We are searching for products of factors whose sum equals the coefficient of the middle term, −23. Factoring begins at this point with two sets of blank parentheses:
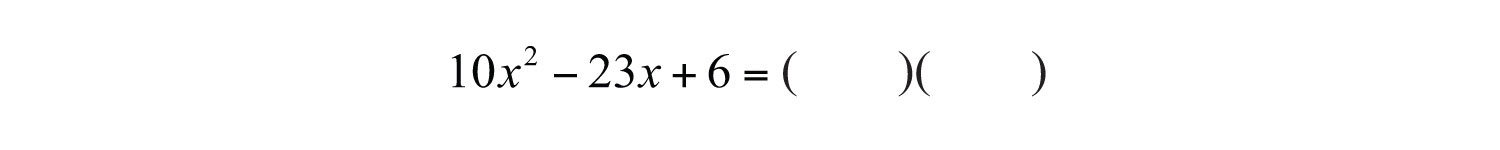
Since the last term is positive and the middle term is negative, we know that both factors of the last term must be negative. Here we list all possible combinations with the factors of .

There is no combination that produces a middle term of . We then move on to the factors of and list all possible combinations:
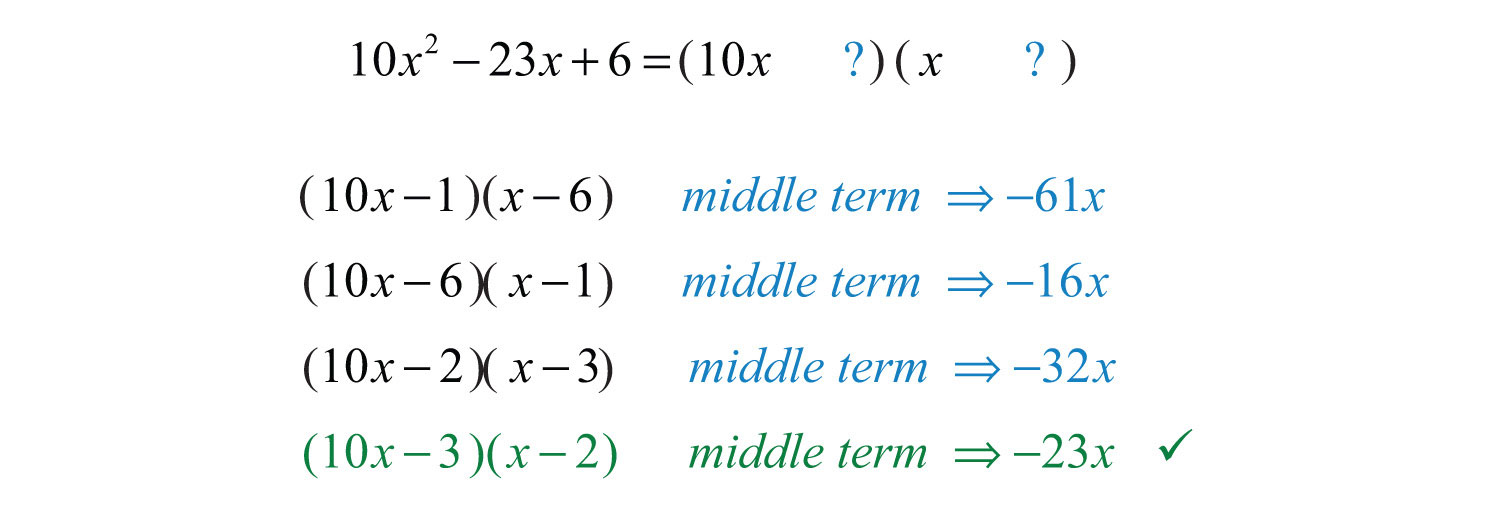
And we can write
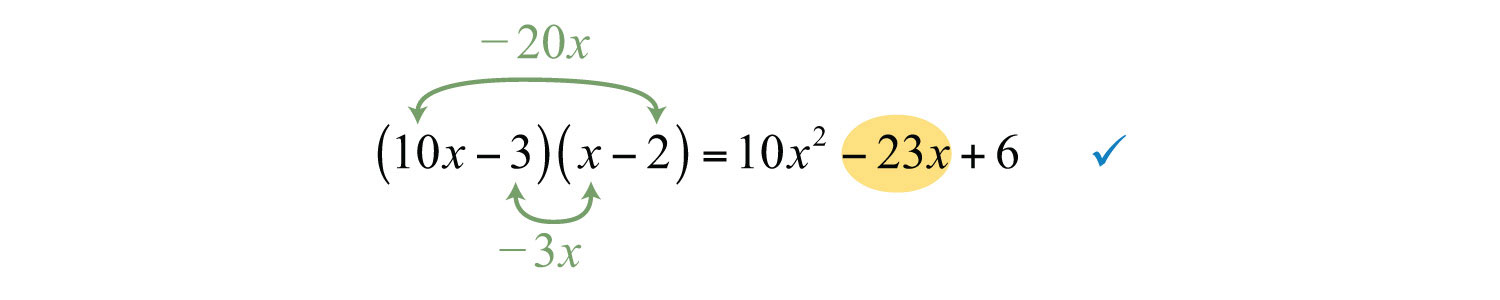
Answer: . The complete check is left to the reader.
We can reduce much of the guesswork involved in factoring trinomials if we consider all of the factors of the first and last terms and their products.
Example 4: Factor: .
Solution: We begin with the factors of 5 and 16.

Since the leading coefficient is prime, we can begin with the following:
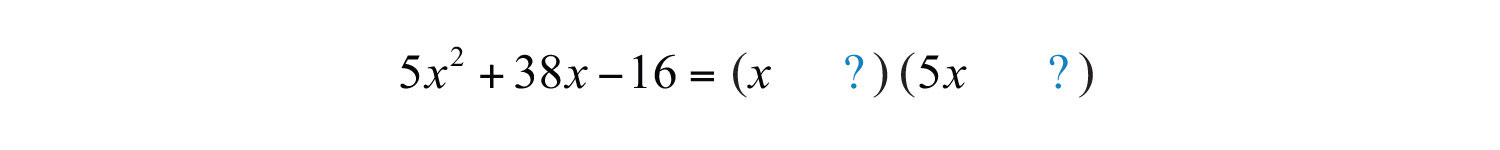
We look for products of the factors of 5 and 16 that could possibly add to 38.

Since the last term is negative, we must look for factors with opposite signs. Here we can see that the products 2 and 40 add up to 38 if they have opposite signs:

Therefore, use −2 and 8 as the factors of 16, making sure that the inner and outer products are and :
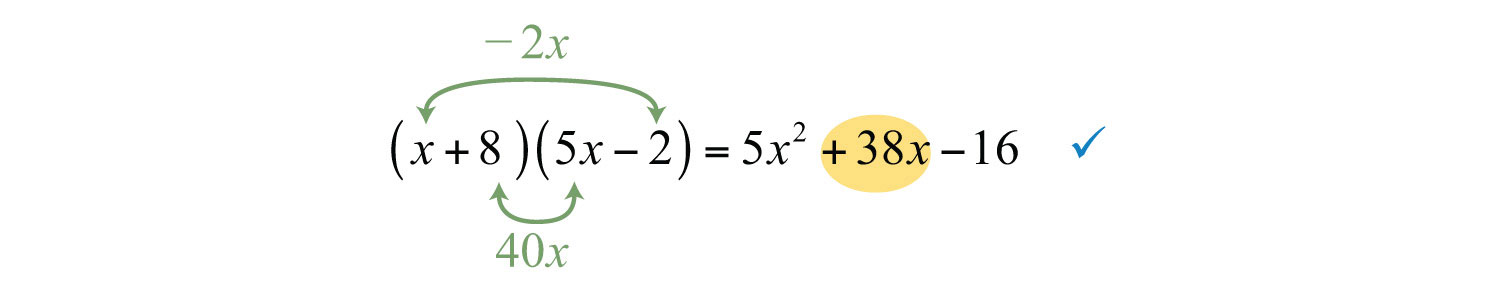
Answer: . The complete check is left to the reader.
After lots of practice, the process described in the previous example can be performed mentally.
Try this! Factor: .
Answer:
Video Solution
(click to see video)When given trinomials with multiple variables, the process is similar.
Example 5: Factor: .
Solution: Search for factors of the first and last terms such that the sum of the inner and outer products equals the middle term.

Add the following products to obtain the middle term: .
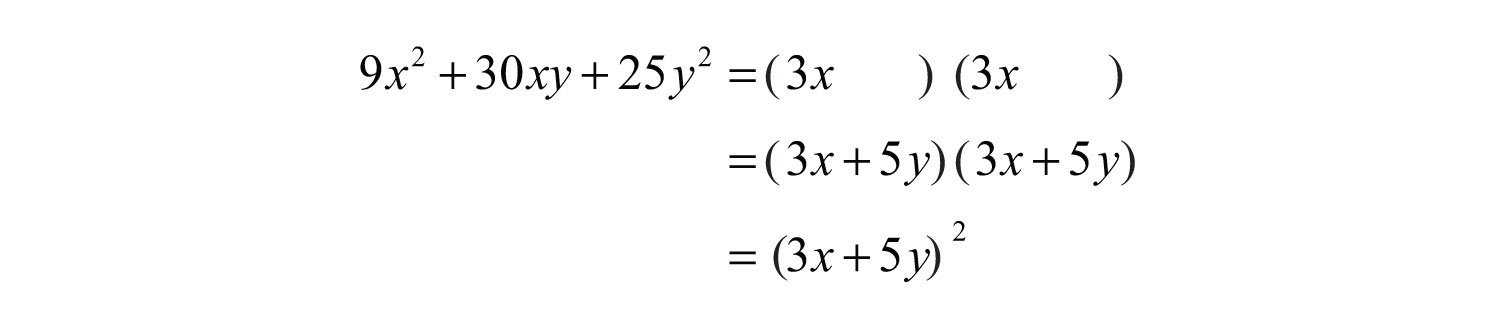
In this example, we have a perfect square trinomial. Check.
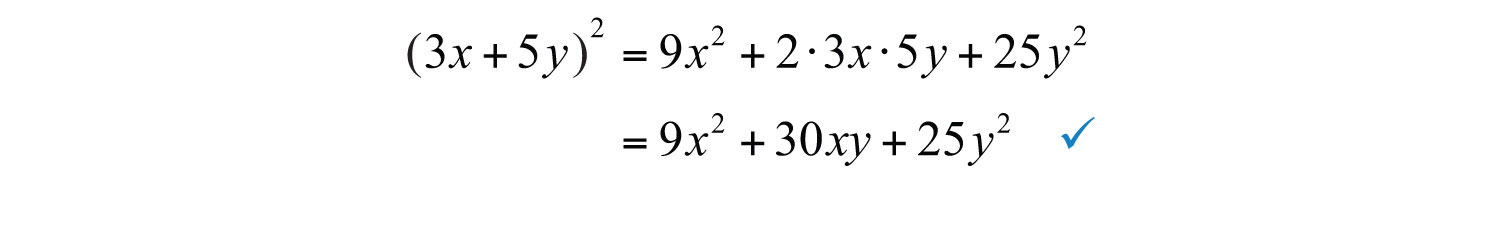
Answer:
Try this! Factor: .
Answer:
Video Solution
(click to see video)Factoring Trinomials with Common Factors
It is a good practice to first factor out the GCF, if there is one. Doing this produces a trinomial factor with smaller coefficients. As we have seen, trinomials with smaller coefficients require much less effort to factor. This commonly overlooked step is worth identifying early.
Example 6: Factor: .
Solution: Begin by factoring out the GCF.
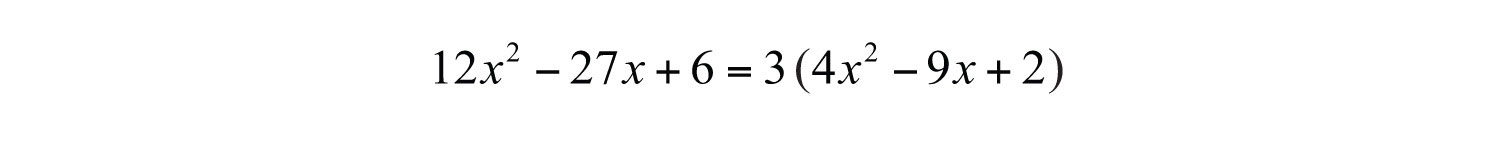
After factoring out 3, the coefficients of the resulting trinomial are smaller and have fewer factors.

After some thought, we can see that the combination that gives the coefficient of the middle term is .
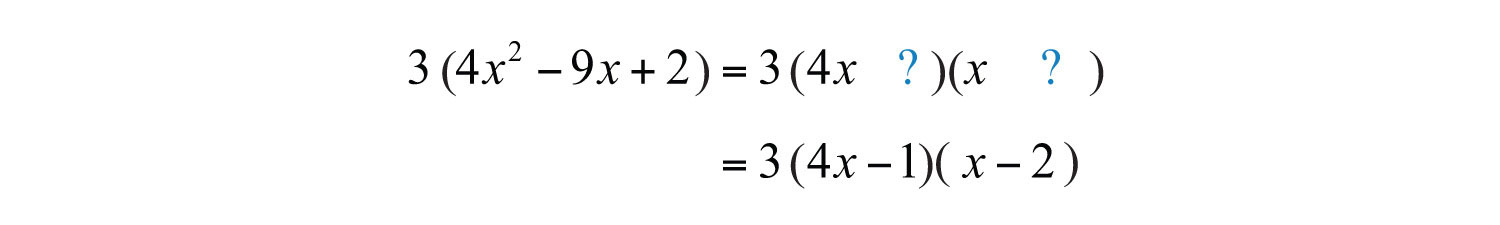
Check.
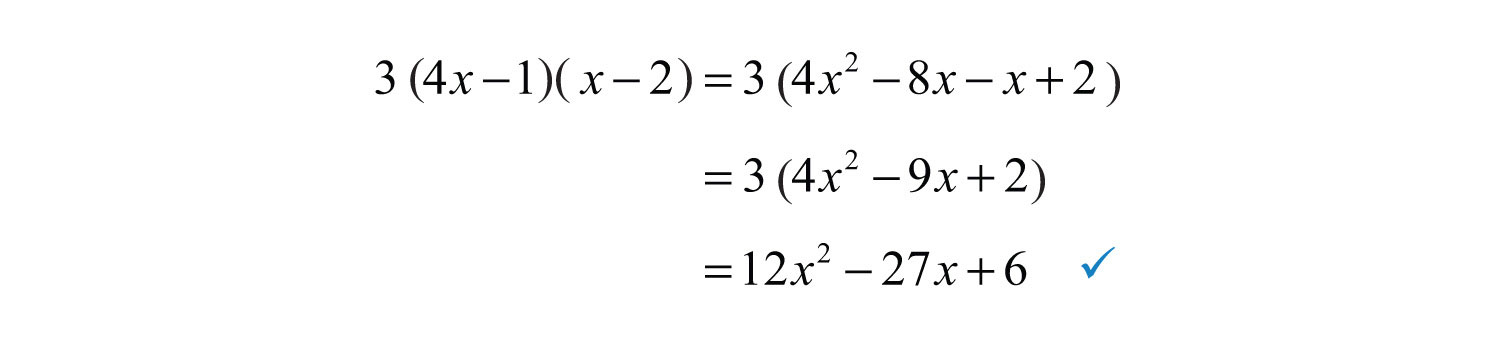
The factor 3 is part of the factored form of the original expression; be sure to include it in the answer.
Answer:
It is a good practice to consistently work with trinomials where the leading coefficient is positive.
Example 7: Factor: .
Solution: In this example, the leading coefficient is −1. Before beginning the factoring process, factor out the −1:
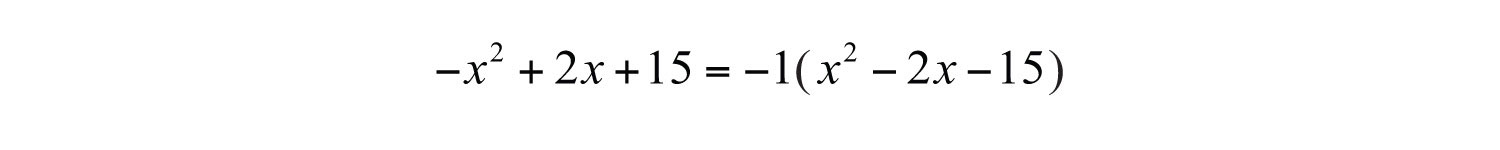
At this point, factor the remaining trinomial as usual, remembering to write the −1 as a factor in your final answer. Because 3 + (−5) = −2, use 3 and 5 as the factors of 15.
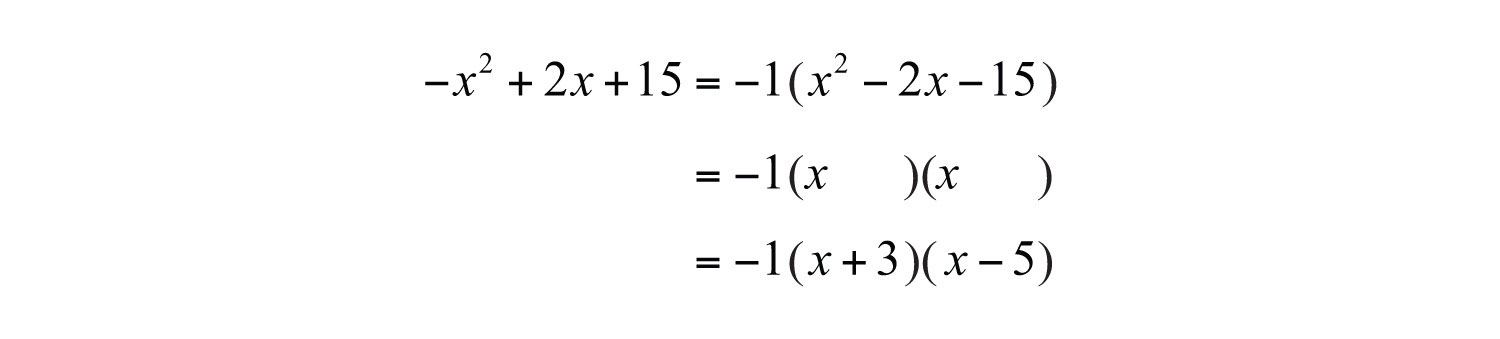
Answer: . The check is left to the reader.
Example 8: Factor: .
Solution: The GCF of all the terms is 5. However, in this case factor out −5 because this produces a trinomial factor where the leading coefficient is positive.
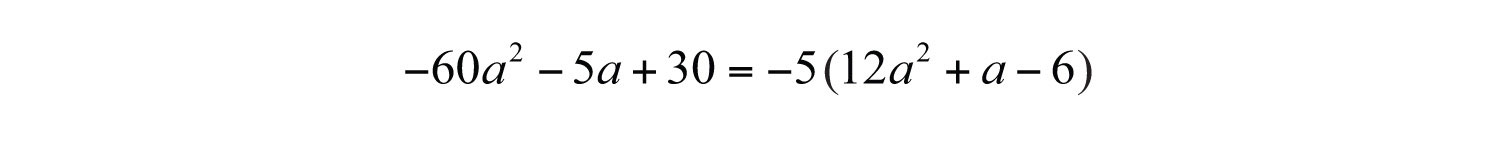
Focus on the factors of 12 and 6 that combine to give the middle coefficient, 1.

After much thought, we find that . Factor the remaining trinomial.
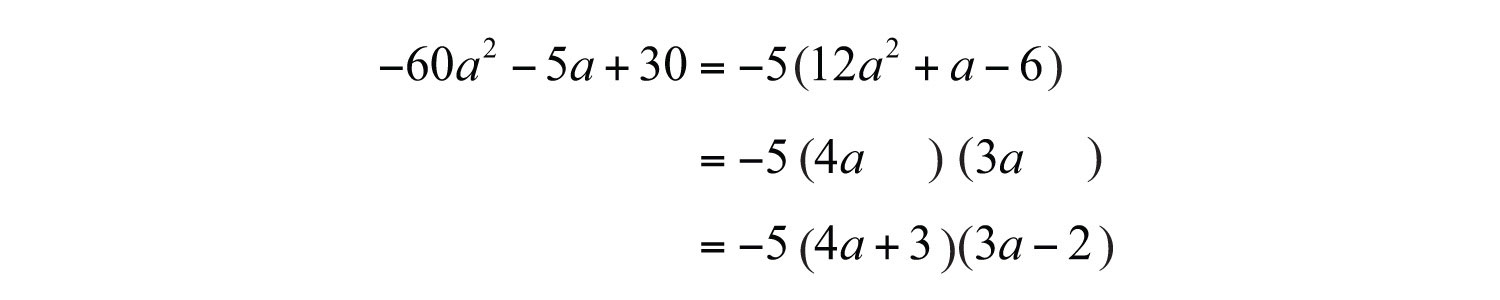
Answer: . The check is left to the reader.
Try this! Factor: .
Answer:
Video Solution
(click to see video)Factoring Using the AC Method
In this section, we factor trinomials of the form using the AC method described previously.
Example 9: Factor using the AC method: .
Solution: Here a = 18, b = −21, and c = 5.
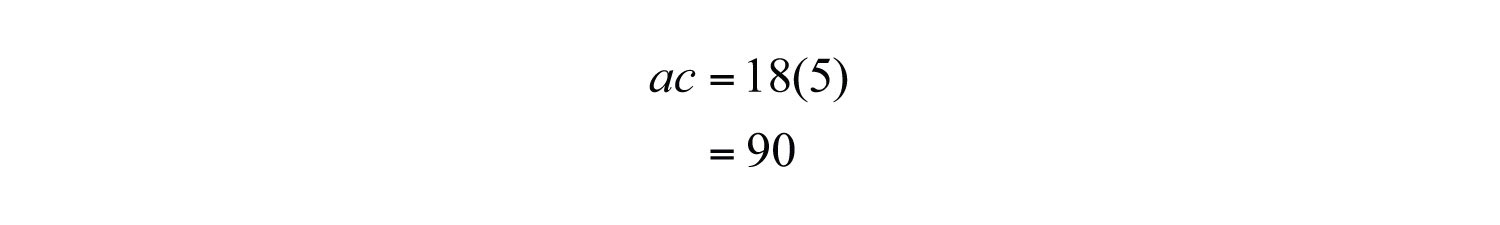
Factor 90 and search for factors whose sum is −21.

In this case, the sum of the factors −6 and −15 equals the middle coefficient, −21. Therefore, , and we can write
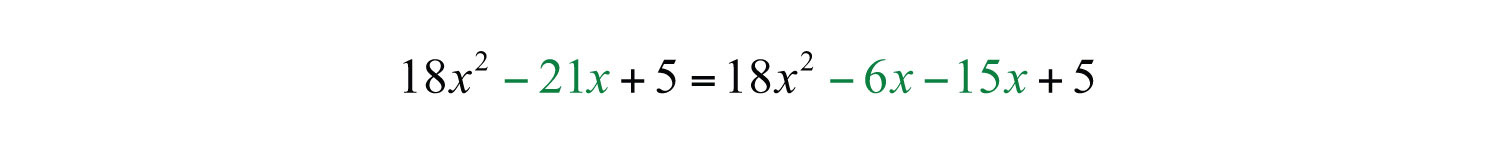
Factor the equivalent expression by grouping.
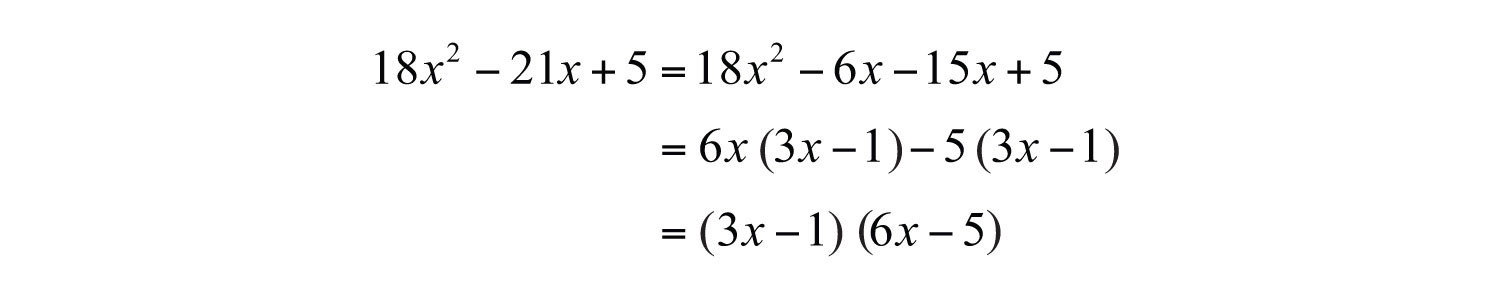
Answer:
Example 10: Factor using the AC method: .
Solution: Here a = 9, b = −61, and c = −14.
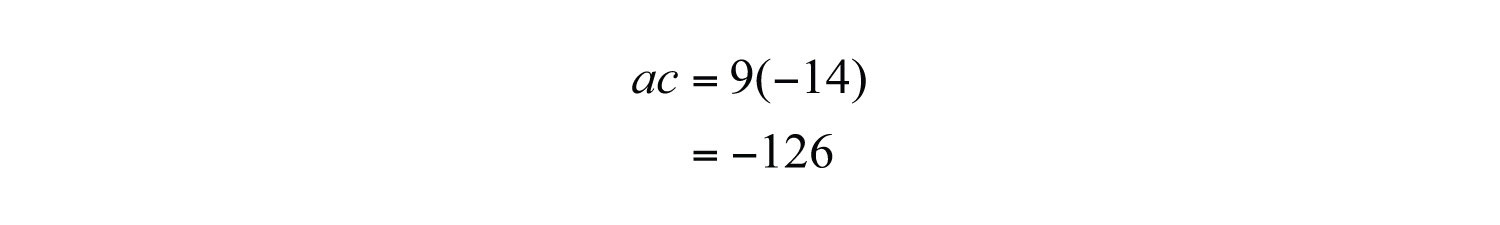
We factor −126 as follows:
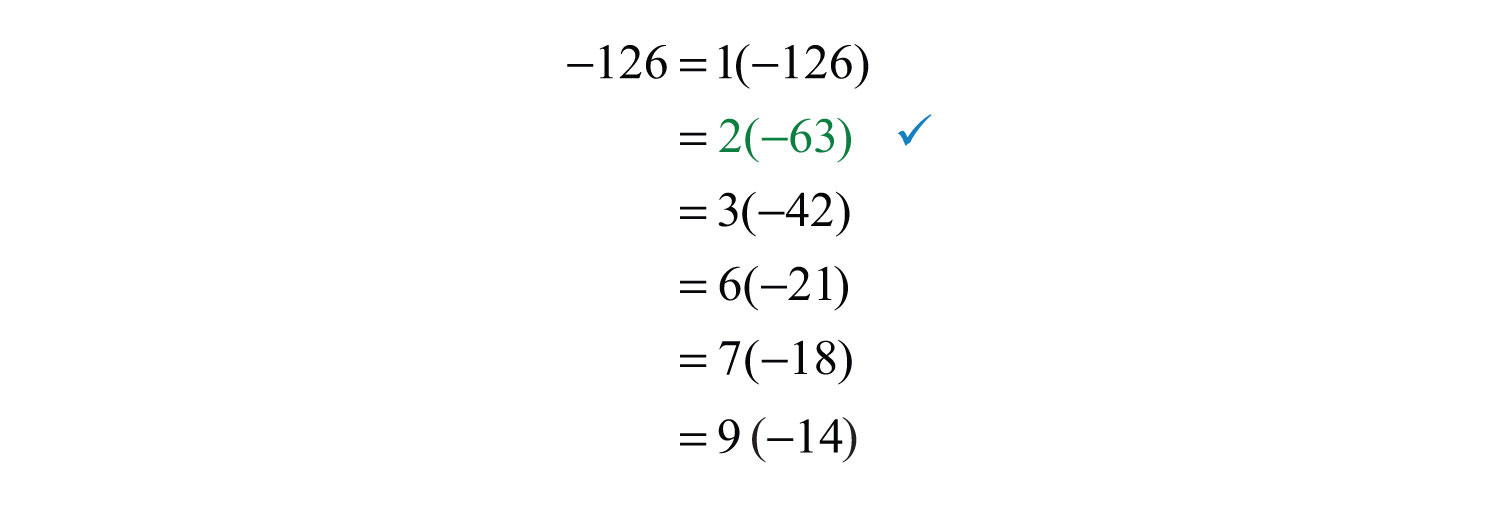
The sum of factors 2 and −63 equals the middle coefficient, −61. Replace with :
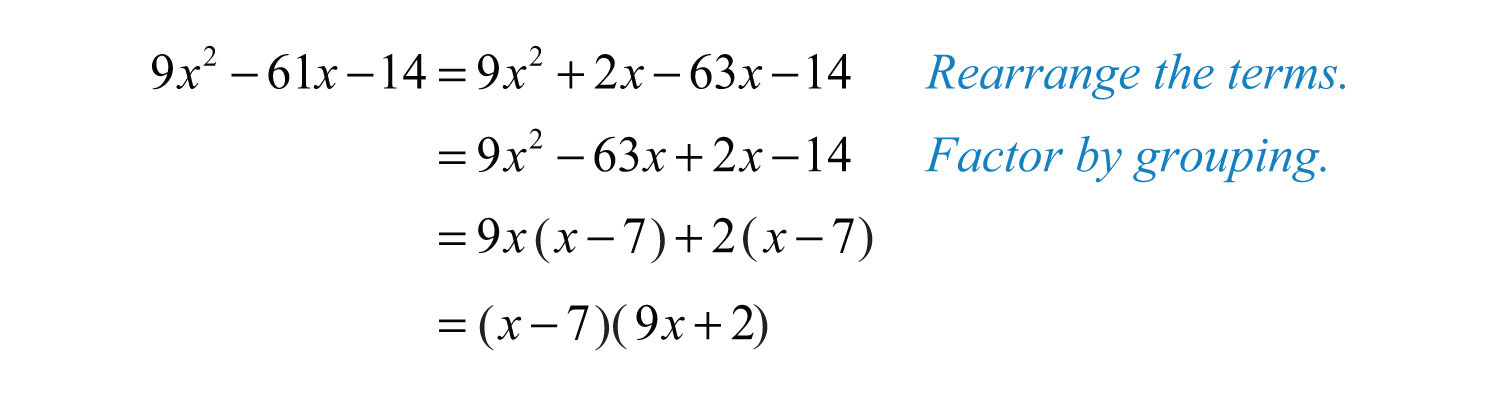
Answer: . The check is left to the reader.
Key Takeaways
- If a trinomial of the form factors into the product of two binomials, then the coefficient of the middle term will be the sum of certain products of factors of the first and last terms.
- If the trinomial has a greatest common factor, then it is a best practice to first factor out the GCF before attempting to factor it into a product of binomials.
- If the leading coefficient of a trinomial is negative, then it is a best practice to factor that negative factor out before attempting to factor the trinomial.
- Factoring trinomials of the form takes lots of practice and patience. It is extremely important to take the time to become proficient by working lots of exercises.
Topic Exercises
Part A: Factoring Trinomials
Factor.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27. The area of a rectangle is given by the function , where x is measured in meters. Rewrite this function in factored form.
28. The area of a rectangle is given by the function , where x is measured in meters. Rewrite this function in factored form.
Part B: Factoring Trinomials with Common Factors
Factor.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
Factor out −1 and then factor further.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
Factor out a negative common factor first and then factor further if possible.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65. The height in feet of a projectile launched from a tower is given by the function , where t represents the number of seconds after launch. Rewrite the given function in factored form.
66. The height in feet of a projectile launched from a tower is given by the function , where t represents the number of seconds after launch. Rewrite the given function in factored form.
Part C: Factoring Using the AC Method
Factor using the AC method.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
Part D: Discussion Board Topics
77. Create your own trinomial of the form that factors. Share it, along with the solution, on the discussion board.
78. Write out your own list of steps for factoring a trinomial of the form and share it on the discussion board.
79. Create a trinomial of the form that does not factor and share it along with the reason why it does not factor.
Answers
1:
3:
5:
7:
9:
11:
13:
15: Prime
17:
19:
21:
23:
25:
27:
29:
31:
33:
35:
37:
39:
41:
43:
45:
47:
49:
51:
53:
55:
57:
59:
61:
63:
65:
67:
69:
71:
73:
75:
6.4 Factoring Special Binomials
Learning Objectives
- Factor binomials that are differences of squares.
- Factor binomials that are sums and differences of cubes.
Difference of Squares
A binomial is a polynomial with two terms. We begin with our first special binomial called difference of squares where a and b represent algebraic expressions.:
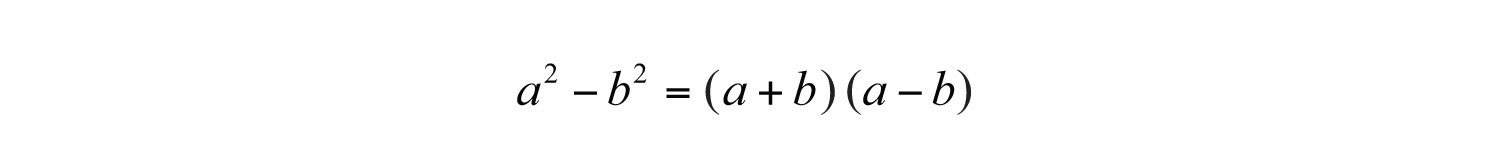
To verify the above formula, multiply:

We use this formula to factor certain special binomials.
Example 1: Factor: .
Solution:
Step 1: Identify the binomial as difference of squares and determine the square factors of each term.
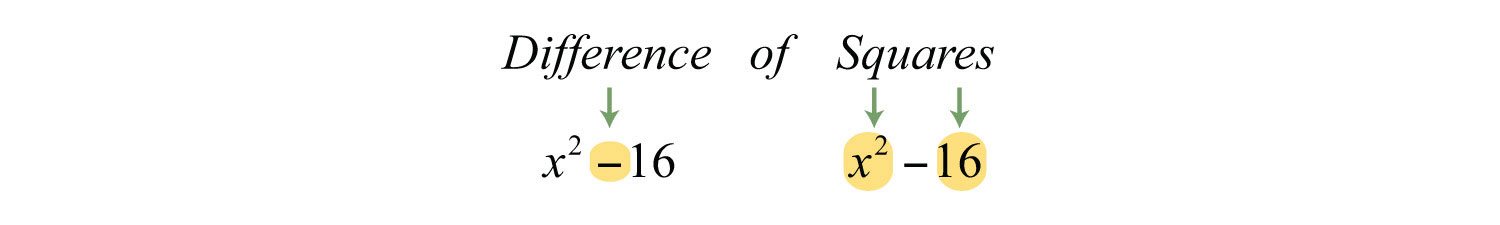
Here we can write
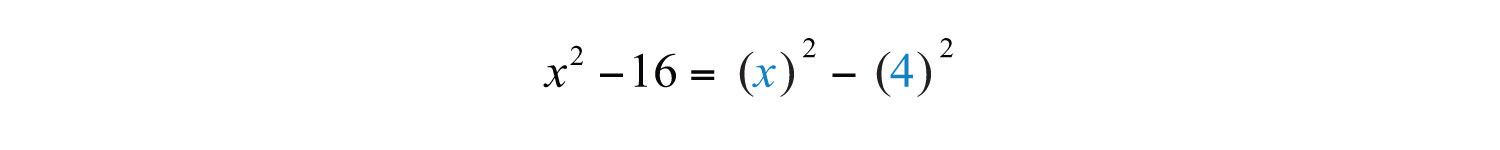
The terms are squares of x and 4. Hence and .
Step 2: Substitute into the difference of squares formula.
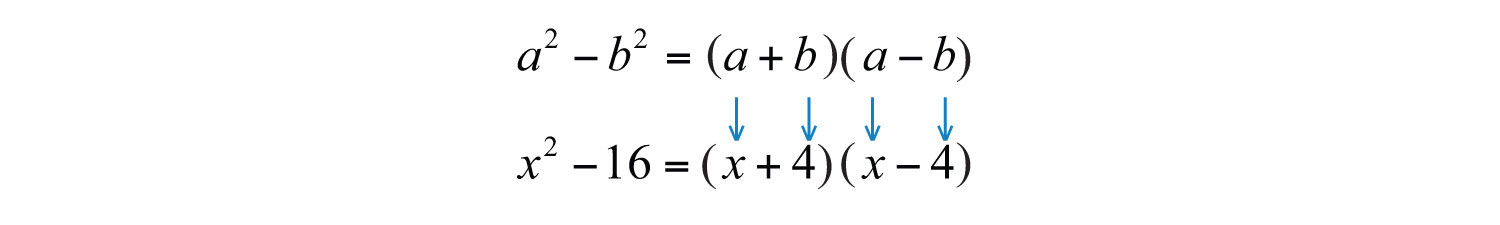
Step 3: Multiply to check. This step is optional.
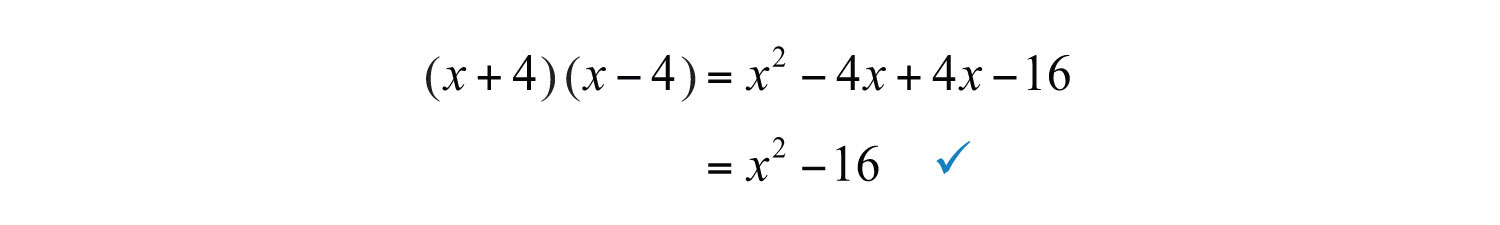
Answer:
It is worth taking some extra time at this point to review all of the squares of integers from 1 to 12.

Recognizing these perfect square integers helps speed the factoring process.
Example 2: Factor: .
Solution: The subtraction indicates that this is a difference. Furthermore, we recognize that the terms are squares.
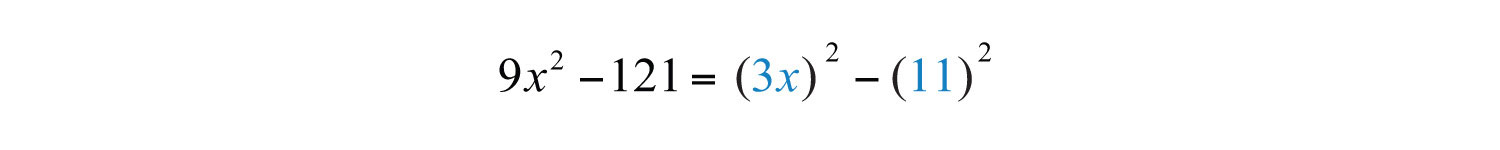
In this case, and . Substitute into the formula for difference of squares.
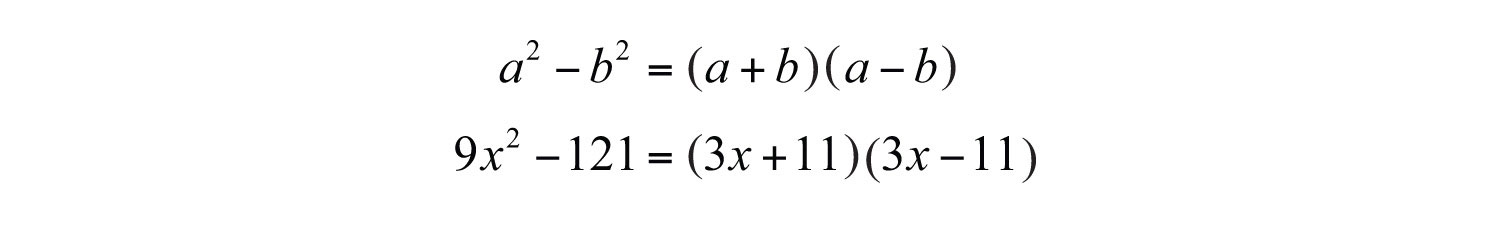
Answer:
It may be the case that the terms of the binomial have a common factor. If so, it will be difficult to identify the perfect squares until we first factor out the GCF.
Example 3: Factor: .
Solution: The terms are not perfect squares. However, notice that they do have a common factor. First, factor out the GCF, 3.
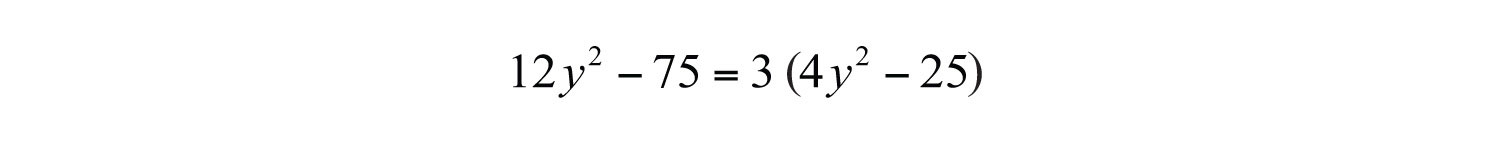
The resulting binomial factor is a difference of squares with and .

Answer:
Example 4: Factor: .
Solution: Here we have a binomial with two variables and recognize that it is a difference of squares.
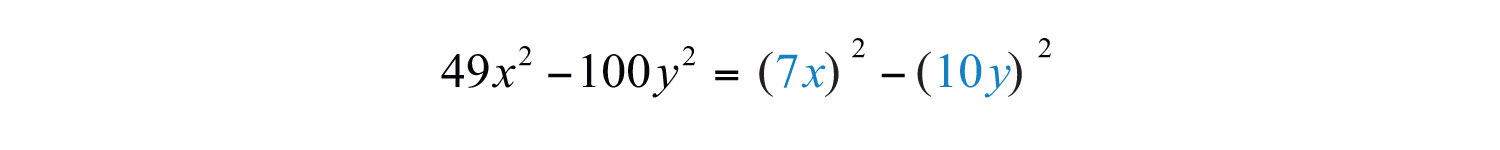
Therefore, and . Substitute into the formula for difference of squares.
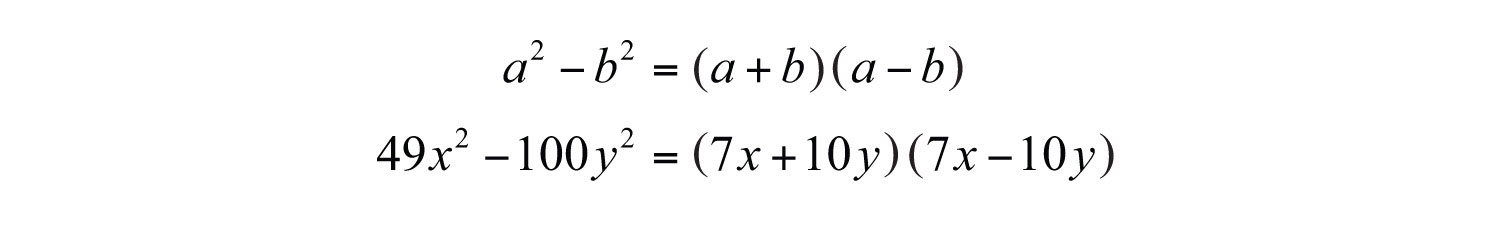
Answer:
Try this! Factor: .
Answer:
Video Solution
(click to see video)Given any real number b, a polynomial of the form is prime. Furthermore, the sum of squares does not have a general factored equivalent. does not have a general factored equivalent. Care should be taken not to confuse this with a perfect square trinomial:
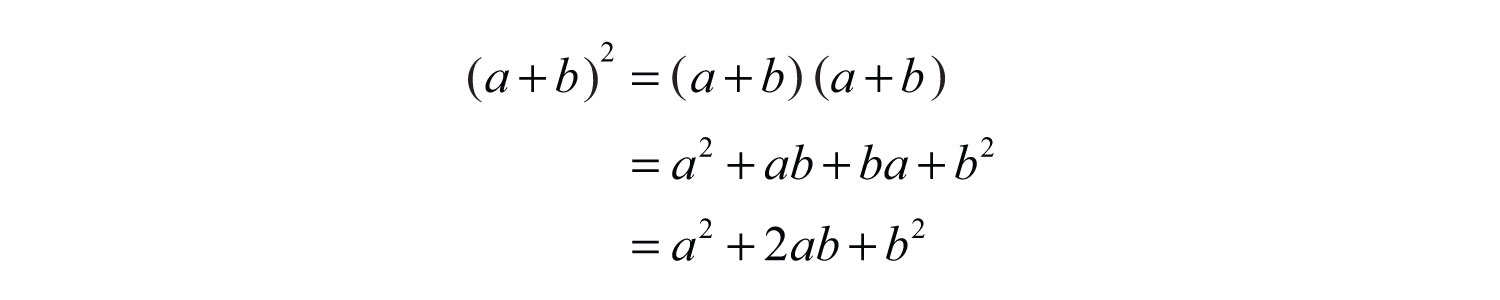
Therefore,
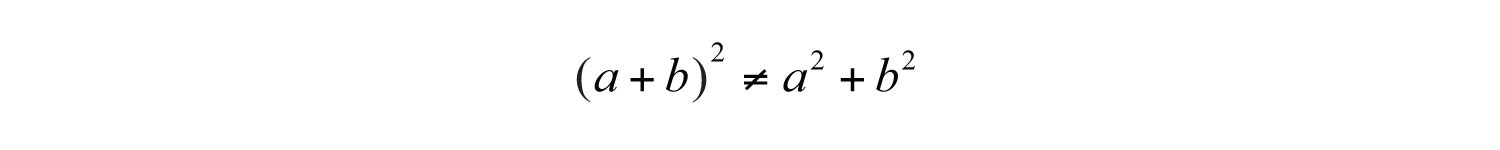
When the degree of the special binomial is greater than two, we may need to apply the difference of squares formula multiple times. A polynomial is completely factored when none of the factors can be factored any further.
Example 5: Factor completely: .
Solution: First, identify what is being squared:
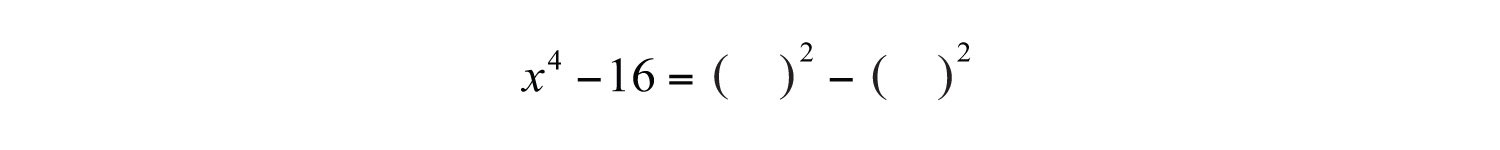
To do this, recall the power rule for exponents, . When exponents are raised to a power, multiply them. With this in mind, determine that and write
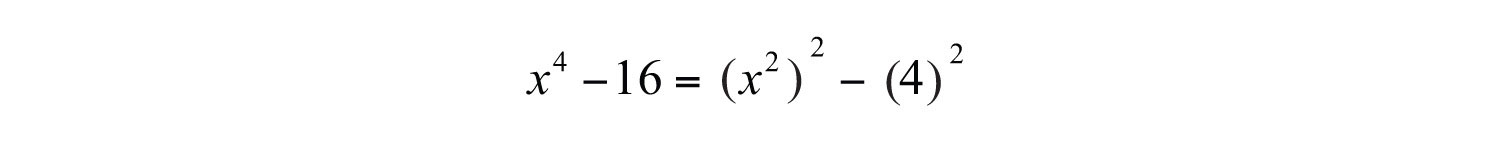
Therefore, and . Substitute into the formula for difference of squares.
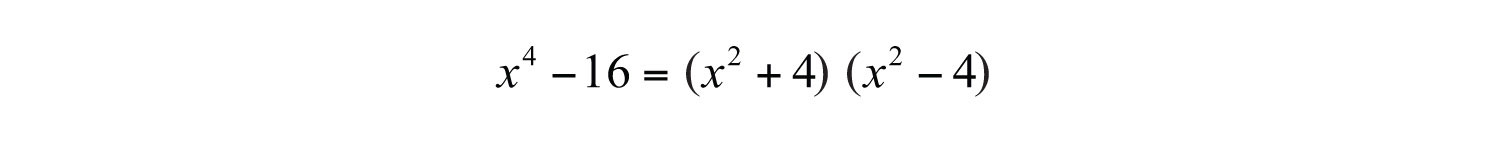
At this point, notice that the factor is itself a difference of two squares and thus can be further factored using and . The factor is a sum of squares, which cannot be factored using real numbers.
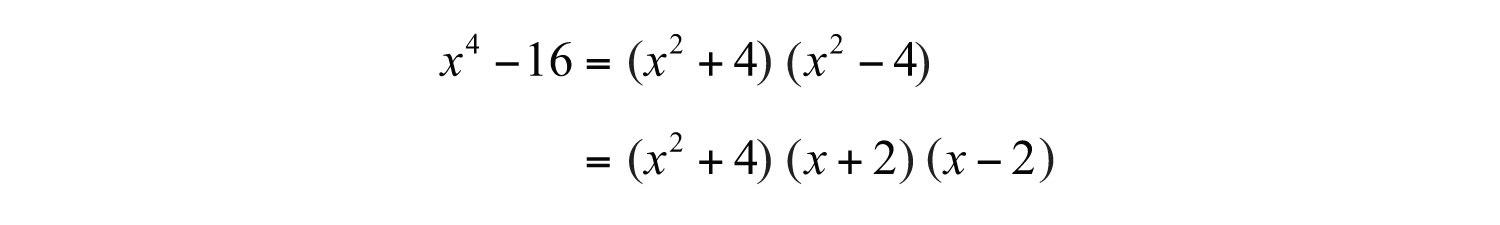
Answer:
Try this! Factor completely: .
Answer:
Video Solution
(click to see video)Sum and Difference of Cubes
Two other special binomials of interest are the sum where a and b represent algebraic expressions. and difference of cubes where a and b represent algebraic expressions.:
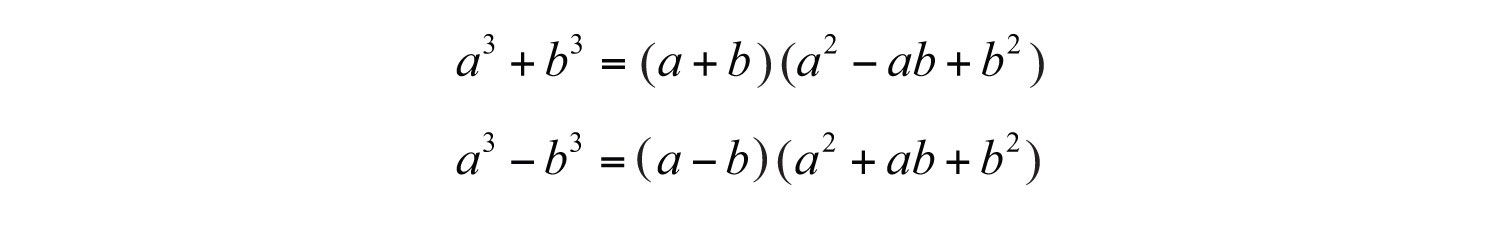
We can verify these formulas by multiplying:
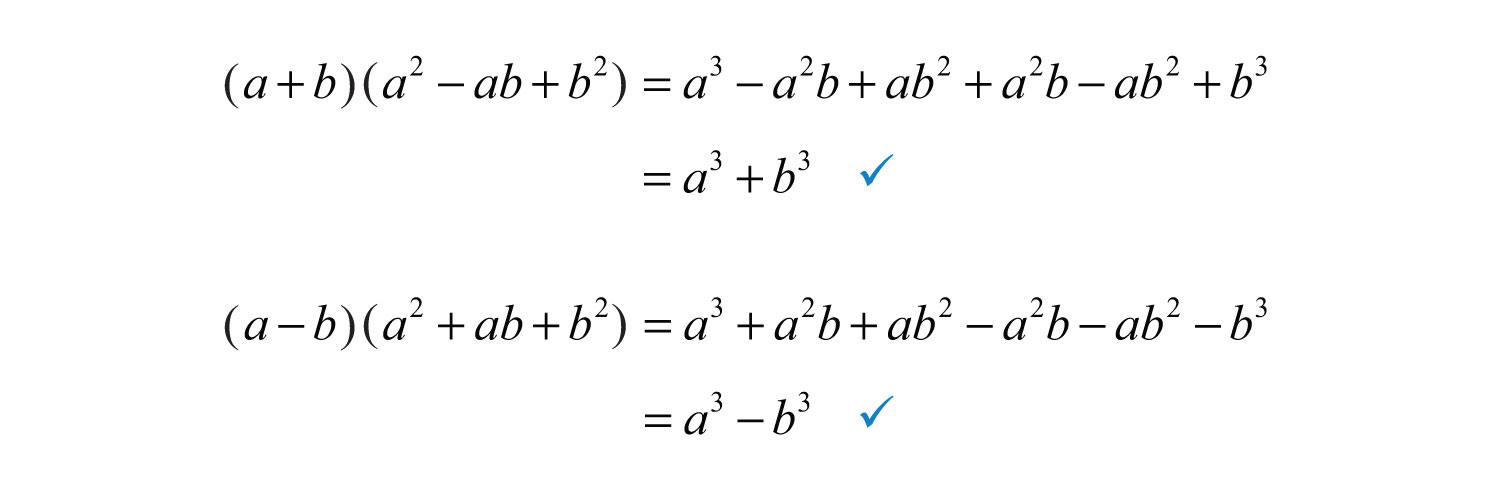
The process for factoring the sum and difference of cubes is very similar to that for the difference of squares. We first identify a and b and then substitute into the appropriate formula. The separate formulas for sum and difference of cubes allow us to always choose a and b to be positive.
Example 6: Factor: .
Solution: The plus sign and the fact that the terms are cubes indicate to us that this is a sum of cubes.
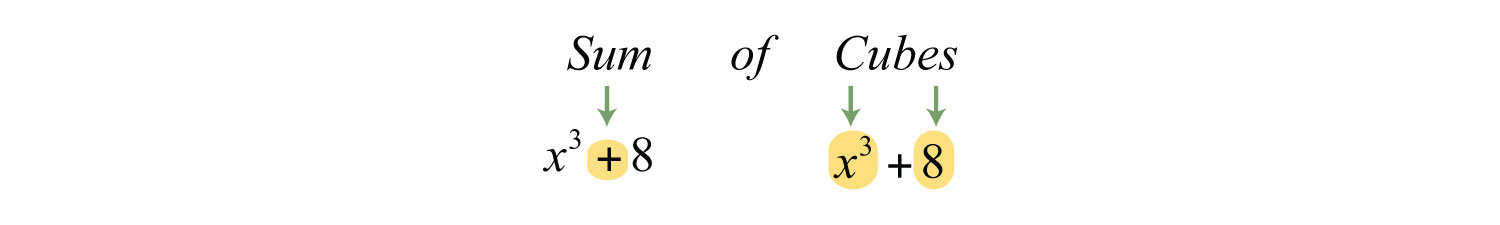
Next, identify what is being cubed.
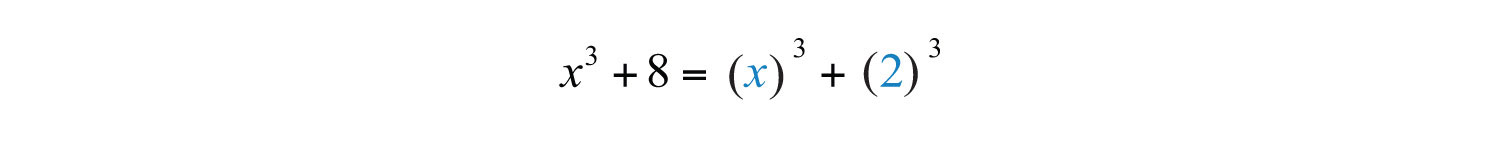
In this case, and . Substitute into the sum of cubes formula.
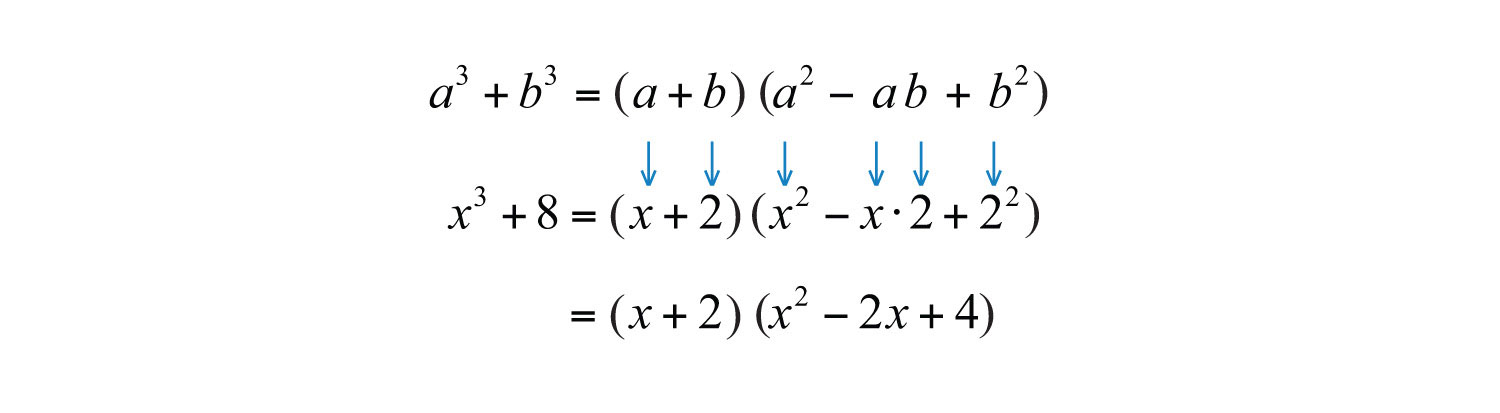
The resulting trinomial is prime and the factoring is complete. We can check this factorization by multiplying.
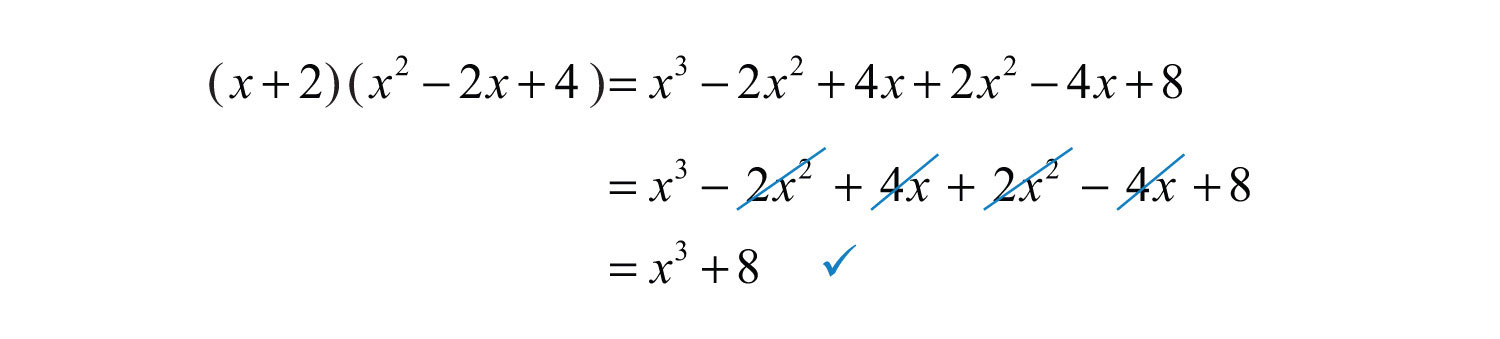
Answer:
It is helpful to review the perfect cubes of integers from 1 to 12. This will aid you in identifying sums and differences of cubes.

Example 7: Factor: .
Solution: In this case, we have a difference of cubes.
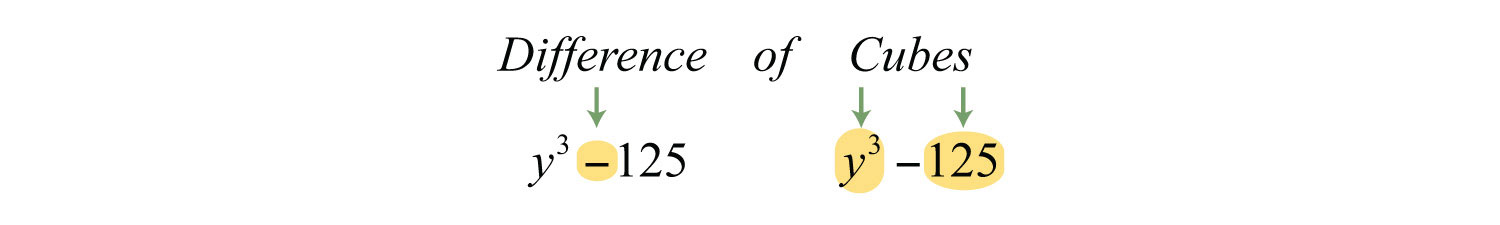
We can write
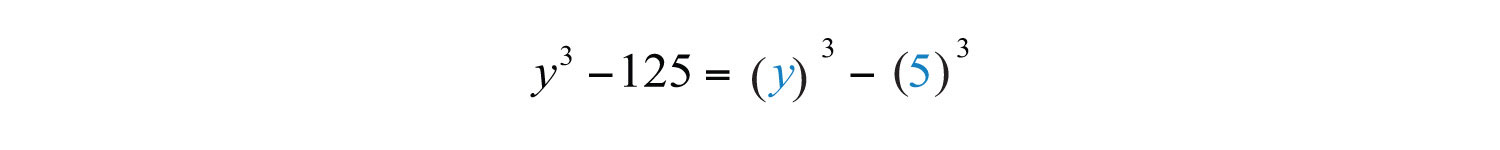
Substitute and into the formula for difference of cubes.
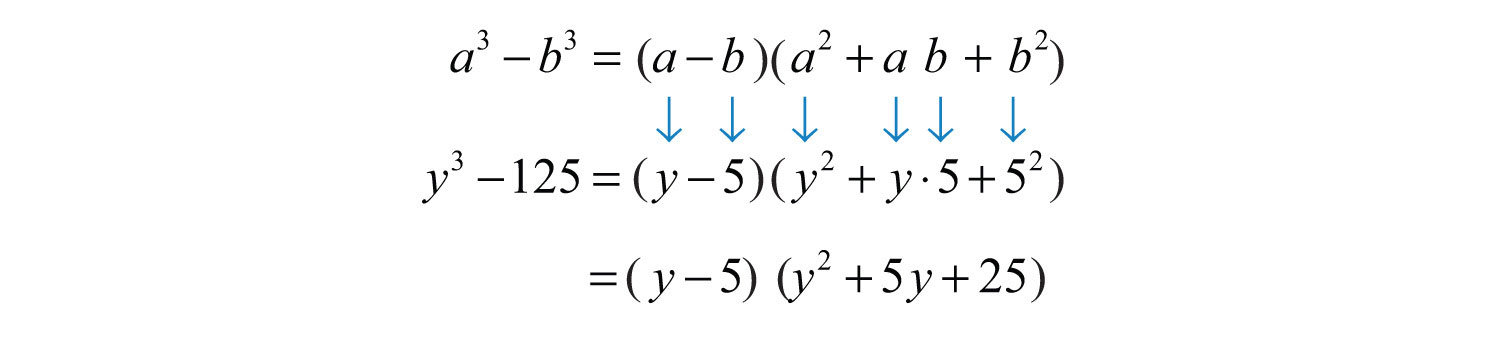
Answer:
Always look for common factors when factoring. If the terms of the binomial have a GCF other than 1, then factor that out first.
Example 8: Factor: .
Solution: Begin by factoring out the GCF .
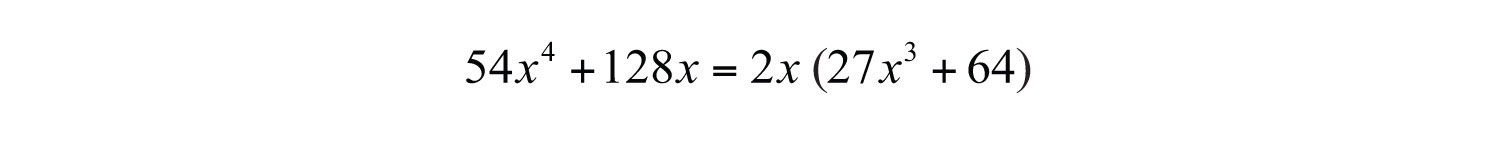
The resulting binomial factor is a sum of cubes, where and .

Answer:
Example 9: Factor: .
Solution: This binomial is a difference of cubes with two variables. Identify what is being cubed.
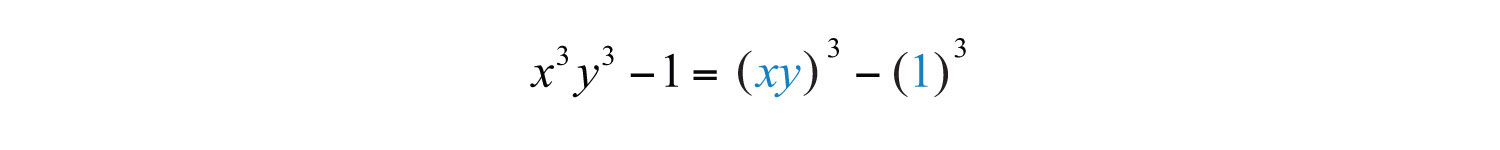
Here and . Substitute into the appropriate formula and simplify.
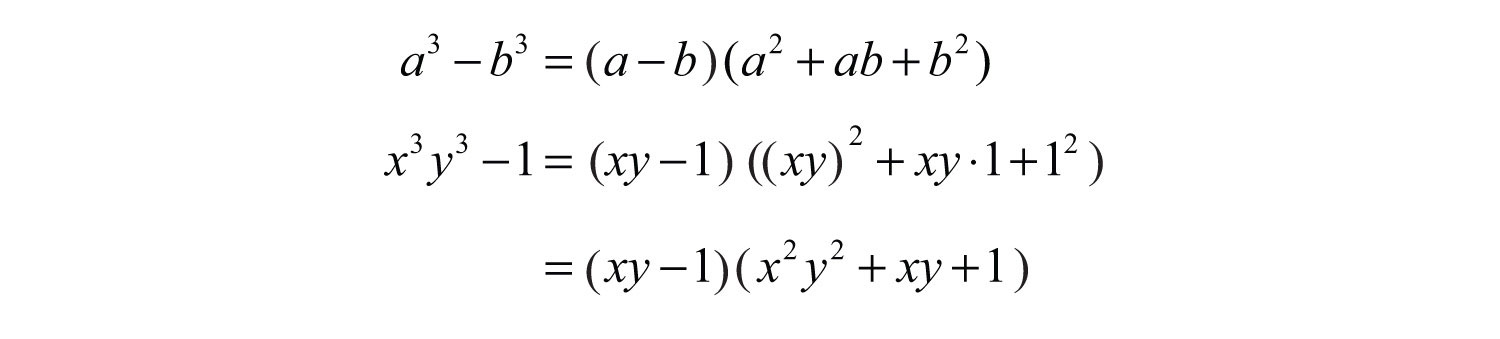
Answer:
Try this! Factor: .
Answer:
Video Solution
(click to see video)When factoring, always look for resulting factors to factor further.
Example 10: Factor completely: .
Solution: When confronted with a binomial that is both a difference of squares and cubes, as this is, make it a rule to factor using difference of squares first.
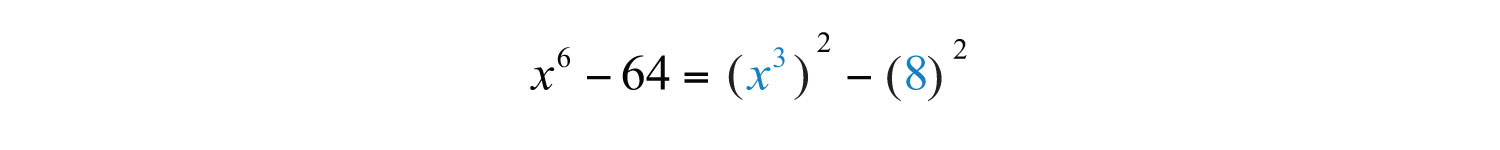
Therefore, and . Substitute into the difference of squares formula.
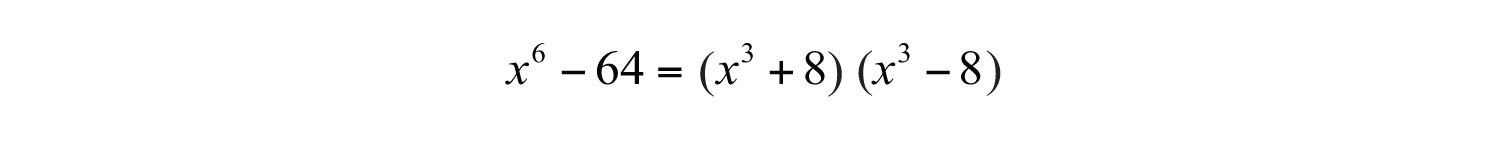
The resulting two binomial factors are a sum and a difference of cubes. Each can be factored further.
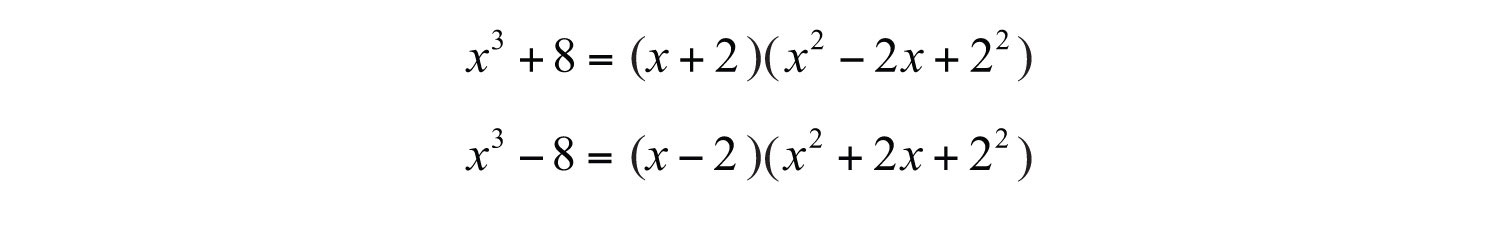
Therefore, we have
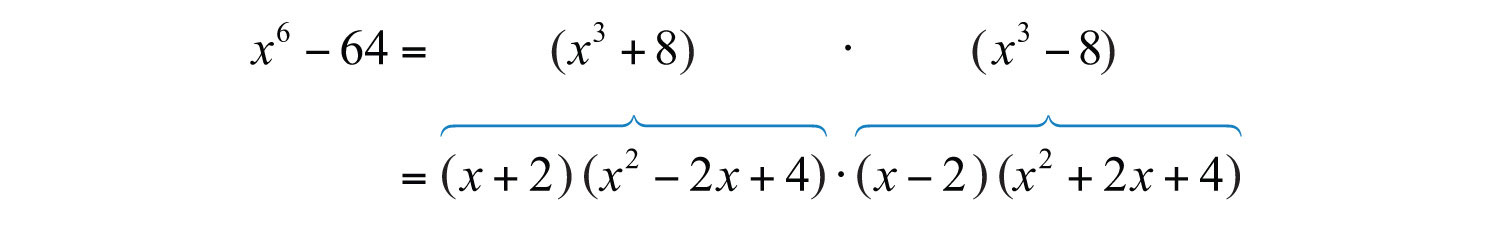
The trinomial factors are prime and the expression is completely factored.
Answer:
As an exercise, factor the previous example as a difference of cubes first and then compare the results. Why do you think we make it a rule to factor using difference of squares first?
Try this! Factor: .
Answer:
Video Solution
(click to see video)Key Takeaways
- When factoring special binomials, the first step is to identify it as a sum or difference. Once we identify the binomial, we then determine the values of a and b and substitute into the appropriate formula.
- The formulas for all of the special binomials should be memorized. In addition, to help facilitate the identification of special binomials, memorize the squares and cubes of integers up to at least 12.
- If a binomial is both a difference of squares and cubes, then first factor it as a difference of squares.
Topic Exercises
Part A: Difference of Squares
Factor completely.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51. The height of a projectile dropped from a 64-foot tower is given by the function , where t represents the time in seconds after it is dropped. Rewrite this function in factored form. (Hint: Factor out −16 first.)
52. The height of a projectile dropped from a 36-foot tower is given by the function , where t represents the time in seconds after it is dropped. Rewrite this function in factored form.
Part B: Sum and Difference of Cubes
Factor completely.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
Part C: Discussion Board Topics
95. If a binomial falls into both categories, difference of squares and difference of cubes, which would be best to factor it as, and why? Create an example that illustrates this situation and factor it using both formulas.
96. What can be said about the degrees of the factors of a polynomial? Give an example.
97. Make up your own difference of squares factoring exercise and provide the answer. Explain how you solved it.
98. Make up your own sum or difference of cubes factoring exercise and provide the answer. Explain how you solved it.
Answers
1:
3:
5: Prime
7:
9:
11:
13:
15:
17:
19:
21:
23:
25:
27:
29:
31:
33:
35:
37:
39:
41:
43:
45:
47:
49:
51:
53:
55:
57:
59:
61:
63:
65:
67:
69:
71: Prime
73:
75:
77:
79:
81:
83:
85:
87:
89:
91:
93:
6.5 General Guidelines for Factoring Polynomials
Learning Objective
- Develop a general strategy for factoring polynomials.
General Factoring Strategy
We have learned various techniques for factoring polynomials with up to four terms. The challenge is to identify the type of polynomial and then decide which method to apply. The following outlines a general guideline for factoring polynomials:
- Check for common factors. If the terms have common factors, then factor out the greatest common factor (GCF) and look at the resulting polynomial factors to factor further.
-
Determine the number of terms in the polynomial.
a. Factor four-term polynomials by grouping.
b. Factor trinomials (three terms) using “trial and error” or the AC method.
c. Factor binomials (two terms) using the following special products:
Difference of squares: Sum of squares: Difference of cubes: Sum of cubes: - Look for factors that can be factored further.
- Check by multiplying.
Note
- If a binomial is both a difference of squares and a difference of cubes, then first factor it as difference of squares and then as a sum and difference of cubes to obtain a more complete factorization.
- Not all polynomials with integer coefficients factor. When this is the case, we say that the polynomial is prime.
If an expression has a GCF, then factor this out first. Doing so is often overlooked and typically results in factors that are easier to work with. Also, look for the resulting factors to factor further; many factoring problems require more than one step. A polynomial is completely factored when none of the factors can be factored further.
Example 1: Factor: .
Solution: This four-term polynomial has a GCF of . Factor this out first.
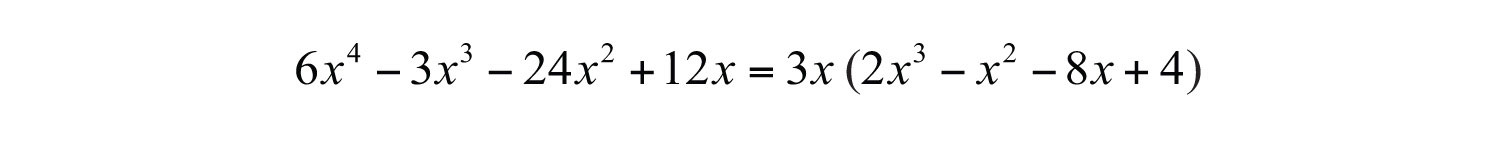
Now factor the resulting four-term polynomial by grouping.
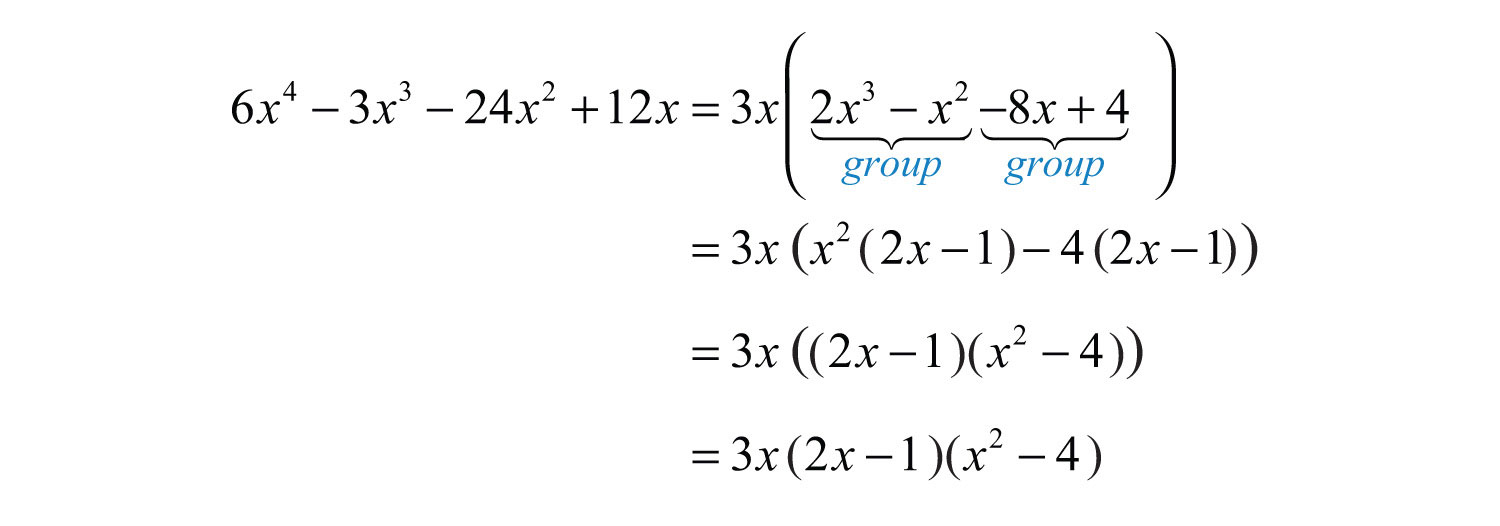
The factor is a difference of squares and can be factored further.
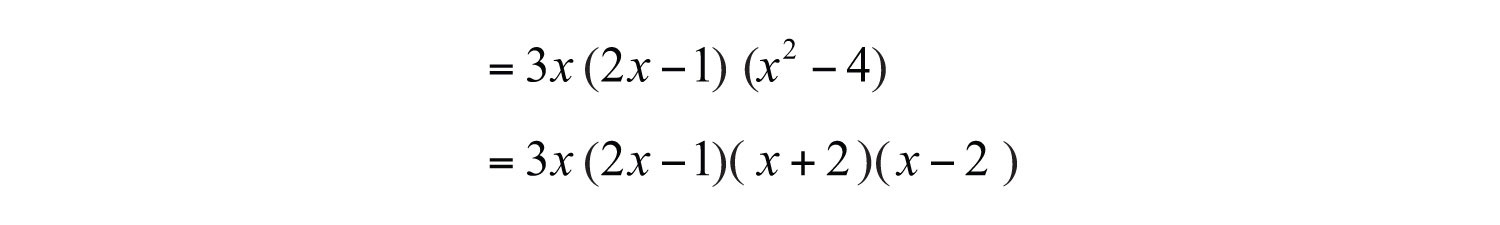
Answer:
Example 2: Factor: .
Solution: This trinomial has a GCF of . Factor this out first.
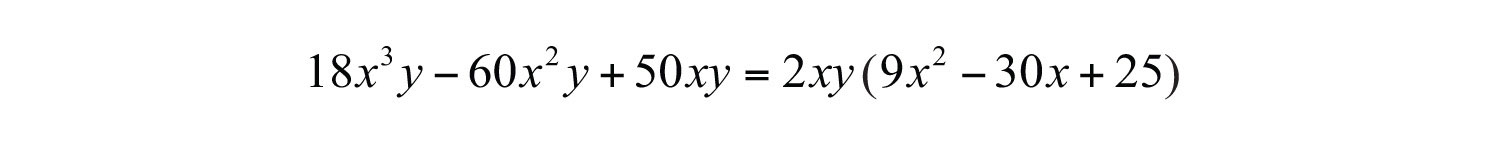
The trinomial factor can be factored further using the trial and error method. Use the factors and . These combine to generate the correct coefficient for the middle term: .
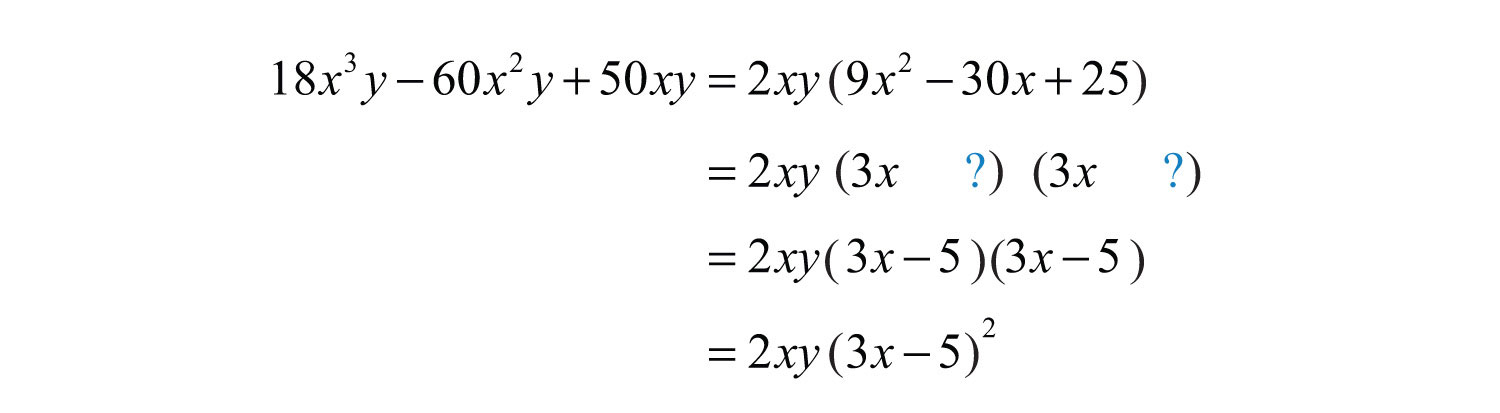
Check.
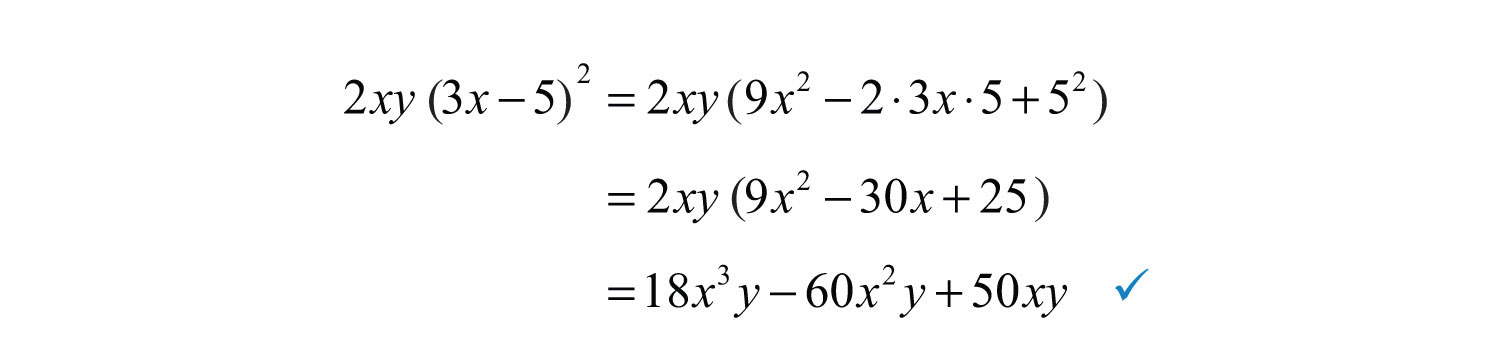
Answer:
Example 3: Factor: .
Solution: This trinomial has a GCF of . Factor this out first.
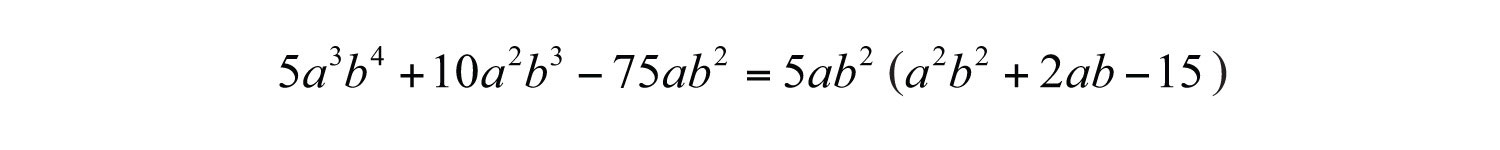
The resulting trinomial factor can be factored as follows:
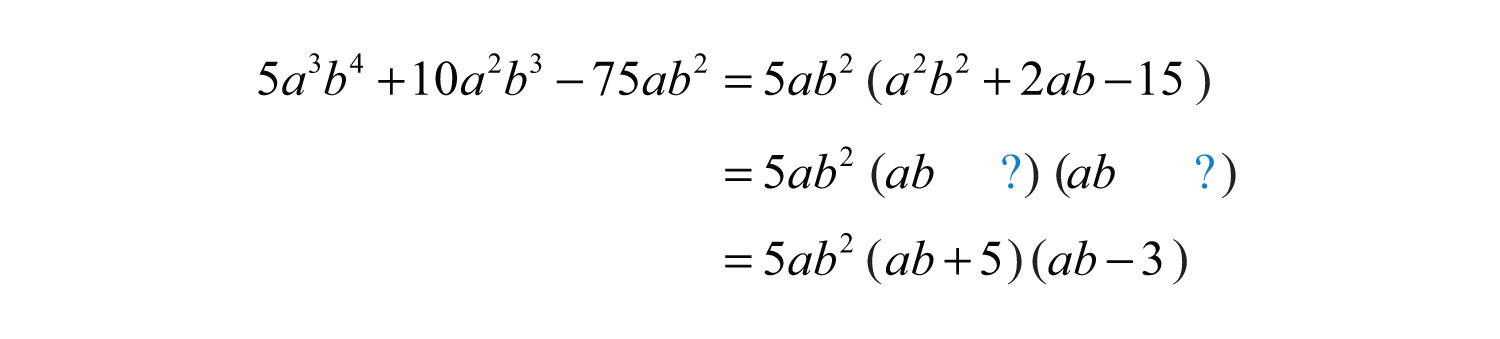
Answer:
Try this! Factor: .
Answer:
Video Solution
(click to see video)
Example 4: Factor: .
Solution: This binomial does not have a GCF. Therefore, begin factoring by identifying it as a difference of squares.
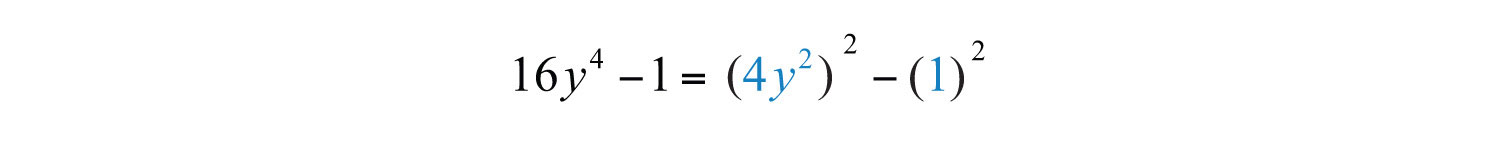
Here and b = 1. Substitute into the formula for difference of squares.

The factor is a sum of squares and is prime. However, is a difference of squares and can be factored further.
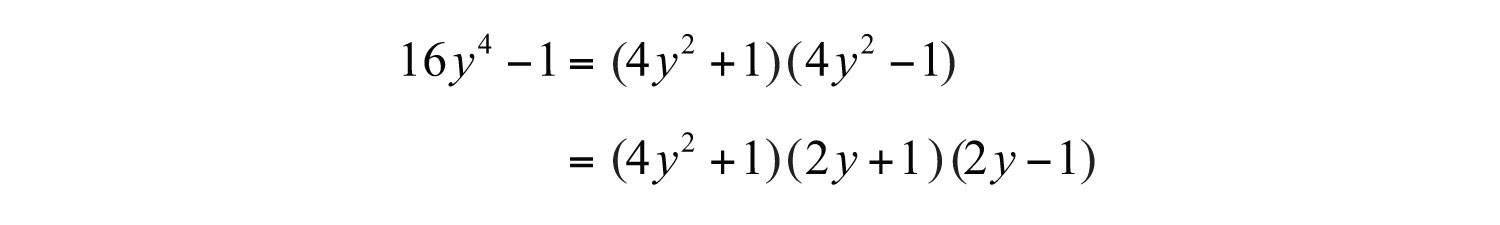
Answer:
Example 5: Factor: .
Solution: This binomial is a difference of squares and a difference of cubes. When this is the case, first factor it as a difference of squares.
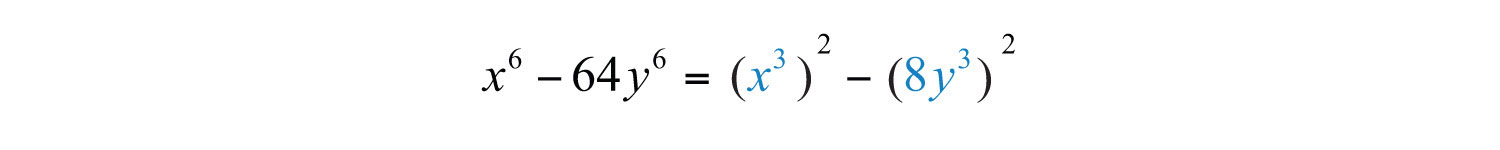
We can write
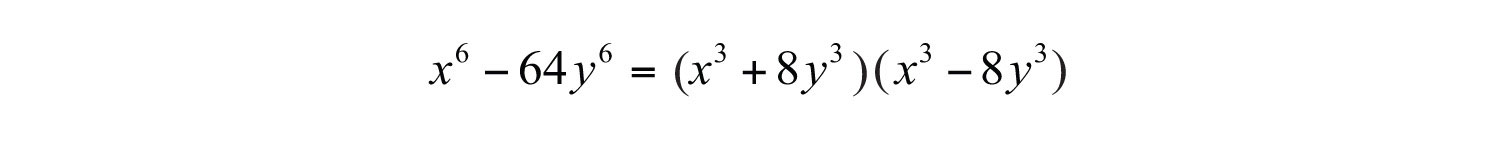
Each factor can be further factored either as a sum or difference of cubes, respectively.
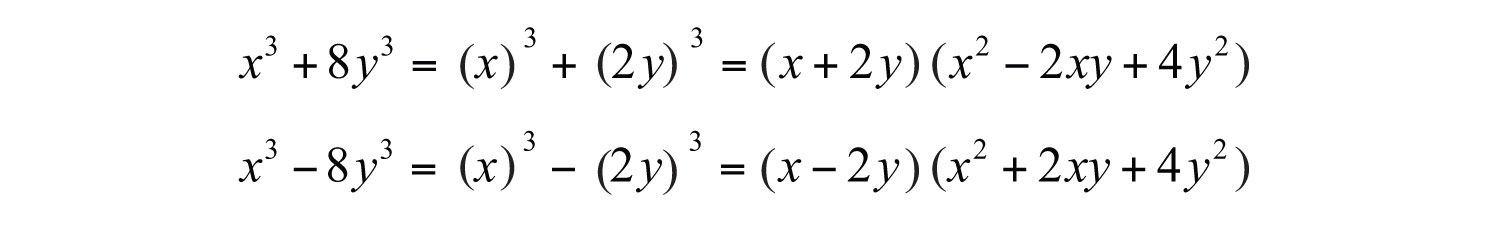
Therefore,
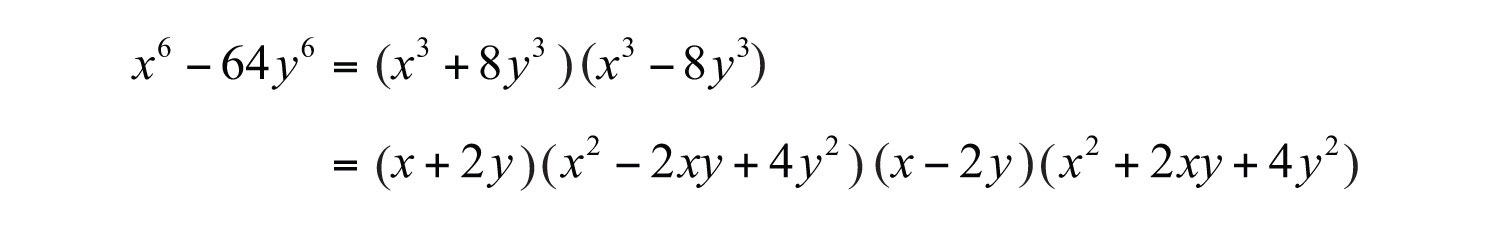
Answer:
Example 6: Factor: .
Solution: First, identify this expression as a difference of squares.
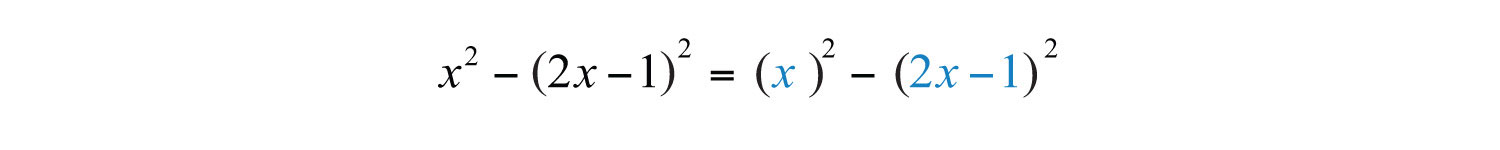
Here use and in the formula for a difference of squares.
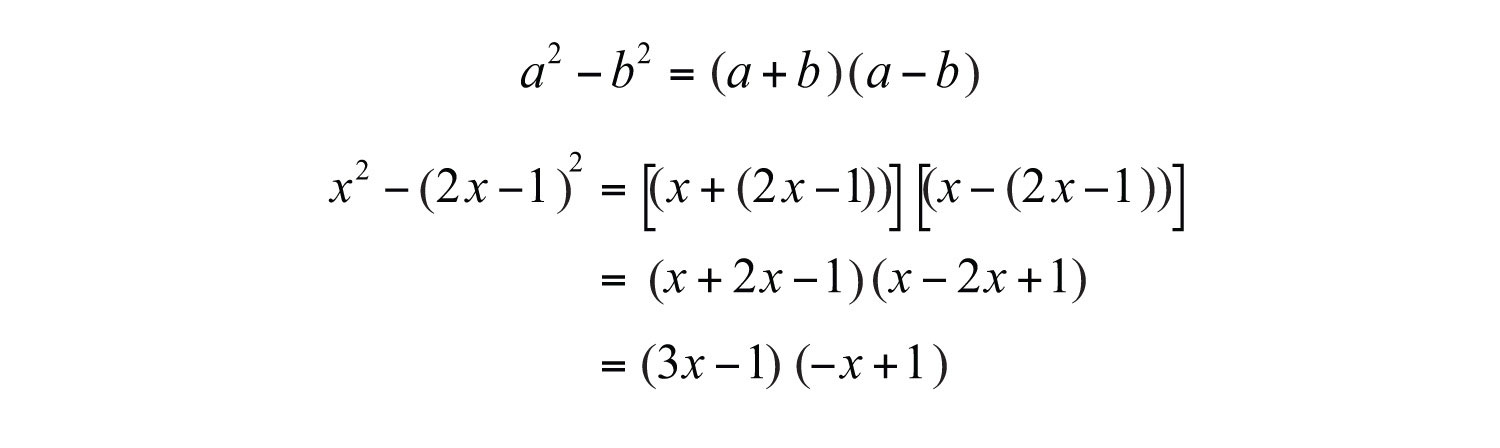
Answer:
Try this! Factor: .
Answer:
Video Solution
(click to see video)Key Takeaways
- Use the polynomial type to determine the method used to factor it.
- It is a best practice to look for and factor out the greatest common factor (GCF) first. This will facilitate further factoring and simplify the process. Be sure to include the GCF as a factor in the final answer.
- Look for resulting factors to factor further. It is often the case that factoring requires more than one step.
- If a binomial can be considered as both a difference of squares and a difference of cubes, then first factor it as a difference of squares. This results in a more complete factorization.
Topic Exercises
Part A: Mixed Factoring
Factor completely.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69. The volume of a certain rectangular solid is given by the function . Write the function in its factored form.
70. The volume of a certain right circular cylinder is given by the function . Write the function in its factored form.
Part B: Discussion Board
71. First, factor the trinomial . Then factor out the GCF. Discuss the significance of factoring out the GCF first. Do you obtain the same result?
72. Discuss a plan for factoring polynomial expressions on an exam. What should you be looking for and what should you be expecting?
Answers
1:
3:
5:
7:
9:
11:
13:
15:
17:
19: Prime
21:
23:
25:
27:
29:
31:
33:
35:
37:
39:
41: Prime
43:
45:
47:
49:
51:
53:
55:
57:
59:
61:
63:
65:
67:
69:
6.6 Solving Equations by Factoring
Learning Objectives
- Verify solutions to quadratic equations.
- Solve quadratic equations by factoring.
- Determine a quadratic equation with given solutions.
- Solve polynomial equations by factoring.
Solving Quadratic Equations by Factoring
Learning how to solve equations is one of our main goals in algebra. Up to this point, we have solved linear equations, which are of degree 1. In this section, we will learn a technique that can be used to solve certain equations of degree 2. A quadratic equationA polynomial equation with one variable of degree 2. is any equation that can be written in the standard formA quadratic equation written in the form
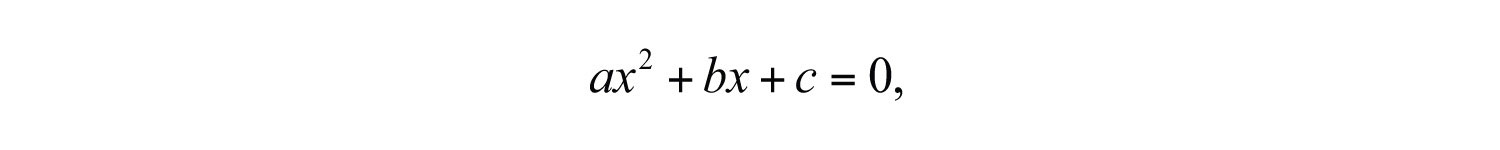
where a, b, and c are real numbers and . The following are some examples of quadratic equations, all of which will be solved in this section:
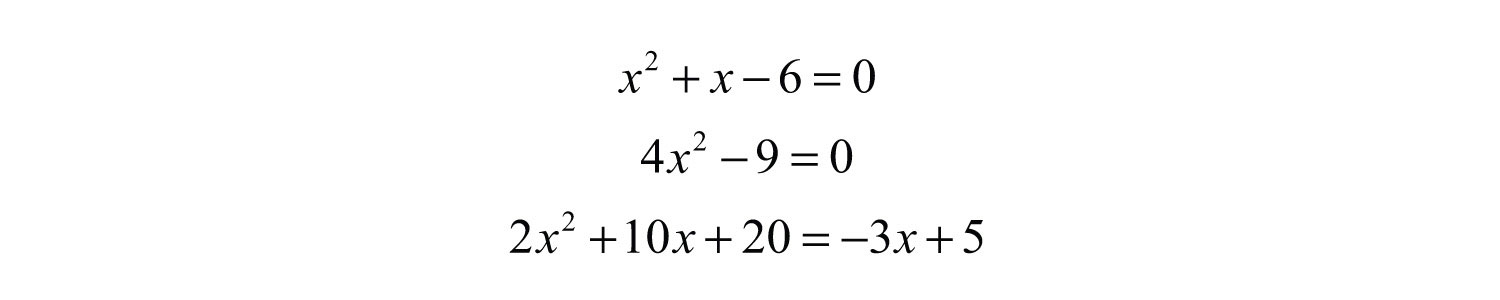
A solution of a quadratic equation in standard form is called a rootA solution to a quadratic equation in standard form.. Quadratic equations can have two real solutions, one real solution, or no real solution. The quadratic equation has two solutions, namely, and .
Example 1: Verify that and are solutions to .
Solution: To verify solutions, substitute the values for x and then simplify to see if a true statement results.

Answer: Both values produce true statements. Therefore, they are both solutions to the equation.
Our goal is to develop algebraic techniques for finding solutions to quadratic equations. The first technique requires the zero-product propertyAny product is equal to zero if and only if at least one of the factors is zero.:
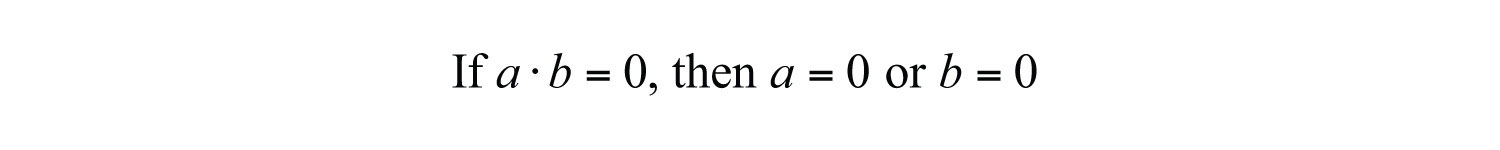
In other words, if any product is equal to zero, then one or both of the variable factors must be equal to zero.
Example 2: Solve: .
Solution: This equation consists of a product of two quantities equal to zero; therefore, the zero-product property applies. One or both of the quantities must be zero.
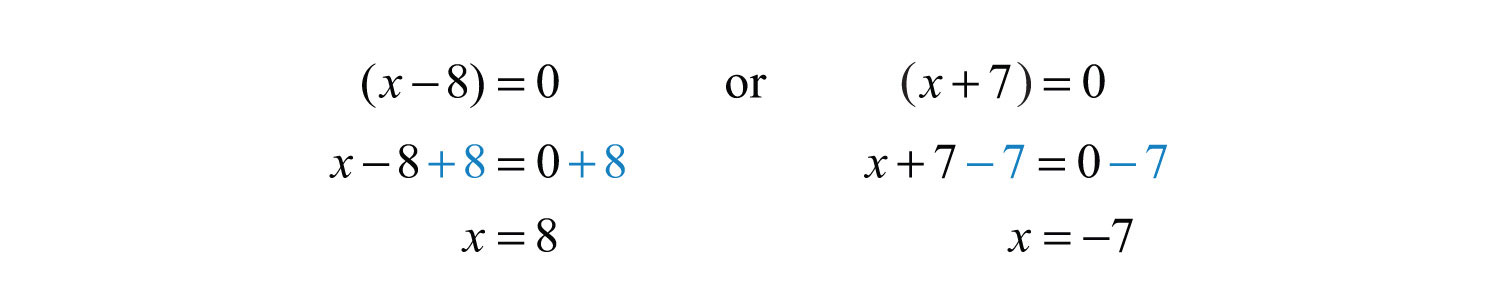
To verify that these are solutions, substitute them for the variable x.

Notice that each solution produces a factor that is equal to zero.
Answer: The solutions are 8 and −7.
The quadratic equation may not be given in its factored form.
Example 3: Solve: .
Solution: The goal is to produce a product that is equal to zero. We can do that by factoring the trinomial on the left side of the equation.
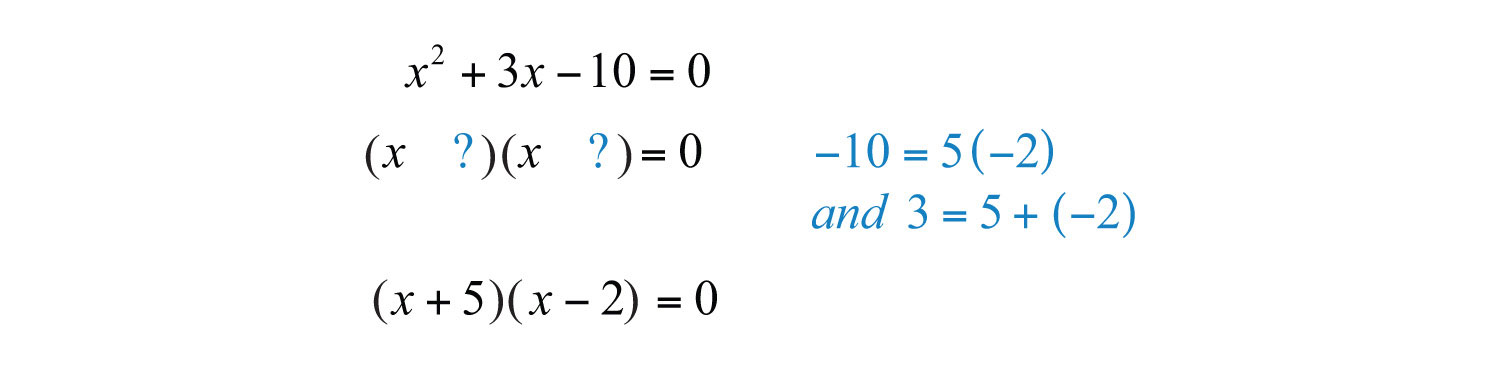
Next, apply the zero-product property and set each factor equal to zero.
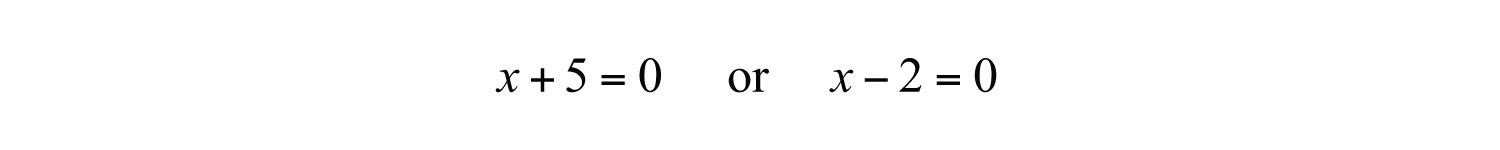
This leaves us with two linear equations, each of which can be solved for .

Check the solutions by substituting into the original equation to verify that we obtain true statements.
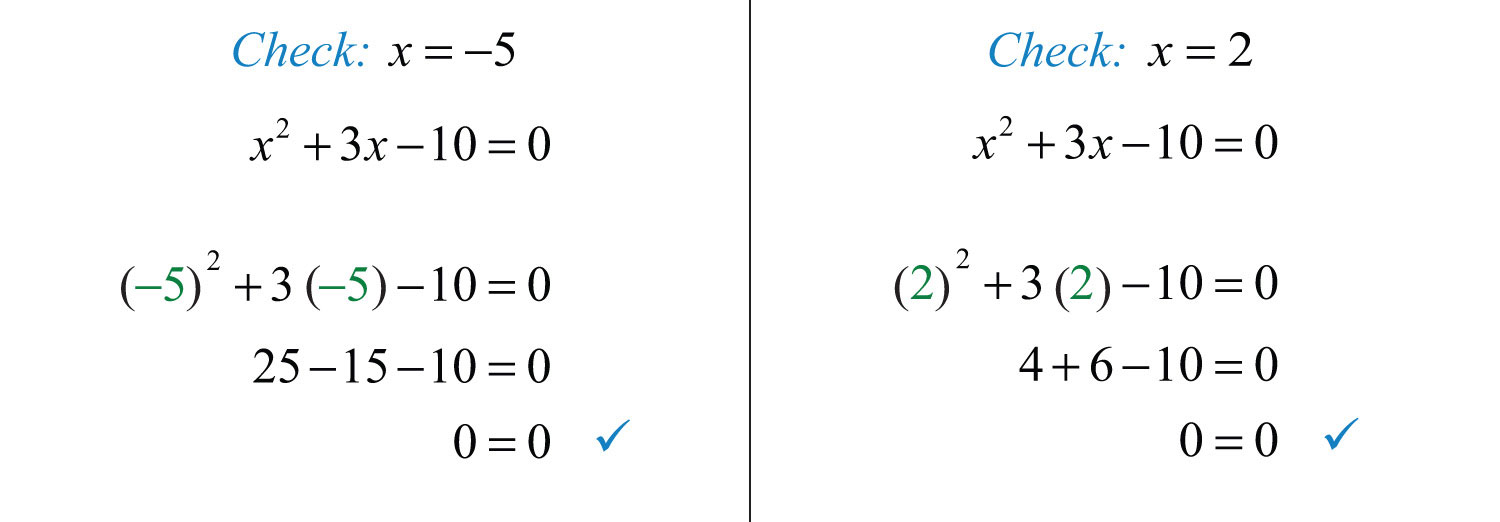
Answer: The solutions are −5 and 2.
Using the zero-product property after factoring a quadratic equation in standard form is the key to this technique. However, the quadratic equation may not be given in standard form, and so there may be some preliminary steps before factoring. The steps required to solve by factoringThe process of solving an equation that is equal to zero by factoring it and then setting each variable factor equal to zero. are outlined in the following example.
Example 4: Solve: .
Solution:
Step 1: Express the quadratic equation in standard form. For the zero-product property to apply, the quadratic expression must be equal to zero. Use the addition and subtraction properties of equality to combine opposite-side like terms and obtain zero on one side of the equation.
In this example, add to and subtract 5 from both sides.
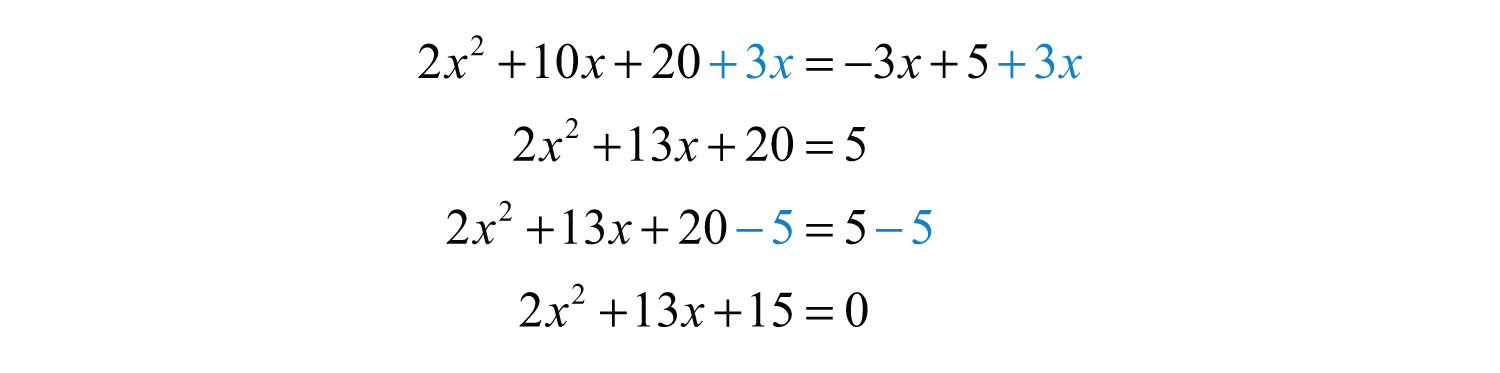
Step 2: Factor the quadratic expression.
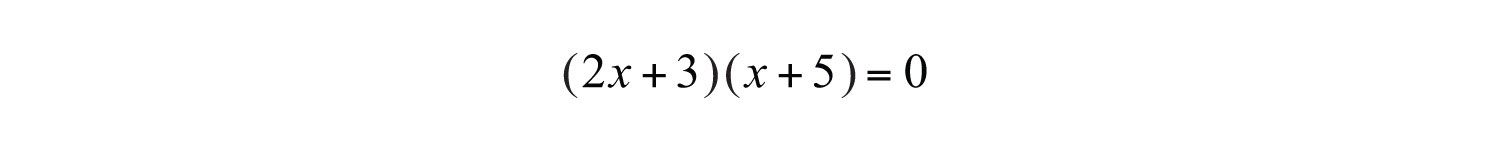
Step 3: Apply the zero-product property and set each variable factor equal to zero.
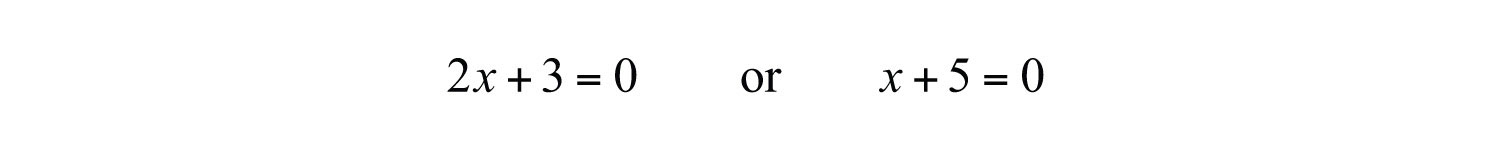
Step 4: Solve the resulting linear equations.
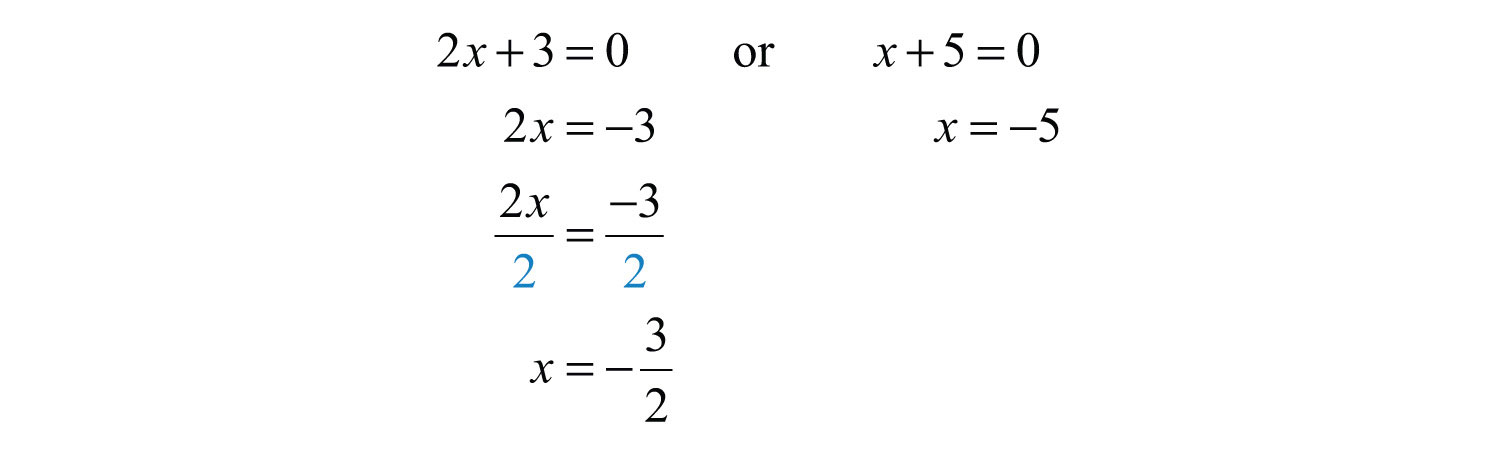
Answer: The solutions are −5 and −3/2. The check is optional.
Example 5: Solve: .
Solution: Write this in standard form by subtracting from both sides.
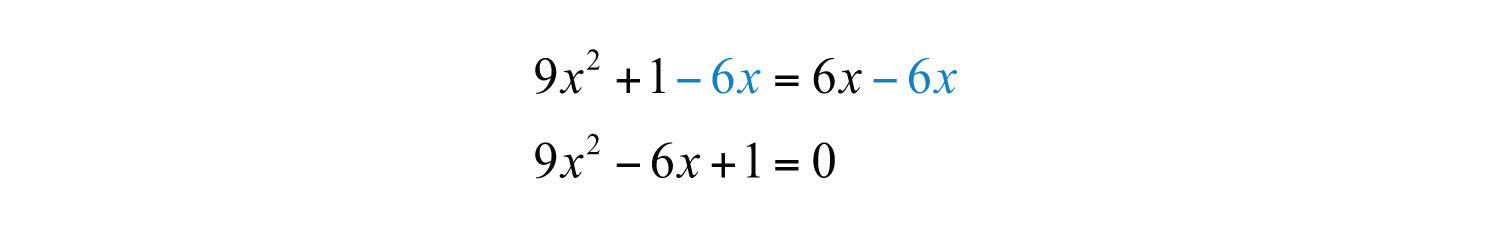
Once the equation is in standard form, equal to zero, factor.
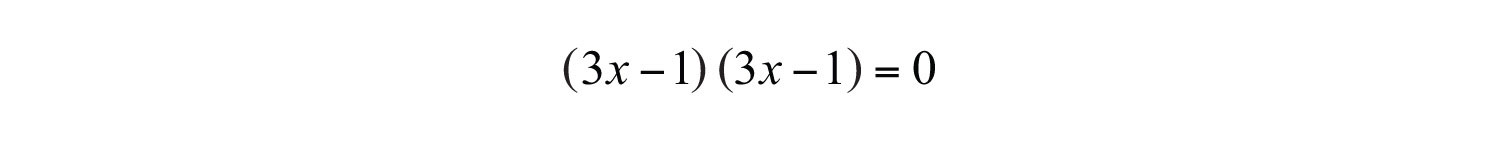
This is a perfect square trinomial. Hence setting each factor equal to zero results in a repeated solution.
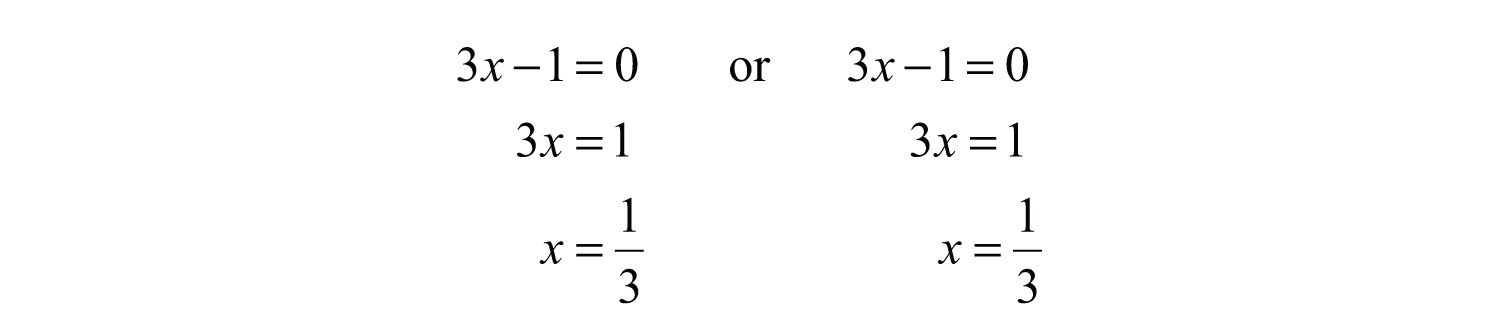
A repeated solution is called a double rootA root that is repeated twice. and does not have to be written twice.
Answer: The solution is 1/3.
Try this! Solve: .
Answer: or
Video Solution
(click to see video)Not all quadratic equations in standard form are trinomials. We often encounter binomials.
Example 6: Solve: .
Solution: This quadratic equation is given in standard form, where the binomial on the left side is a difference of squares. Factor as follows:
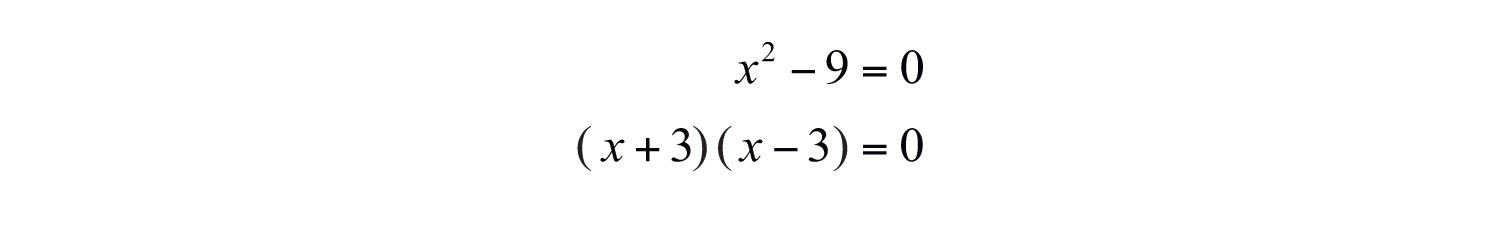
Next, set each factor equal to zero and solve.

Answer: The solutions are 3 and −3, which can also be written as .
Example 7: Solve: .
Solution: By inspection, we see that is a solution to this quadratic equation. Since dividing by zero is undefined, we want to avoid dividing both sides of this equation by x. In general, we wish to avoid dividing both sides of any equation by a variable or an expression containing a variable. We will discuss this in more detail later. The first step is to rewrite this equation in standard form with zero on one side.
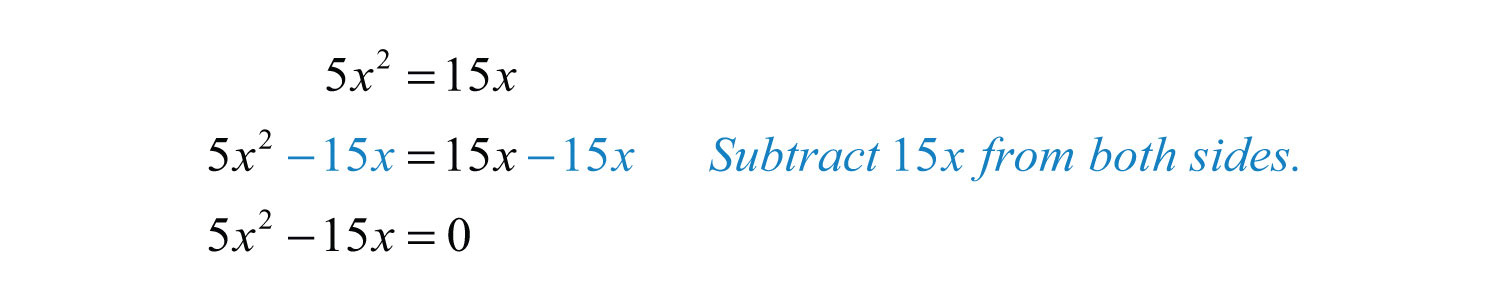
Next, factor the expression. Notice that the binomial on the left has a GCF of .
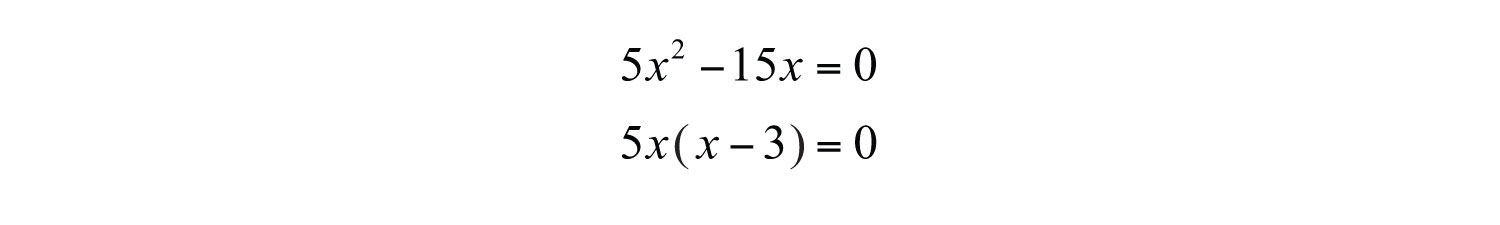
Set each factor to equal to zero.
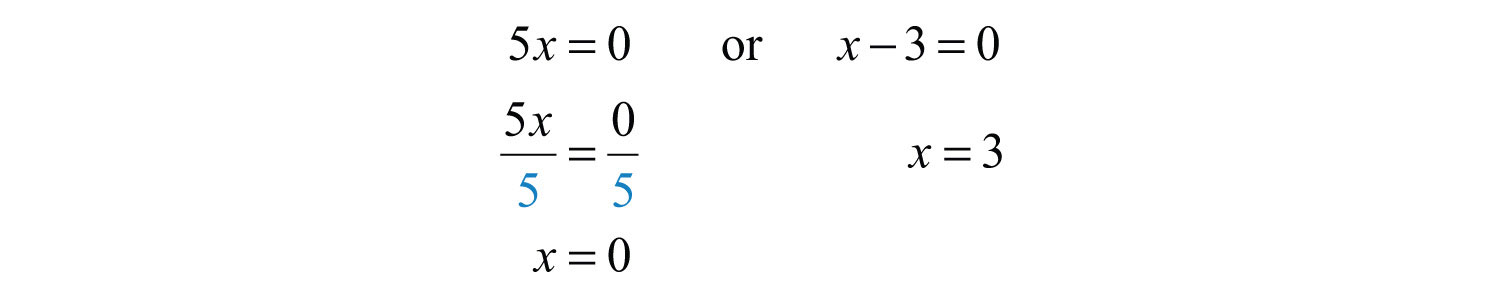
Answer: The solutions are 0 and 3.
Example 8: Solve: .
Solution: This quadratic equation appears to be factored; hence it might be tempting to set each factor equal to 11. However, this would lead to incorrect results. We must rewrite the equation in standard form, equal to zero, so that we can apply the zero-product property.
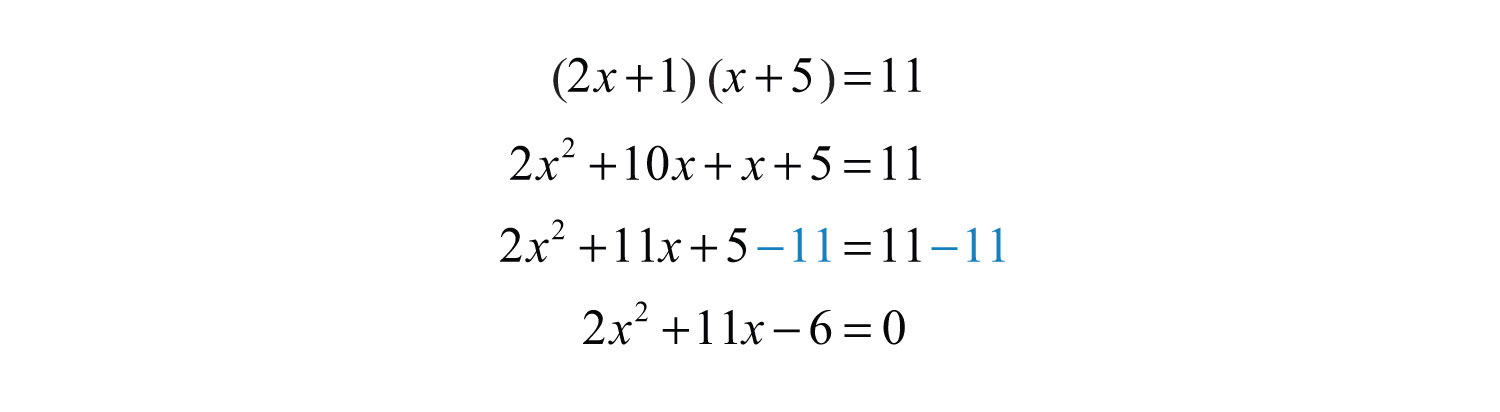
Once it is in standard form, we can factor and then set each factor equal to zero.
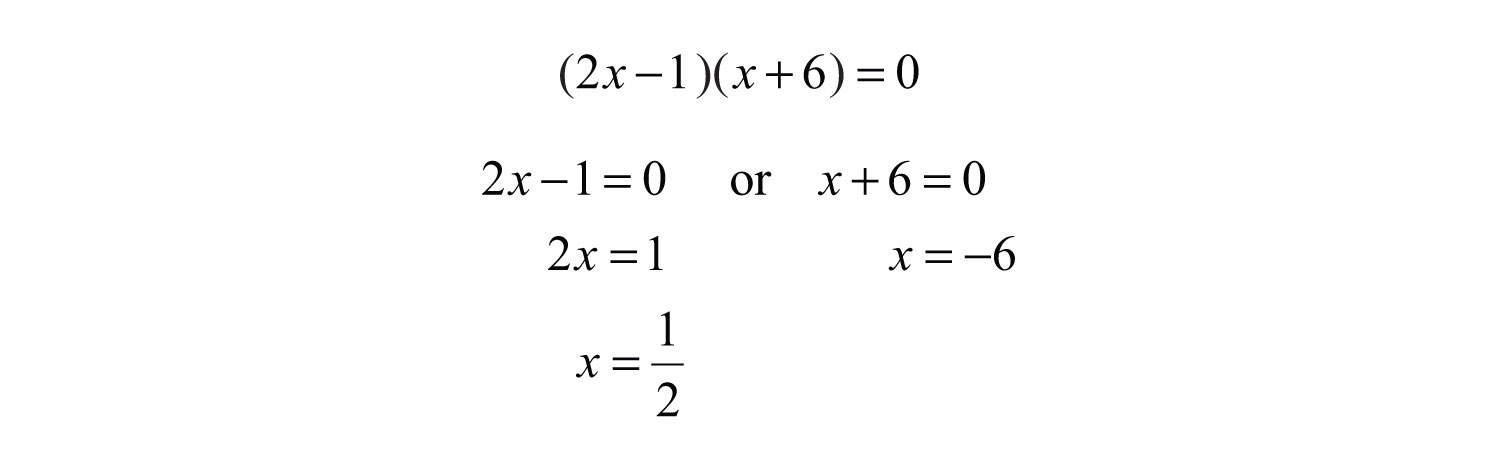
Answer: The solutions are 1/2 and −6.
Example 9: Solve: .
Solution: We begin by factoring out the GCF of 5. Then factor the resulting trinomial.
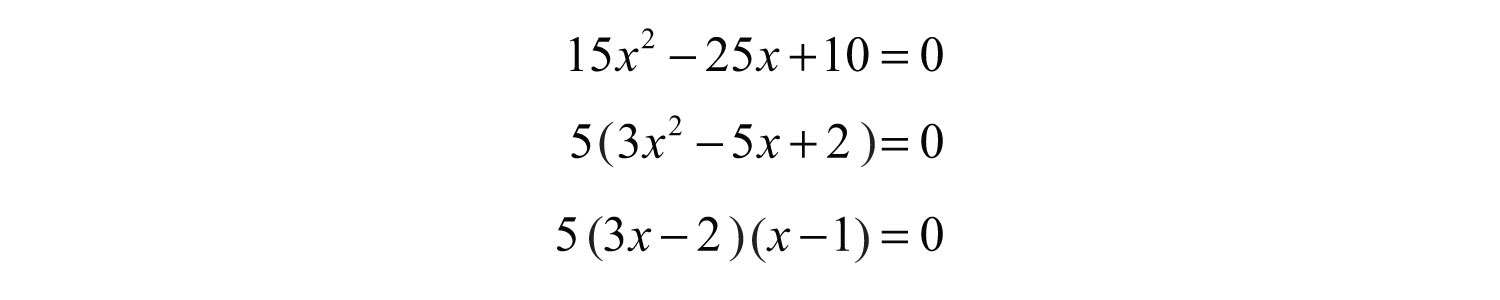
Next, we set each variable factor equal to zero and solve for x.
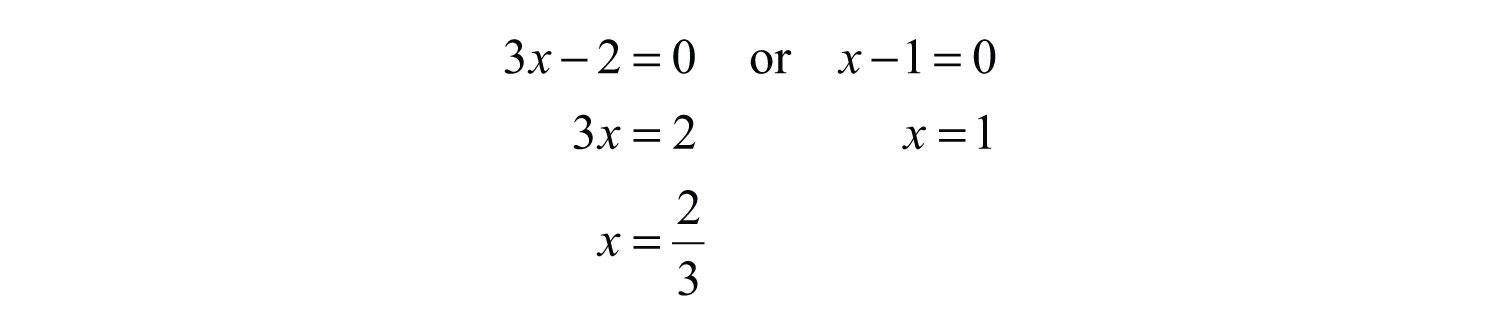
Notice that the factor 5 is not a variable factor and thus did not contribute to the solution set.
Answer: The solutions are 2/3 and 1.
Example 10: Factor: .
Solution: Clear the fractions by multiplying both sides of the equation by the LCD, which is equal to 6.
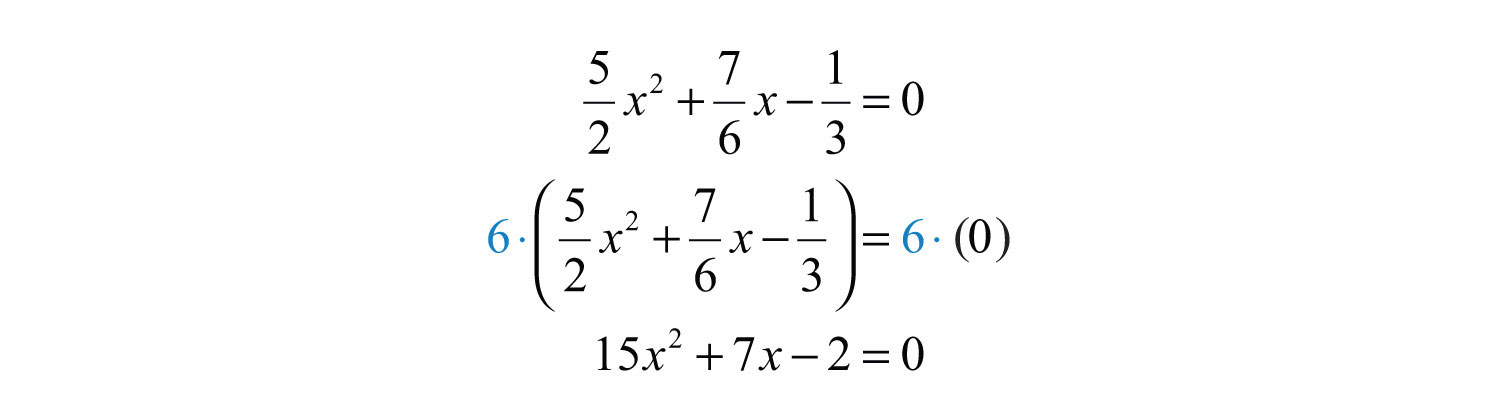
At this point, we have an equivalent equation with integer coefficients and can factor as usual. Begin with the factors of 15 and 2.

The coefficient of the middle term is . Factor as follows:
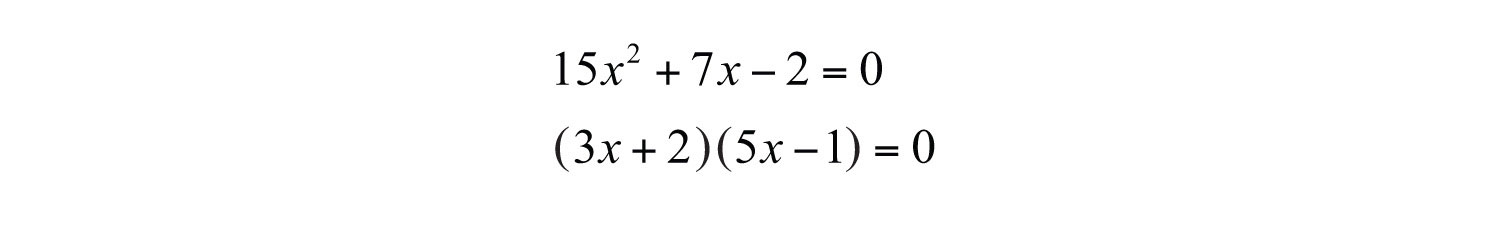
Set each factor equal to zero and solve.
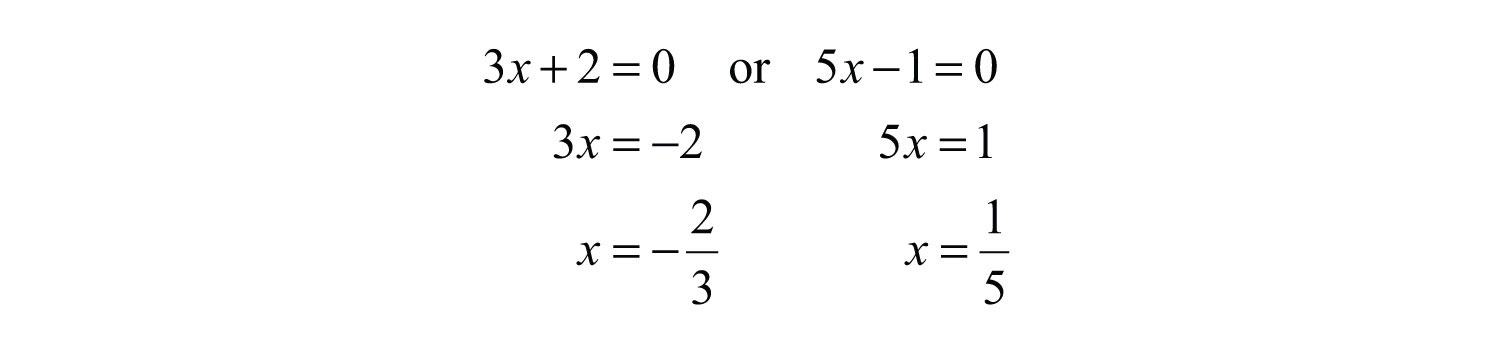
Answer: The solutions are −2/3 and 1/5.
Try this! Solve: .
Answer: −3/2 and 3/2
Video Solution
(click to see video)Finding Equations with Given Solutions
The zero-product property states,
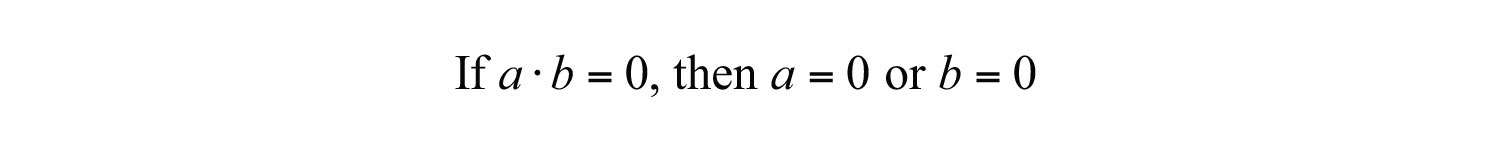
And, in fact, the converse is true as well:
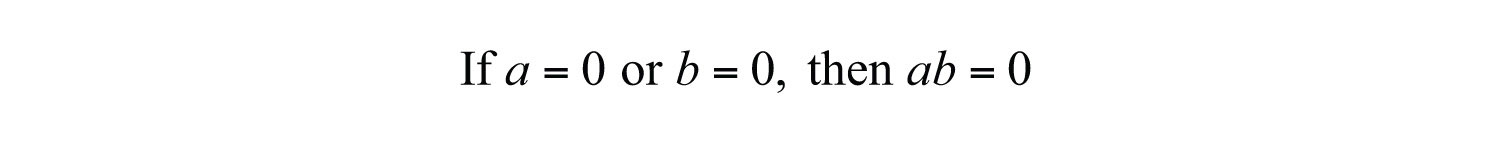
When this is the case, we can write the following:
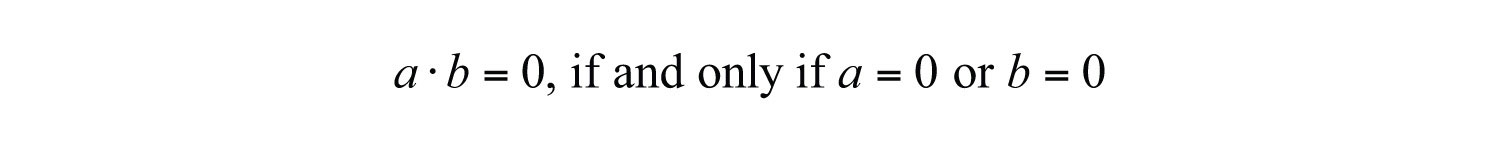
We use this property to find equations, given the solutions. To do this, the steps for solving by factoring are performed in reverse.
Example 11: Find a quadratic equation with solutions −7 and 2.
Solution: Given the solutions, we can determine two linear factors.

The product of these linear factors is equal to zero when or :
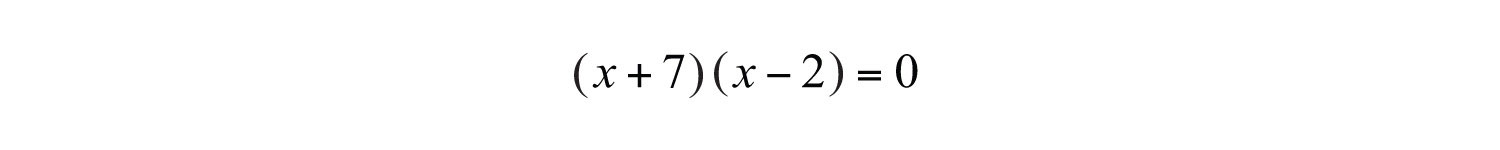
Multiply the binomials and present the equation in standard form.
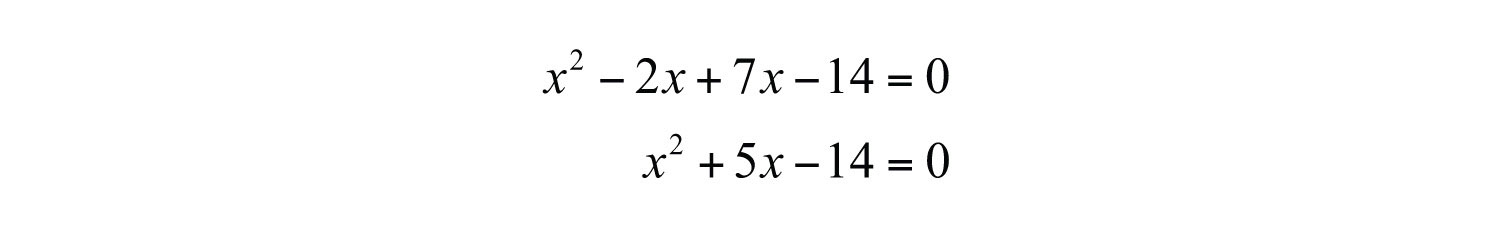
Answer: . We may check our equation by substituting the given answers to see if we obtain a true statement. Also, the equation found above is not unique and so the check becomes essential when our equation looks different from someone else’s. This is left as an exercise.
Example 12: Find a quadratic equation with integer coefficients, given solutions 1/2 and −3/4.
Solution: To avoid fractional coefficients, we first clear the fractions by multiplying both sides by the denominator.
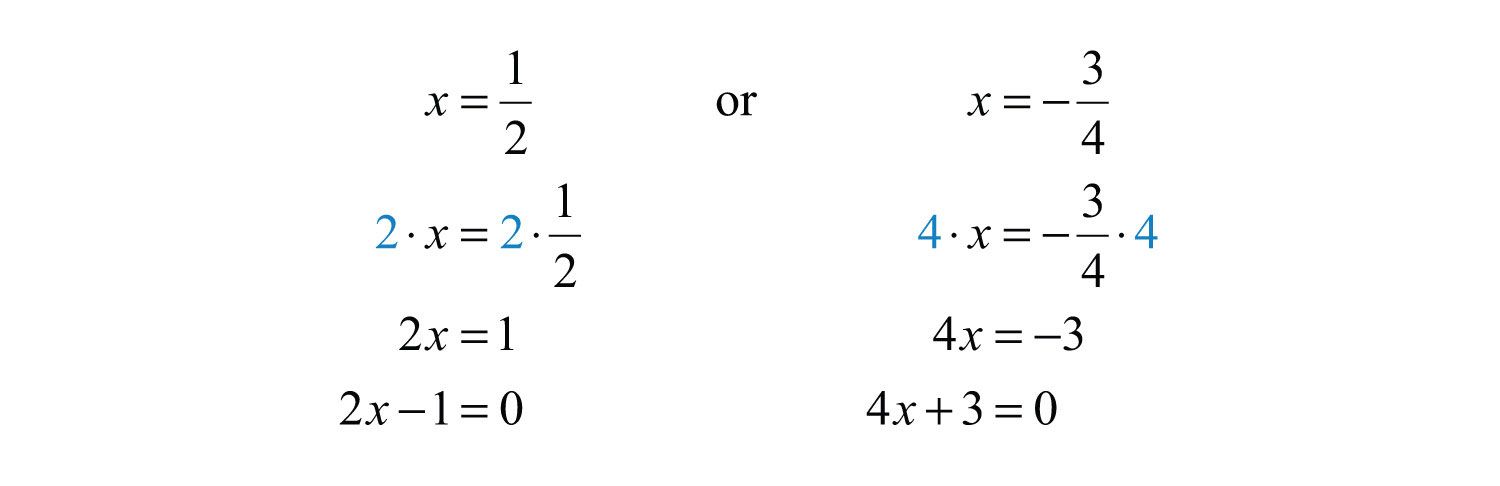
Apply the zero-product property and multiply.
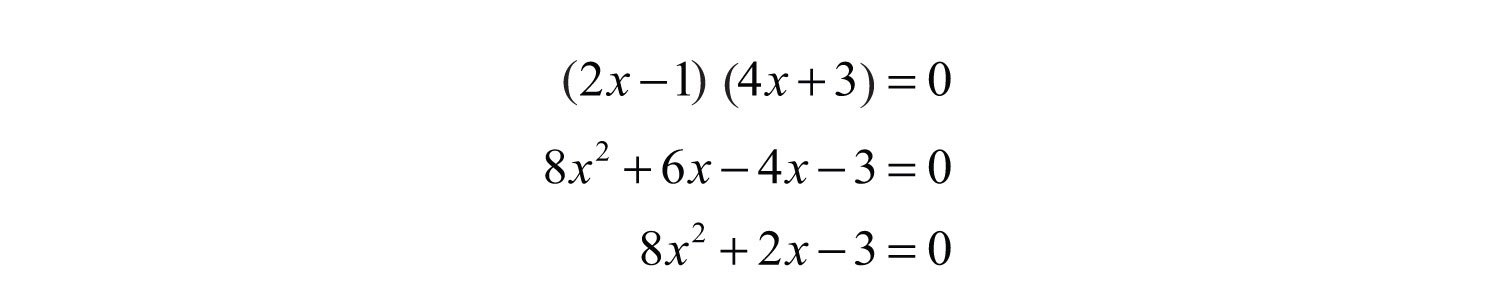
Answer:
Try this! Find a quadratic equation with integer coefficients, given solutions −1 and 2/3.
Answer:
Video Solution
(click to see video)Solving Polynomial Equations by Factoring
The zero-product property is true for any number of factors that make up an equation. If an expression is equal to zero and can be factored into linear factors, then we will be able to set each factor equal to zero and solve for each equation.
Example 13: Solve: .
Solution: Set each variable factor equal to zero and solve.

Answer: The solutions are 0, 5, and 2/3.
Of course, we cannot expect the equation to be given in factored form.
Example 14: Solve: .
Solution: Begin by factoring the left side completely.
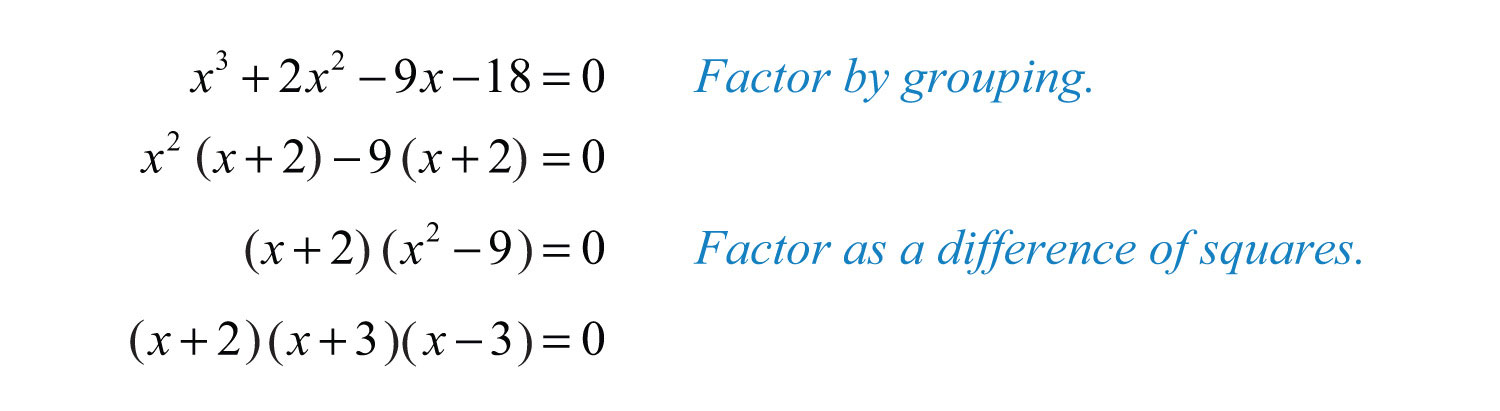
Set each factor equal to zero and solve.
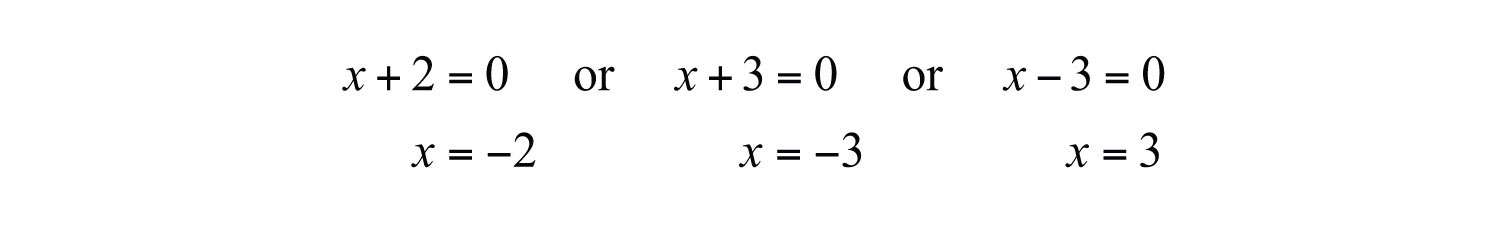
Answer: The solutions are −2, −3, and 3.
Notice that the degree of the polynomial is 3 and we obtained three solutions. In general, for any polynomial equation with one variable of degree n, the fundamental theorem of algebraGuarantees that there will be as many (or fewer) real solutions to a polynomial with one variable as its degree. guarantees n real solutions or fewer. We have seen that many polynomials do not factor. This does not imply that equations involving these unfactorable polynomials do not have real solutions. In fact, many polynomial equations that do not factor do have real solutions. We will learn how to solve these types of equations as we continue in our study of algebra.
Try this! Solve: .
Answer: −2, 0, 1/5
Video Solution
(click to see video)Key Takeaways
- A polynomial can have at most a number of solutions equal to its degree. Therefore, quadratic equations can have up to two real solutions.
- To solve a quadratic equation, first write it in standard form. Once the quadratic expression is equal to zero, factor it and then set each variable factor equal to zero. The solutions to the resulting linear equations are the solutions to the quadratic equation.
- Not all quadratic equations can be solved by factoring. We will learn how to solve quadratic equations that do not factor later in the course.
- To find a quadratic equation with given solutions, perform the process of solving by factoring in reverse.
- If any polynomial is factored into linear factors and is set to zero, then we can determine the solutions by setting each variable factor equal to zero and solving each individually.
Topic Exercises
Part A: Solutions to Quadratic Equations
Determine whether the given set of values are solutions to the quadratic equation.
1. {−3, 5};
2. {7, −1};
3. {−1/2, 1/2};
4. {−3/4, 3/4};
5. {−3, 2};
6. {−5, 1};
Solve.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
Part B: Solve by Factoring
Solve.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
Clear the fractions by first multiplying both sides by the LCD and then solve.
65.
66.
67.
68.
69.
70.
71.
72.
73. The sides of a square measure x + 3 units. If the area is 25 square units, then find x.
74. The height of a triangle is 2 units more than its base. If the area is 40 square units, then find the length of the base.
75. The sides of a right triangle have measures that are consecutive integers. Find the length of the hypotenuse. (Hint: The hypotenuse is the longest side. Apply the Pythagorean theorem.)
76. The profit in dollars generated by producing and selling x custom lamps is given by the function . How many lamps must be sold and produced to break even? (Hint: We break even when the profit is zero.)
Assuming dry road conditions and average reaction times, the safe stopping distance, d in feet of an average car is given using the formula , where v represents the speed of the car in miles per hour. For each problem below, given the stopping distance, determine the safe speed.
77. 15 feet
78. 40 feet
79. 75 feet
80. 120 feet
Part C: Finding Equations with Given Solutions
Find a quadratic equation with integer coefficients, given the following solutions.
81. −3, 1
82. −5, 3
83. −10, −3
84. −7, −4
85. −1, 0
86. 0, 3/5
87. −2, 2
88. −1/2, 1/2
89. −4, 1/3
90. 2/3, 2/5
91. −1/5, −2/3
92. −3/2, 3/4
93. 3, double root
94. −5, double root
Part D: Solving Polynomial Equations
Solve.
95.
96.
97.
98.
99.
100.
101.
102.
103.
104.
105.
106.
107.
108.
109.
110.
Part E: Discussion Board Topics
111. Explain why has two solutions and has three solutions.
112. Make up your own quadratic equation and post it and the solutions on the discussion board.
113. Explain, in your own words, how to solve a quadratic equation in standard form.
Answers
1: Yes
3: Yes
5: No
7: −2, 3
9: 1/2, 4
11: 2
13: 0, 5
15: −3/4, 1/2
17: −2, 4
19: −1, 2
21: −5, 1
23: −5/2, 2/3
25: −2, 3
27: 4, 6
29: 4, 10
31: 5
33: −1/5, 2
35: 7/3
37: −3/2, 1
39: −8, ½
41: −6, 6
43: −9/2, 9/2
45: −2, 2
47: −5/4, 5/4
49: −3, 3
51: −2, 0
53: 0, 2
55: −6, 4
57: 1/5, 4
59: −1, 9
61: −1/2, −1/3
63: −6, 5
65: −3, −2
67: −2/3, 2/3
69: ±7
71: 8
73: 2 units
75: 5 units
77: 10 miles per hour
79: 30 miles per hour
81:
83:
85:
87:
89:
91:
93:
95: −5, 0, 9
97: 0, 1, 10
99: −3, −1, 2
101: −1, 0, 2
103: 0, 1, 2
105: −3, 0, 3
107: −1, 1
109: −3/2, 1/2, 3/2
6.7 Applications Involving Quadratic Equations
Learning Objectives
- Set up and solve applications involving relationships between real numbers.
- Set up and solve applications involving geometric relationships involving area and the Pythagorean theorem.
- Set up and solve applications involving the height of projectiles.
Number Problems
The algebraic setups of the word problems that we have previously encountered led to linear equations. When we translate the applications to algebraic setups in this section, the setups lead to quadratic equations. Just as before, we want to avoid relying on the “guess and check” method for solving applications. Using algebra to solve problems simplifies the process and is more reliable.
Example 1: One integer is 4 less than twice another integer, and their product is 96. Set up an algebraic equation and solve it to find the two integers.
Solution: First, identify the variables. Avoid two variables by using the relationship between the two unknowns.
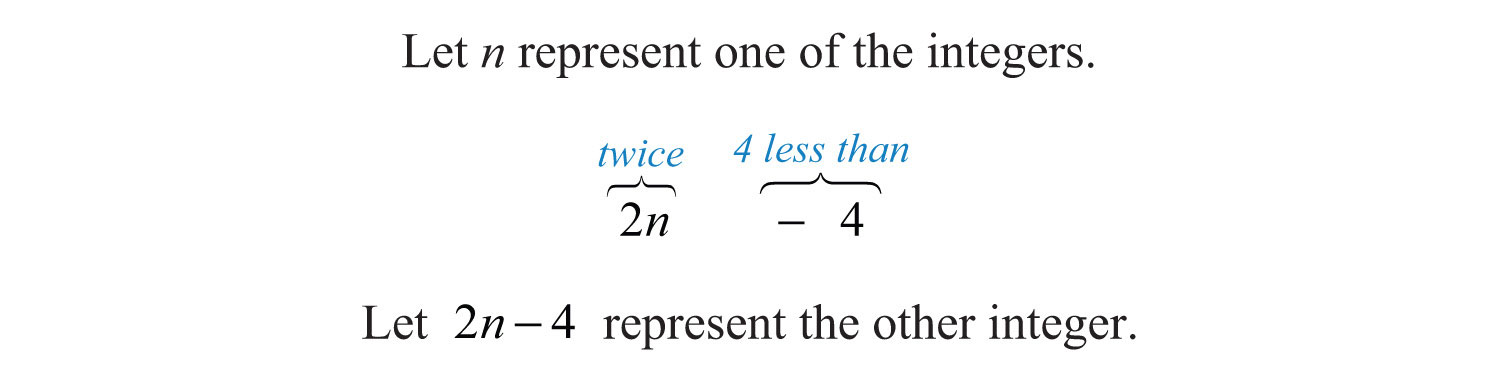
The key phrase, “their product is 96,” indicates that we should multiply and set the product equal to 96.
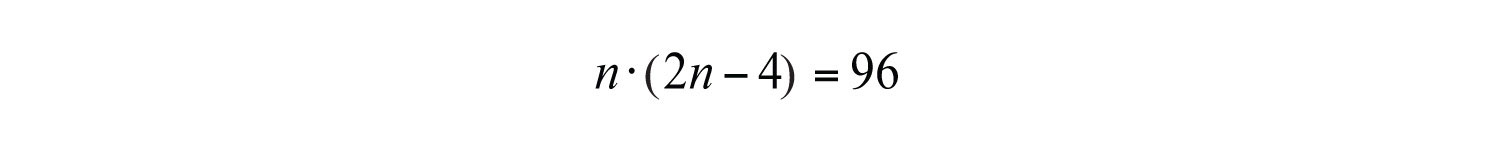
Once we have the problem translated to a mathematical equation, we then solve. In this case, we can solve by factoring. The first step is to write the equation in standard form:

Next, factor completely and set each variable factor equal to zero.

The problem calls for two integers whose product is +96. The product of two positive numbers is positive and the product of two negative numbers is positive. Hence we can have two sets of solutions. Use to determine the other integers.

Answer: Two sets of integers solve this problem: {8, 12} and {−6, −16}. Notice that (8)(12) = 96 and (−6)(−16) = 96; our solutions check out.
With quadratic equations, we often obtain two solutions for the identified unknown. Although it may be the case that both are solutions to the equation, they may not be solutions to the problem. If a solution does not solve the original application, then we disregard it.
Recall that consecutive odd and even integers both are separated by two units.
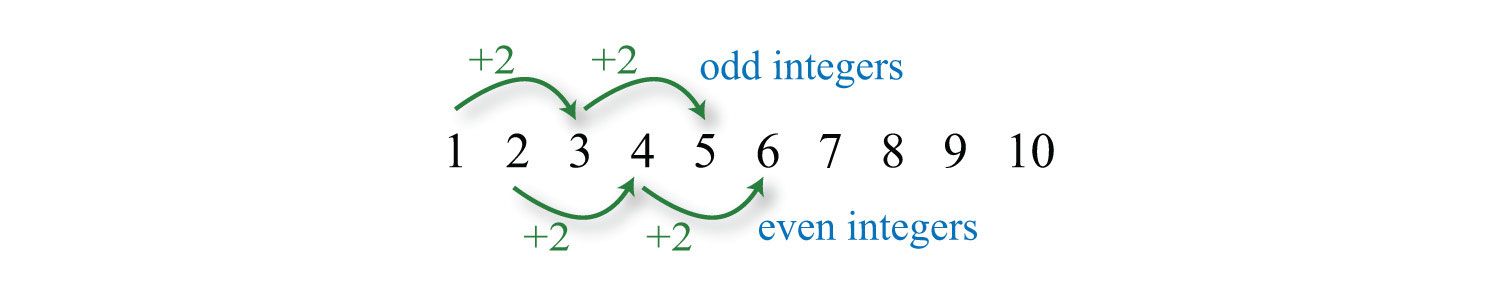
Example 2: The product of two consecutive positive odd integers is 99. Find the integers.
Solution:

The key phase, “product…is 99,” indicates that we should multiply and set the product equal to 99.
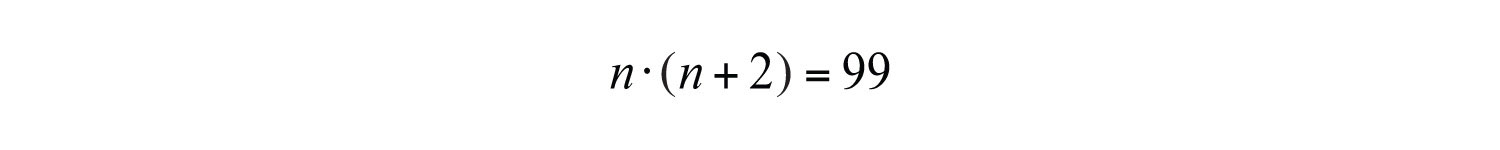
Rewrite the quadratic equation in standard form and solve by factoring.

Because the problem asks for positive integers, is the only solution. Back substitute to determine the next odd integer.
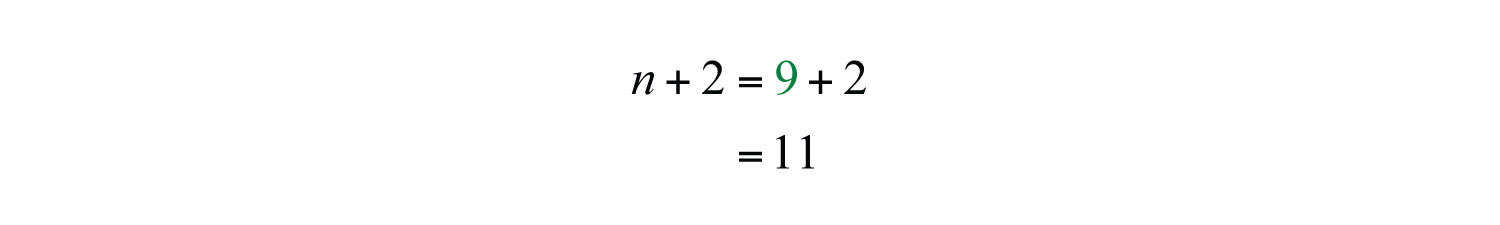
Answer: The consecutive positive odd integers are 9 and 11.
Example 3: Given two consecutive positive odd integers, the product of the larger and twice the smaller is equal to 70. Find the integers.
Solution:

The key phrase “twice the smaller” can be translated to . The phrase “product…is 70” indicates that we should multiply this by the larger odd integer and set the product equal to 70.
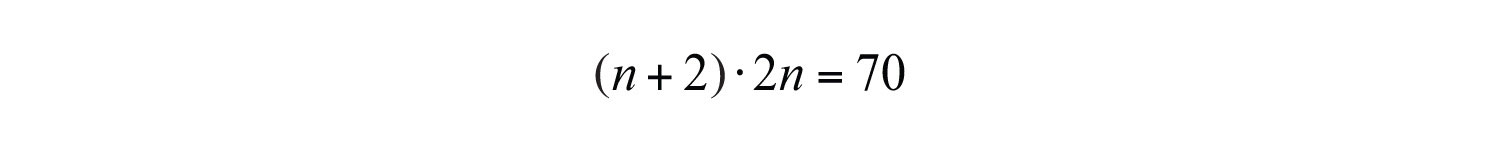
Solve by factoring.

Because the problem asks for positive integers, is the only solution. Back substitute into n + 2 to determine the next odd integer.
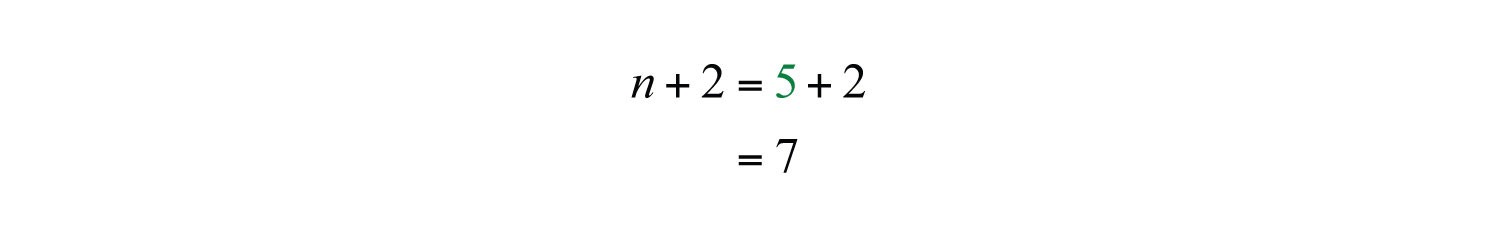
Answer: The positive odd integers are 5 and 7.
Try this! The product of two consecutive positive even integers is 168. Find the integers.
Answer: The positive even integers are 12 and 14.
Video Solution
(click to see video)Geometry Problems
When working with geometry problems, it is helpful to draw a picture. Below are some area formulas that you are expected to know. (Recall that .)
Area of a rectangle, where l represents the length and w represents the width.: |
|
Area of a square, where s represents the length of each side.: |
|
Area of a triangle, where b represents the length of the base and h represents the height.: |
|
Area of a circle, where r represents the radius and the constant .: |
Example 4: The floor of a rectangular room has a length that is 4 feet more than twice its width. If the total area of the floor is 240 square feet, then find the dimensions of the floor.
Solution:
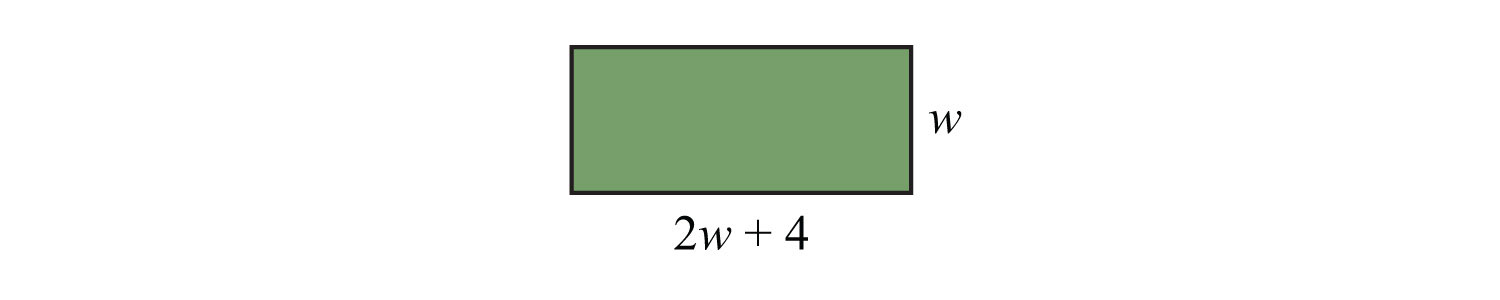
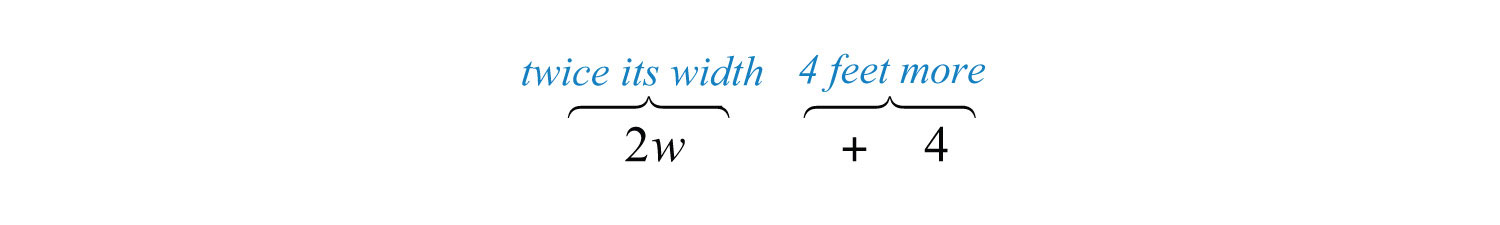
Use the formula and the fact that the area is 240 square feet to set up an algebraic equation.
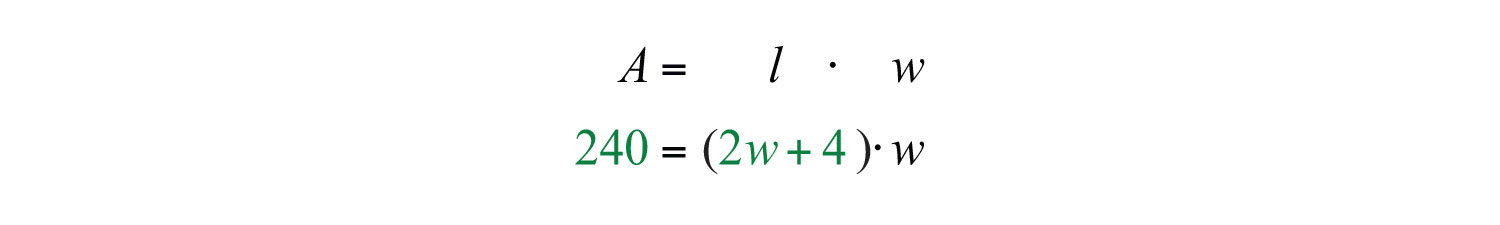
Solve by factoring.
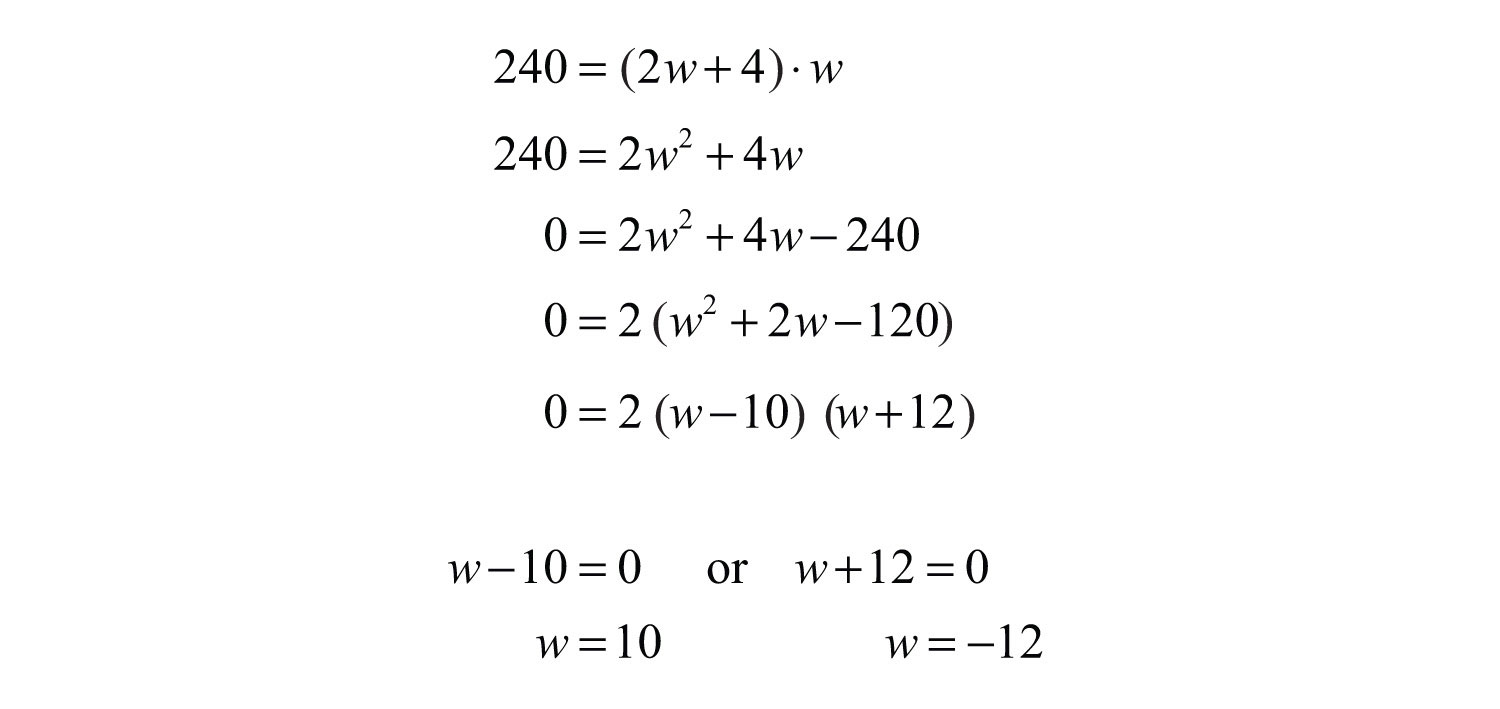
At this point we have two possibilities for the width of the rectangle. However, since a negative width is not defined, choose the positive solution, . Back substitute to find the length.
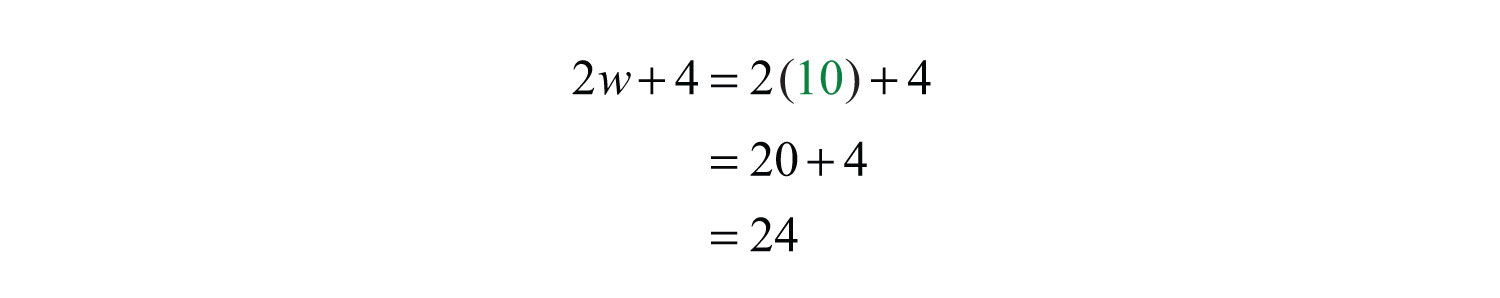
Answer: The width is 10 feet and the length is 24 feet.
It is important to include the correct units in the final presentation of the answer. In the previous example, it would not make much sense to say the width is 10. Make sure to indicate that the width is 10 feet.
Example 5: The height of a triangle is 3 inches less than twice the length of its base. If the total area of the triangle is 7 square inches, then find the lengths of the base and height.
Solution:
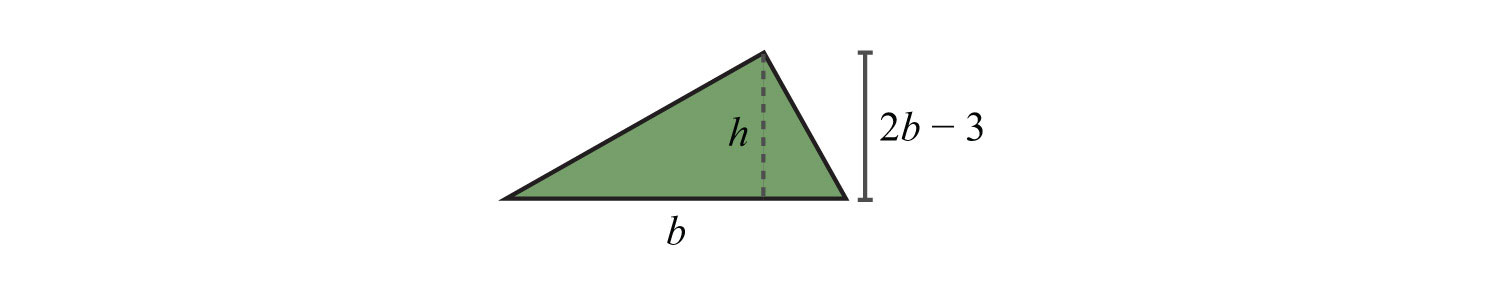

Use the formula and the fact that the area is 7 square inches to set up an algebraic equation.
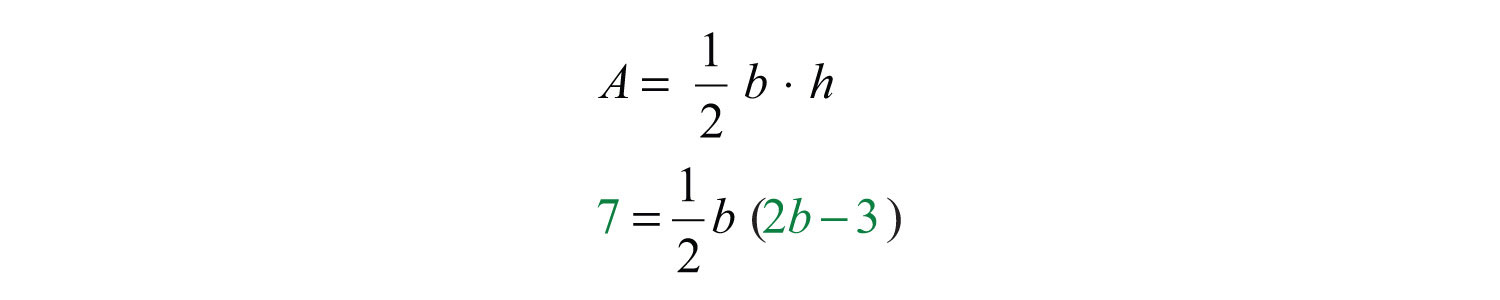
To avoid fractional coefficients, multiply both sides by 2 and then rewrite the quadratic equation in standard form.
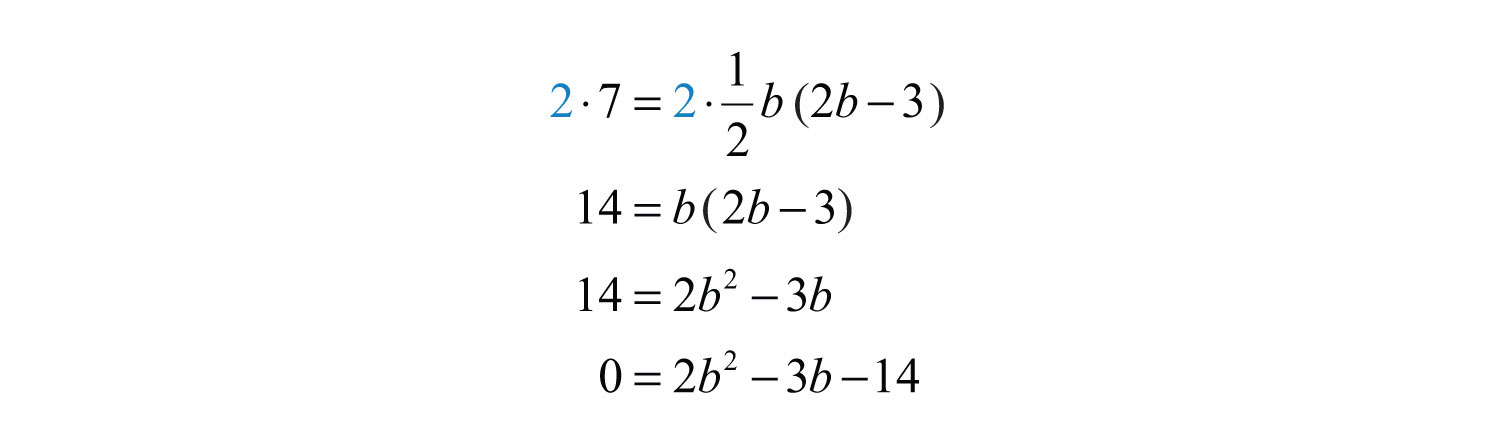
Factor and then set each factor equal to zero.
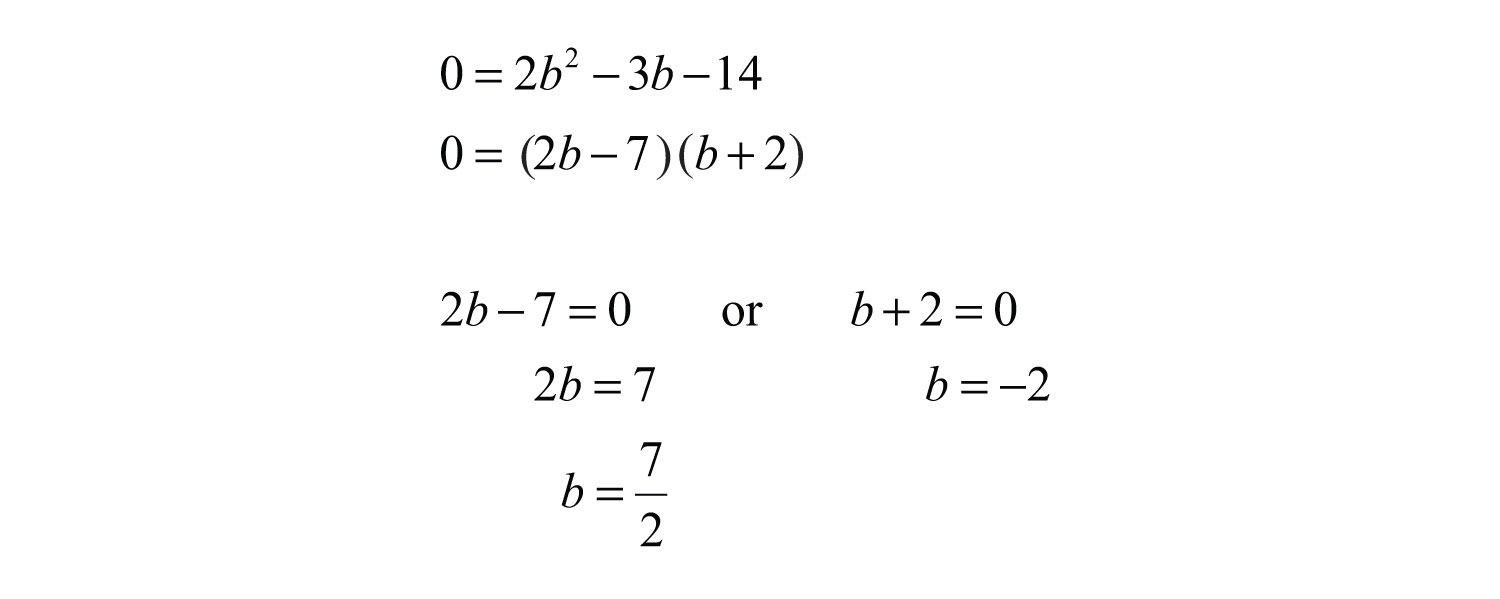
In this case, disregard the negative answer; the length of the base is 7/2 inches long. Use to determine the height of the triangle.
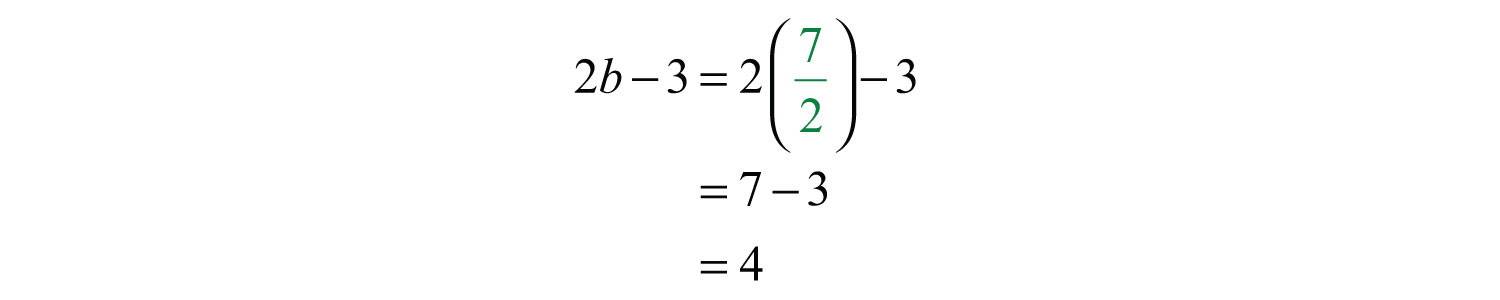
Answer: The base measures 7/2 = 3½ inches and the height is 4 inches.
Try this! The base of a triangle is 5 units less than twice the height. If the area is 75 square units, then what is the length of the base and height?
Answer: The height is 10 units and the base is 15 units.
Video Solution
(click to see video)Recall that a right triangle is a triangle where one of the angles measures 90°. The side opposite of the right angle is the longest side of the triangle and is called the hypotenuse. The Pythagorean theoremGiven any right triangle with legs measuring a and b units and hypotenuse measuring c units, then . gives us a relationship between the legs and hypotenuse of any right triangle, where a and b are the lengths of the legs and c is the length of the hypotenuse:
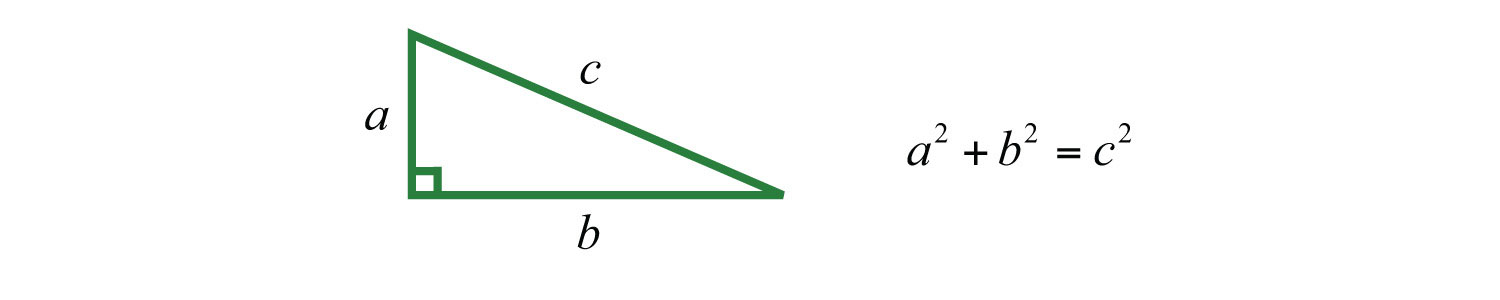
Given certain relationships, we use this theorem when determining the lengths of sides of right triangles.
Example 6: The hypotenuse of a right triangle is 10 inches. If the short leg is 2 inches less than the long leg, then find the lengths of the legs.
Solution:

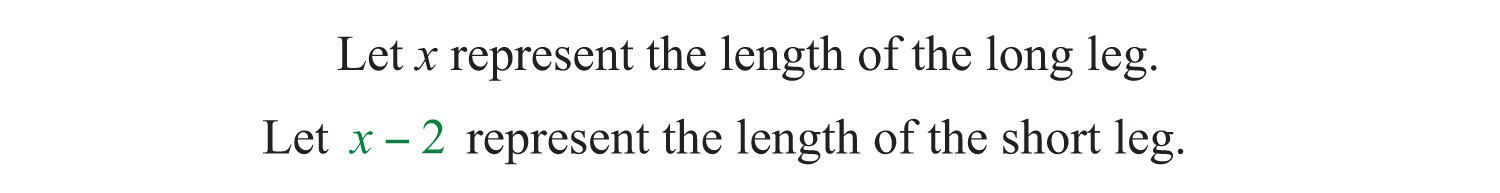
Given that the hypotenuse measures 10 inches, substitute its value into the Pythagorean theorem and obtain a quadratic equation in terms of x.
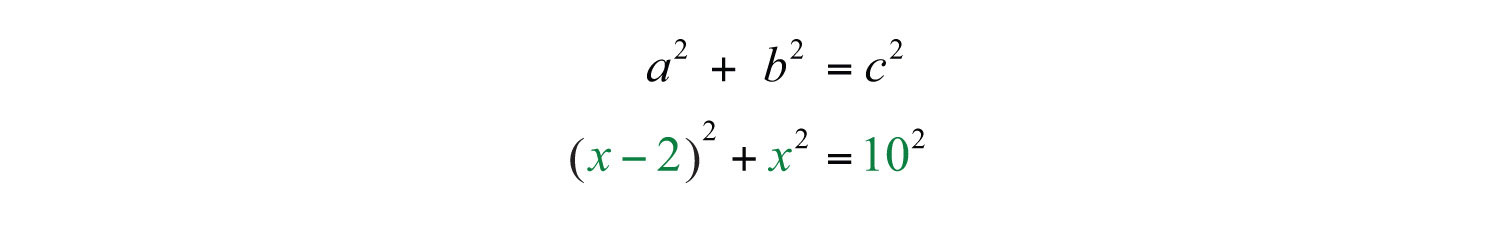
Multiply and rewrite the equation in standard form.
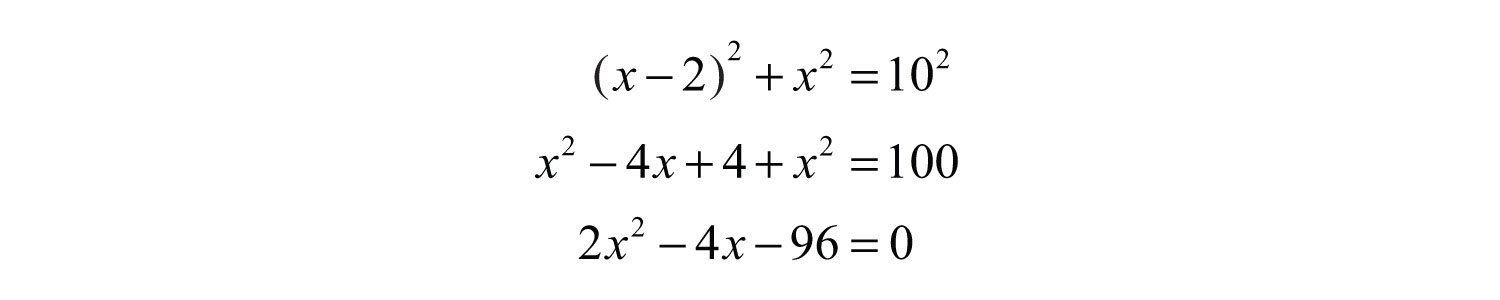
Once it is in standard form, factor and set each variable factor equal to zero.
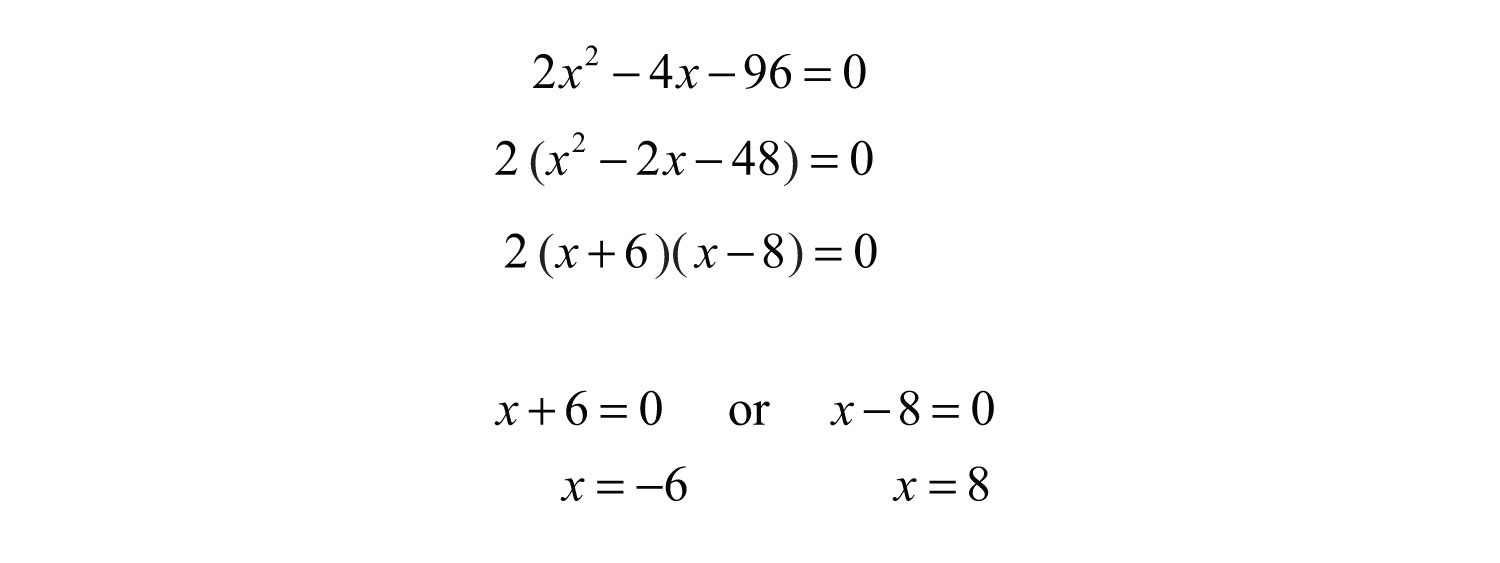
Because lengths cannot be negative, disregard the negative answer. In this case, the long leg measures 8 inches. Use to determine the length of the short leg.
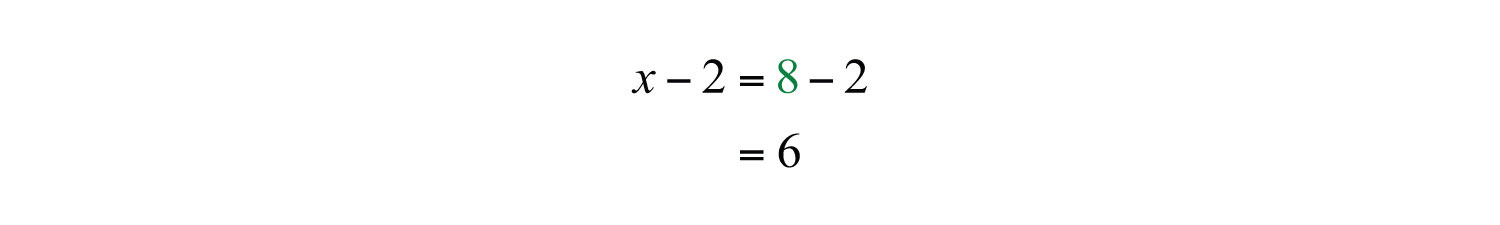
Answer: The short leg measures 6 inches and the long leg measures 8 inches.
Example 7: One leg of a right triangle measures 3 centimeters. The hypotenuse of the right triangle measures 3 centimeters less than twice the length of the unknown leg. Find the measure of all the sides of the triangle.
Solution:
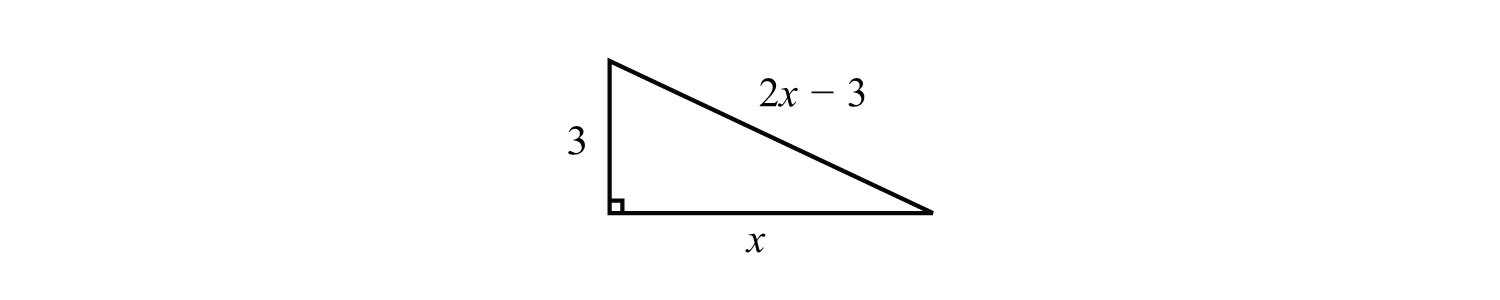

To set up an algebraic equation, we use the Pythagorean theorem.
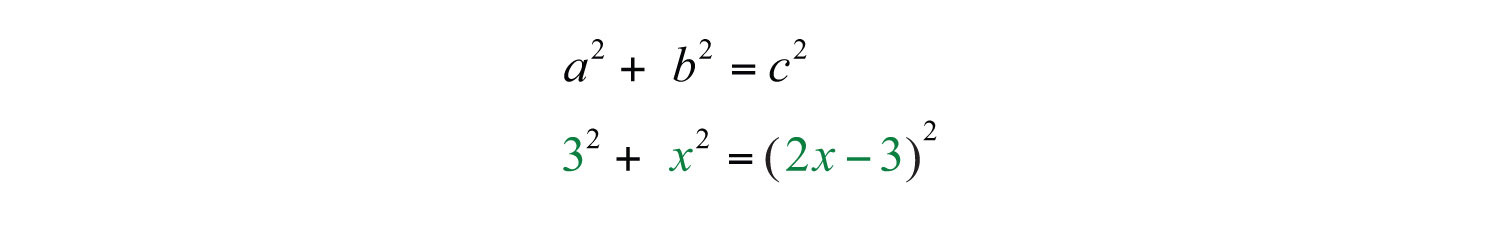
Solve by factoring.
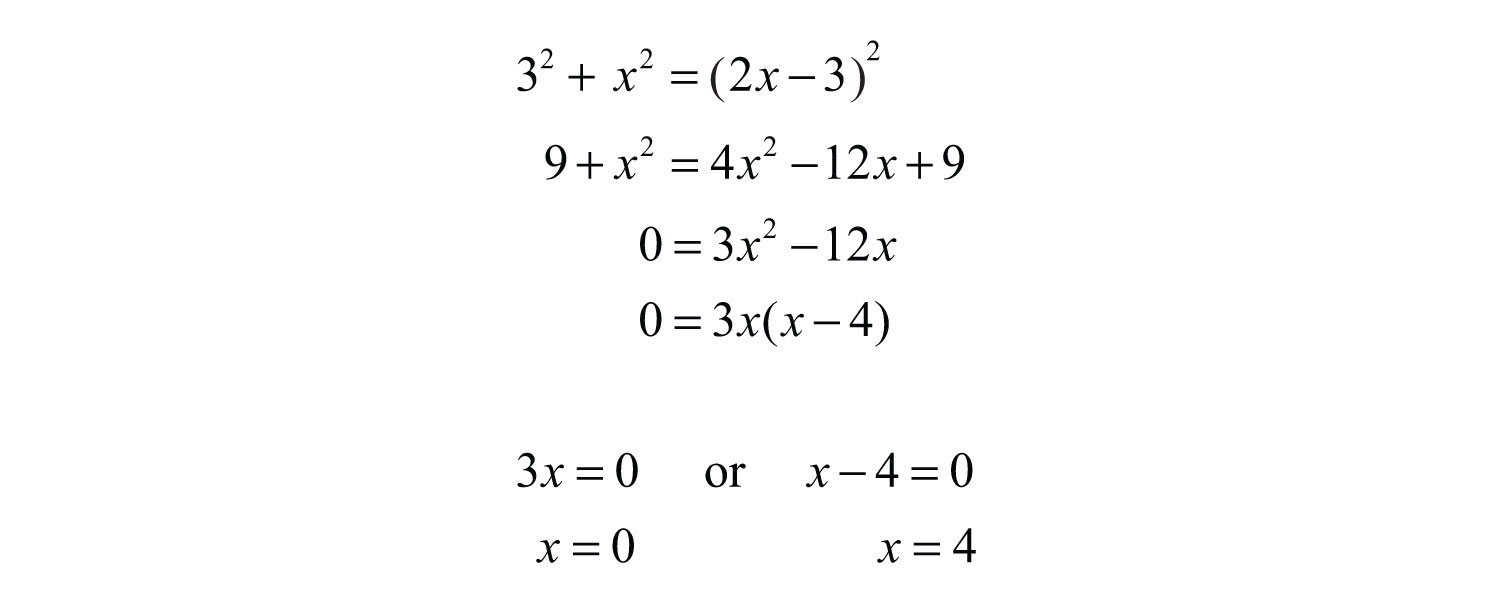
Disregard 0. The length of the unknown leg is 4 centimeters. Use to determine the length of the hypotenuse.
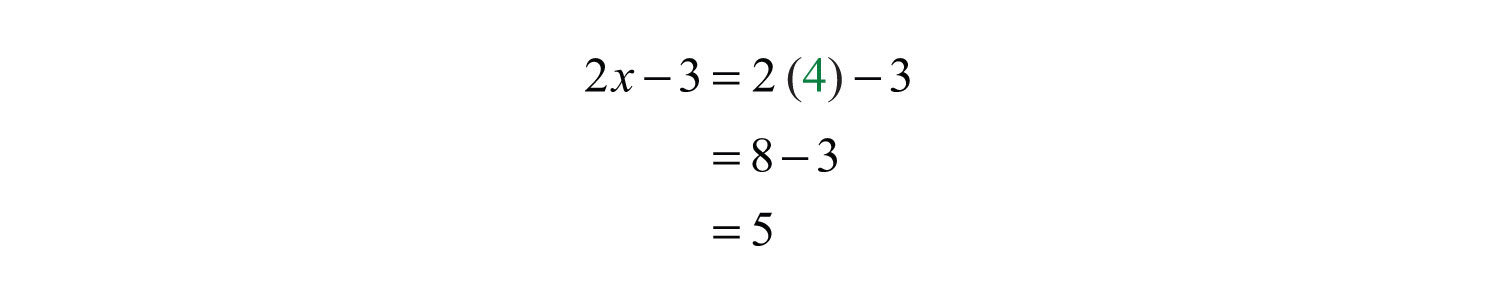
Answer: The sides of the triangle measure 3 centimeters, 4 centimeters, and 5 centimeters.
Try this! The hypotenuse of a right triangle measures 13 units. If one leg is 2 units more than twice that of the other, then find the length of each leg.
Answer: The two legs measure 5 units and 12 units.
Video Solution
(click to see video)Projectile Problems
The height of an object launched upward, ignoring the effects of air resistance, can be modeled with the following formula:
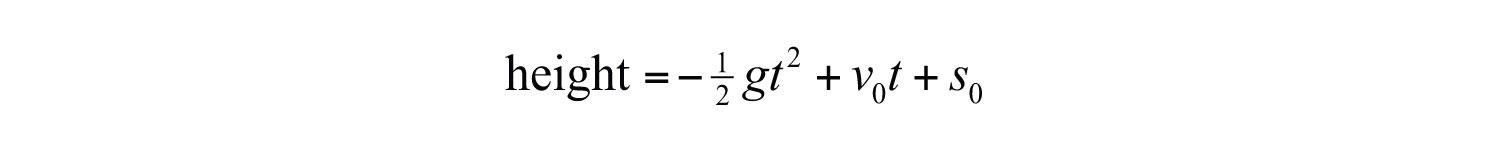
Using function notation, which is more appropriate, we have
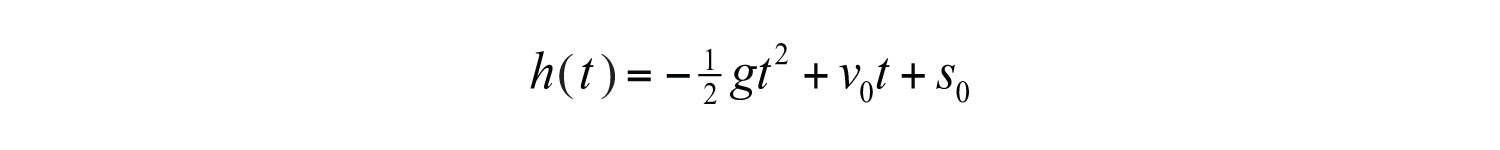
With this formula, the height can be calculated at any given time t after the object is launched. The coefficients represent the following:
The letter g represents the acceleration due to gravity. |
|
“v-naught” represents the initial velocity of the object. |
|
“s-naught” represents the initial height from which the object is launched. |
We consider only problems where the acceleration due to gravity can be expressed as . Therefore, in this section time will be measured in seconds and the height in feet. Certainly though, the formula is valid using units other than these.
Example 8: The height of a projectile launched upward at a speed of 32 feet/second from a height of 128 feet is given by the function . How long does it take to hit the ground?
Solution: An inefficient method for finding the time to hit the ground is to simply start guessing at times and evaluating. To do this, construct a chart.
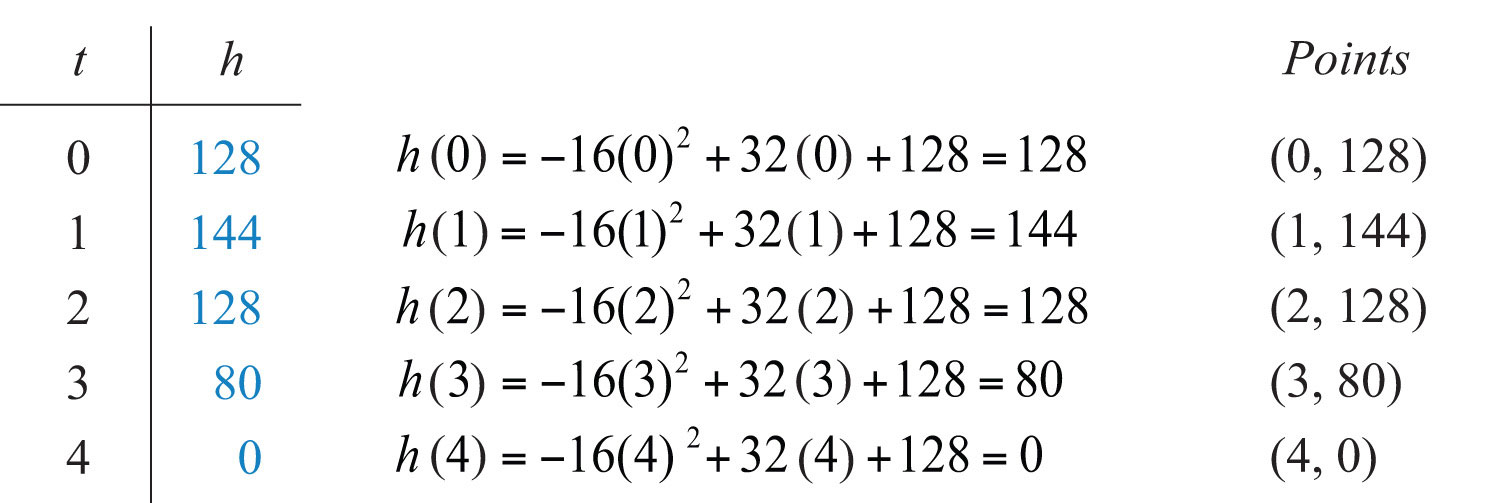
Use the table to sketch the height of the projectile over time.
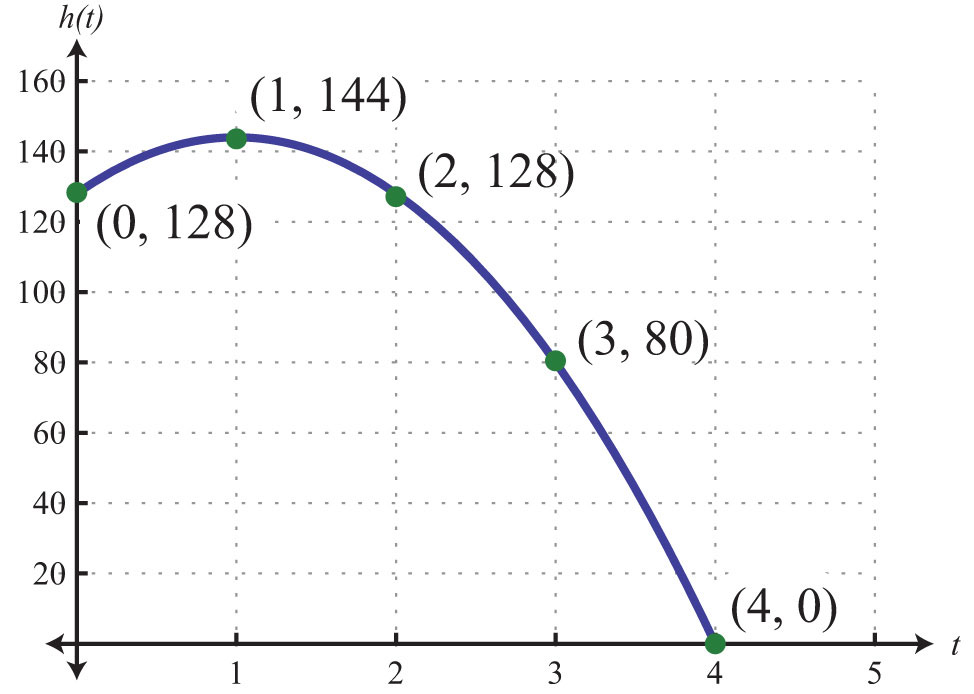
We see that at 4 seconds, the projectile hits the ground. Note that when this occurs, the height is equal to 0. Now we need to solve this problem algebraically. To find the solution algebraically, use the fact that the height is 0 when the object hits the ground. We need to find the time, t, when .
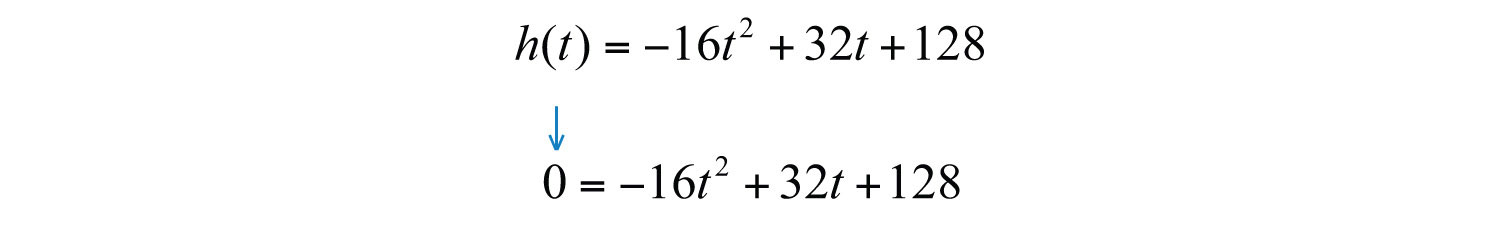
Solve the equation by factoring.
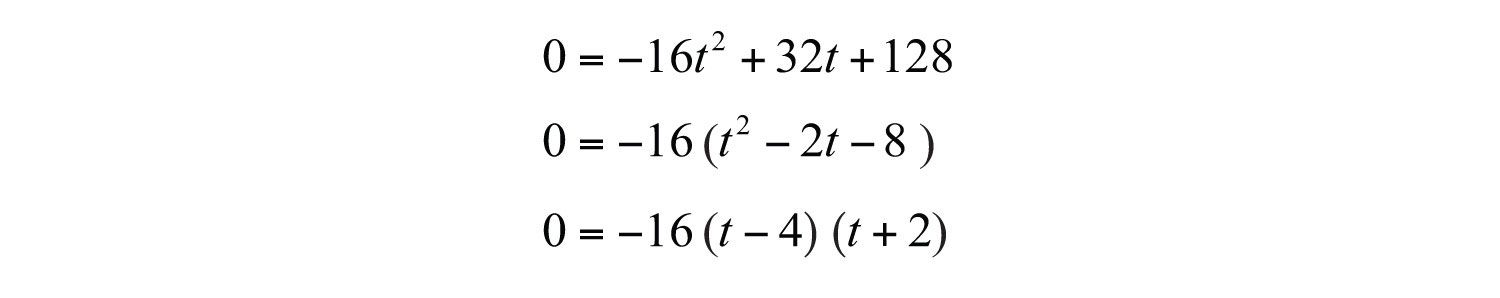
Now set each variable factor to zero.
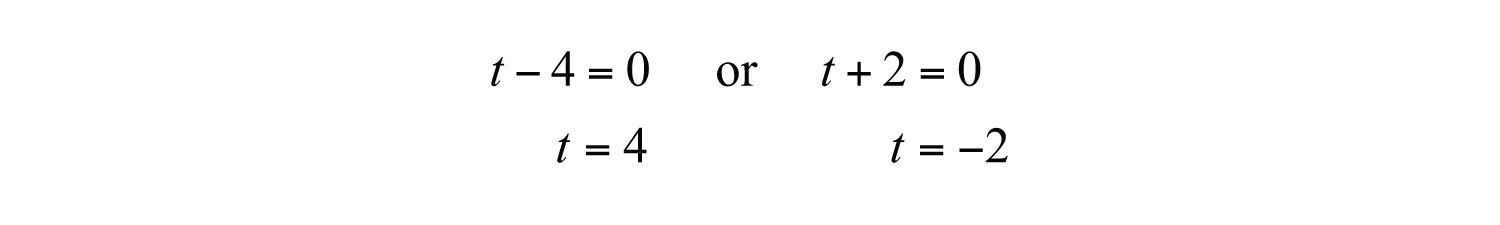
As expected, the projectile hits the ground at seconds. Disregard −2 as a solution because negative time is not defined.
Answer: The projectile hits the ground 4 seconds after it is launched.
Example 9: The height of a certain book dropped from the top of a 144-foot building is given by . How long does it take to hit the ground?
Solution: Find the time t when the height .
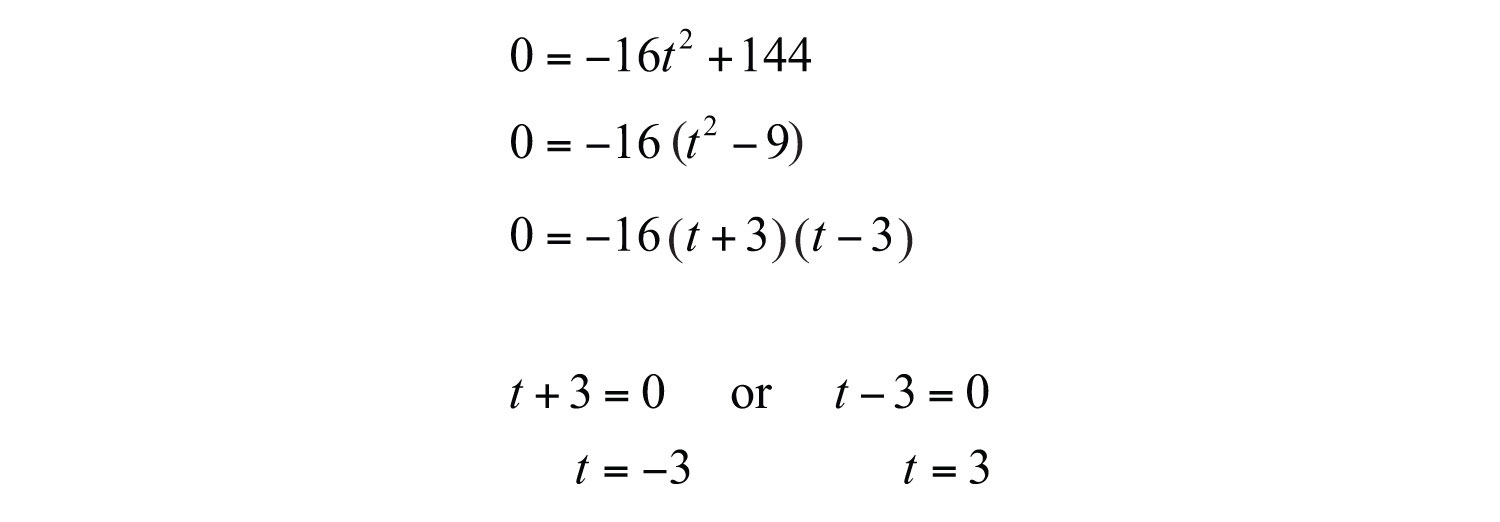
Answer: The book takes 3 seconds to hit the ground when dropped from the top of a 144-foot building.
Try this! The height of a projectile, shot straight up into the air from the ground, is given by . How long does it take to come back down to the ground?
Answer: It will take 5 seconds to come back down to the ground.
Video Solution
(click to see video)Key Takeaways
- It is best to translate a word problem to a mathematical setup and then solve using algebra. Avoid using the “guess and check” method of solving applications in this section.
- When solving applications, check that your solutions make sense in the context of the question. For example, if you wish to find the length of the base of a triangle, then you would disregard any negative solutions.
- It is important to identify each variable and state in a sentence what each variable represents. It is often helpful to draw a picture.
Topic Exercises
Part A: Number Problems
Set up an algebraic equation and then solve.
1. One integer is five times another. If the product of the two integers is 80, then find the integers.
2. One integer is four times another. If the product of the two integers is 36, then find the integers.
3. An integer is one more than four times another. If the product of the two integers is 39, then find the integers.
4. An integer is 3 more than another. If the product of the two integers is 130, then find the integers.
5. An integer is 2 less than twice another. If the product of the two integers is 220, then find the integers.
6. An integer is 3 more than twice another. If the product of the two integers is 90, then find the integers.
7. One integer is 2 units more than another. If the product of the two integers is equal to five times the larger, then find the two integers.
8. A positive integer is 1 less than twice another. If the product of the two integers is equal to fifteen times the smaller, then find the two integers.
9. A positive integer is 3 more than twice a smaller positive integer. If the product of the two integers is equal to six times the larger, then find the integers.
10. One positive integer is 3 more than another. If the product of the two integers is equal to twelve times the smaller, then find the integers.
11. An integer is 3 more than another. If the product of the two integers is equal to 2 more than four times their sum, then find the integers.
12. An integer is 5 more than another. If the product of the two integers is equal to 2 more than twice their sum, then find the integers.
13. The product of two consecutive positive even integers is 120. Find the integers.
14. The product of two consecutive positive odd integers is 99. Find the integers.
15. The product of two consecutive positive integers is 110. Find the integers.
16. The product of two consecutive positive integers is 42. Find the integers.
17. The product of two consecutive positive odd integers is equal to 1 less than seven times the sum of the integers. Find the integers.
18. The product of two consecutive positive even integers is equal to 22 more than eleven times the sum of the integers. Find the integers.
19. The sum of the squares of two consecutive positive odd integers is 74. Find the integers.
20. The sum of the squares of two consecutive positive even integers is 100. Find the integers.
21. The sum of the squares of two consecutive positive integers is 265. Find the integers.
22. The sum of the squares of two consecutive positive integers is 181. Find the integers.
23. For two consecutive positive odd integers, the product of twice the smaller and the larger is 126. Find the integers.
24. For two consecutive positive even integers, the product of the smaller and twice the larger is 160. Find the integers.
Part B: Geometry Problems
Set up an algebraic equation and then solve.
25. The width of a rectangle is 7 feet less than its length. If the area of the rectangle is 170 square feet, then find the length and width.
26. The length of a rectangle is 2 feet more than its width. If the area of the rectangle is 48 square feet, then find the length and width.
27. The width of a rectangle is 3 units less than the length. If the area is 70 square units, then find the dimensions of the rectangle.
28. The width of a rectangle measures one half of the length. If the area is 72 square feet, then find the dimensions of the rectangle.
29. The length of a rectangle is twice that of its width. If the area of the rectangle is 72 square inches, then find the length and width.
30. The length of a rectangle is three times that of its width. If the area of the rectangle is 75 square centimeters, then find the length and width.
31. The length of a rectangle is 2 inches more than its width. The area of the rectangle is equal to 12 inches more than three times the perimeter. Find the length and width of the rectangle.
32. The length of a rectangle is 3 meters more than twice the width. The area of the rectangle is equal to 10 meters less than three times the perimeter. Find the length and width of the rectangle.
33. A uniform border is to be placed around an 8-inch-by-10-inch picture. If the total area including the border must be 224 square inches, then how wide should the border be?
34. A 2-foot brick border is constructed around a square cement slab. If the total area, including the border, is 121 square feet, then what are the dimensions of the slab?
35. The area of a picture frame including a 2-inch wide border is 99 square inches. If the width of the inner area is 2 inches more than its length, then find the dimensions of the inner area.
36. A box can be made by cutting out the corners and folding up the edges of a square sheet of cardboard. A template for a cardboard box with a height of 2 inches is given. What is the length of each side of the cardboard sheet if the volume of the box is to be 50 cubic inches?
37. The height of a triangle is 3 inches more than the length of its base. If the area of the triangle is 44 square inches, then find the length of its base and height.
38. The height of a triangle is 4 units less than the length of the base. If the area of the triangle is 48 square units, then find the length of its base and height.
39. The base of a triangle is twice that of its height. If the area is 36 square centimeters, then find the length of its base and height.
40. The height of a triangle is three times the length of its base. If the area is 73½ square feet, then find the length of the base and height.
41. The height of a triangle is 1 unit more than the length of its base. If the area is 5 units more than four times the height, then find the length of the base and height of the triangle.
42. The base of a triangle is 4 times that of its height. If the area is 3 units more than five times the height, then find the length of the base and height of the triangle.
43. The diagonal of a rectangle measures 5 inches. If the length is 1 inch more than its width, then find the dimensions of the rectangle.
44. The diagonal of a rectangle measures 10 inches. If the width is 2 inches less than the length, then find the area of the rectangle.
45. If the sides of a right triangle are consecutive even integers, then what are their measures?
46. The hypotenuse of a right triangle is 13 units. If the length of one leg is 2 more than twice the other, then what are their lengths?
47. The shortest leg of a right triangle measures 9 centimeters and the hypotenuse measures 3 centimeters more than the longer leg. Find the length of the hypotenuse.
48. The long leg of a right triangle measures 24 centimeters and the hypotenuse measures 4 centimeters more three times the short leg. Find the length of the hypotenuse.
Part C: Projectile Problems
Set up an algebraic equation and then solve.
49. The height of a projectile launched upward at a speed of 32 feet/second from a height of 48 feet is given by the function . How long will it take the projectile to hit the ground?
50. The height of a projectile launched upward at a speed of 16 feet/second from a height of 192 feet is given by the function . How long will it take to hit the ground?
51. An object launched upward at a speed of 64 feet/second from a height of 80 feet. How long will it take the projectile to hit the ground?
52. An object launched upward at a speed of 128 feet/second from a height of 144 feet. How long will it take the projectile to hit the ground?
53. The height of an object dropped from the top of a 64-foot building is given by . How long will it take the object to hit the ground?
54. The height of an object dropped from an airplane at 1,600 feet is given by . How long will it take the object to hit the ground?
55. An object is dropped from a ladder at a height of 16 feet. How long will it take to hit the ground?
56. An object is dropped from a 144-foot building. How long will it take to hit the ground?
57. The height of a projectile, shot straight up into the air from the ground at 128 feet/second, is given by . How long does it take to come back down to the ground?
58. A baseball, tossed up into the air from the ground at 32 feet/second, is given by . How long does it take to come back down to the ground?
59. How long will it take a baseball thrown into the air at 48 feet/second to come back down to the ground?
60. A football is kicked up into the air at 80 feet/second. Calculate how long will it hang in the air.
Part D: Discussion Board Topics
61. Research and discuss the life of Pythagoras.
62. If the sides of a square are doubled, then by what factor is the area increased? Why?
63. Design your own geometry problem involving the area of a rectangle or triangle. Post the question and a complete solution on the discussion board.
64. Write down your strategy for setting up and solving word problems. Share your strategy on the discussion board.
Answers
1: {4, 20} or {−4, −20}
3: 3, 13
5: {11, 20} or {−22, −10}
7: {5, 7} or {−2, 0}
9: 6, 15
11: {7, 10} or {−2, 1}
13: 10, 12
15: 10, 11
17: 13, 15
19: 5, 7
21: 11, 12
23: 7, 9
25: Length: 17 feet; width: 10 feet
27: Length: 10 units; width: 7 units
29: Length: 12 inches; width: 6 inches
31: Length: 14 inches; width: 12 inches
33: 3 inches
35: 5 inches by 7 inches
37: Base: 8 inches; height: 11 inches
39: Base: 12 centimeters; height: 6 centimeters
41: Base: 9 units; height: 10 units
43: 3 inches by 4 inches
45: 6 units, 8 units, and 10 units
47: 15 centimeters
49: 3 seconds
51: 5 seconds
53: 2 seconds
55: 1 second
57: 8 seconds
59: 3 seconds
6.8 Review Exercises and Sample Exam
Review Exercises
Introduction to Factoring
Determine the missing factor.
1.
2.
3.
4.
Factor out the GCF.
5.
6.
7.
8.
9.
10.
Factor by grouping.
11.
12.
13.
14.
15.
16.
Factoring Trinomials of the Form x2 + bx + c
Are the following factored correctly? Check by multiplying.
17.
18.
19.
20.
Factor.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
Factoring Trinomials of the Form ax2 + bx + c
Factor.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
Factoring Special Binomials
Factor completely.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
General Guidelines for Factoring Polynomials
Factor completely.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
Solving Equations by Factoring
Solve.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
Find a quadratic equation with integer coefficients, given the following solutions.
83. −7, 6
84. 0, −10
85. −1/9, 1/2
86. ±3/2
Applications Involving Quadratic Equations
Set up an algebraic equation and then solve the following.
87. An integer is 4 less than twice another. If the product of the two integers is 96, then find the integers.
88. The sum of the squares of two consecutive positive even integers is 52. Find the integers.
89. A 20-foot ladder leaning against a wall reaches a height that is 4 feet more than the distance from the wall to the base of the ladder. How high does the ladder reach?
90. The height of an object dropped from the top of a 196-foot building is given by , where t represents the number of seconds after the object has been released. How long will it take the object to hit the ground?
91. The length of a rectangle is 1 centimeter less than three times the width. If the area is 70 square centimeters, then find the dimensions of the rectangle.
92. The base of a triangle is 4 centimeters more than twice the height. If the area of the triangle is 80 square centimeters, then find the measure of the base.
Sample Exam
1. Determine the GCF of the terms , , and .
2. Determine the missing factor: .
Factor.
3.
4.
5.
6.
7.
8.
Factor completely.
9.
10.
11.
12.
Solve.
13.
14.
15.
16.
17.
18.
19.
20.
For each problem, set up an algebraic equation and then solve.
21. An integer is 4 less than twice another. If the product of the two integers is 70, then find the integers.
22. The sum of the squares of two consecutive positive odd integers is 130. Find the integers.
23. The length of a rectangle is 4 feet more than twice its width. If the area is 160 square feet, then find the dimensions of the rectangle.
24. The height of a triangle is 6 centimeters less than four times the length of its base. If the area measures 27 square centimeters, then what is the height of the triangle?
25. The height of a projectile launched upward at a speed of 64 feet/second from a height of 36 feet is given by the function . How long will it take the projectile to hit the ground?
Review Exercises Answers
1:
3:
5:
7:
9:
11:
13:
15:
17: No
19: Yes
21:
23:
25:
27: Prime
29:
31:
33:
35: Prime
37:
39:
41:
43:
45:
47:
49:
51:
53:
55:
57:
59:
61:
63:
65:
67:
69:
71: 9, −10
73: −1, 1
75: −10, 5
77: ±2
79: −8, 4
81: 0, 8/3
83:
85:
87: {8, 12} or {−6, −16}
89: 16 feet
91: Length: 14 centimeters; width: 5 centimeters
Sample Exam Answers
1:
3:
5:
7:
9:
11:
13: −1/2, 7
15: ±8
17: −3/2, 1/6
19: −1/3, 2
21: {7, 10} or {−14, −5}
23: Width: 8 feet; length: 20 feet
25: 4½ sec




