This is “Polynomials and Their Operations”, chapter 5 from the book Beginning Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
Chapter 5 Polynomials and Their Operations
5.1 Rules of Exponents
Learning Objectives
- Simplify expressions using the rules of exponents.
- Simplify expressions involving parentheses and exponents.
- Simplify expressions involving 0 as an exponent.
Product, Quotient, and Power Rule for Exponents
If a factor is repeated multiple times, then the product can be written in exponential formAn equivalent expression written using a rational exponent. . The positive integer exponent n indicates the number of times the base x is repeated as a factor.
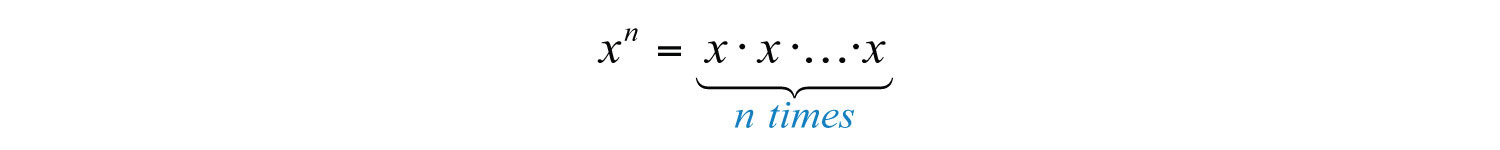
For example,
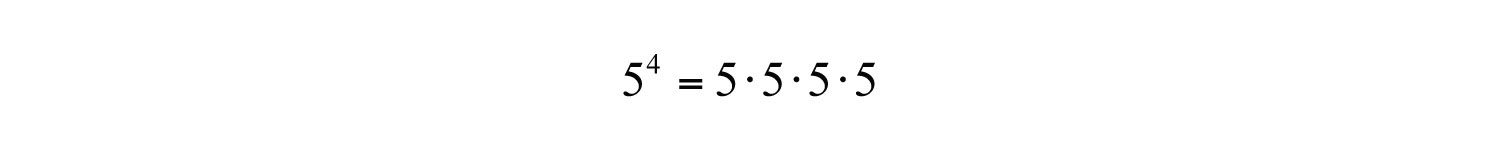
Here the base is 5 and the exponent is 4. Exponents are sometimes indicated with the caret (^) symbol found on the keyboard: 5^4 = 5*5*5*5.
Next consider the product of and ,
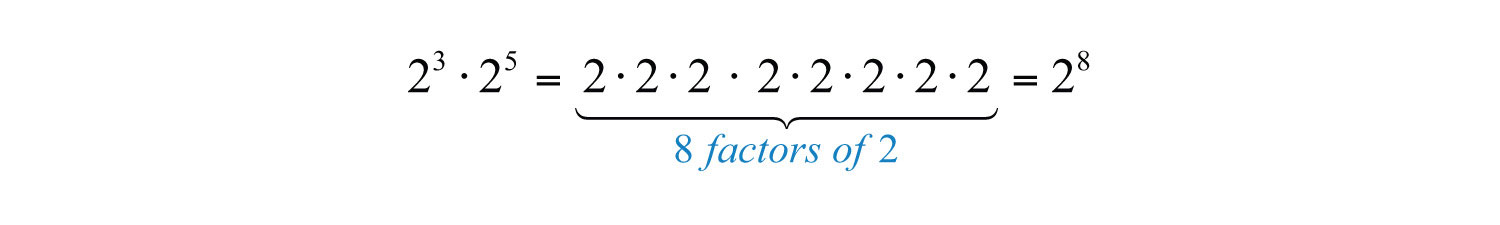
Expanding the expression using the definition produces multiple factors of the base, which is quite cumbersome, particularly when n is large. For this reason, we will develop some useful rules to help us simplify expressions with exponents. In this example, notice that we could obtain the same result by adding the exponents.
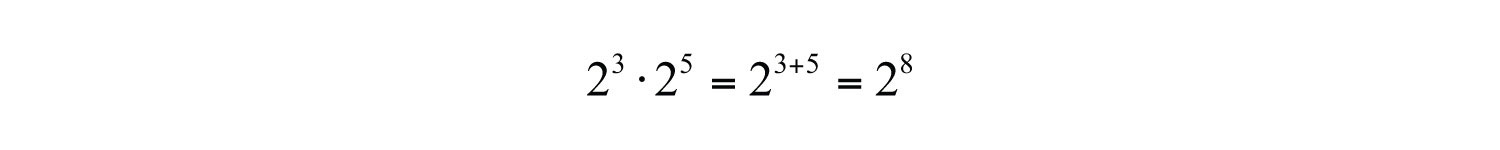
In general, this describes the product rule for exponents; the product of two expressions with the same base can be simplified by adding the exponents.. If m and n are positive integers, then
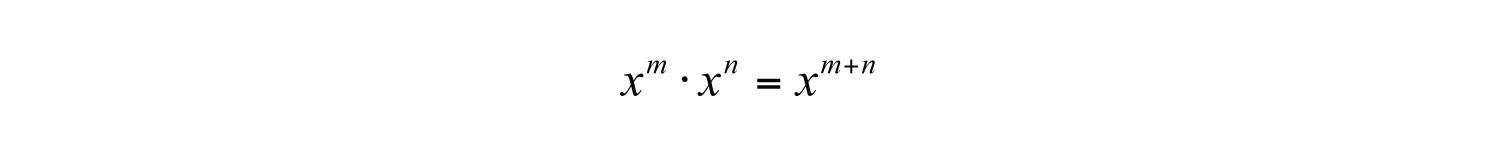
In other words, when multiplying two expressions with the same base, add the exponents.
Example 1: Simplify: .
Solution:
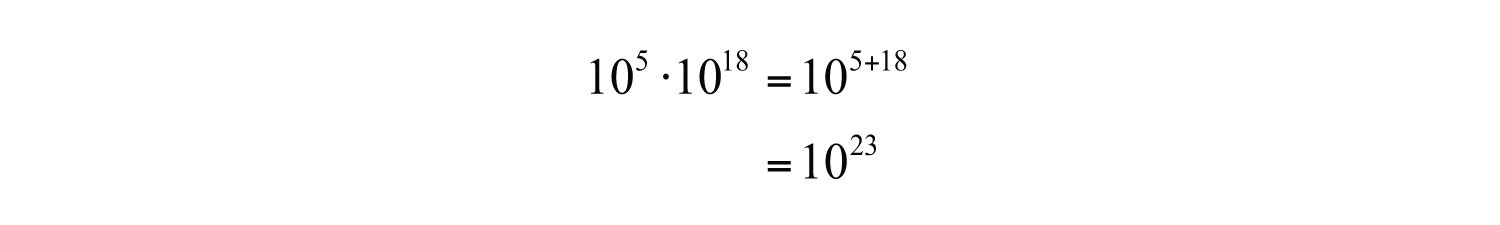
Answer:
In the previous example, notice that we did not multiply the base 10 times itself. When applying the product rule, add the exponents and leave the base unchanged.
Example 2: Simplify: .
Solution: Recall that the variable x is assumed to have an exponent of 1: .
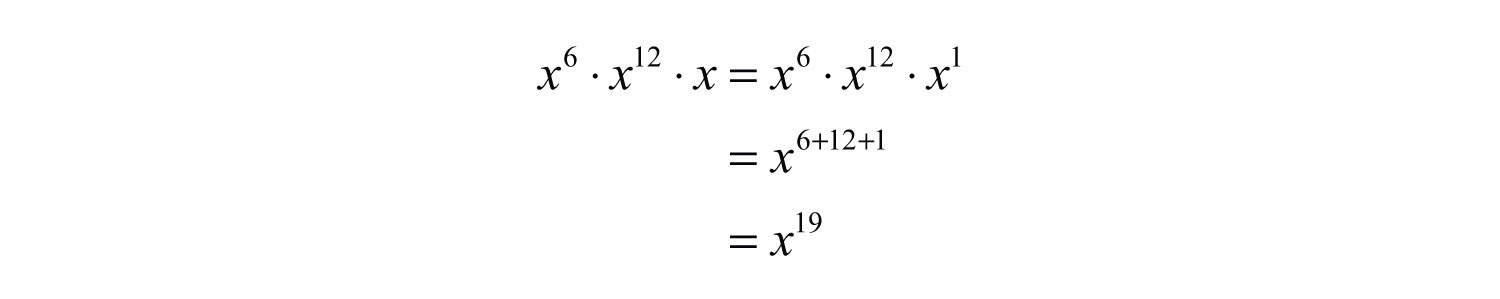
Answer:
The base could be any algebraic expression.
Example 3: Simplify: .
Solution: Treat the expression as the base.
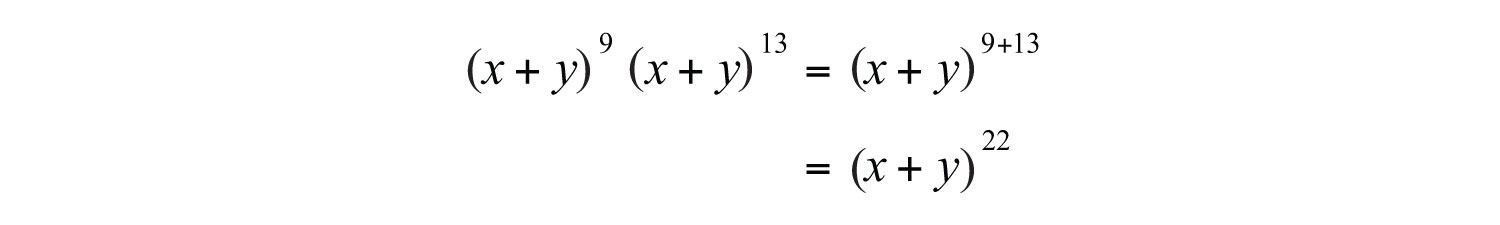
Answer:
The commutative property of multiplication allows us to use the product rule for exponents to simplify factors of an algebraic expression.
Example 4: Simplify: .
Solution: Multiply the coefficients and add the exponents of variable factors with the same base.
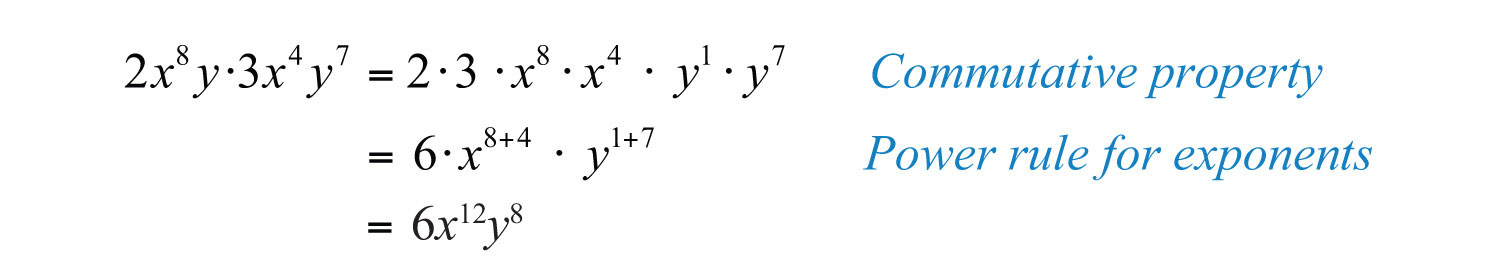
Answer:
Next, we will develop a rule for division by first looking at the quotient of and .
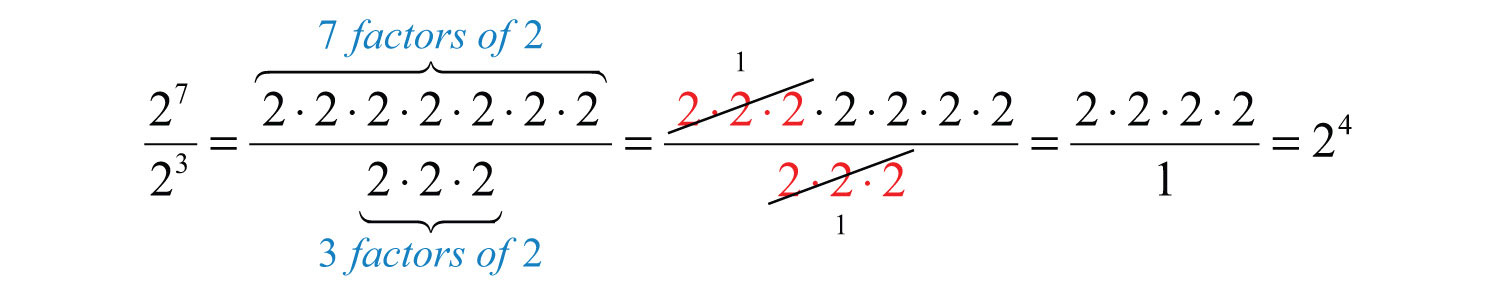
Here we can cancel factors after applying the definition of exponents. Notice that the same result can be obtained by subtracting the exponents.
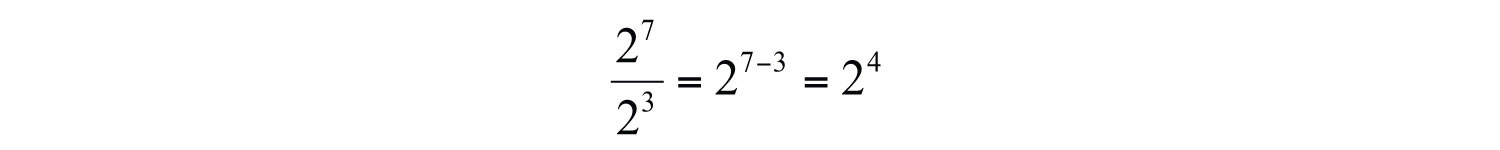
This describes the quotient rule for exponents; the quotient of two expressions with the same base can be simplified by subtracting the exponents.. If m and n are positive integers and , then
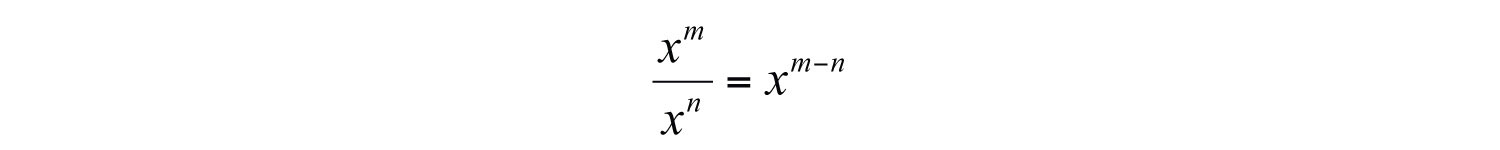
In other words, when you divide two expressions with the same base, subtract the exponents.
Example 5: Simplify: .
Solution: Divide the coefficients and subtract the exponents of the variable y.
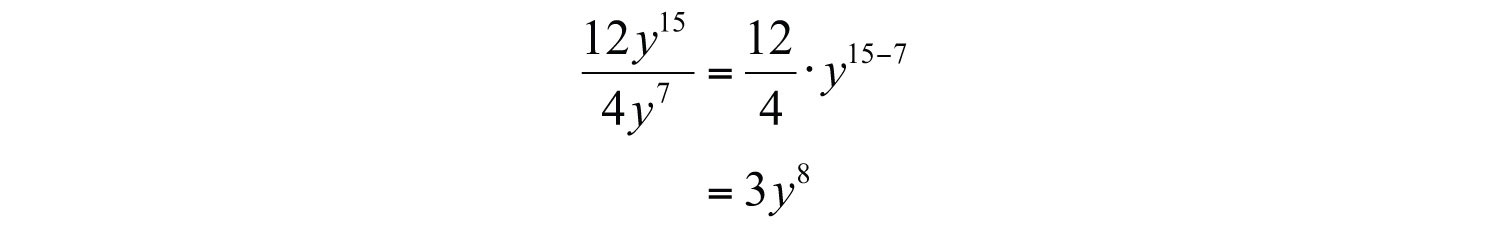
Answer:
Example 6: Simplify: .
Solution:
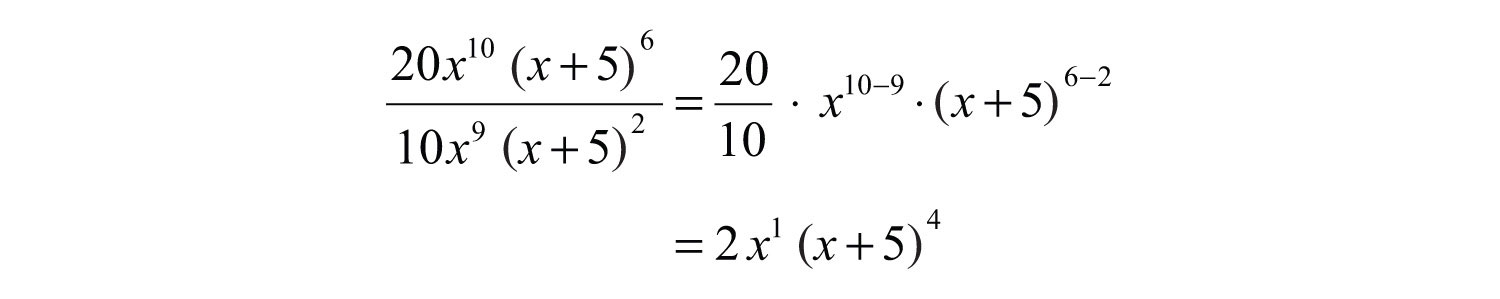
Answer:
Now raise to the fourth power as follows:
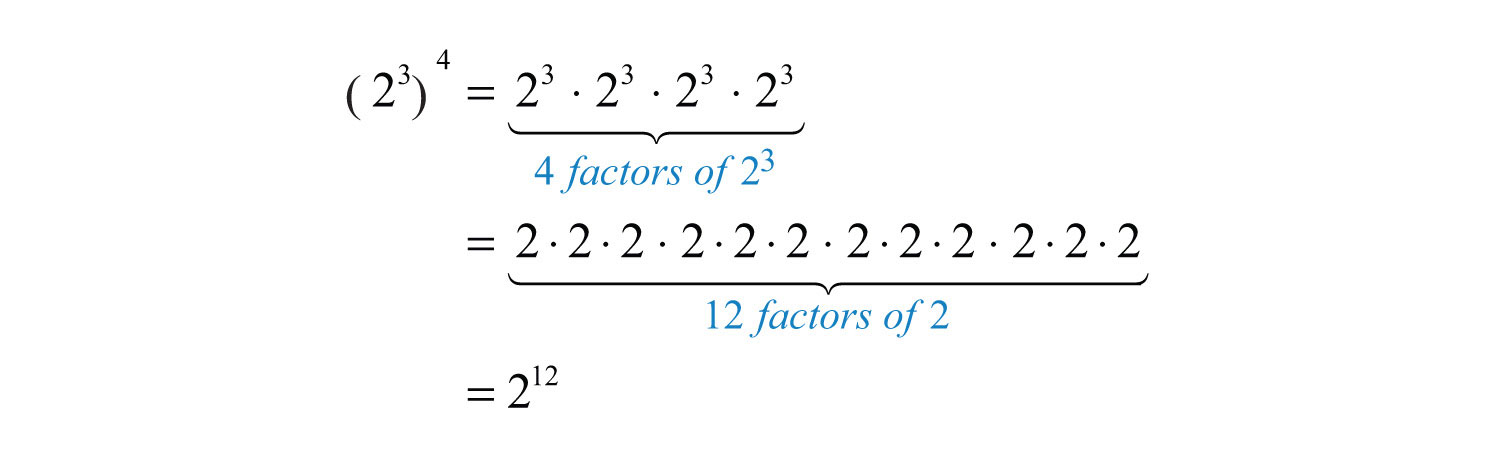
After writing the base as a factor four times, expand to obtain 12 factors of 2. We can obtain the same result by multiplying the exponents.
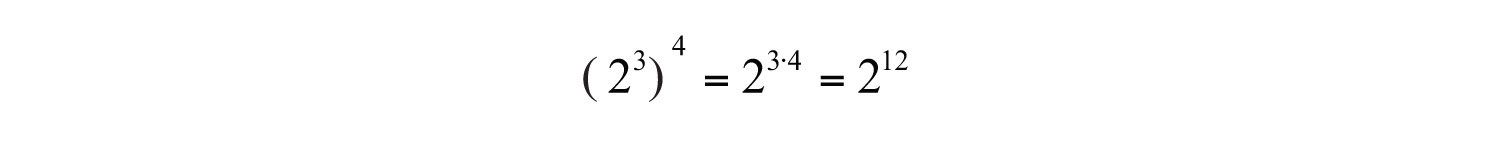
In general, this describes the power rule for exponents; a power raised to a power can be simplified by multiplying the exponents.. Given positive integers m and n, then
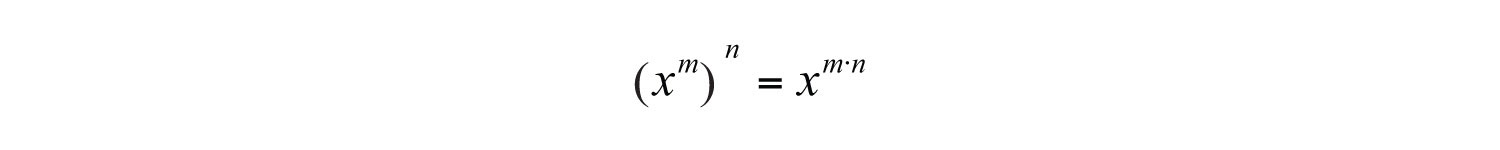
In other words, when raising a power to a power, multiply the exponents.
Example 7: Simplify: .
Solution:
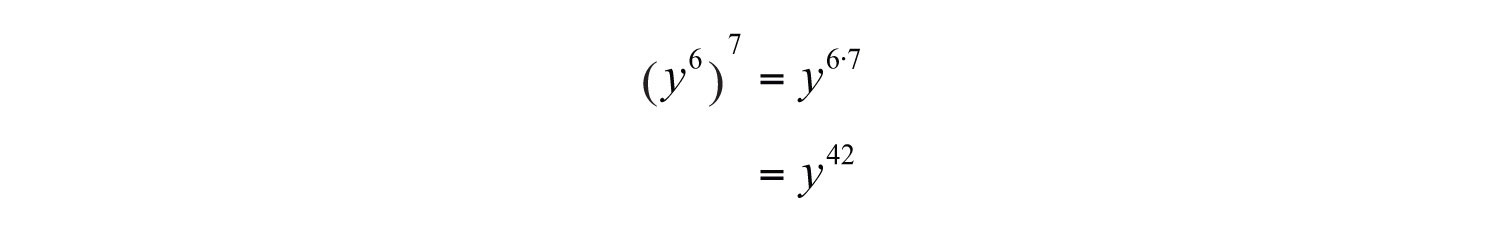
Answer:
To summarize, we have developed three very useful rules of exponents that are used extensively in algebra. If given positive integers m and n, then
| Product rule: | |
| Quotient rule: | |
| Power rule: |
Try this! Simplify: .
Answer:
Video Solution
(click to see video)Power Rules for Products and Quotients
Now we consider raising grouped products to a power. For example,
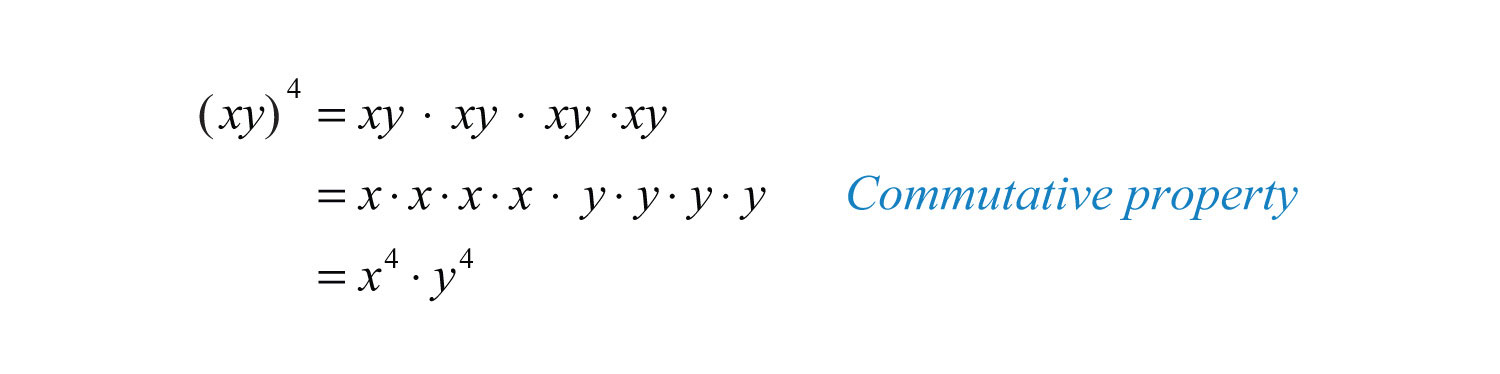
After expanding, we have four factors of the product xy. This is equivalent to raising each of the original factors to the fourth power. In general, this describes the power rule for a product; if a product is raised to a power, then apply that power to each factor in the product.. If n is a positive integer, then
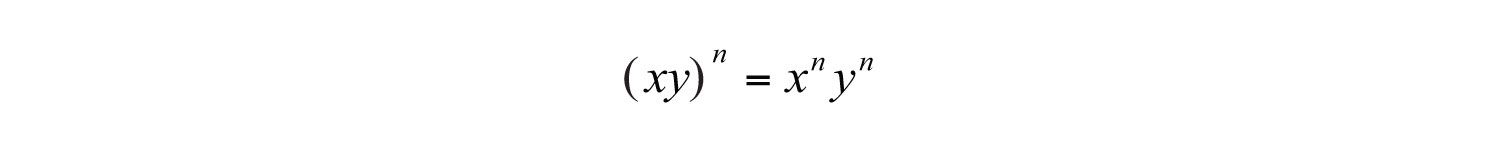
Example 8: Simplify: .
Solution: We must apply the exponent 7 to all the factors, including the coefficient, 2.
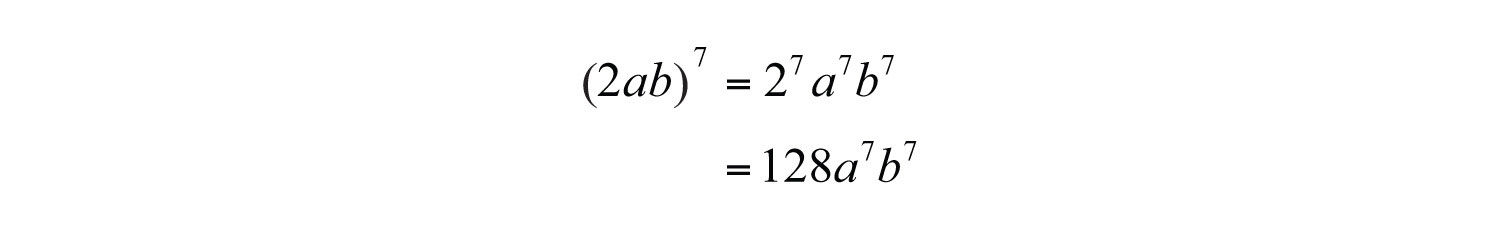
If a coefficient is raised to a relatively small power, then present the real number equivalent, as we did in this example: .
Answer:
In many cases, the process of simplifying expressions involving exponents requires the use of several rules of exponents.
Example 9: Simplify: .
Solution:
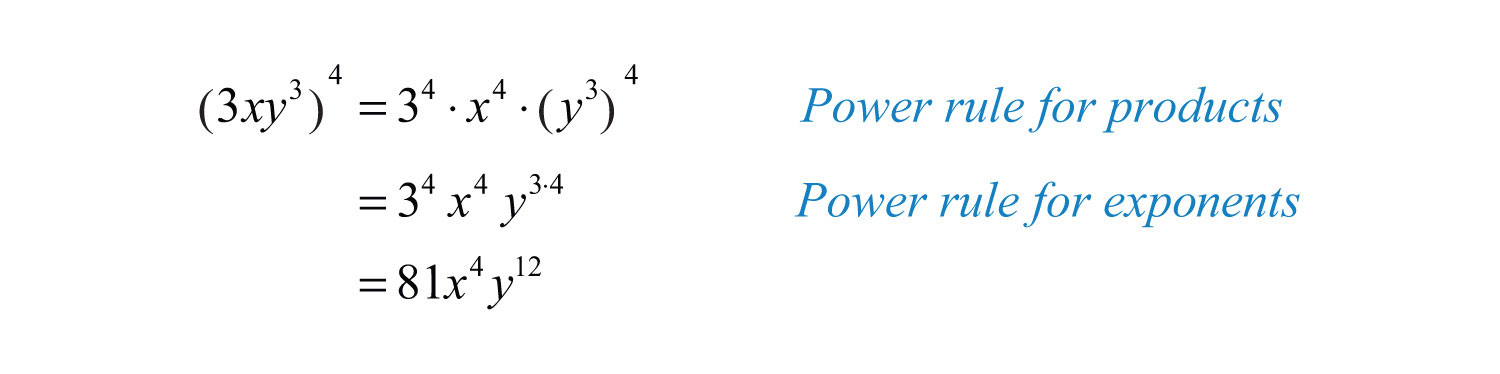
Answer:
Example 10: Simplify: .
Solution:
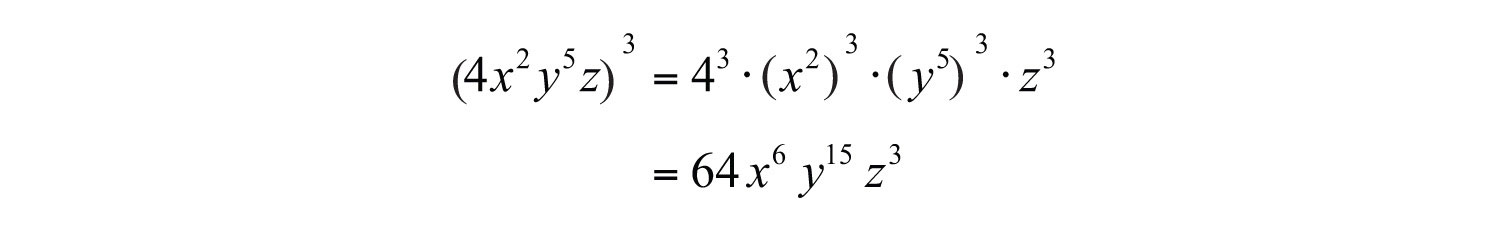
Answer:
Example 11: Simplify: .
Solution:
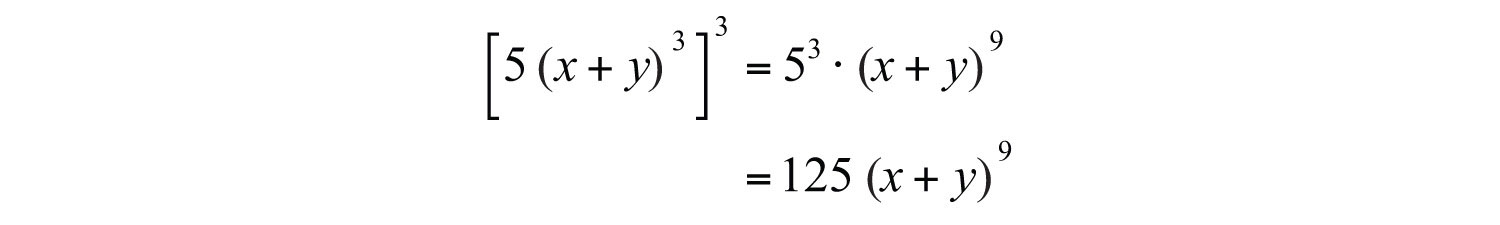
Answer:
Next, consider a quotient raised to a power.
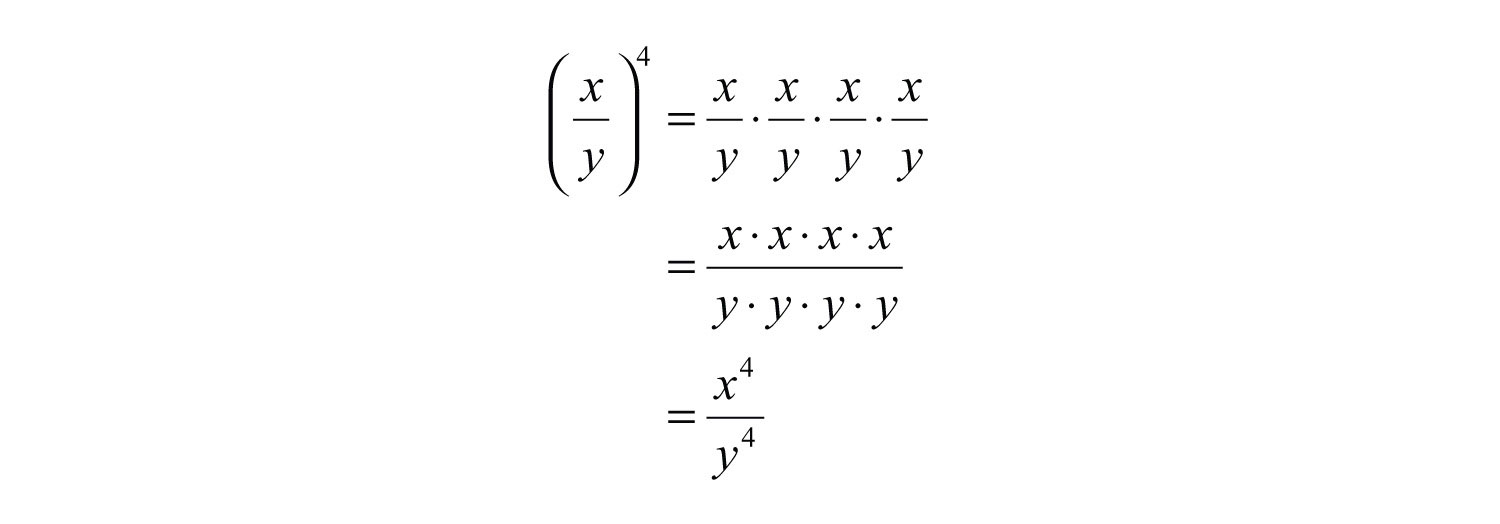
Here we obtain four factors of the quotient, which is equivalent to the numerator and the denominator both raised to the fourth power. In general, this describes the power rule for a quotient; if a quotient is raised to a power, then apply that power to the numerator and the denominator.. If n is a positive integer and , then
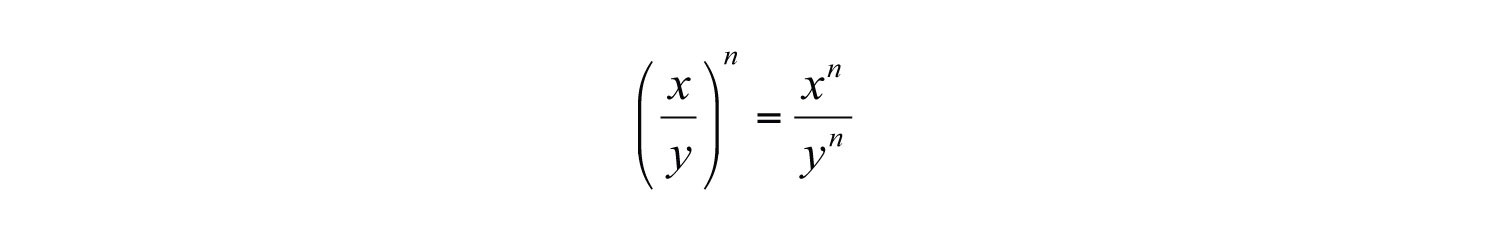
In other words, given a fraction raised to a power, we can apply that exponent to the numerator and the denominator. This rule requires that the denominator is nonzero. We will make this assumption for the remainder of the section.
Example 12: Simplify: .
Solution: First, apply the power rule for a quotient and then the power rule for a product.
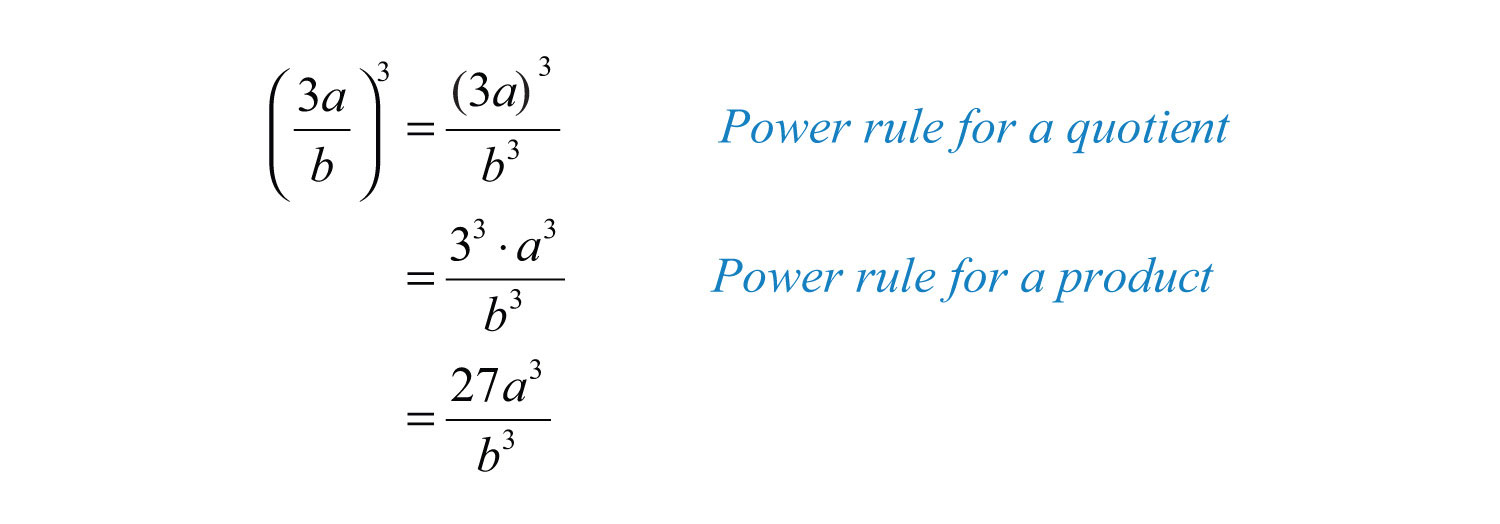
Answer:
In practice, we often combine these two steps by applying the exponent to all factors in the numerator and the denominator.
Example 13: Simplify: .
Solution: Apply the exponent 5 to all of the factors in the numerator and the denominator.
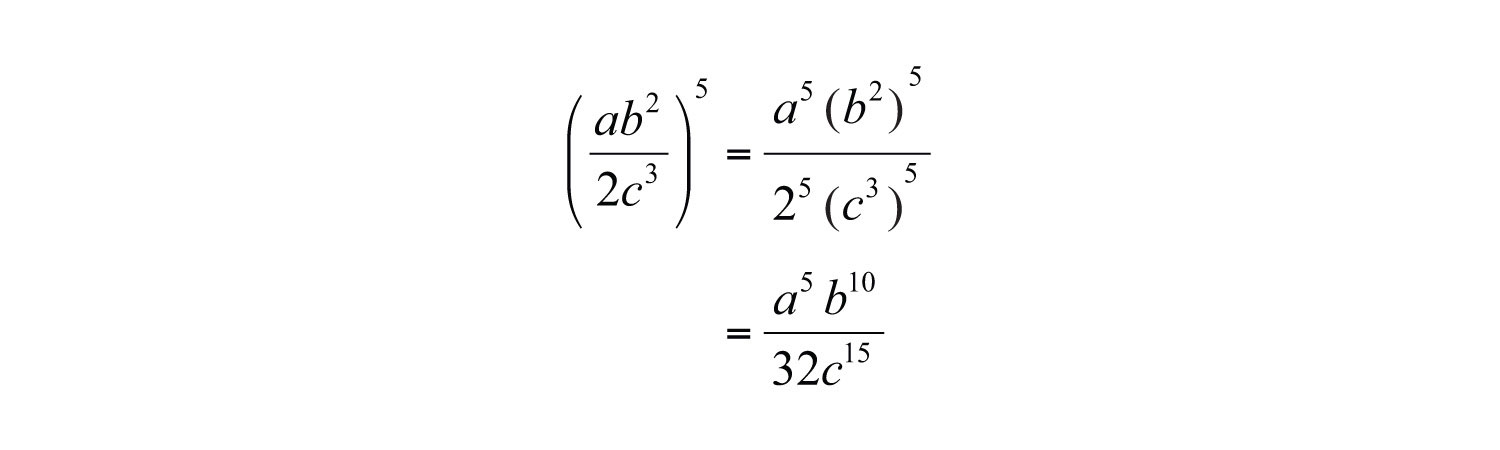
Answer:
Example 14: Simplify: .
Solution:
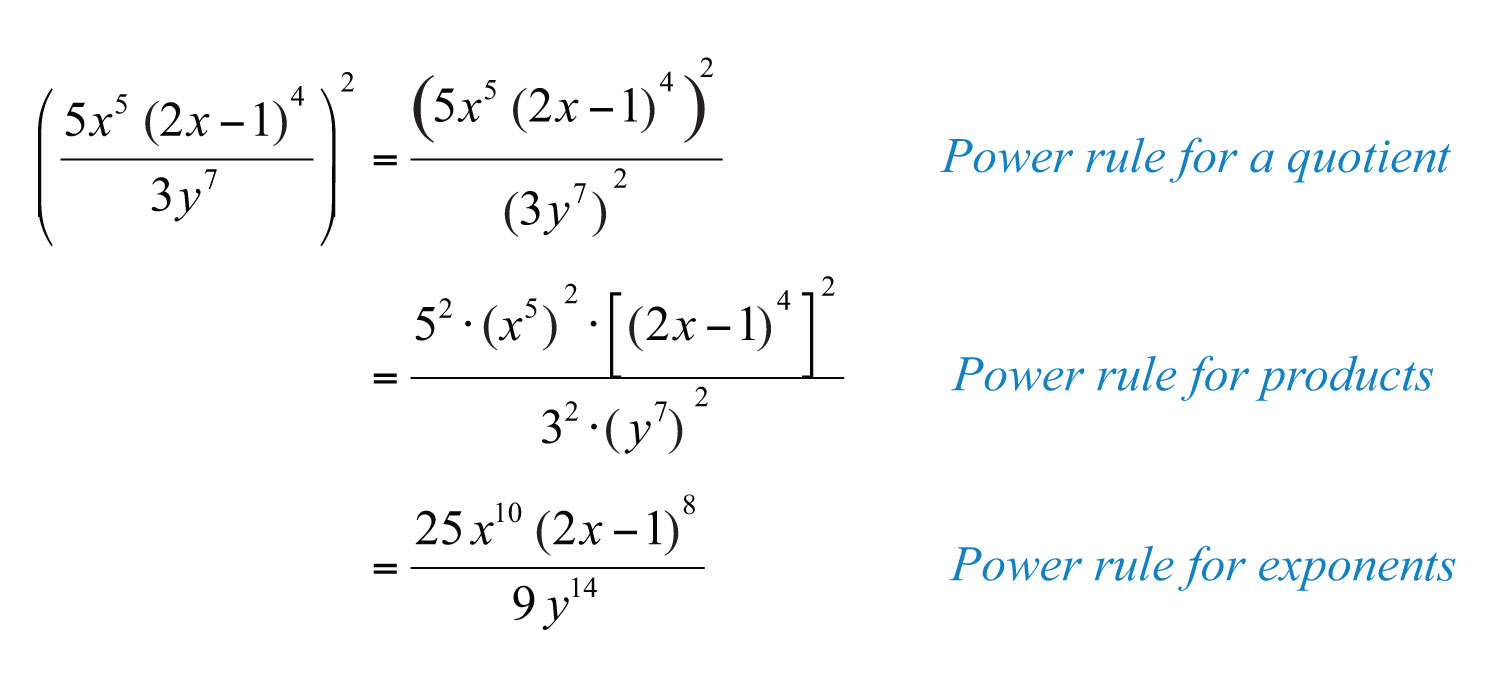
Answer:
It is a good practice to simplify within parentheses before using the power rules; this is consistent with the order of operations.
Example 15: Simplify: .
Solution:

Answer:
To summarize, we have developed two new rules that are useful when grouping symbols are used in conjunction with exponents. If given a positive integer n, where y is a nonzero number, then
| Power rule for a product: | |
| Power rule for a quotient: |
Try this! Simplify: .
Answer:
Video Solution
(click to see video)Zero as an Exponent
Using the quotient rule for exponents, we can define what it means to have 0 as an exponent. Consider the following calculation:
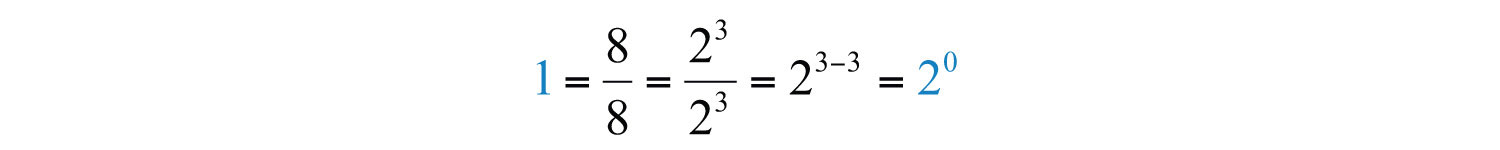
Eight divided by 8 is clearly equal to 1, and when the quotient rule for exponents is applied, we see that a 0 exponent results. This leads us to the definition of zero as an exponent; any nonzero base raised to the 0 power is defined to be 1., where :
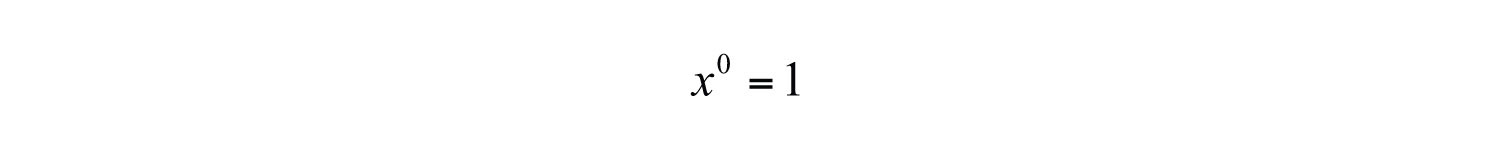
It is important to note that is undefined. If the base is negative, then the result is still +1. In other words, any nonzero base raised to the 0 power is defined to be 1. In the following examples, assume all variables are nonzero.
Example 16: Simplify:
a.
b.
Solution:
a. Any nonzero quantity raised to the 0 power is equal to 1.
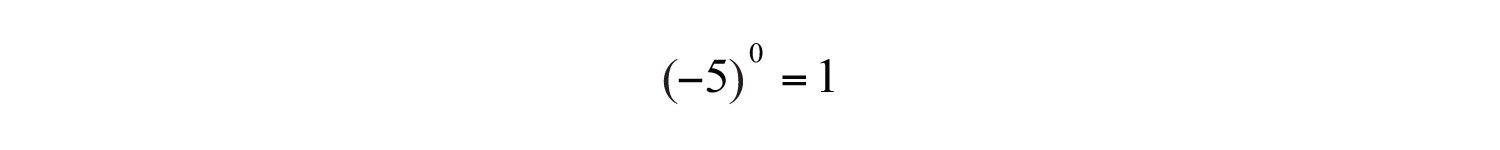
b. In the example , the base is 5, not −5.
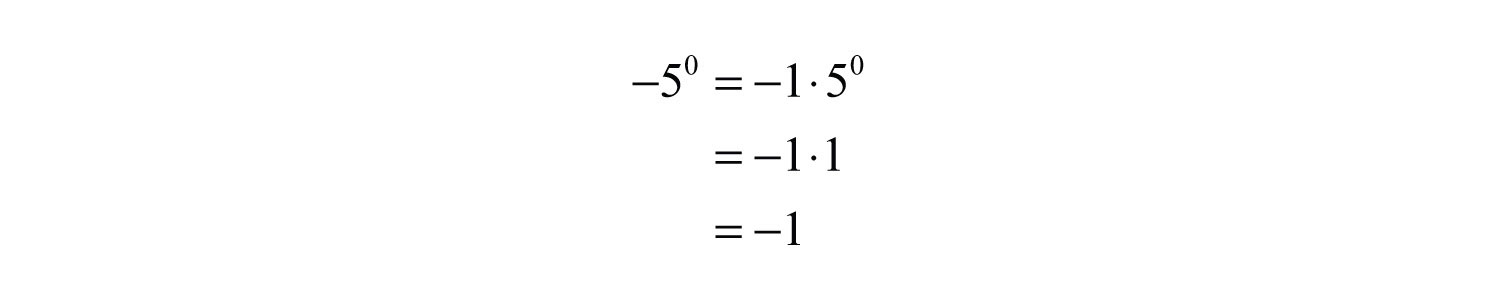
Answers: a. 1; b. −1
Example 17: Simplify: .
Solution: It is good practice to simplify within the parentheses first.
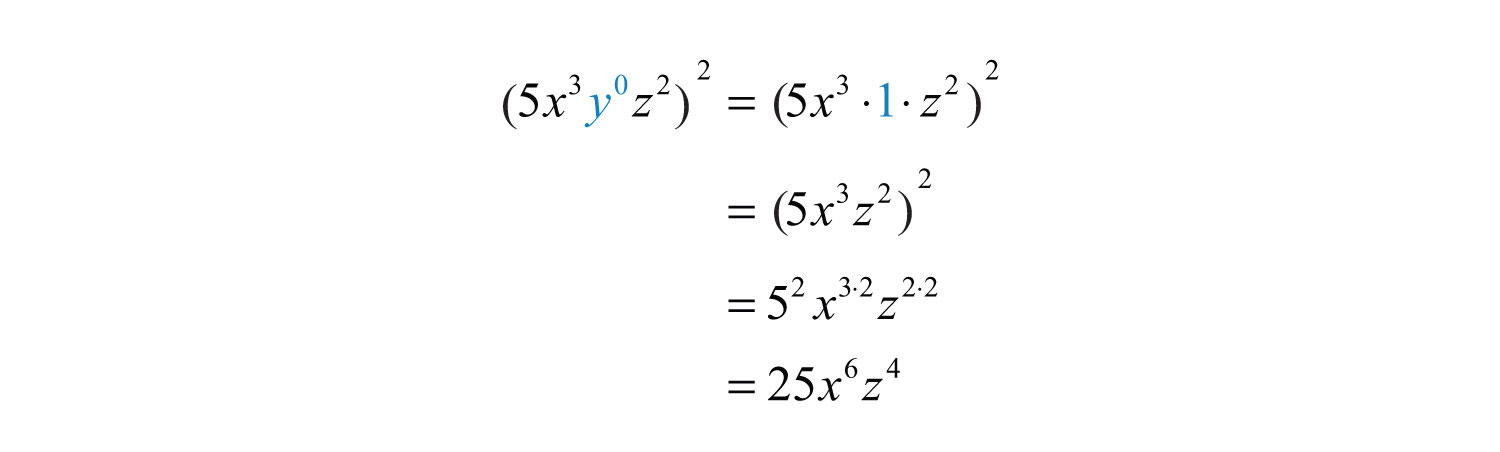
Answer:
Example 18: Simplify: .
Solution:
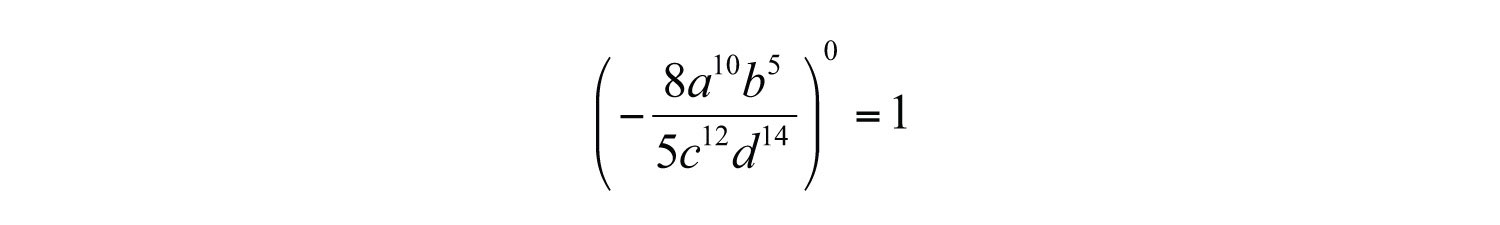
Answer: 1
Try this! Simplify: and .
Answer: and
Video Solution
(click to see video)Key Takeaways
- The rules of exponents allow you to simplify expressions involving exponents.
- When multiplying two quantities with the same base, add exponents: .
- When dividing two quantities with the same base, subtract exponents: .
- When raising powers to powers, multiply exponents: .
- When a grouped quantity involving multiplication and division is raised to a power, apply that power to all of the factors in the numerator and the denominator: and .
- Any nonzero quantity raised to the 0 power is defined to be equal to 1: .
Topic Exercises
Part A: Product, Quotient, and Power Rule for Exponents
Write each expression using exponential form.
1.
2.
3.
4.
5.
6.
Simplify.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
Simplify.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
Part B: Power Rules for Products and Quotients
Simplify.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91. The probability of tossing a fair coin and obtaining n heads in a row is given by the formula . Determine the probability, as a percent, of tossing 5 heads in a row.
92. The probability of rolling a single fair six-sided die and obtaining n of the same faces up in a row is given by the formula . Determine the probability, as a percent, of obtaining the same face up two times in a row.
93. If each side of a square measures units, then determine the area in terms of the variable x.
94. If each edge of a cube measures units, then determine the volume in terms of the variable x.
Part C: Zero Exponents
Simplify. (Assume variables are nonzero.)
95.
96.
97.
98.
99.
100.
101.
102.
103.
104.
105.
106.
107.
108.
109.
Part D: Discussion Board Topics
110. René Descartes (1637) established the usage of exponential form: , , and so on. Before this, how were exponents denoted?
111. Discuss the accomplishments accredited to Al-Karismi.
112. Why is undefined?
113. Explain to a beginning student why .
Answers
1:
3:
5:
7:
9: −16
11: −27
13:
15:
17:
19:
21:
23:
25:
27:
29:
31:
33:
35:
37:
39:
41:
43:
45:
47:
49:
51:
53:
55:
57:
59:
61:
63:
65:
67:
69:
71:
73:
75:
77:
79:
81:
83:
85:
87:
89:
91:
93:
95: 1
97: −1
99: 1
101: −4
103:
105:
107: 1
109:
5.2 Introduction to Polynomials
Learning Objectives
- Identify a polynomial and determine its degree.
- Evaluate a polynomial for given values of the variables.
- Evaluate a polynomial using function notation.
Definitions
A polynomialAn algebraic expression consisting of terms with real number coefficients and variables with whole number exponents. is a special algebraic expression with terms that consist of real number coefficients and variable factors with whole number exponents.
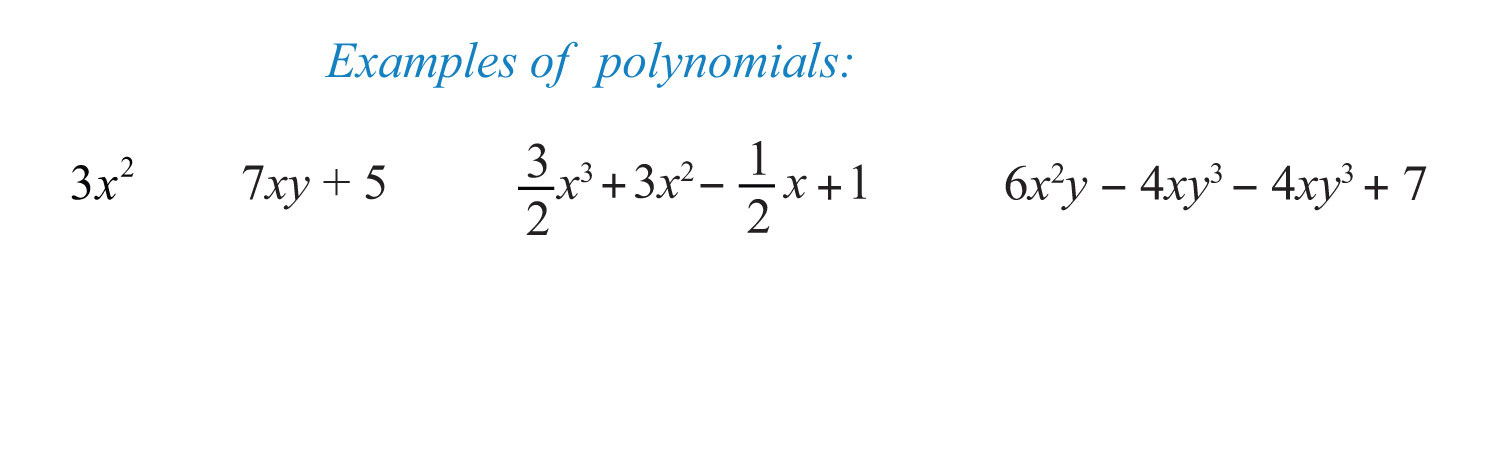
Polynomials do not have variables in the denominator of any term.
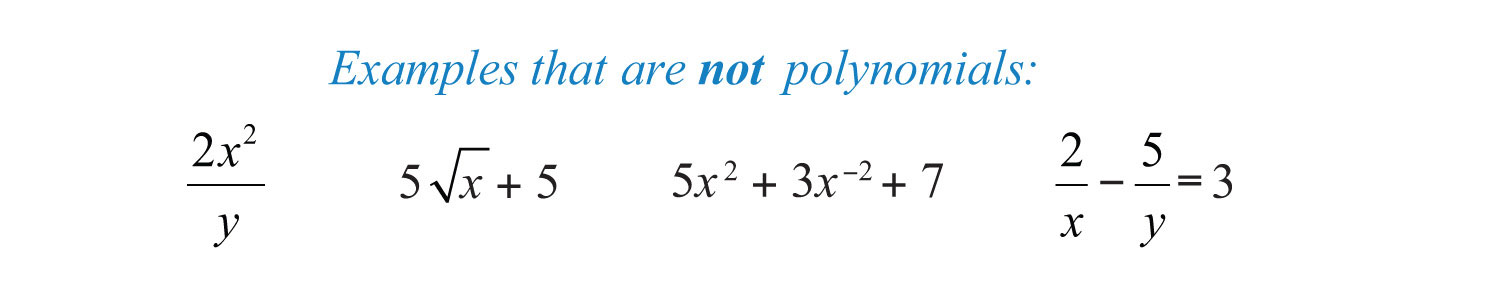
The degree of a termThe exponent of the variable; if there is more than one variable in the term, the degree of the term is the sum their exponents. in a polynomial is defined to be the exponent of the variable, or if there is more than one variable in the term, the degree is the sum of their exponents. Recall that ; any constant term can be written as a product of and itself. Hence the degree of a constant term is 0.
| Term | Degree |
|---|---|
, since |
|
1, since |
The degree of a polynomialThe largest degree of all of its terms. is the largest degree of all of its terms.
| Polynomial | Degree |
|---|---|
, because has degree 4. |
|
1, because |
We classify polynomials by the number of terms and the degree as follows:
| Expression | Classification | Degree |
|---|---|---|
MonomialPolynomial with one term. (one term) |
7 |
|
BinomialPolynomial with two terms. (two terms) |
6 |
|
TrinomialPolynomial with three terms. (three terms) |
2 |
|
PolynomialAn algebraic expression consisting of terms with real number coefficients and variables with whole number exponents. (many terms) |
3 |
In this text, we will call polynomials with four or more terms simply polynomials.
Example 1: Classify and state the degree: .
Solution: Here there are three terms. The highest variable exponent is 5. Therefore, this is a trinomial of degree 5.
Answer: Trinomial; degree 5
Example 2: Classify and state the degree: .
Solution: Since the expression consists of only multiplication, it is one term, a monomial. The variable part can be written as ; hence its degree is .
Answer: Monomial; degree 9
Example 3: Classify and state the degree: .
Solution: The term has degree 3; has degree 5; has degree 6; and the constant term 4 has degree 0. Therefore, the polynomial has 4 terms with degree 6.
Answer: Polynomial; degree 6
Of particular interest are polynomials with one variableA polynomial where each term has the form , where is any real number and n is any whole number., where each term is of the form . Here is any real number and n is any whole number. Such polynomials have the standard form
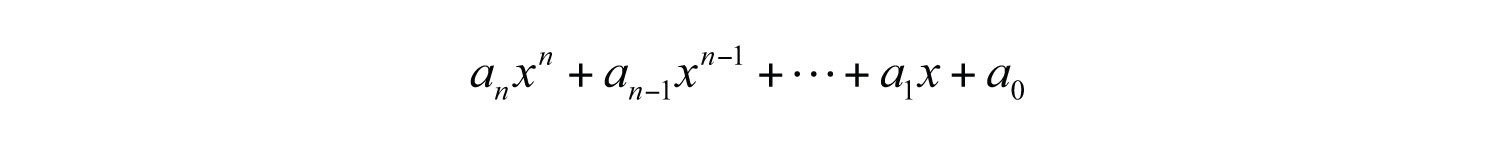
Typically, we arrange terms of polynomials in descending order based on the degree of each term. The leading coefficientThe coefficient of the term with the largest degree. is the coefficient of the variable with the highest power, in this case, .
Example 4: Write in standard form: .
Solution: Since terms are separated by addition, write the following:
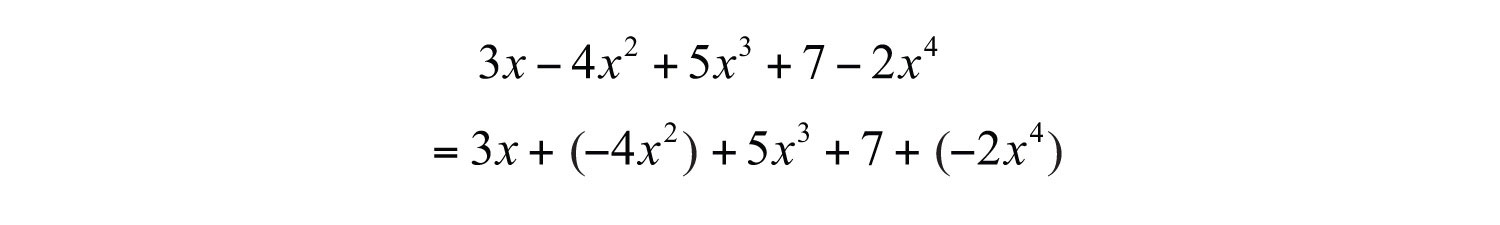
In this form, we can see that the subtraction in the original corresponds to negative coefficients. Because addition is commutative, we can write the terms in descending order based on the degree of each term as follows:
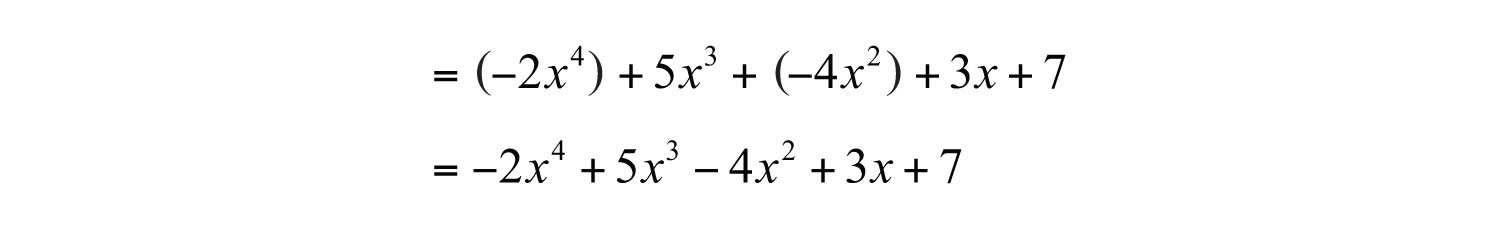
Answer:
We can further classify polynomials with one variable by their degree as follows:
| Polynomial | Name |
|---|---|
5 |
Constant (degree 0) |
Linear (degree 1) |
|
Quadratic (degree 2) |
|
Cubic (degree 3) |
|
Fourth-degree polynomial |
In this text, we call any polynomial of degree an nth-degree polynomial. In other words, if the degree is 4, we call the polynomial a fourth-degree polynomial. If the degree is 5, we call it a fifth-degree polynomial, and so on.
Evaluating Polynomials
Given the values for the variables in a polynomial, we can substitute and simplify using the order of operations.
Example 5: Evaluate: , where .
Solution: First, replace the variable with parentheses and then substitute the given value.
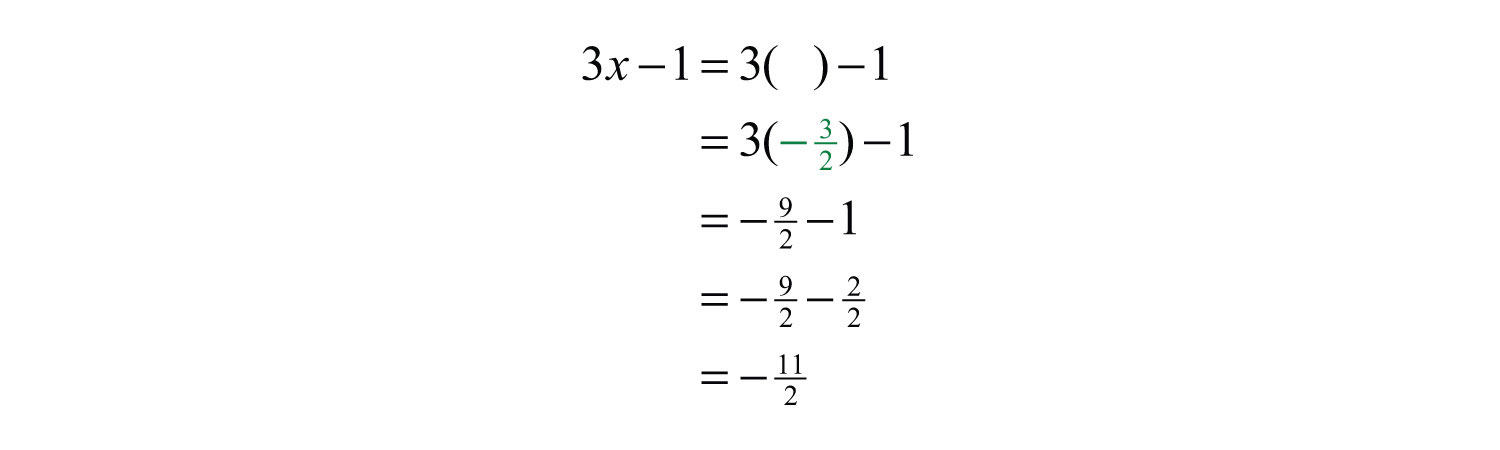
Answer: −11/2
Example 6: Evaluate: , where .
Solution:
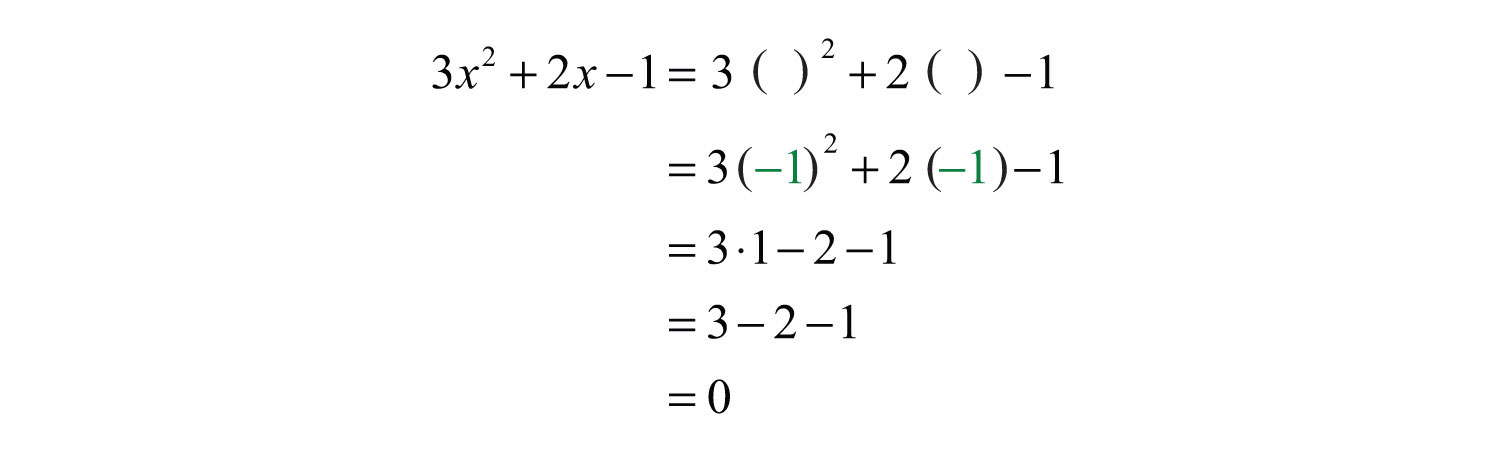
Answer: 0
Example 7: Evaluate: , where and .
Solution:

Answer: 41
Example 8: The volume of a sphere in cubic units is given by the formula , where r is the radius. Calculate the volume of a sphere with radius meters.
Solution:
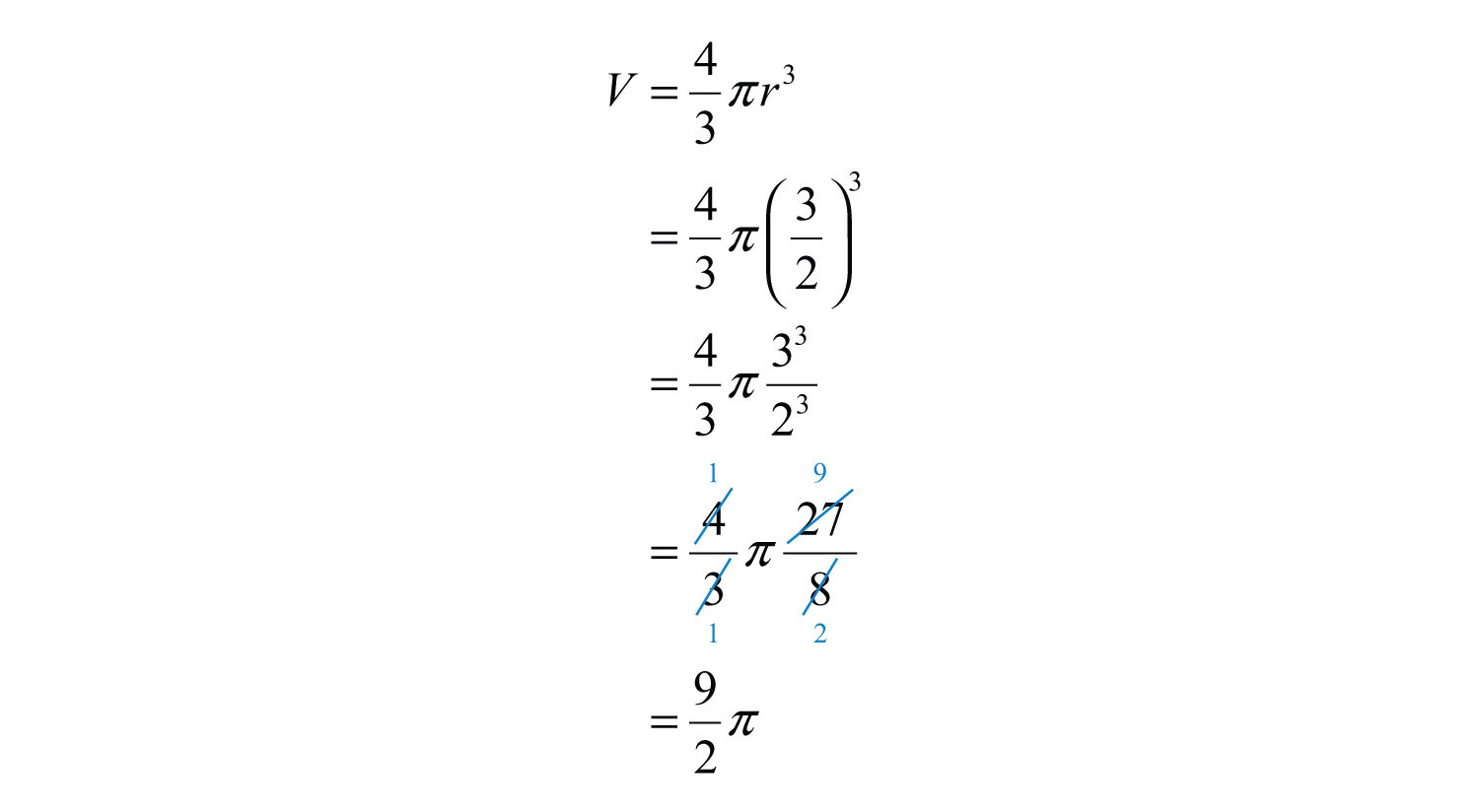
Answer: cubic meters
Try this! Evaluate: , where .
Answer: −50
Video Solution
(click to see video)Polynomial Functions
Polynomial functions with one variable are functions that can be written in the form
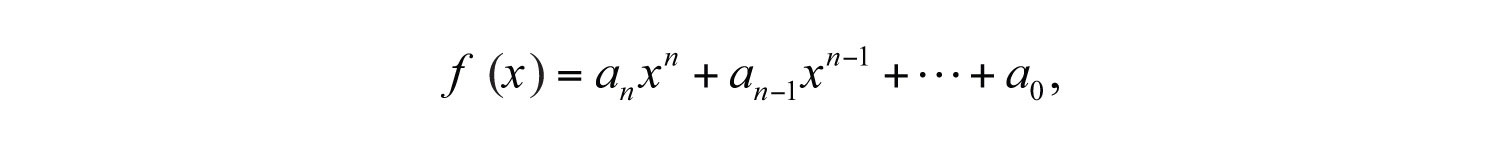
where is any real number and n is any whole number. Some examples of the different classes of polynomial functions are listed below:
| Polynomial function | Name |
|---|---|
Constant functionA polynomial function with degree 0. (degree 0) |
|
Linear functionA polynomial function with degree 1. (degree 1) |
|
Quadratic functionA polynomial function with degree 2. (degree 2) |
|
Cubic functionA polynomial function with degree 3. (degree 3) |
|
Polynomial function |
Since there are no restrictions on the values for x, the domain of any polynomial function consists of all real numbers.
Example 9: Calculate: , given .
Solution: Recall that the function notation indicates we should evaluate the function when . Replace every instance of the variable x with the value 5.
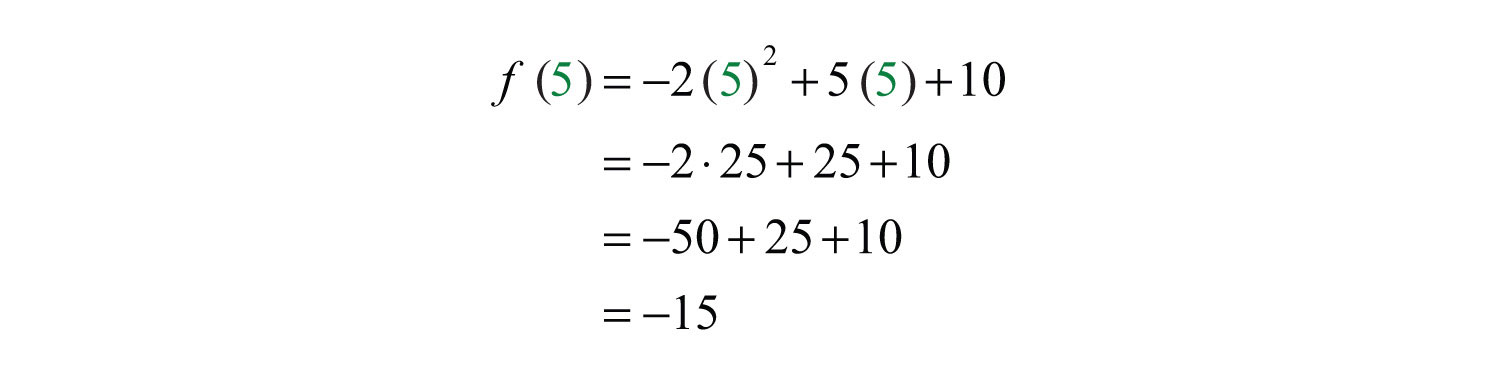
Answer:
Example 10: Calculate: , given .
Solution: Replace the variable x with −1.
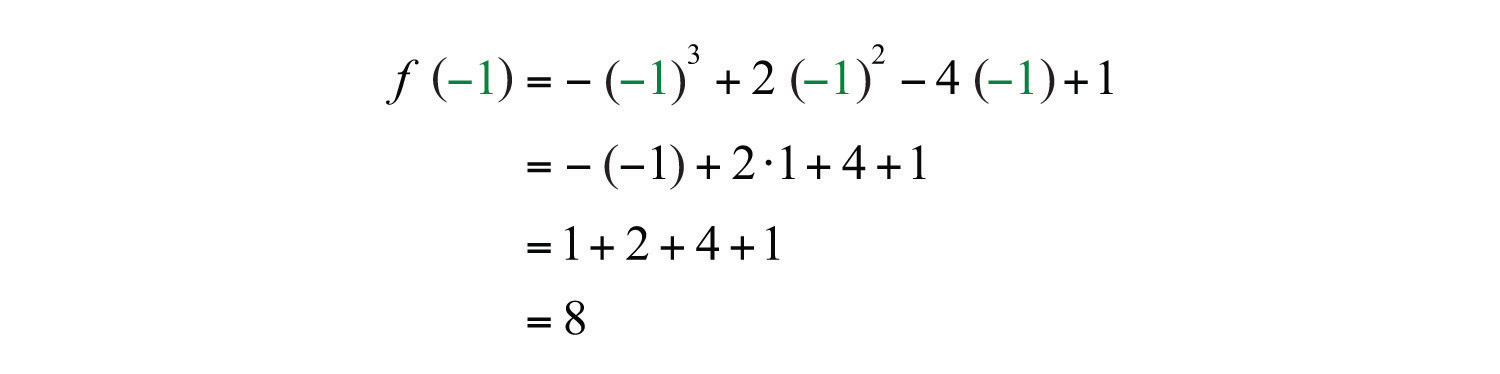
Answer:
Try this! Given , calculate .
Answer:
Video Solution
(click to see video)Key Takeaways
- Polynomials are special algebraic expressions where the terms are the products of real numbers and variables with whole number exponents.
- The degree of a polynomial with one variable is the largest exponent of the variable found in any term.
- The terms of a polynomial are typically arranged in descending order based on the degree of each term.
- When evaluating a polynomial, it is a good practice to replace all variables with parentheses and then substitute the appropriate values.
- All polynomials are functions.
Topic Exercises
Part A: Definitions
Classify the given polynomial as linear, quadratic, or cubic.
1.
2.
3.
4.
5.
6.
Classify the given polynomial as a monomial, binomial, or trinomial and state the degree.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
Write the following polynomials in standard form.
31.
32.
33.
34.
Part B: Evaluating Polynomials
35. Fill in the following chart:
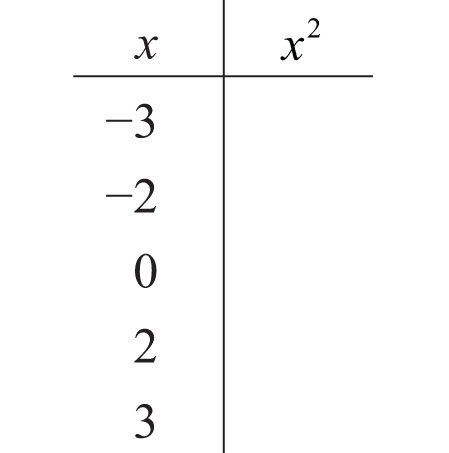
36. Fill in the following chart:
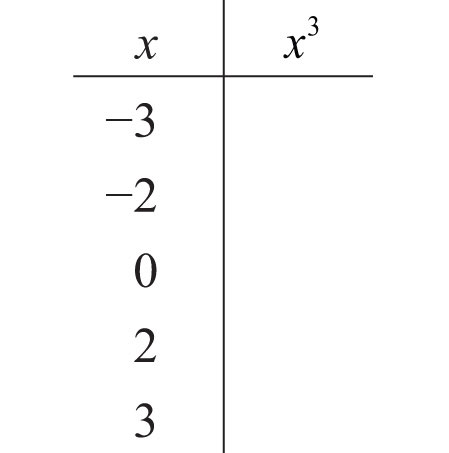
Evaluate.
37. , where
38. , where
39. , where
40. , where
41. , where
42. , where
43. , where
44. , where
45. , where
46. , where
47. , where
48. , where
49. , where and
50. , where and
51. , where and
52. , where and
53. , where and
54. , where and
For each problem, evaluate , given the following values.
55. , , and
56. , , and
57. , ,
58. , , and
59. , , and
60. , , and
The volume of a sphere in cubic units is given by the formula , where r is the radius. For each problem, calculate the volume of a sphere given the following radii.
61. r = 3 centimeters
62. r = 1 centimeter
63. r = 1/2 feet
64. r = 3/2 feet
65. r = 0.15 in
66. r = 1.3 inches
The height in feet of a projectile launched vertically from the ground with an initial velocity in feet per second is given by the formula , where t represents time in seconds. For each problem, calculate the height of the projectile given the following initial velocity and times.
67. , at times t = 0, 1, 2, 3, 4 seconds
68. , at times t = 0, 1, 2, 2.5, 3, 4, 5 seconds
The stopping distance of a car, taking into account an average reaction time, can be estimated with the formula , where d is in feet and v is the speed in miles per hour. For each problem, calculate the stopping distance of a car traveling at the given speeds.
69. 20 miles per hour
70. 40 miles per hour
71. 80 miles per hour
72. 100 miles per hour
Part C: Polynomial Functions
Given the linear function , evaluate each of the following.
73.
74.
75.
76.
77. Find x when .
78. Find x when .
Given the quadratic function , evaluate each of the following.
79.
80.
81.
82.
Given the cubic function , evaluate each of the following.
83.
84.
85.
86.
The height in feet of a projectile launched vertically from the ground with an initial velocity of 128 feet per second is given by the function , where t is in seconds. Calculate and interpret the following.
87.
88.
89.
90.
91.
92.
93.
94.
Part D: Discussion Board Topics
95. Find and share some graphs of polynomial functions.
96. Explain how to convert feet per second into miles per hour.
97. Find and share the names of fourth-degree, fifth-degree, and higher polynomials.
Answers
1: Linear
3: Quadratic
5: Cubic
7: Binomial; degree 3
9: Trinomial; degree 5
11: Monomial; degree 5
13: Trinomial; degree 3
15: Trinomial; degree 5
17: Binomial; degree 1
19: Not a polynomial
21: Monomial; degree 0
23: Trinomial; degree 6
25: Monomial; degree 6
27: Binomial; degree 2
29: Polynomial; degree 14
31:
33:
35:
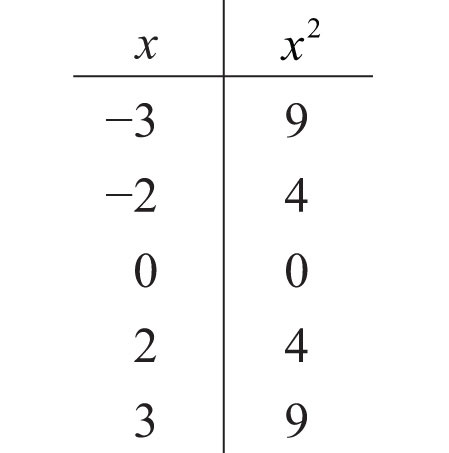
37: 3
39: 1/2
41: −5
43: −3
45: −15
47: 7/6
49: 6
51: −11
53: −35
55: 0
57: 25
59: 14
61: 36π cubic centimeters
63: π/6 cubic feet
65: 0.014 cubic inches
67:
| Time | Height |
|---|---|
| t = 0 seconds | h = 0 feet |
| t = 1 second | h = 48 feet |
| t = 2 seconds | h = 64 feet |
| t = 3 seconds | h = 48 feet |
| t = 4 seconds | h = 0 feet |
69: 21.5 feet
71: 321.5 feet
73: 2
75: 6
77:
79: 19
81: 5
83: −15
85: −1
87: The projectile is launched from the ground.
89: The projectile is 112 feet above the ground 1 second after launch.
91: The projectile is 256 feet above the ground 4 seconds after launch.
93: The projectile is 112 feet above the ground 7 seconds after launch.
5.3 Adding and Subtracting Polynomials
Learning Objectives
- Add polynomials.
- Subtract polynomials.
- Add and subtract polynomial functions.
Adding Polynomials
Recall that we combine like terms, or terms with the same variable part, as a means to simplify expressions. To do this, add the coefficients of the terms to obtain a single term with the same variable part. For example,
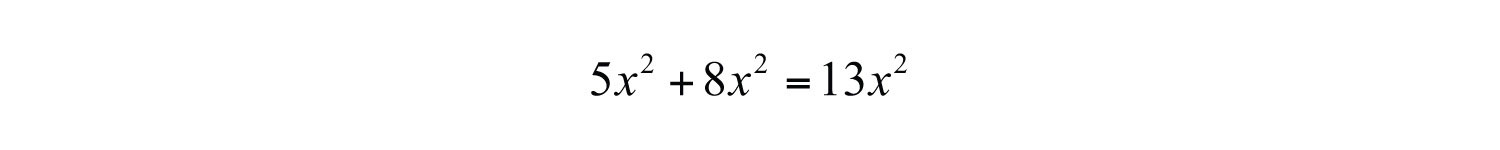
Notice that the variable part, , does not change. This, in addition to the commutative and associative properties of addition, allows us to add polynomialsThe process of combining all like terms of two or more polynomials..
Example 1: Add: .
Solution: The property , which was derived using the distributive property, allows us to remove the parentheses so that we can add like terms.
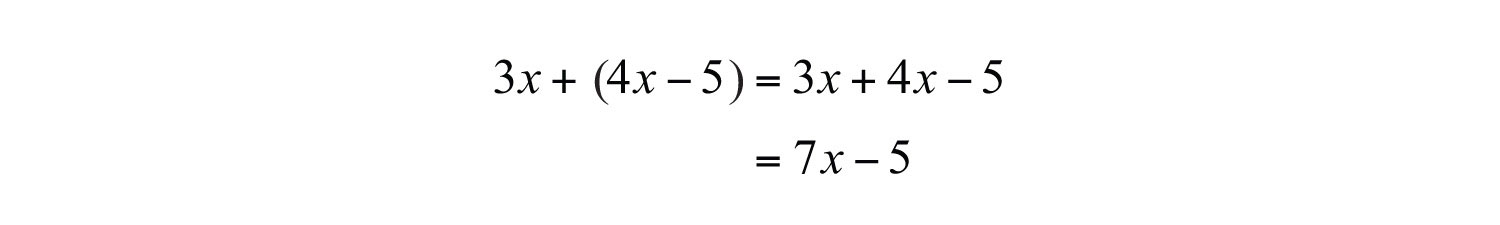
Answer:
Example 2: Add: .
Solution: Remove the parentheses and then combine like terms.
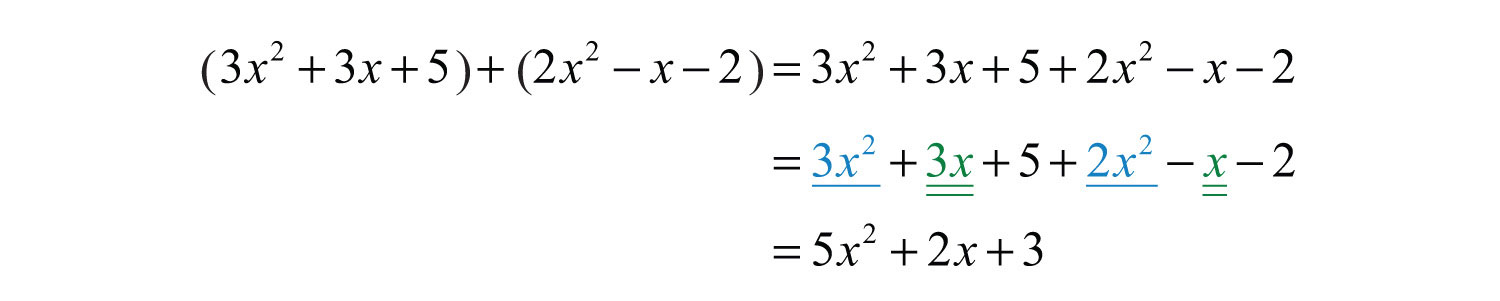
Answer:
Example 3: Add: .
Solution: Remember that the variable parts have to be exactly the same before we can add the coefficients.
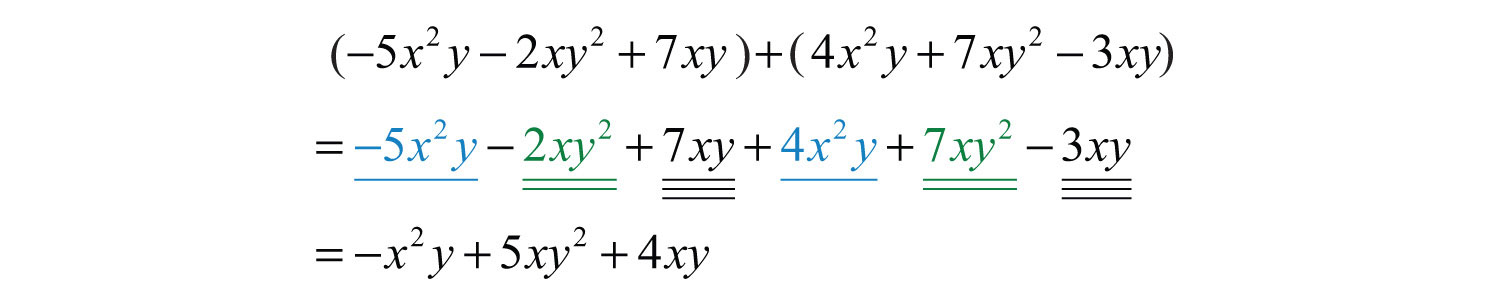
Answer:
It is common practice to present the terms of the simplified polynomial expression in descending order based on their degree. In other words, we typically present polynomials in standard form, with terms in order from highest to lowest degree.
Example 4: Add: .
Solution:
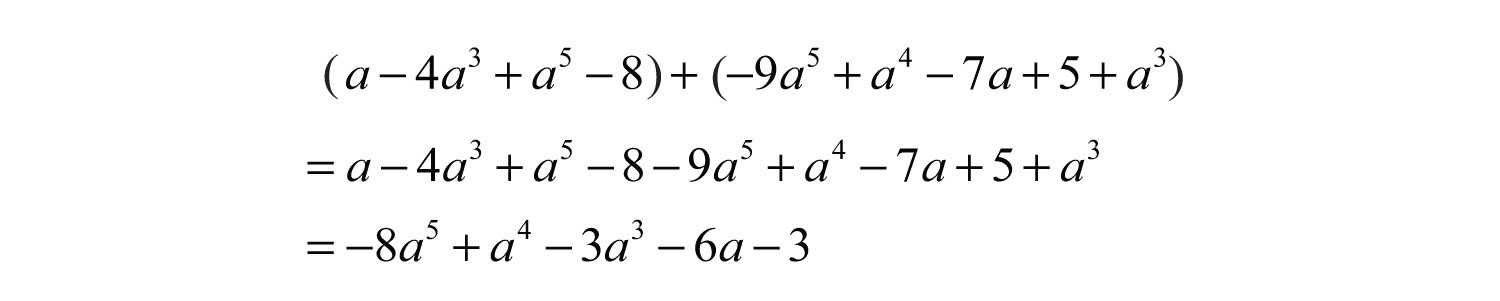
Answer:
Try this! Add: .
Answer:
Video Solution
(click to see video)Subtracting Polynomials
When subtracting polynomialsThe process of subtracting all the terms of one polynomial from another and combining like terms., we see that the parentheses become very important. Recall that the distributive property allowed us to derive the following:
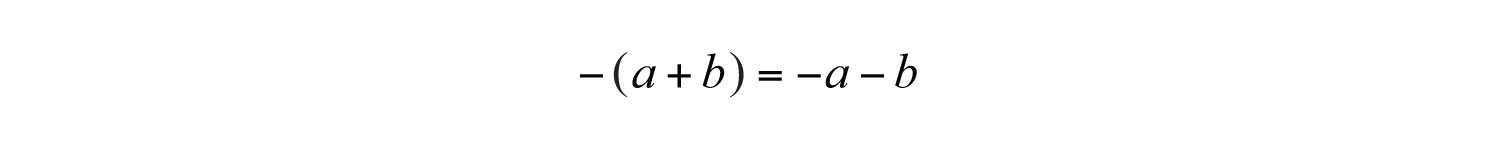
In other words, when subtracting an algebraic expression, we remove the parentheses by subtracting each term.
Example 5: Subtract: .
Solution: Subtract each term within the parentheses and then combine like terms.
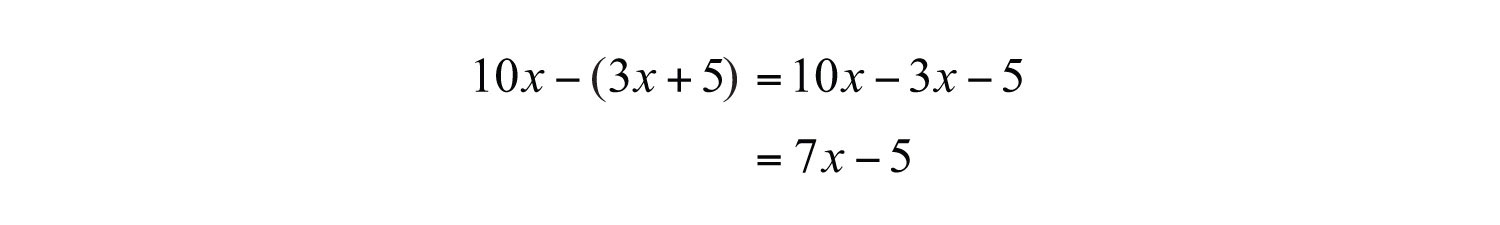
Answer:
Subtracting a quantity is equivalent to multiplying it by −1.
Example 6: Subtract: .
Solution: Distribute the −1, remove the parentheses, and then combine like terms.
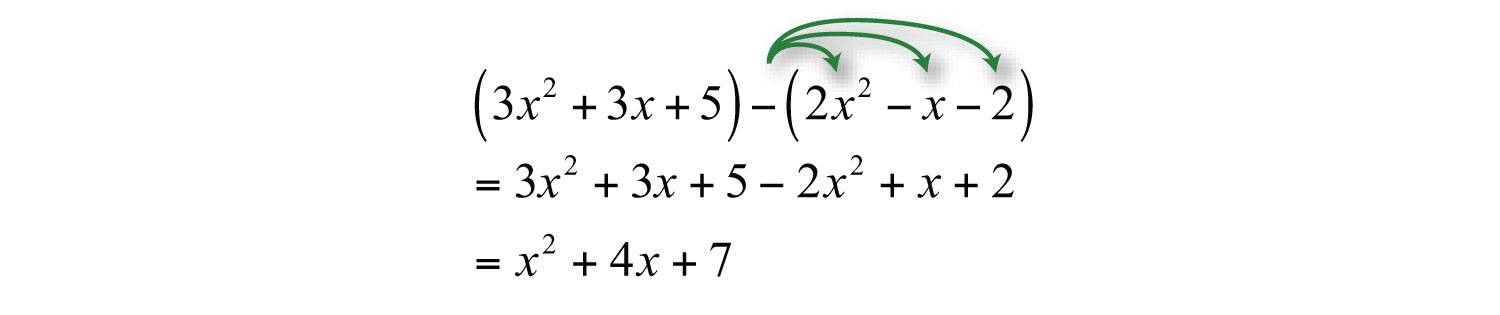
Answer:
Multiplying the terms of a polynomial by −1 changes all the signs.
Example 7: Subtract: .
Solution: Distribute the −1, remove the parentheses, and then combine like terms.
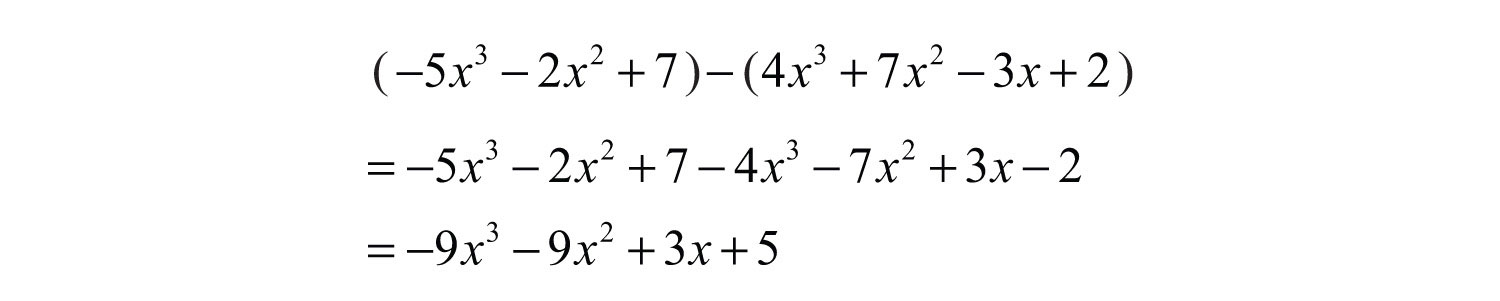
Answer:
Example 8: Subtract from .
Solution: Since subtraction is not commutative, we must take care to set up the difference correctly. First, write the quantity ; from this, subtract the quantity .
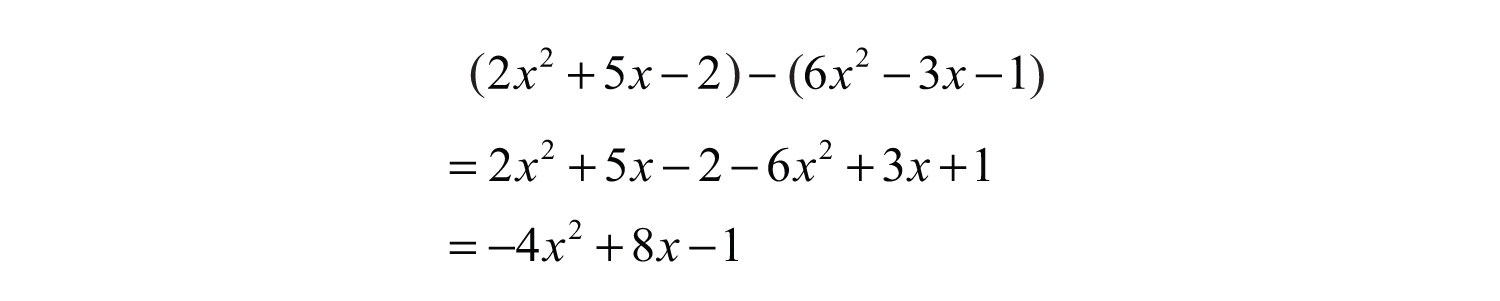
Answer:
Example 9: Simplify: .
Solution: Apply the distributive property, remove the parentheses, and then combine like terms.
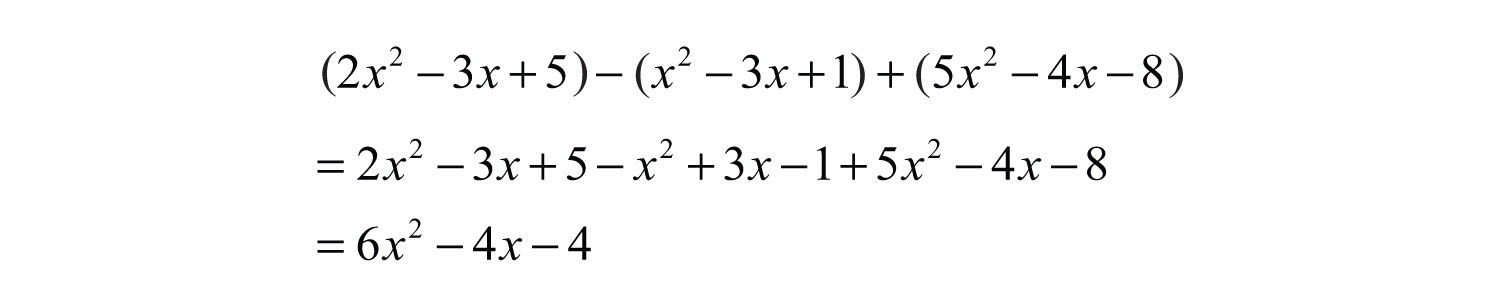
Answer:
Try this! Subtract: .
Answer:
Video Solution
(click to see video)Adding and Subtracting Polynomial Functions
We use function notation to indicate addition and subtraction of functions as follows:
| Addition of functions: | |
| Subtraction of functions: |
When using function notation, be careful to group the entire function and add or subtract accordingly.
Example 10: Calculate: , given and .
Solution: The notation indicates that you should add the functions and collect like terms.
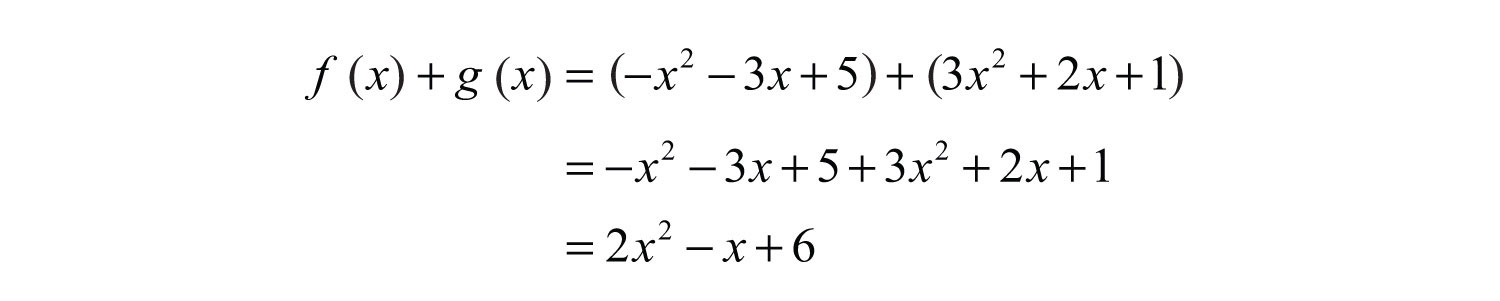
Answer:
Example 11: Calculate: , given and .
Solution: The notation indicates that you should subtract the functions :
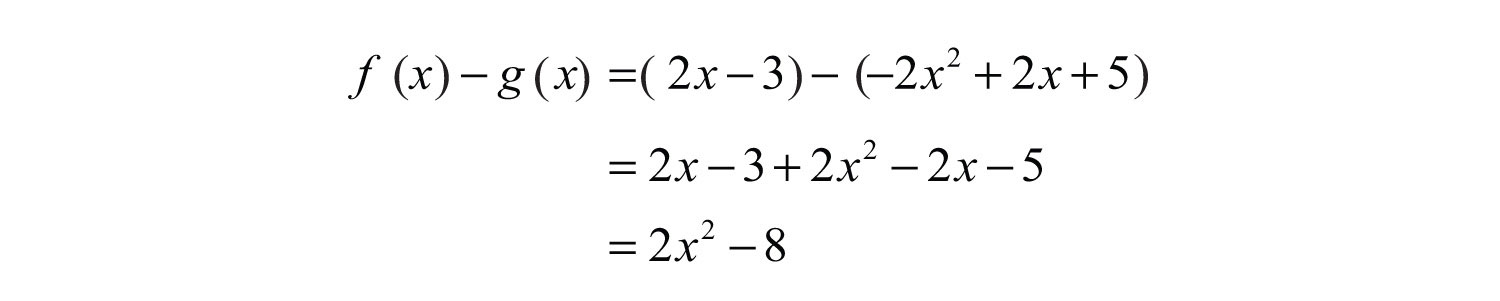
Answer:
We may be asked to evaluate the sum or difference of two functions. We have the option to first find the sum or difference and use the resulting function to evaluate for the given variable, or to first evaluate each function and then find the sum or difference.
Example 12: Calculate: , given and .
Solution: First, find .
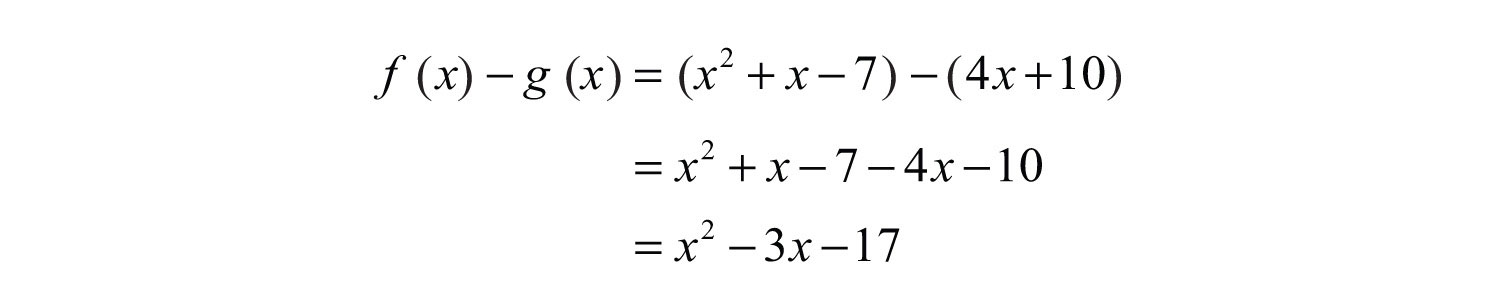
Therefore,
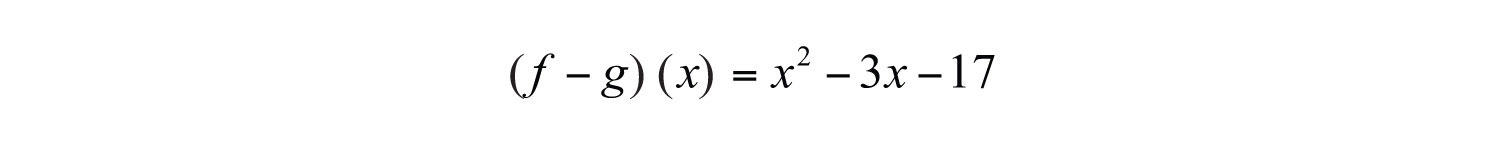
Next, substitute 5 for the variable x.
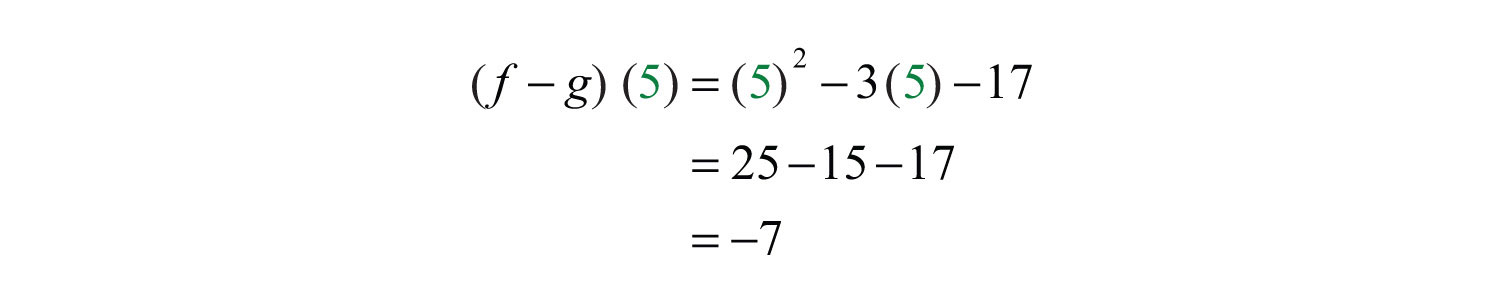
Answer:
Alternate Solution: Since , we can find and and then subtract the results.
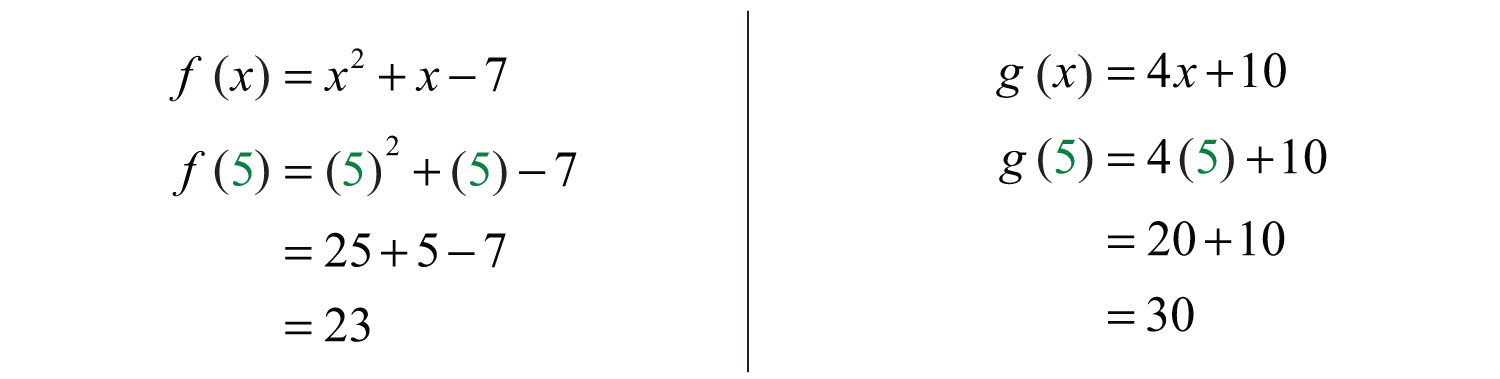
Therefore, we have
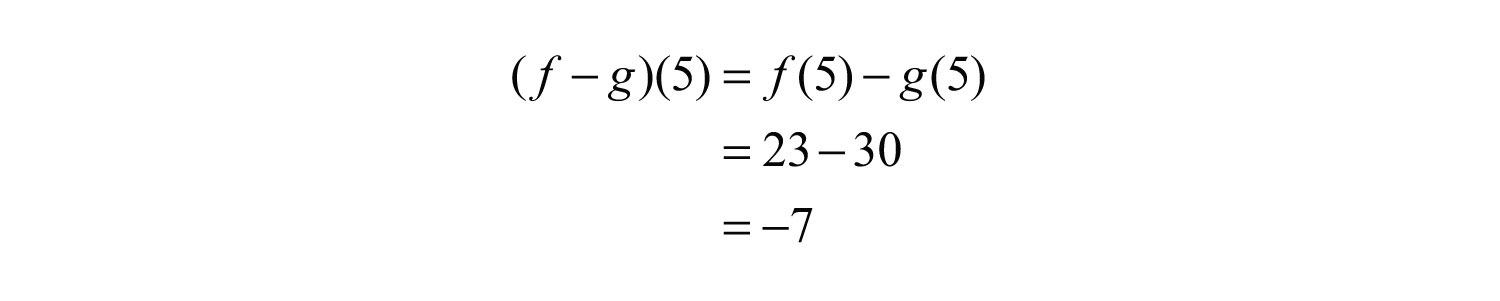
Answer:
Key Takeaways
- When adding polynomials, remove the associated parentheses and then combine like terms.
- When subtracting polynomials, distribute the −1 and subtract all the terms before removing the parentheses and combining like terms.
- The notation indicates that you add the functions.
- The notation indicates that you subtract the functions.
Topic Exercises
Part A: Addition of Polynomials
Add.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25. Find the sum of and .
26. Find the sum of and .
27. Find the sum of and .
28. Find the sum of and .
29. Find the sum of and .
30. Find the sum of and .
Part B: Subtraction of Polynomials
Subtract.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51. Subtract from .
52. Subtract from .
53. Find the difference of and .
54. Find the difference of and .
55. The cost in dollars of producing customized coffee mugs with a company logo is given by the formula , where x is the number of cups produced. The revenue from selling the cups in the company store is given by , where x is the number of units sold.
a. Find a formula for the profit. (profit = revenue − cost)
b. Find the profit from producing and selling 100 mugs in the company store.
56. The cost in dollars of producing sweat shirts is given by the formula , where C is the cost and q represents the quantity produced. The revenue generated by selling the sweat shirts for $37 each is given by , where q represents the quantity sold. Determine the profit generated if 125 sweat shirts are produced and sold.
57. The outer radius of a washer is 3 times the radius of the hole.
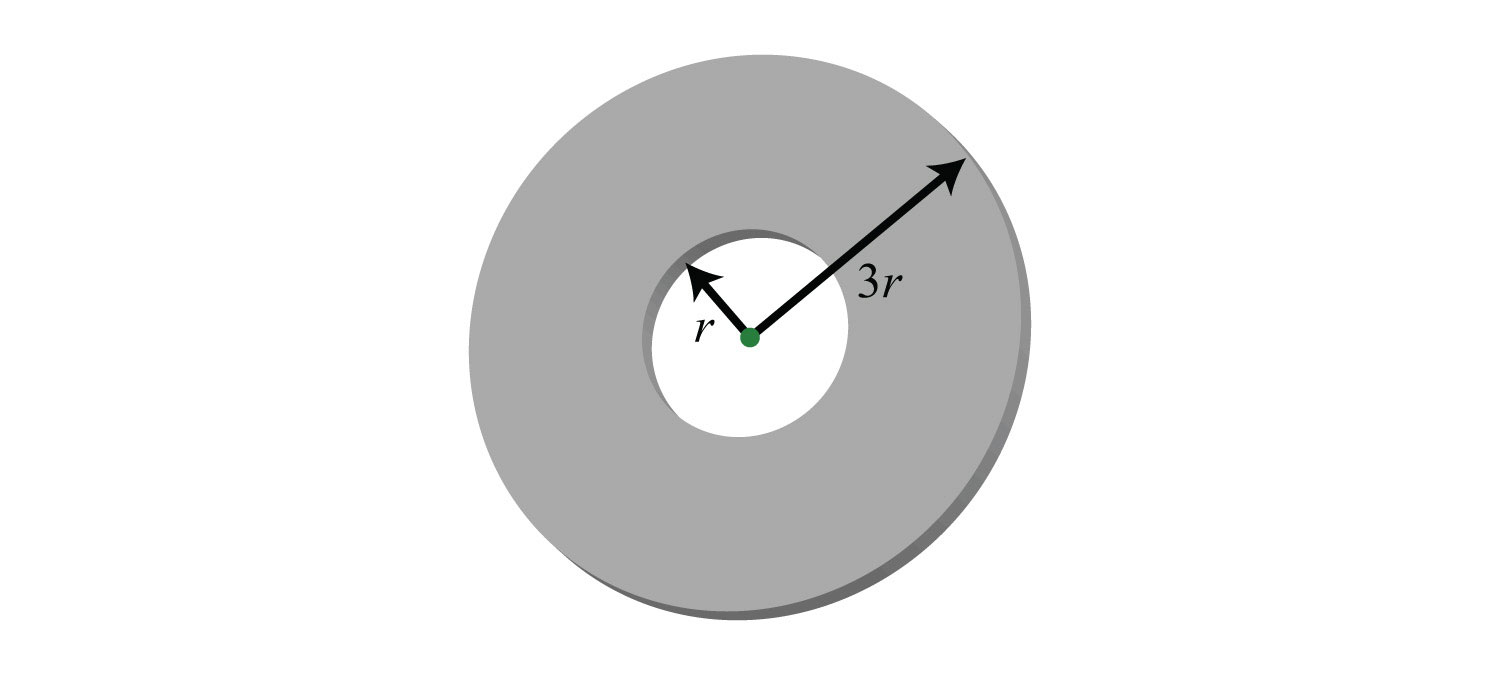
a. Derive a formula for the area of the face of the washer.
b. What is the area of the washer if the hole has a diameter of 10 millimeters?
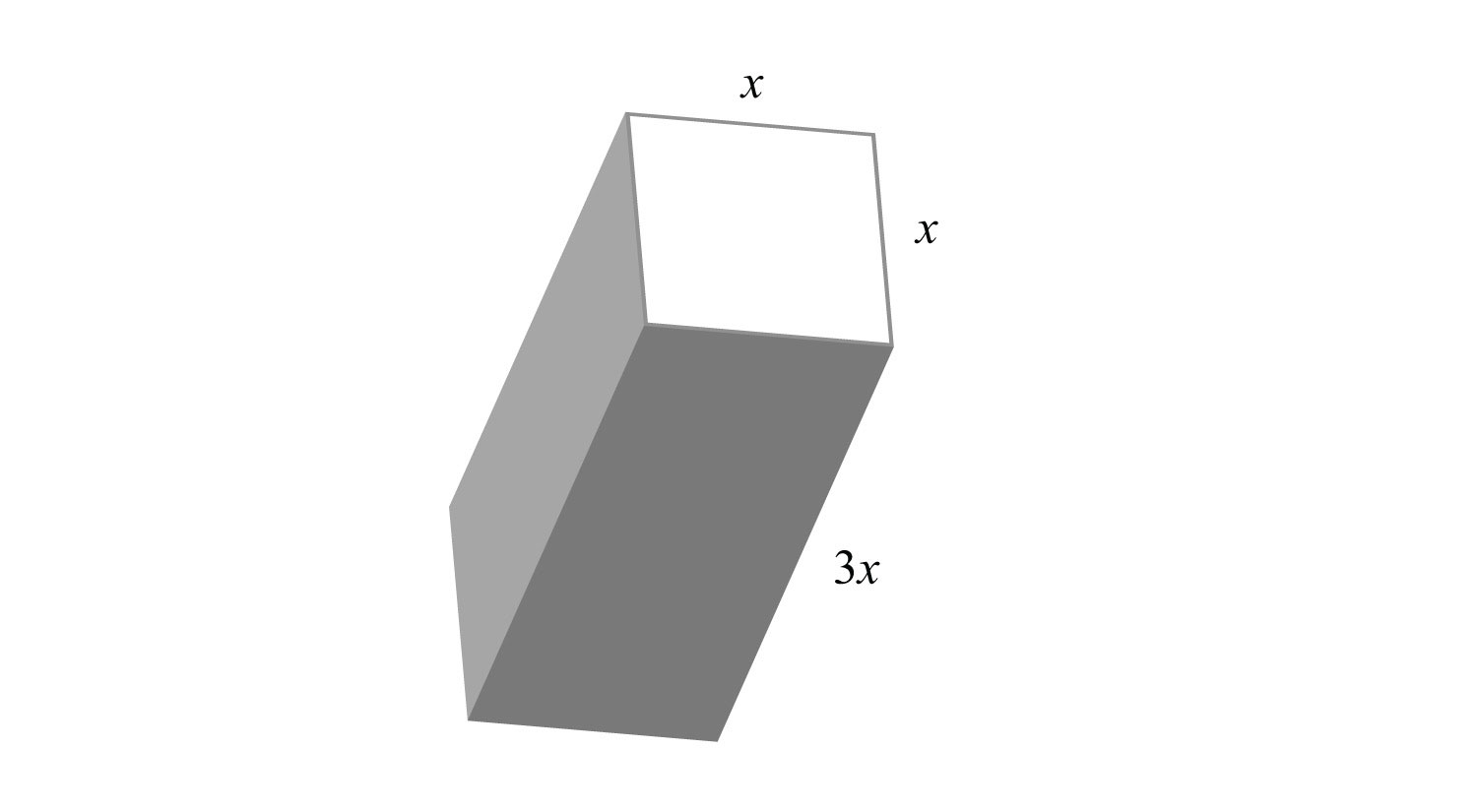
58. Derive a formula for the surface area of the following rectangular solid.
Part C: Addition and Subtraction of Polynomial
Simplify.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
Part D: Addition and Subtraction of Polynomial Functions
Find and , given the following functions.
71. and
72. and
73. and
74. and
75. and
76. and
Given and , find the following.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
Given and , find the following.
89.
90.
91.
92.
93.
94.
95.
96.
Answers
1:
3:
5:
7:
9:
11:
13:
15:
17:
19:
21:
23:
25:
27:
29:
31:
33:
35:
37:
39:
41:
43:
45:
47:
49:
51:
53:
55: a. ; b. $340
57: a. ; b. 628.32 square millimeters
59:
61: 6
63:
65:
67:
69:
71: and
73: and
75: and
77:
79:
81:
83:
85:
87:
89:
91:
93:
95:
5.4 Multiplying Polynomials
Learning Objectives
- Multiply a polynomial by a monomial.
- Multiply a polynomial by a binomial.
- Multiply a polynomial by any size polynomial.
- Recognize and calculate special products.
- Multiply polynomial functions.
Multiplying by a Monomial
Recall the product rule for exponents: if m and n are positive integers, then
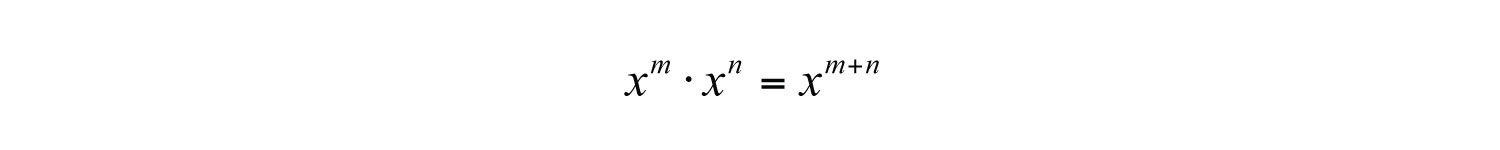
In other words, when multiplying two expressions with the same base, add the exponents. This rule applies when multiplying a monomial by a monomial. To find the product of monomials, multiply the coefficients and add the exponents of variable factors with the same base. For example,
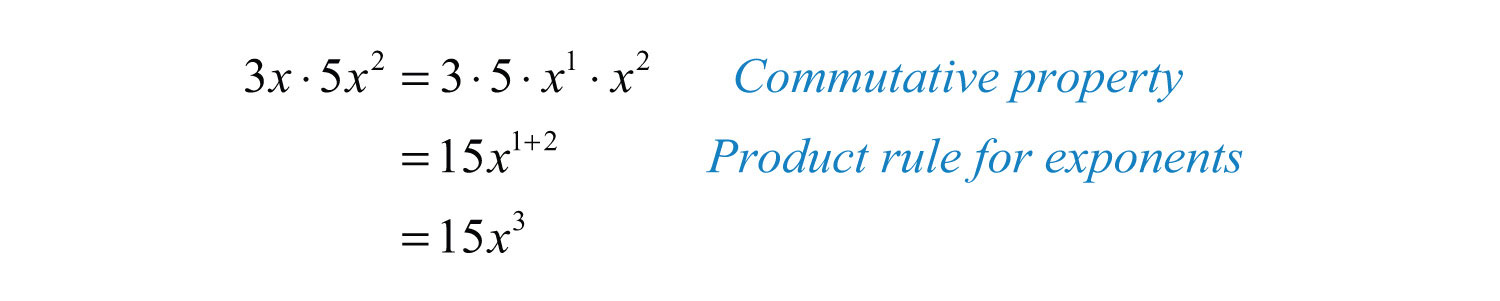
To multiply a polynomial by a monomial, apply the distributive property and then simplify each term.
Example 1: Multiply: .
Solution: In this case, multiply the monomial, , by the binomial, . Apply the distributive property and then simplify.
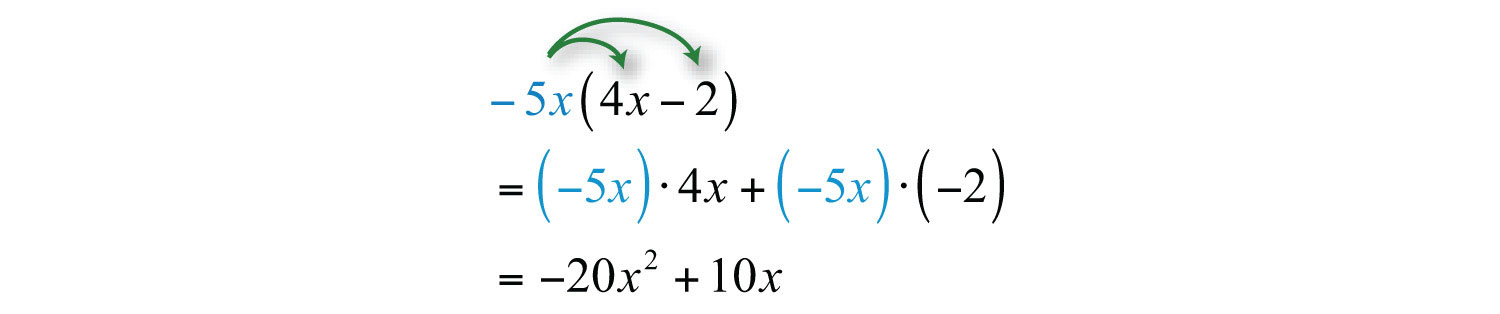
Answer:
Example 2: Multiply: .
Solution: Apply the distributive property and then simplify.
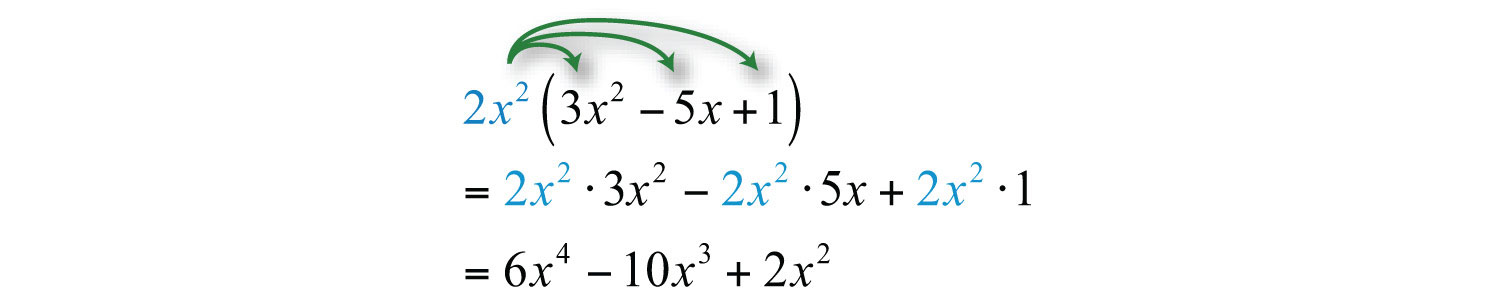
Answer:
Example 3: Multiply: .
Solution:
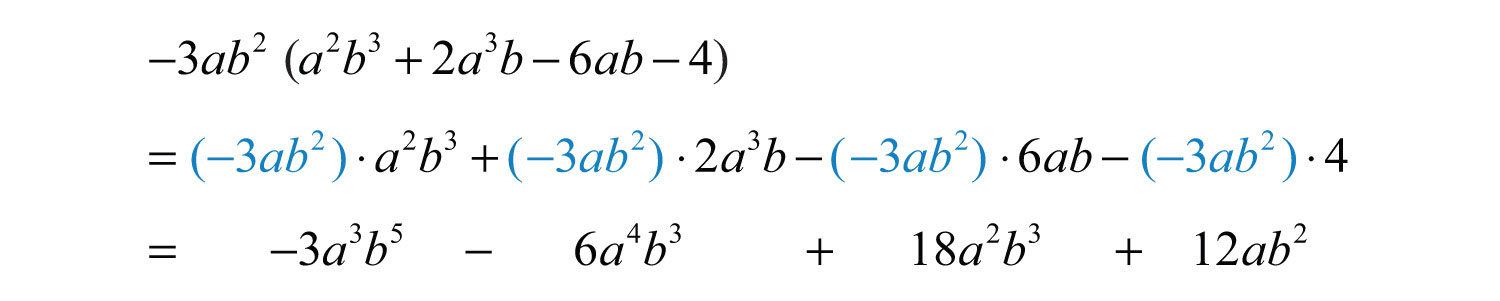
Answer:
To summarize, multiplying a polynomial by a monomial involves the distributive property and the product rule for exponents. Multiply all of the terms of the polynomial by the monomial. For each term, multiply the coefficients and add exponents of variables where the bases are the same.
Try this! Multiply: .
Answer:
Video Solution
(click to see video)Multiplying by a Binomial
In the same way that we used the distributive property to find the product of a monomial and a binomial, we will use it to to find the product of two binomials.
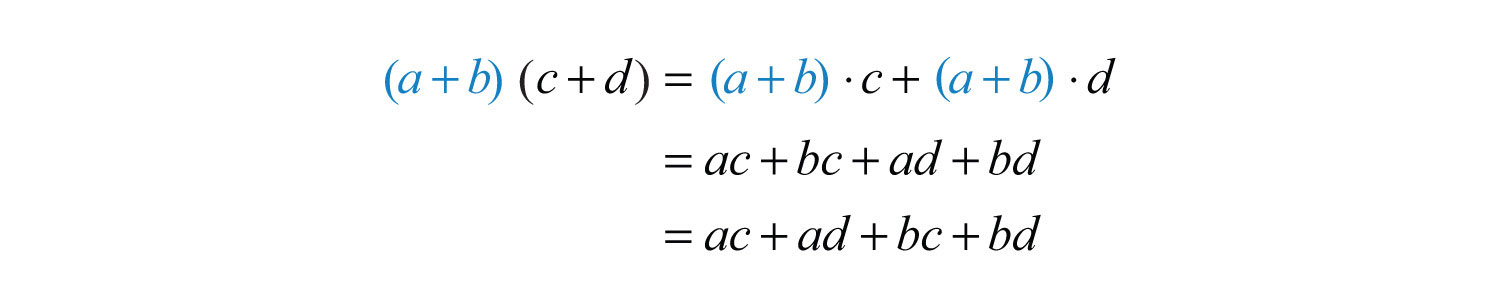
Here we apply the distributive property multiple times to produce the final result. This same result is obtained in one step if we apply the distributive property to a and b separately as follows:
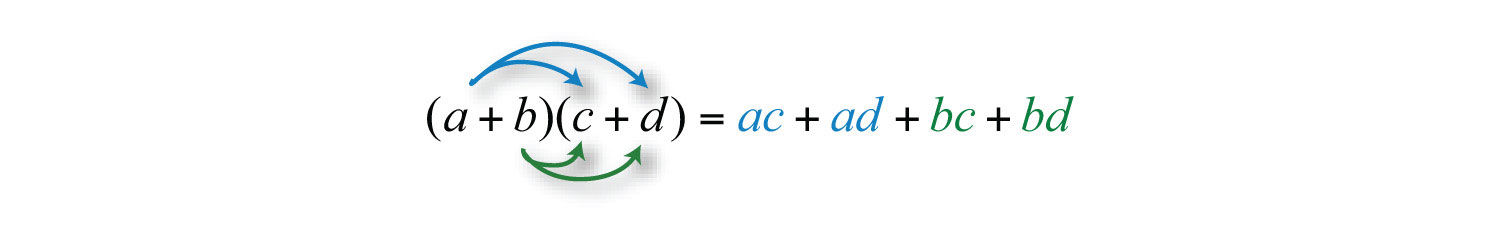
This is often called the FOILWhen multiplying binomials we apply the distributive property multiple times in such a way as to multiply the first terms, outer terms, inner terms, and last terms. method. We add the products of the first terms of each binomial ac, the outer terms ad, the inner terms bc, and finally the last terms bd. This mnemonic device only works for products of binomials; hence it is best to just remember that the distributive property applies.
Example 4: Multiply: .
Solution: Distribute and then distribute 3.
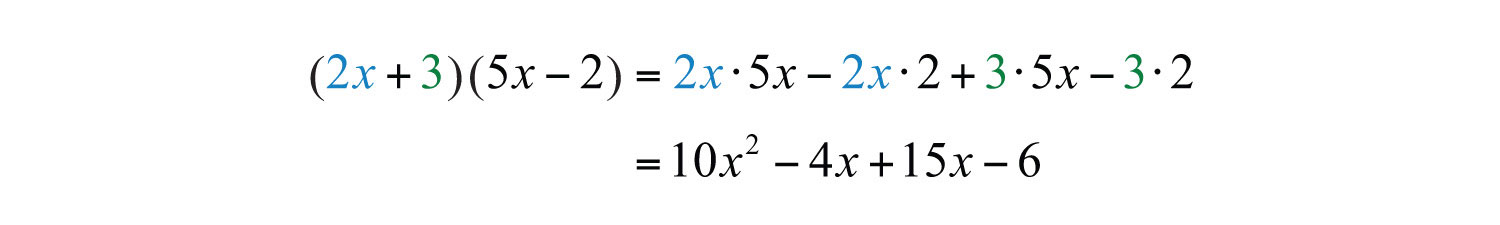
Simplify by combining like terms.
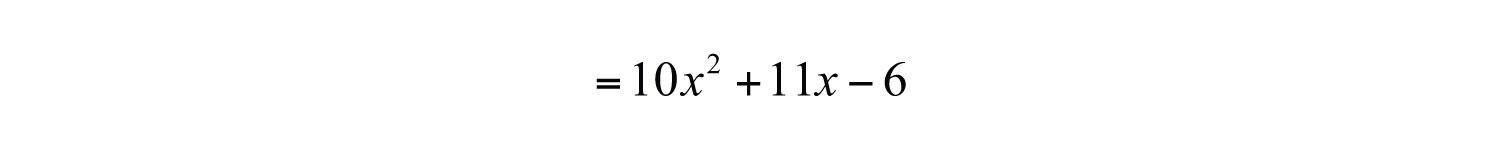
Answer:
Example 5: Multiply: .
Solution: Distribute and then distribute .
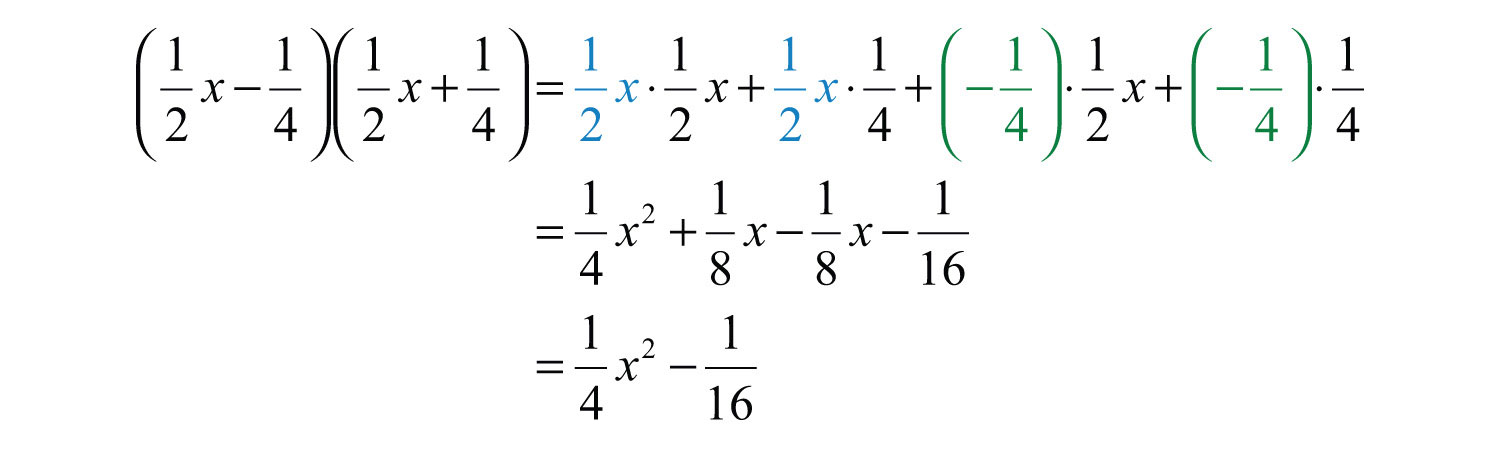
Answer:
Example 6: Multiply: .
Solution:
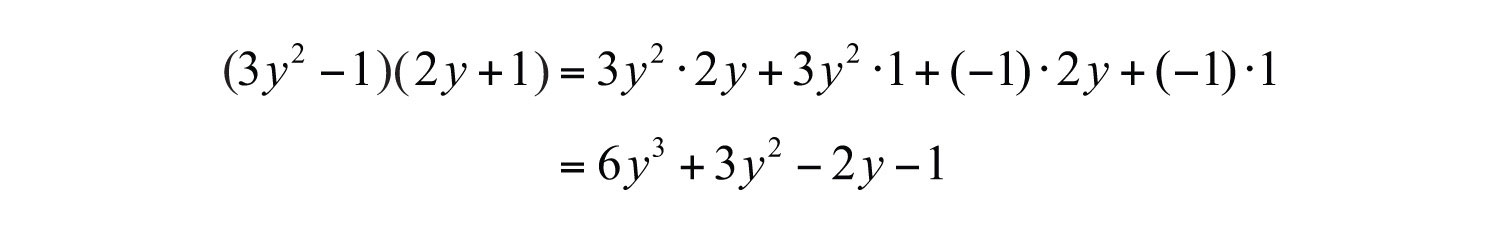
Answer:
After applying the distributive property, combine any like terms.
Example 7: Multiply: .
Solution: After multiplying each term of the trinomial by and , simplify.
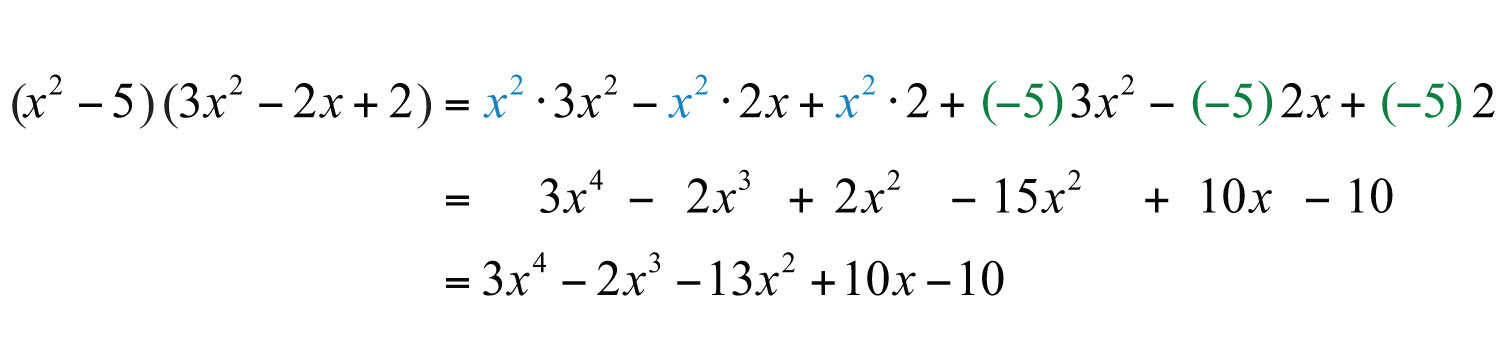
Answer:
Example 8: Multiply: .
Solution: Perform one product at a time.
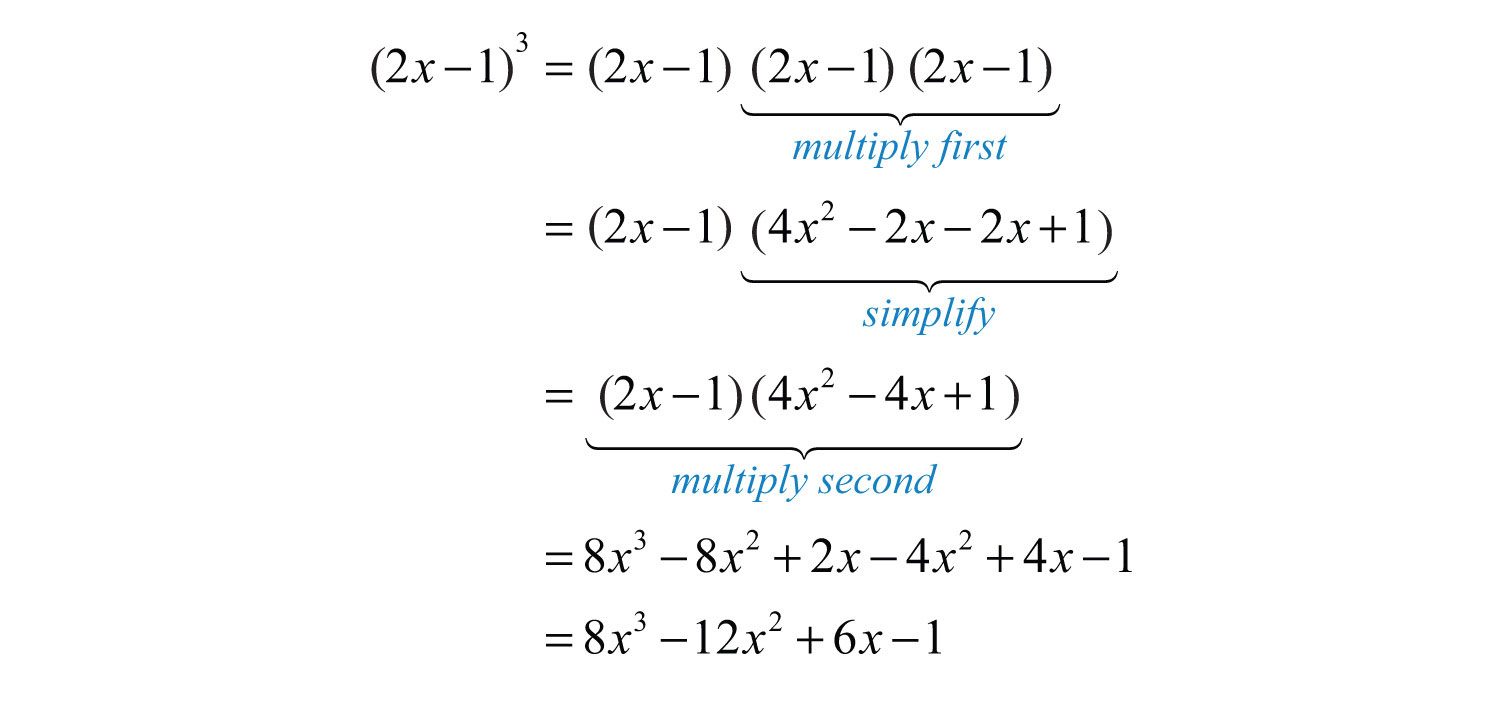
Answer:
At this point, it is worth pointing out a common mistake:
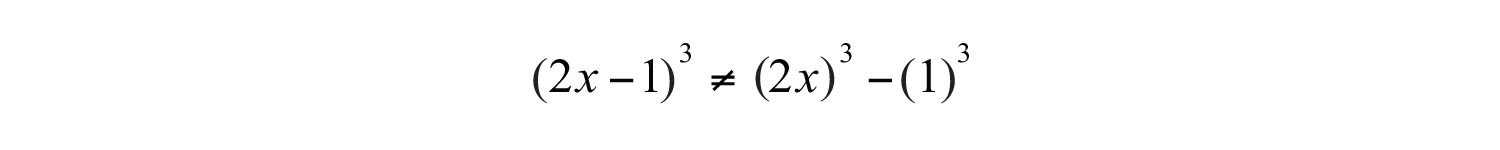
The confusion comes from the product to a power rule of exponents, where we apply the power to all factors. Since there are two terms within the parentheses, that rule does not apply. Care should be taken to understand what is different in the following two examples:
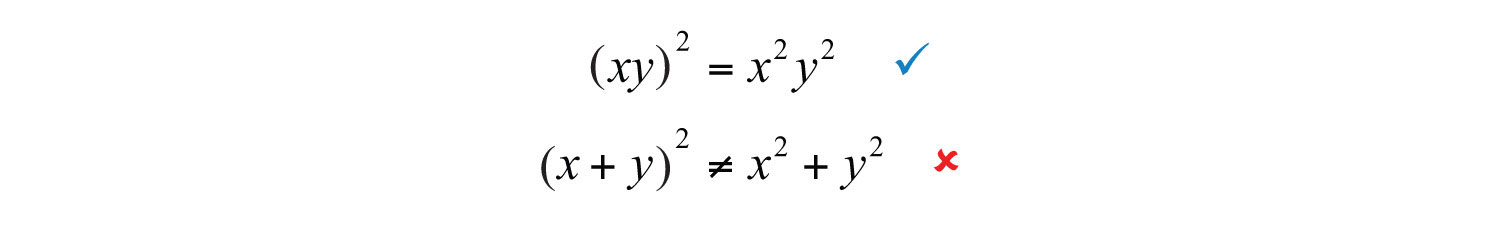
Try this! Multiply: .
Answer:
Video Solution
(click to see video)Product of Polynomials
When multiplying polynomials, we apply the distributive property many times. Multiply all of the terms of each polynomial and then combine like terms.
Example 9: Multiply: .
Solution: Multiply each term of the first trinomial by each term of the second trinomial and then combine like terms.
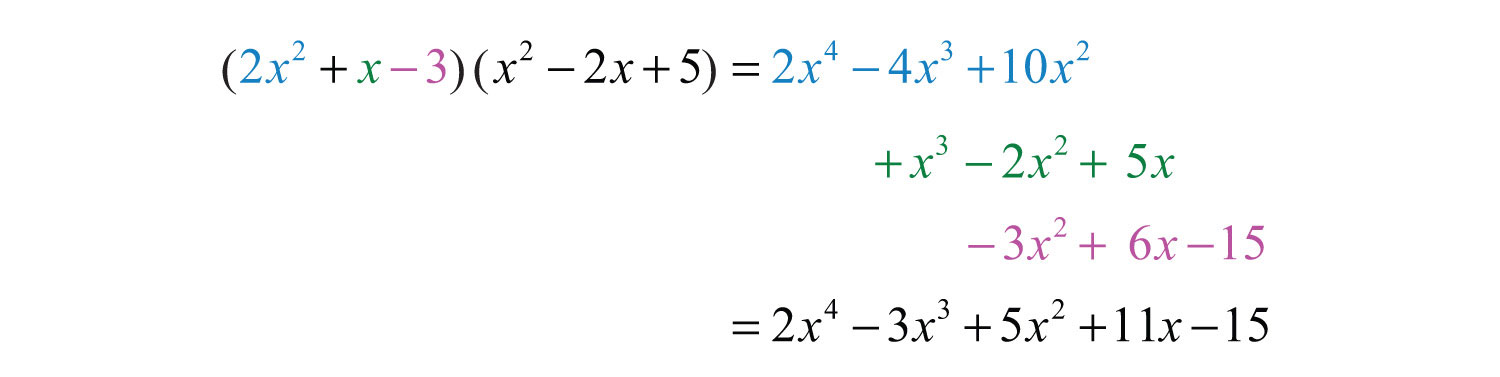
Aligning like terms in columns, as we have here, aids in the simplification process.
Answer:
Notice that when multiplying a trinomial by a trinomial, we obtain nine terms before simplifying. In fact, when multiplying an n-term polynomial by an m-term polynomial, we will obtain n × m terms.
In the previous example, we were asked to multiply and found that
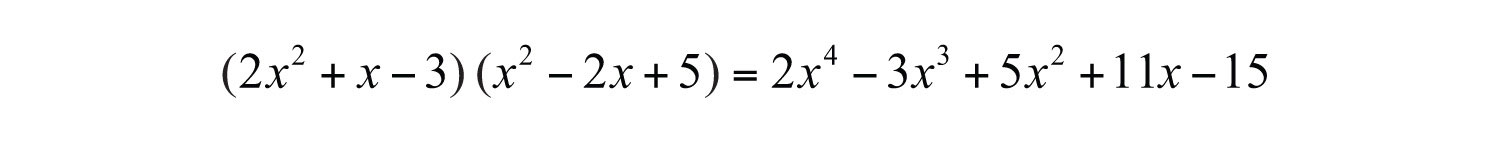
Because it is easy to make a small calculation error, it is a good practice to trace through the steps mentally to verify that the operations were performed correctly. Alternatively, we can check by evaluatingWe can be fairly certain that we have multiplied the polynomials correctly if we check that a few values evaluate to the same results in the original expression and in the answer. any value for x in both expressions to verify that the results are the same. Here we choose x = 2:
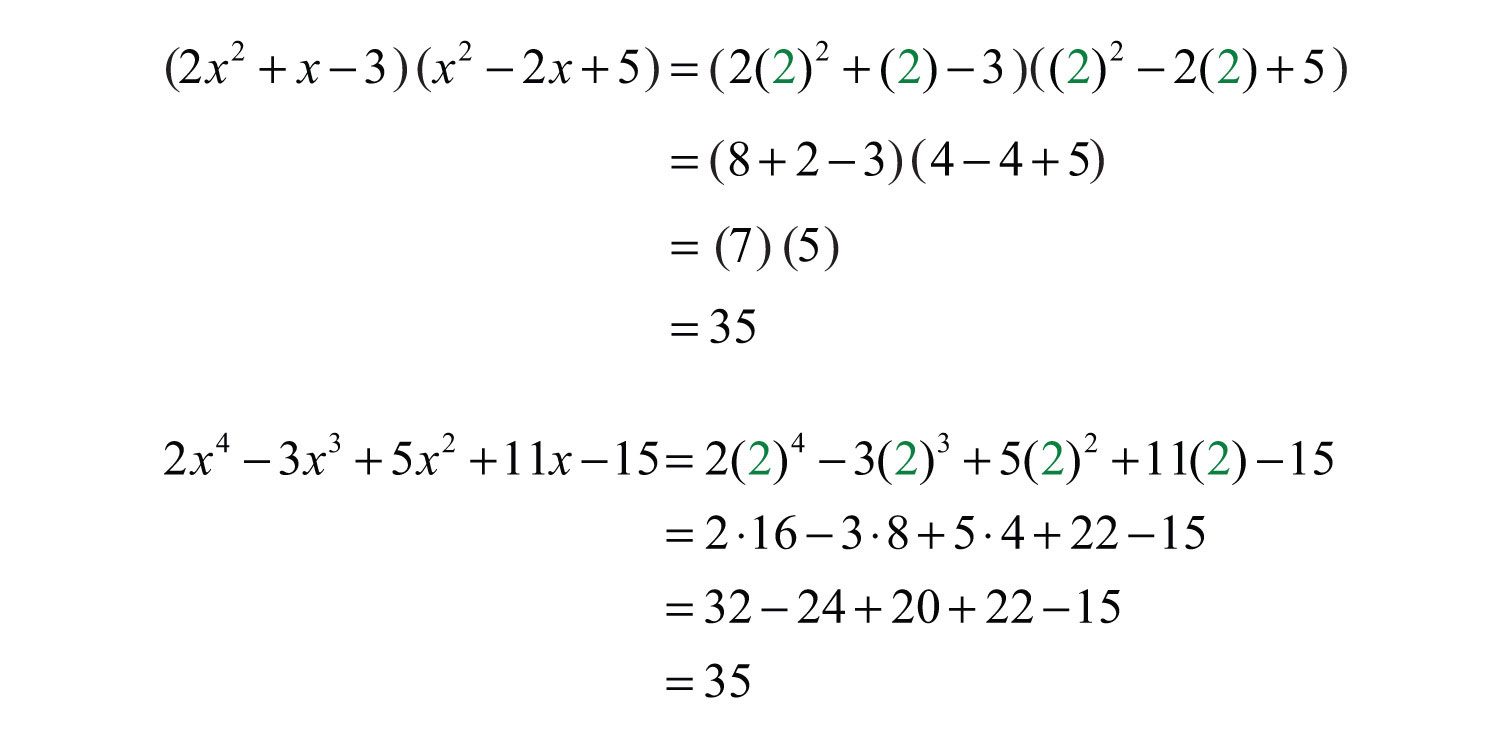
Because the results could coincidentally be the same, a check by evaluating does not necessarily prove that we have multiplied correctly. However, after verifying a few values, we can be fairly confident that the product is correct.
Try this! Multiply: .
Answer:
Video Solution
(click to see video)Special Products
In this section, the goal is to recognize certain special products that occur often in our study of algebra. We will develop three formulas that will be very useful as we move along. The three should be memorized. We begin by considering the following two calculations:
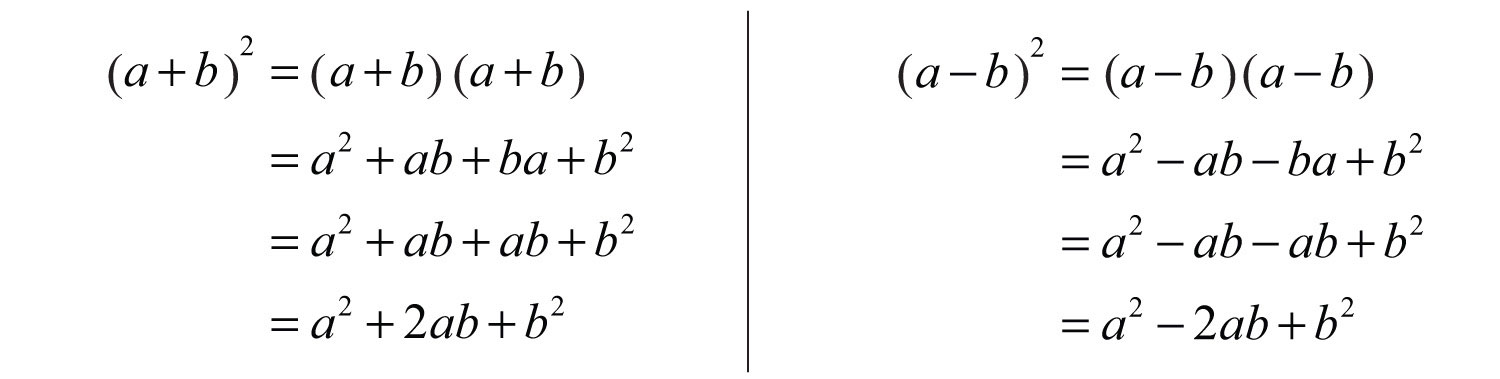
This leads us to two formulas that describe perfect square trinomialsThe trinomials obtained by squaring the binomials and :
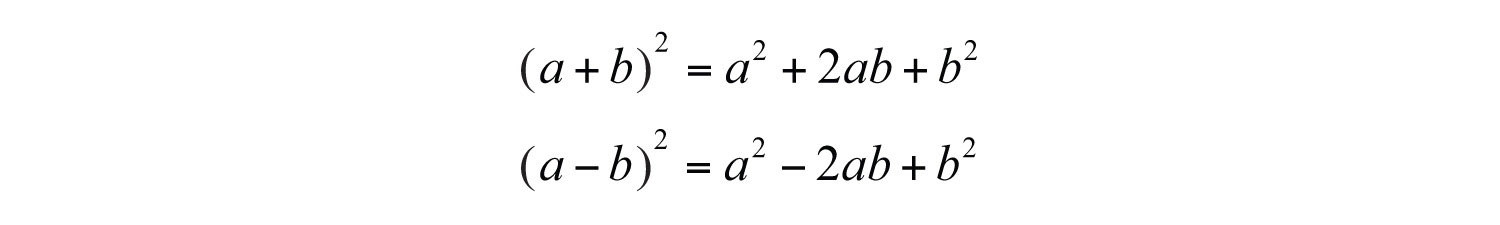
We can use these formulas to quickly square a binomial.
Example 10: Multiply: .
Solution: Here and . Apply the formula:
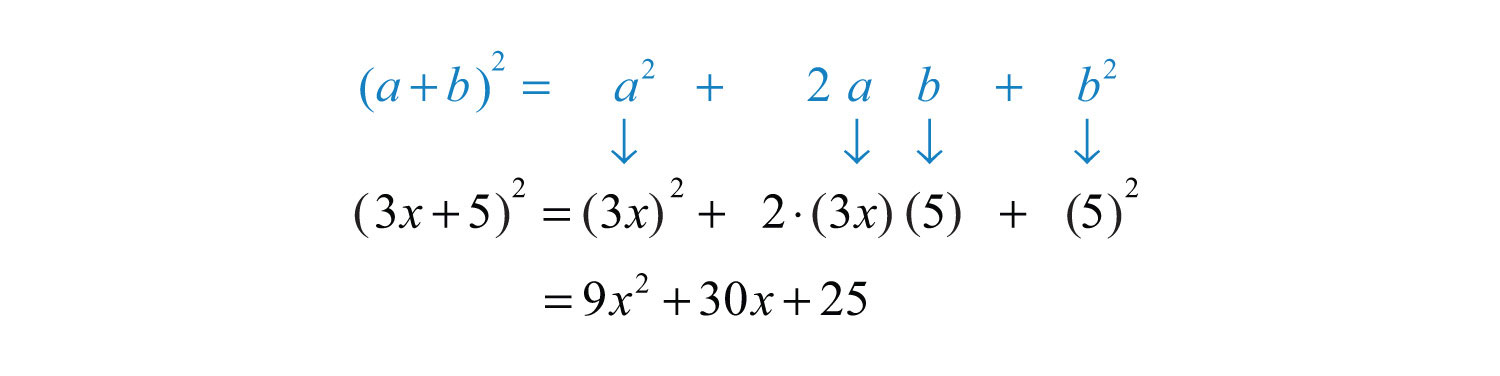
Answer:
This process should become routine enough to be performed mentally.
Example 11: Multiply: .
Solution: Here and . Apply the appropriate formula as follows:
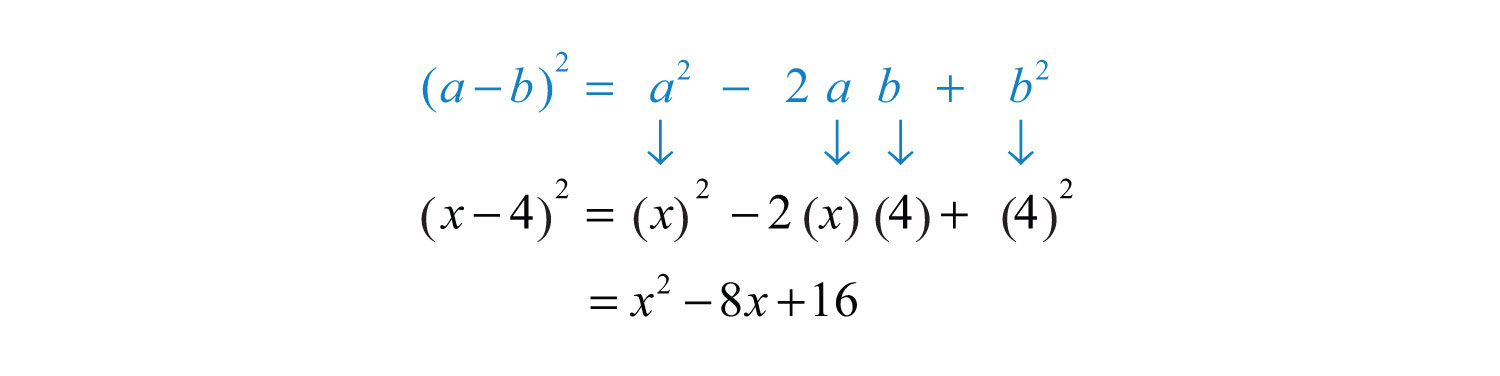
Answer:
Our third special product follows:
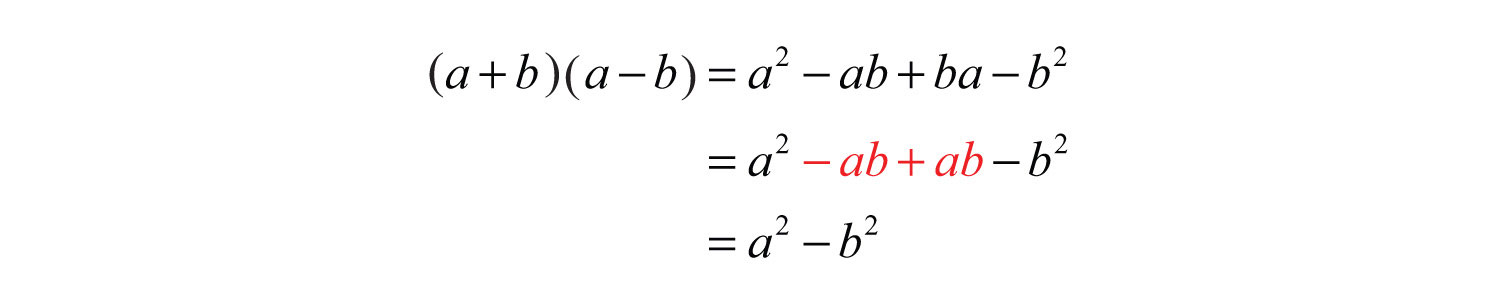
This product is called difference of squares where a and b represent algebraic expressions.:
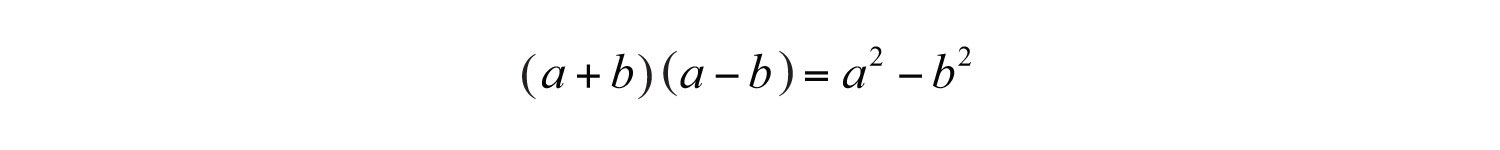
The binomials and are called conjugate binomialsThe binomials and .. Therefore, when conjugate binomials are multiplied, the middle term eliminates, and the product is itself a binomial.
Example 12: Multiply: .
Solution:
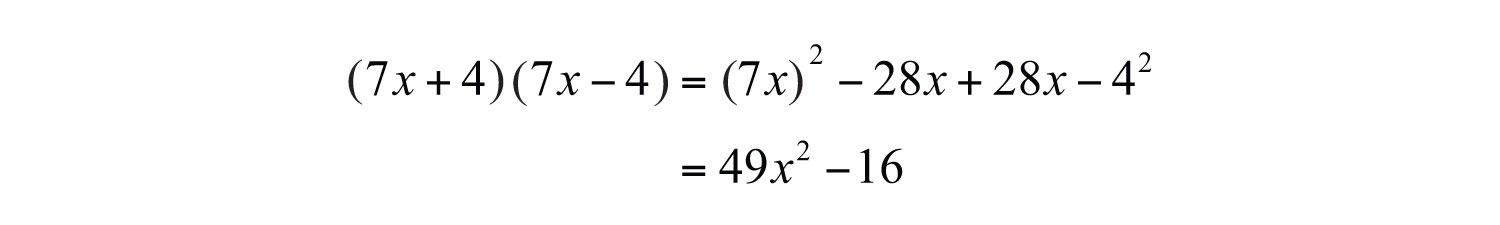
Answer:
Try this! Multiply: .
Answer:
Video Solution
(click to see video)Multiplying Polynomial Functions
We use function notation to indicate multiplication as follows:
| Multiplication of functions: |
Example 13: Calculate: , given and .
Solution: Multiply all terms of the trinomial by the monomial function .
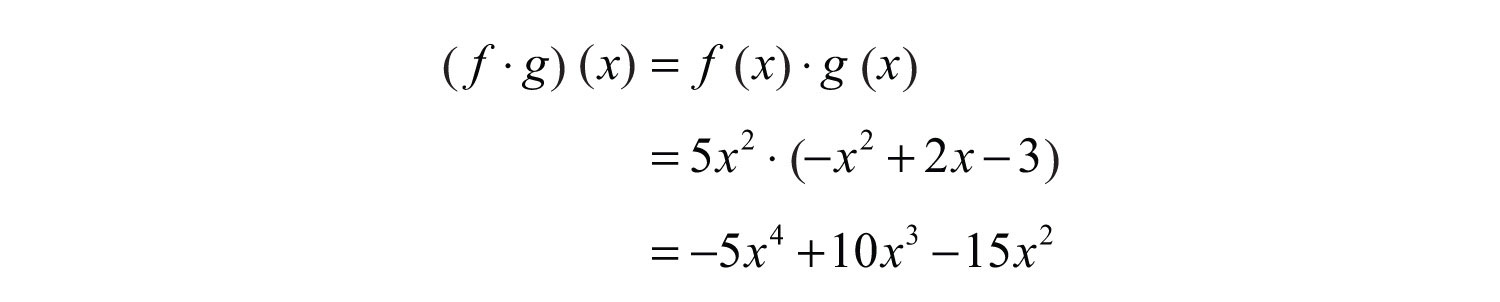
Answer:
Example 14: Calculate: , given and .
Solution: First, determine .
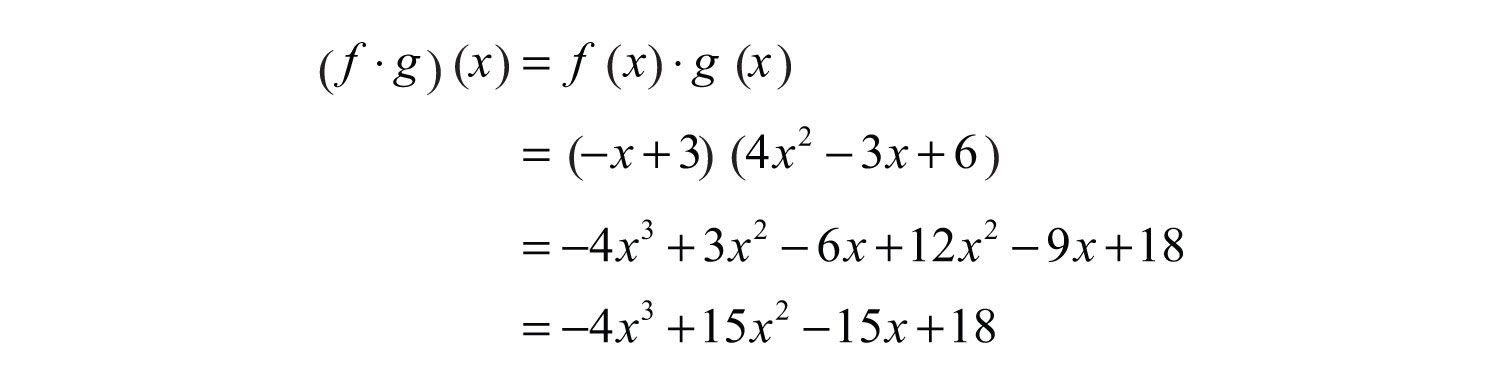
We have
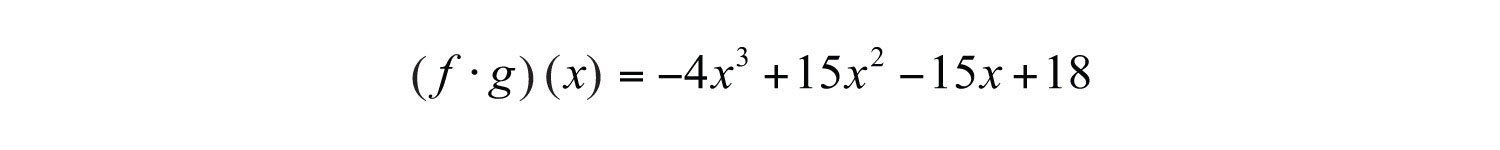
Next, substitute −1 for the variable x.
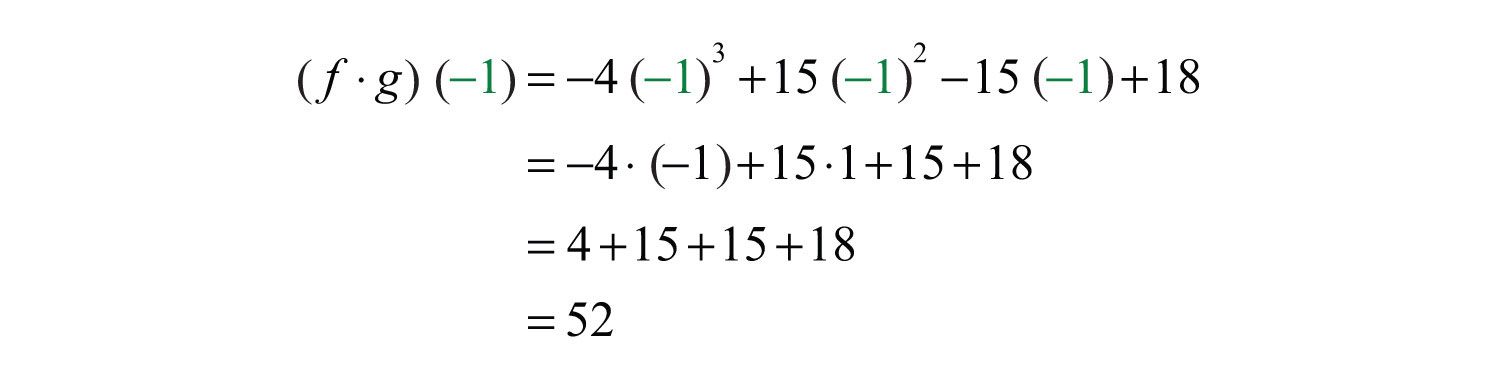
Answer:
Because , we could alternatively calculate and separately and then multiply the results (try this as an exercise). However, if we were asked to evaluate multiple values for the function , it would be best to first determine the general form, as we have in the previous example.
Key Takeaways
- To multiply a polynomial by a monomial, apply the distributive property and then simplify each of the resulting terms.
- To multiply polynomials, multiply each term in the first polynomial with each term in the second polynomial. Then combine like terms.
- The product of an n-term polynomial and an m-term polynomial results in an m × n term polynomial before like terms are combined.
- Check results by evaluating values in the original expression and in your answer to verify that the results are the same.
- Use the formulas for special products to quickly multiply binomials that occur often in algebra.
Topic Exercises
Part A: Product of a Monomial and a Polynomial
Multiply.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29. Find the product of and .
30. Find the product of and .
31. Find the product of and .
32. Find the product of and .
Part B: Product of a Binomial and a Polynomial
Multiply.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
Part C: Product of Polynomials
Multiply.
61.
62.
63.
64.
65.
66.
67.
68.
69. Find the volume of a rectangular solid with sides measuring , , and units.
70. Find the volume of a cube where each side measures units.
Part D: Special Products
Multiply.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
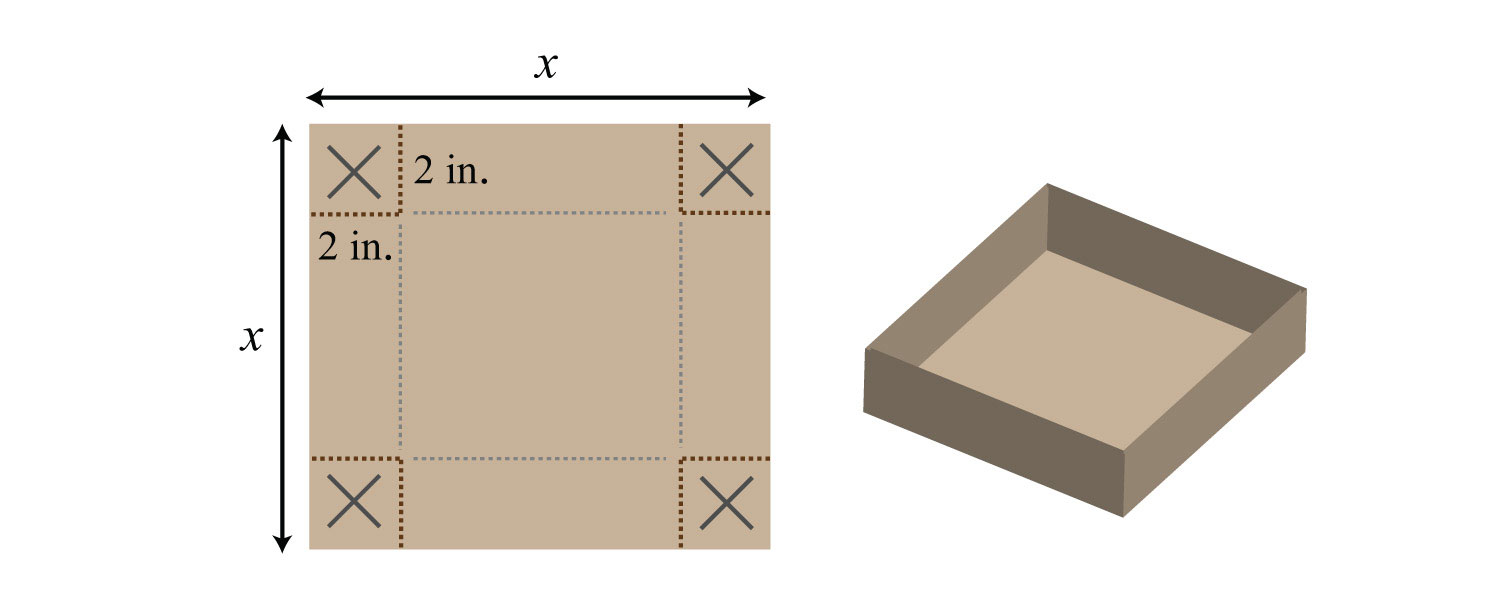
91. A box is made by cutting out the corners and folding up the edges of a square piece of cardboard. A template for a cardboard box with a height of 2 inches is given. Find a formula for the volume, if the initial piece of cardboard is a square with sides measuring x inches.
92. A template for a cardboard box with a height of x inches is given. Find a formula for the volume, if the initial piece of cardboard is a square with sides measuring 12 inches.
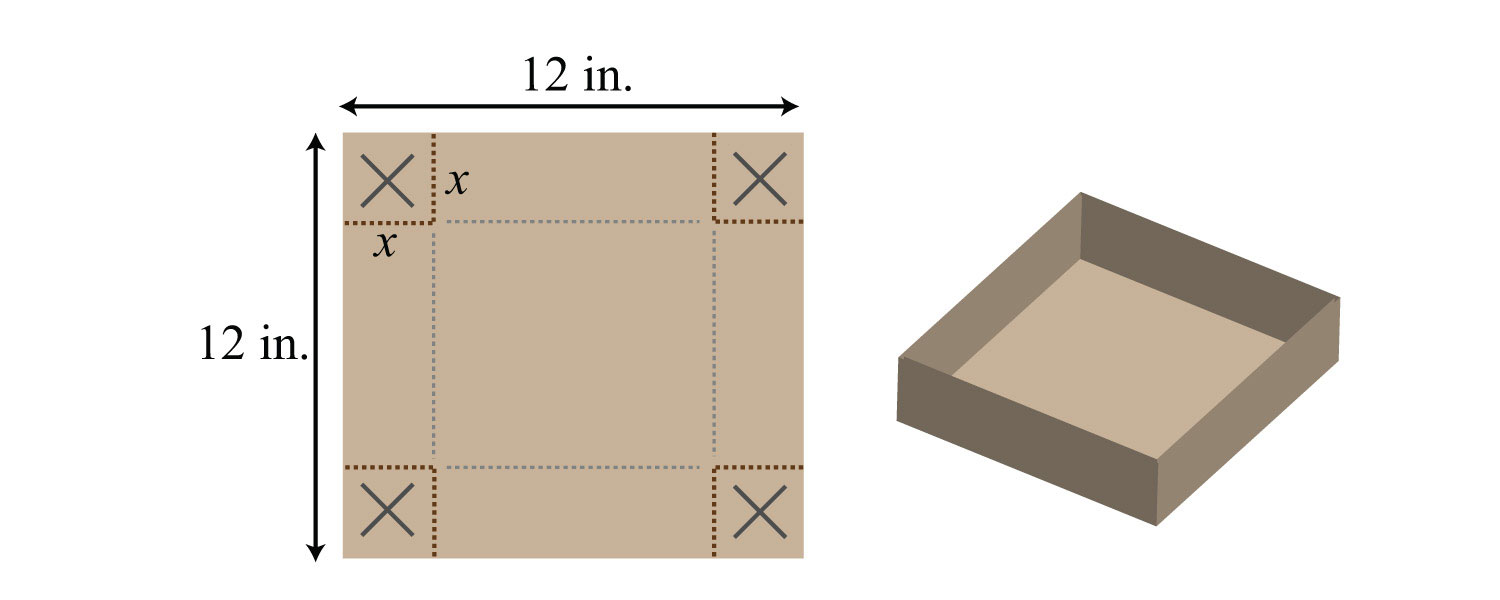
Part E: Multiplying Polynomial Functions
For each problem, calculate , given the functions.
93. and
94. and
95. and
96. and
97. and
98. and
Given and , find the following.
99.
100.
101.
102.
103.
104.
Given and , find the following.
105.
106.
107.
108.
109.
110.
111.
112.
Part F: Discussion Board Topics
113. Explain why .
114. Explain how to quickly multiply a binomial with its conjugate. Give an example.
115. What are the advantages and disadvantages of using the mnemonic device FOIL?
Answers
1:
3:
5:
7:
9:
11:
13:
15:
17:
19:
21:
23:
25:
27:
29:
31:
33:
35:
37:
39:
41:
43:
45:
47:
49:
51:
53:
55:
57:
59:
61:
63:
65:
67:
69:
71:
73:
75:
77:
79:
81:
83:
85:
87:
89:
91: cubic inches
93:
95:
97:
99:
101:
103:
105:
107:
109:
111:
5.5 Dividing Polynomials
Learning Objectives
- Divide by a monomial.
- Divide by a polynomial using the division algorithm.
- Divide polynomial functions.
Dividing by a Monomial
Recall the quotient rule for exponents: if x is nonzero and m and n are positive integers, then
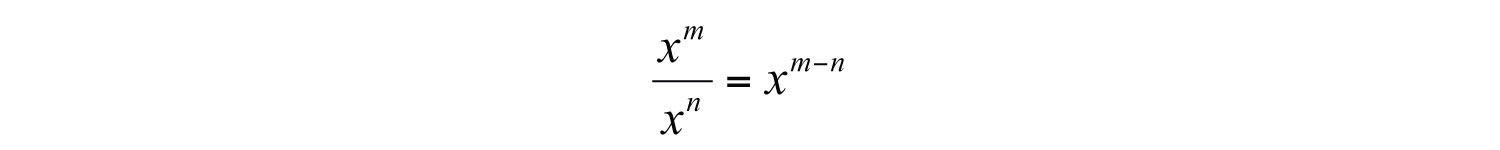
In other words, when dividing two expressions with the same base, subtract the exponents. This rule applies when dividing a monomial by a monomial. In this section, we will assume that all variables in the denominator are nonzero.
Example 1: Divide: .
Solution: Divide the coefficients and subtract the exponents of the variable y.
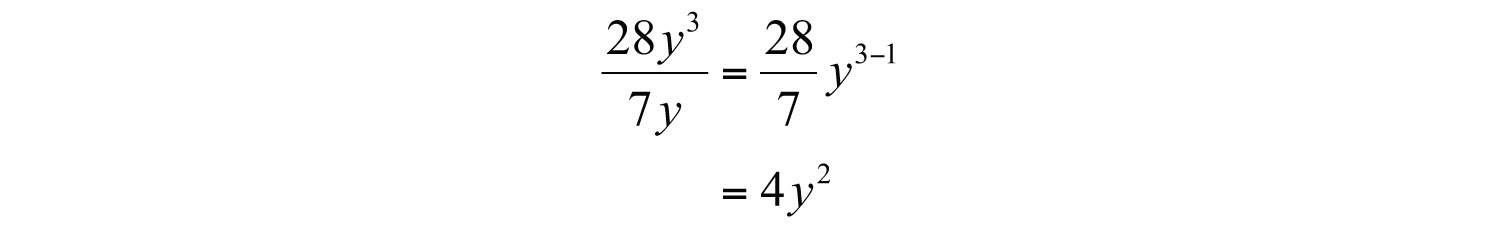
Answer:
Example 2: Divide: .
Solution: Divide the coefficients and apply the quotient rule by subtracting the exponents of the like bases.
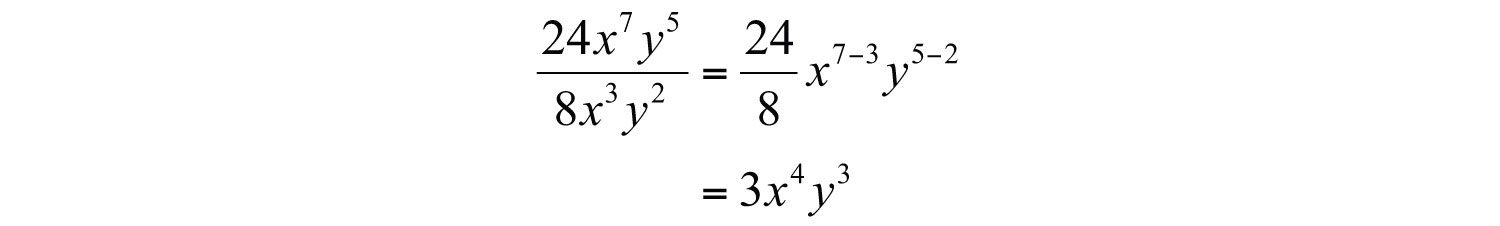
Answer:
When dividing a polynomial by a monomial, we may treat the monomial as a common denominator and break up the fraction using the following property:
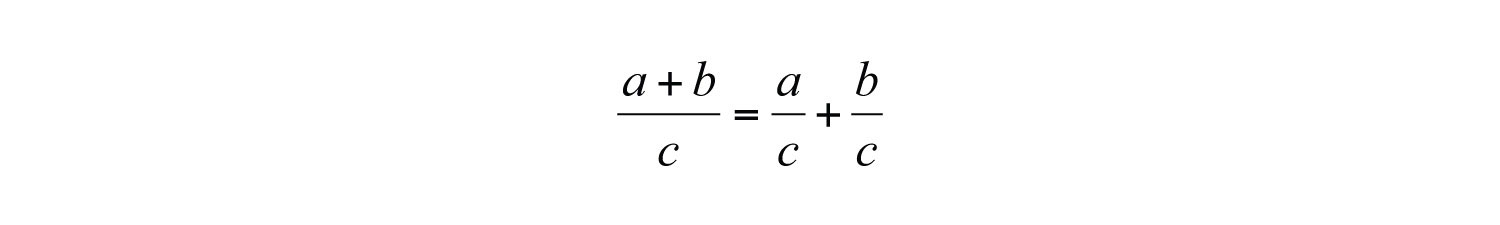
Applying this property results in terms that can be treated as quotients of monomials.
Example 3: Divide: .
Solution: Break up the fraction by dividing each term in the numerator by the monomial in the denominator and then simplify each term.
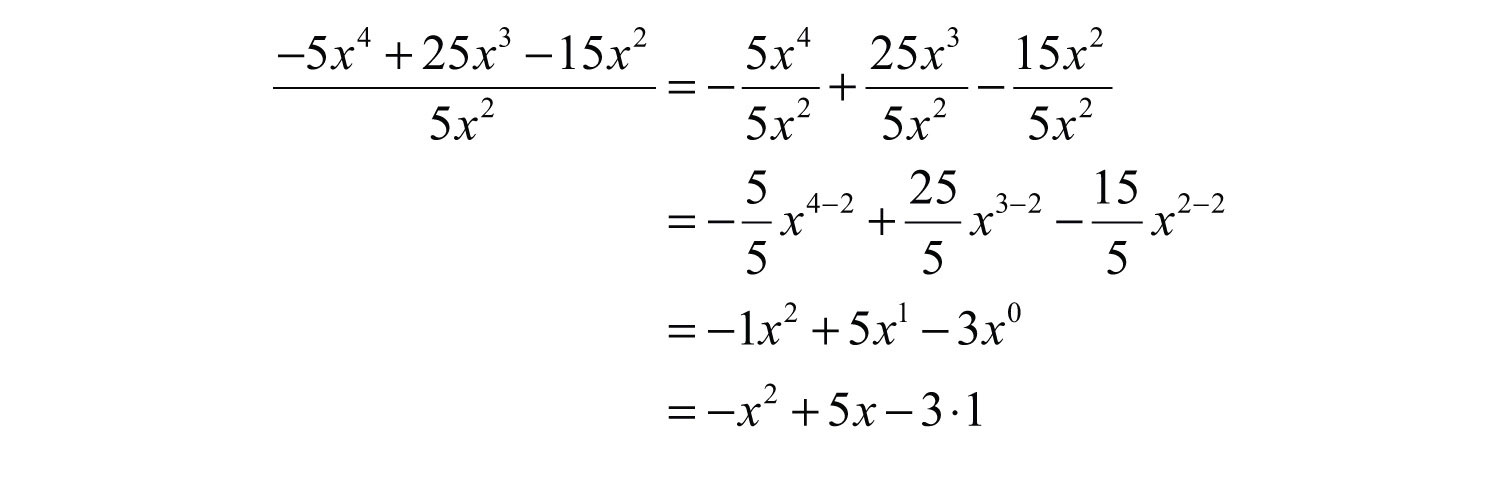
Answer:
Check your division by multiplying the answer, the quotientThe result after dividing., by the monomial in the denominator, the divisorThe denominator of a quotient., to see if you obtain the original numerator, the dividendThe numerator of a quotient..
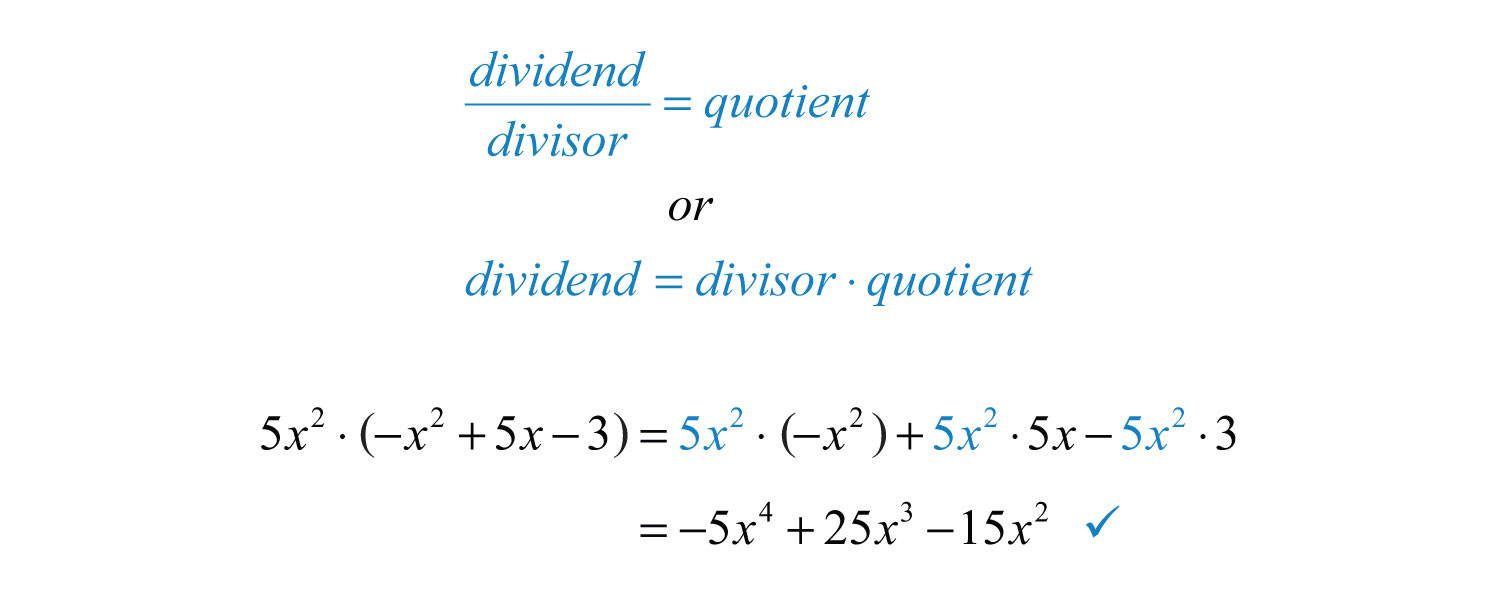
Example 4: Divide: .
Solution:
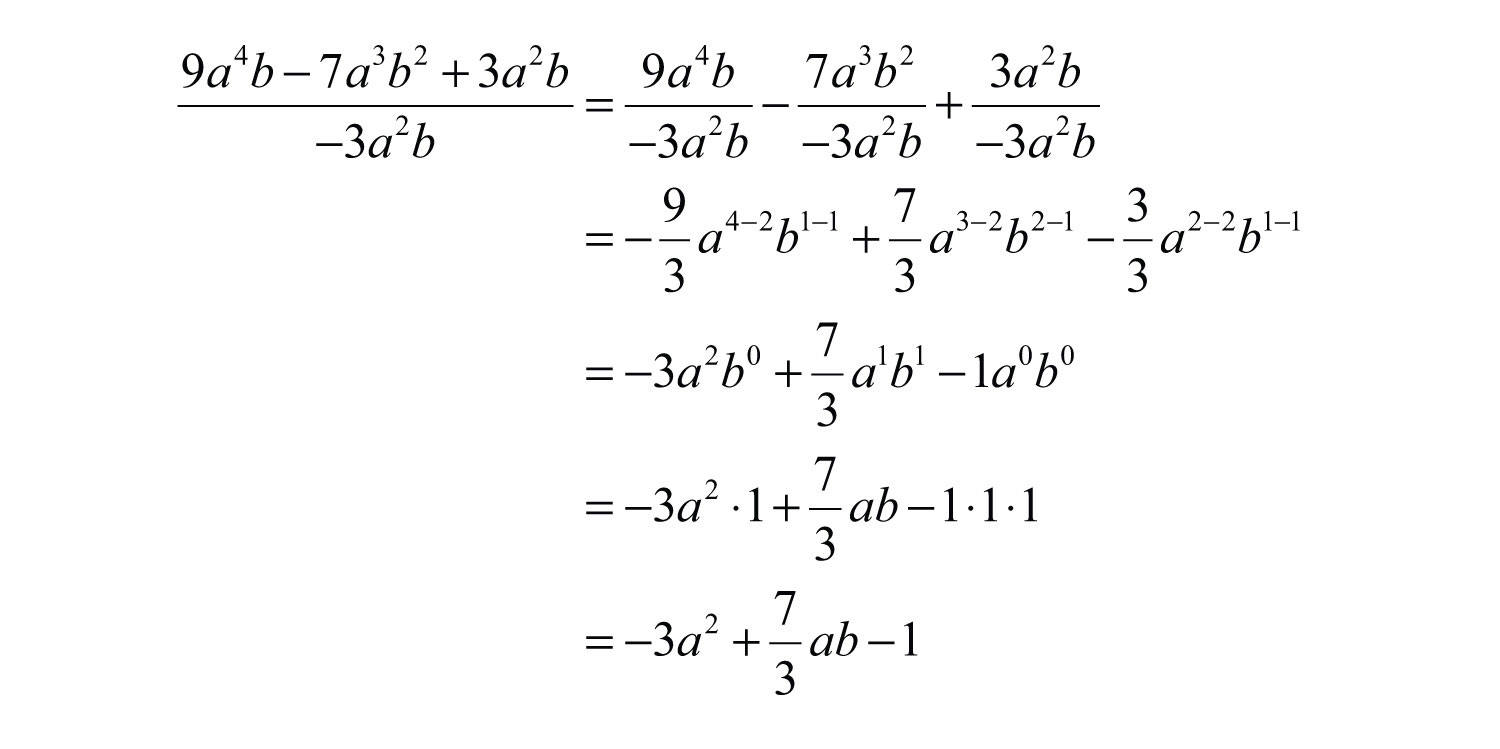
Answer: . The check is optional and is left to the reader.
Try this! Divide: .
Answer:
Video Solution
(click to see video)Dividing by a Polynomial
The same technique outlined for dividing by a monomial does not work for polynomials with two or more terms in the denominator. In this section, we will outline a process called polynomial long divisionThe process of dividing two polynomials using the division algorithm., which is based on the division algorithm for real numbers. For the sake of clarity, we will assume that all expressions in the denominator are nonzero.
Example 5: Divide: .
Solution: Here is the divisor and is the dividend.
Step 1: To determine the first term of the quotient, divide the leading term of the dividend by the leading term of the divisor.
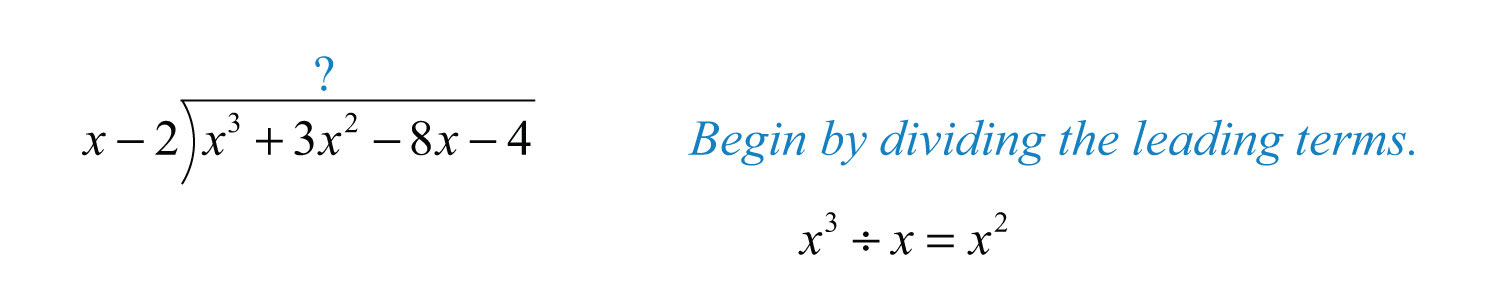
Step 2: Multiply the first term of the quotient by the divisor, remembering to distribute, and line up like terms with the dividend.

Step 3: Subtract the resulting quantity from the dividend. Take care to subtract both terms.
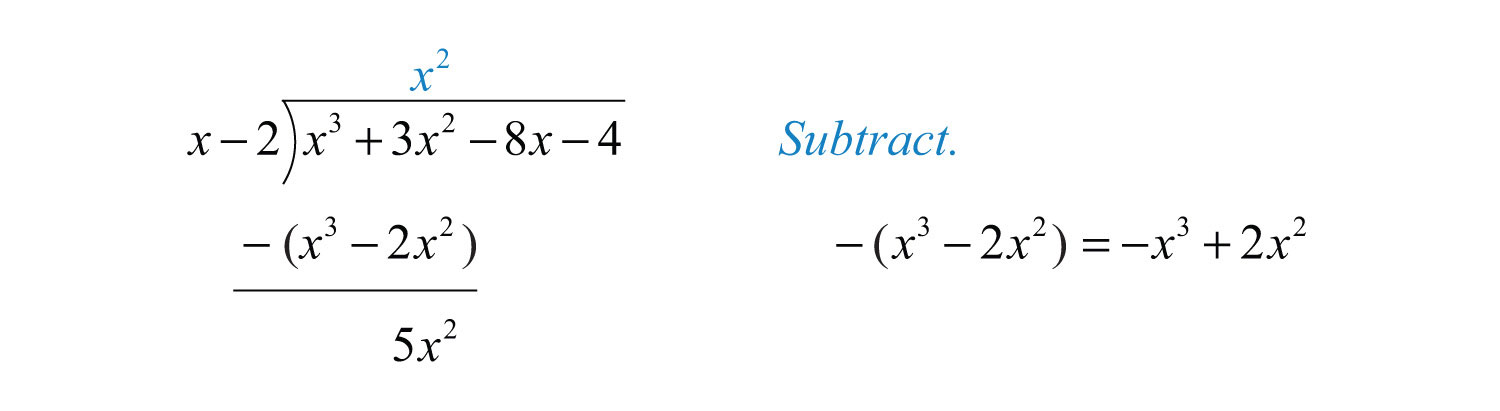
Step 4: Bring down the remaining terms and repeat the process from step 1.

Notice that the leading term is eliminated and that the result has a degree that is one less than the dividend. The complete process is illustrated below:

Polynomial long division ends when the degree of the remainderThe expression that is left after the division algorithm ends. is less than the degree of the divisor. Here the remainder is 0. Therefore, the binomial divides the polynomial evenly and the answer is the quotient shown above the division line.
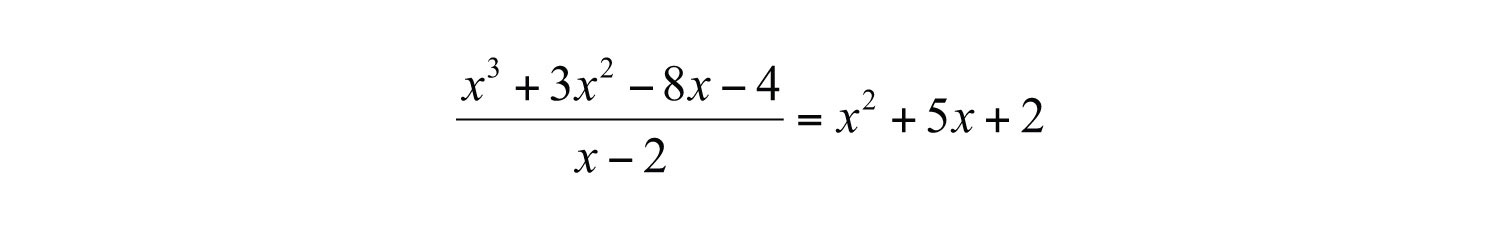
To check the answer, multiply the divisor by the quotient to see if you obtain the dividend:
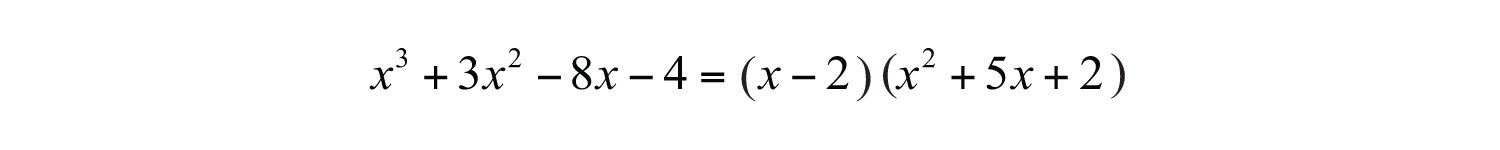
Answer:
Next, we demonstrate the case where there is a nonzero remainder.
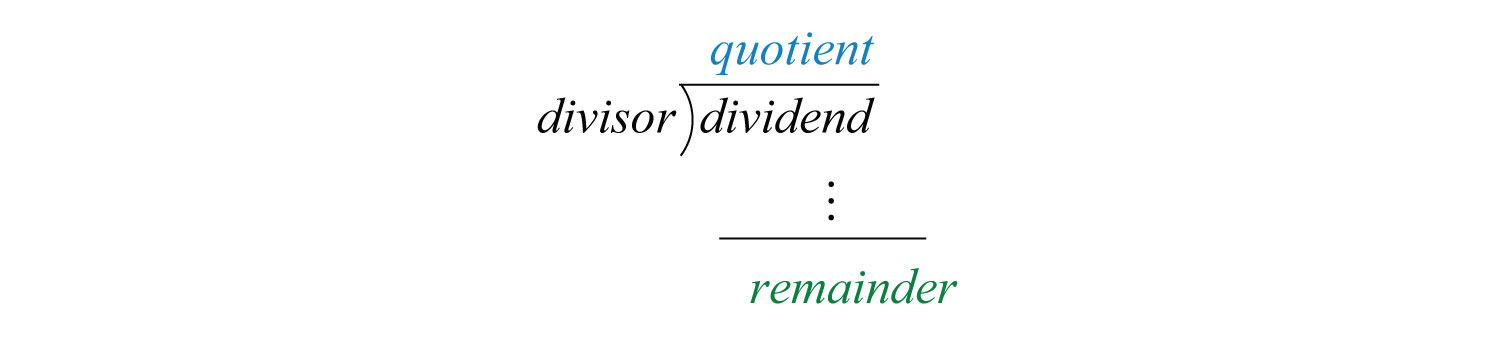
Just as with real numbers, the final answer adds the fraction where the remainder is the numerator and the divisor is the denominator to the quotient. In general, when dividing we have
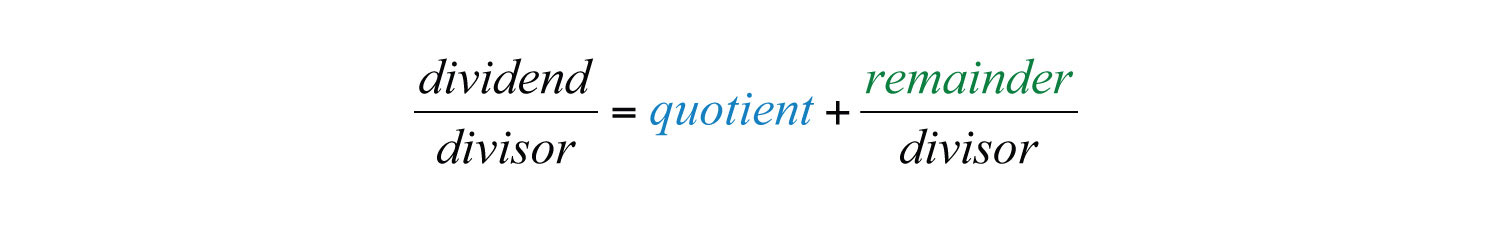
If we multiply both sides by the divisor we obtain
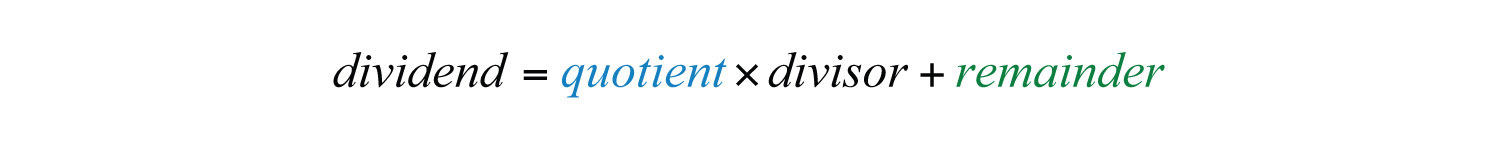
Example 6: Divide: .
Solution: Since the denominator is a binomial, begin by setting up polynomial long division.
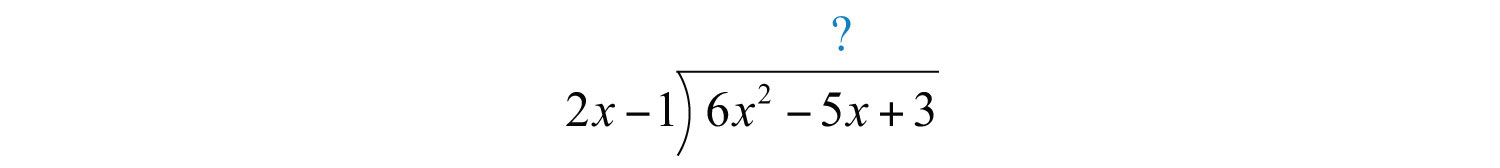
To start, determine what monomial times results in a leading term . This is the quotient of the given leading terms: . Multiply times the divisor and line up the result with like terms of the dividend.
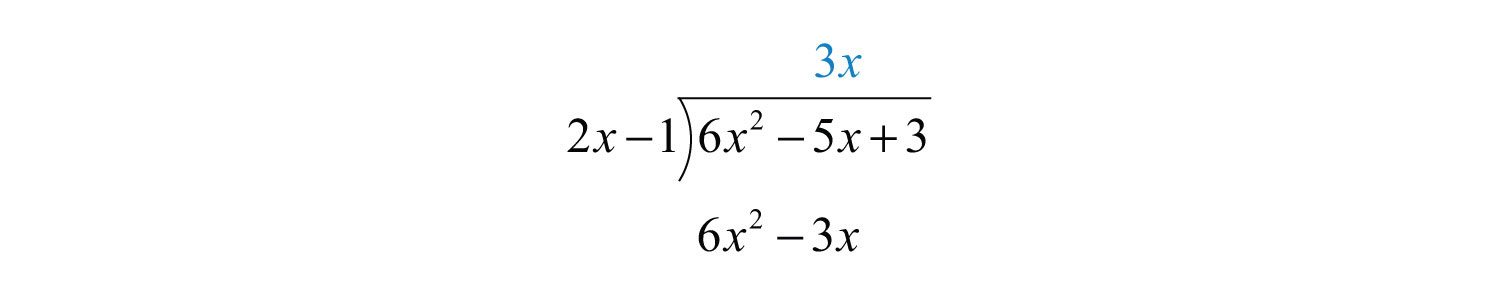
Subtract the result from the dividend and bring down the constant term +3.
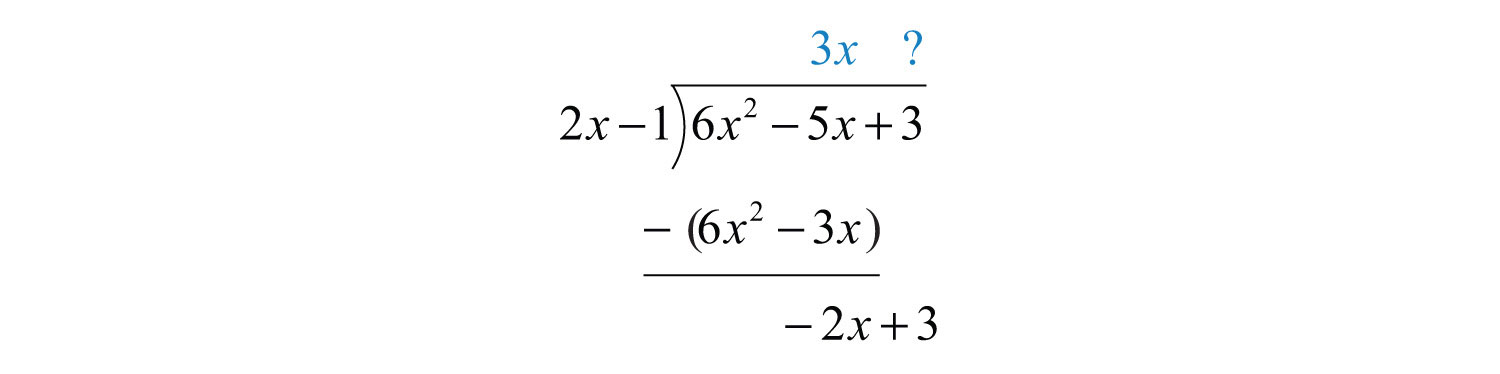
Subtracting eliminates the leading term and . The quotient of and is −1. Multiply by −1 and line up the result.
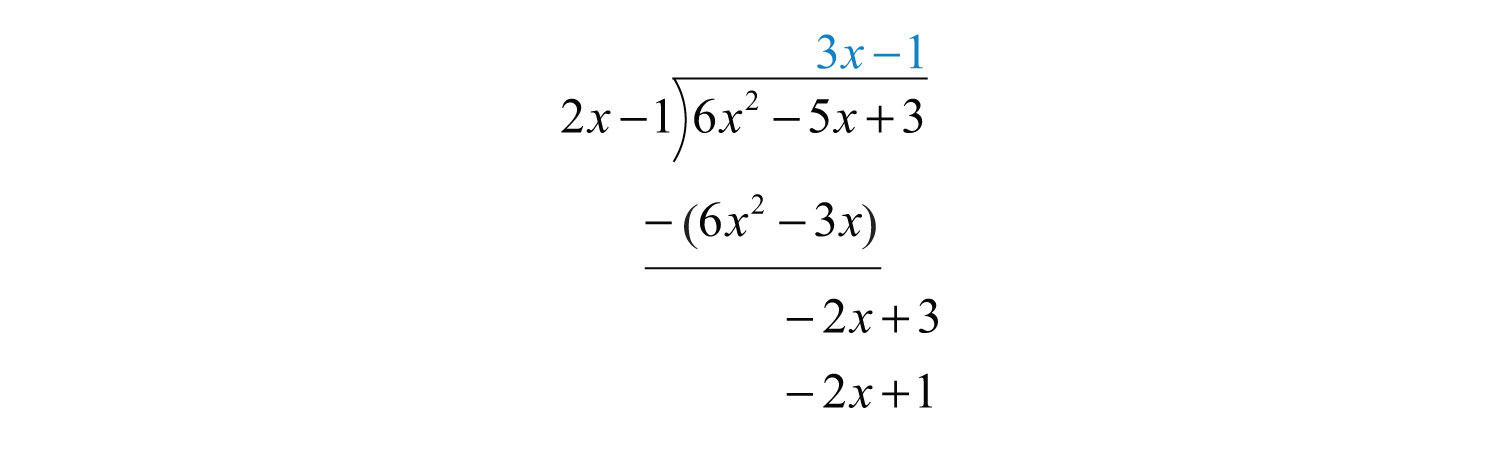
Subtract again and notice that we are left with a remainder.
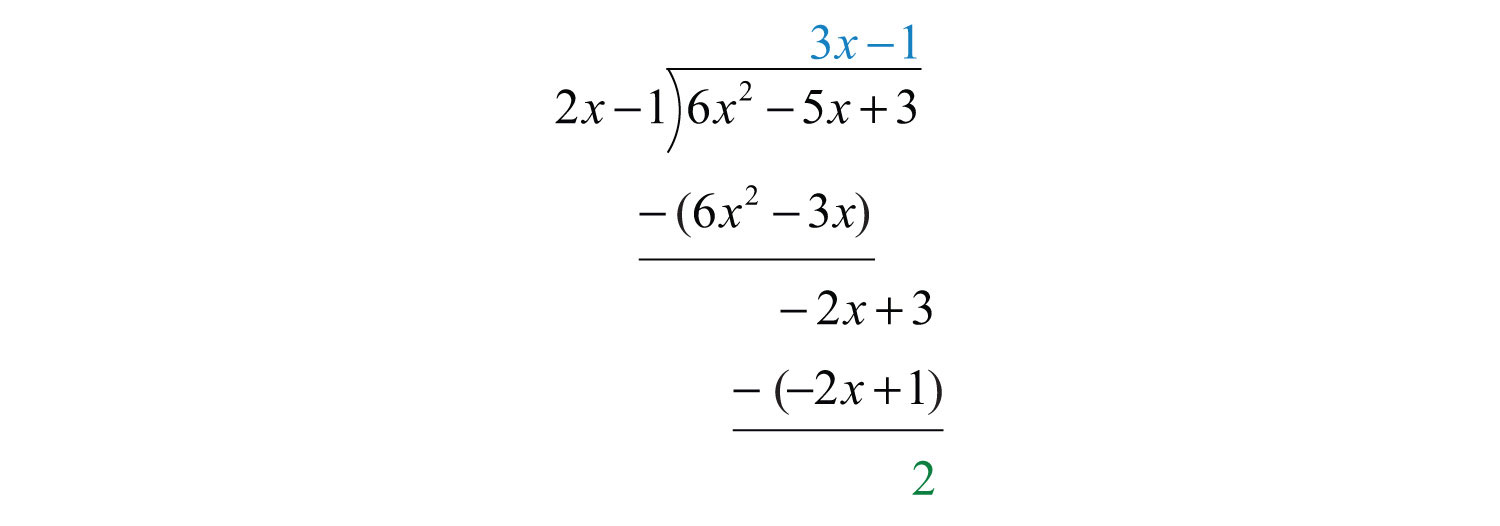
The constant term 2 has degree 0, and thus the division ends. We may write
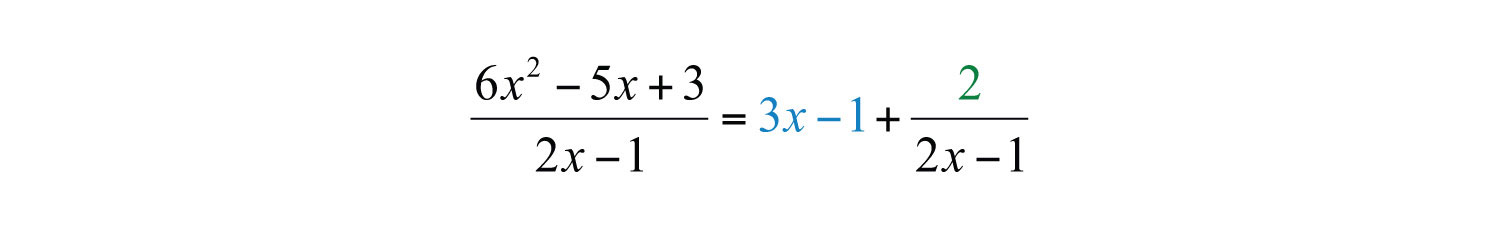
Answer: . To check that this result is correct, we multiply as follows:
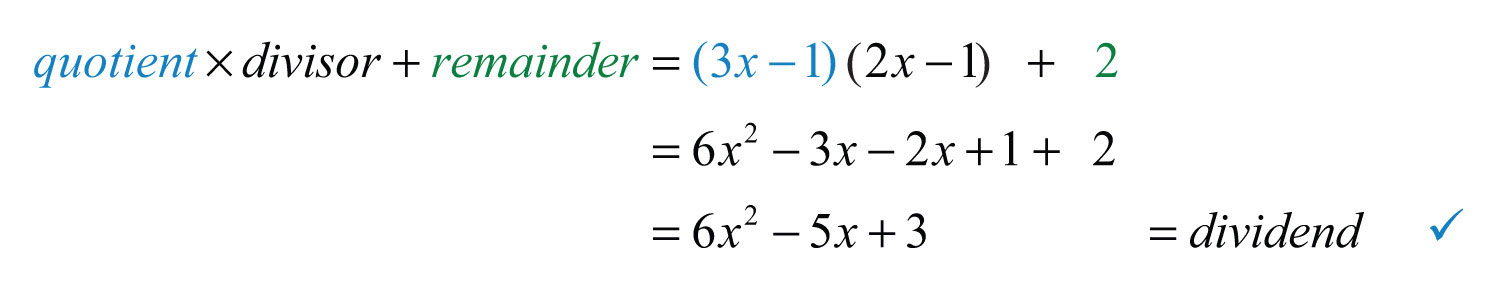
Occasionally, some of the powers of the variables appear to be missing within a polynomial. This can lead to errors when lining up like terms. Therefore, when first learning how to divide polynomials using long division, fill in the missing terms with zero coefficients, called placeholdersTerms with zero coefficients used to fill in all missing exponents within a polynomial..
Example 7: Divide: .
Solution: Notice that the binomial in the numerator does not have terms with degree 2 or 1. The division is simplified if we rewrite the expression with placeholders:
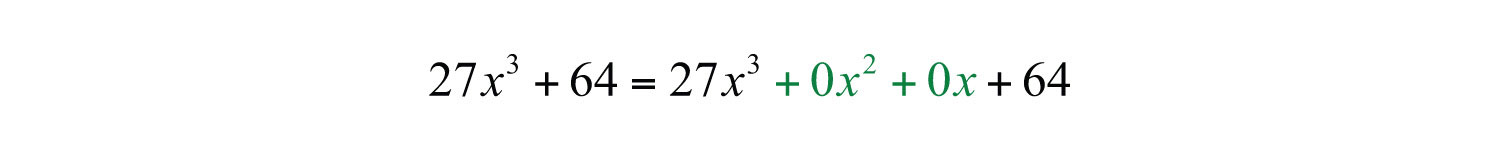
Set up polynomial long division:
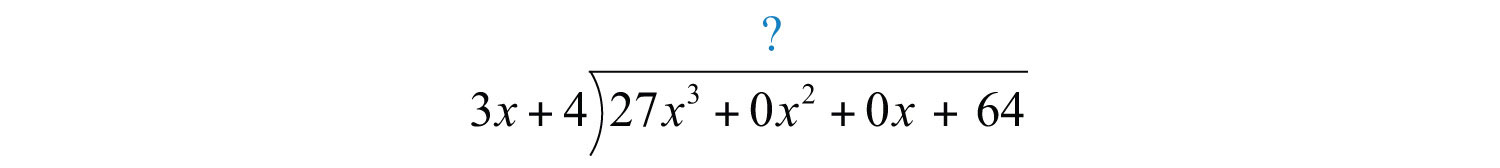
We begin with and work the rest of the division algorithm.
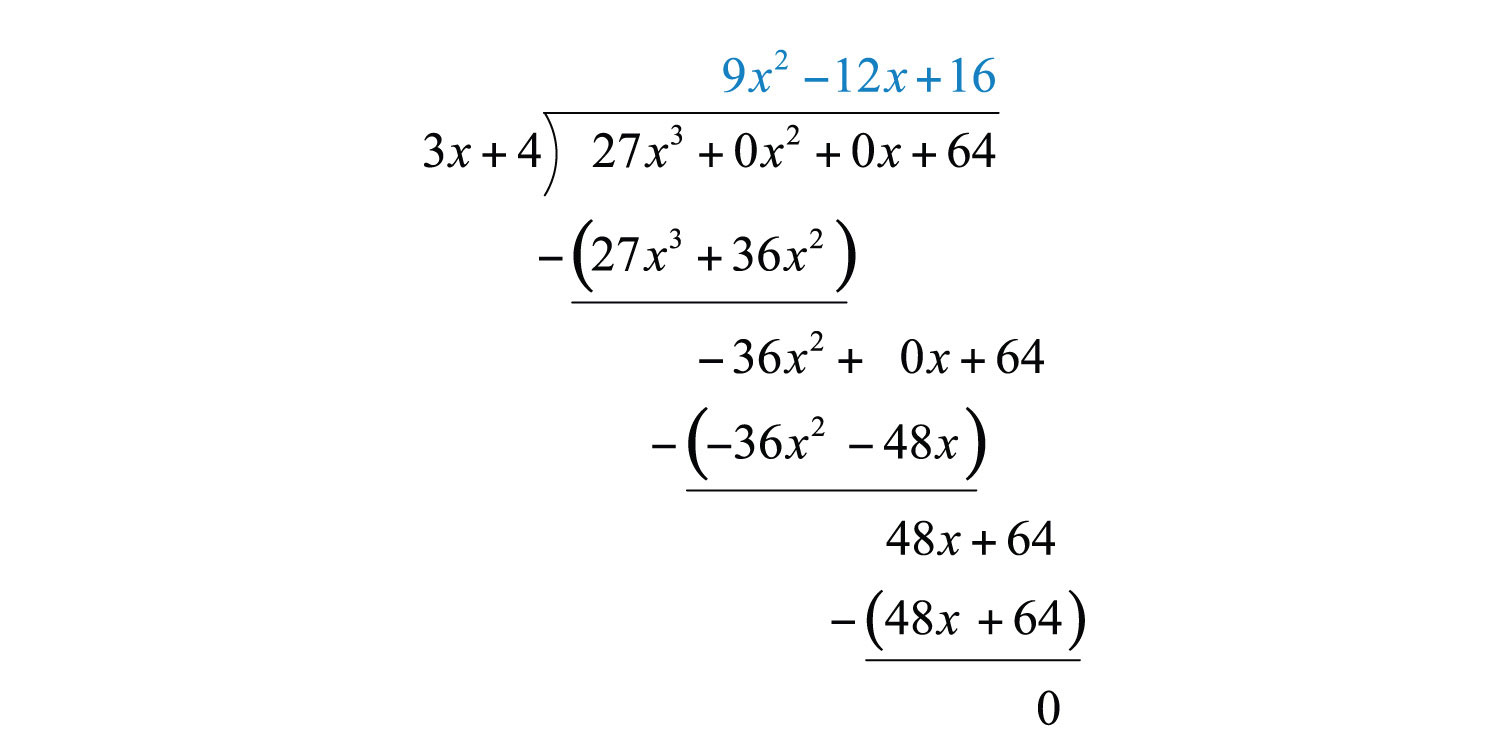
Answer:
Example 8: Divide: .
Solution:
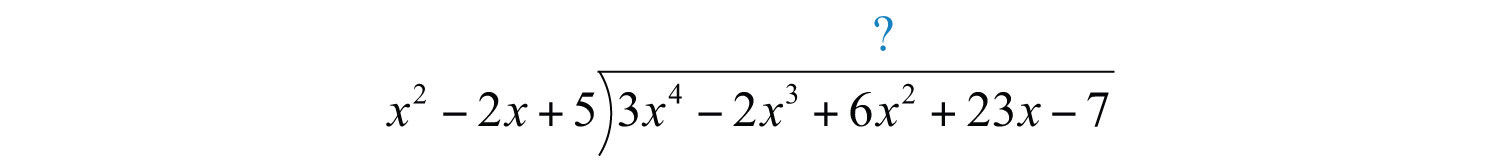
Begin the process by dividing the leading terms to determine the leading term of the quotient . Take care to distribute and line up the like terms. Continue the process until the remainder has a degree less than 2.
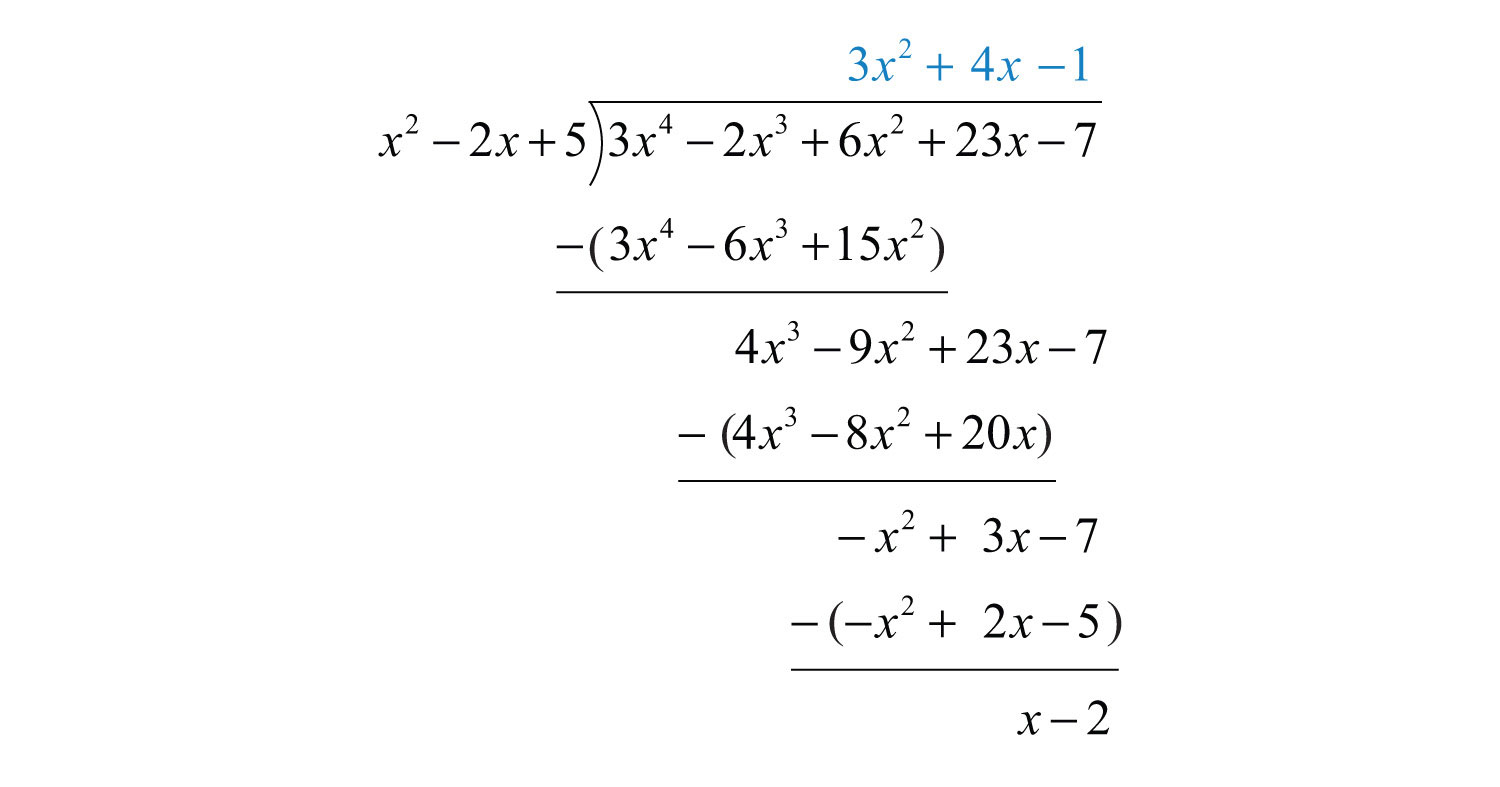
The remainder is . Write the answer with the remainder:
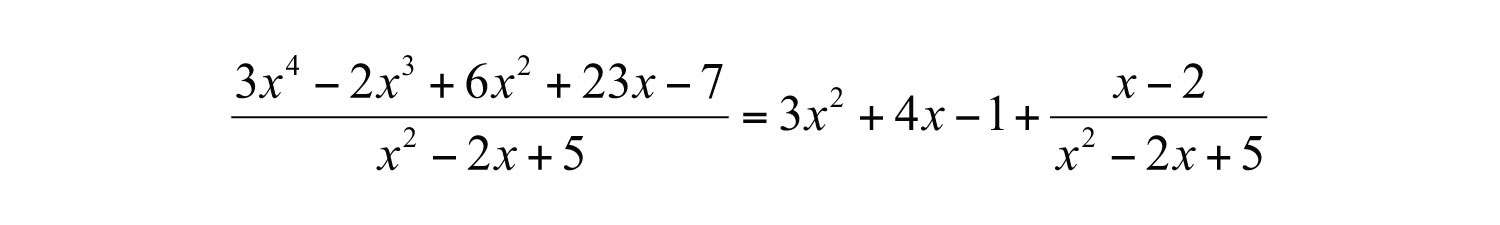
Answer:
Polynomial long division takes time and practice to master. Work lots of problems and remember that you may check your answers by multiplying the quotient by the divisor (and adding the remainder if present) to obtain the dividend.
Try this! Divide: .
Answer:
Video Solution
(click to see video)Dividing Polynomial Functions
We may use function notation to indicate division as follows:
| Division of functions: |
The quotient of two polynomial functions does not necessarily have a domain of all real numbers. The values for x that make the function in the denominator 0 are restricted from the domain. This will be discussed in more detail at a later time. For now, assume all functions in the denominator are nonzero.
Example 9: Calculate: given and .
Solution: The notation indicates that we should divide:
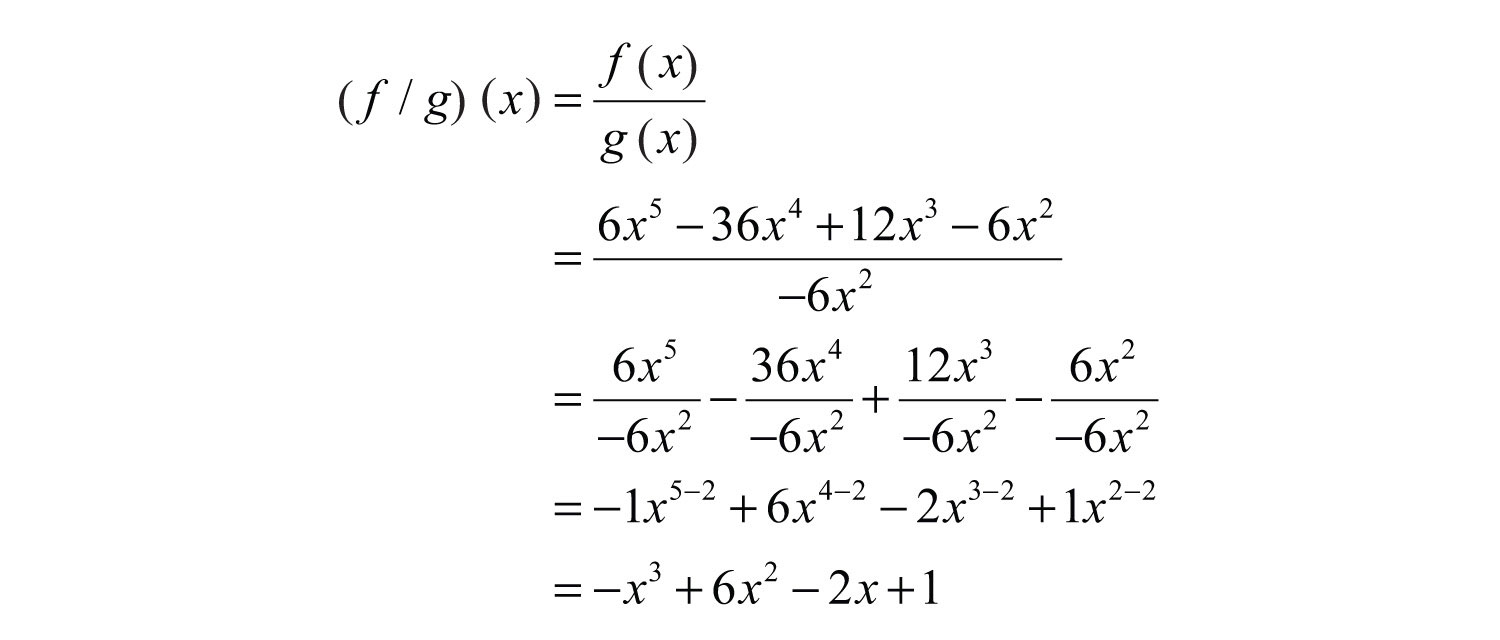
Answer:
Example 10: Calculate: , given and .
Solution: First, determine .
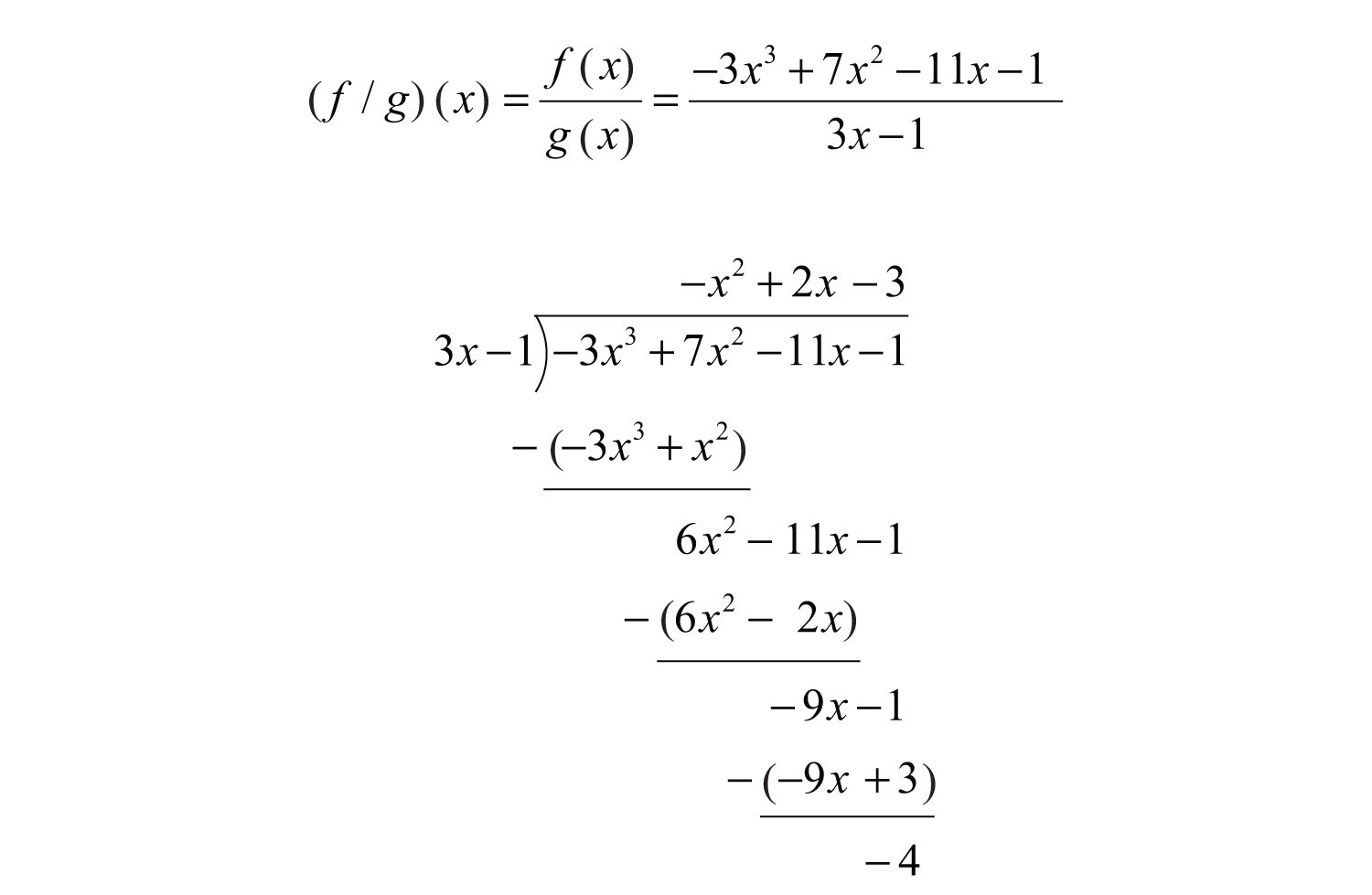
Therefore,
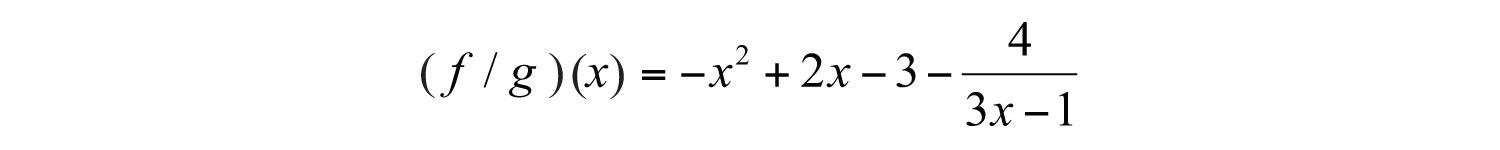
Substitute −1 for the variable .
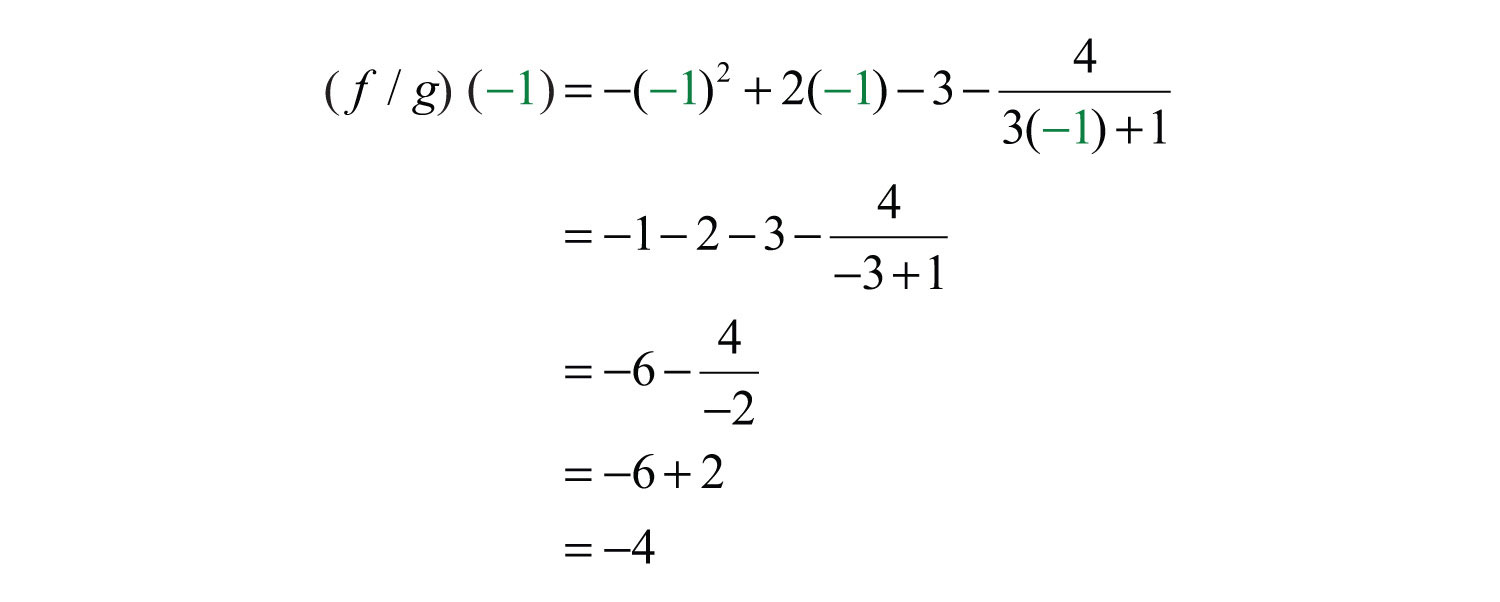
Answer:
Key Takeaways
- When dividing by a monomial, divide all terms in the numerator by the monomial and then simplify each term. To simplify each term, divide the coefficients and apply the quotient rule for exponents.
- When dividing a polynomial by another polynomial, apply the division algorithm.
- To check the answer after dividing, multiply the divisor by the quotient and add the remainder (if necessary) to obtain the dividend.
- It is a good practice to include placeholders when performing polynomial long division.
Topic Exercises
Part A: Dividing by a Monomial
Divide.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23. Find the quotient of and .
24. Find the quotient of and .
25. Find the quotient of and .
26. Find the quotient of and .
Part B: Dividing by a Polynomial
Divide.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67. Divide by .
68. Divide by .
Part C: Dividing Polynomial Functions
Calculate , given the functions.
69. and
70. and
71. and
72. and
73. and
74. and
75. and
76. and
77. and
78. and
Given and , find the following.
79.
80.
81.
82.
Given and , find the following.
83.
84.
85.
86.
Part D: Discussion Board Topics
87. How do you use the distributive property when dividing a polynomial by a monomial?
88. Compare long division of real numbers with polynomial long division. Provide an example of each.
Answers
1:
3:
5:
7:
9:
11:
13:
15:
17:
19:
21:
23:
25:
27:
29:
31:
33:
35:
37:
39:
41:
43:
45:
47:
49:
51:
53:
55:
57:
59:
61:
63:
65:
67:
69:
71:
73:
75:
77:
79:
81:
83:
85:
5.6 Negative Exponents
Learning Objectives
- Simplify expressions with negative integer exponents.
- Work with scientific notation.
Negative Exponents
In this section, we define what it means to have negative integer exponents. We begin with the following equivalent fractions:
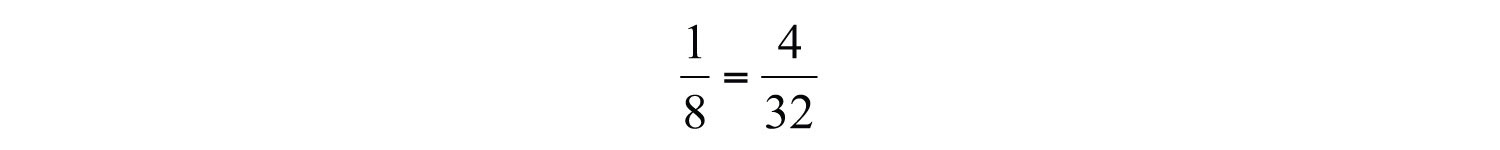
Notice that 4, 8, and 32 are all powers of 2. Hence we can write , , and .
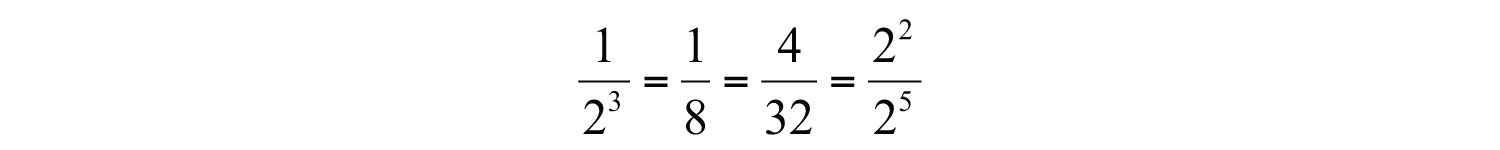
If the exponent of the term in the denominator is larger than the exponent of the term in the numerator, then the application of the quotient rule for exponents results in a negative exponent. In this case, we have the following:
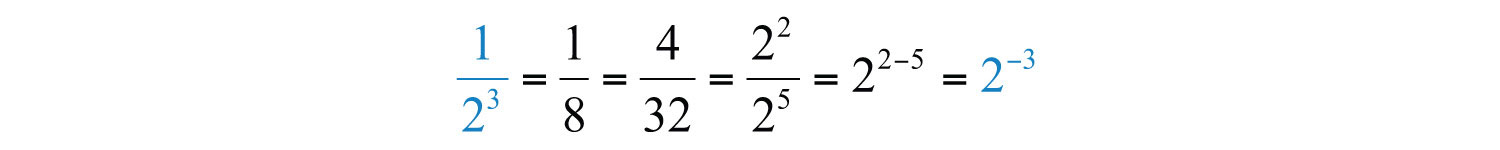
We conclude that . This is true in general and leads to the definition of negative exponents given any integer n, where x is nonzero.. Given any integer n and , then
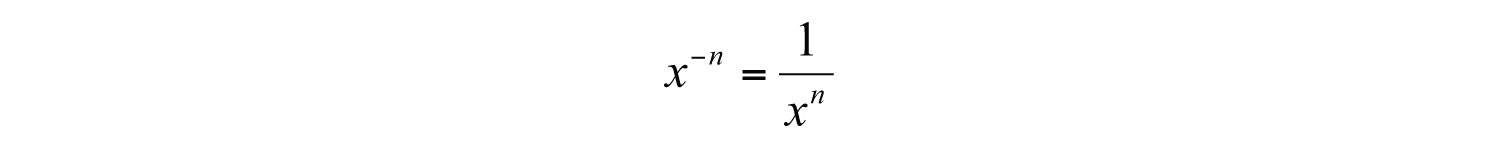
Here because is undefined. For clarity, in this section, assume all variables are nonzero.
Simplifying expressions with negative exponents requires that we rewrite the expression with positive exponents.
Example 1: Simplify: .
Solution:
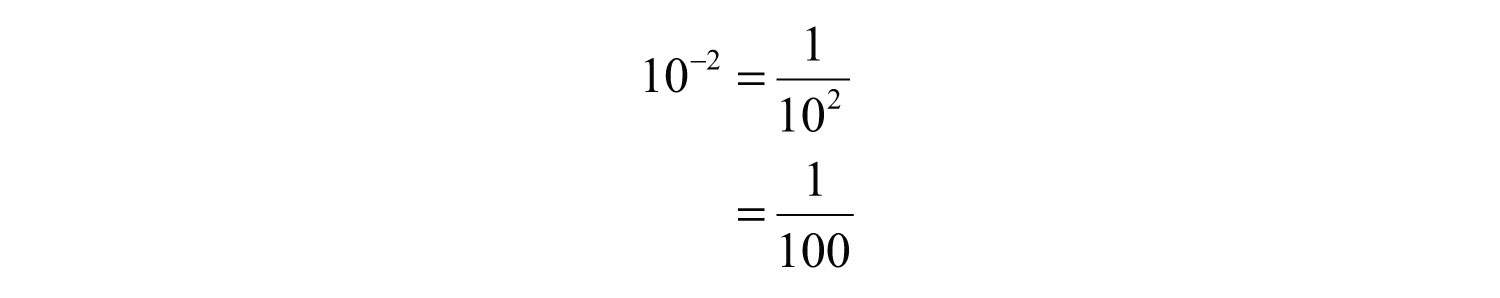
Answer:
Example 2: Simplify: .
Solution:
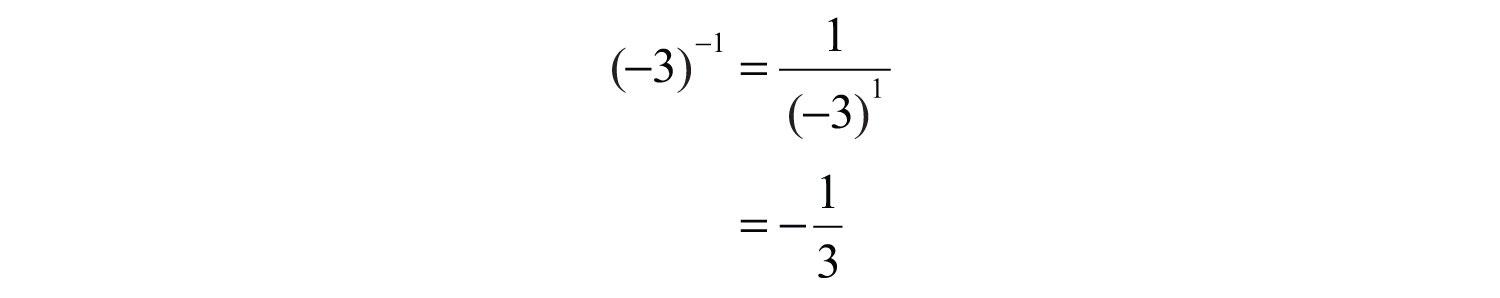
Answer:
Example 3: Simplify: .
Solution:
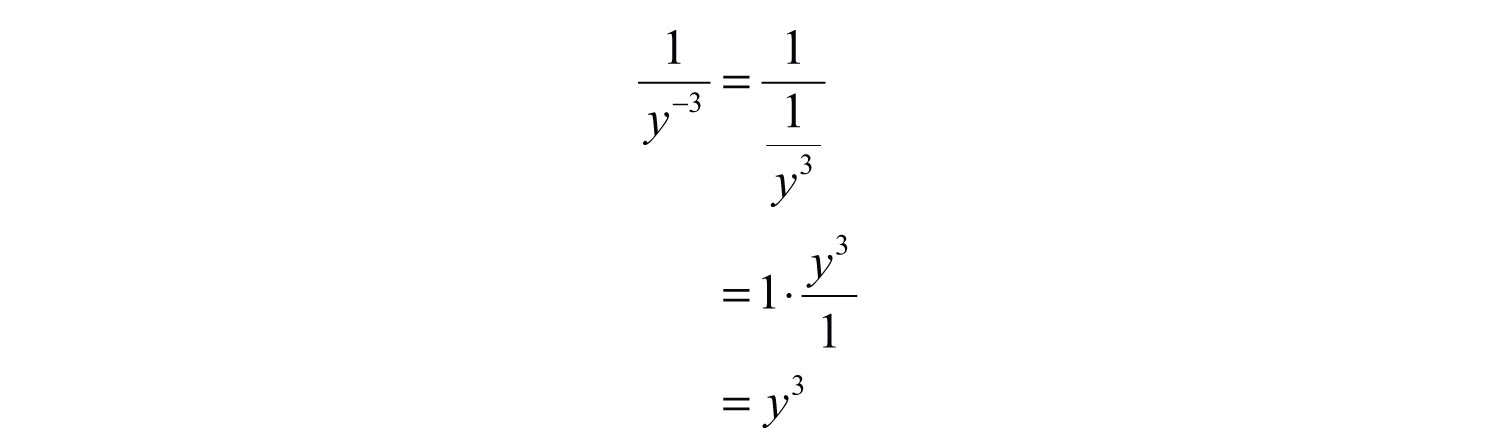
Answer:
At this point we highlight two very important examples,

If the grouped quantity is raised to a negative exponent, then apply the definition and write the entire grouped quantity in the denominator. If there is no grouping, then apply the definition only to the base preceding the exponent.
Example 4: Simplify: .
Solution: First, apply the definition of −3 as an exponent and then apply the power of a product rule.

Answer:
Example 5: Simplify: .
Solution:
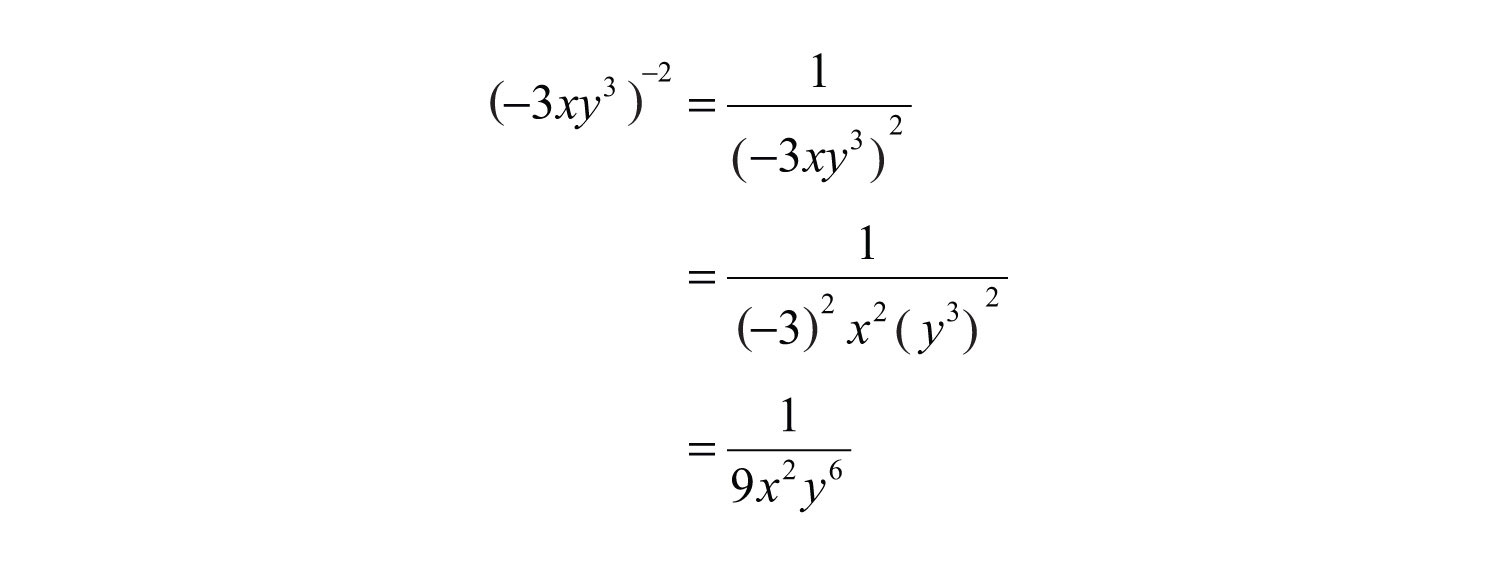
Answer:
Example 6: Simplify: .
Solution:
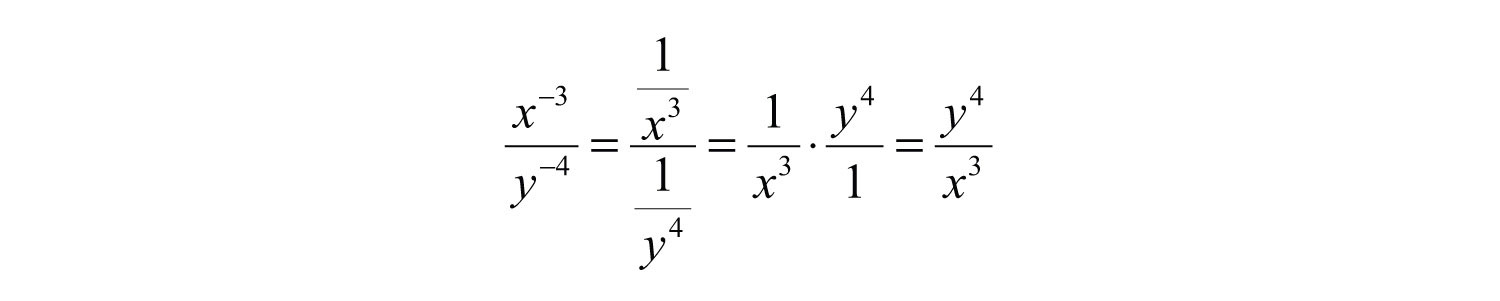
Answer:
The previous example suggests a property of quotients with negative exponents, given any integers m and n, where and .. If given any integers m and n, where and , then
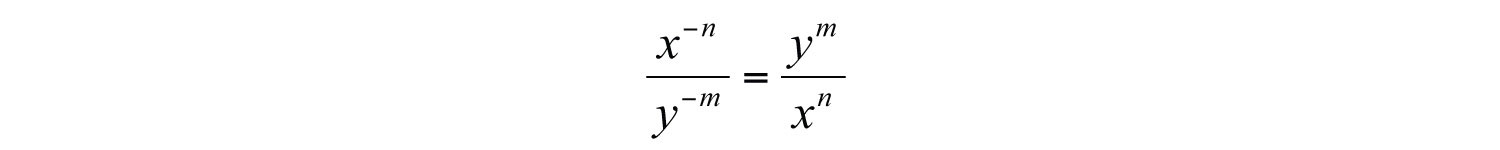
In other words, negative exponents in the numerator can be written as positive exponents in the denominator, and negative exponents in the denominator can be written as positive exponents in the numerator.
Example 7: Simplify: .
Solution: Take care with the coefficient −2; recognize that this is the base and that the exponent is actually +1: . Hence the rules of negative exponents do not apply to this coefficient; leave it in the numerator.
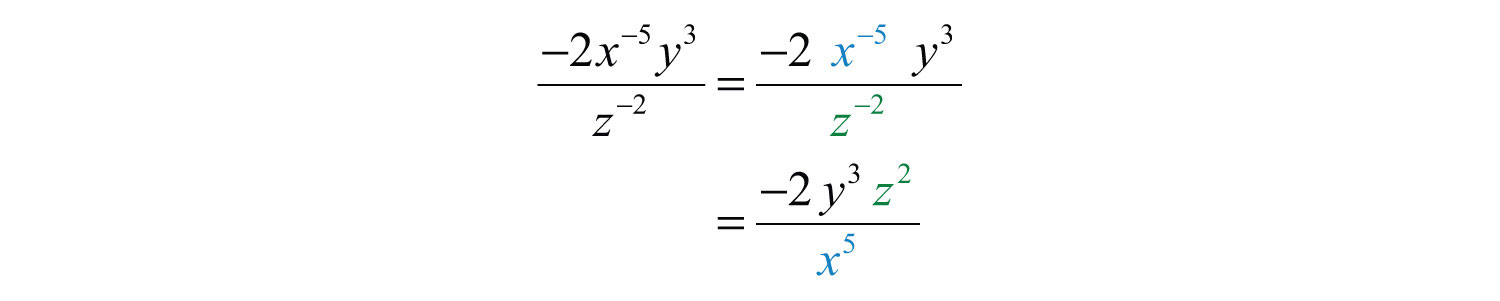
Answer:
Example 8: Simplify: .
Solution: Apply the power of a product rule before applying negative exponents.

Answer:
Example 9: Simplify: .
Solution:
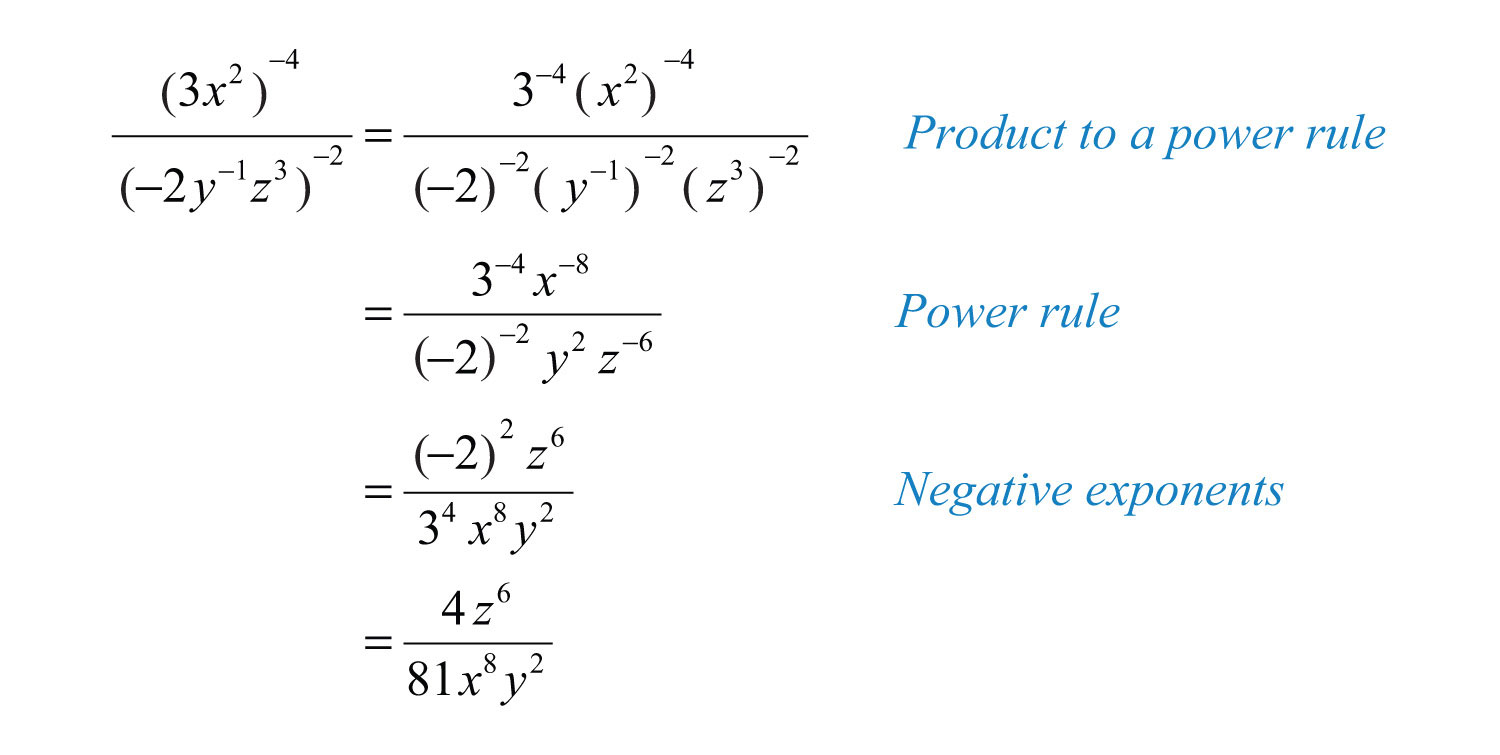
Answer:
Example 10: Simplify: .
Solution: First, apply the power of a product rule and then the quotient rule.
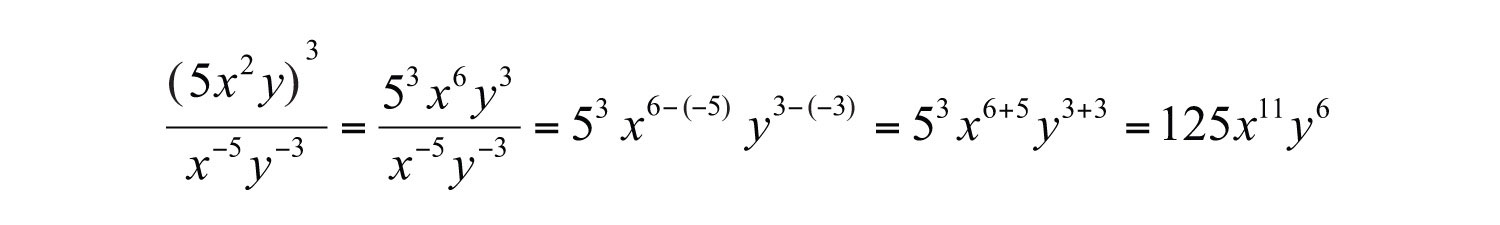
Answer:
To summarize, we have the following rules for negative integer exponents with nonzero bases:
| Negative exponents: | |
| Quotients with negative exponents: |
Try this! Simplify: .
Answer:
Video Solution
(click to see video)Scientific Notation
Real numbers expressed in scientific notationReal numbers expressed in the form , where n is an integer and . have the form
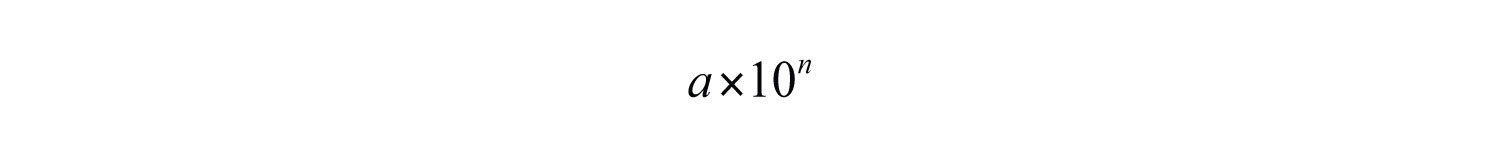
where n is an integer and . This form is particularly useful when the numbers are very large or very small. For example,
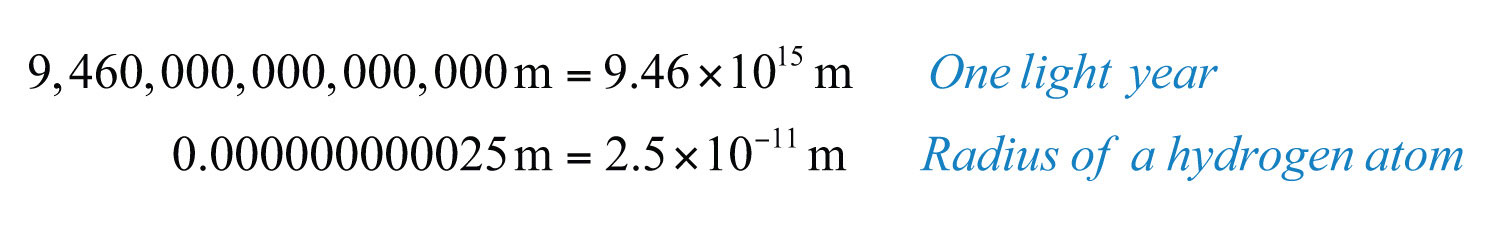
It is cumbersome to write all the zeros in both of these cases. Scientific notation is an alternative, compact representation of these numbers. The factor indicates the power of 10 to multiply the coefficient by to convert back to decimal form:
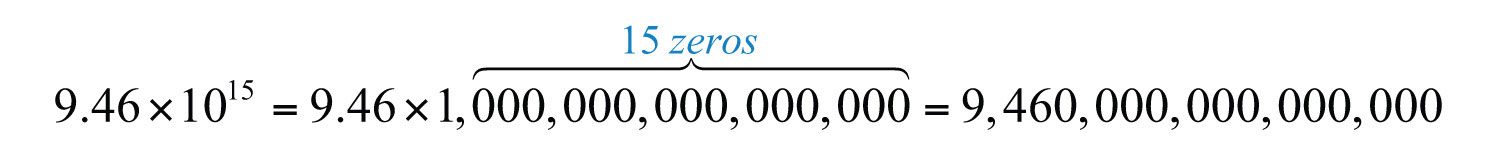
This is equivalent to moving the decimal in the coefficient fifteen places to the right. A negative exponent indicates that the number is very small:

This is equivalent to moving the decimal in the coefficient eleven places to the left.
Converting a decimal number to scientific notation involves moving the decimal as well. Consider all of the equivalent forms of with factors of 10 that follow:
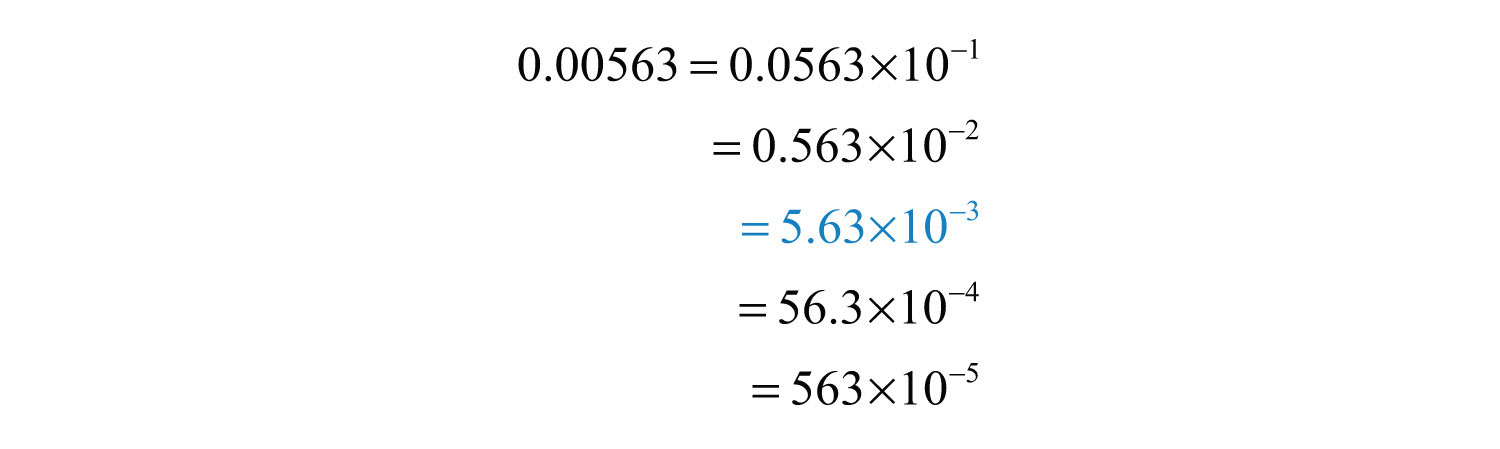
While all of these are equal, is the only form considered to be expressed in scientific notation. This is because the coefficient 5.63 is between 1 and 10 as required by the definition. Notice that we can convert back to decimal form, as a check, by moving the decimal to the left three places.
Example 11: Write using scientific notation.
Solution: Here we count twelve decimal places to the left of the decimal point to obtain the number 1.075.
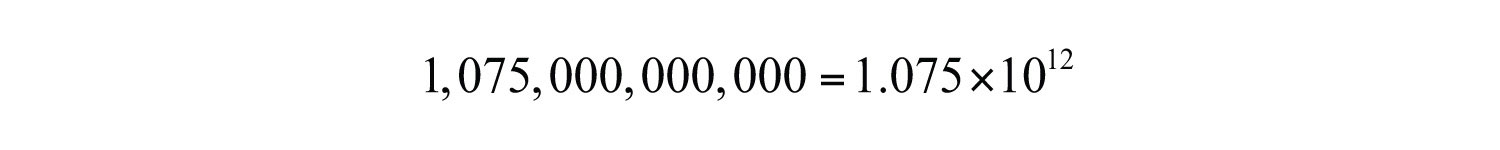
Answer:
Example 12: Write using scientific notation.
Solution: Here we count six decimal places to the right to obtain 3.045.
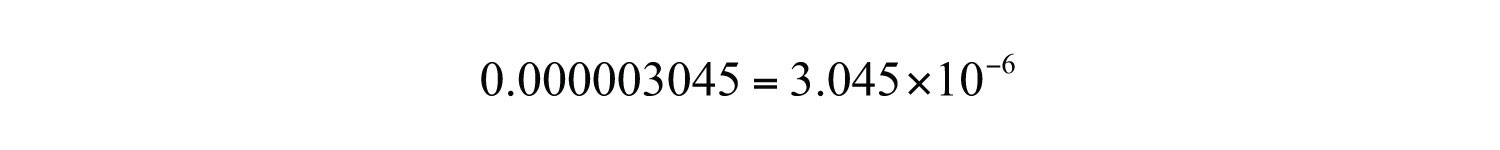
Answer:
Often we will need to perform operations when using numbers in scientific notation. All the rules of exponents developed so far also apply to numbers in scientific notation.
Example 13: Multiply: .
Solution: Use the fact that multiplication is commutative and apply the product rule for exponents.
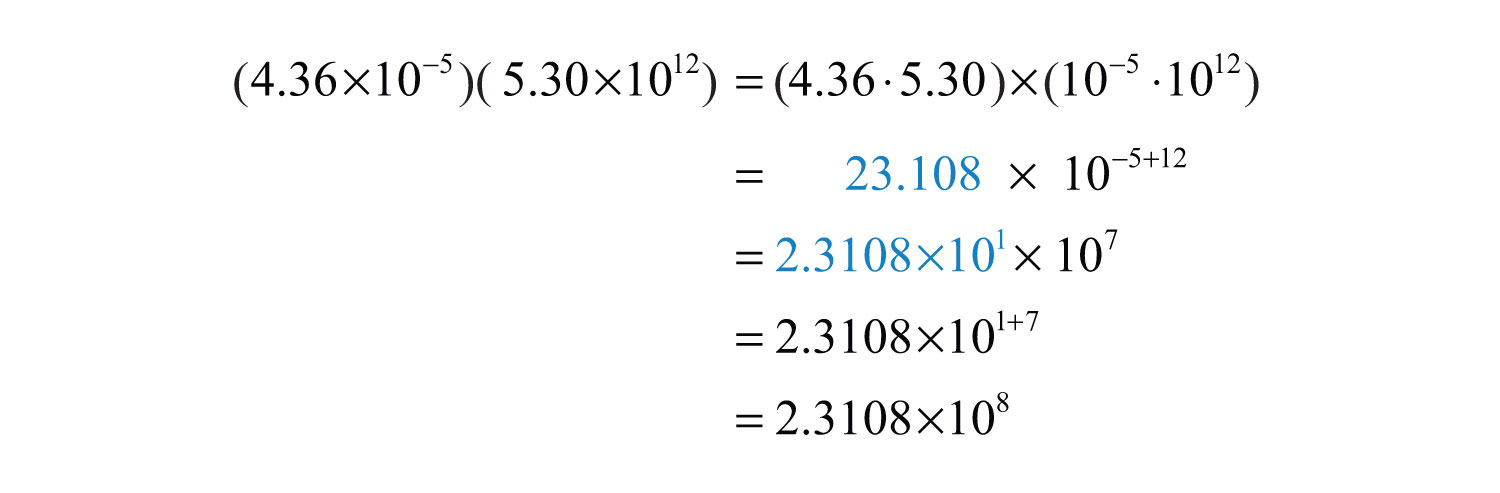
Answer:
Example 14: Divide: .
Solution:
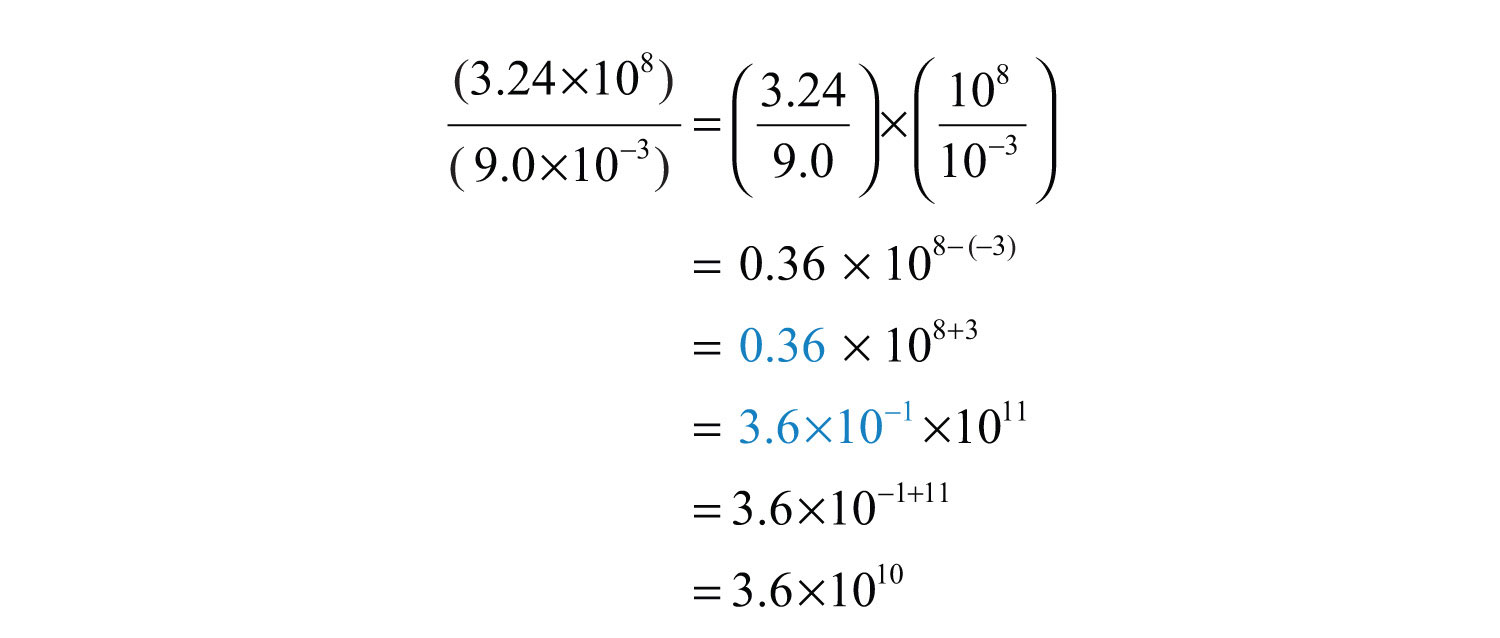
Answer:
Example 15: The speed of light is approximately miles per hour. Express this speed in miles per second.
Solution: A unit analysis indicates that we must divide the number by 3,600.

Answer: The speed of light is approximately miles per second.
Example 16: By what factor is the radius of the sun larger than the radius of earth?
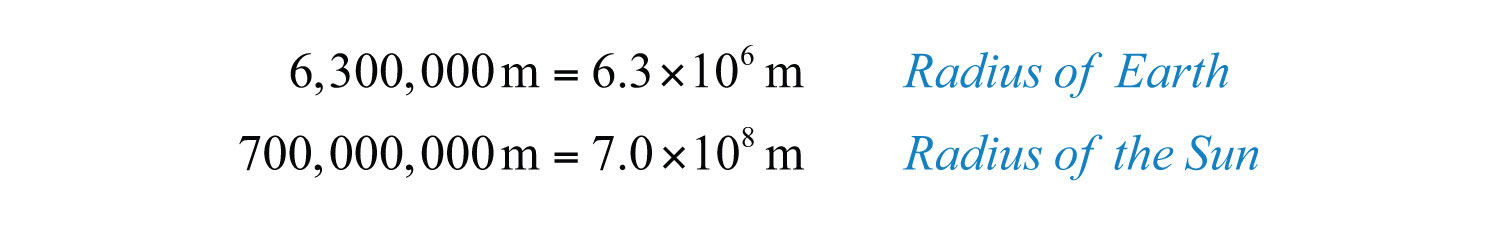
Solution: We want to find the number that when multiplied times the radius of earth equals the radius of the sun.

Source: NASA and European Space Agency, from http://solarsystem.nasa.gov/multimedia/display.cfm?IM_ID=188.
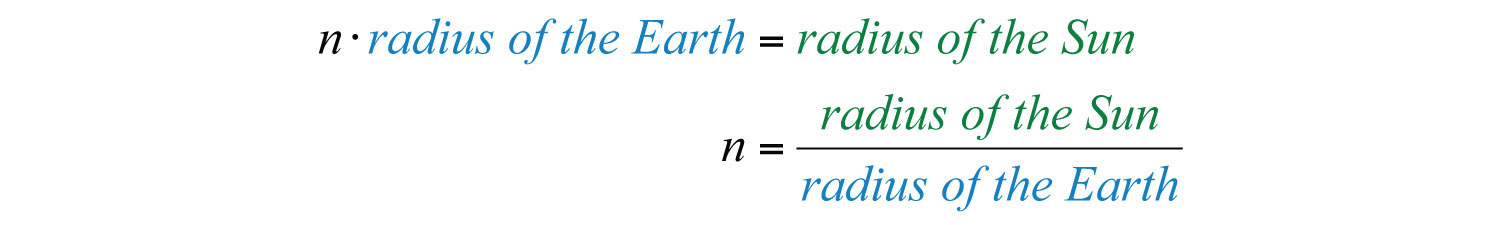
Therefore,
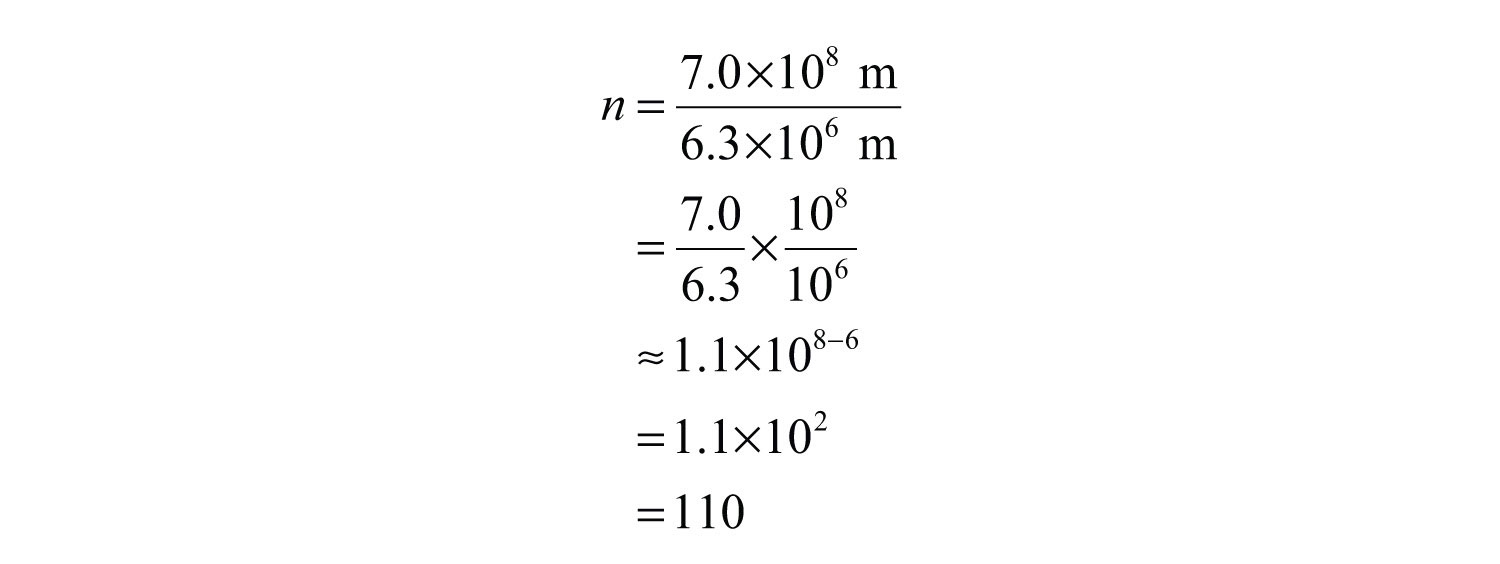
Answer: The radius of the sun is approximately 110 times that of earth.
Try this! Divide: .
Answer:
Video Solution
(click to see video)Key Takeaways
- Expressions with negative exponents in the numerator can be rewritten as expressions with positive exponents in the denominator.
- Expressions with negative exponents in the denominator can be rewritten as expressions with positive exponents in the numerator.
- Take care to distinguish negative coefficients from negative exponents.
- Scientific notation is particularly useful when working with numbers that are very large or very small.
Topic Exercises
Part A: Negative Exponents
Simplify. (Assume variables are nonzero.)
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
The value in dollars of a new MP3 player can be estimated by using the formula , where t is the number of years after purchase.
47. How much was the MP3 player worth new?
48. How much will the MP3 player be worth in 1 year?
49. How much will the MP3 player be worth in 4 years?
50. How much will the MP3 player be worth in 9 years?
51. How much will the MP3 player be worth in 99 years?
52. According to the formula, will the MP3 ever be worthless? Explain.
Part B: Scientific Notation
Convert to a decimal number.
53.
54.
55.
56.
57.
58.
59.
60.
Rewrite using scientific notation.
61. 500,000,000
62. 407,300,000,000,000
63. 9,740,000
64. 100,230
65. 0.0000123
66. 0.000012
67. 0.000000010034
68. 0.99071
Perform the indicated operations.
69.
70.
71.
72.
73.
74.
75.
76.
77. 59,000,000,000,000 × 0.000032
78. 0.0000000000432 × 0.0000000000673
79. 1,030,000,000,000,000,000 ÷ 2,000,000
80. 6,045,000,000,000,000 ÷ 0.00000005
81. The population density of earth refers to the number of people per square mile of land area. If the total land area on earth is square miles and the population in 2007 was estimated to be people, then calculate the population density of earth at that time.
82. In 2008 the population of New York City was estimated to be 8.364 million people. The total land area is 305 square miles. Calculate the population density of New York City.
83. The mass of earth is kilograms and the mass of the moon is kilograms. By what factor is the mass of earth greater than the mass of the moon?
84. The mass of the sun is kilograms and the mass of earth is kilograms. By what factor is the mass of the sun greater than the mass of earth? Express your answer in scientific notation.
85. The radius of the sun is miles and the average distance from earth to the moon is miles. By what factor is the radius of the sun larger than the average distance from earth to the moon?
86. One light year, meters, is the distance that light travels in a vacuum in one year. If the distance to the nearest star to our sun, Proxima Centauri, is estimated to be meters, then calculate the number of years it would take light to travel that distance.
87. It is estimated that there are about 1 million ants per person on the planet. If the world population was estimated to be 6.67 billion people in 2007, then estimate the world ant population at that time.
88. The sun moves around the center of the galaxy in a nearly circular orbit. The distance from the center of our galaxy to the sun is approximately 26,000 light years. What is the circumference of the orbit of the sun around the galaxy in meters?
89. Water weighs approximately 18 grams per mole. If one mole is about molecules, then approximate the weight of each molecule of water.
90. A gigabyte is bytes and a megabyte is bytes. If the average song in the MP3 format consumes about 4.5 megabytes of storage, then how many songs will fit on a 4-gigabyte memory card?
Answers
1:
3:
5:
7:
9:
11:
13:
15:
17:
19:
21:
23:
25:
27:
29:
31:
33:
35:
37:
39:
41:
43:
45:
47: $100
49: $20
51: $1
53: 9,300,000,000
55: 60,800,000,000
57: 0.000000401
59: 0.0099
61:
63:
65:
67:
69:
71:
73:
75:
77:
79:
81: About 116 people per square mile
83: 81.2
85: 1.807
87: ants
89: grams
5.7 Review Exercises and Sample Exam
Review Exercises
Rules of Exponents
Simplify.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11. Each side of a square measures units. Find the area of the square in terms of x.
12. Each side of a cube measures units. Find the volume of the cube in terms of x.
Introduction to Polynomials
Classify the given polynomial as a monomial, binomial, or trinomial and state the degree.
13.
14.
15.
16. 10
Write the following polynomials in standard form.
17.
18.
Evaluate.
19. , where
20. , where
21. , where , , and
22. , where and
23. , where and
24. , where and
25. Given , find .
26. Given , find .
27. The surface area of a rectangular solid is given by the formula , where l, w, and h represent the length, width, and height, respectively. If the length of a rectangular solid measures 2 units, the width measures 3 units, and the height measures 5 units, then calculate the surface area.
28. The surface area of a sphere is given by the formula , where r represents the radius of the sphere. If a sphere has a radius of 5 units, then calculate the surface area.
Adding and Subtracting Polynomials
Perform the operations.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39. Subtract from .
40. Subtract from .
41. Given and , find .
42. Given and , find .
43. Given and , find .
44. Given and , find .
Multiplying Polynomials
Multiply.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59. Find the product of and .
60. Find the product of and .
61. Given and , find .
62. Given and , find .
63. Given and , find .
64. Given and , find .
Dividing Polynomials
Divide.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79. Given and , find .
80. Given and , find .
81. Given and , find .
82. Given and , find .
Negative Exponents
Simplify.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
The value in dollars of a new laptop computer can be estimated by using the formula , where t represents the number of years after the purchase.
94. Estimate the value of the laptop when it is 1½ years old.
95. What was the laptop worth new?
Rewrite using scientific notation.
96. 2,030,000,000
97. 0.00000004011
Perform the indicated operations.
98.
99.
100.
101.
102. 5,000,000,000,000 × 0.0000023
103. 0.0003/120,000,000,000,000
Sample Exam
Simplify.
1.
2.
3.
4. a. ; b.
Evaluate.
5. , where
6. , where and
Perform the operations.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
Simplify.
17.
18.
19.
20.
21. Subtract from .
22. If each side of a cube measures units, calculate the volume in terms of x.
23. The height of a projectile in feet is given by the formula , where t represents time in seconds. Calculate the height of the projectile at 1½ seconds.
24. The cost in dollars of producing custom t-shirts is given by the formula , where x represents the number of t-shirts produced. The revenue generated by selling the t-shirts for $6.50 each is given by the formula , where x represents the number of t-shirts sold.
a. Find a formula for the profit. (profit = revenue − cost)
b. Use the formula to calculate the profit from producing and selling 150 t-shirts.
25. The total volume of water in earth’s oceans, seas, and bays is estimated to be cubic feet. By what factor is the volume of the moon, cubic feet, larger than the volume of earth’s oceans? Round to the nearest tenth.
Review Exercises Answers
1:
3:
5:
7:
9:
11:
13: Binomial; degree 3
15: Monomial; degree 3
17:
19: 22
21: 6
23: −7
25:
27: 62 square units
29:
31:
33:
35:
37:
39:
41:
43:
45:
47:
49:
51:
53:
55:
57:
59:
61:
63:
65:
67:
69:
71:
73:
75:
77:
79:
81:
83:
85:
87:
89:
91:
93:
95: $1,200
97:
99:
101:
103:
Sample Exam Answers
1:
3:
5: 60
7:
9:
11:
13:
15:
17:
19:
21:
23: 118 feet
25: 16.4




