This is “Rules of Exponents”, section 5.1 from the book Beginning Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
5.1 Rules of Exponents
Learning Objectives
- Simplify expressions using the rules of exponents.
- Simplify expressions involving parentheses and exponents.
- Simplify expressions involving 0 as an exponent.
Product, Quotient, and Power Rule for Exponents
If a factor is repeated multiple times, then the product can be written in exponential formAn equivalent expression written using a rational exponent. . The positive integer exponent n indicates the number of times the base x is repeated as a factor.
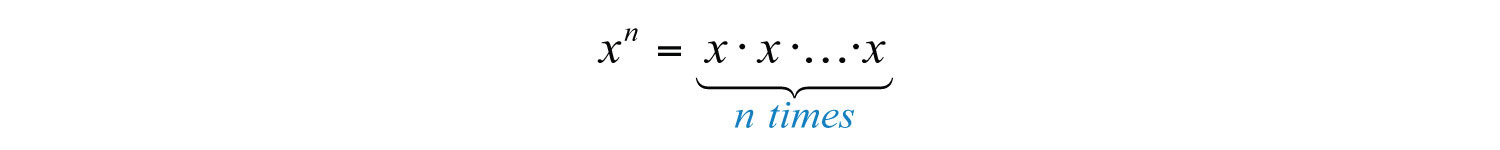
For example,
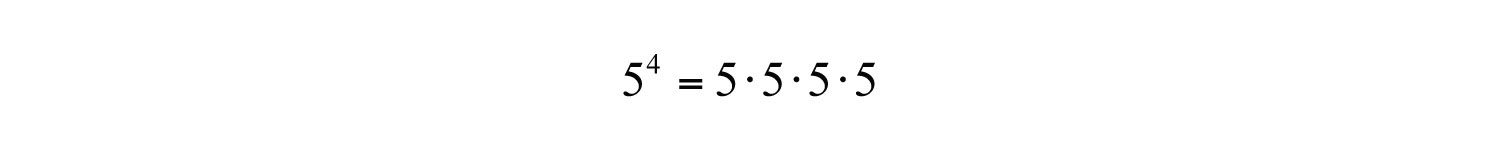
Here the base is 5 and the exponent is 4. Exponents are sometimes indicated with the caret (^) symbol found on the keyboard: 5^4 = 5*5*5*5.
Next consider the product of and ,
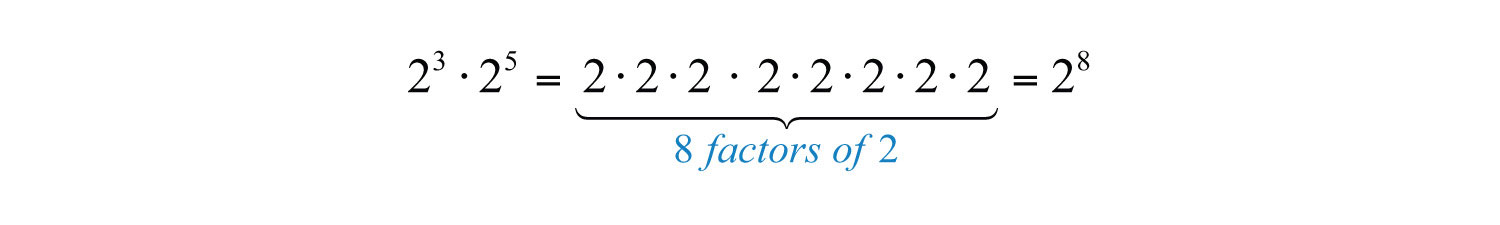
Expanding the expression using the definition produces multiple factors of the base, which is quite cumbersome, particularly when n is large. For this reason, we will develop some useful rules to help us simplify expressions with exponents. In this example, notice that we could obtain the same result by adding the exponents.
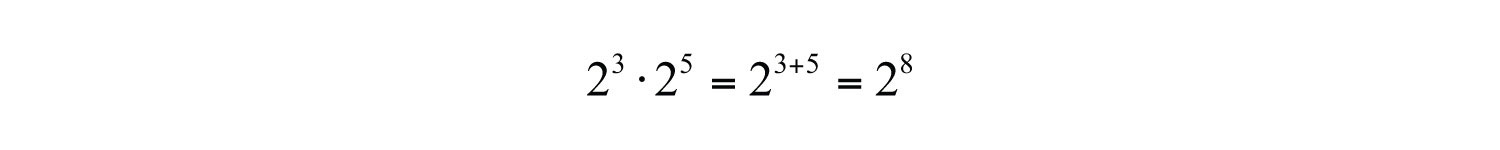
In general, this describes the product rule for exponents; the product of two expressions with the same base can be simplified by adding the exponents.. If m and n are positive integers, then
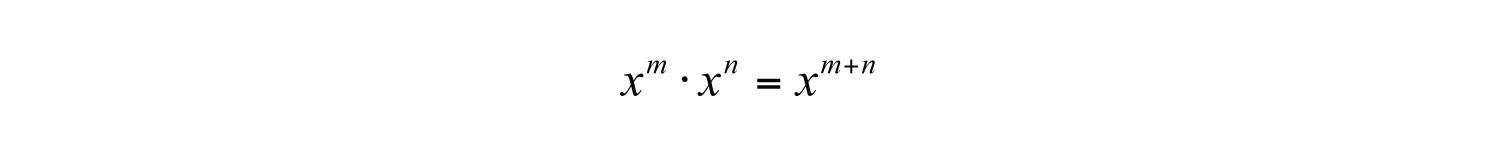
In other words, when multiplying two expressions with the same base, add the exponents.
Example 1: Simplify: .
Solution:
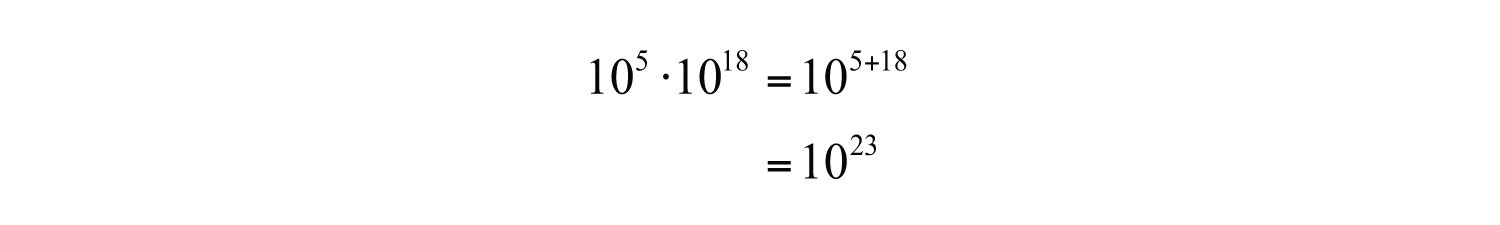
Answer:
In the previous example, notice that we did not multiply the base 10 times itself. When applying the product rule, add the exponents and leave the base unchanged.
Example 2: Simplify: .
Solution: Recall that the variable x is assumed to have an exponent of 1: .
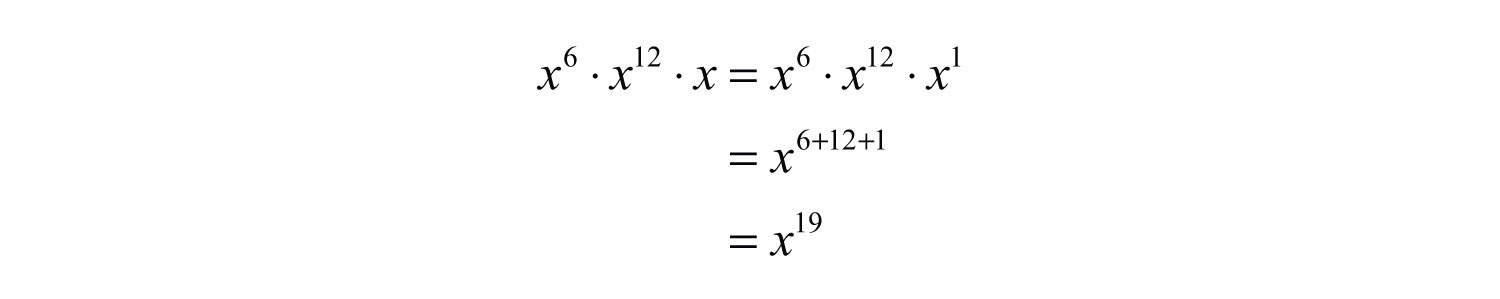
Answer:
The base could be any algebraic expression.
Example 3: Simplify: .
Solution: Treat the expression as the base.
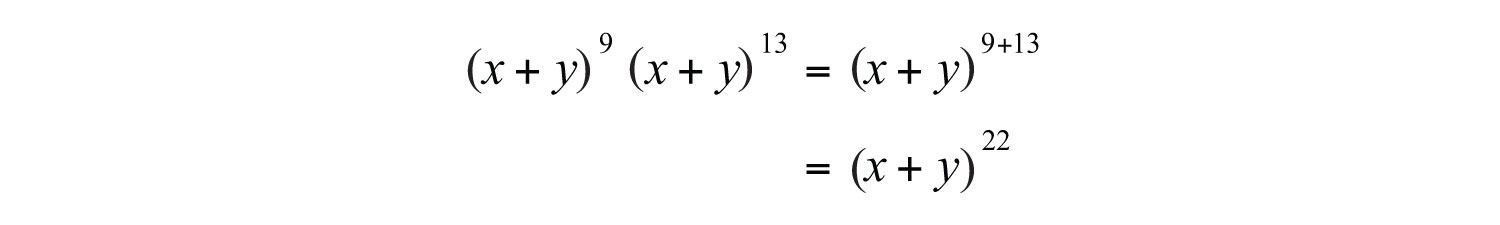
Answer:
The commutative property of multiplication allows us to use the product rule for exponents to simplify factors of an algebraic expression.
Example 4: Simplify: .
Solution: Multiply the coefficients and add the exponents of variable factors with the same base.
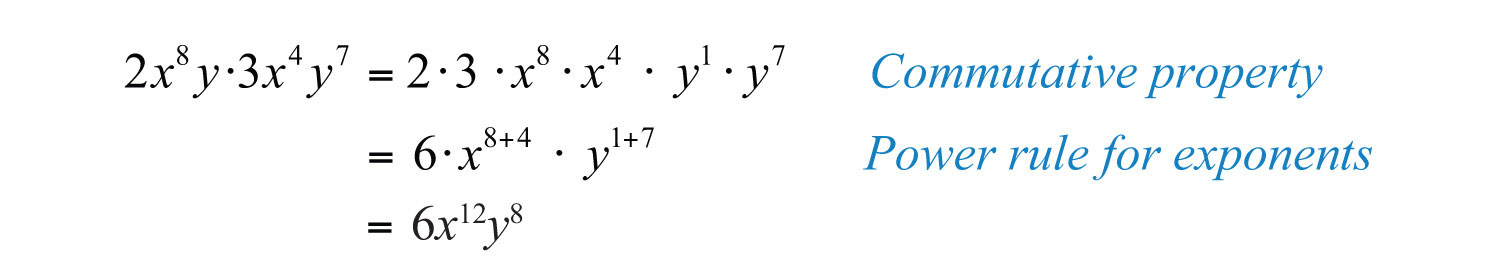
Answer:
Next, we will develop a rule for division by first looking at the quotient of and .
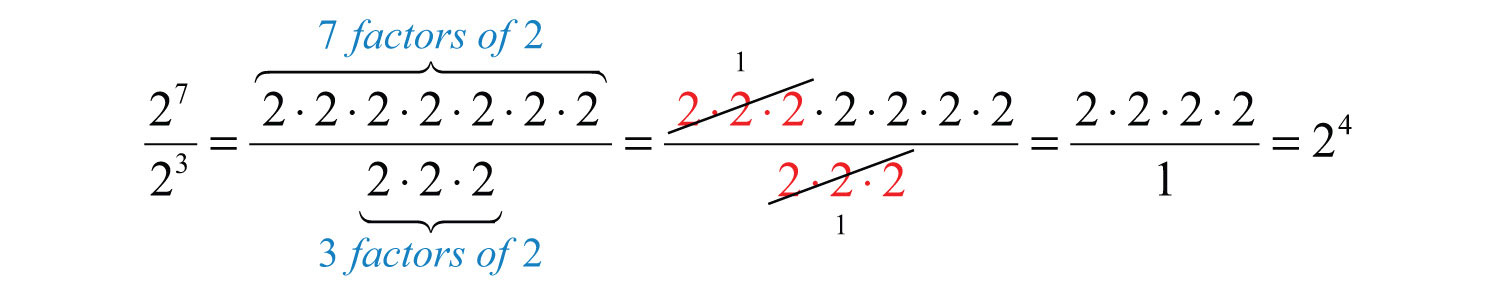
Here we can cancel factors after applying the definition of exponents. Notice that the same result can be obtained by subtracting the exponents.
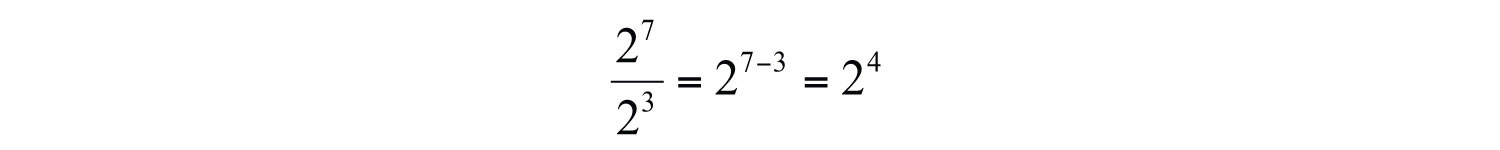
This describes the quotient rule for exponents; the quotient of two expressions with the same base can be simplified by subtracting the exponents.. If m and n are positive integers and , then
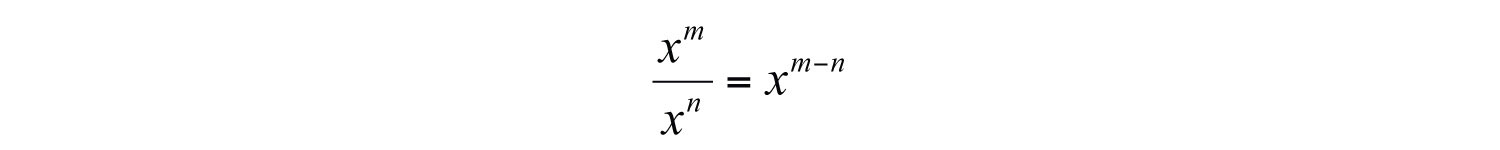
In other words, when you divide two expressions with the same base, subtract the exponents.
Example 5: Simplify: .
Solution: Divide the coefficients and subtract the exponents of the variable y.
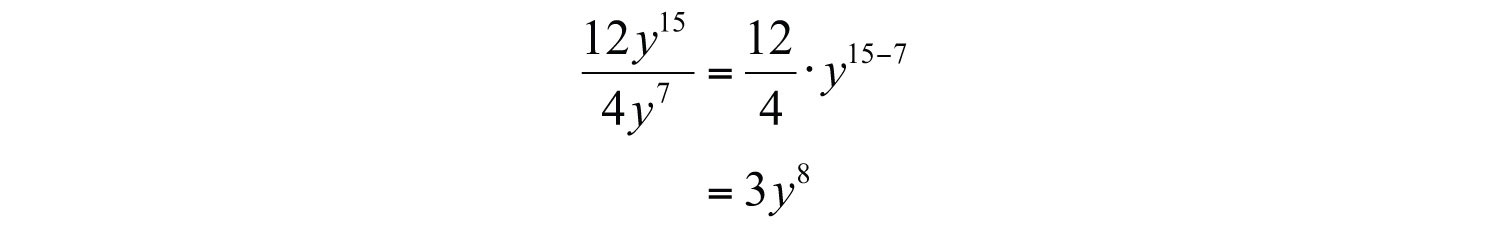
Answer:
Example 6: Simplify: .
Solution:
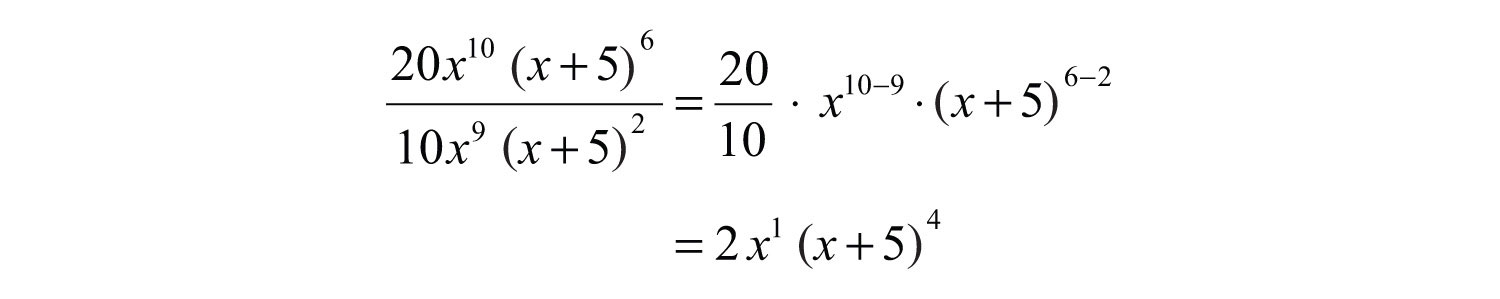
Answer:
Now raise to the fourth power as follows:
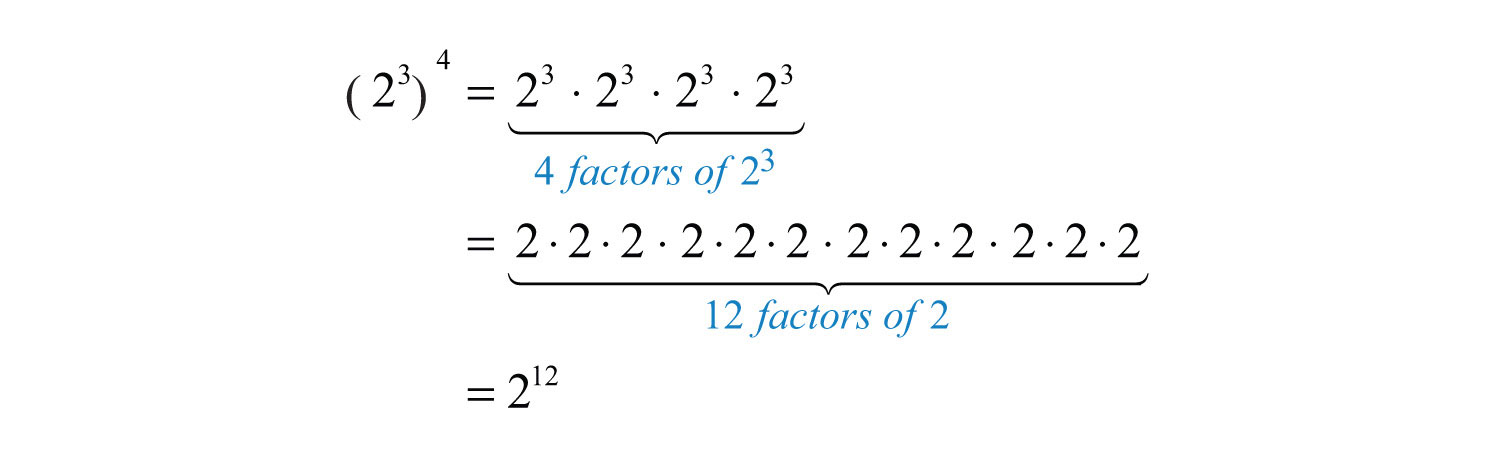
After writing the base as a factor four times, expand to obtain 12 factors of 2. We can obtain the same result by multiplying the exponents.
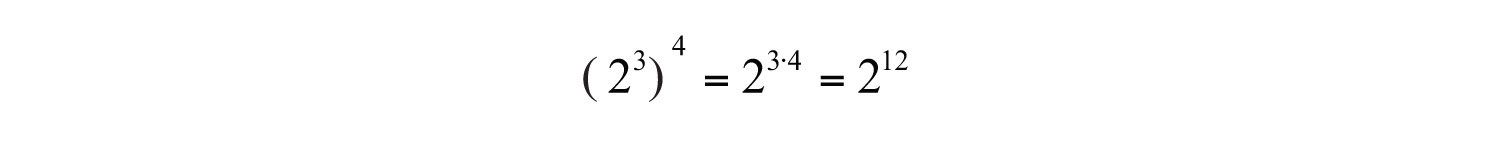
In general, this describes the power rule for exponents; a power raised to a power can be simplified by multiplying the exponents.. Given positive integers m and n, then
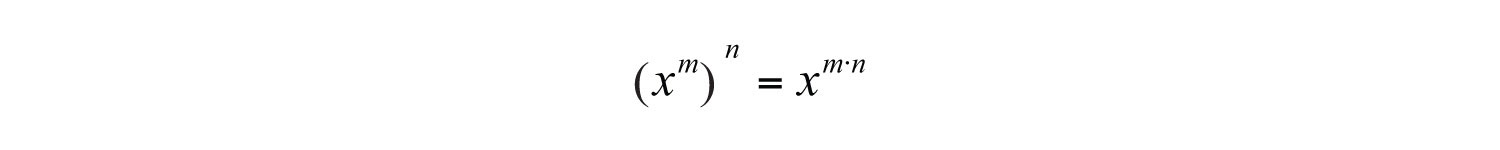
In other words, when raising a power to a power, multiply the exponents.
Example 7: Simplify: .
Solution:
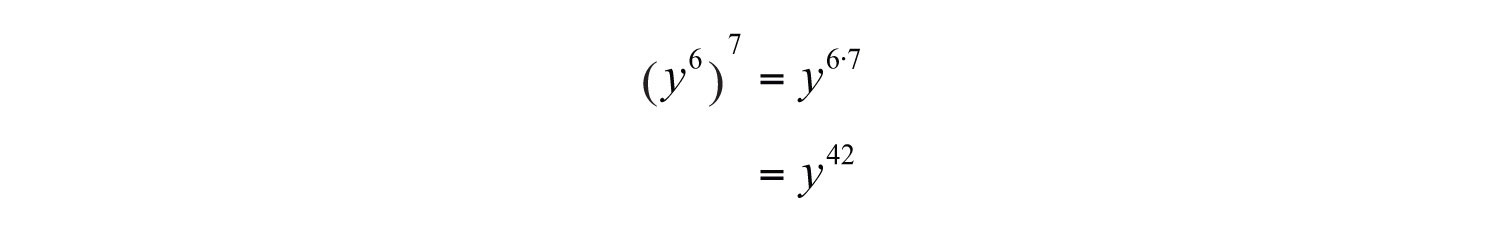
Answer:
To summarize, we have developed three very useful rules of exponents that are used extensively in algebra. If given positive integers m and n, then
| Product rule: | |
| Quotient rule: | |
| Power rule: |
Try this! Simplify: .
Answer:
Video Solution
(click to see video)Power Rules for Products and Quotients
Now we consider raising grouped products to a power. For example,
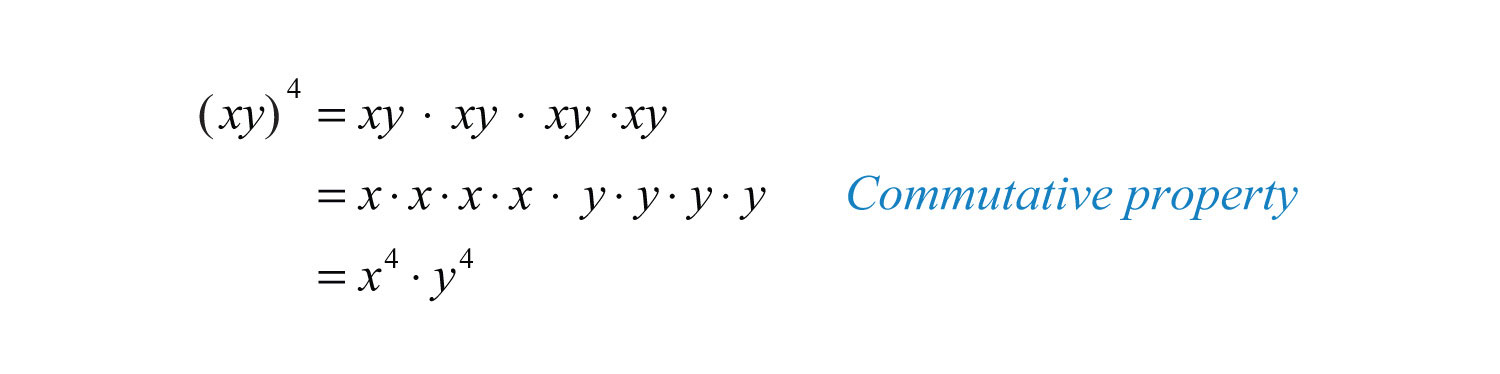
After expanding, we have four factors of the product xy. This is equivalent to raising each of the original factors to the fourth power. In general, this describes the power rule for a product; if a product is raised to a power, then apply that power to each factor in the product.. If n is a positive integer, then
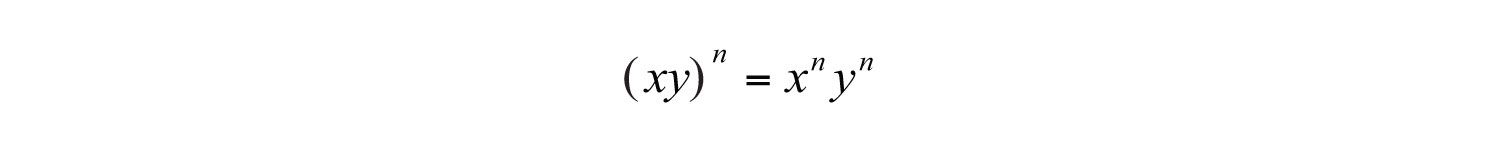
Example 8: Simplify: .
Solution: We must apply the exponent 7 to all the factors, including the coefficient, 2.
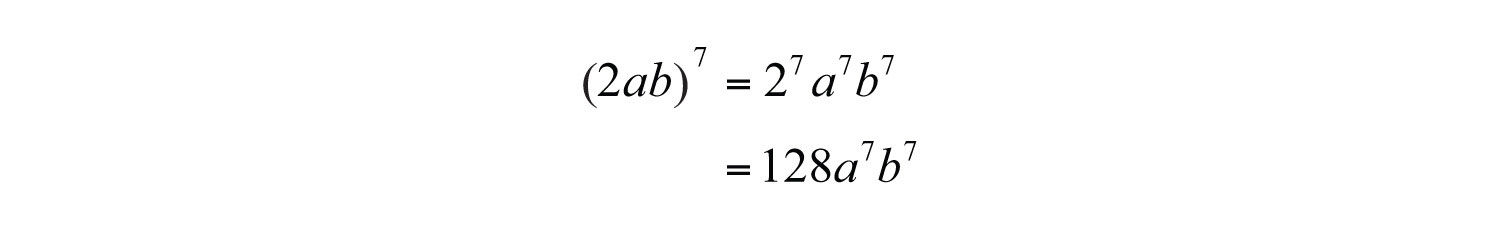
If a coefficient is raised to a relatively small power, then present the real number equivalent, as we did in this example: .
Answer:
In many cases, the process of simplifying expressions involving exponents requires the use of several rules of exponents.
Example 9: Simplify: .
Solution:
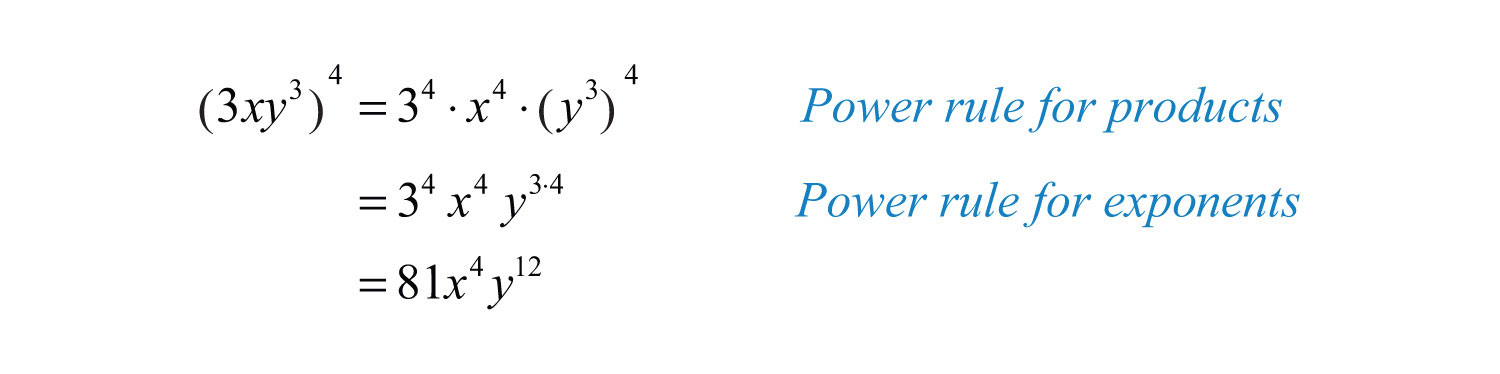
Answer:
Example 10: Simplify: .
Solution:
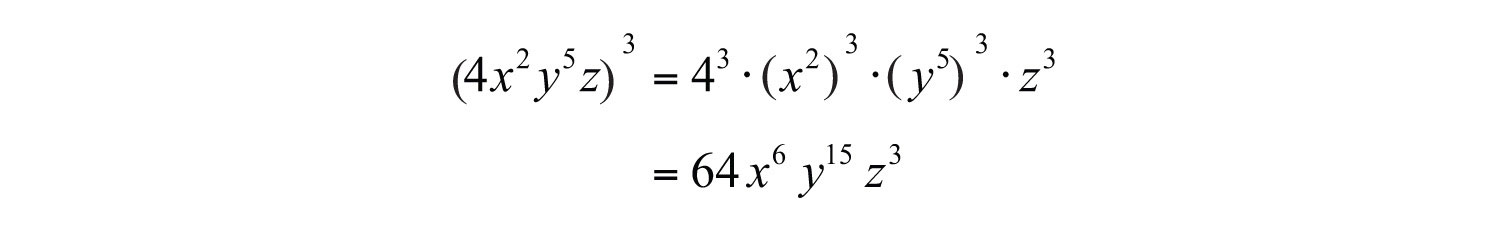
Answer:
Example 11: Simplify: .
Solution:
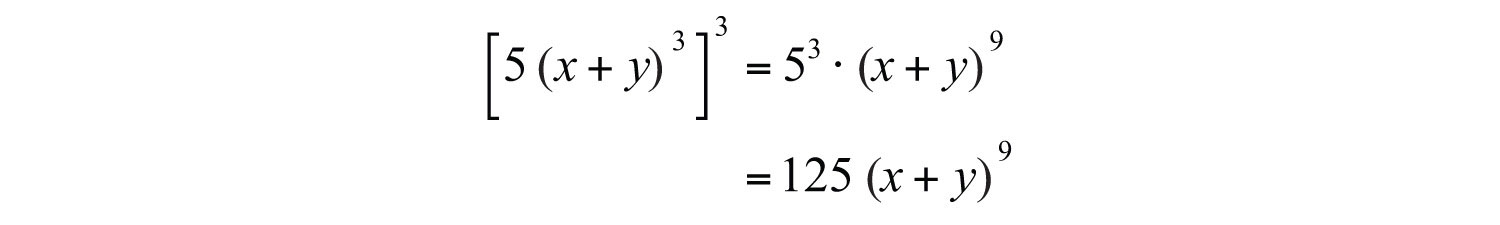
Answer:
Next, consider a quotient raised to a power.
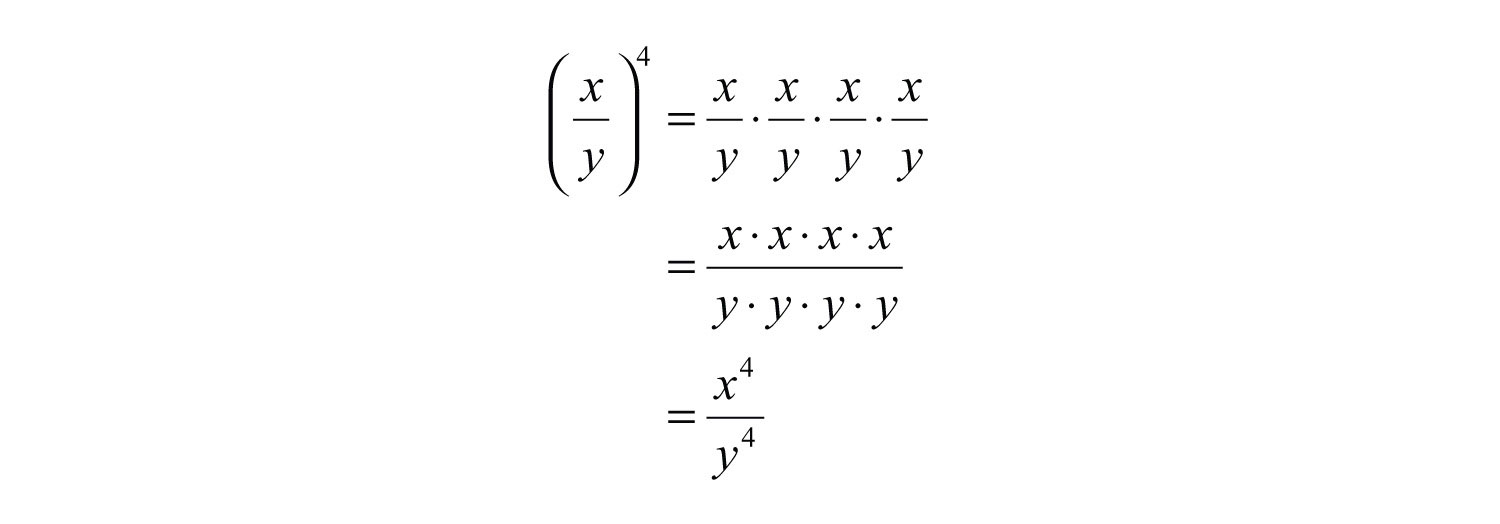
Here we obtain four factors of the quotient, which is equivalent to the numerator and the denominator both raised to the fourth power. In general, this describes the power rule for a quotient; if a quotient is raised to a power, then apply that power to the numerator and the denominator.. If n is a positive integer and , then
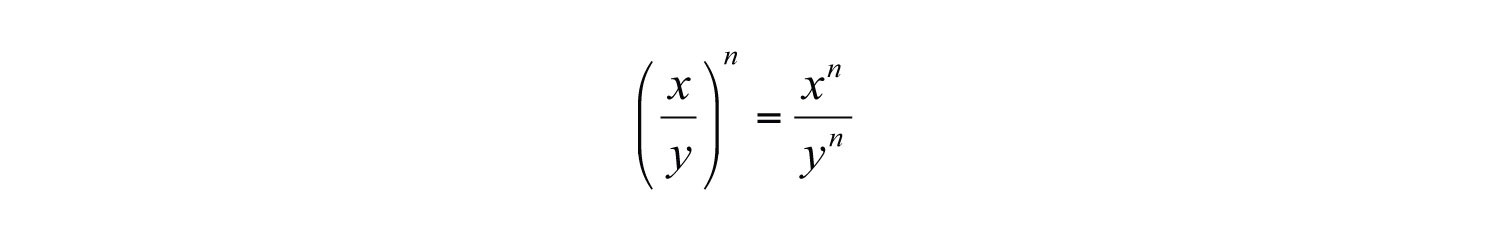
In other words, given a fraction raised to a power, we can apply that exponent to the numerator and the denominator. This rule requires that the denominator is nonzero. We will make this assumption for the remainder of the section.
Example 12: Simplify: .
Solution: First, apply the power rule for a quotient and then the power rule for a product.
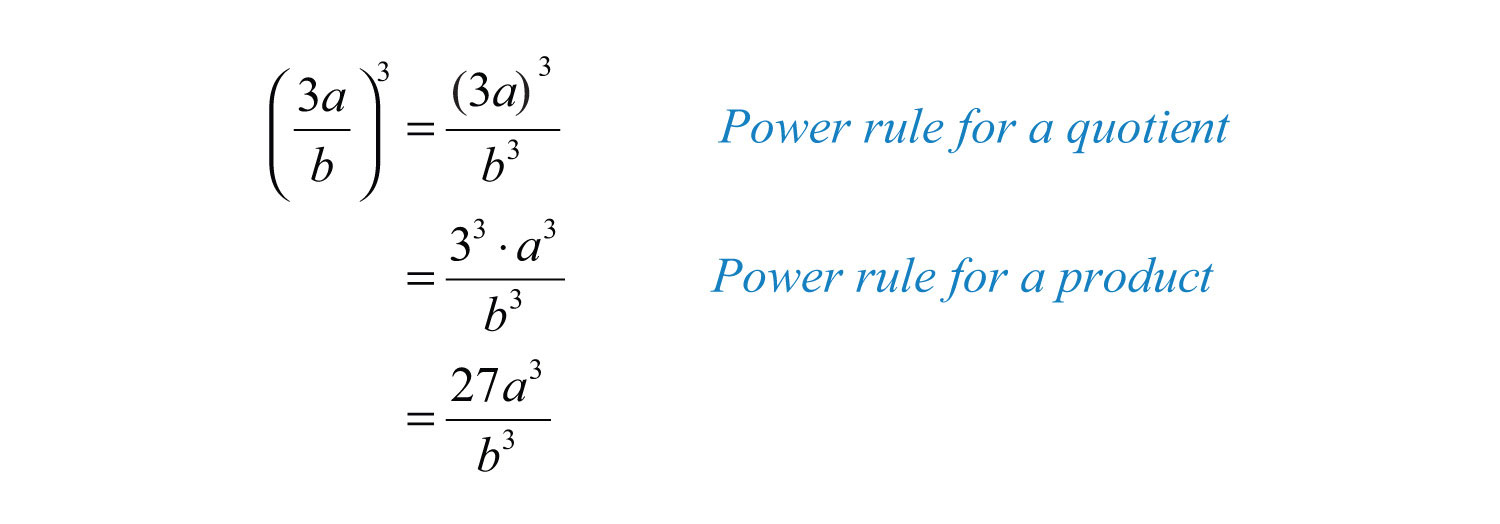
Answer:
In practice, we often combine these two steps by applying the exponent to all factors in the numerator and the denominator.
Example 13: Simplify: .
Solution: Apply the exponent 5 to all of the factors in the numerator and the denominator.
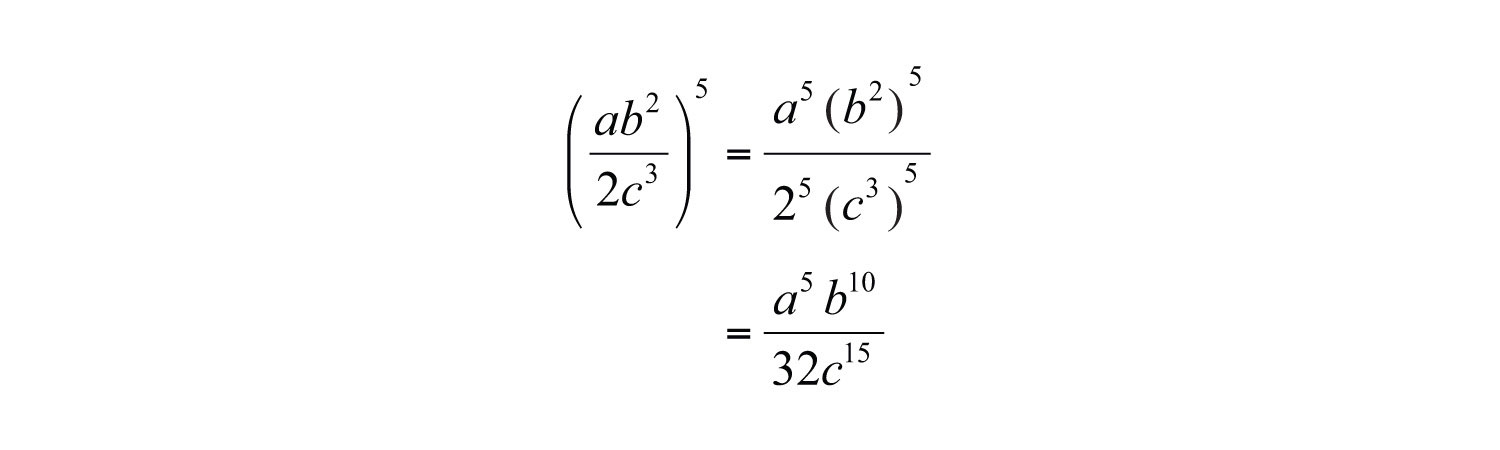
Answer:
Example 14: Simplify: .
Solution:
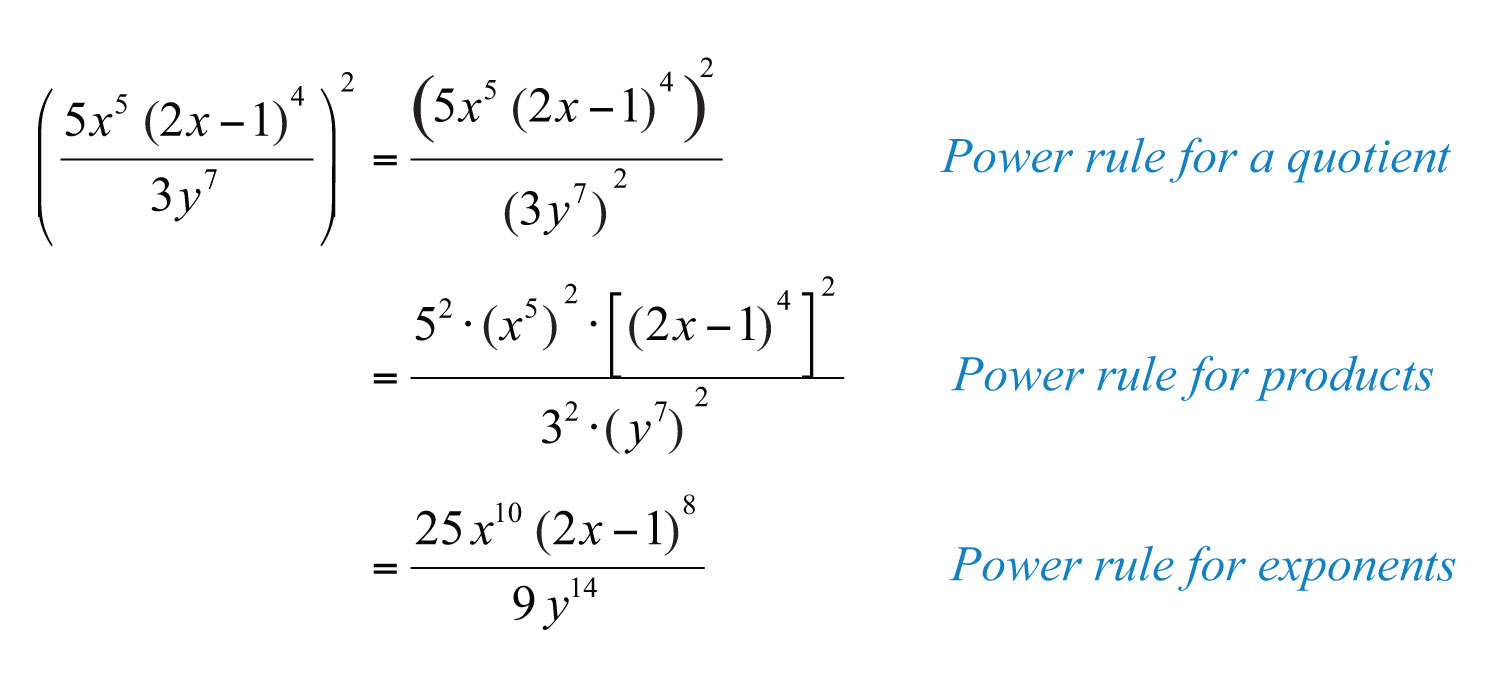
Answer:
It is a good practice to simplify within parentheses before using the power rules; this is consistent with the order of operations.
Example 15: Simplify: .
Solution:

Answer:
To summarize, we have developed two new rules that are useful when grouping symbols are used in conjunction with exponents. If given a positive integer n, where y is a nonzero number, then
| Power rule for a product: | |
| Power rule for a quotient: |
Try this! Simplify: .
Answer:
Video Solution
(click to see video)Zero as an Exponent
Using the quotient rule for exponents, we can define what it means to have 0 as an exponent. Consider the following calculation:
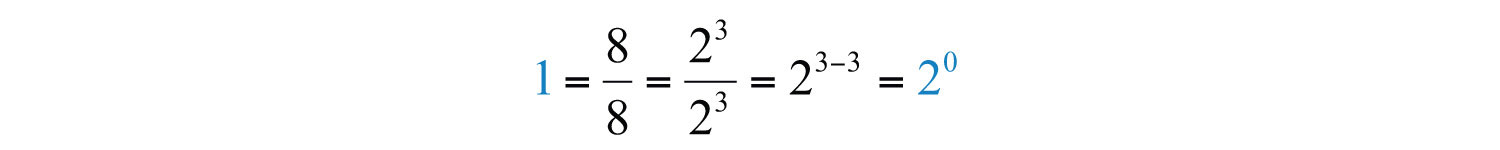
Eight divided by 8 is clearly equal to 1, and when the quotient rule for exponents is applied, we see that a 0 exponent results. This leads us to the definition of zero as an exponent; any nonzero base raised to the 0 power is defined to be 1., where :
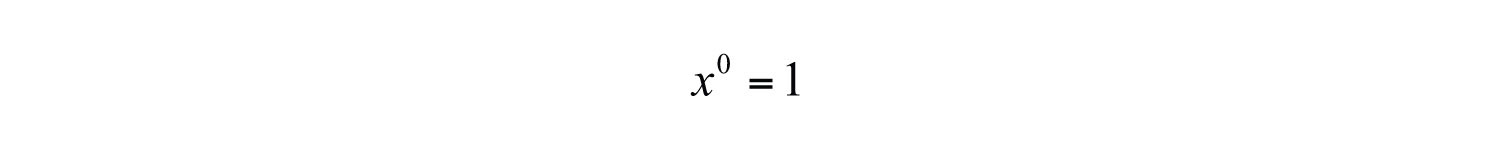
It is important to note that is undefined. If the base is negative, then the result is still +1. In other words, any nonzero base raised to the 0 power is defined to be 1. In the following examples, assume all variables are nonzero.
Example 16: Simplify:
a.
b.
Solution:
a. Any nonzero quantity raised to the 0 power is equal to 1.
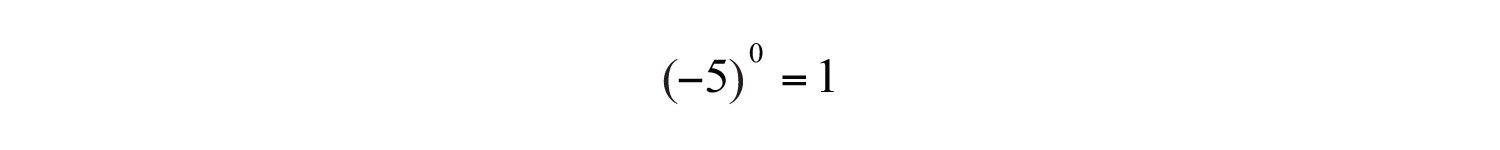
b. In the example , the base is 5, not −5.
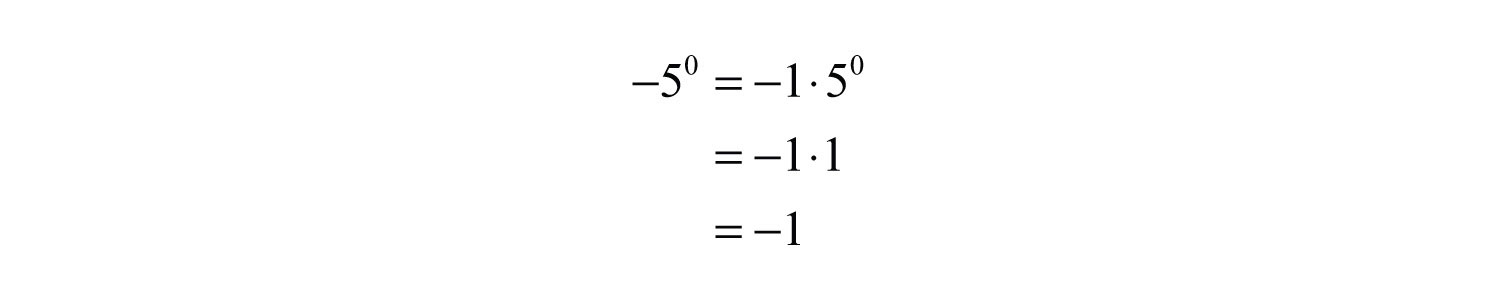
Answers: a. 1; b. −1
Example 17: Simplify: .
Solution: It is good practice to simplify within the parentheses first.
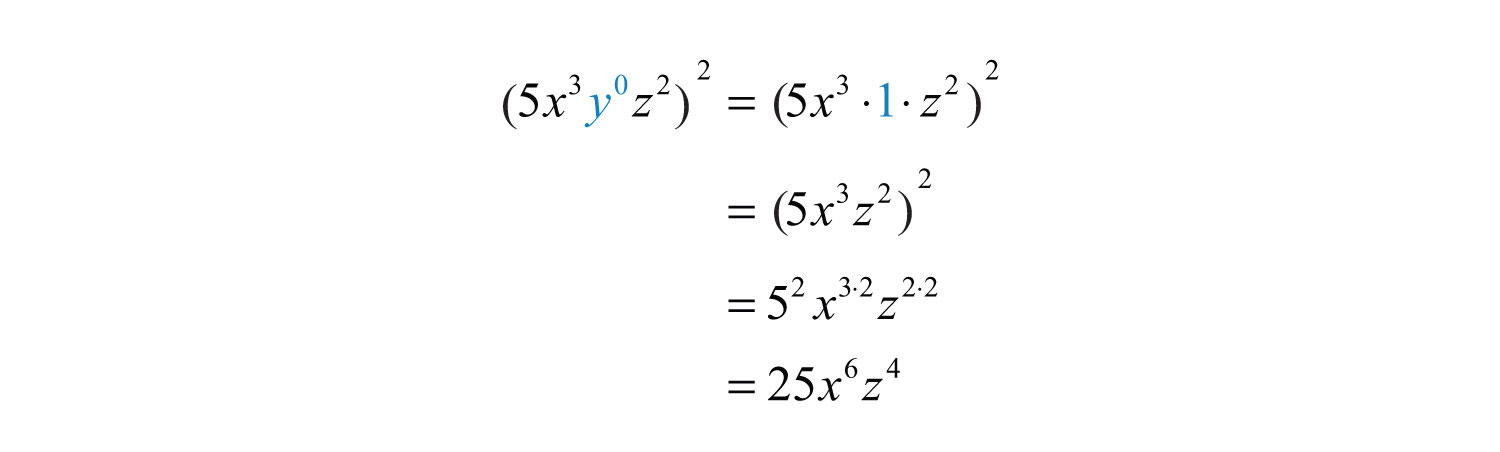
Answer:
Example 18: Simplify: .
Solution:
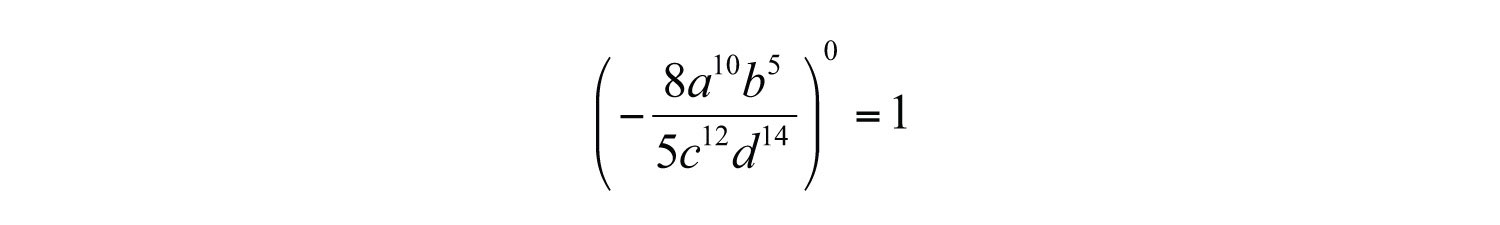
Answer: 1
Try this! Simplify: and .
Answer: and
Video Solution
(click to see video)Key Takeaways
- The rules of exponents allow you to simplify expressions involving exponents.
- When multiplying two quantities with the same base, add exponents: .
- When dividing two quantities with the same base, subtract exponents: .
- When raising powers to powers, multiply exponents: .
- When a grouped quantity involving multiplication and division is raised to a power, apply that power to all of the factors in the numerator and the denominator: and .
- Any nonzero quantity raised to the 0 power is defined to be equal to 1: .
Topic Exercises
Part A: Product, Quotient, and Power Rule for Exponents
Write each expression using exponential form.
1.
2.
3.
4.
5.
6.
Simplify.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
Simplify.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
Part B: Power Rules for Products and Quotients
Simplify.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91. The probability of tossing a fair coin and obtaining n heads in a row is given by the formula . Determine the probability, as a percent, of tossing 5 heads in a row.
92. The probability of rolling a single fair six-sided die and obtaining n of the same faces up in a row is given by the formula . Determine the probability, as a percent, of obtaining the same face up two times in a row.
93. If each side of a square measures units, then determine the area in terms of the variable x.
94. If each edge of a cube measures units, then determine the volume in terms of the variable x.
Part C: Zero Exponents
Simplify. (Assume variables are nonzero.)
95.
96.
97.
98.
99.
100.
101.
102.
103.
104.
105.
106.
107.
108.
109.
Part D: Discussion Board Topics
110. René Descartes (1637) established the usage of exponential form: , , and so on. Before this, how were exponents denoted?
111. Discuss the accomplishments accredited to Al-Karismi.
112. Why is undefined?
113. Explain to a beginning student why .
Answers
1:
3:
5:
7:
9: −16
11: −27
13:
15:
17:
19:
21:
23:
25:
27:
29:
31:
33:
35:
37:
39:
41:
43:
45:
47:
49:
51:
53:
55:
57:
59:
61:
63:
65:
67:
69:
71:
73:
75:
77:
79:
81:
83:
85:
87:
89:
91:
93:
95: 1
97: −1
99: 1
101: −4
103:
105:
107: 1
109:




