This is “Review Exercises and Sample Exam”, section 4.6 from the book Beginning Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
4.6 Review Exercises and Sample Exam
Review Exercises
Solving Linear Systems by Graphing
Determine whether the given ordered pair is a solution to the given system.
1. (1, −3);
2. (−3, −4);
3. (−1, 1/5);
4. (1/2, −1);
Given the graph, determine the simultaneous solution.
5.
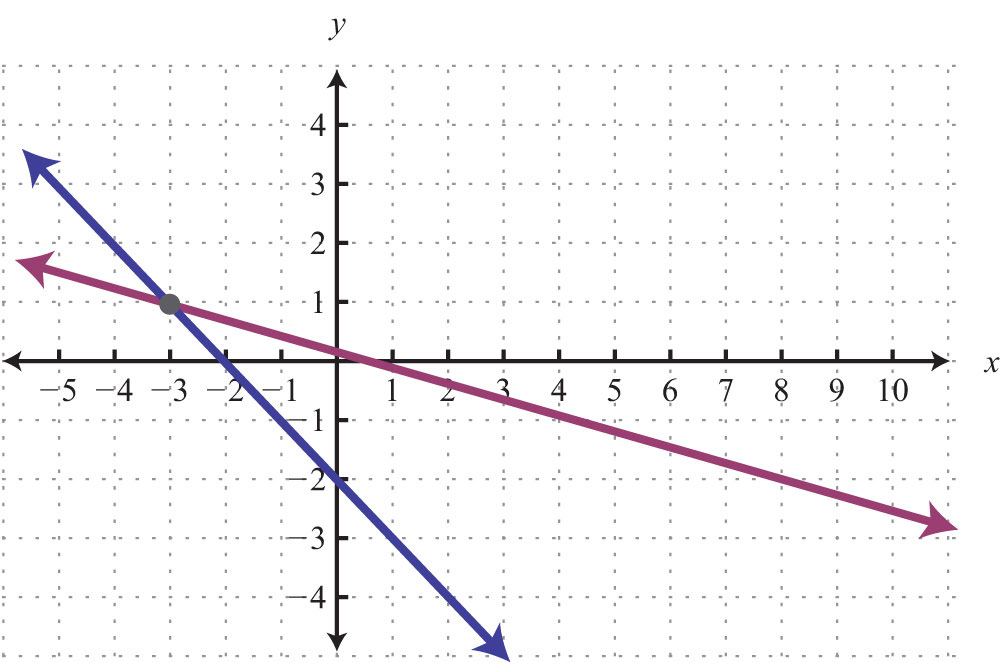
6.
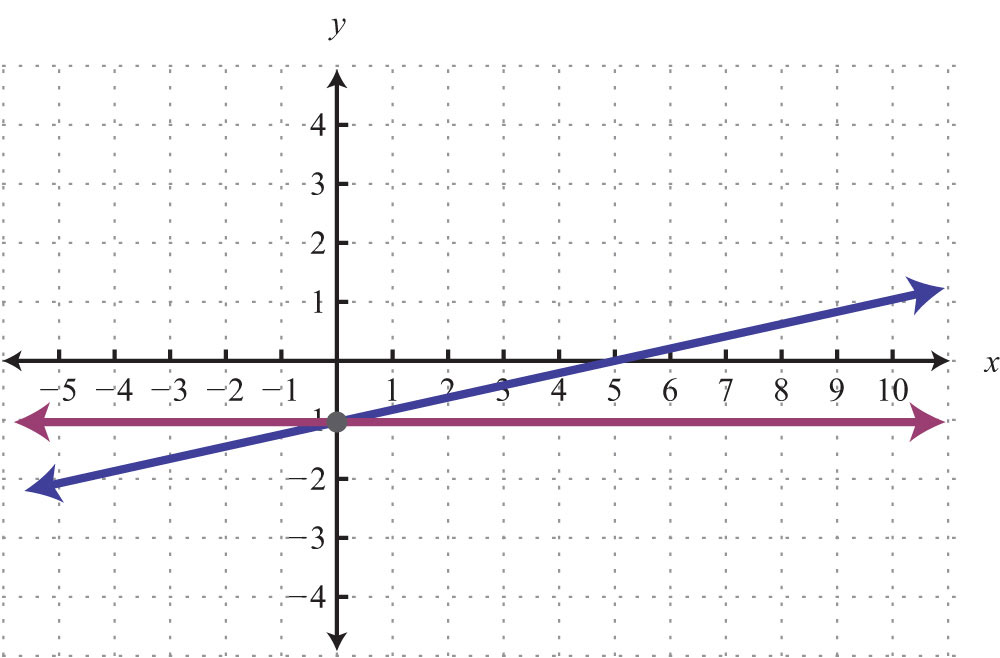
7.
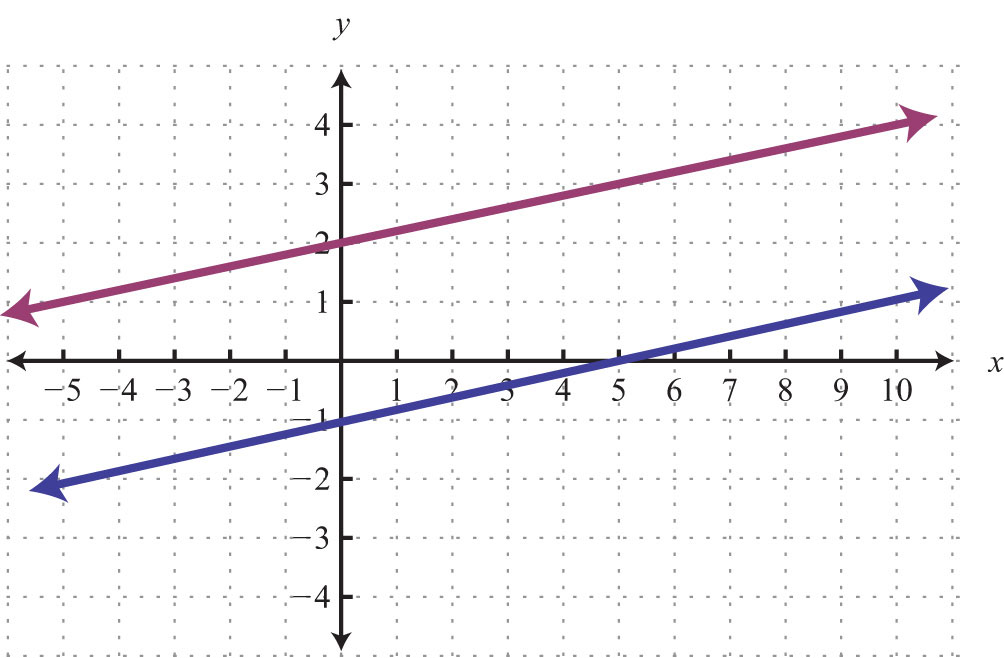
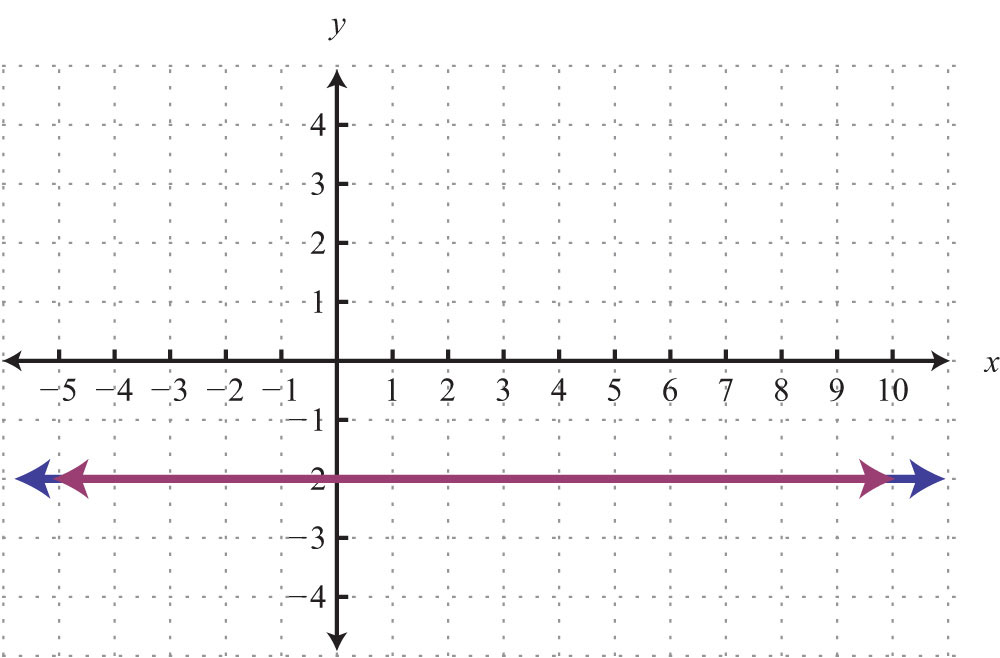
8.
Solve by graphing.
9.
10.
11.
12.
13.
14.
Solving Linear Systems by Substitution
Solve by substitution.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
Solving Linear Systems by Elimination
Solve by elimination.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
Applications of Linear Systems
Set up a linear system and solve.
39. The sum of two numbers is 74 and their difference is 38. Find the numbers.
40. The sum of two numbers is 34. When the larger is subtracted from twice the smaller, the result is 8. Find the numbers.
41. A jar full of 40 coins consisting of dimes and nickels has a total value of $2.90. How many of each coin are in the jar?
42. A total of $9,600 was invested in two separate accounts earning 5.5% and 3.75% annual interest. If the total simple interest earned for the year was $491.25, then how much was invested in each account?
43. A 1% saline solution is to be mixed with a 3% saline solution to produce 6 ounces of a 1.8% saline solution. How much of each is needed?
44. An 80% fruit juice concentrate is to be mixed with water to produce 10 gallons of a 20% fruit juice mixture. How much of each is needed?
45. An executive traveled a total of 4½ hours and 435 miles to a conference by car and by light aircraft. Driving to the airport by car, he averaged 50 miles per hour. In the air, the light aircraft averaged 120 miles per hour. How long did it take him to drive to the airport?
46. Flying with the wind, an airplane traveled 1,065 miles in 3 hours. On the return trip, against the wind, the airplane traveled 915 miles in 3 hours. What is the speed of the wind?
Systems of Linear Inequalities (Two Variables)
Determine whether the given point is a solution to the system of linear inequalities.
47. (5, −2);
48. (2, 3);
49. (2, −10);
50. (0, −2);
Graph the solution set.
51.
52.
53.
54.
55.
56.
Sample Exam
1. Is (−3, 2) a solution to the system ?
2. Is (−2, 9) a solution to the system ?
Given the graph, determine the simultaneous solution.
3.
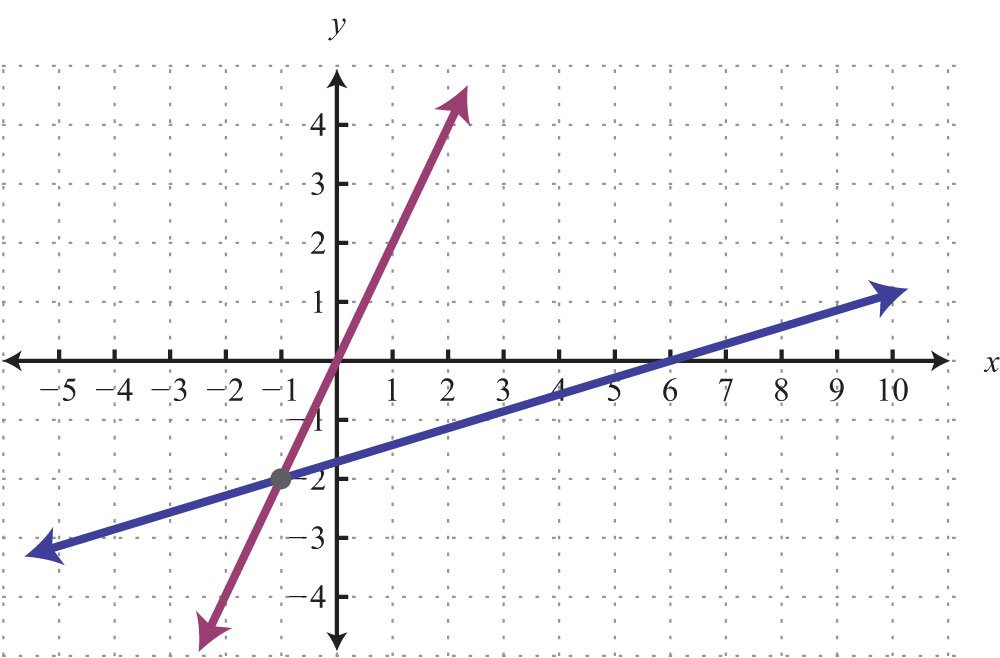
4.
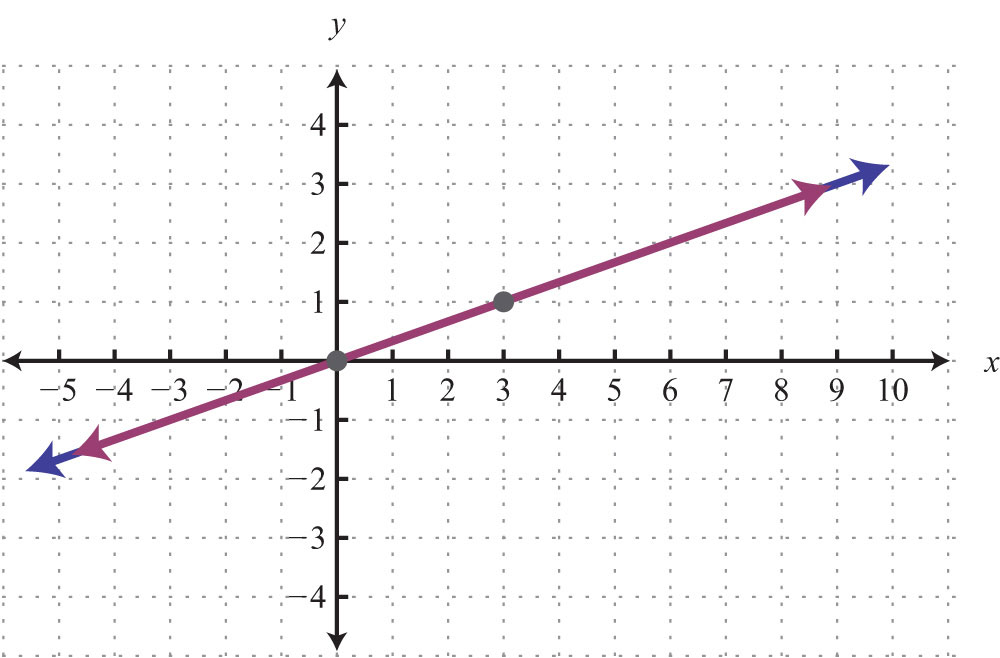
Solve using the graphing method.
5.
6.
7.
8.
Solve using the substitution method.
9.
10.
11.
12.
Solve using the elimination method.
13.
14.
15.
16.
17.
18.
Graph the solution set.
19.
20.
Set up a linear system of two equations and two variables and solve it using any method.
21. The sum of two integers is 23. If the larger integer is one less than twice the smaller, then find the two integers.
22. James has $2,400 saved in two separate accounts. One account earns 3% annual interest and the other earns 4%. If his interest for the year totals $88, then how much is in each account?
23. Mary drives 110 miles to her grandmother’s house in a total of 2 hours. On the freeway, she averages 62 miles per hour. In the city she averages 34 miles per hour. How long does she spend on the freeway?
24. A 15% acid solution is to be mixed with a 35% acid solution to produce 12 ounces of a 22% acid solution. How much of each is needed?
25. Joey has bag full of 52 dimes and quarters with a total value of $8.35. How many of each coin does Joey have?
Review Exercises Answers
1: Yes
3: Yes
5: (−3, 1)
7: Ø
9: (4, −1)
11: (6, 3)
13:
15: (1, 5)
17: (4, 4)
19: (1/2, −1/3)
21: Ø
23: (−1, 1/2)
25: (7, 2)
27: (−4, −5)
29: (−1/2, 3/4)
31: (0.2, −0.5)
33:
35: (5, 6)
37: (−3, 3/2)
39: 18 and 56
41: 18 dimes and 22 nickels
43: 3.6 ounces of the 1% saline solution and 2.4 ounces of the 3% saline solution
45: It took him 1½ hours to drive to the airport.
47: Yes
49: No
51:
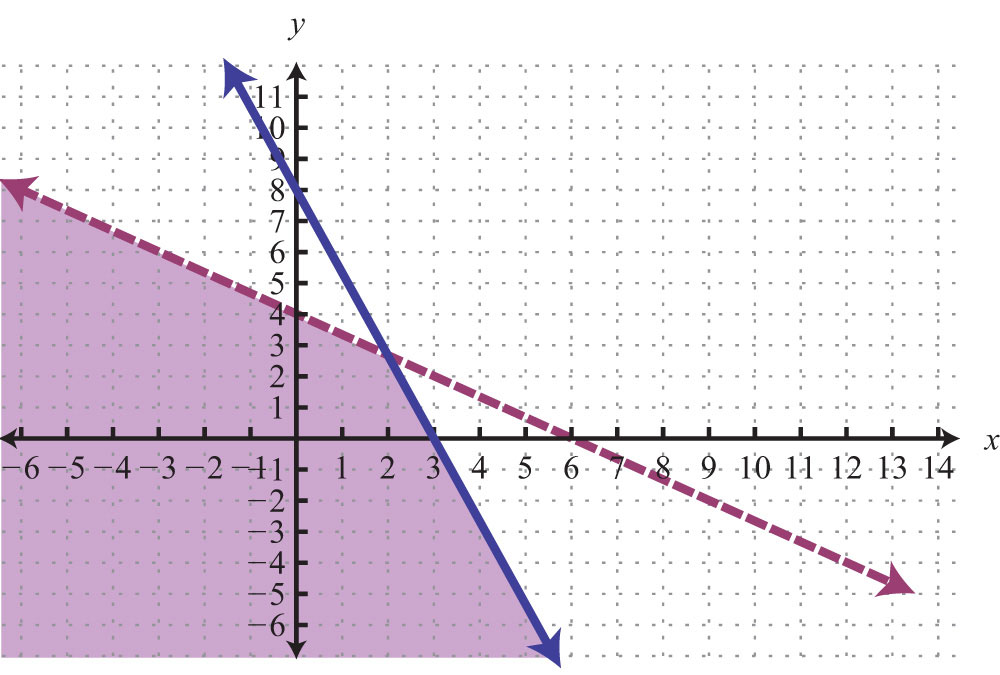
53:
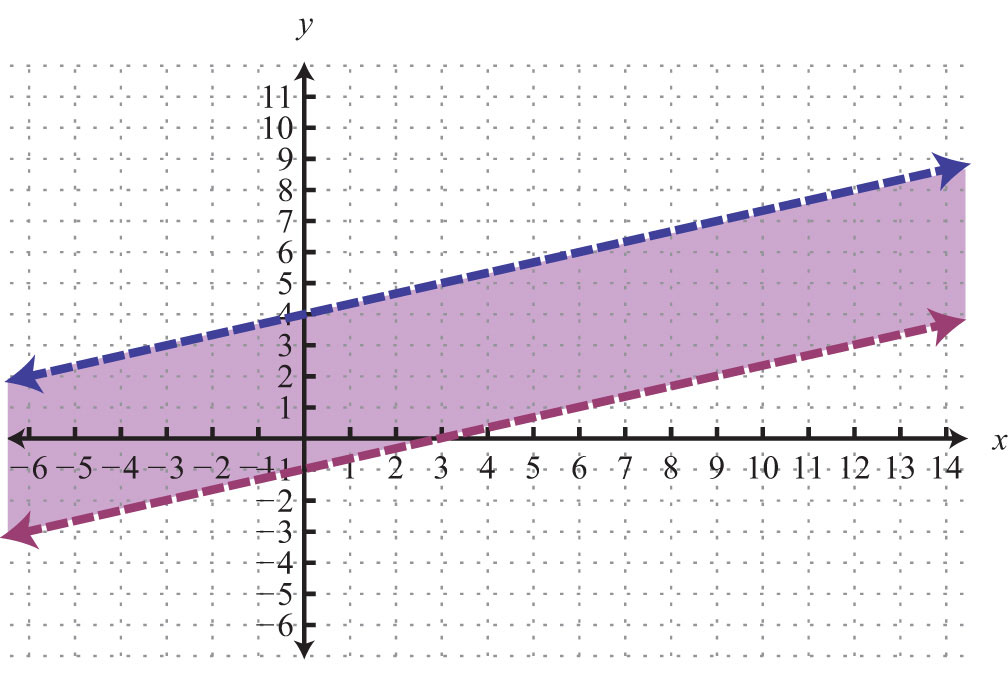
55:
Sample Exam Answers
1: Yes
3: (−1, −2)
5: (4, 1)
7: (1, 2)
9: (−3, 1)
11: Ø
13: (3, −1)
15: Ø
17: (1/2, 2)
19:
21: 8 and 15
23: She drives 1½ hours on the freeway.
25: 21 quarters and 31 dimes




