This is “Review Exercises and Sample Exam”, section 2.9 from the book Beginning Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
2.9 Review Exercises and Sample Exam
Review Exercises
Introduction to Algebra
Evaluate.
1. , where
2. , where
3. , where
4. , where
5. , where , , and
6. , where , , and
7. , where
8. , where
9. Calculate the simple interest earned on a 3-year investment of $750 at an annual interest rate of 8%.
10. A bus traveled for hours at an average speed of 48 miles per hour. What distance did the bus travel?
11. Calculate the area of a rectangle with dimensions 4½ feet by 6 feet.
12. Calculate the volume of a rectangular box with dimensions 4½ feet by 6 feet by 1 foot.
Simplifying Algebraic Expressions
Multiply.
13.
14.
15.
16.
17.
18.
Simplify.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31. Subtract from .
32. Subtract from twice the quantity .
Solving Linear Equations: Part I
Is the given value a solution to the linear equation?
33. ;
34. ;
35. ;
36. ;
Solve.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51. The sum of 9x and 6 is 51.
52. The difference of 3x and 8 is 25.
Solving Linear Equations: Part II
Solve.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69. The sum of 4x and 3 is equal to the difference of 7x and 8.
70. The difference of 5x and 1 is equal to the sum of 12x and 1.
71. Solve for x:
72. Solve for y:
73. Solve for l:
74. Solve for b:
Applications of Linear Equations
75. A larger integer is 3 more than twice a smaller integer. If their sum is 39, then find the integers.
76. A larger integer is 5 more than 3 times a smaller integer. If their sum is 49, then find the integers.
77. The sum of three consecutive odd integers is 45. Find the integers.
78. The sum of three consecutive even integers is 72. Find the integers.
79. The sum of three consecutive integers is 60. Find the integers.
80. The length of a rectangle is 7 centimeters less than twice its width. If the perimeter measures 46 centimeters, then find the dimensions of the rectangle.
81. A triangle has sides whose measures are consecutive even integers. If the perimeter is 24 meters, then find the measure of each side.
82. The circumference of a circle measures 24π inches. Find the radius of the circle.
83. Mary invested $1,800 in two different accounts. One account earned 3.5% simple interest and the other earned 4.8%. If the total interest after 1 year was $79.25, then how much did she invest in each account?
84. James has $6 in dimes and quarters. If he has 4 fewer quarters than he does dimes, then how many of each coin does he have?
85. Two brothers leave the house at the same time traveling in opposite directions. One averages 40 miles per hour and the other 36 miles per hour. How long does it take for the distance between them to reach 114 miles?
86. Driving to her grandmother’s house, Jill made several stops and was only able to average 40 miles per hour. The return trip took 2 hours less time because she drove nonstop and was able to average 60 miles per hour. How long did it take Jill to drive home from her grandmother’s house?
Ratio and Proportion Applications
Solve.
87.
88.
89.
90.
91.
92.
93.
94.
95. Find two numbers in the proportion 4 to 5 whose sum is 27.
96. A larger number is 2 less than twice a smaller number. If the two numbers are in the proportion 5 to 9, then find the numbers.
97. A recipe calls for 1½ teaspoons of vanilla extract for every 3 cups of batter. How many teaspoons of vanilla extract should be used with 7 cups of batter?
98. The ratio of female to male employees at a certain bank is 4 to 5. If there are 80 female employees at the bank, then determine the total number of employees.
If triangle ABC is similar to triangle RST, then find the remaining two sides given the following.
99. , , , and
100. , , , and
101. At the same time of day, a pole casts a 27-foot shadow and 4-foot boy casts a 6-foot shadow. Calculate the height of the pole.
102. An equilateral triangle with sides measuring 10 units is similar to another equilateral triangle with scale factor of 2:3. Find the perimeter of the unknown triangle.
Introduction to Inequalities and Interval Notation
Graph all solutions on a number line and provide the corresponding interval notation.
103.
104.
105.
106.
107.
108.
109.
110.
Determine the inequality given the answers expressed in interval notation.
111.
112.
113.
114.
115.
116.
Linear Inequalities (One Variable)
Solve and graph. In addition, present the solution set in interval notation.
117.
118.
119.
120.
121.
122.
123.
124.
125.
126.
127.
128.
129.
130.
Sample Exam
1. Evaluate , where , , and .
2. Determine the area of a triangle given that the base measures 10 centimeters and the height measures 5 centimeters. ()
Simplify.
3.
4.
5.
6.
Solve.
7.
8.
9.
10.
11.
12.
13.
14. Solve for b: .
Solve and graph the solution set. In addition, present the solution set in interval notation.
15.
16.
17.
18.
19.
20. An algebra student earns 75, 79, and 89 points on the first three quizzes. What must she score on the fourth quiz to earn an average of at least 80?
21. The sum of three consecutive odd integers is 117. Find the integers.
22. The length of a rectangle is 6 inches less than twice the width. If the perimeter measures 39 inches, then find the dimensions of the rectangle.
23. Millie invested her $5,350 savings in two accounts. One account earns 5% annual interest and the other earns 6.2% in annual interest. If she earned $317.30 simple interest in 1 year, then how much was in each account?
24. Because of traffic, Joe was only able to drive an average of 42 miles per hour on the trip to a conference. He was able to average 63 miles per hour on the return trip and it took 1 hour less time. How long did it take Joe to drive home from the conference?
25. A graphic designer wishes to crop an image in the width-to-height ratio of 3:2. If the height is required to be 400 pixels, then to how many pixels should the width be set?
Review Exercises Answers
1: −1
3: −1/10
5: −6
7: 24
9: $180
11: 27 square feet
13:
15:
17:
19:
21:
23:
25:
27:
29:
31:
33: No
35: Yes
37: 2
39: 32
41: −7
43: −3/7
45: 3
47: −21
49: 7/5
51: 5
53: 4
55: 12
57: 2
59: 3/8
61: Ø
63: 8
65: 7/8
67: R
69: 11/3
71:
73:
75: 12, 27
77: 13, 15, 17
79: 19, 20, 21
81: 6 meters, 8 meters, 10 meters
83: Mary invested $550 at 3.5% and $1,250 at 4.8%.
85: They will be 114 miles apart in 1½ hours.
87: 6
89: 11/5
91: 5/6
93: 2/3
95: 12, 15
97: 3½ teaspoons
99: t = 4, r = 4/3
101: 18 feet
103:
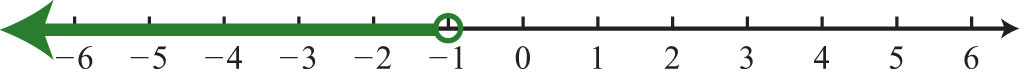
105:

107:

109:

111:
113:
115:
117: ;

119: ;
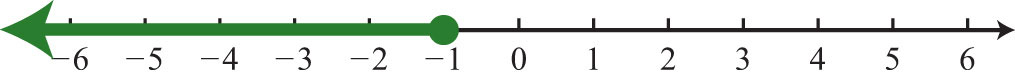
121: ;
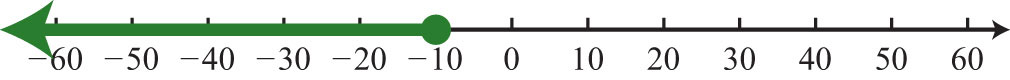
123: ;

125: ;

127: ;

129: ;
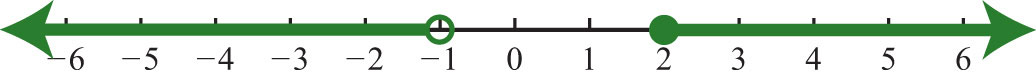
Sample Exam Answers
1: 6
3:
5:
7: −5
9: 1
11: Ø
13: −3
15: ;

17: ;

19: ;

21: The three odd integers are 37, 39, and 41.
23: Millie invested $1,200 in the account earning 5% annual interest and $4,150 in the account earning 6.2%.
25: The width should be set to 600 pixels.




