This is “Polynomial and Rational Functions”, chapter 4 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
Chapter 4 Polynomial and Rational Functions
4.1 Algebra of Functions
Learning Objectives
- Identify and evaluate polynomial functions.
- Add and subtract functions.
- Multiply and divide functions.
- Add functions graphically.
Polynomial Functions
Any polynomial with one variable is a function and can be written in the form
Here represents any real number and n represents any whole number. The degree of a polynomial with one variable is the largest exponent of all the terms. Typically, we arrange terms of polynomials in descending order based on their degree and classify them as follows:
In this textbook, we call any polynomial with degree higher than 3 an nth-degree polynomial. For example, if the degree is 4, we call it a fourth-degree polynomial; if the degree is 5, we call it a fifth-degree polynomial, and so on.
Example 1
Given , find and
Solution:
Replace each instance of x with the value given inside the parentheses.
|
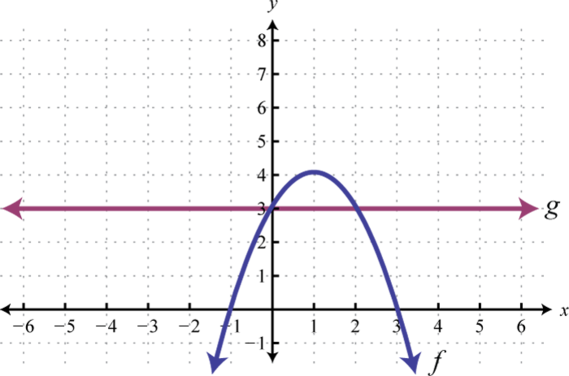
We can write and Remember that and so we can interpret these results on the graph as follows:

Answer: ;
Often we will be asked to evaluate polynomials for algebraic expressions.
Example 2
Given , find and
Solution:
Replace x with the expressions given inside the parentheses.
Answer: and
The height of an object launched upward, ignoring the effects of air resistance, can be modeled with the following quadratic function:
With this formula, the height can be calculated at any given time t after the object is launched. The letter g represents acceleration due to gravity on the surface of the Earth, which is 32 feet per second squared (or, using metric units, g = 9.8 meters per second squared). The variable , pronounced “v-naught,” or sometimes “v-zero,” represents the initial velocity of the object, and represents the initial height from which the object was launched.
Example 3
An object is launched from the ground at a speed of 64 feet per second. Write a function that models the height of the object and use it to calculate the objects height at 1 second and at 3.5 seconds.
Solution:
We know that the acceleration due to gravity is feet per second squared and we are given the initial velocity feet per second. Since the object is launched from the ground, the initial height is feet. Create the mathematical model by substituting these coefficients into the following formula:
Use this model to calculate the height of the object at 1 second and 3.5 seconds.
Answer: ; At 1 second the object is at a height of 48 feet, and at 3.5 seconds it is at a height of 28 feet.
Try this! An object is dropped from a height of 6 meters. Write a function that models the height of the object and use it to calculate the object’s height 1 second after it is dropped.
Answer: ; At 1 second the object is at a height of 1.1 meters.
Adding and Subtracting Functions
The notation used to indicate additionAdd functions as indicated by the notation: and subtractionSubtract functions as indicated by the notation: of functions follows:
When using function notation, be careful to group the entire function and add or subtract accordingly.
Example 4
Given and , find and
Solution:
The notation indicates that we should add the given expressions.
The notation indicates that we should subtract the given expressions. When subtracting, the parentheses become very important. Recall that we can eliminate them after applying the distributive property.
Answer: and
We may be asked to evaluate the sum or difference of two functions. We have the option to first find the sum or difference in general and then use the resulting function to evaluate for the given variable, or evaluate each first and then find the sum or difference.
Example 5
Evaluate given and
Solution:
First, find
Therefore,
Next, substitute 3 in for the variable x.
Hence
Alternate Solution: Since , we can find and and then subtract the results.
|
|
Therefore,
Notice that we obtain the same answer.
Answer:
Note: If multiple values are to be evaluated, it is best to find the sum or difference in general first and then use it to evaluate.
Multiplying and Dividing Functions
The notation used to indicate multiplicationMultiply functions as indicated by the notation: and divisionDivide functions as indicated by the notation: , where of functions follows:
Multiplication of functions: |
|
Division of functions: |
Example 6
Given and , find and
Solution:
The notation indicates that we should multiply. Apply the distributive property and simplify.
The notation indicates that we should divide. For this quotient, assume
Answer: and where
Example 7
Given and , evaluate and
Solution:
Begin by finding
Therefore , and we have,
Answer: and
Adding Functions Graphically
Here we explore the geometry of adding functions. One way to do this is to use the fact that Add the functions together using x-values for which both and are defined.
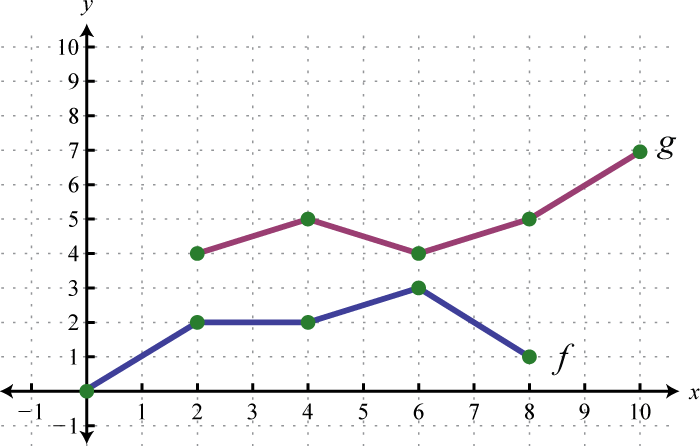
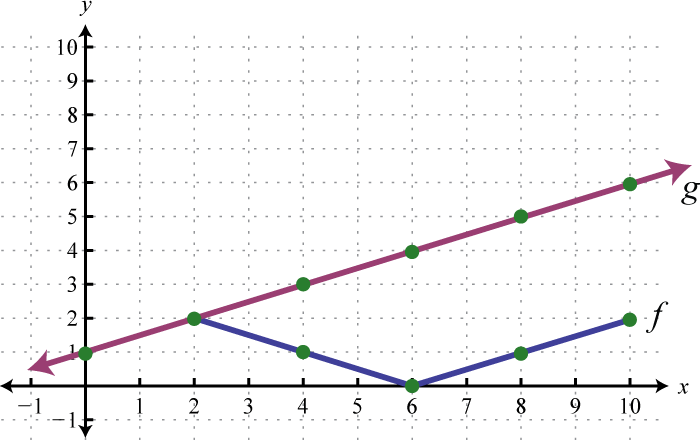
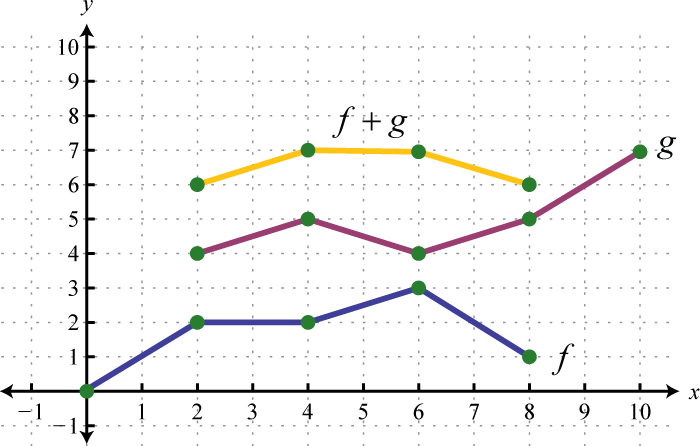
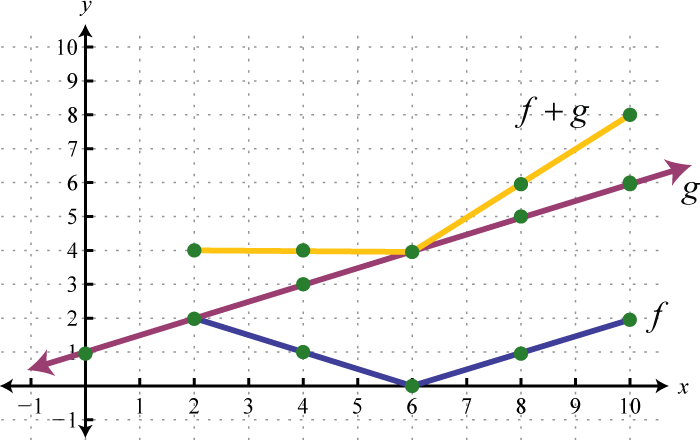
Example 8
Use the graphs of and to graph Also, give the domain of
Solution:
In this case, both functions are defined for x-values between 2 and 6. We will use 2, 4, and 6 as representative values in the domain of to sketch its graph.
Sketch the graph of using the three ordered pair solutions , , and
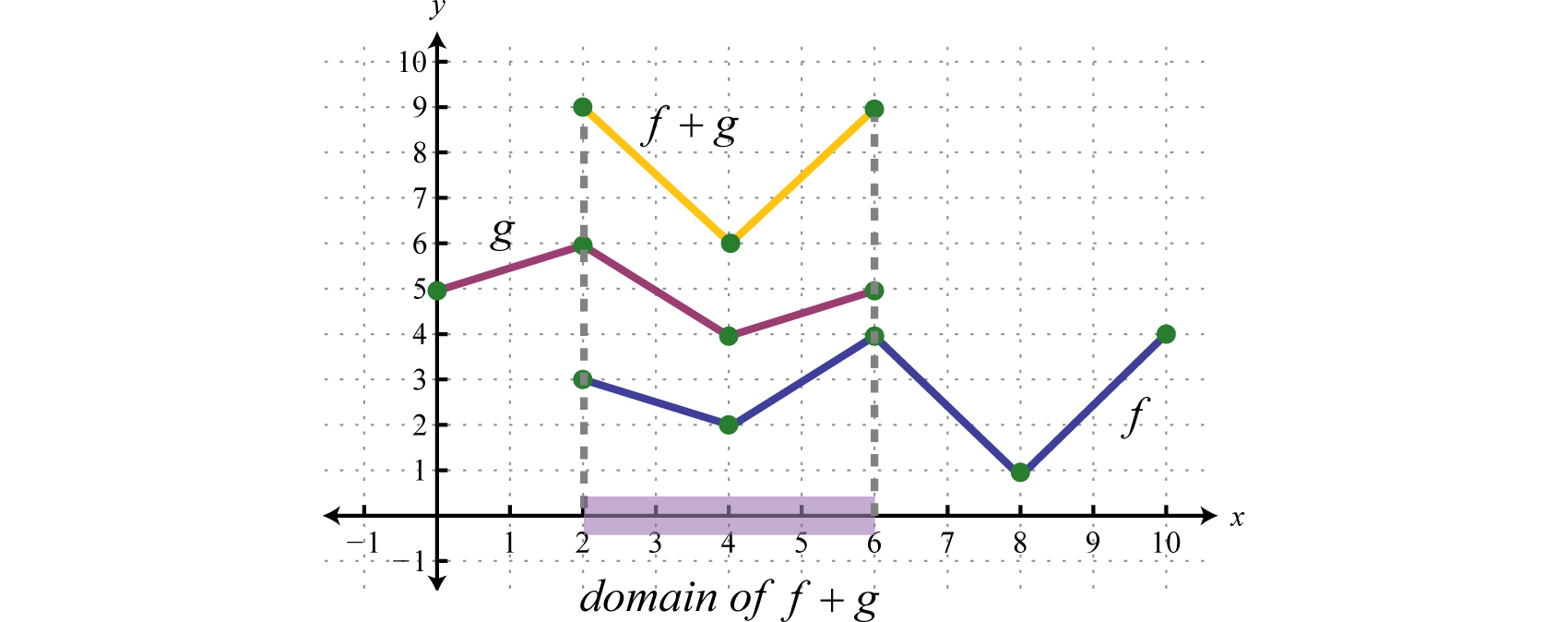
Answer: graphed above has domain
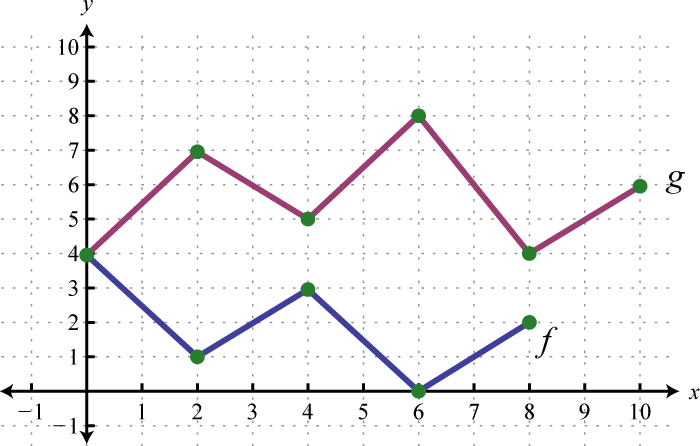
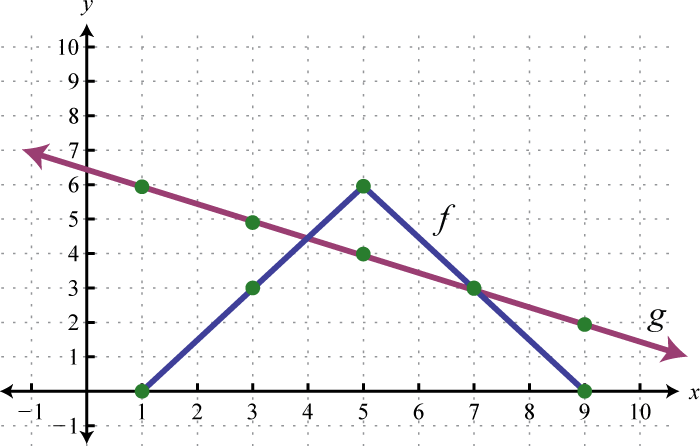
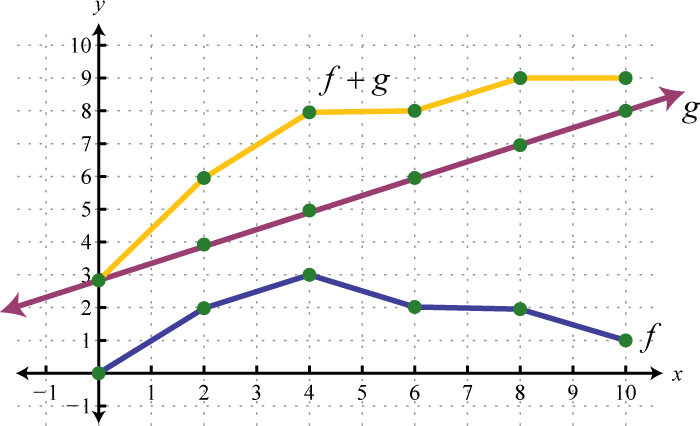
Example 9
Use the graphs of and to graph Also, give the domain of
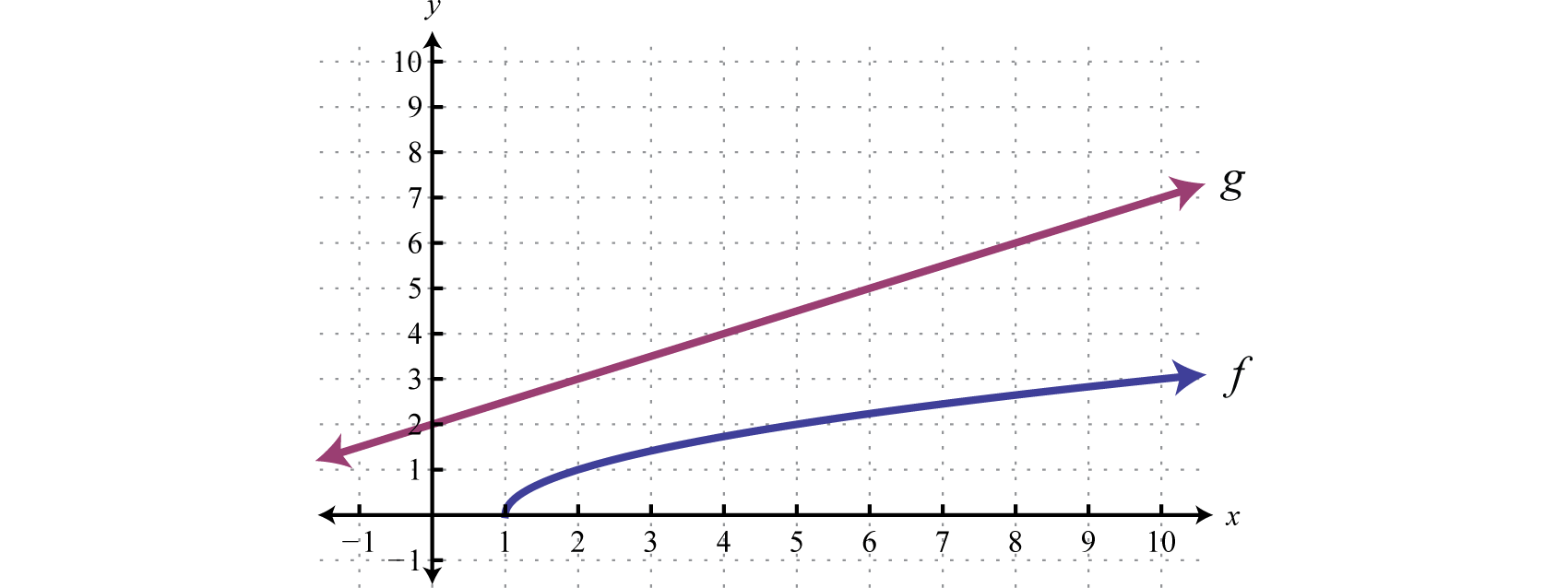
Solution:
Another way to add nonnegative functions graphically is to copy the line segment formed from the x-axis to one of the functions onto the other as illustrated below.
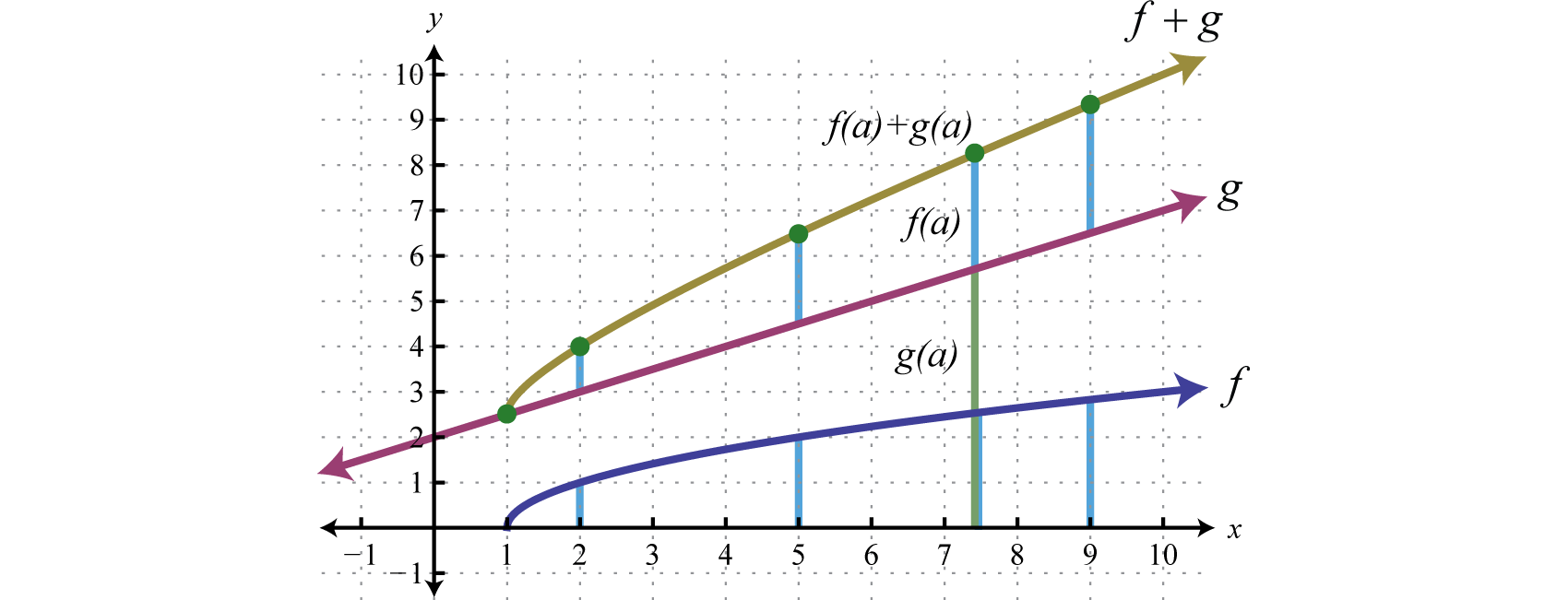
The line segment from the x-axis to the function represents Copy this line segment onto the other function over the same point; the endpoint represents Doing this for a number of points allows us to obtain a quick sketch of the combined graph. In this example, the domain of is limited to the x-values for which is defined.
Answer: Domain:
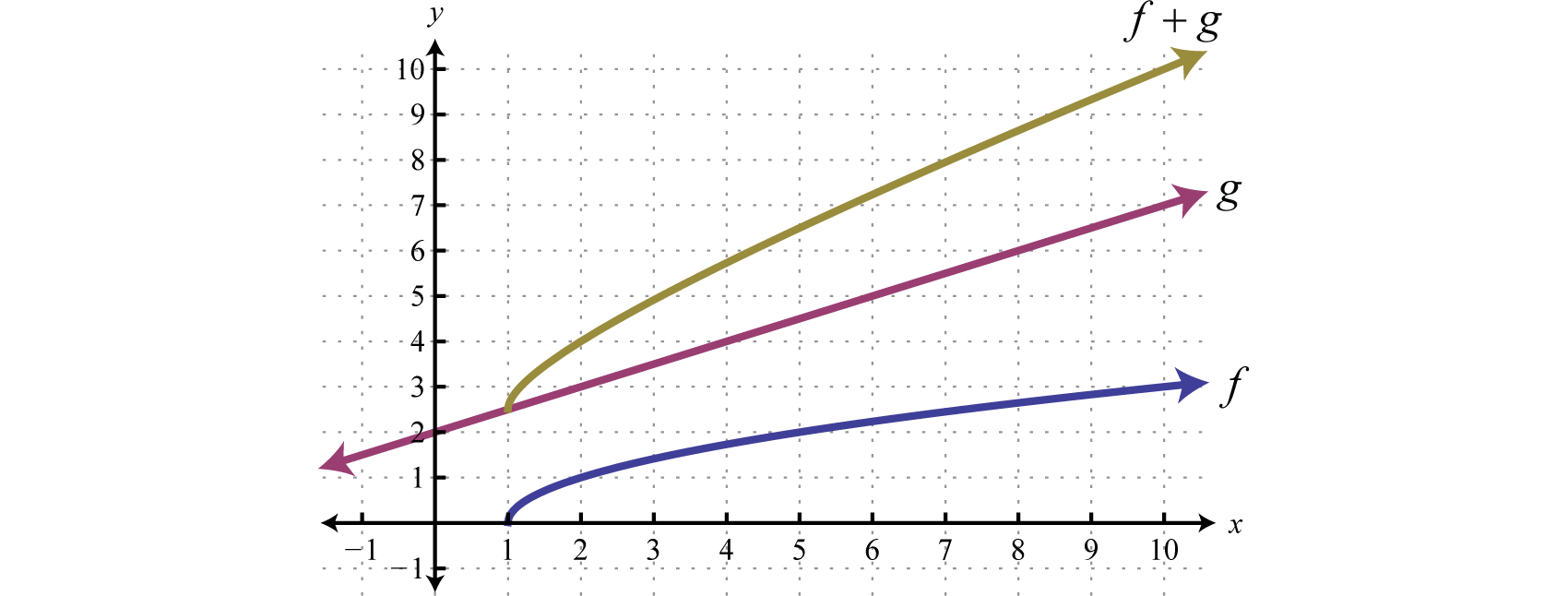
In general, the domain of is the intersection of the domain of with the domain of In fact, this is the case for all of the arithmetic operations with an extra consideration for division. When dividing functions, we take extra care to remove any values that make the denominator zero. This will be discussed in more detail as we progress in algebra.
Key Takeaways
- Any polynomial with one variable is a function and can be written in the form The degree of the polynomial is the largest exponent of all the terms.
- Use function notation to streamline the evaluating process. Substitute the value or expression inside the parentheses for each instance of the variable.
- The notation indicates that we should add
- The notation indicates that we should subtract
- The notation indicates that we should multiply
- The notation indicates that we should divide
- The domain of the function that results from these arithmetic operations is the intersection of the domain of each function. The domain of a quotient is further restricted to values that do not evaluate to zero in the denominator.
Topic Exercises
-
Given , find , , and
-
Given , find , , and
-
Given , find , , and
-
Given , find , , and
-
Given , find , , and
-
Given , find , , and
-
Given , find , , and
-
Given , find , and
-
Given , find and
-
Given , find and
-
Given , find and
-
Given , find and
-
Given , find and
-
Given , find and
-
Given , find and
-
Given , find and
-
-
-
-
-
Find , , and
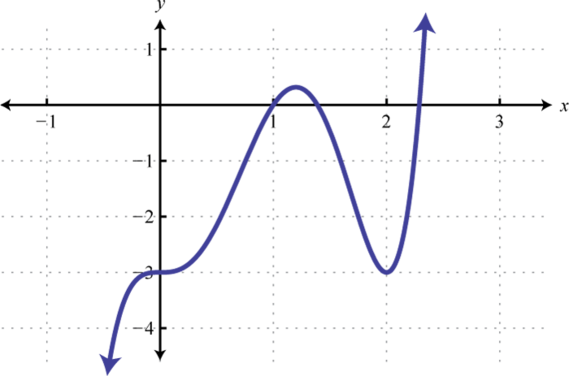
-
Find , , and
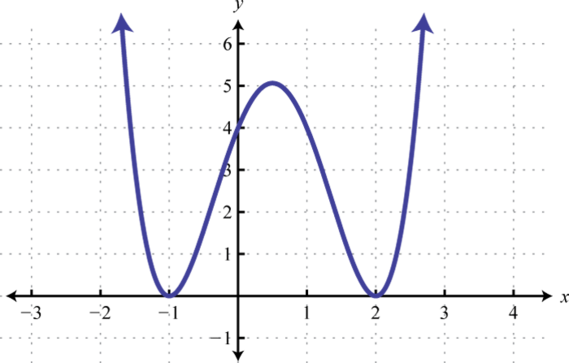
-
Find , , and
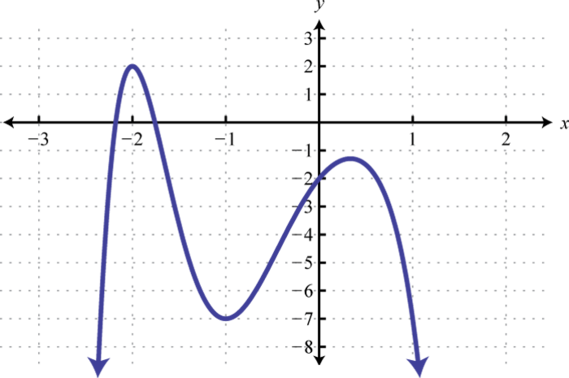
-
Find , , and
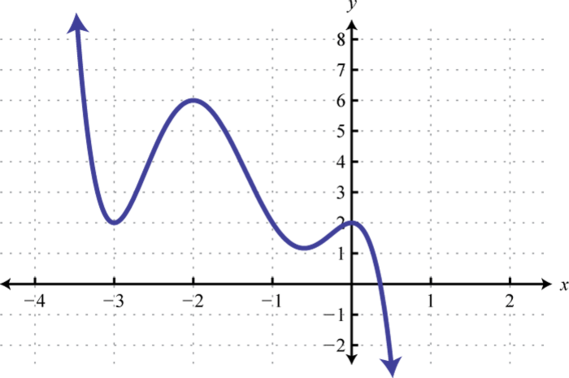
-
A projectile is launched upward from the ground at a speed of 48 feet per second. Write a function that models the height of the projectile and use it to calculate the height every 1/2 second after launch. Sketch a graph that shows the height of the projectile with respect to time.
-
An object is tossed upward from a 48-foot platform at a speed of 32 feet per second. Write a function that models the height of the object and use it to calculate the height every 1/2 second after the object is tossed. Sketch a graph that shows the height of the object with respect to time.
-
An object is dropped from a 128-foot bridge. Write a function that models the height of the object, and use it to calculate the height at 1 second and 2 seconds after it has been dropped.
-
An object is dropped from a 500-foot building. Write a function that models the height of the object, and use it to calculate the distance the object falls in the 1st second, 2nd second, and the 3rd second.
-
A bullet is fired straight up into the air at 320 meters per second. Ignoring the effects of air friction, write a function that models the height of the bullet, and use it to calculate the bullet’s height 1 minute after it was fired into the air.
-
A book is dropped from a height of 10 meters. Write a function that gives the height of the book, and use it to determine how far it will fall in 1¼ seconds.
Part A: Polynomial Functions
Evaluate.
Given the function calculate
Given the graph of the polynomial function find the function values.
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Part B: Adding and Subtracting Functions
Given functions and , find and
Given and , evaluate the following.
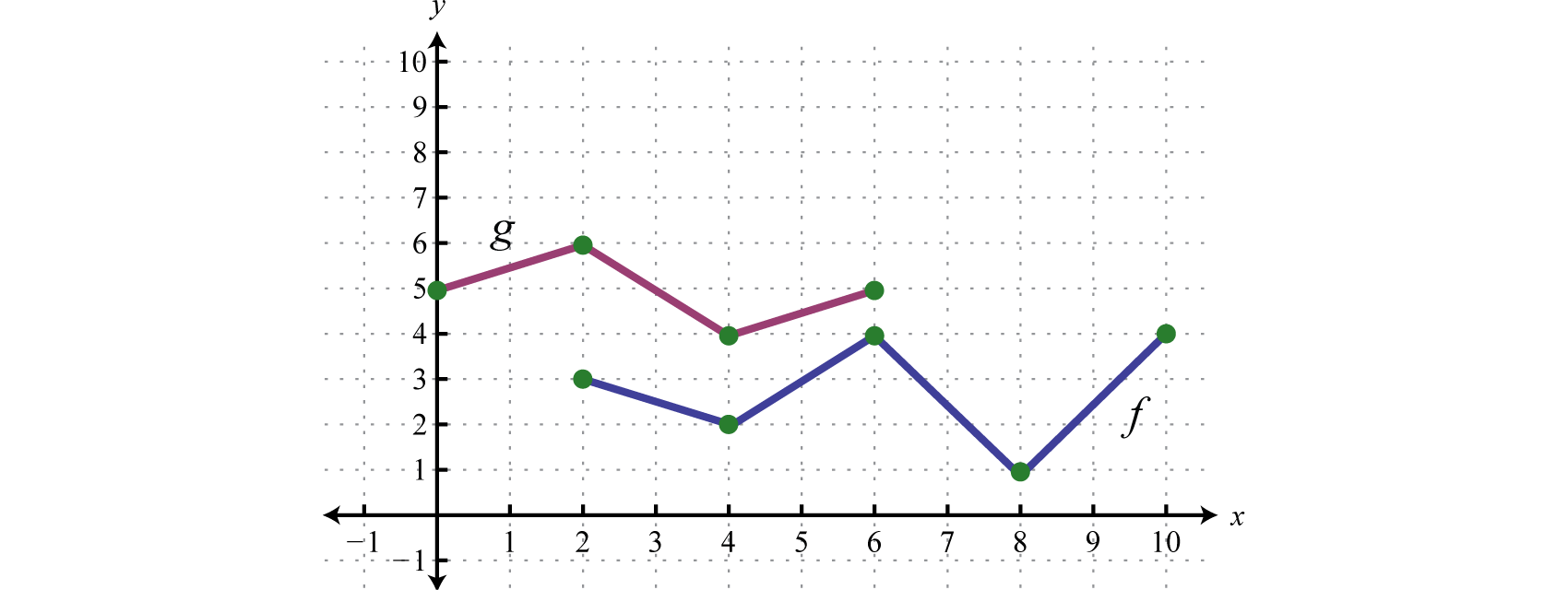
Given the graphs of and , evaluate the following.
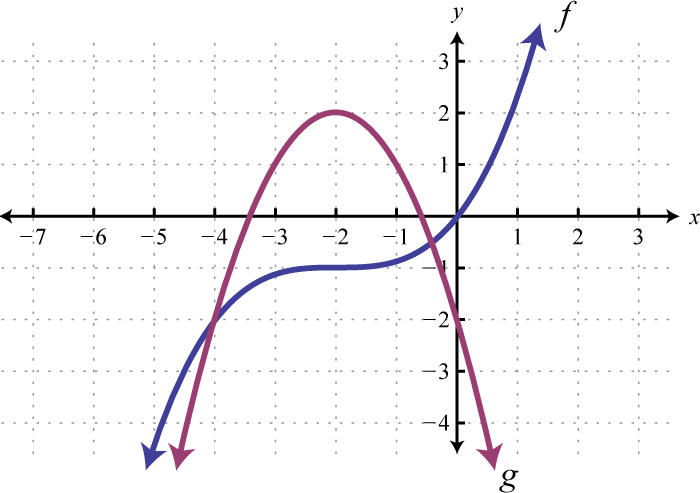
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
The revenue in dollars from selling MP3 players is given by the function , where n represents the number of units sold . The cost in dollars of producing the MP3 players is given by the formula where n represents the number of units produced. Write a function that models the profit of producing and selling n MP3 players. Use the function to determine the profit generated from producing and selling 225 MP3 players. Recall that profit equals revenues less costs.
-
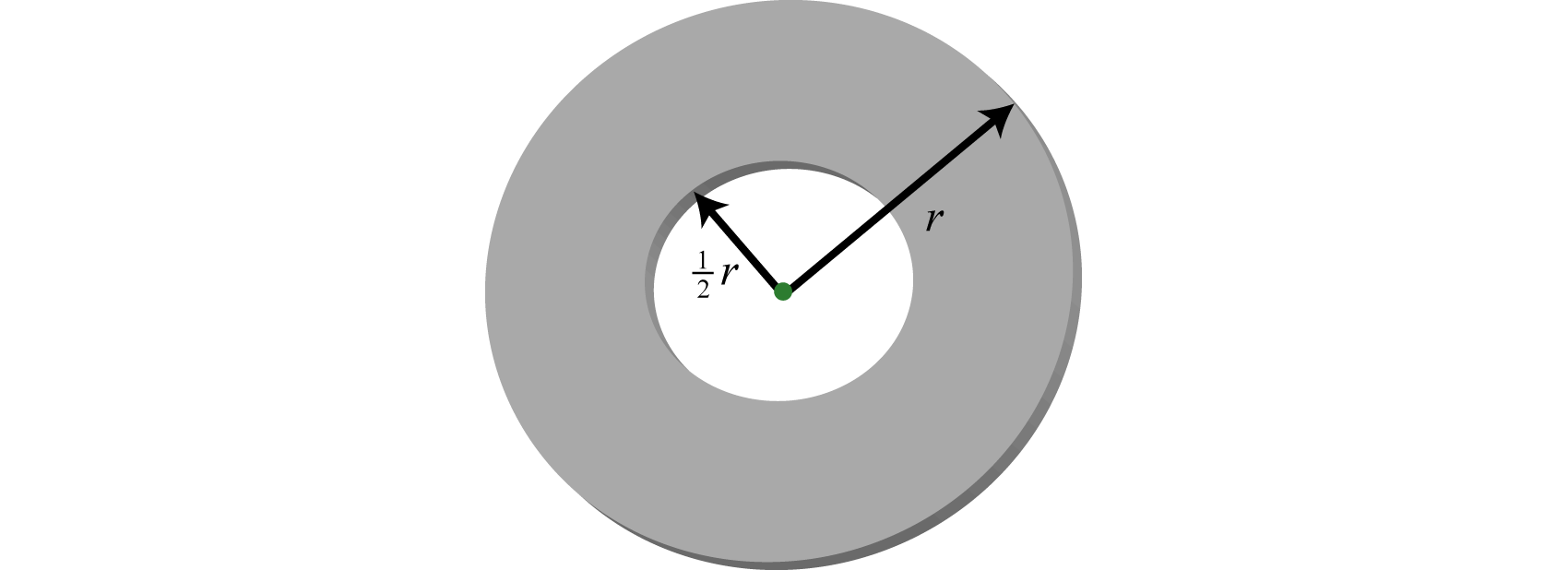
The inner radius of a washer is that of the outer radius.
Part C: Multiplying and Dividing Functions
Given and , find
Given and , find (Assume all expressions in the denominator are nonzero.)
Given and evaluate the following.
Given the graphs of and evaluate the following.
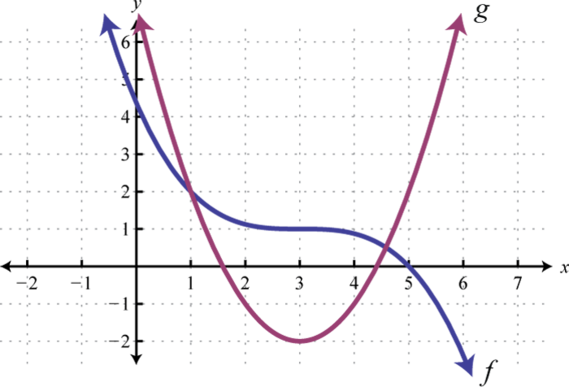
Given , , and , find the following. (Assume all expressions in the denominator are nonzero.)
Part D: Adding Functions Geometrically
Use the graphs of and to graph Also, give the domain of
-
Which arithmetic operations on functions are commutative? Explain.
-
Explore ways we can add functions graphically if they happen to be negative.
Part E: Discussion Board
Answers
-
; ;
-
-
; ;
-
-
; ;
-
-
; ;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
-
-
-
-
; ;
-
-
; ;
-
-
;
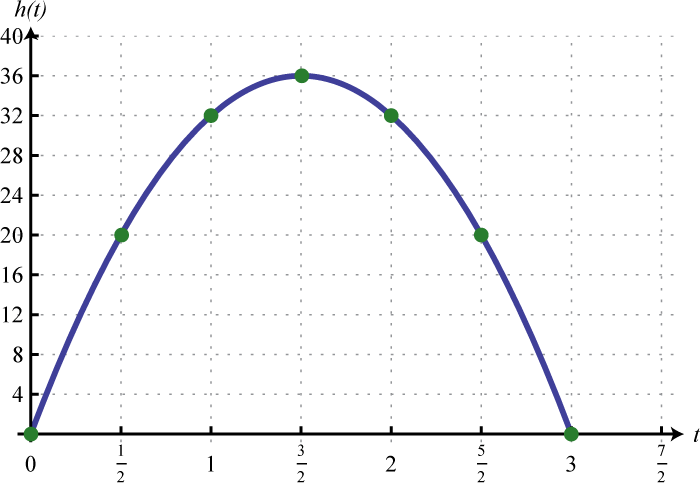
-
-
; At 1 second the object’s height is 112 feet and at 2 seconds its height is 64 feet.
-
-
; 1,560 meters
-
-
;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
11
-
-
−27
-
-
27
-
-
−10
-
-
−4
-
-
1
-
-
−2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
50
-
-
15
-
-
0
-
-
25
-
-
−2
-
-
0
-
-
4
-
-
-
-
-
-
-
-
-
-
; $9,881.25
-
-
Answer may vary
-
4.2 Factoring Polynomials
Learning Objectives
- Determine the greatest common factor (GCF) of monomials.
- Factor out the GCF of a polynomial.
- Factor a four-term polynomial by grouping.
- Factor special binomials.
Determining the GCF of Monomials
The process of writing a number or expression as a product is called factoringThe process of writing a number or expression as a product.. If we write the monomial , we say that the product is a factorizationAny combination of factors, multiplied together, resulting in the product. of and that and are factorsAny of the numbers or expressions that form a product.. Typically, there are many ways to factor a monomial. Some factorizations of follow:
Given two or more monomials, it will be useful to find the greatest common monomial factor (GCF)The product of the common variable factors and the GCF of the coefficients. of each. The GCF of the monomials is the product of the common variable factors and the GCF of the coefficients.
Example 1
Find the GCF of and
Solution:
Begin by finding the GCF of the coefficients. In this case, and It should be clear that
Next determine the common variable factors with the smallest exponents.
The common variable factors are , , and Therefore, given the two monomials,
Answer:
It is worth pointing out that the GCF divides both expressions evenly.
Furthermore, we can write the following:
The factors and share no common monomial factors other than 1; they are relatively primeExpressions that share no common factors other than 1..
Example 2
Determine the GCF of the following three expressions: , , and
Solution:
Begin by finding the GCF of the coefficients. To do this, determine the prime factorization of each and then multiply the common factors with the smallest exponents.
Therefore, the GCF of the coefficients of the three monomials is
Next, determine the common factors of the variables.
The variable factors in common are , , and Therefore,
Note that the variable c is not common to all three expressions and thus is not included in the GCF.
Answer:
Factoring out the GCF
The application of the distributive property is the key to multiplying polynomials. For example,
The process of factoring a polynomial involves applying the distributive property in reverse to write each polynomial as a product of polynomial factors.
Consider factoring the result of the opening example:
We see that the distributive property allows us to write the polynomial as a product of the two factors and Note that in this case, is the GCF of the terms of the polynomial.
Factoring out the greatest common factor (GCF)The process of rewriting a polynomial as a product using the GCF of all of its terms. of a polynomial involves rewriting it as a product where a factor is the GCF of all of its terms.
To factor out the GCF of a polynomial, we first determine the GCF of all of its terms. Then we can divide each term of the polynomial by this factor as a means to determine the remaining factor after applying the distributive property in reverse.
Example 3
Factor out the GCF:
Solution:
In this case, the GCF(18, 30, 6) = 6, and the common variable factor with the smallest exponent is The GCF of the polynomial is
The missing factor can be found by dividing each term of the original expression by the GCF.
Apply the distributive property (in reverse) using the terms found in the previous step.
If the GCF is the same as one of the terms, then, after the GCF is factored out, a constant term 1 will remain. The importance of remembering the constant term becomes clear when performing the check using the distributive property.
Answer:
Example 4
Factor out the GCF:
Solution:
The GCF of the terms is The last term does not have a variable factor of z, and thus z cannot be a part of the greatest common factor. If we divide each term by , we obtain
and can write
Answer:
Of course, not every polynomial with integer coefficients can be factored as a product of polynomials with integer coefficients other than 1 and itself. If this is the case, then we say that it is a prime polynomialA polynomial with integer coefficients that cannot be factored as a product of polynomials with integer coefficients other than 1 and itself.. For example, a linear factor such as is prime. However, it can be factored as follows:
If an x is factored out, the resulting factor is not a polynomial. If any constant is factored out, the resulting polynomial factor will not have integer coefficients. Furthermore, some linear factors are not prime. For example,
In general, any linear factor of the form , where a and b are relatively prime integers, is prime.
Factoring by Grouping
In this section, we outline a technique for factoring polynomials with four terms. First, review a preliminary example where the terms have a common binomial factor.
Example 5
Factor:
Solution:
Begin by rewriting the second term as Next, consider as a common binomial factor and factor it out as follows:
Answer:
Factoring by groupingA technique for factoring polynomials with four terms. is a technique that enables us to factor polynomials with four terms into a product of binomials. This involves an intermediate step where a common binomial factor will be factored out. For example, we wish to factor
Begin by grouping the first two terms and the last two terms. Then factor out the GCF of each grouping:
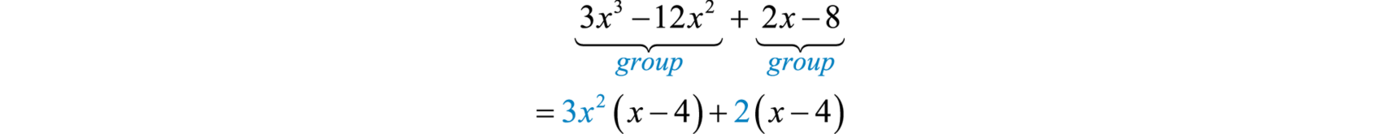
In this form, the polynomial is a binomial with a common binomial factor,
Therefore,
We can check by multiplying.
Example 6
Factor by grouping:
Solution:
The GCF for the first group is We have to choose 5 or −5 to factor out of the second group.
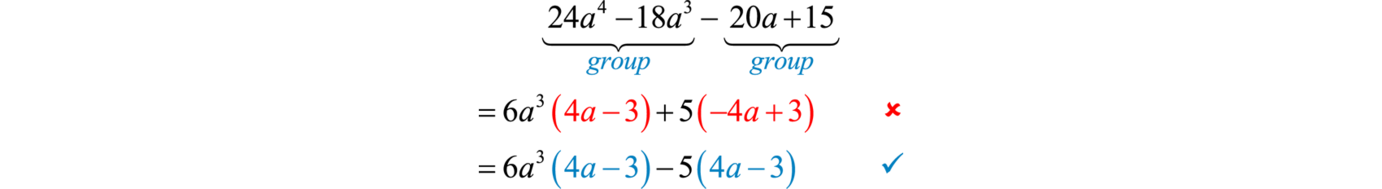
Factoring out +5 does not result in a common binomial factor. If we choose to factor out −5, then we obtain a common binomial factor and can proceed. Note that when factoring out a negative number, we change the signs of the factored terms.

Answer: Check by multiplying; this is left to the reader as an exercise.
Sometimes we must first rearrange the terms in order to obtain a common factor.
Example 7
Factor:
Solution:
Simply factoring the GCF out of the first group and last group does not yield a common binomial factor.
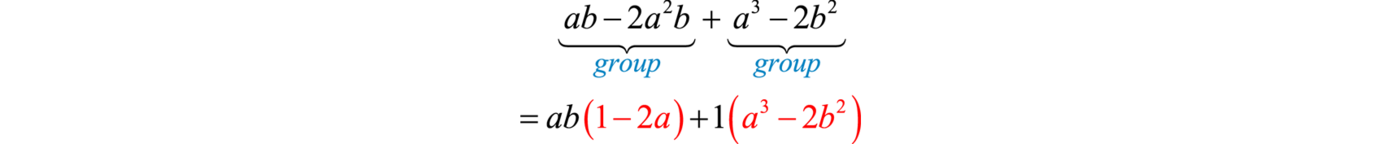
We must rearrange the terms, searching for a grouping that produces a common factor. In this example, we have a workable grouping if we switch the terms and

Answer:
Not all factorable four-term polynomials can be factored with this technique. For example,
This four-term polynomial cannot be grouped in any way to produce a common binomial factor. Despite this, the polynomial is not prime and can be written as a product of polynomials. It can be factored as follows:
Factoring such polynomials is something that we will learn to do as we move further along in our study of algebra. For now, we will limit our attempt to factor four-term polynomials to using the factor by grouping technique.
Factoring Special Binomials
A binomial is a polynomial with two terms. We begin with the special binomial called difference of squares where a and b represent algebraic expressions.:
To verify the above formula, multiply.
We use this formula to factor certain special binomials.
Example 8
Factor:
Solution:
Identify the binomial as difference of squares and determine the square factors of each term.
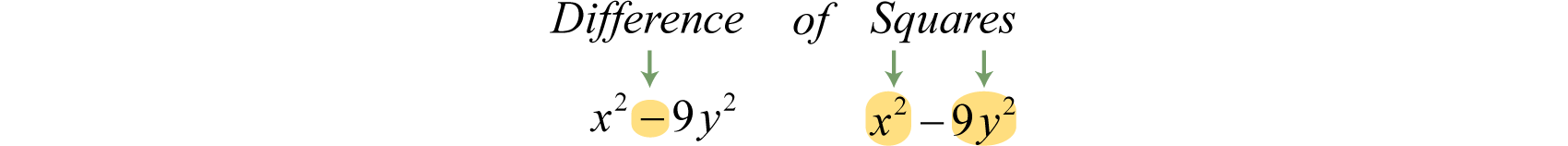
Here we can write
Substitute into the difference of squares formula where and
Multiply to check.
Answer:
Example 9
Factor:
Solution:
First, identify this expression as a difference of squares.
Use and in the formula for a difference of squares and then simplify.
Answer:
Given any real number b, a polynomial of the form is prime. Furthermore, the sum of squares where a and b represent algebraic expressions. This does not have a general factored equivalent. does not have a general factored equivalent. Care should be taken not to confuse this with a perfect square trinomial.
Therefore,
For example, the sum of squares binomial is prime. Two other special binomials of interest are the sum, where a and b represent algebraic expressions. and difference of cubes, where a and b represent algebraic expressions.:
We can verify these formulas by multiplying.
The process for factoring sums and differences of cubes is very similar to that of differences of squares. We first identify a and b and then substitute into the appropriate formula. The separate formulas for the sum and difference of cubes allow us to always choose a and b to be positive.
Example 10
Factor:
Solution:
First, identify this binomial as a difference of cubes.
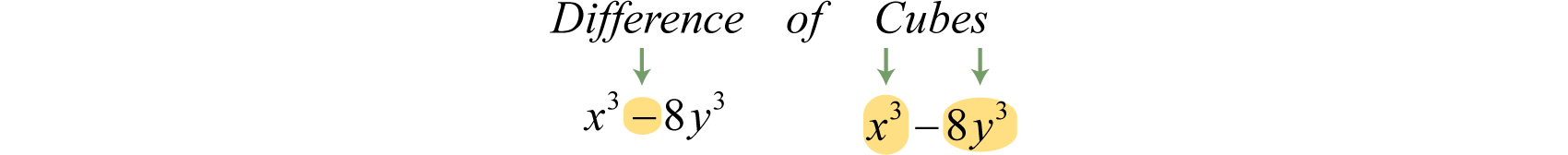
Next, identify what is being cubed.
In this case, and Substitute into the difference of cubes formula.
We can check this factorization by multiplying.
Answer:
It may be the case that the terms of the binomial have a common factor. If so, it will be difficult to identify it as a special binomial until we first factor out the GCF.
Example 11
Factor:
Solution:
The terms are not perfect squares or perfect cubes. However, notice that they do have a common factor. First, factor out the GCF,
The resulting binomial factor is a sum of cubes with and
Answer:
When the degree of the special binomial is greater than two, we may need to apply the formulas multiple times to obtain a complete factorization. A polynomial is completely factoredA polynomial that is prime or written as a product of prime polynomials. when it is prime or is written as a product of prime polynomials.
Example 12
Factor completely:
Solution:
First, identify what is being squared.
To do this, recall the power rule for exponents, When exponents are raised to a power, multiply them. With this in mind, we find
Therefore, and Substitute into the formula for difference of squares.
At this point, notice that the factor is itself a difference of two squares and thus can be further factored using and The factor is prime and cannot be factored using real numbers.
Answer:
When factoring, always look for resulting factors to factor further.
Example 13
Factor completely:
Solution:
This binomial is both a difference of squares and difference of cubes.
When confronted with a binomial that is a difference of both squares and cubes, as this is, make it a rule to factor using difference of squares first. Therefore, and Substitute into the difference of squares formula.
The resulting two binomial factors are sum and difference of cubes. Each can be factored further. Therefore, we have

The trinomial factors are prime and the expression is completely factored.
Answer:
As an exercise, factor the previous example as a difference of cubes first and then compare the results. Why do you think we make it a rule to factor using difference of squares first?
Key Takeaways
- The GCF of two or more monomials is the product of the GCF of the coefficients and the common variable factors with the smallest power.
- If the terms of a polynomial have a greatest common factor, then factor out that GCF using the distributive property. Divide each term of the polynomial by the GCF to determine the terms of the remaining factor.
- Some four-term polynomials can be factored by grouping the first two terms and the last two terms. Factor out the GCF of each group and then factor out the common binomial factor.
- When factoring by grouping, you sometimes have to rearrange the terms to find a common binomial factor. After factoring out the GCF, the remaining binomial factors must be the same for the technique to work.
- When factoring special binomials, the first step is to identify it as a sum or difference. Once we identify the binomial, we then determine the values of a and b and then substitute into the appropriate formula.
- If a binomial is both a difference of squares and cubes, then first factor it as a difference of squares.
Topic Exercises
-
, ,
-
, ,
-
, ,
-
, ,
-
, ,
-
, ,
-
, ,
-
, ,
-
, ,
-
, ,
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Part A: Factoring out the GCF
Determine the GCF of the given expressions.
Determine the missing factor.
Factor out the GCF.
Part B: Factoring by Grouping
Factor by grouping.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Given , show that
-
Given , show that
-
Given , show that
-
Given , show that
-
Given , show that
-
Given , show that
Part C: Factoring Special Binomials
Factor.
-
What can be said about the degree of a factor of a polynomial? Give an example.
-
If a binomial falls into both categories, difference of squares and difference of cubes, which would be best to use for factoring, and why? Create an example that illustrates this situation and factor it using both formulas.
-
Write your own examples for each of the three special types of binomial. Factor them and share your results.
Part D: Discussion Board
Answers
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Answer may vary
-
-
Answer may vary
-
-
Answer may vary
-
-
Answer may vary
-
-
Answer may vary
4.3 Factoring Trinomials
Learning Objectives
- Factor trinomials of the form
- Factor trinomials of higher degree.
- Factor trinomials of the form
- Factor trinomials using the AC method.
Factoring Trinomials of the Form
Some trinomials of the form can be factored as a product of binomials. If a trinomial of this type factors, then we have:
This gives us
In short, if the leading coefficient of a factorable trinomial is 1, then the factors of the last term must add up to the coefficient of the middle term. This observation is the key to factoring trinomials using the technique known as the trial and error (or guess and check) methodDescribes the method of factoring a trinomial by systematically checking factors to see if their product is the original trinomial..
Example 1
Factor:
Solution:
We begin by writing two sets of blank parentheses. If a trinomial of this form factors, then it will factor into two linear binomial factors.
Write the factors of the first term in the first space of each set of parentheses. In this case, factor
Determine the factors of the last term whose sum equals the coefficient of the middle term. To do this, list all of the factorizations of 20 and search for factors whose sum equals 12.
Choose 20 = 2 ⋅ 10 because 2 + 10 = 12. Write in the last term of each binomial using the factors determined in the previous step.
This can be visually interpreted as follows:
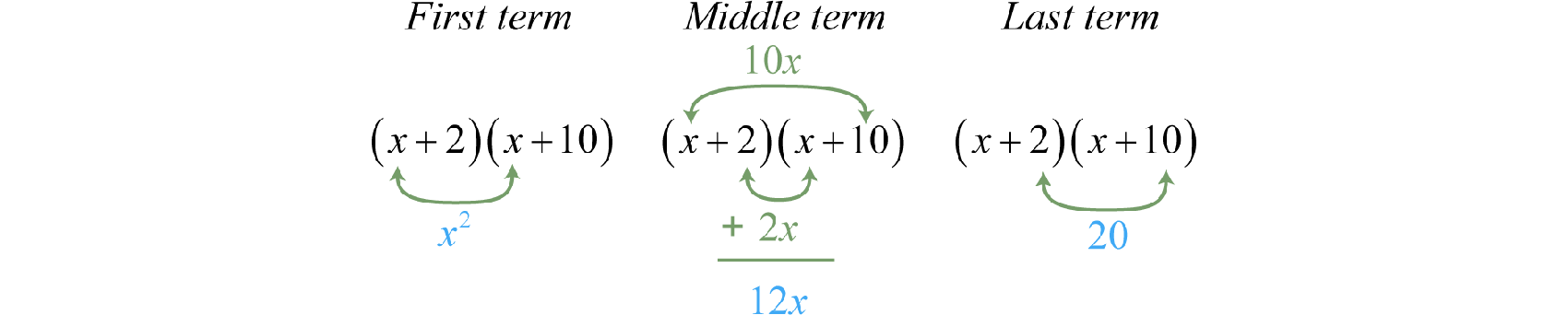
Check by multiplying the two binomials.
Answer:
Since multiplication is commutative, the order of the factors does not matter.
If the last term of the trinomial is positive, then either both of the constant factors must be negative or both must be positive.
Example 2
Factor:
Solution:
First, factor
Next, search for factors of 12 whose sum is −7.
In this case, choose −3 and −4 because and
Check.
Answer:
If the last term of the trinomial is negative, then one of its factors must be negative.
Example 3
Factor:
Solution:
Begin by factoring the first term
The factors of 12 are listed below. In this example, we are looking for factors whose sum is −4.
Therefore, the coefficient of the last term can be factored as , where Because the last term has a variable factor of , use and factor the trinomial as follows:
Multiply to check.
Answer:
Often our first guess will not produce a correct factorization. This process may require repeated trials. For this reason, the check is very important and is not optional.
Example 4
Factor:
Solution:
The first term of this trinomial, , factors as
Consider the factors of 24:
Suppose we choose the factors 4 and 6 because 4 + 6 = 10, the coefficient of the middle term. Then we have the following incorrect factorization:
When we multiply to check, we find the error.
In this case, the middle term is correct but the last term is not. Since the last term in the original expression is negative, we need to choose factors that are opposite in sign. Therefore, we must try again. This time we choose the factors −2 and 12 because
Now the check shows that this factorization is correct.
Answer:
If we choose the factors wisely, then we can reduce much of the guesswork in this process. However, if a guess is not correct, do not get discouraged; just try a different set of factors. Keep in mind that some polynomials are prime. For example, consider the trinomial and the factors of 20:
There are no factors of 20 whose sum is 3. Therefore, the original trinomial cannot be factored as a product of two binomials with integer coefficients. The trinomial is prime.
Factoring Trinomials of Higher Degree
We can use the trial and error technique to factor trinomials of higher degree.
Example 5
Factor:
Solution:
Begin by factoring the first term
Since 5 is prime and the coefficient of the middle term is positive, choose +1 and +5 as the factors of the last term.
Notice that the variable part of the middle term is and the factorization checks out.
Answer:
Example 6
Factor: where n is a positive integer.
Solution:
Begin by factoring the first term
Factor because and write
Answer: The check is left to the reader.
Factoring Trinomials of the Form
Factoring trinomials of the form can be challenging because the middle term is affected by the factors of both and In general,
This gives us,
In short, when the leading coefficient of a trinomial is something other than 1, there will be more to consider when determining the factors using the trial and error method. The key lies in the understanding of how the middle term is obtained. Multiply and carefully follow the formation of the middle term.

As we have seen before, the product of the first terms of each binomial is equal to the first term of the trinomial. The middle term of the trinomial is the sum of the products of the outer and inner terms of the binomials. The product of the last terms of each binomial is equal to the last term of the trinomial. Visually, we have the following:

For this reason, we need to look for products of the factors of the first and last terms whose sum is equal to the coefficient of the middle term. For example, to factor , look at the factors of 6 and 35.
The combination that produces the coefficient of the middle term is Make sure that the outer terms have coefficients 2 and 7, and that the inner terms have coefficients 5 and 3. Use this information to factor the trinomial.
We can always check by multiplying; this is left to the reader.
Example 7
Factor:
Solution:
Since the leading coefficient and the last term are both prime, there is only one way to factor each.
Begin by writing the factors of the first term, , as follows:
The middle and last term are both positive; therefore, the factors of 3 are chosen as positive numbers. In this case, the only choice is in which grouping to place these factors.
Determine which grouping is correct by multiplying each expression.
Answer:
Example 8
Factor:
Solution:
First, consider the factors of the coefficients of the first and last terms.
We are searching for products of factors whose sum equals the coefficient of the middle term, −1. After some thought, we can see that the sum of 8 and −9 is −1 and the combination that gives this follows:
Factoring begins at this point with two sets of blank parentheses.
Use and as factors of
Next use the factors 1 and 4 in the correct order so that the inner and outer products are and respectively.
Answer: The complete check is left to the reader.
It is a good practice to first factor out the GCF, if there is one. Doing this produces a trinomial factor with smaller coefficients. As we have seen, trinomials with smaller coefficients require much less effort to factor. This commonly overlooked step is worth identifying early.
Example 9
Factor:
Solution:
Begin by factoring out the GCF.
After factoring out , the coefficients of the resulting trinomial are smaller and have fewer factors. We can factor the resulting trinomial using and Notice that these factors can produce −13 in two ways:
Because the last term is −5, the correct combination requires the factors 1 and 5 to be opposite signs. Here we use 2(1) = 2 and 3(−5) = −15 because the sum is −13 and the product of (1)(−5) = −5.
Check.
The factor is part of the factored form of the original expression; be sure to include it in the answer.
Answer:
It is a good practice to consistently work with trinomials where the leading coefficient is positive. If the leading coefficient is negative, factor it out along with any GCF. Note that sometimes the factor will be −1.
Example 10
Factor:
Solution:
In this example, the GCF is Because the leading coefficient is negative we begin by factoring out
At this point, factor the remaining trinomial as usual, remembering to write the as a factor in the final answer. Use 6 = 1(6) and −4 = 4(−1) because Therefore,
Answer: The check is left to the reader.
Factoring Using the AC Method
An alternate technique for factoring trinomials, called the AC methodMethod used for factoring trinomials by replacing the middle term with two terms that allow us to factor the resulting four-term polynomial by grouping., makes use of the grouping method for factoring four-term polynomials. If a trinomial in the form can be factored, then the middle term, bx, can be replaced with two terms with coefficients whose sum is b and product is ac. This substitution results in an equivalent expression with four terms that can be factored by grouping.
Example 11
Factor using the AC method:
Solution:
Here a = 18, b = −31, and c = 6.
Factor 108, and search for factors whose sum is −31.
In this case, the sum of the factors −27 and −4 equals the middle coefficient, −31. Therefore, , and we can write
Factor the equivalent expression by grouping.
Answer:
Example 12
Factor using the AC method:
Solution:
Here a = 4, b = −7, and c = −15.
Factor −60 and search for factors whose sum is −7.
The sum of factors 5 and −12 equals the middle coefficient, −7. Replace with
Answer: The check is left to the reader.
If factors of ac cannot be found to add up to b then the trinomial is prime.
Key Takeaways
- If a trinomial of the form factors into the product of two binomials, then the coefficient of the middle term is the sum of factors of the last term.
- If a trinomial of the form factors into the product of two binomials, then the coefficient of the middle term will be the sum of certain products of factors of the first and last terms.
- If the trinomial has a greatest common factor, then it is a best practice to first factor out the GCF before attempting to factor it into a product of binomials.
- If the leading coefficient of a trinomial is negative, then it is a best practice to first factor that negative factor out before attempting to factor the trinomial.
- Factoring is one of the more important skills required in algebra. For this reason, you should practice working as many problems as it takes to become proficient.
Topic Exercises
Part A: Factoring Trinomials of the Form
Factor.
Part B: Factoring Trinomials of the Form
Factor.
Factor.
-
Create your own trinomial of the form that factors. Share it, along with the solution, on the discussion board.
-
Create a trinomial of the form that does not factor and share it along with the reason why it does not factor.
Part D: Discussion Board
Answers
-
-
-
-
-
-
-
Prime
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Prime
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Prime
-
-
-
-
Answer may vary
-
4.4 Solve Polynomial Equations by Factoring
Learning Objectives
- Review general strategies for factoring.
- Solve polynomial equations by factoring.
- Find roots of a polynomial function.
- Find polynomial equations given the solutions.
Reviewing General Factoring Strategies
We have learned various techniques for factoring polynomials with up to four terms. The challenge is to identify the type of polynomial and then decide which method to apply. The following outlines a general guideline for factoring polynomials:
- Check for common factors. If the terms have common factors, then factor out the greatest common factor (GCF).
-
Determine the number of terms in the polynomial.
- Factor four-term polynomials by grouping.
- Factor trinomials (3 terms) using “trial and error” or the AC method.
-
Factor binomials (2 terms) using the following special products:
- Look for factors that can be factored further.
- Check by multiplying.
Note: If a binomial is both a difference of squares and a difference cubes, then first factor it as difference of squares. This will result in a more complete factorization. In addition, not all polynomials with integer coefficients factor. When this is the case, we say that the polynomial is prime.
If an expression has a GCF, then factor this out first. Doing so is often overlooked and typically results in factors that are easier to work with. Furthermore, look for the resulting factors to factor further; many factoring problems require more than one step. A polynomial is completely factored when none of the factors can be factored further.
Example 1
Factor:
Solution:
This four-term polynomial has a GCF of Factor this out first.
Now factor the resulting four-term polynomial by grouping and look for resulting factors to factor further.
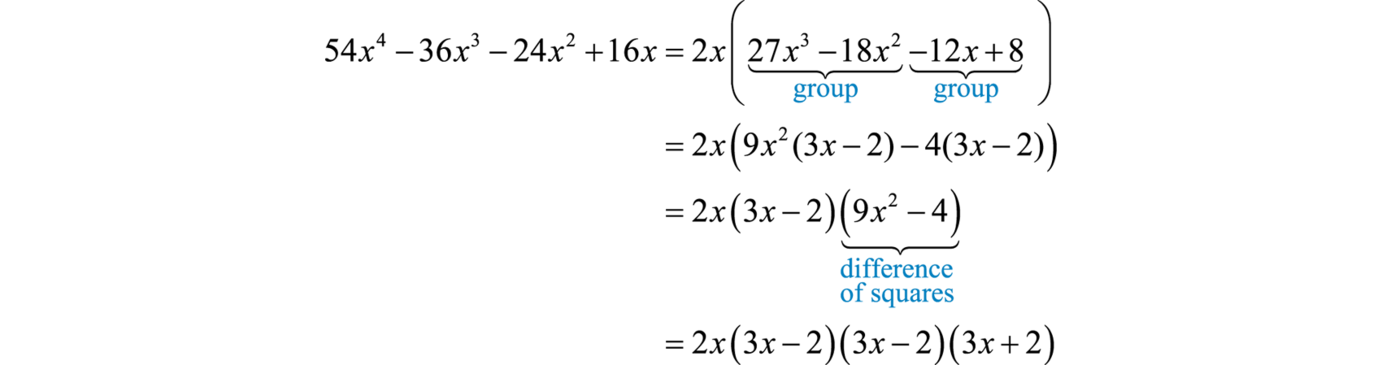
Answer: The check is left to the reader.
Example 2
Factor:
Solution:
This trinomial does not have a GCF.
The factor is prime and the trinomial is completely factored.
Answer:
Example 3
Factor:
Solution:
Begin by factoring and look for the factors of 16 that add to 6.
The factor cannot be factored any further using integers and the factorization is complete.
Answer:
Solving Polynomial Equations by Factoring
In this section, we will review a technique that can be used to solve certain polynomial equations. We begin with the zero-product propertyA product is equal to zero if and only if at least one of the factors is zero.:
The zero-product property is true for any number of factors that make up an equation. In other words, if any product is equal to zero, then at least one of the variable factors must be equal to zero. If an expression is equal to zero and can be factored into linear factors, then we will be able to set each factor equal to zero and solve for each equation.
Example 4
Solve:
Solution:
Set each variable factor equal to zero and solve.
To check that these are solutions we can substitute back into the original equation to see if we obtain a true statement. Note that each solution produces a zero factor. This is left to the reader.
Answer: The solutions are 0, 4, and
Of course, most equations will not be given in factored form.
Example 5
Solve:
Solution:
Begin by factoring the left side completely.
Set each factor equal to zero and solve.
Answer: The solutions are , −5, and 5.
Using the zero-product property after factoring an equation that is equal to zero is the key to this technique. However, the equation may not be given equal to zero, and so there may be some preliminary steps before factoring. The steps required to solve by factoringThe process of solving an equation that is equal to zero by factoring it and then setting each variable factor equal to zero. are outlined in the following example.
Example 6
Solve:
Solution:
Step 1: Express the equation in standard form, equal to zero. In this example, subtract from and add 7 to both sides.
Step 2: Factor the expression.
Step 3: Apply the zero-product property and set each variable factor equal to zero.
Step 4: Solve the resulting linear equations.
Answer: The solutions are and The check is optional.
Example 7
Solve:
Solution:
This quadratic equation appears to be factored; hence it might be tempting to set each factor equal to 4. However, this would lead to incorrect results. We must rewrite the equation equal to zero, so that we can apply the zero-product property.
Once it is in standard form, we can factor and then set each factor equal to zero.
Answer: The solutions are and −2.
Finding Roots of Functions
Recall that any polynomial with one variable is a function and can be written in the form,
A rootA value in the domain of a function that results in zero. of a function is a value in the domain that results in zero. In other words, the roots occur when the function is equal to zero,
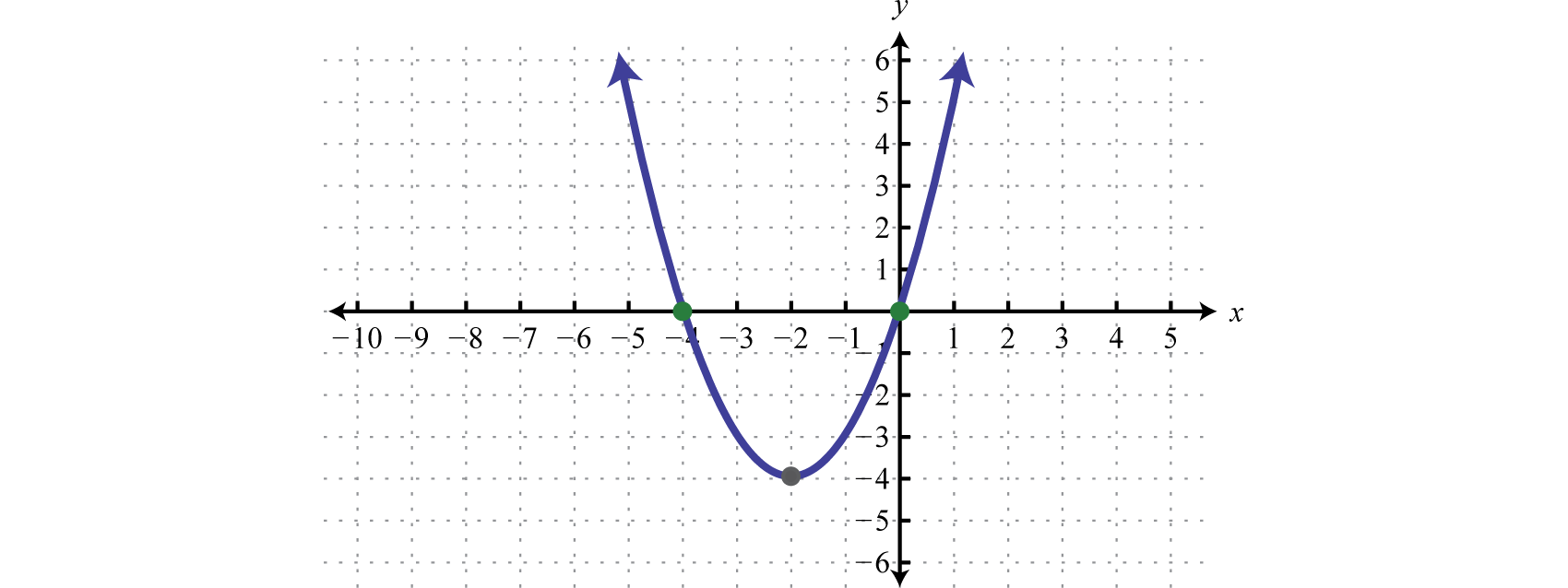
Example 8
Find the roots:
Solution:
To find roots we set the function equal to zero and solve.
Next, set each factor equal to zero and solve.
We can show that these x-values are roots by evaluating.
Answer: The roots are 0 and −4.
If we graph the function in the previous example we will see that the roots correspond to the x-intercepts of the function. Here the function is a basic parabola shifted 2 units to the left and 4 units down.
Example 9
Find the roots:
Solution:
To find roots we set the function equal to zero and solve.
Next, set each factor equal to zero and solve.
Answer: The roots are −1, 1, −2, and 2.
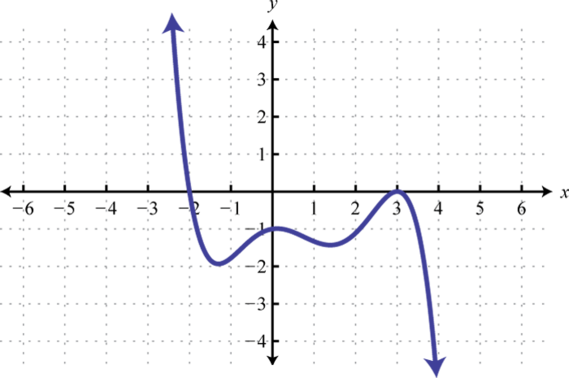
Graphing the previous function is not within the scope of this course. However, the graph is provided below:
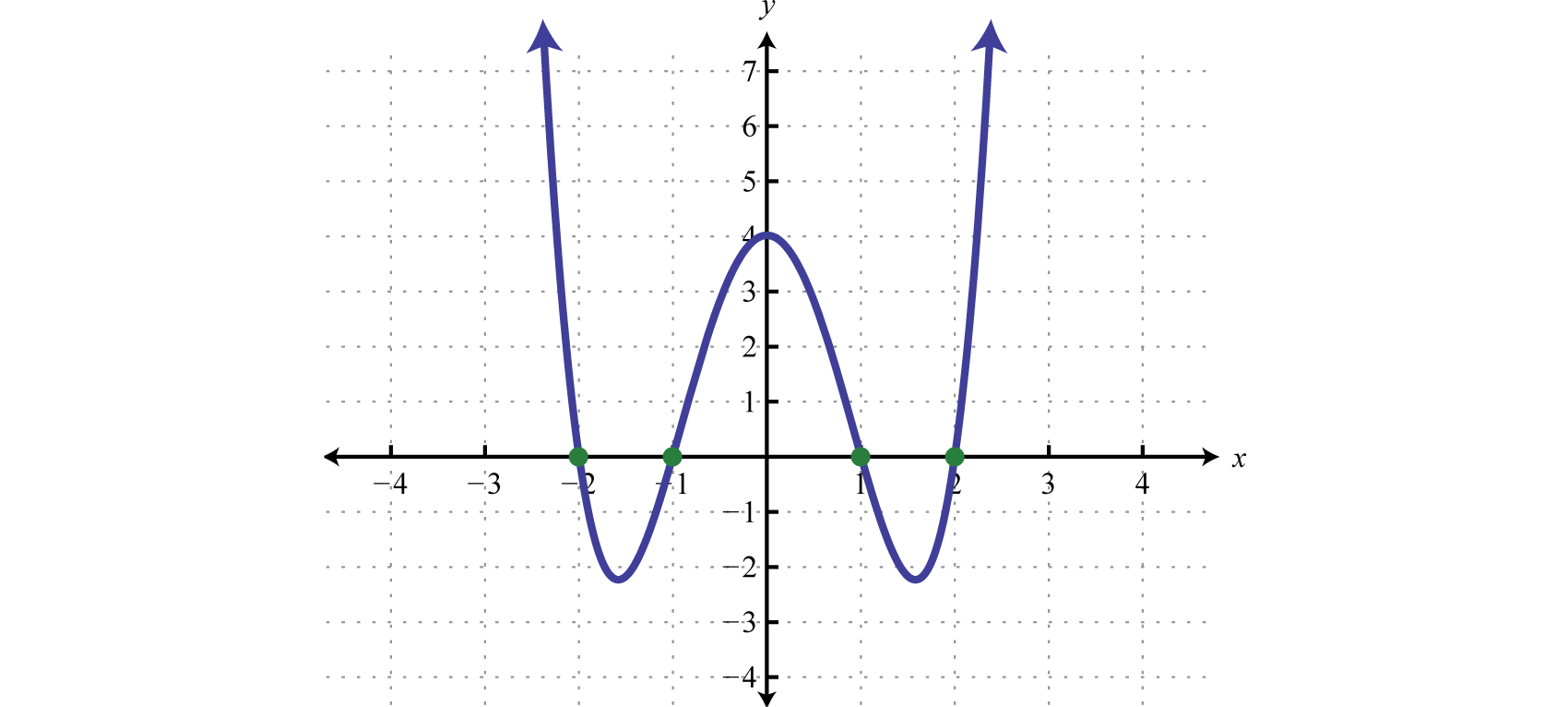
Notice that the degree of the polynomial is 4 and we obtained four roots. In general, for any polynomial function with one variable of degree n, the fundamental theorem of algebraGuarantees that there will be as many (or fewer) roots to a polynomial function with one variable as its degree. guarantees n real roots or fewer. We have seen that many polynomials do not factor. This does not imply that functions involving these unfactorable polynomials do not have real roots. In fact, many polynomial functions that do not factor do have real solutions. We will learn how to find these types of roots as we continue in our study of algebra.
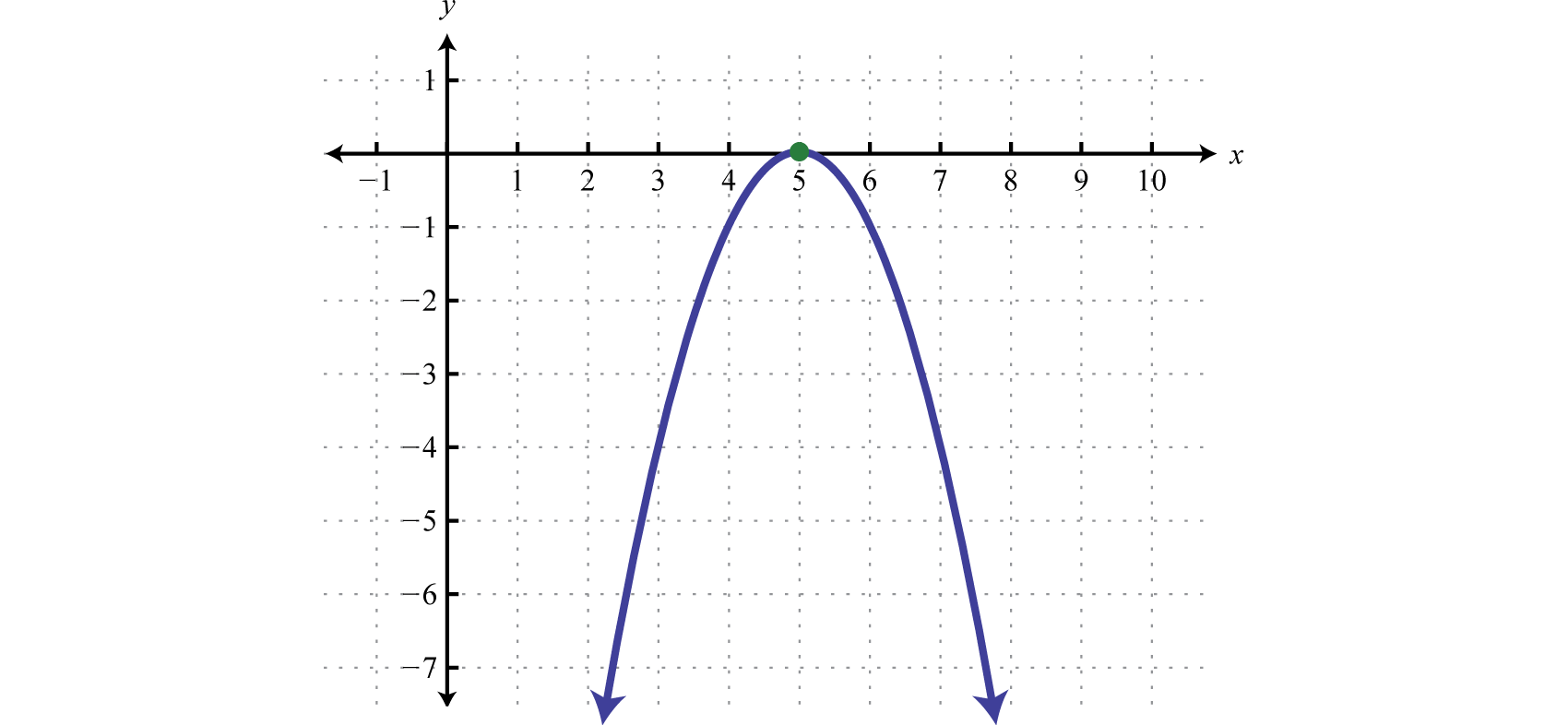
Example 10
Find the roots:
Solution:
To find roots we set the function equal to zero and solve.
Next, set each variable factor equal to zero and solve.
A solution that is repeated twice is called a double rootA root that is repeated twice.. In this case, there is only one solution.
Answer: The root is 5.
The previous example shows that a function of degree 2 can have one root. From the factoring step, we see that the function can be written
In this form, we can see a reflection about the x-axis and a shift to the right 5 units. The vertex is the x-intercept, illustrating the fact that there is only one root.
Example 11
Assuming dry road conditions and average reaction times, the safe stopping distance in feet is given by , where x represents the speed of the car in miles per hour. Determine the safe speed of the car if you expect to stop in 40 feet.
Solution:
We are asked to find the speed x where the safe stopping distance feet.
To solve for x, rewrite the resulting equation in standard form. In this case, we will first multiply both sides by 20 to clear the fraction.
Next factor and then set each factor equal to zero.
The negative answer does not make sense in the context of this problem. Consider miles per hour to be the only solution.
Answer: 20 miles per hour
Finding Equations with Given Solutions
We can use the zero-product property to find equations, given the solutions. To do this, the steps for solving by factoring are performed in reverse.
Example 12
Find a quadratic equation with integer coefficients, given solutions and
Solution:
Given the solutions, we can determine two linear factors. To avoid fractional coefficients, we first clear the fractions by multiplying both sides by the denominator.
The product of these linear factors is equal to zero when or
Multiply the binomials and present the equation in standard form.
We may check our equation by substituting the given answers to see if we obtain a true statement. Also, the equation found above is not unique and so the check becomes essential when our equation looks different from someone else’s. This is left as an exercise.
Answer:
Example 13
Find a polynomial function with real roots 1, −2, and 2.
Solution:
Given solutions to we can find linear factors.
Apply the zero-product property and multiply.
Answer:
Try this! Find a polynomial equation with integer coefficients, given solutions and
Answer:
Key Takeaways
- Factoring and the zero-product property allow us to solve equations.
- To solve a polynomial equation, first write it in standard form. Once it is equal to zero, factor it and then set each variable factor equal to zero. The solutions to the resulting equations are the solutions to the original.
- Not all polynomial equations can be solved by factoring. We will learn how to solve polynomial equations that do not factor later in the course.
- A polynomial function can have at most a number of real roots equal to its degree. To find roots of a function, set it equal to zero and solve.
- To find a polynomial equation with given solutions, perform the process of solving by factoring in reverse.
Topic Exercises
Part A: General Factoring
Factor completely.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
The sides of a square measure units. If the area is 36 square units, then find x.
-
The sides of a right triangle have lengths that are consecutive even integers. Find the lengths of each side. (Hint: Apply the Pythagorean theorem)
-
The profit in dollars generated by producing and selling n bicycles per week is given by the formula How many bicycles must be produced and sold to break even?
-
The height in feet of an object dropped from the top of a 64-foot building is given by where t represents the time in seconds after it is dropped. How long will it take to hit the ground?
-
A box can be made by cutting out the corners and folding up the edges of a square sheet of cardboard. A template for a cardboard box of height 2 inches is given.
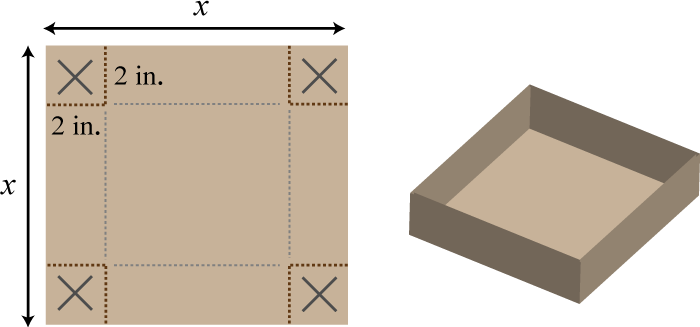
What is the length of each side of the cardboard sheet if the volume of the box is to be 98 cubic inches?
-
The height of a triangle is 4 centimeters less than twice the length of its base. If the total area of the triangle is 48 square centimeters, then find the lengths of the base and height.
-
A uniform border is to be placed around an inch picture.
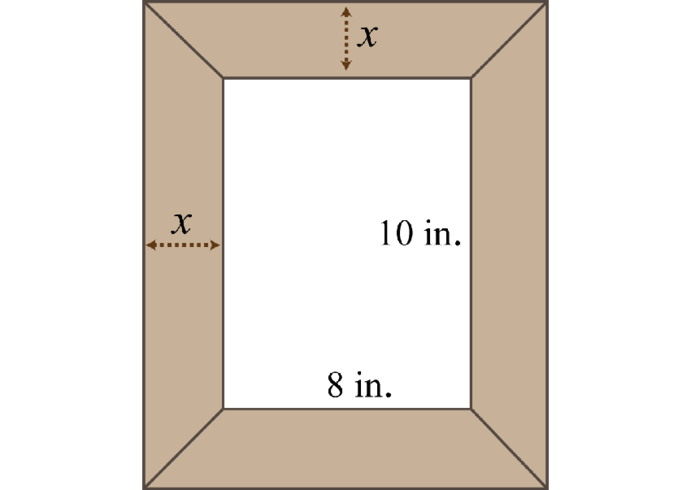
If the total area including the border must be 168 square inches, then how wide should the border be?
-
The area of a picture frame including a 3-inch wide border is 120 square inches.
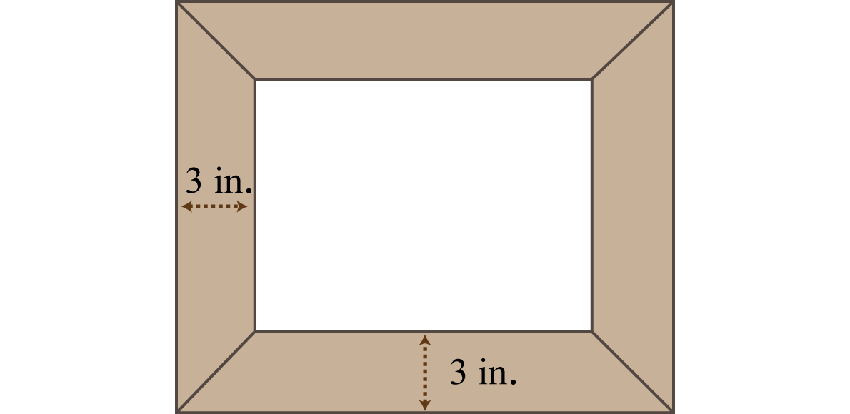
If the width of the inner area is 2 inches less than its length, then find the dimensions of the inner area.
-
Assuming dry road conditions and average reaction times, the safe stopping distance in feet is given by where x represents the speed of the car in miles per hour. Determine the safe speed of the car if you expect to stop in 75 feet.
-
A manufacturing company has determined that the daily revenue in thousands of dollars is given by the formula where n represents the number of palettes of product sold . Determine the number of palettes sold in a day if the revenue was 45 thousand dollars.
Part B: Solving Polynomial Equations by Factoring
Solve.
Find the roots of the given functions.
Given the graph of a function, determine the real roots.
-
−3, 5
-
−1, 8
-
2,
-
, 5
-
0, −4
-
0,7
-
±7
-
±2
-
−3, 1, 3
-
−5, −1, 1
-
,
-
,
-
-
-
5 double root
-
−3 double root
-
−1, 0, 3
-
−5, 0, 2
-
-
-
-
-
-
Part C: Finding Equations with Given Solutions
Find a polynomial equation with the given solutions.
Find a function with the given roots.
Recall that if , then or Use this to solve the following absolute value equations.
-
Explain to a beginning algebra student the difference between an equation and an expression.
-
What is the difference between a root and an x-intercept? Explain.
-
Create a function with three real roots of your choosing. Graph it with a graphing utility and verify your results. Share your function on the discussion board.
-
Research and discuss the fundamental theorem of algebra.
Part D: Discussion Board
Answers
-
−7,
-
-
0, ,
-
-
, 1,
-
-
−6, 4
-
-
,
-
-
5, 10
-
-
, 1
-
-
, 5
-
-
, 6
-
-
, 8
-
-
2, 6
-
-
0, , 5
-
-
0,
-
-
−4, 0,
-
-
±6,
-
-
,
-
-
±1, ±2
-
-
2, −12
-
-
, 4
-
-
-
-
, 0
-
-
-
-
, 5
-
-
±2, ±3
-
-
−6, −4
-
-
-
-
−3, −1, 0, 2
-
-
−2, 3
-
-
8 units
-
-
20 or 60 bicycles
-
-
11 in
-
-
2 inches
-
-
30 miles per hour
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
±4, 0
-
-
±1, 3
-
-
−2, 1, 4
-
-
Answer may vary
-
-
Answer may vary
-
4.5 Rational Functions: Multiplication and Division
Learning Objectives
- Identify restrictions to the domain of a rational function.
- Simplify rational functions.
- Multiply and divide rational functions.
Identifying Restrictions and Simplifying Rational Functions
Rational functionsFunctions of the form , where and are polynomials and have the form where and are polynomials and The domain of a rational functionThe set of real numbers for which the rational function is defined. consists of all real numbers x except those where the denominator RestrictionsThe set of real numbers for which a rational function is not defined. are the real numbers for which the expression is not defined. We often express the domain of a rational function in terms of its restrictions. For example, consider the function
which can be written in factored form
Because rational expressions are undefined when the denominator is 0, we wish to find the values for x that make it 0. To do this, apply the zero-product property. Set each factor in the denominator equal to 0 and solve.
Therefore, the original function is defined for any real number except 2 and 3. We can express its domain using notation as follows:
The restrictions to the domain of a rational function are determined by the denominator. Once the restrictions are determined we can cancel factors and obtain an equivalent function as follows:

It is important to note that 1 is not a restriction to the domain because the expression is defined as 0 when the numerator is 0. In fact, is a root. This function is graphed below:
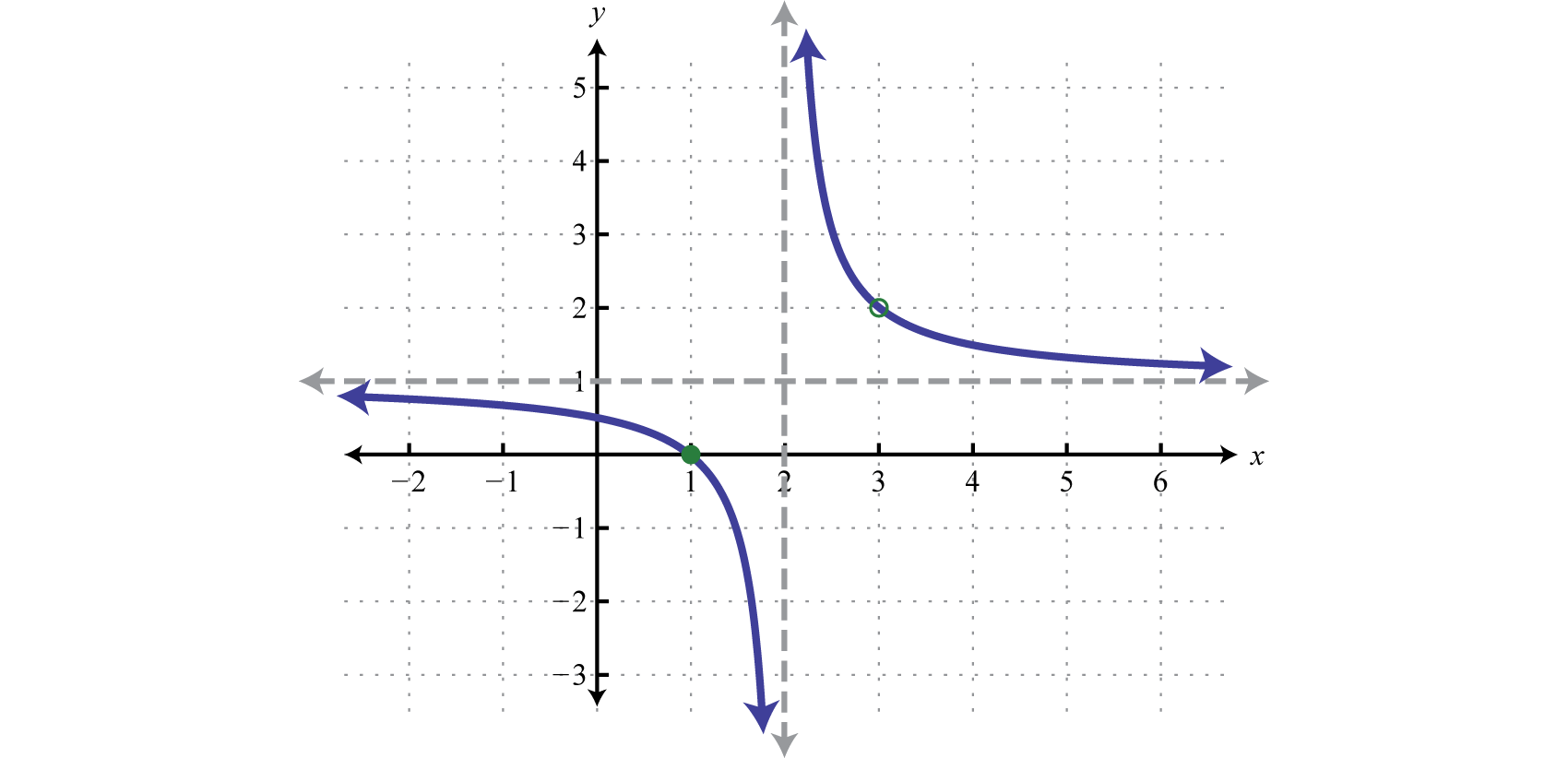
Notice that there is a vertical asymptote at the restriction and the graph is left undefined at the restriction as indicated by the open dot, or hole, in the graph. Graphing rational functions in general is beyond the scope of this textbook. However, it is useful at this point to know that the restrictions are an important part of the graph of rational functions.
Example 1
State the restrictions and simplify:
Solution:
In this example, the function is undefined where x is 0.
Therefore, the domain consists of all real numbers x, where With this understanding, we can simplify by reducing the rational expression to lowest terms. Cancel common factors.
Answer: , where
Example 2
State the restrictions and simplify:
Solution:
First, factor the numerator and denominator.
Any x-value that makes the denominator zero is a restriction. To find the restrictions, first set the denominator equal to zero and then solve
Therefore, With this understanding, we can cancel any common factors.
Answer: , where
We define the opposite of a polynomial P to be −P. Finding the opposite of a polynomial requires the application of the distributive property. For example, the opposite of the polynomial is written as
This leads us to the opposite binomial propertyIf given a binomial , then the opposite is , Care should be taken not to confuse this with the fact that This is the case because addition is commutative. In general,
Also, it is important to recall that
In other words, a negative fraction is shown by placing the negative sign in either the numerator, in front of the fraction bar, or in the denominator. Generally, negative denominators are avoided.
Example 3
State the restrictions and simplify:
Solution:
Begin by factoring the numerator and denominator.
Answer: , where
It is important to remember that we can only cancel factors of a product. A common mistake is to cancel terms. For example,
In some examples, we will make a broad assumption that the denominator is nonzero. When we make that assumption, we do not need to determine the restrictions.
Example 4
Simplify: (Assume all denominators are nonzero.)
Solution:
Factor the numerator by grouping. Factor the denominator using the formula for a difference of squares.
Next, cancel common factors.
Note: When the entire numerator or denominator cancels out a factor of 1 always remains.
Answer:
Example 5
Given , simplify
Solution:
Begin by calculating
Next, substitute into the quotient that is to be simplified.
Answer: , where
An important quantity in higher level mathematics is the difference quotientThe mathematical quantity , where , which represents the slope of a secant line through a function f.:
This quantity represents the slope of the line connecting two points on the graph of a function. The line passing through the two points is called a secant lineLine that intersects two points on the graph of a function..
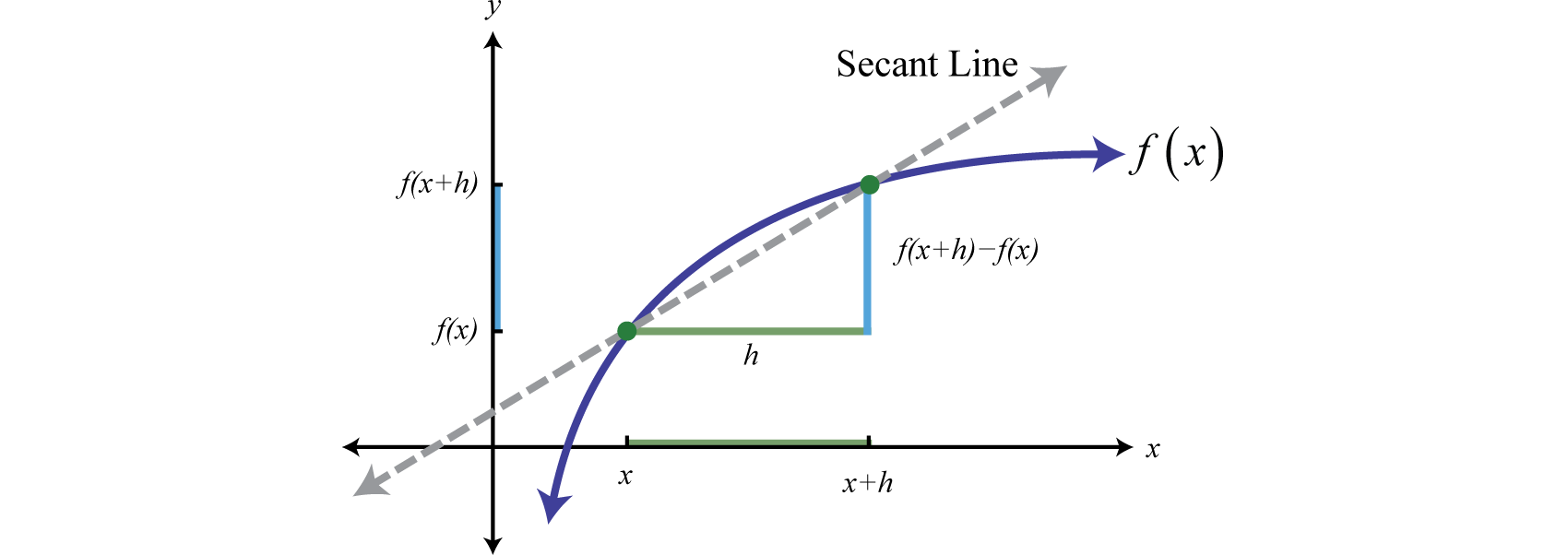
Calculating the difference quotient for many different functions is an important skill to learn in intermediate algebra. We will encounter this quantity often as we proceed in this textbook. When calculating the difference quotient we assume the denominator is nonzero.
Example 6
Given , simplify
Solution:
Answer:
Multiplying and Dividing Rational Functions
When multiplying fractions, we can multiply the numerators and denominators together and then reduce. Multiplying rational expressions is performed in a similar manner. In general, given polynomials P, Q, R, and S, where and , we have
The restrictions to the domain of a product consist of the restrictions of each function.
Example 7
Given and , find and determine the restrictions to the domain.
Solution:
In this case, the domain of consists of all real numbers except 5, and the domain of consists of all real numbers except Therefore, the domain of the product consists of all real numbers except 5 and Multiply the functions and then simplify the result.
Answer: , where
To divide two fractions, we multiply by the reciprocal of the divisor. Dividing rational expressions is performed in a similar manner. In general, given polynomials P, Q, R, and S, where , , and , we have
The restrictions to the domain of a quotient will consist of the restrictions of each function as well as the restrictions on the reciprocal of the divisor.
Example 8
Given and , find and determine the restrictions.
Solution:
In this case, the domain of consists of all real numbers except −3 and 7, and the domain of consists of all real numbers except 7 and −7. In addition, the reciprocal of has a restriction of −3 and Therefore, the domain of this quotient consists of all real numbers except −3, , and ±7.
Answer: , where
Recall that multiplication and division operations are to be performed from left to right.
Example 9
Simplify: (Assume all denominators are nonzero.)
Solution:
Begin by replacing the factor that is to be divided by multiplication of its reciprocal.
Answer:
Try this! Given and , calculate and determine the restrictions.
Answer: , where
If a cost function represents the cost of producing x units, then the average costThe total cost divided by the number of units produced, which can be represented by , where is a cost function. is the cost divided by the number of units produced.
Example 10
A manufacturer has determined that the cost in dollars of producing sweaters is given by , where x represents the number of sweaters produced daily. Determine the average cost of producing 100, 200, and 300 sweaters per day.
Solution:
Set up a function representing the average cost.
Next, calculate , , and
Answer: The average cost of producing 100 sweaters per day is $10.00 per sweater. If 200 sweaters are produced, the average cost per sweater is $5.00. If 300 are produced, the average cost per sweater is $4.00.
Key Takeaways
- Simplifying rational expressions is similar to simplifying fractions. First, factor the numerator and denominator and then cancel the common factors. Rational expressions are simplified if there are no common factors other than 1 in the numerator and the denominator.
- Simplified rational functions are equivalent for values in the domain of the original function. Be sure to state the restrictions unless the problem states that the denominators are assumed to be nonzero.
- After multiplying rational expressions, factor both the numerator and denominator and then cancel common factors. Make note of the restrictions to the domain. The values that give a value of 0 in the denominator for all expressions are the restrictions.
- To divide rational expressions, multiply the numerator by the reciprocal of the divisor.
- The restrictions to the domain of a product consist of the restrictions to the domain of each factor.
Topic Exercises
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Given , simplify
-
Given , simplify
-
Given , simplify
-
Given , simplify
-
Given , simplify
-
Given , simplify
-
-
-
-
-
-
-
-
-
-
Part A: Simplifying Rational Functions
Simplify the function and state its domain using interval notation.
State the restrictions and simplify the given rational expressions.
Simplify the given rational expressions. Assume all variable expressions in the denominator are nonzero.
Given the function, simplify the rational expression.
For the given function, simplify the difference quotient
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
A manufacturer has determined that the cost in dollars of producing bicycles is given by , where x represents the number of bicycles produced weekly. Determine the average cost of producing 50, 100, and 150 bicycles per week.
-
The cost in dollars of producing custom lighting fixtures is given by the function , where x represents the number of fixtures produced in a week. Determine the average cost per unit if 20, 40, and 50 units are produced in a week.
-
A manufacturer has determined that the cost in dollars of producing electric scooters is given by the function , where x represents the number of scooters produced in a month. Determine the average cost per scooter if 50 are produced in a month.
-
The cost in dollars of producing a custom injected molded part is given by , where n represents the number of parts produced. Calculate the average cost of each part if 2,500 custom parts are ordered.
-
The cost in dollars of an environmental cleanup is given by the function , where p represents the percentage of the area to be cleaned up . Use the function to determine the cost of cleaning up 50% of an affected area and the cost of cleaning up 80% of the area.
-
The value of a new car is given by the function where t represents the age of the car in years. Determine the value of the car when it is 6 years old.
Part B: Multiplying and Dividing Rational Functions
Simplify the product and state its domain using interval notation.
Simplify the quotient and state its domain using interval notation.
Multiply or divide as indicated, state the restrictions, and simplify.
Perform the operations and simplify. Assume all variable expressions in the denominator are nonzero.
-
Describe the restrictions to the rational expression . Explain.
-
Describe the restrictions to the rational expression . Explain.
-
Explain why is a restriction to
-
Explain to a beginning algebra student why we cannot cancel x in the rational expression
-
Research and discuss the importance of the difference quotient. What does it represent and in what subject does it appear?
Part D: Discussion Board
Answers
-
;
Domain:
-
-
; Domain:
-
-
; Domain:
-
-
; Domain:
-
-
; Domain:
-
-
;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
, where
-
-
, where
-
-
, where
-
-
5
-
-
-
-
-
-
-
-
-
-
; Domain:
-
-
; Domain:
-
-
; Domain:
-
-
; Domain:
-
-
; Domain:
-
-
; Domain:
-
-
;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
-
-
-
-
-
-
-
-
-
-
If 50 bicycles are produced, the average cost per bicycle is $148. If 100 are produced, the average cost is $111. If 150 bicycles are produced, the average cost is $115.33.
-
-
If 50 scooters are produced, the average cost of each is $490.
-
-
A 50% cleanup will cost $25,000. An 80% cleanup will cost $100,000.
-
-
Answer may vary
-
-
Answer may vary
-
-
Answer may vary
4.6 Rational Functions: Addition and Subtraction
Learning Objectives
- Add and subtract rational functions.
- Simplify complex rational expressions.
Adding and Subtracting Rational Functions
Adding and subtracting rational expressions is similar to adding and subtracting fractions. Recall that if the denominators are the same, we can add or subtract the numerators and write the result over the common denominator. When working with rational expressions, the common denominator will be a polynomial. In general, given polynomials P, Q, and R, where , we have the following:
The set of restrictions to the domain of a sum or difference of rational expressions consists of the restrictions to the domains of each expression.
Example 1
Subtract:
Solution:
The denominators are the same. Hence we can subtract the numerators and write the result over the common denominator. Take care to distribute the negative 1.
Answer: , where
To add rational expressions with unlike denominators, first find equivalent expressions with common denominators. Do this just as you have with fractions. If the denominators of fractions are relatively prime, then the least common denominator (LCD) is their product. For example,
Multiply each fraction by the appropriate form of 1 to obtain equivalent fractions with a common denominator.
In general, given polynomials P, Q, R, and S, where and , we have the following:
Example 2
Given and , find and state the restrictions.
Solution:
Here the LCD is the product of the denominators Multiply by the appropriate factors to obtain rational expressions with a common denominator before adding.
The domain of f consists all real numbers except , and the domain of g consists of all real numbers except −1. Therefore, the domain of f + g consists of all real numbers except −1 and
Answer: , where
It is not always the case that the LCD is the product of the given denominators. Typically, the denominators are not relatively prime; thus determining the LCD requires some thought. Begin by factoring all denominators. The LCD is the product of all factors with the highest power.
Example 3
Given and , find and state the restrictions to the domain.
Solution:
To determine the LCD, factor the denominator of
In this case the Multiply by 1 in the form of to obtain equivalent algebraic fractions with a common denominator and then subtract.
The domain of f consists of all real numbers except , and the domain of g consists of all real numbers except 1 and Therefore, the domain of f − g consists of all real numbers except 1 and
Answer: , where
Example 4
Simplify and state the restrictions:
Solution:
Begin by applying the opposite binomial property
Next, find equivalent fractions with the and then simplify.
Answer: , where
Rational expressions are sometimes expressed using negative exponents. In this case, apply the rules for negative exponents before simplifying the expression.
Example 5
Simplify and state the restrictions:
Solution:
Recall that . Begin by rewriting the rational expressions with negative exponents as fractions.
Then find the LCD and add.
Answer: , where
Simplifying Complex Rational Expressions
A complex rational expressionA rational expression that contains one or more rational expressions in the numerator or denominator or both. is defined as a rational expression that contains one or more rational expressions in the numerator or denominator or both. For example, is a complex rational expression. We simplify a complex rational expression by finding an equivalent fraction where the numerator and denominator are polynomials. There are two methods for simplifying complex rational expressions, and we will outline the steps for both methods. For the sake of clarity, assume that variable expressions used as denominators are nonzero.
Method 1: Simplify Using Division
We begin our discussion on simplifying complex rational expressions using division. Before we can multiply by the reciprocal of the denominator, we must simplify the numerator and denominator separately. The goal is to first obtain single algebraic fractions in the numerator and the denominator. The steps for simplifying a complex algebraic fraction are illustrated in the following example.
Example 6
Simplify: .
Solution:
Step 1: Simplify the numerator and denominator to obtain a single algebraic fraction divided by another single algebraic fraction. In this example, find equivalent terms with a common denominator in both the numerator and denominator before adding and subtracting.
At this point we have a single algebraic fraction divided by another single algebraic fraction.
Step 2: Multiply the numerator by the reciprocal of the denominator.
Step 3: Factor all numerators and denominators completely.
Step 4: Cancel all common factors.
Answer:
Example 7
Simplify: .
Solution:
Obtain a single algebraic fraction in the numerator and in the denominator.
Next, multiply the numerator by the reciprocal of the denominator, factor, and then cancel.
Answer:
Sometimes complex rational expressions are expressed using negative exponents.
Example 8
Simplify: .
Solution:
We begin by rewriting the expression without negative exponents.
Obtain single algebraic fractions in the numerator and denominator and then multiply by the reciprocal of the denominator.
Apply the opposite binomial property and then cancel.
Answer:
Method 2: Simplify Using the LCD
An alternative method for simplifying complex rational expressions involves clearing the fractions by multiplying the expression by a special form of 1. In this method, multiply the numerator and denominator by the least common denominator (LCD) of all given fractions.
Example 9
Simplify: .
Solution:
Step 1: Determine the LCD of all the fractions in the numerator and denominator. In this case, the denominators of the given fractions are 1, , and Therefore, the LCD is
Step 2: Multiply the numerator and denominator by the LCD. This step should clear the fractions in both the numerator and denominator.
This leaves us with a single algebraic fraction with a polynomial in the numerator and in the denominator.
Step 3: Factor the numerator and denominator completely.
Step 4: Cancel all common factors.
Note: This was the same problem presented in Example 6 and the results here are the same. It is worth taking the time to compare the steps involved using both methods on the same problem.
Answer:
It is important to point out that multiplying the numerator and denominator by the same nonzero factor is equivalent to multiplying by 1 and does not change the problem.
Key Takeaways
- Adding and subtracting rational expressions is similar to adding and subtracting fractions. A common denominator is required. If the denominators are the same, then we can add or subtract the numerators and write the result over the common denominator.
- The set of restrictions to the domain of a sum or difference of rational functions consists of the restrictions to the domains of each function.
- Complex rational expressions can be simplified into equivalent expressions with a polynomial numerator and polynomial denominator. They are reduced to lowest terms if the numerator and denominator are polynomials that share no common factors other than 1.
- One method of simplifying a complex rational expression requires us to first write the numerator and denominator as a single algebraic fraction. Then multiply the numerator by the reciprocal of the denominator and simplify the result.
- Another method for simplifying a complex rational expression requires that we multiply it by a special form of 1. Multiply the numerator and denominator by the LCD of all the denominators as a means to clear the fractions. After doing this, simplify the remaining rational expression.
Topic Exercises
Part A: Adding and Subtracting Rational Functions
State the restrictions and simplify.
Given and , simplify the sum and difference Also, state the domain using interval notation.
State the restrictions and simplify.
Simplify the given algebraic expressions. Assume all variable expressions in the denominator are nonzero.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Given , simplify
-
Given , simplify
-
Given , simplify the difference quotient
-
Given , simplify the difference quotient
Part B: Simplifying Complex Rational Expressions
Simplify. Assume all variable expressions in the denominators are nonzero.
-
Explain why the domain of a sum of rational functions is the same as the domain of the difference of those functions.
-
Two methods for simplifying complex rational expressions have been presented in this section. Which of the two methods do you feel is more efficient, and why?
Part C: Discussion Board
Answers
-
;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
;
-
-
; ; Domain:
-
-
; ; Domain:
-
-
; ; Domain:
-
-
; ; Domain:
-
-
; ; Domain:
-
-
;
-
-
;
-
-
;
-
-
;
-
-
0;
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Answer may vary
-
4.7 Solving Rational Equations
Learning Objectives
- Solve rational equations.
- Solve literal equations, or formulas, involving rational expressions.
- Solve applications involving the reciprocal of unknowns.
Solving Rational Equations
A rational equationAn equation containing at least one rational expression. is an equation containing at least one rational expression. Rational expressions typically contain a variable in the denominator. For this reason, we will take care to ensure that the denominator is not 0 by making note of restrictions and checking our solutions. Solving rational equations involves clearing fractions by multiplying both sides of the equation by the least common denominator (LCD).
Example 1
Solve:
Solution:
We first make a note of the restriction on x, We then multiply both sides by the LCD, which in this case equals
Check your answer. Substitute into the original equation and see if you obtain a true statement.
Answer: The solution is 5.
After multiplying both sides of the previous example by the LCD, we were left with a linear equation to solve. This is not always the case; sometimes we will be left with quadratic equation.
Example 2
Solve:
Solution:
In this example, there are two restrictions, and Begin by multiplying both sides by the LCD,
After distributing and simplifying both sides of the equation, a quadratic equation remains. To solve, rewrite the quadratic equation in standard form, factor, and then set each factor equal to 0.
Check to see if these values solve the original equation.
Check |
Check |
|---|---|
|
Answer: The solutions are 0 and −4.
Up to this point, all of the possible solutions have solved the original equation. However, this may not always be the case. Multiplying both sides of an equation by variable factors may lead to extraneous solutionsA solution that does not solve the original equation., which are solutions that do not solve the original equation. A complete list of steps for solving a rational equation is outlined in the following example.
Example 3
Solve:
Solution:
Step 1: Factor all denominators and determine the LCD.
The LCD is
Step 2: Identify the restrictions. In this case, and
Step 3: Multiply both sides of the equation by the LCD. Distribute carefully and then simplify.
Step 4: Solve the resulting equation. Here the result is a quadratic equation. Rewrite it in standard form, factor, and then set each factor equal to 0.
Step 5: Check for extraneous solutions. Always substitute into the original equation, or the factored equivalent. In this case, choose the factored equivalent to check:
Check |
Check |
|---|---|
|
|
Here 5 is an extraneous solution and is not included in the solution set. It is important to note that 5 is a restriction.
Answer: The solution is
If this process produces a solution that happens to be a restriction, then disregard it as a solution.
Sometimes all potential solutions are extraneous, in which case we say that there is no solution to the original equation. In the next two examples, we demonstrate two ways in which rational equation can have no solutions.
Example 4
Solve: .
Solution:
To identify the LCD, first factor the denominators.
Multiply both sides by the LCD, , distributing carefully.
The equation is a contradiction and thus has no solution.
Answer: No solution,
Example 5
Solve: .
Solution:
First, factor the denominators.
Take note that the restrictions on the domain are To clear the fractions, multiply by the LCD,
Both of these values are restrictions of the original equation; hence both are extraneous.
Answer: No solution,
It is important to point out that this technique for clearing algebraic fractions only works for equations. Do not try to clear algebraic fractions when simplifying expressions. As a reminder, an example of each is provided below.
Expression |
Equation |
|---|---|
Expressions are to be simplified and equations are to be solved. If we multiply the expression by the LCD, , we obtain another expression that is not equivalent.
Incorrect |
Correct |
|---|---|
|
Rational equations are sometimes expressed using negative exponents.
Example 6
Solve:
Solution:
Begin by removing the negative exponents.
Here we can see the restriction, Next, multiply both sides by the LCD,
Answer: ,
A proportionA statement of equality of two ratios. is a statement of equality of two ratios.
This proportion is often read “a is to b as c is to d.” Given any nonzero real numbers a, b, c, and d that satisfy a proportion, multiply both sides by the product of the denominators to obtain the following:
This shows that cross products are equal, and is commonly referred to as cross multiplicationIf then .
Cross multiply to solve proportions where terms are unknown.
Example 7
Solve:
Solution:
When cross multiplying, be sure to group

Apply the distributive property in the next step.
Answer:
Cross multiplication can be used as an alternate method for solving rational equations. The idea is to simplify each side of the equation to a single algebraic fraction and then cross multiply.
Example 8
Solve:
Solution:
Obtain a single algebraic fraction on the left side by subtracting the equivalent fractions with a common denominator.
Note that , cross multiply, and then solve for x.
Next, set each variable factor equal to zero.
The check is left to the reader.
Answer: −8, 4
Solving Literal Equations and Applications Involving Reciprocals
Literal equations, or formulas, are often rational equations. Hence the techniques described in this section can be used to solve for particular variables. Assume that all variable expressions in the denominator are nonzero.
Example 9
The reciprocal of the combined resistance of two resistors and in parallel is given by the formula Solve for in terms of and

Solution:
The goal is to isolate on one side of the equation. Begin by multiplying both sides of the equation by the LCD,
Answer:
Recall that the reciprocal of a nonzero number n is For example, the reciprocal of 5 is and In this section, the applications will often involve the key word “reciprocal.” When this is the case, we will see that the algebraic setup results in a rational equation.
Example 10
A positive integer is 3 less than another. If the reciprocal of the smaller integer is subtracted from twice the reciprocal of the larger, then the result is Find the two integers.
Solution:
Let n represent the larger positive integer.
Let n − 3 represent the smaller positive integer.
Set up an algebraic equation.
Solve this rational expression by multiplying both sides by the LCD. The LCD is
Here we have two viable possibilities for the larger integer n. For this reason, we will we have two solutions to this problem.
If , then
If , then
As a check, perform the operations indicated in the problem.
Check 8 and 5. |
Check 15 and 12. |
|---|---|
Answer: Two sets of positive integers solve this problem: {5, 8} and {12, 15}.
Try this! When the reciprocal of the larger of two consecutive even integers is subtracted from 4 times the reciprocal of the smaller, the result is Find the integers.
Answer: 4, 6
Key Takeaways
- Begin solving rational equations by multiplying both sides by the LCD. The resulting equivalent equation can be solved using the techniques learned up to this point.
- Multiplying both sides of a rational equation by a variable expression introduces the possibility of extraneous solutions. Therefore, we must check the solutions against the set of restrictions. If a solution is a restriction, then it is not part of the domain and is extraneous.
- When multiplying both sides of an equation by an expression, distribute carefully and multiply each term by that expression.
- If all of the resulting solutions are extraneous, then the original equation has no solutions.
Topic Exercises
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Given , find x when
-
Given , find x when
-
Given , find x when
-
Given , find x when
-
-
-
-
-
-
-
,
-
,
-
,
-
,
-
-
-
-
-
-
Part A: Solving Rational Equations
Solve.
Solve the following equations involving negative exponents.
Solve by cross multiplying.
Simplify or solve, whichever is appropriate.
Find the roots of the given function.
Find the x- and y-intercepts.
Find the points where the given functions coincide. (Hint: Find the points where )
Recall that if , then or Use this to solve the following absolute value equations.
-
Solve for P:
-
Solve for A:
-
Solve for t:
-
Solve for n:
-
Solve for y:
-
Solve for :
-
Solve for y:
-
Solve for y:
-
Solve for y:
-
Solve for y:
-
Solve for x:
-
Solve for y:
-
The value in dollars of a tablet computer is given by the function , where t represents the age of the tablet. Determine the age of the tablet if it is now worth $100.
-
The value in dollars of a car is given by the function , where t represents the age of the car. Determine the age of the car if it is now worth $6,000.
-
When 2 is added to 5 times the reciprocal of a number, the result is 12. Find the number.
-
When 1 is subtracted from 4 times the reciprocal of a number, the result is 11. Find the number.
-
The sum of the reciprocals of two consecutive odd integers is Find the integers.
-
The sum of the reciprocals of two consecutive even integers is Find the integers.
-
An integer is 4 more than another. If 2 times the reciprocal of the larger is subtracted from 3 times the reciprocal of the smaller, then the result is Find the integers.
-
An integer is 2 more than twice another. If 2 times the reciprocal of the larger is subtracted from 3 times the reciprocal of the smaller, then the result is Find the integers.
-
If 3 times the reciprocal of the larger of two consecutive integers is subtracted from 2 times the reciprocal of the smaller, then the result is Find the two integers.
-
If 3 times the reciprocal of the smaller of two consecutive integers is subtracted from 7 times the reciprocal of the larger, then the result is Find the two integers.
-
A positive integer is 5 less than another. If the reciprocal of the smaller integer is subtracted from 3 times the reciprocal of the larger, then the result is Find the two integers.
-
A positive integer is 6 less than another. If the reciprocal of the smaller integer is subtracted from 10 times the reciprocal of the larger, then the result is Find the two integers.
Part B: Solving Literal Equations
Solve for the given variable.
Use algebra to solve the following applications.
Solve for the unknowns.
-
Explain how we can tell the difference between a rational expression and a rational equation. How do we treat them differently? Give an example of each.
-
Research and discuss reasons why multiplying both sides of a rational equation by the LCD sometimes produces extraneous solutions.
Part C: Discussion Board
Answers
-
-
-
−4
-
-
−7, 3
-
-
, 2
-
-
−2,
-
-
-
-
-
-
Ø
-
-
−2,
-
-
-
-
6
-
-
Ø
-
-
−8, 2
-
-
5
-
-
−6, 4
-
-
10
-
-
-
-
-
-
−3, −1
-
-
−6, 4
-
-
-
-
-
-
−16
-
-
-
-
−2, 0
-
-
−3, 2
-
-
Solve; −3,
-
-
Simplify;
-
-
Simplify;
-
-
Solve;
-
-
-
-
±9
-
-
-
-
-
-
-
-
x-intercept: ; y-intercept: (0, 5)
-
-
x-intercept: ; y-intercept:
-
-
x-intercept: ; y-intercept: none
-
-
(−1, −1) and (1, 1)
-
-
(1, 2) and (3, 4)
-
-
,
-
-
2, 10
-
-
−3, −2, −1, 6
-
-
-
-
-
-
-
-
-
-
-
-
-
-
3.6 years old
-
-
-
-
5, 7
-
-
{−8, −4} and {12, 16}
-
-
{1, 2} or {−4, −3}
-
-
{4, 9} or {15, 20}
-
-
Answer may vary
-
4.8 Applications and Variation
Learning Objectives
- Solve applications involving uniform motion (distance problems).
- Solve work-rate applications.
- Set up and solve applications involving direct, inverse, and joint variation.
Solving Uniform Motion Problems
Uniform motion (or distance)Described by the formula , where the distance D is given as the product of the average rate r and the time t traveled at that rate. problems involve the formula , where the distance D is given as the product of the average rate r and the time t traveled at that rate. If we divide both sides by the average rate r, then we obtain the formula
For this reason, when the unknown quantity is time, the algebraic setup for distance problems often results in a rational equation. We begin any uniform motion problem by first organizing our data with a chart. Use this information to set up an algebraic equation that models the application.
Example 1
Sally traveled 15 miles on the bus and then another 72 miles on a train. The train was 18 miles per hour faster than the bus, and the total trip took 2 hours. What was the average speed of the train?
Solution:
First, identify the unknown quantity and organize the data.
Let x represent the average speed (in miles per hour) of the bus.
Let represent the average speed of the train.

To avoid introducing two more variables for the time column, use the formula The time for each leg of the trip is calculated as follows:
Use these expressions to complete the chart.
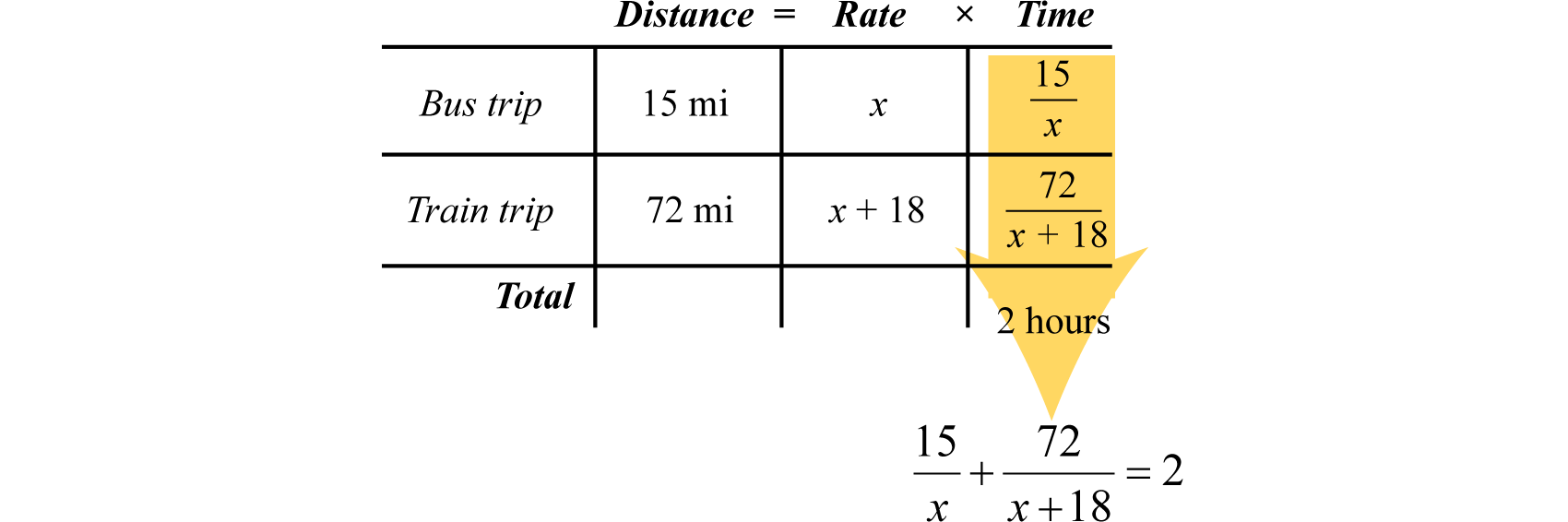
The algebraic setup is defined by the time column. Add the time spent on each leg of the trip to obtain a total of 2 hours:

We begin solving this equation by first multiplying both sides by the LCD,
Solve the resulting quadratic equation by factoring.
Since we are looking for an average speed we will disregard the negative answer and conclude the bus averaged 30 mph. Substitute in the expression identified as the speed of the train.
Answer: The speed of the train was 48 mph.
Example 2
A boat can average 12 miles per hour in still water. On a trip downriver the boat was able to travel 29 miles with the current. On the return trip the boat was only able to travel 19 miles in the same amount of time against the current. What was the speed of the current?
Solution:
First, identify the unknown quantities and organize the data.
Let c represent the speed of the river current.
Next, organize the given data in a chart. Traveling downstream, the current will increase the speed of the boat, so it adds to the average speed of the boat. Traveling upstream, the current slows the boat, so it will subtract from the average speed of the boat.
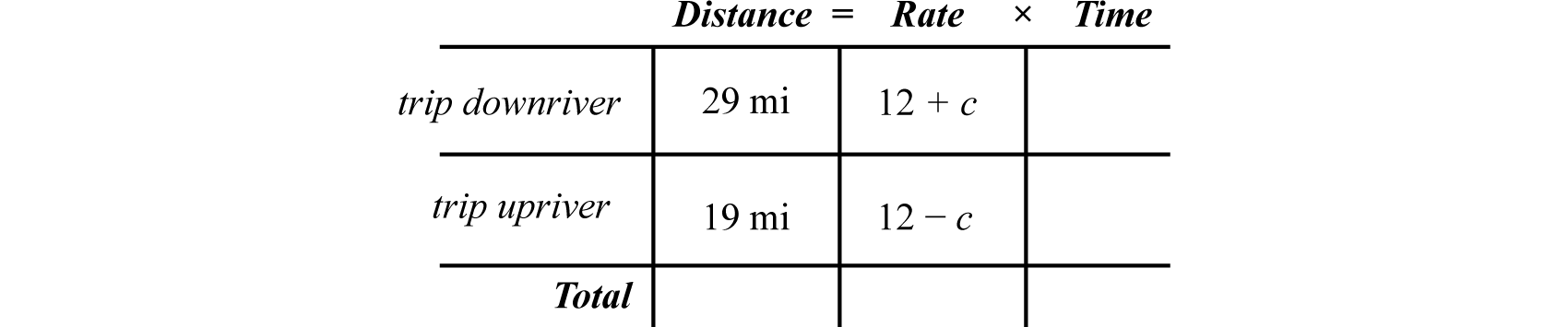
Use the formula to fill in the time column.

Because the boat traveled the same amount of time downriver as it did upriver, finish the algebraic setup by setting the expressions that represent the times equal to each other.
Since there is a single algebraic fraction on each side, we can solve this equation using cross multiplication.
Answer: The speed of the current was miles per hour.
Try this! A jet aircraft can average 160 miles per hour in calm air. On a trip, the aircraft traveled 600 miles with a tailwind and returned the 600 miles against a headwind of the same speed. If the total round trip took 8 hours, then what was the speed of the wind?
Answer: 40 miles per hour
Solving Work-Rate Problems
The rate at which a task can be performed is called a work rateThe rate at which a task can be performed.. For example, if a painter can paint a room in 6 hours, then the task is to paint the room, and we can write
In other words, the painter can complete of the task per hour. If he works for less than 6 hours, then he will perform a fraction of the task. If he works for more than 6 hours, then he can complete more than one task. For example,
Obtain the amount of the task completed by multiplying the work rate by the amount of time the painter works. Typically, work-rate problems involve people or machines working together to complete tasks. In general, if t represents the time two people work together, then we have the following work-rate formula, where and are the individual work rates and t is the time it takes to complete the task working together.:
Here and are the individual work rates.
Example 3
Joe can paint a typical room in 2 hours less time than Mark. If Joe and Mark can paint 5 rooms working together in a 12 hour shift, how long does it take each to paint a single room?
Solution:
Let x represent the time it takes Mark to paint a typical room.
Let x − 2 represent the time it takes Joe to paint a typical room.
Therefore, Mark’s individual work-rate is rooms per hour and Joe’s is rooms per hour. Both men worked for 12 hours. We can organize the data in a chart, just as we did with distance problems.

Working together, they can paint 5 total rooms in 12 hours. This leads us to the following algebraic setup:
Multiply both sides by the LCD,
Solve the resulting quadratic equation by factoring.
We can disregard because back substituting into x − 2 would yield a negative time to paint a room. Take x = 6 to be the only solution and use it to find the time it takes Joe to paint a typical room.
Answer: Joe can paint a typical room in 4 hours and Mark can paint a typical room in 6 hours. As a check we can multiply both work rates by 12 hours to see that together they can paint 5 rooms.
Example 4
It takes Bill twice as long to lay a tile floor by himself as it does Manny. After working together with Bill for 4 hours, Manny was able to complete the job in 2 additional hours. How long would it have taken Manny working alone?
Solution:
Let x represent the time it takes Manny to lay the floor alone.
Let 2x represent the time it takes Bill to lay the floor alone.
Manny’s work rate is of the floor per hour and Bill’s work rate is Bill worked on the job for 4 hours and Manny worked on the job for 6 hours.
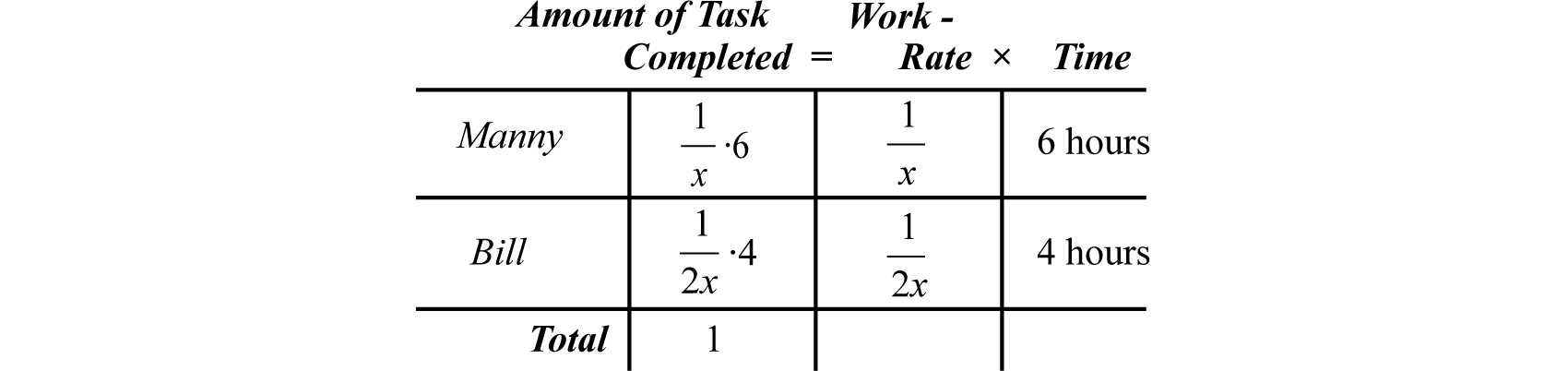
This leads us to the following algebraic setup:
Solve.
Answer: It would have taken Manny 8 hours to complete the floor by himself.
Consider the work-rate formula where one task is to be completed.
Factor out the time t and then divide both sides by t. This will result in equivalent specialized work-rate formulas:
In summary, we have the following equivalent work-rate formulas:
Try this! Matt can tile a countertop in 2 hours, and his assistant can do the same job in 3 hours. If Matt starts the job and his assistant joins him 1 hour later, then how long will it take to tile the countertop?
Answer: hours
Solving Problems involving Direct, Inverse, and Joint variation
Many real-world problems encountered in the sciences involve two types of functional relationships. The first type can be explored using the fact that the distance s in feet an object falls from rest, without regard to air resistance, can be approximated using the following formula:
Here t represents the time in seconds the object has been falling. For example, after 2 seconds the object will have fallen feet.
Time t in seconds |
Distance in feet |
|---|---|
0 |
0 |
1 |
16 |
2 |
64 |
3 |
144 |
4 |
256 |
In this example, we can see that the distance varies over time as the product of a constant 16 and the square of the time t. This relationship is described as direct variationDescribes two quantities x and y that are constant multiples of each other: and 16 is called the constant of variationThe nonzero multiple k, when quantities vary directly or inversely.. Furthermore, if we divide both sides of by we have
In this form, it is reasonable to say that s is proportional to t2, and 16 is called the constant of proportionalityUsed when referring to the constant of variation.. In general, we have
Key words |
Translation |
|---|---|
“y varies directly as x” |
|
“y is directly proportional to x” |
|
“y is proportional to x” |
Used when referring to direct variation.
Here k is nonzero and is called the constant of variation or the constant of proportionality. Typically, we will be given information from which we can determine this constant.
Example 5
An object’s weight on Earth varies directly to its weight on the Moon. If a man weighs 180 pounds on Earth, then he will weigh 30 pounds on the Moon. Set up an algebraic equation that expresses the weight on Earth in terms of the weight on the Moon and use it to determine the weight of a woman on the Moon if she weighs 120 pounds on Earth.
Solution:
Let y represent weight on Earth.
Let x represent weight on the Moon.
We are given that the “weight on Earth varies directly to the weight on the Moon.”
To find the constant of variation k, use the given information. A 180-lb man on Earth weighs 30 pounds on the Moon, or when
Solve for k.
Next, set up a formula that models the given information.
This implies that a person’s weight on Earth is 6 times his weight on the Moon. To answer the question, use the woman’s weight on Earth, y = 120 lbs, and solve for x.
Answer: The woman weighs 20 pounds on the Moon.
The second functional relationship can be explored using the formula that relates the intensity of light I to the distance from its source d.
Here k represents some constant. A foot-candle is a measurement of the intensity of light. One foot-candle is defined to be equal to the amount of illumination produced by a standard candle measured one foot away. For example, a 125-Watt fluorescent growing light is advertised to produce 525 foot-candles of illumination. This means that at a distance foot, foot-candles and we have:
Using we can construct a formula which gives the light intensity produced by the bulb:
Here d represents the distance the growing light is from the plants. In the following chart, we can see that the amount of illumination fades quickly as the distance from the plants increases.
distance t in feet |
Light Intensity
|
|---|---|
1 |
525 |
2 |
131.25 |
3 |
58.33 |
4 |
32.81 |
5 |
21 |
This type of relationship is described as an inverse variationDescribes two quantities x and y, where one variable is directly proportional to the reciprocal of the other: . We say that I is inversely proportionalUsed when referring to inverse variation. to the square of the distance d, where 525 is the constant of proportionality. In general, we have
Key words |
Translation |
|---|---|
“y varies inversely as x” |
|
“y is inversely proportional to x” |
Again, k is nonzero and is called the constant of variation or the constant of proportionality.
Example 6
The weight of an object varies inversely as the square of its distance from the center of Earth. If an object weighs 100 pounds on the surface of Earth (approximately 4,000 miles from the center), how much will it weigh at 1,000 miles above Earth’s surface?
Solution:
Let w represent the weight of the object.
Let d represent the object’s distance from the center of Earth.
Since “w varies inversely as the square of d,” we can write
Use the given information to find k. An object weighs 100 pounds on the surface of Earth, approximately 4,000 miles from the center. In other words, w = 100 when d = 4,000:
Solve for k.
Therefore, we can model the problem with the following formula:
To use the formula to find the weight, we need the distance from the center of Earth. Since the object is 1,000 miles above the surface, find the distance from the center of Earth by adding 4,000 miles:
To answer the question, use the formula with d = 5,000.
Answer: The object will weigh 64 pounds at a distance 1,000 miles above the surface of Earth.
Lastly, we define relationships between multiple variables, described as joint variationDescribes a quantity y that varies directly as the product of two other quantities x and z: . In general, we have
Key Words |
Translation |
|---|---|
“y varies jointly as x and z” |
|
“y is jointly proportional to x and z” |
Used when referring to joint variation.
Here k is nonzero and is called the constant of variation or the constant of proportionality.
Example 7
The area of an ellipse varies jointly as a, half of the ellipse’s major axis, and b, half of the ellipse’s minor axis as pictured. If the area of an ellipse is , where and , what is the constant of proportionality? Give a formula for the area of an ellipse.

Solution:
If we let A represent the area of an ellipse, then we can use the statement “area varies jointly as a and b” to write
To find the constant of variation k, use the fact that the area is when and
Therefore, the formula for the area of an ellipse is
Answer: The constant of proportionality is and the formula for the area of an ellipse is
Try this! Given that y varies directly as the square of x and inversely with z, where y = 2 when x = 3 and z = 27, find y when x = 2 and z = 16.
Answer:
Key Takeaways
- When solving distance problems where the time element is unknown, use the equivalent form of the uniform motion formula, , to avoid introducing more variables.
- When solving work-rate problems, multiply the individual work rate by the time to obtain the portion of the task completed. The sum of the portions of the task results in the total amount of work completed.
- The setup of variation problems usually requires multiple steps. First, identify the key words to set up an equation and then use the given information to find the constant of variation k. After determining the constant of variation, write a formula that models the problem. Once a formula is found, use it to answer the question.
Topic Exercises
-
Every morning Jim spends 1 hour exercising. He runs 2 miles and then he bikes 16 miles. If Jim can bike twice as fast as he can run, at what speed does he average on his bike?
-
Sally runs 3 times as fast as she walks. She ran for of a mile and then walked another miles. The total workout took hours. What was Sally’s average walking speed?
-
On a business trip, an executive traveled 720 miles by jet and then another 80 miles by helicopter. If the jet averaged 3 times the speed of the helicopter, and the total trip took 4 hours, what was the average speed of the jet?
-
A triathlete can run 3 times as fast as she can swim and bike 6 times as fast as she can swim. The race consists of a mile swim, 3 mile run, and a 12 mile bike race. If she can complete all of these events in hour, then how fast can she swim, run and bike?
-
On a road trip, Marty was able to drive an average 4 miles per hour faster than George. If Marty was able to drive 39 miles in the same amount of time George drove 36 miles, what was Marty’s average speed?
-
The bus is 8 miles per hour faster than the trolley. If the bus travels 9 miles in the same amount of time the trolley can travel 7 miles, what is the average speed of each?
-
Terry decided to jog the 5 miles to town. On the return trip, she walked the 5 miles home at half of the speed that she was able to jog. If the total trip took 3 hours, what was her average jogging speed?
-
James drove the 24 miles to town and back in 1 hour. On the return trip, he was able to average 20 miles per hour faster than he averaged on the trip to town. What was his average speed on the trip to town?
-
A light aircraft was able to travel 189 miles with a 14 mile per hour tailwind in the same time it was able to travel 147 miles against it. What was the speed of the aircraft in calm air?
-
A jet flew 875 miles with a 30 mile per hour tailwind. On the return trip, against a 30 mile per hour headwind, it was able to cover only 725 miles in the same amount of time. How fast was the jet in calm air?
-
A helicopter averaged 90 miles per hour in calm air. Flying with the wind it was able to travel 250 miles in the same amount of time it took to travel 200 miles against it. What is the speed of the wind?
-
Mary and Joe took a road-trip on separate motorcycles. Mary’s average speed was 12 miles per hour less than Joe’s average speed. If Mary drove 115 miles in the same time it took Joe to drive 145 miles, what was Mary’s average speed?
-
A boat averaged 12 miles per hour in still water. On a trip downstream, with the current, the boat was able to travel 26 miles. The boat then turned around and returned upstream 33 miles. How fast was the current if the total trip took 5 hours?
-
If the river current flows at an average 3 miles per hour, a tour boat can make an 18-mile tour downstream with the current and back the 18 miles against the current in hours. What is the average speed of the boat in still water?
-
Jose drove 10 miles to his grandmother’s house for dinner and back that same evening. Because of traffic, he averaged 20 miles per hour less on the return trip. If it took hour longer to get home, what was his average speed driving to his grandmother’s house?
-
Jerry paddled his kayak, upstream against a 1 mph current, for 12 miles. The return trip, downstream with the 1 mph current, took one hour less time. How fast did Jerry paddle the kayak in still water?
-
James and Mildred left the same location in separate cars and met in Los Angeles 300 miles away. James was able to average 10 miles an hour faster than Mildred on the trip. If James arrived 1 hour earlier than Mildred, what was Mildred’s average speed?
-
A bus is 20 miles per hour faster than a bicycle. If Bill boards a bus at the same time and place that Mary departs on her bicycle, Bill will arrive downtown 5 miles away hour earlier than Mary. What is the average speed of the bus?
Part A: Solving Uniform Motion Problems
Use algebra to solve the following applications.
-
Mike can paint the office by himself in hours. Jordan can paint the office in 6 hours. How long will it take them to paint the office working together?
-
Barry can lay a brick driveway by himself in days. Robert does the same job in 5 days. How long will it take them to lay the brick driveway working together?
-
A larger pipe fills a water tank twice as fast as a smaller pipe. When both pipes are used, they fill the tank in 10 hours. If the larger pipe is left off, how long would it take the smaller pipe to fill the tank?
-
A newer printer can print twice as fast as an older printer. If both printers working together can print a batch of flyers in 45 minutes, then how long would it take the older printer to print the batch working alone?
-
Mary can assemble a bicycle for display in 2 hours. It takes Jane 3 hours to assemble a bicycle. How long will it take Mary and Jane, working together, to assemble 5 bicycles?
-
Working alone, James takes twice as long to assemble a computer as it takes Bill. In one 8-hour shift, working together, James and Bill can assemble 6 computers. How long would it take James to assemble a computer if he were working alone?
-
Working alone, it takes Harry one hour longer than Mike to install a fountain. Together they can install 10 fountains in 12 hours. How long would it take Mike to install 10 fountains by himself?
-
Working alone, it takes Henry 2 hours longer than Bill to paint a room. Working together they painted rooms in 6 hours. How long would it have taken Henry to paint the same amount if he were working alone?
-
Manny, working alone, can install a custom cabinet in 3 hours less time than his assistant. Working together they can install the cabinet in 2 hours. How long would it take Manny to install the cabinet working alone?
-
Working alone, Garret can assemble a garden shed in 5 hours less time than his brother. Working together, they need 6 hours to build the garden shed. How long would it take Garret to build the shed working alone?
-
Working alone, the assistant-manager takes 2 more hours than the manager to record the inventory of the entire shop. After working together for 2 hours, it took the assistant-manager 1 additional hour to complete the inventory. How long would it have taken the manager to complete the inventory working alone?
-
An older printer can print a batch of sales brochures in 16 minutes. A newer printer can print the same batch in 10 minutes. After working together for some time, the newer printer was shut down and it took the older printer 3 more minutes to complete the job. How long was the newer printer operating?
Part B: Solving Work-Rate Problems
Use algebra to solve the following applications.
-
The distance D an automobile can travel is directly proportional to the time t that it travels at a constant speed.
-
The extension of a hanging spring d is directly proportional to the weight w attached to it.
-
An automobile’s braking distance d is directly proportional to the square of the automobile’s speed v.
-
The volume V of a sphere varies directly as the cube of its radius r.
-
The volume V of a given mass of gas is inversely proportional to the pressure p exerted on it.
-
Every particle of matter in the universe attracts every other particle with a force F that is directly proportional to the product of the masses and of the particles, and it is inversely proportional to the square of the distance d between them.
-
Simple interest I is jointly proportional to the annual interest rate r and the time t in years a fixed amount of money is invested.
-
The time t it takes an object to fall is directly proportional to the square root of the distance d it falls.
-
y varies directly as x, and y = 30 when x = 6.
-
y varies directly as x, and y = 52 when x = 4.
-
y is directly proportional to x, and y = 12 when x = 3.
-
y is directly proportional to x, and y = 120 when x = 20.
-
y is inversely proportional to x, and y = 3 when x = 9.
-
y is inversely proportional to x, and y = 21 when x = 3.
-
y varies inversely as x, and y = 2 when
-
y varies inversely as x, and when
-
y is jointly proportional to x and z, where y = 2 when x = 1 and z = 3.
-
y is jointly proportional to x and z, where y = 15 when x = 3 and z = 7.
-
y varies jointly as x and z, where when and z = 12.
-
y varies jointly as x and z, where y = 5 when and
-
y varies directly as the square of x, where y = 45 when x = 3.
-
y varies directly as the square of x, where y = 3 when
-
y is inversely proportional to the square of x, where y = 27 when
-
y is inversely proportional to the square of x, where y = 9 when
-
y varies jointly as x and the square of z, where y = 6 when and
-
y varies jointly as x and z and inversely as the square of w, where y = 5 when x = 1, z = 3, and
-
y varies directly as the square root of x and inversely as the square of z, where y = 15 when x = 25 and z = 2.
-
y varies directly as the square of x and inversely as z and the square of w, where y = 14 when x = 4, w = 2, and z = 2.
-
Revenue in dollars is directly proportional to the number of branded sweatshirts sold. The revenue earned from selling 25 sweatshirts is $318.75. Determine the revenue if 30 sweatshirts are sold.
-
The sales tax on the purchase of a new car varies directly as the price of the car. If an $18,000 new car is purchased, then the sales tax is $1,350. How much sales tax is charged if the new car is priced at $22,000?
-
The price of a share of common stock in a company is directly proportional to the earnings per share (EPS) of the previous 12 months. If the price of a share of common stock in a company is $22.55, and the EPS is published to be $1.10, determine the value of the stock if the EPS increases by $0.20.
-
The distance traveled on a road trip varies directly with the time spent on the road. If a 126-mile trip can be made in 3 hours, then what distance can be traveled in 4 hours?
-
The circumference of a circle is directly proportional to its radius. The circumference of a circle with radius 7 centimeters is measured as centimeters. What is the constant of proportionality?
-
The area of circle varies directly as the square of its radius. The area of a circle with radius 7 centimeters is determined to be square centimeters. What is the constant of proportionality?
-
The surface area of a sphere varies directly as the square of its radius. When the radius of a sphere measures 2 meters, the surface area measures square meters. Find the surface area of a sphere with radius 3 meters.
-
The volume of a sphere varies directly as the cube of its radius. When the radius of a sphere measures 3 meters, the volume is cubic meters. Find the volume of a sphere with radius 1 meter.
-
With a fixed height, the volume of a cone is directly proportional to the square of the radius at the base. When the radius at the base measures 10 centimeters, the volume is 200 cubic centimeters. Determine the volume of the cone if the radius of the base is halved.
-
The distance d an object in free fall drops varies directly with the square of the time t that it has been falling. If an object in free fall drops 36 feet in 1.5 seconds, then how far will it have fallen in 3 seconds?
-
A hanging spring is stretched 5 inches when a 20-pound weight is attached to it. Determine its spring constant.
-
A hanging spring is stretched 3 centimeters when a 2-kilogram weight is attached to it. Determine the spring constant.
-
If a hanging spring is stretched 3 inches when a 2-pound weight is attached, how far will it stretch with a 5-pound weight attached?
-
If a hanging spring is stretched 6 centimeters when a 4-kilogram weight is attached to it, how far will it stretch with a 2-kilogram weight attached?
-
It takes 36 feet to stop a particular automobile moving at a speed of 30 miles per hour. How much breaking distance is required if the speed is 35 miles per hour?
-
After an accident, it was determined that it took a driver 80 feet to stop his car. In an experiment under similar conditions, it takes 45 feet to stop the car moving at a speed of 30 miles per hour. Estimate how fast the driver was moving before the accident.
-
A balloon is filled to a volume of 216 cubic inches on a diving boat under 1 atmosphere of pressure. If the balloon is taken underwater approximately 33 feet, where the pressure measures 2 atmospheres, then what is the volume of the balloon?
-
A balloon is filled to 216 cubic inches under a pressure of 3 atmospheres at a depth of 66 feet. What would the volume be at the surface, where the pressure is 1 atmosphere?
-
To balance a seesaw, the distance from the fulcrum that a person must sit is inversely proportional to his weight. If a 72-pound boy is sitting 3 feet from the fulcrum, how far from the fulcrum must a 54-pound boy sit to balance the seesaw?
-
The current I in an electrical conductor is inversely proportional to its resistance R. If the current is ampere when the resistance is 100 ohms, what is the current when the resistance is 150 ohms?
-
The amount of illumination I is inversely proportional to the square of the distance d from a light source. If 70 foot-candles of illumination is measured 2 feet away from a lamp, what level of illumination might we expect foot away from the lamp?
-
The amount of illumination I is inversely proportional to the square of the distance d from a light source. If 40 foot-candles of illumination is measured 3 feet away from a lamp, at what distance can we expect 10 foot-candles of illumination?
-
The number of men, represented by y, needed to lay a cobblestone driveway is directly proportional to the area A of the driveway and inversely proportional to the amount of time t allowed to complete the job. Typically, 3 men can lay 1,200 square feet of cobblestone in 4 hours. How many men will be required to lay 2,400 square feet of cobblestone in 6 hours?
-
The volume of a right circular cylinder varies jointly as the square of its radius and its height. A right circular cylinder with a 3-centimeter radius and a height of 4 centimeters has a volume of cubic centimeters. Find a formula for the volume of a right circular cylinder in terms of its radius and height.
-
The period T of a pendulum is directly proportional to the square root of its length L. If the length of a pendulum is 1 meter, then the period is approximately 2 seconds. Approximate the period of a pendulum that is 0.5 meter in length.
-
The time t it takes an object to fall is directly proportional to the square root of the distance d it falls. An object dropped from 4 feet will take second to hit the ground. How long will it take an object dropped from 16 feet to hit the ground?
-
If two objects with masses 50 kilograms and 100 kilograms are meter apart, then they produce approximately newtons (N) of force. Calculate the gravitational constant.
-
Use the gravitational constant from the previous exercise to write a formula that approximates the force F in newtons between two masses and , expressed in kilograms, given the distance d between them in meters.
-
Calculate the force in newtons between Earth and the Moon, given that the mass of the Moon is approximately kilograms, the mass of Earth is approximately kilograms, and the distance between them is on average meters.
-
Calculate the force in newtons between Earth and the Sun, given that the mass of the Sun is approximately kilograms, the mass of Earth is approximately kilograms, and the distance between them is on average meters.
-
If y varies directly as the square of x, then how does y change if x is doubled?
-
If y varies inversely as square of t, then how does y change if t is doubled?
-
If y varies directly as the square of x and inversely as the square of t, then how does y change if both x and t are doubled?
Part C: Solving Variation Problems
Translate each of the following sentences into a mathematical formula.
Construct a mathematical model given the following:
Solve applications involving variation.
Hooke’s law suggests that the extension of a hanging spring is directly proportional to the weight attached to it. The constant of variation is called the spring constant.
Figure 4.1

Robert Hooke (1635—1703)
The braking distance of an automobile is directly proportional to the square of its speed.
Figure 4.2

Robert Boyle (1627—1691)
Boyle’s law states that if the temperature remains constant, the volume V of a given mass of gas is inversely proportional to the pressure p exerted on it.
Newton’s universal law of gravitation states that every particle of matter in the universe attracts every other particle with a force F that is directly proportional to the product of the masses and of the particles and inversely proportional to the square of the distance d between them. The constant of proportionality is called the gravitational constant.
Figure 4.3

Sir Isaac Newton (1643—1727)
Source: Portrait of Isaac Newton by Sir Godfrey Kneller, from http://commons.wikimedia.org/wiki/File:GodfreyKneller-IsaacNewton-1689.
http://commons.wikimedia.org/wiki/File:Frans_Hals_-_Portret_
_van_Ren%C3%A9_Descartes.jpg.
Answers
-
20 miles per hour
-
-
240 miles per hour
-
-
52 miles per hour
-
-
5 miles per hour
-
-
112 miles per hour
-
-
10 miles per hour
-
-
1 mile per hour
-
-
40 miles per hour
-
-
50 miles per hour
-
-
hours
-
-
30 hours
-
-
6 hours
-
-
20 hours
-
-
3 hours
-
-
4 hours
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
$382.50
-
-
$26.65
-
-
-
-
square meters
-
-
50 cubic centimeters
-
-
-
-
7.5 inches
-
-
49 feet
-
-
108 cubic inches
-
-
4 feet
-
-
1,120 foot-candles
-
-
4 men
-
-
1.4 seconds
-
-
-
-
-
-
y changes by a factor of 4
-
-
y remains unchanged
4.9 Review Exercises and Sample Exam
Review Exercises
-
Given , find , , and
-
Given , find , , and
-
Given , find , and
-
Given , find , and
-
The following graph gives the height in feet of a projectile over time in seconds.
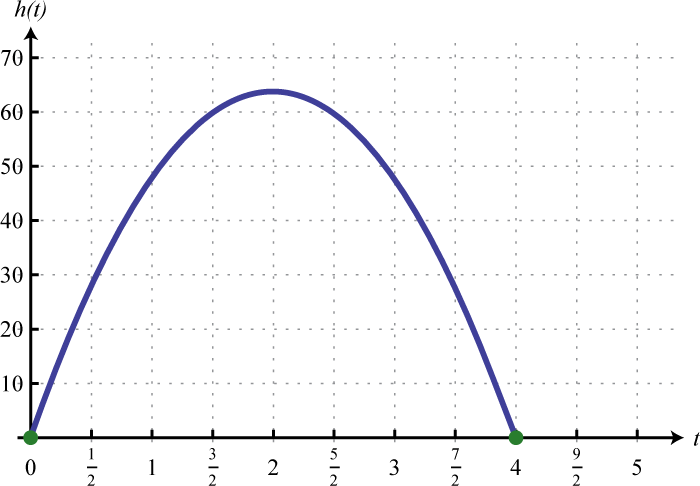
- Use the graph to determine the height of the projectile at 2.5 seconds.
- At what time does the projectile reach its maximum height?
- How long does it take the projectile to return to the ground?
-
Given the graph of the function , find , and
-
From the ground, a bullet is fired straight up into the air at 340 meters per second. Ignoring the effects of air friction, write a function that models the height of the bullet and use it to calculate the bullet’s height after one-quarter of a second. (Round off to the nearest meter.)
-
An object is tossed into the air at an initial speed of 30 feet per second from a rooftop 10 feet high. Write a function that models the height of the object and use it to calculate the height of the object after 1 second.
-
Given and , find
-
Given and , find
-
Given and , find
-
Given and , find
-
Given , find
-
Given , find
-
-
-
-
-
-
-
-
Algebra of Functions
Evaluate
Perform the operations.
Given , , and , find the following:
Factoring Polynomials
Factor out the greatest common factor (GCF).
Factor by grouping.
Factor the special binomials.
Factoring Trinomials
Factor.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
The height in feet of an object dropped from the top of a 16-foot ladder is given by , where t represents the time in seconds after the object has been dropped. How long will it take to hit the ground?
-
The length of a rectangle is 2 centimeters less than twice its width. If the area of the rectangle is 112 square centimeters, find its dimensions.
-
A triangle whose base is equal in measure to its height has an area of 72 square inches. Find the length of the base.
-
A box can be made by cutting out the corners and folding up the edges of a sheet of cardboard. A template for a rectangular cardboard box of height 2 inches is given.
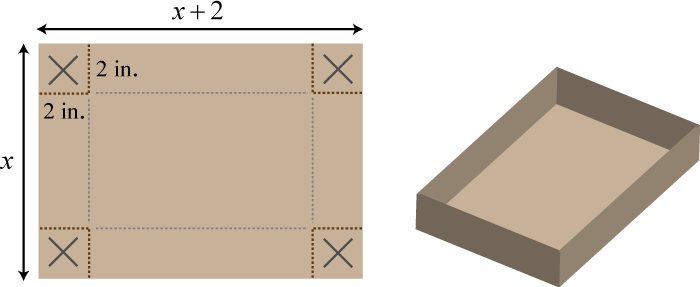
What are the dimensions of a cardboard sheet that will make a rectangular box with volume 240 cubic inches?
-
-
-
-
-
-
-
5, −2
-
-
-
±10
-
−4, 0, 3
-
−8 double root
Solve Polynomial Equations by Factoring
Factor completely.
Solve by factoring.
Find the roots of the given functions.
Solve or factor.
Find a polynomial equation with integer coefficients, given the solutions.
-
-
-
-
-
-
-
-
-
-
-
-
-
Given and , find
-
Given and , find
-
Given and , find
-
Given and , find
-
The daily cost in dollars of running a small business is given by where x represents the number of hours the business is in operation. Determine the average cost per hour if the business is in operation for 8 hours in a day.
-
An electric bicycle manufacturer has determined that the cost of producing its product in dollars is given by the function where n represents the number of electric bicycles produced in a day. Determine the average cost per bicycle if 10 and 20 are produced in a day.
-
Given , simplify
-
Given , simplify
Rational Functions: Multiplication and Division
State the restrictions and simplify.
Perform the operations and simplify. Assume all variable expressions in the denominator are nonzero.
Perform the operations and state the restrictions.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Given and , find
-
Given and , find
-
Given and , find
-
Given and , find
Rational Functions: Addition and Subtraction
State the restrictions and simplify.
Simplify. Assume that all variable expressions used as denominators are nonzero.
Perform the operations and state the restrictions.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Solve for a:
-
Solve for y:
-
A positive integer is 4 less than another. If the reciprocal of the larger integer is subtracted from twice the reciprocal of the smaller, the result is Find the two integers.
-
If 3 times the reciprocal of the larger of two consecutive odd integers is added to 7 times the reciprocal of the smaller, the result is Find the integers.
-
If the reciprocal of the smaller of two consecutive integers is subtracted from three times the reciprocal of the larger, the result is Find the integers.
-
A positive integer is twice that of another. The sum of the reciprocals of the two positive integers is Find the two integers.
Solving Rational Equations
Solve.
-
Manuel traveled 8 miles on the bus and another 84 miles on a train. If the train was 16 miles per hour faster than the bus, and the total trip took 2 hours, what was the average speed of the train?
-
A boat can average 10 miles per hour in still water. On a trip downriver, the boat was able to travel 7.5 miles with the current. On the return trip, the boat was only able to travel 4.5 miles in the same amount of time against the current. What was the speed of the current?
-
Susan can jog, on average, miles per hour faster than her husband Bill. Bill can jog 10 miles in the same amount of time it takes Susan to jog 13 miles. How fast, on average, can Susan jog?
-
In the morning, Raul drove 8 miles to visit his grandmother and then returned later that evening. Because of traffic, his average speed on the return trip was that of his average speed that morning. If the total driving time was of an hour, what was his average speed on the return trip?
-
One pipe can completely fill a water tank in 6 hours while another smaller pipe takes 8 hours to fill the same tank. How long will it take to fill the tank to capacity if both pipes are turned on?
-
It takes Bill 3 minutes longer than Jerry to fill an order. Working together they can fill 15 orders in 30 minutes. How long does it take Bill to fill an order by himself?
-
Manny takes twice as long as John to assemble a skateboard. If they work together, they can assemble a skateboard in 6 minutes. How long would it take Manny to assemble the skateboard without John’s help?
-
Working alone, Joe can complete the yard work in 30 minutes. It takes Mike 45 minutes to complete work on the same yard. How long would it take them working together?
-
y varies directly as x, where y = 30 when x = 5.
-
y varies inversely as x, where y = 3 when x = −2.
-
y is jointly proportional to x and z, where y = −50 when x = −2 and z = 5.
-
y is directly proportional to the square of x and inversely proportional to z, where y = −6 when x = 2 and z = −8.
-
The distance an object in free fall varies directly with the square of the time that it has been falling. It is observed that an object falls 36 feet in seconds. Find an equation that models the distance an object will fall, and use it to determine how far it will fall in seconds.
-
After the brakes are applied, the stopping distance d of an automobile varies directly with the square of the speed s of the car. If a car traveling 55 miles per hour takes 181.5 feet to stop, how many feet will it take to stop if it is moving 65 miles per hour?
-
The weight of an object varies inversely as the square of its distance from the center of the Earth. If an object weighs 180 lbs on the surface of the Earth (approximately 4,000 miles from the center), then how much will it weigh at 2,000 miles above the Earth’s surface?
-
The cost per person of renting a limousine varies inversely with the number of people renting it. If 5 people go in on the rental, the limousine will cost $112 per person. How much will the rental cost per person if 8 people go in on the rental?
-
To balance a seesaw, the distance from the fulcrum that a person must sit is inversely proportional to his weight. If a 52-pound boy is sitting 3 feet away from the fulcrum, then how far from the fulcrum must a 44-pound boy sit? Round to the nearest tenth of a foot.
Applications and Variation
Use algebra to solve the following applications.
Construct a mathematical model given the following:
Answers
-
; ;
-
-
; ;
-
-
a. 60 feet; b. 2 seconds; c. 4 seconds
-
-
; at 0.25 second, the bullet’s height is about 85 meters.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Prime
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Prime
-
-
, 0
-
-
2, 10
-
-
−1,
-
-
0, 3
-
-
-
-
−4, 0, 6
-
-
0,
-
-
±2
-
-
−9, 0, 6
-
-
1 second
-
-
12 inches
-
-
Factor;
-
-
Solve;
-
-
Factor;
-
-
-
-
-
-
-
-
;
-
-
;
-
-
;
-
-
;
-
-
-
-
-
-
;
-
-
;
-
-
$63.75 per hour
-
-
3
-
-
;
-
-
;
-
-
;
-
-
;
-
-
-
-
;
-
-
-
-
-
-
-
-
;
-
-
;
-
-
−9
-
-
−1, 4
-
-
−11, 0
-
-
Ø
-
-
−4
-
-
-
-
-
-
-
-
{8, 12}
-
-
{5, 6}
-
-
48 miles per hour
-
-
6.5 miles per hour
-
-
Approximately 2.6 hours
-
-
18 minutes
-
-
-
-
-
-
; 100 feet
-
-
80 lbs
-
-
Approximately 3.5 feet
Sample Exam
-
-
-
-
-
-
-
-
-
-
-
-
Find a quadratic equation with integer coefficients given the solutions
-
Given , simplify , where
-
-
-
-
-
-
Find the root of the function defined by
-
Solve for y:
-
The height of an object dropped from a 64-foot building is given by the function , where t represents time in seconds after it was dropped.
- Determine the height of the object at of a second.
- How long will it take the object to hit the ground?
-
One positive integer is 3 units more than another. When the reciprocal of the larger is subtracted from twice the reciprocal of the smaller, the result is Find the two positive integers.
-
A light airplane can average 126 miles per hour in still air. On a trip, the airplane traveled 222 miles with a tailwind. On the return trip, against a headwind of the same speed, the plane was only able to travel 156 miles in the same amount of time. What was the speed of the wind?
-
On the production line, it takes John 2 minutes less time than Mark to assemble a watch. Working together they can assemble 5 watches in 12 minutes. How long does it take John to assemble a watch working alone?
-
Write an equation that relates x and y, given that y varies inversely with the square of x, where when Use it to find y when
Given , , and , find the following:
Factor.
Solve.
Simplify and state the restrictions.
Assume all variable expressions in the denominator are nonzero and simplify.
Solve.
Use algebra to solve.
Answers
-
-
-
-
-
-
-
-
-
−4, 0
-
-
, 5
-
-
-
-
;
-
-
-
-
-
-
a. 55 feet; b. 2 seconds
-
-
22 miles per hour
-
-
;