This is “Solving Linear Systems”, chapter 3 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
Chapter 3 Solving Linear Systems
3.1 Linear Systems with Two Variables and Their Solutions
Learning Objectives
- Check solutions to systems of linear equations.
- Solve linear systems using the graphing method.
- Identify dependent and inconsistent systems.
Definition of a Linear System with Two Variables
Real-world applications are often modeled using more than one variable and more than one equation. A system of equationsA set of two or more equations with the same variables. consists of a set of two or more equations with the same variables. In this section, we will study linear systemsA set of two or more linear equations with the same variables. consisting of two linear equations each with two variables. For example,
A solution to a linear systemGiven a linear system with two equations and two variables, a solution is an ordered pair that satisfies both equations and corresponds to a point of intersection., or simultaneous solutionUsed when referring to a solution of a system of equations., is an ordered pair (x, y) that solves both of the equations. In this case, (3, 2) is the only solution. To check that an ordered pair is a solution, substitute the corresponding x- and y-values into each equation and then simplify to see if you obtain a true statement for both equations.
Check: (3, 2) |
|
|---|---|
Equation 1: |
Equation 2: |
Example 1
Determine whether or not (1, 0) is a solution to the system .
Solution:
Substitute the appropriate values into both equations.
Check: (1, 0) |
|
|---|---|
Equation 1: |
Equation 2: |
Answer: Since (1, 0) does not satisfy both equations, it is not a solution.
Solve by Graphing
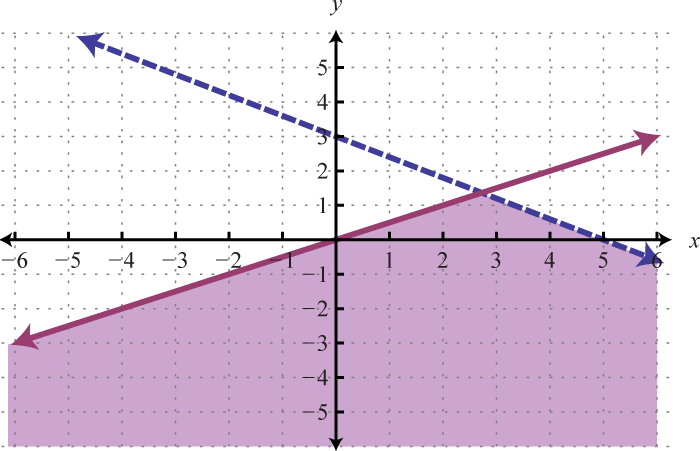
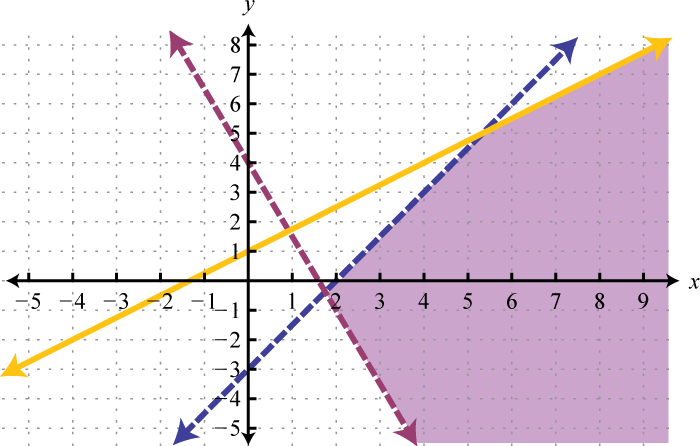
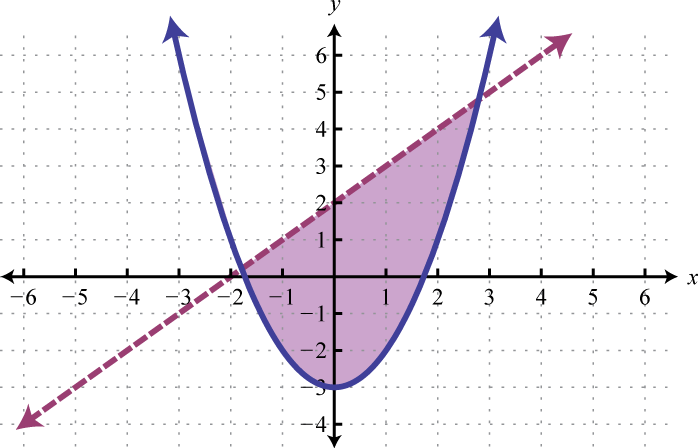
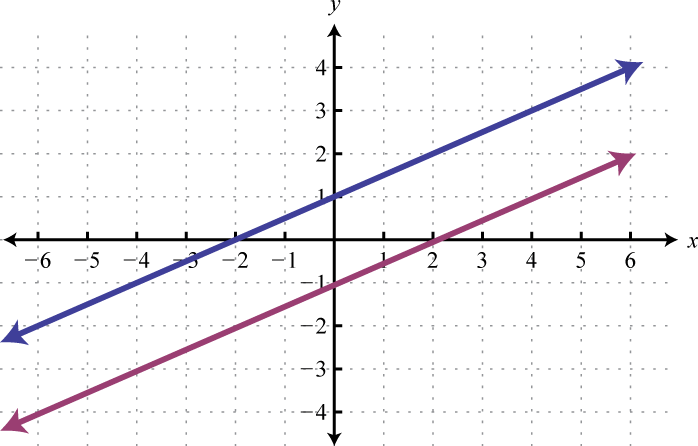
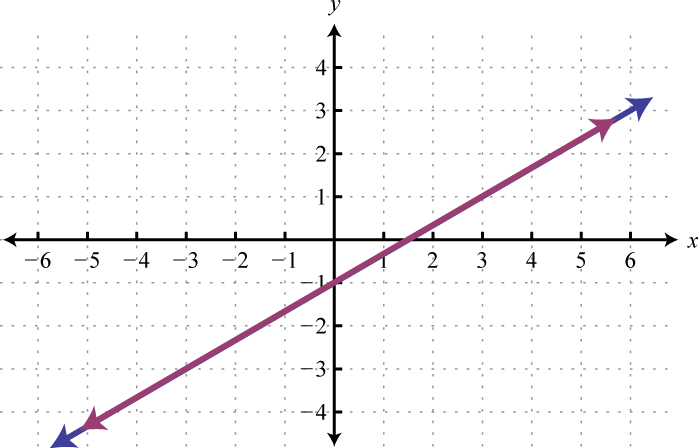
Geometrically, a linear system consists of two lines, where a solution is a point of intersection. To illustrate this, we will graph the following linear system with a solution of (3, 2):
First, rewrite the equations in slope-intercept form so that we may easily graph them.
Next, replace these forms of the original equations in the system to obtain what is called an equivalent systemA system consisting of equivalent equations that share the same solution set.. Equivalent systems share the same solution set.
If we graph both of the lines on the same set of axes, then we can see that the point of intersection is indeed (3, 2), the solution to the system.

To summarize, linear systems described in this section consist of two linear equations each with two variables. A solution is an ordered pair that corresponds to a point where the two lines intersect in the rectangular coordinate plane. Therefore, one way to solve linear systems is by graphing both lines on the same set of axes and determining the point where they cross. This describes the graphing methodA means of solving a system by graphing the equations on the same set of axes and determining where they intersect. for solving linear systems.
When graphing the lines, take care to choose a good scale and use a straightedge to draw the line through the points; accuracy is very important here.
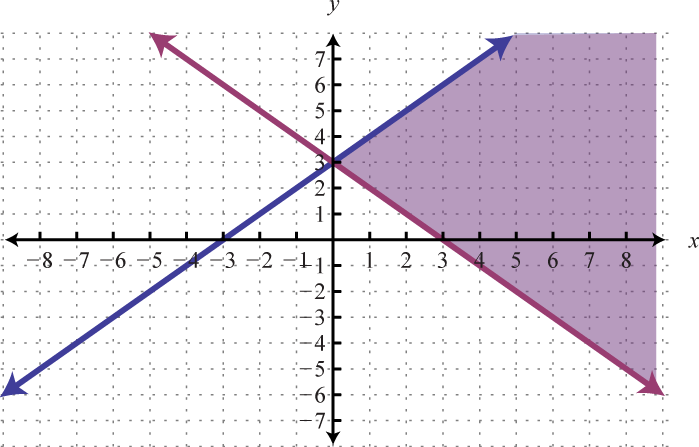
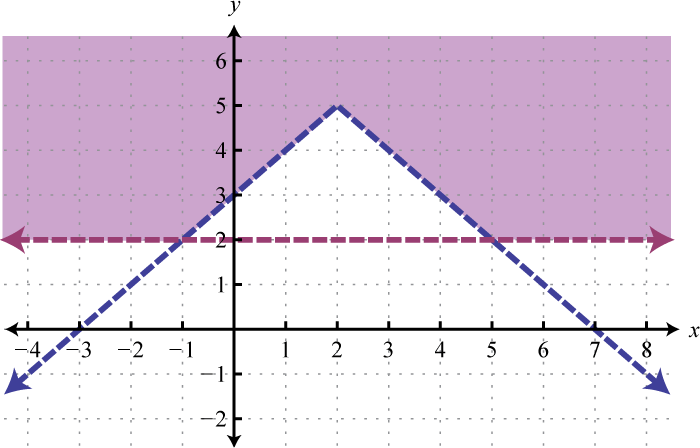
Example 2
Solve by graphing: .
Solution:
Rewrite the linear equations in slope-intercept form.
Write the equivalent system and graph the lines on the same set of axes.
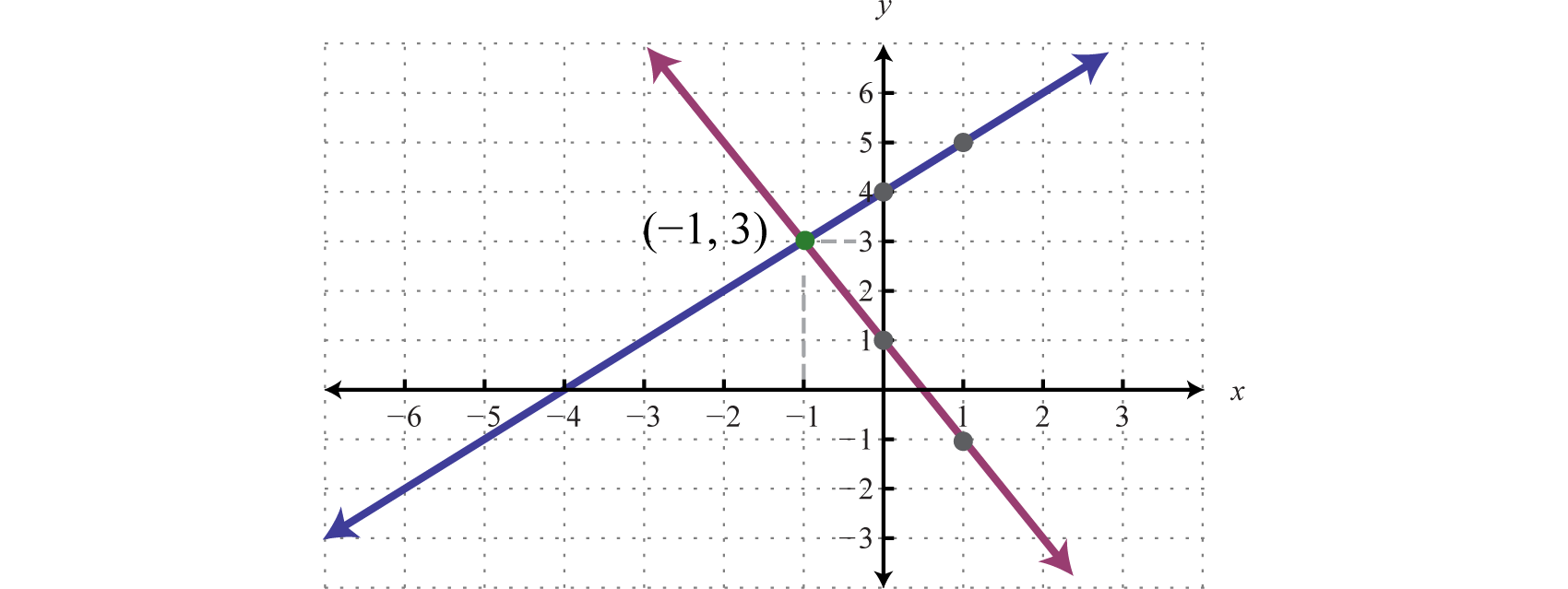
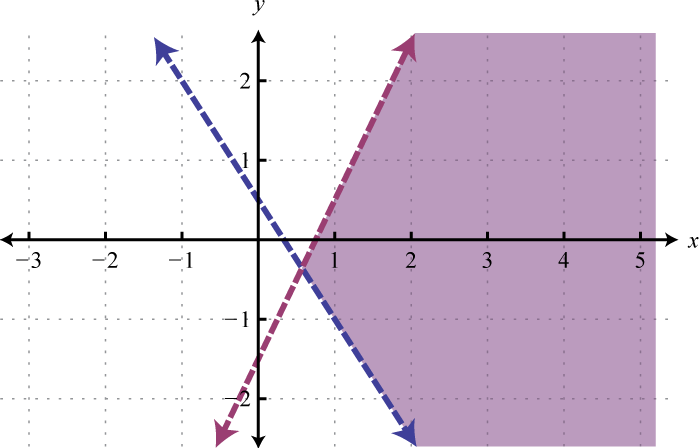
Use the graph to estimate the point where the lines intersect and check to see if it solves the original system. In the above graph, the point of intersection appears to be (−1, 3).
Check: (−1, 3) |
|
|---|---|
Line 1: |
Line 2: |
Answer: (−1, 3)
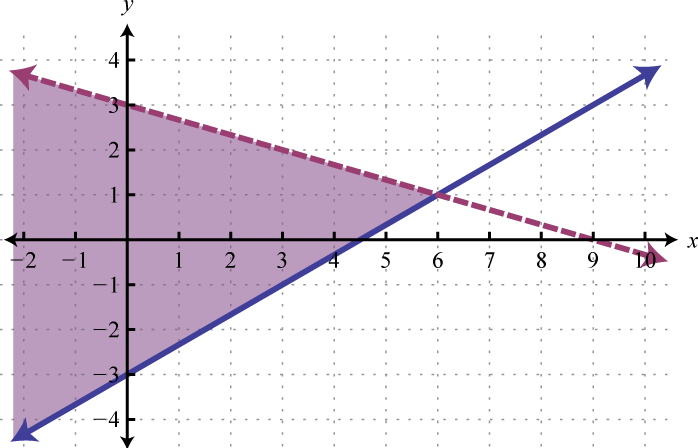
Example 3
Solve by graphing: .
Solution:
We first solve each equation for y to obtain an equivalent system where the lines are in slope-intercept form.
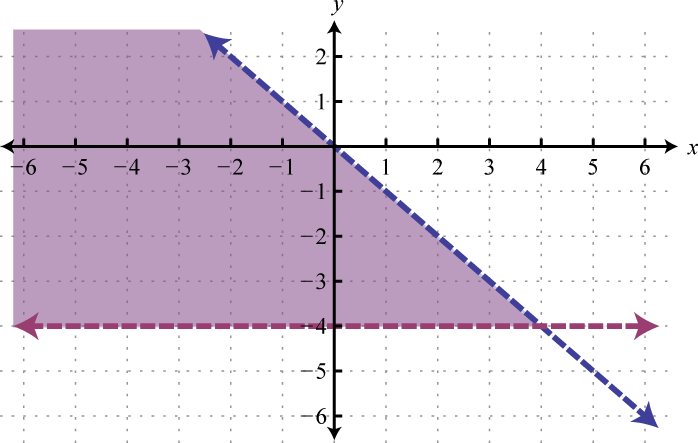
Graph the lines and determine the point of intersection.
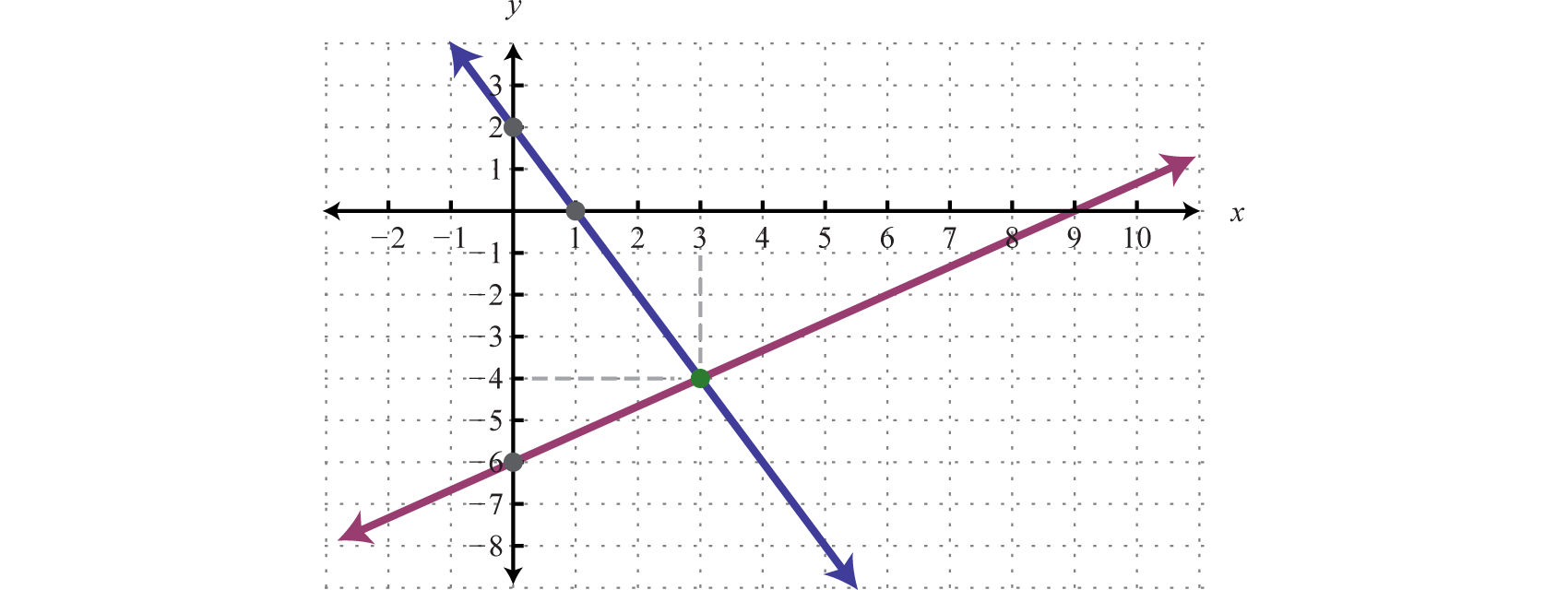
Check: (3, −4) |
|
|---|---|
Answer: (3, −4)
Example 4
Solve by graphing: .
Solution:
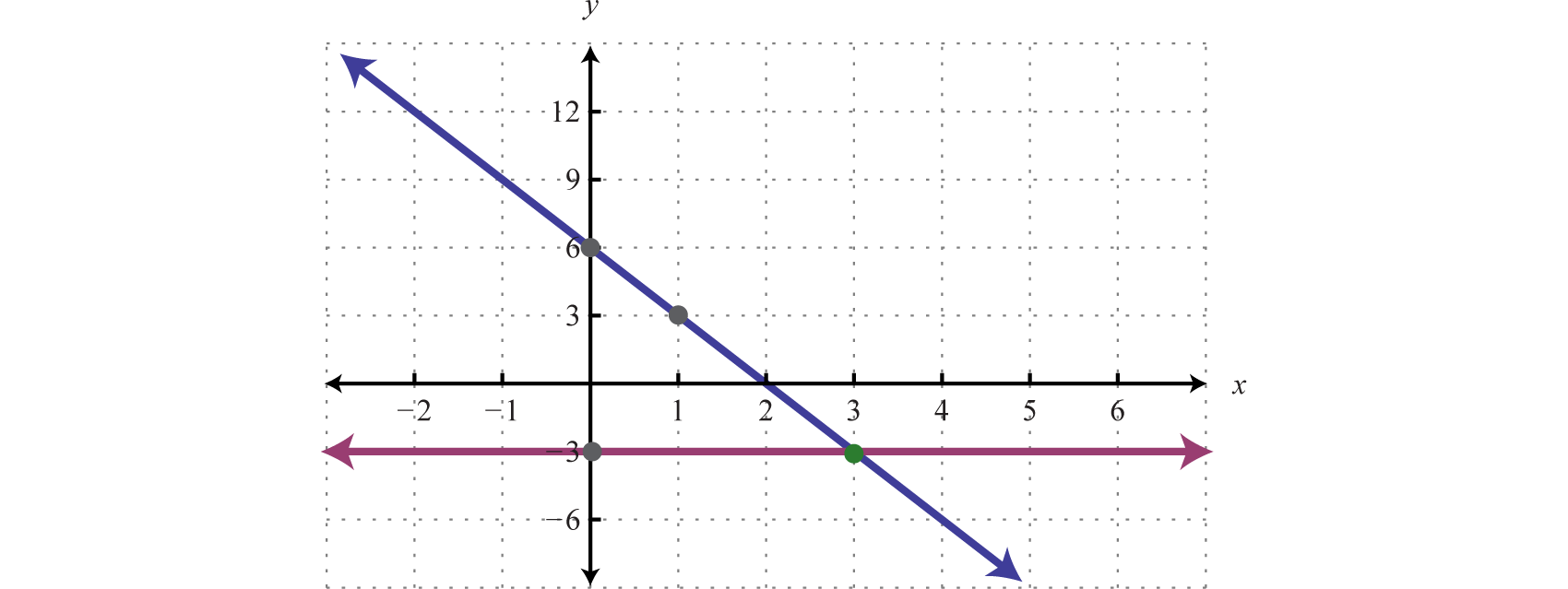
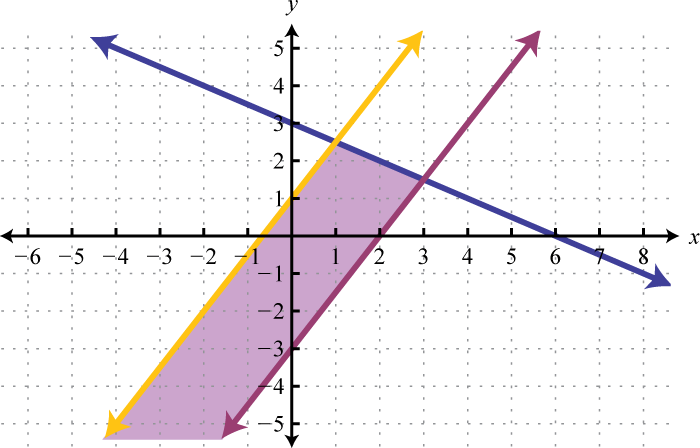
Check: (3, −3) |
|
|---|---|
Answer: (3, −3)
The graphing method for solving linear systems is not ideal when a solution consists of coordinates that are not integers. There will be more accurate algebraic methods in sections to come, but for now, the goal is to understand the geometry involved when solving systems. It is important to remember that the solutions to a system correspond to the point, or points, where the graphs of the equations intersect.
Dependent and Inconsistent Systems
A system with at least one solution is called a consistent systemA system with at least one solution.. Up to this point, all of the examples have been of consistent systems with exactly one ordered pair solution. It turns out that this is not always the case. Sometimes systems consist of two linear equations that are equivalent. If this is the case, the two lines are the same and when graphed will coincide. Hence, the solution set consists of all the points on the line. This is a dependent systemA linear system with two variables that consists of equivalent equations. It has infinitely many ordered pair solutions, denoted by .. Given a consistent linear system with two variables, there are two possible results:
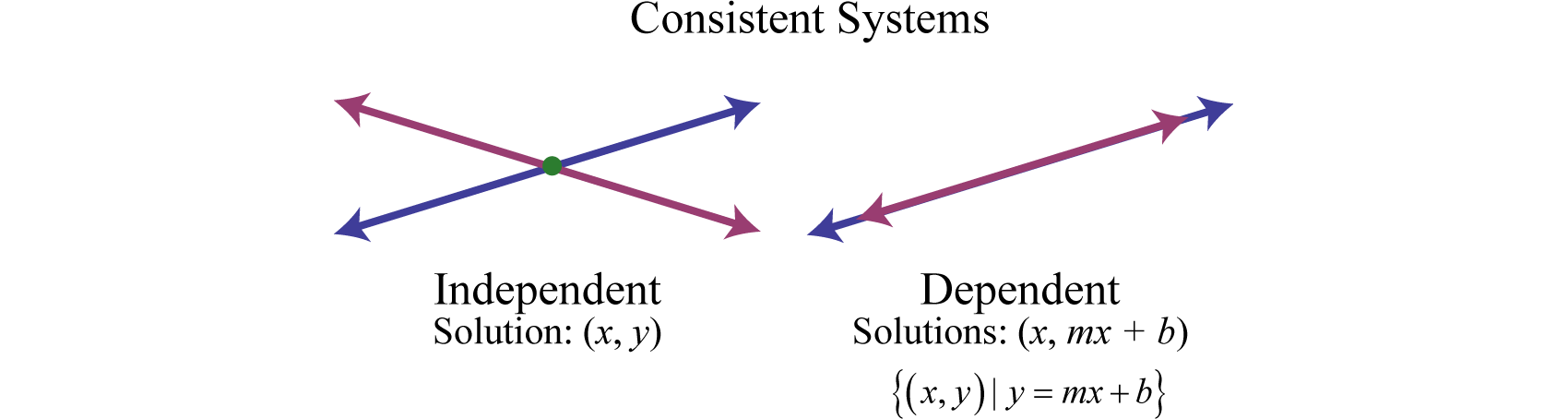
A solution to an independent systemA linear system with two variables that has exactly one ordered pair solution. is an ordered pair (x, y). The solution to a dependent system consists of infinitely many ordered pairs (x, y). Since any line can be written in slope-intercept form,, we can express these solutions, dependent on x, as follows:
In this text we will express all the ordered pair solutions in the shortened form , where x is any real number.
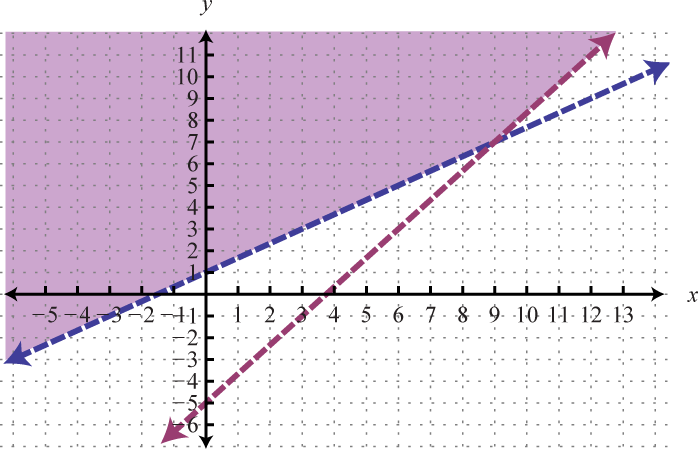
Example 5
Solve by graphing: .
Solution:
Determine slope-intercept form for each linear equation in the system.
In slope-intercept form, we can easily see that the system consists of two lines with the same slope and same y-intercept. They are, in fact, the same line. And the system is dependent.
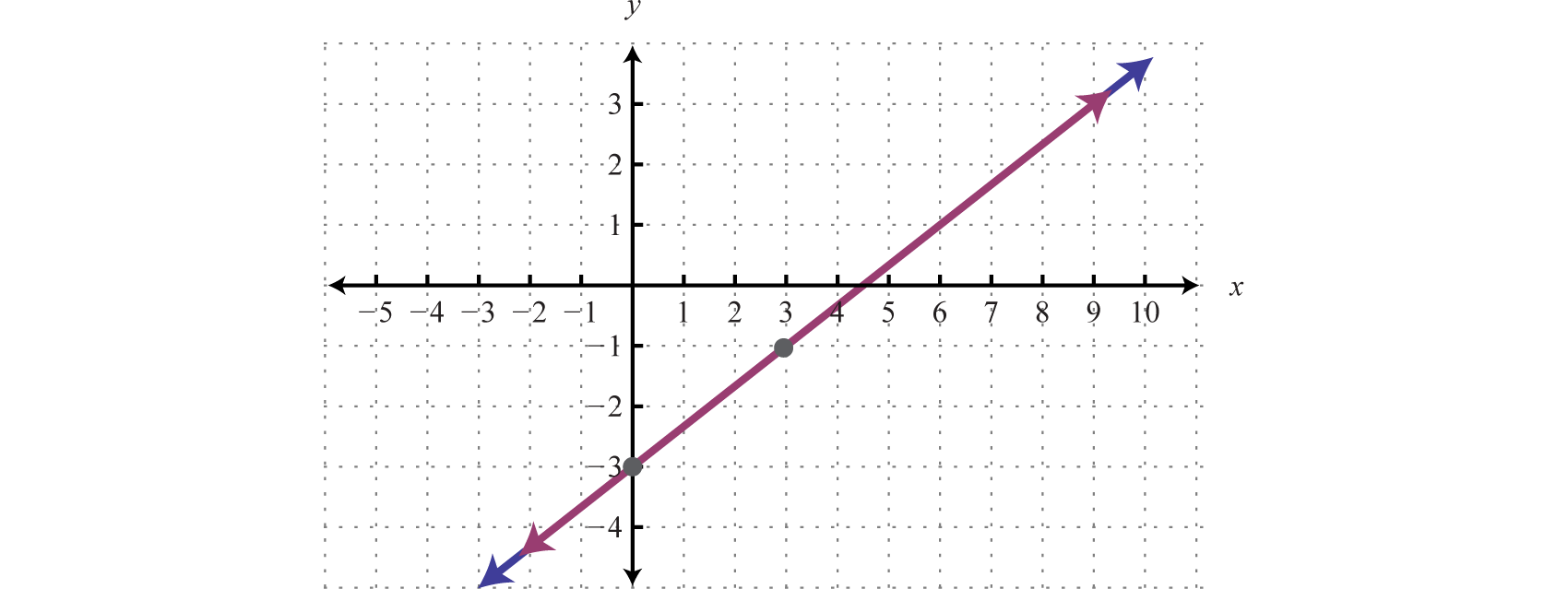
Answer:
In this example, it is important to notice that the two lines have the same slope and same y-intercept. This tells us that the two equations are equivalent and that the simultaneous solutions are all the points on the line . This is a dependent system, and the infinitely many solutions are expressed using the form . Other resources may express this set using set notation, {(x, y) | }, which reads “the set of all ordered pairs (x, y) such that .”
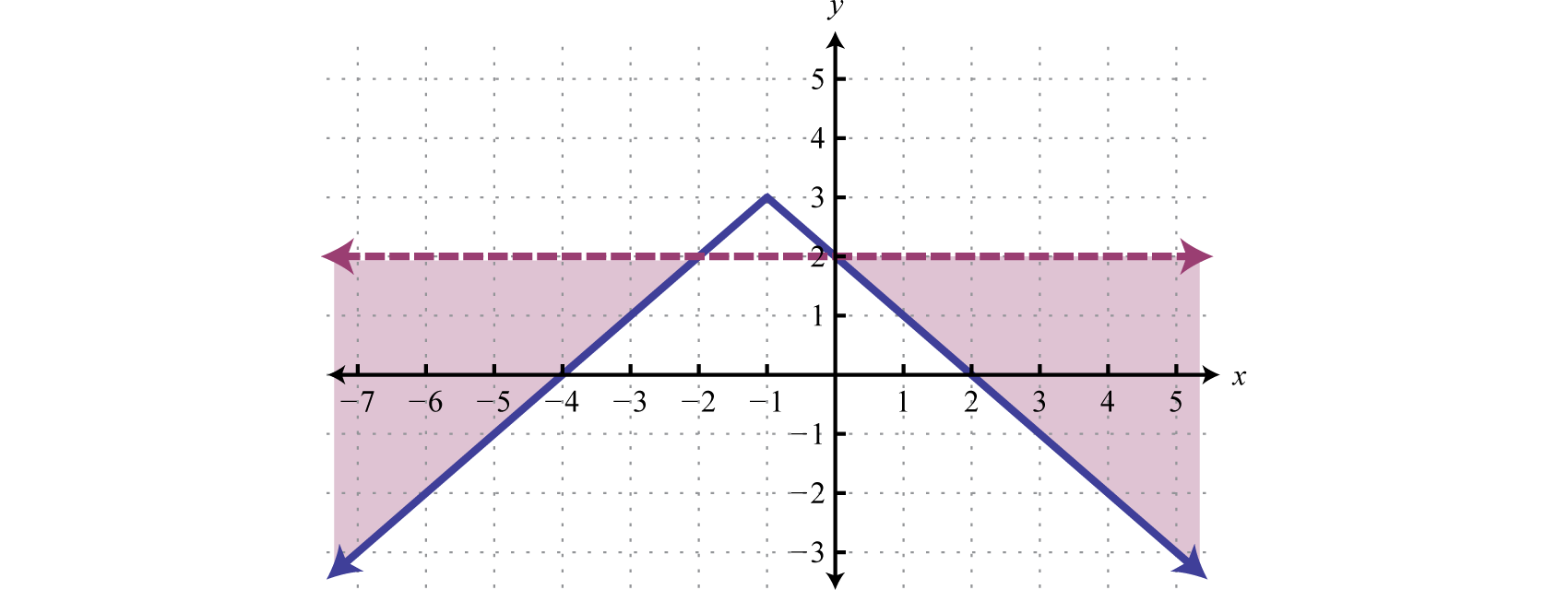
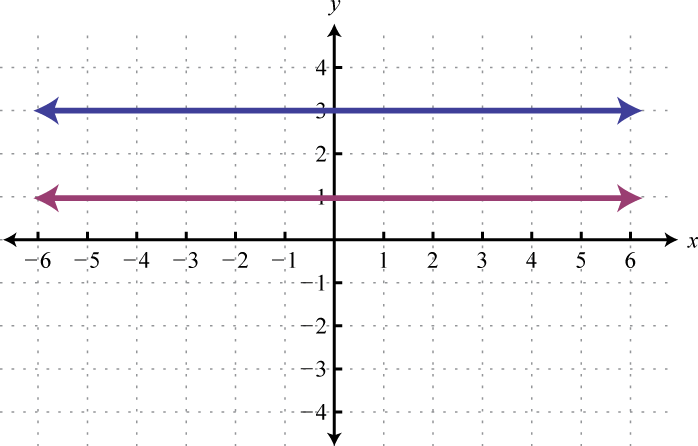
Sometimes the lines do not cross and there is no point of intersection. Such a system has no solution, Ø, and is called an inconsistent systemA system with no simultaneous solution..

Example 6
Solve by graphing: .
Solution:
Determine slope-intercept form for each linear equation.
In slope-intercept form, we can easily see that the system consists of two lines with the same slope and different y-intercepts. Therefore, the lines are parallel and will never intersect.
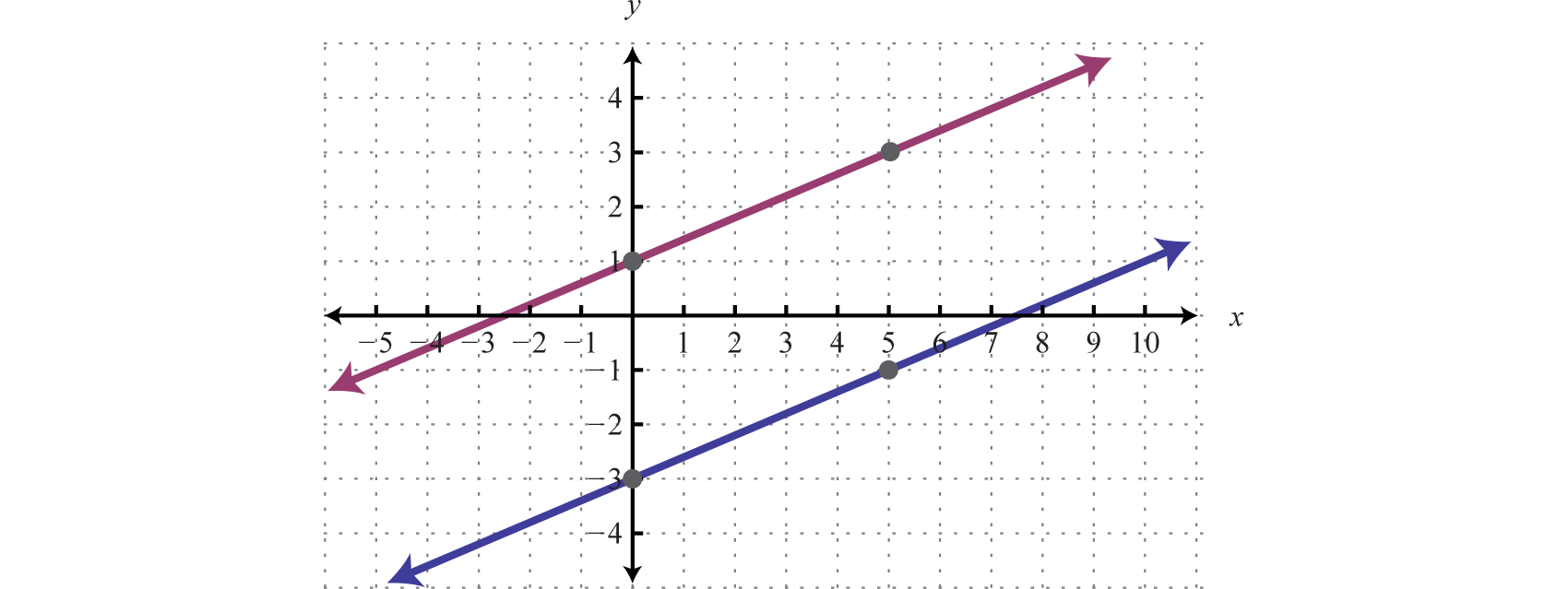
Answer: There is no simultaneous solution, Ø.
Key Takeaways
- In this section, we limit our study to systems of two linear equations with two variables. Solutions to such systems, if they exist, consist of ordered pairs that satisfy both equations. Geometrically, solutions are the points where the graphs intersect.
- The graphing method for solving linear systems requires us to graph both of the lines on the same set of axes as a means to determine where they intersect.
- The graphing method is not the most accurate method for determining solutions, particularly when a solution has coordinates that are not integers. It is a good practice to always check your solutions.
- Some linear systems have no simultaneous solution. These systems consist of equations that represent parallel lines with different y-intercepts and do not intersect in the plane. They are called inconsistent systems and the solution set is the empty set, .
- Some linear systems have infinitely many simultaneous solutions. These systems consist of equations that are equivalent and represent the same line. They are called dependent systems and their solutions are expressed using the notation , where x is any real number.
Topic Exercises
-
(3, −2);
-
(−5, 0);
-
(−2, −6);
-
(2, −7);
-
(0, −3);
-
;
-
;
-
(−3, 4);
-
(−5, −3);
-
(4, 2);
-
-
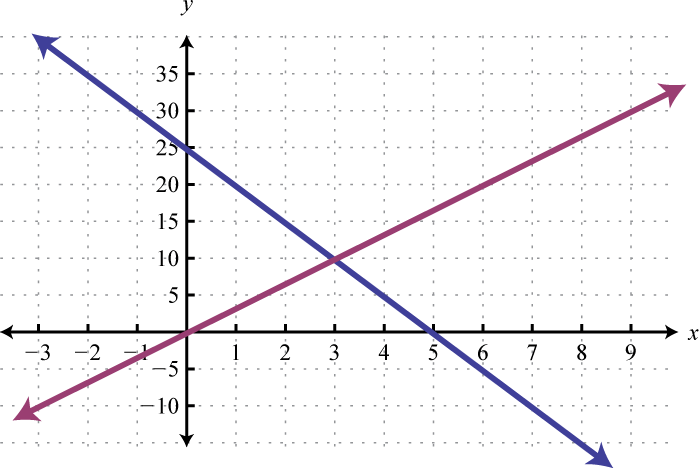
-
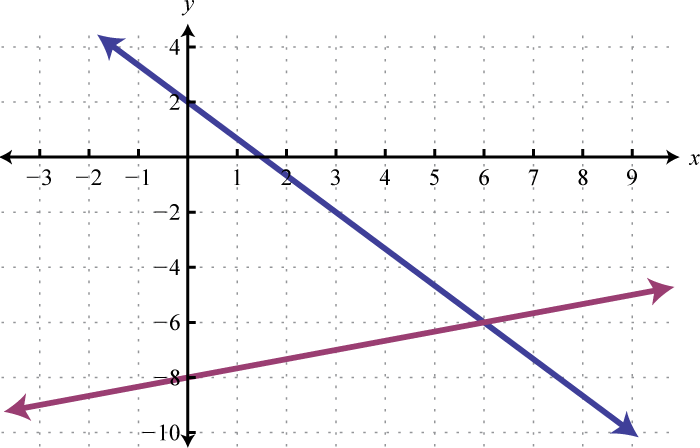
-
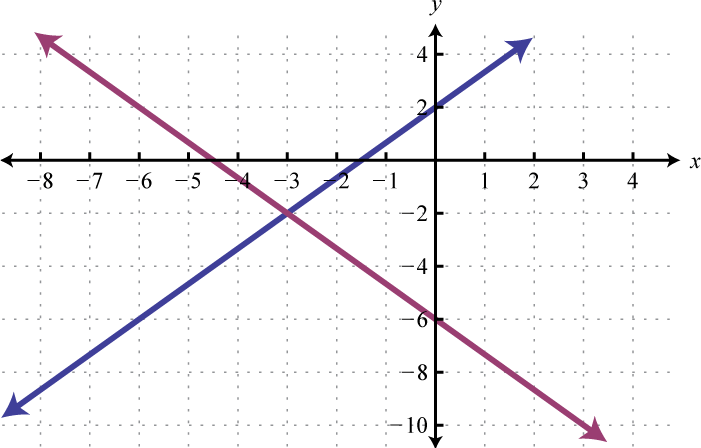
-
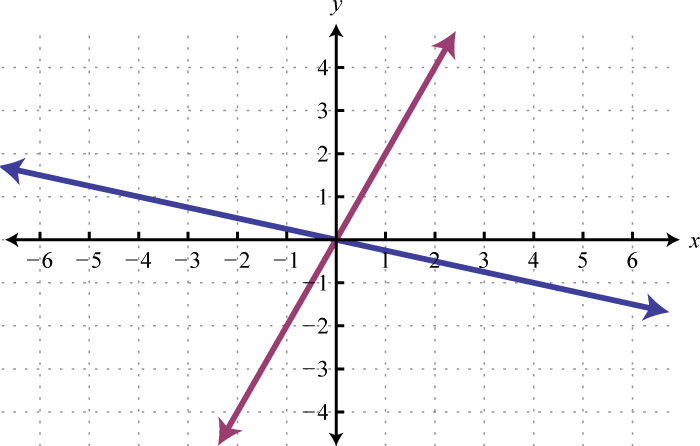
-
-
-
-
-
Part A: Definitions
Determine whether or not the given ordered pair is a solution to the given system.
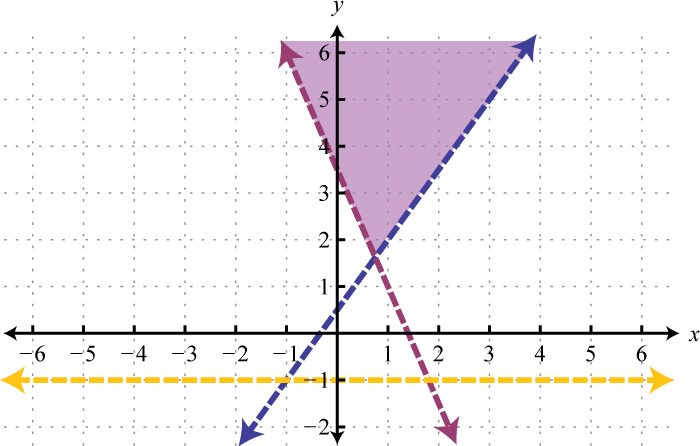
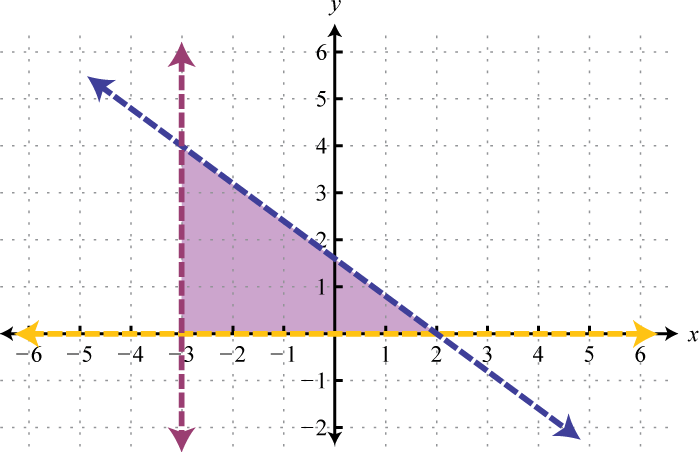
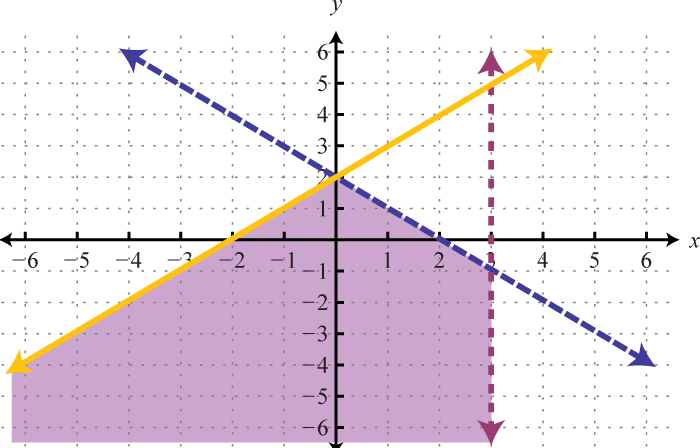
Given the graphs, determine the simultaneous solution.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Assuming m is nonzero solve the system:
-
Assuming b is nonzero solve the system:
-
Find the equation of the line perpendicular to and passing through . Graph this line and the given line on the same set of axes and determine where they intersect.
-
Find the equation of the line perpendicular to and passing through . Graph this line and the given line on the same set of axes and determine where they intersect.
-
Find the equation of the line perpendicular to and passing through . Graph both lines on the same set of axes.
-
Find the equation of the line perpendicular to the y-axis and passing through the origin.
-
Use the graph of to determine the x-value where . Verify your answer using algebra.
-
Use the graph of to determine the x-value where . Verify your answer using algebra.
Part B: Solve by Graphing
Solve by graphing.
-
Discuss the weaknesses of the graphing method for solving systems.
-
Explain why the solution set to a dependent linear system is denoted by .
-
Draw a picture of a dependent linear system as well as a picture of an inconsistent linear system. What would you need to determine the equations of the lines that you have drawn?
Part C: Discussion Board Topics
Answers
-
No
-
-
No
-
-
Yes
-
-
No
-
-
Yes
-
-
(5, 0)
-
-
(6, −6)
-
-
(0, 0)
-
-
-
-
-
-
(−2, 3)
-
-
(3, −1)
-
-
(5, 3)
-
-
(−3, −2)
-
-
(10, 0)
-
-
-
-
(3, 4)
-
-
(−3, −5)
-
-
(6, 2)
-
-
-
-
-
-
(2, −3)
-
-
(10, 5)
-
-
(−9, 6)
-
-
-
-
(−5, 4)
-
-
(0, 0)
-
-
-
-
-
-
-
-
-
-
;
-
-
-
-
-
-
Answer may vary
-
-
Answer may vary
3.2 Solving Linear Systems with Two Variables
Learning Objectives
- Solve linear systems using the substitution method.
- Solve linear systems using the elimination method.
- Identify the strengths and weaknesses of each method.
The Substitution Method
In this section, we review a completely algebraic technique for solving systems, the substitution methodA means of solving a linear system by solving for one of the variables and substituting the result into the other equation.. The idea is to solve one equation for one of the variables and substitute the result into the other equation. After performing this substitution step, we are left with a single equation with one variable, which can be solved using algebra.
Example 1
Solve by substitution: .
Solution:
Solve for either variable in either equation. If you choose the first equation, you can isolate y in one step.
Substitute the expression for the variable y in the other equation.

This leaves us with an equivalent equation with one variable, which can be solved using the techniques learned up to this point. Solve for the remaining variable.
Back substituteOnce a value is found for a variable, substitute it back into one of the original equations, or its equivalent, to determine the corresponding value of the other variable. to find the other coordinate. Substitute x = −2 into either of the original equations or their equivalents. Typically, we use the equivalent equation that we found when isolating a variable in the first step.
Remember to present the solution as an ordered pair: . Verify that these coordinates solve both equations of the original system:
Check: (−2, 1) |
|
|---|---|
Equation 1 |
Equation 2 |
The graph of this linear system follows:
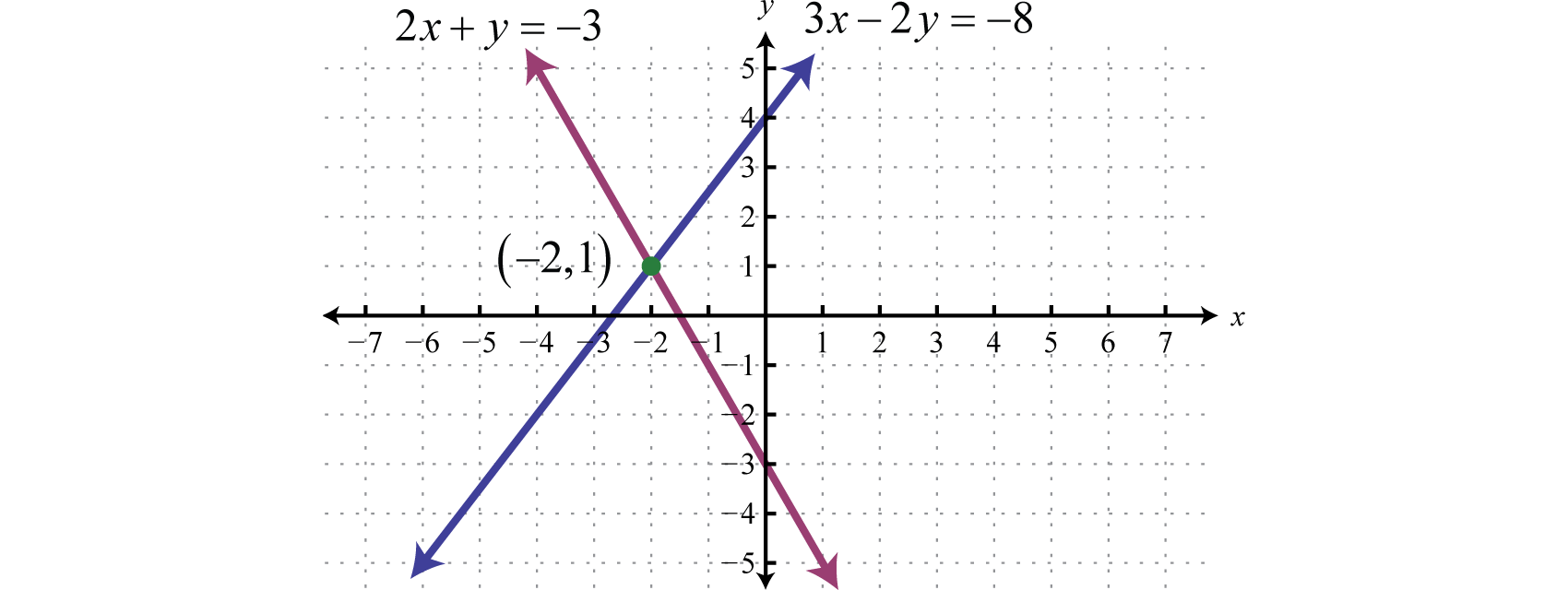
The substitution method for solving systems is a completely algebraic method. Thus graphing the lines is not required.
Answer: (−2, 1)
Example 2
Solve by substitution: .
Solution:
It does not matter which variable we choose to isolate first. In this case, begin by solving for x in the first equation.
Next, substitute into the second equation and solve for y.
Back substitute into the equation used in the substitution step:
Answer:
As we know, not all linear systems have only one ordered pair solution. Next, we explore what happens when using the substitution method to solve a dependent system.
Example 3
Solve by substitution: .
Solution:
Since the first equation has a term with coefficient 1, we choose to solve for that first.
Next, substitute this expression in for y in the second equation.
This process led to a true statement; hence the equation is an identity and any real number is a solution. This indicates that the system is dependent. The simultaneous solutions take the form , or in this case, , where x is any real number.
Answer:
To have a better understanding of the previous example, rewrite both equations in slope-intercept form and graph them on the same set of axes.
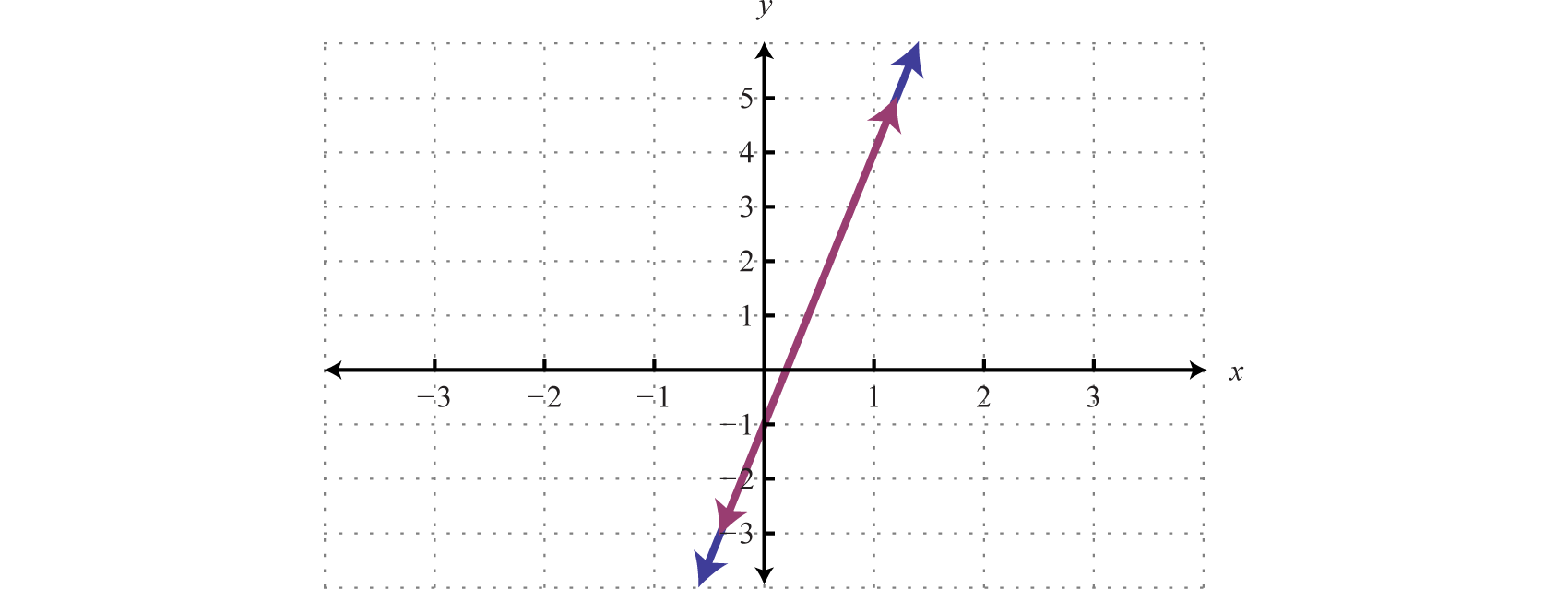
We can see that both equations represent the same line, and thus the system is dependent. Now explore what happens when solving an inconsistent system using the substitution method.
Example 4
Solve by substitution: .
Solution:
Solve for y in the first equation.
Substitute into the second equation and solve.
Solving leads to a false statement. This indicates that the equation is a contradiction. There is no solution for x and hence no solution to the system.
Answer: Ø
A false statement indicates that the system is inconsistent, or in geometric terms, that the lines are parallel and do not intersect. To illustrate this, determine the slope-intercept form of each line and graph them on the same set of axes.
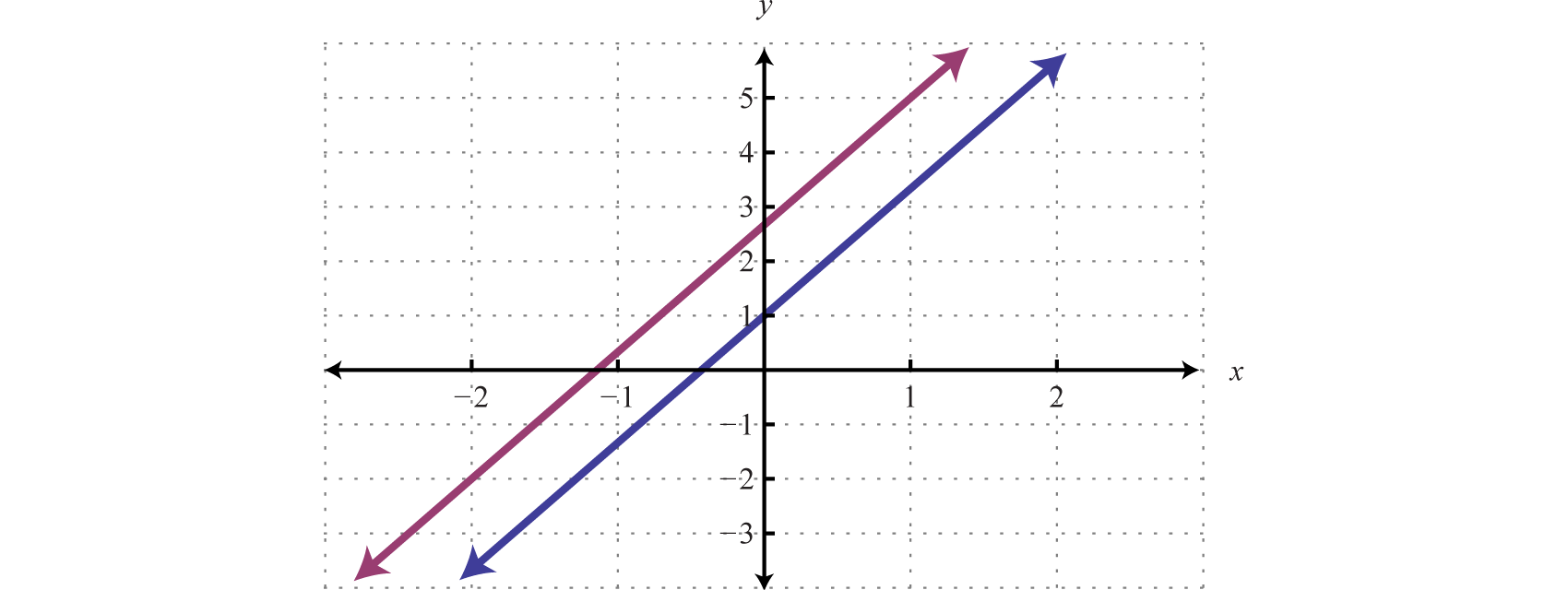
In slope-intercept form, it is easy to see that the two lines have the same slope but different y-intercepts.
The Elimination Method
In this section, the goal is to review another completely algebraic method for solving a system of linear equations called the elimination methodA means of solving a system by adding equivalent equations in such a way as to eliminate a variable. or addition methodOften used when referring to the elimination method for solving systems.. This method depends on the addition property of equationsIf A, B, C, and D are algebraic expressions, where A = B and C = D, then A + C = B + D.: given algebraic expressions A, B, C, and D we have
Consider the following system:
We can add the equations together to eliminate the variable y.
This leaves us with a linear equation with one variable that can be easily solved:
At this point, we have the x-coordinate of the simultaneous solution, so all that is left to do is back substitute to find the corresponding y-value.
The solution to the system is (3, 2). Of course, the variable is not always so easily eliminated. Typically, we have to find an equivalent system by applying the multiplication property of equality to one or both of the equations as a means to line up one of the variables to eliminate. The goal is to arrange that either the x terms or the y terms are opposites, so that when the equations are added, the terms eliminate.
Example 5
Solve by elimination: .
Solution:
We choose to eliminate the terms with variable y because the coefficients have different signs. To do this, we first determine the least common multiple of the coefficients; in this case, the LCM(3, 2) is 6. Therefore, multiply both sides of both equations by the appropriate values to obtain coefficients of −6 and 6. This results in the following equivalent system:
The terms involving y are now lined up to eliminate. Add the equations together and solve for x.
Back substitute.
Therefore the simultaneous solution is (1, 2). The check follows.
Check: (1, 2) |
|
|---|---|
Equation 1: |
Equation 2: |
Answer: (1, 2)
Sometimes linear systems are not given in standard form . When this is the case, it is best to rearrange the equations before beginning the steps to solve by elimination. Also, we can eliminate either variable. The goal is to obtain a solution for one of the variables and then back substitute to find a solution for the other.
Example 6
Solve by elimination: .
Solution:
First, rewrite the second equation in standard form.
This results in an equivalent system in standard form, where like terms are aligned in columns.
We can eliminate the term with variable x if we multiply the second equation by −4.
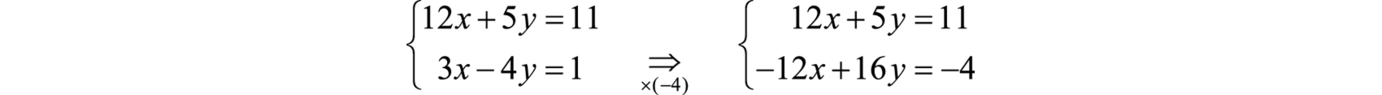
Next, we add the equations together,
Back substitute.
Answer:
At this point, we explore what happens when solving dependent and inconsistent systems using the elimination method.
Example 7
Solve by elimination: .
Solution:
To eliminate the variable x, we could multiply the first equation by −2.
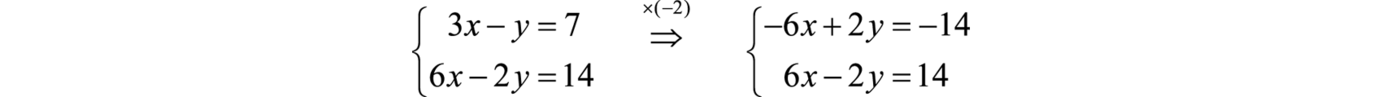
Now adding the equations we have
A true statement indicates that this is a dependent system. The lines coincide, and we need y in terms of x to present the solution set in the form . Choose one of the original equations and solve for y. Since the equations are equivalent, it does not matter which one we choose.
Answer:
Given a linear system where the equations have fractional coefficients, it is usually best to clear the fractions before beginning the elimination method.
Example 8
Solve: .
Solution:
Recall that we can clear fractions by multiplying both sides of an equation by the least common multiple of the denominators (LCD). Take care to distribute and then simplify.
Equation 1 |
Equation 2 |
This results in an equivalent system where the equations have integer coefficients,
Solve using the elimination method.
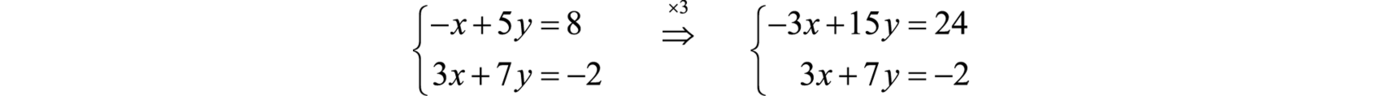
Back substitute.
Answer: (−3, 1)
We can use a similar technique to clear decimals before solving.
Summary of the Methods for Solving Linear Systems
We have reviewed three methods for solving linear systems of two equations with two variables. Each method is valid and can produce the same correct result. In this section, we summarize the strengths and weaknesses of each method.
The graphing method is useful for understanding what a system of equations is and what the solutions must look like. When the equations of a system are graphed on the same set of axes, we can see that the solution is the point where the graphs intersect. The graphing is made easy when the equations are in slope-intercept form. For example,
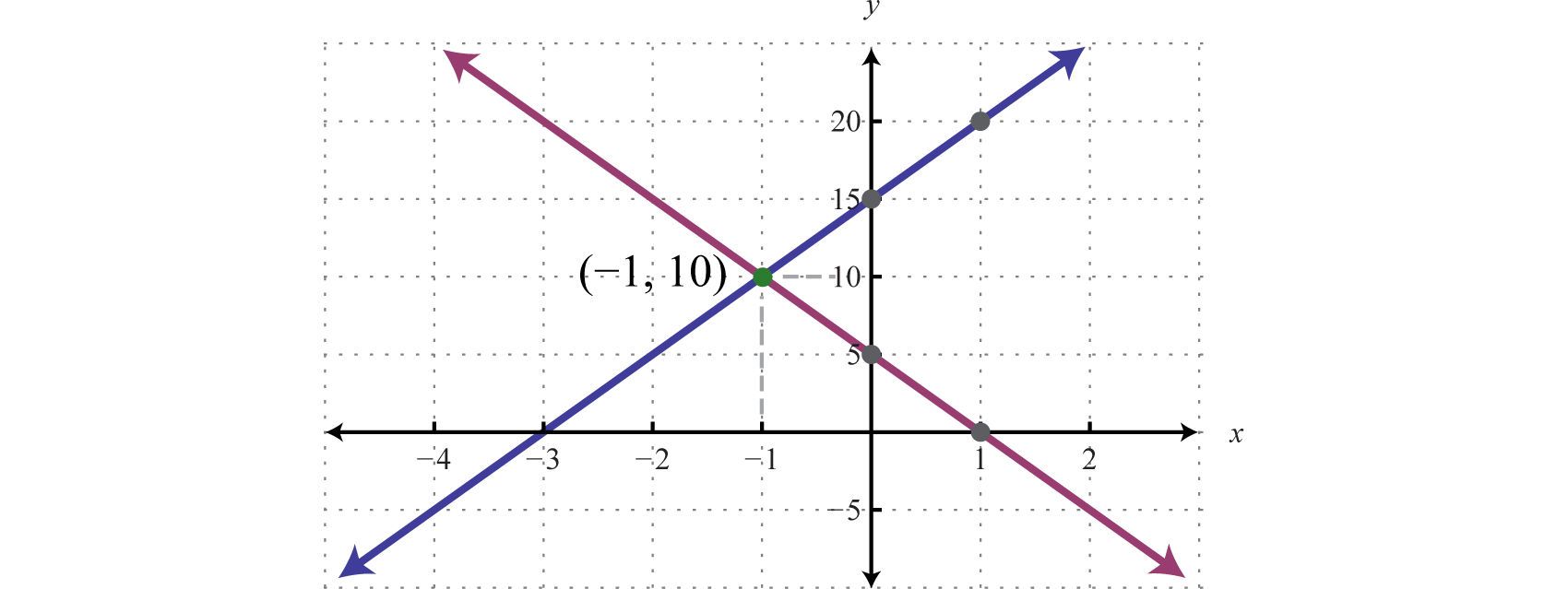
The simultaneous solution (−1, 10) corresponds to the point of intersection. One drawback of this method is that it is very inaccurate. When the coordinates of the solution are not integers, the method is practically unusable. If we have a choice, we typically avoid this method in favor of the more accurate algebraic techniques.
The substitution method, on the other hand, is a completely algebraic method. It requires you to solve for one of the variables and substitute the result into the other equation. The resulting equation has one variable for which you can solve. This method is particularly useful when there is a variable within the system with coefficient of 1. For example,
In this case, it is easy to solve for y in the first equation and then substitute the result into the other equation. One drawback of this method is that it often leads to equivalent equations with fractional coefficients, which are tedious to work with. If there is not a coefficient of 1, then it usually is best to choose the elimination method.
The elimination method is a completely algebraic method which makes use of the addition property of equations. We multiply one or both of the equations to obtain equivalent equations where one of the variables is eliminated if we add them together. For example,
To eliminate the terms involving x, we would multiply both sides of the first equation by 5 and both sides of the second equation by −2. This results in an equivalent system where the variable x is eliminated when we add the equations together. Of course, there are other combinations of numbers that achieve the same result. We could even choose to eliminate the variable y. No matter which variable is eliminated first, the solution will be the same. Note that the substitution method, in this case, would require tedious calculations with fractional coefficients. One weakness of the elimination method, as we will see later in our study of algebra, is that it does not always work for nonlinear systems.
Key Takeaways
- The substitution method requires that we solve for one of the variables and then substitute the result into the other equation. After performing the substitution step, the resulting equation has one variable and can be solved using the techniques learned up to this point.
- The elimination method is another completely algebraic method for solving a system of equations. Multiply one or both of the equations in a system by certain numbers to obtain an equivalent system where at least one variable in both equations have opposite coefficients. Adding these equivalent equations together eliminates that variable, and the resulting equation has one variable for which you can solve.
- It is a good practice to first rewrite the equations in standard form before beginning the elimination method.
- Solutions to systems of two linear equations with two variables, if they exist, are ordered pairs (x, y).
- If the process of solving a system of equations leads to a false statement, then the system is inconsistent and there is no solution, .
- If the process of solving a system of equations leads to an identity, then the system is dependent and there are infinitely many solutions that can be expressed using the form .
Topic Exercises
Part A: Substitution Method
Solve by substitution.
Part B: Elimination Method
Solve by elimination.
Part C: Mixed Practice
Solve using any method.
-
Explain to a beginning algebra student how to choose a method for solving a system of two linear equations. Also, explain what solutions look like and why.
-
Make up your own linear system with two variables and solve it using all three methods. Explain which method was preferable in your exercise.
Part D: Discussion Board
Answers
-
(−2, 11)
-
-
(2, 2)
-
-
-
-
-
-
(4, −2)
-
-
(3, −2)
-
-
(3, −4)
-
-
-
-
-
-
-
-
(2, −3)
-
-
-
-
-
-
(1, 1)
-
-
-
-
-
-
(0, 0)
-
-
(1, 2)
-
-
-
-
-
-
(−4, 2)
-
-
(−8, −1)
-
-
-
-
-
-
-
-
(−1, −2)
-
-
(−28, 0)
-
-
-
-
(1, 2)
-
-
(−1, −4)
-
-
(−5, 2)
-
-
-
-
-
-
-
-
(120, 77)
-
-
-
-
-
-
(0.5, −3)
-
-
-
-
-
-
-
-
(−2, −10)
-
-
(3, −1)
-
-
(32, 0)
-
-
-
-
(−4, 3)
-
-
-
-
-
-
(0.8, −5.4)
-
-
Ø
-
-
Answer may vary
-
3.3 Applications of Linear Systems with Two Variables
Learning Objectives
- Set up and solve applications involving relationships between two variables.
- Set up and solve mixture problems.
- Set up and solve uniform motion problems (distance problems).
Problems Involving Relationships between Two Variables
If we translate an application to a mathematical setup using two variables, then we need to form a linear system with two equations. Setting up word problems with two variables often simplifies the entire process, particularly when the relationships between the variables are not so clear.
Example 1
The sum of 4 times a larger integer and 5 times a smaller integer is 7. When twice the smaller integer is subtracted from 3 times the larger, the result is 11. Find the integers.
Solution:
Begin by assigning variables to the larger and smaller integer.
Let x represent the larger integer.
Let y represent the smaller integer.
When using two variables, we need to set up two equations. The first sentence describes a sum and the second sentence describes a difference.


This leads to the following system:
Solve using the elimination method. To eliminate the variable y multiply the first equation by 2 and the second by 5.
Add the equations in the equivalent system and solve for x.
Back substitute to find y.
Answer: The larger integer is 3 and the smaller integer is −1.
Try this! An integer is 1 less than twice that of another. If their sum is 20, find the integers.
Answer: The two integers are 7 and 13.
Next consider applications involving simple interest and money.
Example 2
A total of $12,800 was invested in two accounts. Part was invested in a CD at a annual interest rate and part was invested in a money market fund at a annual interest rate. If the total simple interest for one year was $465, then how much was invested in each account?
Solution:
Begin by identifying two variables.
Let x represent the amount invested at .
Let y represent the amount invested at .
The total amount in both accounts can be expressed as
To set up a second equation, use the fact that the total interest was $465. Recall that the interest for one year is the interest rate times the principal (). Use this to add the interest in both accounts. Be sure to use the decimal equivalents for the interest rates given as percentages.
These two equations together form the following linear system:
Eliminate x by multiplying the first equation by −0.03125.
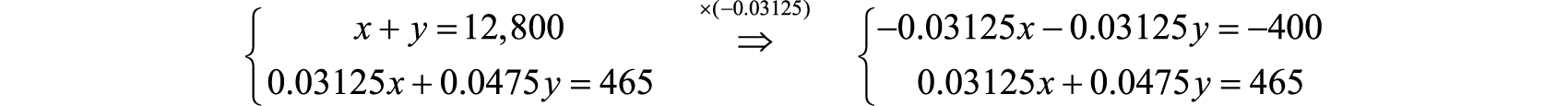
Next, add the resulting equations.
Back substitute to find x.
Answer: $4,000 was invested at and $8,800 was invested at .
Example 3
A jar consisting of only nickels and dimes contains 58 coins. If the total value is $4.20, how many of each coin is in the jar?
Solution:
Let n represent the number of nickels in the jar.
Let d represent the number of dimes in the jar.
The total number of coins in the jar can be expressed using the following equation:
Next, use the value of each coin to determine the total value $4.20.
This leads us to following linear system:
Here we will solve using the substitution method. In the first equation, we can solve for n.

Substitute into the second equation and solve for d.
Now back substitute to find the number of nickels.
Answer: There are 32 nickels and 26 dimes in the jar.
Try this! Joey has a jar full of 40 coins consisting of only quarters and nickels. If the total value is $5.00, how many of each coin does Joey have?
Answer: Joey has 15 quarters and 25 nickels.
Mixture Problems
Mixture problems often include a percentage and some total amount. It is important to make a distinction between these two types of quantities. For example, if a problem states that a 20-ounce container is filled with a 2% saline (salt) solution, then this means that the container is filled with a mixture of salt and water as follows:
|
Percentage |
Amount |
|---|---|---|
Salt |
2% = 0.02 |
0.02(20 ounces) = 0.4 ounces |
Water |
98% = 0.98 |
0.98(20 ounces) = 19.6 ounces |
In other words, we multiply the percentage times the total to get the amount of each part of the mixture.
Example 4
A 1.8% saline solution is to be combined and mixed with a 3.2% saline solution to produce 35 ounces of a 2.2% saline solution. How much of each is needed?
Solution:
Let x represent the amount of 1.8% saline solution needed.
Let y represent the amount of 3.2% saline solution needed.
The total amount of saline solution needed is 35 ounces. This leads to one equation,
The second equation adds up the amount of salt in the correct percentages. The amount of salt is obtained by multiplying the percentage times the amount, where the variables x and y represent the amounts of the solutions. The amount of salt in the end solution is 2.2% of the 35 ounces, or .022(35).
The algebraic setup consists of both equations presented as a system:
Solve.
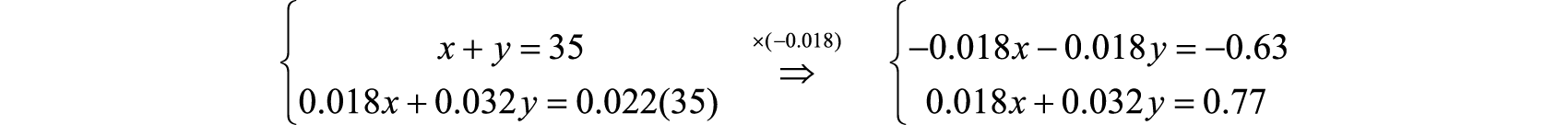
Add the resulting equations together
Back substitute to find x.
Answer: We need 25 ounces of the 1.8% saline solution and 10 ounces of the 3.2% saline solution.
Example 5
An 80% antifreeze concentrate is to be mixed with water to produce a 48-liter mixture containing 25% antifreeze. How much water and antifreeze concentrate is needed?
Solution:
Let x represent the amount of 80% antifreeze concentrate needed.
Let y represent the amount of water needed.
The total amount of the mixture must be 48 liters.
The second equation adds up the amount of antifreeze from each solution in the correct percentages. The amount of antifreeze in the end result is 25% of 48 liters, or 0.25(48).
Now we can form a system of two linear equations and two variables as follows:
Use the second equation to find x:
Back substitute to find y.
Answer: We need to mix 33 liters of water with 15 liters of antifreeze concentrate.
Try this! A chemist wishes to create 100 ml of a solution with 12% acid content. He uses two types of stock solutions, one with 30% acid content and another with 10% acid content. How much of each does he need?
Answer: The chemist will need to mix 10 ml of the 30% acid solution with 90 ml of the 10% acid solution.
Uniform Motion Problems (Distance Problems)
Recall that the distance traveled is equal to the average rate times the time traveled at that rate, . These uniform motion problems usually have a lot of data, so it helps to first organize that data in a chart and then set up a linear system. In this section, you are encouraged to use two variables.
Example 6
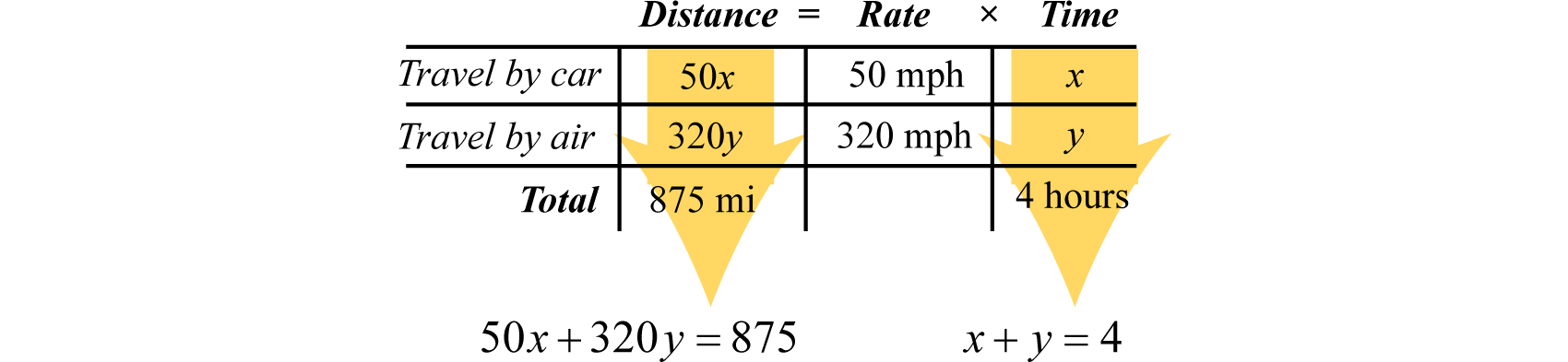
An executive traveled a total of 4 hours and 875 miles by car and by plane. Driving to the airport by car, she averaged 50 miles per hour. In the air, the plane averaged 320 miles per hour. How long did it take her to drive to the airport?
Solution:
We are asked to find the time it takes her to drive to the airport; this indicates that time is the unknown quantity.
Let x represent the time it took to drive to the airport.
Let y represent the time spent in the air.
Fill in the chart with the given information.

Use the formula to fill in the unknown distances.

The distance column and the time column of the chart help us to set up the following linear system.
Solve.
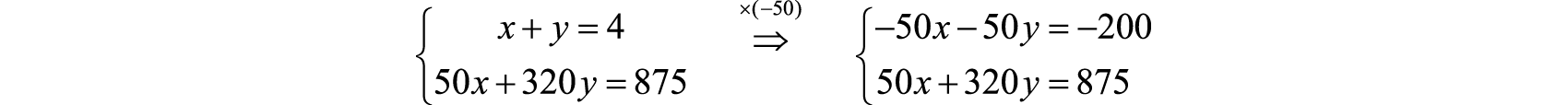
Now back substitute to find the time x it took to drive to the airport:
Answer: It took her hours to drive to the airport.
It is not always the case that time is the unknown quantity. Read the problem carefully and identify what you are asked to find; this defines your variables.
Applications involving simple interest and money.
Applications involving a mixture of amounts usually given as a percentage of some total.
Applications relating distance, average rate, and time.
Example 7
Flying with the wind, a light aircraft traveled 240 miles in 2 hours. The aircraft then turned against the wind and traveled another 135 miles in hours. Find the speed of the airplane and the speed of the wind.
Solution:
Begin by identifying variables.
Let x represent the speed of the airplane.
Let w represent the speed of the wind.
Use the following chart to organize the data:

With the wind, the airplane’s total speed is . Flying against the wind, the total speed is .

Use the rows of the chart along with the formula to construct a linear system that models this problem. Take care to group the quantities that represent the rate in parentheses.
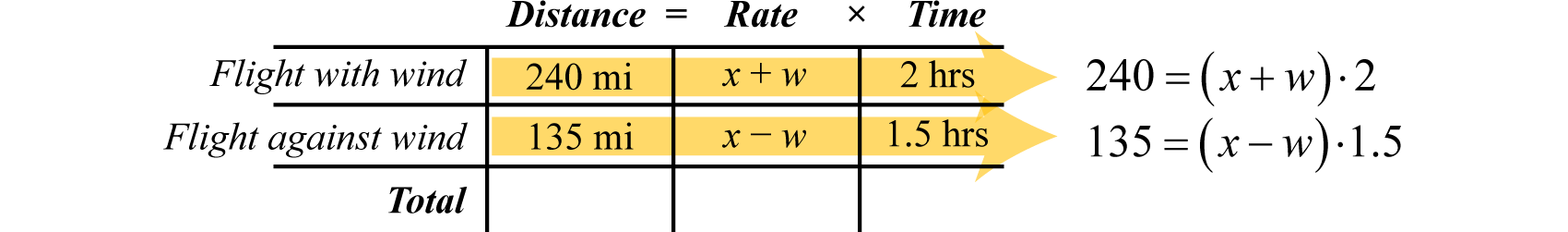
If we divide both sides of the first equation by 2 and both sides of the second equation by 1.5, then we obtain the following equivalent system:
Here w is lined up to eliminate.
Back substitute.
Answer: The speed of the airplane is 105 miles per hour and the speed of the wind is 15 miles per hour.
Try this! A boat traveled 27 miles downstream in 2 hours. On the return trip, which was against the current, the boat was only able to travel 21 miles in 2 hours. What were the speeds of the boat and of the current?
Answer: The speed of the boat was 12 miles per hour and the speed of the current was 1.5 miles per hour.
Key Takeaways
- Use two variables as a means to simplify the algebraic setup of applications where the relationship between unknowns is unclear.
- Carefully read the problem several times. If two variables are used, then remember that you need to set up two linear equations in order to solve the problem.
- Be sure to answer the question in sentence form and include the correct units for the answer.
Topic Exercises
-
The sum of two integers is 45. The larger integer is 3 less than twice the smaller. Find the two integers.
-
The sum of two integers is 126. The larger is 18 less than 5 times the smaller. Find the two integers.
-
The sum of two integers is 41. When 3 times the smaller is subtracted from the larger the result is 17. Find the two integers.
-
The sum of two integers is 46. When the larger is subtracted from twice the smaller the result is 2. Find the two integers.
-
The difference of two integers is 11. When twice the larger is subtracted from 3 times the smaller, the result is 3. Find the integers.
-
The difference of two integers is 6. The sum of twice the smaller and the larger is 72. Find the integers.
-
The sum of 3 times a larger integer and 2 times a smaller is 15. When 3 times the smaller integer is subtracted from twice the larger, the result is 23. Find the integers.
-
The sum of twice a larger integer and 3 times a smaller is 10. When the 4 times the smaller integer is added to the larger, the result is 0. Find the integers.
-
The difference of twice a smaller integer and 7 times a larger is 4. When 5 times the larger integer is subtracted from 3 times the smaller, the result is −5. Find the integers.
-
The difference of a smaller integer and twice a larger is 0. When 3 times the larger integer is subtracted from 2 times the smaller, the result is −5. Find the integers.
-
The length of a rectangle is 5 more than twice its width. If the perimeter measures 46 meters, then find the dimensions of the rectangle.
-
The width of a rectangle is 2 centimeters less than one-half its length. If the perimeter measures 62 centimeters, then find the dimensions of the rectangle.
-
A partitioned rectangular pen next to a river is constructed with a total 136 feet of fencing (see illustration). If the outer fencing measures 114 feet, then find the dimensions of the pen.
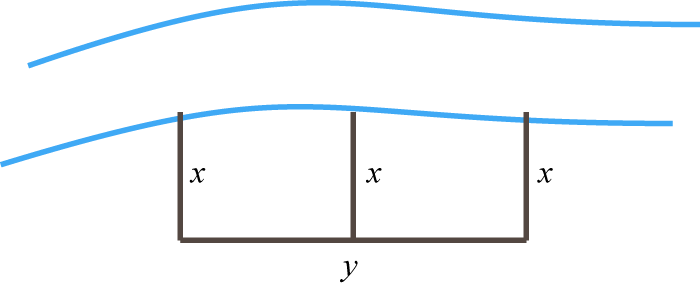
-
A partitioned rectangular pen is constructed with a total 168 feet of fencing (see illustration). If the perimeter measures 138 feet, then find the dimensions of the pen.

-
Find a and b such that the system has solution . (Hint: Substitute the given x- and y-values and solve the resulting linear system in terms of a and b.)
-
Find a and b such that the system has solution .
-
A line passes through two points and . Use these points and to construct a system of two linear equations in terms of m and b and solve it.
-
A line passes through two points and . Use these points and to construct a system of two linear equations in terms of m and b and solve it.
-
A $5,200 principal is invested in two accounts, one earning 3% interest and another earning 6% interest. If the total interest for the year is $210, then how much is invested in each account?
-
Harry’s $2,200 savings is in two accounts. One account earns 2% annual interest and the other earns 4%. His total interest for the year is $69. How much does he have in each account?
-
Janine has two savings accounts totaling $6,500. One account earns annual interest and the other earns . If her total interest for the year is $211, then how much is in each account?
-
Margaret has her total savings of $24,200 in two different CD accounts. One CD earns 4.6% interest and another earns 3.4% interest. If her total interest for the year is $1,007.60, then how much does she have in each CD account?
-
Last year Mandy earned twice as much interest in her Money Market fund as she did in her regular savings account. The total interest from the two accounts was $246. How much interest did she earn in each account?
-
A small business invested $120,000 in two accounts. The account earning 4% annual interest yielded twice as much interest as the account earning 3% annual interest. How much was invested in each account?
-
Sally earns $1,000 per month plus a commission of 2% of sales. Jane earns $200 per month plus 6% of her sales. At what monthly sales figure will both Sally and Jane earn the same amount of pay?
-
The cost of producing specialty book shelves includes an initial set-up fee of $1,200 plus an additional $20 per unit produced. Each shelf can be sold for $60 per unit. Find the number of units that must be produced and sold where the costs equal the revenue generated.
-
Jim was able to purchase a pizza for $12.35 with quarters and dimes. If he uses 71 coins to buy the pizza, then how many of each did he have?
-
A cash register contains $5 bills and $10 bills with a total value of $350. If there are 46 bills total, then how many of each does the register contain?
-
Two families bought tickets for the home basketball game. One family ordered 2 adult tickets and 4 children’s tickets for a total of $36.00. Another family ordered 3 adult tickets and 2 children’s tickets for a total of $32.00. How much did each ticket cost?
-
Two friends found shirts and shorts on sale at a flea market. One bought 4 shirts and 2 shorts for a total of $28.00. The other bought 3 shirts and 3 shorts for a total of $30.75. How much was each shirt and each pair of shorts?
-
A community theater sold 140 tickets to the evening musical for a total of $1,540. Each adult ticket was sold for $12 and each child ticket was sold for $8. How many adult tickets were sold?
-
The campus bookstore sells graphing calculators for $110 and scientific calculators for $16. On the first day of classes 50 calculators were sold for a total of $1,646. How many of each were sold?
-
A jar consisting of only nickels and quarters contains 70 coins. If the total value is $9.10, how many of each coin are in the jar?
-
Jill has $9.20 worth of dimes and quarters. If there are 68 coins in total, how many of each does she have?
Part A: Applications Involving Two Variables
Set up a linear system and solve.
-
A 17% acid solution is to be mixed with a 9% acid solution to produce 8 gallons of a 10% acid solution. How much of each is needed?
-
A nurse wishes to obtain 28 ounces of a 1.5% saline solution. How much of a 1% saline solution must she mix with a 4.5% saline solution to achieve the desired mixture?
-
A customer ordered 4 pounds of a mixed peanut product containing 12% cashews. The inventory consists of only two mixes containing 10% and 26% cashews. How much of each type must be mixed to fill the order?
-
One alcohol solution contains 10% alcohol and another contains 25% alcohol. How much of each should be mixed together to obtain 2 gallons of a 13.75% alcohol solution?
-
How much cleaning fluid concentrate, with 60% alcohol content, must be mixed with water to obtain a 24-ounce mixture with 15% alcohol content?
-
How many pounds of pure peanuts must be combined with a 20% peanut mix to produce 2 pounds of a 50% peanut mix?
-
A 50% fruit juice concentrate can be purchased wholesale. Best taste is achieved when water is mixed with the concentrate in such a way as to obtain a 15% fruit juice mixture. How much water and concentrate is needed to make a 60-ounce fruit juice drink?
-
Pure sugar is to be mixed with a fruit salad containing 10% sugar to produce 65 ounces of a salad containing 18% sugar. How much pure sugar is required?
-
A custom aluminum alloy is created by mixing 150 grams of a 15% aluminum alloy and 350 grams of a 55% aluminum alloy. What percentage of aluminum is in the resulting mixture?
-
A research assistant mixed 500 milliliters of a solution that contained a 12% acid with 300 milliliters of water. What percentage of acid is in the resulting solution?
Part B: Mixture Problems
Set up a linear system and solve.
-
The two legs of a 432-mile trip took 8 hours. The average speed for the first leg of the trip was 52 miles per hour and the average speed for the second leg of the trip was 60 miles per hour. How long did each leg of the trip take?
-
Jerry took two buses on the 265-mile trip from Los Angeles to Las Vegas. The first bus averaged 55 miles per hour and the second bus was able to average 50 miles per hour. If the total trip took 5 hours, then how long was spent in each bus?
-
An executive was able to average 48 miles per hour to the airport in her car and then board an airplane that averaged 210 miles per hour. The 549-mile business trip took 3 hours. How long did it take her to drive to the airport?
-
Joe spends 1 hour each morning exercising by jogging and then cycling for a total of 15 miles. He is able to average 6 miles per hour jogging and 18 miles per hour cycling. How long does he spend jogging each morning?
-
Swimming with the current Jack can swim 2.5 miles in hour. Swimming back, against the same current, he can only swim 2 miles in the same amount of time. How fast is the current?
-
A light aircraft flying with the wind can travel 180 miles in hours. The aircraft can fly the same distance against the wind in 2 hours. Find the speed of the wind.
-
A light airplane flying with the wind can travel 600 miles in 4 hours. On the return trip, against the wind, it will take 5 hours. What are the speeds of the airplane and of the wind?
-
A boat can travel 15 miles with the current downstream in hours. Returning upstream against the current, the boat can only travel miles in the same amount of time. Find the speed of the current.
-
Mary jogged the trail from her car to the cabin at the rate of 6 miles per hour. She then walked back to her car at a rate of 4 miles per hour. If the entire trip took 1 hour, then how long did it take her to walk back to her car?
-
Two trains leave the station traveling in opposite directions. One train is 8 miles per hour faster than the other and in hours they are 230 miles apart. Determine the average speed of each train.
-
Two trains leave the station traveling in opposite directions. One train is 12 miles per hour faster than the other and in 3 hours they are 300 miles apart. Determine the average speed of each train.
-
A jogger can sustain an average running rate of 8 miles per hour to his destination and 6 miles an hour on the return trip. Find the total distance the jogger ran if the total time running was hour.
Part C: Uniform Motion Problems
Set up a linear system and solve.
-
Compose a number or money problem of your own and share it on the discussion board.
-
Compose a mixture problem of your own and share it on the discussion board.
-
Compose a uniform motion problem of your own and share it on the discussion board.
Part E: Discussion Board
Answers
-
The integers are 16 and 29.
-
-
The integers are 6 and 35.
-
-
The integers are 25 and 36.
-
-
The integers are −3 and 7.
-
-
The integers are −5 and −2.
-
-
Length: 17 meters; width: 6 meters
-
-
Width: 22 feet; length: 70 feet
-
-
,
-
-
,
-
-
$3,400 at 3% and $1,800 at 6%
-
-
$2,200 at and $4,300 at
-
-
Savings: $82; Money Market: $164.
-
-
$20,000
-
-
35 quarters and 36 dimes
-
-
Adults $7.00 each and children $5.50 each.
-
-
105 adult tickets were sold.
-
-
The jar contains 42 nickels and 28 quarters.
-
-
7 gallons of the 9% acid solution and 1 gallon of the 17% acid solution
-
-
3.5 pounds of the 10% cashew mix and 0.5 pounds of the 26% cashew mix
-
-
6 ounces of cleaning fluid concentrate
-
-
18 ounces of fruit juice concentrate and 42 ounces of water
-
-
43%
-
-
The first leg of the trip took 6 hours and the second leg took 2 hours.
-
-
It took her hour to drive to the airport.
-
-
0.5 miles per hour.
-
-
Airplane: 135 miles per hour; wind: 15 miles per hour
-
-
hour
-
-
One train averaged 44 miles per hour and the other averaged 56 miles per hour.
-
-
Answer may vary
-
-
Answer may vary
3.4 Solving Linear Systems with Three Variables
Learning Objectives
- Check solutions to linear systems with three variables.
- Solve linear systems with three variables by elimination.
- Identify dependent and inconsistent systems.
- Solve applications involving three unknowns.
Solutions to Linear Systems with Three Variables
Real-world applications are often modeled using more than one variable and more than one equation. In this section, we will study linear systems consisting of three linear equations each with three variables. For example,
A solution to such a linear system is an ordered tripleTriples (x, y, z) that identify position relative to the origin in three-dimensional space. (x, y, z) that solves all of the equations. In this case, (−2, 1, 3) is the only solution. To check that an ordered triple is a solution, substitute in the corresponding x-, y-, and z-values and then simplify to see if you obtain a true statement from all three equations.
Because the ordered triple satisfies all three equations we conclude that it is indeed a solution.
Example 1
Determine whether or not is a solution to the following linear system:
Solution:
Answer: The point does not satisfy all of the equations and thus is not a solution.
An ordered triple such as can be graphed in three-dimensional space as follows:
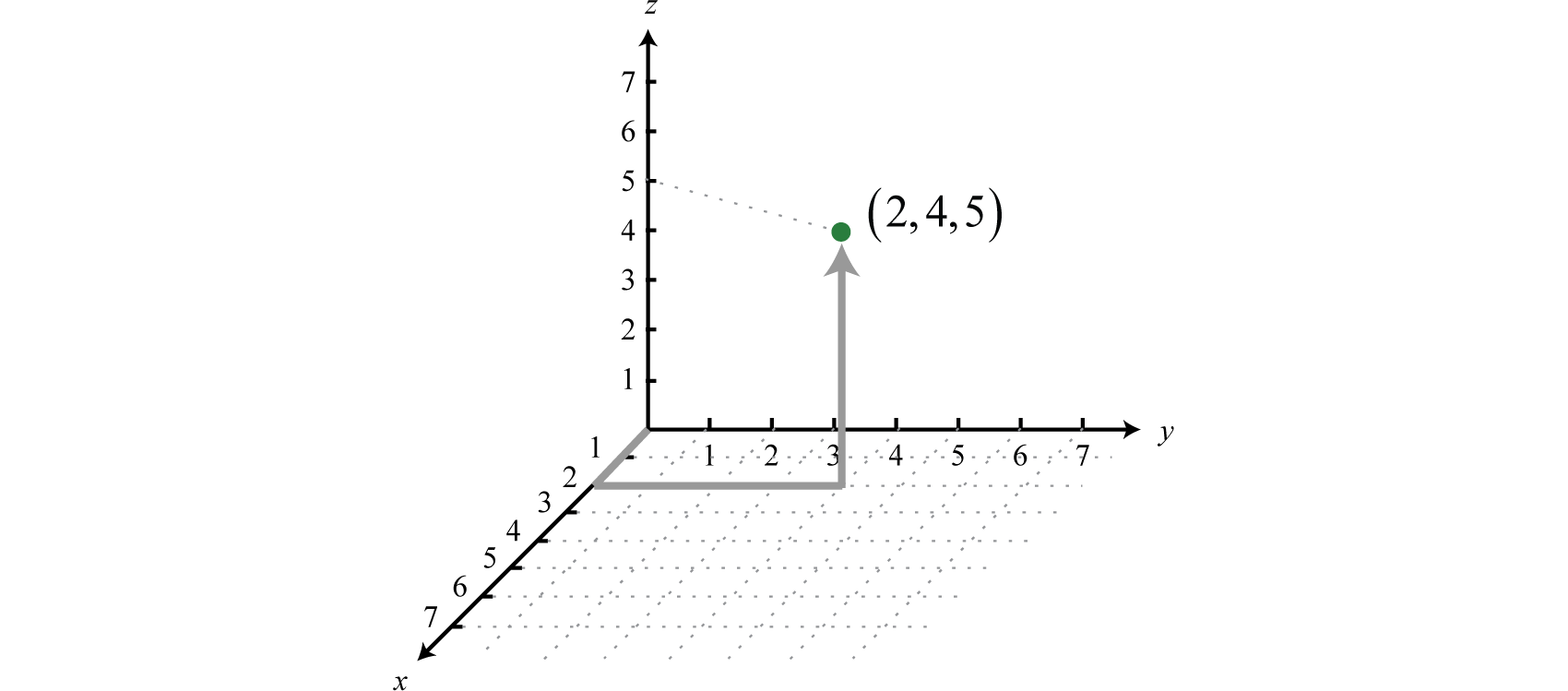
The ordered triple indicates position relative to the origin (0, 0, 0), in this case, 2 units along the x-axis, 4 units parallel to the y-axis, and 5 units parallel to the z-axis. A linear equation with three variablesAn equation that can be written in the standard form where a, b, c, and d are real numbers. is in standard form if where a, b, c, and d are real numbers. For example, is in standard form. Solving for z, we obtain and can consider both x and y to be the independent variables. When graphed in three-dimensional space, its graph will form a straight flat surface called a planeAny flat two-dimensional surface..

Therefore, the graph of a system of three linear equations and three unknowns will consist of three planes in space. If there is a simultaneous solution, the system is consistent and the solution corresponds to a point where the three planes intersect.

Graphing planes in three-dimensional space is not within the scope of this textbook. However, it is always important to understand the geometric interpretation.
Try this! Determine whether or not (3, −1, 2) a solution to the system: .
Answer: Yes, it is a solution.
Solve Linear Systems with Three Variables by Elimination
In this section, the elimination method is used to solve systems of three linear equations with three variables. The idea is to eliminate one of the variables and resolve the original system into a system of two linear equations, after which we can then solve as usual. The steps are outlined in the following example.
Example 2
Solve:
Solution:
All three equations are in standard form. If this were not the case, it would be a best practice to rewrite the equations in standard form before beginning this process.
Step 1: Choose any two of the equations and eliminate a variable. In this case, we can line up the variable z to eliminate if we group 3 times the first equation with the second equation.
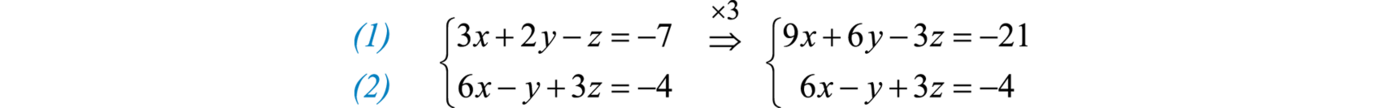
Next, add the equations together.
Step 2: Choose any other two equations and eliminate the same variable. We can line up z to eliminate again if we group −2 times the first equation with the third equation.
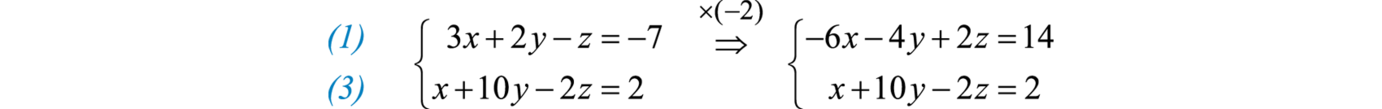
And then add,
Step 3: Solve the resulting system of two equations with two unknowns. Here we solve by elimination. Multiply the second equation by 3 to line up the variable x to eliminate.
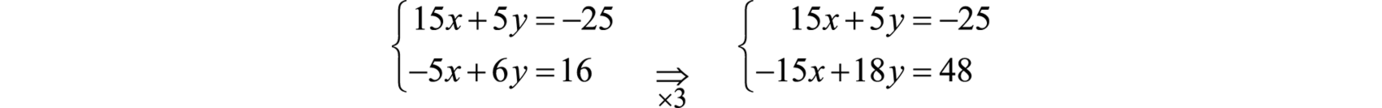
Next, add the equations together.
Step 4: Back substitute and determine all of the coordinates. To find x use the following,
Now choose one of the original equations to find z,
Hence the solution, presented as an ordered triple (x, y, z), is (−2, 1, 3). This is the same system that we checked in the beginning of this section.
Answer: (−2, 1, 3)
It does not matter which variable we initially choose to eliminate, as long as we eliminate it twice with two different sets of equations.
Example 3
Solve: .
Solution:
Because y has coefficient 1 in the second equation, choose to eliminate this variable. Use equations 1 and 2 to eliminate y.
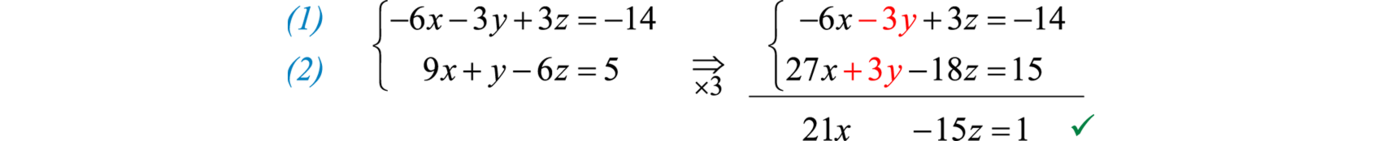
Next use equations 2 and 3 to eliminate y again.
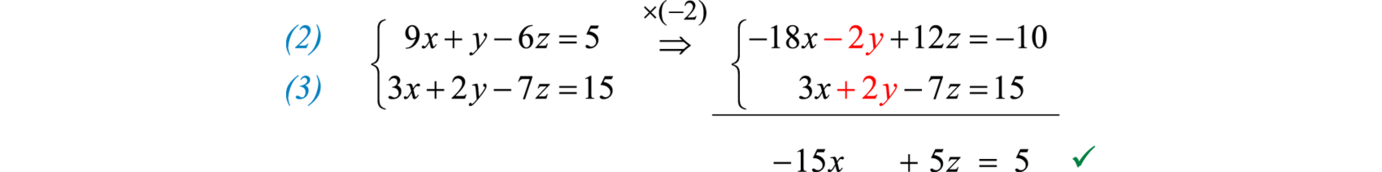
This leaves a system of two equations with two variables x and z,
Multiply the second equation by 3 and eliminate the variable z.
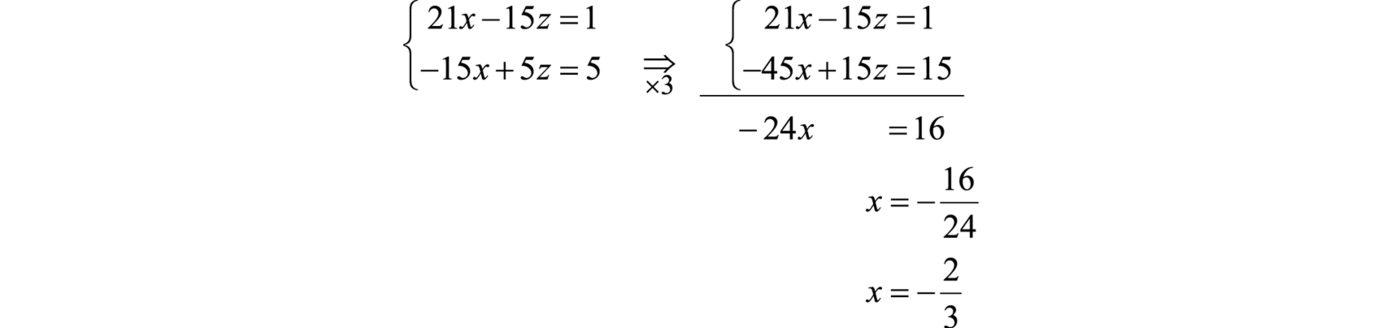
Now back substitute to find z.
Finally, choose one of the original equations to find y.
Answer:
Example 4
Solve:
Solution:
In this example, there is no obvious choice of variable to eliminate. We choose to eliminate x.
Next use equations 2 and 3 to eliminate x again.
This leaves a system of two equations with two variables y and z,
Multiply the first equation by −1 as a means to eliminate the variable y.
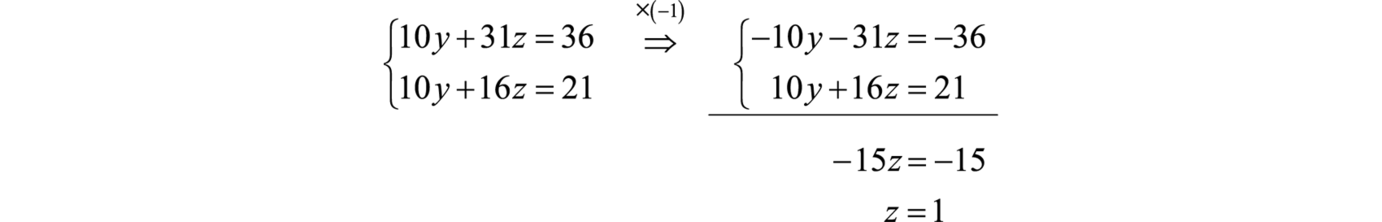
Now back substitute to find y.
Choose any one of the original equations to find x.
Answer:
Dependent and Inconsistent Systems
Just as with linear systems with two variables, not all linear systems with three variables have a single solution. Sometimes there are no simultaneous solutions.
Example 5
Solve the system: .
Solution:
In this case we choose to eliminate the variable y.
Next use equations 2 and 3 to eliminate y again.

This leaves a system of two equations with two variables x and z,
Multiply the first equation by −3 and eliminate the variable z.
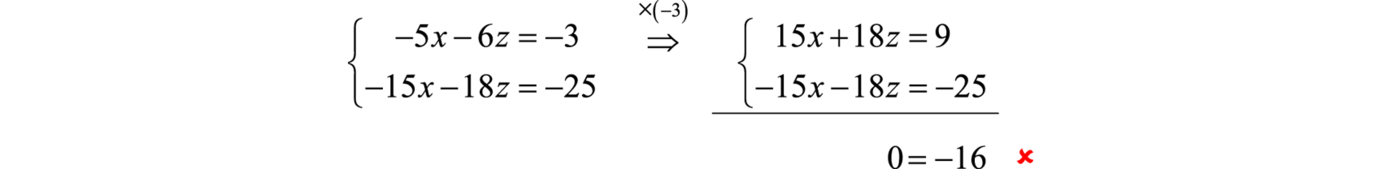
Adding the resulting equations together leads to a false statement, which indicates that the system is inconsistent. There is no simultaneous solution.
Answer: Ø
A system with no solutions is an inconsistent system. Given three planes, no simultaneous solution can occur in a number of ways.

Just as with linear systems with two variables, some linear systems with three variables have infinitely many solutions. Such systems are called dependent systems.
Example 6
Solve the system: .
Solution:
Eliminate z by adding the first and second equations together.
Next use equations 1 and 3 to eliminate z again.
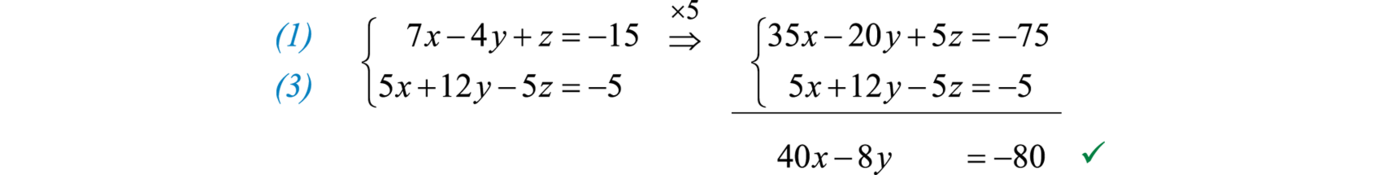
This leaves a system of two equations with two variables x and y,
Line up the variable y to eliminate by dividing the first equation by 2 and the second equation by −8.
A true statement indicates that the system is dependent. To express the infinite number of solutions in terms of one variable, we solve for y and z both in terms of x.
Once we have y in terms of x, we can solve for z in terms of x by back substituting into one of the original equations.
Answer: .
A consistent system with infinitely many solutions is a dependent system. Given three planes, infinitely many simultaneous solutions can occur in a number of ways.

Applications Involving Three Unknowns
Many real-world applications involve more than two unknowns. When an application requires three variables, we look for relationships between the variables that allow us to write three equations.
Example 7
A community theater sold 63 tickets to the afternoon performance for a total of $444. An adult ticket cost $8, a child ticket cost $4, and a senior ticket cost $6. If twice as many tickets were sold to adults as to children and seniors combined, how many of each ticket were sold?
Solution:
Begin by identifying three variables.
Let x represent the number of adult tickets sold.
Let y represent the number of child tickets sold.
Let z represent the number of senior tickets sold.
The first equation comes from the statement that 63 tickets were sold.
The second equation comes from total ticket sales.
The third equation comes from the statement that twice as many adult tickets were sold as child and senior tickets combined.
Therefore, the problem is modeled by the following linear system.
Solving this system is left as an exercise. The solution is .
Answer: The theater sold 42 adult tickets, 9 child tickets, and 12 senior tickets.
Key Takeaways
- A simultaneous solution to a linear system with three equations and three variables is an ordered triple (x, y, z) that satisfies all of the equations. If it does not solve each equation, then it is not a solution.
- We can solve systems of three linear equations with three unknowns by elimination. Choose any two of the equations and eliminate a variable. Next choose any other two equations and eliminate the same variable. This will result in a system of two equations with two variables that can be solved by any method learned previously.
- If the process of solving a system leads to a false statement, then the system is inconsistent and has no solution.
- If the process of solving a system leads to a true statement, then the system is dependent and has infinitely many solutions.
- To solve applications that require three variables, look for relationships between the variables that allow you to write three linear equations.
Topic Exercises
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
-
;
Part A: Linear Systems with Three Variables
Determine whether or not the given ordered triple is a solution to the given system.
Part B: Solving Linear Systems with Three Variables
Solve.
-
The sum of three integers is 38. Two less than 4 times the smaller integer is equal to the sum of the others. The sum of the smaller and larger integer is equal to 2 more than twice that of the other. Find the integers.
-
The sum of three integers is 40. Three times the smaller integer is equal to the sum of the others. Twice the larger is equal to 8 more than the sum of the others. Find the integers.
-
The sum of the angles A, B, and C of a triangle is 180°. The larger angle C is equal to twice the sum of the other two. Four times the smallest angle A is equal to the difference of angle C and B. Find the angles.
-
The sum of the angles A, B, and C of a triangle is 180°. Angle C is equal to the sum of the other two angles. Five times angle A is equal to the sum of angle C and B. Find the angles.
-
A total of $12,000 was invested in three interest earning accounts. The interest rates were 2%, 4%, and 5%. If the total simple interest for one year was $400 and the amount invested at 2% was equal to the sum of the amounts in the other two accounts, then how much was invested in each account?
-
Joe invested his $6,000 bonus in three accounts earning % interest. He invested twice as much in the account earning % as he did in the other two accounts combined. If the total simple interest for the year was $234, how much did Joe invest in each account?
-
A jar contains nickels, dimes, and quarters. There are 105 coins with a total value of $8.40. If there are 3 more than twice as many dimes as quarters, find how many of each coin are in the jar.
-
A billfold holds one-dollar, five-dollar, and ten-dollar bills and has a value of $210. There are 50 bills total where the number of one-dollar bills is one less than twice the number of five-dollar bills. How many of each bill are there?
-
A nurse wishes to prepare a 15-ounce topical antiseptic solution containing 3% hydrogen peroxide. To obtain this mixture, purified water is to be added to the existing 1.5% and 10% hydrogen peroxide products. If only 3 ounces of the 10% hydrogen peroxide solution is available, how much of the 1.5% hydrogen peroxide solution and water is needed?
-
A chemist needs to produce a 32-ounce solution consisting of % acid. He has three concentrates with 5%, 10%, and 40% acid. If he is to use twice as much of the 5% acid solution as the 10% solution, then how many ounces of the 40% solution will he need?
-
A community theater sold 128 tickets to the evening performance for a total of $1,132. An adult ticket cost $10, a child ticket cost $5, and a senior ticket cost $6. If three times as many tickets were sold to adults as to children and seniors combined, how many of each ticket were sold?
-
James sold 82 items at the swap meet for a total of $504. He sold packages of socks for $6, printed t-shirts for $12, and hats for $5. If he sold 5 times as many hats as he did t-shirts, how many of each item did he sell?
-
A parabola passes through three points , and . Use these points and to construct a system of three linear equations in terms of a, b, and c and then solve the system.
-
A parabola passes through three points , and . Use these points and to construct a system of three linear equations in terms of a, b, and c and solve it.
Part C: Applications
Set up a system of equations and use it to solve the following.
-
On a note card, write down the steps for solving a system of three linear equations with three variables using elimination. Use your notes to explain to a friend how to solve one of the exercises in this section.
-
Research and discuss curve fitting. Why is curve fitting an important topic?
Part D: Discussion Board
Answers
-
No
-
-
Yes
-
-
Yes
-
-
No
-
-
No
-
-
(2, −1, −3)
-
-
(4, 1, −3)
-
-
(1, −1, 3)
-
-
Ø
-
-
(5, −10, −6)
-
-
-
-
-
-
-
-
(1, −2, 6)
-
-
(−1, 2, −2)
-
-
(1,−3, 5)
-
-
(1, 1, 0)
-
-
(0, 1, −2)
-
-
(5, 0, 6)
-
-
-
-
-
-
(1, 2, 3)
-
-
8, 12, 18
-
-
A = 20°, B = 40°, and C = 120°
-
-
The amount invested at 2% was $6,000, the amount invested at 4% was $2,000, and the amount invested at 5% was $4,000.
-
-
72 nickels, 23 dimes, and 10 quarters
-
-
10 ounces of the 1.5% hydrogen peroxide solution and 2 ounces of water
-
-
96 adult tickets, 20 child tickets, and 12 senior tickets were sold.
-
-
, , and
-
-
Answer may vary
-
3.5 Matrices and Gaussian Elimination
Learning Objectives
- Use back substitution to solve linear systems in upper triangular form.
- Convert linear systems to equivalent augmented matrices.
- Use matrices and Gaussian elimination to solve linear systems.
Back Substitution
Recall that a linear system of equations consists of a set of two or more linear equations with the same variables. A linear system consisting of three equations in standard form arranged so that the variable x does not appear in any equation after the first and the variable y does not appear in any equation after the second is said to be in upper triangular formA linear system consisting of equations with three variables in standard form arranged so that the variable x does not appear after the first equation and the variable y does not appear after the second equation.. For example,
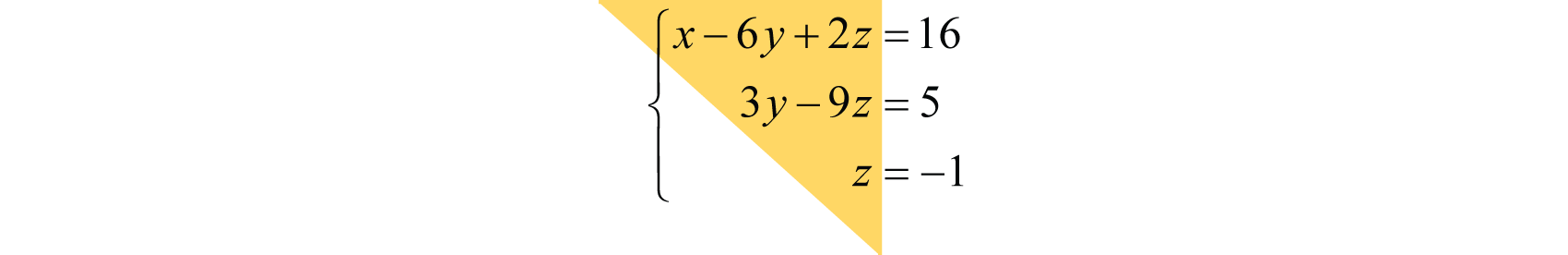
Notice that the system forms a triangle where each successive equation contains one less variable. In general,
If a linear system is in this form, we can easily solve for one of the variables and then back substitute to solve for the remaining variables.
Example 1
Solve: .
Solution:
Recall that solutions to linear systems with two variables, if they exist, are ordered pairs (x, y). We can determine the y-value easily using the second equation.
Next, use the first equation and the fact that to find x.
Answer:
Example 2
Solve: .
Solution:
Recall that solutions to linear systems with three variables, if they exist, are ordered triples (x, y, z). Use the second equation and the fact that to find y.
Next substitute y and z into the first equation.
Answer:
Matrices and Gaussian Elimination
In this section the goal is to develop a technique that streamlines the process of solving linear systems. We begin by defining a matrixA rectangular array of numbers consisting of rows and columns., which is a rectangular array of numbers consisting of rows and columns. Given a linear system in standard form, we create a coefficient matrixThe matrix of coefficients of a linear system in standard form written as they appear lined up without the variables or operations. by writing the coefficients as they appear lined up without the variables or operations as follows.
The rows represent the coefficients in the equations and the columns represent the coefficients of each variable. Furthermore, if we include a column that represents the constants we obtain what is called an augmented matrixThe coefficient matrix with the column of constants included.. For a linear system with two variables,
And for a linear system with three variables we have
Note: The dashed vertical line provides visual separation between the coefficient matrix and the column of constants. In other algebra resources that you may encounter, this is sometimes omitted.
Example 3
Construct the augmented matrix that corresponds to: .
Solution:
This system consists of two linear equations in standard form; therefore, the coefficients in the matrix appear as they do in the system.
Example 4
Construct the augmented matrix that corresponds to: .
Solution:
Since the equations are given in standard form, the coefficients appear in the matrix as they do in the system.
A matrix is in upper triangular form if all elements below the leading nonzero element in each successive row are zero. For example,
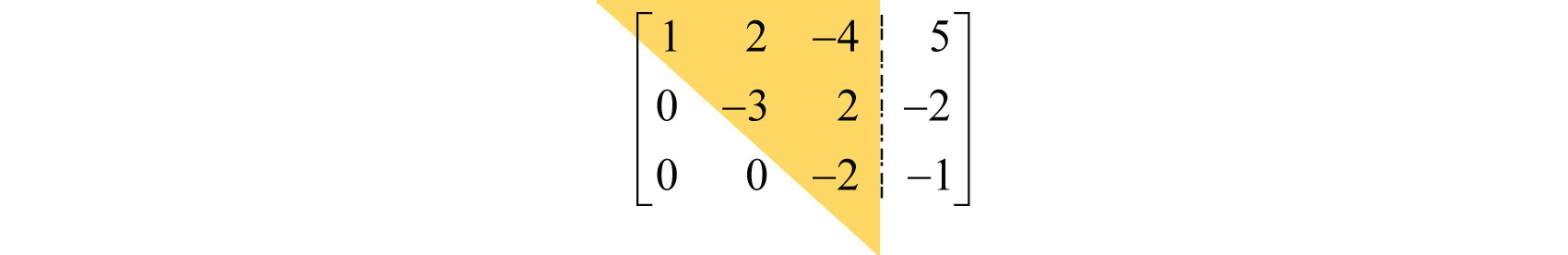
Notice that the elements below the main diagonal are zero and the coefficients above form a triangular shape. In general,
This is important because in this section we outline a process by which certain operations can be made to produce an equivalent linear system in upper triangular form so that it can be solved by using back substitution. An overview of the process is outlined below:
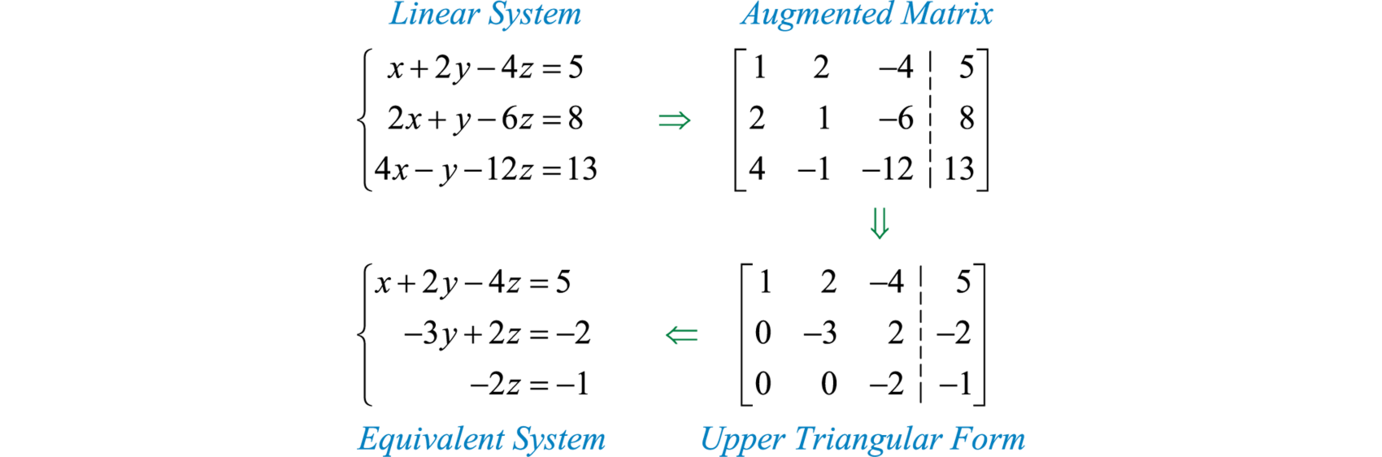
Once the system is in upper triangular form, we can use back substitution to easily solve it. It is important to note that the augmented matrices presented here represent linear systems of equations in standard form.
The following elementary row operationsOperations that can be performed to obtain equivalent linear systems. result in augmented matrices that represent equivalent linear systems:
- Any two rows may be interchanged.
- Each element in a row can be multiplied by a nonzero constant.
- Any row can be replaced by the sum of that row and a multiple of another.
Note: These operations are consistent with the properties used in the elimination method.
To efficiently solve a system of linear equations first construct an augmented matrix. Then apply the appropriate elementary row operations to obtain an augmented matrix in upper triangular form. In this form, the equivalent linear system can easily be solved using back substitution. This process is called Gaussian eliminationSteps used to obtain an equivalent linear system in upper triangular form so that it can be solved using back substitution., named in honor of Carl Friedrich Gauss (1777–1855).
Figure 3.1

Carl Friedrich Gauss (Wikipedia)
The steps for solving a linear equation with two variables using Gaussian elimination are listed in the following example.
Example 5
Solve using matrices and Gaussian elimination: .
Solution:
Ensure that the equations in the system are in standard form before beginning this process.
Step 1: Construct the corresponding augmented matrix.
Step 2: Apply the elementary row operations to obtain upper triangular form. In this case, we need only to eliminate the first element of the second row, −1. To do this, multiply the second row by 9 and add it to the first row.
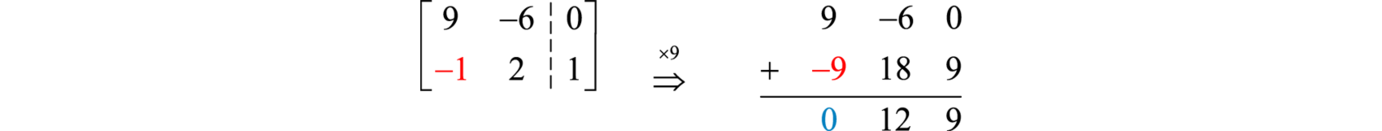
Now use this to replace the second row.
This results in an augmented matrix in upper triangular form.
Step 3: Convert back to a linear system and solve using back substitution. In this example, we have
Solve the second equation for y,
Substitute this value for y into the first equation to find x,
Answer:
The steps for using Gaussian elimination to solve a linear equation with three variables are listed in the following example.
Example 6
Solve using matrices and Gaussian elimination: .
Solution:
Ensure that the equations in the system are in standard form before beginning this process.
Step 1: Construct the corresponding augmented matrix.
Step 2: Apply the elementary row operations to obtain upper triangular form. We begin by eliminating the first element of the second row, 2 in this case. To do this multiply the first row by −2 and then add it to the second row.
Use this to replace the second row.
Next, eliminate the first element of the third row, 4 in this case, by multiplying the first row by −4 and adding it to the third row.
Use this to replace the third row.
This results in an augmented matrix where the elements below the first element of the first row are zero. Next eliminate the second element in the third row, in this case −9. Multiply the second row by −3 and add it to the third row.
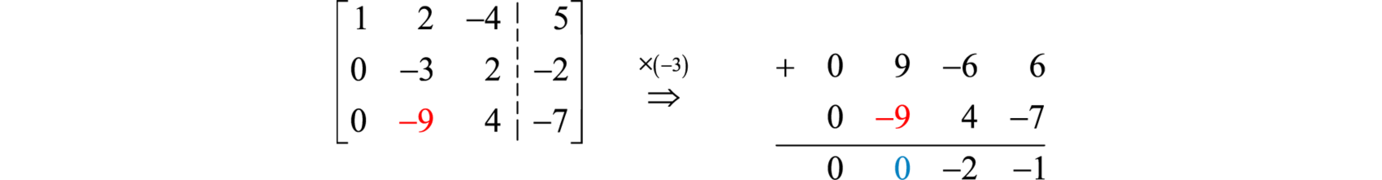
Use this to replace the third row and we can see that we have obtained a matrix in upper triangular form.
Step 3: Convert back to a linear system and solve using back substitution. In this example, we have
Answer: It is left to the reader to verify that the solution is .
Note: Typically, the work involved in replacing a row by multiplying and adding is done on the side using scratch paper.
Example 7
Solve using matrices and Gaussian elimination: .
Solution:
We begin by converting the system to an augmented coefficient matrix.
The elementary row operations are streamlined if the leading nonzero element in a row is 1. For this reason, begin by interchanging row one and two.

Replace row two with the sum of −2 times row one and row two.
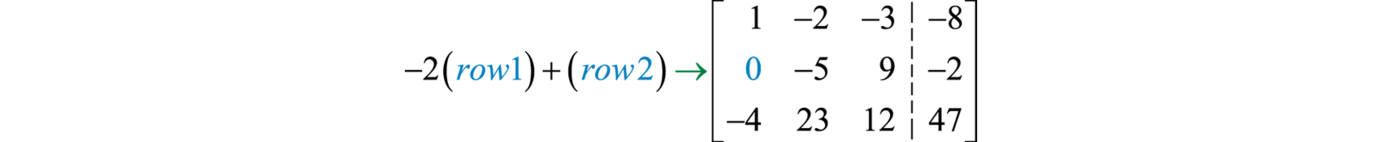
Replace row three with the sum of 4 times row one and row three.
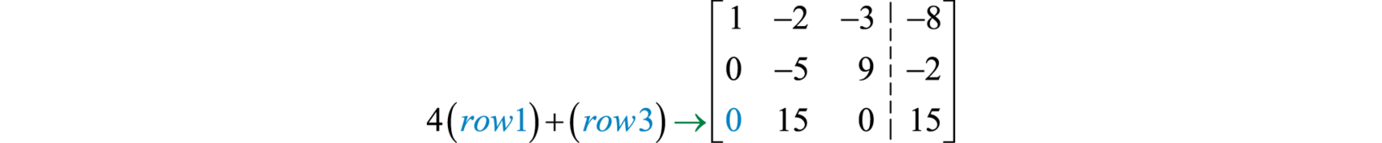
Next divide row 3 by 15.

Interchange row three with row two.

Next replace row 3 with the sum of 5 times row two and row three.

This results in a matrix in upper triangular form. A matrix is in row echelon formA matrix in triangular form where the leading nonzero element of each row is 1. if it is in upper triangular form where the leading nonzero element of each row is 1. We can obtain this form by replacing row three with the results of dividing it by 9.

Convert to a system of linear equations and solve by back substitution.
Here y = 1 and . Substitute into the first equation to find x.
Answer: Therefore the solution is .
Technology note: Many modern calculators and computer algebra systems can perform Gaussian elimination. First you will need to find out how to enter a matrix. Then use the calculator’s functions to find row echelon form. You are encouraged to conduct some web research on this topic for your particular calculator model.
Recall that some consistent linear systems are dependent, that is, they have infinitely many solutions. And some linear systems have no simultaneous solution; they are inconsistent systems.
Example 8
Solve using matrices and Gaussian elimination: .
Solution:
We begin by converting the system to an augmented coefficient matrix.
Replace row two with and replace row three with .
Replace row three with .
The last row indicates that this is a dependent system because converting the augmented matrix back to equations we have,
Note that the row of zeros corresponds to the following identity,
In this case, we can express the infinitely many solutions in terms of z. From the second row we have the following:
And from the first equation,
The solutions take the form where z is any real number.
Answer:
Dependent and inconsistent systems can be identified in an augmented coefficient matrix when the coefficients in one row are all zero.
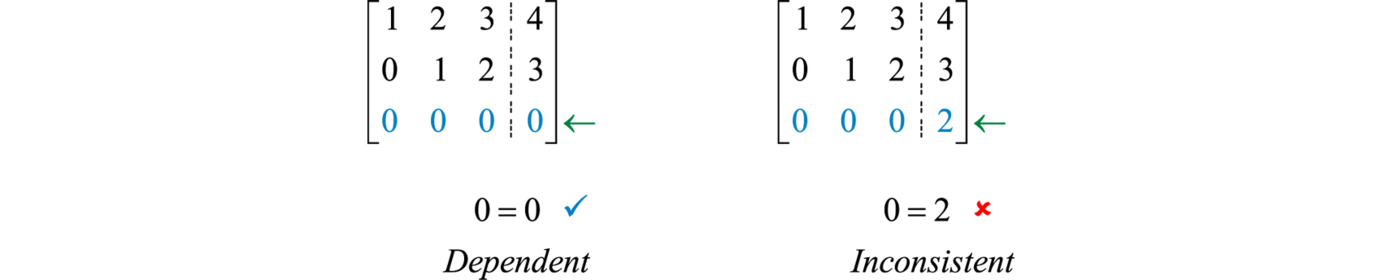
If a row of zeros has a corresponding constant of zero then the matrix represents a dependent system. If the constant is nonzero then the matrix represents an inconsistent system.
Key Takeaways
- A linear system in upper triangular form can easily be solved using back substitution.
- The augmented coefficient matrix and Gaussian elimination can be used to streamline the process of solving linear systems.
- To solve a system using matrices and Gaussian elimination, first use the coefficients to create an augmented matrix. Apply the elementary row operations as a means to obtain a matrix in upper triangular form. Convert the matrix back to an equivalent linear system and solve it using back substitution.
Topic Exercises
Part A: Back Substitution
Solve using back substitution.
Part B: Matrices and Gaussian Elimination
Construct the corresponding augmented matrix (do not solve).
Solve using matrices and Gaussian elimination.
-
Research and discuss the history of Gaussian Elimination. Who is credited for first developing this process? Post something that you found interesting relating to this story.
-
Research and discuss the history of modern matrix notation. Who is credited for the development? In what fields are they used today? Post your findings on the discussion board.
Part C: Discussion Board
Answers
-
-
-
-
-
(−4, 0)
-
-
-
-
(0, 0)
-
-
(−8, 7, 3)
-
-
-
-
-
-
-
-
(−3, 5, 9)
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
(6, −2)
-
-
Ø
-
-
(0, 0)
-
-
-
-
(2, 3, 3)
-
-
(0, 1, 3)
-
-
(1, −1, 2)
-
-
-
-
Ø
-
-
(−7, −13, 7)
-
-
-
-
-
-
-
-
-
-
Ø
-
-
(2, −2, 1)
-
-
Answer may vary
-
3.6 Determinants and Cramer’s Rule
Learning Objectives
- Calculate the determinant of a 2×2 matrix.
- Use Cramer’s rule to solve systems of linear equations with two variables.
- Calculate the determinant of a 3×3 matrix.
- Use Cramer’s rule to solve systems of linear equations with three variables.
Linear Systems of Two Variables and Cramer’s Rule
Recall that a matrix is a rectangular array of numbers consisting of rows and columns. We classify matrices by the number of rows n and the number of columns m. For example, a 3×4 matrix, read “3 by 4 matrix,” is one that consists of 3 rows and 4 columns. A square matrixA matrix with the same number of rows and columns. is a matrix where the number of rows is the same as the number of columns. In this section we outline another method for solving linear systems using special properties of square matrices. We begin by considering the following 2×2 coefficient matrix A,
The determinantA real number associated with a square matrix. of a 2×2 matrix, denoted with vertical lines , or more compactly as det(A), is defined as follows:
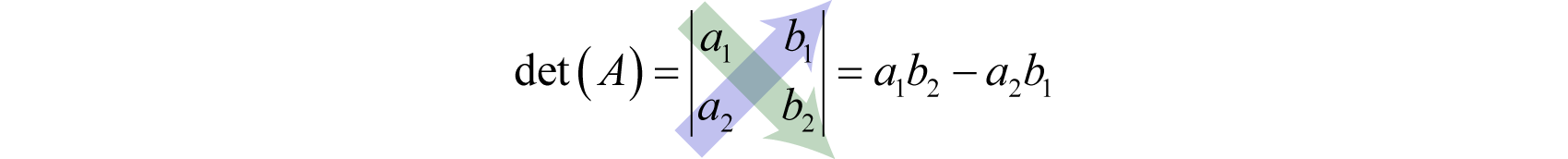
The determinant is a real number that is obtained by subtracting the products of the values on the diagonal.
Example 1
Calculate: .
Solution:
The vertical line on either side of the matrix indicates that we need to calculate the determinant.
Answer: 4
Example 2
Calculate: .
Solution:
Notice that the matrix is given in upper triangular form.
Answer: −18
We can solve linear systems with two variables using determinants. We begin with a general 2×2 linear system and solve for y. To eliminate the variable x, multiply the first equation by and the second equation by .
This results in an equivalent linear system where the variable x is lined up to eliminate. Now adding the equations we have
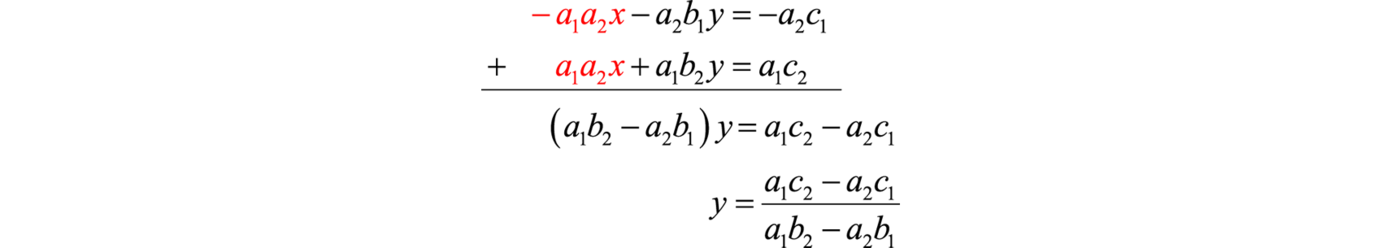
Both the numerator and denominator look very much like a determinant of a 2×2 matrix. In fact, this is the case. The denominator is the determinant of the coefficient matrix. And the numerator is the determinant of the matrix formed by replacing the column that represents the coefficients of y with the corresponding column of constants. This special matrix is denoted .
The value for x can be derived in a similar manner.
In general, we can form the augmented matrix as follows:
and then determine , and by calculating the following determinants.
The solution to a system in terms of determinants described above, when , is called Cramer’s ruleThe solution to an independent system of linear equations expressed in terms of determinants..
This theorem is named in honor of Gabriel Cramer (1704 - 1752).
Figure 3.2

Gabriel Cramer
The steps for solving a linear system with two variables using determinants (Cramer’s rule) are outlined in the following example.
Example 3
Solve using Cramer’s rule: .
Solution:
Ensure the linear system is in standard form before beginning this process.
Step 1: Construct the augmented matrix and form the matrices used in Cramer’s rule.
In the square matrix used to determine , replace the first column of the coefficient matrix with the constants. In the square matrix used to determine , replace the second column with the constants.
Step 2: Calculate the determinants.
Step 3: Use Cramer’s rule to calculate x and y.
Therefore the simultaneous solution .
Step 4: The check is optional; however, we do it here for the sake of completeness.
Equation 1 |
Equation 2 |
|---|---|
Answer: (1, 5)
Example 4
Solve using Cramer’s rule: .
Solution:
The corresponding augmented coefficient matrix follows.
And we have,
Use Cramer’s rule to find the solution.
Answer:
When the determinant of the coefficient matrix D is zero, the formulas of Cramer’s rule are undefined. In this case, the system is either dependent or inconsistent depending on the values of and . When and both and the system is dependent. When and either or is nonzero then the system is inconsistent.
Example 5
Solve using Cramer’s rule: .
Solution:
The corresponding augmented matrix follows.
And we have the following.
If we try to use Cramer’s rule we have,
both of which are indeterminate quantities. Because and both and we know this is a dependent system. In fact, we can see that both equations represent the same line if we solve for y.
Therefore we can represent all solutions where x is a real number.
Answer:
Linear Systems of Three Variables and Cramer’s Rule
Consider the following 3×3 coefficient matrix A,
The determinant of this matrix is defined as follows:
Here each 2×2 determinant is called the minorThe determinant of the matrix that results after eliminating a row and column of a square matrix. of the preceding factor. Notice that the factors are the elements in the first row of the matrix and that they alternate in sign (+ − +).
Example 6
Calculate: .
Solution:
To easily determine the minor of each factor in the first row we line out the first row and the corresponding column. The determinant of the matrix of elements that remain determines the corresponding minor.

Take care to alternate the sign of the factors in the first row. The expansion by minors about the first row follows:
Answer: 12
Expansion by minors can be performed about any row or any column. The sign of the coefficients, determined by the chosen row or column, will alternate according the following sign array.
Therefore, to expand about the second row we will alternate the signs starting with the opposite of the first element. We can expand the previous example about the second row to show that the same answer for the determinant is obtained.

And we can write,
Note that we obtain the same answer 12.
Example 7
Calculate: .
Solution:
The calculations are simplified if we expand about the third column because it contains two zeros.

The expansion by minors about the third column follows:
Answer: 16
It should be noted that there are other techniques used for remembering how to calculate the determinant of a 3×3 matrix. In addition, many modern calculators and computer algebra systems can find the determinant of matrices. You are encouraged to research this rich topic.
We can solve linear systems with three variables using determinants. To do this, we begin with the augmented coefficient matrix,
Let D represent the determinant of the coefficient matrix,
Then determine , , and by calculating the following determinants.
When , the solution to the system in terms of the determinants described above can be calculated using Cramer’s rule:
Use this to efficiently solve systems with three variables.
Example 8
Solve using Cramer’s rule: .
Solution:
Begin by determining the corresponding augmented matrix.
Next, calculate the determinant of the coefficient matrix.
Similarly we can calculate , , and . This is left as an exercise.
Using Cramer’s rule we have,
Answer:
If the determinant of the coefficient matrix D = 0, then the system is either dependent or inconsistent. This will depend on , , and . If they are all zero, then the system is dependent. If at least one of these is nonzero, then it is inconsistent.
Example 9
Solve using Cramer’s rule: .
Solution:
Begin by determining the corresponding augmented matrix.
Next, determine the determinant of the coefficient matrix.
Since D = 0, the system is either dependent or inconsistent.
However, because is nonzero we conclude the system is inconsistent. There is no simultaneous solution.
Answer:
Key Takeaways
- The determinant of a matrix is a real number.
- The determinant of a matrix is obtained by subtracting the product of the values on the diagonals.
- The determinant of a matrix is obtained by expanding the matrix using minors about any row or column. When doing this, take care to use the sign array to help determine the sign of the coefficients.
- Use Cramer’s rule to efficiently determine solutions to linear systems.
- When the determinant of the coefficient matrix is 0, Cramer’s rule does not apply; the system will either be dependent or inconsistent.
Topic Exercises
Part A: Linear Systems with Two Variables
Calculate the determinant.
Solve using Cramer’s rule.
Part B: Linear Systems with Three Variables
Calculate the determinant.
Solve using Cramer’s rule.
-
Research and discuss the history of the determinant. Who is credited for first introducing the notation of a determinant?
-
Research other ways in which we can calculate the determinant of a matrix. Give an example.
Part C: Discussion Board
Answers
-
−2
-
-
11
-
-
3
-
-
0
-
-
4
-
-
-
-
(1, −1)
-
-
-
-
-
-
(0, −2)
-
-
Ø
-
-
-
-
-
-
6
-
-
−39
-
-
0
-
-
3
-
-
24
-
-
-
-
(2, 3, −1)
-
-
(−1, 2, −3)
-
-
-
-
Ø
-
-
(0, −2, 0)
-
-
-
-
(−2, 1, 4)
-
-
-
-
Ø
-
-
(−1, 0, 1)
-
-
-
-
Answer may vary
-
3.7 Solving Systems of Inequalities with Two Variables
Learning Objectives
- Check solutions to systems of inequalities with two variables.
- Graph solution sets of systems of inequalities.
Solutions to Systems of Inequalities
A system of inequalitiesA set of two or more inequalities with the same variables. consists of a set of two or more inequalities with the same variables. The inequalities define the conditions that are to be considered simultaneously. For example,
We know that each inequality in the set contains infinitely many ordered pair solutions defined by a region in a rectangular coordinate plane. When considering two of these inequalities together, the intersection of these sets will define the set of simultaneous ordered pair solutions. When we graph each of the above inequalities separately we have:
And when graphed on the same set of axes, the intersection can be determined.

The intersection is shaded darker and the final graph of the solution set will be presented as follows:
The graph suggests that (3, 2) is a solution because it is in the intersection. To verify this, we can show that it solves both of the original inequalities as follows:
Points on the solid boundary are included in the set of simultaneous solutions and points on the dashed boundary are not. Consider the point (−1, 0) on the solid boundary defined by and verify that it solves the original system:
Notice that this point satisfies both inequalities and thus is included in the solution set. Now consider the point (2, 0) on the dashed boundary defined by and verify that it does not solve the original system:
This point does not satisfy both inequalities and thus is not included in the solution set.
Example 1
Determine whether or not (−3, 3) is a solution to the following system:
Solution:
Substitute the coordinates of (x, y) = (−3, 3) into both inequalities.
Answer: (−3, 3) is not a solution; it does not satisfy both inequalities.
We can graph the solutions of systems that contain nonlinear inequalities in a similar manner. For example, both solution sets of the following inequalities can be graphed on the same set of axes:
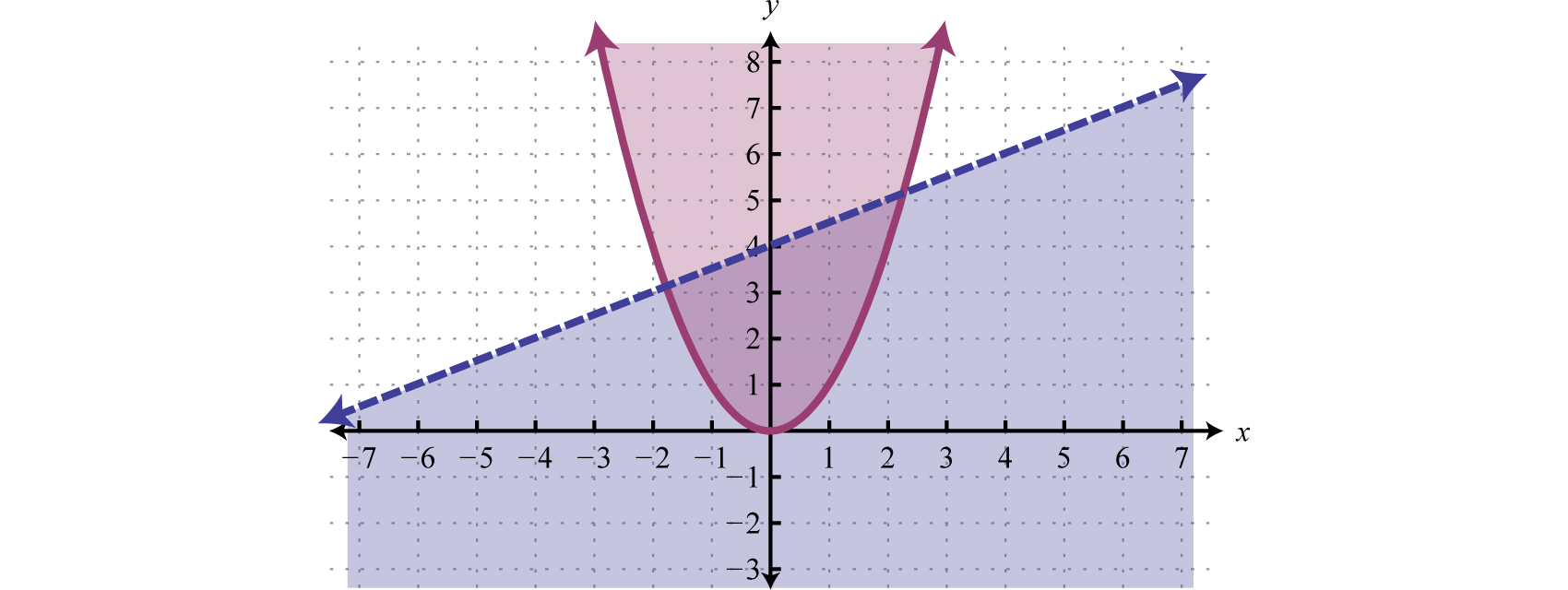
And the intersection of both regions contains the region of simultaneous ordered pair solutions.
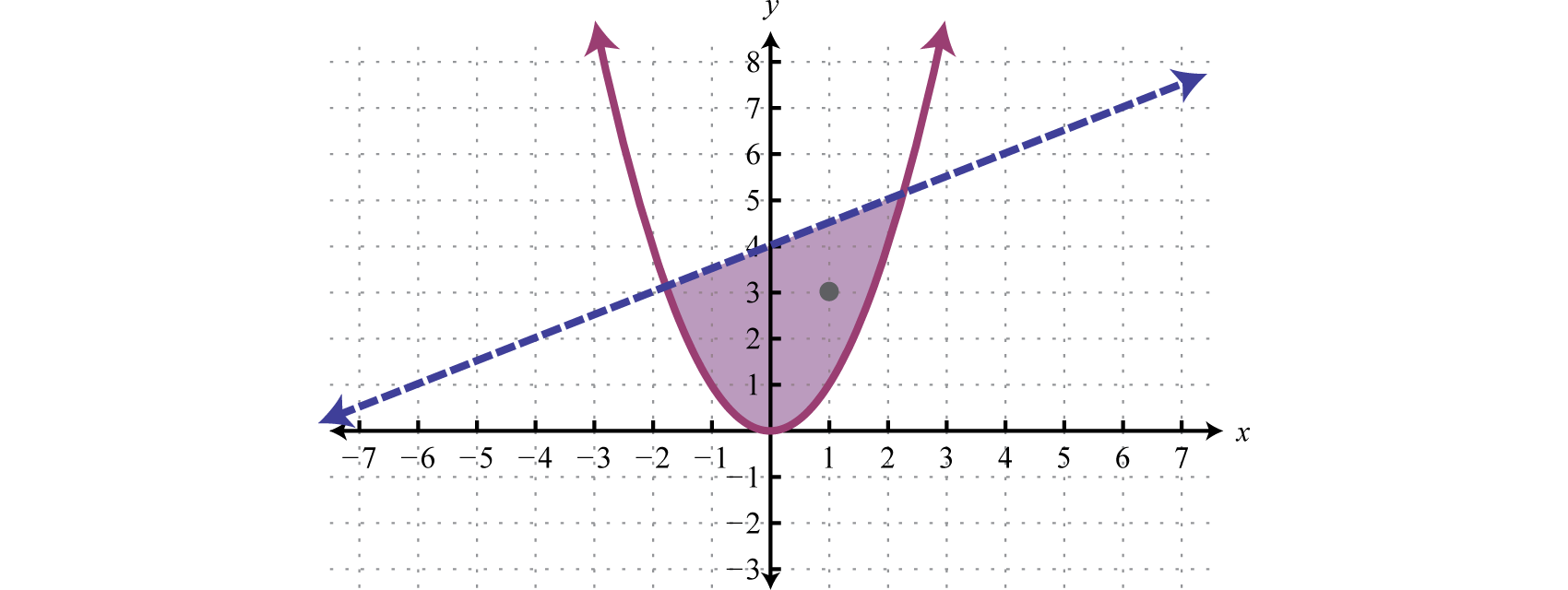
From the graph, we expect the ordered pair (1, 3) to solve both inequalities.
Graphing Solutions to Systems of Inequalities
Solutions to a system of inequalities are the ordered pairs that solve all the inequalities in the system. Therefore, to solve these systems we graph the solution sets of the inequalities on the same set of axes and determine where they intersect. This intersection, or overlap, will define the region of common ordered pair solutions.
Example 2
Graph the solution set: .
Solution:
To facilitate the graphing process, we first solve for y.
For the first inequality, we use a dashed boundary defined by and shade all points above the line. For the second inequality, we use a solid boundary defined by and shade all points below. The intersection is darkened.

Now we present our solution with only the intersection shaded.
Answer:
Example 3
Graph the solution set: .
Solution:
We begin by solving both inequalities for y.
Because of the strict inequalities, we will use a dashed line for each boundary. For the first inequality shade all points above the boundary and for the second inequality shade all points below the boundary.
As we can see, there is no intersection of these two shaded regions. Therefore, there are no simultaneous solutions.
Answer:
Example 4
Graph the solution set: .
Solution:
Begin by graphing the solution sets to all three inequalities.
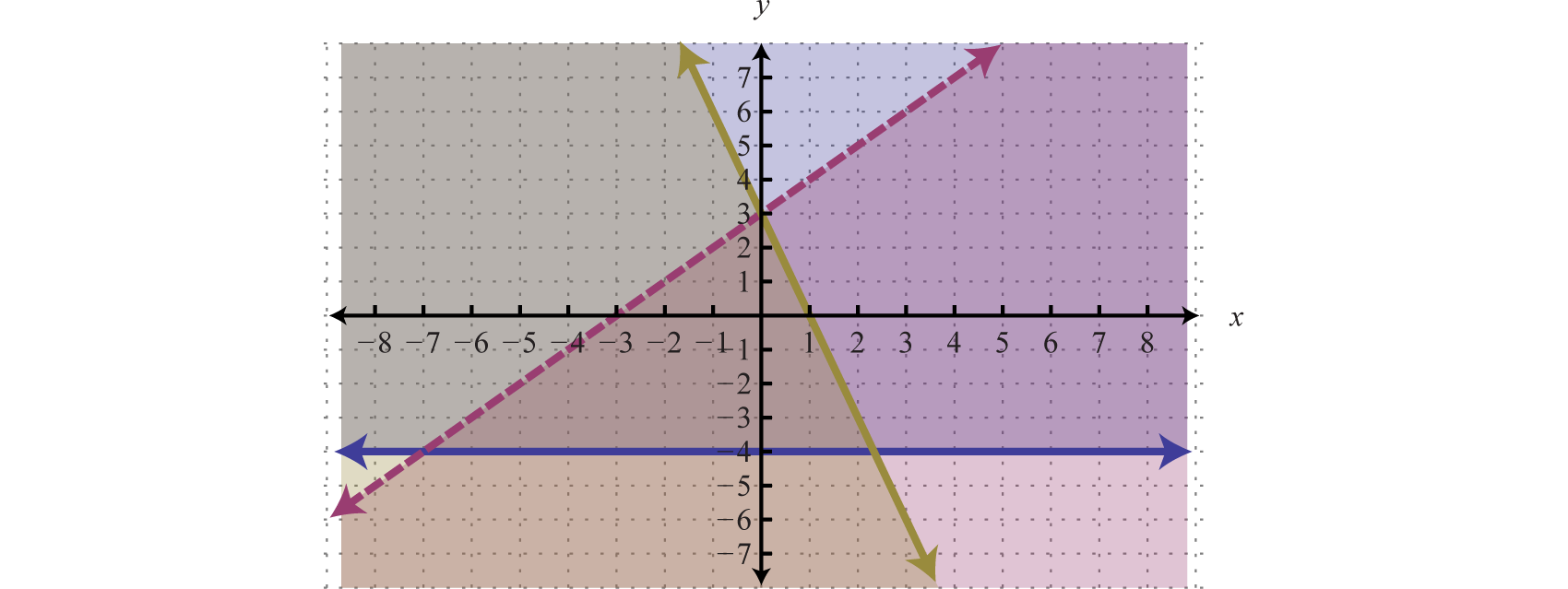
After graphing all three inequalities on the same set of axes, we determine that the intersection lies in the triangular region pictured below.
Answer:
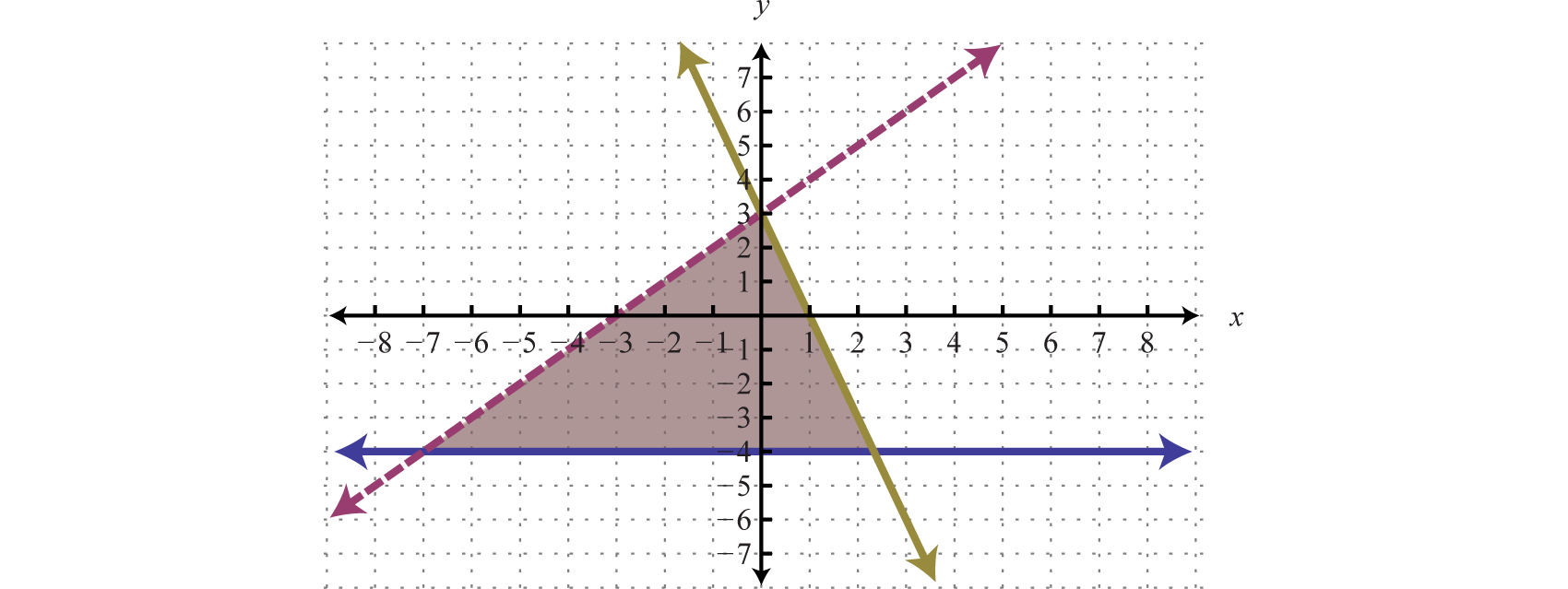
The graph suggests that (−1, 1) is a simultaneous solution. As a check, we could substitute that point into the inequalities and verify that it solves all three conditions.
Use the same technique to graph the solution sets to systems of nonlinear inequalities.
Example 5
Graph the solution set: .
Solution:
The first inequality has a parabolic boundary. This boundary is a horizontal translation of the basic function to the left 1 unit. Because of the strict inequality, the boundary is dashed, indicating that it is not included in the solution set. The second inequality is linear and will be graphed with a solid boundary. Solution sets to both are graphed below.
After graphing the inequalities on the same set of axes, we determine that the intersection lies in the region pictured below.
Answer:
Key Takeaways
- To graph solutions to systems of inequalities, graph the solution sets of each inequality on the same set of axes and determine where they intersect.
- You can check your answer by choosing a few values inside and out of the shaded region to see if they satisfy the inequalities or not. While this is not a proof, doing so will give a good indication that you have graphed the correct region.
Topic Exercises
-
(−2, 1);
-
(−1, −3);
-
(−2, −1);
-
(0, −5);
-
;
-
;
-
(−1, −2);
-
(−5, 2);
-
(0, 3);
-
(1, 1);
-
(−1, 2);
-
(4, 5);
-
(−2, −3);
-
(1, 2);
-
;
-
(−4, 1);
-
;
-
;
-
(4, 2);
-
;
Part A: Solutions to Systems of Inequalities
Determine whether or not the given point is a solution to the given system of inequalities.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Construct a system of linear inequalities that describes all points in the first quadrant.
-
Construct a system of linear inequalities that describes all points in the second quadrant.
-
Construct a system of linear inequalities that describes all points in the third quadrant.
-
Construct a system of linear inequalities that describes all points in the fourth quadrant.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Part B: Solving Systems of Inequalities
Graph the solution set.
Graph the solution set.
Answers
-
Yes
-
-
Yes
-
-
Yes
-
-
Yes
-
-
Yes
-
-
Yes
-
-
No
-
-
Yes
-
-
Yes
-
-
No
-
3.8 Review Exercises and Sample Exam
Review Exercises
-
;
-
;
-
;
-
;
-
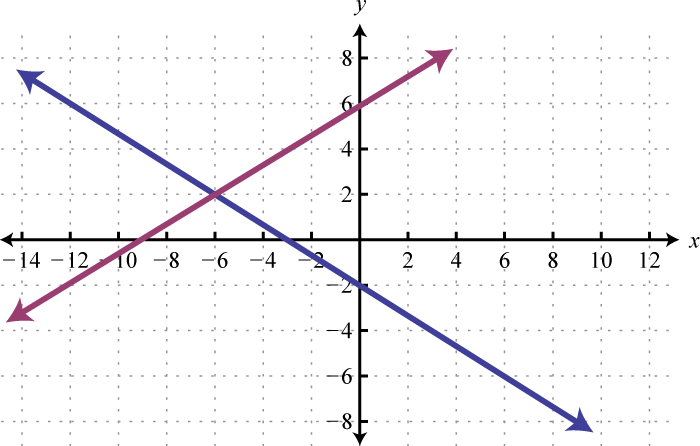
-
-
-
-
-
-
-
-
-
-
-
Linear Systems and Their Solutions
Determine whether or not the given ordered pair is a solution to the given system.
Given the graphs, determine the simultaneous solution.
Solve by graphing.
Solving Linear Systems with Two Variables
Solve by substitution.
Solve by elimination.
Solve using any method.
-
The sum of two integers is 32. The larger is 4 less than twice the smaller. Find the integers.
-
The sum of 2 times a larger integer and 3 times a smaller integer is 54. When twice the smaller integer is subtracted from the larger, the result is −1. Find the integers.
-
The length of a rectangle is 2 centimeters less than three times its width and the perimeter measures 44 centimeters. Find the dimensions of the rectangle.
-
The width of a rectangle is one-third of its length. If the perimeter measures centimeters, then find the dimensions of the rectangle.
-
The sum of a larger integer and 3 times a smaller is 61. When twice the smaller integer is subtracted from the larger, the result is 1. Find the integers.
-
A total of $8,600 was invested in two accounts. One account earned % annual interest and the other earned % annual interest. If the total interest for one year was $431.25, how much was invested in each account?
-
A jar consisting of only nickels and dimes contains 76 coins. If the total value is $6, how many of each coin are in the jar?
-
A nurse wishes to obtain 32 ounces of a 1.2% saline solution. How much of a 1% saline solution must she mix with a 2.6% saline solution to achieve the desired mixture?
-
A light aircraft flying with the wind can travel 330 miles in 2 hours. The aircraft can fly the same distance against the wind in 3 hours. Find the speed of the wind.
-
An executive was able to average 52 miles per hour to the airport in her car and then board an airplane that averaged 340 miles per hour. If the total 640-mile business trip took 4 hours, how long did she spend on the airplane?
Applications of Linear Systems with Two Variables
Set up a linear system and solve.
-
;
-
;
-
;
-
;
-
-
-
-
-
-
-
-
-
The sum of three integers is 24. The larger is equal to the sum of the two smaller integers. Three times the smaller is equal to the larger. Find the integers.
-
The sports center sold 120 tickets to the Friday night basketball game for a total of $942. A general admission ticket cost $12, a student ticket cost $6, and a child ticket cost $4. If the sum of the general admission and student tickets totaled 105, then how many of each ticket were sold?
-
A 16-ounce mixed nut product containing 13.5% peanuts is to be packaged. The packager has a three-mixed nut product containing 6%, 10%, and 50% peanut concentrations in stock. If the amount of 50% peanut product is to be one-quarter that of the 10% peanut product, then how much of each will be needed to produce the desired peanut concentration?
-
Water is to be mixed with two acid solutions to produce a 25-ounce solution containing 6% acid. The acid mixtures on hand contain 10% and 25% acid. If the amount of 25% acid is to be one-half the amount of the 10% acid solution, how much water will be needed?
Solving Linear Systems with Three Variables
Determine whether the given ordered triple is a solution to the given system.
Solve.
Set up a linear system and solve.
Matrices and Gaussian Elimination
Construct the corresponding augmented matrix.
Solve using matrices and Gaussian elimination.
Determinants and Cramer’s Rule
Calculate the determinant.
Solve using Cramer’s rule.
-
(−6, 1);
-
;
-
(−4, −2);
-
;
-
(−3, −2);
-
;
-
-
-
-
-
-
-
-
Systems of Inequalities with Two Variables
Determine whether or not the given point is a solution to the system of inequalities.
Graph the solution set.
Answers
-
Yes
-
-
No
-
-
(−6, 2)
-
-
Ø
-
-
(4, −2)
-
-
-
-
(4, 5)
-
-
(6, 0)
-
-
(2, −4)
-
-
-
-
-
-
(4, 3)
-
-
(5, 2)
-
-
-
-
Ø
-
-
-
-
12, 20
-
-
Length: 16 centimeters; width: 6 centimeters
-
-
12, 25
-
-
The jar contains 32 nickels and 44 dimes.
-
-
27.5 miles per hour
-
-
No
-
-
Yes
-
-
-
-
(−2, −1, 3)
-
-
Ø
-
-
-
-
4, 8, 12
-
-
6 oz of the 6% peanut stock, 8 oz of the 10% peanut stock, and 2 oz of the 50% peanut stock should be mixed.
-
-
-
-
-
-
(5, −4)
-
-
-
-
-
-
(−2, 2, 2)
-
-
−22
-
-
−14
-
-
−1
-
-
0
-
-
-
-
-
-
(2, −5, 1)
-
-
-
-
-
-
Yes
-
-
Yes
-
-
Yes
-
-
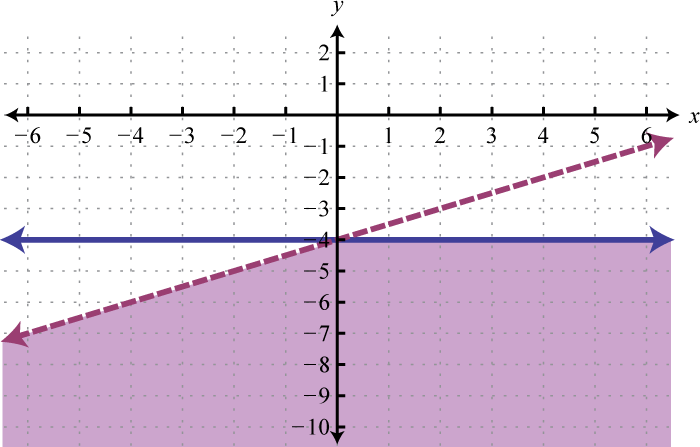
-
-
-
-
-
-
-
Sample Exam
-
Determine whether or not is a solution to .
-
Determine whether or not is a solution to .
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
The length of a rectangle is 1 inch less than twice that of its width. If the perimeter measures 49 inches, then find the dimensions of the rectangle.
-
Joe’s $4,000 savings is in two accounts. One account earns 3.1% annual interest and the other earns 4.9% annual interest. His total interest for the year is $174.40. How much does he have in each account?
-
One solution contains 40% alcohol and another contains 72% alcohol. How much of each should be mixed together to obtain 16 ounces of a 62% alcohol solution?
-
Jerry took two buses on the 193-mile trip to visit his grandmother. The first bus averaged 46 miles per hour and the second bus was able to average 52 miles per hour. If the total trip took 4 hours, then how long was spent in each bus?
-
A total of $8,500 was invested in three interest earning accounts. The interest rates were 2%, 3%, and 6%. If the total simple interest for one year was $380 and the amount invested at 6% was equal to the sum of the amounts in the other two accounts, then how much was invested in each account?
-
A mechanic wishes to mix 6 gallons of a 22% antifreeze solution. In stock he has a 60% and an 80% antifreeze concentrate. Water is to be added in the amount that is equal to twice the amount of both concentrates combined. How much water is needed?
Solve by graphing.
Solve by substitution.
Solve.
Solve using any method.
Graph the solution set.
Use algebra to solve the following.
Answers
-
Yes
-
-
(−4, 1)
-
-
-
-
(−8, −3)
-
-
(4, −3)
-
-
Ø
-
-
-
-
Ø
-
-
(2, 2, 2)
-
-
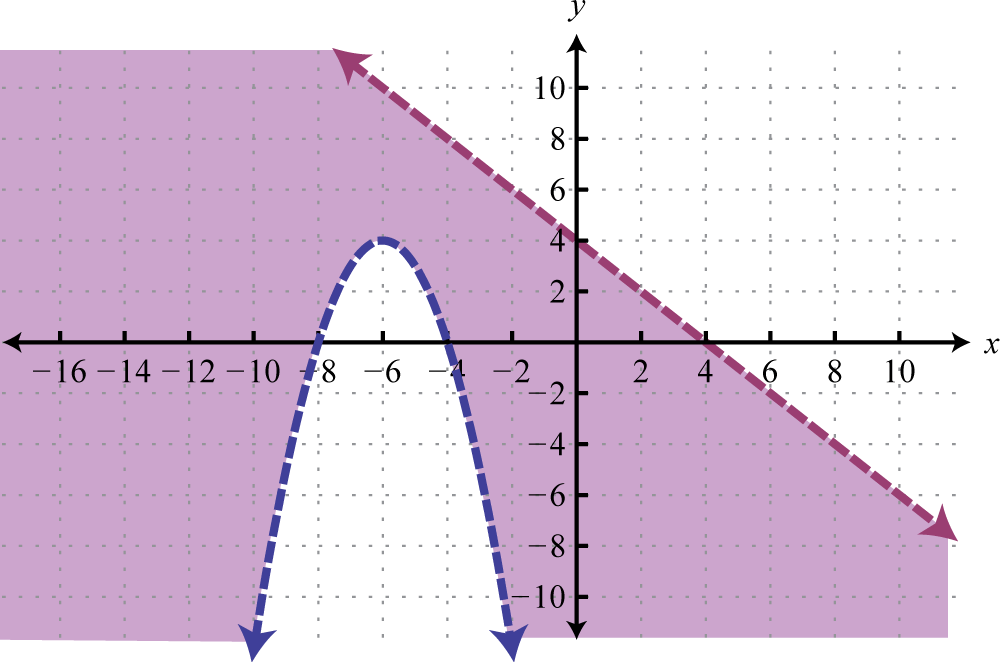
-
-
Joe has $1,200 in the account earning 3.1% interest and $2,800 in the account earning 4.9% interest.
-
-
Jerry spent 2.5 hours in the first bus and 1.5 hours in the second.
-
-
4 gallons of water is needed.