This is “Review Exercises and Sample Exam”, section 4.9 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
4.9 Review Exercises and Sample Exam
Review Exercises
-
Given , find , , and
-
Given , find , , and
-
Given , find , and
-
Given , find , and
-
The following graph gives the height in feet of a projectile over time in seconds.
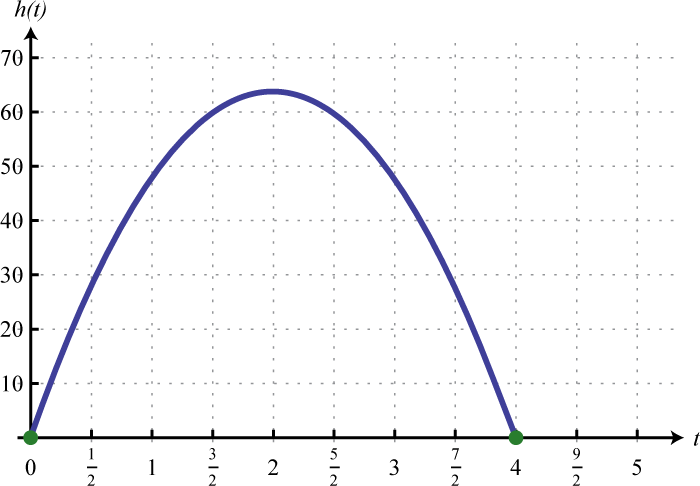
- Use the graph to determine the height of the projectile at 2.5 seconds.
- At what time does the projectile reach its maximum height?
- How long does it take the projectile to return to the ground?
-
Given the graph of the function , find , and
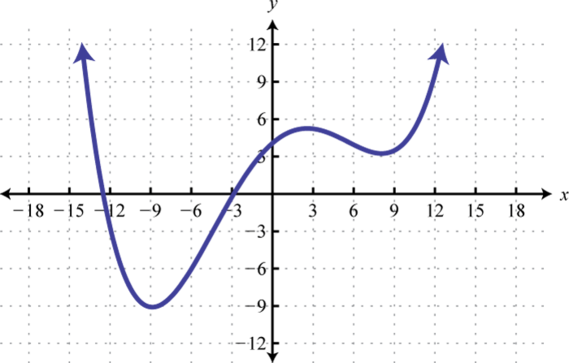
-
From the ground, a bullet is fired straight up into the air at 340 meters per second. Ignoring the effects of air friction, write a function that models the height of the bullet and use it to calculate the bullet’s height after one-quarter of a second. (Round off to the nearest meter.)
-
An object is tossed into the air at an initial speed of 30 feet per second from a rooftop 10 feet high. Write a function that models the height of the object and use it to calculate the height of the object after 1 second.
-
Given and , find
-
Given and , find
-
Given and , find
-
Given and , find
-
Given , find
-
Given , find
-
-
-
-
-
-
-
-
Algebra of Functions
Evaluate
Perform the operations.
Given , , and , find the following:
Factoring Polynomials
Factor out the greatest common factor (GCF).
Factor by grouping.
Factor the special binomials.
Factoring Trinomials
Factor.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
The height in feet of an object dropped from the top of a 16-foot ladder is given by , where t represents the time in seconds after the object has been dropped. How long will it take to hit the ground?
-
The length of a rectangle is 2 centimeters less than twice its width. If the area of the rectangle is 112 square centimeters, find its dimensions.
-
A triangle whose base is equal in measure to its height has an area of 72 square inches. Find the length of the base.
-
A box can be made by cutting out the corners and folding up the edges of a sheet of cardboard. A template for a rectangular cardboard box of height 2 inches is given.
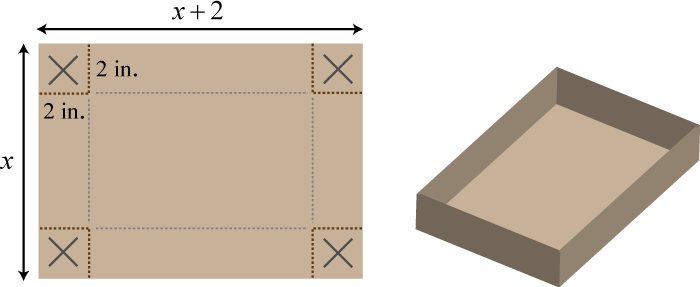
What are the dimensions of a cardboard sheet that will make a rectangular box with volume 240 cubic inches?
-
-
-
-
-
-
-
5, −2
-
-
-
±10
-
−4, 0, 3
-
−8 double root
Solve Polynomial Equations by Factoring
Factor completely.
Solve by factoring.
Find the roots of the given functions.
Solve or factor.
Find a polynomial equation with integer coefficients, given the solutions.
-
-
-
-
-
-
-
-
-
-
-
-
-
Given and , find
-
Given and , find
-
Given and , find
-
Given and , find
-
The daily cost in dollars of running a small business is given by where x represents the number of hours the business is in operation. Determine the average cost per hour if the business is in operation for 8 hours in a day.
-
An electric bicycle manufacturer has determined that the cost of producing its product in dollars is given by the function where n represents the number of electric bicycles produced in a day. Determine the average cost per bicycle if 10 and 20 are produced in a day.
-
Given , simplify
-
Given , simplify
Rational Functions: Multiplication and Division
State the restrictions and simplify.
Perform the operations and simplify. Assume all variable expressions in the denominator are nonzero.
Perform the operations and state the restrictions.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Given and , find
-
Given and , find
-
Given and , find
-
Given and , find
Rational Functions: Addition and Subtraction
State the restrictions and simplify.
Simplify. Assume that all variable expressions used as denominators are nonzero.
Perform the operations and state the restrictions.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Solve for a:
-
Solve for y:
-
A positive integer is 4 less than another. If the reciprocal of the larger integer is subtracted from twice the reciprocal of the smaller, the result is Find the two integers.
-
If 3 times the reciprocal of the larger of two consecutive odd integers is added to 7 times the reciprocal of the smaller, the result is Find the integers.
-
If the reciprocal of the smaller of two consecutive integers is subtracted from three times the reciprocal of the larger, the result is Find the integers.
-
A positive integer is twice that of another. The sum of the reciprocals of the two positive integers is Find the two integers.
Solving Rational Equations
Solve.
-
Manuel traveled 8 miles on the bus and another 84 miles on a train. If the train was 16 miles per hour faster than the bus, and the total trip took 2 hours, what was the average speed of the train?
-
A boat can average 10 miles per hour in still water. On a trip downriver, the boat was able to travel 7.5 miles with the current. On the return trip, the boat was only able to travel 4.5 miles in the same amount of time against the current. What was the speed of the current?
-
Susan can jog, on average, miles per hour faster than her husband Bill. Bill can jog 10 miles in the same amount of time it takes Susan to jog 13 miles. How fast, on average, can Susan jog?
-
In the morning, Raul drove 8 miles to visit his grandmother and then returned later that evening. Because of traffic, his average speed on the return trip was that of his average speed that morning. If the total driving time was of an hour, what was his average speed on the return trip?
-
One pipe can completely fill a water tank in 6 hours while another smaller pipe takes 8 hours to fill the same tank. How long will it take to fill the tank to capacity if both pipes are turned on?
-
It takes Bill 3 minutes longer than Jerry to fill an order. Working together they can fill 15 orders in 30 minutes. How long does it take Bill to fill an order by himself?
-
Manny takes twice as long as John to assemble a skateboard. If they work together, they can assemble a skateboard in 6 minutes. How long would it take Manny to assemble the skateboard without John’s help?
-
Working alone, Joe can complete the yard work in 30 minutes. It takes Mike 45 minutes to complete work on the same yard. How long would it take them working together?
-
y varies directly as x, where y = 30 when x = 5.
-
y varies inversely as x, where y = 3 when x = −2.
-
y is jointly proportional to x and z, where y = −50 when x = −2 and z = 5.
-
y is directly proportional to the square of x and inversely proportional to z, where y = −6 when x = 2 and z = −8.
-
The distance an object in free fall varies directly with the square of the time that it has been falling. It is observed that an object falls 36 feet in seconds. Find an equation that models the distance an object will fall, and use it to determine how far it will fall in seconds.
-
After the brakes are applied, the stopping distance d of an automobile varies directly with the square of the speed s of the car. If a car traveling 55 miles per hour takes 181.5 feet to stop, how many feet will it take to stop if it is moving 65 miles per hour?
-
The weight of an object varies inversely as the square of its distance from the center of the Earth. If an object weighs 180 lbs on the surface of the Earth (approximately 4,000 miles from the center), then how much will it weigh at 2,000 miles above the Earth’s surface?
-
The cost per person of renting a limousine varies inversely with the number of people renting it. If 5 people go in on the rental, the limousine will cost $112 per person. How much will the rental cost per person if 8 people go in on the rental?
-
To balance a seesaw, the distance from the fulcrum that a person must sit is inversely proportional to his weight. If a 52-pound boy is sitting 3 feet away from the fulcrum, then how far from the fulcrum must a 44-pound boy sit? Round to the nearest tenth of a foot.
Applications and Variation
Use algebra to solve the following applications.
Construct a mathematical model given the following:
Answers
-
; ;
-
-
; ;
-
-
a. 60 feet; b. 2 seconds; c. 4 seconds
-
-
; at 0.25 second, the bullet’s height is about 85 meters.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Prime
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Prime
-
-
, 0
-
-
2, 10
-
-
−1,
-
-
0, 3
-
-
-
-
−4, 0, 6
-
-
0,
-
-
±2
-
-
−9, 0, 6
-
-
1 second
-
-
12 inches
-
-
Factor;
-
-
Solve;
-
-
Factor;
-
-
-
-
-
-
-
-
;
-
-
;
-
-
;
-
-
;
-
-
-
-
-
-
;
-
-
;
-
-
$63.75 per hour
-
-
3
-
-
;
-
-
;
-
-
;
-
-
;
-
-
-
-
;
-
-
-
-
-
-
-
-
;
-
-
;
-
-
−9
-
-
−1, 4
-
-
−11, 0
-
-
Ø
-
-
−4
-
-
-
-
-
-
-
-
{8, 12}
-
-
{5, 6}
-
-
48 miles per hour
-
-
6.5 miles per hour
-
-
Approximately 2.6 hours
-
-
18 minutes
-
-
-
-
-
-
; 100 feet
-
-
80 lbs
-
-
Approximately 3.5 feet
Sample Exam
-
-
-
-
-
-
-
-
-
-
-
-
Find a quadratic equation with integer coefficients given the solutions
-
Given , simplify , where
-
-
-
-
-
-
Find the root of the function defined by
-
Solve for y:
-
The height of an object dropped from a 64-foot building is given by the function , where t represents time in seconds after it was dropped.
- Determine the height of the object at of a second.
- How long will it take the object to hit the ground?
-
One positive integer is 3 units more than another. When the reciprocal of the larger is subtracted from twice the reciprocal of the smaller, the result is Find the two positive integers.
-
A light airplane can average 126 miles per hour in still air. On a trip, the airplane traveled 222 miles with a tailwind. On the return trip, against a headwind of the same speed, the plane was only able to travel 156 miles in the same amount of time. What was the speed of the wind?
-
On the production line, it takes John 2 minutes less time than Mark to assemble a watch. Working together they can assemble 5 watches in 12 minutes. How long does it take John to assemble a watch working alone?
-
Write an equation that relates x and y, given that y varies inversely with the square of x, where when Use it to find y when
Given , , and , find the following:
Factor.
Solve.
Simplify and state the restrictions.
Assume all variable expressions in the denominator are nonzero and simplify.
Solve.
Use algebra to solve.
Answers
-
-
-
-
-
-
-
-
-
−4, 0
-
-
, 5
-
-
-
-
;
-
-
-
-
-
-
a. 55 feet; b. 2 seconds
-
-
22 miles per hour
-
-
;




