This is “Applications and Variation”, section 4.8 from the book Advanced Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
4.8 Applications and Variation
Learning Objectives
- Solve applications involving uniform motion (distance problems).
- Solve work-rate applications.
- Set up and solve applications involving direct, inverse, and joint variation.
Solving Uniform Motion Problems
Uniform motion (or distance)Described by the formula , where the distance D is given as the product of the average rate r and the time t traveled at that rate. problems involve the formula , where the distance D is given as the product of the average rate r and the time t traveled at that rate. If we divide both sides by the average rate r, then we obtain the formula
For this reason, when the unknown quantity is time, the algebraic setup for distance problems often results in a rational equation. We begin any uniform motion problem by first organizing our data with a chart. Use this information to set up an algebraic equation that models the application.
Example 1
Sally traveled 15 miles on the bus and then another 72 miles on a train. The train was 18 miles per hour faster than the bus, and the total trip took 2 hours. What was the average speed of the train?
Solution:
First, identify the unknown quantity and organize the data.
Let x represent the average speed (in miles per hour) of the bus.
Let represent the average speed of the train.

To avoid introducing two more variables for the time column, use the formula The time for each leg of the trip is calculated as follows:
Use these expressions to complete the chart.
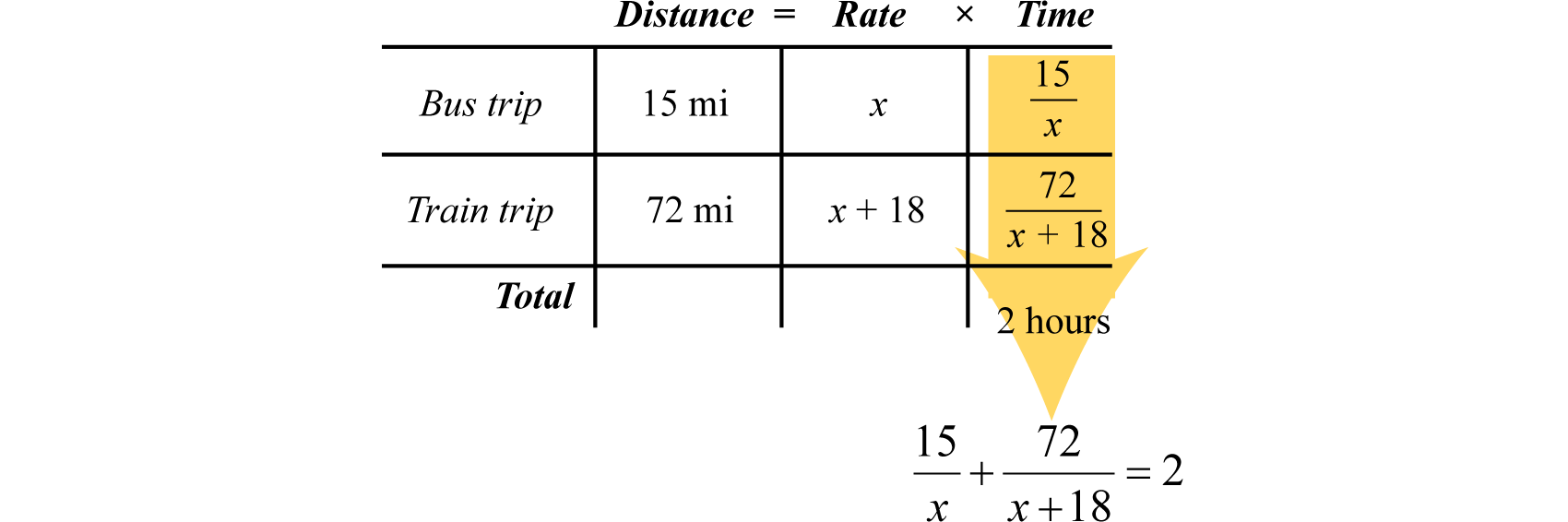
The algebraic setup is defined by the time column. Add the time spent on each leg of the trip to obtain a total of 2 hours:

We begin solving this equation by first multiplying both sides by the LCD,
Solve the resulting quadratic equation by factoring.
Since we are looking for an average speed we will disregard the negative answer and conclude the bus averaged 30 mph. Substitute in the expression identified as the speed of the train.
Answer: The speed of the train was 48 mph.
Example 2
A boat can average 12 miles per hour in still water. On a trip downriver the boat was able to travel 29 miles with the current. On the return trip the boat was only able to travel 19 miles in the same amount of time against the current. What was the speed of the current?
Solution:
First, identify the unknown quantities and organize the data.
Let c represent the speed of the river current.
Next, organize the given data in a chart. Traveling downstream, the current will increase the speed of the boat, so it adds to the average speed of the boat. Traveling upstream, the current slows the boat, so it will subtract from the average speed of the boat.
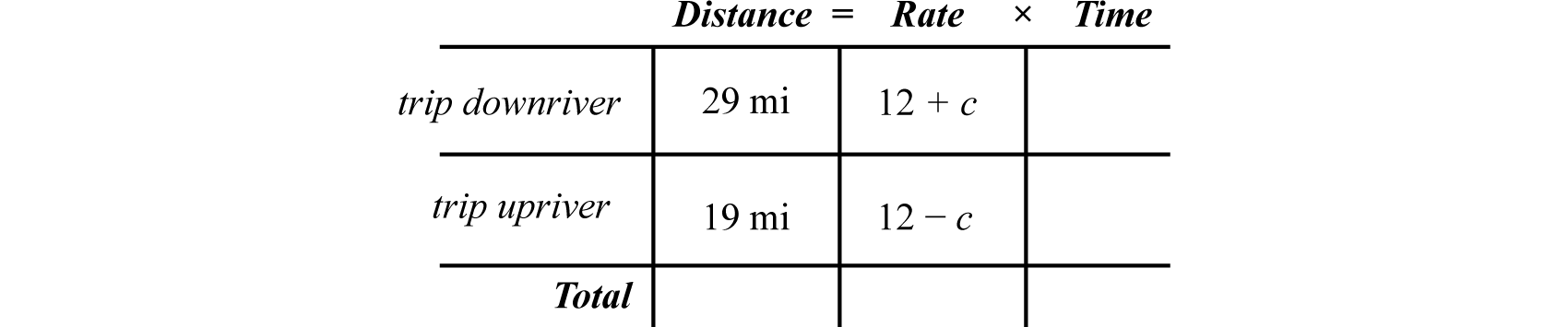
Use the formula to fill in the time column.

Because the boat traveled the same amount of time downriver as it did upriver, finish the algebraic setup by setting the expressions that represent the times equal to each other.
Since there is a single algebraic fraction on each side, we can solve this equation using cross multiplication.
Answer: The speed of the current was miles per hour.
Try this! A jet aircraft can average 160 miles per hour in calm air. On a trip, the aircraft traveled 600 miles with a tailwind and returned the 600 miles against a headwind of the same speed. If the total round trip took 8 hours, then what was the speed of the wind?
Answer: 40 miles per hour
Solving Work-Rate Problems
The rate at which a task can be performed is called a work rateThe rate at which a task can be performed.. For example, if a painter can paint a room in 6 hours, then the task is to paint the room, and we can write
In other words, the painter can complete of the task per hour. If he works for less than 6 hours, then he will perform a fraction of the task. If he works for more than 6 hours, then he can complete more than one task. For example,
Obtain the amount of the task completed by multiplying the work rate by the amount of time the painter works. Typically, work-rate problems involve people or machines working together to complete tasks. In general, if t represents the time two people work together, then we have the following work-rate formula, where and are the individual work rates and t is the time it takes to complete the task working together.:
Here and are the individual work rates.
Example 3
Joe can paint a typical room in 2 hours less time than Mark. If Joe and Mark can paint 5 rooms working together in a 12 hour shift, how long does it take each to paint a single room?
Solution:
Let x represent the time it takes Mark to paint a typical room.
Let x − 2 represent the time it takes Joe to paint a typical room.
Therefore, Mark’s individual work-rate is rooms per hour and Joe’s is rooms per hour. Both men worked for 12 hours. We can organize the data in a chart, just as we did with distance problems.

Working together, they can paint 5 total rooms in 12 hours. This leads us to the following algebraic setup:
Multiply both sides by the LCD,
Solve the resulting quadratic equation by factoring.
We can disregard because back substituting into x − 2 would yield a negative time to paint a room. Take x = 6 to be the only solution and use it to find the time it takes Joe to paint a typical room.
Answer: Joe can paint a typical room in 4 hours and Mark can paint a typical room in 6 hours. As a check we can multiply both work rates by 12 hours to see that together they can paint 5 rooms.
Example 4
It takes Bill twice as long to lay a tile floor by himself as it does Manny. After working together with Bill for 4 hours, Manny was able to complete the job in 2 additional hours. How long would it have taken Manny working alone?
Solution:
Let x represent the time it takes Manny to lay the floor alone.
Let 2x represent the time it takes Bill to lay the floor alone.
Manny’s work rate is of the floor per hour and Bill’s work rate is Bill worked on the job for 4 hours and Manny worked on the job for 6 hours.
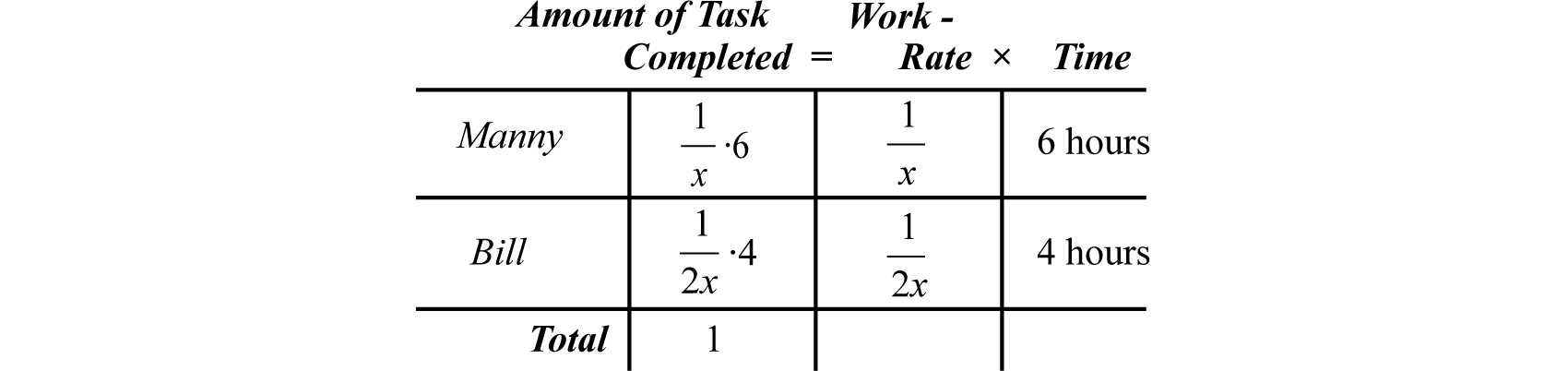
This leads us to the following algebraic setup:
Solve.
Answer: It would have taken Manny 8 hours to complete the floor by himself.
Consider the work-rate formula where one task is to be completed.
Factor out the time t and then divide both sides by t. This will result in equivalent specialized work-rate formulas:
In summary, we have the following equivalent work-rate formulas:
Try this! Matt can tile a countertop in 2 hours, and his assistant can do the same job in 3 hours. If Matt starts the job and his assistant joins him 1 hour later, then how long will it take to tile the countertop?
Answer: hours
Solving Problems involving Direct, Inverse, and Joint variation
Many real-world problems encountered in the sciences involve two types of functional relationships. The first type can be explored using the fact that the distance s in feet an object falls from rest, without regard to air resistance, can be approximated using the following formula:
Here t represents the time in seconds the object has been falling. For example, after 2 seconds the object will have fallen feet.
Time t in seconds |
Distance in feet |
|---|---|
0 |
0 |
1 |
16 |
2 |
64 |
3 |
144 |
4 |
256 |
In this example, we can see that the distance varies over time as the product of a constant 16 and the square of the time t. This relationship is described as direct variationDescribes two quantities x and y that are constant multiples of each other: and 16 is called the constant of variationThe nonzero multiple k, when quantities vary directly or inversely.. Furthermore, if we divide both sides of by we have
In this form, it is reasonable to say that s is proportional to t2, and 16 is called the constant of proportionalityUsed when referring to the constant of variation.. In general, we have
Key words |
Translation |
|---|---|
“y varies directly as x” |
|
“y is directly proportional to x” |
|
“y is proportional to x” |
Used when referring to direct variation.
Here k is nonzero and is called the constant of variation or the constant of proportionality. Typically, we will be given information from which we can determine this constant.
Example 5
An object’s weight on Earth varies directly to its weight on the Moon. If a man weighs 180 pounds on Earth, then he will weigh 30 pounds on the Moon. Set up an algebraic equation that expresses the weight on Earth in terms of the weight on the Moon and use it to determine the weight of a woman on the Moon if she weighs 120 pounds on Earth.
Solution:
Let y represent weight on Earth.
Let x represent weight on the Moon.
We are given that the “weight on Earth varies directly to the weight on the Moon.”
To find the constant of variation k, use the given information. A 180-lb man on Earth weighs 30 pounds on the Moon, or when
Solve for k.
Next, set up a formula that models the given information.
This implies that a person’s weight on Earth is 6 times his weight on the Moon. To answer the question, use the woman’s weight on Earth, y = 120 lbs, and solve for x.
Answer: The woman weighs 20 pounds on the Moon.
The second functional relationship can be explored using the formula that relates the intensity of light I to the distance from its source d.
Here k represents some constant. A foot-candle is a measurement of the intensity of light. One foot-candle is defined to be equal to the amount of illumination produced by a standard candle measured one foot away. For example, a 125-Watt fluorescent growing light is advertised to produce 525 foot-candles of illumination. This means that at a distance foot, foot-candles and we have:
Using we can construct a formula which gives the light intensity produced by the bulb:
Here d represents the distance the growing light is from the plants. In the following chart, we can see that the amount of illumination fades quickly as the distance from the plants increases.
distance t in feet |
Light Intensity
|
|---|---|
1 |
525 |
2 |
131.25 |
3 |
58.33 |
4 |
32.81 |
5 |
21 |
This type of relationship is described as an inverse variationDescribes two quantities x and y, where one variable is directly proportional to the reciprocal of the other: . We say that I is inversely proportionalUsed when referring to inverse variation. to the square of the distance d, where 525 is the constant of proportionality. In general, we have
Key words |
Translation |
|---|---|
“y varies inversely as x” |
|
“y is inversely proportional to x” |
Again, k is nonzero and is called the constant of variation or the constant of proportionality.
Example 6
The weight of an object varies inversely as the square of its distance from the center of Earth. If an object weighs 100 pounds on the surface of Earth (approximately 4,000 miles from the center), how much will it weigh at 1,000 miles above Earth’s surface?
Solution:
Let w represent the weight of the object.
Let d represent the object’s distance from the center of Earth.
Since “w varies inversely as the square of d,” we can write
Use the given information to find k. An object weighs 100 pounds on the surface of Earth, approximately 4,000 miles from the center. In other words, w = 100 when d = 4,000:
Solve for k.
Therefore, we can model the problem with the following formula:
To use the formula to find the weight, we need the distance from the center of Earth. Since the object is 1,000 miles above the surface, find the distance from the center of Earth by adding 4,000 miles:
To answer the question, use the formula with d = 5,000.
Answer: The object will weigh 64 pounds at a distance 1,000 miles above the surface of Earth.
Lastly, we define relationships between multiple variables, described as joint variationDescribes a quantity y that varies directly as the product of two other quantities x and z: . In general, we have
Key Words |
Translation |
|---|---|
“y varies jointly as x and z” |
|
“y is jointly proportional to x and z” |
Used when referring to joint variation.
Here k is nonzero and is called the constant of variation or the constant of proportionality.
Example 7
The area of an ellipse varies jointly as a, half of the ellipse’s major axis, and b, half of the ellipse’s minor axis as pictured. If the area of an ellipse is , where and , what is the constant of proportionality? Give a formula for the area of an ellipse.

Solution:
If we let A represent the area of an ellipse, then we can use the statement “area varies jointly as a and b” to write
To find the constant of variation k, use the fact that the area is when and
Therefore, the formula for the area of an ellipse is
Answer: The constant of proportionality is and the formula for the area of an ellipse is
Try this! Given that y varies directly as the square of x and inversely with z, where y = 2 when x = 3 and z = 27, find y when x = 2 and z = 16.
Answer:
Key Takeaways
- When solving distance problems where the time element is unknown, use the equivalent form of the uniform motion formula, , to avoid introducing more variables.
- When solving work-rate problems, multiply the individual work rate by the time to obtain the portion of the task completed. The sum of the portions of the task results in the total amount of work completed.
- The setup of variation problems usually requires multiple steps. First, identify the key words to set up an equation and then use the given information to find the constant of variation k. After determining the constant of variation, write a formula that models the problem. Once a formula is found, use it to answer the question.
Topic Exercises
-
Every morning Jim spends 1 hour exercising. He runs 2 miles and then he bikes 16 miles. If Jim can bike twice as fast as he can run, at what speed does he average on his bike?
-
Sally runs 3 times as fast as she walks. She ran for of a mile and then walked another miles. The total workout took hours. What was Sally’s average walking speed?
-
On a business trip, an executive traveled 720 miles by jet and then another 80 miles by helicopter. If the jet averaged 3 times the speed of the helicopter, and the total trip took 4 hours, what was the average speed of the jet?
-
A triathlete can run 3 times as fast as she can swim and bike 6 times as fast as she can swim. The race consists of a mile swim, 3 mile run, and a 12 mile bike race. If she can complete all of these events in hour, then how fast can she swim, run and bike?
-
On a road trip, Marty was able to drive an average 4 miles per hour faster than George. If Marty was able to drive 39 miles in the same amount of time George drove 36 miles, what was Marty’s average speed?
-
The bus is 8 miles per hour faster than the trolley. If the bus travels 9 miles in the same amount of time the trolley can travel 7 miles, what is the average speed of each?
-
Terry decided to jog the 5 miles to town. On the return trip, she walked the 5 miles home at half of the speed that she was able to jog. If the total trip took 3 hours, what was her average jogging speed?
-
James drove the 24 miles to town and back in 1 hour. On the return trip, he was able to average 20 miles per hour faster than he averaged on the trip to town. What was his average speed on the trip to town?
-
A light aircraft was able to travel 189 miles with a 14 mile per hour tailwind in the same time it was able to travel 147 miles against it. What was the speed of the aircraft in calm air?
-
A jet flew 875 miles with a 30 mile per hour tailwind. On the return trip, against a 30 mile per hour headwind, it was able to cover only 725 miles in the same amount of time. How fast was the jet in calm air?
-
A helicopter averaged 90 miles per hour in calm air. Flying with the wind it was able to travel 250 miles in the same amount of time it took to travel 200 miles against it. What is the speed of the wind?
-
Mary and Joe took a road-trip on separate motorcycles. Mary’s average speed was 12 miles per hour less than Joe’s average speed. If Mary drove 115 miles in the same time it took Joe to drive 145 miles, what was Mary’s average speed?
-
A boat averaged 12 miles per hour in still water. On a trip downstream, with the current, the boat was able to travel 26 miles. The boat then turned around and returned upstream 33 miles. How fast was the current if the total trip took 5 hours?
-
If the river current flows at an average 3 miles per hour, a tour boat can make an 18-mile tour downstream with the current and back the 18 miles against the current in hours. What is the average speed of the boat in still water?
-
Jose drove 10 miles to his grandmother’s house for dinner and back that same evening. Because of traffic, he averaged 20 miles per hour less on the return trip. If it took hour longer to get home, what was his average speed driving to his grandmother’s house?
-
Jerry paddled his kayak, upstream against a 1 mph current, for 12 miles. The return trip, downstream with the 1 mph current, took one hour less time. How fast did Jerry paddle the kayak in still water?
-
James and Mildred left the same location in separate cars and met in Los Angeles 300 miles away. James was able to average 10 miles an hour faster than Mildred on the trip. If James arrived 1 hour earlier than Mildred, what was Mildred’s average speed?
-
A bus is 20 miles per hour faster than a bicycle. If Bill boards a bus at the same time and place that Mary departs on her bicycle, Bill will arrive downtown 5 miles away hour earlier than Mary. What is the average speed of the bus?
Part A: Solving Uniform Motion Problems
Use algebra to solve the following applications.
-
Mike can paint the office by himself in hours. Jordan can paint the office in 6 hours. How long will it take them to paint the office working together?
-
Barry can lay a brick driveway by himself in days. Robert does the same job in 5 days. How long will it take them to lay the brick driveway working together?
-
A larger pipe fills a water tank twice as fast as a smaller pipe. When both pipes are used, they fill the tank in 10 hours. If the larger pipe is left off, how long would it take the smaller pipe to fill the tank?
-
A newer printer can print twice as fast as an older printer. If both printers working together can print a batch of flyers in 45 minutes, then how long would it take the older printer to print the batch working alone?
-
Mary can assemble a bicycle for display in 2 hours. It takes Jane 3 hours to assemble a bicycle. How long will it take Mary and Jane, working together, to assemble 5 bicycles?
-
Working alone, James takes twice as long to assemble a computer as it takes Bill. In one 8-hour shift, working together, James and Bill can assemble 6 computers. How long would it take James to assemble a computer if he were working alone?
-
Working alone, it takes Harry one hour longer than Mike to install a fountain. Together they can install 10 fountains in 12 hours. How long would it take Mike to install 10 fountains by himself?
-
Working alone, it takes Henry 2 hours longer than Bill to paint a room. Working together they painted rooms in 6 hours. How long would it have taken Henry to paint the same amount if he were working alone?
-
Manny, working alone, can install a custom cabinet in 3 hours less time than his assistant. Working together they can install the cabinet in 2 hours. How long would it take Manny to install the cabinet working alone?
-
Working alone, Garret can assemble a garden shed in 5 hours less time than his brother. Working together, they need 6 hours to build the garden shed. How long would it take Garret to build the shed working alone?
-
Working alone, the assistant-manager takes 2 more hours than the manager to record the inventory of the entire shop. After working together for 2 hours, it took the assistant-manager 1 additional hour to complete the inventory. How long would it have taken the manager to complete the inventory working alone?
-
An older printer can print a batch of sales brochures in 16 minutes. A newer printer can print the same batch in 10 minutes. After working together for some time, the newer printer was shut down and it took the older printer 3 more minutes to complete the job. How long was the newer printer operating?
Part B: Solving Work-Rate Problems
Use algebra to solve the following applications.
-
The distance D an automobile can travel is directly proportional to the time t that it travels at a constant speed.
-
The extension of a hanging spring d is directly proportional to the weight w attached to it.
-
An automobile’s braking distance d is directly proportional to the square of the automobile’s speed v.
-
The volume V of a sphere varies directly as the cube of its radius r.
-
The volume V of a given mass of gas is inversely proportional to the pressure p exerted on it.
-
Every particle of matter in the universe attracts every other particle with a force F that is directly proportional to the product of the masses and of the particles, and it is inversely proportional to the square of the distance d between them.
-
Simple interest I is jointly proportional to the annual interest rate r and the time t in years a fixed amount of money is invested.
-
The time t it takes an object to fall is directly proportional to the square root of the distance d it falls.
-
y varies directly as x, and y = 30 when x = 6.
-
y varies directly as x, and y = 52 when x = 4.
-
y is directly proportional to x, and y = 12 when x = 3.
-
y is directly proportional to x, and y = 120 when x = 20.
-
y is inversely proportional to x, and y = 3 when x = 9.
-
y is inversely proportional to x, and y = 21 when x = 3.
-
y varies inversely as x, and y = 2 when
-
y varies inversely as x, and when
-
y is jointly proportional to x and z, where y = 2 when x = 1 and z = 3.
-
y is jointly proportional to x and z, where y = 15 when x = 3 and z = 7.
-
y varies jointly as x and z, where when and z = 12.
-
y varies jointly as x and z, where y = 5 when and
-
y varies directly as the square of x, where y = 45 when x = 3.
-
y varies directly as the square of x, where y = 3 when
-
y is inversely proportional to the square of x, where y = 27 when
-
y is inversely proportional to the square of x, where y = 9 when
-
y varies jointly as x and the square of z, where y = 6 when and
-
y varies jointly as x and z and inversely as the square of w, where y = 5 when x = 1, z = 3, and
-
y varies directly as the square root of x and inversely as the square of z, where y = 15 when x = 25 and z = 2.
-
y varies directly as the square of x and inversely as z and the square of w, where y = 14 when x = 4, w = 2, and z = 2.
-
Revenue in dollars is directly proportional to the number of branded sweatshirts sold. The revenue earned from selling 25 sweatshirts is $318.75. Determine the revenue if 30 sweatshirts are sold.
-
The sales tax on the purchase of a new car varies directly as the price of the car. If an $18,000 new car is purchased, then the sales tax is $1,350. How much sales tax is charged if the new car is priced at $22,000?
-
The price of a share of common stock in a company is directly proportional to the earnings per share (EPS) of the previous 12 months. If the price of a share of common stock in a company is $22.55, and the EPS is published to be $1.10, determine the value of the stock if the EPS increases by $0.20.
-
The distance traveled on a road trip varies directly with the time spent on the road. If a 126-mile trip can be made in 3 hours, then what distance can be traveled in 4 hours?
-
The circumference of a circle is directly proportional to its radius. The circumference of a circle with radius 7 centimeters is measured as centimeters. What is the constant of proportionality?
-
The area of circle varies directly as the square of its radius. The area of a circle with radius 7 centimeters is determined to be square centimeters. What is the constant of proportionality?
-
The surface area of a sphere varies directly as the square of its radius. When the radius of a sphere measures 2 meters, the surface area measures square meters. Find the surface area of a sphere with radius 3 meters.
-
The volume of a sphere varies directly as the cube of its radius. When the radius of a sphere measures 3 meters, the volume is cubic meters. Find the volume of a sphere with radius 1 meter.
-
With a fixed height, the volume of a cone is directly proportional to the square of the radius at the base. When the radius at the base measures 10 centimeters, the volume is 200 cubic centimeters. Determine the volume of the cone if the radius of the base is halved.
-
The distance d an object in free fall drops varies directly with the square of the time t that it has been falling. If an object in free fall drops 36 feet in 1.5 seconds, then how far will it have fallen in 3 seconds?
-
A hanging spring is stretched 5 inches when a 20-pound weight is attached to it. Determine its spring constant.
-
A hanging spring is stretched 3 centimeters when a 2-kilogram weight is attached to it. Determine the spring constant.
-
If a hanging spring is stretched 3 inches when a 2-pound weight is attached, how far will it stretch with a 5-pound weight attached?
-
If a hanging spring is stretched 6 centimeters when a 4-kilogram weight is attached to it, how far will it stretch with a 2-kilogram weight attached?
-
It takes 36 feet to stop a particular automobile moving at a speed of 30 miles per hour. How much breaking distance is required if the speed is 35 miles per hour?
-
After an accident, it was determined that it took a driver 80 feet to stop his car. In an experiment under similar conditions, it takes 45 feet to stop the car moving at a speed of 30 miles per hour. Estimate how fast the driver was moving before the accident.
-
A balloon is filled to a volume of 216 cubic inches on a diving boat under 1 atmosphere of pressure. If the balloon is taken underwater approximately 33 feet, where the pressure measures 2 atmospheres, then what is the volume of the balloon?
-
A balloon is filled to 216 cubic inches under a pressure of 3 atmospheres at a depth of 66 feet. What would the volume be at the surface, where the pressure is 1 atmosphere?
-
To balance a seesaw, the distance from the fulcrum that a person must sit is inversely proportional to his weight. If a 72-pound boy is sitting 3 feet from the fulcrum, how far from the fulcrum must a 54-pound boy sit to balance the seesaw?
-
The current I in an electrical conductor is inversely proportional to its resistance R. If the current is ampere when the resistance is 100 ohms, what is the current when the resistance is 150 ohms?
-
The amount of illumination I is inversely proportional to the square of the distance d from a light source. If 70 foot-candles of illumination is measured 2 feet away from a lamp, what level of illumination might we expect foot away from the lamp?
-
The amount of illumination I is inversely proportional to the square of the distance d from a light source. If 40 foot-candles of illumination is measured 3 feet away from a lamp, at what distance can we expect 10 foot-candles of illumination?
-
The number of men, represented by y, needed to lay a cobblestone driveway is directly proportional to the area A of the driveway and inversely proportional to the amount of time t allowed to complete the job. Typically, 3 men can lay 1,200 square feet of cobblestone in 4 hours. How many men will be required to lay 2,400 square feet of cobblestone in 6 hours?
-
The volume of a right circular cylinder varies jointly as the square of its radius and its height. A right circular cylinder with a 3-centimeter radius and a height of 4 centimeters has a volume of cubic centimeters. Find a formula for the volume of a right circular cylinder in terms of its radius and height.
-
The period T of a pendulum is directly proportional to the square root of its length L. If the length of a pendulum is 1 meter, then the period is approximately 2 seconds. Approximate the period of a pendulum that is 0.5 meter in length.
-
The time t it takes an object to fall is directly proportional to the square root of the distance d it falls. An object dropped from 4 feet will take second to hit the ground. How long will it take an object dropped from 16 feet to hit the ground?
-
If two objects with masses 50 kilograms and 100 kilograms are meter apart, then they produce approximately newtons (N) of force. Calculate the gravitational constant.
-
Use the gravitational constant from the previous exercise to write a formula that approximates the force F in newtons between two masses and , expressed in kilograms, given the distance d between them in meters.
-
Calculate the force in newtons between Earth and the Moon, given that the mass of the Moon is approximately kilograms, the mass of Earth is approximately kilograms, and the distance between them is on average meters.
-
Calculate the force in newtons between Earth and the Sun, given that the mass of the Sun is approximately kilograms, the mass of Earth is approximately kilograms, and the distance between them is on average meters.
-
If y varies directly as the square of x, then how does y change if x is doubled?
-
If y varies inversely as square of t, then how does y change if t is doubled?
-
If y varies directly as the square of x and inversely as the square of t, then how does y change if both x and t are doubled?
Part C: Solving Variation Problems
Translate each of the following sentences into a mathematical formula.
Construct a mathematical model given the following:
Solve applications involving variation.
Hooke’s law suggests that the extension of a hanging spring is directly proportional to the weight attached to it. The constant of variation is called the spring constant.
Figure 4.1

Robert Hooke (1635—1703)
The braking distance of an automobile is directly proportional to the square of its speed.
Figure 4.2

Robert Boyle (1627—1691)
Boyle’s law states that if the temperature remains constant, the volume V of a given mass of gas is inversely proportional to the pressure p exerted on it.
Newton’s universal law of gravitation states that every particle of matter in the universe attracts every other particle with a force F that is directly proportional to the product of the masses and of the particles and inversely proportional to the square of the distance d between them. The constant of proportionality is called the gravitational constant.
Figure 4.3

Sir Isaac Newton (1643—1727)
Source: Portrait of Isaac Newton by Sir Godfrey Kneller, from http://commons.wikimedia.org/wiki/File:GodfreyKneller-IsaacNewton-1689.
http://commons.wikimedia.org/wiki/File:Frans_Hals_-_Portret_
_van_Ren%C3%A9_Descartes.jpg.
Answers
-
20 miles per hour
-
-
240 miles per hour
-
-
52 miles per hour
-
-
5 miles per hour
-
-
112 miles per hour
-
-
10 miles per hour
-
-
1 mile per hour
-
-
40 miles per hour
-
-
50 miles per hour
-
-
hours
-
-
30 hours
-
-
6 hours
-
-
20 hours
-
-
3 hours
-
-
4 hours
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
$382.50
-
-
$26.65
-
-
-
-
square meters
-
-
50 cubic centimeters
-
-
-
-
7.5 inches
-
-
49 feet
-
-
108 cubic inches
-
-
4 feet
-
-
1,120 foot-candles
-
-
4 men
-
-
1.4 seconds
-
-
-
-
-
-
y changes by a factor of 4
-
-
y remains unchanged




