This is “The Aggregate Production Function”, section 31.26 from the book Theory and Applications of Economics (v. 1.0). For details on it (including licensing), click here.

For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.

Has this book helped you? Consider passing it on:
Help Creative Commons
Creative Commons supports free culture from music to education. Their licenses helped make this book available to you.
Help a Public School
DonorsChoose.org helps people like you help teachers fund their classroom projects, from art supplies to books to calculators.

31.26 The Aggregate Production Function

The aggregate production function describes how total real gross domestic product (real GDP) in an economy depends on available inputs. Aggregate output (real GDP) depends on the following:

  • Physical capital—machines, production facilities, and so forth that are used in production
  • Labor—the number of hours that are worked in the entire economy
  • Human capital—skills and education embodied in the workforce of the economy
  • Knowledge—basic scientific knowledge, and blueprints that describe the available production processes
  • Social infrastructure—the general business, legal and cultural environment
  • The amount of natural resources available in an economy
  • Anything else that we have not yet included

We group the inputs other than labor, physical, and human capital together, and call them technology.

The aggregate production function has several key properties. First, output increases when there are increases in physical capital, labor, and natural resources. In other words, the marginal products of these inputs are all positive.

Second, the increase in output from adding more inputs is lower when we have more of a factor. This is called diminishing marginal product. That is,

  • The more capital we have, the less additional output we obtain from additional capital.
  • The more labor we have, the less additional output we obtain from additional labor.
  • The more natural resources we have, the less additional output we obtain from additional resources.

In addition, increases in output can also come from increases in human capital, knowledge, and social infrastructure. In contrast to capital and labor, we do not assume that there are diminishing returns to human capital and technology. One reason is that we do not have a natural or an obvious measure for human capital, knowledge, or social infrastructure, whereas we do for labor and capital (hours of work and hours of capital usage).

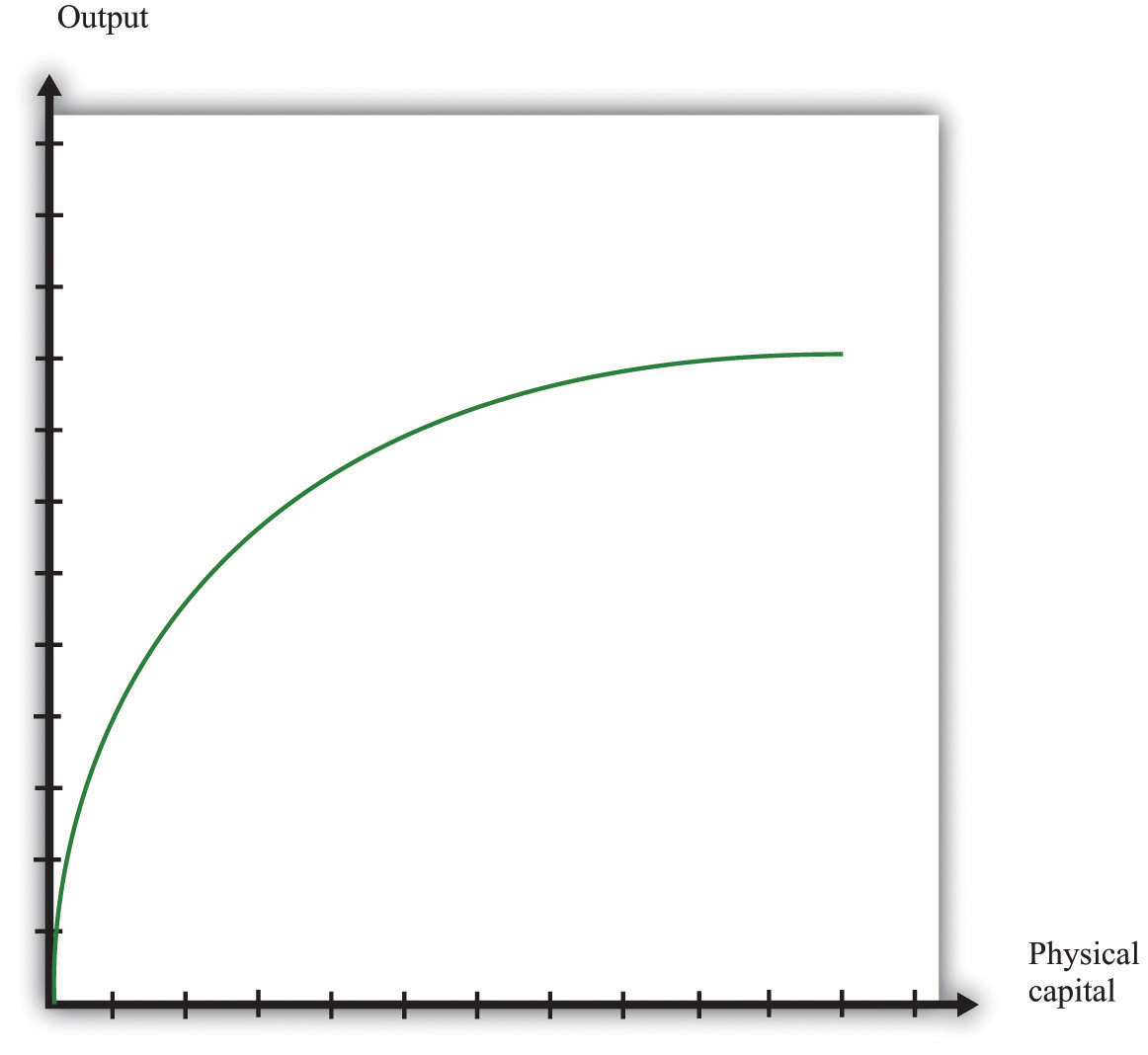
Figure 31.19 shows the relationship between output and capital, holding fixed the level of other inputs. This figure shows two properties of the aggregate production function. As capital input is increased, output increases as well. But the change in output obtained by increasing the capital stock is lower when the capital stock is higher: this is the diminishing marginal product of capital.

Figure 31.19

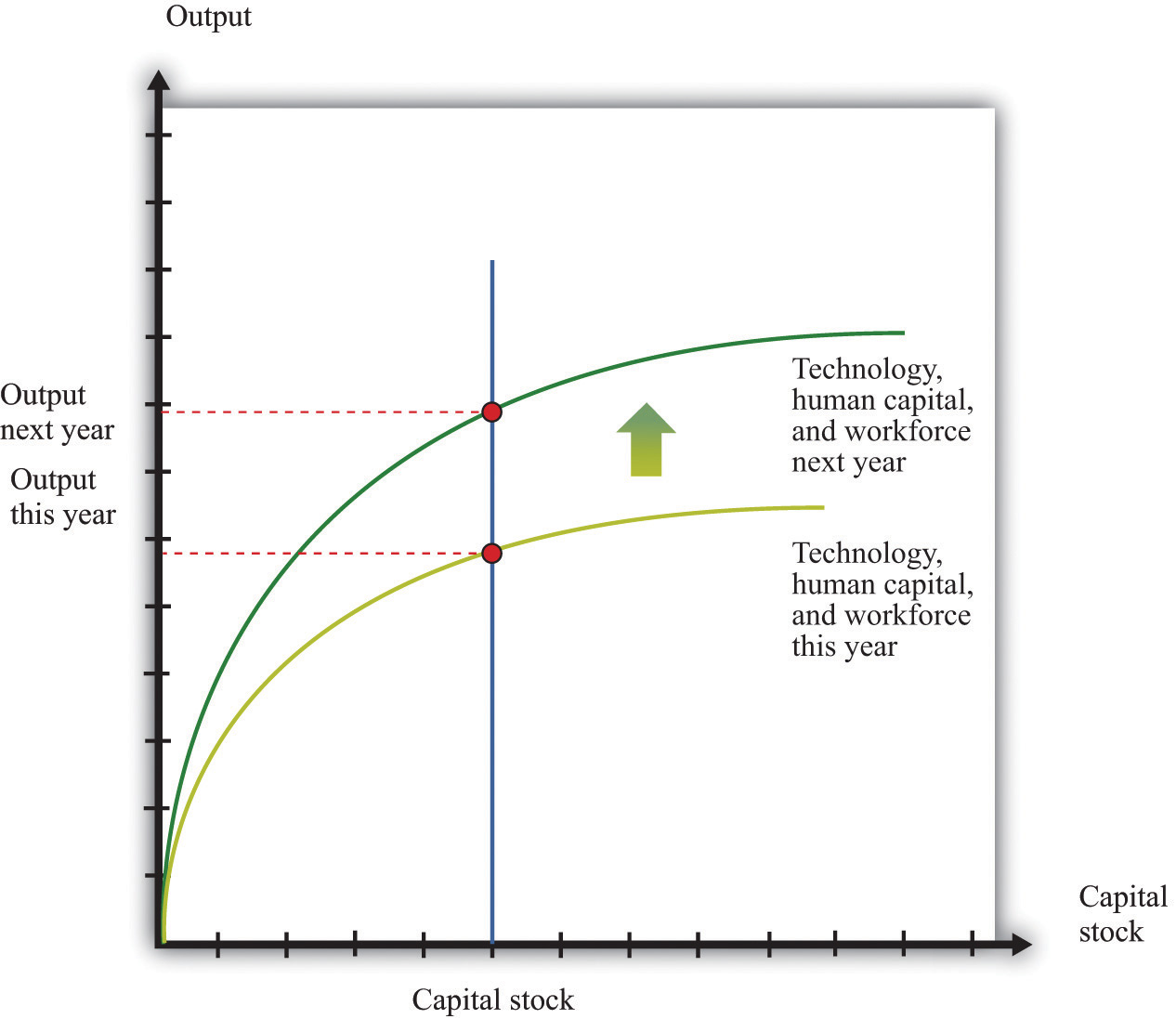
In many applications, we want to understand how the aggregate production function responds to variations in the technology or other inputs. This is illustrated in Figure 31.20. An increase in, say, technology means that for a given level of the capital stock, more output is produced: the production function shifts upward as technology increases. Further, as technology increases, the production function is steeper: the increase in technology increases the marginal product of capital.

Figure 31.20

Key Insight

  • The aggregate production function allows us to determine the output of an economy given inputs of capital, labor, human capital, and technology.

More Formally

Specific Forms for the Production Function

We can write the production function in mathematical form. We use Y to represent real GDP, K to represent the physical capital stock, L to represent labor, H to represent human capital, and A to represent technology (including natural resources). If we want to speak about production completely generally, then we can write Y = F(K,L,H,A). Here F() means “some function of.”

A lot of the time, economists work with a production function that has a specific mathematical form, yet is still reasonably simple:

Y = A × Ka × (L × H)(1 − a),

where a is just a number. This is called a Cobb-Douglas production function. It turns out that this production function does a remarkably good job of summarizing aggregate production in the economy. In fact, we also know that we can describe production in actual economies quite well if we suppose that a = 1/3.