This is “Superconductors”, section 12.7 from the book Principles of General Chemistry (v. 1.0M). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
12.7 Superconductors
Learning Objective
- To become familiar with the properties of superconductors.
The phenomenon of superconductivity was discovered by the Danish physicist H. Kamerlingh Onnes (1853–1926; Nobel Prize in Physics, 1913), who found a way to liquefy helium, which boils at 4.2 K and 1 atm pressure. To exploit the very low temperatures made possible by this new cryogenic fluid, he began a systematic study of the properties of metals, especially their electrical properties. Because the electrical resistance of a sample is technically easier to measure than its conductivity, Onnes measured the resistivity of his samples. The resistivity and conductivity of a material are inversely proportional:
Equation 12.2
In 1911, Onnes discovered that at about 4 K, the resistivity of metallic mercury (melting point = 234 K) decreased suddenly to essentially zero, rather than continuing to decrease only slowly with decreasing temperature as expected (Figure 12.28 "The Temperature Dependence of the Electrical Resistivity of a Normal Metal and a Superconductor"). He called this phenomenon superconductivityThe phenomenon in which a solid at low temperatures exhibits zero resistance to the flow of electrical current. because a resistivity of zero means that an electrical current can flow forever. Onnes soon discovered that many other metallic elements exhibit superconductivity at very low temperatures. Each of these superconductorsA solid that at low temperatures exhibits zero resistance to the flow of electrical current. has a characteristic superconducting transition temperature (Tc)The temperature at which the electrical resistance of a material drops to zero. at which its resistivity drops to zero. At temperatures less than their Tc, superconductors also completely expel a magnetic field from their interior (part (a) in Figure 12.29 "The Meissner Effect"). This phenomenon is called the Meissner effectThe phenomenon in which a superconductor completely expels a magnetic field from its interior. after one of its discoverers, the German physicist Walther Meissner, who described the phenomenon in 1933. Due to the Meissner effect, a superconductor will actually “float” over a magnet, as shown in part (b) in Figure 12.29 "The Meissner Effect".
Figure 12.28 The Temperature Dependence of the Electrical Resistivity of a Normal Metal and a Superconductor

The superconducting transition temperature (Tc) is the temperature at which the resistivity of a superconductor drops to zero.
Figure 12.29 The Meissner Effect

(a) Below its Tc, a superconductor completely expels magnetic lines of force from its interior. (b) In magnetic levitation, a small magnet “floats” over a disk of a high-temperature superconducting material (YBa2Cu3O7−x) cooled in liquid nitrogen.
BCS Theory
For many years, the phenomenon of superconductivity could not be satisfactorily explained by the laws of conventional physics. In the early 1950s, however, American physicists John Bardeen, Leon Cooper, and John Schrieffer formulated a theory for superconductivity that earned them the Nobel Prize in Physics in 1972. According to the BCS theoryA theory used to explain the phenomenon of superconductivity. (named for the initials of their last names), electrons are able to travel through a solid with zero resistance because of attractive interactions involving two electrons that are at some distance from each other. As one electron moves through the lattice, the surrounding nuclei are attracted to it. The motion of the nuclei can create a transient (short-lived) hole that pulls the second electron in the same direction as the first. The nuclei then return to their original positions to avoid colliding with the second electron as it approaches. The pairs of electrons, called Cooper pairsPairs of electrons that migrate through a superconducting material as a unit., migrate through the crystal as a unit. The electrons in Cooper pairs change partners frequently, like dancers in a ballet.
According to the BCS theory, as the temperature of the solid increases, the vibrations of the atoms in the lattice increase continuously, until eventually the electrons cannot avoid colliding with them. The collisions result in the loss of superconductivity at higher temperatures.
The phenomenon of superconductivity suggested many exciting technological applications. For example, using superconducting wires in power cables would result in zero power losses, even over distances of hundreds of miles. Additionally, because superconductors expel magnetic fields, a combination of magnetic rails and superconducting wheels (or vice versa) could be used to produce magnetic levitation of, for example, a train over the track, resulting in friction-free transportation.
Unfortunately, for many years the only superconductors known had serious limitations, especially the need for very low temperatures, which required the use of expensive cryogenic fluids such as liquid He. In addition, the superconducting properties of many substances are destroyed by large electrical currents or even moderately large magnetic fields, making them useless for applications in power cables or high-field magnets. The ability of materials such as NbTi, NbSn, Nb3Si, and Nb3Ge to tolerate rather high magnetic fields, however, has led to a number of commercial applications of superconductors, including high-field magnets for nuclear magnetic resonance (NMR) spectrometers and magnetic resonance imaging (MRI) instruments in medicine, which, unlike x-rays, can detect small changes in soft tissues in the body.
High-Temperature Superconductors
Because of these limitations, scientists continued to search for materials that exhibited superconductivity at temperatures greater than 77 K (the temperature of liquid nitrogen, the least expensive cryogenic fluid). In 1986, Johannes G. Bednorz and Karl A. Müller, working for IBM in Zurich, showed that certain mixed-metal oxides containing La, Ba, and Cu exhibited superconductivity above 30 K. These compounds had been prepared by French workers as potential solid catalysts some years earlier, but their electrical properties had never been examined at low temperatures. Although initially the scientific community was extremely skeptical, the compounds were so easy to prepare that the results were confirmed within a few weeks. These high-temperature superconductorsA material that becomes a superconductor at temperatures greater than 30 K. earned Bednorz and Müller the Nobel Prize in Physics in 1987. Subsequent research has produced new compounds with related structures that are superconducting at temperatures as high as 135 K. The best known of these was discovered by Paul Chu and Maw-Kuen Wu Jr. and is called the “Chu–Wu phase” or the 1-2-3 superconductor.
The formula for the 1-2-3 superconductor is YBa2Cu3O7−x, where x is about 0.1 for samples that superconduct at about 95 K. If x ≈ 1.0, giving a formula of YBa2Cu3O6, the material is an electrical insulator. The superconducting phase is thus a nonstoichiometric compound, with a fixed ratio of metal atoms but a variable oxygen content. The overall equation for the synthesis of this material is as follows:
Equation 12.3
If we assume that the superconducting phase is really stoichiometric YBa2Cu3O7, then the average oxidation states of O, Y, Ba, and Cu are −2, +3, +2, and respectively. The simplest way to view the average oxidation state of Cu is to assume that two Cu atoms per formula unit are present as Cu2+ and one is present as the rather unusual Cu3+. In YBa2Cu3O6, the insulating form, the oxidation state of Cu is so there are two Cu2+ and one Cu+ per formula unit.
As shown in Figure 12.30 "The Relationship of the Structure of a Superconductor Consisting of Y-Ba-Cu-O to a Simple Perovskite Structure", the unit cell of the 1-2-3 superconductor is related to the unit cell of the simple perovskite structure (part (b) in Figure 12.12 "The Perovskite Structure of CaTiO"). The only difference between the superconducting and insulating forms of the compound is that an O atom has been removed from between the Cu3+ ions, which destroys the chains of Cu atoms and leaves the Cu in the center of the unit cell as Cu+. The chains of Cu atoms are crucial to the formation of the superconducting state.
Figure 12.30 The Relationship of the Structure of a Superconductor Consisting of Y-Ba-Cu-O to a Simple Perovskite Structure
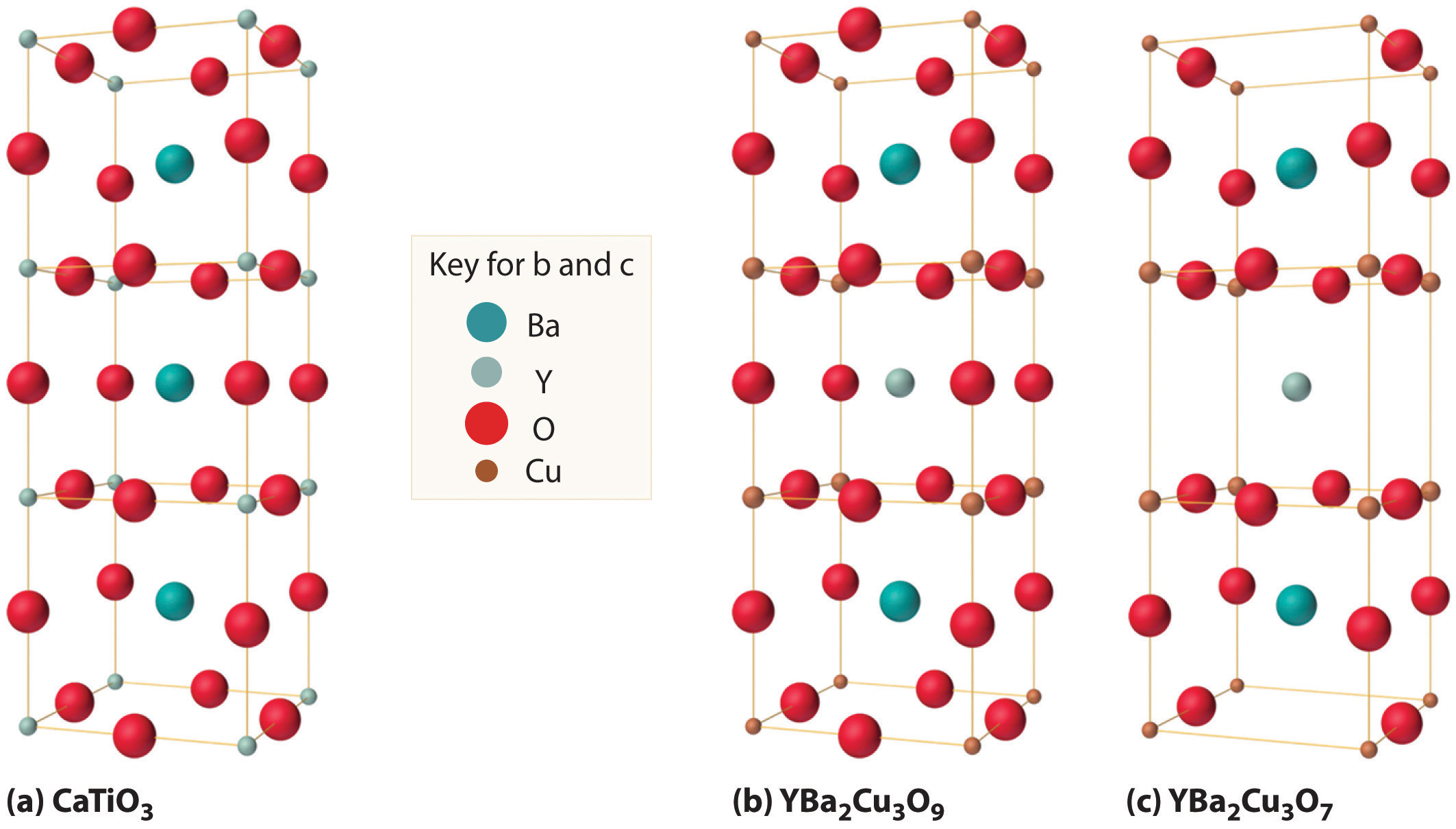
(a) Stacking three unit cells of the Ca-centered CaTiO3 perovskite structure (part (b) in Figure 12.12 "The Perovskite Structure of CaTiO") together with (b) replacement of all Ti atoms by Cu, replacement of Ca in the top and bottom cubes by Ba, and replacement of Ca in the central cube by Y gives a YBa2Cu3O9 stoichiometry. (c) The removal of two oxygen atoms per unit cell gives the nominal YBa2Cu3O7 stoichiometry of the superconducting material.
Table 12.7 "The Composition of Various Superconductors" lists the ideal compositions of some of the known high-temperature superconductors that have been discovered in recent years. Engineers have learned how to process the brittle polycrystalline 1-2-3 and related compounds into wires, tapes, and films that can carry enormous electrical currents. Commercial applications include their use in infrared sensors and in analog signal processing and microwave devices.
Table 12.7 The Composition of Various Superconductors
| Compound | Tc (K) |
|---|---|
| Ba(Pb1−xBix)O3 | 13.5 |
| (La2−xSrx)CuO4 | 35 |
| YBa2Cu3O7−x | 95 |
| Bi2(Sr2−xCax)CuO6* | 80 |
| Bi2Ca2Sr2Cu3O10* | 110 |
| Tl2Ba2Ca2Cu3O10* | 125 |
| HgBa2Ca2Cu3O8* | 133 |
| K3C60 | 18 |
| Rb3C60 | 30 |
| *Nominal compositions only. Oxygen deficiencies or excesses are common in these compounds. | |
Example 9
Calculate the average oxidation state of Cu in a sample of YBa2Cu3O7−x with x = 0.5. How do you expect its structure to differ from those shown in Figure 12.30 "The Relationship of the Structure of a Superconductor Consisting of Y-Ba-Cu-O to a Simple Perovskite Structure" for YBa2Cu3O9 and YBa2Cu3O7?
Given: stoichiometry
Asked for: average oxidation state and structure
Strategy:
A Based on the oxidation states of the other component atoms, calculate the average oxidation state of Cu that would make an electrically neutral compound.
B Compare the stoichiometry of the structures shown in Figure 12.30 "The Relationship of the Structure of a Superconductor Consisting of Y-Ba-Cu-O to a Simple Perovskite Structure" with the stoichiometry of the given compound to predict how the structures differ.
Solution:
A The net negative charge from oxygen is (7.0 − 0.5) (−2) = −13, and the sum of the charges on the Y and Ba atoms is [1 × (+3)] + [2 × (+2)] = +7. This leaves a net charge of −6 per unit cell, which must be compensated for by the three Cu atoms, for a net charge of per Cu.
B The most likely structure would be one in which every other O atom between the Cu atoms in the Cu chains of YBa2Cu3O7 has been removed.
Exercise
Calculate the average oxidation state of Cu in a sample of HgBa2Ca2Cu3O8. Assume that Hg is present as Hg2+.
Answer: +2
Summary
Superconductors are solids that at low temperatures exhibit zero resistance to the flow of electrical current, a phenomenon known as superconductivity. The temperature at which the electrical resistance of a substance drops to zero is its superconducting transition temperature (Tc). Superconductors also expel a magnetic field from their interior, a phenomenon known as the Meissner effect. Superconductivity can be explained by the BCS theory, which says that electrons are able to travel through a solid with no resistance because they couple to form pairs of electrons (Cooper pairs). High-temperature superconductors have Tc values greater than 30 K.
Key Takeaway
- Superconductivity can be described using the BCS theory, in which Cooper pairs of electrons migrate through the crystal as a unit.
Conceptual Problems
-
Why does the BCS theory predict that superconductivity is not possible at temperatures above approximately 30 K?
-
How does the formation of Cooper pairs lead to superconductivity?
Answer
-
According to BCS theory, the interactions that lead to formation of Cooper pairs of electrons are so weak that they should be disrupted by thermal vibrations of lattice atoms above about 30 K.
-




