This is “The Arrangement of Atoms in Crystalline Solids”, section 12.2 from the book Principles of General Chemistry (v. 1.0M). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
12.2 The Arrangement of Atoms in Crystalline Solids
Learning Objectives
- To recognize the unit cell of a crystalline solid.
- To calculate the density of a solid given its unit cell.
Because a crystalline solid consists of repeating patterns of its components in three dimensions (a crystal lattice), we can represent the entire crystal by drawing the structure of the smallest identical units that, when stacked together, form the crystal. This basic repeating unit is called a unit cellThe smallest repeating unit of a crystal lattice.. For example, the unit cell of a sheet of identical postage stamps is a single stamp, and the unit cell of a stack of bricks is a single brick. In this section, we describe the arrangements of atoms in various unit cells.
Unit cells are easiest to visualize in two dimensions. In many cases, more than one unit cell can be used to represent a given structure, as shown for the Escher drawing in the chapter opener and for a two-dimensional crystal lattice in Figure 12.2 "Unit Cells in Two Dimensions". Usually the smallest unit cell that completely describes the order is chosen. The only requirement for a valid unit cell is that repeating it in space must produce the regular lattice. Thus the unit cell in part (d) in Figure 12.2 "Unit Cells in Two Dimensions" is not a valid choice because repeating it in space does not produce the desired lattice (there are triangular holes). The concept of unit cells is extended to a three-dimensional lattice in the schematic drawing in Figure 12.3 "Unit Cells in Three Dimensions".
Figure 12.2 Unit Cells in Two Dimensions
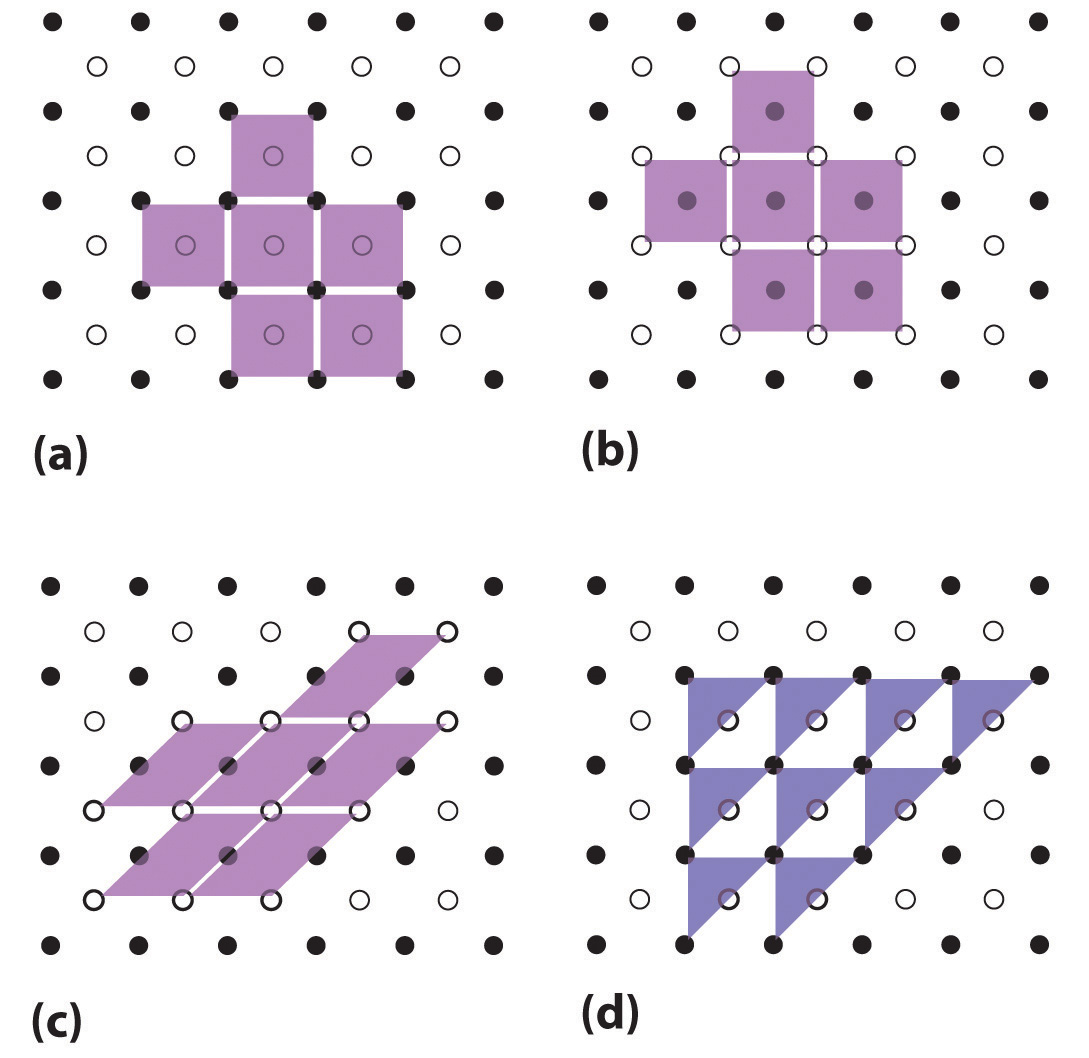
(a–c) Three two-dimensional lattices illustrate the possible choices of the unit cell. The unit cells differ in their relative locations or orientations within the lattice, but they are all valid choices because repeating them in any direction fills the overall pattern of dots. (d) The triangle is not a valid unit cell because repeating it in space fills only half of the space in the pattern.
Figure 12.3 Unit Cells in Three Dimensions
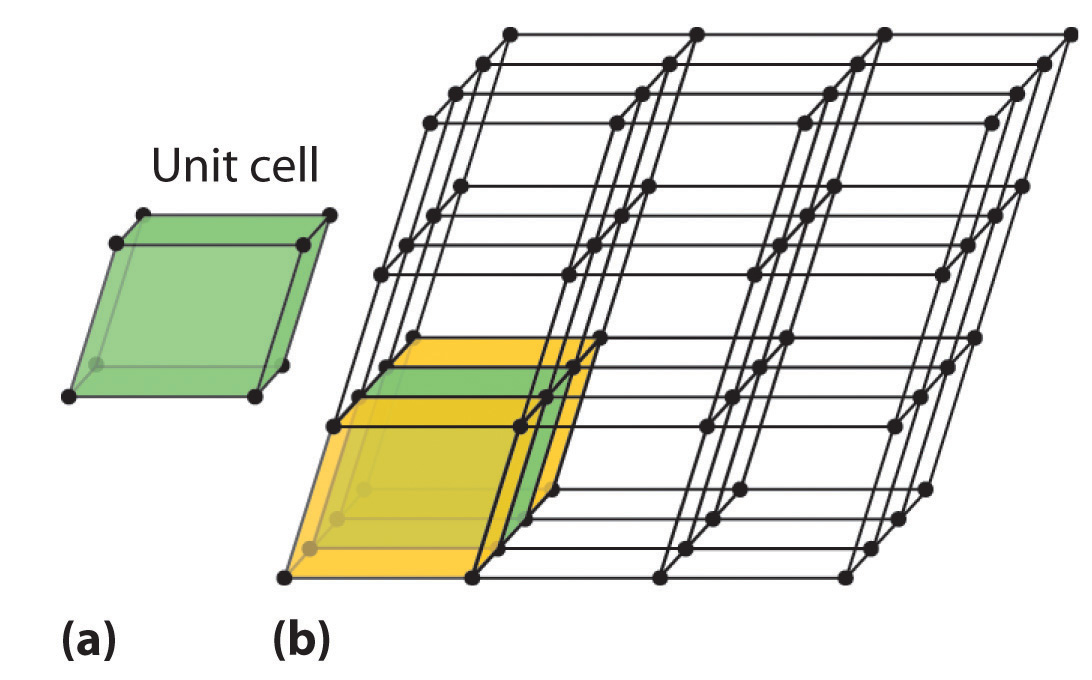
These images show (a) a three-dimensional unit cell and (b) the resulting regular three-dimensional lattice.
The Unit Cell
There are seven fundamentally different kinds of unit cells, which differ in the relative lengths of the edges and the angles between them (Figure 12.4 "The General Features of the Seven Basic Unit Cells"). Each unit cell has six sides, and each side is a parallelogram. We focus primarily on the cubic unit cells, in which all sides have the same length and all angles are 90°, but the concepts that we introduce also apply to substances whose unit cells are not cubic.
Figure 12.4 The General Features of the Seven Basic Unit Cells
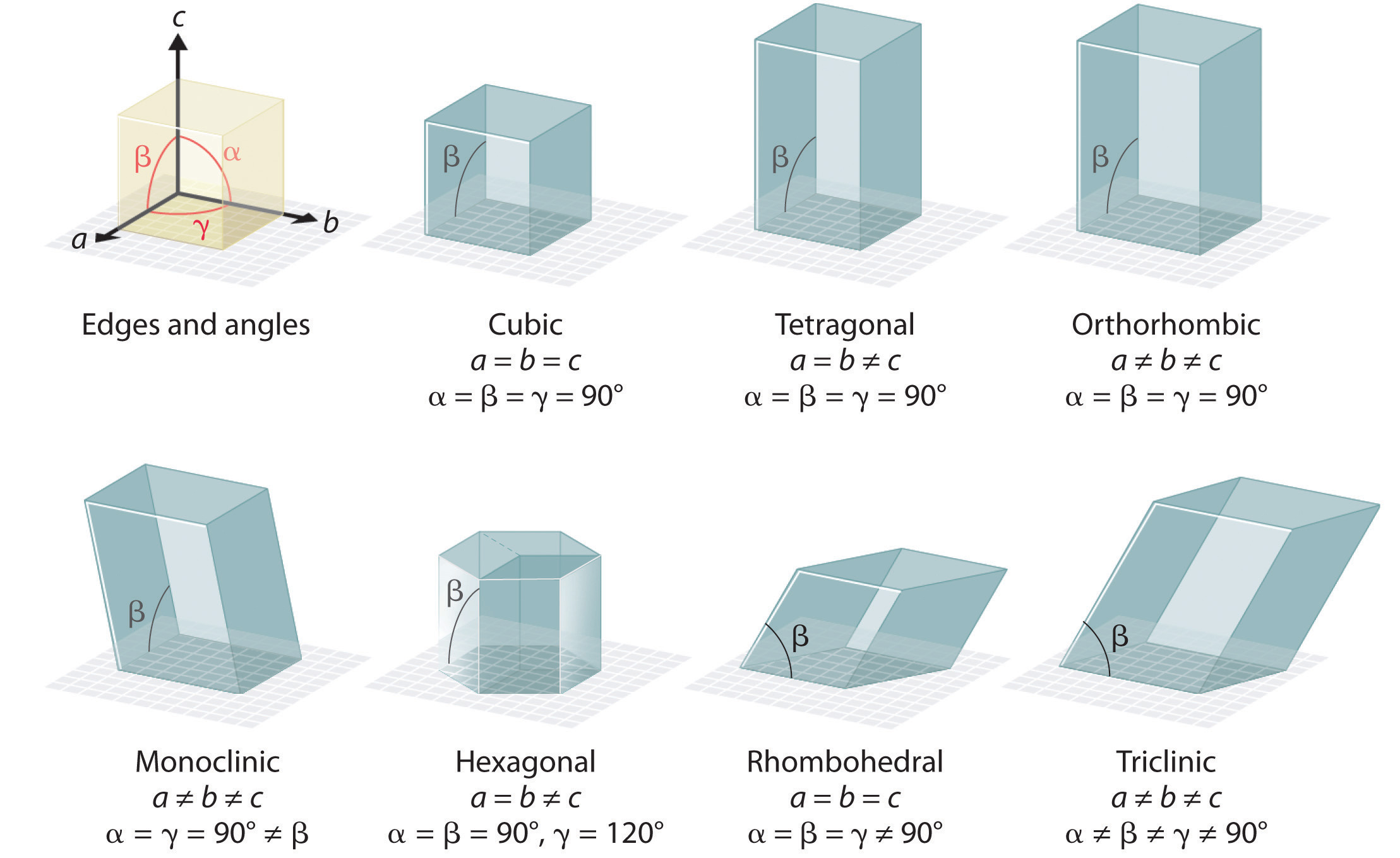
The lengths of the edges of the unit cells are indicated by a, b, and c, and the angles are defined as follows: α, the angle between b and c; β, the angle between a and c; and γ, the angle between a and b.
If the cubic unit cell consists of eight component atoms, molecules, or ions located at the corners of the cube, then it is called simple cubicA cubic unit cell that consists of eight component atoms, molecules, or ions located at the corners of a cube. (part (a) in Figure 12.5 "The Three Kinds of Cubic Unit Cell"). If the unit cell also contains an identical component in the center of the cube, then it is body-centered cubic (bcc)A cubic unit cell with eight component atoms, molecules, or ions located at the corners of a cube plus an identical component in the center of the cube. (part (b) in Figure 12.5 "The Three Kinds of Cubic Unit Cell"). If there are components in the center of each face in addition to those at the corners of the cube, then the unit cell is face-centered cubic (fcc)A cubic unit cell with eight component atoms, molecules, or ions located at the corners of a cube plus an identical component in the center of each face of the cube. (part (c) in Figure 12.5 "The Three Kinds of Cubic Unit Cell").
Figure 12.5 The Three Kinds of Cubic Unit Cell
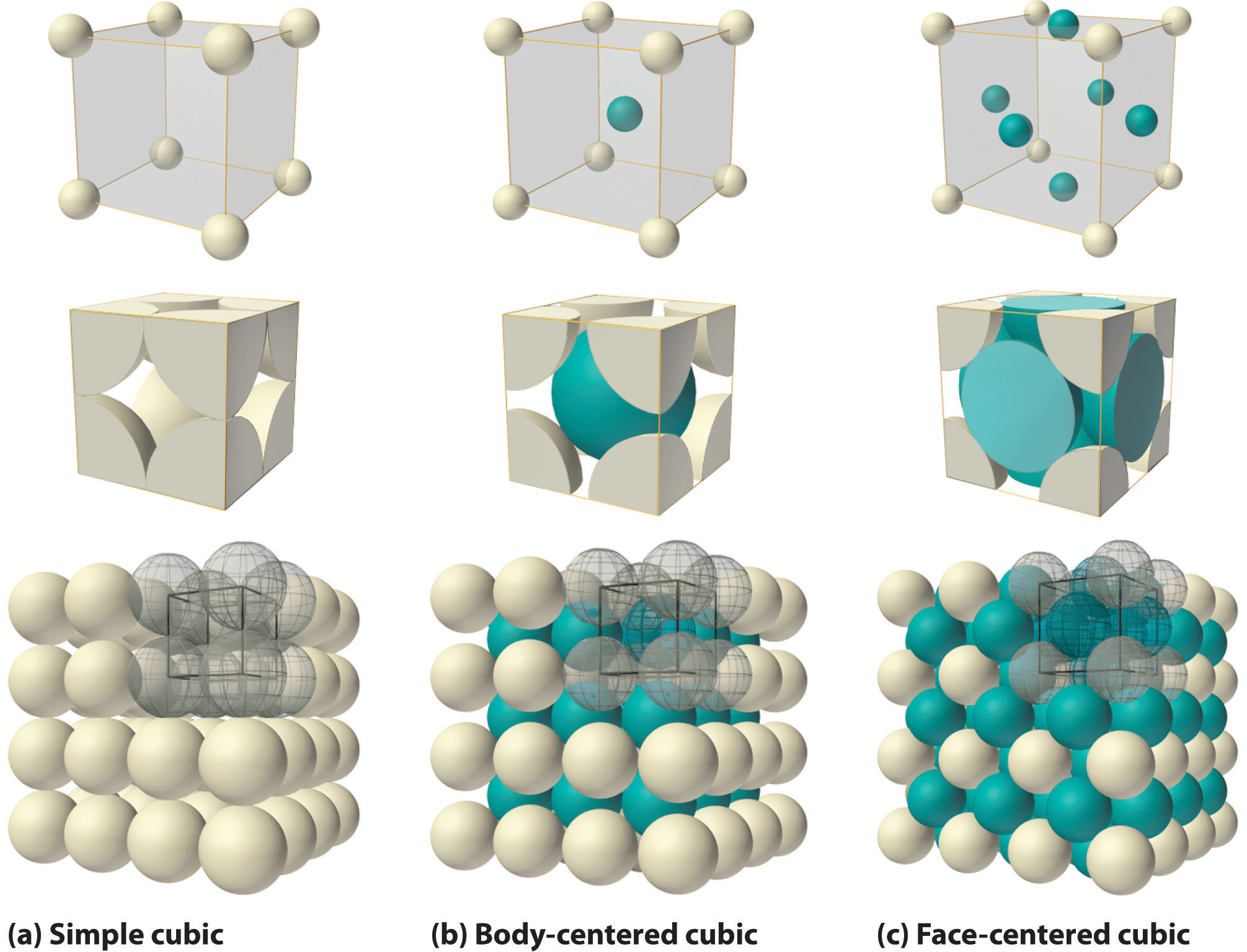
For the three kinds of cubic unit cells, simple cubic (a), body-centered cubic (b), and face-centered cubic (c), there are three representations for each: a ball-and-stick model, a space-filling cutaway model that shows the portion of each atom that lies within the unit cell, and an aggregate of several unit cells.
As indicated in Figure 12.5 "The Three Kinds of Cubic Unit Cell", a solid consists of a large number of unit cells arrayed in three dimensions. Any intensive property of the bulk material, such as its density, must therefore also be related to its unit cell. Because density is the mass of substance per unit volume, we can calculate the density of the bulk material from the density of a single unit cell. To do this, we need to know the size of the unit cell (to obtain its volume), the molar mass of its components, and the number of components per unit cell. When we count atoms or ions in a unit cell, however, those lying on a face, an edge, or a corner contribute to more than one unit cell, as shown in Figure 12.5 "The Three Kinds of Cubic Unit Cell". For example, an atom that lies on a face of a unit cell is shared by two adjacent unit cells and is therefore counted as atom per unit cell. Similarly, an atom that lies on the edge of a unit cell is shared by four adjacent unit cells, so it contributes atom to each. An atom at a corner of a unit cell is shared by all eight adjacent unit cells and therefore contributes atom to each.The statement that atoms lying on an edge or a corner of a unit cell count as or atom per unit cell, respectively, is true for all unit cells except the hexagonal one, in which three unit cells share each vertical edge and six share each corner (Figure 12.4 "The General Features of the Seven Basic Unit Cells"), leading to values of and atom per unit cell, respectively, for atoms in these positions. In contrast, atoms that lie entirely within a unit cell, such as the atom in the center of a body-centered cubic unit cell, belong to only that one unit cell.
Note the Pattern
For all unit cells except hexagonal, atoms on the faces contribute atom to each unit cell, atoms on the edges contribute atom to each unit cell, and atoms on the corners contribute atom to each unit cell.
Example 1
Metallic gold has a face-centered cubic unit cell (part (c) in Figure 12.5 "The Three Kinds of Cubic Unit Cell"). How many Au atoms are in each unit cell?
Given: unit cell
Asked for: number of atoms per unit cell
Strategy:
Using Figure 12.5 "The Three Kinds of Cubic Unit Cell", identify the positions of the Au atoms in a face-centered cubic unit cell and then determine how much each Au atom contributes to the unit cell. Add the contributions of all the Au atoms to obtain the total number of Au atoms in a unit cell.
Solution:
As shown in Figure 12.5 "The Three Kinds of Cubic Unit Cell", a face-centered cubic unit cell has eight atoms at the corners of the cube and six atoms on the faces. Because atoms on a face are shared by two unit cells, each counts as atom per unit cell, giving Au atoms per unit cell. Atoms on a corner are shared by eight unit cells and hence contribute only atom per unit cell, giving Au atom per unit cell. The total number of Au atoms in each unit cell is thus 3 + 1 = 4.
Exercise
Metallic iron has a body-centered cubic unit cell (part (b) in Figure 12.5 "The Three Kinds of Cubic Unit Cell"). How many Fe atoms are in each unit cell?
Answer: two
Now that we know how to count atoms in unit cells, we can use unit cells to calculate the densities of simple compounds. Note, however, that we are assuming a solid consists of a perfect regular array of unit cells, whereas real substances contain impurities and defects that affect many of their bulk properties, including density. Consequently, the results of our calculations will be close but not necessarily identical to the experimentally obtained values.
Example 2
Calculate the density of metallic iron, which has a body-centered cubic unit cell (part (b) in Figure 12.5 "The Three Kinds of Cubic Unit Cell") with an edge length of 286.6 pm.
Given: unit cell and edge length
Asked for: density
Strategy:
A Determine the number of iron atoms per unit cell.
B Calculate the mass of iron atoms in the unit cell from the molar mass and Avogadro’s number. Then divide the mass by the volume of the cell.
Solution:
A We know from Example 1 that each unit cell of metallic iron contains two Fe atoms.
B The molar mass of iron is 55.85 g/mol. Because density is mass per unit volume, we need to calculate the mass of the iron atoms in the unit cell from the molar mass and Avogadro’s number and then divide the mass by the volume of the cell (making sure to use suitable units to get density in g/cm3):
This result compares well with the tabulated experimental value of 7.874 g/cm3.
Exercise
Calculate the density of gold, which has a face-centered cubic unit cell (part (c) in Figure 12.5 "The Three Kinds of Cubic Unit Cell") with an edge length of 407.8 pm.
Answer: 19.29 g/cm3
Packing of Spheres
Our discussion of the three-dimensional structures of solids has considered only substances in which all the components are identical. As we shall see, such substances can be viewed as consisting of identical spheres packed together in space; the way the components are packed together produces the different unit cells. Most of the substances with structures of this type are metals.
Simple Cubic Structure
The arrangement of the atoms in a solid that has a simple cubic unit cell was shown in part (a) in Figure 12.5 "The Three Kinds of Cubic Unit Cell". Each atom in the lattice has only six nearest neighbors in an octahedral arrangement. Consequently, the simple cubic lattice is an inefficient way to pack atoms together in space: only 52% of the total space is filled by the atoms. The only element that crystallizes in a simple cubic unit cell is polonium. Simple cubic unit cells are, however, common among binary ionic compounds, where each cation is surrounded by six anions and vice versa.
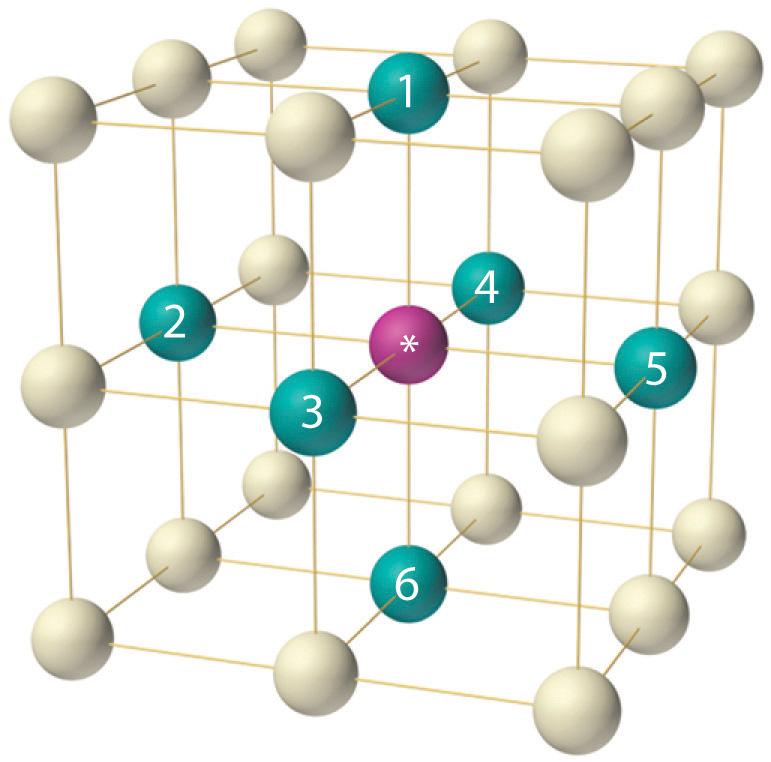
The arrangement of atoms in a simple cubic unit cell. Each atom in the lattice has six nearest neighbors in an octahedral arrangement.
Body-Centered Cubic Structure
The body-centered cubic unit cell is a more efficient way to pack spheres together and is much more common among pure elements. Each atom has eight nearest neighbors in the unit cell, and 68% of the volume is occupied by the atoms. As shown in part (b) in Figure 12.5 "The Three Kinds of Cubic Unit Cell", the body-centered cubic structure consists of a single layer of spheres in contact with each other and aligned so that their centers are at the corners of a square; a second layer of spheres occupies the square-shaped “holes” above the spheres in the first layer. The third layer of spheres occupies the square holes formed by the second layer, so that each lies directly above a sphere in the first layer, and so forth. All the alkali metals, barium, radium, and several of the transition metals have body-centered cubic structures.
Hexagonal Close-Packed and Cubic Close-Packed Structures
The most efficient way to pack spheres is the close-packed arrangement, which has two variants. A single layer of close-packed spheres is shown in part (a) in Figure 12.6 "Close-Packed Layers of Spheres". Each sphere is surrounded by six others in the same plane to produce a hexagonal arrangement. Above any set of seven spheres are six depressions arranged in a hexagon. In principle, all six sites are the same, and any one of them could be occupied by an atom in the next layer. Actually, however, these six sites can be divided into two sets, labeled B and C in part (a) in Figure 12.6 "Close-Packed Layers of Spheres". Sites B and C differ because as soon as we place a sphere at a B position, we can no longer place a sphere in any of the three C positions adjacent to A and vice versa.
Figure 12.6 Close-Packed Layers of Spheres
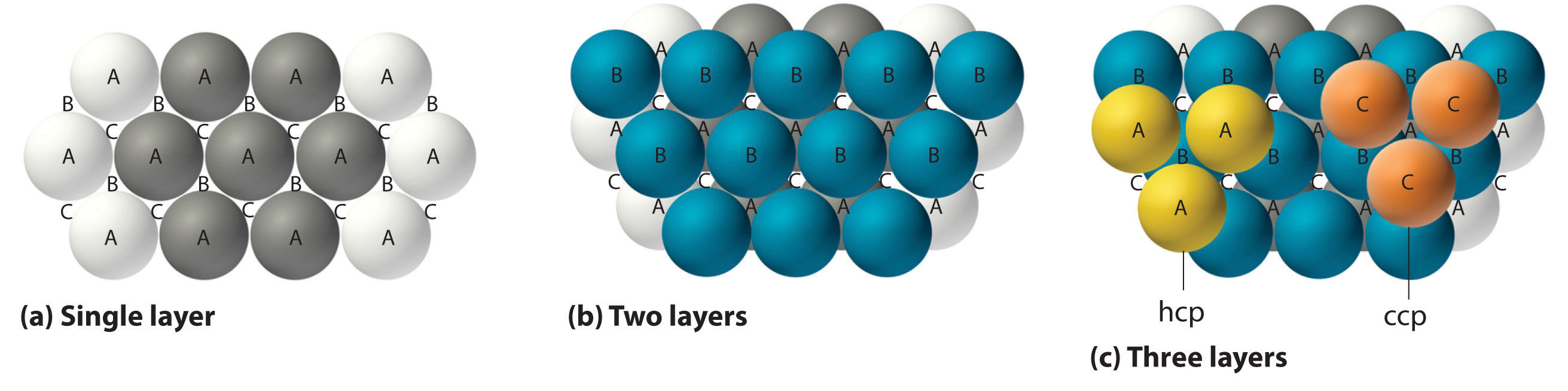
(a) In this single layer of close-packed spheres, each sphere is surrounded by six others in a hexagonal arrangement. (b) Placing an atom at a B position prohibits placing an atom at any of the adjacent C positions and results in all the atoms in the second layer occupying the B positions. (c) Placing the atoms in the third layer over the atoms at A positions in the first layer gives the hexagonal close-packed structure. Placing the third-layer atoms over the C positions gives the cubic close-packed structure.
If we place the second layer of spheres at the B positions in part (a) in Figure 12.6 "Close-Packed Layers of Spheres", we obtain the two-layered structure shown in part (b) in Figure 12.6 "Close-Packed Layers of Spheres". There are now two alternatives for placing the first atom of the third layer: we can place it directly over one of the atoms in the first layer (an A position) or at one of the C positions, corresponding to the positions that we did not use for the atoms in the first or second layers (part (c) in Figure 12.6 "Close-Packed Layers of Spheres"). If we choose the first arrangement and repeat the pattern in succeeding layers, the positions of the atoms alternate from layer to layer in the pattern ABABAB…, resulting in a hexagonal close-packed (hcp) structureOne of two variants of the close-packed arrangement—the most efficient way to pack spheres in a lattice—in which the atomic positions alternate from layer to layer in an ABABAB… pattern. (part (a) in Figure 12.7 "Close-Packed Structures: hcp and ccp"). If we choose the second arrangement and repeat the pattern indefinitely, the positions of the atoms alternate as ABCABC…, giving a cubic close-packed (ccp) structureOne of two variants of the close-packed arrangement—the most efficient way to pack spheres in a lattice—in which the atomic positions alter from layer to layer in an ABCABC… pattern. (part (b) in Figure 12.7 "Close-Packed Structures: hcp and ccp"). Because the ccp structure contains hexagonally packed layers, it does not look particularly cubic. As shown in part (b) in Figure 12.7 "Close-Packed Structures: hcp and ccp", however, simply rotating the structure reveals its cubic nature, which is identical to a fcc structure. The hcp and ccp structures differ only in the way their layers are stacked. Both structures have an overall packing efficiency of 74%, and in both each atom has 12 nearest neighbors (6 in the same plane plus 3 in each of the planes immediately above and below).
Figure 12.7 Close-Packed Structures: hcp and ccp
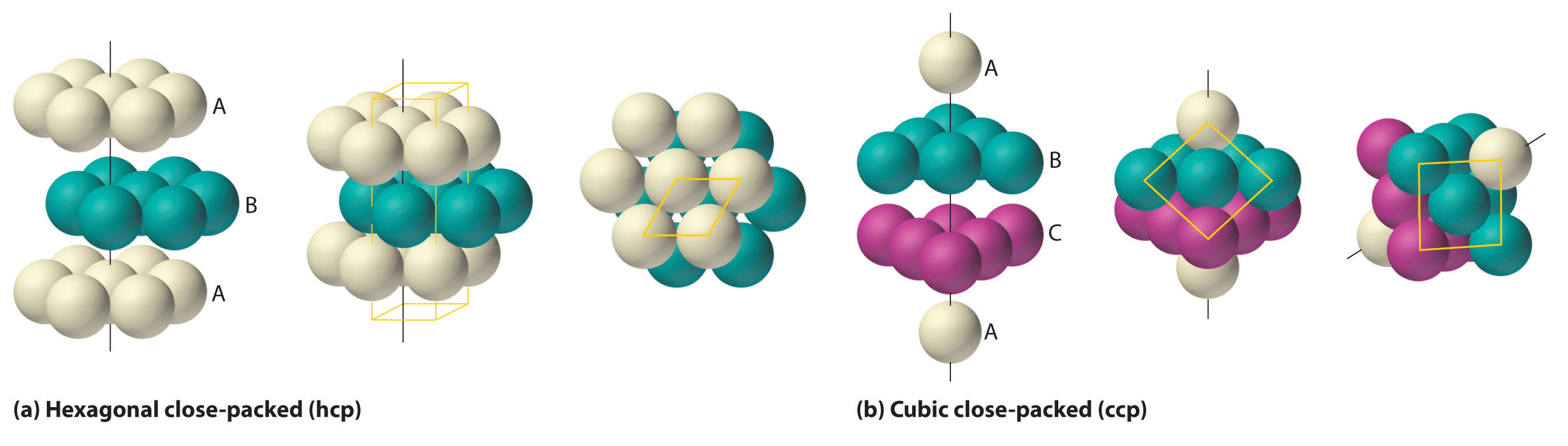
The illustrations in (a) show an exploded view, a side view, and a top view of the hcp structure. The simple hexagonal unit cell is outlined in the side and top views. Note the similarity to the hexagonal unit cell shown in Figure 12.4 "The General Features of the Seven Basic Unit Cells". The ccp structure in (b) is shown in an exploded view, a side view, and a rotated view. The rotated view emphasizes the fcc nature of the unit cell (outlined). The line that connects the atoms in the first and fourth layers of the ccp structure is the body diagonal of the cube.
Table 12.1 "Properties of the Common Structures of Metals" compares the packing efficiency and the number of nearest neighbors for the different cubic and close-packed structures; the number of nearest neighbors is called the coordination numberThe number of nearest neighbors in a solid structure.. Most metals have hcp, ccp, or bcc structures, although several metals exhibit both hcp and ccp structures, depending on temperature and pressure.
Table 12.1 Properties of the Common Structures of Metals
| Structure | Percentage of Space Occupied by Atoms | Coordination Number |
|---|---|---|
| simple cubic | 52 | 6 |
| body-centered cubic | 68 | 8 |
| hexagonal close packed | 74 | 12 |
| cubic close packed (identical to face-centered cubic) | 74 | 12 |
Summary
The smallest repeating unit of a crystal lattice is the unit cell. The simple cubic unit cell contains only eight atoms, molecules, or ions at the corners of a cube. A body-centered cubic (bcc) unit cell contains one additional component in the center of the cube. A face-centered cubic (fcc) unit cell contains a component in the center of each face in addition to those at the corners of the cube. Simple cubic and bcc arrangements fill only 52% and 68% of the available space with atoms, respectively. The hexagonal close-packed (hcp) structure has an ABABAB… repeating arrangement, and the cubic close-packed (ccp) structure has an ABCABC… repeating pattern; the latter is identical to an fcc lattice. The hcp and ccp arrangements fill 74% of the available space and have a coordination number of 12 for each atom in the lattice, the number of nearest neighbors. The simple cubic and bcc lattices have coordination numbers of 6 and 8, respectively.
Key Takeaway
- A crystalline solid can be represented by its unit cell, which is the smallest identical unit that when stacked together produces the characteristic three-dimensional structure.
Conceptual Problems
-
Why is it valid to represent the structure of a crystalline solid by the structure of its unit cell? What are the most important constraints in selecting a unit cell?
-
All unit cell structures have six sides. Can crystals of a solid have more than six sides? Explain your answer.
-
Explain how the intensive properties of a material are reflected in the unit cell. Are all the properties of a bulk material the same as those of its unit cell? Explain your answer.
-
The experimentally measured density of a bulk material is slightly higher than expected based on the structure of the pure material. Propose two explanations for this observation.
-
The experimentally determined density of a material is lower than expected based on the arrangement of the atoms in the unit cell, the formula mass, and the size of the atoms. What conclusion(s) can you draw about the material?
-
Only one element (polonium) crystallizes with a simple cubic unit cell. Why is polonium the only example of an element with this structure?
-
What is meant by the term coordination number in the structure of a solid? How does the coordination number depend on the structure of the metal?
-
Arrange the three types of cubic unit cells in order of increasing packing efficiency. What is the difference in packing efficiency between the hcp structure and the ccp structure?
-
The structures of many metals depend on pressure and temperature. Which structure—bcc or hcp—would be more likely in a given metal at very high pressures? Explain your reasoning.
-
A metal has two crystalline phases. The transition temperature, the temperature at which one phase is converted to the other, is 95°C at 1 atm and 135°C at 1000 atm. Sketch a phase diagram for this substance. The metal is known to have either a ccp structure or a simple cubic structure. Label the regions in your diagram appropriately and justify your selection for the structure of each phase.
Numerical Problems
-
Metallic rhodium has an fcc unit cell. How many atoms of rhodium does each unit cell contain?
-
Chromium has a structure with two atoms per unit cell. Is the structure of this metal simple cubic, bcc, fcc, or hcp?
-
The density of nickel is 8.908 g/cm3. If the metallic radius of nickel is 125 pm, what is the structure of metallic nickel?
-
The density of tungsten is 19.3 g/cm3. If the metallic radius of tungsten is 139 pm, what is the structure of metallic tungsten?
-
An element has a density of 10.25 g/cm3 and a metallic radius of 136.3 pm. The metal crystallizes in a bcc lattice. Identify the element.
-
A 21.64 g sample of a nonreactive metal is placed in a flask containing 12.00 mL of water; the final volume is 13.81 mL. If the length of the edge of the unit cell is 387 pm and the metallic radius is 137 pm, determine the packing arrangement and identify the element.
-
A sample of an alkali metal that has a bcc unit cell is found to have a mass of 1.000 g and a volume of 1.0298 cm3. When the metal reacts with excess water, the reaction produces 539.29 mL of hydrogen gas at 0.980 atm and 23°C. Identify the metal, determine the unit cell dimensions, and give the approximate size of the atom in picometers.
-
A sample of an alkaline earth metal that has a bcc unit cell is found to have a mass 5.000 g and a volume of 1.392 cm3. Complete reaction with chlorine gas requires 848.3 mL of chlorine gas at 1.050 atm and 25°C. Identify the metal, determine the unit cell dimensions, and give the approximate size of the atom in picometers.
-
Lithium crystallizes in a bcc structure with an edge length of 3.509 Å. Calculate its density. What is the approximate metallic radius of lithium in picometers?
-
Vanadium is used in the manufacture of rust-resistant vanadium steel. It forms bcc crystals with a density of 6.11 g/cm3 at 18.7°C. What is the length of the edge of the unit cell? What is the approximate metallic radius of the vanadium in picometers?
-
A simple cubic cell contains one metal atom with a metallic radius of 100 pm.
- Determine the volume of the atom(s) contained in one unit cell [the volume of a sphere = ].
- What is the length of one edge of the unit cell? (Hint: there is no empty space between atoms.)
- Calculate the volume of the unit cell.
- Determine the packing efficiency for this structure.
- Use the steps in Problem 11 to calculate the packing efficiency for a bcc unit cell with a metallic radius of 1.00 Å.
Answers
-
four
-
-
fcc
-
-
molybdenum
-
-
sodium, unit cell edge = 428 pm, r = 185 pm
-
-
d = 0.5335 g/cm3, r =151.9 pm
-
-




