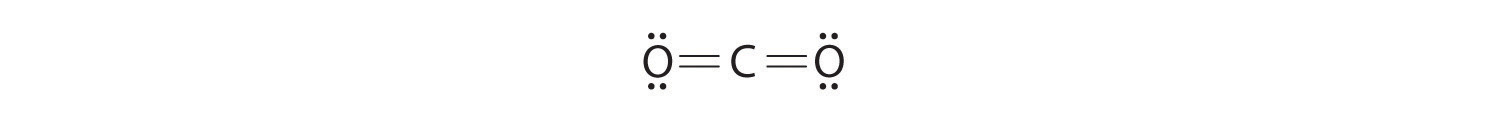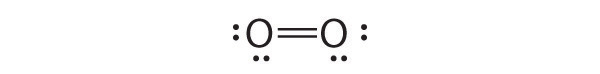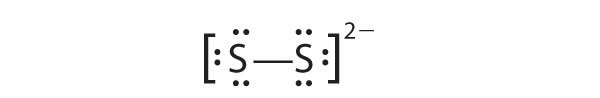This is “Ionic versus Covalent Bonding”, chapter 8 from the book Principles of General Chemistry (v. 1.0M). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
Chapter 8 Ionic versus Covalent Bonding
In Chapter 7 "The Periodic Table and Periodic Trends", we described the relationship between the chemical properties and reactivity of an element and its position in the periodic table. In this chapter and Chapter 9 "Molecular Geometry and Covalent Bonding Models", we describe the interactions that hold atoms together in chemical substances, and we examine the factors that determine how the atoms of a substance are arranged in space. Our goal is to understand how the properties of the component atoms in a chemical compound determine the structure and reactivity of the compound.
The properties described in Chapter 6 "The Structure of Atoms" and Chapter 7 "The Periodic Table and Periodic Trends" were properties of isolated atoms, yet most of the substances in our world consist of atoms held together in molecules, ionic compounds, or metallic solids. The properties of these substances depend on not only the characteristics of the component atoms but also how those atoms are bonded to one another.

Carbon and silicon bonding. Both the group 14 elements carbon and silicon form bonds with oxygen, but how they form those bonds results in a vast difference in physical properties. Because of its simple molecular bond, carbon dioxide is a gas that exists as a volatile molecular solid, known as “dry ice,” at temperatures of −78°C and below. Silicon dioxide is a giant covalent structure, whose strong bonds in three dimensions make it a hard, high-melting-point solid, such as quartz.
What you learn in this chapter about chemical bonding and molecular structure will help you understand how different substances with the same atoms can have vastly different physical and chemical properties. For example, oxygen gas (O2) is essential for life, yet ozone (O3) is toxic to cells, although as you learned in Chapter 3 "Chemical Reactions", ozone in the upper atmosphere shields us from harmful ultraviolet light. Moreover, you saw in Chapter 7 "The Periodic Table and Periodic Trends" that diamond is a hard, transparent solid that is a gemstone; graphite is a soft, black solid that is a lubricant; and fullerenes are molecular species with carbon cage structures—yet all of these are composed of carbon. As you learn about bonding, you will also discover why, although carbon and silicon both have ns2np2 valence electron configurations and form dioxides, CO2 is normally a gas that condenses into the volatile molecular solid known as dry ice, whereas SiO2 is a nonvolatile solid with a network structure that can take several forms, including beach sand and quartz crystals.
8.1 An Overview of Chemical Bonding
Learning Objective
- To present three common features of chemical bonding.
In Chapter 2 "Molecules, Ions, and Chemical Formulas", we defined a chemical bond as the force that holds atoms together in a chemical compound. We also introduced two idealized types of bonding: covalent bondingA type of chemical bonding in which electrons are shared between atoms in a molecule or polyatomic ion., in which electrons are shared between atoms in a molecule or polyatomic ion, and ionic bondingA type of chemical bonding in which positively and negatively charged ions are held together by electrostatic forces., in which positively and negatively charged ions are held together by electrostatic forces. The concepts of covalent and ionic bonding were developed to explain the properties of different kinds of chemical substances. Ionic compounds, for example, typically dissolve in water to form aqueous solutions that conduct electricity. (For more information about solution conductivity, see Chapter 4 "Reactions in Aqueous Solution", Section 4.1 "Aqueous Solutions".) In contrast, most covalent compounds that dissolve in water form solutions that do not conduct electricity. Furthermore, many covalent compounds are volatile, whereas ionic compounds are not.
Despite the differences in the distribution of electrons between these two idealized types of bonding, all models of chemical bonding have three features in common:
- Atoms interact with one another to form aggregates such as molecules, compounds, and crystals because doing so lowers the total energy of the system; that is, the aggregates are more stable than the isolated atoms.
- Energy is required to dissociate bonded atoms or ions into isolated atoms or ions. For ionic solids, in which the ions form a three-dimensional array called a lattice, this energy is called the lattice energy(U)The enthalpy change that occurs when a solid ionic compound (whose ions form a three-dimensional array called a lattice) is transformed into gaseous ions., the enthalpy change that occurs when a solid ionic compound is transformed into gaseous ions. For covalent compounds, this energy is called the bond energyThe enthalpy change that occurs when a given bond in a gaseous molecule is broken., which is the enthalpy change that occurs when a given bond in a gaseous molecule is broken.
- Each chemical bond is characterized by a particular optimal internuclear distance called the bond distance(r0)The optimal internuclear distance between two bonded atoms..
Note the Pattern
Energy is required to dissociate bonded atoms or ions.
We explore these characteristics further, after briefly describing the energetic factors involved in the formation of an ionic bond.
Summary
Chemical bonding is the general term used to describe the forces that hold atoms together in molecules and ions. Two idealized types of bonding are ionic bonding, in which positively and negatively charged ions are held together by electrostatic forces, and covalent bonding, in which electron pairs are shared between atoms. All models of chemical bonding have three common features: atoms form bonds because the products are more stable than the isolated atoms; bonding interactions are characterized by a particular energy (the bond energy or lattice energy), which is the amount of energy required to dissociate the substance into its components; and bonding interactions have an optimal internuclear distance, the bond distance.
Key Takeaway
- Forming bonds lowers the total energy of the system, energy is required to dissociate bonded atoms or ions, and there is an optimal bond distance.
Conceptual Problems
-
Describe the differences between covalent bonding and ionic bonding. Which best describes the bonding in MgCl2 and PF5?
-
What three features do all chemical bonds have in common?
8.2 Ionic Bonding
Learning Objective
- To quantitatively describe the energetic factors involved in the formation of an ionic bond.
Chapter 2 "Molecules, Ions, and Chemical Formulas" explained that ionic bonds are formed when positively and negatively charged ions are held together by electrostatic forces. You learned that the energy of the electrostatic attraction (E), a measure of the force’s strength, is inversely proportional to the internuclear distance between the charged particles (r):
Equation 8.1
where each ion’s charge is represented by the symbol Q. The proportionality constant k is equal to 2.31 × 10−28 J·m.This value of k includes the charge of a single electron (1.6022 × 10−19 C) for each ion. The equation can also be written using the charge of each ion, expressed in coulombs (C), incorporated in the constant. In this case, the proportionality constant, k, equals 8.999 × 109 J·m/C2. In the example given, Q1 = +1(1.6022 × 10−19 C) and Q2 = −1(1.6022 × 10−19 C). If Q1 and Q2 have opposite signs (as in NaCl, for example, where Q1 is +1 for Na+ and Q2 is −1 for Cl−), then E is negative, which means that energy is released when oppositely charged ions are brought together from an infinite distance to form an isolated ion pair. As shown by the green curve in the lower half of Figure 8.1 "A Plot of Potential Energy versus Internuclear Distance for the Interaction between a Gaseous Na", Equation 8.1 predicts that the maximum energy is released when the ions are infinitely close to each other, at r = 0. Because ions occupy space, however, they cannot be infinitely close together. At very short distances, repulsive electron–electron interactions between electrons on adjacent ions become stronger than the attractive interactions between ions with opposite charges, as shown by the red curve in the upper half of Figure 8.1 "A Plot of Potential Energy versus Internuclear Distance for the Interaction between a Gaseous Na". The total energy of the system is a balance between the attractive and repulsive interactions. The purple curve in Figure 8.1 "A Plot of Potential Energy versus Internuclear Distance for the Interaction between a Gaseous Na" shows that the total energy of the system reaches a minimum at r0, the point where the electrostatic repulsions and attractions are exactly balanced. This distance is the same as the experimentally measured bond distance.
Note the Pattern
Energy is released when a bond is formed.
Figure 8.1 A Plot of Potential Energy versus Internuclear Distance for the Interaction between a Gaseous Na+ Ion and a Gaseous Cl− Ion
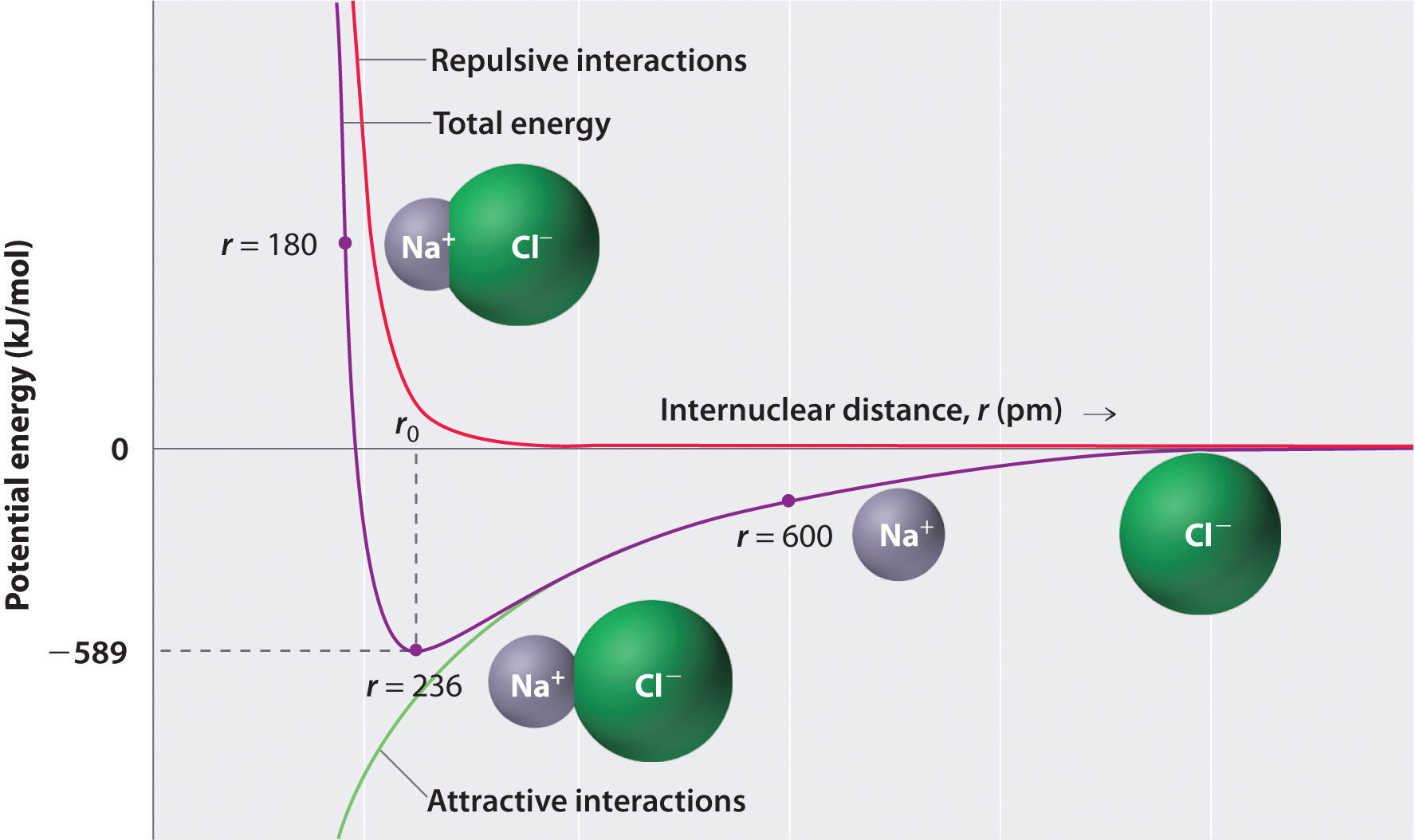
The energy of the system reaches a minimum at a particular distance (r0) when the attractive and repulsive interactions are balanced.
Let’s consider the energy released when a gaseous Na+ ion and a gaseous Cl− ion are brought together from r = ∞ to r = r0. Given that the observed gas-phase internuclear distance is 236 pm, the energy change associated with the formation of an ion pair from an Na+(g) ion and a Cl−(g) ion is as follows:
Equation 8.2
The negative value indicates that energy is released. To calculate the energy change in the formation of a mole of NaCl pairs, we need to multiply the energy per ion pair by Avogadro’s number:
Equation 8.3
This is the energy released when 1 mol of gaseous ion pairs is formed, not when 1 mol of positive and negative ions condenses to form a crystalline lattice. Because of long-range interactions in the lattice structure, this energy does not correspond directly to the lattice energy of the crystalline solid. However, the large negative value indicates that bringing positive and negative ions together is energetically very favorable, whether an ion pair or a crystalline lattice is formed.
We summarize the important points about ionic bonding:
- At r0, the ions are more stable (have a lower potential energy) than they are at an infinite internuclear distance. When oppositely charged ions are brought together from r = ∞ to r = r0, the energy of the system is lowered (energy is released).
- Because of the low potential energy at r0, energy must be added to the system to separate the ions. The amount of energy needed is the bond energy.
- The energy of the system reaches a minimum at a particular internuclear distance (the bond distance).
Example 1
Calculate the amount of energy released when 1 mol of gaseous Li+F− ion pairs is formed from the separated ions. The observed internuclear distance in the gas phase is 156 pm.
Given: cation and anion, amount, and internuclear distance
Asked for: energy released from formation of gaseous ion pairs
Strategy:
Substitute the appropriate values into Equation 8.1 to obtain the energy released in the formation of a single ion pair and then multiply this value by Avogadro’s number to obtain the energy released per mole.
Solution:
Inserting the values for Li+F− into Equation 8.1 (where Q1 = +1, Q2 = −1, and r = 156 pm), we find that the energy associated with the formation of a single pair of Li+F− ions is
Then the energy released per mole of Li+F− ion pairs is
Because Li+ and F− are smaller than Na+ and Cl− (see Figure 7.9 "Ionic Radii (in Picometers) of the Most Common Oxidation States of the "), the internuclear distance in LiF is shorter than in NaCl. Consequently, in accordance with Equation 8.1, much more energy is released when 1 mol of gaseous Li+F− ion pairs is formed (−891 kJ/mol) than when 1 mol of gaseous Na+Cl− ion pairs is formed (−589 kJ/mol).
Exercise
Calculate the amount of energy released when 1 mol of gaseous MgO ion pairs is formed from the separated ions. The internuclear distance in the gas phase is 175 pm.
Answer: −3180 kJ/mol = −3.18 × 103 kJ/mol
Summary
The strength of the electrostatic attraction between ions with opposite charges is directly proportional to the magnitude of the charges on the ions and inversely proportional to the internuclear distance. The total energy of the system is a balance between the repulsive interactions between electrons on adjacent ions and the attractive interactions between ions with opposite charges.
Key Takeaway
- The amount of energy needed to separate a gaseous ion pair is its bond energy.
Conceptual Problems
-
Describe the differences in behavior between NaOH and CH3OH in aqueous solution. Which solution would be a better conductor of electricity? Explain your reasoning.
-
What is the relationship between the strength of the electrostatic attraction between oppositely charged ions and the distance between the ions? How does the strength of the electrostatic interactions change as the size of the ions increases?
-
Which will result in the release of more energy: the interaction of a gaseous sodium ion with a gaseous oxide ion or the interaction of a gaseous sodium ion with a gaseous bromide ion? Why?
-
Which will result in the release of more energy: the interaction of a gaseous chloride ion with a gaseous sodium ion or a gaseous potassium ion? Explain your answer.
-
What are the predominant interactions when oppositely charged ions are
- far apart?
- at internuclear distances close to r0?
- very close together (at a distance that is less than the sum of the ionic radii)?
-
Several factors contribute to the stability of ionic compounds. Describe one type of interaction that destabilizes ionic compounds. Describe the interactions that stabilize ionic compounds.
-
What is the relationship between the electrostatic attractive energy between charged particles and the distance between the particles?
Answer
-
-
-
The interaction of a sodium ion and an oxide ion. The electrostatic attraction energy between ions of opposite charge is directly proportional to the charge on each ion (Q1 and Q2 in Equation 8.1). Thus, more energy is released as the charge on the ions increases (assuming the internuclear distance does not increase substantially). A sodium ion has a +1 charge; an oxide ion, a −2 charge; and a bromide ion, a −1 charge. For the interaction of a sodium ion with an oxide ion, Q1 = +1 and Q2 = −2, whereas for the interaction of a sodium ion with a bromide ion, Q1 = +1 and Q2 = −1. The larger value of Q1 × Q2 for the sodium ion–oxide ion interaction means it will release more energy.
-
-
-
-
Numerical Problems
-
How does the energy of the electrostatic interaction between ions with charges +1 and −1 compare to the interaction between ions with charges +3 and −1 if the distance between the ions is the same in both cases? How does this compare with the magnitude of the interaction between ions with +3 and −3 charges?
-
How many grams of gaseous MgCl2 are needed to give the same electrostatic attractive energy as 0.5 mol of gaseous LiCl? The ionic radii are Li+ = 76 pm, Mg+2 = 72 pm, and Cl− = 181 pm.
-
Sketch a diagram showing the relationship between potential energy and internuclear distance (from r = ∞ to r = 0) for the interaction of a bromide ion and a potassium ion to form gaseous KBr. Explain why the energy of the system increases as the distance between the ions decreases from r = r0 to r = 0.
-
Calculate the magnitude of the electrostatic attractive energy (E, in kilojoules) for 85.0 g of gaseous SrS ion pairs. The observed internuclear distance in the gas phase is 244.05 pm.
-
What is the electrostatic attractive energy (E, in kilojoules) for 130 g of gaseous HgI2? The internuclear distance is 255.3 pm.
Answers
-
According to Equation 8.1, in the first case Q1Q2 = (+1)(−1) = −1; in the second case, Q1Q2 = (+3)(−1) = −3. Thus, E will be three times larger for the +3/−1 ions. For +3/−3 ions, Q1Q2 = (+3)(−3) = −9, so E will be nine times larger than for the +1/−1 ions.
-
-
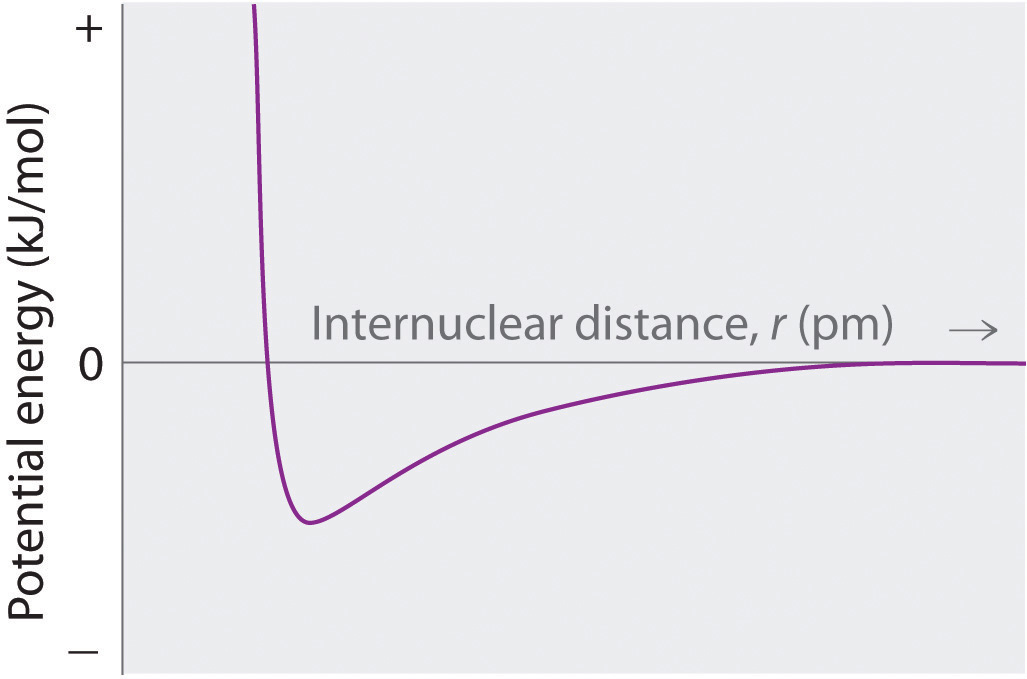
At r < r0, the energy of the system increases due to electron–electron repulsions between the overlapping electron distributions on adjacent ions. At very short internuclear distances, electrostatic repulsions between adjacent nuclei also become important.
-
-
8.3 Lattice Energies in Ionic Solids
Learning Objectives
- To understand the relationship between the lattice energy and physical properties of an ionic compound.
- To use the Born–Haber cycle to calculate lattice energies.
Recall from Chapter 2 "Molecules, Ions, and Chemical Formulas" that the reaction of a metal with a nonmetal usually produces an ionic compound; that is, electrons are transferred from the metal (the reductant) to the nonmetal (the oxidant). Ionic compounds are usually rigid, brittle, crystalline substances with flat surfaces that intersect at characteristic angles. They are not easily deformed, and they melt at relatively high temperatures. NaCl, for example, melts at 801°C. These properties result from the regular arrangement of the ions in the crystalline lattice and from the strong electrostatic attractive forces between ions with opposite charges.
While Equation 8.1 has demonstrated that the formation of ion pairs from isolated ions releases large amounts of energy, even more energy is released when these ion pairs condense to form an ordered three-dimensional array (Figure 7.8 "Definition of Ionic Radius"). In such an arrangement each cation in the lattice is surrounded by more than one anion (typically four, six, or eight) and vice versa, so it is more stable than a system consisting of separate pairs of ions, in which there is only one cation–anion interaction in each pair. Note that r0 may differ between the gas-phase dimer and the lattice.
Note the Pattern
An ionic lattice is more stable than a system consisting of separate ion pairs.
Calculating Lattice Energies
The lattice energy of nearly any ionic solid can be calculated rather accurately using a modified form of Equation 8.1:
Equation 8.4
U, which is always a positive number, represents the amount of energy required to dissociate 1 mol of an ionic solid into the gaseous ions. If we assume that ΔV = 0, then the lattice energy, U, is approximately equal to the change in enthalpy, ΔH (see Chapter 5 "Energy Changes in Chemical Reactions", Section 5.2 "Enthalpy"):
Equation 8.5
As before, Q1 and Q2 are the charges on the ions and r0 is the internuclear distance. We see from Equation 8.4 that lattice energy is directly related to the product of the ion charges and inversely related to the internuclear distance. The value of the constant k′ depends on the specific arrangement of ions in the solid lattice and their valence electron configurations, topics that will be discussed in more detail in Chapter 12 "Solids". Representative values for calculated lattice energies, which range from about 600 to 10,000 kJ/mol, are listed in Table 8.1 "Representative Calculated Lattice Energies". Energies of this magnitude can be decisive in determining the chemistry of the elements.
Table 8.1 Representative Calculated Lattice Energies
| Substance | U (kJ/mol) |
|---|---|
| NaI | 682 |
| CaI2 | 1971 |
| MgI2 | 2293 |
| NaOH | 887 |
| Na2O | 2481 |
| NaNO3 | 755 |
| Ca3(PO4)2 | 10,602 |
| CaCO3 | 2804 |
Source: Data from CRC Handbook of Chemistry and Physics (2004).
Because the lattice energy depends on the product of the charges of the ions, a salt having a metal cation with a +2 charge (M2+) and a nonmetal anion with a −2 charge (X2−) will have a lattice energy four times greater than one with M+ and X−, assuming the ions are of comparable size (and have similar internuclear distances). For example, the calculated value of U for NaF is 910 kJ/mol, whereas U for MgO (containing Mg2+ and O2− ions) is 3795 kJ/mol.
Because lattice energy is inversely related to the internuclear distance, it is also inversely proportional to the size of the ions. This effect is illustrated in Figure 8.2 "A Plot of Lattice Energy versus the Identity of the Halide for the Lithium, Sodium, and Potassium Halides", which shows that lattice energy decreases for the series LiX, NaX, and KX as the radius of X− increases. Because r0 in Equation 8.4 is the sum of the ionic radii of the cation and the anion (r0 = r+ + r−), r0 increases as the cation becomes larger in the series, so the magnitude of U decreases. A similar effect is seen when the anion becomes larger in a series of compounds with the same cation.
Figure 8.2 A Plot of Lattice Energy versus the Identity of the Halide for the Lithium, Sodium, and Potassium Halides
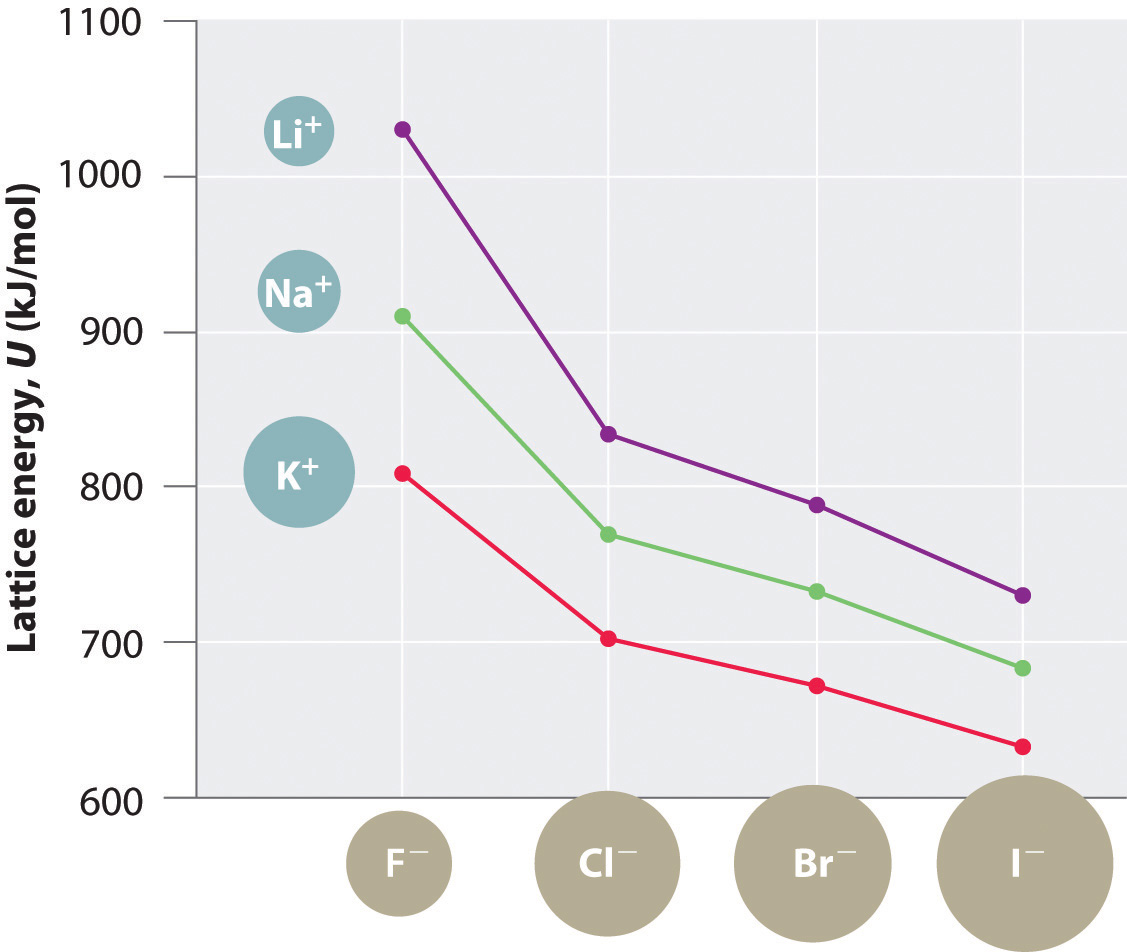
Because the ionic radii of the cations decrease in the order K+ > Na+ > Li+ for a given halide ion, the lattice energy decreases smoothly from Li+ to K+. Conversely, for a given alkali metal ion, the fluoride salt always has the highest lattice energy and the iodide salt the lowest.
Note the Pattern
Lattice energies are highest for substances with small, highly charged ions.
Example 2
Arrange GaP, BaS, CaO, and RbCl in order of increasing lattice energy.
Given: four compounds
Asked for: order of increasing lattice energy
Strategy:
Using Equation 8.4, predict the order of the lattice energies based on the charges on the ions. For compounds with ions with the same charge, use the relative sizes of the ions to make this prediction.
Solution:
The compound GaP, which is used in semiconductor electronics, contains Ga3+ and P3− ions; the compound BaS contains Ba2+ and S2− ions; the compound CaO contains Ca2+ and O2− ions; and the compound RbCl has Rb+ and Cl− ions. We know from Equation 8.4 that lattice energy is directly proportional to the product of the ionic charges. Consequently, we expect RbCl, with a (−1)(+1) term in the numerator, to have the lowest lattice energy, and GaP, with a (+3)(−3) term, the highest. To decide whether BaS or CaO has the greater lattice energy, we need to consider the relative sizes of the ions because both compounds contain a +2 metal ion and a −2 chalcogenide ion. Because Ba2+ lies below Ca2+ in the periodic table, Ba2+ is larger than Ca2+. Similarly, S2− is larger than O2−. Because the cation and the anion in BaS are both larger than the corresponding ions in CaO, the internuclear distance is greater in BaS and its lattice energy will be lower than that of CaO. The order of increasing lattice energy is RbCl < BaS < CaO < GaP.
Exercise
Arrange InAs, KBr, LiCl, SrSe, and ZnS in order of decreasing lattice energy.
Answer: InAs > ZnS > SrSe > LiCl > KBr
The Relationship between Lattice Energies and Physical Properties
The magnitude of the forces that hold an ionic substance together has a dramatic effect on many of its properties. The melting pointThe temperature at which the individual ions in a lattice or the individual molecules in a covalent compound have enough kinetic energy to overcome the attractive forces that hold them together in the solid., for example, is the temperature at which the individual ions have enough kinetic energy to overcome the attractive forces that hold them in place. At the melting point, the ions can move freely, and the substance becomes a liquid. Thus melting points vary with lattice energies for ionic substances that have similar structures. The melting points of the sodium halides (Figure 8.3 "A Plot of Melting Point versus the Identity of the Halide for the Sodium Halides"), for example, decrease smoothly from NaF to NaI, following the same trend as seen for their lattice energies (Figure 8.2 "A Plot of Lattice Energy versus the Identity of the Halide for the Lithium, Sodium, and Potassium Halides"). Similarly, the melting point of MgO is 2825°C, compared with 996°C for NaF, reflecting the higher lattice energies associated with higher charges on the ions. In fact, because of its high melting point, MgO is used as an electrical insulator in heating elements for electric stoves.
Figure 8.3 A Plot of Melting Point versus the Identity of the Halide for the Sodium Halides
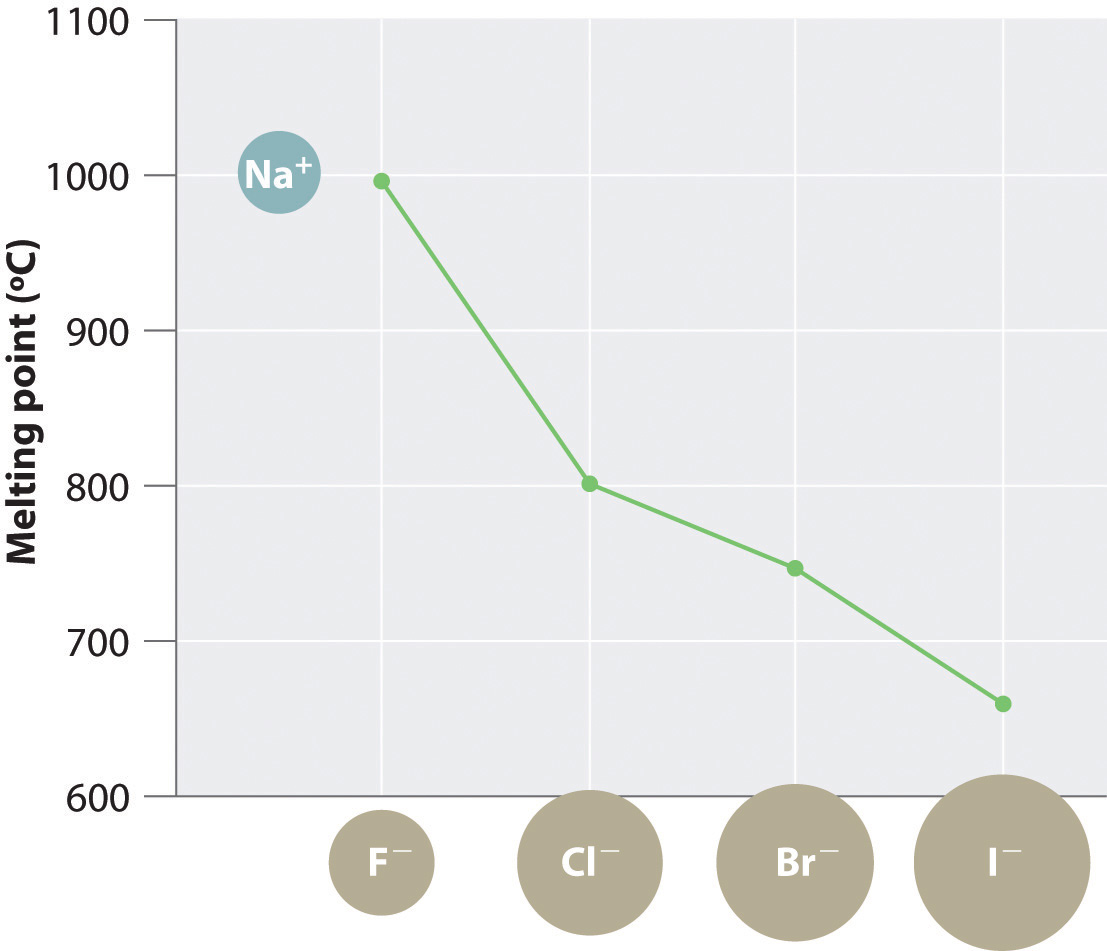
The melting points follow the same trend as the magnitude of the lattice energies in Figure 8.2 "A Plot of Lattice Energy versus the Identity of the Halide for the Lithium, Sodium, and Potassium Halides".
The hardnessThe resistance of ionic materials to scratching or abrasion. of ionic materials—that is, their resistance to scratching or abrasion—is also related to their lattice energies. Hardness is directly related to how tightly the ions are held together electrostatically, which, as we saw, is also reflected in the lattice energy. As an example, MgO is harder than NaF, which is consistent with its higher lattice energy.
In addition to determining melting point and hardness, lattice energies affect the solubilities of ionic substances in water. In general, the higher the lattice energy, the less soluble a compound is in water. For example, the solubility of NaF in water at 25°C is 4.13 g/100 mL, but under the same conditions, the solubility of MgO is only 0.65 mg/100 mL, meaning that it is essentially insoluble.
Note the Pattern
High lattice energies lead to hard, insoluble compounds with high melting points.
The Born–Haber Cycle
In principle, lattice energies could be measured by combining gaseous cations and anions to form an ionic solid and then measuring the heat evolved. Unfortunately, measurable quantities of gaseous ions have never been obtained under conditions where heat flow can be measured. Instead, lattice energies are found using the experimentally determined enthalpy changes for other chemical processes, Hess’s law, and a thermochemical cycle called the Born–Haber cycleA thermochemical cycle that decribes the process in which an ionic solid is conceptually formed from its component elements in a stepwise manner., similar to those introduced in Chapter 5 "Energy Changes in Chemical Reactions". Developed by Max Born and Fritz Haber in 1919, the Born–Haber cycle describes a process in which an ionic solid is conceptually formed from its component elements in a stepwise manner.
Let’s use the Born–Haber cycle to determine the lattice energy of CsF(s). CsF is a nearly ideal ionic compound because Cs is the least electronegative element that is not radioactive and F is the most electronegative element. To construct a thermochemical cycle for the formation of CsF, we need to know its enthalpy of formation, ΔHf, which is defined by the following chemical reaction:
Equation 8.6
Because enthalpy is a state function, the overall ΔH for a series of reactions is the sum of the values of ΔH for the individual reactions. (For more information about state functions and Hess’s law, see Chapter 5 "Energy Changes in Chemical Reactions", Section 5.2 "Enthalpy".) We can therefore use a thermochemical cycle to determine the enthalpy change that accompanies the formation of solid CsF from the parent elements (not ions).
The Born–Haber cycle for calculating the lattice energy of cesium fluoride is shown in Figure 8.4 "The Born–Haber Cycle Illustrating the Enthalpy Changes Involved in the Formation of Solid Cesium Fluoride from Its Elements". This particular cycle consists of six reactions, Equation 8.6 plus the following five reactions:
Figure 8.4 The Born–Haber Cycle Illustrating the Enthalpy Changes Involved in the Formation of Solid Cesium Fluoride from Its Elements

Reaction 1
This equation describes the sublimationThe conversion of a solid directly to a gas (without an intervening liquid phase). of elemental cesium, the conversion of the solid directly to a gas. The accompanying enthalpy change is called the enthalpy of sublimation(ΔHsub)The enthalpy change that accompanies the conversion of a solid directly to a gas. (Table 8.2 "Selected Enthalpies of Sublimation at 298 K") and is always positive because energy is required to sublime a solid.
Table 8.2 Selected Enthalpies of Sublimation at 298 K
| Substance | ΔHsub (kJ/mol) |
|---|---|
| Li | 159.3 |
| Na | 107.5 |
| K | 89.0 |
| Rb | 80.9 |
| Cs | 76.5 |
| Be | 324.0 |
| Mg | 147.1 |
| Ca | 177.8 |
| Sr | 164.4 |
| Ba | 180.0 |
Source: Data from CRC Handbook of Chemistry and Physics (2004).
Reaction 2
This equation describes the ionization of cesium, so the enthalpy change is the first ionization energy of cesium. Recall from Chapter 7 "The Periodic Table and Periodic Trends" that energy is needed to ionize any neutral atom. Hence, regardless of the compound, the enthalpy change for this portion of the Born–Haber cycle is always positive.
Reaction 3
This equation describes the dissociation of fluorine molecules into fluorine atoms, where D is the energy required for dissociation to occur (Table 8.3 "Selected Bond Dissociation Enthalpies at 298 K"). We need to dissociate only mol of F2(g) molecules to obtain 1 mol of F(g) atoms. The ΔH for this reaction, too, is always positive because energy is required to dissociate any stable diatomic molecule into the component atoms.
Table 8.3 Selected Bond Dissociation Enthalpies at 298 K
| Substance | D (kJ/mol) |
|---|---|
| H2(g) | 436.0 |
| N2(g) | 945.3 |
| O2(g) | 498.4 |
| F2(g) | 158.8 |
| Cl2(g) | 242.6 |
| Br2(g) | 192.8 |
| I2(g) | 151.1 |
Source: Data from CRC Handbook of Chemistry and Physics (2004).
Reaction 4
This equation describes the formation of a gaseous fluoride ion from a fluorine atom; the enthalpy change is the electron affinity of fluorine. Recall from Chapter 7 "The Periodic Table and Periodic Trends" that electron affinities can be positive, negative, or zero. In this case, ΔH is negative because of the highly negative electron affinity of fluorine.
Reaction 5
This equation describes the formation of the ionic solid from the gaseous ions. Because Reaction 5 is the reverse of the equation used to define lattice energy and U is defined to be a positive number, ΔH5 is always negative, as it should be in a step that forms bonds.
If the enthalpy of formation of CsF from the elements is known (ΔHf = −553.5 kJ/mol at 298 K), then the thermochemical cycle shown in Figure 8.4 "The Born–Haber Cycle Illustrating the Enthalpy Changes Involved in the Formation of Solid Cesium Fluoride from Its Elements" has only one unknown, the quantity ΔH5 = −U. From Hess’s law, we can write
Equation 8.7
ΔHf = ΔH1 + ΔH2 + ΔH3 + ΔH4 + ΔH5We can rearrange Equation 8.7 to give
Equation 8.8
−ΔH5 = ΔH1 + ΔH2 + ΔH3 + ΔH4 − ΔHfSubstituting for the individual ΔHs, we obtain
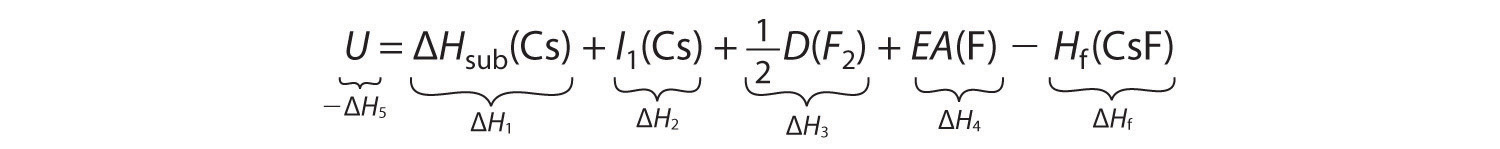
Substituting the appropriate values into this equation gives
Equation 8.9
U = 76.5 kJ/mol + 375.7 kJ/mol + 79.4 kJ/mol + (−328.2 kJ/mole) − (−553.5 kJ/mol) = 756.9 kJ/molU is larger in magnitude than any of the other quantities in Equation 8.9. The process we have used to arrive at this value is summarized in Table 8.4 "Summary of Reactions in the Born–Haber Cycle for the Formation of CsF(s)".
Table 8.4 Summary of Reactions in the Born–Haber Cycle for the Formation of CsF(s)
| Reaction | Enthalpy Change (kJ/mol) | |
|---|---|---|
| (1) | Cs(s) → Cs(g) | ΔHsub = 76.5 |
| (2) | Cs(g) → Cs + (g) + e− | I1 = 375.7 |
| (3) | ½F2(g) → F(g) | ½D = 79.4 |
| (4) | F(g) + e− → F−(g) | EA = −328.2 |
| (5) | Cs + (g) + F−(g) → CsF(s) | −U = −756.9 |
| Cs(s) + ½F2(g) → CsF(s) | ΔHf = −553.5 |
Predicting the Stability of Ionic Compounds
Equation 8.7 may be used as a tool for predicting which ionic compounds are likely to form from particular elements. As we have noted, ΔH1 (ΔHsub), ΔH2 (I), and ΔH3 (D) are always positive numbers, and ΔH2 can be quite large. In contrast, ΔH4 (EA) is comparatively small and can be positive, negative, or zero. Thus the first three terms in Equation 8.7 make the formation of an ionic substance energetically unfavorable, and the fourth term contributes little either way. The formation of an ionic compound will be exothermic (ΔHf < 0) if and only if ΔH5 (−U) is a large negative number. This means that lattice energy is the most important factor in determining the stability of an ionic compound. Another example is the formation of BaO:
Equation 8.10
whose Born–Haber cycle is compared with that for the formation of CsF in Figure 8.5 "Comparison of the Enthalpy Changes Involved in the Formation of Solid CsF and BaO from Their Elements".
Figure 8.5 Comparison of the Enthalpy Changes Involved in the Formation of Solid CsF and BaO from Their Elements
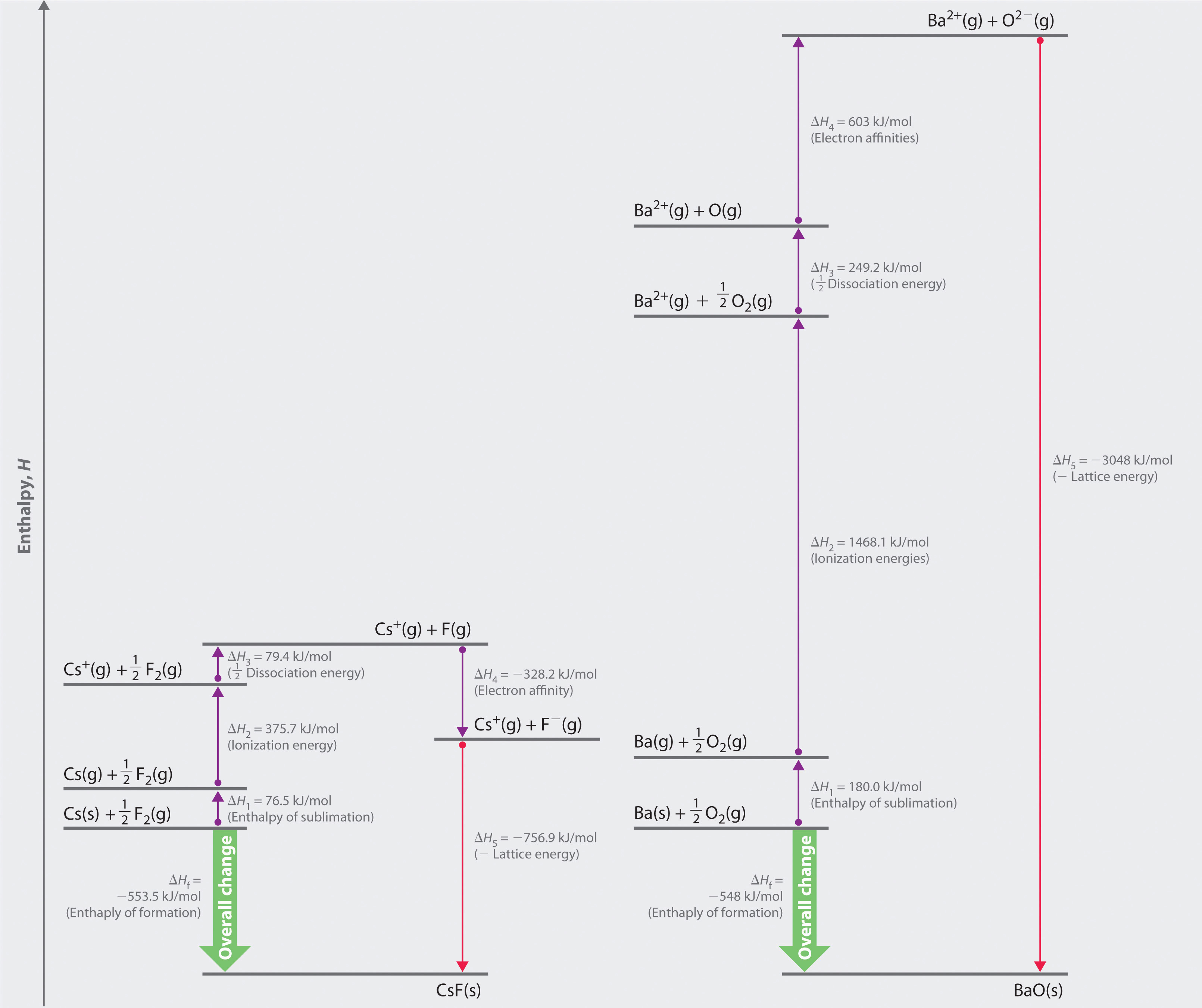
The lattice energy of BaO, with a dipositive cation and a dinegative anion, dominates the Born–Haber cycle.
Reaction 1
More than twice as much energy is required to sublime barium metal (180.0 kJ/mol) as is required to sublime cesium (76.5 kJ/mol).
Reaction 2
Nearly four times the energy is needed to form Ba2+ ions (I1 = 502.9 kJ/mol, I2 = 965.2 kJ/mol, I1 + I2 = 1468.1 kJ/mol) as Cs+ ions (I1 = 375.7 kJ/mol).
Reaction 3
Because the bond energy of O2(g) is 498.4 kJ/mol compared with 158.8 kJ/mol for F2(g), more than three times the energy is needed to form oxygen atoms from O2 molecules as is required to form fluorine atoms from F2.
Reaction 4
Forming gaseous oxide (O2−) ions is energetically unfavorable. Even though adding one electron to an oxygen atom is exothermic (EA1 = −141 kJ/mol), adding a second electron to an O−(g) ion is energetically unfavorable (EA2 = +744 kJ/mol)—so much so that the overall cost of forming O2−(g) from O(g) is energetically prohibitive (EA1 + EA2 = +603 kJ/mol).
If the first four terms in the Born–Haber cycle are all substantially more positive for BaO than for CsF, why does BaO even form? The answer is the formation of the ionic solid from the gaseous ions (Reaction 5):
Reaction 5
Remember from Equation 8.4 that lattice energies are directly proportional to the product of the charges on the ions and inversely proportional to the internuclear distance. Although the internuclear distances are not significantly different for BaO and CsF (275 and 300 pm, respectively), the larger ionic charges in BaO produce a much higher lattice energy. Substituting values for BaO (ΔHf = −548.0 kJ/mol) into the equation and solving for U gives
Thus U for BaO is slightly more than four times greater than U for CsF. The extra energy released when BaO forms from its ions more than compensates for the additional energy required to form Ba2+(g) and O2−(g) ions from Ba(s) and
If the formation of ionic lattices containing multiply charged ions is so energetically favorable, why does CsF contain Cs+ and F− ions rather than Cs2+ and F2− ions? If we assume that U for a Cs2+F2− salt would be approximately the same as U for BaO, the formation of a lattice containing Cs2+ and F2− ions would release 2291 kJ/mol (3048 kJ/mol − 756.9 kJ/mol) more energy than one containing Cs+ and F− ions. To form the Cs2+ ion from Cs+, however, would require removing a 5p electron from a filled inner shell, which calls for a great deal of energy: I2 = 2234.4 kJ/mol for Cs. Furthermore, forming an F2− ion is expected to be even more energetically unfavorable than forming an O2− ion. Not only is an electron being added to an already negatively charged ion, but because the F− ion has a filled 2p subshell, the added electron would have to occupy an empty high-energy 3s orbital. Cesium fluoride, therefore, is not Cs2+F2− because the energy cost of forming the doubly charged ions would be greater than the additional lattice energy that would be gained.
Note the Pattern
Lattice energy is usually the most important energy factor in determining the stability of an ionic compound.
Example 3
Use data from Figure 7.13 "Electron Affinities (in kJ/mol) of the ", Table 7.5 "Successive Ionization Energies (in kJ/mol) for the Elements in the Third Row of the Periodic Table", Table 8.2 "Selected Enthalpies of Sublimation at 298 K", Table 8.3 "Selected Bond Dissociation Enthalpies at 298 K", and Chapter 25 "Appendix A: Standard Thermodynamic Quantities for Chemical Substances at 25°C" to calculate the lattice energy of MgH2.
Given: chemical compound and data from figures and tables
Asked for: lattice energy
Strategy:
A Write a series of stepwise reactions for forming MgH2 from its elements via the gaseous ions.
B Use Hess’s law and data from the specified figures and tables to calculate the lattice energy.
Solution:
A Hess’s law allows us to use a thermochemical cycle (the Born–Haber cycle) to calculate the lattice energy for a given compound. We begin by writing reactions in which we form the component ions from the elements in a stepwise manner and then assemble the ionic solid:
B Table 7.5 "Successive Ionization Energies (in kJ/mol) for the Elements in the Third Row of the Periodic Table" lists the first and second ionization energies for the period 3 elements [I1(Mg) = 737.7 kJ/mol, I2(Mg) = 1450.7 kJ/mol]. First electron affinities for all elements are given in Figure 7.13 "Electron Affinities (in kJ/mol) of the " [EA(H) = −72.8 kJ/mol]. Table 8.2 "Selected Enthalpies of Sublimation at 298 K" lists selected enthalpies of sublimation [ΔHsub(Mg) = 147.1 kJ/mol]. Table 8.3 "Selected Bond Dissociation Enthalpies at 298 K" lists selected bond dissociation energies [D(H2) = 436.0 kJ/mol]. Enthalpies of formation (ΔHf = −75.3 kJ/mol for MgH2) are listed in Chapter 25 "Appendix A: Standard Thermodynamic Quantities for Chemical Substances at 25°C". From Hess’s law, ΔHf is equal to the sum of the enthalpy changes for Reactions 1–5:
For MgH2, U = 2701.2 kJ/mol. Once again, lattice energy provides the driving force for forming this compound because ΔH1, ΔH2, ΔH3 > 0. When solving this type of problem, be sure to write the chemical equation for each step and double-check that the enthalpy value used for each step has the correct sign for the reaction in the direction it is written.
Exercise
Use data from Figure 7.11 "First Ionization Energies of the ", Figure 7.13 "Electron Affinities (in kJ/mol) of the ", Table 8.2 "Selected Enthalpies of Sublimation at 298 K", Table 8.3 "Selected Bond Dissociation Enthalpies at 298 K", and Chapter 25 "Appendix A: Standard Thermodynamic Quantities for Chemical Substances at 25°C" to calculate the lattice energy of Li2O. Remember that the second electron affinity for oxygen [O−(g) + e− → O2−(g)] is positive (+744 kJ/mol; see Equation 7.13).
Answer: 2809 kJ/mol
Summary
Ionic compounds have strong electrostatic attractions between oppositely charged ions in a regular array. The lattice energy (U) of an ionic substance is defined as the energy required to dissociate the solid into gaseous ions; U can be calculated from the charges on the ions, the arrangement of the ions in the solid, and the internuclear distance. Because U depends on the product of the ionic charges, substances with di- or tripositive cations and/or di- or trinegative anions tend to have higher lattice energies than their singly charged counterparts. Higher lattice energies typically result in higher melting points and increased hardness because more thermal energy is needed to overcome the forces that hold the ions together. Lattice energies cannot be measured directly but are obtained from a thermochemical cycle called the Born–Haber cycle, in which Hess’s law is used to calculate the lattice energy from the measured enthalpy of formation of the ionic compound, along with other thermochemical data. The Born–Haber cycle can be used to predict which ionic compounds are likely to form. Sublimation, the conversion of a solid directly to a gas, has an accompanying enthalpy change called the enthalpy of sublimation.
Key Takeaway
- The lattice energy is usually the most important energy factor in determining the stability of an ionic compound.
Conceptual Problems
-
If a great deal of energy is required to form gaseous ions, why do ionic compounds form at all?
-
What are the general physical characteristics of ionic compounds?
-
Ionic compounds consist of crystalline lattices rather than discrete ion pairs. Why?
-
What factors affect the magnitude of the lattice energy of an ionic compound? What is the relationship between ionic size and lattice energy?
-
Which would have the larger lattice energy—an ionic compound consisting of a large cation and a large anion or one consisting of a large anion and a small cation? Explain your answer and any assumptions you made.
-
How would the lattice energy of an ionic compound consisting of a monovalent cation and a divalent anion compare with the lattice energy of an ionic compound containing a monovalent cation and a monovalent anion, if the internuclear distance was the same in both compounds? Explain your answer.
-
Which would have the larger lattice energy—CrCl2 or CrCl3—assuming similar arrangements of ions in the lattice? Explain your answer.
-
Which cation in each pair would be expected to form a chloride salt with the larger lattice energy, assuming similar arrangements of ions in the lattice? Explain your reasoning.
- Na+, Mg2+
- Li+, Cs+
- Cu+, Cu2+
-
Which cation in each pair would be expected to form an oxide with the higher melting point, assuming similar arrangements of ions in the lattice? Explain your reasoning.
- Mg2+, Sr2+
- Cs+, Ba2+
- Fe2+, Fe3+
-
How can a thermochemical cycle be used to determine lattice energies? Which steps in such a cycle require an input of energy?
-
Although NaOH and CH3OH have similar formulas and molecular masses, the compounds have radically different properties. One has a high melting point, and the other is a liquid at room temperature. Which compound is which and why?
Numerical Problems
-
Arrange SrO, PbS, and PrI3 in order of decreasing lattice energy.
-
Compare BaO and MgO with respect to each of the following properties.
- enthalpy of sublimation
- ionization energy of the metal
- lattice energy
- enthalpy of formation
-
Use a thermochemical cycle and data from Figure 7.13 "Electron Affinities (in kJ/mol) of the ", Table 7.5 "Successive Ionization Energies (in kJ/mol) for the Elements in the Third Row of the Periodic Table", Table 8.2 "Selected Enthalpies of Sublimation at 298 K", Table 8.3 "Selected Bond Dissociation Enthalpies at 298 K", and Chapter 25 "Appendix A: Standard Thermodynamic Quantities for Chemical Substances at 25°C" to calculate the lattice energy (U) of magnesium chloride (MgCl2).
-
Would you expect the formation of SrO from its component elements to be exothermic or endothermic? Why or why not? How does the valence electron configuration of the component elements help you determine this?
-
Using the information in Problem 4 and Problem 5, predict whether CaO or MgCl2 will have the higher melting point.
-
Use a thermochemical cycle and data from Table 8.2 "Selected Enthalpies of Sublimation at 298 K", Table 8.3 "Selected Bond Dissociation Enthalpies at 298 K", and Chapter 25 "Appendix A: Standard Thermodynamic Quantities for Chemical Substances at 25°C" to calculate the lattice energy of calcium oxide. The first and second ionization energies of calcium are 589.8 kJ/mol and 1145.4 kJ/mol.
Answers
-
Lattice energy is directly proportional to the product of the ionic charges and inversely proportional to the internuclear distance. Therefore, PrI3 > SrO > PbS.
-
-
U = 2522.2 kJ/mol
-
-
Despite the fact that Mg2+ is smaller than Ca2+, the higher charge of O2− versus Cl− gives CaO a larger lattice energy than MgCl2. Consequently, we expect CaO to have the higher melting point.
-
8.4 Lewis Electron Dot Symbols
Learning Objective
- To use Lewis electron dot symbols to predict the number of bonds an element will form.
At the beginning of the 20th century, the American chemist G. N. Lewis (1875–1946) devised a system of symbols—now called Lewis electron dot symbolsA system that can be used to predict the number of bonds formed by most elements in their compounds., often shortened to Lewis dot symbols—that can be used for predicting the number of bonds formed by most elements in their compounds (Figure 8.6 "G. N. Lewis and the Octet Rule"). Each Lewis dot symbol consists of the chemical symbol for an element surrounded by dots that represent its valence electrons. Cesium, for example, has the electron configuration [Xe]6s1, which indicates one valence electron outside a closed shell. In the Lewis dot symbol, this single electron is represented as a single dot:
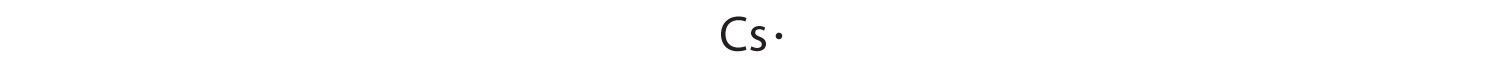
Figure 8.6 G. N. Lewis and the Octet Rule
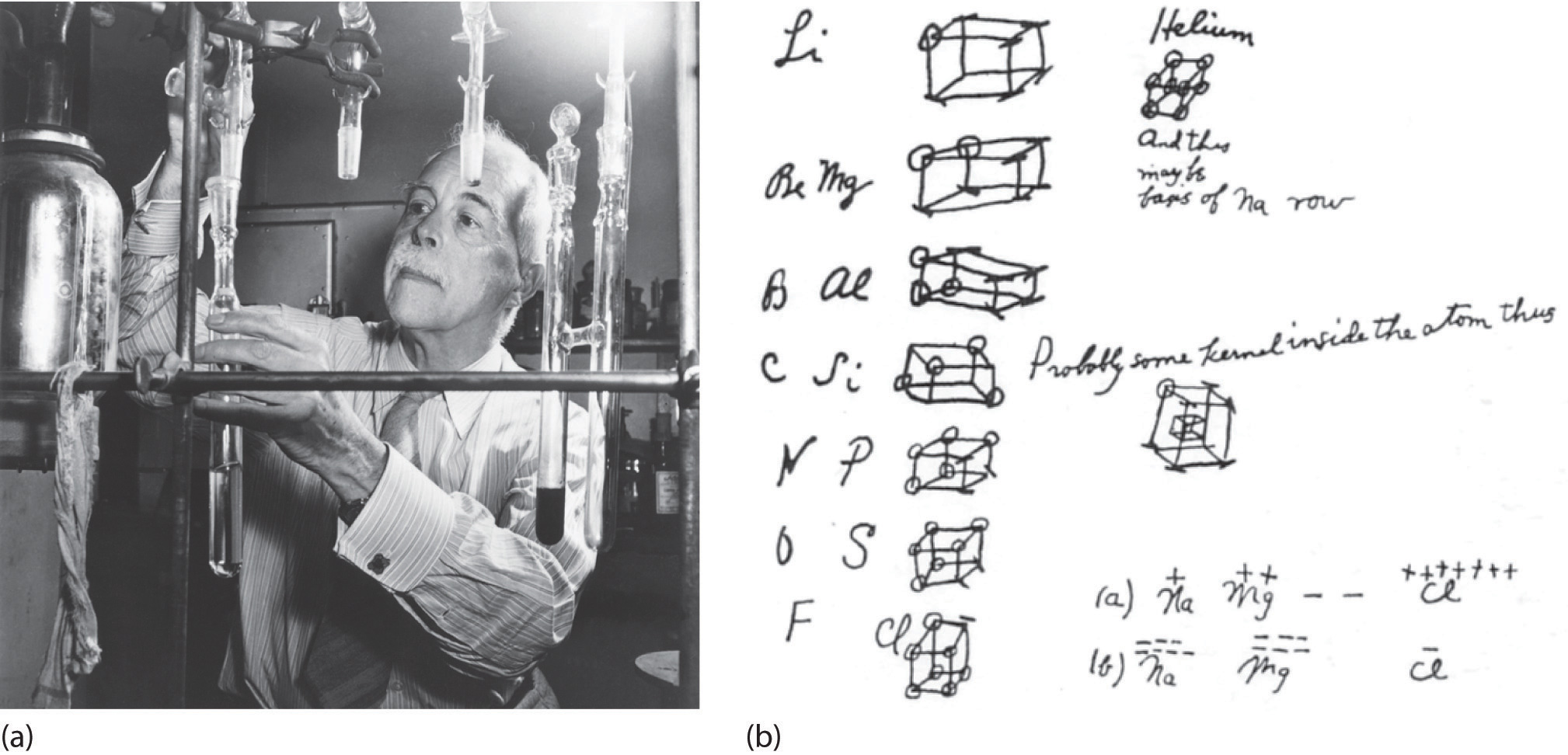
(a) Lewis is working in the laboratory. (b) In Lewis’s original sketch for the octet rule, he initially placed the electrons at the corners of a cube rather than placing them as we do now.
Creating a Lewis Dot Symbol
To write an element’s Lewis dot symbol, we place dots representing its valence electrons, one at a time, around the element’s chemical symbol. Up to four dots are placed above, below, to the left, and to the right of the symbol (in any order, as long as elements with four or fewer valence electrons have no more than one dot in each position). The next dots, for elements with more than four valence electrons, are again distributed one at a time, each paired with one of the first four. Fluorine, for example, with the electron configuration [He]2s22p5, has seven valence electrons, so its Lewis dot symbol is constructed as follows:
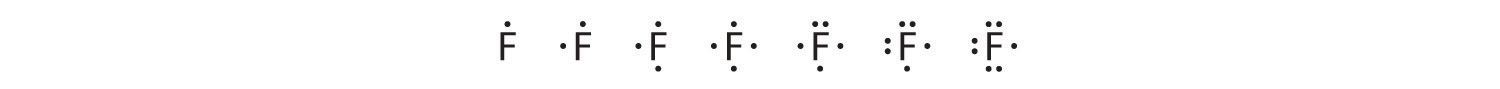
The number of dots in the Lewis dot symbol is the same as the number of valence electrons, which is the same as the last digit of the element’s group number in the periodic table. Lewis dot symbols for the elements in period 2 are given in Figure 8.7 "Lewis Dot Symbols for the Elements in Period 2".
Lewis used the unpaired dots to predict the number of bonds that an element will form in a compound. Consider the symbol for nitrogen in Figure 8.7 "Lewis Dot Symbols for the Elements in Period 2". The Lewis dot symbol explains why nitrogen, with three unpaired valence electrons, tends to form compounds in which it shares the unpaired electrons to form three bonds. Boron, which also has three unpaired valence electrons in its Lewis dot symbol, also tends to form compounds with three bonds, whereas carbon, with four unpaired valence electrons in its Lewis dot symbol, tends to share all of its unpaired valence electrons by forming compounds in which it has four bonds.
Figure 8.7 Lewis Dot Symbols for the Elements in Period 2

The Octet Rule
Lewis’s major contribution to bonding theory was to recognize that atoms tend to lose, gain, or share electrons to reach a total of eight valence electrons, called an octet. This so-called octet ruleThe tendency for atoms to lose, gain, or share electrons to reach a total of eight valence electrons. explains the stoichiometry of most compounds in the s and p blocks of the periodic table. We now know from quantum mechanics that the number eight corresponds to one ns and three np valence orbitals, which together can accommodate a total of eight electrons. Remarkably, though, Lewis’s insight was made nearly a decade before Rutherford proposed the nuclear model of the atom. An exception to the octet rule is helium, whose 1s2 electron configuration gives it a full n = 1 shell, and hydrogen, which tends to gain or share its one electron to achieve the electron configuration of helium.
Lewis dot symbols can also be used to represent the ions in ionic compounds. The reaction of cesium with fluorine, for example, to produce the ionic compound CsF can be written as follows:

No dots are shown on Cs+ in the product because cesium has lost its single valence electron to fluorine. The transfer of this electron produces the Cs+ ion, which has the valence electron configuration of Xe, and the F− ion, which has a total of eight valence electrons (an octet) and the Ne electron configuration. This description is consistent with the statement in Chapter 7 "The Periodic Table and Periodic Trends" that among the main group elements, ions in simple binary ionic compounds generally have the electron configurations of the nearest noble gas. The charge of each ion is written in the product, and the anion and its electrons are enclosed in brackets. This notation emphasizes that the ions are associated electrostatically; no electrons are shared between the two elements.
As you might expect for such a qualitative approach to bonding, there are exceptions to the octet rule, which we describe in Section 8.6 "Exceptions to the Octet Rule". These include molecules in which one or more atoms contain fewer or more than eight electrons. In Section 8.5 "Lewis Structures and Covalent Bonding", however, we explain how to form molecular compounds by completing octets.
Summary
One convenient way to predict the number and basic arrangement of bonds in compounds is by using Lewis electron dot symbols, which consist of the chemical symbol for an element surrounded by dots that represent its valence electrons, grouped into pairs often placed above, below, and to the left and right of the symbol. The structures reflect the fact that the elements in period 2 and beyond tend to gain, lose, or share electrons to reach a total of eight valence electrons in their compounds, the so-called octet rule. Hydrogen, with only two valence electrons, does not obey the octet rule.
Key Takeaway
- Lewis dot symbols can be used to predict the number of bonds formed by most elements in their compounds.
Conceptual Problems
-
The Lewis electron system is a simplified approach for understanding bonding in covalent and ionic compounds. Why do chemists still find it useful?
-
Is a Lewis dot symbol an exact representation of the valence electrons in an atom or ion? Explain your answer.
-
How can the Lewis electron dot system help to predict the stoichiometry of a compound and its chemical and physical properties?
-
How is a Lewis dot symbol consistent with the quantum mechanical model of the atom described in Chapter 6 "The Structure of Atoms"? How is it different?
Answer
-
-
-
Lewis dot symbols allow us to predict the number of bonds atoms will form, and therefore the stoichiometry of a compound. The Lewis structure of a compound also indicates the presence or absence of lone pairs of electrons, which provides information on the compound’s chemical reactivity and physical properties.
-
8.5 Lewis Structures and Covalent Bonding
Learning Objectives
- To use Lewis dot symbols to explain the stoichiometry of a compound.
- To understand the concept of resonance.
We begin our discussion of the relationship between structure and bonding in covalent compounds by describing the interaction between two identical neutral atoms—for example, the H2 molecule, which contains a purely covalent bond. Each hydrogen atom in H2 contains one electron and one proton, with the electron attracted to the proton by electrostatic forces. As the two hydrogen atoms are brought together, additional interactions must be considered (Figure 8.8 "Attractive and Repulsive Interactions between Electrons and Nuclei in the Hydrogen Molecule"):
- The electrons in the two atoms repel each other because they have the same charge (E > 0).
- Similarly, the protons in adjacent atoms repel each other (E > 0).
- The electron in one atom is attracted to the oppositely charged proton in the other atom and vice versa (E < 0).Recall from Chapter 6 "The Structure of Atoms" that it is impossible to specify precisely the position of the electron in either hydrogen atom. Hence the quantum mechanical probability distributions must be used.
Figure 8.8 Attractive and Repulsive Interactions between Electrons and Nuclei in the Hydrogen Molecule
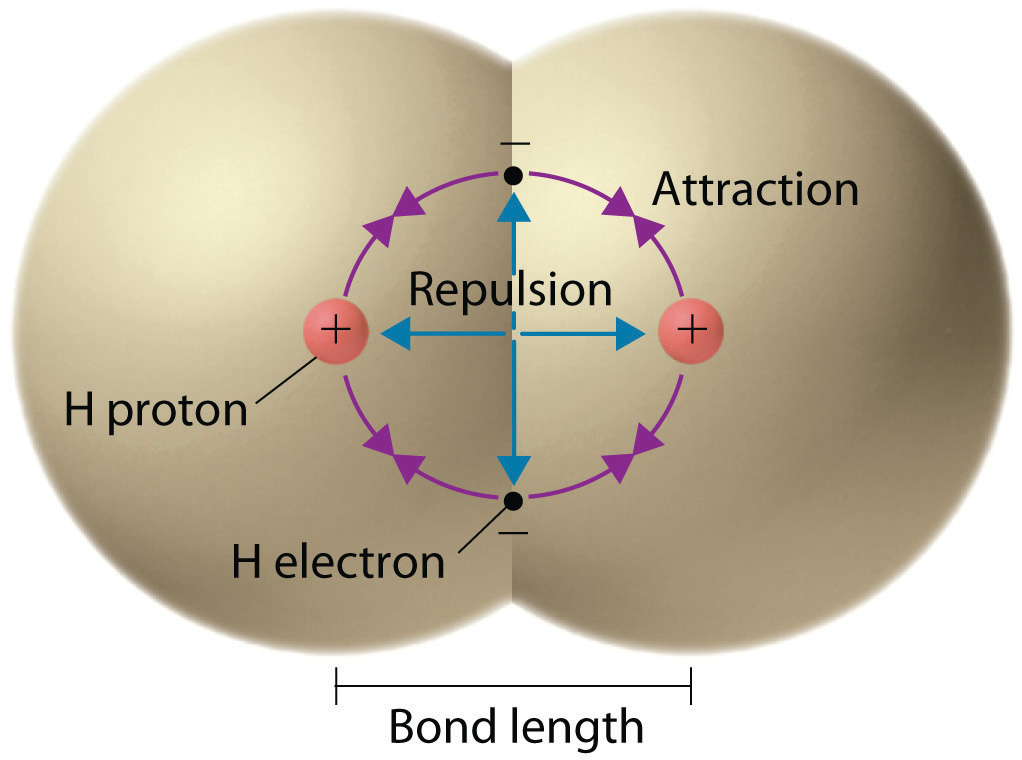
Electron–electron and proton–proton interactions are repulsive; electron–proton interactions are attractive. At the observed bond distance, the repulsive and attractive interactions are balanced.
A plot of the potential energy of the system as a function of the internuclear distance (Figure 8.9 "A Plot of Potential Energy versus Internuclear Distance for the Interaction between Two Gaseous Hydrogen Atoms") shows that the system becomes more stable (the energy of the system decreases) as two hydrogen atoms move toward each other from r = ∞, until the energy reaches a minimum at r = r0 (the observed internuclear distance in H2 is 74 pm). Thus at intermediate distances, proton–electron attractive interactions dominate, but as the distance becomes very short, electron–electron and proton–proton repulsive interactions cause the energy of the system to increase rapidly. Notice the similarity between Figure 8.9 "A Plot of Potential Energy versus Internuclear Distance for the Interaction between Two Gaseous Hydrogen Atoms" and Figure 8.1 "A Plot of Potential Energy versus Internuclear Distance for the Interaction between a Gaseous Na", which described a system containing two oppositely charged ions. The shapes of the energy versus distance curves in the two figures are similar because they both result from attractive and repulsive forces between charged entities.
Figure 8.9 A Plot of Potential Energy versus Internuclear Distance for the Interaction between Two Gaseous Hydrogen Atoms
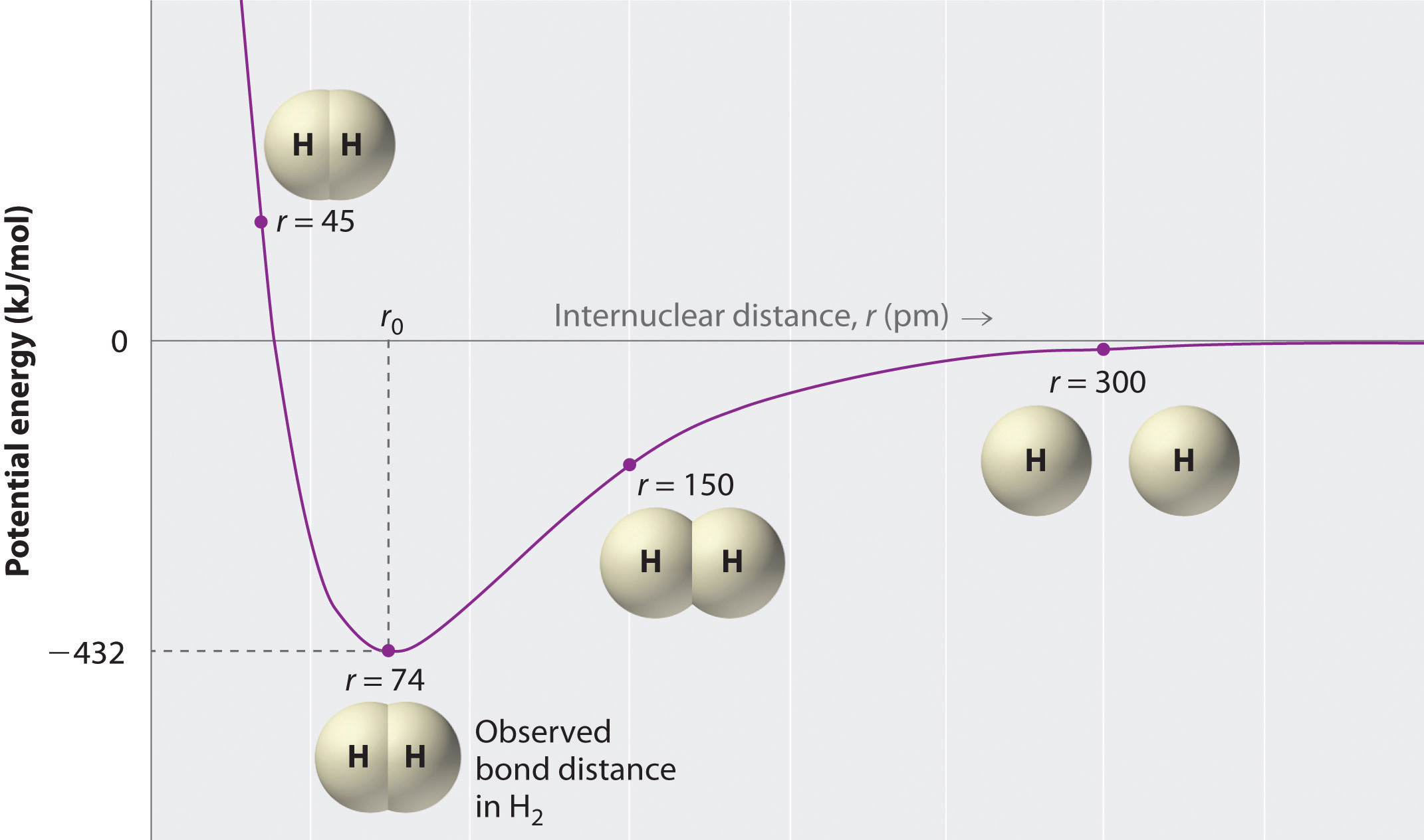
At long distances, both attractive and repulsive interactions are small. As the distance between the atoms decreases, the attractive electron–proton interactions dominate, and the energy of the system decreases. At the observed bond distance, the repulsive electron–electron and proton–proton interactions just balance the attractive interactions, preventing a further decrease in the internuclear distance. At very short internuclear distances, the repulsive interactions dominate, making the system less stable than the isolated atoms.
Using Lewis Dot Symbols to Describe Covalent Bonding
The valence electron configurations of the constituent atoms of a covalent compound are important factors in determining its structure, stoichiometry, and properties. For example, chlorine, with seven valence electrons, is one electron short of an octet. If two chlorine atoms share their unpaired electrons by making a covalent bond and forming Cl2, they can each complete their valence shell:
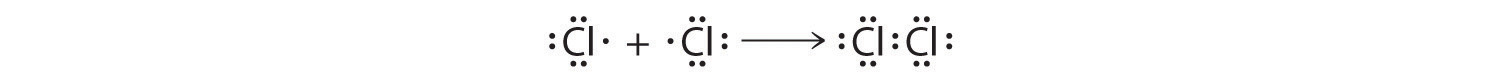
Each chlorine atom now has an octet. The electron pair being shared by the atoms is called a bonding pairA pair of electrons in a Lewis structure that is shared by two atoms, thus forming a covalent bond.; the other three pairs of electrons on each chlorine atom are called lone pairsA pair of electrons in a Lewis structure that is not involved in covalent bonding.. Lone pairs are not involved in covalent bonding. If both electrons in a covalent bond come from the same atom, the bond is called a coordinate covalent bondA covalent bond in which both electrons come from the same atom.. Examples of this type of bonding are presented in Section 8.6 "Exceptions to the Octet Rule" when we discuss atoms with less than an octet of electrons.
We can illustrate the formation of a water molecule from two hydrogen atoms and an oxygen atom using Lewis dot symbols:
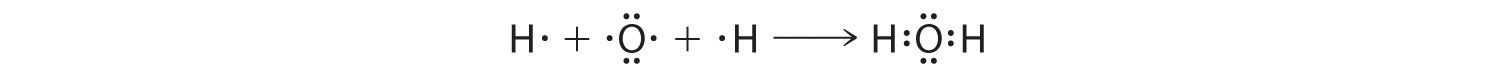
The structure on the right is the Lewis electron structure, or Lewis structure, for H2O. With two bonding pairs and two lone pairs, the oxygen atom has now completed its octet. Moreover, by sharing a bonding pair with oxygen, each hydrogen atom now has a full valence shell of two electrons. Chemists usually indicate a bonding pair by a single line, as shown here for our two examples:

The following procedure can be used to construct Lewis electron structures for more complex molecules and ions:
1. Arrange the atoms to show specific connections. When there is a central atom, it is usually the least electronegative element in the compound. Chemists usually list this central atom first in the chemical formula (as in CCl4 and CO32−, which both have C as the central atom), which is another clue to the compound’s structure. Hydrogen and the halogens are almost always connected to only one other atom, so they are usually terminal rather than central.
Note the Pattern
The central atom is usually the least electronegative element in the molecule or ion; hydrogen and the halogens are usually terminal.
2. Determine the total number of valence electrons in the molecule or ion. Add together the valence electrons from each atom. (Recall from Chapter 6 "The Structure of Atoms" that the number of valence electrons is indicated by the position of the element in the periodic table.) If the species is a polyatomic ion, remember to add or subtract the number of electrons necessary to give the total charge on the ion. For CO32−, for example, we add two electrons to the total because of the −2 charge.
3. Place a bonding pair of electrons between each pair of adjacent atoms to give a single bond. In H2O, for example, there is a bonding pair of electrons between oxygen and each hydrogen.
4. Beginning with the terminal atoms, add enough electrons to each atom to give each atom an octet (two for hydrogen). These electrons will usually be lone pairs.
5. If any electrons are left over, place them on the central atom. We explain in Section 8.6 "Exceptions to the Octet Rule" that some atoms are able to accommodate more than eight electrons.
6. If the central atom has fewer electrons than an octet, use lone pairs from terminal atoms to form multiple (double or triple) bonds to the central atom to achieve an octet. This will not change the number of electrons on the terminal atoms.
Now let’s apply this procedure to some particular compounds, beginning with one we have already discussed.
H2O
1. Because H atoms are almost always terminal, the arrangement within the molecule must be HOH.
2. Each H atom (group 1) has 1 valence electron, and the O atom (group 16) has 6 valence electrons, for a total of 8 valence electrons.
3. Placing one bonding pair of electrons between the O atom and each H atom gives H:O:H, with 4 electrons left over.
4. Each H atom has a full valence shell of 2 electrons.
5. Adding the remaining 4 electrons to the oxygen (as two lone pairs) gives the following structure:

This is the Lewis structure we drew earlier. Because it gives oxygen an octet and each hydrogen two electrons, we do not need to use step 6.
OCl−
1. With only two atoms in the molecule, there is no central atom.
2. Oxygen (group 16) has 6 valence electrons, and chlorine (group 17) has 7 valence electrons; we must add one more for the negative charge on the ion, giving a total of 14 valence electrons.
3. Placing a bonding pair of electrons between O and Cl gives O:Cl, with 12 electrons left over.
4. If we place six electrons (as three lone pairs) on each atom, we obtain the following structure:
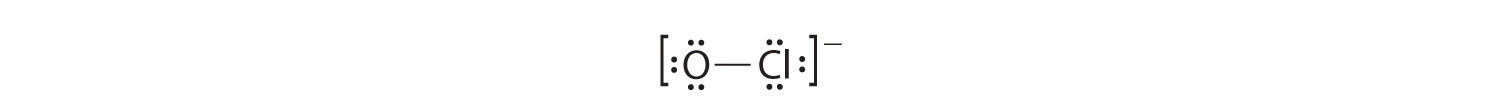
Each atom now has an octet of electrons, so steps 5 and 6 are not needed. The Lewis electron structure is drawn within brackets as is customary for an ion, with the overall charge indicated outside the brackets, and the bonding pair of electrons is indicated by a solid line. OCl− is the hypochlorite ion, the active ingredient in chlorine laundry bleach and swimming pool disinfectant.
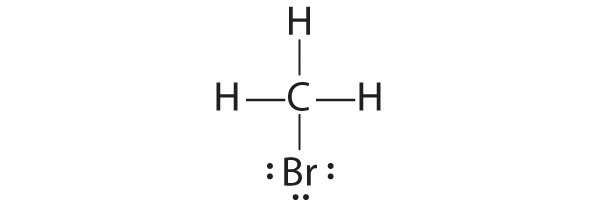
CH2O
1. Because carbon is less electronegative than oxygen and hydrogen is normally terminal, C must be the central atom. One possible arrangement is as follows:

2. Each hydrogen atom (group 1) has one valence electron, carbon (group 14) has 4 valence electrons, and oxygen (group 16) has 6 valence electrons, for a total of [(2)(1) + 4 + 6] = 12 valence electrons.
3. Placing a bonding pair of electrons between each pair of bonded atoms gives the following:

Six electrons are used, and 6 are left over.
4. Adding all 6 remaining electrons to oxygen (as three lone pairs) gives the following:

Although oxygen now has an octet and each hydrogen has 2 electrons, carbon has only 6 electrons.
5. There are no electrons left to place on the central atom.
6. To give carbon an octet of electrons, we use one of the lone pairs of electrons on oxygen to form a carbon–oxygen double bond:

Both the oxygen and the carbon now have an octet of electrons, so this is an acceptable Lewis electron structure. The O has two bonding pairs and two lone pairs, and C has four bonding pairs. This is the structure of formaldehyde, which is used in embalming fluid.
An alternative structure can be drawn with one H bonded to O. Formal charges, discussed later in this section, suggest that such a structure is less stable than that shown previously.
Example 4
Write the Lewis electron structure for each species.
- NCl3
- S22−
- NOCl
Given: chemical species
Asked for: Lewis electron structures
Strategy:
Use the six-step procedure to write the Lewis electron structure for each species.
Solution:
-
Nitrogen is less electronegative than chlorine, and halogen atoms are usually terminal, so nitrogen is the central atom. The nitrogen atom (group 15) has 5 valence electrons and each chlorine atom (group 17) has 7 valence electrons, for a total of 26 valence electrons. Using 2 electrons for each N–Cl bond and adding three lone pairs to each Cl account for (3 × 2) + (3 × 2 × 3) = 24 electrons. Rule 5 leads us to place the remaining 2 electrons on the central N:

Nitrogen trichloride is an unstable oily liquid once used to bleach flour; this use is now prohibited in the United States.
-
In a diatomic molecule or ion, we do not need to worry about a central atom. Each sulfur atom (group 16) contains 6 valence electrons, and we need to add 2 electrons for the −2 charge, giving a total of 14 valence electrons. Using 2 electrons for the S–S bond, we arrange the remaining 12 electrons as three lone pairs on each sulfur, giving each S atom an octet of electrons:
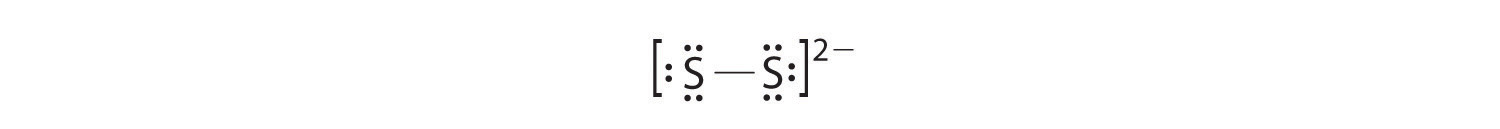
-
Because nitrogen is less electronegative than oxygen or chlorine, it is the central atom. The N atom (group 15) has 5 valence electrons, the O atom (group 16) has 6 valence electrons, and the Cl atom (group 17) has 7 valence electrons, giving a total of 18 valence electrons. Placing one bonding pair of electrons between each pair of bonded atoms uses 4 electrons and gives the following:
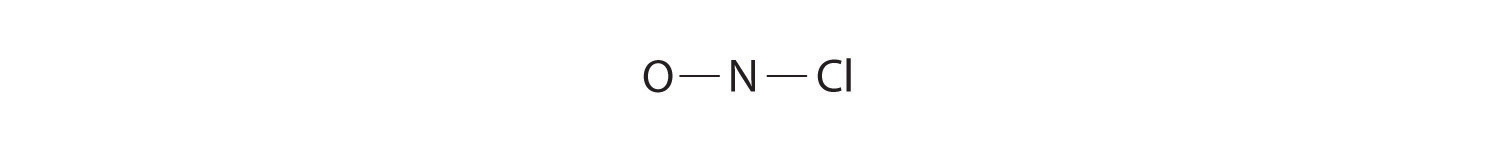
Adding three lone pairs each to oxygen and to chlorine uses 12 more electrons, leaving 2 electrons to place as a lone pair on nitrogen:
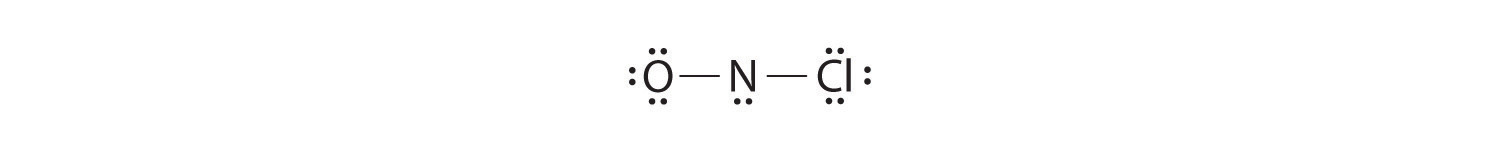
Because this Lewis structure has only 6 electrons around the central nitrogen, a lone pair of electrons on a terminal atom must be used to form a bonding pair. We could use a lone pair on either O or Cl. Because we have seen many structures in which O forms a double bond but none with a double bond to Cl, it is reasonable to select a lone pair from O to give the following:
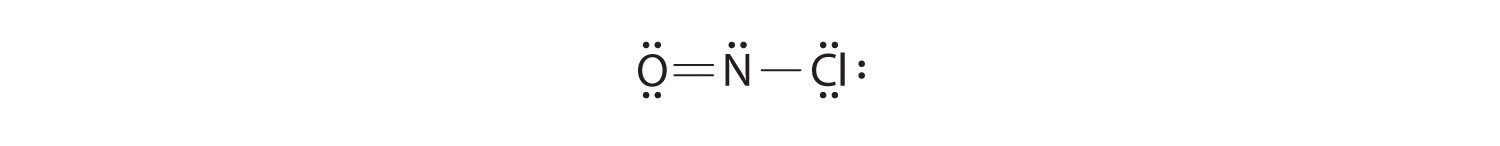
All atoms now have octet configurations. This is the Lewis electron structure of nitrosyl chloride, a highly corrosive, reddish-orange gas.
Exercise
Write Lewis electron structures for CO2 and SCl2, a vile-smelling, unstable red liquid that is used in the manufacture of rubber.
Answer:
Using Lewis Electron Structures to Explain Stoichiometry
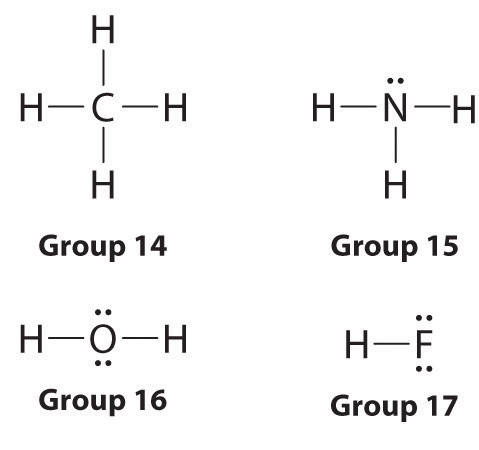
Lewis dot symbols provide a simple rationalization of why elements form compounds with the observed stoichiometries. In the Lewis model, the number of bonds formed by an element in a neutral compound is the same as the number of unpaired electrons it must share with other atoms to complete its octet of electrons. For the elements of group 17 (the halogens), this number is one; for the elements of group 16 (the chalcogens), it is two; for group 15, three; and for group 14, four. These requirements are illustrated by the following Lewis structures for the hydrides of the lightest members of each group:
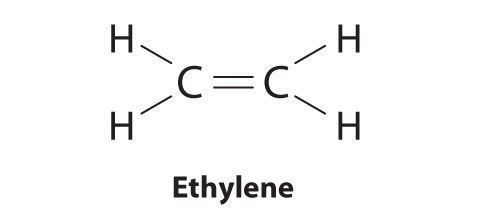
Elements may form multiple bonds to complete an octet. In ethylene, for example, each carbon contributes two electrons to the double bond, giving each carbon an octet (two electrons/bond × four bonds = eight electrons). Neutral structures with fewer or more bonds exist, but they are unusual and violate the octet rule.
Allotropes of an element can have very different physical and chemical properties because of different three-dimensional arrangements of the atoms; the number of bonds formed by the component atoms, however, is always the same. As noted at the beginning of the chapter, diamond is a hard, transparent solid; graphite is a soft, black solid; and the fullerenes have open cage structures. Despite these differences, the carbon atoms in all three allotropes form four bonds, in accordance with the octet rule. Elemental phosphorus also exists in three forms: white phosphorus, a toxic, waxy substance that initially glows and then spontaneously ignites on contact with air; red phosphorus, an amorphous substance that is used commercially in safety matches, fireworks, and smoke bombs; and black phosphorus, an unreactive crystalline solid with a texture similar to graphite (Figure 8.10 "The Three Allotropes of Phosphorus: White, Red, and Black"). Nonetheless, the phosphorus atoms in all three forms obey the octet rule and form three bonds per phosphorus atom.
Note the Pattern
Lewis structures explain why the elements of groups 14–17 form neutral compounds with four, three, two, and one bonded atom(s), respectively.
Figure 8.10 The Three Allotropes of Phosphorus: White, Red, and Black
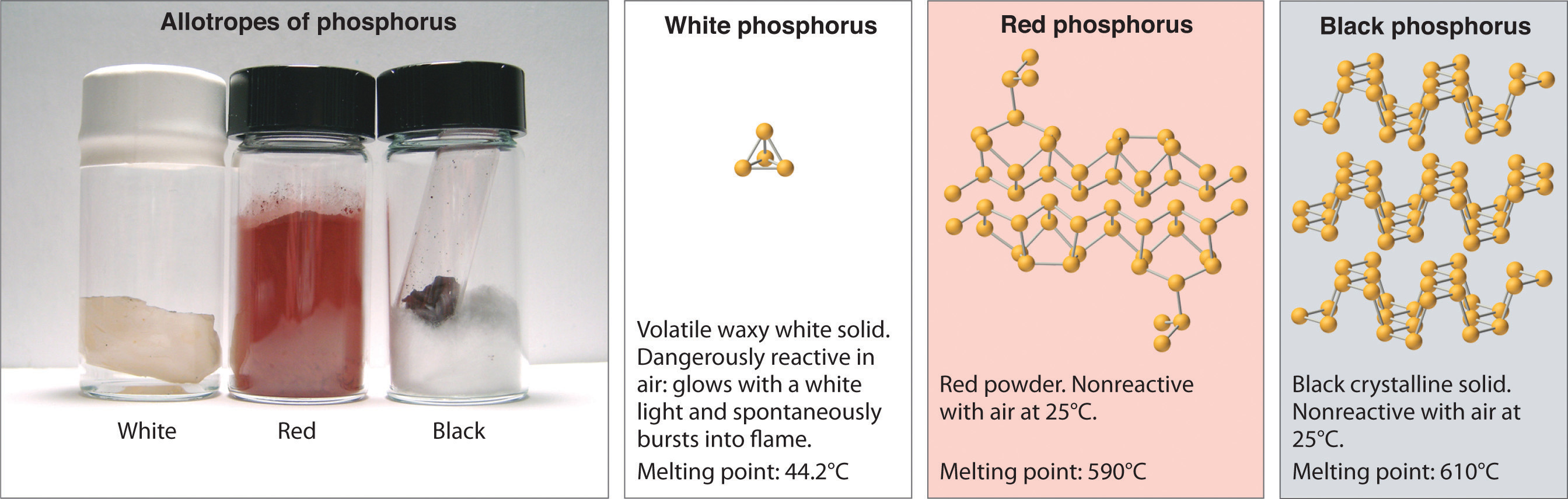
All three forms contain only phosphorus atoms, but they differ in the arrangement and connectivity of their atoms. White phosphorus contains P4 tetrahedra, red phosphorus is a network of linked P8 and P9 units, and black phosphorus forms sheets of six-membered rings. As a result, their physical and chemical properties differ dramatically.
Formal Charges
It is sometimes possible to write more than one Lewis structure for a substance that does not violate the octet rule, as we saw for CH2O, but not every Lewis structure may be equally reasonable. In these situations, we can choose the most stable Lewis structure by considering the formal chargeThe difference between the number of valence electrons in a free atom and the number of electrons assigned to it in a particular Lewis electron structure. on the atoms, which is the difference between the number of valence electrons in the free atom and the number assigned to it in the Lewis electron structure. The formal charge is a way of computing the charge distribution within a Lewis structure; the sum of the formal charges on the atoms within a molecule or an ion must equal the overall charge on the molecule or ion. A formal charge does not represent a true charge on an atom in a covalent bond but is simply used to predict the most likely structure when a compound has more than one valid Lewis structure.
To calculate formal charges, we assign electrons in the molecule to individual atoms according to these rules:
- Nonbonding electrons are assigned to the atom on which they are located.
- Bonding electrons are divided equally between the bonded atoms.
For each atom, we then compute a formal charge:
Equation 8.11
To illustrate this method, let’s calculate the formal charge on the atoms in ammonia (NH3) whose Lewis electron structure is as follows:

A neutral nitrogen atom has five valence electrons (it is in group 15). From its Lewis electron structure, the nitrogen atom in ammonia has one lone pair and shares three bonding pairs with hydrogen atoms, so nitrogen itself is assigned a total of five electrons [2 nonbonding e− + (6 bonding e−/2)]. Substituting into Equation 8.11, we obtain
Equation 8.12
A neutral hydrogen atom has one valence electron. Each hydrogen atom in the molecule shares one pair of bonding electrons and is therefore assigned one electron [0 nonbonding e− + (2 bonding e−/2)]. Using Equation 8.11 to calculate the formal charge on hydrogen, we obtain
Equation 8.13
The hydrogen atoms in ammonia have the same number of electrons as neutral hydrogen atoms, and so their formal charge is also zero. Adding together the formal charges should give us the overall charge on the molecule or ion. In this example, the nitrogen and each hydrogen has a formal charge of zero. When summed the overall charge is zero, which is consistent with the overall charge on the NH3 molecule.
Typically, the structure with the most charges on the atoms closest to zero is the more stable Lewis structure. In cases where there are positive or negative formal charges on various atoms, stable structures generally have negative formal charges on the more electronegative atoms and positive formal charges on the less electronegative atoms. The next example further demonstrates how to calculate formal charges.
Example 5
Calculate the formal charges on each atom in the NH4+ ion.
Given: chemical species
Asked for: formal charges
Strategy:
Identify the number of valence electrons in each atom in the NH4+ ion. Use the Lewis electron structure of NH4+ to identify the number of bonding and nonbonding electrons associated with each atom and then use Equation 8.11 to calculate the formal charge on each atom.
Solution:
The Lewis electron structure for the NH4+ ion is as follows:

The nitrogen atom shares four bonding pairs of electrons, and a neutral nitrogen atom has five valence electrons. Using Equation 8.11, the formal charge on the nitrogen atom is therefore
Each hydrogen atom in has one bonding pair. The formal charge on each hydrogen atom is therefore
The formal charges on the atoms in the NH4+ ion are thus

Adding together the formal charges on the atoms should give us the total charge on the molecule or ion. In this case, the sum of the formal charges is 0 + 1 + 0 + 0 + 0 = +1.
Exercise
Write the formal charges on all atoms in BH4−.
Answer:

If an atom in a molecule or ion has the number of bonds that is typical for that atom (e.g., four bonds for carbon), its formal charge is zero.
Note the Pattern
An atom, molecule, or ion has a formal charge of zero if it has the number of bonds that is typical for that species.
Using Formal Charges to Distinguish between Lewis Structures
As an example of how formal charges can be used to determine the most stable Lewis structure for a substance, we can compare two possible structures for CO2. Both structures conform to the rules for Lewis electron structures.
CO2
1. C is less electronegative than O, so it is the central atom.
2. C has 4 valence electrons and each O has 6 valence electrons, for a total of 16 valence electrons.
3. Placing one electron pair between the C and each O gives O–C–O, with 12 electrons left over.
4. Dividing the remaining electrons between the O atoms gives three lone pairs on each atom:
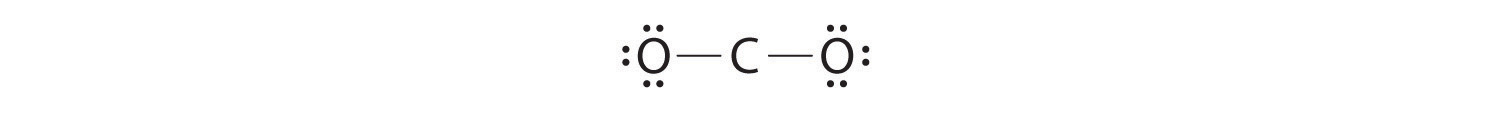
This structure has an octet of electrons around each O atom but only 4 electrons around the C atom.
5. No electrons are left for the central atom.
6. To give the carbon atom an octet of electrons, we can convert two of the lone pairs on the oxygen atoms to bonding electron pairs. There are, however, two ways to do this. We can either take one electron pair from each oxygen to form a symmetrical structure or take both electron pairs from a single oxygen atom to give an asymmetrical structure:
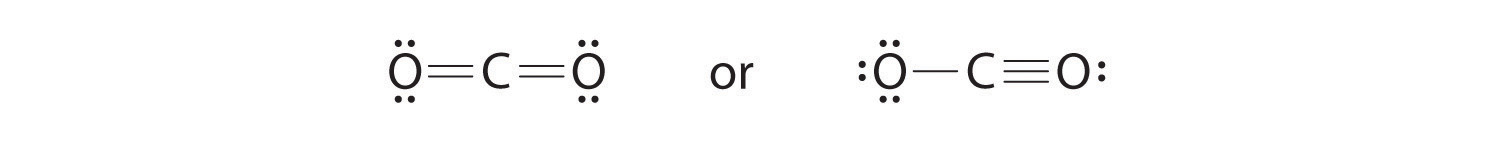
Both Lewis electron structures give all three atoms an octet. How do we decide between these two possibilities? The formal charges for the two Lewis electron structures of CO2 are as follows:

Both Lewis structures have a net formal charge of zero, but the structure on the right has a +1 charge on the more electronegative atom (O). Thus the symmetrical Lewis structure on the left is predicted to be more stable, and it is, in fact, the structure observed experimentally. Remember, though, that formal charges do not represent the actual charges on atoms in a molecule or ion. They are used simply as a bookkeeping method for predicting the most stable Lewis structure for a compound.
Note the Pattern
The Lewis structure with the set of formal charges closest to zero is usually the most stable.
Example 6
The thiocyanate ion (SCN−), which is used in printing and as a corrosion inhibitor against acidic gases, has at least two possible Lewis electron structures. Draw two possible structures, assign formal charges on all atoms in both, and decide which is the preferred arrangement of electrons.
Given: chemical species
Asked for: Lewis electron structures, formal charges, and preferred arrangement
Strategy:
A Use the step-by-step procedure to write two plausible Lewis electron structures for SCN−.
B Calculate the formal charge on each atom using Equation 8.11.
C Predict which structure is preferred based on the formal charge on each atom and its electronegativity relative to the other atoms present.
Solution:
A Possible Lewis structures for the SCN− ion are as follows:
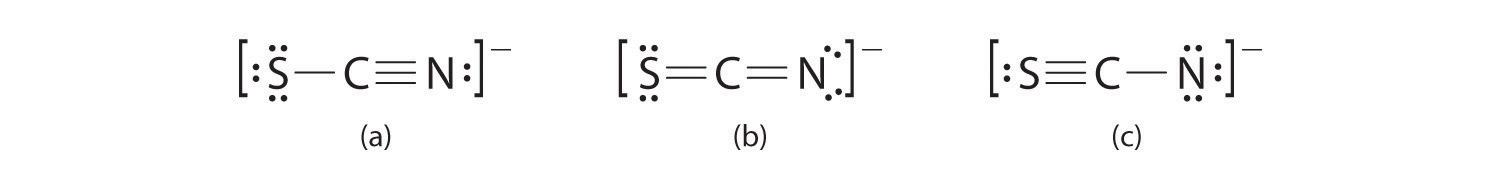
B We must calculate the formal charges on each atom to identify the more stable structure. If we begin with carbon, we notice that the carbon atom in each of these structures shares four bonding pairs, the number of bonds typical for carbon, so it has a formal charge of zero. Continuing with sulfur, we observe that in (a) the sulfur atom shares one bonding pair and has three lone pairs and has a total of six valence electrons. The formal charge on the sulfur atom is therefore In (b), the sulfur atom has two bonding pairs and two lone pairs, giving it a formal charge of zero. In (c), sulfur has a formal charge of +1. Completing our calculations with nitrogen, in (a) the nitrogen atom has three bonding pairs, giving it a formal charge of zero. In (b), the nitrogen atom has two lone pairs and shares two bonding pairs, giving it a formal charge of In (c), nitrogen has a formal charge of −2.
C Which structure is preferred? Structure (b) is preferred because the negative charge is on the more electronegative atom (N), and it has lower formal charges on each atom as compared to structure (c): 0, −1 versus +1, −2.
Exercise
Salts containing the fulminate ion (CNO−) are used in explosive detonators. Draw three Lewis electron structures for CNO− and use formal charges to predict which is more stable. (Note: N is the central atom.)
Answer:
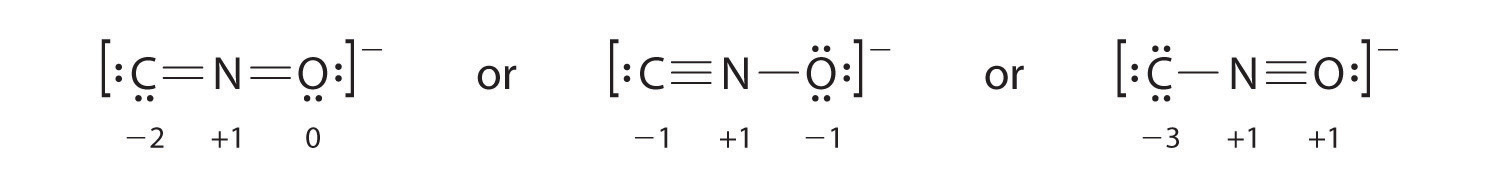
The second structure is predicted to be more stable.
Resonance Structures
Sometimes, even when formal charges are considered, the bonding in some molecules or ions cannot be described by a single Lewis structure. Such is the case for ozone (O3), an allotrope of oxygen with a V-shaped structure and an O–O–O angle of 117.5°.
O3
1. We know that ozone has a V-shaped structure, so one O atom is central:

2. Each O atom has 6 valence electrons, for a total of 18 valence electrons.
3. Assigning one bonding pair of electrons to each oxygen–oxygen bond gives

with 14 electrons left over.
4. If we place three lone pairs of electrons on each terminal oxygen, we obtain

and have 2 electrons left over.
5. At this point, both terminal oxygen atoms have octets of electrons. We therefore place the last 2 electrons on the central atom:

6. The central oxygen has only 6 electrons. We must convert one lone pair on a terminal oxygen atom to a bonding pair of electrons—but which one? Depending on which one we choose, we obtain either
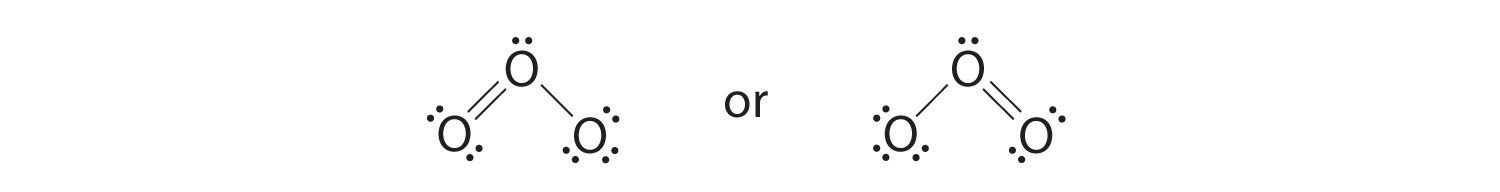
Which is correct? In fact, neither is correct. Both predict one O–O single bond and one O=O double bond. As you will learn in Section 8.8 "Properties of Covalent Bonds", if the bonds were of different types (one single and one double, for example), they would have different lengths. It turns out, however, that both O–O bond distances are identical, 127.2 pm, which is shorter than a typical O–O single bond (148 pm) and longer than the O=O double bond in O2 (120.7 pm).
Equivalent Lewis dot structures, such as those of ozone, are called resonance structuresA Lewis electron structure that has different arrangements of electrons around atoms whose positions do not change.. The position of the atoms is the same in the various resonance structures of a compound, but the position of the electrons is different. Double-headed arrows link the different resonance structures of a compound:

The double-headed arrow indicates that the actual electronic structure is an average of those shown, not that the molecule oscillates between the two structures.
Note the Pattern
When it is possible to write more than one equivalent resonance structure for a molecule or ion, the actual structure is the average of the resonance structures.
CO32−
Like ozone, the electronic structure of the carbonate ion cannot be described by a single Lewis electron structure. Unlike O3, though, the actual structure of CO32− is an average of three resonance structures.
1. Because carbon is the least electronegative element, we place it in the central position:
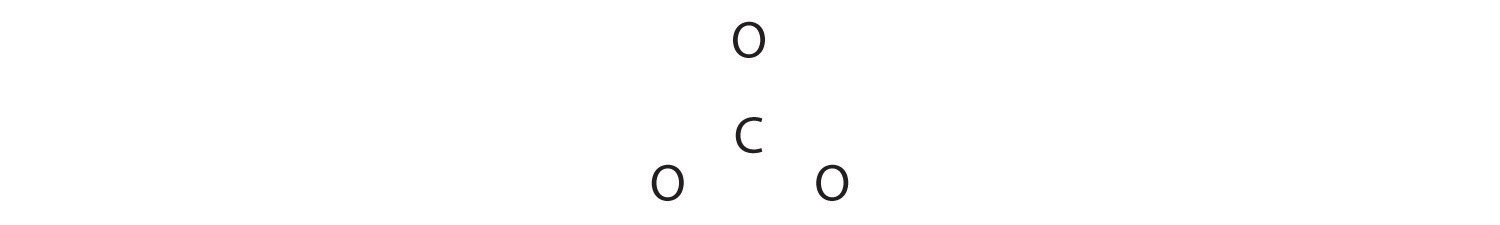
2. Carbon has 4 valence electrons, each oxygen has 6 valence electrons, and there are 2 more for the −2 charge. This gives 4 + (3 × 6) + 2 = 24 valence electrons.
3. Six electrons are used to form three bonding pairs between the oxygen atoms and the carbon:

4. We divide the remaining 18 electrons equally among the three oxygen atoms by placing three lone pairs on each and indicating the −2 charge:

5. No electrons are left for the central atom.
6. At this point, the carbon atom has only 6 valence electrons, so we must take one lone pair from an oxygen and use it to form a carbon–oxygen double bond. In this case, however, there are three possible choices:
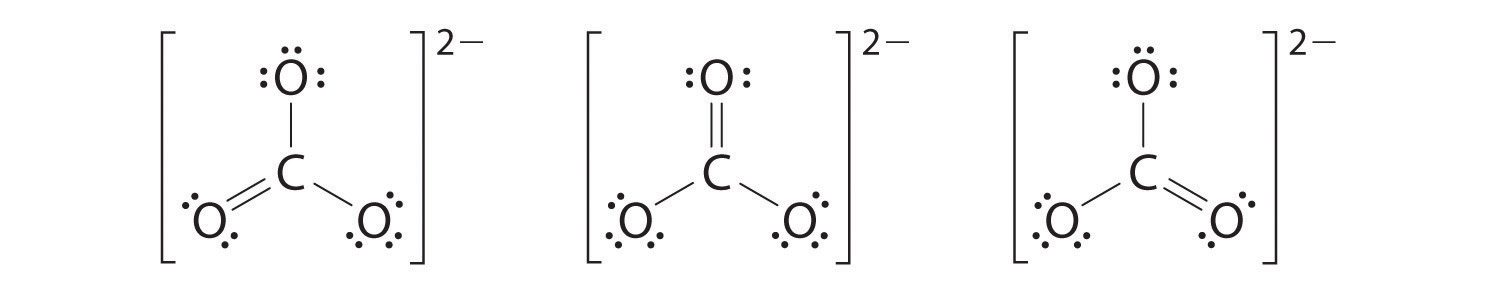
As with ozone, none of these structures describes the bonding exactly. Each predicts one carbon–oxygen double bond and two carbon–oxygen single bonds, but experimentally all C–O bond lengths are identical. We can write resonance structures (in this case, three of them) for the carbonate ion:
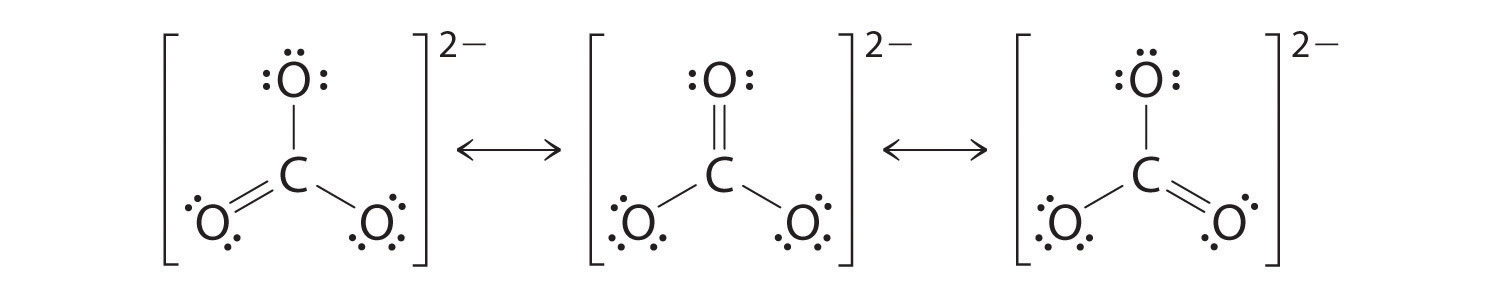
The actual structure is an average of these three resonance structures.
Example 7
Benzene is a common organic solvent that was previously used in gasoline; it is no longer used for this purpose, however, because it is now known to be a carcinogen. The benzene molecule (C6H6) consists of a regular hexagon of carbon atoms, each of which is also bonded to a hydrogen atom. Use resonance structures to describe the bonding in benzene.
Given: molecular formula and molecular geometry
Asked for: resonance structures
Strategy:
A Draw a structure for benzene illustrating the bonded atoms. Then calculate the number of valence electrons used in this drawing.
B Subtract this number from the total number of valence electrons in benzene and then locate the remaining electrons such that each atom in the structure reaches an octet.
C Draw the resonance structures for benzene.
Solution:
A Each hydrogen atom contributes 1 valence electron, and each carbon atom contributes 4 valence electrons, for a total of (6 × 1) + (6 × 4) = 30 valence electrons. If we place a single bonding electron pair between each pair of carbon atoms and between each carbon and a hydrogen atom, we obtain the following:
Each carbon atom in this structure has only 6 electrons and has a formal charge of +1, but we have used only 24 of the 30 valence electrons.
B If the 6 remaining electrons are uniformly distributed pairwise on alternate carbon atoms, we obtain the following:
Three carbon atoms now have an octet configuration and a formal charge of −1, while three carbon atoms have only 6 electrons and a formal charge of +1. We can convert each lone pair to a bonding electron pair, which gives each atom an octet of electrons and a formal charge of 0, by making three C=C double bonds.
C There are, however, two ways to do this:
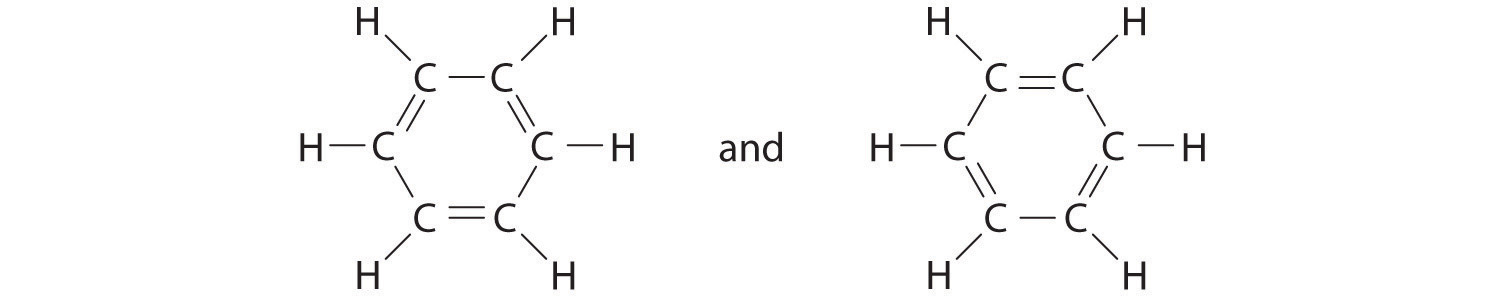
Each structure has alternating double and single bonds, but experimentation shows that each carbon–carbon bond in benzene is identical, with bond lengths (139.9 pm) intermediate between those typically found for a C–C single bond (154 pm) and a C=C double bond (134 pm). We can describe the bonding in benzene using the two resonance structures, but the actual electronic structure is an average of the two. The existence of multiple resonance structures for aromatic hydrocarbons like benzene is often indicated by drawing either a circle or dashed lines inside the hexagon:
Exercise
The sodium salt of nitrite is used to relieve muscle spasms. Draw two resonance structures for the nitrite ion (NO2−).
Answer:

Resonance structures are particularly common in oxoanions of the p-block elements, such as sulfate and phosphate, and in aromatic hydrocarbons, such as benzene and naphthalene.
Summary
A plot of the overall energy of a covalent bond as a function of internuclear distance is identical to a plot of an ionic pair because both result from attractive and repulsive forces between charged entities. In Lewis electron structures, we encounter bonding pairs, which are shared by two atoms, and lone pairs, which are not shared between atoms. If both electrons in a covalent bond come from the same atom, the bond is called a coordinate covalent bond. Lewis structures are an attempt to rationalize why certain stoichiometries are commonly observed for the elements of particular families. Neutral compounds of group 14 elements typically contain four bonds around each atom (a double bond counts as two, a triple bond as three), whereas neutral compounds of group 15 elements typically contain three bonds. In cases where it is possible to write more than one Lewis electron structure with octets around all the nonhydrogen atoms of a compound, the formal charge on each atom in alternative structures must be considered to decide which of the valid structures can be excluded and which is the most reasonable. The formal charge is the difference between the number of valence electrons of the free atom and the number of electrons assigned to it in the compound, where bonding electrons are divided equally between the bonded atoms. The Lewis structure with the lowest formal charges on the atoms is almost always the most stable one. Some molecules have two or more chemically equivalent Lewis electron structures, called resonance structures. These structures are written with a double-headed arrow between them, indicating that none of the Lewis structures accurately describes the bonding but that the actual structure is an average of the individual resonance structures.
Key Takeaway
- Lewis dot symbols provide a simple rationalization of why elements form compounds with the observed stoichiometries.
Conceptual Problems
-
Compare and contrast covalent and ionic compounds with regard to
- volatility.
- melting point.
- electrical conductivity.
- physical appearance.
-
What are the similarities between plots of the overall energy versus internuclear distance for an ionic compound and a covalent compound? Why are the plots so similar?
-
Which atom do you expect to be the central atom in each of the following species?
- SO42−
- NH4+
- BCl3
- SO2Cl2?
-
Which atom is the central atom in each of the following species?
- PCl3
- CHCl3
- SO2
- IF3?
-
What is the relationship between the number of bonds typically formed by the period 2 elements in groups 14, 15, and 16 and their Lewis electron structures?
-
Although formal charges do not represent actual charges on atoms in molecules or ions, they are still useful. Why?
-
Why are resonance structures important?
-
In what types of compounds are resonance structures particularly common?
Numerical Problems
-
Give the electron configuration and the Lewis dot symbol for the following. How many more electrons can each atom accommodate?
- Se
- Kr
- Li
- Sr
- H
-
Give the electron configuration and the Lewis dot symbol for the following. How many more electrons can each atom accommodate?
- Na
- Br
- Ne
- C
- Ga
-
Based on Lewis dot symbols, predict the preferred oxidation state of Be, F, B, and Cs.
-
Based on Lewis dot symbols, predict the preferred oxidation state of Br, Rb, O, Si, and Sr.
-
Based on Lewis dot symbols, predict how many bonds gallium, silicon, and selenium will form in their neutral compounds.
-
Determine the total number of valence electrons in the following.
- Cr
- Cu+
- NO+
- XeF2
- Br2
- CH2Cl2
- NO3−
- H3O+
-
Determine the total number of valence electrons in the following.
- Ag
- Pt2+
- H2S
- OH−
- I2
- CH4
- SO42−
- NH4+.
-
Draw Lewis electron structures for the following.
- F2
- SO2
- AlCl4−
- SO32−
- BrCl
- XeF4
- NO+
- PCl3
-
Draw Lewis electron structures for the following.
- Br2
- CH3Br
- SO42−
- O2
- S22−
- BF3
-
Draw Lewis electron structures for CO2, NO2−, SO2, and NO2+. From your diagram, predict which pair(s) of compounds have similar electronic structures.
-
Write Lewis dot symbols for each pair of elements. For a reaction between each pair of elements, predict which element is the oxidant, which element is the reductant, and the final stoichiometry of the compound formed.
- K, S
- Sr, Br
- Al, O
- Mg, Cl
-
Write Lewis dot symbols for each pair of elements. For a reaction between each pair of elements, predict which element is the oxidant, which element is the reductant, and the final stoichiometry of the compound formed.
- Li, F
- Cs, Br
- Ca, Cl
- B, F
-
Use Lewis dot symbols to predict whether ICl and NO4− are chemically reasonable formulas.
-
Draw a plausible Lewis electron structure for a compound with the molecular formula Cl3PO.
-
Draw a plausible Lewis electron structure for a compound with the molecular formula CH4O.
-
While reviewing her notes, a student noticed that she had drawn the following structure in her notebook for acetic acid:
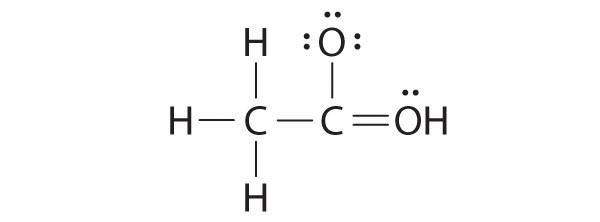
Why is this structure not feasible? Draw an acceptable Lewis structure for acetic acid. Show the formal charges of all nonhydrogen atoms in both the correct and incorrect structures.
-
A student proposed the following Lewis structure shown for acetaldehyde.
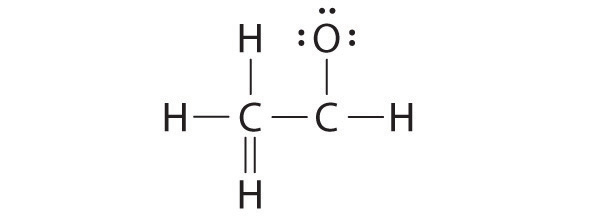
Why is this structure not feasible? Draw an acceptable Lewis structure for acetaldehyde. Show the formal charges of all nonhydrogen atoms in both the correct and incorrect structures.
-
Draw the most likely structure for HCN based on formal charges, showing the formal charge on each atom in your structure. Does this compound have any plausible resonance structures? If so, draw one.
-
Draw the most plausible Lewis structure for NO3−. Does this ion have any other resonance structures? Draw at least one other Lewis structure for the nitrate ion that is not plausible based on formal charges.
-
At least two Lewis structures can be drawn for BCl3. Using arguments based on formal charges, explain why the most likely structure is the one with three B–Cl single bonds.
-
Using arguments based on formal charges, explain why the most feasible Lewis structure for SO42− has two sulfur–oxygen double bonds.
-
At least two distinct Lewis structures can be drawn for N3−. Use arguments based on formal charges to explain why the most likely structure contains a nitrogen–nitrogen double bond.
-
Is H–O–N=O a reasonable structure for the compound HNO2? Justify your answer using Lewis electron dot structures.
-
Is H–O=C–H a reasonable structure for a compound with the formula CH2O? Use Lewis electron dot structures to justify your answer.
-
Explain why the following Lewis structure for SO32− is or is not reasonable.
-
Draw all the resonance structures for each ion.
- HSO4−
- HSO3−
Answers
-
-
[Ar]4s23d104p4
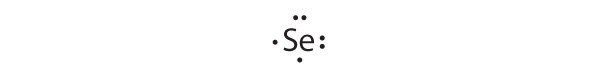
Selenium can accommodate two more electrons, giving the Se2− ion.
-
[Ar]4s23d104p6
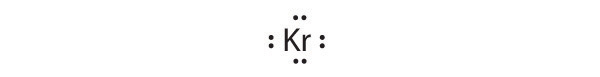
Krypton has a closed shell electron configuration, so it cannot accommodate any additional electrons.
-
1s22s1
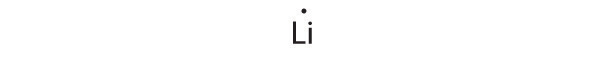
Lithium can accommodate one additional electron in its 2s orbital, giving the Li− ion.
-
[Kr]5s2
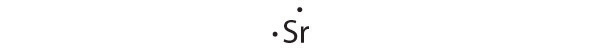
Strontium has a filled 5s subshell, and additional electrons would have to be placed in an orbital with a higher energy. Thus strontium has no tendency to accept an additional electron.
-
1s1

Hydrogen can accommodate one additional electron in its 1s orbital, giving the H− ion.
-
-
-
Be2+, F−, B3+, Cs+
-
-
-
-
- 11
- 8
- 8
- 8
- 14
- 8
- 32
- 8
-
-
-
-
-
-
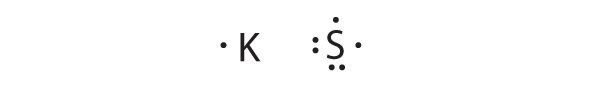
K is the reductant; S is the oxidant. The final stoichiometry is K2S.
-
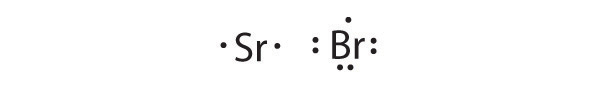
Sr is the reductant; Br is the oxidant. The final stoichiometry is SrBr2.
-
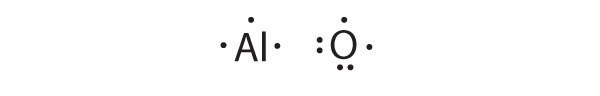
Al is the reductant; O is the oxidant. The final stoichiometry is Al2O3.
-

Mg is the reductant; Cl is the oxidant. The final stoichiometry is MgCl2.
-
-
-
-
-
The only structure that gives both oxygen and carbon an octet of electrons is the following:
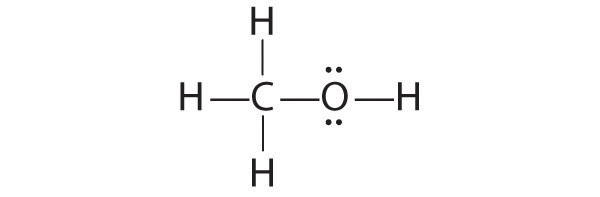
-
-
The student’s proposed structure has two flaws: the hydrogen atom with the double bond has four valence electrons (H can only accommodate two electrons), and the carbon bound to oxygen only has six valence electrons (it should have an octet). An acceptable Lewis structure is
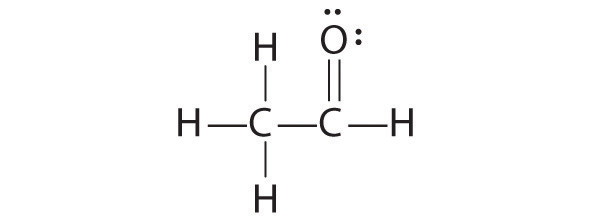
The formal charges on the correct and incorrect structures are as follows:
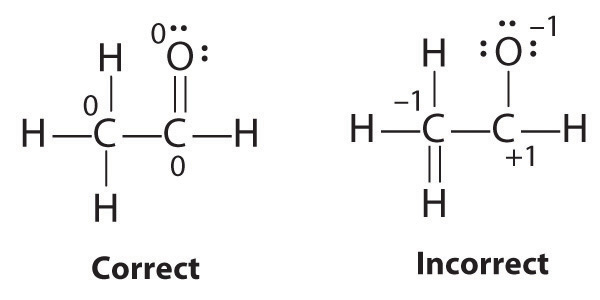
-
-
The most plausible Lewis structure for NO3− is:
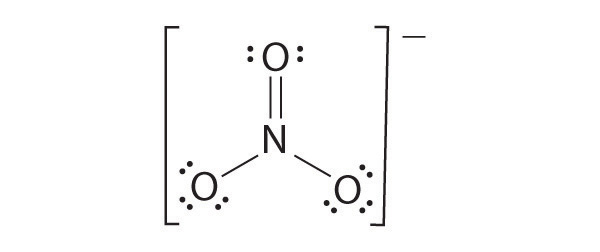
There are three equivalent resonance structures for nitrate (only one is shown), in which nitrogen is doubly bonded to one of the three oxygens. In each resonance structure, the formal charge of N is +1; for each singly bonded O, it is −1; and for the doubly bonded oxygen, it is 0.
The following is an example of a Lewis structure that is not plausible:
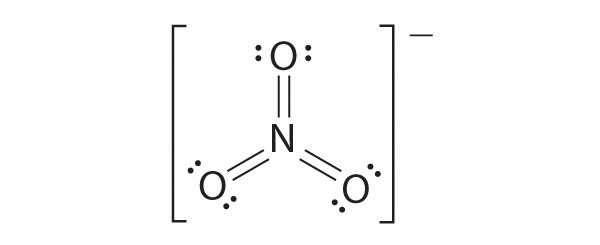
This structure nitrogen has six bonds (nitrogen can form only four bonds) and a formal charge of –1.
-
-
With four S–O single bonds, each oxygen in SO42− has a formal charge of −1, and the central sulfur has a formal charge of +2. With two S=O double bonds, only two oxygens have a formal charge of –1, and sulfur has a formal charge of zero. Lewis structures that minimize formal charges tend to be lowest in energy, making the Lewis structure with two S=O double bonds the most probable.
-
-
Yes. This is a reasonable Lewis structure, because the formal charge on all atoms is zero, and each atom (except H) has an octet of electrons.
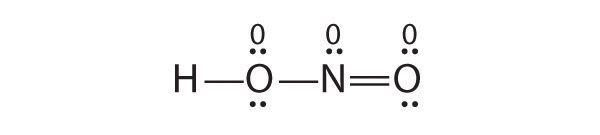
-
-
-
8.6 Exceptions to the Octet Rule
Learning Objective
- To assign a Lewis dot symbol to elements not having an octet of electrons in their compounds.
Lewis dot structures provide a simple model for rationalizing the bonding in most known compounds. However, there are three general exceptions to the octet rule: (1) molecules, such as NO, with an odd number of electrons; (2) molecules in which one or more atoms possess more than eight electrons, such as SF6; and (3) molecules such as BCl3, in which one or more atoms possess less than eight electrons.
Odd Number of Electrons
Because most molecules or ions that consist of s- and p-block elements contain even numbers of electrons, their bonding can be described using a model that assigns every electron to either a bonding pair or a lone pair.Molecules or ions containing d-block elements frequently contain an odd number of electrons, and their bonding cannot adequately be described using the simple approach we have developed so far. Bonding in these compounds will be discussed in Chapter 23 "The ". There are, however, a few molecules containing only p-block elements that have an odd number of electrons. Some important examples are nitric oxide (NO), whose biochemical importance was described in earlier chapters; nitrogen dioxide (NO2), an oxidizing agent in rocket propulsion; and chlorine dioxide (ClO2), which is used in water purification plants. Consider NO, for example. With 5 + 6 = 11 valence electrons, there is no way to draw a Lewis structure that gives each atom an octet of electrons. Molecules such as NO, NO2, and ClO2 require a more sophisticated treatment of bonding, which will be developed in Chapter 9 "Molecular Geometry and Covalent Bonding Models".
More Than an Octet of Electrons
The most common exception to the octet rule is a molecule or an ion with at least one atom that possesses more than an octet of electrons. Such compounds are found for elements of period 3 and beyond. Examples from the p-block elements include SF6, a substance used by the electric power industry to insulate high-voltage lines, and the SO42− and PO43− ions.
Let’s look at sulfur hexafluoride (SF6), whose Lewis structure must accommodate a total of 48 valence electrons [6 + (6 × 7) = 48]. If we arrange the atoms and electrons symmetrically, we obtain a structure with six bonds to sulfur; that is, it is six-coordinate. Each fluorine atom has an octet, but the sulfur atom has 12 electrons surrounding it rather than 8.The third step in our procedure for writing Lewis electron structures, in which we place an electron pair between each pair of bonded atoms, requires that an atom have more than 8 electrons whenever it is bonded to more than 4 other atoms.
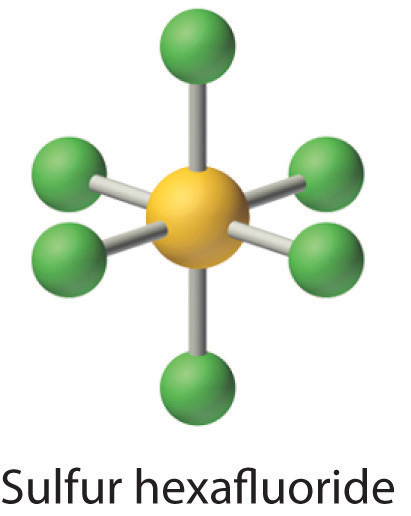

The octet rule is based on the fact that each valence orbital (typically, one ns and three np orbitals) can accommodate only two electrons. To accommodate more than eight electrons, sulfur must be using not only the ns and np valence orbitals but additional orbitals as well. Sulfur has an [Ne]3s23p43d0 electron configuration, so in principle it could accommodate more than eight valence electrons by using one or more d orbitals. Thus species such as SF6 are often called expanded-valence moleculesA compound with more than an octet of electrons around an atom.. Whether or not such compounds really do use d orbitals in bonding is controversial, but this model explains why compounds exist with more than an octet of electrons around an atom.
There is no correlation between the stability of a molecule or an ion and whether or not it has an expanded valence shell. Some species with expanded valences, such as PF5, are highly reactive, whereas others, such as SF6, are very unreactive. In fact, SF6 is so inert that it has many commercial applications. In addition to its use as an electrical insulator, it is used as the coolant in some nuclear power plants, and it is the pressurizing gas in “unpressurized” tennis balls.
An expanded valence shell is often written for oxoanions of the heavier p-block elements, such as sulfate (SO42−) and phosphate (PO43−). Sulfate, for example, has a total of 32 valence electrons [6 + (4 × 6) + 2]. If we use a single pair of electrons to connect the sulfur and each oxygen, we obtain the four-coordinate Lewis structure (a). We know that sulfur can accommodate more than eight electrons by using its empty valence d orbitals, just as in SF6. An alternative structure (b) can be written with S=O double bonds, making the sulfur again six-coordinate. We can draw five other resonance structures equivalent to (b) that vary only in the arrangement of the single and double bonds. In fact, experimental data show that the S-to-O bonds in the SO42− ion are intermediate in length between single and double bonds, as expected for a system whose resonance structures all contain two S–O single bonds and two S=O double bonds. When calculating the formal charges on structures (a) and (b), we see that the S atom in (a) has a formal charge of +2, whereas the S atom in (b) has a formal charge of 0. Thus by using an expanded octet, a +2 formal charge on S can be eliminated.

Note the Pattern
In oxoanions of the heavier p-block elements, the central atom often has an expanded valence shell.
Less Than an Octet of Electrons
Molecules with atoms that possess less than an octet of electrons generally contain the lighter s- and p-block elements, especially beryllium, typically with just four electrons around the central atom, and boron, typically with six. One example, boron trichloride (BCl3) is used to produce fibers for reinforcing high-tech tennis rackets and golf clubs. The compound has 24 valence electrons and the following Lewis structure:

The boron atom has only six valence electrons, while each chlorine atom has eight. A reasonable solution might be to use a lone pair from one of the chlorine atoms to form a B-to-Cl double bond:

This resonance structure, however, results in a formal charge of +1 on the doubly bonded Cl atom and −1 on the B atom. The high electronegativity of Cl makes this separation of charge unlikely and suggests that this is not the most important resonance structure for BCl3. This conclusion is shown to be valid based on the three equivalent B–Cl bond lengths of 173 pm that have no double bond character. Electron-deficient compounds such as BCl3 have a strong tendency to gain an additional pair of electrons by reacting with species with a lone pair of electrons.
Note the Pattern
Molecules with atoms that have fewer than an octet of electrons generally contain the lighter s- and p-block elements.
Note the Pattern
Electron-deficient compounds have a strong tendency to gain electrons in their reactions.
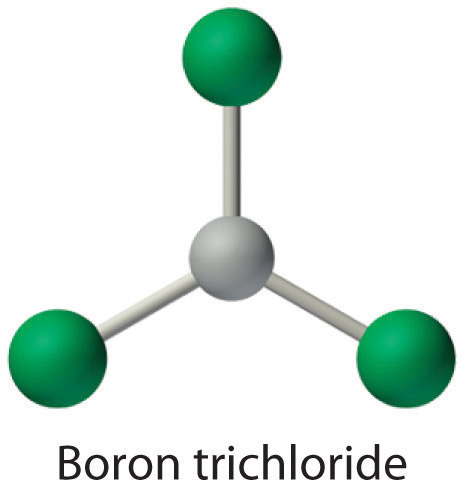
Example 8
Draw Lewis dot structures for each compound.
- BeCl2 gas, a compound used to produce beryllium, which in turn is used to produce structural materials for missiles and communication satellites
- SF4, a compound that reacts violently with water
Include resonance structures where appropriate.
Given: two compounds
Asked for: Lewis electron structures
Strategy:
A Use the procedure given earlier to write a Lewis electron structure for each compound. If necessary, place any remaining valence electrons on the element most likely to be able to accommodate more than an octet.
B After all the valence electrons have been placed, decide whether you have drawn an acceptable Lewis structure.
Solution:
-
A Because it is the least electronegative element, Be is the central atom. The molecule has 16 valence electrons (2 from Be and 7 from each Cl). Drawing two Be–Cl bonds and placing three lone pairs on each Cl gives the following structure:
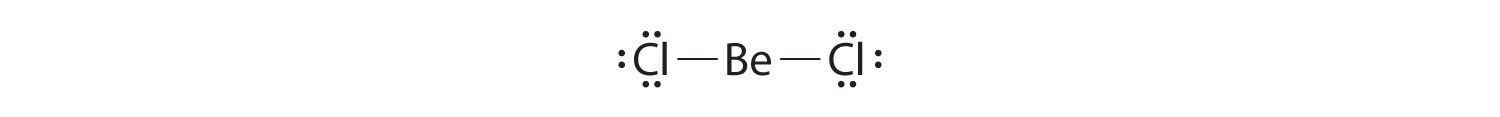
B Although this arrangement gives beryllium only 4 electrons, it is an acceptable Lewis structure for BeCl2. Beryllium is known to form compounds in which it is surrounded by less than an octet of electrons.
-
A Sulfur is the central atom because it is less electronegative than fluorine. The molecule has 34 valence electrons (6 from S and 7 from each F). The S–F bonds use 8 electrons, and another 24 are placed around the F atoms:

The only place to put the remaining 2 electrons is on the sulfur, giving sulfur 10 valence electrons:

B Sulfur can accommodate more than an octet, so this is an acceptable Lewis structure.
Exercise
Draw Lewis dot structures for XeF4.
Answer:

Summary
Molecules with an odd number of electrons are relatively rare in the s and p blocks but rather common among the d- and f-block elements. Compounds with more than an octet of electrons around an atom are called expanded-valence molecules. One model to explain their existence uses one or more d orbitals in bonding in addition to the valence ns and np orbitals. Such species are known for only atoms in period 3 or below, which contain nd subshells in their valence shell.
Key Takeaway
- General exceptions to the octet rule include molecules that have an odd number of electrons and molecules in which one or more atoms possess more or fewer than eight electrons.
Conceptual Problems
-
What regions of the periodic table contain elements that frequently form molecules with an odd number of electrons? Explain your answer.
-
How can atoms expand their valence shell? What is the relationship between an expanded valence shell and the stability of an ion or a molecule?
-
What elements are known to form compounds with less than an octet of electrons? Why do electron-deficient compounds form?
-
List three elements that form compounds that do not obey the octet rule. Describe the factors that are responsible for the stability of these compounds.
Numerical Problems
-
What is the major weakness of the Lewis system in predicting the electron structures of PCl6− and other species containing atoms from period 3 and beyond?
-
The compound aluminum trichloride consists of Al2Cl6 molecules with the following structure (lone pairs of electrons removed for clarity):

Does this structure satisfy the octet rule? What is the formal charge on each atom? Given the chemical similarity between aluminum and boron, what is a plausible explanation for the fact that aluminum trichloride forms a dimeric structure rather than the monomeric trigonal planar structure of BCl3?
-
Draw Lewis electron structures for ClO4−, IF5, SeCl4, and SbF5.
-
Draw Lewis electron structures for ICl3, Cl3PO, Cl2SO, and AsF6−.
-
Draw plausible Lewis structures for the phosphate ion, including resonance structures. What is the formal charge on each atom in your structures?
-
Draw an acceptable Lewis structure for PCl5, a compound used in manufacturing a form of cellulose. What is the formal charge of the central atom? What is the oxidation number of the central atom?
-
Using Lewis structures, draw all of the resonance structures for the BrO3− ion.
-
Draw an acceptable Lewis structure for xenon trioxide (XeO3), including all resonance structures.
Answers
-
-
-
ClO4− (one of four equivalent resonance structures)
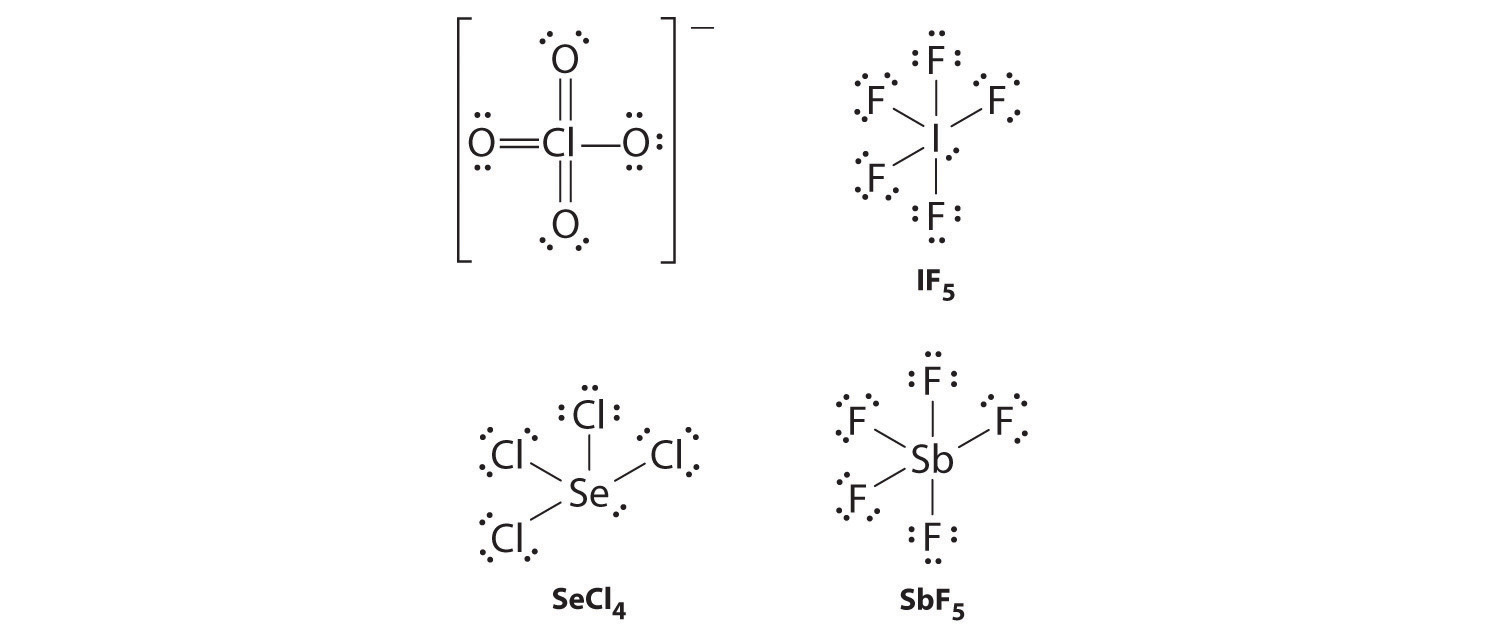
-
-
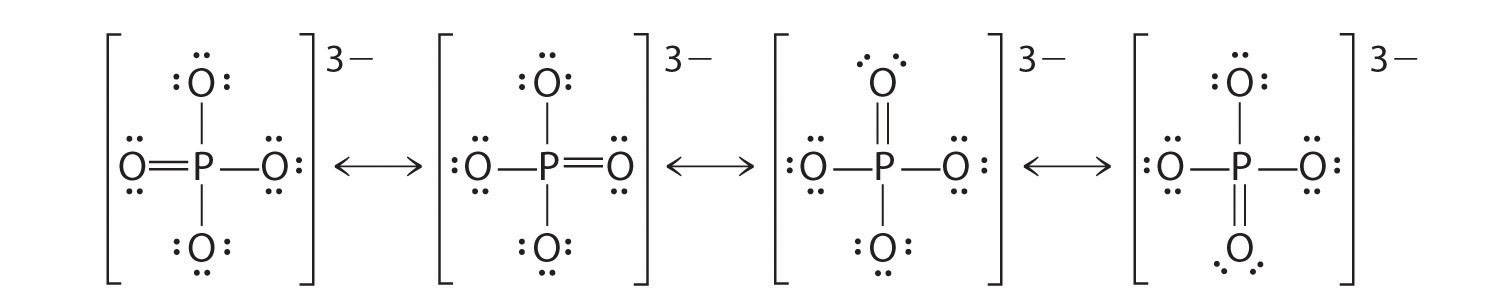
The formal charge on phosphorus is 0, while three oxygen atoms have a formal charge of −1 and one has a formal charge of zero.
-
-

-
8.7 Lewis Acids and Bases
Learning Objective
- To identify Lewis acids and bases.
As you learned in Chapter 4 "Reactions in Aqueous Solution", the Brønsted–Lowry concept of acids and bases defines a base as any species that can accept a proton, and an acid as any substance that can donate a proton. Lewis proposed an alternative definition that focuses on pairs of electrons instead.
A Lewis baseAny species that can donate a pair of electrons. is defined as any species that can donate a pair of electrons, and a Lewis acidAny species that can accept a pair of electrons. is any species that can accept a pair of electrons. All Brønsted–Lowry bases (proton acceptors), such as OH−, H2O, and NH3, are also electron-pair donors. Thus the Lewis definition of acids and bases does not contradict the Brønsted–Lowry definition. Rather, it expands the definition of acids to include substances other than the H+ ion.
Electron-deficient moleculesA compound that has less than an octet of electrons around one atom., such as BCl3, contain less than an octet of electrons around one atom and have a strong tendency to gain an additional pair of electrons by reacting with substances that possess a lone pair of electrons. Lewis’s definition, which is less restrictive than either the Brønsted–Lowry or the Arrhenius definition, grew out of his observation of this tendency.
Note the Pattern
Electron-deficient molecules (those with less than an octet of electrons) are Lewis acids.
A general Brønsted–Lowry acid–base reaction can be depicted in Lewis electron symbols as follows:

The proton (H+), which has no valence electrons, is a Lewis acid because it accepts a lone pair of electrons on the base to form a bond. The proton, however, is just one of many electron-deficient species that are known to react with bases. For example, neutral compounds of boron, aluminum, and the other group 13 elements, which possess only six valence electrons, have a very strong tendency to gain an additional electron pair. Such compounds are therefore potent Lewis acids that react with an electron-pair donor such as ammonia to form an acid–base adductThe product of a reaction between a Lewis acid and a Lewis base with a coordinate covalent bond., a new covalent bond, as shown here for boron trifluoride (BF3):

The bond formed between a Lewis acid and a Lewis base is a coordinate covalent bond because both electrons are provided by only one of the atoms (N, in the case of F3B:NH3). After it is formed, however, a coordinate covalent bond behaves like any other covalent single bond.
Species that are very weak Brønsted–Lowry bases can be relatively strong Lewis bases. For example, many of the group 13 trihalides are highly soluble in ethers (R–O–R′) because the oxygen atom in the ether contains two lone pairs of electrons, just as in H2O. Hence the predominant species in solutions of electron-deficient trihalides in ether solvents is a Lewis acid–base adduct. A reaction of this type is shown in Equation 8.19 for boron trichloride and diethyl ether:
Many molecules with multiple bonds can act as Lewis acids. In these cases, the Lewis base typically donates a pair of electrons to form a bond to the central atom of the molecule, while a pair of electrons displaced from the multiple bond becomes a lone pair on a terminal atom. A typical example is the reaction of the hydroxide ion with carbon dioxide to give the bicarbonate ion, as shown in Equation 8.21. The highly electronegative oxygen atoms pull electron density away from carbon, so the carbon atom acts as a Lewis acid. Arrows indicate the direction of electron flow.

Example 9
Identify the acid and the base in each Lewis acid–base reaction.
- BH3 + (CH3)2S → H3B:S(CH3)2
- CaO + CO2 → CaCO3
- BeCl2 + 2 Cl− → BeCl42−
Given: reactants and products
Asked for: identity of Lewis acid and Lewis base
Strategy:
In each equation, identify the reactant that is electron deficient and the reactant that is an electron-pair donor. The electron-deficient compound is the Lewis acid, whereas the other is the Lewis base.
Solution:
- In BH3, boron has only six valence electrons. It is therefore electron deficient and can accept a lone pair. Like oxygen, the sulfur atom in (CH3)2S has two lone pairs. Thus (CH3)2S donates an electron pair on sulfur to the boron atom of BH3. The Lewis base is (CH3)2S, and the Lewis acid is BH3.
- As in the reaction shown in Equation 8.21, CO2 accepts a pair of electrons from the O2− ion in CaO to form the carbonate ion. The oxygen in CaO is an electron-pair donor, so CaO is the Lewis base. Carbon accepts a pair of electrons, so CO2 is the Lewis acid.
- The chloride ion contains four lone pairs. In this reaction, each chloride ion donates one lone pair to BeCl2, which has only four electrons around Be. Thus the chloride ions are Lewis bases, and BeCl2 is the Lewis acid.
Exercise
Identify the acid and the base in each Lewis acid–base reaction.
- (CH3)2O + BF3 → (CH3)2O:BF3
- H2O + SO3 → H2SO4
Answer:
- Lewis base: (CH3)2O; Lewis acid: BF3
- Lewis base: H2O; Lewis acid: SO3
Summary
A Lewis acid is a compound with a strong tendency to accept an additional pair of electrons from a Lewis base, which can donate a pair of electrons. Such an acid–base reaction forms an adduct, which is a compound with a coordinate covalent bond in which both electrons are provided by only one of the atoms. Electron-deficient molecules, which have less than an octet of electrons around one atom, are relatively common. They tend to acquire an octet electron configuration by reacting with an atom having a lone pair of electrons.
Key Takeaway
- The acid-base behavior of many compounds can be explained by their Lewis electron structures.
Conceptual Problems
-
Construct a table comparing how OH−, NH3, H2O, and BCl3 are classified according to the Arrhenius, the Brønsted–Lowry, and the Lewis definitions of acids and bases.
-
Describe how the proton (H+) can simultaneously behave as an Arrhenius acid, a Brønsted–Lowry acid, and a Lewis acid.
-
Would you expect aluminum to form compounds with covalent bonds or coordinate covalent bonds? Explain your answer.
-
Classify each compound as a Lewis acid or a Lewis base and justify your choice.
- AlCl3
- (CH3)3N
- IO3−
-
Explain how a carboxylate ion (RCO2−) can act as both a Brønsted–Lowry base and a Lewis base.
Numerical Problems
-
In each reaction, identify the Lewis acid and the Lewis base and complete the reaction by writing the products(s).
- (CH3)2O + AlCl3
- SnCl4 + 2 Cl−
-
Use Lewis dot symbols to depict the reaction of BCl3 with dimethyl ether [(CH3)2O]. How is this reaction similar to that in which a proton is added to ammonia?
Answer
-
- AlCl3 is the Lewis acid, and the ether is the Lewis base; AlCl3 + (CH3)2O → AlCl3·O(CH3)2
- SnCl4 is the Lewis acid, and chloride is the Lewis base; SnCl4 + 2 Cl− → SnCl62−
-
8.8 Properties of Covalent Bonds
Learning Objective
- To understand the relationship between bond order, bond length, and bond energy.
In proposing his theory that octets can be completed by two atoms sharing electron pairs, Lewis provided scientists with the first description of covalent bonding. In this section, we expand on this and describe some of the properties of covalent bonds.
Bond Order
When we draw Lewis structures, we place one, two, or three pairs of electrons between adjacent atoms. In the Lewis bonding model, the number of electron pairs that hold two atoms together is called the bond orderThe number of electron pairs that hold two atoms together.. For a single bond, such as the C–C bond in H3C–CH3, the bond order is one. For a double bond (such as H2C=CH2), the bond order is two. For a triple bond, such as HC≡CH, the bond order is three.
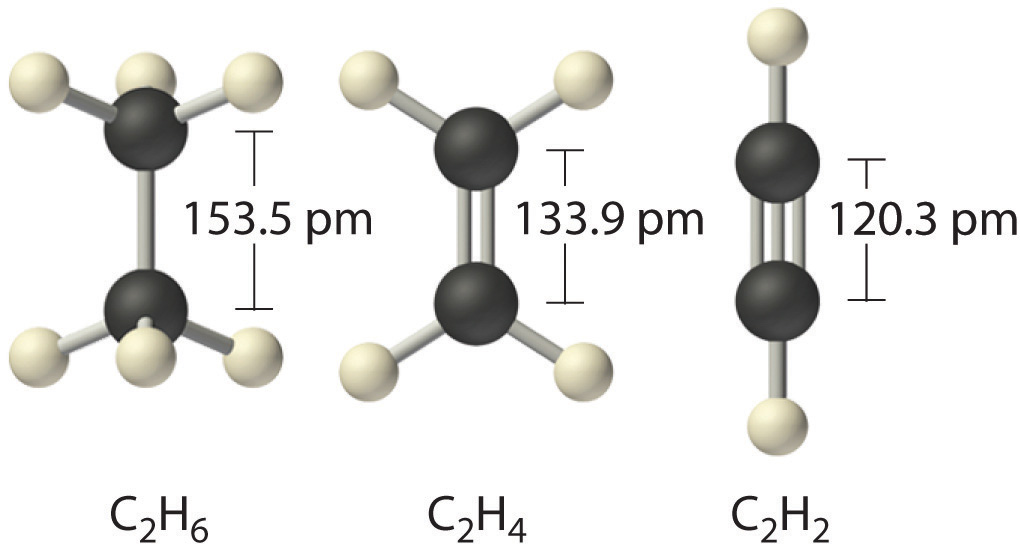
When analogous bonds in similar compounds are compared, bond length decreases as bond order increases. The bond length data in Table 8.5 "Bond Lengths and Bond Dissociation Energies for Bonds with Different Bond Orders in Selected Gas-Phase Molecules at 298 K", for example, show that the C–C distance in H3C–CH3 (153.5 pm) is longer than the distance in H2C=CH2 (133.9 pm), which in turn is longer than that in HC≡CH (120.3 pm). Additionally, as noted in Section 8.5 "Lewis Structures and Covalent Bonding", molecules or ions whose bonding must be described using resonance structures usually have bond distances that are intermediate between those of single and double bonds, as we demonstrated with the C–C distances in benzene. The relationship between bond length and bond order is not linear, however. A double bond is not half as long as a single bond, and the length of a C=C bond is not the average of the lengths of C≡C and C–C bonds. Nevertheless, as bond orders increase, bond lengths generally decrease.
Table 8.5 Bond Lengths and Bond Dissociation Energies for Bonds with Different Bond Orders in Selected Gas-Phase Molecules at 298 K
| Compound | Bond Order | Bond Length (pm) | Bond Dissociation Energy (kJ/mol) | Compound | Bond Order | Bond Length (pm) | Bond Dissociation Energy (kJ/mol) |
|---|---|---|---|---|---|---|---|
| H3C–CH3 | 1 | 153.5 | 376 | H3C–NH2 | 1 | 147.1 | 331 |
| H2C=CH2 | 2 | 133.9 | 728 | H2C=NH | 2 | 127.3 | 644 |
| HC≡CH | 3 | 120.3 | 965 | HC≡N | 3 | 115.3 | 937 |
| H2N–NH2 | 1 | 144.9 | 275.3 | H3C–OH | 1 | 142.5 | 377 |
| HN=NH | 2 | 125.2 | 456 | H2C=O | 2 | 120.8 | 732 |
| N≡N | 3 | 109.8 | 945.3 | O=C=O | 2 | 116.0 | 799 |
| HO–OH | 1 | 147.5 | 213 | C≡O | 3 | 112.8 | 1076.5 |
| O=O | 2 | 120.7 | 498.4 | ||||
Sources: Data from CRC Handbook of Chemistry and Physics (2004); Lange’s Handbook of Chemistry (2005); http://cccbdb.nist.gov.
The Relationship between Bond Order and Bond Energy
As shown in Table 8.5 "Bond Lengths and Bond Dissociation Energies for Bonds with Different Bond Orders in Selected Gas-Phase Molecules at 298 K", triple bonds between like atoms are shorter than double bonds, and because more energy is required to completely break all three bonds than to completely break two, a triple bond is also stronger than a double bond. Similarly, double bonds between like atoms are stronger and shorter than single bonds. Bonds of the same order between different atoms show a wide range of bond energies, however. Table 8.6 "Average Bond Energies (kJ/mol) for Commonly Encountered Bonds at 273 K" lists the average values for some commonly encountered bonds. Although the values shown vary widely, we can observe four trends:
Table 8.6 Average Bond Energies (kJ/mol) for Commonly Encountered Bonds at 273 K
| Single Bonds | Multiple Bonds | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| H–H | 432 | C–C | 346 | N–N | ≈167 | O–O | ≈142 | F–F | 155 | C=C | 602 |
| H–C | 411 | C–Si | 318 | N–O | 201 | O–F | 190 | F–Cl | 249 | C≡C | 835 |
| H–Si | 318 | C–N | 305 | N–F | 283 | O–Cl | 218 | F–Br | 249 | C=N | 615 |
| H–N | 386 | C–O | 358 | N–Cl | 313 | O–Br | 201 | F–I | 278 | C≡N | 887 |
| H–P | ≈322 | C–S | 272 | N–Br | 243 | O–I | 201 | Cl–Cl | 240 | C=O | 749 |
| H–O | 459 | C–F | 485 | P–P | 201 | S–S | 226 | Cl–Br | 216 | C≡O | 1072 |
| H–S | 363 | C–Cl | 327 | S–F | 284 | Cl–I | 208 | N=N | 418 | ||
| H–F | 565 | C–Br | 285 | S–Cl | 255 | Br–Br | 190 | N≡N | 942 | ||
| H–Cl | 428 | C–I | 213 | S–Br | 218 | Br–I | 175 | N=O | 607 | ||
| H–Br | 362 | Si–Si | 222 | I–I | 149 | O=O | 494 | ||||
| H–I | 295 | Si–O | 452 | S=O | 532 | ||||||
Source: Data from J. E. Huheey, E. A. Keiter, and R. L. Keiter, Inorganic Chemistry, 4th ed. (1993).
1. Bonds between hydrogen and atoms in the same column of the periodic table decrease in strength as we go down the column. Thus an H–F bond is stronger than an H–I bond, H–C is stronger than H–Si, H–N is stronger than H–P, H–O is stronger than H–S, and so forth. The reason for this is that the region of space in which electrons are shared between two atoms becomes proportionally smaller as one of the atoms becomes larger (part (a) in Figure 8.11 "The Strength of Covalent Bonds Depends on the Overlap between the Valence Orbitals of the Bonded Atoms").
2. Bonds between like atoms usually become weaker as we go down a column (important exceptions are noted later). For example, the C–C single bond is stronger than the Si–Si single bond, which is stronger than the Ge–Ge bond, and so forth. As two bonded atoms become larger, the region between them occupied by bonding electrons becomes proportionally smaller, as illustrated in part (b) in Figure 8.11 "The Strength of Covalent Bonds Depends on the Overlap between the Valence Orbitals of the Bonded Atoms". Noteworthy exceptions are single bonds between the period 2 atoms of groups 15, 16, and 17 (i.e., N, O, F), which are unusually weak compared with single bonds between their larger congeners. It is likely that the N–N, O–O, and F–F single bonds are weaker than might be expected due to strong repulsive interactions between lone pairs of electrons on adjacent atoms. The trend in bond energies for the halogens is therefore
Cl–Cl > Br–Br > F–F > I–ISimilar effects are also seen for the O–O versus S–S and for N–N versus P–P single bonds.
Note the Pattern
Bonds between hydrogen and atoms in a given column in the periodic table are weaker down the column; bonds between like atoms usually become weaker down a column.
3. Because elements in periods 3 and 4 rarely form multiple bonds with themselves, their multiple bond energies are not accurately known. Nonetheless, they are presumed to be significantly weaker than multiple bonds between lighter atoms of the same families. Compounds containing an Si=Si double bond, for example, have only recently been prepared, whereas compounds containing C=C double bonds are one of the best-studied and most important classes of organic compounds.
Figure 8.11 The Strength of Covalent Bonds Depends on the Overlap between the Valence Orbitals of the Bonded Atoms

The relative sizes of the region of space in which electrons are shared between (a) a hydrogen atom and lighter (smaller) vs. heavier (larger) atoms in the same periodic group; and (b) two lighter versus two heavier atoms in the same group. Although the absolute amount of shared space increases in both cases on going from a light to a heavy atom, the amount of space relative to the size of the bonded atom decreases; that is, the percentage of total orbital volume decreases with increasing size. Hence the strength of the bond decreases.
4. Multiple bonds between carbon, oxygen, or nitrogen and a period 3 element such as phosphorus or sulfur tend to be unusually strong. In fact, multiple bonds of this type dominate the chemistry of the period 3 elements of groups 15 and 16. Multiple bonds to phosphorus or sulfur occur as a result of d-orbital interactions, as we discussed for the SO42− ion in Section 8.6 "Exceptions to the Octet Rule". In contrast, silicon in group 14 has little tendency to form discrete silicon–oxygen double bonds. Consequently, SiO2 has a three-dimensional network structure in which each silicon atom forms four Si–O single bonds, which makes the physical and chemical properties of SiO2 very different from those of CO2.
Note the Pattern
Bond strengths increase as bond order increases, while bond distances decrease.
The Relationship between Molecular Structure and Bond Energy
Bond energy is defined as the energy required to break a particular bond in a molecule in the gas phase. Its value depends on not only the identity of the bonded atoms but also their environment. Thus the bond energy of a C–H single bond is not the same in all organic compounds. For example, the energy required to break a C–H bond in methane varies by as much as 25% depending on how many other bonds in the molecule have already been broken (Table 8.7 "Energies for the Dissociation of Successive C–H Bonds in Methane"); that is, the C–H bond energy depends on its molecular environment. Except for diatomic molecules, the bond energies listed in Table 8.6 "Average Bond Energies (kJ/mol) for Commonly Encountered Bonds at 273 K" are average values for all bonds of a given type in a range of molecules. Even so, they are not likely to differ from the actual value of a given bond by more than about 10%.
Table 8.7 Energies for the Dissociation of Successive C–H Bonds in Methane
| Reaction | D (kJ/mol) |
|---|---|
| CH4(g) → CH3(g) + H(g) | 439 |
| CH3(g) → CH2(g) + H(g) | 462 |
| CH2(g) → CH(g) + H(g) | 424 |
| CH(g) → C(g) + H(g) | 338 |
Source: Data from CRC Handbook of Chemistry and Physics (2004).
We can estimate the enthalpy change for a chemical reaction by adding together the average energies of the bonds broken in the reactants and the average energies of the bonds formed in the products and then calculating the difference between the two. If the bonds formed in the products are stronger than those broken in the reactants, then energy will be released in the reaction (ΔHrxn < 0):
Equation 8.14
The ≈ sign is used because we are adding together average bond energies; hence this approach does not give exact values for ΔHrxn.
Let’s consider the reaction of 1 mol of n-heptane (C7H16) with oxygen gas to give carbon dioxide and water. This is one reaction that occurs during the combustion of gasoline:
Equation 8.15
CH3(CH2)5CH3(l) + 11 O2(g) → 7 CO2(g) + 8 H2O(g)In this reaction, 6 C–C bonds, 16 C–H bonds, and 11 O=O bonds are broken per mole of n-heptane, while 14 C=O bonds (two for each CO2) and 16 O–H bonds (two for each H2O) are formed. The energy changes can be tabulated as follows:
| Bonds Broken (kJ/mol) | Bonds Formed (kJ/mol) | ||
|---|---|---|---|
| 6 C–C | 346 × 6 = 2076 | 14 C=O | 799 × 14 = 11,186 |
| 16 C–H | 411 × 16 = 6576 | 16 O–H | 459 × 16 = 7344 |
| 11 O=O | 494 × 11 = 5434 | Total = 18,530 | |
| Total = 14,086 | |||
The bonds in the products are stronger than the bonds in the reactants by about 4444 kJ/mol. This means that ΔHrxn is approximately −4444 kJ/mol, and the reaction is highly exothermic (which is not too surprising for a combustion reaction).
If we compare this approximation with the value obtained from measured values (ΔHrxn = −4817 kJ/mol), we find a discrepancy of only about 8%, less than the 10% typically encountered. Chemists find this method useful for calculating approximate enthalpies of reaction for molecules whose actual values are unknown. These approximations can be important for predicting whether a reaction is exothermic or endothermic—and to what degree.
Example 10
The compound RDX (Research Development Explosive) is a more powerful explosive than dynamite and is used by the military. When detonated, it produces gaseous products and heat according to the following reaction. Use the approximate bond energies in Table 8.6 "Average Bond Energies (kJ/mol) for Commonly Encountered Bonds at 273 K" to estimate the ΔHrxn per mole of RDX.
Given: chemical reaction, structure of reactant, and Table 8.6 "Average Bond Energies (kJ/mol) for Commonly Encountered Bonds at 273 K"
Asked for: ΔHrxn per mole
Strategy:
A List the types of bonds broken in RDX, along with the bond energy required to break each type. Multiply the number of each type by the energy required to break one bond of that type and then add together the energies. Repeat this procedure for the bonds formed in the reaction.
B Use Equation 8.14 to calculate the amount of energy consumed or released in the reaction (ΔHrxn).
Solution:
We must add together the energies of the bonds in the reactants and compare that quantity with the sum of the energies of the bonds in the products. A nitro group (–NO2) can be viewed as having one N–O single bond and one N=O double bond, as follows:

In fact, however, both N–O distances are usually the same because of the presence of two equivalent resonance structures.
A We can organize our data by constructing a table:
| Bonds Broken (kJ/mol) | Bonds Formed (kJ/mol) | ||
|---|---|---|---|
| 6 C–N | 305 × 6 = 1830 | 3 N≡N | 942 × 3 = 2826 |
| 6 C–H | 411 × 6 = 2466 | 6 C=O | 799 × 6 = 4794 |
| 3 N–N | 167 × 3 = 501 | 6 O–H | 459 × 6 = 2754 |
| 3 N–O | 201 × 3 = 603 | Total = 10,374 | |
| 3 N=O | 607 × 3 = 1821 | ||
| 1.5 O=O | 494 × 1.5 = 741 | ||
| Total = 7962 | |||
B From Equation 8.14, we have
Thus this reaction is also highly exothermic.
Exercise
The molecule HCFC-142b, a hydrochlorofluorocarbon used in place of chlorofluorocarbons (CFCs) such as the Freons, can be prepared by adding HCl to 1,1-difluoroethylene:

Use tabulated bond energies to calculate ΔHrxn.
Answer: −54 kJ/mol
Summary
Bond order is the number of electron pairs that hold two atoms together. Single bonds have a bond order of one, and multiple bonds with bond orders of two (a double bond) and three (a triple bond) are quite common. In closely related compounds with bonds between the same kinds of atoms, the bond with the highest bond order is both the shortest and the strongest. In bonds with the same bond order between different atoms, trends are observed that, with few exceptions, result in the strongest single bonds being formed between the smallest atoms. Tabulated values of average bond energies can be used to calculate the enthalpy change of many chemical reactions. If the bonds in the products are stronger than those in the reactants, the reaction is exothermic and vice versa.
Key Takeaway
- The strength of a covalent bond depends on the overlap between the valence orbitals of the bonded atoms.
Conceptual Problems
-
Which would you expect to be stronger—an S–S bond or an Se–Se bond? Why?
-
Which element—nitrogen, phosphorus, or arsenic—will form the strongest multiple bond with oxygen? Why?
-
Why do multiple bonds between oxygen and period 3 elements tend to be unusually strong?
-
What can bond energies tell you about reactivity?
-
Bond energies are typically reported as average values for a range of bonds in a molecule rather than as specific values for a single bond? Why?
-
If the bonds in the products are weaker than those in the reactants, is a reaction exothermic or endothermic? Explain your answer.
-
A student presumed that because heat was required to initiate a particular reaction, the reaction product would be stable. Instead, the product exploded. What information might have allowed the student to predict this outcome?
Numerical Problems
-
What is the bond order about the central atom(s) of hydrazine (N2H4), nitrogen, and diimide (N2H2)? Draw Lewis electron structures for each compound and then arrange these compounds in order of increasing N–N bond distance. Which of these compounds would you expect to have the largest N–N bond energy? Explain your answer.
-
What is the carbon–carbon bond order in ethylene (C2H4), BrH2CCH2Br, and FCCH? Arrange the compounds in order of increasing C–C bond distance. Which would you expect to have the largest C–C bond energy? Why?
-
From each pair of elements, select the one with the greater bond strength? Explain your choice in each case.
- P–P, Sb–Sb
- Cl–Cl, I–I
- O–O, Se–Se
- S–S, Cl–Cl
- Al–Cl, B–Cl
-
From each pair of elements, select the one with the greater bond strength? Explain your choice in each case.
- Te–Te, S–S
- C–H, Ge–H
- Si–Si, P–P
- Cl–Cl, F–F
- Ga–H, Al–H
-
Approximately how much energy per mole is required to completely dissociate acetone [(CH3)2CO] and urea [(NH2)2CO] into their constituent atoms?
-
Approximately how much energy per mole is required to completely dissociate ethanol, formaldehyde, and hydrazine into their constituent atoms?
-
Is the reaction of diimine (N2H2) with oxygen to produce nitrogen and water exothermic or endothermic? Quantify your answer.
Answer
-
N2H4, bond order 1; N2H2, bond order 2; N2, bond order 3; N–N bond distance: N2 < N2H2 < N2H4; Largest bond energy: N2; Highest bond order correlates with strongest and shortest bond.
-
-
-
-
-
-
8.9 Polar Covalent Bonds
Learning Objective
- To calculate the percent ionic character of a covalent polar bond..
In Chapter 2 "Molecules, Ions, and Chemical Formulas" and Section 8.1 "An Overview of Chemical Bonding", we described the two idealized extremes of chemical bonding: (1) ionic bonding—in which one or more electrons are transferred completely from one atom to another, and the resulting ions are held together by purely electrostatic forces—and (2) covalent bonding, in which electrons are shared equally between two atoms. Most compounds, however, have polar covalent bondsA covalent bond in which the electrons are shared unequally between the bonded atoms., which means that electrons are shared unequally between the bonded atoms. Figure 8.12 "The Electron Distribution in a Nonpolar Covalent Bond, a Polar Covalent Bond, and an Ionic Bond Using Lewis Electron Structures" compares the electron distribution in a polar covalent bond with those in an ideally covalent and an ideally ionic bond. Recall from Chapter 4 "Reactions in Aqueous Solution", Section 4.1 "Aqueous Solutions" that a lowercase Greek delta () is used to indicate that a bonded atom possesses a partial positive charge, indicated by or a partial negative charge, indicated by and a bond between two atoms that possess partial charges is a polar bond.
Figure 8.12 The Electron Distribution in a Nonpolar Covalent Bond, a Polar Covalent Bond, and an Ionic Bond Using Lewis Electron Structures
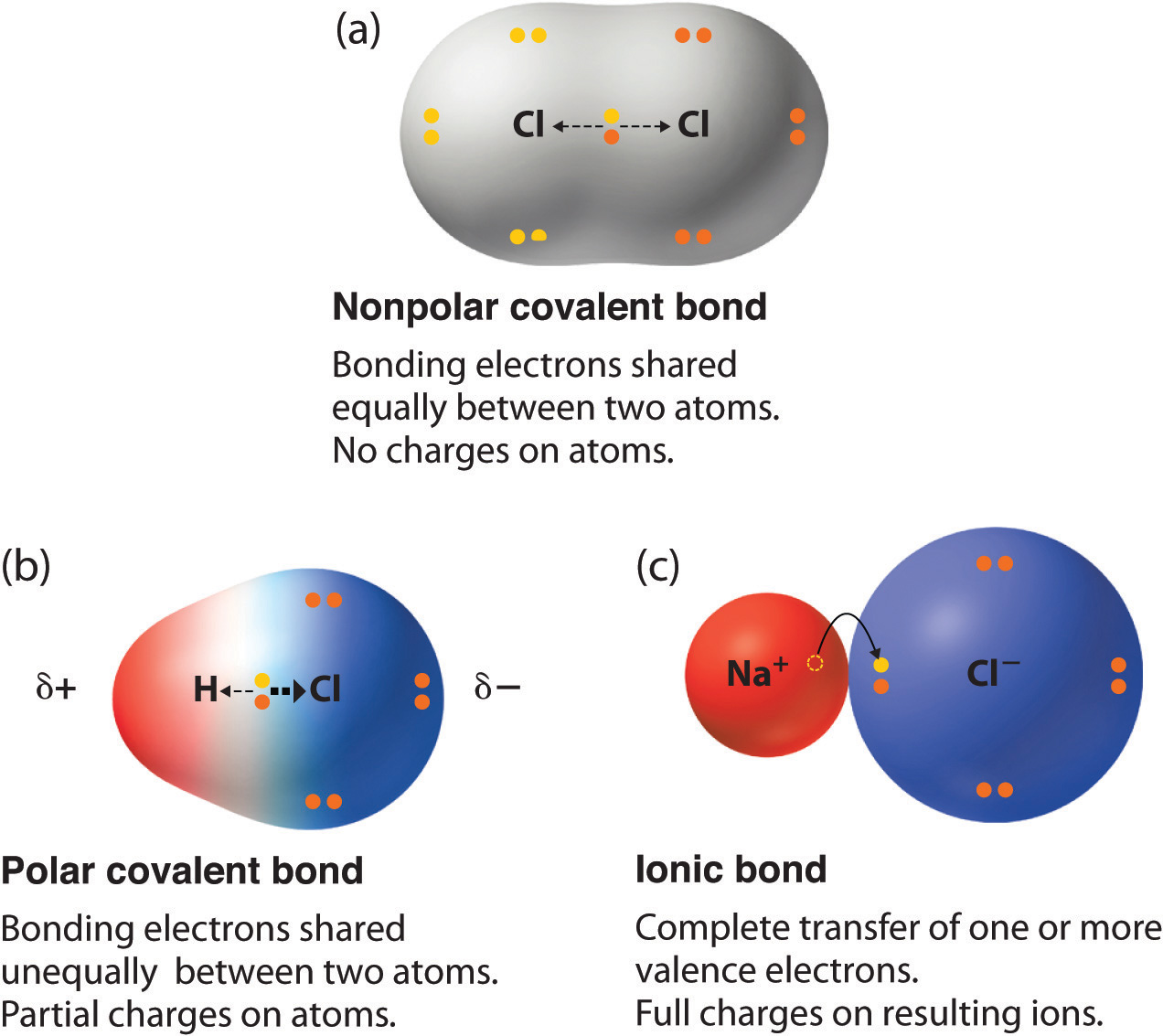
In a purely covalent bond (a), the bonding electrons are shared equally between the atoms. In a purely ionic bond (c), an electron has been transferred completely from one atom to the other. A polar covalent bond (b) is intermediate between the two extremes: the bonding electrons are shared unequally between the two atoms, and the electron distribution is asymmetrical with the electron density being greater around the more electronegative atom. Electron-rich (negatively charged) regions are shown in blue; electron-poor (positively charged) regions are shown in red.
Bond Polarity
The polarity of a bond—the extent to which it is polar—is determined largely by the relative electronegativities of the bonded atoms. In Chapter 7 "The Periodic Table and Periodic Trends", electronegativity (χ) was defined as the ability of an atom in a molecule or an ion to attract electrons to itself. Thus there is a direct correlation between electronegativity and bond polarity. A bond is nonpolar if the bonded atoms have equal electronegativities. If the electronegativities of the bonded atoms are not equal, however, the bond is polarized toward the more electronegative atom. A bond in which the electronegativity of B (χB) is greater than the electronegativity of A (χA), for example, is indicated with the partial negative charge on the more electronegative atom:
One way of estimating the ionic character of a bond—that is, the magnitude of the charge separation in a polar covalent bond—is to calculate the difference in electronegativity between the two atoms: Δχ = χB − χA.
To predict the polarity of the bonds in Cl2, HCl, and NaCl, for example, we look at the electronegativities of the relevant atoms: χCl = 3.16, χH = 2.20, and χNa = 0.93 (see Figure 7.14 "A Plot of Periodic Variation of Electronegativity with Atomic Number for the First Six Rows of the Periodic Table"). Cl2 must be nonpolar because the electronegativity difference (Δχ) is zero; hence the two chlorine atoms share the bonding electrons equally. In NaCl, Δχ is 2.23. This high value is typical of an ionic compound (Δχ ≥ ≈1.5) and means that the valence electron of sodium has been completely transferred to chlorine to form Na+ and Cl− ions. In HCl, however, Δχ is only 0.96. The bonding electrons are more strongly attracted to the more electronegative chlorine atom, and so the charge distribution is
Remember that electronegativities are difficult to measure precisely and different definitions produce slightly different numbers. In practice, the polarity of a bond is usually estimated rather than calculated.
Note the Pattern
Bond polarity and ionic character increase with an increasing difference in electronegativity.
As with bond energies, the electronegativity of an atom depends to some extent on its chemical environment. It is therefore unlikely that the reported electronegativities of a chlorine atom in NaCl, Cl2, ClF5, and HClO4 would be exactly the same.
Dipole Moments
The asymmetrical charge distribution in a polar substance such as HCl produces a dipole momentThe product of the partial charge on the bonded atoms and the distance between the partial charges: , where is measured in coulombs (C) and in meters (m)., abbreviated by the Greek letter mu (µ). The dipole moment is defined as the product of the partial charge Q on the bonded atoms and the distance r between the partial charges:
Equation 8.16
µ = Qrwhere Q is measured in coulombs (C) and r in meters. The unit for dipole moments is the debye (D):
Equation 8.17
1 D = 3.3356 × 10−30 C·mWhen a molecule with a dipole moment is placed in an electric field, it tends to orient itself with the electric field because of its asymmetrical charge distribution (Figure 8.13 "Molecules That Possess a Dipole Moment Partially Align Themselves with an Applied Electric Field").
Figure 8.13 Molecules That Possess a Dipole Moment Partially Align Themselves with an Applied Electric Field
In the absence of a field (a), the HCl molecules are randomly oriented. When an electric field is applied (b), the molecules tend to align themselves with the field, such that the positive end of the molecular dipole points toward the negative terminal and vice versa.
We can measure the partial charges on the atoms in a molecule such as HCl using Equation 8.16. If the bonding in HCl were purely ionic, an electron would be transferred from H to Cl, so there would be a full +1 charge on the H atom and a full −1 charge on the Cl atom. The dipole moment of HCl is 1.109 D, as determined by measuring the extent of its alignment in an electric field, and the reported gas-phase H–Cl distance is 127.5 pm. Hence the charge on each atom is
Equation 8.18
By dividing this calculated value by the charge on a single electron (1.6022 × 10−19 C), we find that the charge on the Cl atom of an HCl molecule is about −0.18, corresponding to about 0.18 e−:
Equation 8.19
To form a neutral compound, the charge on the H atom must be equal but opposite. Thus the measured dipole moment of HCl indicates that the H–Cl bond has approximately 18% ionic character (0.1811 × 100), or 82% covalent character. Instead of writing HCl as we can therefore indicate the charge separation quantitatively as
Our calculated results are in agreement with the electronegativity difference between hydrogen and chlorine χH = 2.20; χCl = 3.16, χCl − χH = 0.96), a value well within the range for polar covalent bonds. We indicate the dipole moment by writing an arrow above the molecule.Mathematically, dipole moments are vectors, and they possess both a magnitude and a direction. The dipole moment of a molecule is the vector sum of the dipoles of the individual bonds. In HCl, for example, the dipole moment is indicated as follows:
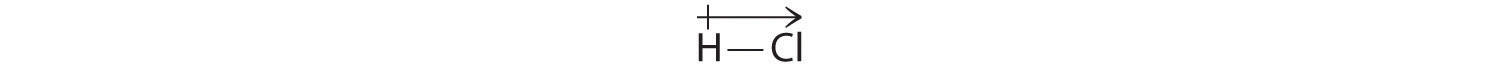
The arrow shows the direction of electron flow by pointing toward the more electronegative atom.
The charge on the atoms of many substances in the gas phase can be calculated using measured dipole moments and bond distances. Figure 8.14 "A Plot of the Percent Ionic Character of a Bond as Determined from Measured Dipole Moments versus the Difference in Electronegativity of the Bonded Atoms" shows a plot of the percent ionic character versus the difference in electronegativity of the bonded atoms for several substances. According to the graph, the bonding in species such as NaCl(g) and CsF(g) is substantially less than 100% ionic in character. As the gas condenses into a solid, however, dipole–dipole interactions between polarized species increase the charge separations. In the crystal, therefore, an electron is transferred from the metal to the nonmetal, and these substances behave like classic ionic compounds. The data in Figure 8.14 "A Plot of the Percent Ionic Character of a Bond as Determined from Measured Dipole Moments versus the Difference in Electronegativity of the Bonded Atoms" show that diatomic species with an electronegativity difference of less than 1.5 are less than 50% ionic in character, which is consistent with our earlier description of these species as containing polar covalent bonds. The use of dipole moments to determine the ionic character of a polar bond is illustrated in Example 11.
Figure 8.14 A Plot of the Percent Ionic Character of a Bond as Determined from Measured Dipole Moments versus the Difference in Electronegativity of the Bonded Atoms
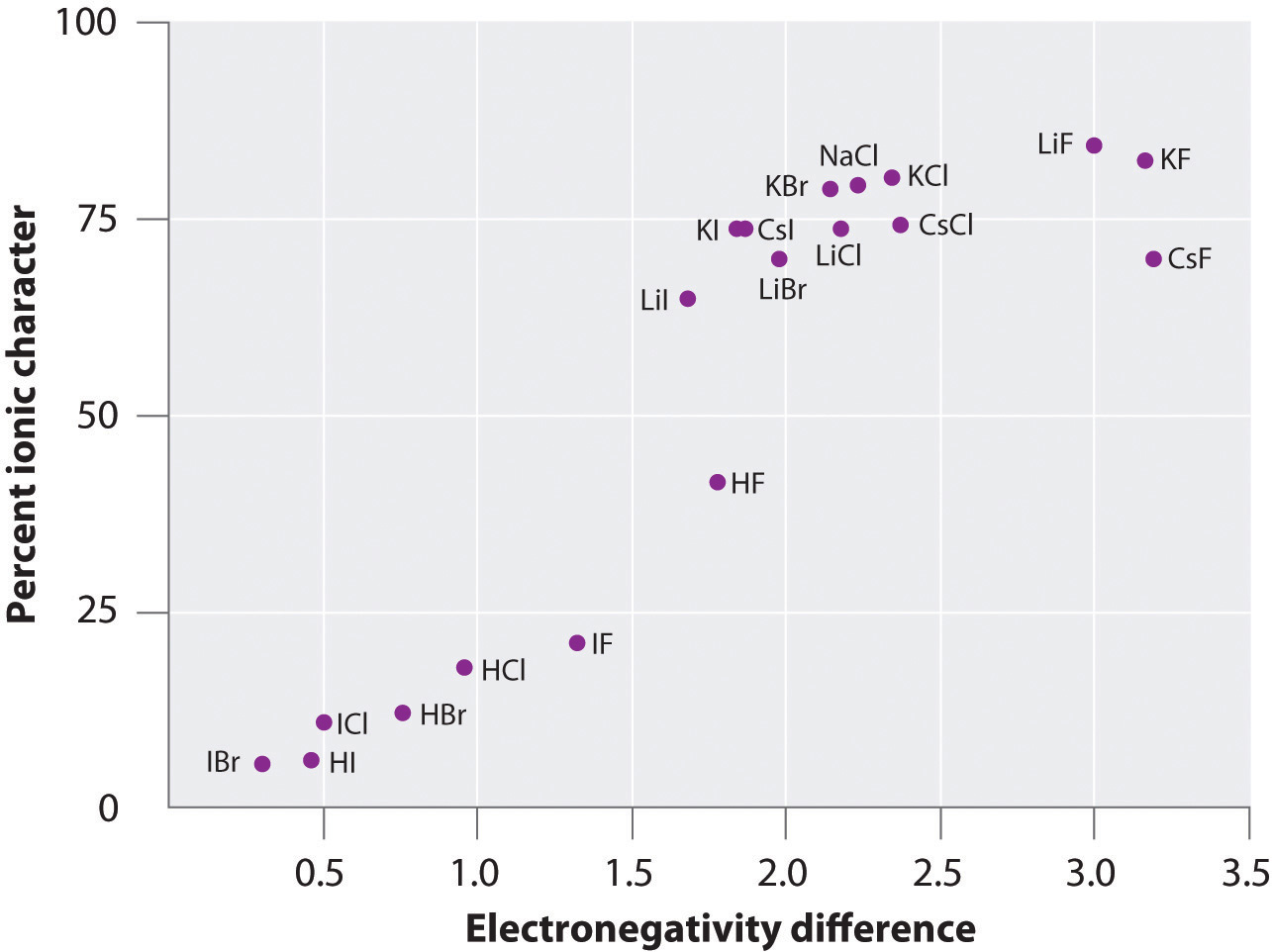
In the gas phase, even CsF, which has the largest possible difference in electronegativity between atoms, is not 100% ionic. Solid CsF, however, is best viewed as 100% ionic because of the additional electrostatic interactions in the lattice.
Example 11
In the gas phase, NaCl has a dipole moment of 9.001 D and an Na–Cl distance of 236.1 pm. Calculate the percent ionic character in NaCl.
Given: chemical species, dipole moment, and internuclear distance
Asked for: percent ionic character
Strategy:
A Compute the charge on each atom using the information given and Equation 8.16.
B Find the percent ionic character from the ratio of the actual charge to the charge of a single electron.
Solution:
A The charge on each atom is given by
Thus NaCl behaves as if it had charges of 1.272 × 10−19 C on each atom separated by 236.1 pm.
B The percent ionic character is given by the ratio of the actual charge to the charge of a single electron (the charge expected for the complete transfer of one electron):
Exercise
In the gas phase, silver chloride (AgCl) has a dipole moment of 6.08 D and an Ag–Cl distance of 228.1 pm. What is the percent ionic character in silver chloride?
Answer: 55.5%
Summary
Compounds with polar covalent bonds have electrons that are shared unequally between the bonded atoms. The polarity of such a bond is determined largely by the relative electronegativites of the bonded atoms. The asymmetrical charge distribution in a polar substance produces a dipole moment, which is the product of the partial charges on the bonded atoms and the distance between them.
Key Takeaway
- Bond polarity and ionic character increase with an increasing difference in electronegativity.
Conceptual Problems
-
Why do ionic compounds such as KI exhibit substantially less than 100% ionic character in the gas phase?
-
Of the compounds LiI and LiF, which would you expect to behave more like a classical ionic compound? Which would have the greater dipole moment in the gas phase? Explain your answers.
Numerical Problems
-
Predict whether each compound is purely covalent, purely ionic, or polar covalent.
- RbCl
- S8
- TiCl2
- SbCl3
- LiI
- Br2
-
Based on relative electronegativities, classify the bonding in each compound as ionic, covalent, or polar covalent. Indicate the direction of the bond dipole for each polar covalent bond.
- NO
- HF
- MgO
- AlCl3
- SiO2
- the C=O bond in acetone
- O3
-
Based on relative electronegativities, classify the bonding in each compound as ionic, covalent, or polar covalent. Indicate the direction of the bond dipole for each polar covalent bond.
- NaBr
- OF2
- BCl3
- the S–S bond in CH3CH2SSCH2CH3
- the C–Cl bond in CH2Cl2
- the O–H bond in CH3OH
- PtCl42−
-
Classify each species as having 0%–40% ionic character, 40%–60% ionic character, or 60%–100% ionic character based on the type of bonding you would expect. Justify your reasoning.
- CaO
- S8
- AlBr3
- ICl
- Na2S
- SiO2
- LiBr
-
If the bond distance in HCl (dipole moment = 1.109 D) were double the actual value of 127.46 pm, what would be the effect on the charge localized on each atom? What would be the percent negative charge on Cl? At the actual bond distance, how would doubling the charge on each atom affect the dipole moment? Would this represent more ionic or covalent character?
-
Calculate the percent ionic character of HF (dipole moment = 1.826 D) if the H–F bond distance is 92 pm.
-
Calculate the percent ionic character of CO (dipole moment = 0.110 D) if the C–O distance is 113 pm.
-
Calculate the percent ionic character of PbS and PbO in the gas phase, given the following information: for PbS, r = 228.69 pm and µ = 3.59 D; for PbO, r = 192.18 pm and µ = 4.64 D. Would you classify these compounds as having covalent or polar covalent bonds in the solid state?
8.10 End-of-Chapter Material
Application Problems
-
Until recently, benzidine was used in forensic medicine to detect the presence of human blood: when mixed with human blood, benzidine turns a characteristic blue color. Because benzidine has recently been identified as a carcinogen, other indicators have replaced it. Draw the complete Lewis dot structure for benzidine. Would you expect this compound to behave as a Lewis acid or a Lewis base?

-
There are three possible ways to connect carbon, nitrogen, and oxygen to form a monoanion: CNO−, CON−, and OCN−. One is the cyanate ion, a common and stable species; one is the fulminate ion, salts of which are used as explosive detonators; and one is so unstable that it has never been isolated. Use Lewis electron structures and the concept of formal charge to determine which isomer is cyanate, which is the fulminate, and which is the least stable.
-
The colorless gas N2O4 is a deadly poison that has been used as an oxidizing agent in rocket fuel. The compound has a single N–N bond, with a formal charge of +1 on each nitrogen atom. Draw resonance structures for this molecule.
-
Naphthalene is an organic compound that is commonly used in veterinary medicine as the active ingredient in dusting powders; it is also used internally as an intestinal antiseptic. From its chemical structure and the ΔHf of CO2 and H2O, estimate the molar enthalpy of combustion and the enthalpy of formation of naphthalene.
-
♦ Compare the combustion of hydrazine (N2H4), which produces nitrogen and water, with the combustion of methanol. Use the chemical structures to estimate which has a higher heat of combustion. Given equal volumes of hydrazine (d = 1.004 g/mL) and methanol (d = 0.791 g/mL), which is the better fuel (i.e., which provides more energy per unit volume during combustion)? Can you think of a reason why hydrazine is not used in internal combustion engines?
-
♦ Race car drivers frequently prefer methanol to isooctane as a fuel. Is this justified based on enthalpies of combustion? If you had a choice between 10 gal of methanol (d = 0.791 g/mL) and the same volume of isooctane (d = 0.688 g/mL), which fuel would you prefer?
-
♦ An atmospheric reservoir species is a molecule that is rather unreactive, but it contains elements that can be converted to reactive forms. For example, chlorine nitrate (ClONO2) is a reservoir species for both chlorine and nitrogen dioxide. In fact, most of the chlorine in the atmosphere is usually bound up in chlorine nitrate as a result of the reaction of ClO with NO2.
- Write a balanced chemical equation for this reaction.
-
Draw Lewis electron structures for each species in this reaction. What difficulty is associated with the structure of the reactants? How does this affect the reactivity of the compounds?
Chlorine nitrate can react in a surface reaction with water to form HClO and nitric acid.
- Draw Lewis electron structures to describe this reaction.
- Identify the Lewis and Brønsted–Lowry acids.
-
♦ Aniline is an oily liquid used to prepare organic dyes, varnishes, and black shoe polishes.
- Draw a complete Lewis structure for the molecule (including the nitrogen atom).
-
The –NH2 bound to the ring contains a lone pair of electrons that can participate in resonance in the following way:

Draw a second Lewis structure for aniline that takes this interaction into account.
- Calculate the formal charge on each nonhydrogen atom in both Lewis structures.
- What other resonance structures can be drawn for aniline that satisfy the octet rule?
Problems marked with a ♦ involve multiple concepts.
Answers
-
This molecule is likely to serve as a Lewis base because of the lone pair of electrons on each nitrogen atom.
-
-

-
-
The balanced chemical reaction is:
N2H4 + O2 → N2 + 2 H2OHydrazine:
ΔHcomb = −573 kJ/mol or −17.9 kJ/mlMethanol (CH3OH):
ΔHcomb = −1286 kJ/mol or –15.9 kJ/mlHydrazine is both extremely toxic and potentially explosive.
-
-
- ClO + NO2 → ClONO2
-

Both reactants have one unpaired electron, which makes them more reactive than might otherwise be expected.
-
ClONO2 + H2O → HClO + HONO2

- Water is acting as a Lewis base, as well as a Brønsted–Lowry acid. A lone pair on oxygen is used to attack the N atom of chlorine nitrate, and an H+ of water is transferred to the ClO−. Chlorine nitrate acts as a Lewis acid, and OH− is transferred to NO2+, which acts as both a Lewis and a Brønsted–Lowry acid.
-