This is “Building Up the Periodic Table”, section 6.6 from the book Principles of General Chemistry (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
6.6 Building Up the Periodic Table
Learning Objective
- To write the electron configuration of any element and relate its electron configuration to its position in the periodic table.
Now you can use the information you learned in Section 6.5 "Atomic Orbitals and Their Energies" to determine the electronic structure of every element in the periodic table. The process of describing each atom’s electronic structure consists, essentially, of beginning with hydrogen and adding one proton and one electron at a time to create the next heavier element in the table.All stable nuclei other than hydrogen also contain one or more neutrons. Because neutrons have no electrical charge, however, they can be ignored in the following discussion. Before demonstrating how to do this, however, we must introduce the concept of electron spin and the Pauli principle.
Electron Spin: The Fourth Quantum Number
When scientists analyzed the emission and absorption spectra of the elements more closely, they saw that for elements having more than one electron, nearly all the lines in the spectra were actually pairs of very closely spaced lines. Because each line represents an energy level available to electrons in the atom, there are twice as many energy levels available as would be predicted solely based on the quantum numbers n, l, and ml. Scientists also discovered that applying a magnetic field caused the lines in the pairs to split farther apart. In 1925, two graduate students in physics in the Netherlands, George Uhlenbeck (1900–1988) and Samuel Goudsmit (1902–1978), proposed that the splittings were caused by an electron spinning about its axis, much as Earth spins about its axis. When an electrically charged object spins, it produces a magnetic moment parallel to the axis of rotation, making it behave like a magnet. Although the electron cannot be viewed solely as a particle, spinning or otherwise, it is indisputable that it does have a magnetic moment. This magnetic moment is called electron spinThe magnetic moment that results when an electron spins. Electrons have two possible orientations (spin up and spin down), which are described by a fourth quantum number (ms)..
Figure 6.31 Electron Spin
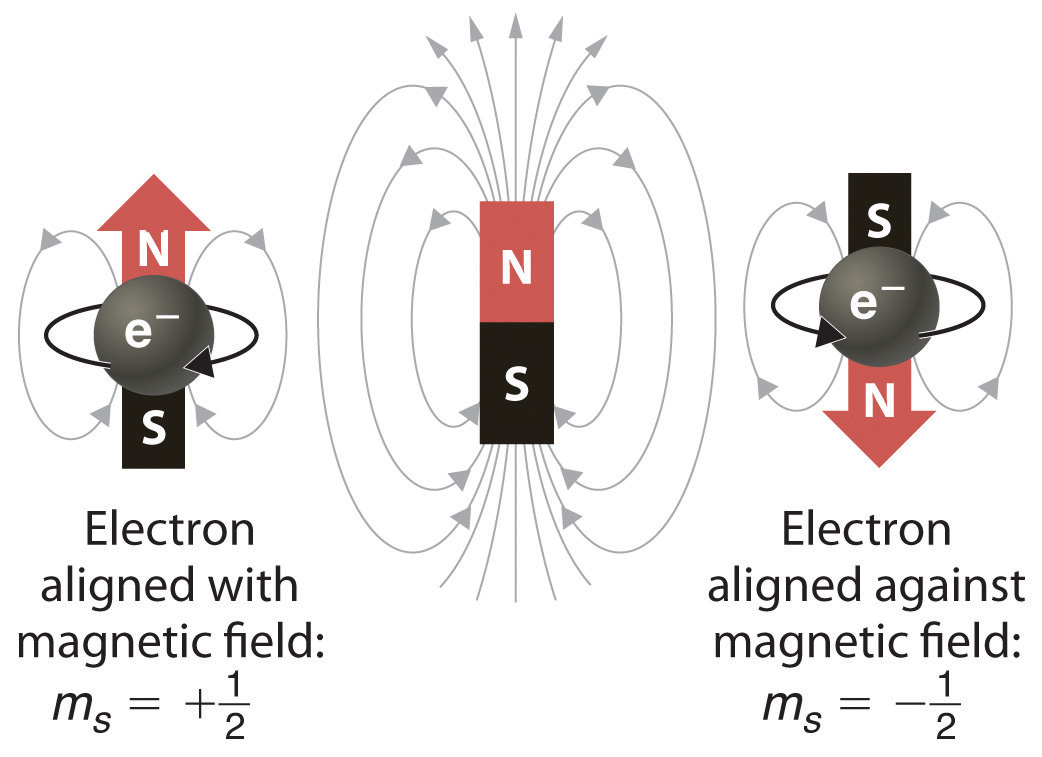
In a magnetic field, an electron has two possible orientations with different energies, one with spin up, aligned with the magnetic field, and one with spin down, aligned against it. All other orientations are forbidden.
In an external magnetic field, the electron has two possible orientations (Figure 6.31 "Electron Spin"). These are described by a fourth quantum number (ms), which for any electron can have only two possible values, designated +½ (up) and −½ (down) to indicate that the two orientations are opposites; the subscript s is for spin. An electron behaves like a magnet that has one of two possible orientations, aligned either with the magnetic field or against it.
The Pauli Principle
The implications of electron spin for chemistry were recognized almost immediately by an Austrian physicist,Wolfgang Pauli (1900–1958; Nobel Prize in Physics, 1945), who determined that each orbital can contain no more than two electrons. He developed the Pauli exclusion principleA principle stating that no two electrons in an atom can have the same value of all four quantum numbers.: No two electrons in an atom can have the same values of all four quantum numbers (n, l, ml, ms).
By giving the values of n, l, and ml, we also specify a particular orbital (e.g., 1s with n = 1, l = 0, ml = 0). Because ms has only two possible values (+½ or −½), two electrons, and only two electrons, can occupy any given orbital, one with spin up and one with spin down. With this information, we can proceed to construct the entire periodic table, which, as you learned in Chapter 1 "Introduction to Chemistry", was originally based on the physical and chemical properties of the known elements.
Example 7
List all the allowed combinations of the four quantum numbers (n, l, ml, ms) for electrons in a 2p orbital and predict the maximum number of electrons the 2p subshell can accommodate.
Given: orbital
Asked for: allowed quantum numbers and maximum number of electrons in orbital
Strategy:
A List the quantum numbers (n, l, ml) that correspond to an n = 2p orbital. List all allowed combinations of (n, l, ml).
B Build on these combinations to list all the allowed combinations of (n, l, ml, ms).
C Add together the number of combinations to predict the maximum number of electrons the 2p subshell can accommodate.
Solution:
A For a 2p orbital, we know that n = 2, l = n − 1 = 1, and ml = −l, (−l +1),…, (l − 1), l. There are only three possible combinations of (n, l, ml): (2, 1, 1), (2, 1, 0), and (2, 1, −1).
B Because ms is independent of the other quantum numbers and can have values of only +½ and −½, there are six possible combinations of (n, l, ml, ms): (2, 1, 1, +½), (2, 1, 1, −½), (2, 1, 0, +½), (2, 1, 0, −½), (2, 1, −1, +½), and (2, 1, −1, −½).
C Hence the 2p subshell, which consists of three 2p orbitals (2px, 2py, and 2pz), can contain a total of six electrons, two in each orbital.
Exercise
List all the allowed combinations of the four quantum numbers (n, l, ml, ms) for a 6s orbital, and predict the total number of electrons it can contain.
Answer: (6, 0, 0, +½), (6, 0, 0, −½); two electrons
Electron Configurations of the Elements
The electron configurationThe arrangement of an element’s electrons in its atomic orbitals. of an element is the arrangement of its electrons in its atomic orbitals. By knowing the electron configuration of an element, we can predict and explain a great deal of its chemistry.
The Aufbau Principle
We construct the periodic table by following the aufbau principleThe process used to build up the periodic table by adding protons one by one to the nucleus and adding the corresponding electrons to the lowest-energy orbital available without violating the Pauli exclusion principle. (from German, meaning “building up”). First we determine the number of electrons in the atom; then we add electrons one at a time to the lowest-energy orbital available without violating the Pauli principle. We use the orbital energy diagram of Figure 6.29 "Orbital Energy Level Diagram for a Typical Multielectron Atom", recognizing that each orbital can hold two electrons, one with spin up ↑, corresponding to ms = +½, which is arbitrarily written first, and one with spin down ↓, corresponding to ms = −½. A filled orbital is indicated by ↑↓, in which the electron spins are said to be paired. Here is a schematic orbital diagram for a hydrogen atom in its ground state:
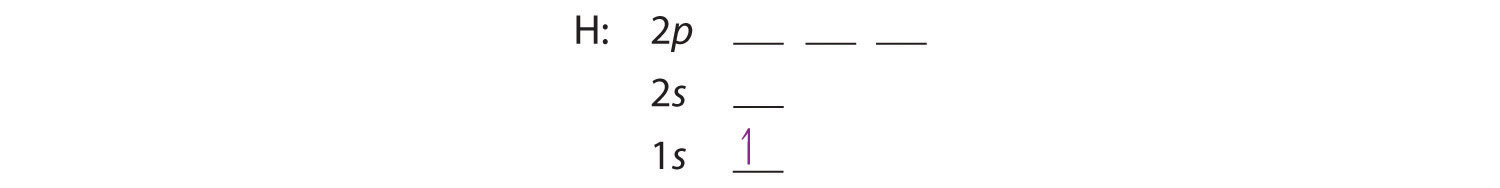
From the orbital diagram, we can write the electron configuration in an abbreviated form in which the occupied orbitals are identified by their principal quantum number n and their value of l (s, p, d, or f), with the number of electrons in the subshell indicated by a superscript. For hydrogen, therefore, the single electron is placed in the 1s orbital, which is the orbital lowest in energy (Figure 6.29 "Orbital Energy Level Diagram for a Typical Multielectron Atom"), and the electron configuration is written as 1s1 and read as “one-s-one.”
A neutral helium atom, with an atomic number of 2 (Z = 2), has two electrons. We place one electron in the orbital that is lowest in energy, the 1s orbital. From the Pauli exclusion principle, we know that an orbital can contain two electrons with opposite spin, so we place the second electron in the same orbital as the first but pointing down, so that the electrons are paired. The orbital diagram for the helium atom is therefore
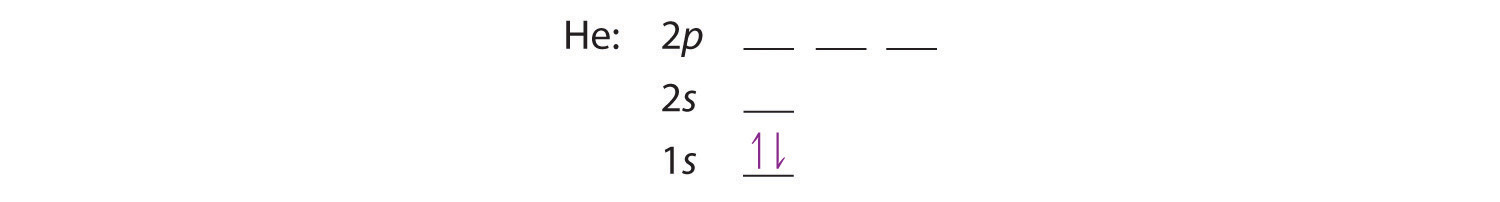
written as 1s2, where the superscript 2 implies the pairing of spins. Otherwise, our configuration would violate the Pauli principle.
The next element is lithium, with Z = 3 and three electrons in the neutral atom. We know that the 1s orbital can hold two of the electrons with their spins paired. Figure 6.29 "Orbital Energy Level Diagram for a Typical Multielectron Atom" tells us that the next lowest energy orbital is 2s, so the orbital diagram for lithium is
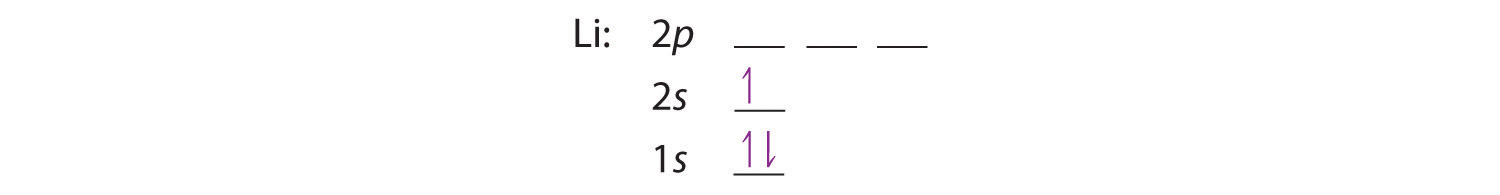
This electron configuration is written as 1s22s1.
The next element is beryllium, with Z = 4 and four electrons. We fill both the 1s and 2s orbitals to achieve a 1s22s2 electron configuration:
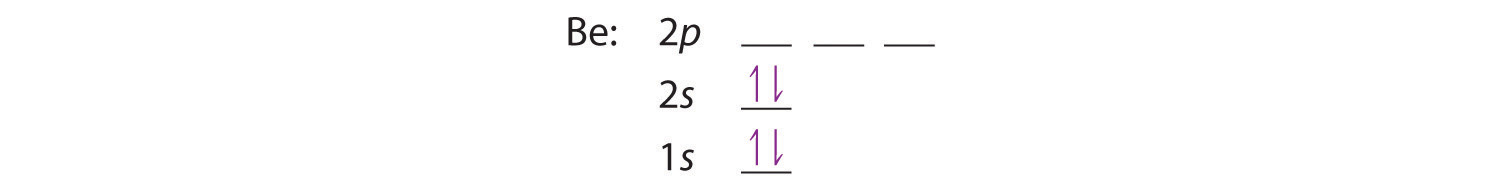
When we reach boron, with Z = 5 and five electrons, we must place the fifth electron in one of the 2p orbitals. Because all three 2p orbitals are degenerate, it doesn’t matter which one we select. The electron configuration of boron is 1s22s22p1:
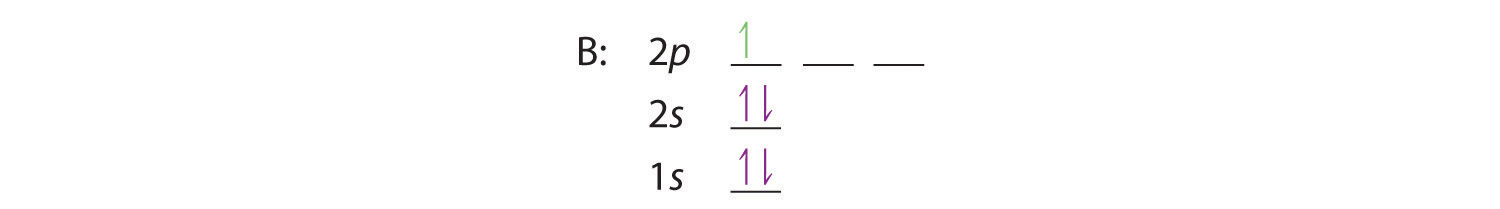
At carbon, with Z = 6 and six electrons, we are faced with a choice. Should the sixth electron be placed in the same 2p orbital that already has an electron, or should it go in one of the empty 2p orbitals? If it goes in an empty 2p orbital, will the sixth electron have its spin aligned with or be opposite to the spin of the fifth? In short, which of the following three orbital diagrams is correct for carbon, remembering that the 2p orbitals are degenerate?
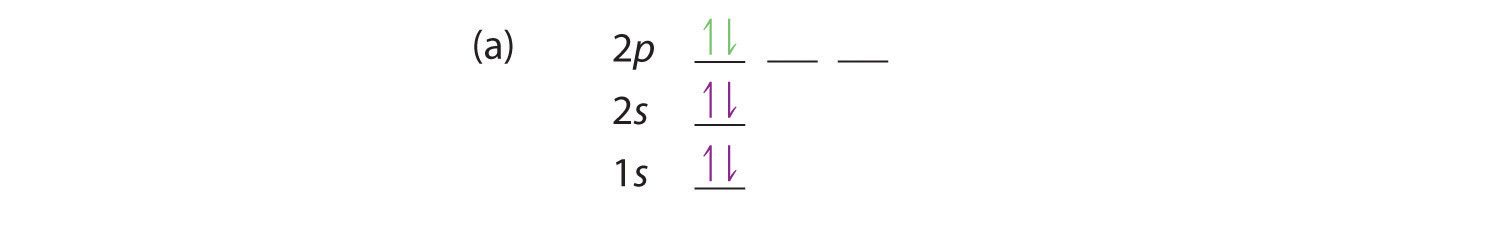
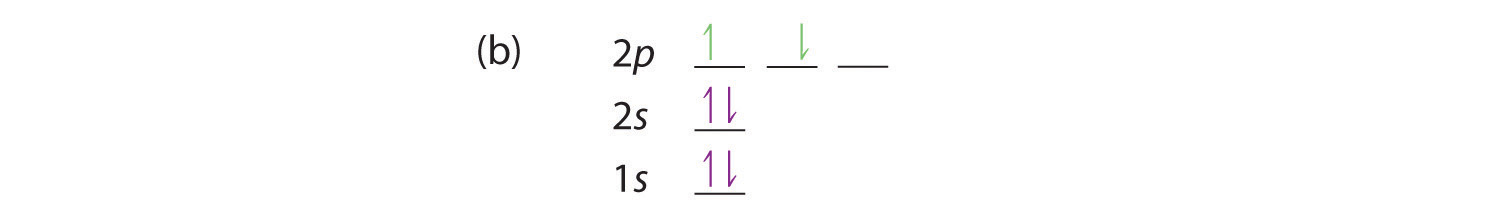
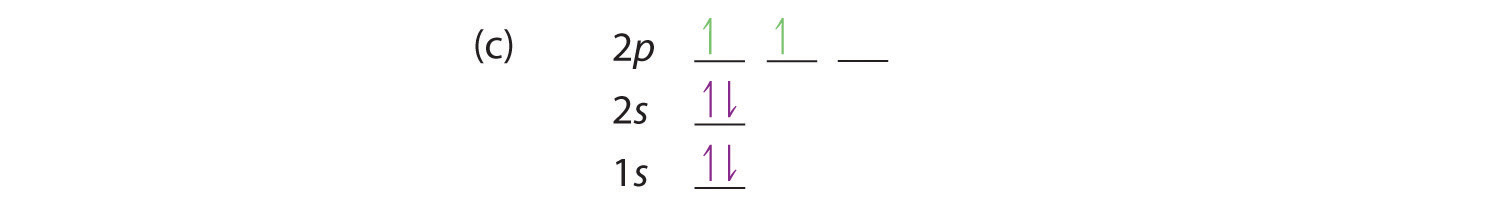
Because of electron-electron repulsions, it is more favorable energetically for an electron to be in an unoccupied orbital than in one that is already occupied; hence we can eliminate choice a. Similarly, experiments have shown that choice b is slightly higher in energy (less stable) than choice c because electrons in degenerate orbitals prefer to line up with their spins parallel; thus, we can eliminate choice b. Choice c illustrates Hund’s ruleA rule stating that the lowest-energy electron configuration for an atom is the one that has the maximum number of electrons with parallel spins in degenerate orbitals. (named after the German physicist Friedrich H. Hund, 1896–1997), which today says that the lowest-energy electron configuration for an atom is the one that has the maximum number of electrons with parallel spins in degenerate orbitals. By Hund’s rule, the electron configuration of carbon, which is 1s22s22p2, is understood to correspond to the orbital diagram shown in c. Experimentally, it is found that the ground state of a neutral carbon atom does indeed contain two unpaired electrons.
When we get to nitrogen (Z = 7, with seven electrons), Hund’s rule tells us that the lowest-energy arrangement is
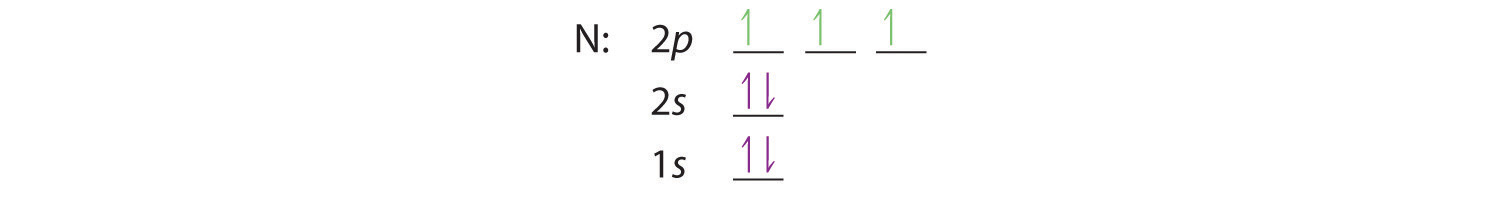
with three unpaired electrons. The electron configuration of nitrogen is thus 1s22s22p3.
At oxygen, with Z = 8 and eight electrons, we have no choice. One electron must be paired with another in one of the 2p orbitals, which gives us two unpaired electrons and a 1s22s22p4 electron configuration. Because all the 2p orbitals are degenerate, it doesn’t matter which one has the pair of electrons.
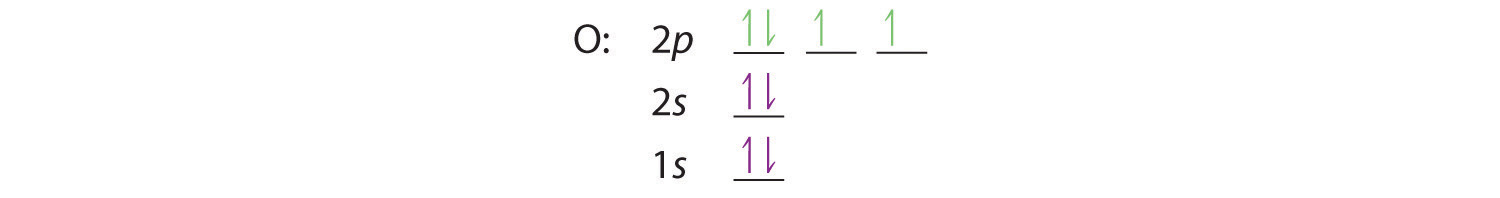
Similarly, fluorine has the electron configuration 1s22s22p5:
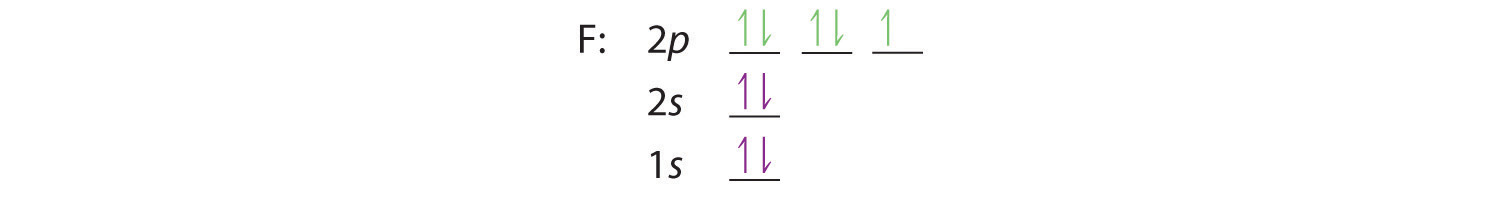
When we reach neon, with Z = 10, we have filled the 2p subshell, giving a 1s22s22p6 electron configuration:
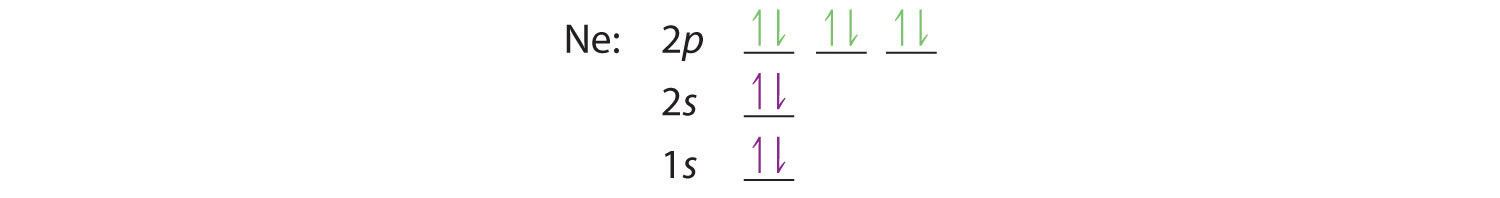
Notice that for neon, as for helium, all the orbitals through the 2p level are completely filled. This fact is very important in dictating both the chemical reactivity and the bonding of helium and neon, as you will see.
Valence Electrons
As we continue through the periodic table in this way, writing the electron configurations of larger and larger atoms, it becomes tedious to keep copying the configurations of the filled inner subshells. In practice, chemists simplify the notation by using a bracketed noble gas symbol to represent the configuration of the noble gas from the preceding row because all the orbitals in a noble gas are filled. For example, [Ne] represents the 1s22s22p6 electron configuration of neon (Z = 10), so the electron configuration of sodium, with Z = 11, which is 1s22s22p63s1, is written as [Ne]3s1:
| Neon | Z = 10 | 1s22s22p6 |
| Sodium | Z = 11 | 1s22s22p63s1 = [Ne]3s1 |
Because electrons in filled inner orbitals are closer to the nucleus and more tightly bound to it, they are rarely involved in chemical reactions. This means that the chemistry of an atom depends mostly on the electrons in its outermost shell, which are called the valence electronsElectrons in the outermost shell of an atom.. The simplified notation allows us to see the valence-electron configuration more easily. Using this notation to compare the electron configurations of sodium and lithium, we have:
| Sodium | 1s22s22p63s1 = [Ne]3s1 |
| Lithium | 1s22s1 = [He]2s1 |
It is readily apparent that both sodium and lithium have one s electron in their valence shell. We would therefore predict that sodium and lithium have very similar chemistry, which is indeed the case.
As we continue to build the eight elements of period 3, the 3s and 3p orbitals are filled, one electron at a time. This row concludes with the noble gas argon, which has the electron configuration [Ne]3s23p6, corresponding to a filled valence shell.
Example 8
Draw an orbital diagram and use it to derive the electron configuration of phosphorus, Z = 15. What is its valence electron configuration?
Given: atomic number
Asked for: orbital diagram and valence electron configuration for phosphorus
Strategy:
A Locate the nearest noble gas preceding phosphorus in the periodic table. Then subtract its number of electrons from those in phosphorus to obtain the number of valence electrons in phosphorus.
B Referring to Figure 6.29 "Orbital Energy Level Diagram for a Typical Multielectron Atom", draw an orbital diagram to represent those valence orbitals. Following Hund’s rule, place the valence electrons in the available orbitals, beginning with the orbital that is lowest in energy. Write the electron configuration from your orbital diagram.
C Ignore the inner orbitals (those that correspond to the electron configuration of the nearest noble gas) and write the valence electron configuration for phosphorus.
Solution:
A Because phosphorus is in the third row of the periodic table, we know that it has a [Ne] closed shell with 10 electrons. We begin by subtracting 10 electrons from the 15 in phosphorus.
B The additional five electrons are placed in the next available orbitals, which Figure 6.29 "Orbital Energy Level Diagram for a Typical Multielectron Atom" tells us are the 3s and 3p orbitals:
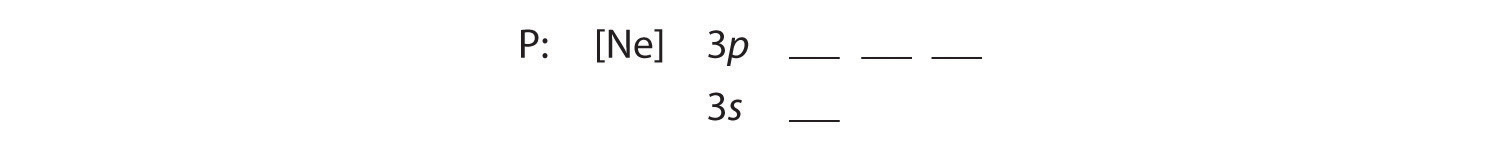
Because the 3s orbital is lower in energy than the 3p orbitals, we fill it first:
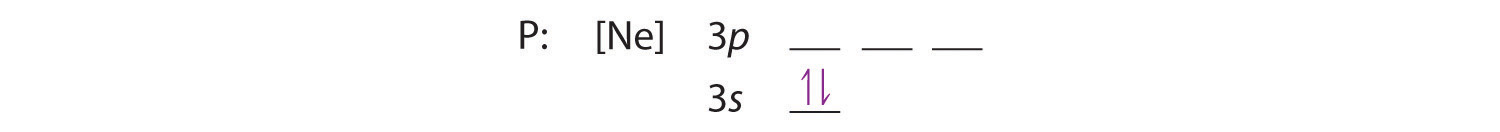
Hund’s rule tells us that the remaining three electrons will occupy the degenerate 3p orbitals separately but with their spins aligned:
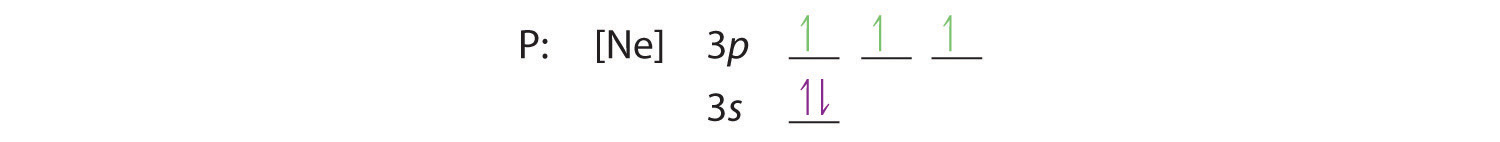
The electron configuration is [Ne]3s23p3.
C We obtain the valence electron configuration by ignoring the inner orbitals, which for phosphorus means that we ignore the [Ne] closed shell. This gives a valence-electron configuration of 3s23p3.
Exercise
Draw an orbital diagram and use it to derive the electron configuration of chlorine, Z = 17. What is its valence electron configuration?
Answer: [Ne]3s23p5; 3s23p5
The general order in which orbitals are filled is depicted in Figure 6.32 "Predicting the Order in Which Orbitals Are Filled in Multielectron Atoms". Subshells corresponding to each value of n are written from left to right on successive horizontal lines, where each row represents a row in the periodic table. The order in which the orbitals are filled is indicated by the diagonal lines running from the upper right to the lower left. Accordingly, the 4s orbital is filled prior to the 3d orbital because of shielding and penetration effects. Consequently, the electron configuration of potassium, which begins the fourth period, is [Ar]4s1, and the configuration of calcium is [Ar]4s2. Five 3d orbitals are filled by the next 10 elements, the transition metals, followed by three 4p orbitals. Notice that the last member of this row is the noble gas krypton (Z = 36), [Ar]4s23d104p6 = [Kr], which has filled 4s, 3d, and 4p orbitals. The fifth row of the periodic table is essentially the same as the fourth, except that the 5s, 4d, and 5p orbitals are filled sequentially.
Figure 6.32 Predicting the Order in Which Orbitals Are Filled in Multielectron Atoms
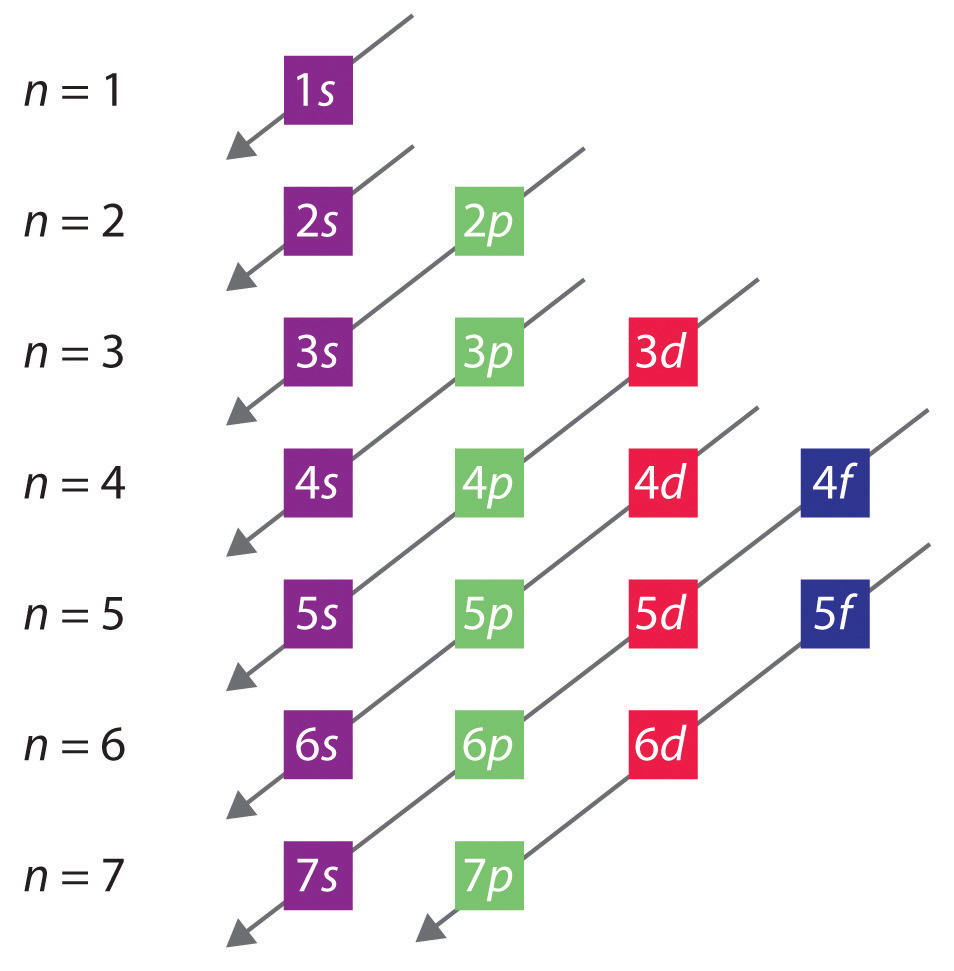
If you write the subshells for each value of the principal quantum number on successive lines, the observed order in which they are filled is indicated by a series of diagonal lines running from the upper right to the lower left.
The sixth row of the periodic table will be different from the preceding two because the 4f orbitals, which can hold 14 electrons, are filled between the 6s and the 5d orbitals. The elements that contain 4f orbitals in their valence shell are the lanthanides. When the 6p orbitals are finally filled, we have reached the next (and last known) noble gas, radon (Z = 86), [Xe]6s24f145d106p6 = [Rn]. In the last row, the 5f orbitals are filled between the 7s and the 6d orbitals, which gives the 14 actinide elements. Because the large number of protons makes their nuclei unstable, all the actinides are radioactive.
Example 9
Write the electron configuration of mercury (Z = 80), showing all the inner orbitals.
Given: atomic number
Asked for: complete electron configuration
Strategy:
Using the orbital diagram in Figure 6.32 "Predicting the Order in Which Orbitals Are Filled in Multielectron Atoms" and the periodic table as a guide, fill the orbitals until all 80 electrons have been placed.
Solution:
By placing the electrons in orbitals following the order shown in Figure 6.32 "Predicting the Order in Which Orbitals Are Filled in Multielectron Atoms" and using the periodic table as a guide, we obtain
| 1s2 | row 1 | 2 electrons |
| 2s22p6 | row 2 | 8 electrons |
| 3s23p6 | row 3 | 8 electrons |
| 4s23d104p6 | row 4 | 18 electrons |
| 5s24d105p6 | row 5 | 18 electrons |
| row 1–5 | 54 electrons |
After filling the first five rows, we still have 80 − 54 = 26 more electrons to accommodate. According to Figure 6.33 "The Periodic Table, Showing How the Elements Are Grouped According to the Kind of Subshell (", we need to fill the 6s (2 electrons), 4f (14 electrons), and 5d (10 electrons) orbitals. The result is mercury’s electron configuration:
1s22s22p63s23p64s23d104p65s24d105p66s24f145d10 = Hg = [Xe]6s24f145d10with a filled 5d subshell, a 6s24f145d10 valence shell configuration, and a total of 80 electrons. (You should always check to be sure that the total number of electrons equals the atomic number.)
Exercise
Although element 114 is not stable enough to occur in nature, two isotopes of element 114 were created for the first time in a nuclear reactor in 1999 by a team of Russian and American scientists. Write the complete electron configuration for element 114.
Answer: 1s22s22p63s23p64s23d104p65s24d105p66s24f145d106p67s25f146d107p2
The electron configurations of the elements are presented in Figure 6.34 "Electron Configurations of the Elements", which lists the orbitals in the order in which they are filled. In several cases, the ground state electron configurations are different from those predicted by Figure 6.32 "Predicting the Order in Which Orbitals Are Filled in Multielectron Atoms". Some of these anomalies occur as the 3d orbitals are filled. For example, the observed ground state electron configuration of chromium is [Ar]4s13d5 rather than the predicted [Ar]4s23d4. Similarly, the observed electron configuration of copper is [Ar]4s13d10 instead of [Ar]s23d9. The actual electron configuration may be rationalized in terms of an added stability associated with a half-filled (ns1, np3, nd5, nf7) or filled (ns2, np6, nd10, nf14) subshell. Given the small differences between higher energy levels, this added stability is enough to shift an electron from one orbital to another. In heavier elements, other more complex effects can also be important, leading to some of the additional anomalies indicated in Figure 6.34 "Electron Configurations of the Elements". For example, cerium has an electron configuration of [Xe]6s24f15d1, which is impossible to rationalize in simple terms. In most cases, however, these apparent anomalies do not have important chemical consequences.
Note the Pattern
Additional stability is associated with half-filled or filled subshells.
Blocks in the Periodic Table
As you have learned, the electron configurations of the elements explain the otherwise peculiar shape of the periodic table. Although the table was originally organized on the basis of physical and chemical similarities between the elements within groups, these similarities are ultimately attributable to orbital energy levels and the Pauli principle, which cause the individual subshells to be filled in a particular order. As a result, the periodic table can be divided into “blocks” corresponding to the type of subshell that is being filled, as illustrated in Figure 6.34 "Electron Configurations of the Elements". For example, the two columns on the left, known as the s blockThe elements in the left two columns of the periodic table in which the ns orbital is being filled., consist of elements in which the ns orbitals are being filled. The six columns on the right, elements in which the np orbitals are being filled, constitute the p blockThe elements in the six columns on the right of the periodic table in which the np orbitals are being filled.. In between are the 10 columns of the d blockThe elements in the periodic table in which the (n − 1)d orbitals are being filled., elements in which the (n − 1)d orbitals are filled. At the bottom lie the 14 columns of the f blockThe elements in the periodic table in which the (n − 2)f orbitals are being filled., elements in which the (n − 2)f orbitals are filled. Because two electrons can be accommodated per orbital, the number of columns in each block is the same as the maximum electron capacity of the subshell: 2 for ns, 6 for np, 10 for (n − 1)d, and 14 for (n − 2)f. Within each column, each element has the same valence electron configuration—for example, ns1 (group 1) or ns2np1 (group 13). As you will see, this is reflected in important similarities in the chemical reactivity and the bonding for the elements in each column.
Note the Pattern
Because each orbital can have a maximum of 2 electrons, there are 2 columns in the s block, 6 columns in the p block, 10 columns in the d block, and 14 columns in the f block.
Figure 6.33 The Periodic Table, Showing How the Elements Are Grouped According to the Kind of Subshell (s, p, d, f) Being Filled with Electrons in the Valence Shell of Each Element
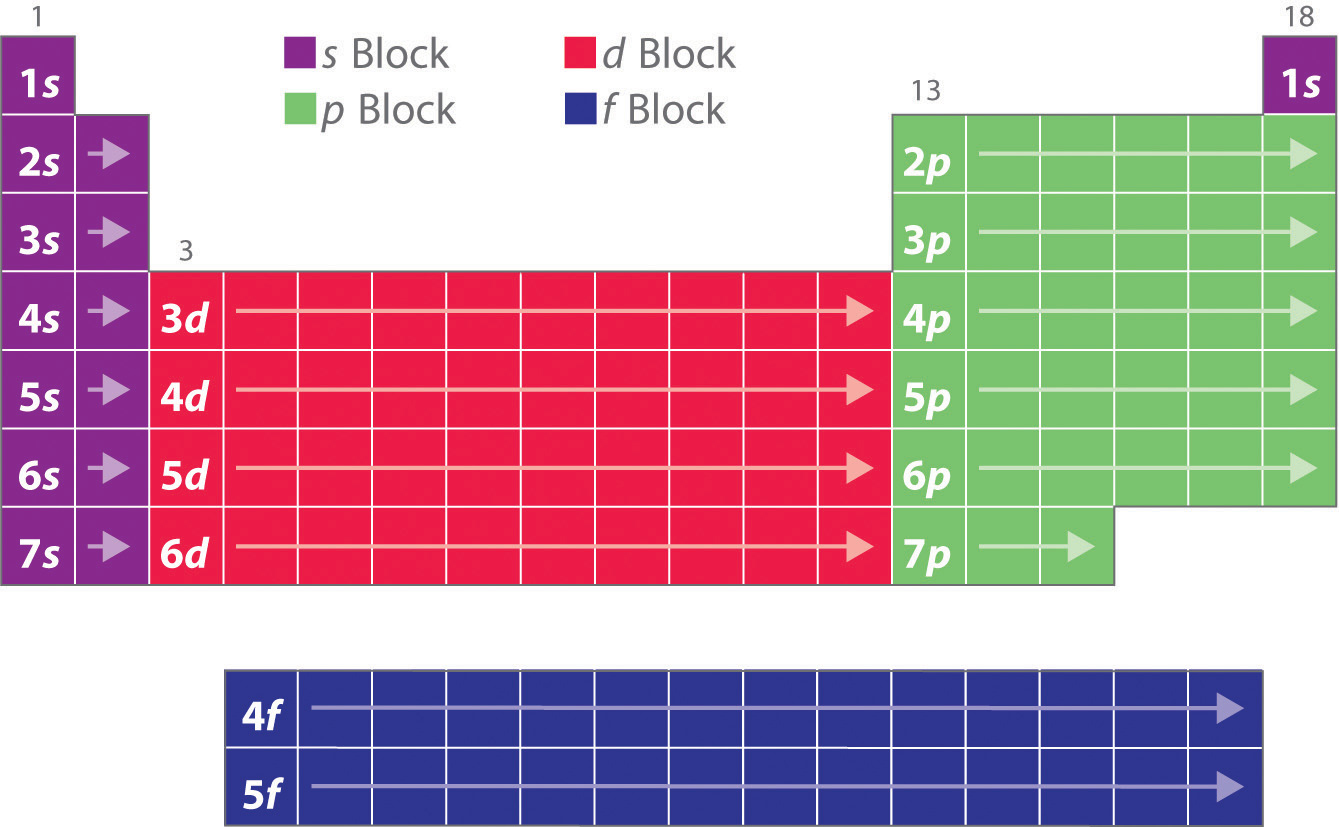
The electron configurations of the elements are in Figure 6.34 "Electron Configurations of the Elements".
Hydrogen and helium are placed somewhat arbitrarily. Although hydrogen is not an alkali metal, its 1s1 electron configuration suggests a similarity to lithium ([He]2s1) and the other elements in the first column. Although helium, with a filled ns subshell, should be similar chemically to other elements with an ns2 electron configuration, the closed principal shell dominates its chemistry, justifying its placement above neon on the right. In Chapter 7 "The Periodic Table and Periodic Trends", we will examine how electron configurations affect the properties and reactivity of the elements.
Figure 6.34 Electron Configurations of the Elements
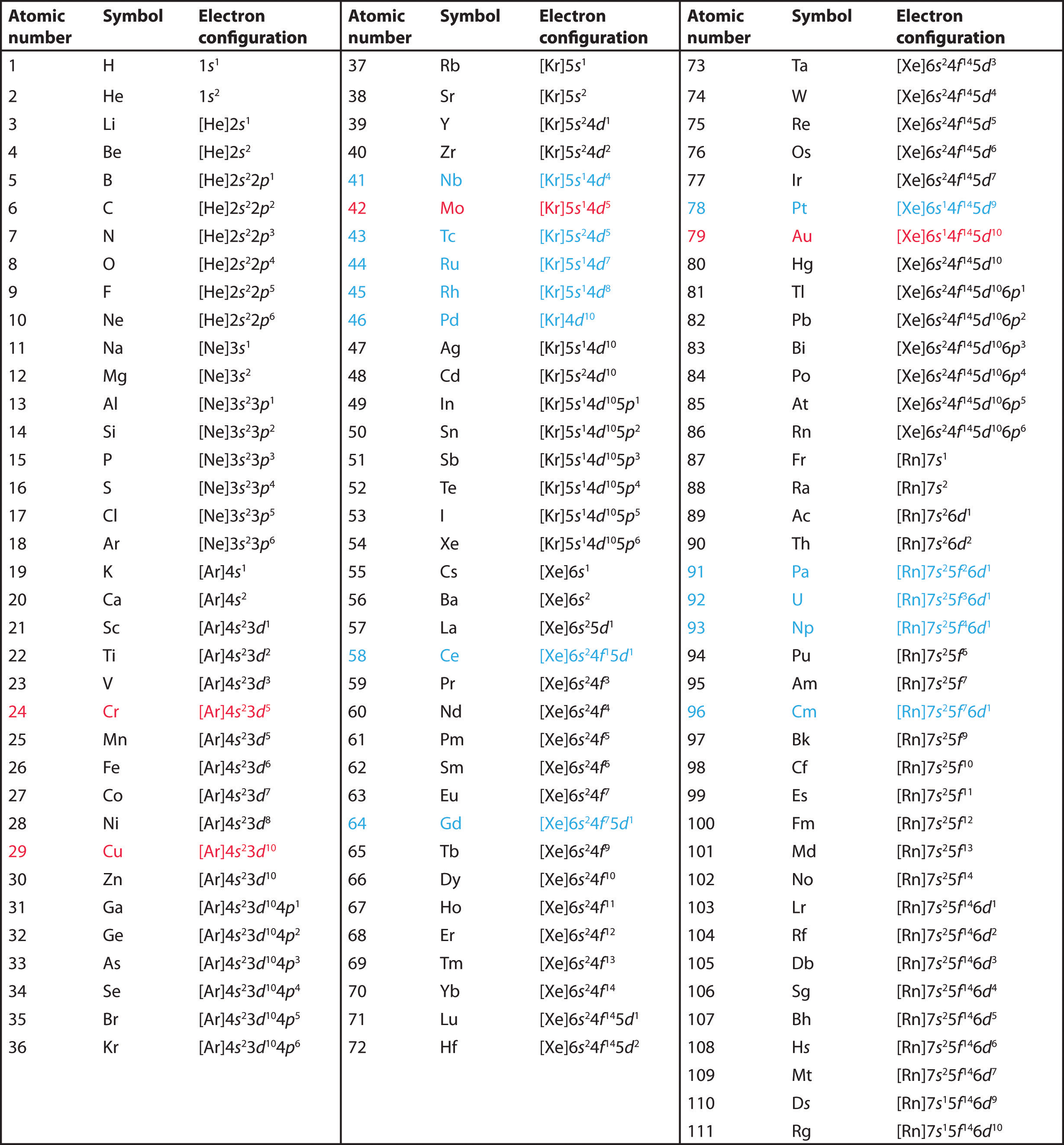
The electron configurations of elements indicated in red are exceptions due to the added stability associated with half-filled and filled subshells. The electron configurations of the elements indicated in blue are also anomalous, but the reasons for the observed configurations are more complex. For elements after No, the electron configurations are tentative.
Example 10
Use the periodic table to predict the valence electron configuration of all the elements of group 2 (beryllium, magnesium, calcium, strontium, barium, and radium).
Given: series of elements
Asked for: valence electron configurations
Strategy:
A Identify the block in the periodic table to which the group 2 elements belong. Locate the nearest noble gas preceding each element and identify the principal quantum number of the valence shell of each element.
B Write the valence electron configuration of each element by first indicating the filled inner shells using the symbol for the nearest preceding noble gas and then listing the principal quantum number of its valence shell, its valence orbitals, and the number of valence electrons in each orbital as superscripts.
Solution:
A The group 2 elements are in the s block of the periodic table, and as group 2 elements, they all have two valence electrons. Beginning with beryllium, we see that its nearest preceding noble gas is helium and that the principal quantum number of its valence shell is n = 2.
B Thus beryllium has an [He]s2 electron configuration. The next element down, magnesium, is expected to have exactly the same arrangement of electrons in the n = 3 principal shell: [Ne]s2. By extrapolation, we expect all the group 2 elements to have an ns2 electron configuration.
Exercise
Use the periodic table to predict the characteristic valence electron configuration of the halogens in group 17.
Answer: All have an ns2np5 electron configuration, one electron short of a noble gas electron configuration. (Note that the heavier halogens also have filled (n − 1)d10 subshells, as well as an (n − 2)f14 subshell for Rn; these do not, however, affect their chemistry in any significant way.
Summary
In addition to the three quantum numbers (n, l, ml) dictated by quantum mechanics, a fourth quantum number is required to explain certain properties of atoms. This is the electron spin quantum number (ms), which can have values of +½ or −½ for any electron, corresponding to the two possible orientations of an electron in a magnetic field. The concept of electron spin has important consequences for chemistry because the Pauli exclusion principle implies that no orbital can contain more than two electrons (with opposite spin). Based on the Pauli principle and a knowledge of orbital energies obtained using hydrogen-like orbitals, it is possible to construct the periodic table by filling up the available orbitals beginning with the lowest-energy orbitals (the aufbau principle), which gives rise to a particular arrangement of electrons for each element (its electron configuration). Hund’s rule says that the lowest-energy arrangement of electrons is the one that places them in degenerate orbitals with their spins parallel. For chemical purposes, the most important electrons are those in the outermost principal shell, the valence electrons. The arrangement of atoms in the periodic table results in blocks corresponding to filling of the ns, np, nd, and nf orbitals to produce the distinctive chemical properties of the elements in the s block, p block, d block, and f block, respectively.
Key Takeaway
- The arrangement of atoms in the periodic table arises from the lowest energy arrangement of electrons in the valence shell.
Conceptual Problems
-
A set of four quantum numbers specifies each wave function. What information is given by each quantum number? What does the specified wave function describe?
-
List two pieces of evidence to support the statement that electrons have a spin.
-
The periodic table is divided into blocks. Identify each block and explain the principle behind the divisions. Which quantum number distinguishes the horizontal rows?
-
Identify the element with each ground state electron configuration.
- [He]2s22p3
- [Ar]4s23d1
- [Kr]5s24d105p3
- [Xe]6s24f 6
-
Identify the element with each ground state electron configuration.
- [He]2s22p1
- [Ar]4s23d8
- [Kr]5s24d105p4
- [Xe]6s2
-
Propose an explanation as to why the noble gases are inert.
Numerical Problems
-
How many magnetic quantum numbers are possible for a 4p subshell? A 3d subshell? How many orbitals are in these subshells?
-
How many magnetic quantum numbers are possible for a 6s subshell? A 4f subshell? How many orbitals does each subshell contain?
-
If l = 2 and ml = 2, give all the allowed combinations of the four quantum numbers (n, l, ml, ms) for electrons in the corresponding 3d subshell.
-
Give all the allowed combinations of the four quantum numbers (n, l, ml, ms) for electrons in a 4d subshell. How many electrons can the 4d orbital accommodate? How would this differ from a situation in which there were only three quantum numbers (n, l, m)?
-
Given the following sets of quantum numbers (n, l, ml, ms), identify each principal shell and subshell.
- 1, 0, 0, ½
- 2, 1, 0, ½
- 3, 2, 0, ½
- 4, 3, 3, ½
-
Is each set of quantum numbers allowed? Explain your answers.
- n = 2; l = 1; ml = 2; ms = +½
- n = 3, l = 0; ml = −1; ms = −½
- n = 2; l = 2; ml = 1; ms = +½
- n = 3; l = 2; ml = 2; ms = +½
-
List the set of quantum numbers for each electron in the valence shell of each element.
- beryllium
- xenon
- lithium
- fluorine
-
List the set of quantum numbers for each electron in the valence shell of each element.
- carbon
- magnesium
- bromine
- sulfur
-
Sketch the shape of the periodic table if there were three possible values of ms for each electron (+½, −½, and 0); assume that the Pauli principle is still valid.
-
Predict the shape of the periodic table if eight electrons could occupy the p subshell.
-
If the electron could only have spin +½, what would the periodic table look like?
-
If three electrons could occupy each s orbital, what would be the electron configuration of each species?
- sodium
- titanium
- fluorine
- calcium
-
If Hund’s rule were not followed and maximum pairing occurred, how many unpaired electrons would each species have? How do these numbers compare with the number found using Hund’s rule?
- phosphorus
- iodine
- manganese
-
Write the electron configuration for each element in the ground state.
- aluminum
- calcium
- sulfur
- tin
- nickel
- tungsten
- neodymium
- americium
-
Write the electron configuration for each element in the ground state.
- boron
- rubidium
- bromine
- germanium
- vanadium
- palladium
- bismuth
- europium
-
Give the complete electron configuration for each element.
- magnesium
- potassium
- titanium
- selenium
- iodine
- uranium
- germanium
-
Give the complete electron configuration for each element.
- tin
- copper
- fluorine
- hydrogen
- thorium
- yttrium
- bismuth
-
Write the valence electron configuration for each element:
- samarium
- praseodymium
- boron
- cobalt
-
Using the Pauli exclusion principle and Hund’s rule, draw valence orbital diagrams for each element.
- barium
- neodymium
- iodine
-
Using the Pauli exclusion principle and Hund’s rule, draw valence orbital diagrams for each element.
- chlorine
- silicon
- scandium
-
How many unpaired electrons does each species contain?
- lead
- cesium
- copper
- silicon
- selenium
-
How many unpaired electrons does each species contain?
- helium
- oxygen
- bismuth
- silver
- boron
-
For each element, give the complete electron configuration, draw the valence electron configuration, and give the number of unpaired electrons present.
- lithium
- magnesium
- silicon
- cesium
- lead
-
Use an orbital diagram to illustrate the aufbau principle, the Pauli exclusion principle, and Hund’s rule for each element.
- carbon
- sulfur
Answers
-
For a 4p subshell, n = 4 and l = 1. The allowed values of the magnetic quantum number, ml, are therefore +1, 0, −1, corresponding to three 4p orbitals. For a 3d subshell, n = 3 and l = 2. The allowed values of the magnetic quantum number, ml, are therefore +2, +1, 0, −1, −2, corresponding to five 3d orbitals.
-
-
n = 3, l = 2, ml = 2, ms = ;n = 3, l = 2, ml = 2, ms =
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-




