This is “The Quantization of Energy”, section 6.2 from the book Principles of General Chemistry (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
6.2 The Quantization of Energy
Learning Objective
- To understand how energy is quantized.
By the late 19th century, many physicists thought their discipline was well on the way to explaining most natural phenomena. They could calculate the motions of material objects using Newton’s laws of classical mechanics, and they could describe the properties of radiant energy using mathematical relationships known as Maxwell’s equations, developed in 1873 by James Clerk Maxwell, a Scottish physicist. The universe appeared to be a simple and orderly place, containing matter, which consisted of particles that had mass and whose location and motion could be accurately described, and electromagnetic radiation, which was viewed as having no mass and whose exact position in space could not be fixed. Thus matter and energy were considered distinct and unrelated phenomena. Soon, however, scientists began to look more closely at a few inconvenient phenomena that could not be explained by the theories available at the time.
Blackbody Radiation
One phenomenon that seemed to contradict the theories of classical physics was blackbody radiationElectromagnetic radiation whose wavelength and color depends on the temperature of the object., the energy emitted by an object when it is heated. The wavelength of energy emitted by an object depends on only its temperature, not its surface or composition. Hence an electric stove burner or the filament of a space heater glows dull red or orange when heated, whereas the much hotter tungsten wire in an incandescent light bulb gives off a yellowish light (Figure 6.5 "Blackbody Radiation").
Figure 6.5 Blackbody Radiation

When heated, all objects emit electromagnetic radiation whose wavelength (and color) depends on the temperature of the object. A relatively low-temperature object, such as an electric stove element, on a low setting appears red, whereas a higher-temperature object, such as the filament of an incandescent light bulb, appears yellow or white.
The intensity of radiation is a measure of the energy emitted per unit area. A plot of the intensity of blackbody radiation as a function of wavelength for an object at various temperatures is shown in Figure 6.6 "Relationship between the Temperature of an Object and the Spectrum of Blackbody Radiation It Emits". One of the major assumptions of classical physics was that energy increased or decreased in a smooth, continuous manner. For example, classical physics predicted that as wavelength decreased, the intensity of the radiation an object emits should increase in a smooth curve without limit at all temperatures, as shown by the broken line for 6000 K in Figure 6.6 "Relationship between the Temperature of an Object and the Spectrum of Blackbody Radiation It Emits". Thus classical physics could not explain the sharp decrease in the intensity of radiation emitted at shorter wavelengths (primarily in the ultraviolet region of the spectrum), which we now refer to as the “ultraviolet catastrophe.” In 1900, however, the German physicist Max Planck (1858–1947) explained the ultraviolet catastrophe by proposing that the energy of electromagnetic waves is quantized rather than continuous. This means that for each temperature, there is a maximum intensity of radiation that is emitted in a blackbody object, corresponding to the peaks in Figure 6.6 "Relationship between the Temperature of an Object and the Spectrum of Blackbody Radiation It Emits", so the intensity does not follow a smooth curve as the temperature increases, as predicted by classical physics. Thus energy could be gained or lost only in integral multiples of some smallest unit of energy, a quantumThe smallest possible unit of energy. Energy can be gained or lost only in integral multiples of a quantum..
Figure 6.6 Relationship between the Temperature of an Object and the Spectrum of Blackbody Radiation It Emits
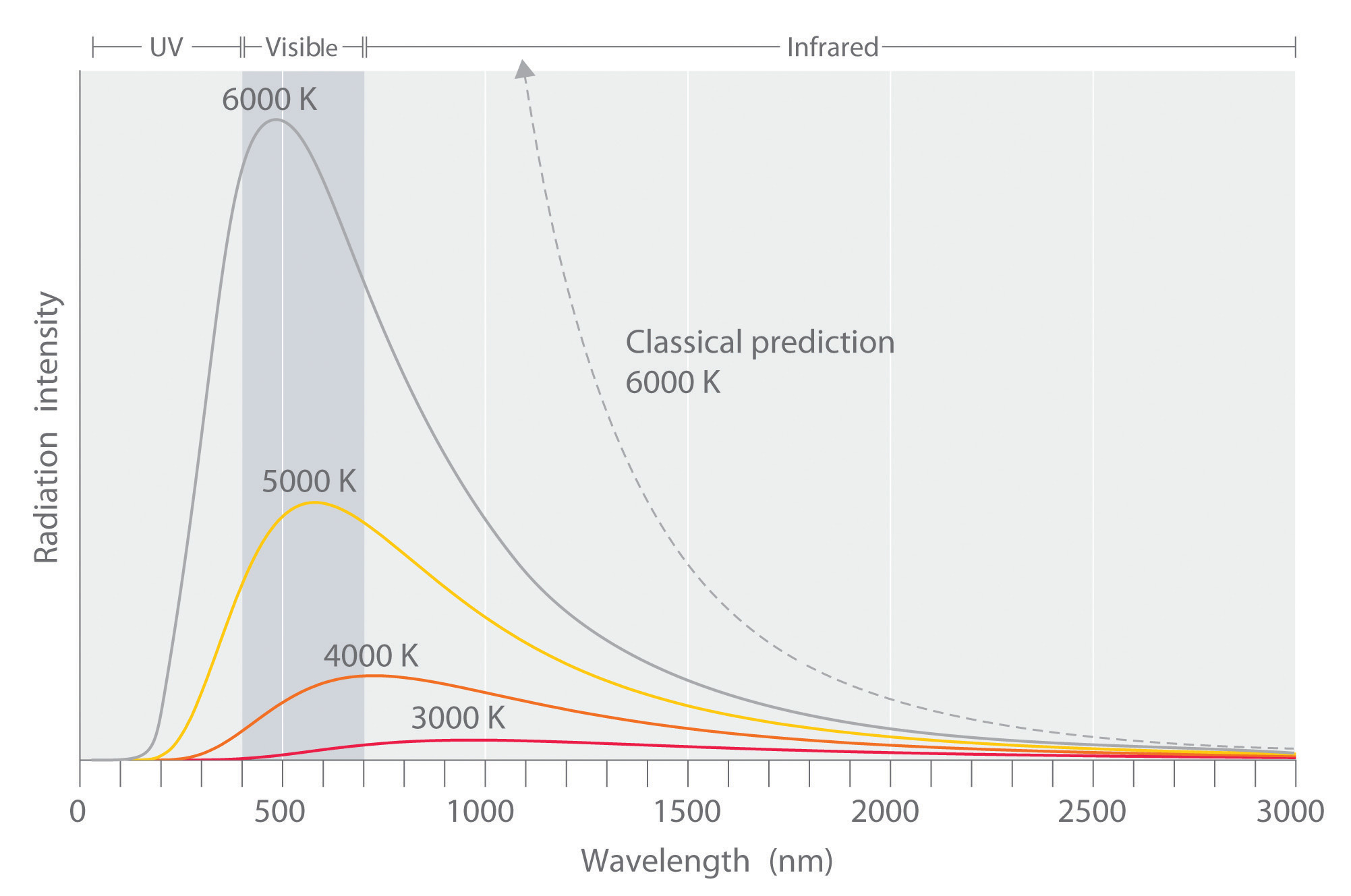
At relatively low temperatures, most radiation is emitted at wavelengths longer than 700 nm, which is in the infrared portion of the spectrum. The dull red glow of the electric stove element in Figure 6.5 "Blackbody Radiation" is due to the small amount of radiation emitted at wavelengths less than 700 nm, which the eye can detect. As the temperature of the object increases, the maximum intensity shifts to shorter wavelengths, successively resulting in orange, yellow, and finally white light. At high temperatures, all wavelengths of visible light are emitted with approximately equal intensities. The white light spectrum shown for an object at 6000 K closely approximates the spectrum of light emitted by the sun (Figure 6.14 "The Visible Spectrum of Sunlight"). Note the sharp decrease in the intensity of radiation emitted at wavelengths below 400 nm, which constituted the ultraviolet catastrophe. The classical prediction fails to fit the experimental curves entirely and does not have a maximum intensity.
Max Planck (1858–1947)
In addition to being a physicist, Planck was a gifted pianist, who at one time considered music as a career. During the 1930s, Planck felt it was his duty to remain in Germany, despite his open opposition to the policies of the Nazi government. One of his sons was executed in 1944 for his part in an unsuccessful attempt to assassinate Hitler, and bombing during the last weeks of World War II destroyed Planck’s home.
Although quantization may seem to be an unfamiliar concept, we encounter it frequently. For example, US money is integral multiples of pennies. Similarly, musical instruments like a piano or a trumpet can produce only certain musical notes, such as C or F sharp. Because these instruments cannot produce a continuous range of frequencies, their frequencies are quantized. Even electrical charge is quantized: an ion may have a charge of −1 or −2 but not −1.33.
Planck postulated that the energy of a particular quantum of radiant energy could be described explicitly by the equation
Equation 6.5
E = hνwhere the proportionality constant h is called Planck’s constant, one of the most accurately known fundamental constants in science. For our purposes, its value to four significant figures is generally sufficient:
h = 6.626 × 10−34 J·s (joule-seconds)As the frequency of electromagnetic radiation increases, the magnitude of the associated quantum of radiant energy increases. By assuming that energy can be emitted by an object only in integral multiples of hν, Planck devised an equation that fit the experimental data shown in Figure 6.6 "Relationship between the Temperature of an Object and the Spectrum of Blackbody Radiation It Emits". We can understand Planck’s explanation of the ultraviolet catastrophe qualitatively as follows: At low temperatures, radiation with only relatively low frequencies is emitted, corresponding to low-energy quanta. As the temperature of an object increases, there is an increased probability of emitting radiation with higher frequencies, corresponding to higher-energy quanta. At any temperature, however, it is simply more probable for an object to lose energy by emitting n lower-energy quanta than a single very high-energy quantum that corresponds to ultraviolet radiation. The result is a maximum in the plot of intensity of emitted radiation versus wavelength, as shown in Figure 6.6 "Relationship between the Temperature of an Object and the Spectrum of Blackbody Radiation It Emits", and a shift in the position of the maximum to lower wavelength (higher frequency) with increasing temperature.
At the time he proposed his radical hypothesis, Planck could not explain why energies should be quantized. Initially, his hypothesis explained only one set of experimental data—blackbody radiation. If quantization were observed for a large number of different phenomena, then quantization would become a law (as defined in Chapter 1 "Introduction to Chemistry"). In time, a theory might be developed to explain that law. As things turned out, Planck’s hypothesis was the seed from which modern physics grew.
The Photoelectric Effect
Only five years after he proposed it, Planck’s quantization hypothesis was used to explain a second phenomenon that conflicted with the accepted laws of classical physics. When certain metals are exposed to light, electrons are ejected from their surface (Figure 6.7 "The Photoelectric Effect"). Classical physics predicted that the number of electrons emitted and their kinetic energy should depend on only the intensity of the light, not its frequency. In fact, however, each metal was found to have a characteristic threshold frequency of light; below that frequency, no electrons are emitted regardless of the light’s intensity. Above the threshold frequency, the number of electrons emitted was found to be proportional to the intensity of the light, and their kinetic energy was proportional to the frequency. This phenomenon was called the photoelectric effectA phenomenon in which electrons are ejected from the surface of a metal that has been exposed to light..
Figure 6.7 The Photoelectric Effect
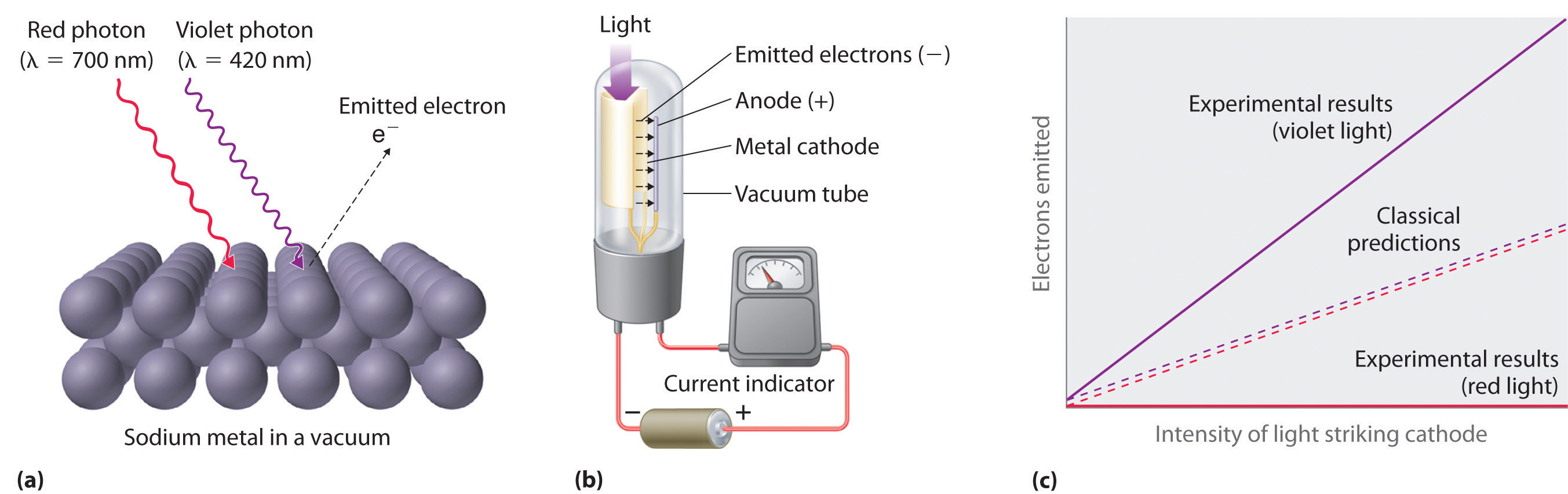
(a) Irradiating a metal surface with photons of sufficiently high energy causes electrons to be ejected from the metal. (b) A photocell that uses the photoelectric effect, similar to those found in automatic door openers. When light strikes the metal cathode, electrons are emitted and attracted to the anode, resulting in a flow of electrical current. If the incoming light is interrupted by, for example, a passing person, the current drops to zero. (c) In contrast to predictions using classical physics, no electrons are emitted when photons of light with energy less than Eo, such as red light, strike the cathode. The energy of violet light is above the threshold frequency, so the number of emitted photons is proportional to the light’s intensity.
Albert Einstein (1879–1955; Nobel Prize in Physics, 1921) quickly realized that Planck’s hypothesis about the quantization of radiant energy could also explain the photoelectric effect. The key feature of Einstein’s hypothesis was the assumption that radiant energy arrives at the metal surface in particles that we now call photonsA quantum of radiant energy, each of which possesses a particular energy given by , each possessing a particular energy E given by Equation 6.5. Einstein postulated that each metal has a particular electrostatic attraction for its electrons that must be overcome before an electron can be emitted from its surface (Eo = hνo). If photons of light with energy less than Eo strike a metal surface, no single photon has enough energy to eject an electron, so no electrons are emitted regardless of the intensity of the light. If a photon with energy greater than Eo strikes the metal, then part of its energy is used to overcome the forces that hold the electron to the metal surface, and the excess energy appears as the kinetic energy of the ejected electron:
Equation 6.6
kinetic energy of ejected electron = E − Eo = hν − hνo = h(ν − νo)When a metal is struck by light with energy above the threshold energy Eo, the number of emitted electrons is proportional to the intensity of the light beam, which corresponds to the number of photons per square centimeter, but the kinetic energy of the emitted electrons is proportional to the frequency of the light. Thus Einstein showed that the energy of the emitted electrons depended on the frequency of the light, contrary to the prediction of classical physics.
Albert Einstein (1879–1955)
In 1900, Einstein was working in the Swiss patent office in Bern. He was born in Germany and throughout his childhood his parents and teachers had worried that he might be developmentally disabled. The patent office job was a low-level civil service position that was not very demanding, but it did allow Einstein to spend a great deal of time reading and thinking about physics. In 1905, he published his paper on the photoelectric effect, for which he received the Nobel Prize in 1921.
Planck’s and Einstein’s postulate that energy is quantized is in many ways similar to Dalton’s description of atoms. Both theories are based on the existence of simple building blocks, atoms in one case and quanta of energy in the other. The work of Planck and Einstein thus suggested a connection between the quantized nature of energy and the properties of individual atoms. In fact, Einstein’s Nobel Prize was awarded for his work on the photoelectric effect (not for his more famous equation E = mc2), demonstrating its fundamental importance.
Recently, scientists have theorized that even our sense of smell has its basis in quantum physics. Preliminary research indicates that odorant molecules absorb a quantum of energy that causes their bonds to vibrate at a specific frequency. Because different assemblages of molecules have different characteristic frequencies, these vibrations seem to act as a molecular signature that can be detected as an odor. Studies with flies show that they can distinguish between similar molecules with different vibrational frequencies. This vibrational theory of smell could serve as a discriminatory process in nature in other ways and is an active area of research.
Example 2
Figure 6.8 A Beam of Red Light Emitted by a Ruby Laser

Ruby lasers, which emit red light at a wavelength of 694.3 nm, are used to read bar codes. When used for commercial applications, such lasers are generally designed to emit radiation over a narrow range of wavelengths to reduce their cost.
A ruby laser, a device that produces light in a narrow range of wavelengths (Section 6.3 "Atomic Spectra and Models of the Atom"), emits red light at a wavelength of 694.3 nm (Figure 6.8 "A Beam of Red Light Emitted by a Ruby Laser"). What is the energy in joules of a
- single photon?
- mole of photons?
Given: wavelength
Asked for: energy of single photon and mole of photons
Strategy:
A Use Equation 6.2 and Equation 6.5 to calculate the energy in joules.
B Multiply the energy of a single photon by Avogadro’s number to obtain the energy in a mole of photons.
Solution:
The energy of a single photon is given by E = hν = hc/λ.
B To calculate the energy in a mole of photons, we multiply the energy of a single photon by the number of photons in a mole (Avogadro’s number). If we write the energy of a photon as 2.861 × 10−19 J/photon, we obtain the energy of a mole of photons with wavelength 694.3 nm:
This energy is of the same magnitude as some of the enthalpies of reaction in Chapter 5 "Energy Changes in Chemical Reactions", and, as you will see in Chapter 8 "Ionic versus Covalent Bonding", it is comparable to the strength of many chemical bonds. As a result, light can be used to initiate chemical reactions. In fact, an entire area of chemistry called photochemistry is devoted to studying such processes. In the phenomenon of photosynthesis, green plants use the energy of visible light to convert carbon dioxide and water into sugars such as glucose.
Exercise
An x-ray generator, such as those used in hospitals, emits radiation with a wavelength of 1.544 Å.
- What is the energy in joules of a single photon?
- What is the energy in joules of a mole of photons?
- How many times more energetic is a single x-ray photon of this wavelength than a photon emitted by a ruby laser?
Answer:
- 1.287 × 10−15 J/photon
- 7.748 × 108 J/mol = 7.748 × 105 kJ/mol
- 4497 times
Summary
The properties of blackbody radiation, the radiation emitted by hot objects, could not be explained with classical physics. Max Planck postulated that energy was quantized and could be emitted or absorbed only in integral multiples of a small unit of energy, known as a quantum. The energy of a quantum is proportional to the frequency of the radiation; the proportionality constant h is a fundamental constant (Planck’s constant). Albert Einstein used Planck’s concept of the quantization of energy to explain the photoelectric effect, the ejection of electrons from certain metals when exposed to light. Einstein postulated the existence of what today we call photons, particles of light with a particular energy, E = hν. Both energy and matter have fundamental building blocks: quanta and atoms, respectively.
Key Takeaway
- The fundamental building blocks of energy are quanta and of matter are atoms.
Conceptual Problems
-
Describe the relationship between the energy of a photon and its frequency.
-
How was the ultraviolet catastrophe explained?
-
If electromagnetic radiation with a continuous range of frequencies above the threshold frequency of a metal is allowed to strike a metal surface, is the kinetic energy of the ejected electrons continuous or quantized? Explain your answer.
-
The vibrational energy of a plucked guitar string is said to be quantized. What do we mean by this? Are the sounds emitted from the 88 keys on a piano also quantized?
-
Which of the following exhibit quantized behavior: a human voice, the speed of a car, a harp, the colors of light, automobile tire sizes, waves from a speedboat?
Answers
-
The energy of a photon is directly proportional to the frequency of the electromagnetic radiation.
-
-
-
-
Quantized: harp, tire size, speedboat waves; continuous: human voice, colors of light, car speed.
Numerical Problems
-
What is the energy of a photon of light with each wavelength? To which region of the electromagnetic spectrum does each wavelength belong?
- 4.33 × 105 m
- 0.065 nm
- 786 pm
-
How much energy is contained in each of the following? To which region of the electromagnetic spectrum does each wavelength belong?
- 250 photons with a wavelength of 3.0 m
- 4.2 × 106 photons with a wavelength of 92 μm
- 1.78 × 1022 photons with a wavelength of 2.1 Å
-
A mole of photons is found to have an energy of 225 kJ. What is the wavelength of the radiation?
-
Use the data in Table 6.1 "Common Wavelength Units for Electromagnetic Radiation" to calculate how much more energetic a single gamma-ray photon is than a radio-wave photon. How many photons from a radio source operating at a frequency of 8 × 105 Hz would be required to provide the same amount of energy as a single gamma-ray photon with a frequency of 3 × 1019 Hz?
-
Use the data in Table 6.1 "Common Wavelength Units for Electromagnetic Radiation" to calculate how much more energetic a single x-ray photon is than a photon of ultraviolet light.
-
A radio station has a transmitter that broadcasts at a frequency of 100.7 MHz with a power output of 50 kW. Given that 1 W = 1 J/s, how many photons are emitted by the transmitter each second?
Answers
-
- 4.59 × 10−31 J/photon, radio
- 3.1 × 10−15 J/photon, gamma ray
- 2.53 × 10−16 J/photon, gamma ray
-
-
532 nm
-
-
-




