This is “Thermochemistry and Nutrition”, section 5.4 from the book Principles of General Chemistry (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
5.4 Thermochemistry and Nutrition
Learning Objective
- To understand the relationship between thermochemistry and nutrition.
The thermochemical quantities that you probably encounter most often are the caloric values of food. Food supplies the raw materials that your body needs to replace cells and the energy that keeps those cells functioning. About 80% of this energy is released as heat to maintain your body temperature at a sustainable level to keep you alive.
The nutritional CalorieA unit used to indicate the caloric content of food. It is equal to 1 kilocalorie (1 kcal). (with a capital C) that you see on food labels is equal to 1 kcal (kilocalorie). The caloric content of food is determined from its enthalpy of combustion (ΔHcomb) per gram, as measured in a bomb calorimeter, using the general reaction
Equation 5.43
food + excess O2(g) → CO2(g) + H2O(l) + N2(g)There are two important differences, however, between the caloric values reported for foods and the ΔHcomb of the same foods burned in a calorimeter. First, the ΔHcomb described in joules (or kilojoules) are negative for all substances that can be burned. In contrast, the caloric content of a food is always expressed as a positive number because it is stored energy. Therefore,
Equation 5.44
caloric content = −ΔHcombSecond, when foods are burned in a calorimeter, any nitrogen they contain (largely from proteins, which are rich in nitrogen) is transformed to N2. In the body, however, nitrogen from foods is converted to urea [(H2N)2C=O], rather than N2 before it is excreted. The ΔHcomb of urea measured by bomb calorimetry is −632.0 kJ/mol. Consequently, the enthalpy change measured by calorimetry for any nitrogen-containing food is greater than the amount of energy the body would obtain from it. The difference in the values is equal to the ΔHcomb of urea multiplied by the number of moles of urea formed when the food is broken down. This point is illustrated schematically in the following equations:
Equation 5.45
All three ΔH values are negative, and, by Hess’s law, ΔH3 = ΔH1 + ΔH2. The magnitude of ΔH1 must be less than ΔH3, the calorimetrically measured ΔHcomb for a food. By producing urea rather than N2, therefore, humans are excreting some of the energy that was stored in their food.
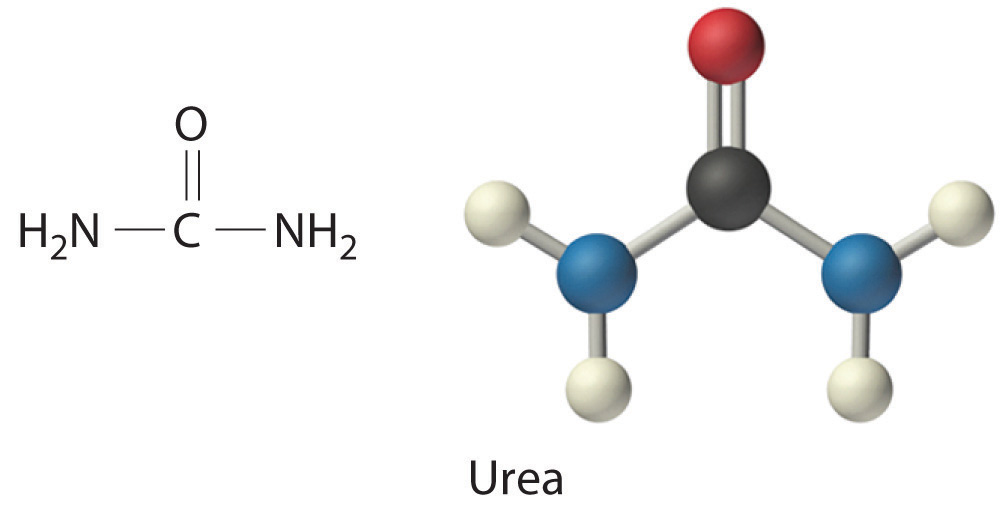
Because of their different chemical compositions, foods vary widely in caloric content. As we saw in Example 5, for instance, a fatty acid such as palmitic acid produces about 39 kJ/g during combustion, while a sugar such as glucose produces 15.6 kJ/g. Fatty acids and sugars are the building blocks of fats and carbohydrates, respectively, two of the major sources of energy in the diet. Nutritionists typically assign average values of 38 kJ/g (about 9 Cal/g) and 17 kJ/g (about 4 Cal/g) for fats and carbohydrates, respectively, although the actual values for specific foods vary because of differences in composition. Proteins, the third major source of calories in the diet, vary as well. Proteins are composed of amino acids, which have the following general structure:
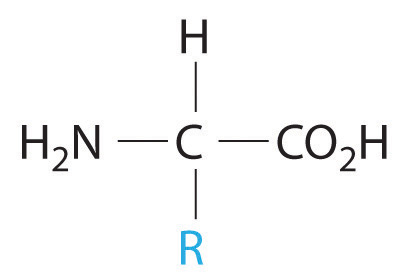
General structure of an amino acid. An amino acid contains an amine group (−NH2) and a carboxylic acid group (−CO2H).
In addition to their amine and carboxylic acid components, amino acids may contain a wide range of other functional groups: R can be hydrogen (–H); an alkyl group (e.g., –CH3); an aryl group (e.g., –CH2C6H5); or a substituted alkyl group that contains an amine, an alcohol, or a carboxylic acid (Figure 5.16 "The Structures of 10 Amino Acids"). Of the 20 naturally occurring amino acids, 10 are required in the human diet; these 10 are called essential amino acids because our bodies are unable to synthesize them from other compounds. Because R can be any of several different groups, each amino acid has a different value of ΔHcomb. Proteins are usually estimated to have an average ΔHcomb of 17 kJ/g (about 4 Cal/g).
Figure 5.16 The Structures of 10 Amino Acids
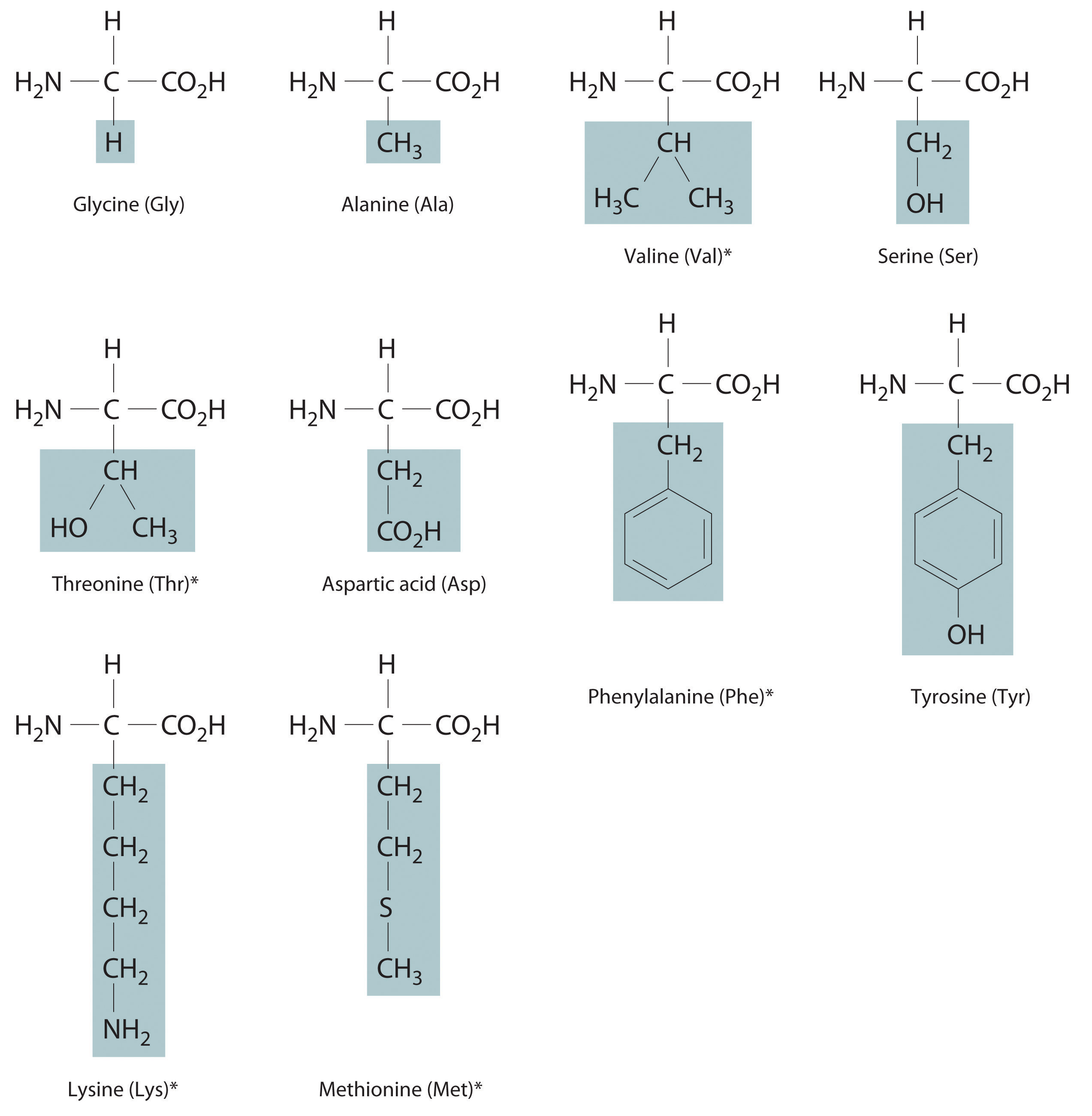
Essential amino acids in this group are indicated with an asterisk.
Example 11
Calculate the amount of available energy obtained from the biological oxidation of 1.000 g of alanine (an amino acid). Remember that the nitrogen-containing product is urea, not N2, so biological oxidation of alanine will yield less energy than will combustion. The value of ΔHcomb for alanine is −1577 kJ/mol.
Given: amino acid and ΔHcomb per mole
Asked for: caloric content per gram
Strategy:
A Write balanced chemical equations for the oxidation of alanine to CO2, H2O, and urea; the combustion of urea; and the combustion of alanine. Multiply both sides of the equations by appropriate factors and then rearrange them to cancel urea from both sides when the equations are added.
B Use Hess’s law to obtain an expression for ΔH for the oxidation of alanine to urea in terms of the ΔHcomb of alanine and urea. Substitute the appropriate values of ΔHcomb into the equation and solve for ΔH for the oxidation of alanine to CO2, H2O, and urea.
C Calculate the amount of energy released per gram by dividing the value of ΔH by the molar mass of alanine.
Solution:
The actual energy available biologically from alanine is less than its ΔHcomb because of the production of urea rather than N2. We know the ΔHcomb values for alanine and urea, so we can use Hess’s law to calculate ΔH for the oxidation of alanine to CO2, H2O, and urea.
A We begin by writing balanced chemical equations for (1) the oxidation of alanine to CO2, H2O, and urea; (2) the combustion of urea; and (3) the combustion of alanine. Because alanine contains only a single nitrogen atom, whereas urea and N2 each contain two nitrogen atoms, it is easier to balance Equations 1 and 3 if we write them for the oxidation of 2 mol of alanine:
Adding Equations 1 and 2 and canceling urea from both sides give the overall chemical equation directly:
B By Hess’s law, ΔH3 = ΔH1 + ΔH2. We know that ΔH3 = 2ΔHcomb (alanine), ΔH2 = ΔHcomb (urea), and ΔH1 = 2ΔH (alanine → urea). Rearranging and substituting the appropriate values gives
Thus ΔH (alanine → urea) = −2522 kJ/(2 mol of alanine) = −1261 kJ/mol of alanine. Oxidation of alanine to urea rather than to nitrogen therefore results in about a 20% decrease in the amount of energy released (−1261 kJ/mol versus −1577 kJ/mol).
C The energy released per gram by the biological oxidation of alanine is
This is equal to −3.382 Cal/g.
Exercise
Calculate the energy released per gram from the oxidation of valine (an amino acid) to CO2, H2O, and urea. Report your answer to three significant figures. The value of ΔHcomb for valine is −2922 kJ/mol.
Answer: −22.2 kJ/g (−5.31 Cal/g)
The reported caloric content of foods does not include ΔHcomb for those components that are not digested, such as fiber. Moreover, meats and fruits are 50%−70% water, which cannot be oxidized by O2 to obtain energy. So water contains no calories. Some foods contain large amounts of fiber, which is primarily composed of sugars. Although fiber can be burned in a calorimeter just like glucose to give carbon dioxide, water, and heat, humans lack the enzymes needed to break fiber down into smaller molecules that can be oxidized. Hence fiber also does not contribute to the caloric content of food.
We can determine the caloric content of foods in two ways. The most precise method is to dry a carefully weighed sample and carry out a combustion reaction in a bomb calorimeter. The more typical approach, however, is to analyze the food for protein, carbohydrate, fat, water, and “minerals” (everything that doesn’t burn) and then calculate the caloric content using the average values for each component that produces energy (9 Cal/g for fats, 4 Cal/g for carbohydrates and proteins, and 0 Cal/g for water and minerals). An example of this approach is shown in Table 5.4 "Approximate Composition and Fuel Value of an 8 oz Slice of Roast Beef" for a slice of roast beef. The compositions and caloric contents of some common foods are given in Table 5.5 "Approximate Compositions and Fuel Values of Some Common Foods".
Table 5.4 Approximate Composition and Fuel Value of an 8 oz Slice of Roast Beef
| Composition | Calories |
|---|---|
| 97.5 g of water | × 0 Cal/g = 0 |
| 58.7 g of protein | × 4 Cal/g = 235 |
| 69.3 g of fat | × 9 Cal/g = 624 |
| 0 g of carbohydrates | × 4 Cal/g = 0 |
| 1.5 g of minerals | × 0 Cal/g = 0 |
| Total mass: 227.0 g | Total calories: about 900 Cal |
Table 5.5 Approximate Compositions and Fuel Values of Some Common Foods
| Food (quantity) | Approximate Composition (%) | Food Value (Cal/g) | Calories | |||
|---|---|---|---|---|---|---|
| Water | Carbohydrate | Protein | Fat | |||
| beer (12 oz) | 92 | 3.6 | 0.3 | 0 | 0.4 | 150 |
| coffee (6 oz) | 100 | ~0 | ~0 | ~0 | ~0 | ~0 |
| milk (1 cup) | 88 | 4.5 | 3.3 | 3.3 | 0.6 | 150 |
| egg (1 large) | 75 | 2 | 12 | 12 | 1.6 | 80 |
| butter (1 tbsp) | 16 | ~0 | ~0 | 79 | 7.1 | 100 |
| apple (8 oz) | 84 | 15 | ~0 | 0.5 | 0.6 | 125 |
| bread, white (2 slices) | 37 | 48 | 8 | 4 | 2.6 | 130 |
| brownie (40 g) | 10 | 55 | 5 | 30 | 4.8 | 190 |
| hamburger (4 oz) | 54 | 0 | 24 | 21 | 2.9 | 326 |
| fried chicken (1 drumstick) | 53 | 8.3 | 22 | 15 | 2.7 | 195 |
| carrots (1 cup) | 87 | 10 | 1.3 | ~0 | 0.4 | 70 |
Because the Calorie represents such a large amount of energy, a few of them go a long way. An average 73 kg (160 lb) person needs about 67 Cal/h (1600 Cal/day) to fuel the basic biochemical processes that keep that person alive. This energy is required to maintain body temperature, keep the heart beating, power the muscles used for breathing, carry out chemical reactions in cells, and send the nerve impulses that control those automatic functions. Physical activity increases the amount of energy required but not by as much as many of us hope (Table 5.6 "Approximate Energy Expenditure by a 160 lb Person Engaged in Various Activities"). A moderately active individual requires about 2500−3000 Cal/day; athletes or others engaged in strenuous activity can burn 4000 Cal/day. Any excess caloric intake is stored by the body for future use, usually in the form of fat, which is the most compact way to store energy. When more energy is needed than the diet supplies, stored fuels are mobilized and oxidized. We usually exhaust the supply of stored carbohydrates before turning to fats, which accounts in part for the popularity of low-carbohydrate diets.
Table 5.6 Approximate Energy Expenditure by a 160 lb Person Engaged in Various Activities
| Activity | Cal/h |
|---|---|
| sleeping | 80 |
| driving a car | 120 |
| standing | 140 |
| eating | 150 |
| walking 2.5 mph | 210 |
| mowing lawn | 250 |
| swimming 0.25 mph | 300 |
| roller skating | 350 |
| tennis | 420 |
| bicycling 13 mph | 660 |
| running 10 mph | 900 |
Example 12
What is the minimum number of Calories expended by a 160 lb person who climbs a 30-story building? (Assume each flight of stairs is 14 ft high.) How many grams of glucose are required to supply this amount of energy? (The energy released during the combustion of glucose was calculated in Example 5.)
Given: mass, height, and energy released by combustion of glucose
Asked for: calories expended and mass of glucose needed
Strategy:
A Convert mass and height to SI units and then substitute these values into Equation 5.6 to calculate the change in potential energy (in kilojoules). Divide the calculated energy by 4.184 Cal/kJ to convert the potential energy change to Calories.
B Use the value obtained in Example 5 for the combustion of glucose to calculate the mass of glucose needed to supply this amount of energy.
Solution:
The energy needed to climb the stairs equals the difference between the person’s potential energy (PE) at the top of the building and at ground level.
A Recall from Section 5.1 "Energy and Work" that PE = mgh. Because m and h are given in non-SI units, we must convert them to kilograms and meters, respectively:
Thus
PE = (72.6 kg)(9.81 m/s2)(128 m) = 8.55 × 104 (kg·m2)/s2 = 91.2 kJTo convert to Calories, we divide by 4.184 kJ/kcal:
B Because the combustion of glucose produces 15.6 kJ/g (Example 5), the mass of glucose needed to supply 85.5 kJ of energy is
This mass corresponds to only about a teaspoonful of sugar! Because the body is only about 30% efficient in using the energy in glucose, the actual amount of glucose required would be higher: (100%/30%) × 5.85 g = 19.5 g. Nonetheless, this calculation illustrates the difficulty many people have in trying to lose weight by exercise alone.
Exercise
Calculate how many times a 160 lb person would have to climb the tallest building in the United States, the 110-story Willis Tower in Chicago, to burn off 1.0 lb of stored fat. Assume that each story of the building is 14 ft high and use a calorie content of 9.0 kcal/g of fat.
Answer: About 55 times
The calculations in Example 12 ignore various factors, such as how fast the person is climbing. Although the rate is irrelevant in calculating the change in potential energy, it is very relevant to the amount of energy actually required to ascend the stairs. The calculations also ignore the fact that the body’s conversion of chemical energy to mechanical work is significantly less than 100% efficient. According to the average energy expended for various activities listed in Table 5.6 "Approximate Energy Expenditure by a 160 lb Person Engaged in Various Activities", a person must run more than 4.5 h at 10 mph or bicycle for 6 h at 13 mph to burn off 1 lb of fat (1.0 lb × 454 g/lb × 9.0 Cal/g = 4100 Cal). But if a person rides a bicycle at 13 mph for only 1 h per day 6 days a week, that person will burn off 50 lb of fat in the course of a year (assuming, of course, the cyclist doesn’t increase his or her intake of calories to compensate for the exercise).
Summary
The nutritional Calorie is equivalent to 1 kcal (4.184 kJ). The caloric content of a food is its ΔHcomb per gram. The combustion of nitrogen-containing substances produces N2(g), but the biological oxidation of such substances produces urea. Hence the actual energy available from nitrogen-containing substances, such as proteins, is less than the ΔHcomb of urea multiplied by the number of moles of urea produced. The typical caloric contents for food are 9 Cal/g for fats, 4 Cal/g for carbohydrates and proteins, and 0 Cal/g for water and minerals.
Key Takeaway
- Thermochemical concepts can be applied to determine the actual energy available in food.
Conceptual Problems
-
Can water be considered a food? Explain your answer.
-
Describe how you would determine the caloric content of a bag of popcorn using a calorimeter.
-
Why do some people initially feel cold after eating a meal and then begin to feel warm?
-
In humans, one of the biochemical products of the combustion/digestion of amino acids is urea. What effect does this have on the energy available from these reactions? Speculate why conversion to urea is preferable to the generation of N2.
Numerical Problems
-
Determine the amount of energy available from the biological oxidation of 1.50 g of leucine (an amino acid, ΔHcomb = −3581.7 kJ/mol).
-
Calculate the energy released (in kilojoules) from the metabolism of 1.5 oz of vodka that is 62% water and 38% ethanol by volume, assuming that the total volume is equal to the sum of the volume of the two components. The density of ethanol is 0.824 g/mL. What is this enthalpy change in nutritional Calories?
-
While exercising, a person lifts an 80 lb barbell 7 ft off the ground. Assuming that the transformation of chemical energy to mechanical energy is only 35% efficient, how many Calories would the person use to accomplish this task? From Figure 5.11 "A Thermochemical Cycle for the Combustion of Glucose", how many grams of glucose would be needed to provide the energy to accomplish this task?
-
A 30 g sample of potato chips is placed in a bomb calorimeter with a heat capacity of 1.80 kJ/°C, and the bomb calorimeter is immersed in 1.5 L of water. Calculate the energy contained in the food per gram if, after combustion of the chips, the temperature of the calorimeter increases to 58.6°C from an initial temperature of 22.1°C.
Please be sure you are familiar with the topics discussed in Essential Skills 4 (Section 5.6 "Essential Skills 4") before proceeding to the Numerical Problems.




