This is “Stoichiometry of Reactions in Solution”, section 4.3 from the book Principles of General Chemistry (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
4.3 Stoichiometry of Reactions in Solution
Learning Objectives
- To balance equations that describe reactions in solution.
- To solve quantitative problems involving the stoichiometry of reactions in solution.
Quantitative calculations involving reactions in solution are carried out in the same manner as we discussed in Chapter 3 "Chemical Reactions". Instead of masses, however, we use volumes of solutions of known concentration to determine the number of moles of reactants. Whether we are dealing with volumes of solutions of reactants or masses of reactants, the coefficients in the balanced chemical equation tell us the number of moles of each reactant needed and the number of moles of each product that can be produced.
Calculating Moles from Volume
An expanded version of the flowchart for stoichiometric calculations illustrated in Figure 3.5 "Steps for Obtaining an Empirical Formula from Combustion Analysis" is shown in Figure 4.10 "An Expanded Flowchart for Stoichiometric Calculations". We can use the balanced chemical equation for the reaction and either the masses of solid reactants and products or the volumes of solutions of reactants and products to determine the amounts of other species, as illustrated in Example 7, Example 8, and Example 9.
Figure 4.10 An Expanded Flowchart for Stoichiometric Calculations

Either the masses or the volumes of solutions of reactants and products can be used to determine the amounts of other species in a balanced chemical equation.
Note the Pattern
The balanced chemical equation for a reaction and either the masses of solid reactants and products or the volumes of solutions of reactants and products can be used in stoichiometric calculations.
Example 7
Gold is extracted from its ores by treatment with an aqueous cyanide solution, which causes a reaction that forms the soluble [Au(CN)2]− ion. Gold is then recovered by reduction with metallic zinc according to the following equation:
Zn(s) + 2[Au(CN)2]−(aq) → [Zn(CN)4]2−(aq) + 2Au(s)What mass of gold would you expect to recover from 400.0 L of a 3.30 × 10−4 M solution of [Au(CN)2]−?
Given: chemical equation and molarity and volume of reactant
Asked for: mass of product
Strategy:
A Check the chemical equation to make sure it is balanced as written; balance if necessary. Then calculate the number of moles of [Au(CN)2]− present by multiplying the volume of the solution by its concentration.
B From the balanced chemical equation, use a mole ratio to calculate the number of moles of gold that can be obtained from the reaction. To calculate the mass of gold recovered, multiply the number of moles of gold by its molar mass.
Solution:
A The equation is balanced as written, so we can proceed to the stoichiometric calculation. We can adapt Figure 4.10 "An Expanded Flowchart for Stoichiometric Calculations" for this particular problem as follows:

As indicated in the strategy, we start by calculating the number of moles of [Au(CN)2]− present in the solution from the volume and concentration of the [Au(CN)2]− solution:
B Because the coefficients of gold and the [Au(CN)2]− ion are the same in the balanced chemical equation, if we assume that Zn(s) is present in excess, the number of moles of gold produced is the same as the number of moles of [Au(CN)2]− we started with (i.e., 0.132 mol of Au). The problem asks for the mass of gold that can be obtained, so we need to convert the number of moles of gold to the corresponding mass using the molar mass of gold:
At a 2011 market price of over $1400 per troy ounce (31.10 g), this amount of gold is worth $1170.
Exercise
What mass of solid lanthanum(III) oxalate nonahydrate [La2(C2O4)3·9H2O] can be obtained from 650 mL of a 0.0170 M aqueous solution of LaCl3 by adding a stoichiometric amount of sodium oxalate?
Answer: 3.89 g
Limiting Reactants in Solutions
The concept of limiting reactants applies to reactions that are carried out in solution as well as to reactions that involve pure substances. If all the reactants but one are present in excess, then the amount of the limiting reactant may be calculated as illustrated in Example 8.
Example 8
Because the consumption of alcoholic beverages adversely affects the performance of tasks that require skill and judgment, in most countries it is illegal to drive while under the influence of alcohol. In almost all US states, a blood alcohol level of 0.08% by volume is considered legally drunk. Higher levels cause acute intoxication (0.20%), unconsciousness (about 0.30%), and even death (about 0.50%). The Breathalyzer is a portable device that measures the ethanol concentration in a person’s breath, which is directly proportional to the blood alcohol level. The reaction used in the Breathalyzer is the oxidation of ethanol by the dichromate ion:
When a measured volume (52.5 mL) of a suspect’s breath is bubbled through a solution of excess potassium dichromate in dilute sulfuric acid, the ethanol is rapidly absorbed and oxidized to acetic acid by the dichromate ions. In the process, the chromium atoms in some of the Cr2O72− ions are reduced from Cr6+ to Cr3+. In the presence of Ag+ ions that act as a catalyst, the reaction is complete in less than a minute. Because the Cr2O72− ion (the reactant) is yellow-orange and the Cr3+ ion (the product) forms a green solution, the amount of ethanol in the person’s breath (the limiting reactant) can be determined quite accurately by comparing the color of the final solution with the colors of standard solutions prepared with known amounts of ethanol.

A Breathalyzer ampul before (a) and after (b) ethanol is added. When a measured volume of a suspect’s breath is bubbled through the solution, the ethanol is oxidized to acetic acid, and the solution changes color from yellow-orange to green. The intensity of the green color indicates the amount of ethanol in the sample.
A typical Breathalyzer ampul contains 3.0 mL of a 0.25 mg/mL solution of K2Cr2O7 in 50% H2SO4 as well as a fixed concentration of AgNO3 (typically 0.25 mg/mL is used for this purpose). How many grams of ethanol must be present in 52.5 mL of a person’s breath to convert all the Cr6+ to Cr3+?
Given: volume and concentration of one reactant
Asked for: mass of other reactant needed for complete reaction
Strategy:
A Calculate the number of moles of Cr2O72− ion in 1 mL of the Breathalyzer solution by dividing the mass of K2Cr2O7 by its molar mass.
B Find the total number of moles of Cr2O72− ion in the Breathalyzer ampul by multiplying the number of moles contained in 1 mL by the total volume of the Breathalyzer solution (3.0 mL).
C Use the mole ratios from the balanced chemical equation to calculate the number of moles of C2H5OH needed to react completely with the number of moles of Cr2O72− ions present. Then find the mass of C2H5OH needed by multiplying the number of moles of C2H5OH by its molar mass.
Solution:
A In any stoichiometry problem, the first step is always to calculate the number of moles of each reactant present. In this case, we are given the mass of K2Cr2O7 in 1 mL of solution, which we can use to calculate the number of moles of K2Cr2O7 contained in 1 mL:
B Because 1 mol of K2Cr2O7 produces 1 mol of Cr2O72− when it dissolves, each milliliter of solution contains 8.5 × 10−7 mol of Cr2O72−. The total number of moles of Cr2O72− in a 3.0 mL Breathalyzer ampul is thus
C The balanced chemical equation tells us that 3 mol of C2H5OH is needed to consume 2 mol of Cr2O72− ion, so the total number of moles of C2H5OH required for complete reaction is
As indicated in the strategy, this number can be converted to the mass of C2H5OH using its molar mass:
Thus 1.8 × 10−4 g or 0.18 mg of C2H5OH must be present. Experimentally, it is found that this value corresponds to a blood alcohol level of 0.7%, which is usually fatal.
Exercise
The compound para-nitrophenol (molar mass = 139 g/mol) reacts with sodium hydroxide in aqueous solution to generate a yellow anion via the reaction
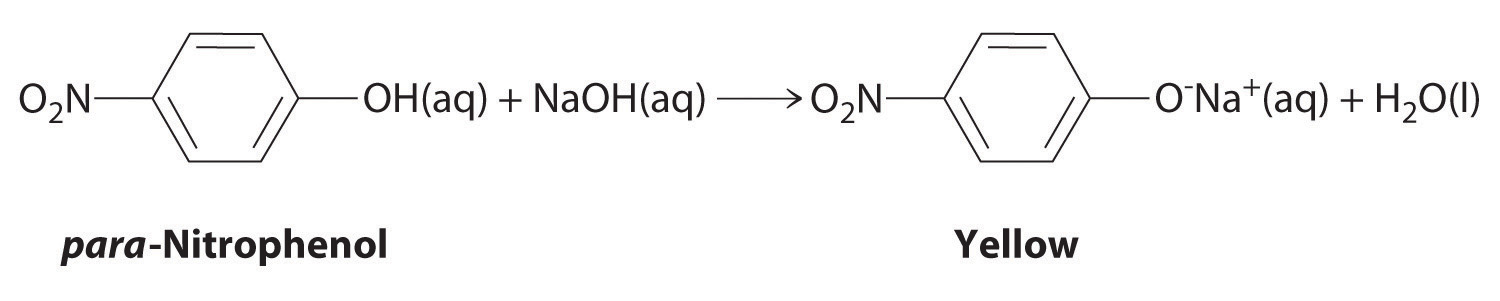
Because the amount of para-nitrophenol is easily estimated from the intensity of the yellow color that results when excess NaOH is added, reactions that produce para-nitrophenol are commonly used to measure the activity of enzymes, the catalysts in biological systems. What volume of 0.105 M NaOH must be added to 50.0 mL of a solution containing 7.20 × 10−4 g of para-nitrophenol to ensure that formation of the yellow anion is complete?
Answer: 4.93 × 10−5 L or 49.3 μL
In Example 7 and Example 8, the identity of the limiting reactant has been apparent: [Au(CN)2]−, LaCl3, ethanol, and para-nitrophenol. When the limiting reactant is not apparent, we can determine which reactant is limiting by comparing the molar amounts of the reactants with their coefficients in the balanced chemical equation, just as we did in Chapter 3 "Chemical Reactions", Section 3.4 "Mass Relationships in Chemical Equations". The only difference is that now we use the volumes and concentrations of solutions of reactants rather than the masses of reactants to calculate the number of moles of reactants, as illustrated in Example 9.
Example 9
When aqueous solutions of silver nitrate and potassium dichromate are mixed, an exchange reaction occurs, and silver dichromate is obtained as a red solid. The overall chemical equation for the reaction is as follows:
2AgNO3(aq) + K2Cr2O7(aq) → Ag2Cr2O7(s) + 2KNO3(aq)What mass of Ag2Cr2O7 is formed when 500 mL of 0.17 M K2Cr2O7 are mixed with 250 mL of 0.57 M AgNO3?
Given: balanced chemical equation and volume and concentration of each reactant
Asked for: mass of product
Strategy:
A Calculate the number of moles of each reactant by multiplying the volume of each solution by its molarity.
B Determine which reactant is limiting by dividing the number of moles of each reactant by its stoichiometric coefficient in the balanced chemical equation.
C Use mole ratios to calculate the number of moles of product that can be formed from the limiting reactant. Multiply the number of moles of the product by its molar mass to obtain the corresponding mass of product.
Solution:
A The balanced chemical equation tells us that 2 mol of AgNO3(aq) reacts with 1 mol of K2Cr2O7(aq) to form 1 mol of Ag2Cr2O7(s) (Figure 4.11 "What Happens at the Molecular Level When Solutions of AgNO"). The first step is to calculate the number of moles of each reactant in the specified volumes:
B Now we can determine which reactant is limiting by dividing the number of moles of each reactant by its stoichiometric coefficient:
Because 0.070 < 0.085, we know that AgNO3 is the limiting reactant.
C Each mole of Ag2Cr2O7 formed requires 2 mol of the limiting reactant (AgNO3), so we can obtain only 0.14/2 = 0.070 mol of Ag2Cr2O7. Finally, we convert the number of moles of Ag2Cr2O7 to the corresponding mass:
Figure 4.11 What Happens at the Molecular Level When Solutions of AgNO3 and K2Cr2O7 Are Mixed
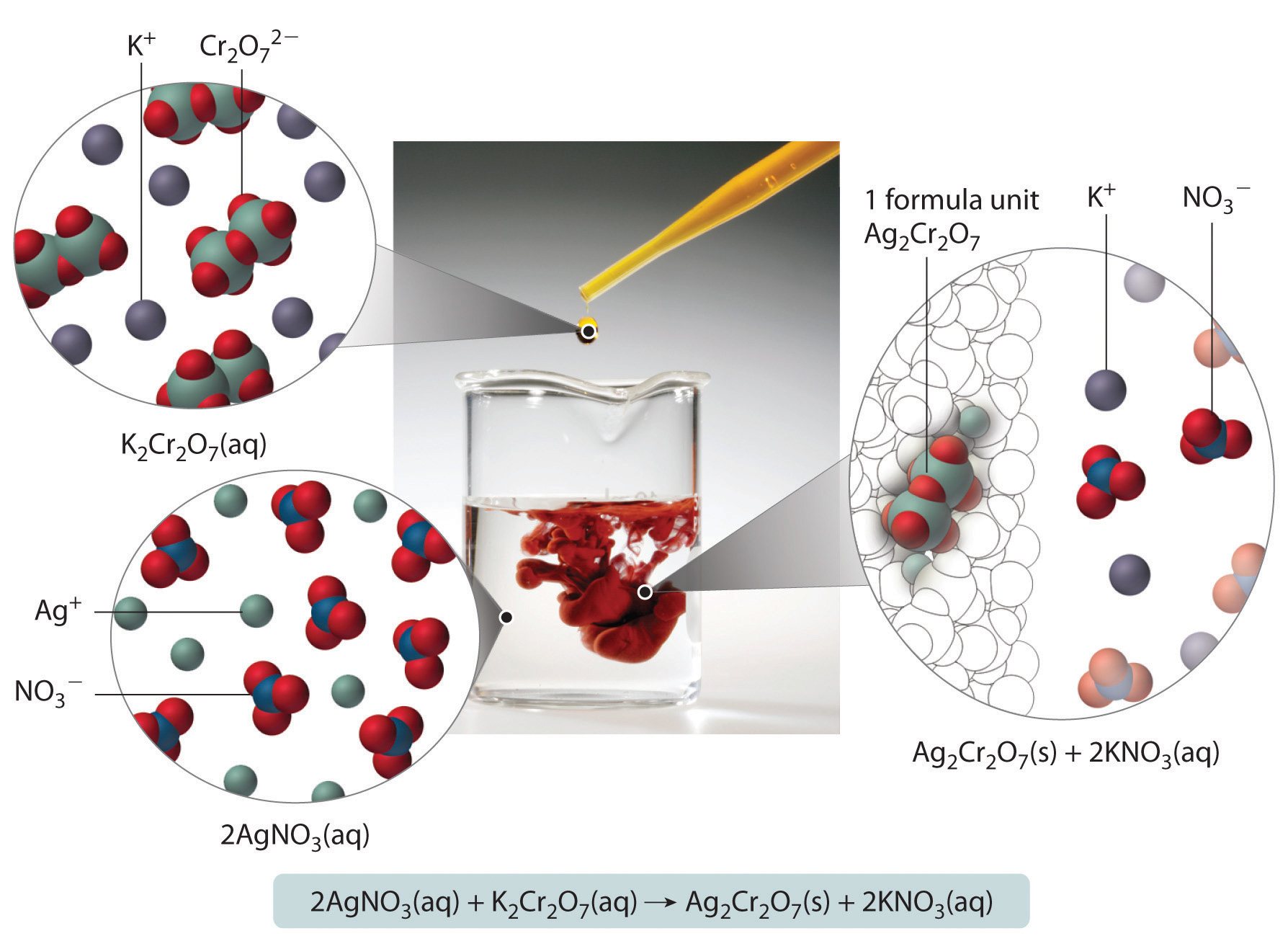
The Ag+ and Cr2O72− ions form a red precipitate of solid Ag2Cr2O7, while the K+ and NO3− ions remain in solution. (Water molecules are omitted from molecular views of the solutions for clarity.)
Exercise
Aqueous solutions of sodium bicarbonate and sulfuric acid react to produce carbon dioxide according to the following equation:
2NaHCO3(aq) + H2SO4(aq) → 2CO2(g) + Na2SO4(aq) + 2H2O(l)If 13.0 mL of 3.0 M H2SO4 are added to 732 mL of 0.112 M NaHCO3, what mass of CO2 is produced?
Answer: 3.4 g
Summary
Quantitative calculations that involve the stoichiometry of reactions in solution use volumes of solutions of known concentration instead of masses of reactants or products. The coefficients in the balanced chemical equation tell how many moles of reactants are needed and how many moles of product can be produced.
Key Takeaway
- Either the masses or the volumes of solutions of reactants and products can be used to determine the amounts of other species in the balanced chemical equation.
Conceptual Problems
-
What information is required to determine the mass of solute in a solution if you know the molar concentration of the solution?
-
Is it possible for one reactant to be limiting in a reaction that does not go to completion?
Numerical Problems
-
Refer to the Breathalyzer test described in Example 8. How much ethanol must be present in 89.5 mL of a person’s breath to consume all the potassium dichromate in a Breathalyzer ampul containing 3.0 mL of a 0.40 mg/mL solution of potassium dichromate?
-
Phosphoric acid and magnesium hydroxide react to produce magnesium phosphate and water. If 45.00 mL of 1.50 M phosphoric acid are used in the reaction, how many grams of magnesium hydroxide are needed for the reaction to go to completion?
-
Barium chloride and sodium sulfate react to produce sodium chloride and barium sulfate. If 50.00 mL of 2.55 M barium chloride are used in the reaction, how many grams of sodium sulfate are needed for the reaction to go to completion?
-
How many grams of sodium phosphate are obtained in solution from the reaction of 75.00 mL of 2.80 M sodium carbonate with a stoichiometric amount of phosphoric acid? A second product is water; what is the third product? How many grams of the third product are obtained?
-
How many grams of ammonium bromide are produced from the reaction of 50.00 mL of 2.08 M iron(II) bromide with a stoichiometric amount of ammonium sulfide? What is the second product? How many grams of the second product are produced?
-
Lead(II) nitrate and hydroiodic acid react to produce lead(II) iodide and nitric acid. If 3.25 g of lead(II) iodide were obtained by adding excess HI to 150.0 mL of lead(II) nitrate, what was the molarity of the lead(II) nitrate solution?
-
Silver nitrate and sodium chloride react to produce sodium nitrate and silver chloride. If 2.60 g of AgCl was obtained by adding excess NaCl to 100 mL of AgNO3, what was the molarity of the silver nitrate solution?




