This is “Chemistry, Matter, and Measurement”, chapter 1 from the book Introduction to Chemistry: General, Organic, and Biological (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
Chapter 1 Chemistry, Matter, and Measurement
Opening Essay
In April 2003, the US Pharmacopeia, a national organization that establishes quality standards for medications, reported a case in which a physician ordered “morphine [a powerful painkiller] 2–3 mg IV [intravenously] every 2–3 hours for pain.” A nurse misread the dose as “23 mg” and thus administered approximately 10 times the proper amount to an 8-year-old boy with a broken leg. The boy stopped breathing but was successfully resuscitated and left the hospital three days later.
Quantities and measurements are as important in our everyday lives as they are in medicine. The posted speed limits on roads and highways, such as 55 miles per hour (mph), are quantities we might encounter all the time. Both parts of a quantity, the amount (55) and the unit (mph), must be properly communicated to prevent potential problems. In chemistry, as in any technical endeavor, the proper expression of quantities is a necessary fundamental skill. As we begin our journey into chemistry, we will learn this skill so that errors—from homework mistakes to traffic tickets to more serious consequences—can be avoided.
The study of chemistry will open your eyes to a fascinating world. Chemical processes are continuously at work all around us. They happen as you cook and eat food, strike a match, shampoo your hair, and even read this page. Chemistry is called the central science because a knowledge of chemical principles is essential for other sciences. You might be surprised at the extent to which chemistry pervades your life.
1.1 What Is Chemistry?
Learning Objectives
- Define chemistry in relation to other sciences.
- Identify the general steps in the scientific method.
ChemistryThe study of matter. is the study of matter—what it consists of, what its properties are, and how it changes. Being able to describe the ingredients in a cake and how they change when the cake is baked is called chemistry. MatterAnything that has mass and takes up space. is anything that has mass and takes up space—that is, anything that is physically real. Some things are easily identified as matter—this book, for example. Others are not so obvious. Because we move so easily through air, we sometimes forget that it, too, is matter.
Chemistry is one branch of science. ScienceThe process by which we learn about the natural universe by observing, testing, and then generating models that explain our observations. is the process by which we learn about the natural universe by observing, testing, and then generating models that explain our observations. Because the physical universe is so vast, there are many different branches of science (Figure 1.1 "The Relationships between Some of the Major Branches of Science"). Thus, chemistry is the study of matter, biology is the study of living things, and geology is the study of rocks and the earth. Mathematics is the language of science, and we will use it to communicate some of the ideas of chemistry.
Although we divide science into different fields, there is much overlap among them. For example, some biologists and chemists work in both fields so much that their work is called biochemistry. Similarly, geology and chemistry overlap in the field called geochemistry. Figure 1.1 "The Relationships between Some of the Major Branches of Science" shows how many of the individual fields of science are related.
Figure 1.1 The Relationships between Some of the Major Branches of Science
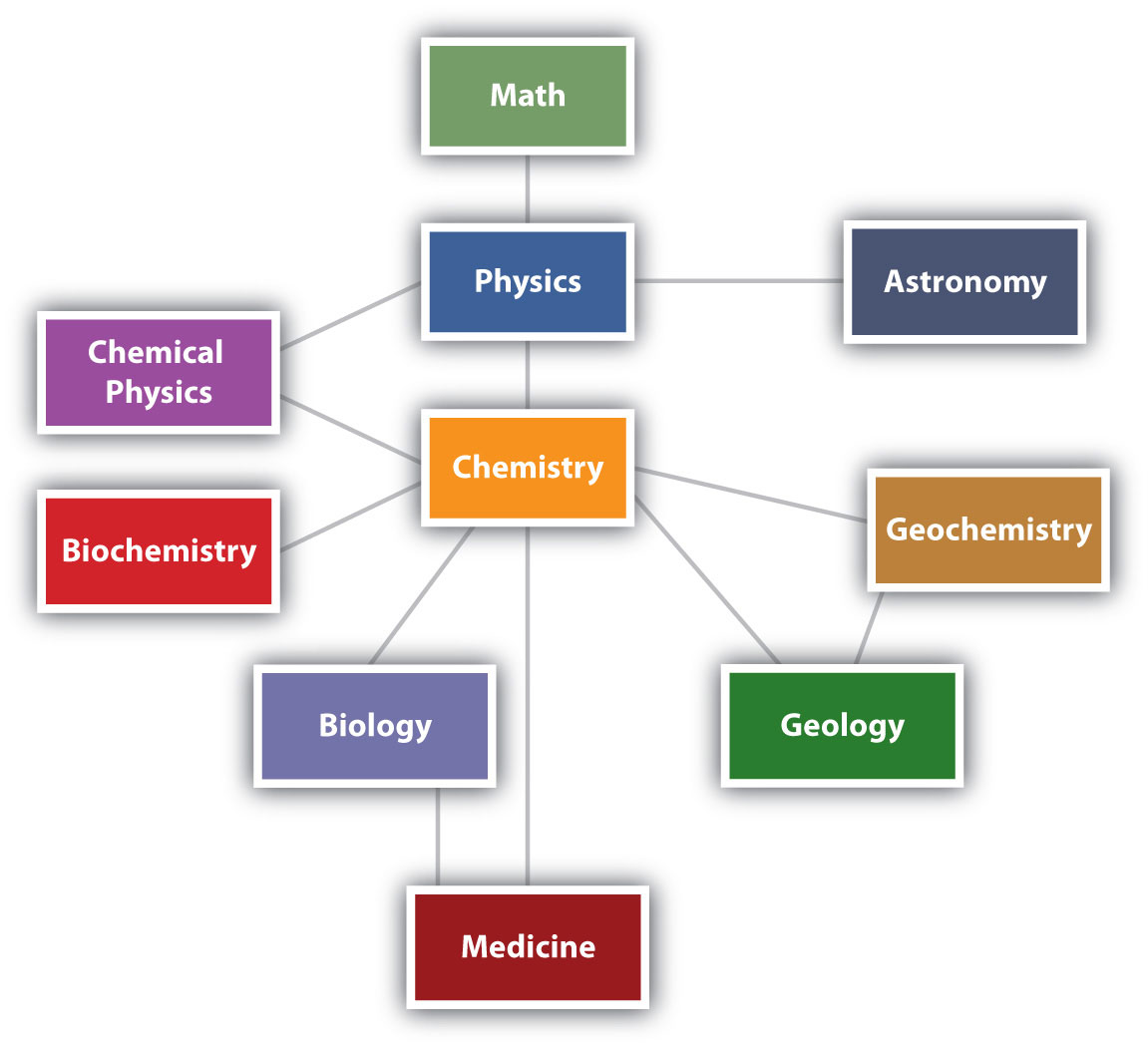
Chemistry lies more or less in the middle, which emphasizes its importance to many branches of science.
Note
There are many other fields of science, in addition to the ones (biology, medicine, etc.) listed here.
Looking Closer: Alchemy
As our understanding of the universe has changed over time, so has the practice of science. Chemistry in its modern form, based on principles that we consider valid today, was developed in the 1600s and 1700s. Before that, the study of matter was known as alchemy and was practiced mainly in China, Arabia, Egypt, and Europe.
Alchemy was a somewhat mystical and secretive approach to learning how to manipulate matter. Practitioners, called alchemists, thought that all matter was composed of different proportions of the four basic elements—fire, water, earth, and air—and believed that if you changed the relative proportions of these elements in a substance, you could change the substance. The long-standing attempts to “transmute” common metals into gold represented one goal of alchemy. Alchemy’s other major goal was to synthesize the philosopher’s stone, a material that could impart long life—even immortality. Alchemists used symbols to represent substances, some of which are shown in the accompanying figure. This was not done to better communicate ideas, as chemists do today, but to maintain the secrecy of alchemical knowledge, keeping others from sharing in it.

Alchemists used symbols like these to represent substances.
© Thinkstock
In spite of this secrecy, in its time alchemy was respected as a serious, scholarly endeavor. Isaac Newton, the great mathematician and physicist, was also an alchemist.
Example 1
Which fields of study are branches of science? Explain.
- sculpture
- astronomy
Solution
- Sculpture is not considered a science because it is not a study of some aspect of the natural universe.
- Astronomy is the study of stars and planets, which are part of the natural universe. Astronomy is therefore a field of science.
Skill-Building Exercise
-
politics
-
physiology (the study of the function of an animal’s or a plant’s body)
-
geophysics
-
agriculture
Which fields of study are branches of science?
How do scientists work? Generally, they follow a process called the scientific method. The scientific methodAn organized procedure for learning answers to questions. is an organized procedure for learning answers to questions. To find the answer to a question (for example, “Why do birds fly toward Earth’s equator during the cold months?”), a scientist goes through the following steps, which are also illustrated in Figure 1.2 "The General Steps of the Scientific Method":
Figure 1.2 The General Steps of the Scientific Method

The steps may not be as clear-cut in real life as described here, but most scientific work follows this general outline.
- Propose a hypothesis. A scientist generates a testable idea, or hypothesisA testable idea., to try to answer a question or explain how the natural universe works. Some people use the word theory in place of hypothesis, but the word hypothesis is the proper word in science. For scientific applications, the word theoryA general statement that describes a large set of observations and data. is a general statement that describes a large set of observations and data. A theory represents the highest level of scientific understanding.
- Test the hypothesis. A scientist evaluates the hypothesis by devising and carrying out experiments to test it. If the hypothesis passes the test, it may be a proper answer to the question. If the hypothesis does not pass the test, it may not be a good answer.
- Refine the hypothesis if necessary. Depending on the results of experiments, a scientist may want to modify the hypothesis and then test it again. Sometimes the results show the original hypothesis to be completely wrong, in which case a scientist will have to devise a new hypothesis.
Not all scientific investigations are simple enough to be separated into these three discrete steps. But these steps represent the general method by which scientists learn about our natural universe.
Concept Review Exercises
-
Define science and chemistry.
-
Name the steps of the scientific method.
Answers
-
Science is a process by which we learn about the natural universe by observing, testing, and then generating models that explain our observations. Chemistry is the study of matter.
-
propose a hypothesis, test the hypothesis, and refine the hypothesis if necessary
Key Takeaways
- Chemistry is the study of matter and how it behaves.
- The scientific method is the general process by which we learn about the natural universe.
Exercises
-
Based on what you know, which fields are branches of science?
- meteorology (the study of weather)
- astrophysics (the physics of planets and stars)
- economics (the study of money and monetary systems)
- astrology (the prediction of human events based on planetary and star positions)
- political science (the study of politics)
-
Based on what you know, which fields are a branches of science?
- history (the study of past events)
- ornithology (the study of birds)
- paleontology (the study of fossils)
- zoology (the study of animals)
- phrenology (using the shape of the head to determine personal characteristics)
-
Which of the following are examples of matter?
- a baby
- an idea
- the Empire State Building
- an emotion
- the air
- Alpha Centauri, the closest known star (excluding the sun) to our solar system
-
Which of the following are examples of matter?
- your textbook
- brain cells
- love
- a can of soda
- breakfast cereal
-
Suggest a name for the science that studies the physics of rocks and the earth.
-
Suggest a name for the study of the physics of living organisms.
-
Engineering is the practical application of scientific principles and discoveries to develop things that make our lives easier. Is medicine science or engineering? Justify your answer.
-
Based on the definition of engineering in Exercise 7, would building a bridge over a river or road be considered science or engineering? Justify your answer.
-
When someone says, “I have a theory that excess salt causes high blood pressure,” does that person really have a theory? If it is not a theory, what is it?
-
When a person says, “My hypothesis is that excess calcium in the diet causes kidney stones,” what does the person need to do to determine if the hypothesis is correct?
-
Some people argue that many scientists accept many scientific principles on faith. Using what you know about the scientific method, how might you argue against that assertion?
-
Most students take multiple English classes in school. Does the study of English use the scientific method?
Answers
-
- science
- science
- not science
- not science
- not science
-
-
- matter
- not matter
- matter
- not matter
- matter
- matter
-
-
geophysics
-
-
Medicine is probably closer to a field of engineering than a field of science, but this may be arguable. Ask your doctor.
-
-
In scientific terms, this person has a hypothesis.
-
-
Science is based on reproducible facts, not blind belief.
-
1.2 The Classification of Matter
Learning Objectives
- Use physical and chemical properties, including phase, to describe matter.
- Identify a sample of matter as an element, a compound, or a mixture.
Part of understanding matter is being able to describe it. One way chemists describe matter is to assign different kinds of properties to different categories.
Physical and Chemical Properties
The properties that chemists use to describe matter fall into two general categories. Physical propertiesA charactristic that describes matter, such as size, shape, and color. are characteristics that describe matter. They include characteristics such as size, shape, color, and mass. Chemical propertiesA characteristic that describes how matter changes its chemical structure or composition. are characteristics that describe how matter changes its chemical structure or composition. An example of a chemical property is flammability—a material’s ability to burn—because burning (also known as combustion) changes the chemical composition of a material.
Elements and Compounds
Any sample of matter that has the same physical and chemical properties throughout the sample is called a substanceAny sample of matter that has the same physical and chemical properties throughout the sample.. There are two types of substances. A substance that cannot be broken down into chemically simpler components is an elementA substance that cannot be broken down into chemically simpler components.. Aluminum, which is used in soda cans, is an element. A substance that can be broken down into chemically simpler components (because it has more than one element) is a compoundA substance that can be broken down into chemically simpler components. (Figure 1.2 "The General Steps of the Scientific Method"). Water is a compound composed of the elements hydrogen and oxygen. Today, there are about 118 elements in the known universe. In contrast, scientists have identified tens of millions of different compounds to date.
Note
Sometimes the word pure is added to substance, but this is not absolutely necessary. By definition, any single substance is pure.
The smallest part of an element that maintains the identity of that element is called an atomThe smallest part of an element that maintains the identity of that element.. Atoms are extremely tiny; to make a line 1 inch long, you would need 217 million iron atoms. The smallest part of a compound that maintains the identity of that compound is called a moleculeThe smallest part of a compound that maintains the identity of that compound.. Molecules are composed of atoms that are attached together and behave as a unit. Scientists usually work with millions and millions of atoms and molecules at a time. When a scientist is working with large numbers of atoms or molecules at a time, the scientist is studying the macroscopicA view of the universe in which one is working with large numbers of atoms or molecules at a time. view of the universe. However, scientists can also describe chemical events on the level of individual atoms or molecules, which is referred to as the microscopicA view of the universe in which one is working with a few atoms or molecules at a time. viewpoint. We will see examples of both macroscopic and microscopic viewpoints throughout this book (Figure 1.3 "How Many Particles Are Needed for a Period in a Sentence?").
Figure 1.3 How Many Particles Are Needed for a Period in a Sentence?
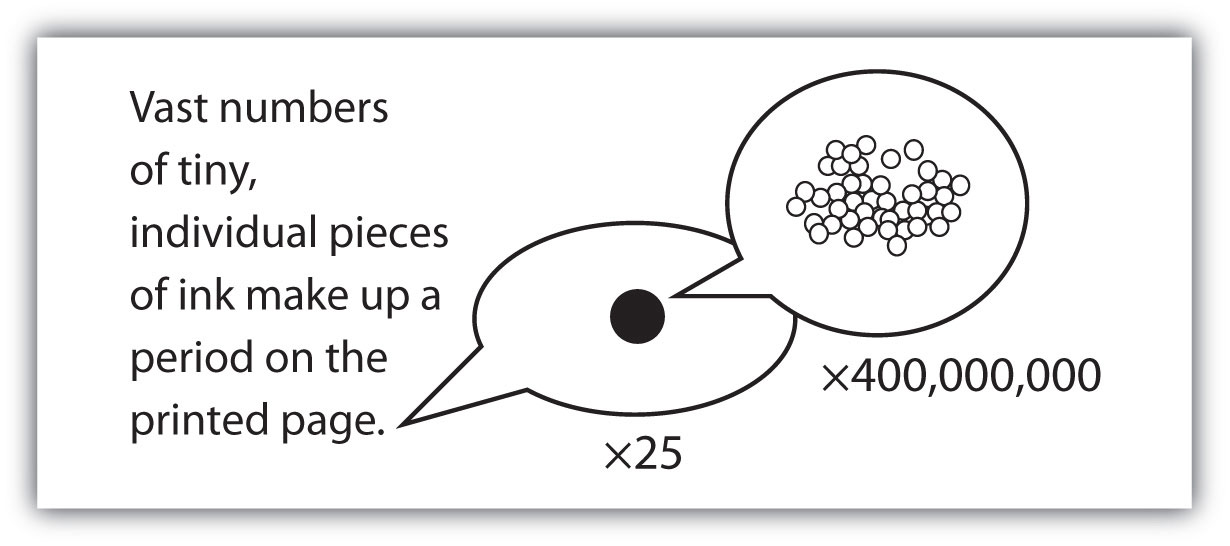
Although we do not notice it from a macroscopic perspective, matter is composed of microscopic particles so tiny that billions of them are needed to make a speck we can see with the naked eye. The ×25 and ×400,000,000 indicate the number of times the image is magnified.
Mixtures
A material composed of two or more substances is a mixtureA sample composed of two or more substances.. In a mixture, the individual substances maintain their chemical identities. Many mixtures are obvious combinations of two or more substances, such as a mixture of sand and water. Such mixtures are called heterogeneous mixturesA mixture that is a combination of two or more substances.. In some mixtures, the components are so intimately combined that they act like a single substance (even though they are not). Mixtures with a consistent composition throughout are called homogeneous mixtures (or solutions)A mixture that acts as a single substance so that it is not obvious that two or more substances are present.. Sugar dissolved in water is an example of a solution. A metal alloy, such as steel, is an example of a solid solution. Air, a mixture of mainly nitrogen and oxygen, is a gaseous solution.
Example 2
How would a chemist categorize each example of matter?
- saltwater
- soil
- water
- oxygen
Solution
- Saltwater acts as if it were a single substance even though it contains two substances—salt and water. Saltwater is a homogeneous mixture, or a solution.
- Soil is composed of small pieces of a variety of materials, so it is a heterogeneous mixture.
- Water is a substance; more specifically, because water is composed of hydrogen and oxygen, it is a compound.
- Oxygen, a substance, is an element.
Skill-Building Exercise
-
coffee
-
hydrogen
-
an egg
How would a chemist categorize each example of matter?
Phases
Another way to classify matter is to describe it as a solid, a liquid, or a gas, which was done in the examples of solutions. These three descriptions, each implying that the matter has certain physical properties, represent the three phasesA certain form of matter that includes a specific set of physical properties. of matter. A solid has a definite shape and a definite volume. Liquids ordinarily have a definite volume but not a definite shape; they take the shape of their containers. Gases have neither a definite shape nor a definite volume, and they expand to fill their containers. We encounter matter in each phase every day; in fact, we regularly encounter water in all three phases: ice (solid), water (liquid), and steam (gas).
We know from our experience with water that substances can change from one phase to another if the conditions are right. Typically, varying the temperature of a substance (and, less commonly, the pressure exerted on it) can cause a phase changeA physical process in which a substance goes from one phase to another., a physical process in which a substance goes from one phase to another (Figure 1.4 "Boiling Water"). Phase changes have particular names depending on what phases are involved, as summarized in Table 1.1 "Phase Changes".
Table 1.1 Phase Changes
| Change | Name |
|---|---|
| solid to liquid | melting, fusion |
| solid to gas | sublimation |
| liquid to gas | boiling, evaporation |
| liquid to solid | solidification, freezing |
| gas to liquid | condensation |
| gas to solid | deposition |
Figure 1.4 Boiling Water

When liquid water boils to make gaseous water, it undergoes a phase change.
© Thinkstock
Figure 1.5 "The Classification of Matter" illustrates the relationships between the different ways matter can be classified.
Figure 1.5 The Classification of Matter
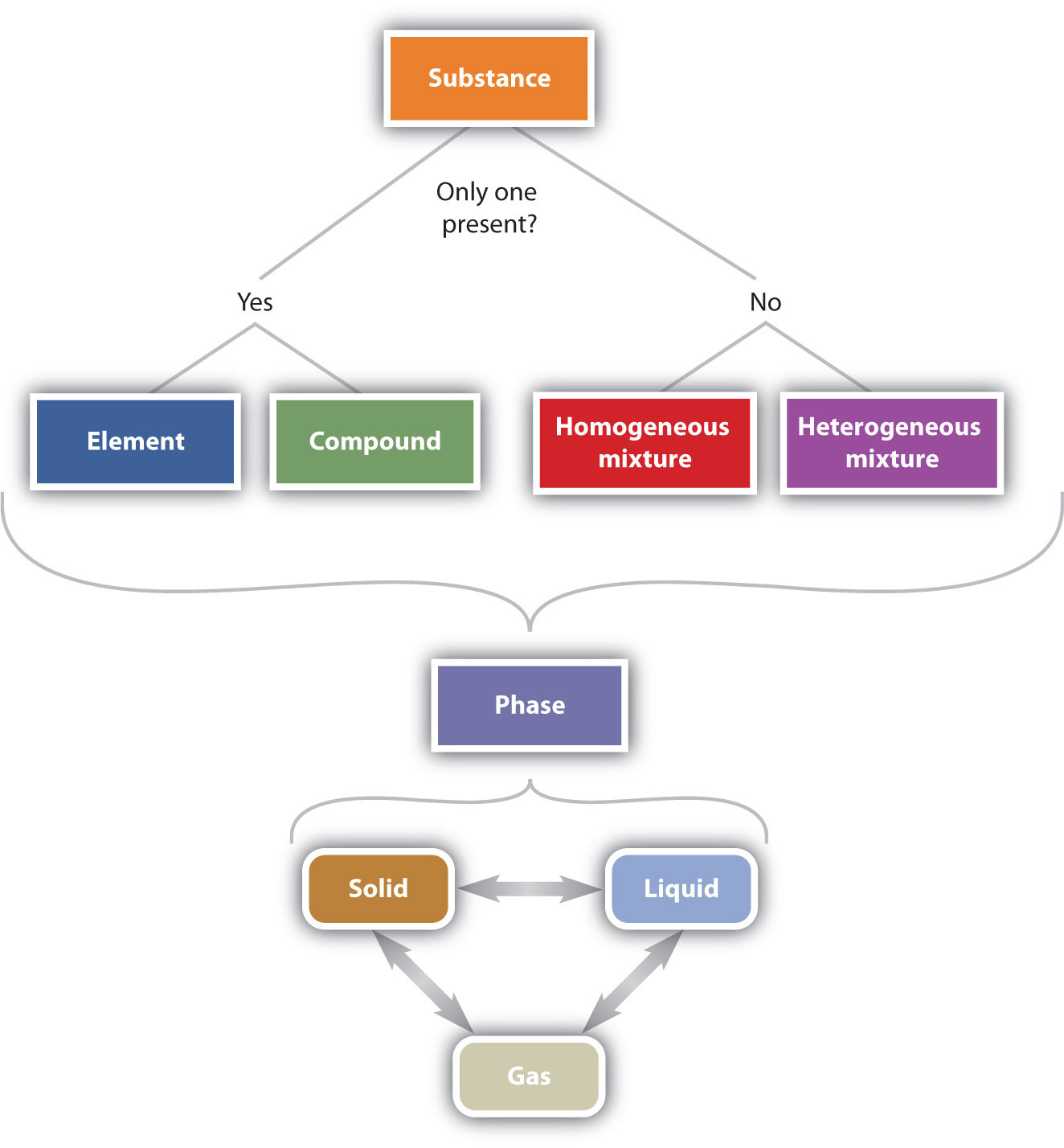
Matter can be classified in a variety of ways, depending on its properties.
Concept Review Exercises
-
Explain the differences between the physical properties of matter and the chemical properties of matter.
-
What is the difference between a heterogeneous mixture and a homogeneous mixture? Give an example of each.
-
Give at least two examples of a phase change and state the phases involved in each.
Answers
-
Physical properties describe the existence of matter, and chemical properties describe how substances change into other substances.
-
A heterogeneous mixture is obviously a mixture, such as dirt; a homogeneous mixture behaves like a single substance, such as saltwater.
-
solid to liquid (melting) and liquid to gas (boiling) (answers will vary)
Key Takeaways
- Matter can be described with both physical properties and chemical properties.
- Matter can be identified as an element, a compound, or a mixture.
Exercises
-
Does each statement refer to a chemical property or a physical property?
- Balsa is a very light wood.
- If held in a flame, magnesium metal burns in air.
- Mercury has a density of 13.6 g/mL.
- Human blood is red.
-
Does each statement refer to a chemical property or a physical property?
- The elements sodium and chlorine can combine to make table salt.
- The metal tungsten does not melt until its temperature exceeds 3,000°C.
- The ingestion of ethyl alcohol can lead to disorientation and confusion.
- The boiling point of isopropyl alcohol, which is used to sterilize cuts and scrapes, is lower than the boiling point of water.
-
Define element. How does it differ from a compound?
-
Define compound. How does it differ from an element?
-
Give two examples of a heterogeneous mixture.
-
Give two examples of a homogeneous mixture.
-
Identify each substance as an element, a compound, a heterogeneous mixture, or a solution.
- xenon, a substance that cannot be broken down into chemically simpler components
- blood, a substance composed of several types of cells suspended in a salty solution called plasma
- water, a substance composed of hydrogen and oxygen
-
Identify each substance as an element, a compound, a heterogeneous mixture, or a solution.
- sugar, a substance composed of carbon, hydrogen, and oxygen
- hydrogen, the simplest chemical substance
- dirt, a combination of rocks and decaying plant matter
-
Identify each substance as an element, a compound, a heterogeneous mixture, or a solution.
- air, primarily a mixture of nitrogen and oxygen
- ringer’s lactate, a standard fluid used in medicine that contains salt, potassium, and lactate compounds all dissolved in sterile water
- tartaric acid, a substance composed of carbon, hydrogen, and oxygen
-
Identify each material as an element, a compound, a heterogeneous mixture, or a solution.
- equal portions of salt and sand placed in a beaker and shaken up
- a combination of beeswax dissolved in liquid hexane
- hydrogen peroxide, a substance composed of hydrogen and oxygen
-
What word describes each phase change?
- solid to liquid
- liquid to gas
- solid to gas
-
What word describes each phase change?
- liquid to solid
- gas to liquid
- gas to solid
Answers
-
- physical property
- chemical property
- physical property
- physical property
-
-
An element is a substance that cannot be broken down into chemically simpler components. Compounds can be broken down into simpler substances.
-
-
a salt and pepper mix and a bowl of cereal (answers will vary)
-
-
- element
- heterogeneous mixture
- compound
-
-
- solution
- solution
- compound
-
-
- melting or fusion
- boiling or evaporation
- sublimation
-
1.3 Measurements
Learning Objective
- Express quantities properly, using a number and a unit.
A coffee maker’s instructions tell you to fill the coffeepot with 4 cups of water and use 3 scoops of coffee. When you follow these instructions, you are measuring. When you visit a doctor’s office, a nurse checks your temperature, height, weight, and perhaps blood pressure (Figure 1.6 "Measuring Blood Pressure"). The nurse is also measuring.
Figure 1.6 Measuring Blood Pressure

A nurse or a doctor measuring a patient’s blood pressure is taking a measurement.
© Thinkstock
Chemists measure the properties of matter and express these measurements as quantities. A quantityAn amount of something. is an amount of something and consists of a numberHow many (or how much) of something in a quantity. and a unitThe scale of measurement for a quantity.. The number tells us how many (or how much), and the unit tells us what the scale of measurement is. For example, when a distance is reported as “5 kilometers,” we know that the quantity has been expressed in units of kilometers and that the number of kilometers is 5. If you ask a friend how far he or she walks from home to school, and the friend answers “12” without specifying a unit, you do not know whether your friend walks—for example, 12 miles, 12 kilometers, 12 furlongs, or 12 yards. Both a number and a unit must be included to express a quantity properly.
To understand chemistry, we need a clear understanding of the units chemists work with and the rules they follow for expressing numbers. The next two sections examine the rules for expressing numbers.
Example 3
Identify the number and the unit in each quantity.
- one dozen eggs
- 2.54 centimeters
- a box of pencils
- 88 meters per second
Solution
- The number is one, and the unit is dozen eggs.
- The number is 2.54, and the unit is centimeter.
- The number 1 is implied because the quantity is only a box. The unit is box of pencils.
- The number is 88, and the unit is meters per second. Note that in this case the unit is actually a combination of two units: meters and seconds.
Skill-Building Exercise
-
99 bottles of soda
-
60 miles per hour
-
32 fluid ounces
-
98.6 degrees Fahrenheit
Identify the number and the unit in each quantity.
Concept Review Exercise
-
What are the two necessary parts of a quantity?
Answer
-
The two necessary parts are the number and the unit.
To Your Health: Dosages
As we saw in the chapter-opening essay, a medicine can be more harmful than helpful if it is not taken in the proper dosage. A dosage (or dose) is the specific amount of a medicine that is known to be therapeutic for an ailment in a patient of a certain size. Dosages of the active ingredient in medications are usually described by units of mass, typically grams or milligrams, and generally are equated with a number of capsules or teaspoonfuls to be swallowed or injected. (For more information about mass, see Section 1.6 "The International System of Units".) The amount of the active ingredient in a medicine is carefully controlled so that the proper number of pills or spoonfuls contains the proper dose.
Most drugs must be taken in just the right amount. If too little is taken, the desired effects will not occur (or will not occur fast enough for comfort); if too much is taken, there may be potential side effects that are worse than the original ailment. Some drugs are available in multiple dosages. For example, tablets of the medication levothyroxine sodium, a synthetic thyroid hormone for those suffering from decreased thyroid gland function, are available in 11 different doses, ranging from 25 micrograms (µg) to 300 µg. It is a doctor’s responsibility to prescribe the correct dosage for a patient, and it is a pharmacist’s responsibility to provide the patient with the correct medicine at the dosage prescribed. Thus, proper quantities—which are expressed using numbers and their associated units—are crucial for keeping us healthy.
Key Takeaway
- Identify a quantity properly with a number and a unit.
Exercises
-
Why are both parts of a quantity important when describing it?
-
Why are measurements an important part of any branch of science, such as chemistry?
-
You ask a classmate how much homework your chemistry professor assigned. Your classmate answers, “twenty.” Is that a proper answer? Why or why not?
-
Identify the number and the unit in each quantity.
- five grandchildren
- 16 candles
- four score and seven years
- 40 days and 40 nights
- 12.01 grams
- 9.8 meters per second squared
- 55 miles per hour
- 98.6 degrees Fahrenheit
Answers
-
The number states how much, and the unit states of what. Without the number and the unit, a quantity cannot be properly communicated.
-
-
No, it is not a proper answer; you do not know whether the professor meant homework problem number 20 or 20 homework problems.
-
1.4 Expressing Numbers: Scientific Notation
Learning Objective
- Express a large number or a small number in scientific notation.
The instructions for making a pot of coffee specified 3 scoops (rather than 12,000 grounds) because any measurement is expressed more efficiently with units that are appropriate in size. In science, however, we often must deal with quantities that are extremely small or incredibly large. For example, you may have 5,000,000,000,000 red blood cells in a liter of blood, and the diameter of an iron atom is 0.000000014 inches. Numbers with many zeros can be cumbersome to work with, so scientists use scientific notation.
Scientific notationA system for expressing very large or very small numbers in a compact manner. is a system for expressing very large or very small numbers in a compact manner. It uses the idea that such numbers can be rewritten as a simple number multiplied by 10 raised to a certain exponent, or powerThe exponent in a number expressed in scientific notation..
Let us look first at large numbers. Suppose a spacecraft is 1,500,000 miles from Mars. The number 1,500,000 can be thought of as follows:

That is, 1,500,000 is the same as 1.5 times 1 million, and 1 million is 10 × 10 × 10 × 10 × 10 × 10, or 106 (which is read as “ten to the sixth power”). Therefore, 1,500,000 can be rewritten as 1.5 times 106, or 1.5 × 106. The distance of the spacecraft from Mars can therefore be expressed as 1.5 × 106 miles.
100 = 1
101 = 10
102 = 100
103 = 1,000
104 = 10,000
and so forth
The convention for expressing numbers in scientific notation is to write a single nonzero first digit, a decimal point, and the rest of the digits, excluding any trailing zeros. This figure is followed by a multiplication sign and then by 10 raised to the power necessary to reproduce the original number. For example, although 1,500,000 can also be written as 15. × 105 (which would be 15. × 100,000), the convention is to have only one digit before the decimal point. How do we know to what power 10 is raised? The power is the number of places you have to move the decimal point to the left to make it follow the first digit, so that the number being multiplied is between 1 and 10:

Example 4
Express each number in scientific notation.
- 67,000,000,000
- 1,689
- 12.6
Solution
- Moving the decimal point 10 places to the left gives 6.7 × 1010.
- The decimal point is assumed to be at the end of the number, so moving it three places to the left gives 1.689 × 103.
- In this case, we need to move the decimal point only one place to the left, which yields 1.26 × 101.
Skill-Building Exercise
-
1,492
-
102,000,000
-
101,325
Express each number in scientific notation.
To change scientific notation to standard notation, we reverse the process, moving the decimal point to the right. Add zeros to the end of the number being converted, if necessary, to produce a number of the proper magnitude.
Example 5
Express each number in standard, or nonscientific, notation.
- 5.27 × 104
- 1.0008 × 106
Solution
- Rather than moving the decimal to the left, we move it four places to the right and add zeros to give 52,700.
- Moving the decimal six places to the right gives 1,000,800.
Skill-Building Exercise
-
6.98 × 108
-
1.005 × 102
Express each number in standard, or nonscientific, notation.
We can also use scientific notation to express numbers whose magnitudes are less than 1. For example, the number 0.006 can be expressed as follows:

10−1 = 1/10
10−2 = 1/100
10−3 = 1/1,000
10−4 = 1/10,000
10−5 = 1/100,000
and so forth
We use a negative number as the power to indicate the number of places we have to move the decimal point to the right to follow the first nonzero digit. This is illustrated as follows:

In scientific notation, numbers with a magnitude greater than one have a positive power, while numbers with a magnitude less than one have a negative power.
Example 6
Express each number in scientific notation.
- 0.000006567
- −0.0004004
- 0.000000000000123
Solution
- Move the decimal point six places to the right to get 6.567 × 10−6.
- Move the decimal point four places to the right to get −4.004 × 10−4. The negative sign on the number itself does not affect how we apply the rules of scientific notation.
- Move the decimal point 13 places to the right to get 1.23 × 10−13.
Skill-Building Exercise
-
0.000355
-
0.314159
Express each number in scientific notation.
As with numbers with positive powers of 10, when changing from scientific notation to standard notation, we reverse the process.
Example 7
Express each number in standard notation.
- 6.22 × 10−2
- 9.9 × 10−9
Solution
- 0.0622
- 0.0000000099
Skill-Building Exercise
-
9.98 × 10−5
-
5.109 × 10−8
Express each number in standard notation.
Although calculators can show 8 to 10 digits in their display windows, that is not always enough when working with very large or very small numbers. For this reason, many calculators are designed to handle scientific notation. The method for entering scientific notation differs for each calculator model, so take the time to learn how to do it properly on your calculator, asking your instructor for assistance if necessary. If you do not learn to enter scientific notation into your calculator properly, you will not get the correct final answer when performing a calculation.
Concept Review Exercises
-
Why it is easier to use scientific notation to express very large or very small numbers?
-
What is the relationship between how many places a decimal point moves and the power of 10 used in changing a conventional number into scientific notation?
Answers
-
Scientific notation is more convenient than listing a large number of zeros.
-
The number of places the decimal point moves equals the power of 10—positive if the decimal point moves to the left and negative if the decimal point moves to the right.
Key Takeaway
- Large or small numbers are expressed in scientific notation, which use powers of 10.
Exercises
-
Why is scientific notation useful in expressing numbers?
-
What is the relationship between the power and the number of places a decimal point is moved when going from standard to scientific notation?
-
Express each number in scientific notation.
- 0.00064
- 5,230,000
- −56,200
- 0.000000000220
- 1.0
-
Express each number in scientific notation.
- 678
- −1,061
- 0.000560
- 0.0000003003
- 100,000,000
-
Express each number in standard form.
- 6.72 × 104
- 2.088 × 10−4
- −3 × 106
- 9.98 × 10−7
-
Express each number in standard form.
- 9.05 × 105
- 1.0 × 10−3
- 6.022 × 1023
- 8.834 × 10−12
-
Complete the following table:
Incorrect Scientific Notation Correct Scientific Notation 54.7 × 104 0.0066 × 103 3,078 × 100 -
Complete the following table:
Incorrect Scientific Notation Correct Scientific Notation 234.0 × 101 36 × 10−4 0.993 × 105
Answers
-
Scientific notation is more convenient than listing a large number of zeros.
-
-
- 6.4 × 10−4
- 5.23 × 106
- −5.62 × 104
- 2.20 × 10−10
- 1.0 × 100
-
-
- 67,200
- 0.0002088
- −3,000,000
- 0.000000998
-
-
Incorrect Scientific Notation Correct Scientific Notation 54.7 × 104 5.47 × 105 0.0066 × 103 6.6 × 100 3,078 × 100 3.078 × 103 -
1.5 Expressing Numbers: Significant Figures
Learning Objectives
- Identify the number of significant figures in a reported value.
- Use significant figures correctly in arithmetical operations.
Scientists have established certain conventions for communicating the degree of precision of a measurement. Imagine, for example, that you are using a meterstick to measure the width of a table. The centimeters (cm) are marked off, telling you how many centimeters wide the table is. Many metersticks also have millimeters (mm) marked off, so we can measure the table to the nearest millimeter. But most metersticks do not have any finer measurements indicated, so you cannot report the table’s width any more exactly than to the nearest millimeter. All you can do is estimate the next decimal place in the measurement (Figure 1.7 "Measuring an Object to the Correct Number of Digits").
Figure 1.7 Measuring an Object to the Correct Number of Digits
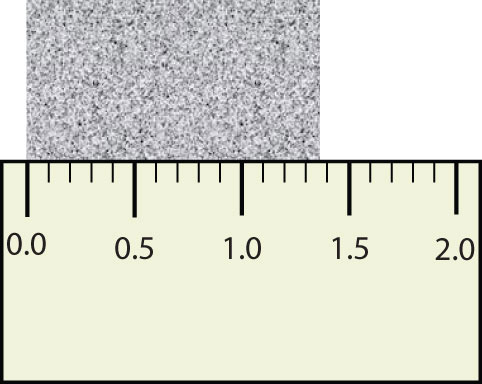
How many digits should be reported for the length of this object?
The concept of significant figures takes this limitation into account. The significant figuresAll the digits of a measured quantity known with certainty and the first uncertain, or estimated, digit. of a measured quantity are defined as all the digits known with certainty and the first uncertain, or estimated, digit. It makes no sense to report any digits after the first uncertain one, so it is the last digit reported in a measurement. Zeros are used when needed to place the significant figures in their correct positions. Thus, zeros may not be significant figures.
Note
“Sig figs” is a common abbreviation for significant figures.
For example, if a table is measured and reported as being 1,357 mm wide, the number 1,357 has four significant figures. The 1 (thousands), the 3 (hundreds), and the 5 (tens) are certain; the 7 (units) is assumed to have been estimated. It would make no sense to report such a measurement as 1,357.0 or 1,357.00 because that would suggest the measuring instrument was able to determine the width to the nearest tenth or hundredth of a millimeter, when in fact it shows only tens of millimeters and the units have to be estimated.
On the other hand, if a measurement is reported as 150 mm, the 1 (hundreds) and the 5 (tens) are known to be significant, but how do we know whether the zero is or is not significant? The measuring instrument could have had marks indicating every 10 mm or marks indicating every 1 mm. Is the zero an estimate, or is the 5 an estimate and the zero a placeholder?
The rules for deciding which digits in a measurement are significant are as follows:
- All nonzero digits are significant. In 1,357, all the digits are significant.
- Captive (or embedded) zeros, which are zeros between significant digits, are significant. In 405, all the digits are significant.
- Leading zeros, which are zeros at the beginning of a decimal number less than 1, are not significant. In 0.000458, the first four digits are leading zeros and are not significant. The zeros serve only to put the digits 4, 5, and 8 in the correct positions. This number has three significant figures.
- Trailing zeros, which are zeros at the end of a number, are significant only if the number has a decimal point. Thus, in 1,500, the two trailing zeros are not significant because the number is written without a decimal point; the number has two significant figures. However, in 1,500.00, all six digits are significant because the number has a decimal point.
Example 8
How many significant digits does each number have?
- 6,798,000
- 6,000,798
- 6,000,798.00
- 0.0006798
Solution
- four (by rules 1 and 4)
- seven (by rules 1 and 2)
- nine (by rules 1, 2, and 4)
- four (by rules 1 and 3)
Skill-Building Exercise
-
2.1828
-
0.005505
-
55,050
-
5
-
500
How many significant digits does each number have?
Combining Numbers
It is important to be aware of significant figures when you are mathematically manipulating numbers. For example, dividing 125 by 307 on a calculator gives 0.4071661238… to an infinite number of digits. But do the digits in this answer have any practical meaning, especially when you are starting with numbers that have only three significant figures each? When performing mathematical operations, there are two rules for limiting the number of significant figures in an answer—one rule is for addition and subtraction, and one rule is for multiplication and division.
For addition or subtraction, the rule is to stack all the numbers with their decimal points aligned and then limit the answer’s significant figures to the rightmost column for which all the numbers have significant figures. Consider the following:
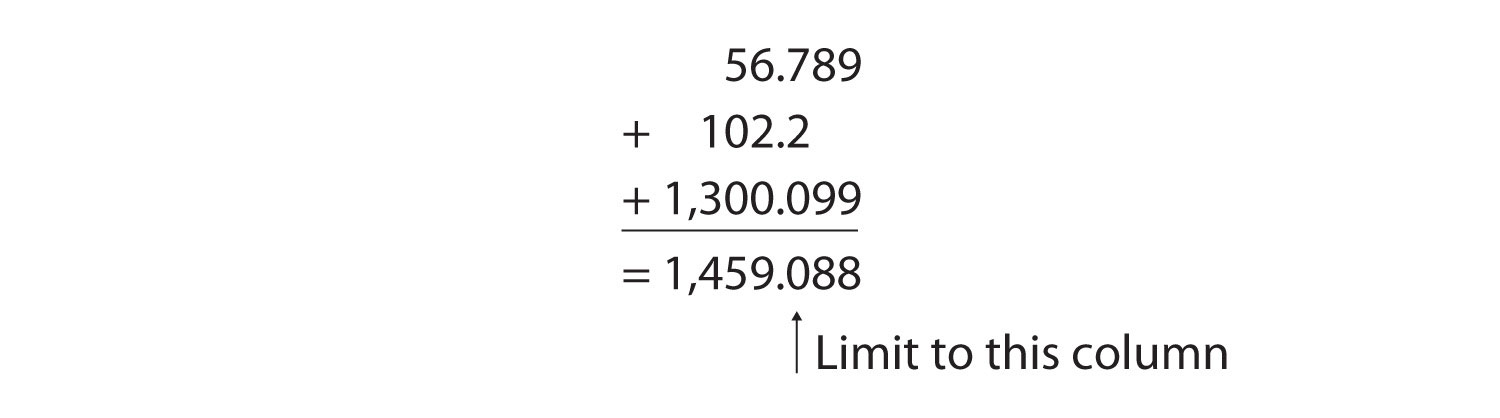
The arrow points to the rightmost column in which all the numbers have significant figures—in this case, the tenths place. Therefore, we will limit our final answer to the tenths place. Is our final answer therefore 1,459.0? No, because when we drop digits from the end of a number, we also have to roundThe process of assessing the final significant figure of a quantity to determine if it should be kept or moved higher. the number. Notice that the second dropped digit, in the hundredths place, is 8. This suggests that the answer is actually closer to 1,459.1 than it is to 1,459.0, so we need to round up to 1,459.1. The rules in rounding are simple: If the first dropped digit is 5 or higher, round up. If the first dropped digit is lower than 5, do not round up.
For multiplication or division, the rule is to count the number of significant figures in each number being multiplied or divided and then limit the significant figures in the answer to the lowest count. An example is as follows:
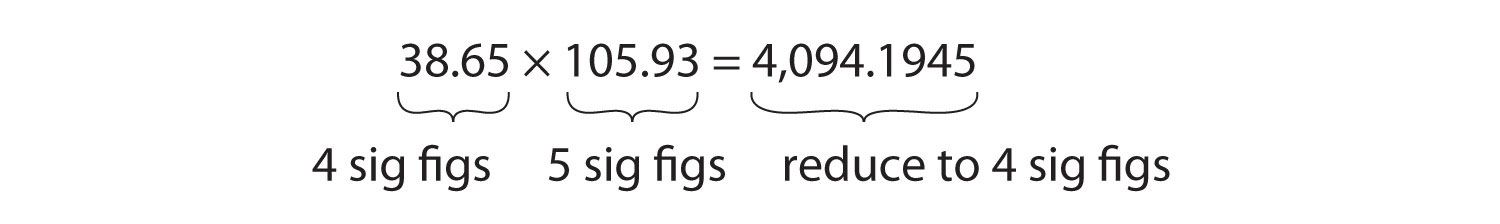
The final answer, limited to four significant figures, is 4,094. The first digit dropped is 1, so we do not round up.
Scientific notation provides a way of communicating significant figures without ambiguity. You simply include all the significant figures in the leading number. For example, the number 450 has two significant figures and would be written in scientific notation as 4.5 × 102, whereas 450.0 has four significant figures and would be written as 4.500 × 102. In scientific notation, all significant figures are listed explicitly.
Example 9
Write the answer for each expression using scientific notation with the appropriate number of significant figures.
- 23.096 × 90.300
- 125 × 9.000
- 1,027 + 610 + 363.06
Solution
- The calculator answer is 2,085.5688, but we need to round it to five significant figures. Because the first digit to be dropped (in the hundredths place) is greater than 5, we round up to 2,085.6, which in scientific notation is 2.0856 × 103.
- The calculator gives 1,125 as the answer, but we limit it to three significant figures and convert into scientific notation: 1.13 × 103.
- The calculator gives 2,000.06 as the answer, but because 610 has its farthest-right significant figure in the tens column, our answer must be limited to the tens position: 2.0 × 103.
Skill-Building Exercise
-
217 ÷ 903
-
13.77 + 908.226 + 515
-
255.0 − 99
-
0.00666 × 321
Write the answer for each expression using scientific notation with the appropriate number of significant figures.
Remember that calculators do not understand significant figures. You are the one who must apply the rules of significant figures to a result from your calculator.
Concept Review Exercises
-
Explain why the concept of significant figures is important in numerical calculations.
-
State the rules for determining the significant figures in a measurement.
-
When do you round a number up, and when do you not round a number up?
Answers
-
Significant figures represent all the known digits of a measurement plus the first estimated one.
-
All nonzero digits are significant; zeros between nonzero digits are significant; zeros at the end of a nondecimal number or the beginning of a decimal number are not significant; zeros at the end of a decimal number are significant.
-
Round up only if the first digit dropped is 5 or higher.
Key Takeaways
- Significant figures properly report the number of measured and estimated digits in a measurement.
- There are rules for applying significant figures in calculations.
Exercises
-
Define significant figures. Why are they important?
-
Define the different types of zeros found in a number and explain whether or not they are significant.
-
How many significant figures are in each number?
- 140
- 0.009830
- 15,050
- 221,560,000
- 5.67 × 103
- 2.9600 × 10−5
-
How many significant figures are in each number?
- 1.05
- 9,500
- 0.0004505
- 0.00045050
- 7.210 × 106
- 5.00 × 10−6
-
Round each number to three significant figures.
- 34,705
- 34,750
- 34,570
-
Round each number to four significant figures.
- 34,705
- 0.0054109
- 8.90443 × 108
-
Perform each operation and express the answer to the correct number of significant figures.
- 467.88 + 23.0 + 1,306 = ?
- 10,075 + 5,822.09 − 34.0 = ?
- 0.00565 + 0.002333 + 0.0991 = ?
-
Perform each operation and express the answer to the correct number of significant figures.
- 0.9812 + 1.660 + 8.6502 = ?
- 189 + 3,201.8 − 1,100 = ?
- 675.0 − 24 + 1,190 = ?
-
Perform each operation and express the answer to the correct number of significant figures.
- 439 × 8,767 = ?
- 23.09 ÷ 13.009 = ?
- 1.009 × 876 = ?
-
Perform each operation and express the answer to the correct number of significant figures.
- 3.00 ÷ 1.9979 = ?
- 2,300 × 185 = ?
- 16.00 × 4.0 = ?
-
Use your calculator to solve each equation. Express each answer in proper scientific notation and with the proper number of significant figures. If you do not get the correct answers, you may not be entering scientific notation into your calculator properly, so ask your instructor for assistance.
- (5.6 × 103) × (9.04 × 10−7) = ?
- (8.331 × 10−2) × (2.45 × 105) = ?
- 983.09 ÷ (5.390 × 105) = ?
- 0.00432 ÷ (3.9001 × 103) = ?
-
Use your calculator to solve each equation. Express each answer in proper scientific notation and with the proper number of significant figures. If you do not get the correct answers, you may not be entering scientific notation into your calculator properly, so ask your instructor for assistance.
- (5.2 × 106) × (3.33 × 10−2) = ?
- (7.108 × 103) × (9.994 × 10−5) = ?
- (6.022 × 107) ÷ (1.381 × 10−8) = ?
- (2.997 × 108) ÷ (1.58 × 1034) = ?
Answers
-
Significant figures represent all the known digits plus the first estimated digit of a measurement; they are the only values worth reporting in a measurement.
-
-
- two
- four
- four
- five
- three
- five
-
-
- 34,700
- 34,800
- 34,600
-
-
- 1,797
- 15,863
- 0.1071
-
-
- 3,850,000
- 1.775
- 884
-
-
- 5.1 × 10−3
- 2.04 × 104
- 1.824 × 10−3
- 1.11 × 10−6
-
1.6 The International System of Units
Learning Objective
- Recognize the SI base units and explain the system of prefixes used with them.
Now that we have discussed some of the conventions for expressing numbers, let us focus on the other component of a quantity—the units.
People who live in the United States measure weight in pounds, height in feet and inches, and a car’s speed in miles per hour. In contrast, chemistry and other branches of science use the International System of Units (also known as SI after Système Internationale d’Unités), which was established so that scientists around the world could communicate efficiently with each other. Many countries have also adopted SI units for everyday use as well. The United States is one of the few countries that has not.
Base SI Units
Base (or basic) unitsA fundamental unit of SI., are the fundamental units of SI. There are seven base units, which are listed in Table 1.2 "The Seven Base SI Units". Chemistry uses five of the base units: the mole for amount, the kilogram for mass, the meter for length, the second for time, and the kelvin for temperature. The degree Celsius (°C) is also commonly used for temperature. The numerical relationship between kelvins and degrees Celsius is as follows:
K = °C + 273Table 1.2 The Seven Base SI Units
| Property | Unit | Abbreviation |
|---|---|---|
| length | meter | m |
| mass | kilogram | kg |
| time | second | s |
| amount | mole | mol |
| temperature | kelvin | K |
| electrical current | ampere | amp |
| luminous intensity | candela | cd |
Note
The United States uses the English system of units for many quantities. Inches, feet, miles, gallons, pounds, and so forth, are all units connected with the English system of units.
The size of each base unit is defined by international convention. For example, the kilogram is defined as the quantity of mass of a special metal cylinder kept in a vault in France (Figure 1.8 "The Kilogram"). The other base units have similar definitions. The sizes of the base units are not always convenient for all measurements. For example, a meter is a rather large unit for describing the width of something as narrow as human hair. Instead of reporting the diameter of hair as 0.00012 m or even 1.2 × 10−4 m, SI also provides a series of prefixes that can be attached to the units, creating units that are larger or smaller by powers of 10.
Figure 1.8 The Kilogram

The standard for the kilogram is a platinum-iridium cylinder kept in a special vault in France.
Source: Photo reproduced by permission of the Bureau International des Poids et Mesures, who retain full internationally protected copyright.
Common prefixes and their multiplicative factors are listed in Table 1.3 "Prefixes Used with SI Units". (Perhaps you have already noticed that the base unit kilogram is a combination of a prefix, kilo- meaning 1,000 ×, and a unit of mass, the gram.) Some prefixes create a multiple of the original unit: 1 kilogram equals 1,000 grams, and 1 megameter equals 1,000,000 meters. Other prefixes create a fraction of the original unit. Thus, 1 centimeter equals 1/100 of a meter, 1 millimeter equals 1/1,000 of a meter, 1 microgram equals 1/1,000,000 of a gram, and so forth.
Table 1.3 Prefixes Used with SI Units
| Prefix | Abbreviation | Multiplicative Factor | Multiplicative Factor in Scientific Notation |
|---|---|---|---|
| giga- | G | 1,000,000,000 × | 109 × |
| mega- | M | 1,000,000 × | 106 × |
| kilo- | k | 1,000 × | 103 × |
| deca- | D | 10 × | 101 × |
| deci- | d | 1/10 × | 10−1 × |
| centi- | c | 1/100 × | 10−2 × |
| milli- | m | 1/1,000 × | 10−3 × |
| micro- | µ* | 1/1,000,000 × | 10−6 × |
| nano- | n | 1/1,000,000,000 × | 10−9 × |
| *The letter µ is the Greek lowercase letter for m and is called “mu,” which is pronounced “myoo.” | |||
Both SI units and prefixes have abbreviations, and the combination of a prefix abbreviation with a base unit abbreviation gives the abbreviation for the modified unit. For example, kg is the abbreviation for kilogram. We will be using these abbreviations throughout this book.
Derived SI Units
Derived unitsA combinations of the SI base units. are combinations of SI base units. Units can be multiplied and divided, just as numbers can be multiplied and divided. For example, the area of a square having a side of 2 cm is 2 cm × 2 cm, or 4 cm2 (read as “four centimeters squared” or “four square centimeters”). Notice that we have squared a length unit, the centimeter, to get a derived unit for area, the square centimeter.
Volume is an important quantity that uses a derived unit. VolumeThe amount of space that a given substance occupies. is the amount of space that a given substance occupies and is defined geometrically as length × width × height. Each distance can be expressed using the meter unit, so volume has the derived unit m × m × m, or m3 (read as “meters cubed” or “cubic meters”). A cubic meter is a rather large volume, so scientists typically express volumes in terms of 1/1,000 of a cubic meter. This unit has its own name—the liter (L). A liter is a little larger than 1 US quart in volume. (Table 1.4 "Approximate Equivalents to Some SI Units" gives approximate equivalents for some of the units used in chemistry.) As shown in Figure 1.9 "The Liter", a liter is also 1,000 cm3. By definition, there are 1,000 mL in 1 L, so 1 milliliter and 1 cubic centimeter represent the same volume.
1 mL = 1 cm3Figure 1.9 The Liter
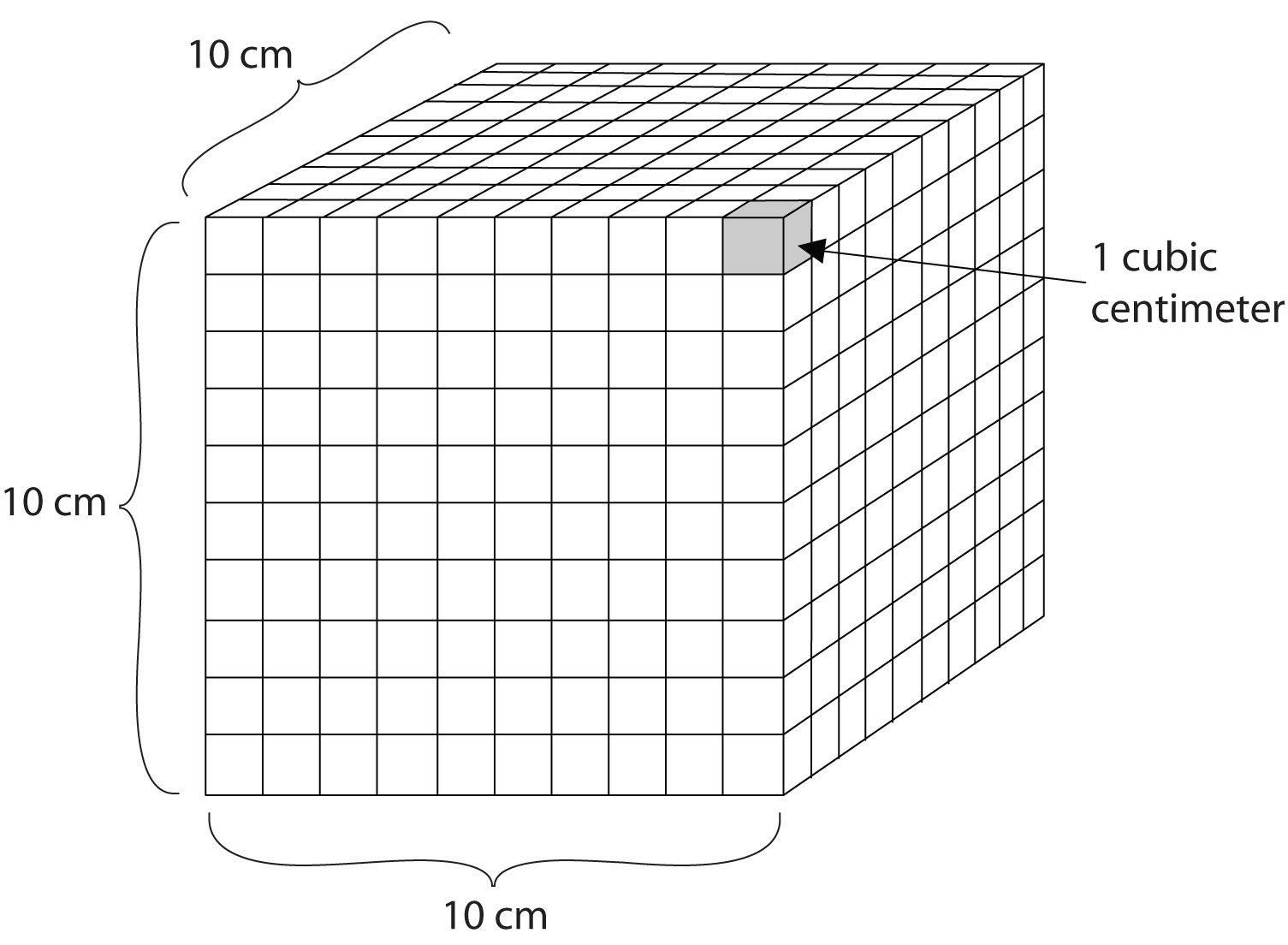
A liter is defined as a cube 10 cm (1/10th of a meter) on a side. A milliliter, 1/1,000th of a liter, is equal to 1 cubic centimeter.
Table 1.4 Approximate Equivalents to Some SI Units
| 1 m ≈ 39.36 in. ≈ 3.28 ft ≈ 1.09 yd |
| 1 cm ≈ 2.54 in. |
| 1 km ≈ 0.62 mi |
| 1 kg ≈ 2.20 lb |
| 1 lb ≈ 454 g |
| 1 L ≈ 1.06 qt |
| 1 qt ≈ 0.946 L |
EnergyThe ability to perform work., another important quantity in chemistry, is the ability to perform work, such as moving a box of books from one side of a room to the other side. It has a derived unit of kg·m2/s2. (The dot between the kg and m units implies the units are multiplied together.) Because this combination is cumbersome, this collection of units is redefined as a jouleThe SI unit of energy. (J). An older unit of energy, the calorie (cal), is also widely used. There are 4.184 J in 1 cal. All chemical processes occur with a simultaneous change in energy. (For more information on energy changes, see Chapter 7 "Energy and Chemical Processes".)
To Your Health: Energy and Food
The food in our diet provides the energy our bodies need to function properly. The energy contained in food could be expressed in joules or calories, which are the conventional units for energy, but the food industry prefers to use the kilocalorie and refers to it as the Calorie (with a capital C). The average daily energy requirement of an adult is about 2,000–2,500 Calories, which is 2,000,000–2,500,000 calories (with a lowercase c).
If we expend the same amount of energy that our food provides, our body weight remains stable. If we ingest more Calories from food than we expend, however, our bodies store the extra energy in high-energy-density compounds, such as fat, and we gain weight. On the other hand, if we expend more energy than we ingest, we lose weight. Other factors affect our weight as well—genetic, metabolic, behavioral, environmental, cultural factors—but dietary habits are among the most important.
In 2008 the US Centers for Disease Control and Prevention issued a report stating that 73% of Americans were either overweight or obese. More alarmingly, the report also noted that 19% of children aged 6–11 and 18% of adolescents aged 12–19 were overweight—numbers that had tripled over the preceding two decades. Two major reasons for this increase are excessive calorie consumption (especially in the form of high-fat foods) and reduced physical activity. Partly because of that report, many restaurants and food companies are working to reduce the amounts of fat in foods and provide consumers with more healthy food options.
DensityThe mass of an object divided by its volume. is defined as the mass of an object divided by its volume; it describes the amount of matter contained in a given amount of space.
Thus, the units of density are the units of mass divided by the units of volume: g/cm3 or g/mL (for solids and liquids), g/L (for gases), kg/m3, and so forth. For example, the density of water is about 1.00 g/cm3, while the density of mercury is 13.6 g/mL. (Remember that 1 mL equals 1 cm3.) Mercury is over 13 times as dense as water, meaning that it contains over 13 times the amount of matter in the same amount of space. The density of air at room temperature is about 1.3 g/L.
Example 10
Give the abbreviation for each unit and define the abbreviation in terms of the base unit.
- kiloliter
- microsecond
- decimeter
- nanogram
Solution
- The abbreviation for a kiloliter is kL. Because kilo means “1,000 ×,” 1 kL equals 1,000 L.
- The abbreviation for microsecond is µs. Micro implies 1/1,000,000th of a unit, so 1 µs equals 0.000001 s.
- The abbreviation for decimeter is dm. Deci means 1/10th, so 1 dm equals 0.1 m.
- The abbreviation for nanogram is ng and equals 0.000000001 g.
Skill-Building Exercise
-
kilometer
-
milligram
-
nanosecond
-
centiliter
Give the abbreviation for each unit and define the abbreviation in terms of the base unit.
Example 11
What is the density of a section of bone if a 25.3 cm3 sample has a mass of 27.8 g?
Solution
Because density is defined as the mass of an object divided by its volume, we can set up the following relationship:
Note that we have limited our final answer to three significant figures.
Skill-Building Exercise
-
What is the density of oxygen gas if a 15.0 L sample has a mass of 21.7 g?
Concept Review Exercises
-
What is the difference between a base unit and a derived unit? Give two examples of each type of unit.
-
Do units follow the same mathematical rules as numbers do? Give an example to support your answer.
Answers
-
Base units are the seven fundamental units of SI; derived units are constructed by making combinations of the base units; base units: kilograms and meters (answers will vary); derived units: grams per milliliter and joules (answers will vary).
-
yes; (answers will vary)
Key Takeaways
- Recognize the SI base units.
- Combining prefixes with base units creates new units of larger or smaller sizes.
Exercises
-
List four base units.
-
List four derived units.
-
How many meters are in 1 km? How many centimeters are in 1 m?
-
How many grams are in 1 Mg? How many microliters are in 1 L?
-
Complete the following table:
Unit Abbreviation centiliter ms cm kL micrometer -
Complete the following table:
Unit Abbreviation microliter kilosecond dL ns millimeter -
What are some appropriate units for density?
-
A derived unit for velocity, which is the change of position with respect to time, is meters per second (m/s). Give three other derived units for velocity.
Answers
-
second, meter, kilogram, and kelvin (answers will vary)
-
-
1,000; 100
-
-
Unit Abbreviation centiliter cL millisecond ms centimeter cm kiloliter kL micrometer µm -
-
grams per liter, grams per milliliter, and kilograms per liter (answers will vary)
-
1.7 Converting Units
Learning Objective
- Convert a value reported in one unit to a corresponding value in a different unit.
The ability to convert from one unit to another is an important skill. For example, a nurse with 50 mg aspirin tablets who must administer 0.2 g of aspirin to a patient needs to know that 0.2 g equals 200 mg, so 4 tablets are needed. Fortunately, there is a simple way to convert from one unit to another.
Conversion Factors
If you learned the SI units and prefixes described in Section 1.6 "The International System of Units", then you know that 1 cm is 1/100th of a meter.
or 100 cm = 1 mSuppose we divide both sides of the equation by 1 m (both the number and the unit):
As long as we perform the same operation on both sides of the equals sign, the expression remains an equality. Look at the right side of the equation; it now has the same quantity in the numerator (the top) as it has in the denominator (the bottom). Any fraction that has the same quantity in the numerator and the denominator has a value of 1:
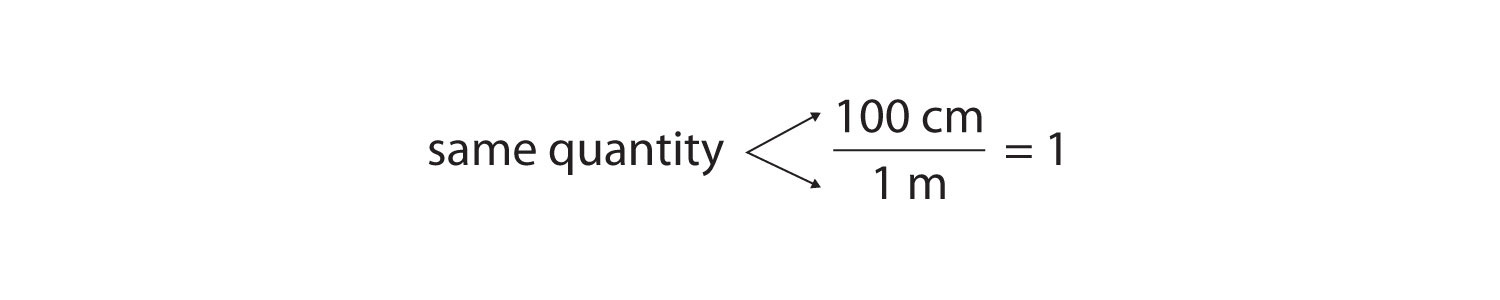
We know that 100 cm is 1 m, so we have the same quantity on the top and the bottom of our fraction, although it is expressed in different units. A fraction that has equivalent quantities in the numerator and the denominator but expressed in different units is called a conversion factorA fraction that has equivalent quantities in the numerator and the denominator but expressed in different units..
Here is a simple example. How many centimeters are there in 3.55 m? Perhaps you can determine the answer in your head. If there are 100 cm in every meter, then 3.55 m equals 355 cm. To solve the problem more formally with a conversion factor, we first write the quantity we are given, 3.55 m. Then we multiply this quantity by a conversion factor, which is the same as multiplying it by 1. We can write 1 as and multiply:
The 3.55 m can be thought of as a fraction with a 1 in the denominator. Because m, the abbreviation for meters, occurs in both the numerator and the denominator of our expression, they cancel out:
The final step is to perform the calculation that remains once the units have been canceled:
In the final answer, we omit the 1 in the denominator. Thus, by a more formal procedure, we find that 3.55 m equals 355 cm. A generalized description of this process is as follows:
quantity (in old units) × conversion factor = quantity (in new units)You may be wondering why we use a seemingly complicated procedure for a straightforward conversion. In later studies, the conversion problems you will encounter will not always be so simple. If you can master the technique of applying conversion factors, you will be able to solve a large variety of problems.
In the previous example, we used the fraction as a conversion factor. Does the conversion factor also equal 1? Yes, it does; it has the same quantity in the numerator as in the denominator (except that they are expressed in different units). Why did we not use that conversion factor? If we had used the second conversion factor, the original unit would not have canceled, and the result would have been meaningless. Here is what we would have gotten:
For the answer to be meaningful, we have to construct the conversion factor in a form that causes the original unit to cancel out. Figure 1.10 "A Concept Map for Conversions" shows a concept map for constructing a proper conversion. The steps for doing a unit conversion problem are summarized in the margin.
Figure 1.10 A Concept Map for Conversions
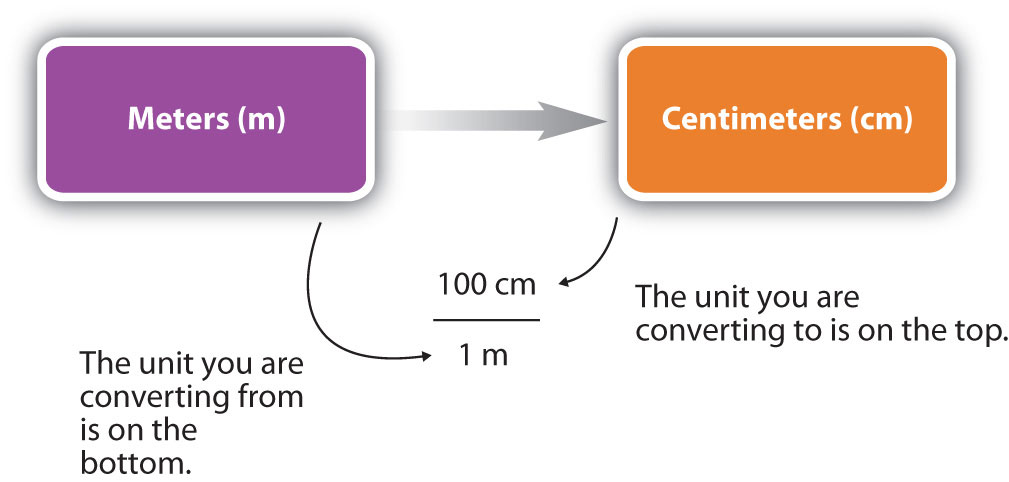
This is how you construct a conversion factor to convert from one unit to another.
Significant Figures in Conversions
How do conversion factors affect the determination of significant figures? Numbers in conversion factors based on prefix changes, such as kilograms to grams, are not considered in the determination of significant figures in a calculation because the numbers in such conversion factors are exact. Exact numbersA number that is defined or counted. are defined or counted numbers, not measured numbers, and can be considered as having an infinite number of significant figures. (In other words, 1 kg is exactly 1,000 g, by the definition of kilo-.) Counted numbers are also exact. If there are 16 students in a classroom, the number 16 is exact. In contrast, conversion factors that come from measurements (such as density, as we will see shortly) or are approximations have a limited number of significant figures and should be considered in determining the significant figures of the final answer.
Example 12
- The average volume of blood in an adult male is 4.7 L. What is this volume in milliliters?
- A hummingbird can flap its wings once in 18 ms. How many seconds are in 18 ms?
Solution
-
We start with what we are given, 4.7 L. We want to change the unit from liters to milliliters. There are 1,000 mL in 1 L. From this relationship, we can construct two conversion factors:
We use the conversion factor that will cancel out the original unit, liters, and introduce the unit we are converting to, which is milliliters. The conversion factor that does this is the one on the right.
Because the numbers in the conversion factor are exact, we do not consider them when determining the number of significant figures in the final answer. Thus, we report two significant figures in the final answer.
-
We can construct two conversion factors from the relationships between milliseconds and seconds:
To convert 18 ms to seconds, we choose the conversion factor that will cancel out milliseconds and introduce seconds. The conversion factor on the right is the appropriate one. We set up the conversion as follows:
The conversion factor’s numerical values do not affect our determination of the number of significant figures in the final answer.
Skill-Building Exercise
-
101,000 ns to seconds
-
32.08 kg to grams
Perform each conversion.
Conversion factors can also be constructed for converting between different kinds of units. For example, density can be used to convert between the mass and the volume of a substance. Consider mercury, which is a liquid at room temperature and has a density of 13.6 g/mL. The density tells us that 13.6 g of mercury have a volume of 1 mL. We can write that relationship as follows:
13.6 g mercury = 1 mL mercuryThis relationship can be used to construct two conversion factors:
Which one do we use? It depends, as usual, on the units we need to cancel and introduce. For example, suppose we want to know the mass of 16 mL of mercury. We would use the conversion factor that has milliliters on the bottom (so that the milliliter unit cancels) and grams on top so that our final answer has a unit of mass:
In the last step, we limit our final answer to two significant figures because the volume quantity has only two significant figures; the 1 in the volume unit is considered an exact number, so it does not affect the number of significant figures. The other conversion factor would be useful if we were given a mass and asked to find volume, as the following example illustrates.
Note
Density can be used as a conversion factor between mass and volume.
Example 13
A mercury thermometer for measuring a patient’s temperature contains 0.750 g of mercury. What is the volume of this mass of mercury?
Solution
Because we are starting with grams, we want to use the conversion factor that has grams in the denominator. The gram unit will cancel algebraically, and milliliters will be introduced in the numerator.
We have limited the final answer to three significant figures.
Skill-Building Exercise
-
What is the volume of 100.0 g of air if its density is 1.3 g/L?
Looking Closer: Density and the Body
The densities of many components and products of the body have a bearing on our health.
Bones. Bone density is important because bone tissue of lower-than-normal density is mechanically weaker and susceptible to breaking. The density of bone is, in part, related to the amount of calcium in one’s diet; people who have a diet deficient in calcium, which is an important component of bones, tend to have weaker bones. Dietary supplements or adding dairy products to the diet seems to help strengthen bones. As a group, women experience a decrease in bone density as they age. It has been estimated that fully half of women over age 50 suffer from excessive bone loss, a condition known as osteoporosis. Exact bone densities vary within the body, but for a healthy 30-year-old female, it is about 0.95–1.05 g/cm3. Osteoporosis is diagnosed if the bone density is below 0.6–0.7 g/cm3.
Urine. The density of urine can be affected by a variety of medical conditions. Sufferers of diabetes insipidus produce an abnormally large volume of urine with a relatively low density. In another form of diabetes, called diabetes mellitus, there is excess glucose dissolved in the urine, so that the density of urine is abnormally high. The density of urine may also be abnormally high because of excess protein in the urine, which can be caused by congestive heart failure or certain renal (kidney) problems. Thus, a urine density test can provide clues to various kinds of health problems. The density of urine is commonly expressed as a specific gravity, which is a unitless quantity defined as . Normal values for the specific gravity of urine range from 1.002 to 1.028.
Body Fat. The overall density of the body is one indicator of a person’s total body fat. Fat is less dense than muscle and other tissues, so as it accumulates, the overall density of the body decreases. Measurements of a person’s weight and volume provide the overall body density, which can then be correlated to the percentage of body fat. (The body’s volume can be measured by immersion in a large tank of water. The amount of water displaced is equal to the volume of the body.)
Sometimes you will have to perform more than one conversion to obtain the desired unit. For example, suppose you want to convert 54.7 km into millimeters. You can either memorize the relationship between kilometers and millimeters, or you can do the conversion in steps. Most people prefer to convert in steps.
To do a stepwise conversion, we first convert the given amount to the base unit. In this example, the base unit is meters. We know that there are 1,000 m in 1 km:
Then we take the result (54,700 m) and convert it to millimeters, remembering that there are 1,000 mm for every 1 m:
We have expressed the final answer in scientific notation.
As a shortcut, both steps in the conversion can be combined into a single, multistep expression:
Either method—one step at a time or all the steps together—is acceptable. If you do all the steps together, the restriction for the proper number of significant figures should be done after the last step. As long as the math is performed correctly, you should get the same answer no matter which method you use.
Example 14
Convert 58.2 ms to megaseconds in one multistep calculation.
Solution
First, convert the given unit to the base unit—in this case, seconds—and then convert seconds to the final unit, megaseconds:
Neither conversion factor affects the number of significant figures in the final answer.
Skill-Building Exercise
-
Convert 43.007 ng to kilograms in one multistep calculation.
Career Focus: Pharmacist
A pharmacist dispenses drugs that have been prescribed by a doctor. Although that may sound straightforward, pharmacists in the United States must hold a doctorate in pharmacy and be licensed by the state in which they work. Most pharmacy programs require four years of education in a specialty pharmacy school.
Pharmacists must know a lot of chemistry and biology so they can understand the effects that drugs (which are chemicals, after all) have on the body. Pharmacists can advise physicians on the selection, dosage, interactions, and side effects of drugs. They can also advise patients on the proper use of their medications, including when and how to take specific drugs properly. Pharmacists can be found in drugstores, hospitals, and other medical facilities.
Curiously, an outdated name for pharmacist is chemist, which was used when pharmacists formerly did a lot of drug preparation, or compounding. In modern times, pharmacists rarely compound their own drugs, but their knowledge of the sciences, including chemistry, helps them provide valuable services in support of everyone’s health.

A pharmacist is a person who needs to know a lot of chemistry. Curiously, an old name for pharmacist is chemist.
© Thinkstock
Concept Review Exercises
-
How do you determine which quantity in a conversion factor goes in the denominator of the fraction?
-
State the guidelines for determining significant figures when using a conversion factor.
Answers
-
The unit you want to cancel from the numerator goes in the denominator of the conversion factor.
-
Exact numbers that appear in many conversion factors do not affect the number of significant figures; otherwise, the normal rules of multiplication and division for significant figures apply.
Key Takeaway
- A unit can be converted to another unit of the same type with a conversion factor.
Exercises
-
Give the two conversion factors you can construct using each pair of units.
- meters and kilometers
- liters and microliters
- seconds and milliseconds
-
Give the two conversion factors you can construct using each pair of units.
- grams and centigrams
- millimeters and meters
- liters and megaliters
-
How many meters are in 56.2 km?
-
How many seconds are in 209.7 ms?
-
How many microliters are in 44.1 L?
-
How many megagrams are in 90.532 g?
-
Convert 109.6 kg into micrograms. Express your final answer in scientific notation.
-
Convert 3.8 × 105 mm into kilometers. Express your final answer in scientific notation.
-
Convert 3.009 × 10−5 ML into centiliters. Express your final answer in scientific notation.
-
Convert 99.04 dm into micrometers. Express your final answer in scientific notation.
-
The density of ethyl alcohol is 0.79 g/mL. What is the mass of 340 mL of ethyl alcohol?
-
The density of a certain fraction of crude oil is 1.209 g/mL. What is the mass of 13,500 mL of this fraction?
-
The density of ethyl alcohol is 0.79 g/mL. What is the volume of 340 g of ethyl alcohol?
-
The density of a certain component of crude oil is 1.209 g/mL. What is the volume of 13,500 g of this component?
-
Vitamin C tablets can come in 500 mg tablets. How many of these tablets are needed to obtain 10 g of vitamin C?
-
A tablet of penicillin contains 250 mg of the antibacterial drug. A prescription contains 44 tablets. What is the total mass of penicillin in the prescription?
Answers
-
-
-
5.62 × 104 m
-
-
4.41 × 107 µL
-
-
1.096 × 108 µg
-
-
3.009 × 103 cL
-
-
270 g
-
-
430 mL
-
-
20 tablets
-
1.8 End-of-Chapter Material
Chapter Summary
To ensure that you understand the material in this chapter, you should review the meanings of the bold terms in the following summary and ask yourself how they relate to the topics in the chapter.
Chemistry is the study of matter, which is anything that has mass and takes up space. Chemistry is one branch of science, which is the study of the natural universe. Like all branches of science, chemistry relies on the scientific method, which is a process of learning about the world around us. In the scientific method, a guess or hypothesis is tested through experiment and measurement.
Matter can be described in a number of ways. Physical properties describe characteristics of a sample that do not change the chemical identity of the material (size, shape, color, and so on), while chemical properties describe how a sample of matter changes its chemical composition. A substance is any material that has the same physical and chemical properties throughout. An element is a substance that cannot be broken down into chemically simpler components. The smallest chemically identifiable piece of an element is an atom. A substance that can be broken down into simpler chemical components is a compound. The smallest chemically identifiable piece of a compound is a molecule. Two or more substances combine physically to make a mixture. If the mixture is composed of discrete regions that maintain their own identity, the mixture is a heterogeneous mixture. If the mixture is so thoroughly mixed that the different components are evenly distributed throughout, it is a homogeneous mixture. Another name for a homogeneous mixture is a solution. Substances can also be described by their phase: solid, liquid, or gas.
Scientists learn about the universe by making measurements of quantities, which consist of numbers (how many) and units (of what). The numerical portion of a quantity can be expressed using scientific notation, which is based on powers, or exponents, of 10. Large numbers have positive powers of 10, while numbers less than 1 have negative powers of 10. The proper reporting of a measurement requires proper use of significant figures, which are all the known digits of a measurement plus the first estimated digit. The number of figures to report in the result of a calculation based on measured quantities depends on the numbers of significant figures in those quantities. For addition and subtraction, the number of significant figures is determined by position; for multiplication and division, it is decided by the number of significant figures in the original measured values. Nonsignificant digits are dropped from a final answer in accordance with the rules of rounding.
Chemistry uses SI, a system of units based on seven basic units. The most important ones for chemistry are the units for length, mass, amount, time, and temperature. Basic units can be combined with numerical prefixes to change the size of the units. They can also be combined with other units to make derived units, which are used to express other quantities such as volume, density, or energy. A formal conversion from one unit to another uses a conversion factor, which is constructed from the relationship between the two units. Numbers in conversion factors may affect the number of significant figures in a calculated quantity, depending on whether the conversion factor is exact. Conversion factors can be applied in separate computations, or several can be used at once in a single, longer computation.
Additional Exercises
-
A sample of urine has a density of 1.105 g/cm3. What is the mass of 0.255 L of this urine?
-
The hardest bone in the body is tooth enamel, which has a density of 2.91 g/cm3. What is the volume, in liters, of 75.9 g of tooth enamel?
-
Some brands of aspirin have 81 mg of aspirin in each tablet. If a person takes 8 tablets per day, how many grams of aspirin is that person consuming every day?
-
The US government has a recommended daily intake (RDI) of 5 µg of vitamin D per day. (The name recommended daily allowance was changed to RDI in 1997.) If milk contains 1.2 µg per 8 oz glass, how many ounces of milk are needed to supply the RDI of vitamin D?
-
The population of the United States, according to the 2000 census, was 281.4 million people.
- How many significant figures does this number have?
- What is the unit in this quantity?
- Express this quantity in proper scientific notation.
-
The United States produces 34,800,000,000 lb of sugar each year, and much of it is exported to other countries.
- How many significant figures does this number have?
- What is the unit in this quantity?
- Express this quantity in proper scientific notation.
-
Construct a conversion factor that can convert from one unit to the other in each pair of units.
- from millimeters to kilometers
- from kilograms to micrograms
- from centimeters to micrometers
-
Construct a conversion factor that can convert from one unit to the other in each pair of units.
- from kilometers to micrometers
- from decaliters to milliliters
- from megagrams to milligrams
-
What is the density of a dextrose solution if 355 mL of the solution has a mass of 406.9 g?
-
What is the density of a dental amalgam (an alloy used to fill cavities) if 1.005 kg of the material has a volume of 433 mL? Express your final answer in grams per milliliter.
-
Approximately how many inches are in 4.76 m?
-
Approximately how many liters are in 1 gal, which is exactly 4 qt?
-
Approximately how many kilograms are in a person who weighs 170 lb?
-
The average distance between Earth and the sun is 9.3 × 107 mi. How many kilometers is that?
-
Show mathematically that 1 L equals 1 dm3.
-
Show mathematically that 1 L equals 1,000 cm3.
For Exercises 11–16, see the accompanying table for the relationships between English and SI units.
| 1 m ≈ 39.36 in. ≈ 3.28 ft ≈ 1.09 yd |
| 1 cm ≈ 2.54 in. |
| 1 km ≈ 0.62 mi |
| 1 kg ≈ 2.20 lb |
| 1 lb ≈ 454 g |
| 1 L ≈ 1.06 qt |
| 1 qt ≈ 0.946 L |
Answers
-
282 g
-
-
650 mg
-
-
- four significant figures
- people
- 2.841 × 108 people
-
-
-
-
1.15 g/mL
-
-
187 in.
-
-
77 kg
-
-
-




