This is “Short-Run Determinants of Exchange Rates”, section 18.4 from the book Finance, Banking, and Money (v. 2.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
18.4 Short-Run Determinants of Exchange Rates
Learning Objectives
- What are the short-run determinants of exchange rates?
- What is the interest parity condition and when and why does it hold?
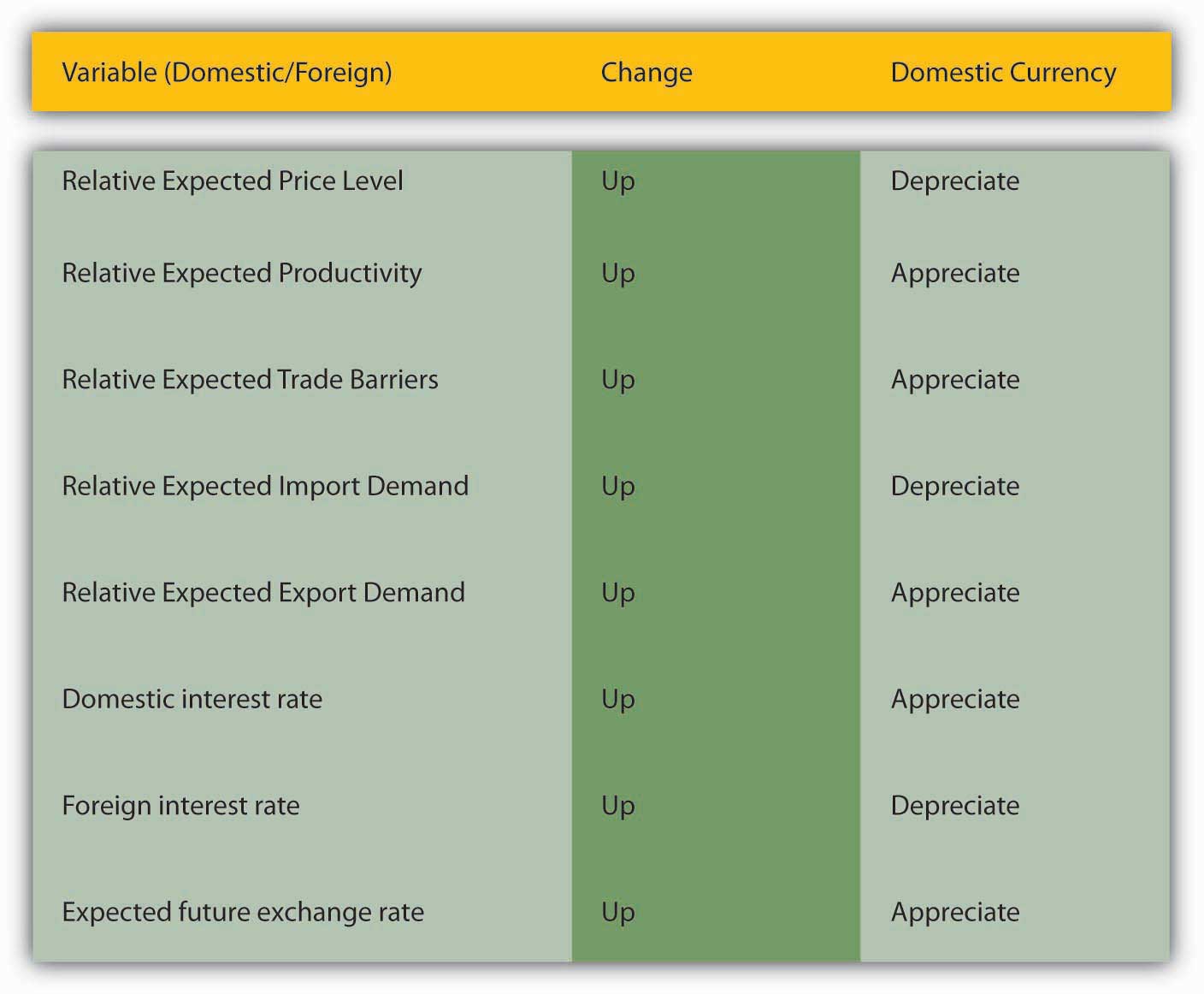
As Figure 18.6 "South Africa-United States exchange rate, June 2006" shows, exchange rates can be very volatile. In a single month (June 2006), the South African rand depreciated from about 6.6 to 7.4 rand to 1 USD, with various ups and downs along the way. The rand then reversed course and appreciated toward 7.1 rand/USD. Such fluctuations are by no means unusual. Why do exchange rates undergo such gyrations? Figure 18.7 "Determinants of exchange rates in the short run" summarizes the major factors affecting exchange rates in the short run. Note that it looks very much like Figure 18.5 "Determinants of exchange rates in the long run" but with three key differences. First, instead of actual relative price levels, trade barriers, exports, imports, and productivity driving changes, expectations of their future direction drive changes. This should not be surprising given the basic rationality of most financial markets. Second, two additional variables have entered the equation: foreign and domestic interest rates. The intuition behind the first variables is the same as those discussed above, but in the short run, the mere expectation of a change in a variable moves the market. The intuition behind the interest rates is also straightforward. If something increases demand for the domestic currency, like domestic interest rates increasing or foreign interest rates decreasing, it will appreciate. If something reduces demand for the domestic currency, like domestic interest rates decreasing or foreign interest rates increasing, it will depreciate. Because expectations and interest rates change frequently, so, too, do exchange rates under the current floating rate regime.
Figure 18.6 South Africa-United States exchange rate, June 2006
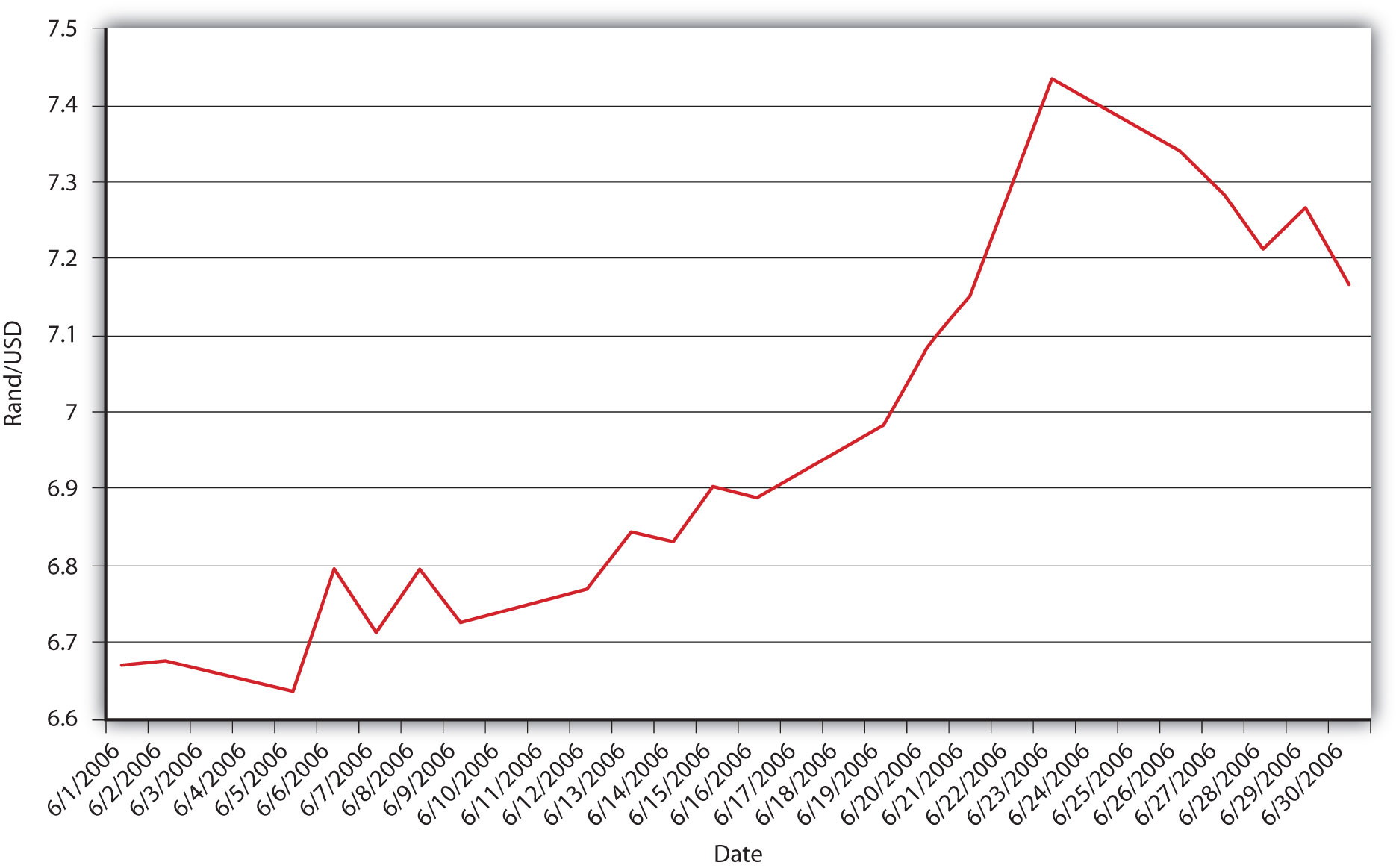
Figure 18.7 Determinants of exchange rates in the short run
Stop and Think Box
There is an important distinction between real and nominal interest rates. Through the Fisher Equation, we know that the nominal interest rate equals the real interest rate plus inflation expectations. Is that distinction important when considering foreign exchange markets?
Absolutely, and here is why. An increase in nominal interest rates caused by a rise in the real interest rate would leave expectations about future exchange rates unchanged and hence would cause the domestic currency to appreciate. An increase in nominal interest rates caused solely by an increase in inflation expectations, by contrast, would cause the expected future exchange rate to decrease through the expected and actual price level effects. So the domestic currency would depreciate instead.
The third difference between the long and short terms is that, in the short term, the expectation of the future direction of the exchange rate plays an important role. The easiest way to see this is to compare two investments with a one-year time horizon: a domestic (say, USD-denominated) bank account that pays 5 percent per year and a foreign (say, pound-sterling-denominated) account paying 6 percent per year. Before you jump for the sterling (6 > 5), you need to consider that, in a year, you’re going to want dollars again because you reside in the United States and need USD to buy lunch, pay the rent, and so forth. If the dollar appreciates more than 1 percent over the course of the year, you’d be better off with the dollar deposit. Say that you invest $10,000 in sterling when the exchange rate is $1.50/£1 or, in other words, £.6667/$1. Your investment today would buy 10,000 × .6667 = £6,667. Multiply that by the interest on the sterling deposit (1.06) and you get £7,067.02 in a year. If the exchange rate is unchanged, you’re cool because you’ll have 7,067.02 × 1.50 = $10,600.53, which is greater than $10,000 invested at 5 percent, which equals 10,000 × 1.05 = $10,500.00. But what if, over the course of that year, the dollar appreciated strongly, to $1.25 per pound? Then your £7,067.02 would buy you only 7,067.02 × 1.25 = $8,833.78. You just took a bath, and not the good kind, because you should have invested in the dollar deposit! Of course, if the dollar depreciated to, say, $1.75, you’ll be pheeling phat at 7,067.02 × 1.75 = $12,367.29.
Stop and Think Box
Increases in the growth rate of the money supply will eventually cause the price level to increase, but its effect on nominal interest rates in the short term can vary: rates can dip strongly, then rebound but remain permanently lower than the previous level, decrease temporarily before increasing permanently, or increase immediately. What does this mean for the market for foreign exchange?
The fact that a major short-run determinant of the exchange rate, foreign and domestic interest rates, moves around a lot helps to explain why the foreign exchange market is volatile. That market is also volatile because expectations of many things, including future differential price levels, productivity, and trading levels, will affect it via the expected future exchange rate (the Eef variable in the equation introduced below).
As noted above, the markets for foreign exchange and bonds/deposits are highly competitive and efficient, so we wouldn’t expect discrepancies in returns to last long. The law of one price, of course, applies most stringently to financial markets in which international capital mobility is allowed because huge sums of money (deposits) can be sent hither and thither almost immediately and cost-free, ideal conditions for the law of one price to prevail. So what economists call the interest parity condition often holds (is true). More formally,
where:
iD = domestic interest rate
iF = foreign interest rate
Eef = expected future exchange rate
Et = exchange rate today
(Note: express all variables as decimals, e.g. 6% = .06; 5 = 500%.)
In plain English, if the so-called interest parity condition holds, the domestic interest rate should equal the foreign interest rate minus the expected appreciation of the domestic currency. If iF is > iD, the domestic currency must be expected to appreciate; otherwise, everyone would sell their domestic deposits to buy the foreign ones. If iF is < iD, the domestic currency must be expected to depreciate (have a negative sign, two of which make a positive, augmenting iF); otherwise, everyone would sell the foreign deposits and buy the domestic ones. If you find this confusing, there is another, more intuitive way of stating it: the domestic interest rate must equal the foreign interest rate plus the expected appreciation of the foreign currency. If iF is < iD, the expected appreciation of the foreign currency compensates for the lower interest rate, allowing equilibrium. You can practice calculating interest parity in the following Exercise.
Exercise
-
Use the interest parity formula (iD = iF − (Eef − Et)/Et) to calculate the following:
Foreign Interest Rate Expected Future Exchange Rate Exchange Rate Today Answer: Domestic Interest Rate 0.05 1 1 0.05 0.05 1.01 1 0.04 0.05 1.02 1 0.03 0.05 1.03 1 0.02 0.05 0.9 1 0.15 0.05 0.8 1 0.25 0.05 0.7 1 0.35 0.06 1 1 0.06 0.06 1 1.1 0.15 0.06 1 1.2 0.23 0.06 1 1.3 0.29 0.06 1 0.99 0.05 0.06 1 0.95 0.01 0.1 1 0.95 0.05 0.15 1 1 0.15 0.15 1.1 1 0.05 0.15 1 10 1.05 Expected Future Exchange Rate Exchange Rate Today Domestic Interest Rate Answer: Foreign Interest Rate 1 1 0.02 0.02 1.1 1 0.02 0.12 1.2 1 0.02 0.22 1.3 1 0.02 0.32 0.9 1 0.11 0.01 0.8 1 0.21 0.01 0.7 1 0.31 0.01 1 1 0.1 0.10 1 1.1 0.1 0.01 1 1.2 0.2 0.03 1 1.3 0.25 0.02 1 0.9 0.1 0.21 1 0.8 0.1 0.35 1 0.7 0.1 0.53 1 1 0 0.00 10 1 0 9.00 1 5 1 0.20
Key Takeaways
- Because foreign exchange markets are efficient, in the short run, the mere expectation of changes in relative inflation, exports, imports, trade barriers, and productivity moves the markets.
- Also in the short run, differences in interest rates and expectations of the future exchange rate play key roles in exchange rate determination.
- The interest parity condition equates the domestic interest rate to the foreign interest rate minus the appreciation of the domestic currency. (Or, by rearranging the terms, it equates the foreign interest rate to the domestic interest rate plus the expected appreciation of the domestic currency.)
- The interest parity condition holds whenever there is capital mobility, whenever deposits (units of account) can move freely and cheaply from one country to another.
- It holds under those conditions because if it didn’t, an arbitrage condition would exist, inducing arbitrageurs to sell the overvalued deposit (side of the equation) and buy the undervalued one until the equation held.




