21.2 The IS-LM Model

The Keynesian cross diagram framework is great, as far as it goes. Note that it has nothing to say about interest rates or money, a major shortcoming for us students of money, banking, and monetary policy! It does, however, help us to build a more powerful model that examines equilibrium in the markets for goods and money, the IS (investment-savings) and the LM (liquidity preference–money) curves, respectively (hence the name of the model).

Interest rates are negatively related to I and to NX. The reasoning here is straightforward. When interest rates (i) are high, companies would rather invest in bonds than in physical plant (because fewer projects are positive net present valueA project likely to be profitable at a given interest rate after comparing the present values of both expenditures and revenues. This will make more sense after you navigate Chapter 4 "Interest Rates". or +NPVSee positive net present value.) or inventory (because it has a high opportunity cost), so I (investment) is low. When rates are low, new physical plant and inventories look cheap and many more projects are +NPV (i has come down in the denominator of the present value formula), so I is high. Similarly, when i is low, as we learned in Chapter 18 "Foreign Exchange", the domestic currency will be weak, all else equal. Exports will be facilitated and imports will decline because foreign goods will look expensive. Thus, NX will be high (exports > imports). When i is high, by contrast, the domestic currency will be in demand and hence strong. That will hurt exports and increase imports, so NX will drop and perhaps become negative (exports < imports).

Now think of Y_ad on a Keynesian cross diagram. As we saw above, aggregate output will rise as I and NX do. So we know that as i increases, Y_ad decreases, ceteris paribus. Plotting the interest rate on the vertical axis against aggregate output on the horizontal axis, as below, gives us a downward sloping curve. That’s the IS curve! For each interest rate, it tells us at what point the market for goods (I and NX, get it?) is in equilibrium. For all points to the right of the curve, there is an excess supply of goods for that interest rate, which causes firms to decrease inventories, leading to a fall in output toward the curve. For all points to the left of the IS curve, an excess demand for goods persists, which induces firms to increase inventories, leading to increased output toward the curve.

Obviously, the IS curve alone is as insufficient to determine i or Y as demand alone is to determine prices or quantities in the standard supply and demand microeconomic price model. We need another curve, one that slopes the other way, which is to say, upward. That curve is called the LM curve and it represents equilibrium points in the market for money. Recall from our discussions of liquidity preference in Chapter 5 "The Economics of Interest-Rate Fluctuations" and Chapter 20 "Money Demand" that the demand for money is positively related to income because more income means more transactions and because more income means more assets, and money is one of those assets. So we can immediately plot an upward sloping LM curve. To the left of the LM curve there is an excess supply of money given the interest rate and the amount of output. That’ll cause people to use their money to buy bonds, thus driving bond prices up, and hence i down to the LM curve. To the right of the LM curve, there is an excess demand for money, inducing people to sell bonds for cash, which drives bond prices down and hence i up to the LM curve.

Figure 21.4 IS-LM diagram: equilibrium in the markets for money and goods

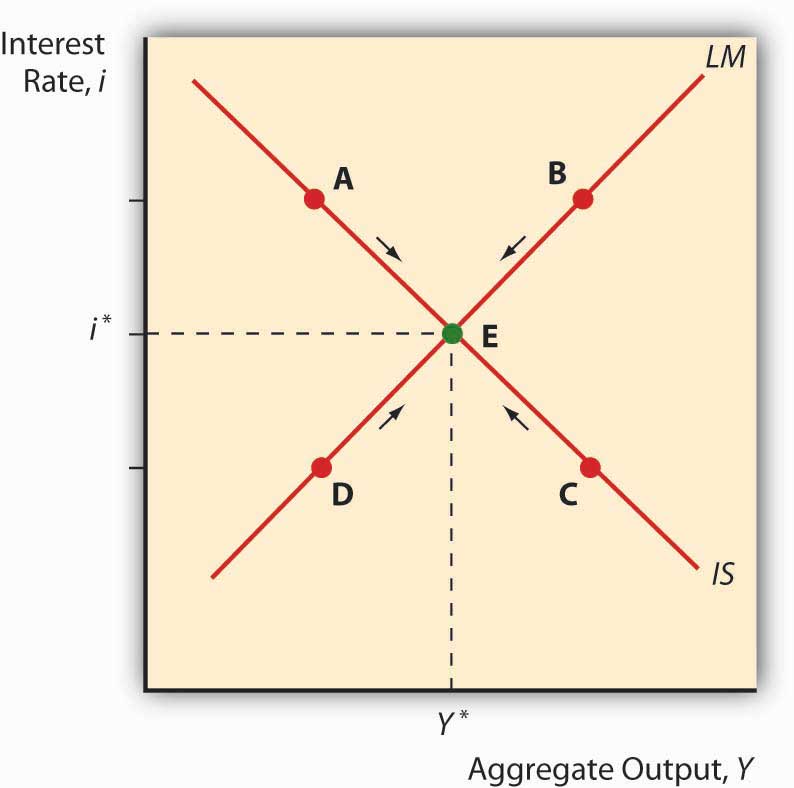
When we put the IS and LM curves on the graph at the same time, as in Figure 21.4 "IS-LM diagram: equilibrium in the markets for money and goods", we immediately see that there is only one point, their intersection, where the markets for both goods and money are in equilibrium. Both the interest rate and aggregate output are determined by that intersection. We can then shift the IS and LM curves around to see how they affect interest rates and output, i* and Y*. In the next chapter, we’ll see how policymakers manipulate those curves to increase output. But we still won’t be done because, as mentioned above, the IS-LM model has one major drawback: it works only in the short term or when the price level is otherwise fixed.

Stop and Think Box

Does Figure 21.5 "Real gross private domestic investment, 1925–2010" make sense? Why or why not? What does Figure 21.6 "Net exports, 1945–2010" mean? Why is Figure 21.7 "Federal government expenditures, 1945–2010" not a good representation of G?

Figure 21.5 Real gross private domestic investment, 1925–2010

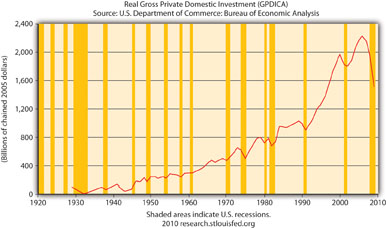
Figure 21.6 Net exports, 1945–2010

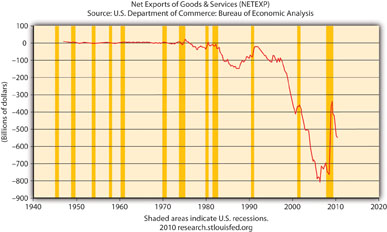
Figure 21.7 Federal government expenditures, 1945–2010

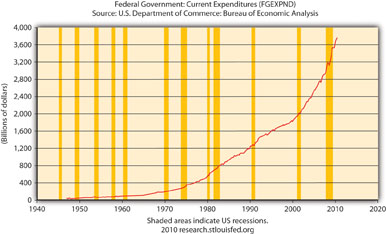
Figure 21.5 "Real gross private domestic investment, 1925–2010" makes perfectly good sense because it depicts I in the equation Y = Y_ad = C + I + G + NX, and the shaded areas represent recessions, that is, decreases in Y. Note that before almost every recession in the twentieth century, I dropped.

Figure 21.6 "Net exports, 1945–2010" means that NX in the United States is considerably negative, that exports < imports by a large margin, creating a significant drain on Y (GDP). Note that NX improved (became less negative) during the crisis and resulting recession but dipped downward again during the 2010 recovery.

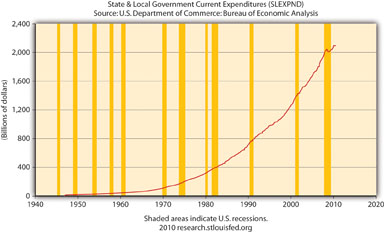
Figure 21.7 "Federal government expenditures, 1945–2010" is not a good representation of G because it ignores state and local government expenditures, which are significant in the United States, as Figure 21.8 "State and local government expenditures, 1945–2010" shows.

Figure 21.8 State and local government expenditures, 1945–2010