This is “A Simple Model of Multiple Deposit Creation”, section 14.3 from the book Finance, Banking, and Money (v. 1.1). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
14.3 A Simple Model of Multiple Deposit Creation
Learning Objectives
- What is the multiple deposit creation process?
- What is the money multiplier?
- What are the major limitations of the simple deposit multiplier?
As shown above, the central bank pretty much controls the size of the monetary base. (The check clearing process and the government’s banking activities can cause some short-term flutter, but generally the central bank can anticipate such fluctuations and respond accordingly.) That does not mean, however, that the central bank controls the money supply, which, if you recall from Chapter 3 "Money", consists of more than just MB. (M1, for example, also includes checkable deposits.) The reason is that each $1 (or €1, etc.) of additional MB creates some multiple > 1 of new deposits in a process called multiple deposit creation.
Suppose the central bank buys $1 million of securities from Some Bank. We know that the following will occur:
| Some Bank | |
|---|---|
| Liabilities | |
| Securities −$1 million | |
| Reserves +$1 million | |
| Central Bank | |
|---|---|
| Assets | Liabilities |
| Securities +$1 million | Reserves +$1 million |
Some Bank suddenly has $1 million in excess reserves. (Its deposits are unchanged, but it has $1 million more in cash.) What will the bank do? Likely what banks do best: make loans. So its T-account will be the following:
| Some Bank | |
|---|---|
| Assets | Liabilities |
| Loans +$1 million | Deposits +$1 million |
Recall from Chapter 9 "Bank Management" that deposits are created in the process of making the loan. The bank has effectively increased M1 by $1 million. The borrower will not leave the proceeds of the loan in the bank for long but instead will use it, within the guidelines set by the loan’s covenants, to make payments. As the deposits flow out of Some Bank, its excess reserves decline until finally Some Bank has essentially swapped securities for loans:
| Some Bank | |
|---|---|
| Assets | Liabilities |
| Securities −$1 million | |
| Loans +$1 million | |
But now there is another $1 million of checkable deposits out there and they rarely rest. Suppose, for simplicity’s sake, they all end up at Another Bank. Its T-account would be the following:
| Another Bank | |
|---|---|
| Assets Bank | Liabilities |
| Reserves +$1 million | Checkable deposits +$1 million |
If the required reserve ratio (rr) is 10 percent, Another Bank can, and likely will, use those deposits to fund a loan, making its T-account:
| Another Bank | |
|---|---|
| Assets | Liabilities |
| Reserves +$.1 million | Checkable Deposits +$1 million |
| Loans +$.9 million | |
That loan will also eventually be paid out to others and deposited into other banks, which in turn will lend 90 percent of them (1 − rr) to other borrowers. Even if a bank decides to invest in securities instead of loans, as long as it buys the bonds from anyone but the central bank, the multiple deposit creation expansion will continue, as in Figure 14.1 "Multiple deposit creation, with an increase in reserves of $1 million, if rr = .10".
Figure 14.1 Multiple deposit creation, with an increase in reserves of $1 million, if rr = .10
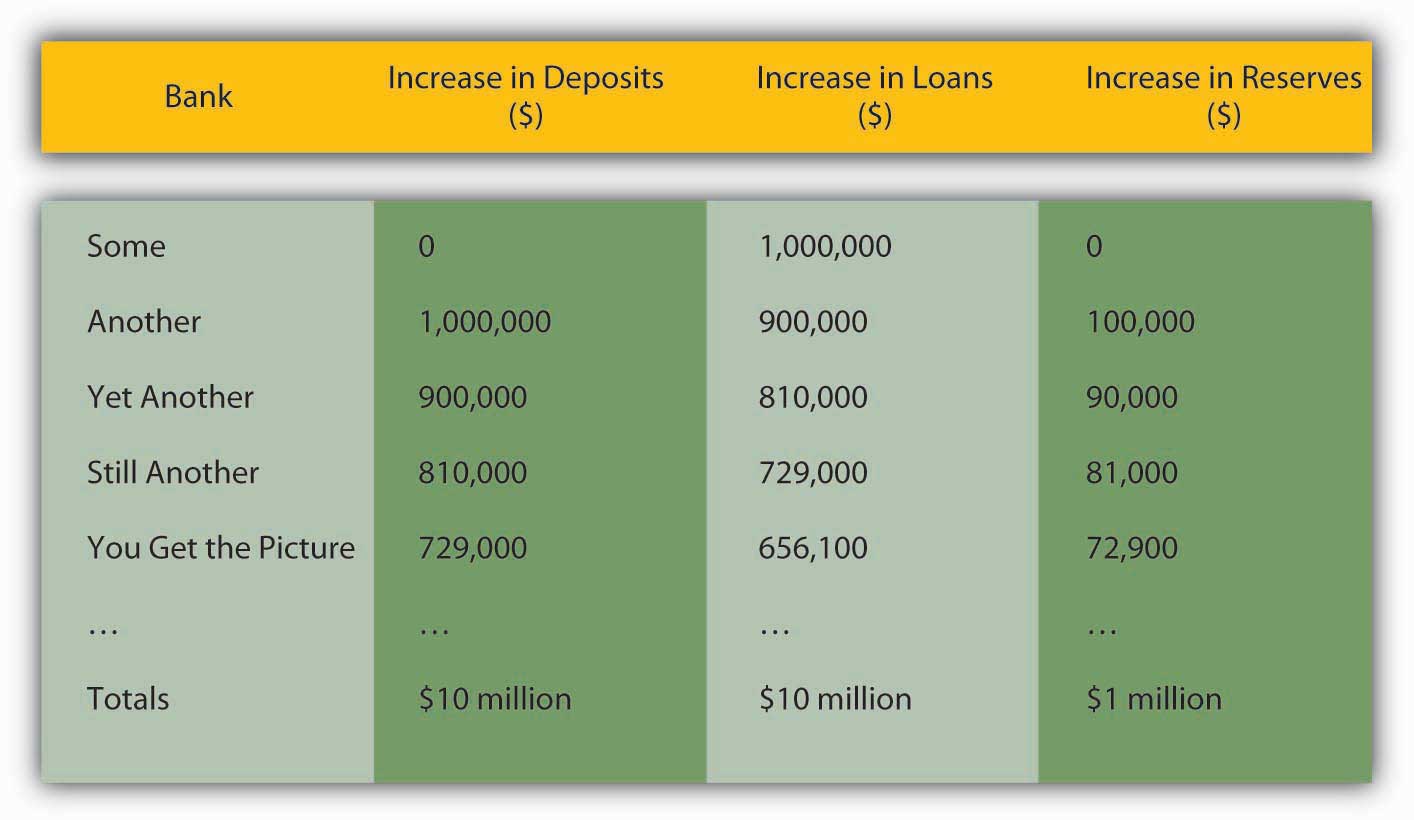
Notice that the increase in deposits is the same as the increase in loans from the previous bank. The increase in reserves is the increase in deposits times the required reserve ratio of .10, and the increase in loans is the increase in deposits times the remainder, .90. Rather than working through this rather clunky process every time, you can calculate the effects of increasing reserves with the so-called simple deposit multiplier formula:
where:
∆D = change in deposits
∆R = change in reserves
Rr = required reserve ratio
1/.1 × 1 million = 10 million, just as in Figure 14.1 "Multiple deposit creation, with an increase in reserves of $1 million, if rr = .10"Practice calculating the simple deposit multiplier in Exercise 2.
Exercise
-
Use the simple deposit multiplier ∆D = (1/rr) × ∆R to calculate the change in deposits given the following conditions:
Required Reserve Ratio Change in Reserves Answer: Change in Deposits .1 10 100 .5 10 20 1 10 10 .1 −10 −100 .1 100 1,000 0 43.5 ERROR—cannot divide by 0
Stop and Think Box
Suppose the Federal Reserve wants to increase the amount of checkable deposits by $1,000,000 by conducting open market operations. Using the simple model of multiple deposit creation, determine what value of securities the Fed should purchase, assuming a required reserve ratio of 5 percent. What two major assumptions does the simple model of multiple deposit creation make? Show the appropriate equation and work.
The Fed should purchase $50,000 worth of securities. The simple model of multiple deposit creation is ∆D = (1/rr) ×∆R, which of course is the same as ∆R = ∆D/(1/rr). So for this problem 1,000,000/(1/.05) = $50,000 worth of securities should be purchased. This model assumes that money is not held as cash and that banks do not hold excess reserves.
Pretty easy, eh? Too bad the simple deposit multiplier isn’t very accurate. It provides an upper bound to the deposit creation process. The model simply isn’t very realistic. Sometimes banks hold excess reserves, and people sometimes prefer to hold cash instead of deposits, thereby stopping the multiple deposit creation process cold. That is why, at the beginning of the chapter, we said that depositors, borrowers, and banks were also important players in the money supply determination process. In the next chapter, we’ll take their decisions into account.
Key Takeaways
- The multiple deposit creation process works like this: say that the central bank buys $100 of securities from Bank 1, which lends the $100 in cash it receives to some borrower. Said borrower writes checks against the $100 in deposits created by the loan until all the money rests in Bank 2. Its deposits and reserves increased by $100, Bank 2 lends as much as it can, say (1 – rr = .9) or $90, to another borrower, who writes checks against it until it winds up in Bank 3, which also lends 90 percent of it. Bank 4 lends 90 percent of that, Bank 5 lends 90 percent of that, and so on, until a $100 initial increase in reserves has led to a $1,000 increase in deposits (and loans).
- The simple deposit multiplier is ∆D = (1/rr) × ∆R, where ∆D = change in deposits; ∆R = change in reserves; rr = required reserve ratio.
- The simple deposit multiplier assumes that banks hold no excess reserves and that the public holds no currency. We all know what happens when we assume or ass|u|me. These assumptions mean that the simple deposit multiplier overestimates the multiple deposit creation process, providing us with an upper-bound estimate.




