This is “Asset Bubbles”, section 12.2 from the book Finance, Banking, and Money (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
12.2 Asset Bubbles
Learning Objective
- What are asset bubbles and what role does leverage play in their creation?
Asset bubblesIn this context, a rapid increase in asset prices that is not easily justified by fundamentals like expected earnings, interest rates, and the like. are rapid increases in the value of some asset, like bonds, commodities (cotton, gold, oil, tulips), equities, or real estate. Some combination of low interest rates, new technology, unprecedented increases in demand for the asset, and leverage typically create bubbles.
Low interest rates can cause bubbles by lowering the total cost of asset ownership. Recall from Chapter 4 "Interest Rates" that interest rates and bond prices are inversely related. Algebraically, the i term is in the denominator of the PV formula—PV = FV/(1 + i)n—so as it gets smaller, PV must get larger (holding FV constant, of course).
Stop and Think Box
In colonial New York in the 1740s and 1750s, interest rates on mortgages were generally 8 percent. In the late 1750s and early 1760s, they fell to about 4 percent, and expected revenues from land ownership increased by about 50 percent. What happened to real estate prices? Why?
They rose significantly because it was cheaper to borrow money, thus lowering the total cost of real estate ownership, and because the land was expected to create higher revenues. Thinking of the land as a perpetuity and FV as the expected revenues arising from it:
And that is just the real estate effect. Increasing FV by £50 leads to the following:
In 1762, Benjamin Franklin reported that the “Rent of old Houses, and Value of Lands, . . . are trebled in the last Six Years.”For more on the crisis, see Tim Arango, “The Housing-Bubble Revolution,” New York Times (30 November 2008), WK 5. http://www.nytimes.com/2008/11/30/weekinreview/30arango.html?_r=2&pagewanted=1&ref=weekinreview
The effect of new technology can be thought of as increasing FV, leading, of course, to a higher PV. Or, in the case of equities, low interest rates decrease k (required return) and new inventions increase g (constant growth rate) in the Gordon growth model—P = E × (1 + g)/(k – g)—both of which lead to a higher price.
Large increases in the demand for an asset occur for a variety of reasons. Demand can be increased merely by investors’ expectations of higher prices in the future, as in the one period valuation model—P = E/(1 + k) + P1/(1 + k). If many investors believe that P1 must be greater than P a year (or any other period) hence, demand for the asset will increase and the expectation of a higher P1 will be vindicated. That sometimes leads investors to believe that P2 will be higher than P1, leading to a self-fulfilling cycle that repeats through P3 to Px. At some point, the value of the asset becomes detached from fundamental reality, driven solely by expectations of yet higher future prices. In fact, some scholars verify the existence of an asset bubble when news about the price of an asset affects the economy, rather than the economy affecting the price of the asset.
To increase their returns, investors often employ leverage, or borrowing. Compare three investors, one who buys asset X entirely with his own money, one who borrows half of the price of asset X, and one who borrows 90 percent of the price of asset X. Their returns (not including the cost of borrowing, which as noted above is usually low during bubbles) will be equal to those calculated in Figure 12.1 "The effects of leverage on returns in a rising market".
Figure 12.1 The effects of leverage on returns in a rising market
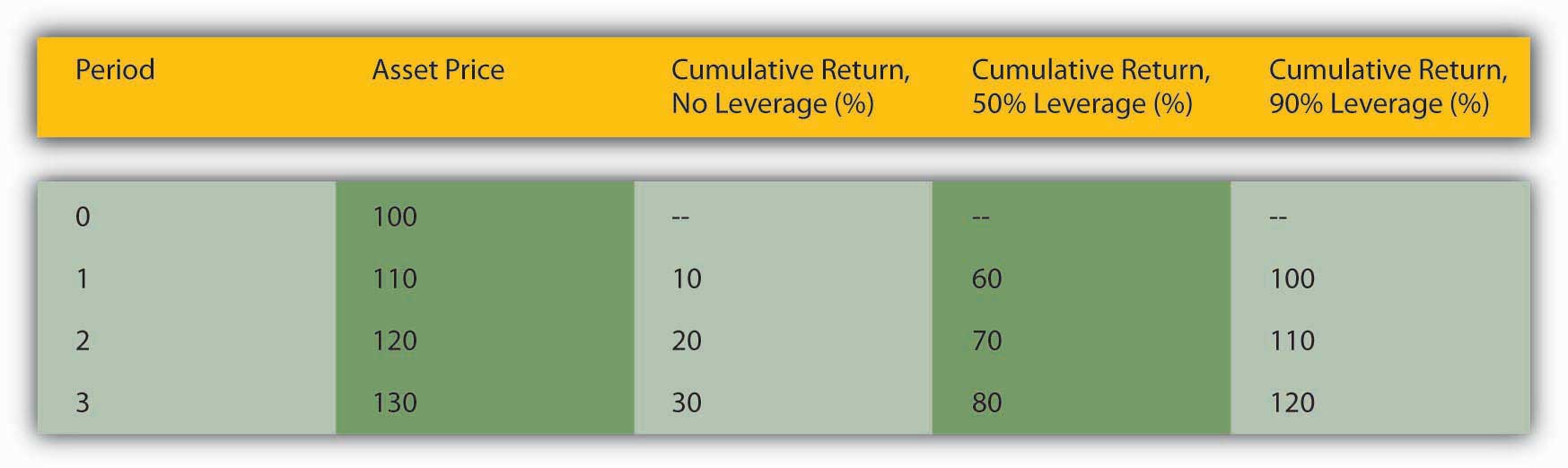
The figures were calculated using the rate of return formula: R = (C + Pt1 – Pt0)/Pt0 discussed in Chapter 4 "Interest Rates". Here, coupons are zero and hence drop out so that R = (Pt1 – Pt0)/Pt0.
In this example, returns for the unleveraged investor are great:
But the returns are not as high as the investor who borrowed half the cash, in essence paying only $50 of his own money for the $100 asset at the outset:
But even he looks like a chump compared to the investor who borrowed most of the money to finance the original purchase, putting up only $10 of his own money:
If you are thinking the most highly leveraged investor is the smart one, go back and reread the section of Chapter 2 "The Financial System" that discusses the trade-off between risk and return before continuing.
Key Takeaways
- Asset bubbles occur when the prices of some asset, like stocks or real estate, increase rapidly due to some combination of low interest rates, high leverage, new technology, and large, often self-fulfilling shifts in demand.
- The expectation of higher prices in the future, combined with high levels of borrowing, allow asset prices to detach from their underlying economic fundamentals.




