This is “In a Set of Financial Statements, What Information Is Conveyed about Noncurrent Liabilities Such as Bonds?”, chapter 14 from the book Business Accounting (v. 2.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
Chapter 14 In a Set of Financial Statements, What Information Is Conveyed about Noncurrent Liabilities Such as Bonds?
Video Clip
(click to see video)In this video, Professor Joe Hoyle introduces the essential points covered in Chapter 14 "In a Set of Financial Statements, What Information Is Conveyed about Noncurrent Liabilities Such as Bonds?".
14.1 Debt Financing
Learning Objectives
At the end of this section, students should be able to meet the following objectives:
- List and explain the advantages of debt financing.
- List and explain the disadvantages of debt financing.
- Describe and illustrate the use of financial leverage.
- Define notes and bonds as used in debt financing.
The Cost and Risk of Debt
Question: Businesses and other organizations need monetary funds to finance their operations and possible expansions. Such amounts can be quite significant. A portion of these resources normally come from investors who choose to become owners through the purchase of shares of capital stock directly from the company. Monetary amounts can also be generated internally by means of profitable operations. If net income each period exceeds the dividends that are paid to stockholders, a company has an ongoing source of financing.
However, many companies obtain a large part of the funding needed to support themselves and their growth through borrowing. If those debts will not be paid within the following year, they are listed on the balance sheet as noncurrent liabilities. The Xerox Corporation, for example, listed noncurrent liabilities on its December 31, 2010, balance sheet of $11.7 billion.
Creditors expect their entire loan balance to be repaid plus interestThe charge for using money over time, often associated with long-term loans; even if not specifically mentioned in the debt agreement, financial accounting rules require it to be computed and reported based on a reasonable rate. at the specified due date. The money has to be available. Consequently, incurring debts of such large amounts exposes the organization to risks. What problems and potential dangers does an entity face when liabilities—especially those of significant size—are owed?
Answer: Few things in life are free. The most obvious problem with financing an organization through debt is that it has a cost. A bank or other creditor will demand interest in exchange for the use of its money. For example, Xerox Corporation reported interest expense for the year ending December 31, 2010, of approximately $592 million. The rate of interest charged on debt will vary based on economic conditions and the perceived financial health of the debtor. As should be expected, strong companies are able to borrow money at a lower rate than weaker ones.
In addition, debt brings risk. A business must be able to generate enough surplus cash to satisfy creditors as liabilities come due. Xerox owes noncurrent liabilities of $11.7 billion. Eventually, company officials will have to find sufficient money to satisfy these obligations. Those funds might well be generated by profitable operations or contributed by investors. Or Xerox may simply borrow more money to pay off debts as they mature. This type of rollover financing is common but only as long as the debtor remains economically strong. Whatever the approach, the company has to manage its financial resources in such a way that all debts are settled in a timely manner.
The most serious risk associated with debt financing is the possibility of bankruptcy. As has become unfortunately commonplace during the recent economic crisis, organizations that are unable to pay their liabilities can be forced into legal bankruptcy.A company can seek protection from its creditors by voluntarily asking the court to allow it to enter bankruptcy. Or, three creditors holding a minimum amount of debt can push a company into bankruptcy, an event known as an involuntary bankruptcy filing. The end result of bankruptcyA formal court process that often results in the liquidation of a debtor’s assets when it cannot pay liabilities as they come due; in some cases, bankrupt companies are allowed to reorganize their finances and continue operations so that liquidation is not necessary. is frequently the liquidation of company assets with the distribution of those proceeds to creditors. However, under U.S. law, financial reorganization and continued existence is also a possibility. When Circuit City entered bankruptcy, company officials tried to reorganize to save the company. Eventually, Circuit City sold its assets and went out of business. In contrast, Delta Air Lines was able to leave bankruptcy protection in 2007 as a business that had been completely reorganized in hopes of remaining a viable entity.Information on the bankruptcy and subsequent legal reorganization of Delta Air Lines can be found at http://money.cnn.com/2007/04/30/news/companies/delta_bankruptcy/index.htm.
Given the cost and risk associated with owing large amounts of debt, the desire of decision makers to receive adequate and clear information is understandable. Few areas of financial accounting have been more discussed over the decades than the reporting of noncurrent liabilities.
The Benefits of Debt Financing
Question: Debt is a costly and possibly risky method of financing a company’s operations and growth. Some advantages must exist or no company would ever incur any noncurrent liabilities. What are the advantages to an organization of using debt to generate funding for operations and other vital activities?
Answer: One advantage of borrowing money is that interest expense is tax deductible. A company will essentially recoup a significant portion of all interest costs from the government. As mentioned above, Xerox incurred interest expense of $592 million. This interest reduced the company’s taxable income by that amount. If the assumption is made that Xerox has an effective income tax rate of 35 percent, the total amount paid to the government is lowered by $207.2 million (35 percent times $592 million). Xerox pays interest of $592 million, which reduces its income taxes by $207.2 million so that the net cost of borrowing for the period was $384.8 million.
Another advantage associated with debt financing is that it can be eliminated. Liabilities are not permanent. If the economic situation changes, a company can rid itself of all debt by making payments as each balance comes due. In contrast, if money is raised by issuing capital stock, the new shareholders can maintain their ownership indefinitely.
However, the biggest advantage commonly linked to debt is the benefit provided by financial leverageA company’s ability to earn more on borrowed money than the associated interest cost so that net income increases; often viewed as a wise business strategy although risks (such as possible bankruptcy) are elevated.. This term refers to an organization’s ability to increase its reported net income by earning more money on borrowed funds than the associated cost of interest. For example, if a company borrows $1 million on a debt that charges interest of 5 percent per year, annual interest is $50,000. If the $1 million that is received can be used to generate profit of $80,000 (added revenue minus added operating expenses), net income has gone up $30,000 ($80,000 - $50,000) using funds provided solely by creditors. The owners did not have to contribute any additional funds to increase profits by $30,000.
Over the decades, many companies have adopted a strategy of being highly leveraged, meaning that most of their funds come from debt financing. If profitable, the owners can earn huge profits with little or no investment of their own. Unfortunately, companies that take this approach face a much greater risk of falling into bankruptcy because of the large amounts of interest that have to be paid at regular intervals.
Test Yourself
Question:
James Thorpe invests $100,000 to start a new business. He immediately borrows another $400,000 at a 6 percent annual interest rate. The business earns a profit on its assets of 10 percent per year. At the end of one year, Thorpe liquidates all assets at book value and closes the business. What rate of return did he earn on this investment during this year of operations? Ignore income taxes.
- 10 percent
- 14 percent
- 15 percent
- 26 percent
Answer:
The correct answer is choice d: 26 percent.
Explanation:
The business is heavily debt financed; 80 percent of assets came from debt. Assets of $500,000 earn a profit of 10 percent, or $50,000. Interest cost is only $24,000 ($400,000 × 6 percent). The profit is $26,000 ($50,000 less $24,000). A profit of $26,000 is earned from the owner’s investment of $100,000, a return of 26 percent in one year. A profit of 10 percent was made from borrowed funds that cost 6 percent to obtain. The residual profit goes to the owners. This is financial leverage.
Raising Funds by Issuing Notes and Bonds
Question: Long-term financing typically comes from the issuance of notes or bonds. What are notes and bonds and how do they differ from each other?
Answer: Both notes and bonds are written contracts (often referred to as indentures) that specify the payment of designated amounts of cash by the debtor on stated dates. The two terms have become somewhat interchangeable over the years and clear distinctions are not likely to be found in practice.
- In this textbook, for convenience, the term “note” is used when a contract is negotiated directly between two parties. For example, assume officials from Jones Company go to City Street Bank and borrow $1.2 million to construct a new warehouse. The contract between these parties to establish the specific requirements of this loan agreement will be referred to as a note.
- The term “bond” will be used to describe a contract or group of contracts created by a debtor and then issued for money, often to members of the general public. Jones Company could opt to raise the $1.2 million needed for its new warehouse by printing 1,200 $1,000 bonds that it then sells to a wide array of creditors around the world. Such bonds are prepared in a wide variety of denominations.
Typically, the issuance of debt to multiple parties enables a company to raise extremely large amounts of money. A news story from the end of 2010 confirms the magnitude of these transactions: “Corporate bond sales worldwide topped $3 trillion for a second straight year.”Tim Catts and Sapna Maheshwari, “GE Leads $3.19 Trillion in Corporate Bond Sales: Credit Markets,” December 30, 2010, http://www.bloomberg.com/news/2010-12-30/ge-leads-3-trillion-in-company-bond-sales-as-yields-fall-credit-markets.html. If securities are being issued to the public in this way, the legal rules and regulations of the U.S. Securities and Exchange Commission must be followed, which adds another layer of cost to the raising of funds.
Key Takeaway
Most companies have a periodic need to raise money for operations and capital improvements. Debt financing is common for this purpose, although it leads to an interest charge and increased risk, even the possibility of bankruptcy. The cost of debt is offset somewhat because interest expense is tax deductible. Incurring liabilities also allows a business to use financial leverage to boost reported profits but only if the proceeds received generate more income than the cost of the related interest. Notes and bonds are debt contracts that spell out the specific legal rights and responsibilities of both parties. In this textbook, notes will indicate that loans have been negotiated between two parties whereas bonds will refer to debt instruments that are issued, often to the public.
14.2 Issuance of Notes and Bonds
Learning Objectives
At the end of this section, students should be able to meet the following objectives:
- Identify common terms found in a note or bond contract such as face value, stated cash interest rate, and various types of security agreements or covenants.
- Record notes and bonds that are issued at face value where periodic interest payments are made on dates other than the year-end.
- Explain the handling of notes and bonds that are sold between interest dates and make the journal entries for both the issuance and the first interest payment.
Debt Contracts
Question: Notes and bonds are contracts that facilitate the borrowing of money. They are produced with great care by attorneys who are knowledgeable in contract law. What legal terms are typically included in a debt instrument?
Answer: The specific terms written into a loan indenture vary considerably depending on what a debtor is willing to promise in hopes of enticing a creditor to turn over needed financial resources. Some of the most common are as follows.
Face valueMonetary amount of a note or bond to be repaid at the end of the contract; it serves as the basis for computing interest payments and is also known as the maturity value. (or maturity value). The noteA written contract to convey money as a loan at a specified interest rate and repayment schedule between two parties. or bondA written contract created by a debtor that is issued (to specific parties or to the members of the general public) to raise money; the contract specifies the amount and time of repayment as well as other terms and covenants promised by the debtor. will specify the amount to be repaid at the end of the contract term. A $1,000 bond, for example, has a face value of $1,000—the payment to be made on a designated maturity date. The face value can be set at any figure of the debtor’s choosing.
Payment pattern. With some debts, no part of the face value is scheduled for repayment until the conclusion of the contract period. These loans are often referred to as term notes or term bondsA type of debt instrument where interest is paid at regular time intervals with the entire face value due at the end of the contract period.. The entire amount of the face value is paid when the contract reaches the end of its term (sometimes referred to as a balloon payment). For many debtors, accumulating this amount of cash at one time might pose a significant financial burden.
Other loans, known as serial debtsA type of debt instrument where a set repayment is to be made each period to cover both interest and a portion of the face value; home mortgages and automobile loans are common examples., require many individual payments of the face value to be made periodically over time. Home mortgages, for example, are commonly structured as serial notes. Part of each scheduled payment reduces the face value of the obligation so that no large amount remains to be paid on the maturity date.
Notes and bonds can also be set up to allow the debtor the choice of repaying part or all of the face value prior to the due date. Such debts are referred to as “callable.” This feature is popular because it permits refinancing if interest rates fall. If a new loan can be obtained at a cheaper interest rate, the money is used to pay off any callable debt that charges a higher interest rate. Sometimes a penalty payment is required if a note or bond is paid prematurely.
Interest rate. Creditors require the promise of interest before they are willing to risk loaning money to a debtor. Therefore, within the debt contract, a stated cash interest rateThe rate for interest on a debt can be identified by any of several terms. Cash rate, stated rate, contract rate, and coupon rate are all examples of the same information: the rate of interest to be paid by the debtor at specified times. is normally included. A loan that is identified as having a $100,000 face value with a stated annual interest rate of 5 percent informs both parties that $5,000 in interest ($100,000 × 5 percent) will be conveyed from debtor to creditor each year.
For example, the 2010 financial statements for the Intel Corporation indicated that the company had issued over $1 billion in bonds during 2009 that paid a stated annual interest ratePercentage rate established in a debt contract to be paid by the debtor in addition to the face value usually at specified time intervals; it is also called the cash rate, contract rate or coupon rate. of 3.25 percent with a maturity date in 2039.
Interest payment dates. The stated amount of interest is paid at the times identified in the contract. Payments can range from monthly to quarterly to semiannually to annually to the final day of the debt term.
Security. Many companies are not able to borrow money (or cannot borrow money without paying a steep rate of interest) unless some additional security is provided for the creditor. Any reduction of risk makes a note or bond instrument more appealing to potential lenders.
For example, some loans (often dealing with the purchase of real estate) are mortgage agreements that provide the creditor with an interest in identified property. Although specific rights can vary based on state law and the wording of the contract, this type of security usually allows the creditor to repossess the property or force its liquidation if the debtor fails to make payments in a timely manner. The recent downturn in the housing market has seen many debtor defaults that have led to bank foreclosures on homes across the country because of such mortgage agreements.
A debentureA debt contract that does not contain any type of security for the creditor; these contracts are usually offered by debtors that are considered financially strong so that no additional security is required by creditors to reduce their chance of loss. is a debt contract that does not contain any security. The debtor is viewed as so financially strong that money can be obtained at a reasonable interest rate without having to add extra security agreements to the contract.
CovenantsPromises made by the issuer of a debt contract to help ensure that sufficient money will be available to make required payments at their scheduled times. and other terms. Notes and bonds can contain an almost infinite list of other agreements. In legal terms, a covenant is a promise to do a certain action or a promise not to do a certain action. Most loan covenants are promises made by the debtor to help ensure that adequate money will be available to make required payments when they come due. For example, the debtor might agree to limit the size of any dividend payments, keep its current ratio above a minimum standard, or not exceed a maximum amount of debt.
Debts can also be convertible so that the creditor can swap them for something else of value (often the capital stock of the debtor) if that seems a prudent move. The notes to the financial statements for the Ford Motor Company as of December 31, 2010, and the year then ended describe one such noncurrent liability. “At December 31, 2010, we had outstanding $883 million principal of 4.25% Senior Convertible Notes due December 15, 2016 (‘2016 Convertible Notes’). The 2016 Convertible Notes pay interest semiannually at a rate of 4.25% per annum. The 2016 Convertible Notes are convertible into shares of Ford Common Stock, based on a conversion rate (subject to adjustment) of 107.5269 shares per $1,000 principal amount.”
Recording a Note Issued at Face Value
Question: The financial reporting of a debt contract appears to be fairly straightforward. Assume, for example, that Brisbane Company borrows $400,000 in cash from a local bank on May 1, Year One. The face value of this loan is to be repaid in exactly five years. In the interim, interest payments at an annual rate of 6 percent will be made every six months beginning on November 1, Year One. What journal entries are appropriate to record a debt issued for a cash amount equal to the face value of the contract?
Answer: Brisbane receives $400,000 in cash but also accepts a noncurrent liability for the same amount. The resulting journal entry is shown in Figure 14.1 "May 1, Year One—Cash of $400,000 Borrowed on Long-term Note Payable".
Figure 14.1 May 1, Year One—Cash of $400,000 Borrowed on Long-term Note Payable

The first semiannual interest payment will be made on November 1, Year One. Because the 6 percent interest rate stated in the contract is for a full year, it must be adjusted to calculate the payment that covers each six-month interval. These payments will be for $12,000 ($400,000 face value × 6 percent annual stated interest rate × 6/12 year). The recording of the first payment is presented in Figure 14.2 "November 1, Year One—Payment of Interest for Six Months".
Figure 14.2 November 1, Year One—Payment of Interest for Six Months

By December 31, Year One, when financial statements are to be prepared, interest for two additional months (November and December) has accrued. This amount ($4,000 or $400,000 × 6 percent × 2/12 year) is recognized at that time so (a) the amount due on the balance sheet date will be presented fairly and (b) the cost of the debt for these two months is included on the Year One income statement. No transaction occurs on that date but the adjusting entry in Figure 14.3 "December 31, Year One—Accrual of Interest for Two Months" brings all reported figures up to date.
Figure 14.3 December 31, Year One—Accrual of Interest for Two Months

When the next $12,000 interest payment is made by Brisbane on May 1, Year Two, the recorded $4,000 liability is extinguished and interest for four additional months (January through April) is recognized. The appropriate expense for this period is $8,000 ($400,000 × 6 percent × 4/12 year). Mechanically, this payment could be recorded in more than one way but the journal entry shown in Figure 14.4 "May 1, Year Two—Payment of Interest for Six Months" is probably the easiest to follow. Interest expense for the first two months was recorded in Year One with interest for the next four months recorded here in Year Two.
Figure 14.4 May 1, Year Two—Payment of Interest for Six Months

Interest payments and the recording process will continue in this same way until all five years have passed and the face value is paid.
Except for the initial entry, these events are recorded in an identical fashion if Brisbane had signed this same note to acquire an asset—such as a piece of machinery—directly from the seller. The only reporting difference is that the asset replaces cash in Figure 14.1 "May 1, Year One—Cash of $400,000 Borrowed on Long-term Note Payable" above.
Test Yourself
Question:
On January 1, Year One, the Leaver Company signs a nine-year note payable with a face value of $800,000 and a stated annual cash interest rate of 7 percent. Interest will be paid annually beginning on January 1, Year Two. Which of the following statements is true?
- Interest expense of $56,000 is recognized on January 1, Year Two.
- Interest payable of $56,000 is reduced on January 1, Year Two.
- No interest expense is reported for Year One because no interest was paid in that year.
- No interest liability is recorded at the end of Year One because payment is not due until Year Two.
Answer:
The correct answer is choice b: Interest payable of $56,000 is reduced on January 1, Year Two.
Explanation:
Interest was incurred throughout Year One on the borrowed funds and is recognized through a year-end adjusting entry. Both the interest expense and the interest payable for the period are reported in that way. On the following day, when payment is made, the liability is removed and cash is reduced. No additional interest expense is recognized on January 1, Year Two, because no time has yet passed since the interest was recognized at the end of Year One.
Issuance of Bonds between Interest Dates
Question: Bonds can be issued to a group of known investors or to the public in general. Often, companies will print bond indentures but not offer them to buyers until monetary levels run low. Thus, bonds are frequently issued on a day that falls between two interest dates. Payment must still be made to creditors as specified by the contract regardless of the length of time that the debt has been outstanding. If an interest payment is required, the debtor is legally obligated.
To illustrate, assume that the Brisbane Company plans to issue bonds with a face value of $400,000 to a consortium of twenty wealthy individuals. As in the previous example, these bonds pay a 6 percent annual interest rate with payments every May 1 and November 1. However, this transaction is not finalized until October 1, Year One, when Brisbane has need for the cash.
The first six-month interest payment must still be made on November 1 as stated in the contract. After just one month, the debtor is forced to pay interest for six months. That is not fair, and Brisbane would be foolish to agree to this arrangement. How does a company that issues a bond between interest payment dates ensure that the transaction is fair to both parties?
Answer: As indicated in this question, the issuance of a bond between interest dates is common. Thus, a standard system of aligning the first interest payment with the time that the debt has been outstanding is necessary. Because of the terms of the contract, Brisbane must pay interest for six months on November 1 even though the cash proceeds have been held for only one month. In this first payment, the creditor receives interest for an extra five months.
Consequently, such bonds are normally issued for a stated amount plus accrued interest. The accrued interest is measured from the previous interest payment date to the present and is charged to the buyer. Later, when the first payment is made, the net effect reflects just the time that the bond has been outstanding. If issued on October 1, Year One, the creditors should pay for the bonds plus five months of accrued interest. Later, when Brisbane makes the first required interest payment on November 1 for six months, the net effect is interest for one month—the period that has passed since the date of issuance (six months minus five months).
Assume that the creditors buy these bonds on October 1, Year One, for face value plus accrued interest. Because five months have passed since the previous interest date (May 1), interest on the bonds as of the issuance date is $10,000 ($400,000 × 6 percent × 5/12 year). Thus, the creditors pay $400,000 for the bond and an additional $10,000 for the interest that has accrued to that date. Once again, the actual recording can be made in more than one way but the entry presented in Figure 14.5 "Issuance of Bond on October 1 at Face Value plus Accrued Interest Recognized for Five Months" seems easiest.
Figure 14.5 Issuance of Bond on October 1 at Face Value plus Accrued Interest Recognized for Five Months

One month later, Brisbane makes the first interest payment of $12,000. However, interest expense of only $2,000 is actually recognized in the entry in Figure 14.6 "November 1, Year One—Payment of First Interest Payment". That amount is the appropriate interest for the month of October ($400,000 × 6 percent × 1/12 year). This expense reflects the cost associated with the period that the bond has been outstanding. Interest of $10,000 for five months was collected initially by Brisbane. Interest of $12,000 was later paid by Brisbane for the entire six month period. Interest expense of $2,000 is the net result for that one month.
Figure 14.6 November 1, Year One—Payment of First Interest Payment

After this entry, the recording of interest follows the process demonstrated previously in Figure 14.3 "December 31, Year One—Accrual of Interest for Two Months" and Figure 14.4 "May 1, Year Two—Payment of Interest for Six Months".
Test Yourself
Question:
On January 1, Year One, the Halenstein Corporation creates bond indentures with a total face value of $1.5 million that pay annual interest of 10 percent every December 31. The company had expected to sell the bonds on that date. However, the company’s monetary needs changed and the bonds were not issued until August 1. On that date they were sold for face value plus accrued interest. Thereafter, the bonds were serviced normally until their maturity on December 31, Year Four. Which of the following statements is true in connection with the Year One transactions?
- Halenstein receives $1,587,500 (August 1) and pays $150,000 (December 31).
- Halenstein receives $1,562,500 (August 1) and pays $150,000 (December 31).
- Halenstein receives $1,650,000 (August 1) and pays $62,500 (December 31).
- Halenstein receives $1,650,000 (August 1) and pays $87,500 (December 31).
Answer:
The correct answer is choice a: Halenstein receives $1,587,500 (August 1) and pays $150,000 (December 31).
Explanation:
Seven months pass before the bond is issued (January 1 to August 1). The interest that has accrued on this bond by that date is $87,500 ($1.5 million × 10 percent interest × 7/12 year). Thus, the buyers pay $1.5 million for the bond and $87,500 to cover the accrued interest. On the last day of the year, the contract calls for the payment of interest for a full year or $150,000 ($1.5 million face value × 10 percent stated interest rate).
Key Takeaway
Bond and note contracts include numerous terms that define the specific rights of both the debtor and the creditor. The face value of the debt and the payment patterns should be identified in these indentures as well as stated cash interest amounts and dates. Security agreements and other covenants are also commonly included to reduce the risk for potential creditors. For debts that are issued at face value, interest is recorded as paid and also at the end of each year to reflect any accrued amount. Bonds are frequently issued between interest dates so that an adjustment in the cash price must be made. Such debts are issued at a stated price plus accrued interest so that the agreement is fair to both parties. The journal entry at the time of the first payment then removes the amount recorded for this accrued interest.
14.3 Accounting for Zero-Coupon Bonds
Learning Objectives
At the end of this section, students should be able to meet the following objectives:
- Identify the characteristics of a zero-coupon bond.
- Explain how interest is earned by a creditor on a zero-coupon bond.
- Understand the method of arriving at an effective interest rate for a bond.
- Calculate the price of a zero-coupon bond and list the variables that affect this computation.
- Prepare journal entries for a zero-coupon bond using the effective rate method.
- Explain the term “compounding.”
- Describe the theoretical problems associated with the straight-line method, and identify the situation in which this method can be applied.
The Issuance of a Zero-Coupon Bond
Question: A wide array of bonds and other types of financial instruments can be issued by parties (businesses and other organizations) seeking money. A zero-coupon bond is one that is popular because of its ease. The face value of a zero-coupon bond is paid to the creditor after a specified period of time, but no further cash is ever exchanged. Thus, no stated cash interest rate is paid. Money is received when the bond is issued and money is paid at the end of the term but no other payments are made. Why does any investor choose to purchase a zero-coupon bond if no interest is paid?
Answer: No investor would buy a note or bond that did not pay interest. That makes no economic sense. Because zero-coupon bonds are widely issued, some form of interest must be included.
These bonds are sold at a discount below face value with that reduction serving as interest. If a bond is issued for $37,000 and the company eventually repays its face value of $40,000, the $3,000 difference is the interest on the debt. That additional payment is the charge paid for the use of the money that was borrowed. The price reduction below face value can be so significant that zero-coupon bonds are sometimes referred to as deep discount bonds.
To illustrate, assume that on January 1, Year One, a company offers a $20,000 two-year zero-coupon bondA debt instrument that includes no interest payments; these bonds are issued at a discount with the difference between the cash received at the beginning and the cash paid on the maturity date serving as interest for that period of time. to the public. A single payment of $20,000 will be made to the holder of this bond on December 31, Year Two. According to the contract, no other cash will be paid. An investor who wishes to earn 7 percent annual interest can mathematically compute the exact amount to bid for this contract. The debtor must then decide whether to accept this offer.
Often, the actual exchange price for a bond is the result of a serious negotiation process to establish the interest rate to be earned. The potential creditor might initially offer an amount that equates to interest at an annual rate of 7 percent. The debtor could then counter by suggesting that an annual rate of 5 percent is more reasonable. After some discussion, the two parties might compromise by settling on a price that provides an annual interest rate of 6 percent. In the bond market, interest rates are the subject of intense negotiations. After the effective rateThe interest rate determined by negotiation and market forces that is used to set the price of a bond; it is also called the yield rate and often varies from the interest rate stated on the indenture that is used to establish cash interest payments. (also called the yield or negotiated rate) has been agreed on by both parties, the actual price of the bond is simply a mathematical computation.
Agreeing on a Price for a Bond
Question: A $20,000 zero-coupon bond is being issued by a company. According to the indenture, it comes due in exactly two years. The parties have negotiated an annual interest rate to be earned of 6 percent. How is the actual price to be paid for a bond mathematically determined after an effective rate of interest has been established?
Answer: Calculation of the price of a bond is based on the present value of the cash payments in the same manner as demonstrated previously in the coverage of intangible assets. Future cash payments are first identified and then valued by the mathematical removal of interest (the present value computation).
Here, a single cash payment of $20,000 is to be made by the debtor in two years. The parties have negotiated an annual 6 percent effective interest rate. Thus, a portion of the future cash ($20,000) serves as interest at an annual rate of 6 percent for this two-year period of time. In a present value computation, interest at the designated rate is calculated and subtracted to leave the principal amount of those payments. That is the price of the bond. Interest at a 6 percent annual rate for two years is removed. The remainder is the amount paid for the bond.
Present Value of $1
http://www.principlesofaccounting.com/ART/fv.pv.tables/pvof1.htm
The present value of $1 in two years at an annual rate of interest of 6 percent is $0.8900. This can be found in a chart (through the link presented or in the tables at the end of this book), by formula, or by use of an Excel spreadsheet.As explained in the chapter on acquiring intangible assets, the present value of $1 can be mathematically determined using the formula $1/(1 + i)n. Here, i is 0.06 and n is two periods. Present value can also be determined using an Excel spreadsheet. If a spreadsheet is used, the present value of $1 at 6 percent in two periods is found by typing the following formula into a cell: =PV(.06,2,,1,0). Because the actual payment is $20,000 and not $1, the present value of the cash flows from this bond (its price) can be found as follows:
present value = future cash payment × $0.8900 present value = $20,000 × $0.8900 present value = $17,800Bond prices are often stated as a percentage of face value. Thus, this bond is sold to the investor at “89” ($17,800/$20,000), which indicates that the price is 89 percent of the $20,000 face value. The price is the future cash payments with the negotiated rate of interest removed. If the investor pays $17,800 today and the debtor returns $20,000 in two years, the additional $2,200 is the interest. Mathematically, this extra $2,200 is equal to interest at 6 percent per year.
The issuance is recorded through the entry presented in Figure 14.8 "January 1, Year One—Zero-Coupon Bond Issued at Effective Annual Interest Rate of 6 Percent".The entry shown in Figure 14.8 "January 1, Year One—Zero-Coupon Bond Issued at Effective Annual Interest Rate of 6 Percent" can also be recorded in a slightly different manner. Under this alternative, the liability is entered into the records at its face value of $20,000 along with a separate discount of $2,200. The discount serves as a contra account to reduce the net liability balance to its principal amount. Although visually different, the liability is still reported as $17,800.
Figure 14.6 
Figure 14.8 January 1, Year One—Zero-Coupon Bond Issued at Effective Annual Interest Rate of 6 Percent

Test Yourself
Question:
On January 1, Year One, the Leisinger Company offers a ten-year zero-coupon bond with a face value of $80,000 to an investor. Leisinger hopes to issue this bond at an annual interest rate of 4 percent. The investor wants 7 percent and they finally agree on 5 percent. The present value of $1 at 4 percent annual interest for 10 years is $0.6756 and at 5 percent for ten years is $0.6139. The present value of an ordinary annuity of $1 for ten years at 4 percent annual interest is $8.1109 and at 5 percent is $7.7217. What amount does Leisinger Company receive (rounded)?
- $49,112
- $54,048
- $61,774
- $64,887
Answer:
The correct answer is choice a: $49,112.
Explanation:
The negotiated effective (or yield) interest rate is 5 percent per year. A single payment will be made in ten years. Using the rate for $1 (a single amount) in ten years at 5 percent interest per year, the present value is the cash of $80,000 times $0.6139 or $49,112. The present value factors have been mathematically determined to compute the appropriate interest which is then removed to leave the principal. At an annual rate of 5 percent, $49,112 will grow to be exactly $80,000 in ten years.
Recognizing Interest on a Zero-Coupon Bond
Question: The $20,000 zero-coupon bond discussed above is issued for $17,800 so that a 6 percent annual interest rate will be earned. As shown in Figure 14.8 "January 1, Year One—Zero-Coupon Bond Issued at Effective Annual Interest Rate of 6 Percent", the bond is initially recorded at this principal amount.
Subsequently, two problems must be addressed by the accountant.
- First, the company actually has to pay $20,000. Over time, the $17,800 principal balance must be raised to that face value. At the end of Year Two, the liability should be reported as $20,000.
- Second, the $2,200 difference between the amount received and the eventual repayment ($20,000 less $17,800) has to be recognized as interest expense over these two years. The additional payment is the cost of the debt for this period, the interest.
To arrive at fairly presented figures, both of these problems must be resolved. How is a zero-coupon bond reported in the period after its issuance?
Answer: In the earlier discussion of present value and the purchase of assets (such as a patent), the effective rate method was demonstrated. It solves the two accounting problems mentioned here. The reported debt balance is raised gradually to the face value and interest expense equal to 6 percent is reported each year until maturity.
Interest recognized for Year One should be the $17,800 principal balance multiplied by the effective interest rate of 6 percent or $1,068. However, no cash interest payment is made for this zero-coupon bond. Thus, as is shown in Figure 14.9 "December 31, Year One—Interest on Zero-Coupon Bond at 6 Percent Rate Is Recognized and Compounded", this interest is compounded—added to the principal of the debt. Interest that is recognized but not paid at that time is compounded, included in the balance of the liability.
Figure 14.9 December 31, Year One—Interest on Zero-Coupon Bond at 6 Percent Rate Is Recognized and CompoundedIf a discount is recorded in the initial entry, as is shown in endnote 6, the credit shown in Figure 14.9 "December 31, Year One—Interest on Zero-Coupon Bond at 6 Percent Rate Is Recognized and Compounded" is to the Discount account and not directly to the bond payable. Because the contra account is reduced, the net liability balance increases by $1,068. Thus, overall reporting of the interest and the liability is not impacted by the method used in recording the issuance of the bond.

The compounding of this interest raises the principal by $1,068 from $17,800 to $18,868. The balances to be reported in the financial statements at the end of Year One are as follows:
| Year One—Interest Expense (Income Statement) | $1,068 |
| December 31, Year One—Bond Payable (Balance Sheet) | $18,868 |
The principal is higher in Year Two because of the compounding (addition) of the first year interest. As the principal increases, interest for subsequent periods must also go up. As reflected in Figure 14.10 "December 31, Year Two—Interest on Zero-Coupon Bond at 6 Percent Rate Is Recognized and Compounded", interest for Year Two is 6 percent of the new liability balance of $18,868 or $1,132 (rounded).
Figure 14.10 December 31, Year Two—Interest on Zero-Coupon Bond at 6 Percent Rate Is Recognized and Compounded

Note that the bond payable balance has now been raised to $20,000 as of the date of payment ($17,800 + $1,068 + $1,132). In addition, interest expense of $2,200 ($1,068 + $1,132) has been recognized over the two years. Reported interest was exactly 6 percent of the principal in each year. Total interest reported for this zero-coupon bond is equal to the difference between the amount received by the debtor and the face value eventually repaid. Both of the accounting problems have been resolved through the application of the effective rate method.
The $17,800 price of the bond was computed mathematically based on the following:
- The cash payment ($20,000)
- The time periods (two)
- The effective rate of interest (the 6 percent negotiated rate)
- The pattern of cash flows (a single payment in the future)
Interest is then recognized each period based on this same set of variables. Thus, the resulting numbers will reconcile. Interest expense reported for the two years is $2,200 and the final liability balance comes back to $20,000.
Test Yourself
Question:
The O’Neil Company issues a six-year $40,000 zero-coupon bond on January 1, Year One. At that time, most companies are able to borrow money at an annual rate of 10 percent. O’Neil is in such good financial health that the bond is sold for $25,207 to yield a negotiated rate of 8 percent per year. What is reported in O’Neil’s financial statements at the end of Year One if the effective rate method is applied? (All numbers are rounded.)
- Interest expense of $2,017 and a bond payable of $27,224.
- Interest expense of $2,112 and a bond payable of $27,319.
- Interest expense of $2,215 and a bond payable of $27,422.
- Interest expense of $2,521 and a bond payable of $27,728.
Answer:
The correct answer is choice a: Interest expense of $2,017 and a bond payable of $27,224.
Explanation:
Interest to be reported for the first year is the 8 percent negotiated rate times the principal of $25,207 or $2,017 (rounded). This is a zero-coupon bond so no interest is paid as time passes. Because no cash interest is actually paid, this entire amount of interest for the first year is compounded to raise the principal by $2,017 from $25,207 to $27,224. In this manner, the principal balance should reach $40,000 after six years.
Test Yourself
Question:
Johnson Company issues an eight-year $50,000 zero-coupon bond on January 1, Year One. After serious negotiations between the company and the investor, this bond is sold for $31,371 to yield an effective annual rate of 6 percent. What is reported in Johnson’s financial statements at the end of Year Two if the effective rate method is applied? (All numbers are rounded.)
- Interest expense of $1,882 and a bond payable of $33,253.
- Interest expense of $1,882 and a bond payable of $35,135.
- Interest expense of $1,995 and a bond payable of $35,248.
- Interest expense of $2,015 and a bond payable of $35,285.
Answer:
The correct answer is choice c: Interest expense of $1,995 and a bond payable of $35,248.
Explanation:
Interest for the first year is the $31,371 principal times the effective annual rate of 6 percent or $1,882. As a zero-coupon bond, no interest is paid. The entire $1,882 is compounded by adding it to the principal so that the balance is $33,253. For Year Two, interest expense is now recognized as $1,995 or 6 percent times the updated principal of $33,253. Again, the interest is compounded so the liability is reported at $35,248. In this manner, the balance will be $50,000 after 8 years.
Recognizing Interest Using the Straight-Line Method
Question: The previous zero-coupon bond was sold at the present value of its future cash flows based on a rate of interest negotiated by the parties involved. Interest was then recognized each year by applying the effective rate method. Is the effective rate method the only acceptable technique that can be used to compute and report interest when the face value of a debt differs from its issue price?
Answer: When a zero-coupon bond is issued at a discount, interest to be reported each year can also be calculated by a simpler approach known as the straight-line method. According to this technique, an equal amount of the discount is assigned to interest each period over the life of the bond. This zero-coupon bond was issued for $2,200 below face value to provide interest to the buyer. Payment of the face value will be made in two years. As is shown in Figure 14.11 "December 31, Years One and Two—Interest on Zero-Coupon Bond at 6 Percent Rate—Straight-Line Method", the straight-line method recognizes interest of $1,100 annually ($2,200/2 years).
Figure 14.11 December 31, Years One and Two—Interest on Zero-Coupon Bond at 6 Percent Rate—Straight-Line Method

Once again, the bond payable balance has been raised to $20,000 by the end of the second year ($17,800 + $1,100 + $1,100) and total interest expense over the life of the bond equals the $2,200 discount ($1,100 + $1,100). However, a theoretical question should be raised as to whether the information reported under this method is a fairly presented portrait of the events that took place. Although the bond was sold to earn 6 percent annual interest, this rate is not reported for either period.
Year One: $1,100 interest/$17,800 principal = 6.2 percent
Compounding of the interest raises the principal by $1,100 to $18,900
Year Two: $1,100 interest/$18,900 principal = 5.8 percent
The debtor and creditor agreed on an annual rate of exactly 6 percent for the entire two-year period. When applying the straight-line method, this rate is not reported for either year. Furthermore, the interest rate appears to float (6.2 percent to 5.8 percent) as if a different rate was negotiated for each year. That change does not reflect reality. A single 6 percent annual interest rate was established by these two parties.
Although the straight-line method creates some theoretical concerns, it can still be applied according to U.S. GAAP but only if the reported results are not materially different from those derived using the effective rate method.
Test Yourself
Question:
The Reynolda Company issues an eight-year $80,000 zero-coupon bond on January 1, Year One. After serious negotiations, this bond is sold for $54,144 to yield an effective annual rate of 5 percent. What is reported in Reynolda’s financial statements at the end of Year Two if the straight-line method is applied to this discount? (All numbers are rounded.)
- Interest expense of $3,198 and a bond payable of $60,540.
- Interest expense of $3,232 and a bond payable of $60,608.
- Interest expense of $3,268 and a bond payable of $60,680.
- Interest expense of $3,304 and a bond payable of $60,752.
Answer:
The correct answer is choice b: Interest expense of $3,232 and a bond payable of $60,608.
Explanation:
This bond was sold at a discount of $25,856 ($80,000 less $54,144) to provide interest over the eight-year life of this bond. If the straight-line method is used, this discount is allocated equally to interest each period. That annual amount is $3,232 ($25,856/8 years). No cash interest is being paid during the life of this bond. Thus, the recognized interest each period is compounded to arrive at a principal balance of $60,608 after two years ($54,144 plus $3,232 plus $3,232).
Key Takeaway
Zero-coupon bonds pay no explicitly-stated cash interest. Instead, they are issued at a discount with the difference between the price and face value serving as interest. The price of the bond is determined by computing the present value of the required cash flows based on the effective interest rate negotiated by the two parties. The present value figure represents the principal of the debt with all future interest mathematically removed. The bond is issued for this amount. Interest is subsequently determined each period using the effective (or yield) rate. Because no interest is paid, the entire amount recognized must be compounded (added) to the principal. The straight-line method can also be used to record interest if the resulting numbers are not materially different from the effective rate method. This alternative assigns an equal amount of the discount to interest each period over the bond’s life.
14.4 Pricing and Reporting Term Bonds
Learning Objectives
At the end of this section, students should be able to meet the following objectives:
- Understand the difference between a stated cash interest rate in a debt contract and an effective interest rate negotiated by the debtor and creditor.
- Compute the price of a term bond when the stated cash interest rate is different from the effective interest rate.
- Determine the amount of interest to be compounded each period when the stated cash interest rate specified on a bond contract is different from the effective interest rate established by the parties.
- Prepare all journal entries for a term bond when the stated cash interest rate is different from the effective interest rate.
Determining the Price of a Term Bond
Question: Although zero-coupon bonds are popular, most bonds actually do pay a stated rate of cash interest, one that is specified in the contract. If the buyer and seller negotiate an effective rate of interest that is the same as this stated rate, an amount equal to face value is paid for the bond. For example, if the stated interest is 7 percent per year and a negotiated annual rate of 7 percent is accepted by the parties, the bond is issued at its face value. No discount or premium results; the debtor and creditor are both satisfied with the interest being paid. The effective rate method is not needed because the cash interest and the effective interest are the same—7 percent is paid each period and recognized as interest.
However, the negotiated rate often differs from the cash rate stated in the bond contract. Market interest rate conditions change quickly. The interest that creditors demand will often shift between the printing of the indenture and the actual issuance day. Or the financial reputation of the company might move up or down during this time. Information travels so quickly in this technology age that news about companies—both good and bad—spreads rapidly.
To illustrate, assume that Smith Corporation decides to issue $1 million in term bonds to the public on January 1, Year One. The face value of these bonds comes due in four years. During the interim, annual interest at a stated rate of 5 percent will be paid starting on December 31, Year One.
No investors can be found who want to purchase Smith Corporation bonds with only a 5 percent annual return. Therefore, in setting an issuance price, annual interest of 6 percent is negotiated. Possibly, interest offered by other similar companies is 6 percent so that Smith had to match this rate to entice investors to buy its bonds. Or some recent event has made Smith seem slightly more risky causing potential creditors to demand a higher rate of return. A list of market conditions that can impact the price of a bond would be almost unlimited. How is the price of a bond calculated when the stated cash interest rate differs from the effective rate negotiated by the two parties involved?
Answer: The pricing of a bond always begins by identifying the cash flows specified by the contract. These amounts are set and will not be affected by the eventual sales price. The debtor is legally obligated to make these payments regardless of whether the bond is sold for $1 or $10 million.
Here, Smith Corporation must pay $50,000 per year in interest ($1 million × 5 percent) for four years and then the $1 million face value:
| Future Cash Flows Set by Bond Contract |
|---|
| $50,000 annually for four years (5 percent stated rate) |
| $1,000,000 in four years (face value of term bond) |
After the cash flows are identified, the present value of each is calculated based on the negotiated yield rate. These two present values are then summed to arrive at the price to be paid for the bond. The $50,000 annual interest payments form an annuity—equal amounts are paid at equal time intervals. Because interest is paid at the end of each period starting on December 31, Year One, these payments constitute an ordinary annuity.As mentioned in earlier discussions about the acquisition of intangible assets, an annuity with payments made at the beginning of each period is known as an annuity due. If the interest had been paid starting on January 1, Year One, the payments here would form an annuity due rather than an ordinary annuity. The cash flow pattern for notes and bonds is more likely to be in the form of an ordinary annuity since interest is not typically paid in advance.
As determined by table, formula, or Excel spreadsheet, the present value of an ordinary annuity of $1 at an effective annual interest rate of 6 percent over four years is $3.46511.The mathematical formula to determine the present value of an ordinary annuity of $1 is (1 – 1/[1 + i]n)/i, where i is the appropriate interest rate (6 percent in this illustration) and n is the number of payment periods (four). If using an Excel spreadsheet, the present value of a $1 per period ordinary annuity for four periods at an annual rate of interest of 6 percent can be found by typing the following data into a cell: =PV(.06,4,1,,0). Thus, the present value of the four interest payments is $50,000 times $3.46511 or $173,256 (rounded). Note that the present value computation requires the multiplication of one annuity payment ($50,000) rather than the total amount of all interest payments ($200,000).
Present Value of an Ordinary Annuity of $1
http://www.principlesofaccounting.com/ART/fv.pv.tables/pvofordinaryannuity.htm
The second part of the cash flows promised by this bond is a single payment of $1 million in four years. The present value of a payment of $1 in four years at a 6 percent annual rate is $0.79209 so the present value of the entire $1 million is $792,090.
Present Value of $1
http://www.principlesofaccounting.com/ART/fv.pv.tables/pvof1.htm
Based on an annual interest rate of 6 percent for four years, the present value of the cash flows required by this term bond contract is $173,256 (cash interest) plus $792,090 (face value) or a total of $965,346. Smith receives this amount on January 1, Year One, but must pay back $50,000 per year for four years followed by a single payment of $1 million. Mathematically, that is equivalent to a 6 percent rate of interest each year for four years. The journal entry to record the issuance is shown in Figure 14.12 "January 1, Year One—Term Bonds Issued at an Effective Rate of 6 Percent".
Figure 14.12 January 1, Year One—Term Bonds Issued at an Effective Rate of 6 Percent

Test Yourself
Question:
The Venture Company issues a twenty-year bond with a face value of $500,000 on January 1, Year One. According to the bond contract, cash interest at a stated rate of 2 percent will be paid each year beginning on December 31, Year One. The Manhattan Investment Company wants to buy this bond but demands an effective annual interest rate of 9 percent. After some discussion, both parties agree that the bond will be sold to earn an annual interest rate of 8 percent. The present value of $1 in twenty years at a rate of 8 percent is $0.21455. The present value of an ordinary annuity of $1 per year for twenty years at a rate of 8 percent per year is $9.81815. The present value of an annuity due of $1 per year for twenty years at a rate of 8 percent per year is $10.60360. How much does Manhattan Investment Company pay the Venture Company for this bond (rounded)?
- $205,457
- $209,145
- $213,311
- $217,445
Answer:
The correct answer is choice a: $205,457.
Explanation:
Cash interest of $10,000 is paid annually for twenty years ($500,000 × 2 percent). This is an ordinary annuity, since payments are made at each year’s end. A single payment of $500,000 is also due in twenty years. Present value of the interest is $10,000 times $9.81815, or $98,182. Present value of the face value is $500,000 times $0.21455, or $107,275. Total present value is $205,457. That amount is offered by the creditor and accepted by the debtor because it equals 8 percent per year.
Calculating Interest When a Term Bond Is Issued at a Discount
Question: After the previously described term bond was issued at a discount, the debtor has the same two accounting problems that were discussed previously for zero-coupon bonds.
- First, the recorded principal must be raised gradually over four years from $965,346 (as shown in Figure 14.12 "January 1, Year One—Term Bonds Issued at an Effective Rate of 6 Percent") to the $1 million face value.
- Second, the cash interest of 5 percent paid each year has to be adjusted to the annual 6 percent effective rate negotiated by the two parties.
How does a debtor report a bond payable over its life if the stated cash interest rate and the effective rate differ?
Answer: At the end of Year One, Smith Corporation pays $50,000 cash interest to the bondholders as specified in the contract ($1 million face value × 5 percent annual stated rate). However, interest expense must be reported on the income statement based on the agreed upon rate of 6 percent. That was the negotiated rate that led to the initial payment of $965,346. This discounted price was accepted by Smith (the debtor) as a means of increasing the actual rate of return from 5 percent per year to 6 percent.
The effective rate is reflected in the financial statements by recognizing interest in Year One of $57,921 (rounded), which is the $965,346 principal balance times 6 percent. The $7,921 difference between the effective interest expense of $57,921 and the cash interest payment of $50,000 will eventually be paid at the end of the four-year term when $1 million rather than $965,346 is conveyed to the bondholders. Therefore, at the current time, this extra $7,921 is compounded (increasing the liability balance). Note that only the portion of this interest that is not paid is added to the principal. Earlier, with the zero-coupon bond, the entire amount of interest each year was compounded, but that was because no cash interest payment was made.
The cash interest payment is recorded in Figure 14.13 "December 31, Year One—Payment of Cash Interest at 5 Percent Rate" with the compounding entry shown in Figure 14.14 "December 31, Year One—Compounding Entry to Adjust Interest to Effective Annual Rate of 6 Percent". These two entries can be recorded separately or combined.
Figure 14.13 December 31, Year One—Payment of Cash Interest at 5 Percent Rate

Figure 14.14 December 31, Year One—Compounding Entry to Adjust Interest to Effective Annual Rate of 6 Percent

The interest expense reported on the income statement for Year One of $57,921 ($50,000 + $7,921) equals the 6 percent effective rate times the principal of the debt for that period. The liability on the balance sheet at the end of Year One has begun to move closer to the $1 million face value. The reported figure is now $973,267 ($965,346 + $7,921) as a result of the compounding.
As shown in Figure 14.15 "Reported Bond Figures for Remaining Three Years until Maturity", reported figures for the remaining three years of this bond contract can be calculated to verify that the ending balance does grow to $1 million by the time of payment.
Figure 14.15 Reported Bond Figures for Remaining Three Years until MaturityInterest expense for the final year has been increased by $3 so that the final bond payable balance is exactly equal to the $1 million debt that must be paid. Slight adjustments of this type are common to compensate for numbers having been rounded.
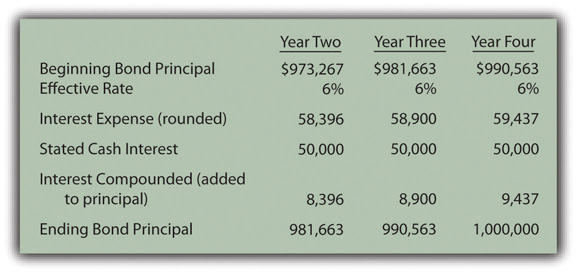
Through the use of the effective rate method, interest expense of 6 percent is recognized each period and the principal balance reported for the liability does gradually grow to equal the face value of the bond on the maturity date.
Test Yourself
Question:
On June 30, Year One, a company issues ten-year term bonds with a total face value of $600,000. Only interest at a 4 percent annual rate is paid each June 30 and December 31 beginning at the end of Year One. These bonds were issued for $375,680 to earn a negotiated rate of 10 percent per year over the ten-year term. What does the company report on its December 31, Year One, balance sheet for this liability?
- $380,775
- $381,225
- $382,464
- $383,646
Answer:
The correct answer is choice c: $382,464.
Explanation:
After six months, the company pays interest to the creditors of $12,000 ($600,000 × 4% × 1/2 year). Interest for the same period—based on an annual yield rate of 10 percent—is $18,784 ($375,680 × 10% × 1/2). The extra interest recognized over the amount paid ($6,784 or $18,784 less $12,000) is compounded to begin moving the principal to the $600,000 face value. At the end of Year One, the bond payable has been raised to $382,464, the original principal of $375,680 plus the compound interest of $6,784.
Key Takeaway
The stated cash interest rate for a term bond is often different from the effective interest rate negotiated between the creditor and the debtor. To compute the amount of money to be exchanged for the bond, the cash flows are determined based on the terms of the contract. The present value of these payments is then calculated. The resulting total is the amount initially paid so that the agreed upon rate of interest is earned over the life of the bond. Cash interest payments are conveyed thereafter with the interest balance adjusted each period based on the effective rate. The interest rate stated in the contract times the face value provides the amount of each cash payment. The principal of the debt times the effective rate gives the interest expense to be recognized for the period. The difference in the effective interest and the cash payment is compounded (added to the principal of the debt). On the maturity date, the liability balance should be equal to the face value of the debt instrument.
14.5 Issuing and Accounting for Serial Bonds
Learning Objectives
At the end of this section, students should be able to meet the following objectives:
- Define a serial bond.
- Identify the steps to calculate the price of a serial bond and provide the proper accounting for the issuance.
- Record the interest and payments on a serial bond over its life.
- Explain the determination of interest expense for a serial bond and the amount that must be compounded each period.
Recording the Issuance of a Serial Bond
Question: The previous section examined the recording of term bonds. Interest was paid each period but no payment was made on the face value until the maturity date. How do these procedures differ for a serial bond where both interest and a portion of the face value are paid periodically?
To demonstrate this process, assume that Smith Corporation issues a four-year, $1 million serial bond on January 1, Year One. This bond will pay a 5 percent stated interest rate at the end of each year on the unpaid face value for the period. The indenture further specifies that $250,000 of the face value is to be paid annually at the same time as the interest. Smith officials negotiate with potential investors and finally agree on a 6 percent annual effective rate. What accounting is appropriate for a serial bond?
Answer: From the previous coverage, the reporting of a term bond where the stated cash interest and the effective rate are different can be divided into five steps:
- The cash flows required by the bond contract are identified.
- The total present value of these cash flows is determined using the effective rate of interest negotiated by the parties. Present value mathematically removes all future interest at the appropriate rate leaving only the principal of the debt. Thus, this resulting figure is the exact amount to be paid so that the agreed-upon interest rate is earned over the life of the bond.
- The bond is recorded at the principal (present value) amount paid by the investors.
- The debtor pays the stated rate of interest periodically on the dates indicated in the contract.
- The effective rate method is applied. Interest to be reported for each period is determined by multiplying the liability’s principal balance times the effective interest rate. The cash interest figure is adjusted to this calculated amount with the difference compounded (added to the principal).The series of steps shown here is also used when a bond is issued at a premium above face value. If the effective interest rate negotiated by the parties is below the stated cash rate, the amount paid for the bond (the present value) will be above face value rather than below. In effect, the high rate of cash interest makes the bond more valuable. Thereafter, the effective interest recognized each period will be below the cash interest. Adjustment is made to lower the cash interest rate to the effective rate, which also reduces the reported principal balance moving it toward face value. Thus, when the negotiated rate is below the stated cash rate, a premium is created rather than a discount. The subsequent accounting process is not affected except that the increases and decreases are reversed from the examples shown here for a discount.
This same process is applied when a serial bond is issued. The sole difference is that regular payments are also made to reduce the face value of the debt over time. To account for the Smith Corporation serial bond described above, the following five steps are required.
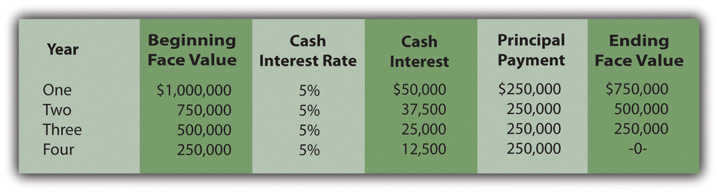
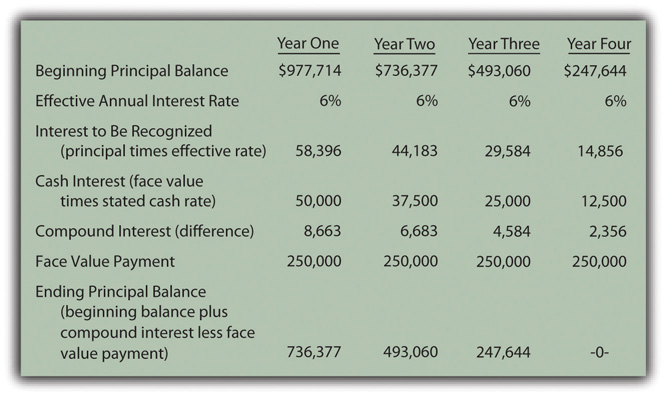
Identify cash flows specified in the bond contract. As shown in Figure 14.16 "Cash Payments Required by Serial Bond Contract", Smith is required to make an annual $250,000 payment to reduce the face value of this serial bond. In addition, interest must be paid each year. During Year One, the unpaid face value is the original $1 million. The stated rate is 5 percent necessitating a $50,000 year-end interest payment ($1,000,000 × 5 percent).
Following the $250,000 payment on December 31, Year One, the face value of the bond drops to $750,000 throughout the second year. Consequently, the interest payment at the end of Year Two is only $37,500 ($750,000 × 5 percent). As a serial bond, the annual payments cause the face value to get smaller so that the interest payments are less each year.
Based on the terms of the contract, the cash flows required by this bond are identified in Figure 14.16 "Cash Payments Required by Serial Bond Contract".
Figure 14.16 Cash Payments Required by Serial Bond Contract
Determine present value of the cash flows. These required cash flows can be organized in either of two ways.
- First, they can be viewed as an ordinary annuity of $250,000 per year for four years plus four separate single amounts of $50,000 (one year), $37,500 (two years), $25,000 (three years) and $12,500 (four years). The pattern is that of an ordinary annuity rather than an annuity due because the payments are at the end of each period. The present value computation for this version of the cash flows is shown in Figure 14.17 "Computation of Present Value of Serial Bond—First Pattern of Cash Flows".
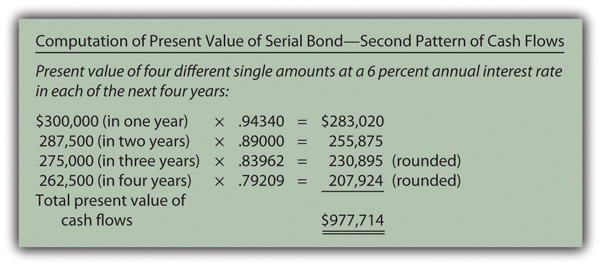
- Second, the payments of the face value and interest can be combined into four separate single amounts of $300,000 (one year), $287,500 (two years), $275,000 (three years), and $262,500 (four years). The present value computation for this version of the cash flows is shown in Figure 14.18 "Computation of Present Value of Serial Bond—Second Pattern of Cash Flows".
The same cash flows are described in both cases. Thus, as proven by a comparison of Figure 14.17 "Computation of Present Value of Serial Bond—First Pattern of Cash Flows" and Figure 14.18 "Computation of Present Value of Serial Bond—Second Pattern of Cash Flows", the resulting present value will be identical ($977,714) regardless of the approach that is followed. A link to the tables for the present value of an ordinary annuity of $1 and the present value of $1 are provided here but those tables are also included at the end of this textbook.
Present Value of an Ordinary Annuity of $1
http://www.principlesofaccounting.com/ART/fv.pv.tables/pvofordinaryannuity.htm
Present Value of $1
http://www.principlesofaccounting.com/ART/fv.pv.tables/pvof1.htm
Figure 14.17 Computation of Present Value of Serial Bond—First Pattern of Cash Flows
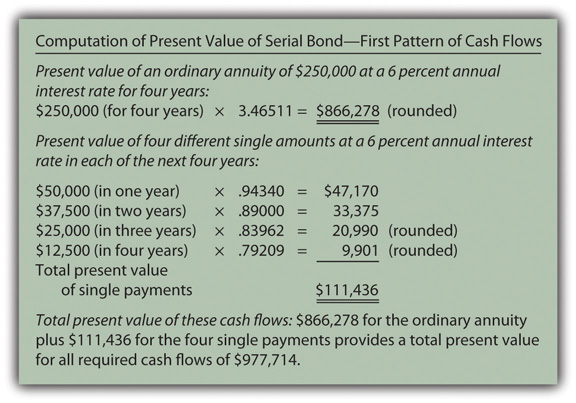
Figure 14.18 Computation of Present Value of Serial Bond—Second Pattern of Cash Flows
Record the principal amount received in the issuance of the bond. Based on either of these computations, $977,714 in cash is exchanged for this four-year $1 million serial bond with an annual stated rate of 5 percent. That payment amount creates an effective rate of interest of 6 percent per year. The issuance of the bond is recorded through the journal entry shown in Figure 14.19 "January 1, Year One—Issuance of $1 Million Serial Bonds Paying 5 Percent Annual Interest with an Effective Rate of 6 Percent".
Figure 14.19 January 1, Year One—Issuance of $1 Million Serial Bonds Paying 5 Percent Annual Interest with an Effective Rate of 6 Percent

Payment of stated cash interest at 5 percent annual rate. Because of the terms specified in the bond contract, interest of $50,000 will be paid at the end of Year One, $37,500 at the end of Year Two, and so on. The Year One interest payment is recorded in Figure 14.20 "December 31, Year One—Payment of 5 Percent Interest on Serial Bond". To better illustrate the handling of interest in a serial bond, the $250,000 payments on the face value are shown separately in Figure 14.22 "December 31, Year One—Payment on Face Value of Serial Bond".
Figure 14.20 December 31, Year One—Payment of 5 Percent Interest on Serial Bond

Effective rate method is applied to recognize the interest rate that was negotiated by the two parties. For the first year, the principal balance of this debt is the original issuance price of $977,714. The yield rate agreed on by the two parties was 6 percent. Thus, the interest to be recognized for Year One is $58,663 ($977,714 × 6 percent).
As shown in Figure 14.20 "December 31, Year One—Payment of 5 Percent Interest on Serial Bond", the cash interest paid is only 5 percent of the face value or $50,000. The $8,663 in extra interest for the period ($58,663 less $50,000) is compounded—added to the principal of the bond payable. The interest to be compounded is added to the principal in Figure 14.21 "December 31, Year One—Adjustment of Interest from Cash Rate to Effective Rate".
The journal entries shown in Figure 14.20 "December 31, Year One—Payment of 5 Percent Interest on Serial Bond" and Figure 14.21 "December 31, Year One—Adjustment of Interest from Cash Rate to Effective Rate" are often combined in practice. They are separated here for discussion purposes.
Figure 14.21 December 31, Year One—Adjustment of Interest from Cash Rate to Effective Rate

In addition, as a serial bond, the first payment of the face value is made at the end of Year One and shown in Figure 14.22 "December 31, Year One—Payment on Face Value of Serial Bond".
Figure 14.22 December 31, Year One—Payment on Face Value of Serial Bond

Whether a long-term liability is a term bond or a serial bond, the accounting process is the same. It follows the five steps that have been listed above and demonstrated here. All the amounts to be recorded over the four-year life of this bond can be computed to verify that the final payment does appropriately remove the remainder of the debt. Those figures are presented in Figure 14.23 "Balances to be Reported Over the Four-year Life of Serial Bond".
Figure 14.23 Balances to be Reported Over the Four-year Life of Serial BondThe interest recognized in the final year has been adjusted by $3 to compensate for the rounding of several computations so that the liability balance drops precisely to zero at the end of the four years.
Test Yourself
Question:
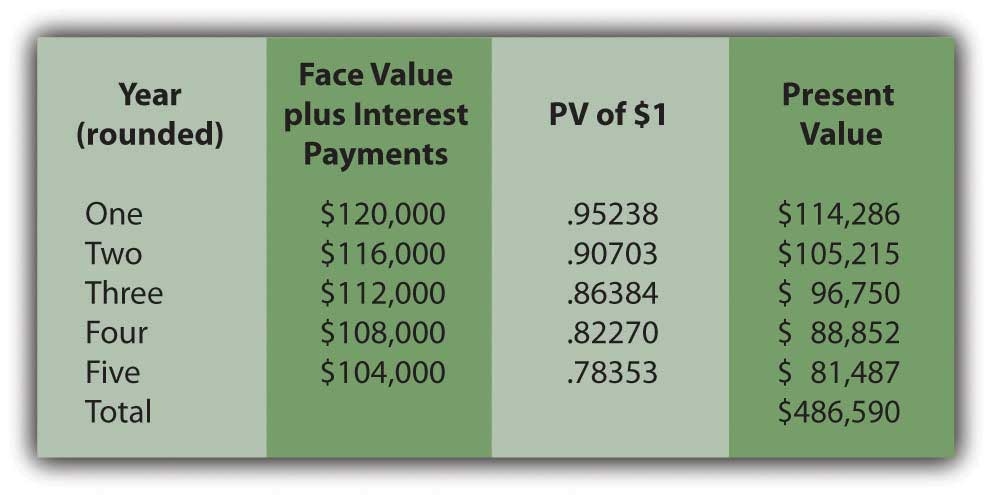
The Heyman Company issues a $500,000 serial bond on January 1, Year One. At the end of each year, the bond pays $100,000 of the face value plus interest at a 4 percent rate on the unpaid balance for the period. The bond was sold at an effective yield rate of 5 percent per year. The present value of $1 at a 5 percent annual rate in one year is $0.95238, in two years is $0.90703, in three years is $0.86384, in four years is $0.82270, and in five years is $0.78353. The present value of an ordinary annuity at a 5 percent annual rate for five years is $4.32948. What amount did Heyman Company receive when the bond was issued (rounded)?
- $483,865
- $486,590
- $490,130
- $492,545
Answer:
The correct answer is choice b: $486,590.
Explanation:
As a serial bond, cash payments of $100,000 are made each year. In addition, interest payments for each year are as follows.
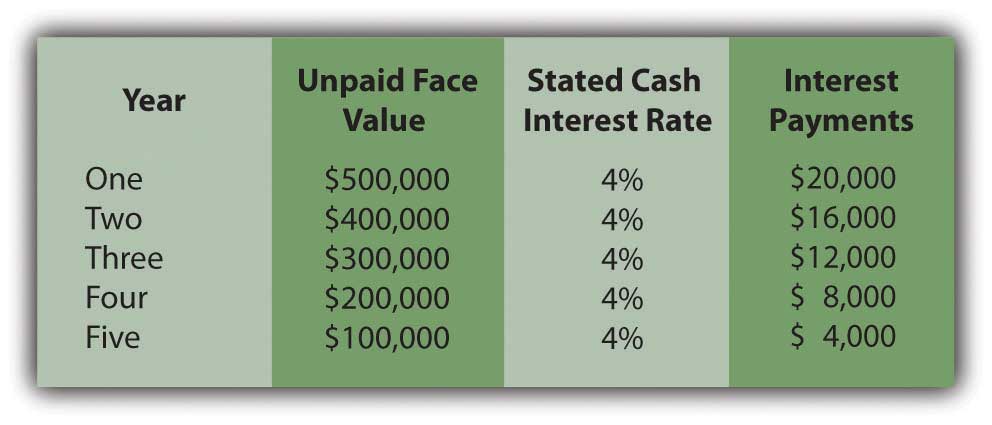
By combining the face value payments with the interest, the present value at an annual rate of 5 percent can be calculated.
Test Yourself
Question:
The Mullins Company issues a $500,000 serial bond on January 1, Year One. At the end of each year, the bond pays $100,000 of the face value plus interest at a 3 percent rate on the unpaid balance for the period. The bond was sold for $473,200 to yield an effective rate of 5 percent per year. What will Mullins report for this bond on its December 31, Year Two, balance sheet?
- $288,953
- $292,875
- $295,445
- $297,905
Answer:
The correct answer is choice a: $288,953.
Explanation:
Effective interest for Year One is $473,200 × the yield rate of 5 percent or $23,660. Because only $15,000 ($500,000 times 3 percent) is paid, the extra $8,660 is compounded. The $473,200 goes up by this $8,660 but down by the $100,000 payment to $381,860. Interest for Year Two is $19,093 ($381,860 × 5 percent). Only $12,000 ($400,000 × 3 percent) is paid so the $7,093 difference is compounded. The $381,860 plus $7,093 but less the next $100,000 payment leaves a balance of $288,953.
Key Takeaway
The issuance price for bonds (whether serial bonds or term bonds) can be computed and the subsequent accounting outlined in five general steps: (1) determine the cash payments required by the bond contract, (2) calculate the present value of those cash flows based on the negotiated effective rate of interest, a computation that sets the price to be paid for the bond, (3) record the bond at this exchange price (the present value amount), (4) over time, record each periodic cash interest payment, and (5) adjust the stated cash interest amounts to the effective interest rate through a compounding entry. A serial bond extends this process slightly because a portion of the face value is also paid periodically. The debt principal goes up each year as a result of interest compounding. However, in recording a serial bond, the principal also goes down because of the periodic payments of the face value.
14.6 Bonds with Other Than Annual Interest Payments
Learning Objectives
At the end of this section, students should be able to meet the following objectives:
- Realize that cash interest payments are often made more frequently than once a year, such as each quarter or semiannually.
- Determine the stated interest rate, the effective interest rate, and the number of time periods to be used in a present value computation when interest payments cover a period of time of less than a year.
- Compute the stated cash interest payments and the effective interest rate when interest is paid on a bond more frequently than once each year.
- Prepare journal entries for a bond when the interest payments are made for a period of time shorter than a year.
Question: In the previous examples, both the interest rates and payments always covered a full year. How is this process affected if interest payments are made at other time intervals such as each quarter or semiannually?
As an illustration, assume that on January 1, Year One, an entity issues term bonds with a face value of $500,000 that will come due in six years. Cash interest payments at a 6 percent annual rate are required by the contract. However, the actual disbursements are made every six months on June 30 and December 31. In setting a price for these bonds, the debtor and the creditor negotiate an effective interest rate of 8 percent per year. How is the price of a bond determined and the debt reported if interest payments occur more often than once each year?
Answer: None of the five basic steps for issuing and reporting a bond is affected by a change in the frequency of interest payments. However, both the stated cash rate and the effective rate must be set to agree with the time interval between payment dates. The number of time periods used in the present value computation also varies based on the time that passes from one payment to the next.
In this current example, interest is paid semiannually, so each time period is only six months in length. The stated cash interest rate to be paid during that period is 3 percent or 6/12 of the annual 6 percent rate listed in the bond contract. Similarly, the effective interest rate is 4 percent or 6/12 of the annual 8 percent negotiated rate. Both of these interest rates must align with the specific amount of time between payments. Over the six years until maturity, the bond is outstanding for twelve of these six-month periods of time.
Thus, for this bond, the cash flows will be the interest payments followed by settlement of the face value.
- Interest Payments: $500,000 face value times 3 percent stated rate for a $15,000 interest payment every six months during these twelve periods. Equal payments are made at equal time intervals making this an annuity. Because payments are made at the end of each period, these payments constitute an ordinary annuity.
- Face value: $500,000 is paid at the end of these same twelve periods. This cash payment is a single amount.
As indicated, the effective rate to be used in determining the present value of these cash payments is 4 percent per period or 6/12 times 8 percent.
Present Value of Annuity Due of $1
http://www.principlesofaccounting.com/ART/fv.pv.tables/pvof1.htm
Present Value of Ordinary Annuity of $1
http://www.principlesofaccounting.com/ART/fv.pv.tables/pvofordinaryannuity.htm
- The present value of $1 in twelve periods at an effective rate of 4 percent per period is $0.62460.
- The present value of an ordinary annuity of $1 for twelve periods at an effective rate of 4 percent per period is $9.38507.
- The present value of the face value cash payment is $500,000 times $0.62460 or $312,300.
- The present value of the cash interest payments every six months is $15,000 times $9.38507 or $140,776 (rounded).
- The total present value of the cash flows established by this contract is $312,300 plus $140,776 or $453,076. As shown in Figure 14.24 "January 1, Year One—Issuance of $500,000 Bond with a 3 Percent Stated Rate to Yield Effective Rate of 4 Percent Semiannually", the bond is issued for this present value amount. With this payment, the agreed-upon effective rate of interest (8 percent for a full year or 4 percent for each six-month period) will be earned by the investor over the entire life of the bond.
Figure 14.24 January 1, Year One—Issuance of $500,000 Bond with a 3 Percent Stated Rate to Yield Effective Rate of 4 Percent Semiannually

On June 30, Year One, the first $15,000 interest payment is made as reported in Figure 14.25 "June 30, Year One—Cash Interest Paid on Bond for Six-Month Period". However, the effective interest rate for that period is the principal of $453,076 times the six-month negotiated rate of 4 percent or $18,123 (rounded). Therefore, the interest to be compounded for this first six-month period is $3,123 ($18,123 interest less $15,000 payment). That is the amount of interest recognized but not yet paid that is added to the liability as shown in Figure 14.26 "June 30, Year One—Interest on Bond Adjusted to Effective Rate".
Figure 14.25 June 30, Year One—Cash Interest Paid on Bond for Six-Month Period

Figure 14.26 June 30, Year One—Interest on Bond Adjusted to Effective Rate

The compound interest recorded previously raises the bond’s principal to $456,199 ($453,076 principal plus $3,123 in compound interest). The principal is gradually moving to the $500,000 face value. Another $15,000 in cash interest is paid on December 31, Year One (Figure 14.27 "December 31, Year One—Cash Interest Paid on Bond for Six-Month Period"). The effective interest for this second six-month period is $18,248 (rounded) or $456,199 times 4 percent interest. The compound interest recognized on December 31, Year One, is $3,248 ($18,248 less $15,000), a balance that is recognized by the entry presented in Figure 14.28 "December 31, Year One—Interest on Bond Adjusted to Effective Rate".
Figure 14.27 December 31, Year One—Cash Interest Paid on Bond for Six-Month Period

Figure 14.28 December 31, Year One—Interest on Bond Adjusted to Effective Rate

The Year One income statement will report interest expense of $18,123 for the first six months and $18,248 for the second, giving a total for that year of $36,371. The second amount is larger than the first because of compounding.
The December 31, Year One, balance sheet reports the bond payable as a noncurrent liability of $459,447. That is the original principal (present value) of $453,076 plus compound interest of $3,123 (first six months) and $3,248 (second six months). Once again, interest each period has been adjusted from the cash rate stated in the bond contract to the effective rate negotiated by the two parties. Here, the annual rates had to be halved because payments were made semiannually.
Test Yourself
Question:
Friday Corporation issues a two-year bond on January 1, Year One, with a $300,000 face value and a stated annual cash rate of 8 percent. The bond was sold to earn an effective annual rate of 12 percent. Interest payments are made quarterly beginning on April 1, Year One. The present value of $1 at a 3 percent rate in eight periods is $0.78941. The present value of $1 at a 12 percent rate in two periods is $0.79719. The present value of an ordinary annuity of $1 at a 3 percent rate for eight periods is $7.01969. The present value of an ordinary annuity of $1 at a 12 percent rate for two periods is $1.69005. What amount will Friday receive for this bond?
- $276,055
- $278,941
- $284,785
- $285,179
Answer:
The correct answer is choice b: $278,941.
Explanation:
This bond pays interest of $6,000 every three months ($300,000 × 8 percent × 3/12) and $300,000 in two years. Based on quarterly payments, effective interest is 3 percent (12 percent × 3/12 year) and cash flows are for eight periods (every three months for two years). Present value of the interest is $6,000 × $7.01969, or $42,118. Present value of the face value is $300,000 × $0.78941, or $236,823. Total present value (price of the bond) is $42,118 + $236,823, or $278,941.
Key Takeaway
Bonds often pay interest more frequently than once a year—for example, at an interval such as every three months or six months. If the stated cash rate and the effective rate differ, determination of present value is still required to arrive at the principal amount to be paid when the bond is issued. However, the present value computation must be adjusted to reflect the change in the length of a time period. The amount of time between payments is considered one period. The stated cash interest rate, the effective rate negotiated by the parties, and the number of time periods until maturity are all set for that particular time. The actual accounting and reporting are not affected, merely the method by which the interest rates and the number of periods are calculated.
Talking With a Real Investing Pro (Continued)
Following is a continuation of our interview with Kevin G. Burns.
Question: Assume that you are investigating two similar companies. You are thinking about recommending one of them to your clients as an investment possibility. The financial statements look much the same except that one of these companies has an especially low amount of noncurrent liabilities whereas the other has a noncurrent liability total that seems quite high. How does that difference impact your thinking? Long-term liabilities are a great way to gain financing because a company can make use of someone else’s money. However, debt does increase risk.
Kevin Burns: I have managed to do well now for many years by being a conservative investor. My preference is always for the company that is debt free or as close to debt free as possible. I do not like financial leverage, never have. I even paid off my own home mortgage more than ten years ago.
On the other hand, long-term liabilities have to be analyzed as they are so very common. Is any of the debt convertible into capital stock so that it could potentially dilute everyone’s ownership in the company? Is the company forced to pay a high rate of interest? Why was the debt issued? In other words, how did the company use all that cash that it received? As with virtually every area of financial reporting, you have to look behind the numbers to see what is actually happening. That is why transparency is important. If the debt was issued at a low interest rate in order to make a smart acquisition, I am impressed. If the debt has a high rate of interest and the money was not well used, that is not attractive to me at all.
Video Clip
(click to see video)Professor Joe Hoyle talks about the five most important points in Chapter 14 "In a Set of Financial Statements, What Information Is Conveyed about Noncurrent Liabilities Such as Bonds?".
14.7 End-of-Chapter Exercises
Questions
- The Lohr Company needs $40 million in cash to expand several of its facilities. Company officials chose to issue bonds to raise this money rather than capital stock. What are some of the possible reasons for this decision?
- Officials for the Bohannon Corporation have always avoided incurring noncurrent liabilities as a company policy. Over the years, they have raised long-term financing through operations or from the issuance of capital stock. Why might these officials have preferred that money be raised by means other than noncurrent liabilities?
- The president of the Nelson Company is a fan of financial leverage. He wants to expand operations into California and Oregon and borrows $70 million on 8 percent term bonds to finance this decision. How does he hope to make financial leveraging work for the Nelson Company in this expansion?
- What is a term bond?
- What is a serial bond?
- What is an indenture?
- A company is forced into bankruptcy. Assuming that the bankruptcy petition is not dismissed by the court, what are the two possible outcomes of a bankruptcy?
- The Arapo Corporation issued $10 million in term bonds that are callable. What information does the term “callable” indicate to decision makers?
- On January 1, Year One, the Rexal Company issues term bonds with a face value of $30 million that pay a stated cash interest rate of 6 percent. The bonds are actually issued for $27 million to yield an effective interest rate of 8 percent. If the first payment is made on December 31, Year One, how much cash is paid?
- What is a mortgage agreement?
- The Philadelphia Corporation issues $17 million in debentures. What is a debenture?
- A company issues $12 million in term bonds on March 1, Year One, for face value. The bonds pay a stated cash interest rate of 10 percent per year. Interest payments are made every February 28 and August 31. On financial statements for Year One, what is recognized as interest expense on the income statements? What interest payable is reported on the December 31, Year One, balance sheet?
- A company issues $18 million in term bonds on March 1, Year One, for face value plus accrued interest. The bonds pay a stated cash interest rate of 10 percent per year. Interest payments are made every January 31 and July 31. Prepare journal entries on March 1, Year One, July 31, Year One, and December 31, Year One?
- The Shelby Corporation issues $10 million in zero-coupon bonds. What is a zero-coupon bond? Why would an investor be willing to acquire a zero-coupon bond? How is the price of a zero-coupon bond determined?
- What is meant by the term “compounding”?
- On January 1, Year One, a zero-coupon bond with a face value of $12 million is issued for $7.8 million to create an effective annual interest rate of 9 percent. The bond will be paid in exactly five years. If the effective rate method is applied, what liability balance is reported on December 31, Year One, and also on December 31, Year Two?
- Do Problem 16 again but assume that the straight-line method is used rather than the effective rate method.
- Why is the straight-line method of recognizing interest on a bond that is issued at a discount not viewed as theoretically appropriate? When can the straight-line method be used in connection with the reporting of bond interest?
- On January 1, Year One, a company issues term bonds with a face value of $20 million and an annual stated cash interest rate of 6 percent. Assume the bonds are issued for $18 million to earn an effective yield rate of 8 percent per year. If the first interest payment is made on December 31, Year One, what is the liability balance reported on the balance sheet at the end of that day?
- On January 1, Year One, the Vallee Corporation issues a five-year $10 million serial bond paying a stated annual cash interest rate each December 31 of 5 percent. What are the cash payments specified by this bond contract?
True or False
- ____ A company borrows $1 million on a term bond that pays 8 percent cash interest each year. The money is used by the company to create additional profits of $93,000 per year. This company is using financial leverage.
- ____ One advantage of debt financing is that the payments made on the liability are tax deductible.
- ____ Companies that are forced into bankruptcy will have their assets liquidated with the resulting money going to pay the creditors.
- ____ Banks typically charge stronger companies higher interest rates than weaker ones because a financially healthy company can better afford to pay the extra amounts each period.
- ____ All bonds are issued for cash amounts equal to their face value.
- ____ A callable bond can be exchanged by the creditor for the capital stock of the debtor company.
- ____ A serial bond is a debt that pays interest more frequently than just once each year.
- ____ A debenture is a debt that is not secured.
- ____ The term “indenture” refers to a bond contract.
- ____ A term bond pays interest each February 1 and August 1. It is issued on February 1, Year One. The company will report interest expense on its Year One income statement for 11 months.
- ____ When a company issues a bond between interest dates, the first interest payment will be reduced.
- ____ A zero-coupon bond is issued for a price determined by computing the present value of the stated cash interest payments.
- ____ A company recognizes interest expense for the current year of $23,000 but pays cash interest of only $18,000. The $5,000 difference is compounded.
- ____ On January 1, Year One, a company issues a $1 million term bond that pays a stated cash interest rate of 8 percent per year at the end of each year. To determine the price of this bond, the present value of a single amount of $1 million must be determined along with the present value of an annuity due of $80,000.
- ____ A company issues a $1 million term bond for $700,000. The $300,000 discount can never be recognized as interest expense through the use of the straight-line method.
- ____ A serial bond is issued on December 31, Year One, for $885,000. Interest of $17,000 is compounded at the end of Year Two, and the first principal payment of $50,000 is made on that date. The liability balance to be reported on the December 31, Year Two, balance sheet is $818,000.
Multiple Choice
-
A company needs to raise $9 million and issues bonds for that amount rather than additional capital stock. Which of the following is not a likely reason the company chose debt financing?
- Management hopes to increase profits by using financial leveraging.
- The cost of borrowing is reduced because interest expense is tax deductible.
- Adding new owners increases the possibility of bankruptcy if economic conditions get worse.
- If money becomes available, the company can rid itself of debts.
-
A company issues bonds with a face value of $12 million on June 1, Year One, for the face value plus accrued interest. The bonds pay an annual cash interest rate of 10 percent with payments made on April 1 and October 1 of each year. On financial statements as of December 31, Year One, and the year then ended, which of the following balances will appear?
- Interest expense: $400,000; interest payable: -0-
- Interest expense: $600,000; interest payable: -0-
- Interest expense: $700,000; interest payable: $300,000
- Interest expense: $900,000; interest payable: $300,000
-
The Akimbo Company issues bonds with a face value of $12 million on June 1, Year One, for 93 percent of face value plus accrued interest. The bonds pay an annual cash interest rate of 10 percent with payments made on April 1 and October 1 of each year. The bonds were sold at a discount to create an effective interest rate of 12 percent per year. What amount of cash interest will Akimbo actually pay during Year One?
- $400,000
- $600,000
- $700,000
- $900,000
-
Kitten Inc. issued $105,000 in bonds on September 1 for face value plus any accrued interest. The annual interest rate is 6 percent, and interest is paid on the bonds every June 30 and December 31. When the bonds are issued on September 1, how much cash will the company collect?
- $105,000
- $106,050
- $106,575
- $108,150
-
The Alexander Company issues a fifteen-year, zero-coupon bond with a face value of $500,000. The effective interest negotiated by the parties to the exchange was an annual rate of 7 percent. The present value of $1 in 15 periods at an annual interest rate of 7 percent is $0.36245. The present value of an ordinary annuity of $1 for 15 periods at an annual interest rate of 7 percent is $9.10791. The present value of an annuity due of $1 for 15 periods at an annual interest rate of 7 percent is $9.74547. What was the exchange price for the bond (rounded)?
- $181,225
- $192,687
- $318,777
- $341,091
-
A zero coupon bond with a face value of $900,000 is issued on January 1, Year One. It will mature in ten years and was issued for $502,550 to earn an annual effective rate of 6 percent. If the effective rate method is used, what interest expense does the company recognize for Year Two (rounded)?
- $30,153
- $31,962
- $38,128
- $39,745
-
A zero coupon bond with a face value of $600,000 is issued on January 1, Year One. It will mature in five years and was issued for $408,350 to earn an annual effective rate of 8 percent. If the effective rate method is used, what liability balance does the company report at the end of Year Two (rounded)?
- $476,299
- $478,821
- $482,678
- $485,010
-
A zero coupon bond with a face value of $800,000 is issued on January 1, Year One. It will mature in eight years and was issued for $541,470 to earn an annual effective rate of 5 percent. If the straight-line method is used, what liability balance does the company report at the end of Year Two (rounded)?
- $601,350
- $602,974
- $604,755
- $606,102
-
On January 1, Krystal Corporation issued bonds with a face value of $100,000 and a 4 percent annual stated interest rate. The effective annual rate of interest negotiated by the parties was 6 percent. Interest is paid semiannually on June 30 and December 31. The bonds mature in ten years. The present value of $1 in 10 periods at a 4 percent interest rate is $0.67556, in 10 periods at 6 percent interest is $0.55839, in 20 periods at a 2 percent interest rate is $0.67297, and in 20 periods at a 3 percent interest rate is $0.55368. The present value of an ordinary annuity of $1 for 10 periods at a 4 percent interest rate is $8.11090, for 10 periods at 6 percent interest is $7.36009, for 20 periods at a 2 percent interest rate is $16.35143, and in 20 periods at a 3 percent interest rate is $14.87747. What will be the price of the bonds on January 1 (rounded)?
- $85,123
- $85,279
- $86,054
- $86,311
-
On January 1, Year One, Giant Company decides to issue term bonds with a total face value of $1 million. The bonds come due in ten years and pay cash interest of 4 percent each year on December 31. An investor is found for these bonds, but that person wants to earn an annual effective rate of 8 percent. After some serious negotiations, Giant agrees to a 7 percent annual rate, and the bonds are issued for a total of $789,292. The effective rate method is applied to recognize interest. What amount of interest expense should be recognized by Giant on its Year Two income statement (rounded)?
- $48,515
- $50,375
- $52,936
- $56,318
-
On January 1, Year One, Super Company decides to issue term bonds with a total face value of $600,000. The bonds come due in six years and pay cash interest of 3 percent each year on December 31. An investor is found and an effective annual interest rate of 8 percent is agreed to by all parties. As a result, the bond is issued for $461,315. The effective rate method is applied. What was the reported balance of this liability at the end of Year One (rounded)?
- $473,018
- $476,550
- $477,105
- $480,220
-
On January 1, Year One, the Elizabeth Corporation issues a $1 million serial bond. Beginning on December 31, Year One, the company will pay $100,000 per year plus interest at an 8 percent rate on the unpaid balance during that year. The bond will be issued at an effective rate of 9 percent per year. How much cash will the company pay on December 31, Year Two?
- $162,000
- $172,000
- $180,000
- $184,000
-
On January 1, Year One, the Benson Company issues a $400,000 serial bond. Beginning on December 31, Year One, the company will pay $100,000 per year plus interest at a 4 percent rate on the unpaid balance during that year. The bond is issued for $373,740 to earn an effective annual interest rate of 7 percent. What is the liability balance reported on this company’s balance sheet as of December 31, Year One (rounded)?
- $278,750
- $281,865
- $283,902
- $285,776
Video Problems
Professor Joe Hoyle discusses the answers to these two problems at the links that are indicated. After formulating your answers, watch each video to see how Professor Hoyle answers these questions.
-
Your roommate is an English major. The roommate’s parents own a chain of ice cream shops located throughout Florida. One day, while warming up to go jogging, your roommate poses this question: “My parents plan to build four new shops in the next year or so. They will need several million dollars to construct these facilities and add the necessary equipment and furniture. I thought they were going to obtain this money by adding one or two new owners. Instead, they borrowed the money by issuing bonds to a number of investors throughout the state. I don’t like debt; it scares me. I don’t understand why they would have taken on so much debt when they could simply have gotten new ownership involved. Why would they have made this decision? How will this affect their financial statements in the future?” How would you respond?
-
Your uncle and two friends started a small office supply store several years ago. The company has grown and now has several large locations. Your uncle knows that you are taking a financial accounting class and asks you the following question: “We are beginning a major expansion project that will cost us about $10 million. We plan to raise the needed money by issuing bonds. One of my partners wants to issue zero-coupon bonds. Our lawyer tells us that we really should issue serial bonds. Our financial advisor suggests term bonds. I am not even sure I know the difference. Can you explain how these three types of bonds differ? How do those differences impact the financial reporting?” How would you respond?
Problems
-
Joni Corporation borrows $500,000 from Friendly Bank on February 1, Year One. The principal will not be repaid until the end of six years, but interest payments are due every February 1 and August 1 beginning on August 1, Year One. The interest rate is 4 percent annually. Record the journal entry or adjusting entry necessary for each of the following.
- The signing of the loan on February 1, Year One.
- The payment of interest on August 1, Year One.
- The recognition of accrued interest on December 31, Year One.
- The payment of interest on February 1, Year Two.
-
Colson Corporation produces women’s clothing. Company officials decide to issue $50,000 in long-term bonds to finance an expansion of its swimwear line. These bonds are issued for face value on April 1, Year One and pay interest in the amount of 5 percent annually. Interest payments are made semiannually, every April 1 and October 1. Record the journal entry or the adjusting necessary for each of the following.
- The issuance of the bonds.
- The first payment of interest on October 1, Year One.
- The accrual of interest on December 31, Year One, so that financial statements can be prepared.
- The payment of interest on April 1, Year Two.
-
Assume the same facts as in problem 2, but instead of April 1, Year One, the bonds are issued on July 1, Year One. The bonds are issued for face value plus accrued interest. Record the journal entry or adjusting entry necessary for each of the following.
- The issuance of the bonds on July 1, Year One.
- The first payment of interest on October 1, Year One.
- The accrual of interest on December 31, Year One, so that financial statements can be prepared.
- The payment of interest on April 1, Year Two.
-
Keller Corporation offers to issue zero-coupon bonds of $80,000 on January 1, Year One. The bonds will come due on December 31, Year Three. Keller and several potential creditors negotiate an annual interest rate of 7 percent on the bonds. The present value of $1 in 3 periods at an annual interest rate of 7 percent is $0.81630. The present value of an ordinary annuity of $1 for 3 periods at an annual interest rate of 7 percent is $2.62432. The present value of an annuity due of $1 for 3 periods at an annual interest rate of 7 percent is $2.80802.
- Determine the amount the creditors will pay on January 1, Year One, for these bonds.
- Record the issuance of the bonds on January 1, Year One.
- Make the necessary adjusting entry at the end of Year One. What is the liability balance at the end of Year One?
- Make the necessary adjusting entry at the end of Year Two. What is the liability balance at the end of Year Two?
- The Rangaletta Company issues a five-year, zero-coupon bond on January 1, Year One. The bond has a face value of $200,000 and is issued to yield an effective interest rate of 9 percent. Rangaletta receives $129,986. On January 1, Year Three, Rangaletta pays off the bond early by making a payment of $155,000 to the bondholder. Make all journal entries from January 1, Year One, through January 1, Year Three assuming the effective rate method is applied.
- Do problem 5 again but assume that the straight-line method is used.
-
A company issues $600,000 in zero-coupon bonds on January 1, Year One. They come due in exactly six years and are sold to yield an effective interest rate of 4 percent per year. They are issued for $474,186. The effective rate method is applied.
- What interest expense was recognized for Year One and for Year Two?
- How would the company’s net income have been affected in each of the first two years if the straight-line method had been used rather than the effective rate method?
-
On January 1, Year One, Gijulka Corporation offers to issue a $100,000 bond coming due in exactly ten years. This bond pays a stated cash interest rate of 6 percent per year on December 31. A buyer is found. After some negotiations, the parties agree on an effective annual yield rate of 7 percent. Consequently, the bond is issued for $92,974. The effective rate method is applied.
- What figures will be reported for this bond in Gijulka’s Year One financial statements?
- What figures will be reported for this bond in Gijulka’s Year Two financial statements?
-
Jaguar Corporation issues term bonds with a face value of $300,000 on January 1, Year One. The bonds have a stated rate of interest of 7 percent per year and a life of four years. They pay this interest annually on December 31. Because the market rate of interest at that time was 9 percent, the bonds were issued at a discount to create an effective annual rate of 9 percent. The present value of $1 in 4 periods at an annual interest rate of 9 percent is $0.70843. The present value of an ordinary annuity of $1 for 4 periods at an annual interest rate of 9 percent is $3.23972.
- What amount will Jaguar receive when the bonds are issued?
- What journal entry does the company make on January 1, Year One, when the bonds are issued?
- What journal entry or entries does the company make on December 31, Year One?
- What is the liability balance reported on the December 31, Year One, balance sheet?
- What journal entry or entries does the company make on December 31, Year Two?
- What is the liability balance reported on the December 31, Year Two, balance sheet?
-
Arizona Corporation issues term bonds with a face value of $800,000 on January 1, Year One. The bonds have a stated rate of interest of 7 percent per year and a life of six years. They pay interest annually on December 31. These bonds were issued at $695,470 to create an effective annual rate of 10 percent.
- What journal entry does the company make on January 1, Year One, when the bonds are issued?
- What journal entry or entries does the company make on December 31, Year One?
- What is the liability balance reported on the December 31, Year One, balance sheet?
- What journal entry or entries does the company make on December 31, Year Two?
- What is the liability balance reported on the December 31, Year Two, balance sheet?
-
Collins Company issues term bonds with a face value of $100,000 on January 1, Year One. The bonds have an annual stated rate of interest of 4 percent and a life of ten years. They pay interest semiannually on June 30 and December 31. The bonds were issued to yield an effective annual interest rate of 6 percent.
The present value of $1 in 10 periods at a 4 percent interest rate is $0.67556, in 10 periods at 6 percent interest is $0.55839, in 20 periods at a 2 percent interest rate is $0.67297, and in 20 periods at a 3 percent interest rate is $0.55368.
The present value of an ordinary annuity of $1 for 10 periods at a 4 percent interest rate is $8.11090, for 10 periods at 6 percent interest is $7.36009, for 20 periods at a 2 percent interest rate is $16.35143, and in 20 periods at a 3 percent interest rate is $14.87747.
- Prepare the journal entry to record the issuance of the bonds on January 1, Year One.
- Prepare the journal entry to record the first payment of interest on June 30, Year One.
- Prepare the journal entry to record the second payment of interest on December 31, Year One.
- What amount of interest expense is reported on the Year One income statement?
- What is the liability balance to be reported for this bond on a December 31, Year One, balance sheet?
-
Chyrsalys Corporation issues $4,000,000 in serial bonds on January 1, Year One, with a stated cash interest rate of 4 percent. The bonds are issued at face value. The bond terms specify that interest and $2,000,000 in principal will be paid on December 31, Year One and December 31, Year Two.
- What journal entry, or entries, is recorded on December 31, Year One?
- What journal entry, or entries, is recorded on December 31, Year Two?
-
The Empire Company issues $3 million in bonds on January 1, Year One. The bonds are for three years with $1 million paid at the end of each year plus interest of 6 percent on the unpaid balance for that period. These bonds are sold to yield an effective rate of 8 percent per year. The present value of $1 at an 8 percent interest rate in one year is $0.92593, in two years is $0.85734, and in three years is $0.79383. The present value of an ordinary annuity of $1 at an 8 percent interest rate over three years is $2.57710.
- What amount of cash will Empire pay on December 31 of each of these three years?
- What is the present value of these cash payments at an 8 percent effective annual interest rate?
- What journal entry or entries is recorded on December 31, Year One?
- What journal entry or entries is recorded on December 31, Year Two?
-
The Althenon Corporation issues bonds with a $1 million face value on January 1, Year One. The bonds pay a stated interest rate of 5 percent each year on December 31. They come due in eight years. The Zephyr Corporation also issues bonds with a $1 million face value on January 1, Year One. These bonds pay a stated interest rate of 8 percent each year on December 31. They come due in eight years. Both companies actually issue their bonds to yield an effective annual interest rate of 10 percent. Both companies use the effective rate method. The present value of $1 at a 10 percent interest rate in eight years is $0.46651. The present value of an ordinary annuity of $1 at a 10 percent interest rate over eight years is $5.33493.
- What interest expense does Althenon report for Year One and also for Year Two?
- What interest expense does Zephyr report for Year One and also for Year Two?
-
On January 1, Year One, the Pulaski Corporation issues bonds with a face value of $1 million. These bonds come due in twenty years and pay an annual stated interest rate (each December 31) of 5 percent. An investor offers to buy the entire group of bonds for an amount that will yield an effective interest rate of 10 percent per year. Company officials negotiate and are able to reduce the effective rate by 2 percent to 8 percent per year. The present value of $1 at a 10 percent interest rate in twenty years is $0.14864. The present value of an ordinary annuity of $1 at a 10 percent interest rate over twenty years is $8.51356. The present value of $1 at an 8 percent interest rate in twenty years is $0.21455. The present value of an ordinary annuity of $1 at an 8 percent interest rate over twenty years is $9.81815.
- As a result of the 2 percent reduction in the annual effective interest for this bond, what is the decrease in the amount of interest expense that Pulaski recognizes in Year One?
- As a result of the 2 percent reduction in the annual effective interest for this bond, what is the decrease in the amount of interest expense that Pulaski recognizes in Year Two?
Comprehensive Problem
This problem will carry through several chapters, building in difficulty. It allows students to continually practice skills and knowledge learned in previous chapters.
In Chapter 13 "In a Set of Financial Statements, What Information Is Conveyed about Current and Contingent Liabilities?", financial statements for January were prepared for Webworks. They are included here as a starting point for the required recording for February.
Figure 14.29 Webworks Financial Statements
Figure 14.30

Figure 14.31
The following events occur during February:
- Webworks starts and completes nine more sites and bills clients for $5,400.
- Webworks purchases supplies worth $150 on account.
- At the beginning of February, Webworks had nineteen keyboards costing $117 each and ten flash drives costing $20 each. Webworks uses periodic FIFO to cost its inventory.
- On account, Webworks purchases seventy keyboards for $118 each and one hundred of the new flash drives for $22 each.
- On February 1, Webworks borrows $3,000 from Local Area Bank. The loan plus accrued interest will be repaid at the end of two years. The interest rate is 6 percent.
- Webworks purchases new computer equipment for use in designing Web sites. The equipment costs $5,500 and was paid for in cash.
- Webworks pays Nancy Po (company employee) $800 for her work during the first three weeks of February.
- Webworks sells seventy keyboards for $11,250 and ninety of the new flash drives for $2,700 cash.
- Webworks collects $5,200 in accounts receivable.
- Webworks purchases one hundred shares of RST Company for $18 per share in cash. This is considered a trading security.
- Webworks pays off its salaries payable from January.
- Webworks is hired to design Web sites for a local photographer and bakery. It is paid $600 in advance.
- Webworks pays off $11,300 of its accounts payable.
- Webworks pays Leon Jackson (company owner) a salary of $2,000.
- Webworks completes the salon Web site and earns the $450 paid in January.
- RST Company pays Webworks a dividend of $25.
-
Webworks pays taxes of $1,558 in cash.
Required:
- Prepare journal entries for the previous events.
- Post the journal entries to T-accounts.
- Prepare an unadjusted trial balance for Webworks for February.
- Prepare adjusting entries for the following and post them to your T-accounts.
- Webworks owes Nancy Po $220 for her work during the last week of February.
- Leon’s parents let him know that Webworks owes $300 toward the electricity bill. Webworks will pay them in March.
- Webworks determines that it has $70 worth of supplies remaining at the end of January.
- Prepaid rent should be adjusted for February’s portion.
- Prepaid advertising should be adjusted for February’s portion.
- Webworks is continuing to accrue bad debts at 10 percent of accounts receivable.
- Webworks continues to depreciate its equipment over four years and its furniture over five years, using the straight-line method. The new equipment will also be depreciated over five years using the straight-line method.
- The license agreement should be amortized over its one-year life.
- QRS Company is selling for $12 per share and RST is selling for $16 per share on February 28.
- Interest should be accrued for February.
-
Record cost of goods sold.
- Prepare an adjusted trial balance.
- Prepare financial statements for February.
Research Assignment
Assume that you take a job as a summer employee for an investment advisory service. One of the partners for that firm is currently looking at the possibility of investing in Marriott International. The partner is aware that Marriott builds a lot of hotels and, therefore, probably has to borrow a significant amount of money. The partner is curious as to the cost of the interest on the money that Marriott borrows. The partner asks you to look at the 2010 financial statements for Marriott by following this path:
- Go to http://www.marriott.com.
- At the bottom of this screen, click on “About Marriott.”
- At the top of the next screen, on the right, click on “Investors.”
- On the next screen, on the right side, click on “2010 Annual Report” to download.
- On the next screen, click on “Financials” at the top right side.
- On the next screen, click on “Financial Statements” on the left side.
- The company’s income statement should appear. Review the contents of that statement.
- Click the number 2 at the top of the screen to see the balance sheet. Review the contents of that statement.
- On the left side of the screen, click on “Notes to Financial Statements.”
- Go to note 13 “Long-term debt.” A schedule of the company’s senior notes can be found in that note.
- What was the amount of interest expense the company recognized on its 2010 income statement? How did that number compare with the interest expense recognized in 2009?
- What was the amount of long-term debt reported by the company on its balance sheet at the end of 2010? How did that number compare with the long-term debt at the end of 2009?
- According to the information in note 13, what was the stated cash interest rate for the various senior notes that the company has outstanding? What was the effective interest rate on each of these senior notes?




