This is “Pricing and Reporting Term Bonds”, section 14.4 from the book Business Accounting (v. 2.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
14.4 Pricing and Reporting Term Bonds
Learning Objectives
At the end of this section, students should be able to meet the following objectives:
- Understand the difference between a stated cash interest rate in a debt contract and an effective interest rate negotiated by the debtor and creditor.
- Compute the price of a term bond when the stated cash interest rate is different from the effective interest rate.
- Determine the amount of interest to be compounded each period when the stated cash interest rate specified on a bond contract is different from the effective interest rate established by the parties.
- Prepare all journal entries for a term bond when the stated cash interest rate is different from the effective interest rate.
Determining the Price of a Term Bond
Question: Although zero-coupon bonds are popular, most bonds actually do pay a stated rate of cash interest, one that is specified in the contract. If the buyer and seller negotiate an effective rate of interest that is the same as this stated rate, an amount equal to face value is paid for the bond. For example, if the stated interest is 7 percent per year and a negotiated annual rate of 7 percent is accepted by the parties, the bond is issued at its face value. No discount or premium results; the debtor and creditor are both satisfied with the interest being paid. The effective rate method is not needed because the cash interest and the effective interest are the same—7 percent is paid each period and recognized as interest.
However, the negotiated rate often differs from the cash rate stated in the bond contract. Market interest rate conditions change quickly. The interest that creditors demand will often shift between the printing of the indenture and the actual issuance day. Or the financial reputation of the company might move up or down during this time. Information travels so quickly in this technology age that news about companies—both good and bad—spreads rapidly.
To illustrate, assume that Smith Corporation decides to issue $1 million in term bonds to the public on January 1, Year One. The face value of these bonds comes due in four years. During the interim, annual interest at a stated rate of 5 percent will be paid starting on December 31, Year One.
No investors can be found who want to purchase Smith Corporation bonds with only a 5 percent annual return. Therefore, in setting an issuance price, annual interest of 6 percent is negotiated. Possibly, interest offered by other similar companies is 6 percent so that Smith had to match this rate to entice investors to buy its bonds. Or some recent event has made Smith seem slightly more risky causing potential creditors to demand a higher rate of return. A list of market conditions that can impact the price of a bond would be almost unlimited. How is the price of a bond calculated when the stated cash interest rate differs from the effective rate negotiated by the two parties involved?
Answer: The pricing of a bond always begins by identifying the cash flows specified by the contract. These amounts are set and will not be affected by the eventual sales price. The debtor is legally obligated to make these payments regardless of whether the bond is sold for $1 or $10 million.
Here, Smith Corporation must pay $50,000 per year in interest ($1 million × 5 percent) for four years and then the $1 million face value:
| Future Cash Flows Set by Bond Contract |
|---|
| $50,000 annually for four years (5 percent stated rate) |
| $1,000,000 in four years (face value of term bond) |
After the cash flows are identified, the present value of each is calculated based on the negotiated yield rate. These two present values are then summed to arrive at the price to be paid for the bond. The $50,000 annual interest payments form an annuity—equal amounts are paid at equal time intervals. Because interest is paid at the end of each period starting on December 31, Year One, these payments constitute an ordinary annuity.As mentioned in earlier discussions about the acquisition of intangible assets, an annuity with payments made at the beginning of each period is known as an annuity due. If the interest had been paid starting on January 1, Year One, the payments here would form an annuity due rather than an ordinary annuity. The cash flow pattern for notes and bonds is more likely to be in the form of an ordinary annuity since interest is not typically paid in advance.
As determined by table, formula, or Excel spreadsheet, the present value of an ordinary annuity of $1 at an effective annual interest rate of 6 percent over four years is $3.46511.The mathematical formula to determine the present value of an ordinary annuity of $1 is (1 – 1/[1 + i]n)/i, where i is the appropriate interest rate (6 percent in this illustration) and n is the number of payment periods (four). If using an Excel spreadsheet, the present value of a $1 per period ordinary annuity for four periods at an annual rate of interest of 6 percent can be found by typing the following data into a cell: =PV(.06,4,1,,0). Thus, the present value of the four interest payments is $50,000 times $3.46511 or $173,256 (rounded). Note that the present value computation requires the multiplication of one annuity payment ($50,000) rather than the total amount of all interest payments ($200,000).
Present Value of an Ordinary Annuity of $1
http://www.principlesofaccounting.com/ART/fv.pv.tables/pvofordinaryannuity.htm
The second part of the cash flows promised by this bond is a single payment of $1 million in four years. The present value of a payment of $1 in four years at a 6 percent annual rate is $0.79209 so the present value of the entire $1 million is $792,090.
Present Value of $1
http://www.principlesofaccounting.com/ART/fv.pv.tables/pvof1.htm
Based on an annual interest rate of 6 percent for four years, the present value of the cash flows required by this term bond contract is $173,256 (cash interest) plus $792,090 (face value) or a total of $965,346. Smith receives this amount on January 1, Year One, but must pay back $50,000 per year for four years followed by a single payment of $1 million. Mathematically, that is equivalent to a 6 percent rate of interest each year for four years. The journal entry to record the issuance is shown in Figure 14.12 "January 1, Year One—Term Bonds Issued at an Effective Rate of 6 Percent".
Figure 14.12 January 1, Year One—Term Bonds Issued at an Effective Rate of 6 Percent

Test Yourself
Question:
The Venture Company issues a twenty-year bond with a face value of $500,000 on January 1, Year One. According to the bond contract, cash interest at a stated rate of 2 percent will be paid each year beginning on December 31, Year One. The Manhattan Investment Company wants to buy this bond but demands an effective annual interest rate of 9 percent. After some discussion, both parties agree that the bond will be sold to earn an annual interest rate of 8 percent. The present value of $1 in twenty years at a rate of 8 percent is $0.21455. The present value of an ordinary annuity of $1 per year for twenty years at a rate of 8 percent per year is $9.81815. The present value of an annuity due of $1 per year for twenty years at a rate of 8 percent per year is $10.60360. How much does Manhattan Investment Company pay the Venture Company for this bond (rounded)?
- $205,457
- $209,145
- $213,311
- $217,445
Answer:
The correct answer is choice a: $205,457.
Explanation:
Cash interest of $10,000 is paid annually for twenty years ($500,000 × 2 percent). This is an ordinary annuity, since payments are made at each year’s end. A single payment of $500,000 is also due in twenty years. Present value of the interest is $10,000 times $9.81815, or $98,182. Present value of the face value is $500,000 times $0.21455, or $107,275. Total present value is $205,457. That amount is offered by the creditor and accepted by the debtor because it equals 8 percent per year.
Calculating Interest When a Term Bond Is Issued at a Discount
Question: After the previously described term bond was issued at a discount, the debtor has the same two accounting problems that were discussed previously for zero-coupon bonds.
- First, the recorded principal must be raised gradually over four years from $965,346 (as shown in Figure 14.12 "January 1, Year One—Term Bonds Issued at an Effective Rate of 6 Percent") to the $1 million face value.
- Second, the cash interest of 5 percent paid each year has to be adjusted to the annual 6 percent effective rate negotiated by the two parties.
How does a debtor report a bond payable over its life if the stated cash interest rate and the effective rate differ?
Answer: At the end of Year One, Smith Corporation pays $50,000 cash interest to the bondholders as specified in the contract ($1 million face value × 5 percent annual stated rate). However, interest expense must be reported on the income statement based on the agreed upon rate of 6 percent. That was the negotiated rate that led to the initial payment of $965,346. This discounted price was accepted by Smith (the debtor) as a means of increasing the actual rate of return from 5 percent per year to 6 percent.
The effective rate is reflected in the financial statements by recognizing interest in Year One of $57,921 (rounded), which is the $965,346 principal balance times 6 percent. The $7,921 difference between the effective interest expense of $57,921 and the cash interest payment of $50,000 will eventually be paid at the end of the four-year term when $1 million rather than $965,346 is conveyed to the bondholders. Therefore, at the current time, this extra $7,921 is compounded (increasing the liability balance). Note that only the portion of this interest that is not paid is added to the principal. Earlier, with the zero-coupon bond, the entire amount of interest each year was compounded, but that was because no cash interest payment was made.
The cash interest payment is recorded in Figure 14.13 "December 31, Year One—Payment of Cash Interest at 5 Percent Rate" with the compounding entry shown in Figure 14.14 "December 31, Year One—Compounding Entry to Adjust Interest to Effective Annual Rate of 6 Percent". These two entries can be recorded separately or combined.
Figure 14.13 December 31, Year One—Payment of Cash Interest at 5 Percent Rate

Figure 14.14 December 31, Year One—Compounding Entry to Adjust Interest to Effective Annual Rate of 6 Percent

The interest expense reported on the income statement for Year One of $57,921 ($50,000 + $7,921) equals the 6 percent effective rate times the principal of the debt for that period. The liability on the balance sheet at the end of Year One has begun to move closer to the $1 million face value. The reported figure is now $973,267 ($965,346 + $7,921) as a result of the compounding.
As shown in Figure 14.15 "Reported Bond Figures for Remaining Three Years until Maturity", reported figures for the remaining three years of this bond contract can be calculated to verify that the ending balance does grow to $1 million by the time of payment.
Figure 14.15 Reported Bond Figures for Remaining Three Years until MaturityInterest expense for the final year has been increased by $3 so that the final bond payable balance is exactly equal to the $1 million debt that must be paid. Slight adjustments of this type are common to compensate for numbers having been rounded.
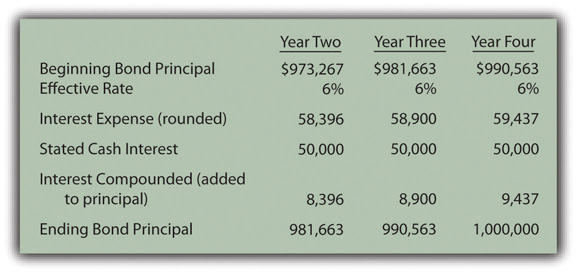
Through the use of the effective rate method, interest expense of 6 percent is recognized each period and the principal balance reported for the liability does gradually grow to equal the face value of the bond on the maturity date.
Test Yourself
Question:
On June 30, Year One, a company issues ten-year term bonds with a total face value of $600,000. Only interest at a 4 percent annual rate is paid each June 30 and December 31 beginning at the end of Year One. These bonds were issued for $375,680 to earn a negotiated rate of 10 percent per year over the ten-year term. What does the company report on its December 31, Year One, balance sheet for this liability?
- $380,775
- $381,225
- $382,464
- $383,646
Answer:
The correct answer is choice c: $382,464.
Explanation:
After six months, the company pays interest to the creditors of $12,000 ($600,000 × 4% × 1/2 year). Interest for the same period—based on an annual yield rate of 10 percent—is $18,784 ($375,680 × 10% × 1/2). The extra interest recognized over the amount paid ($6,784 or $18,784 less $12,000) is compounded to begin moving the principal to the $600,000 face value. At the end of Year One, the bond payable has been raised to $382,464, the original principal of $375,680 plus the compound interest of $6,784.
Key Takeaway
The stated cash interest rate for a term bond is often different from the effective interest rate negotiated between the creditor and the debtor. To compute the amount of money to be exchanged for the bond, the cash flows are determined based on the terms of the contract. The present value of these payments is then calculated. The resulting total is the amount initially paid so that the agreed upon rate of interest is earned over the life of the bond. Cash interest payments are conveyed thereafter with the interest balance adjusted each period based on the effective rate. The interest rate stated in the contract times the face value provides the amount of each cash payment. The principal of the debt times the effective rate gives the interest expense to be recognized for the period. The difference in the effective interest and the cash payment is compounded (added to the principal of the debt). On the maturity date, the liability balance should be equal to the face value of the debt instrument.




