Purchases Made with Future Cash Payments

Question: A company buys a patent from an inventor on January 1, Year One, for $1 million to be paid immediately. The accounting here is straightforward; the patent is recognized as an intangible asset and reported at the historical cost of $1 million. Accounting rules are clear on the handling of such acquisitions.

Assume, instead, that the company offers to pay this $1 million but not until five years have passed. The seller agrees to that proposal. The purchase is made now, but payment is delayed. Is the $1 million still being paid solely for the patent? Does the entire $1 million reflect the historical cost of this intangible? What reporting is appropriate if an asset such as a patent, building, or land is bought but payment will not take place for several years? In such cases, how is historical cost determined?

 

Answer: More than forty years ago, the accounting body that was viewed as authoritative at the time ruled that when cash is paid for a purchaseSimilar rules apply when an asset is sold and the money is to be collected over a period of future years. For convenience, the illustrations in this chapter will focus solely on cash payments made in an acquisition. over an extended period of time, two distinct reasons for the payments always exist.The Accounting Principles Board (APB) was the primary group in charge of creating U.S. GAAP from 1962 until 1973 when it was replaced by the Financial Accounting Standards Board (FASB). During those years, the APB produced thirty-one opinions. Its Opinion 21, “Interest of Receivables and Payables” was issued in August 1971 and established the rules described here. Within the new Accounting Standards Codification, information on the reporting of interest can be found at FASB ASC 835-30.

• The first is obviously the acquisition of the property such as the patent in this example.
• The second is interestThe charge for using money over time, often associated with long-term loans; even if not specifically mentioned in the debt agreement, financial accounting rules require it to be computed and reported based on a reasonable rate.. Interest is the charge for the use of money over time.

This rule assumes that no reasonable seller would allow cash payments to be spread over several years without some interest charge being factored into the negotiated amounts. In other words, interest (the charge for the use of the money over time) is included whether it can be seen or not. The accounting demonstrated here is the result of that assertion.

In many purchases where payments are made over time, interest payments are explicitly included. For example, the contract to buy this patent could have required payment of the $1 million after five years plus interest at a 7 percent rate to be paid each year. With those terms, the accounting process is not complicated. The $1 million is the historical cost of the patent while the annual $70,000 payments ($1 million × 7 percent) are recorded each year by the buyer as interest expense. The two amounts are clearly differentiated based on the terms of the agreement.

A theoretical problem arises if interest is not identified in the contract. In the current illustration, assume that the company agrees to make a single $1 million payment in five years with no mention of interest. According to U.S. GAAP, interest is still present and must be recognized because the conveyance of cash has been delayed. This means that only part of the $1 million is actually paid for the patent with the rest serving as interest. Authoritative accounting rules hold that an interest charge is always present when payment is put off into the future. Payment has been deferred for five years; some part of that amount serves to compensate the seller for having to wait to receive the money.

However, the specific allocation of the $1 million between patent and interest is not readily apparent. To calculate the interest included within the price, an introduction to present valueThe amount associated with cash flows after all future interest—computed at a reasonable rate—has been mathematically removed; this figure is the principal of those future cash flows. computations is necessary.

In simple terms, the present value of future cash flows is the amount left after all future interest is removed (hence the term “present value”). The present value is the portion within the $1 million that is being paid for the patent. The remainder will be recognized as interest expense over the five-year period until payment is made.

To determine the present value of future cash flows, a reasonable interest rate is needed. Then, the amount of interest for these five years can be mathematically calculated and removed. An appropriate interest rate is often viewed as the one the buyer would be charged if the money were borrowed from a local bank.

Assume here that 10 percent is a reasonable annual interest rate. Fortunately, present value conversion factors have already been mechanically computed. They can serve to remove the future amount of interest so that only the present value (the amount paid for the patent) is left. The formula to determine the present value of $1 at a designated point in the future is $1 divided by (1 + i) raised to the n^th power with “n” being the number of periods and “i” the appropriate interest rate. In this case, because payment is due in five years, the present value $1 is $1/(1.10)⁵, or 0.62092. This factor can then be multiplied by the actual cash payment to determine its present value.

In an Excel spreadsheet, the present value of $1 at 10 percent for five years is derived by entering the following formula into one of the cells: =PV(.10,5,0,1). Thus, the present value of $1,000,000 is found in Excel by entering =PV(.10,5,0,1000000).

Regardless of the method being applied, if $1 is paid in five years for an asset and a reasonable rate of interest is 10 percent per year, then the $0.62 (rounded) present value is the portion being paid for the asset with the remaining $0.38 representing interest for those years. The present value computation mathematically determines the interest and then removes it to leave the cost of the asset.

Predetermined present value tables are available as well as calculators and computer spreadsheets that make this computation relatively easy. Present value tables can be found at the end of this book as well as through Internet links provided at appropriate spots throughout the chapters.

On a table created to provide the present value of a single amount of $1, the factor is found by looking under the specific interest rate column (10 percent) at the line for the number of applicable time periods (five).

The present value today of paying $1 million in five years assuming a 10 percent annual interest rate is $1 million times 0.62092 or $620,920. This is the cost before any future interest is accrued over time. Mathematically, the interest for these five years has been computed and removed to arrive at this figure. The remainder of the payment ($379,080) will be reported as interest expense by the buyer over the subsequent five years using a 10 percent annual rate. The total ($620,920 for the patent plus $379,080 in interest) equals the $1 million payment.

The journal entries for Year One are shown in Figure 11.5 "Present Value—Acquisition of Patent with Future Payment of Cash and Recognition of Year One Interest". On January 1, the patent and the liability are reported at present value. No time has passed so no interest is recognized. However, at the end of that first year, interest expense of $62,092 should be reported. That amount is 10 percent of the liability’s principal balance for that year ($620,920).The effective rate method of computing interest is demonstrated here. The principal balance is multiplied by the reasonable interest rate to get the amount of interest to be recorded each period. The effective rate method is the preferred approach according to U.S. GAAP. In Chapter 14 "In a Set of Financial Statements, What Information Is Conveyed about Noncurrent Liabilities Such as Bonds?", an alternative method known as the straight-line method is also demonstrated. It is also allowed by U.S. GAAP if the differences are not viewed as material.

Notice in the December 31 entry that no interest is paid on that date. Payment of this additional charge actually occurs in five years when $1 million is paid and not just $620,920. Because interest was recognized in Year One but not paid, the amount of the liability (the principal) has grown. Increasing a debt to reflect the accrual of interest is referred to as “compounding.” Whenever interest is recognized but not paid, it is compounded which means that it is added to the principal of the liability.

In the second year, the expense to be recognized is higher because the principal has increased from $620,920 to $683,012 ($620,920 plus $62,092) as a result of compounding the Year One interest. The ongoing compounding raises the principal each year so that the interest expense also increases as can be seen in the series of entries in Figure 11.6 "Present Value—Recognition and Compounding of Interest".

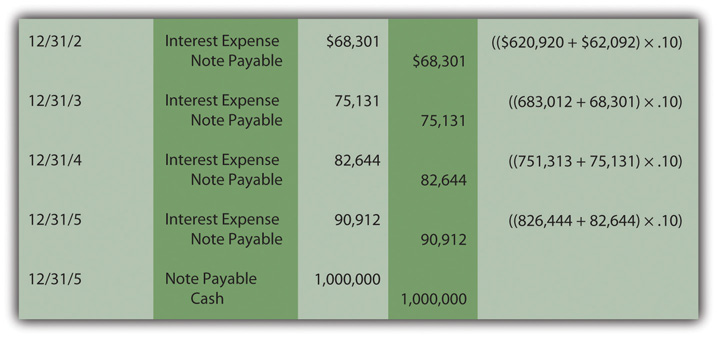
These journal entries show that three goals are achieved by this reporting process.

• The patent is recorded at its historical cost of $620,920, the total amount to be paid less a reasonable interest rate for the five year delay until payment is made.
• The compounding process adds the interest back into the liability that was removed in determining the present value so that the reported balance returns to $1 million as of the due date.
• Interest expense of $379,080 is recognized over the five-year period ($62,092 + $68,301 + $75,131 + $82,644 + $90,912). Although interest was not mentioned in the contract, U.S. GAAP requires it to be computed and reported over these five years.

The Present Value of Cash Flows Paid as an Annuity

Question: Does the application of present value change substantially if cash is paid each year rather than as a lump sum at the end of the term? What reporting is appropriate if an intangible asset is purchased by making a down payment today followed by a series of equal payments in the future?

To illustrate, assume a company acquires a copyright from an artist by paying $10,000 on January 1, Year One, and agreeing to pay an additional $10,000 at the beginning of each subsequent year until January 1, Year Five. The total cash amount is $50,000. As with the previous example, no separate interest is paid so that a present value computation is required. What is the historical cost to be reported for this intangible asset and what interest should be recorded on the liability over these future years?

 

Answer: Cash is conveyed over an extended period of time in this purchase. However, a reasonable rate of interest is not being explicitly paid to compensate for the delay in payments. Once again, accounting believes that interest exists within the cash amounts. A present value computation is necessary to pull out the appropriate amount of interest and leave just the cost of the newly acquired asset. As before, the present value of the payments is the cash paid after all future interest is mathematically removed. The idea behind the process has not changed. Here, though, cash is not conveyed as a single amount but rather as an annuityA series of equal payments made at equal time intervals.—an equal amount paid at equal time intervals. An annuity can be either of the following:

• An ordinary annuityAn annuity with payments made at the end of each period; it is also referred to as an annuity in arrears. with payments made at the end of each period
• An annuity dueAn annuity with payments made at the beginning of each period; it is also referred to as an annuity in advance. with payments starting immediately at the beginning of each period

The specific series of payments in this question is an annuity due pattern because the first $10,000 is conveyed immediately when the contract is signed. As before, the applicable present value factor to remove the interest can be determined by a calculatorThe mathematical formula to determine the present value of an annuity due of $1 per period is present value of an annuity due = [(1 - 1/[1 + i]ⁿ)/i] × (1 + i), where i is the appropriate interest rate and n is the number of payment periods.The mathematical formula to determine the present value of an ordinary annuity of $1 per period is present value of an ordinary annuity = (1 - 1/[1 + i]ⁿ)/i, where i is the appropriate interest rate and n is the number of payment periods. or computer spreadsheet.On an Excel spreadsheet, the present value of a $1 per year annuity due for five periods at a reasonable rate of 12 percent is computed by typing the following data into a cell: =PV(.12,5,1,,1). Therefore, the present value of seven annual payments of $25,000 made as annuity due with a reasonable interest rate of 9 percent would be found by entering =PV(.09,7,25000,,1)If this had been an ordinary annuity because the initial payment was delayed until the end of the first period, present value of that $1 per year ordinary annuity is =PV(.12,5,1,,0). The present value of seven annual payments of $25,000 made as an ordinary annuity with a reasonable interest rate of 9 percent would be found by entering =PV(.09,7,25000,,0) Tables are also available at the end of this book or through the following Internet link.

Regardless of the approach applied, if a reasonable rate is assumed to be 12 percent per year, the present value of a $1 per year annuity due for five periods is 4.0374. Thus, the present value of paying $10,000 annually for five years beginning immediately is $10,000 times 4.0374 or $40,374. For annuities, the computation is constructed so that a single payment ($10,000) is multiplied rather than the total cash amount ($50,000).

Of the total cash to be paid, $40,374 (the present value) is the cost of the copyright with the remaining $9,626 ($50,000 total less $40,374) representing the interest expense over this period. The initial journal entry to record this acquisition is shown in Figure 11.7 "Acquisition of Intangible Asset—Present Value of an Annuity Due". No interest is reported because no time has yet passed.

At the end of the first year, amortization of the cost of the copyright must be recognized along with interest expense on the liability. Assuming a life of ten years and no residual value, annual amortization is $40,374 divided by ten years, or $4,037. Interest for the period is the $30,374 principal of the liability times the 12 percent reasonable rate, or $3,645 (rounded). Because no interest is explicitly paid in this contract, all of this interest is compounded (added to the liability). The year-end adjusting entries are shown in Figure 11.8 "Intangible Asset—Recognition of Interest and Amortization for Year One".

The second scheduled payment is made on January 1, Year Two, and reduces the amount of the liability.

At the end of Year Two, both amortization of the asset’s cost and interest expense on the liability must be recognized again to reflect the passage of another period. The amortization figure remains the same (assuming application of the straight-line method) but interest must be recomputed. The principal of the liability was $30,374 for the first year, but interest of $3,645 was then compounded at the end of that period followed by another $10,000 payment. As shown in Figure 11.10 "Computation of Liability Principal Throughout Year Two", these changes result in a liability principal throughout Year Two of $24,019.

Thus, during the second year, the principal amount of the liability is $24,019 and the interest, at the reasonable rate of 12 percent, is $2,882 (rounded).

This pattern of entries will continue until the liability has been extinguished and the capitalized cost of the asset amortized to expense.