This is “The Sampling Distribution of the Sample Mean”, section 6.2 from the book Beginning Statistics (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
6.2 The Sampling Distribution of the Sample Mean
Learning Objectives
- To learn what the sampling distribution of is when the sample size is large.
- To learn what the sampling distribution of is when the population is normal.
The Central Limit Theorem
In Note 6.5 "Example 1" in Section 6.1 "The Mean and Standard Deviation of the Sample Mean" we constructed the probability distribution of the sample mean for samples of size two drawn from the population of four rowers. The probability distribution is:
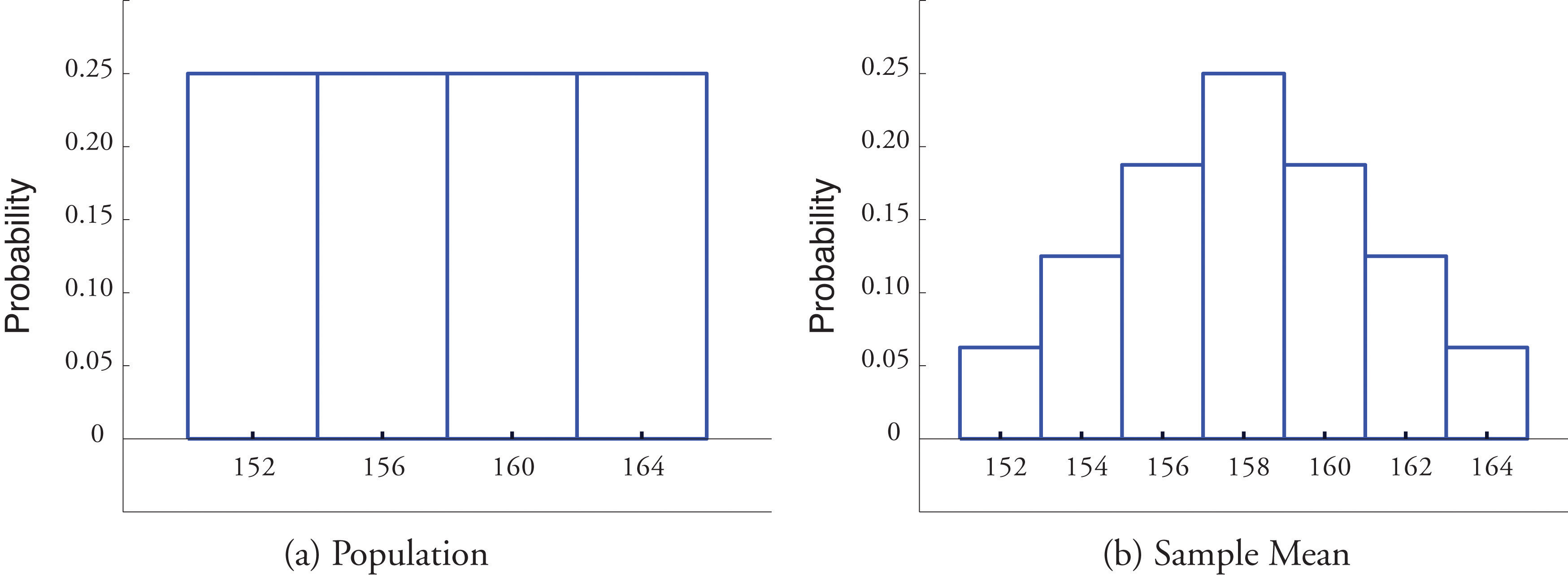
Figure 6.1 "Distribution of a Population and a Sample Mean" shows a side-by-side comparison of a histogram for the original population and a histogram for this distribution. Whereas the distribution of the population is uniform, the sampling distribution of the mean has a shape approaching the shape of the familiar bell curve. This phenomenon of the sampling distribution of the mean taking on a bell shape even though the population distribution is not bell-shaped happens in general. Here is a somewhat more realistic example.
Figure 6.1 Distribution of a Population and a Sample Mean
Suppose we take samples of size 1, 5, 10, or 20 from a population that consists entirely of the numbers 0 and 1, half the population 0, half 1, so that the population mean is 0.5. The sampling distributions are:
n = 1:
n = 5:
n = 10:
n = 20:
Histograms illustrating these distributions are shown in Figure 6.2 "Distributions of the Sample Mean".
Figure 6.2 Distributions of the Sample Mean
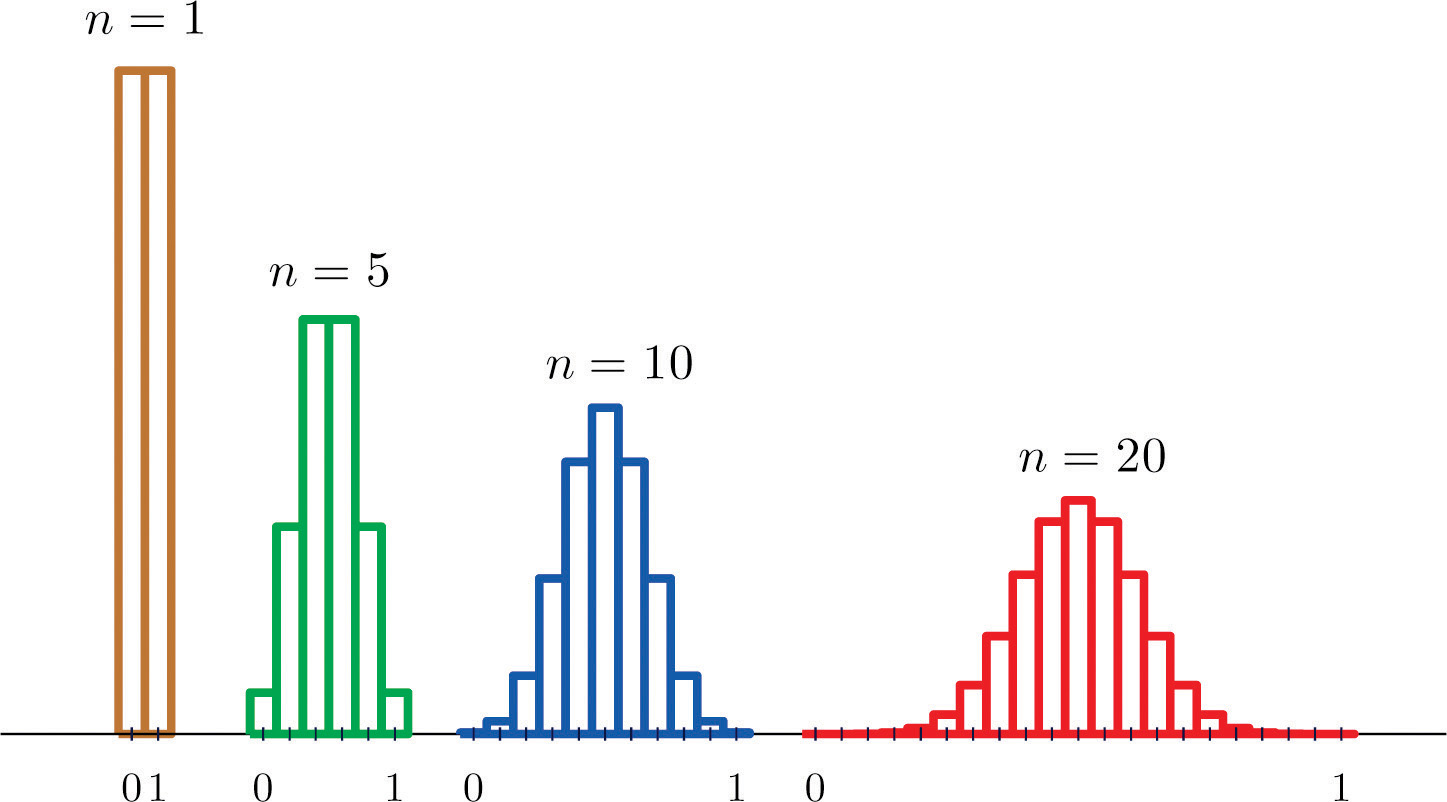
As n increases the sampling distribution of evolves in an interesting way: the probabilities on the lower and the upper ends shrink and the probabilities in the middle become larger in relation to them. If we were to continue to increase n then the shape of the sampling distribution would become smoother and more bell-shaped.
What we are seeing in these examples does not depend on the particular population distributions involved. In general, one may start with any distribution and the sampling distribution of the sample mean will increasingly resemble the bell-shaped normal curve as the sample size increases. This is the content of the Central Limit Theorem.
The Central Limit Theorem
For samples of size 30 or more, the sample mean is approximately normally distributed, with mean and standard deviation , where n is the sample size. The larger the sample size, the better the approximation.
The Central Limit Theorem is illustrated for several common population distributions in Figure 6.3 "Distribution of Populations and Sample Means".
Figure 6.3 Distribution of Populations and Sample Means
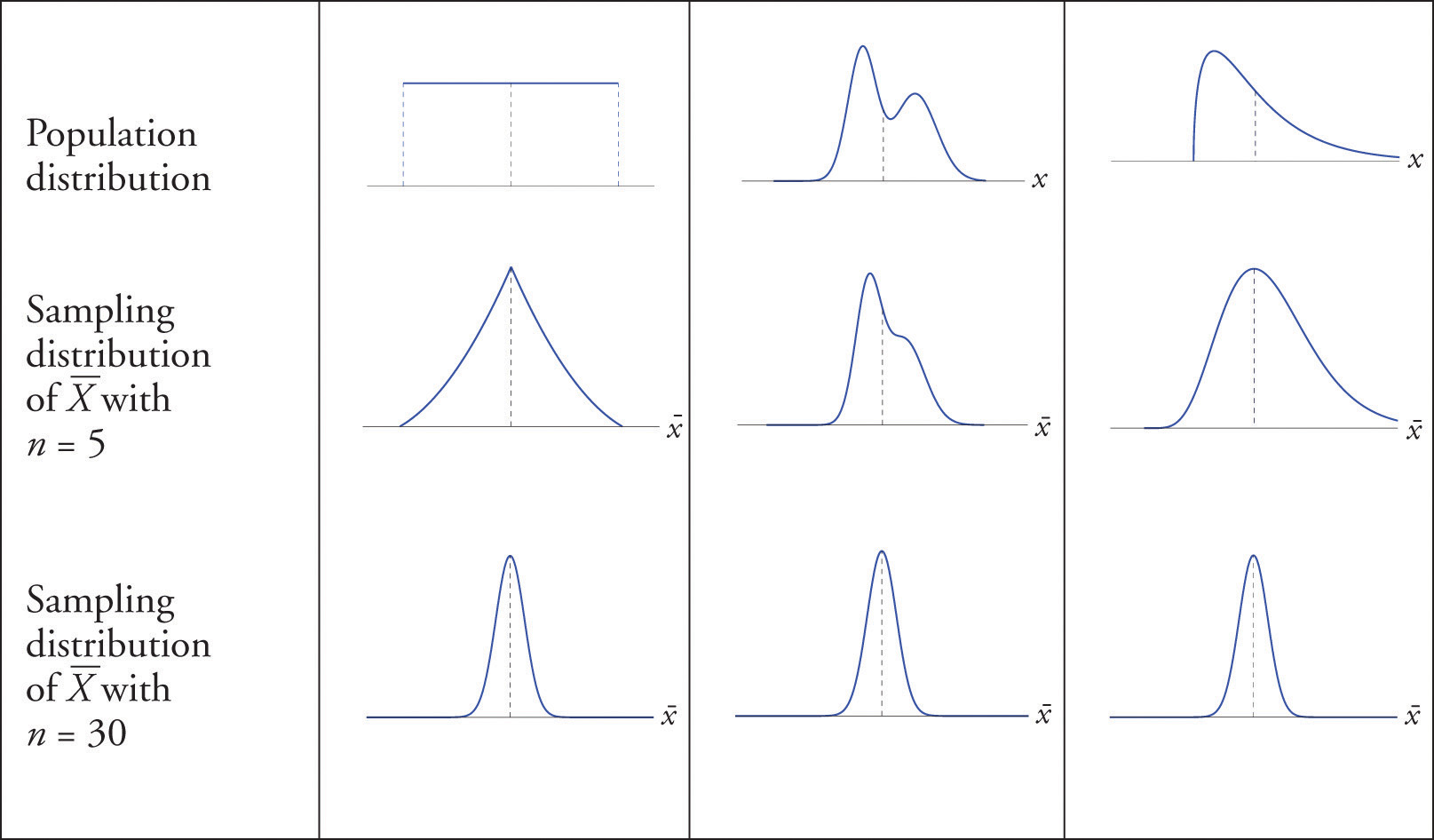
The dashed vertical lines in the figures locate the population mean. Regardless of the distribution of the population, as the sample size is increased the shape of the sampling distribution of the sample mean becomes increasingly bell-shaped, centered on the population mean. Typically by the time the sample size is 30 the distribution of the sample mean is practically the same as a normal distribution.
The importance of the Central Limit Theorem is that it allows us to make probability statements about the sample mean, specifically in relation to its value in comparison to the population mean, as we will see in the examples. But to use the result properly we must first realize that there are two separate random variables (and therefore two probability distributions) at play:
- X, the measurement of a single element selected at random from the population; the distribution of X is the distribution of the population, with mean the population mean μ and standard deviation the population standard deviation σ;
- , the mean of the measurements in a sample of size n; the distribution of is its sampling distribution, with mean and standard deviation
Example 3
Let be the mean of a random sample of size 50 drawn from a population with mean 112 and standard deviation 40.
- Find the mean and standard deviation of
- Find the probability that assumes a value between 110 and 114.
- Find the probability that assumes a value greater than 113.
Solution
-
By the formulas in the previous section
-
Since the sample size is at least 30, the Central Limit Theorem applies: is approximately normally distributed. We compute probabilities using Figure 12.2 "Cumulative Normal Probability" in the usual way, just being careful to use and not σ when we standardize:
-
Similarly
Note that if in Note 6.11 "Example 3" we had been asked to compute the probability that the value of a single randomly selected element of the population exceeds 113, that is, to compute the number P(X > 113), we would not have been able to do so, since we do not know the distribution of X, but only that its mean is 112 and its standard deviation is 40. By contrast we could compute even without complete knowledge of the distribution of X because the Central Limit Theorem guarantees that is approximately normal.
Example 4
The numerical population of grade point averages at a college has mean 2.61 and standard deviation 0.5. If a random sample of size 100 is taken from the population, what is the probability that the sample mean will be between 2.51 and 2.71?
Solution
The sample mean has mean and standard deviation , so
Normally Distributed Populations
The Central Limit Theorem says that no matter what the distribution of the population is, as long as the sample is “large,” meaning of size 30 or more, the sample mean is approximately normally distributed. If the population is normal to begin with then the sample mean also has a normal distribution, regardless of the sample size.
For samples of any size drawn from a normally distributed population, the sample mean is normally distributed, with mean and standard deviation , where n is the sample size.
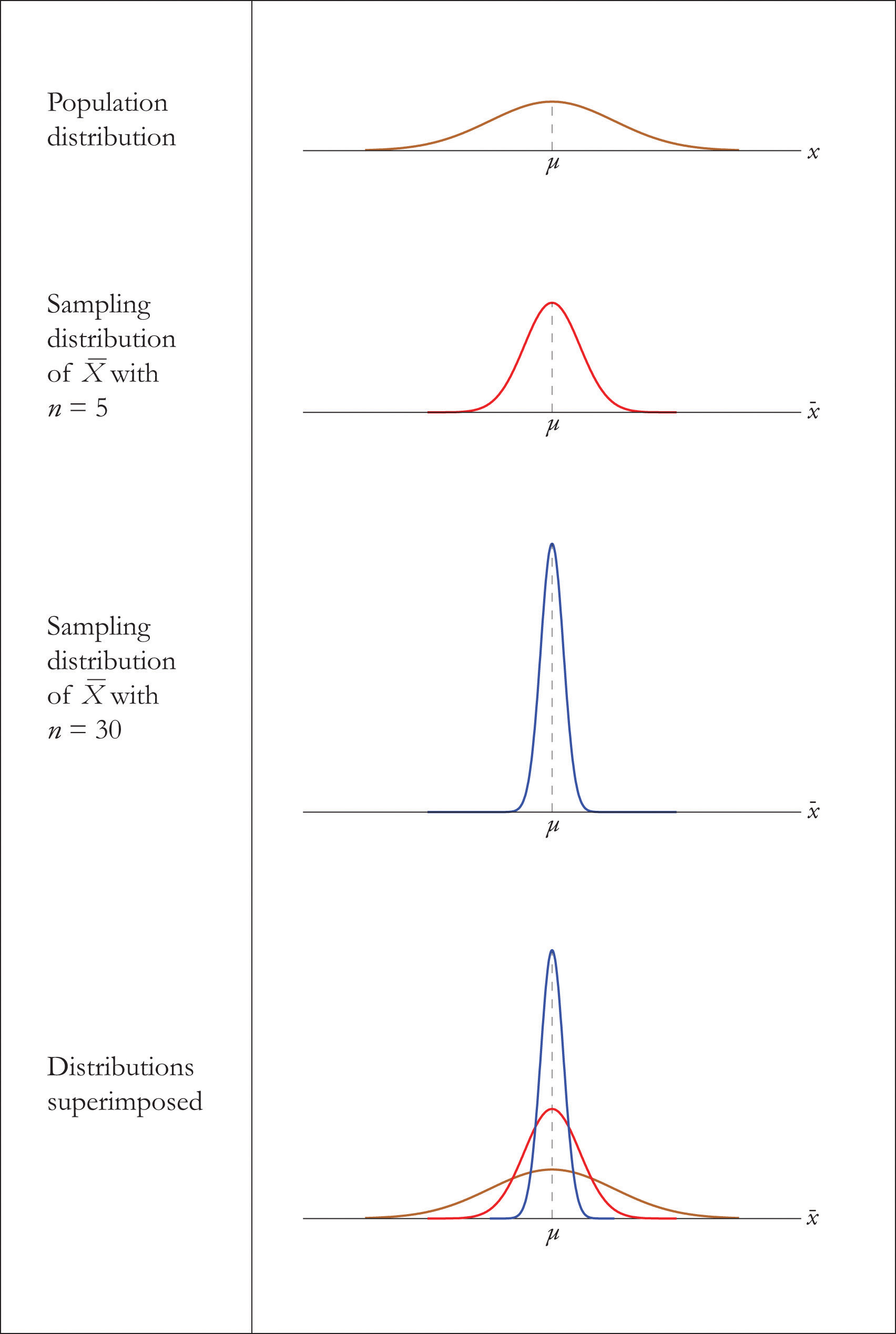
The effect of increasing the sample size is shown in Figure 6.4 "Distribution of Sample Means for a Normal Population".
Figure 6.4 Distribution of Sample Means for a Normal Population
Example 5
A prototype automotive tire has a design life of 38,500 miles with a standard deviation of 2,500 miles. Five such tires are manufactured and tested. On the assumption that the actual population mean is 38,500 miles and the actual population standard deviation is 2,500 miles, find the probability that the sample mean will be less than 36,000 miles. Assume that the distribution of lifetimes of such tires is normal.
Solution
For simplicity we use units of thousands of miles. Then the sample mean has mean and standard deviation Since the population is normally distributed, so is , hence
That is, if the tires perform as designed, there is only about a 1.25% chance that the average of a sample of this size would be so low.
Example 6
An automobile battery manufacturer claims that its midgrade battery has a mean life of 50 months with a standard deviation of 6 months. Suppose the distribution of battery lives of this particular brand is approximately normal.
- On the assumption that the manufacturer’s claims are true, find the probability that a randomly selected battery of this type will last less than 48 months.
- On the same assumption, find the probability that the mean of a random sample of 36 such batteries will be less than 48 months.
Solution
-
Since the population is known to have a normal distribution
-
The sample mean has mean and standard deviation Thus
Key Takeaways
- When the sample size is at least 30 the sample mean is normally distributed.
- When the population is normal the sample mean is normally distributed regardless of the sample size.
Exercises
-
A population has mean 128 and standard deviation 22.
- Find the mean and standard deviation of for samples of size 36.
- Find the probability that the mean of a sample of size 36 will be within 10 units of the population mean, that is, between 118 and 138.
-
A population has mean 1,542 and standard deviation 246.
- Find the mean and standard deviation of for samples of size 100.
- Find the probability that the mean of a sample of size 100 will be within 100 units of the population mean, that is, between 1,442 and 1,642.
-
A population has mean 73.5 and standard deviation 2.5.
- Find the mean and standard deviation of for samples of size 30.
- Find the probability that the mean of a sample of size 30 will be less than 72.
-
A population has mean 48.4 and standard deviation 6.3.
- Find the mean and standard deviation of for samples of size 64.
- Find the probability that the mean of a sample of size 64 will be less than 46.7.
-
A normally distributed population has mean 25.6 and standard deviation 3.3.
- Find the probability that a single randomly selected element X of the population exceeds 30.
- Find the mean and standard deviation of for samples of size 9.
- Find the probability that the mean of a sample of size 9 drawn from this population exceeds 30.
-
A normally distributed population has mean 57.7 and standard deviation 12.1.
- Find the probability that a single randomly selected element X of the population is less than 45.
- Find the mean and standard deviation of for samples of size 16.
- Find the probability that the mean of a sample of size 16 drawn from this population is less than 45.
-
A population has mean 557 and standard deviation 35.
- Find the mean and standard deviation of for samples of size 50.
- Find the probability that the mean of a sample of size 50 will be more than 570.
-
A population has mean 16 and standard deviation 1.7.
- Find the mean and standard deviation of for samples of size 80.
- Find the probability that the mean of a sample of size 80 will be more than 16.4.
-
A normally distributed population has mean 1,214 and standard deviation 122.
- Find the probability that a single randomly selected element X of the population is between 1,100 and 1,300.
- Find the mean and standard deviation of for samples of size 25.
- Find the probability that the mean of a sample of size 25 drawn from this population is between 1,100 and 1,300.
-
A normally distributed population has mean 57,800 and standard deviation 750.
- Find the probability that a single randomly selected element X of the population is between 57,000 and 58,000.
- Find the mean and standard deviation of for samples of size 100.
- Find the probability that the mean of a sample of size 100 drawn from this population is between 57,000 and 58,000.
-
A population has mean 72 and standard deviation 6.
- Find the mean and standard deviation of for samples of size 45.
- Find the probability that the mean of a sample of size 45 will differ from the population mean 72 by at least 2 units, that is, is either less than 70 or more than 74. (Hint: One way to solve the problem is to first find the probability of the complementary event.)
-
A population has mean 12 and standard deviation 1.5.
- Find the mean and standard deviation of for samples of size 90.
- Find the probability that the mean of a sample of size 90 will differ from the population mean 12 by at least 0.3 unit, that is, is either less than 11.7 or more than 12.3. (Hint: One way to solve the problem is to first find the probability of the complementary event.)
Basic
-
Suppose the mean number of days to germination of a variety of seed is 22, with standard deviation 2.3 days. Find the probability that the mean germination time of a sample of 160 seeds will be within 0.5 day of the population mean.
-
Suppose the mean length of time that a caller is placed on hold when telephoning a customer service center is 23.8 seconds, with standard deviation 4.6 seconds. Find the probability that the mean length of time on hold in a sample of 1,200 calls will be within 0.5 second of the population mean.
-
Suppose the mean amount of cholesterol in eggs labeled “large” is 186 milligrams, with standard deviation 7 milligrams. Find the probability that the mean amount of cholesterol in a sample of 144 eggs will be within 2 milligrams of the population mean.
-
Suppose that in one region of the country the mean amount of credit card debt per household in households having credit card debt is $15,250, with standard deviation $7,125. Find the probability that the mean amount of credit card debt in a sample of 1,600 such households will be within $300 of the population mean.
-
Suppose speeds of vehicles on a particular stretch of roadway are normally distributed with mean 36.6 mph and standard deviation 1.7 mph.
- Find the probability that the speed X of a randomly selected vehicle is between 35 and 40 mph.
- Find the probability that the mean speed of 20 randomly selected vehicles is between 35 and 40 mph.
-
Many sharks enter a state of tonic immobility when inverted. Suppose that in a particular species of sharks the time a shark remains in a state of tonic immobility when inverted is normally distributed with mean 11.2 minutes and standard deviation 1.1 minutes.
- If a biologist induces a state of tonic immobility in such a shark in order to study it, find the probability that the shark will remain in this state for between 10 and 13 minutes.
- When a biologist wishes to estimate the mean time that such sharks stay immobile by inducing tonic immobility in each of a sample of 12 sharks, find the probability that mean time of immobility in the sample will be between 10 and 13 minutes.
-
Suppose the mean cost across the country of a 30-day supply of a generic drug is $46.58, with standard deviation $4.84. Find the probability that the mean of a sample of 100 prices of 30-day supplies of this drug will be between $45 and $50.
-
Suppose the mean length of time between submission of a state tax return requesting a refund and the issuance of the refund is 47 days, with standard deviation 6 days. Find the probability that in a sample of 50 returns requesting a refund, the mean such time will be more than 50 days.
-
Scores on a common final exam in a large enrollment, multiple-section freshman course are normally distributed with mean 72.7 and standard deviation 13.1.
- Find the probability that the score X on a randomly selected exam paper is between 70 and 80.
- Find the probability that the mean score of 38 randomly selected exam papers is between 70 and 80.
-
Suppose the mean weight of school children’s bookbags is 17.4 pounds, with standard deviation 2.2 pounds. Find the probability that the mean weight of a sample of 30 bookbags will exceed 17 pounds.
-
Suppose that in a certain region of the country the mean duration of first marriages that end in divorce is 7.8 years, standard deviation 1.2 years. Find the probability that in a sample of 75 divorces, the mean age of the marriages is at most 8 years.
-
Borachio eats at the same fast food restaurant every day. Suppose the time X between the moment Borachio enters the restaurant and the moment he is served his food is normally distributed with mean 4.2 minutes and standard deviation 1.3 minutes.
- Find the probability that when he enters the restaurant today it will be at least 5 minutes until he is served.
- Find the probability that average time until he is served in eight randomly selected visits to the restaurant will be at least 5 minutes.
Applications
-
A high-speed packing machine can be set to deliver between 11 and 13 ounces of a liquid. For any delivery setting in this range the amount delivered is normally distributed with mean some amount μ and with standard deviation 0.08 ounce. To calibrate the machine it is set to deliver a particular amount, many containers are filled, and 25 containers are randomly selected and the amount they contain is measured. Find the probability that the sample mean will be within 0.05 ounce of the actual mean amount being delivered to all containers.
-
A tire manufacturer states that a certain type of tire has a mean lifetime of 60,000 miles. Suppose lifetimes are normally distributed with standard deviation miles.
- Find the probability that if you buy one such tire, it will last only 57,000 or fewer miles. If you had this experience, is it particularly strong evidence that the tire is not as good as claimed?
- A consumer group buys five such tires and tests them. Find the probability that average lifetime of the five tires will be 57,000 miles or less. If the mean is so low, is that particularly strong evidence that the tire is not as good as claimed?
Additional Exercises
Answers
-
- ,
- 0.9936
-
-
- ,
- 0.0005
-
-
- 0.0918
- ,
- 0.0000
-
-
- ,
- 0.0043
-
-
- 0.5818
- ,
- 0.9998
-
-
- ,
- 0.0250
-
-
0.9940
-
-
0.9994
-
-
- 0.8036
- 1.0000
-
-
0.9994
-
-
- 0.2955
- 0.8977
-
-
0.9251
-
-
0.9982
-




