This is “The Binomial Distribution”, section 4.3 from the book Beginning Statistics (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
4.3 The Binomial Distribution
Learning Objectives
- To learn the concept of a binomial random variable.
- To learn how to recognize a random variable as being a binomial random variable.
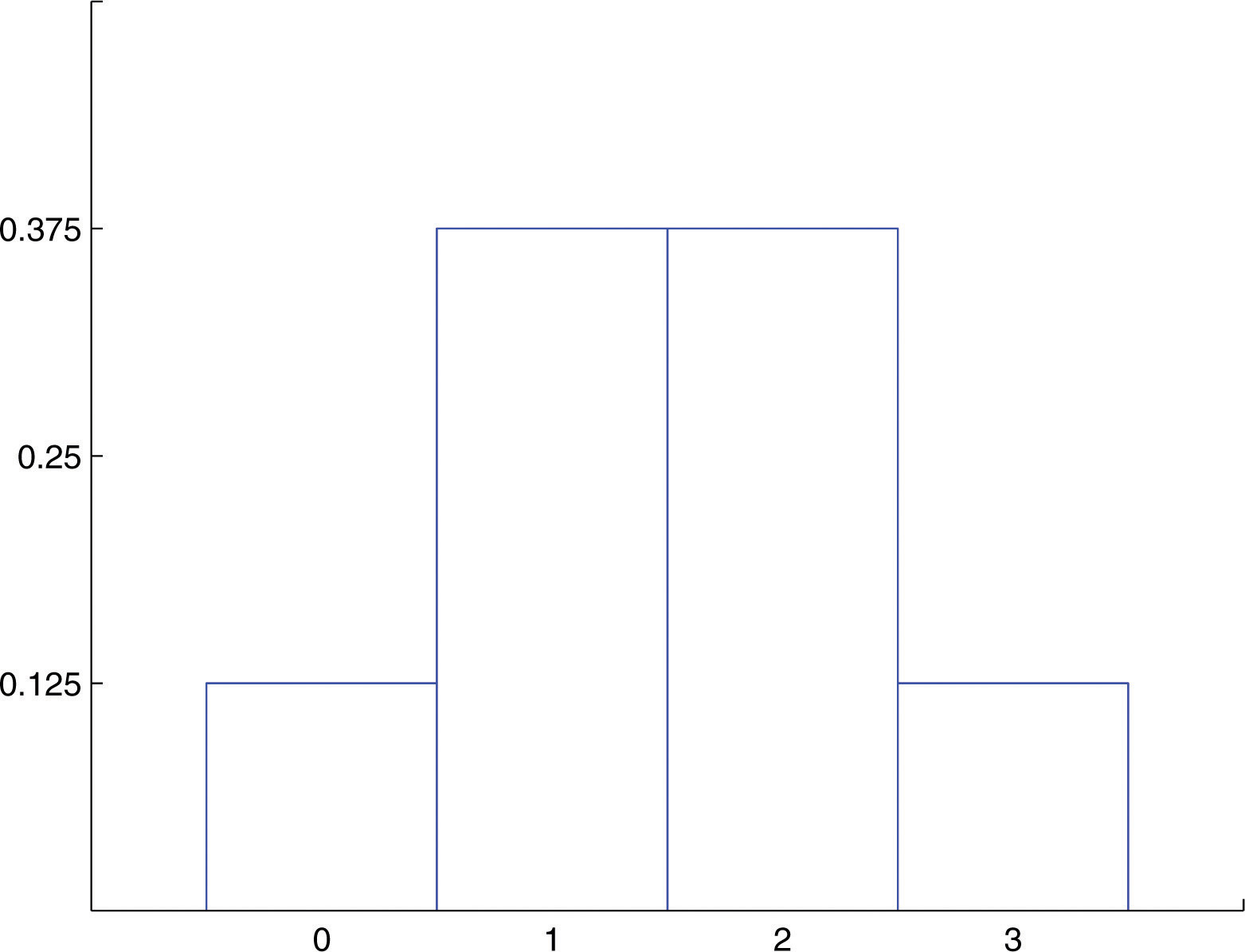
The experiment of tossing a fair coin three times and the experiment of observing the genders according to birth order of the children in a randomly selected three-child family are completely different, but the random variables that count the number of heads in the coin toss and the number of boys in the family (assuming the two genders are equally likely) are the same random variable, the one with probability distribution
A histogram that graphically illustrates this probability distribution is given in Figure 4.4 "Probability Distribution for Three Coins and Three Children". What is common to the two experiments is that we perform three identical and independent trials of the same action, each trial has only two outcomes (heads or tails, boy or girl), and the probability of success is the same number, 0.5, on every trial. The random variable that is generated is called the binomial random variableA random variable that counts successes in a fixed number of independent, identical trials of a success/failure experiment. with parameters n = 3 and p = 0.5. This is just one case of a general situation.
Figure 4.4 Probability Distribution for Three Coins and Three Children
Definition
Suppose a random experiment has the following characteristics.
- There are n identical and independent trials of a common procedure.
- There are exactly two possible outcomes for each trial, one termed “success” and the other “failure.”
- The probability of success on any one trial is the same number p.
Then the discrete random variable X that counts the number of successes in the n trials is the binomial random variable with parameters n and p. We also say that X has a binomial distribution with parameters n and p.
The following four examples illustrate the definition. Note how in every case “success” is the outcome that is counted, not the outcome that we prefer or think is better in some sense.
- A random sample of 125 students is selected from a large college in which the proportion of students who are females is 57%. Suppose X denotes the number of female students in the sample. In this situation there are n = 125 identical and independent trials of a common procedure, selecting a student at random; there are exactly two possible outcomes for each trial, “success” (what we are counting, that the student be female) and “failure;” and finally the probability of success on any one trial is the same number p = 0.57. X is a binomial random variable with parameters n = 125 and p = 0.57.
- A multiple-choice test has 15 questions, each of which has five choices. An unprepared student taking the test answers each of the questions completely randomly by choosing an arbitrary answer from the five provided. Suppose X denotes the number of answers that the student gets right. X is a binomial random variable with parameters n = 15 and
- In a survey of 1,000 registered voters each voter is asked if he intends to vote for a candidate Titania Queen in the upcoming election. Suppose X denotes the number of voters in the survey who intend to vote for Titania Queen. X is a binomial random variable with n = 1000 and p equal to the true proportion of voters (surveyed or not) who intend to vote for Titania Queen.
- An experimental medication was given to 30 patients with a certain medical condition. Suppose X denotes the number of patients who develop severe side effects. X is a binomial random variable with n = 30 and p equal to the true probability that a patient with the underlying condition will experience severe side effects if given that medication.
Probability Formula for a Binomial Random Variable
Often the most difficult aspect of working a problem that involves the binomial random variable is recognizing that the random variable in question has a binomial distribution. Once that is known, probabilities can be computed using the following formula.
If X is a binomial random variable with parameters n and p, then
where and where for any counting number m, (read “m factorial”) is defined by
and in general
Example 7
Seventeen percent of victims of financial fraud know the perpetrator of the fraud personally.
- Use the formula to construct the probability distribution for the number X of people in a random sample of five victims of financial fraud who knew the perpetrator personally.
- A investigator examines five cases of financial fraud every day. Find the most frequent number of cases each day in which the victim knew the perpetrator.
- A investigator examines five cases of financial fraud every day. Find the average number of cases per day in which the victim knew the perpetrator.
Solution:
-
The random variable X is binomial with parameters n = 5 and p = 0.17; The possible values of X are 0, 1, 2, 3, 4, and 5.
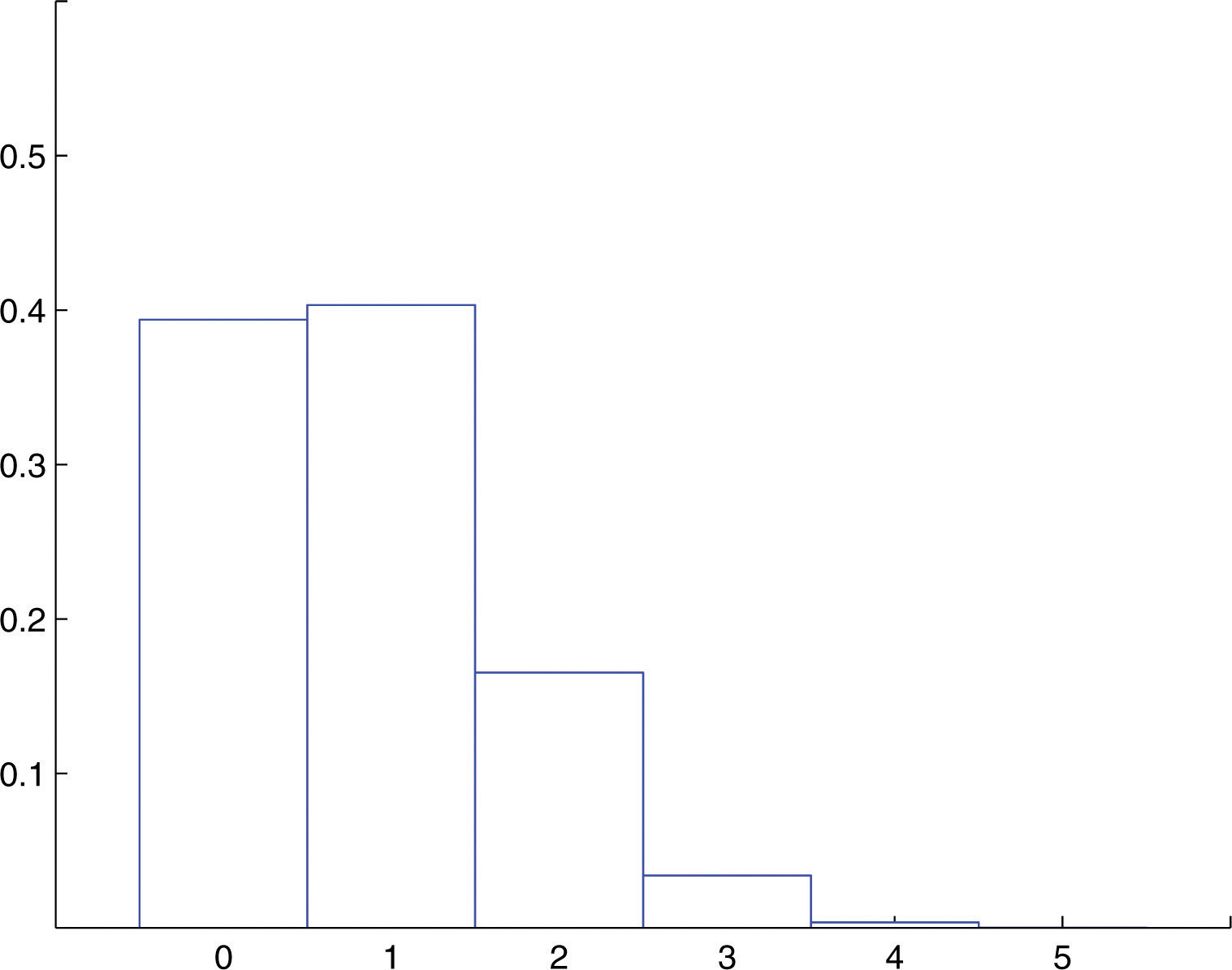
The remaining three probabilities are computed similarly, to give the probability distribution
The probabilities do not add up to exactly 1 because of rounding.
This probability distribution is represented by the histogram in Figure 4.5 "Probability Distribution of the Binomial Random Variable in ", which graphically illustrates just how improbable the events X = 4 and X = 5 are. The corresponding bar in the histogram above the number 4 is barely visible, if visible at all, and the bar above 5 is far too short to be visible.
Figure 4.5 Probability Distribution of the Binomial Random Variable in Note 4.29 "Example 7"
- The value of X that is most likely is X = 1, so the most frequent number of cases seen each day in which the victim knew the perpetrator is one.
-
The average number of cases per day in which the victim knew the perpetrator is the mean of X, which is
Special Formulas for the Mean and Standard Deviation of a Binomial Random Variable
Since a binomial random variable is a discrete random variable, the formulas for its mean, variance, and standard deviation given in the previous section apply to it, as we just saw in Note 4.29 "Example 7" in the case of the mean. However, for the binomial random variable there are much simpler formulas.
If X is a binomial random variable with parameters n and p, then
where
Example 8
Find the mean and standard deviation of the random variable X of Note 4.29 "Example 7".
Solution:
The random variable X is binomial with parameters n = 5 and p = 0.17, and Thus its mean and standard deviation are
and
The Cumulative Probability Distribution of a Binomial Random Variable
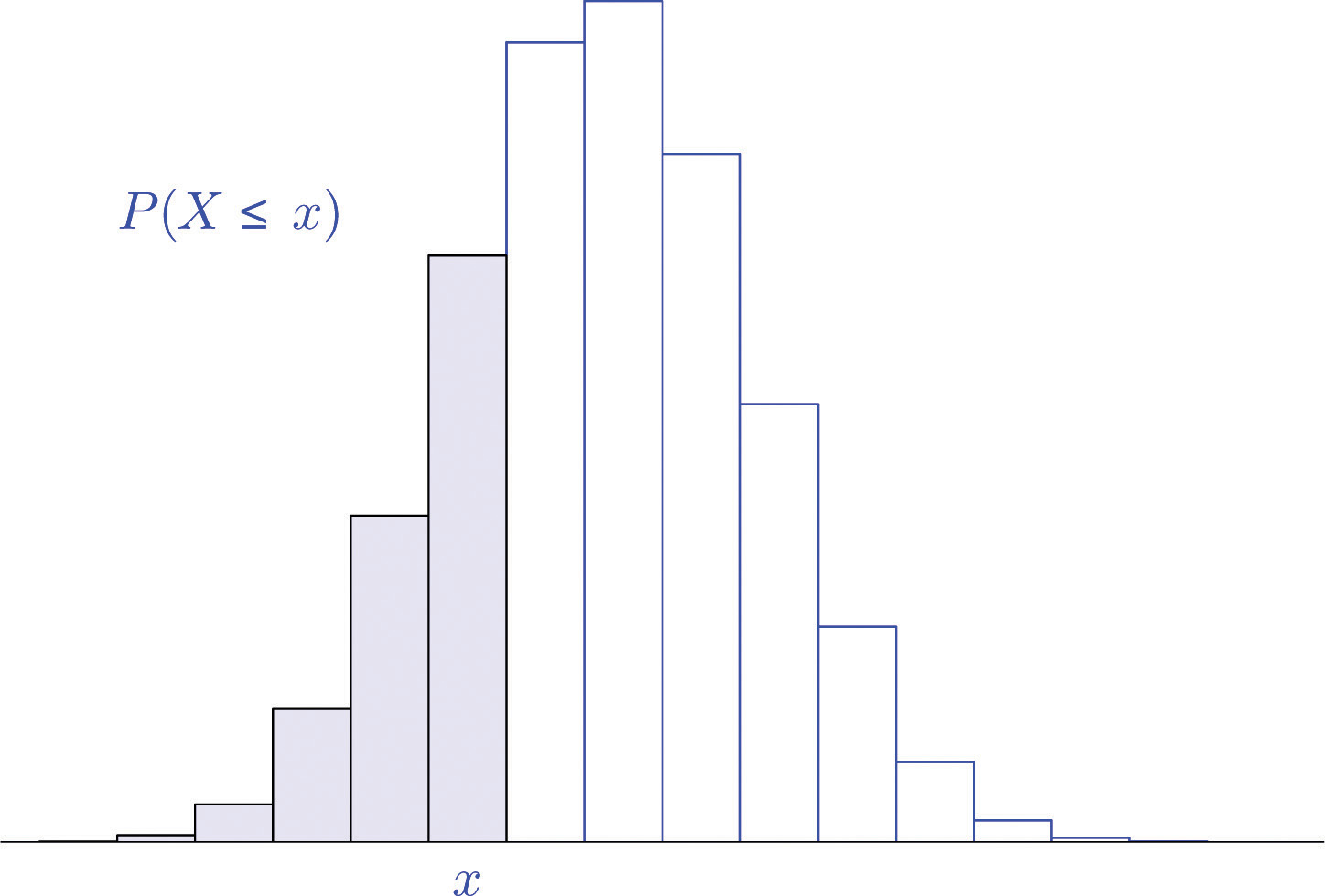
In order to allow a broader range of more realistic problems Chapter 12 "Appendix" contains probability tables for binomial random variables for various choices of the parameters n and p. These tables are not the probability distributions that we have seen so far, but are cumulative probability distributions. In the place of the probability the table contains the probability
This is illustrated in Figure 4.6 "Cumulative Probabilities". The probability entered in the table corresponds to the area of the shaded region. The reason for providing a cumulative table is that in practical problems that involve a binomial random variable typically the probability that is sought is of the form or The cumulative table is much easier to use for computing since all the individual probabilities have already been computed and added. The one table suffices for both or and can be used to readily obtain probabilities of the form , too, because of the following formulas. The first is just the Probability Rule for Complements.
Figure 4.6 Cumulative Probabilities
If X is a discrete random variable, then
Example 9
A student takes a ten-question true/false exam.
- Find the probability that the student gets exactly six of the questions right simply by guessing the answer on every question.
- Find the probability that the student will obtain a passing grade of 60% or greater simply by guessing.
Solution:
Let X denote the number of questions that the student guesses correctly. Then X is a binomial random variable with parameters n = 10 and p = 0.50.
-
The probability sought is The formula gives
Using the table,
-
The student must guess correctly on at least 60% of the questions, which is questions. The probability sought is not (an easy mistake to make), but
Instead of computing each of these five numbers using the formula and adding them we can use the table to obtain
which is much less work and of sufficient accuracy for the situation at hand.
Example 10
An appliance repairman services five washing machines on site each day. One-third of the service calls require installation of a particular part.
- The repairman has only one such part on his truck today. Find the probability that the one part will be enough today, that is, that at most one washing machine he services will require installation of this particular part.
- Find the minimum number of such parts he should take with him each day in order that the probability that he have enough for the day's service calls is at least 95%.
Solution:
Let X denote the number of service calls today on which the part is required. Then X is a binomial random variable with parameters n = 5 and
-
Note that the probability in question is not , but rather P(X ≤ 1). Using the cumulative distribution table in Chapter 12 "Appendix",
- The answer is the smallest number x such that the table entry is at least 0.9500. Since is less than 0.95, two parts are not enough. Since is as large as 0.95, three parts will suffice at least 95% of the time. Thus the minimum needed is three.
Key Takeaways
- The discrete random variable X that counts the number of successes in n identical, independent trials of a procedure that always results in either of two outcomes, “success” or “failure,” and in which the probability of success on each trial is the same number p, is called the binomial random variable with parameters n and p.
- There is a formula for the probability that the binomial random variable with parameters n and p will take a particular value x.
- There are special formulas for the mean, variance, and standard deviation of the binomial random variable with parameters n and p that are much simpler than the general formulas that apply to all discrete random variables.
- Cumulative probability distribution tables, when available, facilitate computation of probabilities encountered in typical practical situations.
Exercises
-
Determine whether or not the random variable X is a binomial random variable. If so, give the values of n and p. If not, explain why not.
- X is the number of dots on the top face of fair die that is rolled.
- X is the number of hearts in a five-card hand drawn (without replacement) from a well-shuffled ordinary deck.
- X is the number of defective parts in a sample of ten randomly selected parts coming from a manufacturing process in which 0.02% of all parts are defective.
- X is the number of times the number of dots on the top face of a fair die is even in six rolls of the die.
- X is the number of dice that show an even number of dots on the top face when six dice are rolled at once.
-
Determine whether or not the random variable X is a binomial random variable. If so, give the values of n and p. If not, explain why not.
- X is the number of black marbles in a sample of 5 marbles drawn randomly and without replacement from a box that contains 25 white marbles and 15 black marbles.
- X is the number of black marbles in a sample of 5 marbles drawn randomly and with replacement from a box that contains 25 white marbles and 15 black marbles.
- X is the number of voters in favor of proposed law in a sample 1,200 randomly selected voters drawn from the entire electorate of a country in which 35% of the voters favor the law.
- X is the number of fish of a particular species, among the next ten landed by a commercial fishing boat, that are more than 13 inches in length, when 17% of all such fish exceed 13 inches in length.
- X is the number of coins that match at least one other coin when four coins are tossed at once.
-
X is a binomial random variable with parameters n = 12 and p = 0.82. Compute the probability indicated.
-
X is a binomial random variable with parameters n = 16 and p = 0.74. Compute the probability indicated.
-
X is a binomial random variable with parameters n = 5, p = 0.5. Use the tables in Chapter 12 "Appendix" to compute the probability indicated.
- P(X ≤ 3)
- P(X ≥ 3)
-
X is a binomial random variable with parameters n = 5, Use the table in Chapter 12 "Appendix" to compute the probability indicated.
- P(X ≤ 2)
- P(X ≥ 2)
-
X is a binomial random variable with the parameters shown. Use the tables in Chapter 12 "Appendix" to compute the probability indicated.
- n = 10, p = 0.25, P(X ≤ 6)
- n = 10, p = 0.75, P(X ≤ 6)
- n = 15, p = 0.75, P(X ≤ 6)
- n = 15, p = 0.75,
- n = 15, ,
-
X is a binomial random variable with the parameters shown. Use the tables in Chapter 12 "Appendix" to compute the probability indicated.
- n = 5, p = 0.05, P(X ≤ 1)
- n = 5, p = 0.5, P(X ≤ 1)
- n = 10, p = 0.75, P(X ≤ 5)
- n = 10, p = 0.75,
- n = 10, ,
-
X is a binomial random variable with the parameters shown. Use the special formulas to compute its mean μ and standard deviation σ.
- n = 8, p = 0.43
- n = 47, p = 0.82
- n = 1200, p = 0.44
- n = 2100, p = 0.62
-
X is a binomial random variable with the parameters shown. Use the special formulas to compute its mean μ and standard deviation σ.
- n = 14, p = 0.55
- n = 83, p = 0.05
- n = 957, p = 0.35
- n = 1750, p = 0.79
-
X is a binomial random variable with the parameters shown. Compute its mean μ and standard deviation σ in two ways, first using the tables in Chapter 12 "Appendix" in conjunction with the general formulas and , then using the special formulas and
- n = 5,
- n = 10, p = 0.75
-
X is a binomial random variable with the parameters shown. Compute its mean μ and standard deviation σ in two ways, first using the tables in Chapter 12 "Appendix" in conjunction with the general formulas and , then using the special formulas and
- n = 10, p = 0.25
- n = 15, p = 0.1
-
X is a binomial random variable with parameters n = 10 and Use the cumulative probability distribution for X that is given in Chapter 12 "Appendix" to construct the probability distribution of X.
-
X is a binomial random variable with parameters n = 15 and Use the cumulative probability distribution for X that is given in Chapter 12 "Appendix" to construct the probability distribution of X.
-
In a certain board game a player's turn begins with three rolls of a pair of dice. If the player rolls doubles all three times there is a penalty. The probability of rolling doubles in a single roll of a pair of fair dice is 1/6. Find the probability of rolling doubles all three times.
-
A coin is bent so that the probability that it lands heads up is 2/3. The coin is tossed ten times.
- Find the probability that it lands heads up at most five times.
- Find the probability that it lands heads up more times than it lands tails up.
Basic
-
An English-speaking tourist visits a country in which 30% of the population speaks English. He needs to ask someone directions.
- Find the probability that the first person he encounters will be able to speak English.
- The tourist sees four local people standing at a bus stop. Find the probability that at least one of them will be able to speak English.
-
The probability that an egg in a retail package is cracked or broken is 0.025.
- Find the probability that a carton of one dozen eggs contains no eggs that are either cracked or broken.
- Find the probability that a carton of one dozen eggs has (i) at least one that is either cracked or broken; (ii) at least two that are cracked or broken.
- Find the average number of cracked or broken eggs in one dozen cartons.
-
An appliance store sells 20 refrigerators each week. Ten percent of all purchasers of a refrigerator buy an extended warranty. Let X denote the number of the next 20 purchasers who do so.
- Verify that X satisfies the conditions for a binomial random variable, and find n and p.
- Find the probability that X is zero.
- Find the probability that X is two, three, or four.
- Find the probability that X is at least five.
-
Adverse growing conditions have caused 5% of grapefruit grown in a certain region to be of inferior quality. Grapefruit are sold by the dozen.
- Find the average number of inferior quality grapefruit per box of a dozen.
- A box that contains two or more grapefruit of inferior quality will cause a strong adverse customer reaction. Find the probability that a box of one dozen grapefruit will contain two or more grapefruit of inferior quality.
-
The probability that a 7-ounce skein of a discount worsted weight knitting yarn contains a knot is 0.25. Goneril buys ten skeins to crochet an afghan.
- Find the probability that (i) none of the ten skeins will contain a knot; (ii) at most one will.
- Find the expected number of skeins that contain knots.
- Find the most likely number of skeins that contain knots.
-
One-third of all patients who undergo a non-invasive but unpleasant medical test require a sedative. A laboratory performs 20 such tests daily. Let X denote the number of patients on any given day who require a sedative.
- Verify that X satisfies the conditions for a binomial random variable, and find n and p.
- Find the probability that on any given day between five and nine patients will require a sedative (include five and nine).
- Find the average number of patients each day who require a sedative.
- Using the cumulative probability distribution for X in Chapter 12 "Appendix", find the minimum number of doses of the sedative that should be on hand at the start of the day so that there is a 99% chance that the laboratory will not run out.
-
About 2% of alumni give money upon receiving a solicitation from the college or university from which they graduated. Find the average number monetary gifts a college can expect from every 2,000 solicitations it sends.
-
Of all college students who are eligible to give blood, about 18% do so on a regular basis. Each month a local blood bank sends an appeal to give blood to 250 randomly selected students. Find the average number of appeals in such mailings that are made to students who already give blood.
-
About 12% of all individuals write with their left hands. A class of 130 students meets in a classroom with 130 individual desks, exactly 14 of which are constructed for people who write with their left hands. Find the probability that exactly 14 of the students enrolled in the class write with their left hands.
-
A travelling salesman makes a sale on 65% of his calls on regular customers. He makes four sales calls each day.
- Construct the probability distribution of X, the number of sales made each day.
- Find the probability that, on a randomly selected day, the salesman will make a sale.
- Assuming that the salesman makes 20 sales calls per week, find the mean and standard deviation of the number of sales made per week.
-
A corporation has advertised heavily to try to insure that over half the adult population recognizes the brand name of its products. In a random sample of 20 adults, 14 recognized its brand name. What is the probability that 14 or more people in such a sample would recognize its brand name if the actual proportion p of all adults who recognize the brand name were only 0.50?
Applications
-
When dropped on a hard surface a thumbtack lands with its sharp point touching the surface with probability 2/3; it lands with its sharp point directed up into the air with probability 1/3. The tack is dropped and its landing position observed 15 times.
- Find the probability that it lands with its point in the air at least 7 times.
- If the experiment of dropping the tack 15 times is done repeatedly, what is the average number of times it lands with its point in the air?
-
A professional proofreader has a 98% chance of detecting an error in a piece of written work (other than misspellings, double words, and similar errors that are machine detected). A work contains four errors.
- Find the probability that the proofreader will miss at least one of them.
- Show that two such proofreaders working independently have a 99.96% chance of detecting an error in a piece of written work.
- Find the probability that two such proofreaders working independently will miss at least one error in a work that contains four errors.
-
A multiple choice exam has 20 questions; there are four choices for each question.
- A student guesses the answer to every question. Find the chance that he guesses correctly between four and seven times.
- Find the minimum score the instructor can set so that the probability that a student will pass just by guessing is 20% or less.
-
In spite of the requirement that all dogs boarded in a kennel be inoculated, the chance that a healthy dog boarded in a clean, well-ventilated kennel will develop kennel cough from a carrier is 0.008.
- If a carrier (not known to be such, of course) is boarded with three other dogs, what is the probability that at least one of the three healthy dogs will develop kennel cough?
- If a carrier is boarded with four other dogs, what is the probability that at least one of the four healthy dogs will develop kennel cough?
- The pattern evident from parts (a) and (b) is that if dogs are boarded together, one a carrier and K healthy dogs, then the probability that at least one of the healthy dogs will develop kennel cough is , where X is the binomial random variable that counts the number of healthy dogs that develop the condition. Experiment with different values of K in this formula to find the maximum number of dogs that a kennel owner can board together so that if one of the dogs has the condition, the chance that another dog will be infected is less than 0.05.
-
Investigators need to determine which of 600 adults have a medical condition that affects 2% of the adult population. A blood sample is taken from each of the individuals.
- Show that the expected number of diseased individuals in the group of 600 is 12 individuals.
- Instead of testing all 600 blood samples to find the expected 12 diseased individuals, investigators group the samples into 60 groups of 10 each, mix a little of the blood from each of the 10 samples in each group, and test each of the 60 mixtures. Show that the probability that any such mixture will contain the blood of at least one diseased person, hence test positive, is about 0.18.
- Based on the result in (b), show that the expected number of mixtures that test positive is about 11. (Supposing that indeed 11 of the 60 mixtures test positive, then we know that none of the 490 persons whose blood was in the remaining 49 samples that tested negative has the disease. We have eliminated 490 persons from our search while performing only 60 tests.)
Additional Exercises
Answers
-
- not binomial; not success/failure.
- not binomial; trials are not independent.
- binomial; n = 10, p = 0.0002
- binomial; n = 6, p = 0.5
- binomial; n = 6, p = 0.5
-
-
- 0.2434
- 0.2151
- 0
-
-
- 0.8125
- 0.5000
- 0.3125
- 0.0313
- 0.0312
-
-
- 0.9965
- 0.2241
- 0.0042
- 0.2252
- 0.5390
-
-
- μ = 3.44, σ = 1.4003
- μ = 38.54, σ = 2.6339
- μ = 528, σ = 17.1953
- μ = 1302, σ = 22.2432
-
-
- μ = 1.6667, σ = 1.0541
- μ = 7.5, σ = 1.3693
-
-
-
-
0.0046
-
-
- 0.3
- 0.7599
-
-
- n = 20, p = 0.1
- 0.1216
- 0.5651
- 0.0432
-
-
- 0.0563 and 0.2440
- 2.5
- 2
-
-
40
-
-
0.1019
-
-
0.0577
-
-
- 0.0776
- 0.9996
- 0.0016
-
-
- 0.0238
- 0.0316
- 6
-




