This is “Information”, chapter 18 from the book Beginning Economic Analysis (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
Chapter 18 Information
An important advantage of the price system is that it economizes on information. A typical consumer needs to know only the prices of goods and his or her own personal preferences in order to make a sensible choice of purchases, and manufacturers need to know only the prices of goods in order to decide what to produce. Such economies of information are an advantage over centrally planned economies, which attempt to direct production and consumption decisions using something other than prices, and centrally planned economies typically experience chronic shortages and occasional surpluses. Shortages of important inputs to production may have dramatic effects; the shortages aren’t remedied by the price of the input rising in a centrally planned economy and thus often persist for long periods of time.
There are circumstances, however, where the prices are not the only necessary information required for firms and consumers to make good decisions. In such circumstances, information itself and how it is distributed among individuals in the market can lead to market failures.
18.1 Market for Lemons
Learning Objective
- Can information held by sellers but relevant to buyers be an impediment to trade?
Nobel laureate George Akerlof (1940– ) examined the market for used cars and considered a situation known as the market for lemonsA model where sellers are better informed about quality than buyers., where the sellers are better informed than the buyers. This is quite reasonable because sellers have owned the car for a while and are likely to know its quirks and potential problems. Akerlof showed that this differential information may cause the used car market to collapse; that is, the information possessed by sellers of used cars destroys the market and the opportunities for profitable exchange.
To understand Akerlof’s insight, suppose that the quality of used cars lies on a 0 to 1 scale and that the population of used cars is uniformly distributed on the interval from 0 to 1. In addition, let that quality represent the value a seller places on the car, and suppose buyers put a value that is 50% higher than the seller. Finally, the seller knows the actual quality, while the buyer does not.
Can a buyer and seller trade in such a situation? First, note that trade is a good thing because the buyer values the car more than the seller. That is, both the buyer and seller know that they should trade. But can they agree on a price? Consider a price p. At this price, any seller who values the car less than p will be willing to trade. But because of our uniform distribution assumption, this means the distribution of qualities of cars offered for trade at price p will be uniform on the interval 0 to p. Consequently, the average quality of these cars will be ½ p, and the buyer values these cars 50% more, which yields ¾ p. Thus, the buyer is not willing to pay the price p for the average car offered at price p.
The effect of the informed seller and uninformed buyer produces a “lemons” problem. At any given price, all the lemons and only a few of the good cars are offered, and the buyer—not knowing the quality of the car—isn’t willing to pay as much as the actual value of a high-value car offered for sale. This causes the market to collapse; and only the worthless cars trade at a price around zero. Economists call this situation, where some parties have information that others do not, an informational asymmetrySituation in which some parties have information that others do not..
In the real world, of course, the market has found partial or imperfect solutions to the lemons problem identified by Akerlof. First, buyers can become informed and regularly hire their own mechanic to inspect a car they are considering. Inspections reduce the informational asymmetry but are costly in their own right. Second, intermediaries offer warranties and certification to mitigate the lemons problem. The existence of both of these solutions, which involve costs in their own right, is itself evidence that the lemons problem is a real and significant problem, even though competitive markets find ways to ameliorate the problems.
An important example of the lemons problem is the inventor who creates an idea that is difficult or impossible to patent. Consider an innovation that would reduce the cost of manufacturing computers. The inventor would like to sell it to a computer company, but she or he can’t tell the computer company what the innovation entails prior to price negotiations because then the computer company could just copy the innovation. Similarly, the computer company can’t possibly offer a price for the innovation in advance of knowing what the innovation is. As a result, such innovations usually require the inventor to enter the computer manufacturing business, rather than selling to an existing manufacturer, entailing many otherwise unnecessary costs.
Key Takeaways
- Information itself can lead to market failures.
- The market for lemons refers to a situation where sellers are better informed than buyers about the quality of the good for sale, like used cars.
- The informational asymmetry—sellers know more than buyers—causes the market to collapse.
- Inspections, warranties, and certification mitigate the lemons problem. The existence of these costly solutions is itself evidence that the lemons problem (informational asymmetry is an impediment to trade) is a real and significant problem.
- An example of the lemons problem is the inventor who creates an idea that is difficult or impossible to patent and cannot be verified without being revealed.
Exercise
- In Akerlof’s market for lemons model, suppose it is possible to certify cars, verifying that they are better than a particular quality q. Thus, a market for cars “at least as good as q” is possible. What price or prices are possible in this market? (Hint: sellers offer cars only if q ≤ quality ≤ p.) What quality maximizes the expected gains from trade?
18.2 Myerson-Satterthwaite Theorem
Learning Objective
- Can information about values and costs that is not relevant to the other party be an impediment to trade?
The lemons problem is a situation where the buyers are relatively uninformed and care about the information held by sellers. Lemons problems are limited to situations where the buyer isn’t well-informed, and these problems can be mitigated by making information public. In many transactions, the buyer knows the quality of the product, so lemons concerns aren’t a significant issue. There can still be a market failure, however, if there are a limited number of buyers and sellers.
Consider the case of one buyer and one seller bargaining over the sale of a good. The buyer knows his own value v for the good, but not the seller’s cost. The seller knows her own cost c for the good, but not the buyer’s value. The buyer views the seller’s cost as uniformly distributed on the interval [0,1], and, similarly, the seller views the buyer’s value as uniformly distributed on [0,1].The remarkable fact proved by Roger Myerson and Mark Satterthwaite (“Efficient Mechanisms for Bilateral Trade,” Journal of Economic Theory 28 [1983]: 265–281) is that the distributions don’t matter; the failure of efficient trade is a fully general property. Philip Reny and Preston McAfee (“Correlated Information and Mechanism Design,” Econometrica 60, no. 2 [March 1992]: 395–421) show the nature of the distribution of information matters, and Preston McAfee (“Efficient Allocation with Continuous Quantities,” Journal of Economic Theory 53, no. 1 [February 1991]: 51–74.) showed that continuous quantities can overturn the Myerson-Satterthwaite theorem. Can efficient trade take place? Efficient trade requires that trade occurs whenever v > c, and the remarkable answer is that it is impossible to arrange efficient trade if the buyer and seller are to trade voluntarily. This is true even if a third party is used to help arrange trade, provided the third party isn’t able to subsidize the transaction.
The total gains from trade under efficiency are
A means of arranging trade, known as a mechanismA means of arranging a trade.,A mechanism is a game for achieving an objective, in this case to arrange trades. asks the buyer and seller for their value and cost, respectively, and then orders trade if the value exceeds the cost and dictates a payment p by the buyer to the seller. Buyers need not make honest reports to the mechanism, however, and the mechanisms must be designed to induce the buyer and seller to report honestly to the mechanism so that efficient trades can be arranged.Inducing honesty is without loss of generality. Suppose that the buyer of type v reported the type z(v). Then we can add a stage to the mechanism in which the buyer reports a type, which is converted via the function z to a report, and then that report is given to the original mechanism. In the new mechanism, reporting v is tantamount to reporting z(v) to the original mechanism.
Consider a buyer who actually has value v but reports a value r. The buyer trades with the seller if the seller has a cost less than r, which occurs with probability r.
The buyer gets the actual value v with probability r, and makes a payment that depends on the buyer’s report and the seller’s report. But we can take expectations over the seller’s report to eliminate it (from the buyer’s perspective), and this is denoted Ecp(r, c), which is just the expected payment given the report r. For the buyer to choose to be honest, u must be maximized at r = v for every v; otherwise, some buyers would lie and some trades would not be efficiently arranged. Thus, we can concludeWe maintain an earlier notation that the subscript refers to a partial derivative, so that if we have a function f, f1 is the partial derivative of f with respect to the first argument of f.
The first equality is just the total derivative of u(v,v) because there are two terms: the second equality because u is maximized over the first argument r at r = v, and the first-order condition ensures u1 = 0. Finally, u2 is just r, and we are evaluating the derivative at the point r = v. A buyer who has a value v + Δ, but who reports v, trades with probability v and makes the payment Ecp(v, c). Such a buyer gets Δv more in utility than the buyer with value v. Thus, a Δ increase in value produces an increase in utility of at least Δv, showing that and hence that A similar argument considering a buyer with value v who reports v + Δ shows that equality occurs.
The value u(v,v) is the gain accruing to a buyer with value v who reports having value v. Because the buyer with value 0 gets zero, the total gain accruing to the average buyer can be computed by integrating by parts
In the integration by parts, dv = d – (1 – v) is used. The remarkable conclusion is that if the buyer is induced to truthfully reveal the buyer’s value, the buyer must obtain the entire gains from trade. This is actually a quite general proposition. If you offer the entire gains from trade to a party, that party is induced to maximize the gains from trade. Otherwise, he or she will want to distort away from maximizing the entire gains from trade, which will result in a failure of efficiency.
The logic with respect to the seller is analogous: the only way to get the seller to report her cost honestly is to offer her the entire gains from trade.
The Myerson-Satterthwaite theoremA theorem that shows private information about value may prevent efficient trade. shows that private information about value may prevent efficient trade. Thus, the gains from trade are insufficient to induce honesty by both parties. (Indeed, they are half the necessary amount.) Thus, any mechanism for arranging trades between the buyer and the seller must suffer some inefficiency. Generally this occurs because buyers act like they value the good less than they do, and sellers act like their costs are higher than they truly are.
It turns out that the worst-case scenario is a single buyer and a single seller. As markets get “thick,” the per capita losses converge to zero, and markets become efficient. Thus, informational problems of this kind are a small-numbers issue. However, many markets do in fact have small numbers of buyers or sellers. In such markets, it seems likely that informational problems will be an impediment to efficient trade.
Key Takeaways
- The Myerson-Satterthwaite theorem shows that the gains from trade are insufficient to induce honesty about values and costs by a buyer and seller. Any mechanism for arranging trades between the buyer and the seller must suffer some inefficiency.
- Generally this inefficiency occurs because buyers act like they value the good less than they do, and sellers act like their costs are higher than they truly are, resulting in an inefficiently low level of trade.
- As markets get “thick,” the per capita losses converge to zero, and markets become efficient. Informational problems of this kind are a small-numbers issue.
Exercise
-
Let h(r, c) be the gains of a seller who has cost c and reports r, h(r, c) = p(v, r) – (1 – r)c.
Noting that the highest cost seller (c = 1) never sells and thus obtains zero profits, show that honesty by the seller implies the expected value of h is 1/16.
18.3 Signaling
Learning Objectives
- Why do people spend so much money on things that aren’t much better than the cheap versions?
- Why do people who study ancient Greek get good jobs that don’t involve reading ancient Greek?
An interesting approach to solving informational problems involves signalingExpenditures of time or money whose purpose is to convince others of something..Signaling was introduced by Nobel laureate Michael Spence in his dissertation, part of which was reprinted in “Job Market Signaling,” Quarterly Journal of Economics 87 (August 1973): 355–74. Signaling, in economic jargon, means expenditures of time or money whose purpose is to convince others of something. Thus, people signal wealth by wearing Rolex watches, driving expensive cars, or sailing in the America’s Cup. They signal erudition by tossing quotes from Kafka or Tacitus into conversations. They signal being chic by wearing the “right” clothes and listening to cool music. Signaling is also rampant in the animal world, from peacock feathers to elk battles, and it is the subject of a vibrant and related research program.
A university education serves not just to educate but also to signal the ability to learn. Businesses often desire employees who are able to adapt to changing circumstances and who can easily and readily learn new strategies and approaches. Education signals such abilities because it will be easier for quick learners to perform well at university. A simple model suffices to illustrate the point. Suppose there are two types of people. Type A has a low cost cA of learning, and type B has a higher cost cB of learning. It is difficult to determine from an interview whether someone is type A or type B. Type A is worth more to businesses, and the competitive wage wA (expressed as a present value of lifetime earnings) for type A’s is higher than the wage wB for type B’s.
A person can signal that she is a type A by pursuing a sufficient amount of education. Suppose the person devotes an amount of time x to learning at university, thus incurring the cost cA x. If x is large enough so that wA – cA x > wB > wA – cB x, it pays the type A to obtain the education, but not the type B, if education in fact signals that the student is type A. Thus, a level of education x in this case signals a trait (ease of learning) that is valued by business, and it does so by voluntary choice—those with a high cost of learning choose not to obtain the education, even though they could do it. This works as a signal because only type A would voluntarily obtain the education in return for being perceived to be a type A.
There are several interesting aspects to this kind of signaling. First, the education embodied in x need not be valuable in itself; the student could be studying astronomy or ancient Greek, neither of which are very useful in most businesses but are nevertheless strong signals of the ability to learn. Second, the best subject matter for signaling is that in which the difference in cost between the type desired by employers and the less desirable type is greatest—that is, where cB – cA is greatest. Practical knowledge is somewhat unlikely to make this difference great; instead, challenging and abstract problem solving may be a better separator. Clearly, it is desirable to have the subject matter be useful, if it can still do the signaling job. But interpreting long medieval poems could more readily signal the kind of flexible mind desired in management than studying accounting, not because the desirable type is good at it or that it is useful, but because the less desirable type is so much worse at it.
Third, one interprets signals by asking, “What kinds of people would make this choice?” while understanding that the person makes the choice hoping to send the signal. Successful law firms have very fine offices, generally much finer than the offices of their clients. Moreover, there are back rooms at most law firms, where much of the real work is done, that aren’t nearly so opulent. The purpose of the expensive offices is to signal success, essentially proclaiming, “We couldn’t afford to waste money on such expensive offices if we weren’t very successful. Thus, you should believe we are successful.”
The law firm example is similar to the education example. Here, the cost of the expenditures on fancy offices is different for different law firms because more successful firms earn more money and thus value the marginal dollar less. Consequently, more successful firms have a lower cost of a given level of office luxury. What is interesting about signaling is that it is potentially quite wasteful. A student spends 4 years studying boring poems and dead languages in order to demonstrate a love of learning, and a law firm pays $75,000 for a conference table that it rarely uses and gets no pleasure out of in order to convince a client that the firm is extremely successful. In both cases, it seems like a less costly solution should be available. The student can take standardized tests, and the law firm could show its win-loss record to the potential client. But standardized tests may measure test-taking skills rather than learning ability, especially if what matters is the learning ability over a long time horizon. Win-loss records can be “massaged,” and in the majority of all legal disputes, the case settles and both sides consider themselves the winner. Consequently, statistics may not be a good indicator of success, and the expensive conference table may be a better guide.
Key Takeaways
- Signaling means expenditures of time or money whose purpose is to convince others of something.
- A university education signals the ability to learn. The education need not be useful in itself to be helpful in signaling. The best subject matter for signaling is something that is easy for fast learners and difficult for slower learners.
- Signals are interpreted by asking, “What kinds of people would make this choice?” while understanding that the person makes the choice hoping to send the signal.
18.4 Search and Price Dispersion
Learning Objectives
- Why do we see such random prices at the grocery store?
- Why are prices unpredictable?
Decades ago, economists used to make a big deal about the law of one priceIdentical goods sell at the same price., which states that identical goods sell at the same price. The argument in favor of the law of one price is theoretical. Well-informed consumers will buy identical goods from the lowest-price seller. Consequently, the only seller to make any sales is the low-price seller. This kind of consumer behavior forces all sellers to sell at the same price.
There are few markets where the law of one price is actually observed to hold. Organized exchanges, like stock, bond, and commodity markets, will satisfy the law of one price. In addition, gas stations across the street from each other will often offer identical prices, but often is not always.
Many economists believed that the Internet would force prices of standardized goods—DVD players, digital cameras, MP3 players—to a uniform, and uniformly low, price. However, this has not occurred. Moreover, it probably can’t occur in the sense that pure price competition would put the firms out of business and hence can’t represent equilibrium behavior.
There are many markets where prices appear unpredictable to consumers. The price of airline tickets is notorious for unpredictability. The price of milk, soft drinks, paper towels, and canned tuna varies 50% or more depending on whether or not the store has an advertised sale of the item. Prices of goods sold on the Internet vary substantially from day to day.It is often very challenging to assess Internet prices because of variations in shipping charges. Such variation of price across stores is known as price dispersionPrice variation across stores. by economists. It is different from price discrimination because price dispersion entails a given store quoting the same price to all customers; the variation is across stores, while price discrimination varies across customers.
Why are prices so unpredictable? We now develop a model that shows they have to be.
To understand price dispersion, we divide consumers into two types: shoppers and loyal customers. Loyal customers won’t pay more than a price pm for the good, but they consult a particular store. If that store has the good for less than the price pm, the loyal customer buys; otherwise, he or she does not. In contrast, the shoppers buy only from the store offering the lowest price; shoppers are informed about the prices offered by all stores. We let the proportion of shoppers be s. The loyal customers are allocated to the other stores equally so that if there are n stores, each store gets a fraction (1 – s)/n of the customers. Let the marginal cost of the good be c, and assume that c < pm. Both kinds of customers buy only one unit.
For the purposes of this analysis, we will assume that prices can be chosen from the continuum. This makes the analysis more straightforward, but there is an alternate version of the analysis (not developed here) that makes the more reasonable assumption of prices that are an integer number of pennies.
First note that there is no pure strategy equilibrium. To see this, consider the lowest price p charged by any firm. If that price is c, the firm makes no money, so it would do better by raising its price to pm and selling only to the loyal customers. Thus, the lowest price p exceeds c. If there is a tie at p, it pays to break the tie by charging a billionth of a cent less than p, and thereby capturing all the shoppers rather than sharing them with the other firm charging p. So there can’t be a tie.
But no tie at p means the next-lowest firm is charging something strictly greater than p, which means the lowest-price firm can increase price somewhat and not suffer any loss of sales. This contradicts profit maximization for that firm. The conclusion is that firms must randomize and that no pure strategy equilibrium exists.
But how do they randomize? We are going to look for a distribution of prices. Each firm will choose a price from the continuous distribution F, where F(x) is the probability the firm charges a price less than x. What must F look like? We use the logic of mixed strategies: the firm must get the same profits for all prices that might actually be charged under the mixed strategy; otherwise, it would not be willing to randomize.
A firm that charges price p ≤ pm always sells to its captive customers. In addition, it sells to the shoppers if the other firms have higher prices, which occurs with probability Thus, the firm’s profits are
On each sale, the firm earns p – c. The firm always sells to its loyal customers and in addition captures the shoppers if the other firms price higher. Because no firm will exceed pm, the profits must be the same as the level arising from charging pm, and this gives
This equation is readily solved for F:
The lower bound of prices arises at the point L where F(L) = 0, or
These two equations provide a continuous distribution of prices charged by each firm, which is an equilibrium to the pricing game. That is, each firm randomizes over the interval [L, pm], according to the continuous distribution F. Any price in the interval [L,pm] produces the same profits for each firm, so the firms are willing to randomize over this interval.
The loyal customers get a price chosen randomly from F, so we immediately see that the shoppers make life better for the loyal customers by pushing average price down. (An increase in s directly increases F, which means prices fall—recall that F gives the probability that prices are below a given level, so an increase in F is an increase in the probability of low prices.)
Similarly loyal customers make life worse for shoppers, increasing prices on average to shoppers. The distribution of prices facing shoppers is actually the distribution of the minimum price. Because all firms charge a price exceeding p with probability (1 – F(p))n, at least one charges a price less than p with probability 1 – (1 – F(p))n, and this is the distribution of prices facing shoppers. That is, the distribution of prices charged to shoppers is
How does a price-dispersed industry perform? First, average industry profits are
An interesting aspect of this equation is that it doesn’t depend on the number of firms, only on the number of loyal customers. Essentially, the industry profits are the same that it would earn as if the shoppers paid marginal cost and the loyal customers paid the monopoly price, although that isn’t what happens in the industry, except in the limit as the number of firms goes to infinity. Note that this formula for industry profits does not work for a monopoly. To capture monopoly, one must set s = 0 because shoppers have no alternative under monopoly.
As the number of firms gets large, the price charged by any one firm converges to the monopoly price pm. However, the lowest price offered by any firm actually converges to c, marginal cost. Thus, in the limit as the number of firms gets large, shoppers obtain price equal to marginal cost and loyal firms pay the monopoly price.
Figure 18.1 Expected Prices in Search Equilibrium
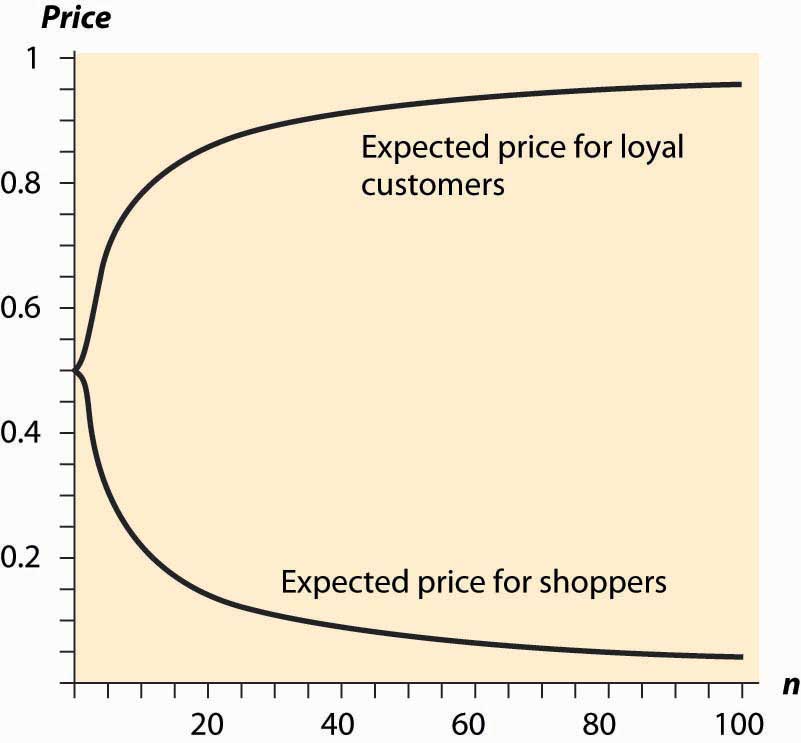
The average price charged to shoppers and nonshoppers is a complicated object, so we consider the case where there are n firms, s = ½, pm = 1, and c = 0. Then the expected prices for shoppers and loyal customers are given in Figure 18.1 "Expected Prices in Search Equilibrium", letting the number of firms vary. Thus, with many firms, most of the gains created by the shoppers flow to shoppers. In contrast, with few firms, a significant fraction of the gains created by shoppers goes instead to the loyal customers.
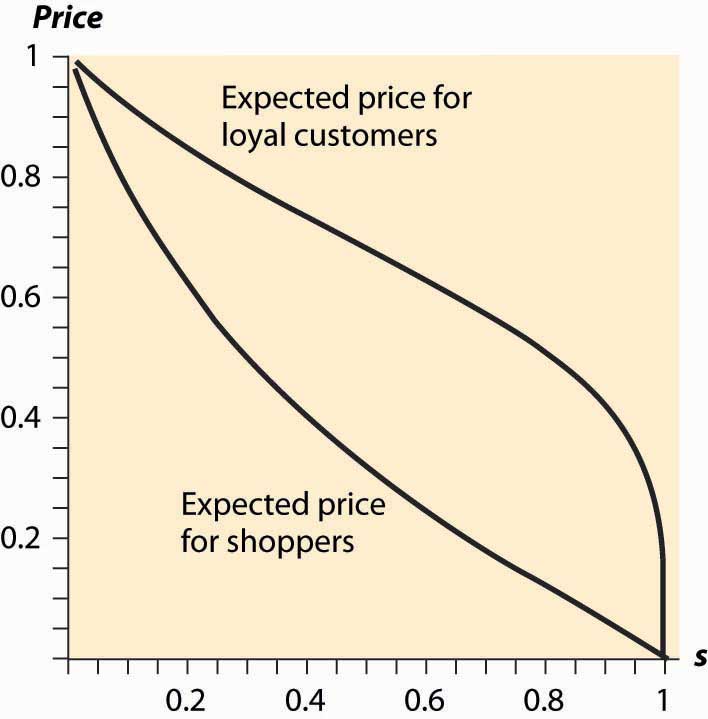
Similarly, we can examine the average prices for loyal customers and shoppers when the proportion of shoppers varies. Increasing the proportion of shoppers has two effects. First, it makes low prices more attractive, thus encouraging price competition because capturing the shoppers is more valuable. Second, it lowers industry profits because the set of loyal customers is reduced. Figure 18.2 "Expected Prices (" plots the average price for loyal customers and shoppers, as the proportion of shoppers ranges from zero to one, when there are five firms, pm = 1 and c = 0.
People who are price-sensitive and shop around convey a positive externality on other buyers by encouraging price competition. Similarly, people who are less price-sensitive and don’t shop around convey a negative externality on the other buyers. In markets with dispersed information about the best prices, where some buyers are informed and some are not, randomized prices are a natural outcome. That is, randomization of prices, and the failure of the law of one price, is just a reflection of the different willingness or ability to search on the part of consumers.
Figure 18.2 Expected Prices (s = Proportion of Shoppers)
This difference in the willingness to search could arise simply because search is itself costly. That is, the shoppers could be determined by their choice to shop in such a way that the cost of shopping just balances the expected gains from searching. The proportion of shoppers may adjust endogenously to ensure that the gains from searching exactly equal the costs of searching. In this way, a cost of shopping is translated into a randomized price equilibrium in which there is a benefit from shopping and all consumers get the same total cost of purchase on average.
Key Takeaways
- The law of one price, which states that identical goods sell at the same price, is unfortunately empirically false.
- There are many markets where prices appear unpredictable to consumers. Price variation over time or across stores is known as price dispersion.
- The basic price-dispersion model involves firms setting prices simultaneously and selling to two types of customers: one loyal to a particular store, the other (“shoppers”) buying from the cheapest store.
- There is no pure strategy equilibrium because firms either want to be just barely the cheapest or at the monopoly price. The only candidate for an equilibrium is a mixed strategy.
- There is a mixed strategy involving randomizing over an interval of prices.
- Industry profits in price dispersion arise from the number of loyal customers and are independent of the number of firms.
- An increase in the number of firms is good for shoppers and bad for loyal customers. In the limit as the number of firms goes to infinity, the shoppers pay marginal cost and loyal customers pay the monopoly price.
- Shoppers convey a positive externality on other buyers by encouraging price competition.




