This is “Energy and Chemistry”, chapter 7 from the book Beginning Chemistry (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
Chapter 7 Energy and Chemistry
Opening Essay
It takes energy to launch a spaceship into space. If it takes 1 energy unit to warm 0.25 g of water by 1°C, then it takes over 15,100 energy units to put that 0.25 g of water into earth orbit. The most powerful engines designed to lift rockets into space were part of the Saturn V rocket, that was built by the National Aeronautics and Space Administration (NASA). The rocket had three stages, with the first stage having the capability of launching about 3.5 million kg of mass. About 2.3 million kg was the actual fuel for the first stage; rockets in space have the unpleasant task of having to take their own chemicals with them to provide thrust.

It takes a lot of energy to launch a rocket into space. The Saturn V rocket used five of the most powerful engines ever built to take its initial step into orbit.
© Thinkstock
Having to carry its own fuel puts a lot of mass burden on an engine in space. This is why NASA is developing other types of engines to minimize fuel mass. An ion thruster uses xenon atoms that have had at least one electron removed from their atoms. The resulting ions can be accelerated by electric fields, causing a thrust. Because xenon atoms are very large for atoms, the thrusting efficiency is high even though the actual thrust is low. Because of this, ion engines are useful only in space.

Ion drives have low thrust but high efficiency. They have already been used on several space missions, including NASA’s Deep Space 1 spacecraft and Japan’s Hayabusa asteroid sampling probe.
Source: Photo courtesy of NASA, http://commons.wikimedia.org/wiki/File:Ion_Engine_Test_Firing_-_GPN-2000-000482.jpg.
Energy is a very important quantity in science and the world around us. Although most of our energy ultimately comes from the sun, much of the energy we use on a daily basis is rooted in chemical reactions. The gasoline in your car, the electricity in your house, the food in your diet—all provide substances for chemical reactions to provide energy (gasoline, food) or are produced from chemical reactions (electricity, about 50% of which is generated by burning coal). As such, it is only natural that the study of chemistry involves energy.
7.1 Energy
Learning Objectives
- Define energy.
- Know the units of energy.
- Understand the law of conservation of energy.
EnergyThe ability to do work. is the ability to do work. Think about it: when you have a lot of energy, you can do a lot of work; but if you’re low on energy, you don’t want to do much work. Work (w) itself is defined as a force (F) operating over a distance (Δx):
w = F × ΔxIn SI, force has units of newtons (N), while distance has units of meters. Therefore, work has units of N·m. This compound unit is redefined as a jouleThe SI unit of energy. (J):
1 joule = 1 newton·meter 1 J = 1 N·mBecause energy is the ability to do work, energy is also measured in joules. This is the primary unit of energy we will use here.
How much is 1 J? It is enough to warm up about one-fourth of a gram of water by 1°C. It takes about 12,000 J to warm a cup of coffee from room temperature to 50°C. So a joule is not a lot of energy. It will not be uncommon to measure energies in thousands of joules, so the kilojoule (kJ) is a common unit of energy, with 1 kJ equal to 1,000 J.
An older—but still common—unit of energy is the calorie. The calorie (cal) was originally defined in terms of warming up a given quantity of water. The modern definition of calorie equates it to joules:
1 cal = 4.184 JOne area where the calorie is used is in nutrition. Energy contents of foods are often expressed in calories. However, the calorie unit used for foods is actually the kilocalorie (kcal). Most foods indicate this by spelling the word with a capital C—Calorie. Figure 7.1 "Calories on Food Labels" shows one example. So be careful counting calories when you eat!
Figure 7.1 Calories on Food Labels

This label expresses the energy content of the food, but in Calories (which are actually kilocalories).
© Thinkstock
Example 1
The label in Figure 7.1 "Calories on Food Labels" states that the serving has 38 Cal. How many joules is this?
Solution
We recognize that with a capital C, the Calories unit is actually kilocalories. To determine the number of joules, we convert first from kilocalories to calories (using the definition of the kilo- prefix) and then from calories to joules (using the relationship between calories and joules). So
Test Yourself
A serving of breakfast cereal usually has 110 Cal. How many joules of energy is this?
Answer
460,000 J
In the study of energy, we use the term systemThe part of the universe under study. to describe the part of the universe under study: a beaker, a flask, or a container whose contents are being observed and measured. An isolated systemA system that does not allow a transfer of energy or matter into or out of the system. is a system that does not allow a transfer of energy or matter into or out of the system. A good approximation of an isolated system is a closed, insulated thermos-type bottle. The fact that the thermos-type bottle is closed keeps matter from moving in or out, and the fact that it is insulated keeps energy from moving in or out.
One of the fundamental ideas about the total energy of an isolated system is that is does not increase or decrease. When this happens to a quantity, we say that the quantity is conserved. The statement that the total energy of an isolated system does not change is called the law of conservation of energyThe total energy of an isolated system does not increase or decrease.. As a scientific law, this concept occupies the highest level of understanding we have about the natural universe.
Key Takeaways
- Energy is the ability to do work and uses the unit joule.
- The law of conservation of energy states that the total energy of an isolated system does not increase or decrease.
Exercises
-
Define energy. How is work related to energy?
-
Give two units of energy and indicate which one is preferred.
-
Express the quantity of 422 J in calories.
-
Express the quantity of 3.225 kJ in calories.
-
Express the quantity 55.69 cal in joules.
-
Express the quantity 965.33 kcal in joules.
-
How does a Calorie differ from a calorie?
-
Express the quantity 965.33 Cal in joules.
-
What is the law of conservation of energy?
-
What does the word conserved mean as applied to the law of conservation of energy?
Answers
-
Energy is the ability to do work. Work is a form of energy.
-
-
101 cal
-
-
233.0 J
-
-
A Calorie is actually a kilocalorie, or 1,000 calories.
-
-
The total energy of an isolated system does not increase or decrease.
-
7.2 Work and Heat
Learning Objectives
- Define a type of work in terms of pressure and volume.
- Define heat.
- Relate the amount of heat to a temperature change.
We have already defined work as a force acting through a distance. It turns out that there are other equivalent definitions of work that are also important in chemistry.
When a certain volume of a gas expands, it works against an external pressure to expand (Figure 7.2 "Volume versus Pressure"). That is, the gas must perform work. Assuming that the external pressure Pext is constant, the amount of work done by the gas is given by the equation
w = −Pext × ΔVwhere ΔV is the change in volume of the gas. This term is always the final volume minus the initial volume,
ΔV = Vfinal − Vinitialand can be positive or negative, depending on whether Vfinal is larger (is expanding) or smaller (is contracting) than Vinitial. The negative sign in the equation for work is important and implies that as volume expands (ΔV is positive), the gas in the system is losing energy as work. On the other hand, if the gas is contracting, ΔV is negative, and the two negative signs make the work positive, so energy is being added to the system.
Figure 7.2 Volume versus Pressure
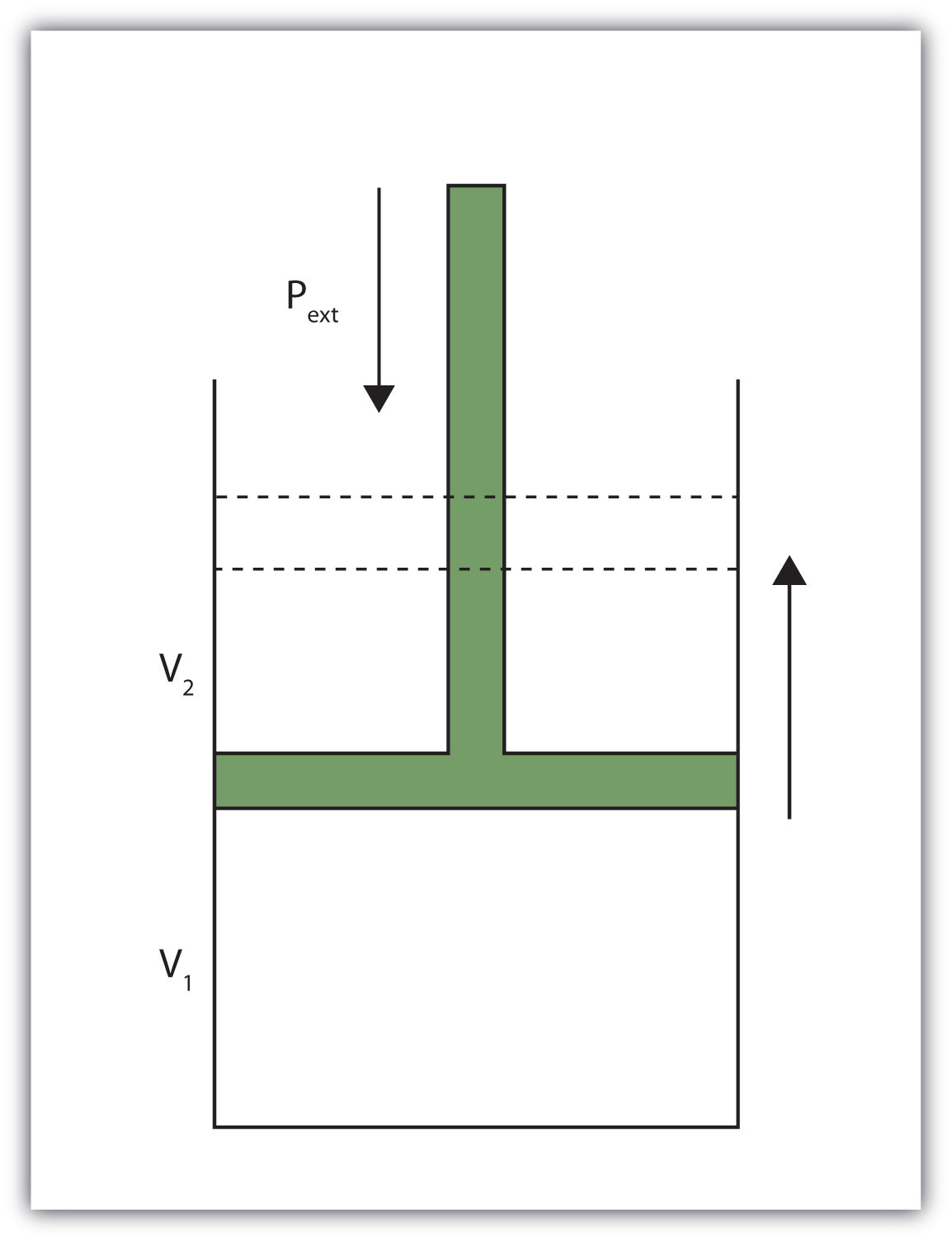
When a gas expands against an external pressure, the gas does work.
Finally, let us consider units. Volume changes are usually expressed in units like liters, while pressures are usually expressed in atmospheres. When we use the equation to determine work, the unit for work comes out as liter·atmospheres, or L·atm. This is not a very common unit for work. However, there is a conversion factor between L·atm and the common unit of work, joules:
1 L·atm = 101.32 JUsing this conversion factor and the previous equation for work, we can calculate the work performed when a gas expands or contracts.
Example 2
What is the work performed by a gas if it expands from 3.44 L to 6.19 L against a constant external pressure of 1.26 atm? Express the final answer in joules.
Solution
First we need to determine the change in volume, ΔV. A change is always the final value minus the initial value:
ΔV = Vfinal − Vinitial = 6.19 L − 3.44 L = 2.75 LNow we can use the definition of work to determine the work done:
w = −Pext · ΔV = −(1.26 atm)(2.75 L) = −3.47 L·atmNow we construct a conversion factor from the relationship between liter·atmospheres and joules:
We limit the final answer to three significant figures, as appropriate.
Test Yourself
What is the work performed when a gas expands from 0.66 L to 1.33 L against an external pressure of 0.775 atm?
Answer
−53 J
Heat is another aspect of energy. HeatThe transfer of energy from one body to another due to a difference in temperature. is the transfer of energy from one body to another due to a difference in temperature. For example, when we touch something with our hands, we interpret that object as either hot or cold depending on how energy is transferred: If energy is transferred into your hands, the object feels hot. If energy is transferred from your hands to the object, your hands feel cold. Because heat is a measure of energy transfer, heat is also measured in joules.
For a given object, the amount of heat (q) involved is proportional to two things: the mass of the object (m) and the temperature change (ΔT) evoked by the energy transfer. We can write this mathematically as
where ∝ means “is proportional to.” To make a proportionality an equality, we include a proportionality constant. In this case, the proportionality constant is labeled c and is called the specific heat capacityThe proportionality constant between heat, mass, and temperature change; also called specific heat., or, more succinctly, specific heat:
q = mcΔTwhere the mass, specific heat, and change in temperature are multiplied together. Specific heat is a measure of how much energy is needed to change the temperature of a substance; the larger the specific heat, the more energy is needed to change the temperature. The units for specific heat are or , depending on what the unit of ΔT is. You may note a departure from the insistence that temperature be expressed in Kelvin. That is because a change in temperature has the same value whether the temperatures are expressed in degrees Celsius or kelvins.
Example 3
Calculate the heat involved when 25.0 g of Fe increase temperature from 22°C to 76°C. The specific heat of Fe is 0.449 J/g·°C.
Solution
First we need to determine ΔT. A change is always the final value minus the initial value:
ΔT = 76°C − 22°C = 54°CNow we can use the expression for q, substitute for all variables, and solve for heat:
Note how the g and °C units cancel, leaving J, a unit of heat. Also note that this value of q is inherently positive, meaning that energy is going into the system.
Test Yourself
Calculate the heat involved when 76.5 g of Ag increase temperature from 17.8°C to 144.5°C. The specific heat of Ag is 0.233 J/g·°C.
Answer
2,260 J
As with any equation, when you know all but one variable in the expression for q, you can determine the remaining variable by using algebra.
Example 4
It takes 5,408 J of heat to raise the temperature of 373 g of Hg by 104°C. What is the specific heat of Hg?
Solution
We can start with the equation for q, but now different values are given, and we need to solve for specific heat. Note that ΔT is given directly as 104°C. Substituting,
5,408 J = (373 g)c(104°C)We divide both sides of the equation by 373 g and 104°C:
Combining the numbers and bringing together all the units, we get
Test Yourself
Gold has a specific heat of 0.129 J/g·°C. If 1,377 J are needed to increase the temperature of a sample of gold by 99.9°C, what is the mass of the gold?
Answer
107 g
Table 7.1 "Specific Heats of Various Substances" lists the specific heats of some substances. Specific heat is a physical property of substances, so it is a characteristic of the substance. The general idea is that the lower the specific heat, the less energy is required to change the temperature of the substance by a certain amount.
Table 7.1 Specific Heats of Various Substances
| Substance | Specific Heat (J/g·°C) |
|---|---|
| water | 4.184 |
| iron | 0.449 |
| gold | 0.129 |
| mercury | 0.139 |
| aluminum | 0.900 |
| ethyl alcohol | 2.419 |
| magnesium | 1.03 |
| helium | 5.171 |
| oxygen | 0.918 |
Key Takeaways
- Work can be defined as a gas changing volume against a constant external pressure.
- Heat is the transfer of energy due to temperature differences.
- Heat can be calculated in terms of mass, temperature change, and specific heat.
Exercises
-
Give two definitions of work.
-
What is the sign on work when a sample of gas increases its volume? Explain why work has that sign.
-
What is the work when a gas expands from 3.00 L to 12.60 L against an external pressure of 0.888 atm?
-
What is the work when a gas expands from 0.666 L to 2.334 L against an external pressure of 2.07 atm?
-
What is the work when a gas contracts from 3.45 L to 0.97 L under an external pressure of 0.985 atm?
-
What is the work when a gas contracts from 4.66 L to 1.22 L under an external pressure of 3.97 atm?
-
Like work, the sign on heat can be positive or negative. What is happening to the total energy of a system if heat is positive?
-
Like work, the sign on heat can be positive or negative. What is happening to the total energy of a system if heat is negative?
-
What is the heat when 55.6 g of Fe increase temperature from 25.6°C to 177.9°C? The heat capacity of Fe is in Table 7.1 "Specific Heats of Various Substances".
-
What is the heat when 0.444 g of Au increases temperature from 17.8°C to 222.5°C? The heat capacity of Au is in Table 7.1 "Specific Heats of Various Substances".
-
What is the heat when 245 g of H2O cool from 355 K to 298 K? The heat capacity of H2O is in Table 7.1 "Specific Heats of Various Substances".
-
What is the heat when 100.0 g of Mg cool from 725 K to 552 K? The heat capacity of Mg is in Table 7.1 "Specific Heats of Various Substances".
-
It takes 452 J of heat to raise the temperature of a 36.8 g sample of a metal from 22.9°C to 98.2°C. What is the heat capacity of the metal?
-
It takes 2,267 J of heat to raise the temperature of a 44.5 g sample of a metal from 33.9°C to 288.3°C. What is the heat capacity of the metal?
-
An experimenter adds 336 J of heat to a 56.2 g sample of Hg. What is its change in temperature? The heat capacity of Hg is in Table 7.1 "Specific Heats of Various Substances".
-
To a 0.444 g sample of H2O, 23.4 J of heat are added. What is its change in temperature? The heat capacity of H2O is in Table 7.1 "Specific Heats of Various Substances".
-
An unknown mass of Al absorbs 187.9 J of heat and increases its temperature from 23.5°C to 35.6°C. What is the mass of the aluminum? How many moles of aluminum is this?
-
A sample of He goes from 19.4°C to 55.9°C when 448 J of energy are added. What is the mass of the helium? How many moles of helium is this?
Answers
-
Work is a force acting through a distance or a volume changing against some pressure.
-
-
−864 J
-
-
248 J
-
-
When heat is positive, the total energy of the system is increasing.
-
-
3.80 × 103 J
-
-
−58,400 J
-
-
0.163 J/g·°C
-
-
43.0°C
-
-
17.3 g; 0.640 mol
-
7.3 Enthalpy and Chemical Reactions
Learning Objectives
- Define enthalpy.
- Properly express the enthalpy change of chemical reactions.
- Explain how enthalpy changes are measured experimentally.
Now that we have shown how energy, work, and heat are related, we are ready to consider energy changes in chemical reactions. A fundamental concept is that every chemical reaction occurs with a concurrent change in energy. Now we need to learn how to properly express these energy changes.
Our study of gases in Chapter 6 "Gases" and our definition of work in Section 7.2 "Work and Heat" indicate that conditions like pressure, volume, and temperature affect the energy content of a system. What we need is a definition of energy that holds when some of these conditions are specified (somewhat similar to our definition of standard temperature and pressure in our study of gases). We define the enthalpy changeThe heat of a process at constant pressure; denoted . (ΔH) as the heat of a process when pressure is held constant:
The letter H stands for “enthalpy,” a kind of energy, while the Δ implies a change in the quantity. We will always be interested in the change in H, rather than the absolute value of H itself.
When a chemical reaction occurs, there is a characteristic change in enthalpy. The enthalpy change for a reaction is typically written after a balanced chemical equation and on the same line. For example, when two moles of hydrogen react with one mole of oxygen to make two moles of water, the characteristic enthalpy change is 570 kJ. We write the equation as
2H2(g) + O2(g) → 2H2O(ℓ) ΔH = −570 kJA chemical equation that includes an enthalpy change is called a thermochemical equationA chemical equation that includes an enthalpy change.. A thermochemical equation is assumed to refer to the equation in molar quantities, which means it must be interpreted in terms of moles, not individual molecules.
Example 5
Write the thermochemical equation for the reaction of PCl3(g) with Cl2(g) to make PCl5(g), which has an enthalpy change of −88 kJ.
Solution
The thermochemical equation is
PCl3(g) + Cl2(g) → PCl5(g) ΔH = −88 kJTest Yourself
Write the thermochemical equation for the reaction of N2(g) with O2(g) to make 2NO(g), which has an enthalpy change of 181 kJ.
Answer
N2(g) + O2(g) → 2NO(g) ΔH = 181 kJYou may have noticed that the ΔH for a chemical reaction may be positive or negative. The number is assumed to be positive if it has no sign; a + sign can be added explicitly to avoid confusion. A chemical reaction that has a positive ΔH is said to be endothermicA chemical reaction that has a positive change in enthalpy., while a chemical reaction that has a negative ΔH is said to be exothermicA chemical reaction that has a negative change in enthalpy..
What does it mean if the ΔH of a process is positive? It means that the system in which the chemical reaction is occurring is gaining energy. If one considers the energy of a system as being represented as a height on a vertical energy plot, the enthalpy change that accompanies the reaction can be diagrammed as in part (a) in Figure 7.3 "Reaction Energy": the energy of the reactants has some energy, and the system increases its energy as it goes to products. The products are higher on the vertical scale than the reactants. Endothermic, then, implies that the system gains, or absorbs, energy.
An opposite situation exists for an exothermic process, as shown in part (b) in Figure 7.3 "Reaction Energy". If the enthalpy change of a reaction is negative, the system is losing energy, so the products have less energy than the reactants, and the products are lower on the vertical energy scale than the reactants are. Exothermic, then, implies that the system loses, or gives off, energy.
Figure 7.3 Reaction Energy
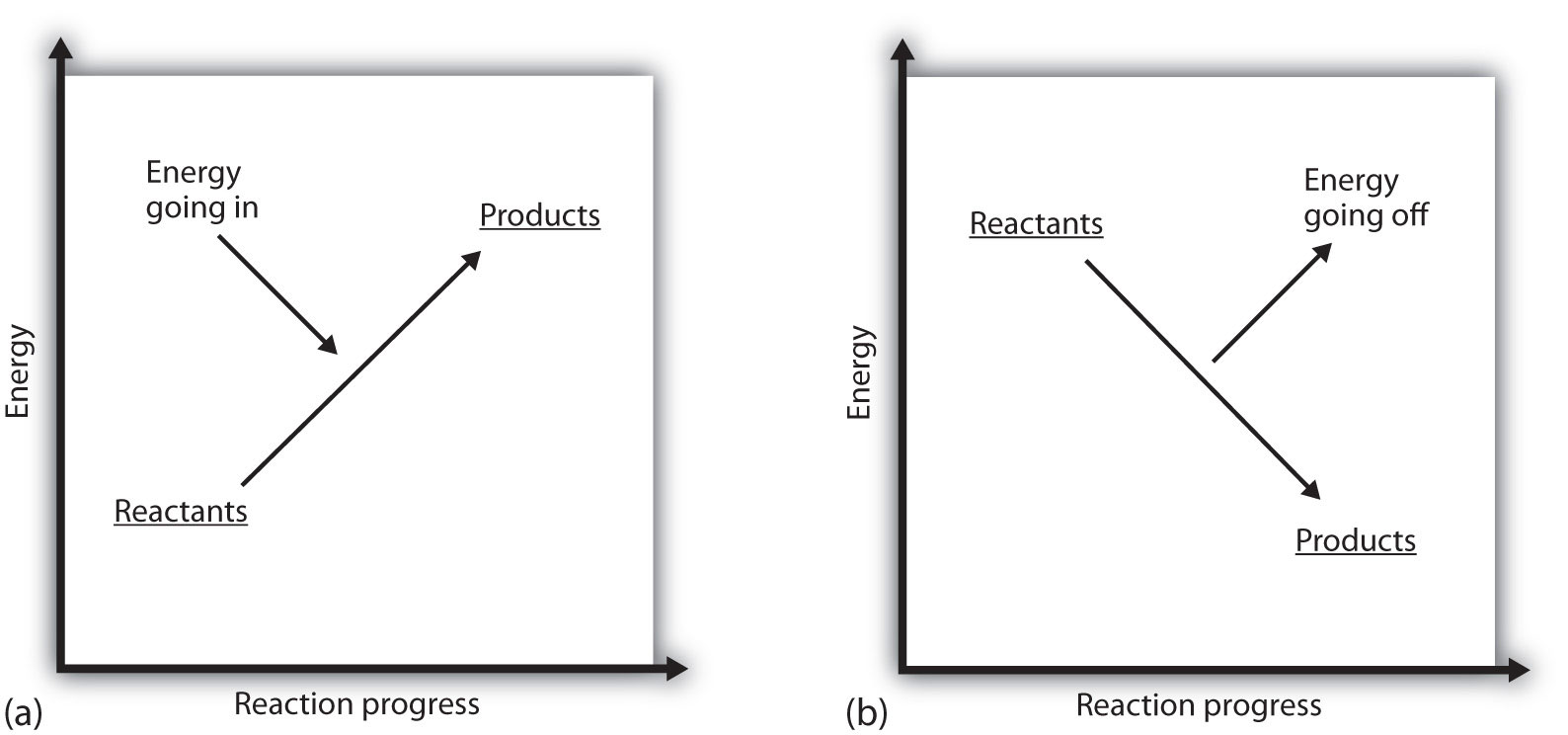
(a) In an endothermic reaction, the energy of the system increases (i.e., moves higher on the vertical scale of energy). (b) In an exothermic reaction, the energy of the system decreases (i.e., moves lower on the vertical scale of energy).
Example 6
Consider this thermochemical equation.
2CO(g) + O2(g) → 2CO2(g) ΔH = −565 kJIs it exothermic or endothermic? How much energy is given off or absorbed?
Solution
By definition, a chemical reaction that has a negative ΔH is exothermic, meaning that this much energy—in this case, 565 kJ—is given off by the reaction.
Test Yourself
Consider this thermochemical equation.
CO2(g) + H2(g) → CO(g) + H2O(g) ΔH = 42 kJIs it exothermic or endothermic? How much energy is given off or absorbed?
Answer
Endothermic; 42 kJ are absorbed.
How are ΔH values measured experimentally? Actually, ΔH is not measured; q is measured. But the measurements are performed under conditions of constant pressure, so ΔH is equal to the q measured.
Experimentally, q is measured by taking advantage of the equation
q = mcΔTWe premeasure the mass of the chemicals in a system. Then we let the chemical reaction occur and measure the change in temperature (ΔT) of the system. If we know the specific heat of the materials in the system (typically, we do), we can calculate q. That value of q is numerically equal to the ΔH of the process, which we can scale up to a molar scale. The container in which the system resides is typically insulated, so any energy change goes into changing the temperature of the system, rather than being leaked from the system. The container is referred to as a calorimeterA container used to measure the heat of a chemical reaction., and the process of measuring changes in enthalpy is called calorimetryThe process of measuring enthalpy changes for chemical reactions..
Figure 7.4 Calorimeters
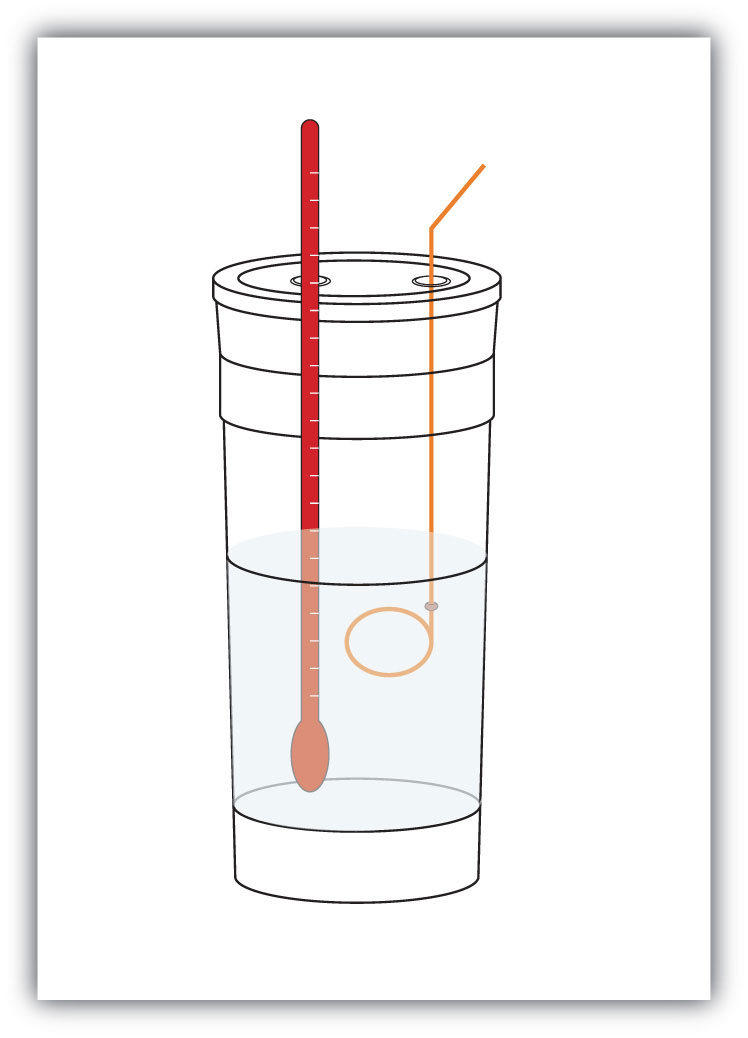
A simple calorimeter can be constructed from some nested foam coffee cups, a cover, a thermometer, and a stirrer.
For example, suppose 4.0 g of NaOH, or 0.10 mol of NaOH, are dissolved to make 100.0 mL of aqueous solution, while 3.65 g of HCl, or 0.10 mol of HCl, are dissolved to make another 100.0 mL of aqueous solution. The two solutions are mixed in an insulated calorimeter, a thermometer is inserted, and the calorimeter is covered (see Figure 7.4 "Calorimeters" for an example setup). The thermometer measures the temperature change as the following chemical reaction occurs:
NaOH (aq) + HCl(aq) → NaCl(aq) + H2O(ℓ)An observer notes that the temperature increases from 22.4°C to 29.1°C. Assuming that the heat capacities and densities of the solutions are the same as those of pure water, we now have the information we need to determine the enthalpy change of the chemical reaction. The total amount of solution is 200.0 mL, and with a density of 1.00 g/mL, we thus have 200.0 g of solution. Using the equation for q, we substitute for our experimental measurements and the specific heat of water (Table 7.1 "Specific Heats of Various Substances"):
Solving for q, we get
The heat q is equal to the ΔH for the reaction because the chemical reaction occurs at constant pressure. However, the reaction is giving off this amount of energy, so the actual sign on ΔH is negative:
ΔH = −5,600 J for the reactionThus, we have the following thermochemical equation for the chemical reaction that occurred in the calorimeter:
The 1/10 coefficients are present to remind us that we started with one-tenth of a mole of each reactant, so we make one-tenth of a mole of each product. Typically, however, we report thermochemical equations in terms of moles, not one-tenth of a mole. To scale up to molar quantities, we must multiply the coefficients by 10. However, when we do this, we get 10 times as much energy. Thus, we have
NaOH (aq) + HCl(aq) → NaCl(aq) + H2O(ℓ) ΔH = −56,000 JThe ΔH can be converted into kJ units, so our final thermochemical equation is
NaOH (aq) + HCl(aq) → NaCl(aq) + H2O(ℓ) ΔH = −56 kJWe have just taken our experimental data from calorimetry and determined the enthalpy change of a chemical reaction. Similar measurements on other chemical reactions can determine the ΔH values of any chemical reaction you want to study.
Example 7
A 100 mL solution of 0.25 mol of Ca2+(aq) was mixed with 0.50 mol of F−(aq) ions, and CaF2 was precipitated:
Ca2+(aq) + 2F−(aq) → CaF2(s)The temperature of the solution increased by 10.5°C. What was the enthalpy change for the chemical reaction? What was the enthalpy change for the production of 1 mol of CaF2? Assume that the solution has the same density and specific heat as water.
Solution
Because we are given ΔT directly, we can determine the heat of the reaction, which is equal to ΔH:
Solving for q, we get
q = 4,400 JTherefore, ΔH = −4,400 J.
According to the stoichiometry of the reaction, exactly 0.25 mol of CaF2 will form, so this quantity of heat is for 0.25 mol. For 1 mol of CaF2, we need to scale up the heat by a factor of four:
q = 4,400 J × 4 = 17,600 J for 1 mol CaF2On a molar basis, the change in enthalpy is
ΔH = −17,600 J = −17.6 kJTest Yourself
In a calorimeter at constant pressure, 0.10 mol of CH4(g) and 0.20 mol of O2(g) are reacted.
CH4(g) + 2O2(g) → CO2(g) + 2H2O(ℓ)The reaction warms 750.0 g of H2O by 28.4°C. What is ΔH for the reaction on a molar scale?
Answer
−891 kJ
Key Takeaways
- Every chemical reaction occurs with a concurrent change in energy.
- The change in enthalpy equals heat at constant pressure.
- Enthalpy changes can be expressed by using thermochemical equations.
- Enthalpy changes are measured by using calorimetry.
Exercises
-
Under what circumstances are q and ΔH the same?
-
Under what circumstances are q and ΔH different?
-
Hydrogen gas and chlorine gas react to make hydrogen chloride gas with an accompanying enthalpy change of −184 kJ. Write a properly balanced thermochemical equation for this process.
-
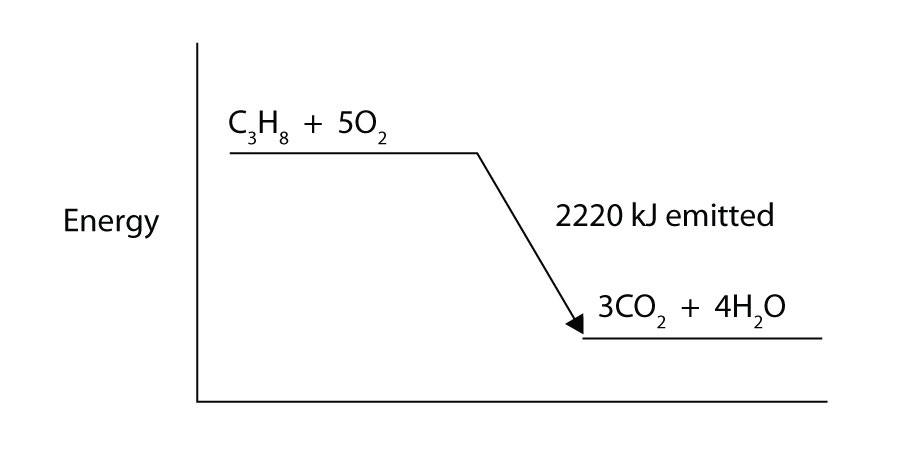
Propane (C3H8) reacts with elemental oxygen gas to produce carbon dioxide and liquid water with an accompanying enthalpy change of −2,220 kJ. Write a properly balanced thermochemical equation for this process.
-
Nitrogen gas reacts with oxygen gas to make NO(g) while absorbing 180 kJ. Write a properly balanced thermochemical equation for this process.
-
Solid sodium reacts with chlorine gas to make solid sodium chloride while giving off 772 kJ. Write a properly balanced thermochemical equation for this process.
-
Hydrogen gas and chlorine gas react to make hydrogen chloride gas with an accompanying enthalpy change of −184 kJ. Is this process endothermic or exothermic?
-
Propane (C3H8) reacts with elemental oxygen gas to produce carbon dioxide while giving off 2,220 kJ of energy. Is this process endothermic or exothermic?
-
Nitrogen gas reacts with oxygen gas to make NO(g) while absorbing 180 kJ. Is this process exothermic or endothermic?
-
Sodium metal can react with nitrogen to make sodium azide (NaN3) with a ΔH of 21.72 kJ. Is this process exothermic or endothermic?
-
Draw an energy level diagram for the chemical reaction in Exercise 8. (See Figure 7.3 "Reaction Energy" for an example.)
-
Draw an energy level diagram for the chemical reaction in Exercise 9. (See Figure 7.3 "Reaction Energy" for an example.)
-
In a 250 mL solution, 0.25 mol of KOH(aq) and 0.25 mol of HNO3(aq) are combined. The temperature of the solution increases from 22.5°C to 35.9°C. Assume the solution has the same density and heat capacity of water. What is the heat of the reaction, and what is the ΔH of the reaction on a molar basis?
-
In a 600 mL solution, 0.50 mol of Ca(OH)2(aq) and 0.50 mol of H2SO4(aq) are combined. The temperature of the solution increases by 22.3°C. What is the heat of the reaction, and what is the ΔH of the reaction on a molar basis? Assume the solution has the same density and heat capacity of water.
-
To warm 400.0 g of H2O, 0.050 mol of ethanol (C2H5OH) is burned. The water warms from 24.6°C to 65.6°C. What is the heat of the reaction, and what is the ΔH of the reaction on a molar basis?
-
To warm 100.0 g of H2O, 0.066 mol beeswax is burned. The water warms from 21.4°C to 25.5°C. What is the heat of the reaction, and what is the ΔH of the reaction on a molar basis?
Answers
-
under conditions of constant pressure
-
-
H2(g) + Cl2(g) → 2HCl(g) ΔH = −184 kJ
-
-
N2(g) + O2(g) → 2NO(g) ΔH = 180 kJ
-
-
exothermic
-
-
endothermic
-
-
-
-
heat of reaction = −14.0 kJ; ΔH = −56.0 kJ/mol of reactants
-
-
heat of reaction = −68.6 kJ; ΔH = −1,370 kJ/mole of ethanol
-
7.4 Stoichiometry Calculations Using Enthalpy
Learning Objective
- Perform stoichiometry calculations using energy changes from thermochemical equations.
In Chapter 5 "Stoichiometry and the Mole", we related quantities of one substance to another in a chemical equation by performing calculations that used the balanced chemical equation; the balanced chemical equation provided equivalences that we used to construct conversion factors. For example, in the balanced chemical equation
2H2(g) + O2(g) → 2H2O(ℓ)we recognized the equivalences
2 mol H2 ⇔ 1 mol O2 ⇔ 2 mol H2Owhere ⇔ is the mathematical symbol for “is equivalent to.” In our thermochemical equation, however, we have another quantity—energy change:
2H2(g) + O2(g) → 2H2O(ℓ) ΔH = −570 kJThis new quantity allows us to add another equivalence to our list:
2 mol H2 ⇔ 1 mol O2 ⇔ 2 mol H2O ⇔ −570 kJThat is, we can now add an energy amount to the equivalences—the enthalpy change of a balanced chemical reaction. This equivalence can also be used to construct conversion factors so that we can relate enthalpy change to amounts of substances reacted or produced.
Note that these equivalences address a concern. When an amount of energy is listed for a balanced chemical reaction, what amount(s) of reactants or products does it refer to? The answer is that relates to the number of moles of the substance as indicated by its coefficient in the balanced chemical reaction. Thus, 2 mol of H2 are related to −570 kJ, while 1 mol of O2 is related to −570 kJ. This is why the unit on the energy change is kJ, not kJ/mol.
For example, consider the thermochemical equation
H2(g) + Cl2(g) → 2HCl(g) ΔH = −184.6 kJThe equivalences for this thermochemical equation are
1 mol H2 ⇔ 1 mol Cl2 ⇔ 2 mol HCl ⇔ −184.6 kJSuppose we asked how much energy is given off when 8.22 mol of H2 react. We would construct a conversion factor between the number of moles of H2 and the energy given off, −184.6 kJ:
The negative sign means that this much energy is given off.
Example 8
Given the thermochemical equation
N2(g) + 3H2(g) → 2NH3(g) ΔH = −91.8 kJhow much energy is given off when 222.4 g of N2 reacts?
Solution
The balanced thermochemical equation relates the energy change to moles, not grams, so we first convert the amount of N2 to moles and then use the thermochemical equation to determine the energy change:
Test Yourself
Given the thermochemical equation
N2(g) + 3H2(g) → 2NH3(g) ΔH = −91.8 kJhow much heat is given off when 1.00 g of H2 reacts?
Answer
−15.1 kJ
Like any stoichiometric quantity, we can start with energy and determine an amount, rather than the other way around.
Example 9
Given the thermochemical equation
N2(g) + O2(g) → 2NO(g) ΔH = 180.6 kJif 558 kJ of energy are supplied, what mass of NO can be made?
Solution
This time, we start with an amount of energy:
Test Yourself
How many grams of N2 will react if 100.0 kJ of energy are supplied?
N2(g) + O2(g) → 2NO(g) ΔH = 180.6 kJAnswer
15.5 g
Chemistry Is Everywhere: Welding with Chemical Reactions
One very energetic reaction is called the thermite reaction. Its classic reactants are aluminum metal and iron(III) oxide; the reaction produces iron metal and aluminum oxide:
2Al(s) + Fe2O3(s) → Al2O3(s) + 2Fe(s) ΔH = −850.2 kJWhen properly done, the reaction gives off so much energy that the iron product comes off as a liquid. (Iron normally melts at 1,536°C.) If carefully directed, the liquid iron can fill spaces between two or more metal parts and, after it quickly cools, can weld the metal parts together.
Thermite reactions are used for this purpose even today. For civilian purposes, they are used to reweld broken locomotive axles that cannot be easily removed for repair. They are used to weld railroad tracks together. Thermite reactions can also be used to separate thin pieces of metal if, for whatever reason, a torch doesn’t work.

A small clay pot contains a thermite mixture. It is reacting at high temperature in the photo and will eventually produce molten metal to join the railroad tracks below it.
Source: Photo courtesy of Skatebiker, http://commons.wikimedia.org/wiki/File:Velp-thermitewelding-1.jpg.
Thermite reactions are also used for military purposes. Thermite mixtures are frequently used with additional components as incendiary devices—devices that start fires. Thermite reactions are also useful in disabling enemy weapons: a piece of artillery doesn’t work so well when it has a hole melted into its barrel because of a thermite reaction!
Key Takeaway
- The energy change of a chemical reaction can be used in stoichiometry calculations.
Exercises
-
Write the equivalences that this balanced thermochemical equation implies.
PCl3(g) + Cl2(g) → PCl5(g) ΔH = −87.9 kJ -
Write the equivalences that this balanced thermochemical equation implies.
2SO3(g) → 2SO2(g) + O2(g) ΔH = 197.9 kJ -
How many kilojoules are given off when 17.8 mol of CH4(g) react?
CH4(g) + 2O2(g) → CO2(g) + 2H2O(ℓ) ΔH = −890.1 kJ -
How many kilojoules are absorbed when 0.772 mol of N2(g) reacts?
N2(g) + 2NO(g) → 2N2O(g) ΔH = 73.8 kJ -
How many kilojoules are absorbed when 23.09 mol of C6H6(ℓ) are formed?
6C(s) + 3H2(g) → C6H6(ℓ) ΔH = 49.0 kJ -
How many kilojoules are given off when 8.32 mol of Mg react?
2Mg(s) + O2(g) → 2MgO(s) ΔH = −1,213 kJ -
Glucose is the main fuel metabolized in animal cells:
C6H12O6 + 6O2 → 6CO2 + 6H2O ΔH = −2,799 kJHow much energy is given off when 100.0 g of C6H12O6 react?
-
Given the thermochemical equation
2Al(s) + Fe2O3(s) → Al2O3(s) + 2Fe(s) ΔH = −850.2 kJhow much energy is given off when 288 g of Fe are produced?
-
Given the thermochemical equation
2CO2(g) → 2CO(g) + O2(g) ΔH = 566 kJhow much energy is absorbed when 85.2 g of CO2 are reacted?
-
Given the thermochemical equation
2Na+(aq) + SO42−(aq) → Na2SO4(s) ΔH = 819.8 kJhow much energy is absorbed when 55.9 g of Na+(aq) are reacted?
-
NaHCO3 decomposes when exposed to heat:
2NaHCO3(s) → Na2CO3(s) + CO2(g) + H2O(ℓ) ΔH = 91.5 kJWhat mass of NaHCO3 is decomposed by 256 kJ?
-
HgO decomposes when exposed to heat:
2HgO(s) → 2Hg(ℓ) + O2(g) ΔH = 181.6 kJWhat mass of O2 can be made with 100.0 kJ?
-
For the thermochemical equation
Fe2O3(s) + 3SO3(g) → Fe2(SO4)3 (s) ΔH = −570.2 kJwhat mass of SO3 is needed to generate 1,566 kJ?
-
For the thermochemical equation
H2(g) + Br2(ℓ) → 2HBr(g) ΔH = −72.6 kJwhat mass of HBr will be formed when 553 kJ of energy are given off?
Answers
-
1 mol of PCl3 ⇔ 1 mol of Cl2 ⇔ 1 mol of PCl5 ⇔ −87.9 kJ
-
-
15,800 kJ
-
-
1,130 kJ
-
-
1,554 kJ
-
-
548 kJ
-
-
470 g
-
-
6.60 × 102 g
-
7.5 Hess’s Law
Learning Objective
- Learn how to combine chemical equations and their enthalpy changes.
Now that we understand that chemical reactions occur with a simultaneous change in energy, we can apply the concept more broadly. To start, remember that some chemical reactions are rather difficult to perform. For example, consider the combustion of carbon to make carbon monoxide:
2C(s) + O2(g) → 2CO(g) ΔH = ?In reality, this is extremely difficult to do; given the opportunity, carbon will react to make another compound, carbon dioxide:
2C(s) + O2(g) → 2CO2(g) ΔH = −393.5 kJIs there a way around this? Yes. It comes from the understanding that chemical equations can be treated like algebraic equations, with the arrow acting like the equals sign. Like algebraic equations, chemical equations can be combined, and if the same substance appears on both sides of the arrow, it can be canceled out (much like a spectator ion in ionic equations). For example, consider these two reactions:
2C(s) + 2O2(g) → 2CO2(g) 2CO2(g) → 2CO(g) + O2(g)If we added these two equations by combining all the reactants together and all the products together, we would get
2C(s) + 2O2(g) + 2CO2(g) → 2CO2(g) + 2CO(g) + O2(g)We note that 2CO2(g) appears on both sides of the arrow, so they cancel:
We also note that there are 2 mol of O2 on the reactant side, and 1 mol of O2 on the product side. We can cancel 1 mol of O2 from both sides:
What do we have left?
2C(s) + O2(g) → 2CO(g)This is the reaction we are looking for! So by algebraically combining chemical equations, we can generate new chemical equations that may not be feasible to perform.
What about the enthalpy changes? Hess’s lawWhen chemical equations are combined algebraically, their enthalpies can be combined in exactly the same way. states that when chemical equations are combined algebraically, their enthalpies can be combined in exactly the same way. Two corollaries immediately present themselves:
- If a chemical reaction is reversed, the sign on ΔH is changed.
- If a multiple of a chemical reaction is taken, the same multiple of the ΔH is taken as well.
What are the equations being combined? The first chemical equation is the combustion of C, which produces CO2:
2C(s) + 2O2(g) → 2CO2(g)This reaction is two times the reaction to make CO2 from C(s) and O2(g), whose enthalpy change is known:
C(s) + O2(g) → CO2(g) ΔH = −393.5 kJAccording to the first corollary, the first reaction has an energy change of two times −393.5 kJ, or −787.0 kJ:
2C(s) + 2O2(g) → 2CO2(g) ΔH = −787.0 kJThe second reaction in the combination is related to the combustion of CO(g):
2CO(g) + O2(g) → 2CO2(g) ΔH = −566.0 kJThe second reaction in our combination is the reverse of the combustion of CO. When we reverse the reaction, we change the sign on the ΔH:
2CO2(g) → 2CO(g) + O2(g) ΔH = +566.0 kJNow that we have identified the enthalpy changes of the two component chemical equations, we can combine the ΔH values and add them:
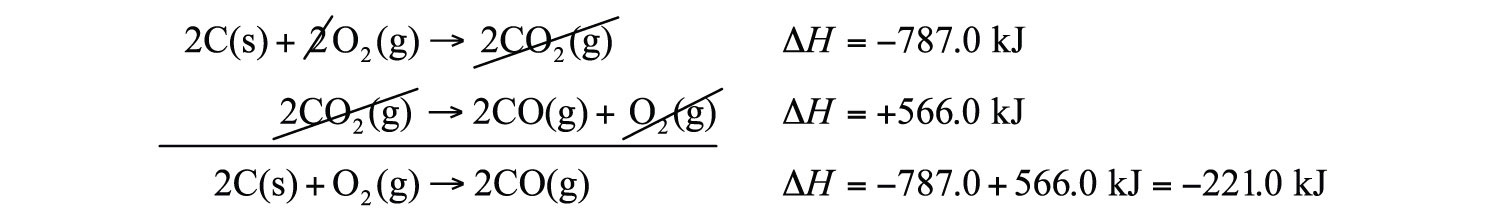
Hess’s law is very powerful. It allows us to combine equations to generate new chemical reactions whose enthalpy changes can be calculated, rather than directly measured.
Example 10
Determine the enthalpy change of
C2H4 + 3O2 → 2CO2 + 2H2O ΔH = ?from these reactions:
C2H2 + H2 → C2H4 ΔH = −174.5 kJ 2C2H2 + 5O2 → 4CO2 + 2H2O ΔH = −1,692.2 kJ 2CO2 + H2 → 2O2 + C2H2 ΔH = −167.5 kJSolution
We will start by writing chemical reactions that put the correct number of moles of the correct substance on the proper side. For example, our desired reaction has C2H4 as a reactant, and only one reaction from our data has C2H4. However, it has C2H4 as a product. To make it a reactant, we need to reverse the reaction, changing the sign on the ΔH:
C2H4 → C2H2 + H2 ΔH = +174.5 kJWe need CO2 and H2O as products. The second reaction has them on the proper side, so let us include one of these reactions (with the hope that the coefficients will work out when all our reactions are added):
2C2H2 + 5O2 → 4CO2 + 2H2O ΔH = −1,692.2 kJWe note that we now have 4 mol of CO2 as products; we need to get rid of 2 mol of CO2. The last reaction has 2CO2 as a reactant. Let us use it as written:
2CO2 + H2 → 2O2 + C2H2 ΔH = −167.5 kJWe combine these three reactions, modified as stated:
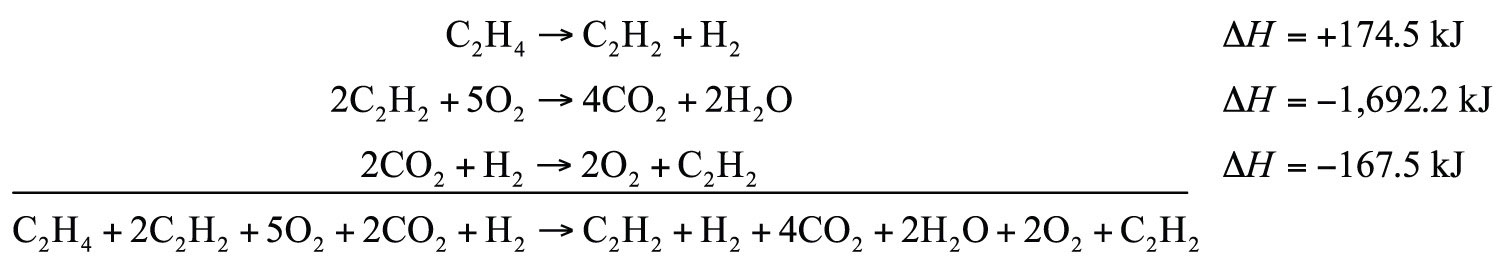
What cancels? 2C2H2, H2, 2O2, and 2CO2. What is left is
C2H4 + 3O2 → 2CO2 + 2H2Owhich is the reaction we are looking for. The ΔH of this reaction is the sum of the three ΔH values:
ΔH = +174.5 − 1,692.2 − 167.5 = −1,685.2 kJTest Yourself
Given the thermochemical equations
Pb + Cl2 → PbCl2 ΔH = −223 kJ PbCl2 + Cl2 → PbCl4 ΔH = −87 kJdetermine ΔH for
2PbCl2 → Pb + PbCl4Answer
+136 kJ
Key Takeaway
- Hess’s law allows us to combine reactions algebraically and then combine their enthalpy changes the same way.
Exercises
-
Define Hess’s law.
-
What does Hess’s law require us to do to the ΔH of a thermochemical equation if we reverse the equation?
-
If the ΔH for
C2H4 + H2 → C2H6is −65.6 kJ, what is the ΔH for this reaction?
C2H6 → C2H4 + H2 -
If the ΔH for
2Na + Cl2 → 2NaClis −772 kJ, what is the ΔH for this reaction:
2NaCl → 2Na + Cl2 -
If the ΔH for
C2H4 + H2 → C2H6is −65.6 kJ, what is the ΔH for this reaction?
2C2H4 + 2H2 → 2C2H6 -
If the ΔH for
2C2H6 + 7O2 → 4CO2 + 6H2Ois −2,650 kJ, what is the ΔH for this reaction?
6C2H6 + 21O2 → 12CO2 + 18H2O -
The ΔH for
C2H4 + H2O → C2H5OHis −44 kJ. What is the ΔH for this reaction?
2C2H5OH → 2C2H4 + 2H2O -
The ΔH for
N2 + O2 → 2NOis 181 kJ. What is the ΔH for this reaction?
NO → 1/2N2 + 1/2O2 -
Determine the ΔH for the reaction
Cu + Cl2 → CuCl2given these data:
2Cu + Cl2 → 2CuCl ΔH = −274 kJ 2CuCl + Cl2 → 2CuCl2 ΔH = −166 kJ -
Determine ΔH for the reaction
2CH4 → 2H2 + C2H4given these data:
CH4 + 2O2 → CO2 + 2H2O ΔH = −891 kJ C2H4 + 3O2 → 2CO2 + 2H2O ΔH = −1,411 kJ 2H2 + O2 → 2H2O ΔH = −571 kJ -
Determine ΔH for the reaction
Fe2(SO4)3 → Fe2O3 + 3SO3given these data:
4Fe + 3O2 → 2Fe2O3 ΔH = −1,650 kJ 2S + 3O2 → 2SO3 ΔH = −792 kJ 2Fe + 3S + 6O2 → Fe2(SO4)3 ΔH = −2,583 kJ -
Determine ΔH for the reaction
CaCO3 → CaO + CO2given these data:
2Ca + 2C + 3O2 → 2CaCO3 ΔH = −2,414 kJ C + O2 → CO2 ΔH = −393.5 kJ 2Ca + O2 → 2CaO ΔH = −1,270 kJ
Answers
-
If chemical equations are combined, their energy changes are also combined.
-
-
ΔH = 65.6 kJ
-
-
ΔH = −131.2 kJ
-
-
ΔH = 88 kJ
-
-
ΔH = −220 kJ
-
-
ΔH = 570 kJ
-
7.6 Formation Reactions
Learning Objectives
- Define a formation reaction and be able to recognize one.
- Use enthalpies of formation to determine the enthalpy of reaction.
Hess’s law allows us to construct new chemical reactions and predict what their enthalpies of reaction will be. This is a very useful tool because now we don’t have to measure the enthalpy changes of every possible reaction. We need measure only the enthalpy changes of certain benchmark reactions and then use these reactions to algebraically construct any possible reaction and combine the enthalpies of the benchmark reactions accordingly.
But what are the benchmark reactions? We need to have some agreed-on sets of reactions that provide the central data for any thermochemical equation.
Formation reactionsA chemical reaction that forms one mole of a substance from its constituent elements in their standard states. are chemical reactions that form one mole of a substance from its constituent elements in their standard states. By standard states we mean as a diatomic molecule if that is how the element exists and the proper phase at normal temperatures (typically room temperature). The product is one mole of substance, which may require that coefficients on the reactant side be fractional (a change from our normal insistence that all coefficients be whole numbers). For example, the formation reaction for methane (CH4) is
C(s) + 2H2(g) → CH4(g)The formation reaction for carbon dioxide (CO2) is
C(s) + O2(g) → CO2(g)In both cases, one of the elements is a diatomic molecule because that is the standard state for that particular element. The formation reaction for H2O—
2H2(g) + O2(g) → 2H2O(ℓ)—is not in a standard state because the coefficient on the product is 2; for a proper formation reaction, only one mole of product is formed. Thus, we have to divide all coefficients by 2:
H2(g) + 1/2O2(g) → H2O(ℓ)On a molecular scale, we are using half of an oxygen molecule, which may be problematic to visualize. However, on a molar level, it implies that we are reacting only half of a mole of oxygen molecules, which should be an easy concept for us to understand.
Example 11
Which of the following are proper formation reactions?
- H2(g) + Cl2(g) → 2HCl(g)
- Si(s) + 2F2(g) → SiF4(g)
- CaO(s) + CO2 → CaCO3(s)
Solution
- In this reaction, two moles of product are produced, so this is not a proper formation reaction.
- In this reaction, one mole of a substance is produced from its elements in their standard states, so this is a proper formation reaction.
- One mole of a substance is produced, but it is produced from two other compounds, not its elements. So this is not a proper formation reaction.
Test Yourself
Is this a proper formation reaction? Explain why or why not.
2Fe(s) + 3P(s) + 12O(g) → Fe2(PO4)3(s)Answer
This is not a proper formation reaction because oxygen is not written as a diatomic molecule.
Given the formula of any substance, you should be able to write the proper formation reaction for that substance.
Example 12
Write formation reactions for each of the following.
- FeO(s)
- C2H6(g)
Solution
In both cases, there is one mole of the substance as product, and the coefficients of the reactants may have to be fractional to balance the reaction.
- Fe(s) + 1/2O2(g) → FeO(s)
- 2C(s) + 3H2(g) → C2H6(g)
Test Yourself
Write the equation for the formation of CaCO3(s).
Answer
Ca(s) + C(s) + 3/2O2(g) → CaCO3(s)The enthalpy change for a formation reaction is called the enthalpy of formationThe enthalpy change for a formation reaction; denoted . and is given the symbol ΔHf. The subscript f is the clue that the reaction of interest is a formation reaction. Thus, for the formation of FeO(s),
Note that now we are using kJ/mol as the unit because it is understood that the enthalpy change is for one mole of substance. Note, too, by definition, that the enthalpy of formation of an element is exactly zero because making an element from an element is no change. For example,
H2(g) → H2(g) ΔHf = 0Formation reactions and their enthalpies are important because these are the thermochemical data that are tabulated for any chemical reaction. Table 7.2 "Enthalpies of Formation for Various Substances" lists some enthalpies of formation for a variety of substances; in some cases, however, phases can be important (e.g., for H2O).
It is easy to show that any general chemical equation can be written in terms of the formation reactions of its reactants and products, some of them reversed (which means the sign must change in accordance with Hess’s law). For example, consider
2NO2(g) → N2O4(g)We can write it in terms of the (reverse) formation reaction of NO2 and the formation reaction of N2O4:
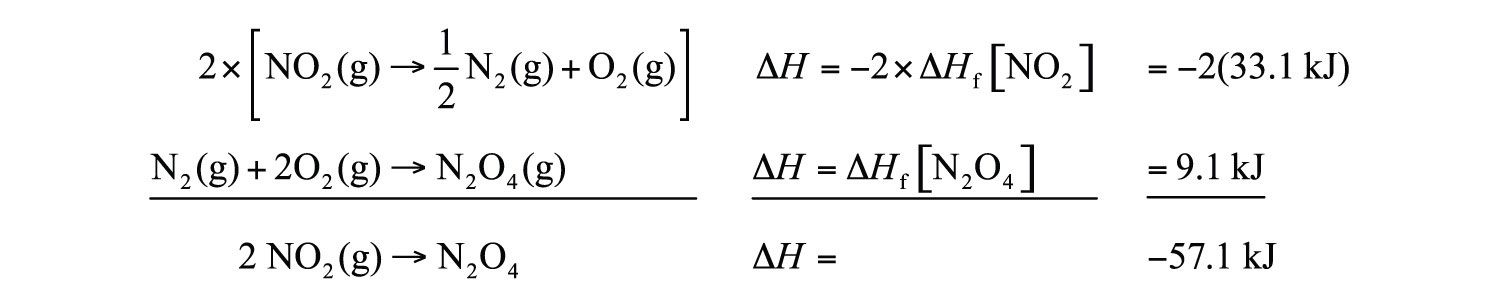
We must multiply the first reaction by 2 to get the correct overall balanced equation. We are simply using Hess’s law in combining the ΔHf values of the formation reactions.
Table 7.2 Enthalpies of Formation for Various Substances
| Compound | ΔHf (kJ/mol) | Compound | ΔHf (kJ/mol) | Compound | ΔHf (kJ/mol) | Compound | ΔHf (kJ/mol) |
|---|---|---|---|---|---|---|---|
| Ag(s) | 0 | Ca(s) | 0 | Hg2Cl2(s) | −265.37 | NaHCO3(s) | −950.81 |
| AgBr(s) | −100.37 | CaCl2(s) | −795.80 | I2(s) | 0 | NaN3(s) | 21.71 |
| AgCl(s) | −127.01 | CaCO3(s, arag) | −1,207.1 | K(s) | 0 | Na2CO3(s) | −1,130.77 |
| Al(s) | 0 | CaCO3(s, calc) | −1,206.9 | KBr(s) | −393.8 | Na2O(s) | −417.98 |
| Al2O3(s) | −1,675.7 | Cl2(g) | 0 | KCl(s) | −436.5 | Na2SO4(s) | −331.64 |
| Ar(g) | 0 | Cr(s) | 0 | KF(s) | −567.3 | Ne(g) | 0 |
| Au(s) | 0 | Cr2O3(s) | −1,134.70 | KI(s) | −327.9 | Ni(s) | 0 |
| BaSO4(s) | −1,473.19 | Cs(s) | 0 | Li(s) | 0 | O2(g) | 0 |
| Br2(ℓ) | 0 | Cu(s) | 0 | LiBr(s) | −351.2 | O3(g) | 142.67 |
| C(s, dia) | 1.897 | F2(g) | 0 | LiCl(s) | −408.27 | PH3(g) | 22.89 |
| C(s, gra) | 0 | Fe(s) | 0 | LiF(s) | −616.0 | Pb(s) | 0 |
| CCl4(ℓ) | −128.4 | Fe2(SO4)3(s) | −2,583.00 | LiI(s) | −270.4 | PbCl2(s) | −359.41 |
| CH2O(g) | −115.90 | Fe2O3(s) | −825.5 | Mg(s) | 0 | PbO2(s) | −274.47 |
| CH3COOH(ℓ) | −483.52 | Ga(s) | 0 | MgO(s) | −601.60 | PbSO4(s) | −919.97 |
| CH3OH(ℓ) | −238.4 | HBr(g) | −36.29 | NH3(g) | −45.94 | Pt(s) | 0 |
| CH4(g) | −74.87 | HCl(g) | −92.31 | NO(g) | 90.29 | S(s) | 0 |
| CO(g) | −110.5 | HF(g) | −273.30 | NO2(g) | 33.10 | SO2(g) | −296.81 |
| CO2(g) | −393.51 | HI(g) | 26.5 | N2(g) | 0 | SO3(g) | −395.77 |
| C2H5OH(ℓ) | −277.0 | HNO2(g) | −76.73 | N2O(g) | 82.05 | SO3(ℓ) | −438 |
| C2H6(g) | −83.8 | HNO3(g) | −134.31 | N2O4(g) | 9.08 | Si(s) | 0 |
| C6H12(ℓ) | −157.7 | H2(g) | 0 | N2O5(g) | 11.30 | U(s) | 0 |
| C6H12O6(s) | −1277 | H2O(g) | −241.8 | Na(s) | 0 | UF6(s) | −2,197.0 |
| C6H14(ℓ) | −198.7 | H2O(ℓ) | −285.83 | NaBr(s) | −361.1 | UO2(s) | −1,085.0 |
| C6H5CH3(ℓ) | 12.0 | H2O(s) | −292.72 | NaCl(s) | −385.9 | Xe(g) | 0 |
| C6H6(ℓ) | 48.95 | He(g) | 0 | NaF(s) | −576.6 | Zn(s) | 0 |
| C10H8(s) | 77.0 | Hg(ℓ) | 0 | NaI(s) | −287.8 | ZnCl2(s) | −415.05 |
| C12H22O11(s) | −2,221.2 |
Sources: National Institute of Standards and Technology’s Chemistry WebBook, http://webbook.nist.gov/chemistry; D. R. Lide, ed., CRC Handbook of Chemistry and Physics, 89th ed. (Boca Raton, FL: CRC Press, 2008); J. A. Dean, ed., Lange’s Handbook of Chemistry, 14th ed. (New York: McGraw-Hill, 1992).
Example 13
Show that the reaction
Fe2O3(s) + 3SO3(g) → Fe2(SO4)3(s)can be written as a combination of formation reactions.
Solution
There will be three formation reactions. The one for the products will be written as a formation reaction, while the ones for the reactants will be written in reverse. Furthermore, the formation reaction for SO3 will be multiplied by 3 because there are three moles of SO3 in the balanced chemical equation. The formation reactions are as follows:
2Fe(s) + 3S(s) + 6O2(g) → Fe2(SO4)3(s)When these three equations are combined and simplified, the overall reaction is
Fe2O3(s) + 3SO3(s) → Fe2(SO4)3(s)Test Yourself
Write the formation reactions that will yield
2SO2(g) + O2(g) → 2SO3(g).Answer
Now that we have established formation reactions as the major type of thermochemical reaction we will be interested in, do we always need to write all the formation reactions when we want to determine the enthalpy change of any random chemical reaction? No. There is an easier way. You may have noticed in all our examples that we change the signs on all the enthalpies of formation of the reactants, and we don’t change the signs on the enthalpies of formation of the products. We also multiply the enthalpies of formation of any substance by its coefficient—technically, even when it is just 1. This allows us to make the following statement: the enthalpy change of any chemical reaction is equal to the sum of the enthalpies of formation of the products minus the sum of the enthalpies of formation of the reactants. In mathematical terms,
where np and nr are the number of moles of products and reactants, respectively (even if they are just 1 mol), and ΔHf,p and ΔHf,r are the enthalpies of formation of the product and reactant species, respectively. This products-minus-reactants scheme is very useful in determining the enthalpy change of any chemical reaction, if the enthalpy of formation data are available. Because the mol units cancel when multiplying the amount by the enthalpy of formation, the enthalpy change of the chemical reaction has units of energy (joules or kilojoules) only.
Example 14
Use the products-minus-reactants approach to determine the enthalpy of reaction for
Solution
The enthalpies of formation are multiplied by the number of moles of each substance in the chemical equation, and the total enthalpy of formation for reactants is subtracted from the total enthalpy of formation of the products:
All the mol units cancel. Multiplying and combining all the values, we get
ΔHrxn = −112.0 kJTest Yourself
What is the enthalpy of reaction for this chemical equation?
Answer
+2.8 kJ
Food and Drink App: Calories and Nutrition
Section 7.1 "Energy" mentioned the connection between the calorie unit and nutrition: the calorie is the common unit of energy used in nutrition, but we really consider the kilocalorie (spelled Calorie with a capital C). A daily diet of 2,000 Cal is actually 2,000,000 cal, or over 8,000,000 J, of energy.
Nutritionists typically generalize the Calorie content of foods by separating it into the three main food types: proteins, carbohydrates, and fats. The general rule of thumb is as follows:
| If the food is | It has this energy content |
|---|---|
| protein | 4 Cal/g |
| carbohydrate | 4 Cal/g |
| fat | 9 Cal/g |
This table is very useful. Assuming a 2,000 Cal daily diet, if our diet consists solely of proteins and carbohydrates, we need only about 500 g of food for sustenance—a little more than a pound. If our diet consists solely of fats, we need only about 220 g of food—less than a half pound. Of course, most of us have a mixture of proteins, carbohydrates, and fats in our diets. Water has no caloric value in the diet, so any water in the diet is calorically useless. (However, it is important for hydration; also, many forms of water in our diet are highly flavored and sweetened, which bring other nutritional issues to bear.)
When your body works, it uses calories provided by the diet as its energy source. If we eat more calories than our body uses, we gain weight—about 1 lb of weight for every additional 3,500 Cal we ingest. Similarly, if we want to lose weight, we need to expend an extra 3,500 Cal than we ingest to lose 1 lb of weight. No fancy or fad diets are needed; maintaining an ideal body weight is a straightforward matter of thermochemistry—pure and simple.
Key Takeaways
- A formation reaction is the formation of one mole of a substance from its constituent elements.
- Enthalpies of formation are used to determine the enthalpy change of any given reaction.
Exercises
-
Define formation reaction and give an example.
-
Explain the importance of formation reactions in thermochemical equations.
-
Which of the following reactions is a formation reaction? If it is not a formation reaction, explain why.
- H2(g) + S(s) → H2S(g)
- 2HBr(g) + Cl2(g) → 2HCl(g) + Br2(ℓ)
-
Which of the following reactions is a formation reaction? If it is not a formation reaction, explain why.
- Fe(g) + 1/2O2(g) → FeO(s)
- Hg(ℓ) + 1/2O2(g) → HgO(s)
-
Which of the following reactions is a formation reaction? If it is not a formation reaction, explain why.
- H2(g) + S(s) + 2O2(g) → H2SO4(ℓ)
- C3H8(g) + 5O2(g) → 3CO2(g) + 4H2O(ℓ)
-
Which of the following reactions is a formation reaction? If it is not a formation reaction, explain why.
- Zn(s) + 2HCl(aq) → ZnCl2(aq) + H2(g)
- 2Na(s) + C(s) + 3/2O2(g) → Na2CO3(s)
-
Write a proper formation reaction for each substance.
- H3PO4(s)
- Na2O(s)
- C3H7OH(ℓ)
-
Write a proper formation reaction for each substance.
- N2O5(g)
- BaSO4(s)
- Fe(OH)3(s)
-
Write a proper formation reaction for each substance.
- C12H22O11(s)
- Zn(NO3)2(s)
- Al(OH)3(s)
-
Write a proper formation reaction for each substance.
- O3(g)
- Na2O2(s)
- PCl5(g)
-
Write this reaction in terms of formation reactions.
MgCO3(s) → MgO(s) + CO2(g) -
Write this reaction in terms of formation reactions.
2NO + 4NO2 → 2N2O5 + N2 -
Write this reaction in terms of formation reactions.
2CuCl(s) → Cu(s) + CuCl2(s) -
Write this reaction in terms of formation reactions.
SiH4 + 4F2 → SiF4 + 4HF -
Determine the enthalpy change of this reaction. Data can be found in Table 7.2 "Enthalpies of Formation for Various Substances".
CH2O(g) + O2 → CO2(g) + H2O(ℓ) -
Determine the enthalpy change of this reaction. Data can be found in Table 7.2 "Enthalpies of Formation for Various Substances".
2AgBr(s) + Cl2(g) → 2AgCl(s) + Br2(ℓ) -
Determine the enthalpy change of this reaction. Data can be found in Table 7.2 "Enthalpies of Formation for Various Substances".
Mg(s) + N2O5(g) → MgO(s) + 2NO2(g) -
Determine the enthalpy change of this reaction. Data can be found in Table 7.2 "Enthalpies of Formation for Various Substances".
2C6H6(ℓ) + 15O2(g) → 12CO2(g) + 6H2O(ℓ)
Answers
-
A formation reaction is a reaction that produces one mole of a substance from its elements. Example: C(s) + O2(g) → CO2(g)
-
-
- formation reaction
- It is not the formation of a single substance, so it is not a formation reaction.
-
-
- formation reaction
- It is not the formation of a single substance, so it is not a formation reaction.
-
-
- 3/2H2(g) + P(s) + 2O2(g) → H3PO4(s)
- 2Na(s) + 1/2O2(g) → Na2O(s)
- 3C(s) + 1/2O2(g) + 4H2(g) → C3H7OH(ℓ)
-
-
- 12C(s) + 11H2(g) + 11/2O2(g) → C12H22O11(s)
- Zn(s) + N2(g) + 3O2(g) → Zn(NO3)2
- Al(s) + 3/2O2(g) + 3/2H2(g) → Al(OH)3(s)
-
-
MgCO3(s) → Mg(s) + C(s) + 3/2O2(g)
Mg(s) + 1/2O2(g) → MgO(s)
C(s) + O2(g) → CO2(g)
-
-
2 × [CuCl(s) → Cu(s) + 1/2Cl2(g)]
Cu(s) → Cu(s)
Cu(s) + Cl2(g) → CuCl2(s)
-
-
ΔH = −563.44 kJ
-
-
ΔH = −546.7 kJ
-
7.7 End-of-Chapter Material
Additional Exercises
-
What is the work when 124 mL of gas contract to 72.0 mL under an external pressure of 822 torr?
-
What is the work when 2,345 mL of gas contract to 887 mL under an external pressure of 348 torr?
-
A 3.77 L volume of gas is exposed to an external pressure of 1.67 atm. As the gas contracts, 156 J of work are added to the gas. What is the final volume of the gas?
-
A 457 mL volume of gas contracts when 773 torr of external pressure act on it. If 27.4 J of work are added to the gas, what is its final volume?
-
What is the heat when 1,744 g of Hg increase in temperature by 334°C? Express your final answer in kJ.
-
What is the heat when 13.66 kg of Fe cool by 622°C? Express your final answer in kJ.
-
What is final temperature when a 45.6 g sample of Al at 87.3°C gains 188 J of heat?
-
What is final temperature when 967 g of Au at 557°C lose 559 J of heat?
-
Plants take CO2 and H2O and make glucose (C6H12O6) and O2. Write a balanced thermochemical equation for this process. Use data in Table 7.2 "Enthalpies of Formation for Various Substances".
-
Exercise 9 described the formation of glucose in plants, which take in CO2 and H2O and give off O2. Is this process exothermic or endothermic? If exothermic, where does the energy go? If endothermic, where does the energy come from?
-
The basic reaction in the refining of aluminum is to take Al2O3(s) and turn it into Al(s) and O2(g). Write the balanced thermochemical equation for this process. Use data in Table 7.2 "Enthalpies of Formation for Various Substances".
-
Is the enthalpy change of the reaction
H2O(ℓ) → H2O(g)zero or nonzero? Use data in Table 7.2 "Enthalpies of Formation for Various Substances" to determine the answer.
-
What mass of H2O can be heated from 22°C to 80°C in the combustion of 1 mol of CH4? You will need the balanced thermochemical equation for the combustion of CH4. Use data in Table 7.2 "Enthalpies of Formation for Various Substances".
-
What mass of H2O can be heated from 22°C to 80°C in the combustion of 1 mol of C2H6? You will need the balanced thermochemical equation for the combustion of C2H6. Use data in Table 7.2 "Enthalpies of Formation for Various Substances". Compare your answer to Exercise 13.
-
What is the enthalpy change for the unknown reaction?
Pb(s) + Cl2(g) → PbCl2(s) ΔH = −359 kJ PbCl2(s) + Cl2(g) → PbCl4(ℓ) ΔH = ? Pb(s) + 2Cl2(g) → PbCl4(ℓ) ΔH = −329 kJ -
What is the enthalpy change for the unknown reaction?
P(s) + 3/2Br2(ℓ) → PBr3(ℓ) ΔH = −185 kJ PI3(s) → P(s) + 3/2I2(s) ΔH = ? PI3(s) + 3/2Br2(ℓ) → PBr3(ℓ) + 3/2I2(s) ΔH = −139 kJ -
What is the ΔH for this reaction? The label gra means graphite, and the label dia means diamond. What does your answer mean?
C(s, gra) → C(s, dia) -
Without consulting any tables, determine the ΔH for this reaction. Explain your answer.
H2O(ℓ, 25°C) → H2O(ℓ, 25°C)
Answers
-
5.70 J
-
-
4.69 L
-
-
80.97 kJ
-
-
91.9°C
-
-
6CO2(g) + 6H2O(ℓ) → C6H12O6(s) + 6O2(g) ΔH = 2,799 kJ
-
-
2Al2O3(s) → 4Al(s) + 3O2(g) ΔH = 3351.4 kJ
-
-
3,668 g
-
-
ΔH = 30 kJ
-
-
ΔH = 1.897 kJ; the reaction is endothermic.
-




