This is “Introduction to Complex Numbers and Complex Solutions”, section 9.6 from the book Beginning Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
9.6 Introduction to Complex Numbers and Complex Solutions
Learning Objectives
- Perform operations with complex numbers.
- Solve quadratic equations with complex solutions.
Introduction to Complex Numbers
Up to this point, the square root of a negative number has been left undefined. For example, we know that is not a real a number.

There is no real number that when squared results in a negative number. We begin the resolution of this issue by defining the imaginary unitDefined as and ., i, as the square root of −1.
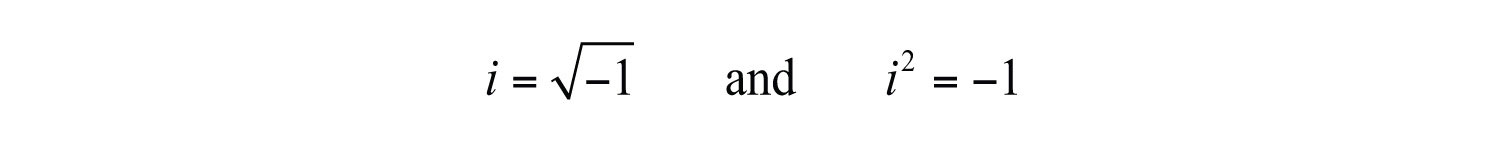
To express a square root of a negative number in terms of the imaginary unit i, we use the following property, where a represents any nonnegative real number:

With this we can write

If , then we would expect that 3i squared equals −9:

Therefore, the square root of any negative real number can be written in terms of the imaginary unit. Such numbers are often called imaginary numbersThe square roots of any negative real numbers..
Example 1: Rewrite in terms of the imaginary unit i.
a.
b.
c.
Solution:
a.
b.
c.
Notation Note
When an imaginary number involves a radical, place i in front of the radical. Consider the following:
Since multiplication is commutative, these numbers are equivalent. However, in the form , the imaginary unit i is often misinterpreted to be part of the radicand. To avoid this confusion, it is a best practice to place the i in front of the radical and use
A complex numberNumbers of the form , where a and b are real numbers. is any number of the form

where a and b are real numbers. Here a is called the real partThe real number a of a complex number . and b is called the imaginary partThe real number b of a complex number .. For example, is a complex number with a real part, 3, and an imaginary part, −4. It is important to note that any real number is also a complex number. For example, the real number 5 is also a complex number because it can be written as with a real part of 5 and an imaginary part of 0. Hence the set of real numbers, denoted R, is a subset of the set of complex numbers, denoted C.
Adding and subtracting complex numbers is similar to adding and subtracting like terms. Add or subtract the real parts and then the imaginary parts.
Example 2: Add: .
Solution: Add the real parts and then add the imaginary parts.
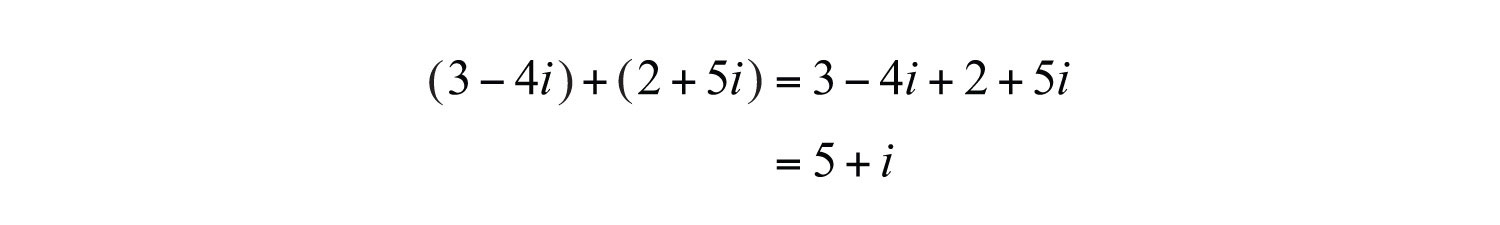
Answer:
To subtract complex numbers, subtract the real parts and subtract the imaginary parts. This is consistent with the use of the distributive property.
Example 3: Subtract: .
Solution: Distribute the negative one and then combine like terms.

Answer:
The distributive property also applies when multiplying complex numbers. Make use of the fact that to resolve the result into standard form: .
Example 4: Multiply: .
Solution: Begin by applying the distributive property.

Answer:
Example 5: Multiply: .
Solution:

Answer:
Given a complex number , its complex conjugateTwo complex numbers whose real parts are the same and imaginary parts are opposite. If given , then its complex conjugate is . is . We next explore the product of complex conjugates.
Example 6: Multiply: .
Solution:

Answer: 25
In general, the product of complex conjugatesThe real number that results from multiplying complex conjugates: follows:

Note that the result does not involve the imaginary unit; hence the result is real. This leads us to the very useful property:

To divide complex numbers, we apply the technique used to rationalize the denominator. Multiply the numerator and denominator (dividend and divisor) by the conjugate of the denominator. The result can then be resolved into standard form, .
Example 7: Divide: .
Solution: In this example, the conjugate of the denominator is . Multiply by 1 in the form .
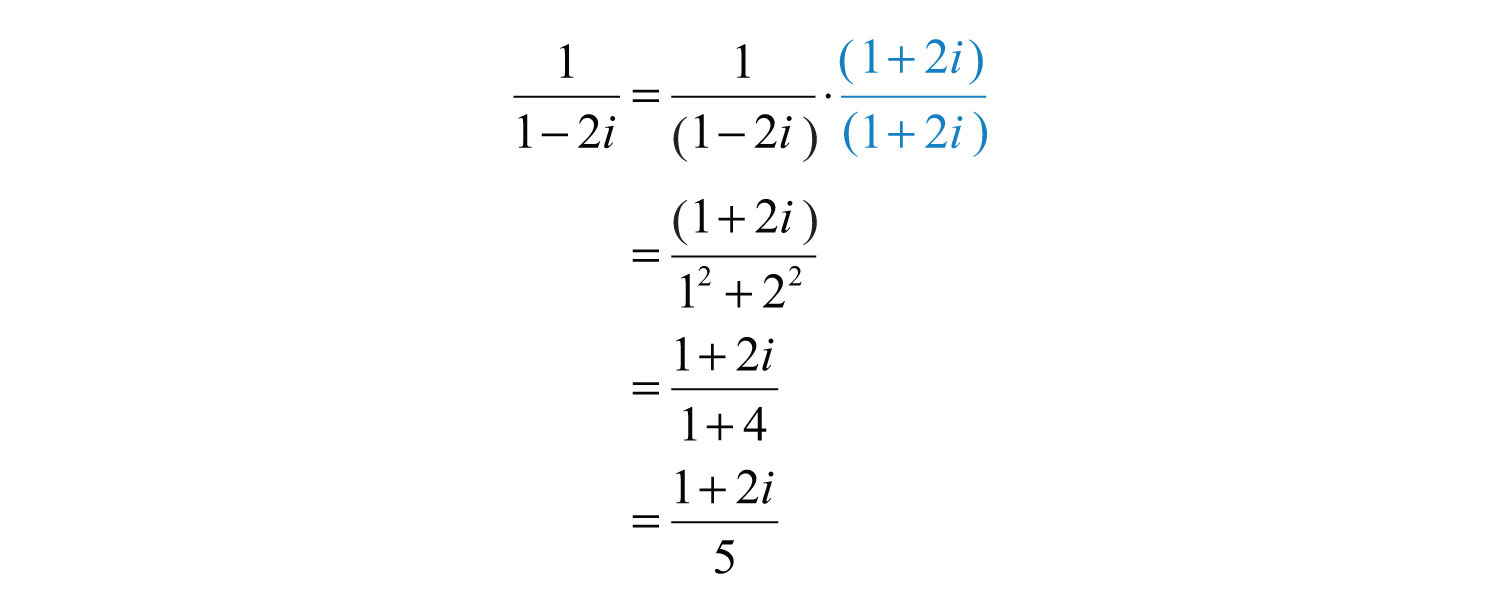
To express this complex number in standard form, write each term over the common denominator 5.

Answer:
Example 8: Divide: .
Solution:
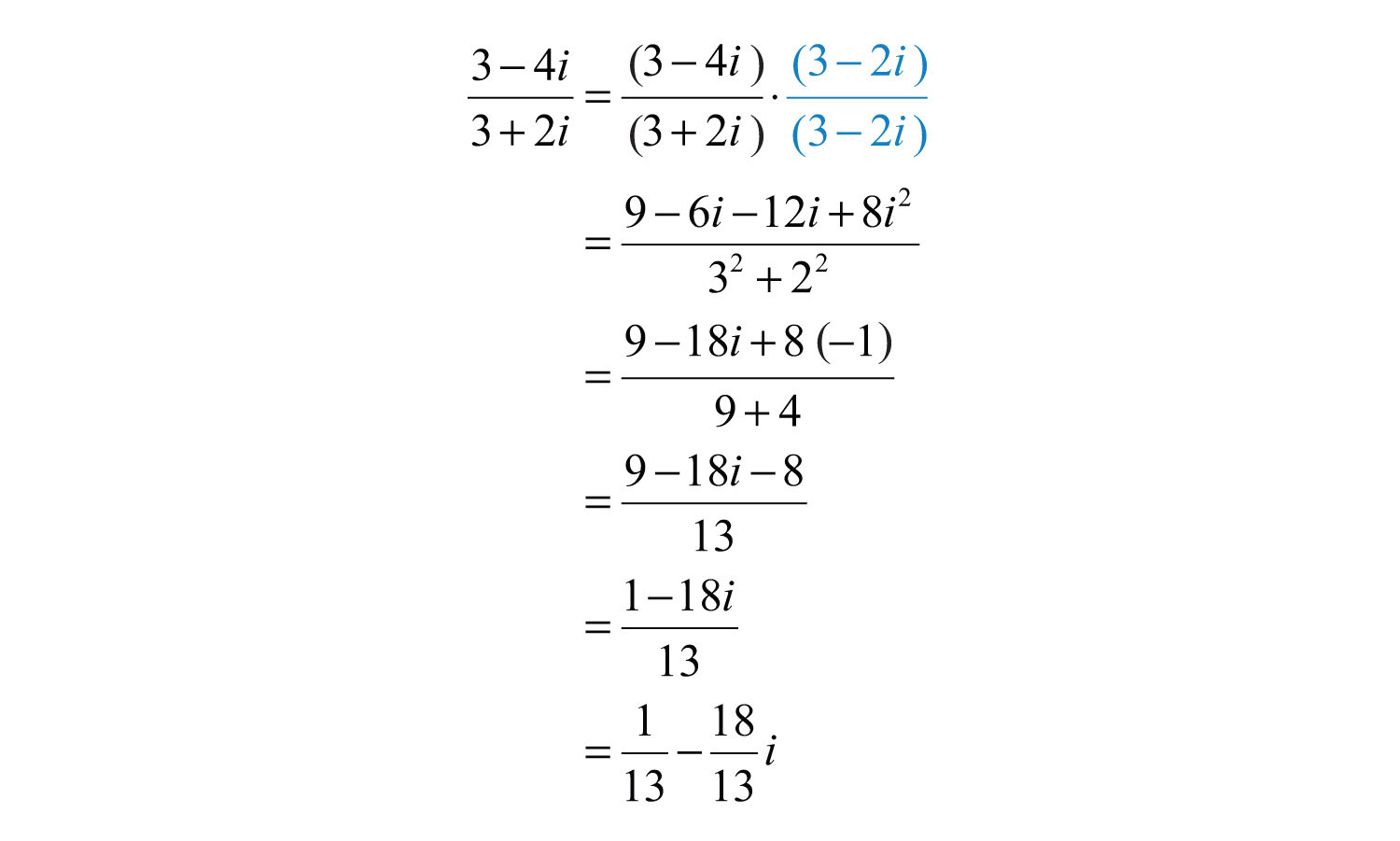
Answer:
Try this! Divide: .
Answer:
Video Solution
(click to see video)Quadratic Equations with Complex Solutions
Now that complex numbers are defined, we can complete our study of solutions to quadratic equations. Often solutions to quadratic equations are not real.
Example 9: Solve using the quadratic formula:
Solution: Begin by identifying a, b, and c. Here

Substitute these values into the quadratic formula and then simplify.

Check these solutions by substituting them into the original equation.

Answer: The solutions are and .
The equation may not be given in standard form. The general steps for solving using the quadratic formula are outlined in the following example.
Example 10: Solve: .
Solution:
Step 1: Write the quadratic equation in standard form.

Step 2: Identify a, b, and c for use in the quadratic formula. Here

Step 3: Substitute the appropriate values into the quadratic formula and then simplify.
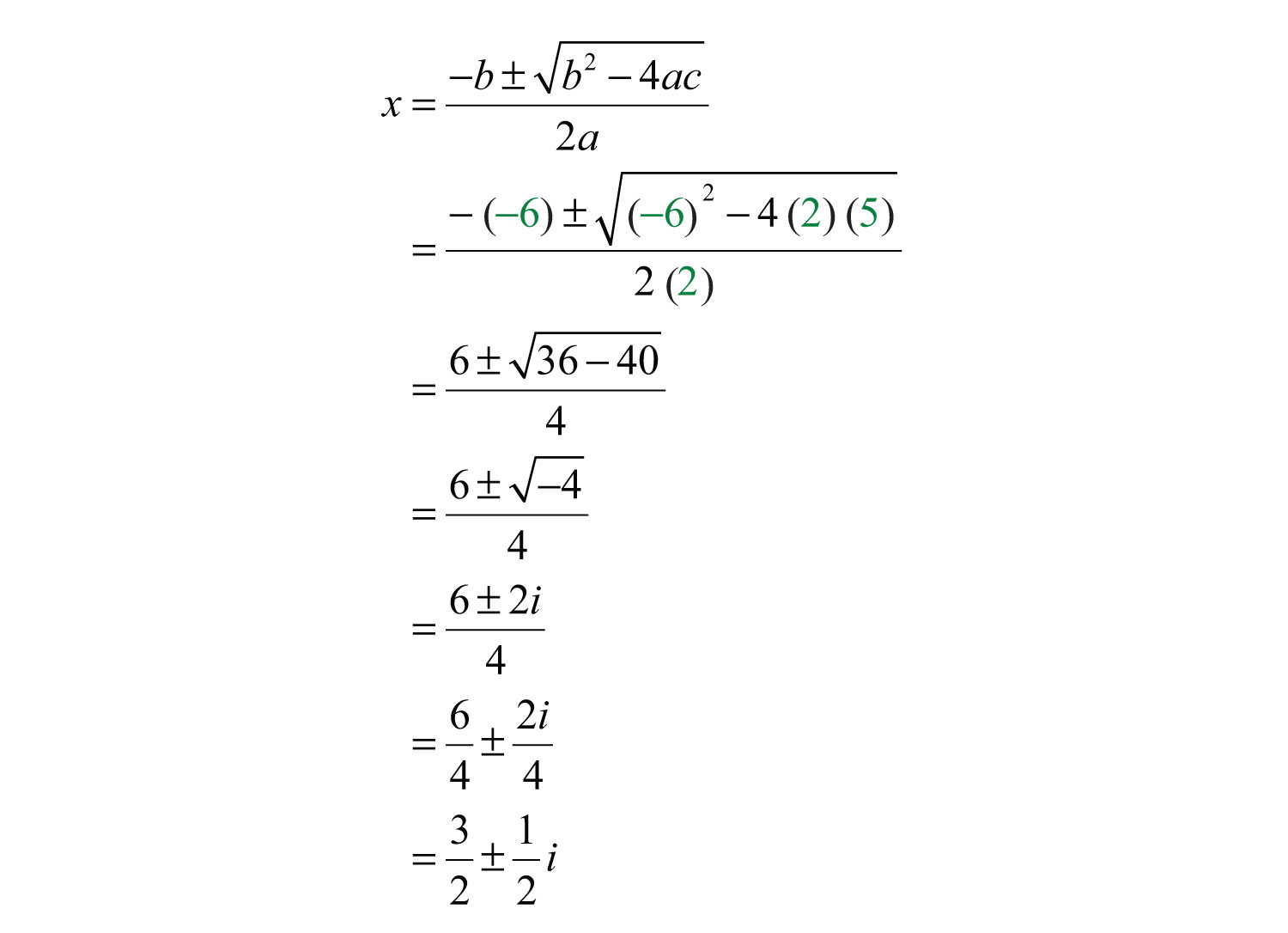
Answer: The solution is . The check is optional.
Example 11: Solve: .
Solution: Begin by rewriting the equation in standard form.

Here , , and . Substitute these values into the quadratic formula.

Answer: The solutions are and .
Notation Note
Consider the following:
Both numbers are equivalent and is in standard form, where the real part is −1 and the imaginary part is . However, this number is often expressed as , even though this expression is not in standard form. Again, this is done to avoid the possibility of misinterpreting the imaginary unit as part of the radicand.
Try this! Solve: .
Answer:
Video Solution
(click to see video)Key Takeaways
- The result of adding, subtracting, multiplying, and dividing complex numbers is a complex number.
- Use complex numbers to describe solutions to quadratic equations that are not real.
Topic Exercises
Part A: Introduction to Complex Numbers
Rewrite in terms of i.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Perform the operations.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
Part B: Complex Roots
Solve by extracting the roots and then solve by using the quadratic formula. Check answers.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
Solve using the quadratic formula.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
Part C: Discussion Board
91. Explore the powers of i. Share your discoveries on the discussion board.
92. Research and discuss the rich history of imaginary numbers.
93. Research and discuss real-world applications involving complex numbers.
Answers
1:
3:
5:
7:
9:
11:
13:
15:
17:
19:
21:
23:
25:
27:
29:
31:
33: 20
35:
37:
39:
41:
43:
45:
47:
49:
51:
53:
55:
57:
59:
61:
63:
65:
67:
69:
71:
73:
75:
77:
79:
81:
83:
85:
87:
89:




