Completing the Square

9.2 Completing the Square

Learning Objective

Solve quadratic equations by completing the square.

Completing the Square

In this section, we will devise a method for rewriting any quadratic equation of the form

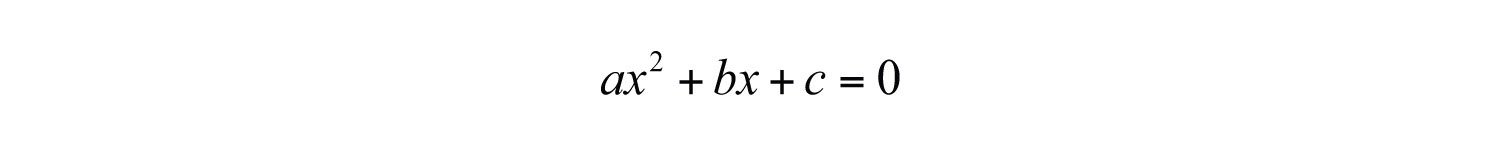
in the form

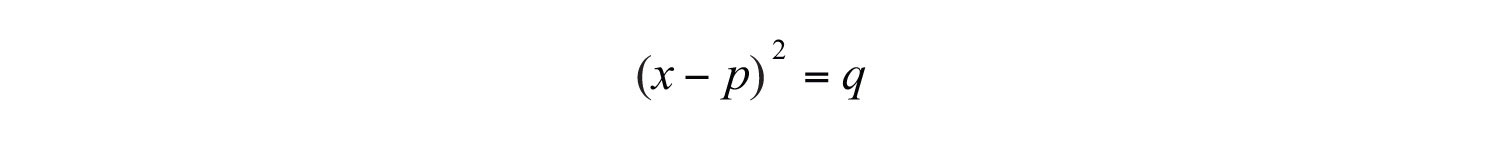
This process is called completing the squareThe process of rewriting a quadratic equation in the form ${(x - p)}^{2} = q$ .. As we have seen, quadratic equations in this form can easily be solved by extracting roots. We begin by examining perfect square trinomials:

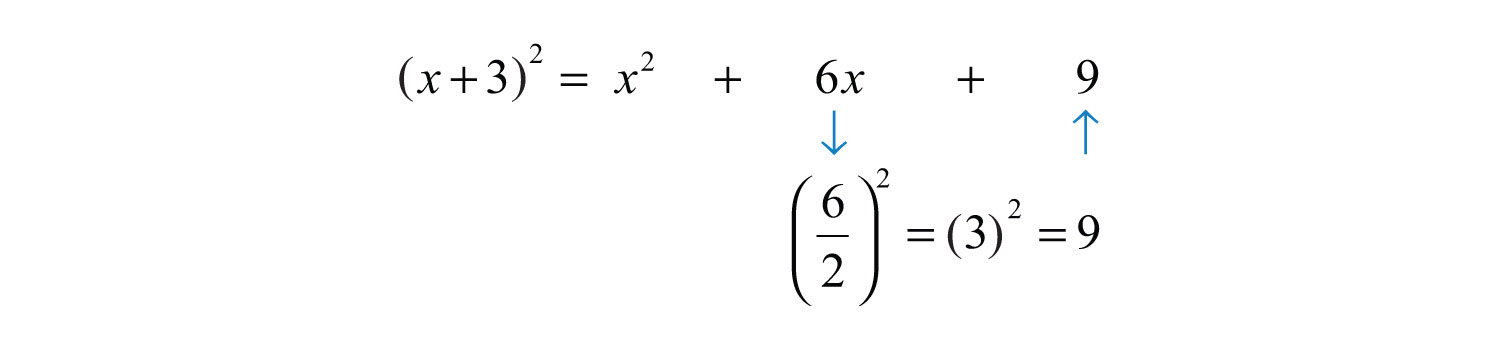
The last term, 9, is the square of one-half of the coefficient of x. In general, this is true for any perfect square trinomial of the form $x^{2} + b x + c$ .

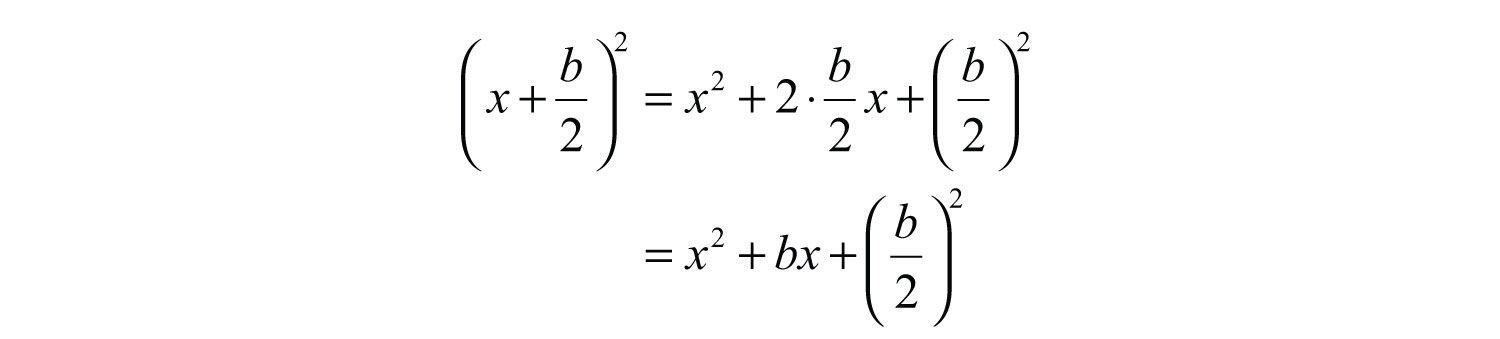
In other words, any trinomial of the form $x^{2} + b x + c$ will be a perfect square trinomial if

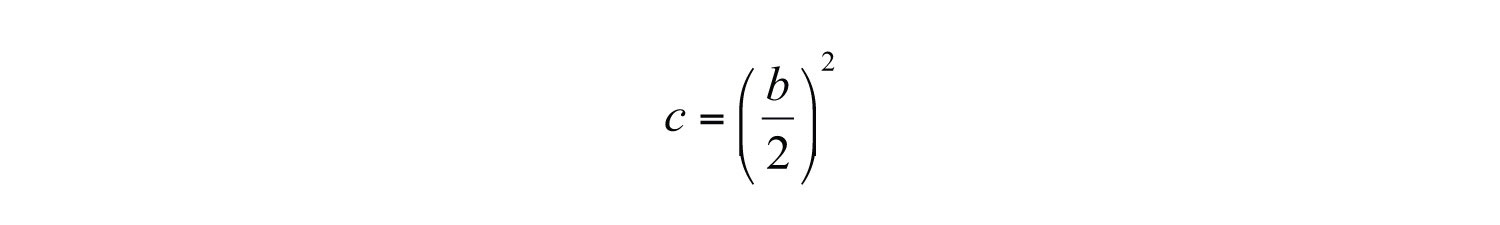
Note

It is important to point out that the leading coefficient must be equal to 1 for this to be true.

Example 1: Complete the square: $x^{2} + 8 x + ? = {(x + ?)}^{2}$ .

Solution: In this example, the coefficient of the middle term b = 8, so find the value that completes the square as follows:

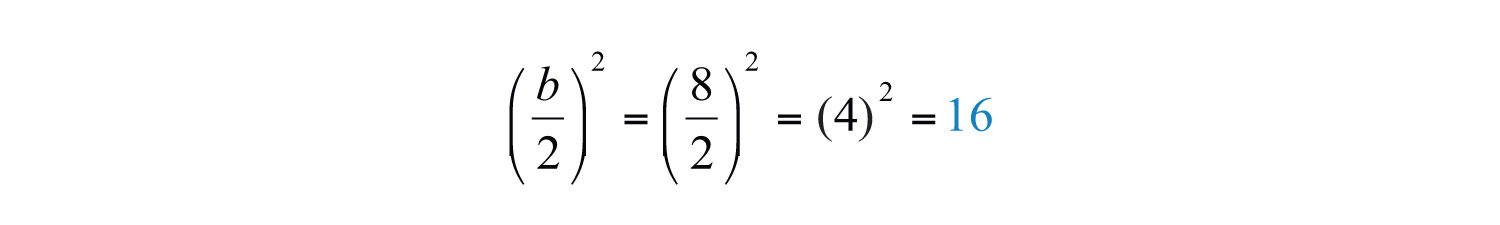
The value that completes the square is 16.

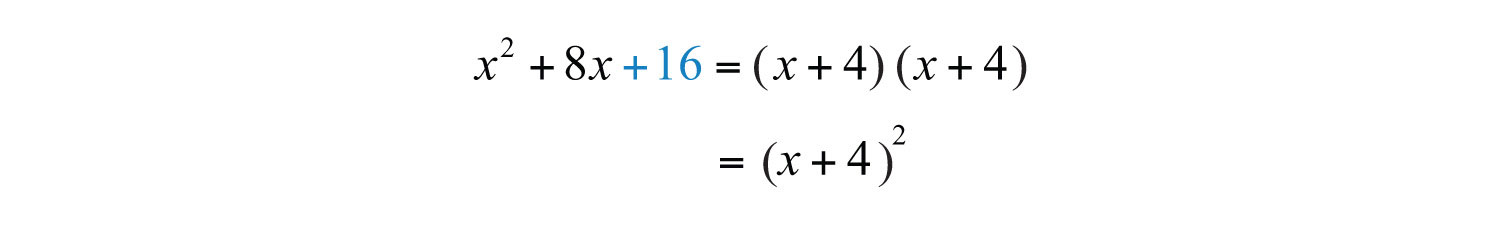
Answer: $x^{2} + 8 x + 16 = {(x + 4)}^{2}$

Example 2: Complete the square: $x^{2} + 3 x + ? = {(x + ?)}^{2}$ .

Solution: Here b = 3, so find the value that will complete the square as follows:

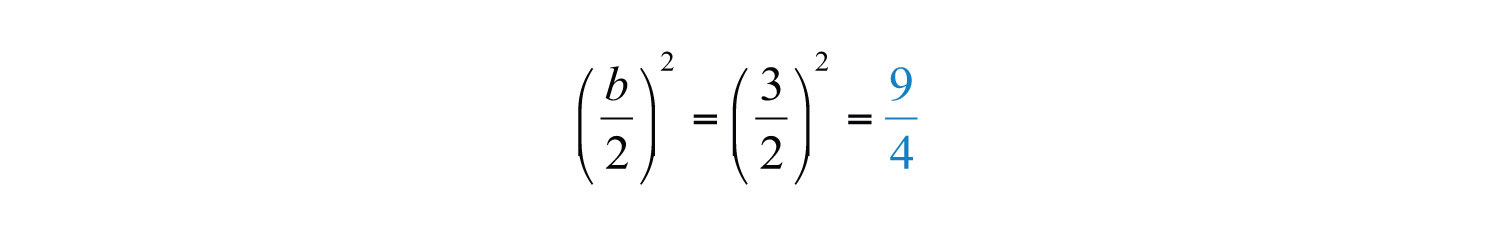
The value 9/4 completes the square:

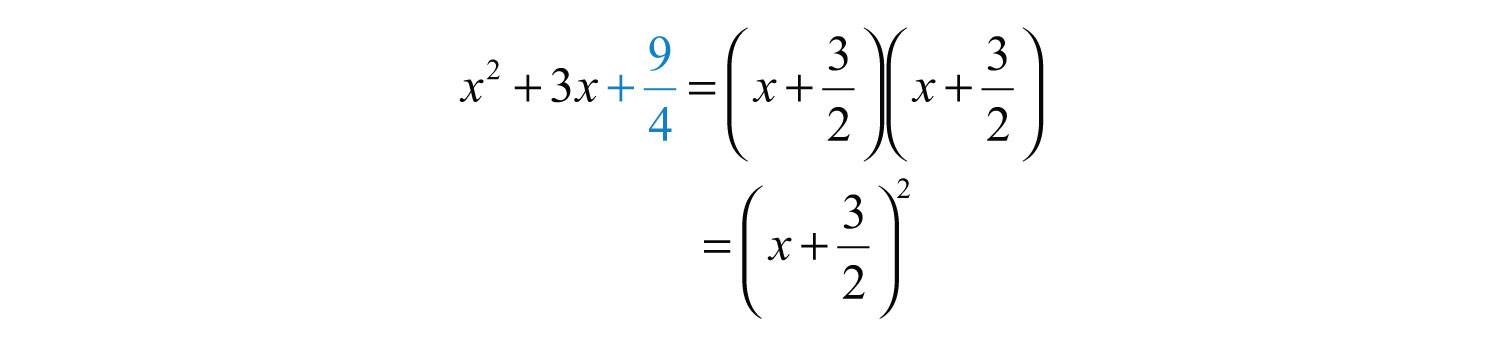
Answer: $x^{2} + 3 x + \frac{9}{4} = {(x + \frac{3}{2})}^{2}$

We can use this technique to solve quadratic equations. The idea is to take any quadratic equation in standard form and complete the square so that we can solve it by extracting roots. The following are general steps for solving a quadratic equation with a leading coefficient of 1 in standard form by completing the square.

Example 3: Solve by completing the square: $x^{2} + 14 x + 46 = 0$ .

Solution:

Step 1: Add or subtract the constant term to obtain the equation in the form $x^{2} + b x = c$ . In this example, subtract 46 to move it to the right side of the equation.

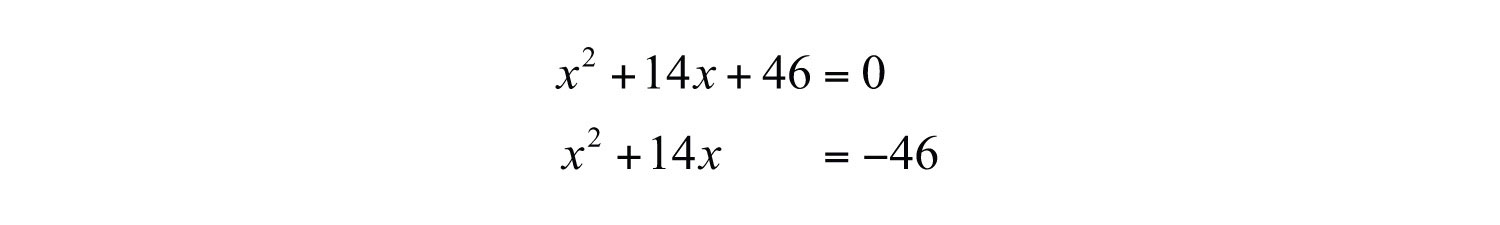
Step 2: Use ${(\frac{b}{2})}^{2}$ to determine the value that completes the square. Here b = 14:

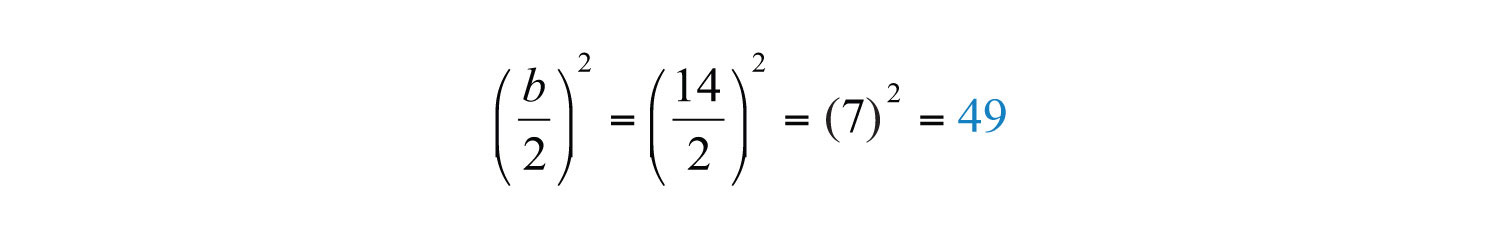
Step 3: Add ${(\frac{b}{2})}^{2}$ to both sides of the equation and complete the square.

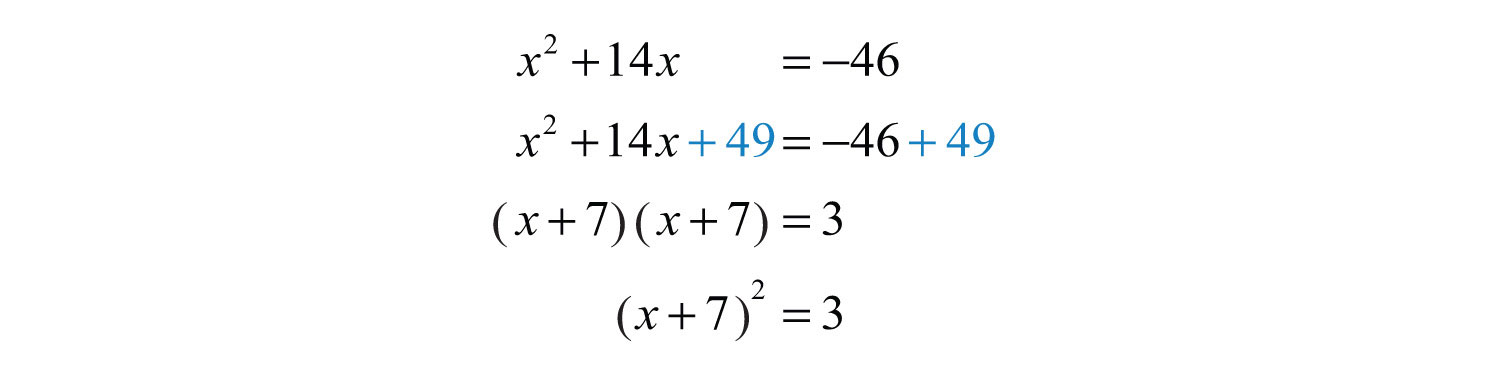
Step 4: Solve by extracting roots.

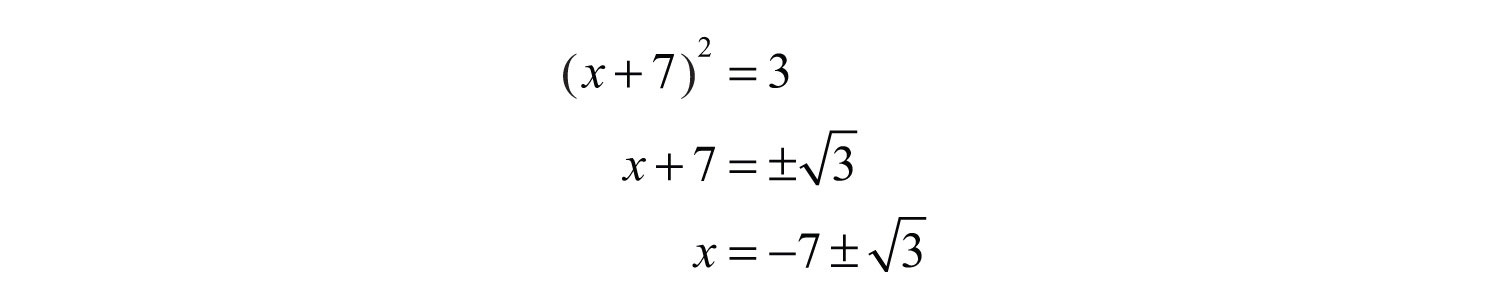
Answer: The solutions are $- 7 - \sqrt{3}$ or $- 7 + \sqrt{3}$ . The check is optional.

Example 4: Solve by completing the square: $x^{2} - 18 x + 72 = 0$ .

Solution: Begin by subtracting 72 from both sides.

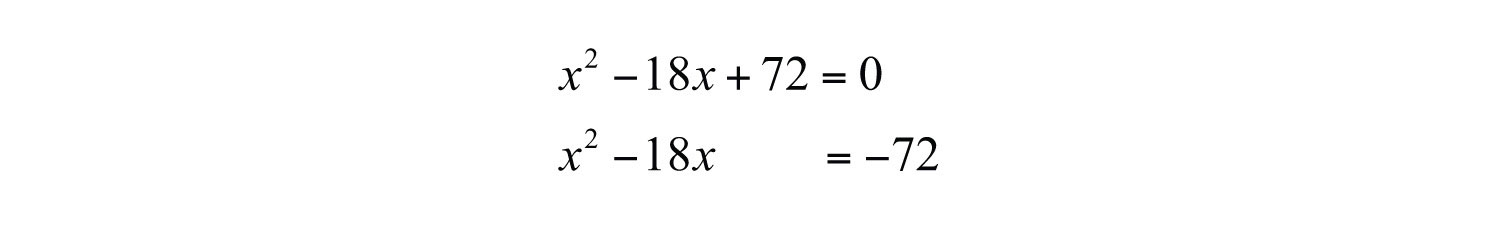
Next, find the value that completes the square using b = −18.

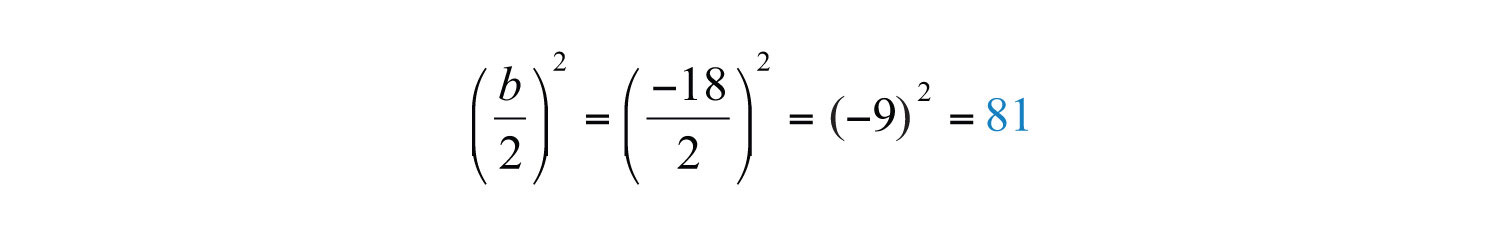
To complete the square, add 81 to both sides, complete the square, and then solve by extracting the roots.

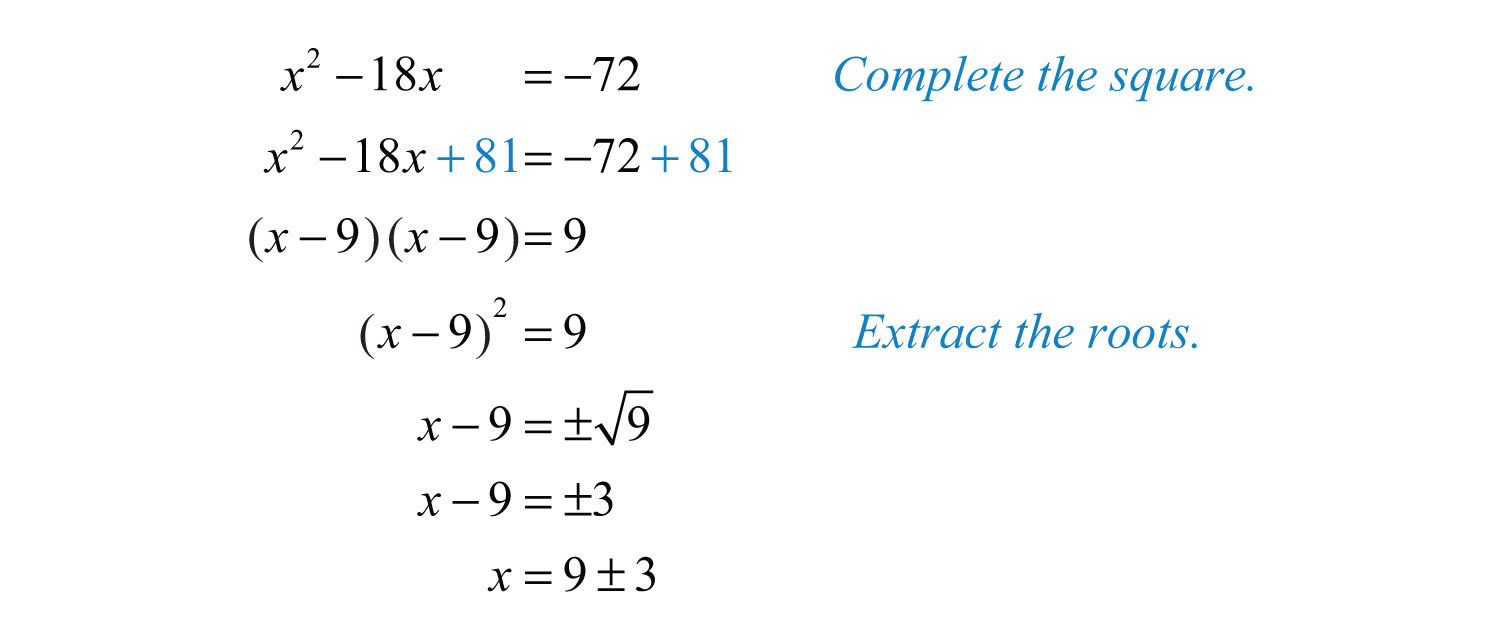
At this point, separate the “plus or minus” into two equations and solve each.

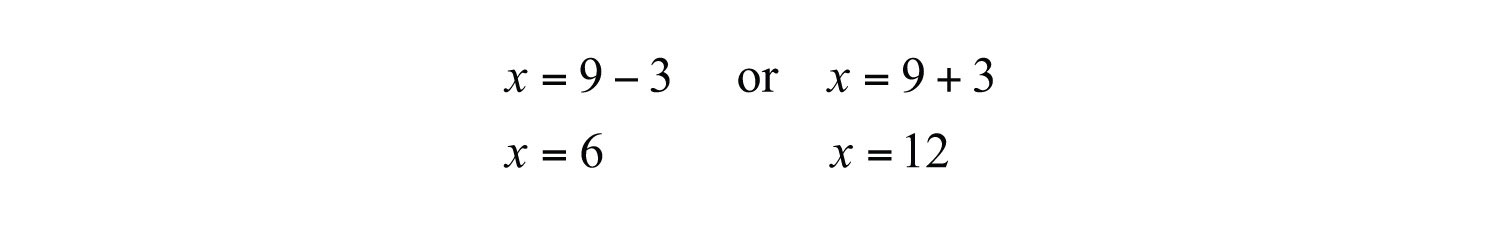
Answer: The solutions are 6 and 12.

Note that in the previous example the solutions are integers. If this is the case, then the original equation will factor.

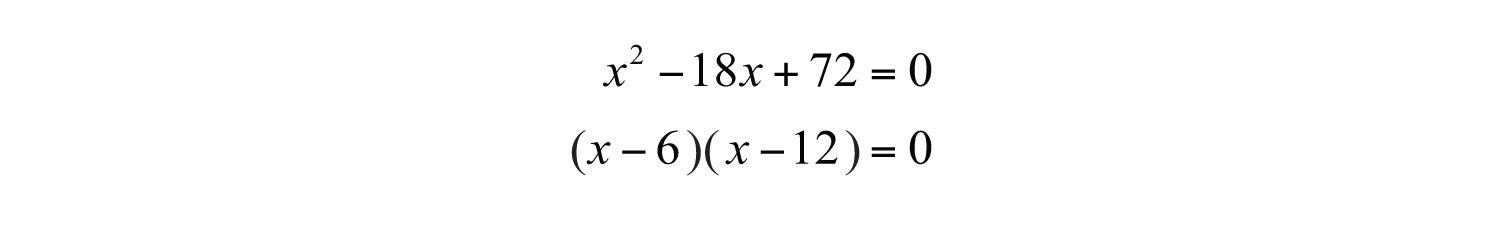
If it factors, we can solve it by factoring. However, not all quadratic equations will factor.

Example 5: Solve by completing the square: $x^{2} + 10 x + 1 = 0$ .

Solution: Begin by subtracting 1 from both sides of the equation.

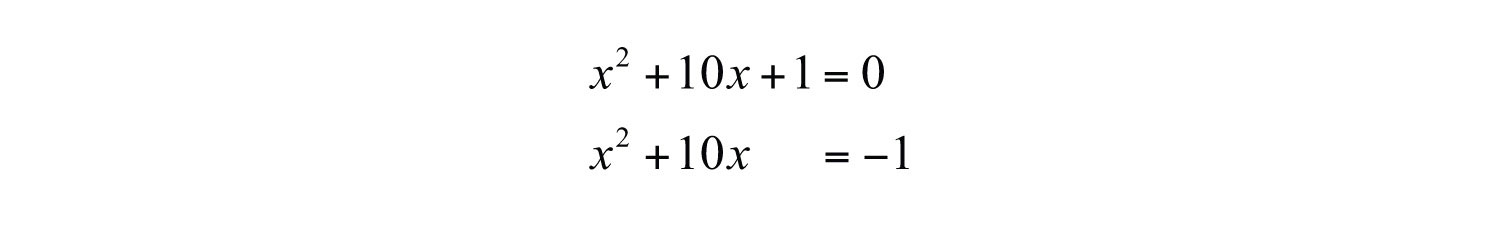
Here b = 10, and we determine the value that completes the square as follows:

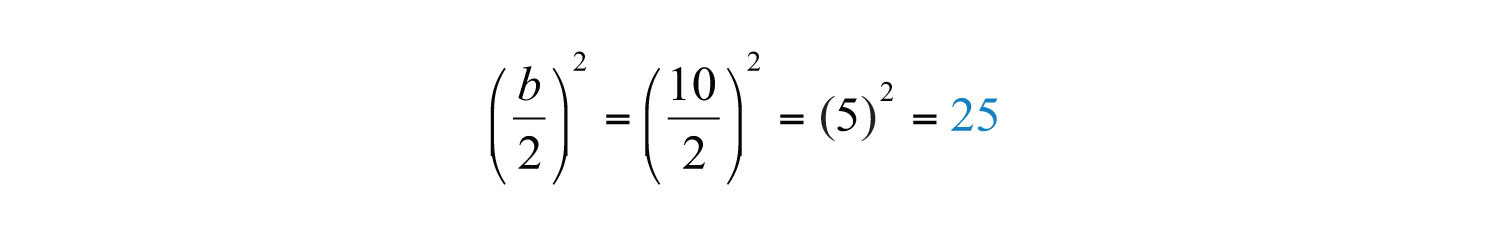
To complete the square, add 25 to both sides of the equation.

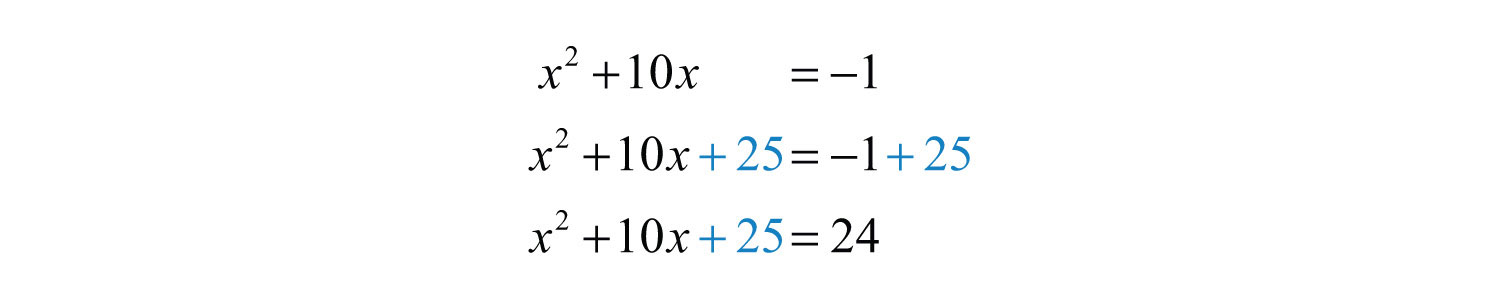
Factor and then solve by extracting roots.

Answer: The solutions are $- 5 - 2 \sqrt{6}$ and $- 5 + 2 \sqrt{6}$ .

Sometimes quadratic equations do not have real solutions.

Example 6: Solve by completing the square: $x^{2} - 2 x + 3 = 0$ .

Solution: Begin by subtracting 3 from both sides of the equation.

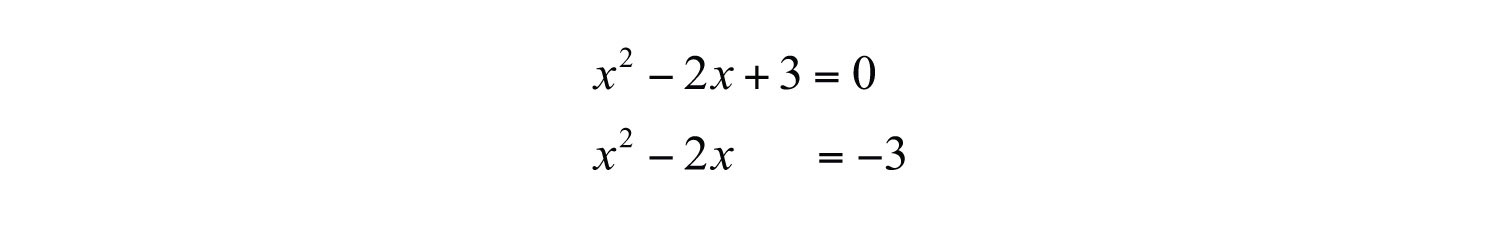
Here b = −2, and we have

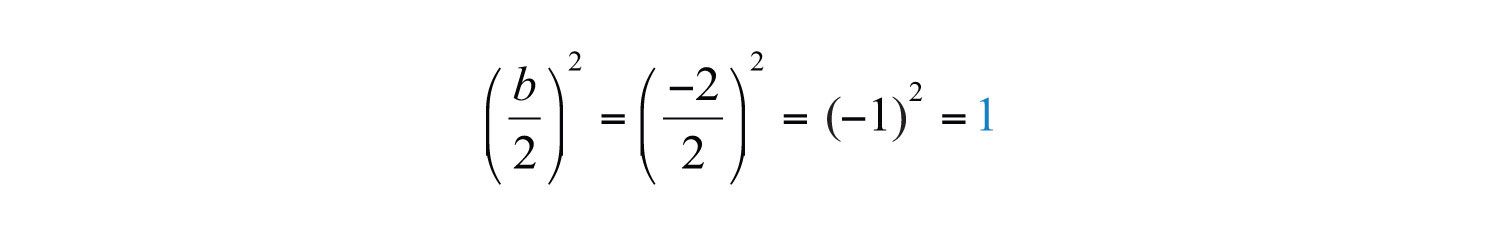
Therefore,

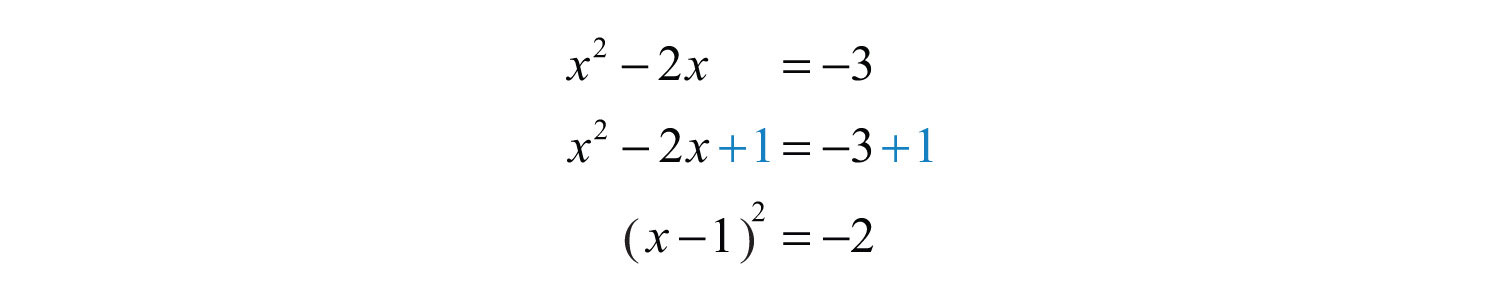
At this point we see that extracting the root leads to the square root of a negative number.

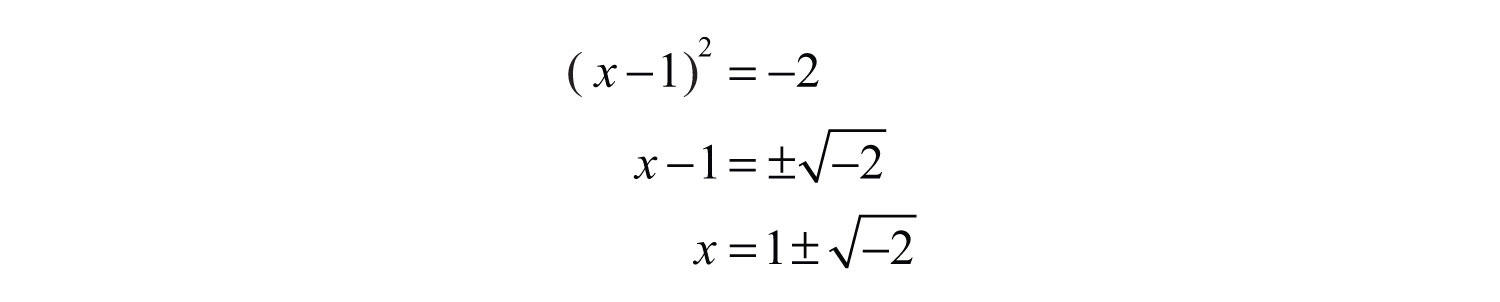
Answer: No real solution

Try this! Solve by completing the square: $x^{2} - 2 x - 27 = 0$ .

Answer: $x = 1 \pm 2 \sqrt{7}$

Video Solution

(click to see video)

The coefficient of x is not always divisible by 2.

Example 7: Solve by completing the square: $x^{2} + 3 x - 2 = 0$ .

Solution: Begin by adding 2 to both sides.

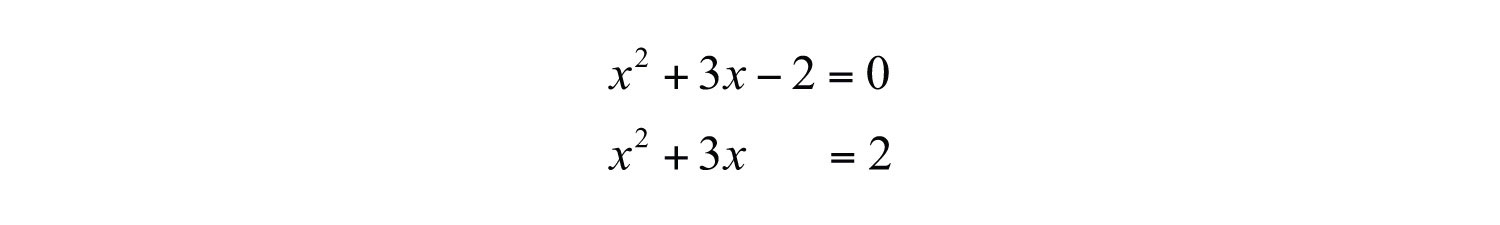
Use b = 3 to find the value that completes the square:

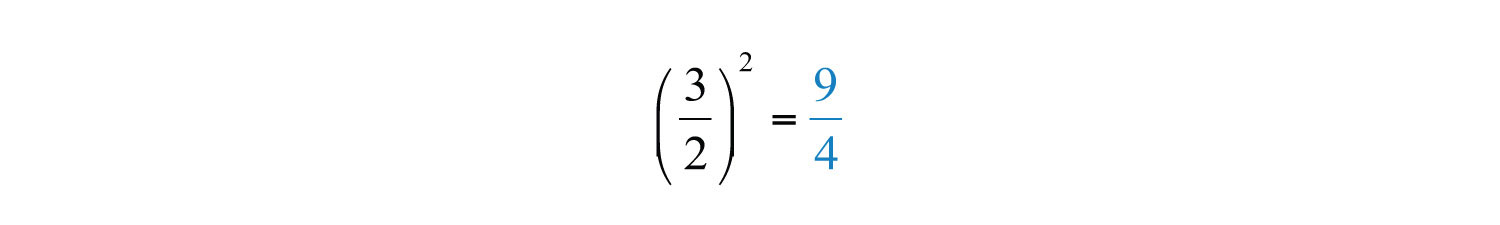
To complete the square, add 9/4 to both sides of the equation.

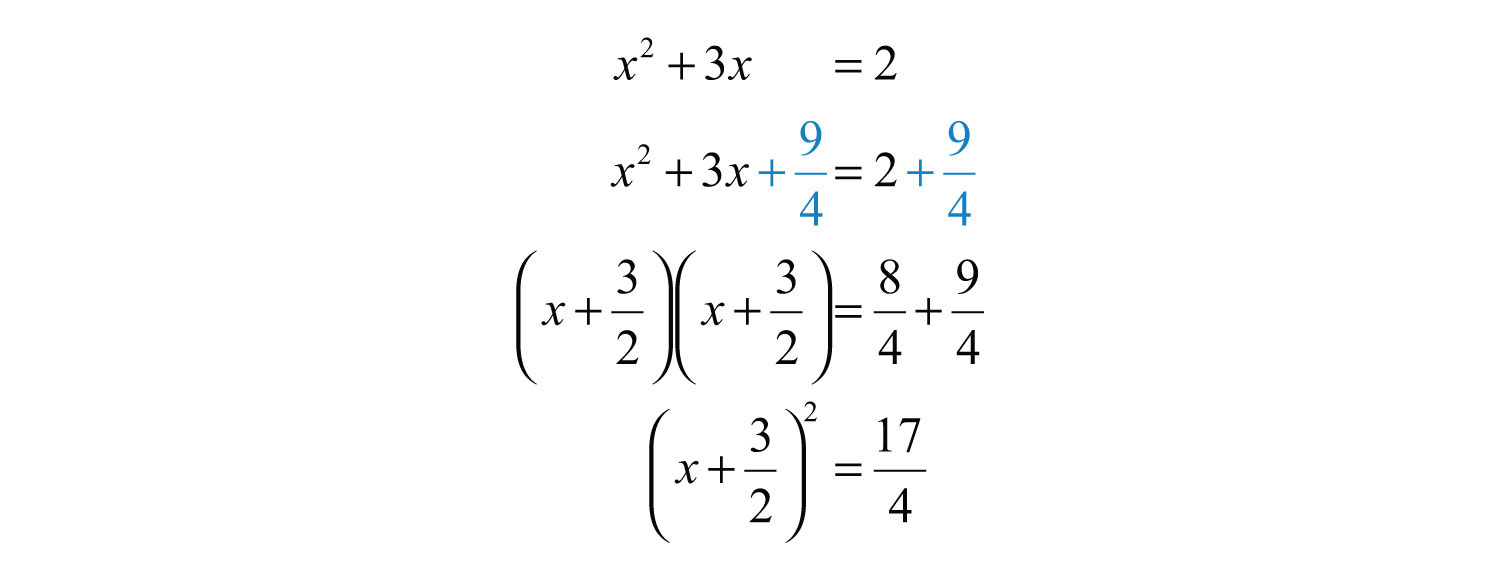
Solve by extracting roots.

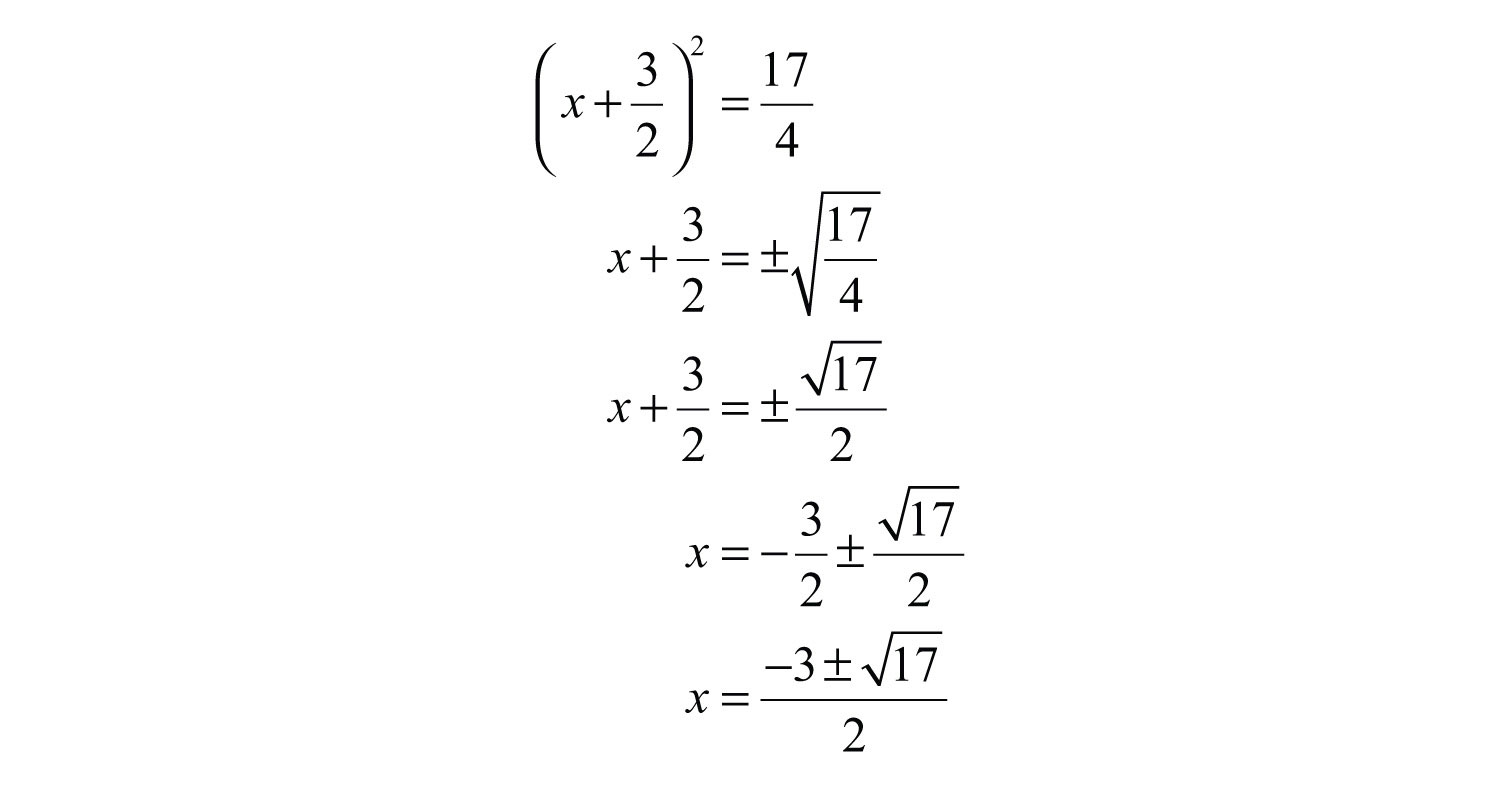
Answer: The solutions are $\frac{- 3 \pm \sqrt{17}}{2}$ .

So far, all of the examples have had a leading coefficient of 1. The formula ${(\frac{b}{2})}^{2}$ determines the value that completes the square only if the leading coefficient is 1. If this is not the case, then simply divide both sides by the leading coefficient.

Example 8: Solve by completing the square: $2 x^{2} + 5 x - 1 = 0$ .

Solution: Notice that the leading coefficient is 2. Therefore, divide both sides by 2 before beginning the steps required to solve by completing the square.

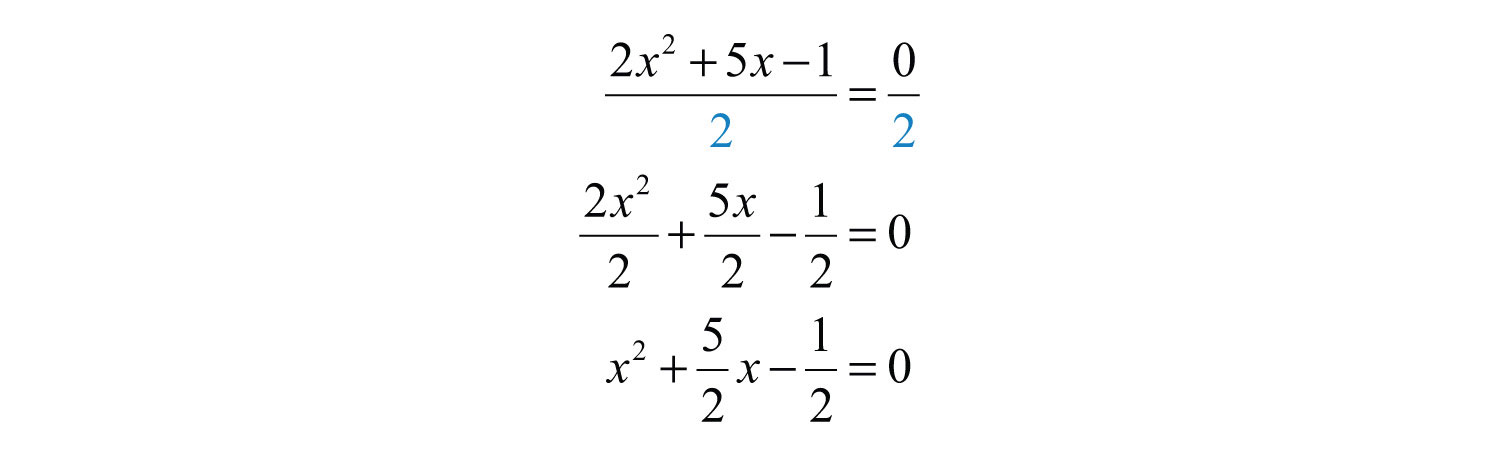
Begin by adding 1/2 to both sides of the equation.

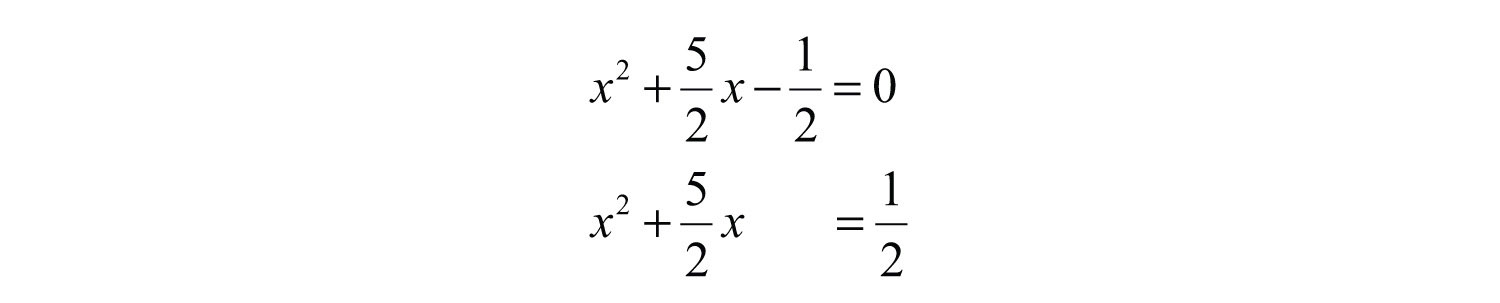
Here b = 5/2, and we can find the value that completes the square as follows:

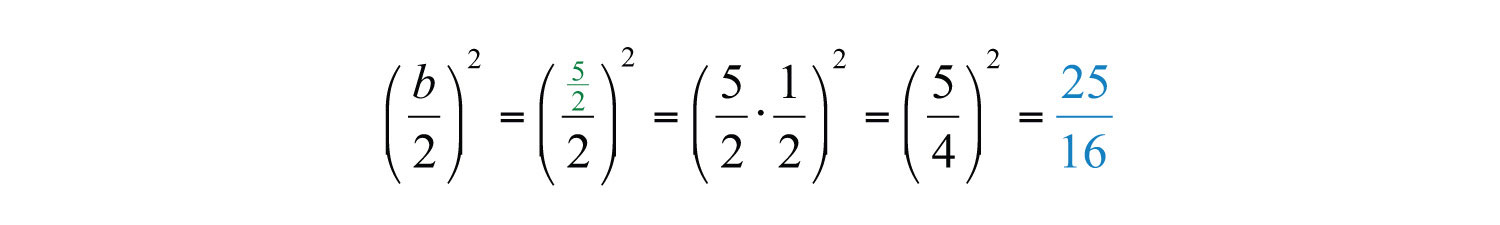
To complete the square, add 25/16 to both sides of the equation.

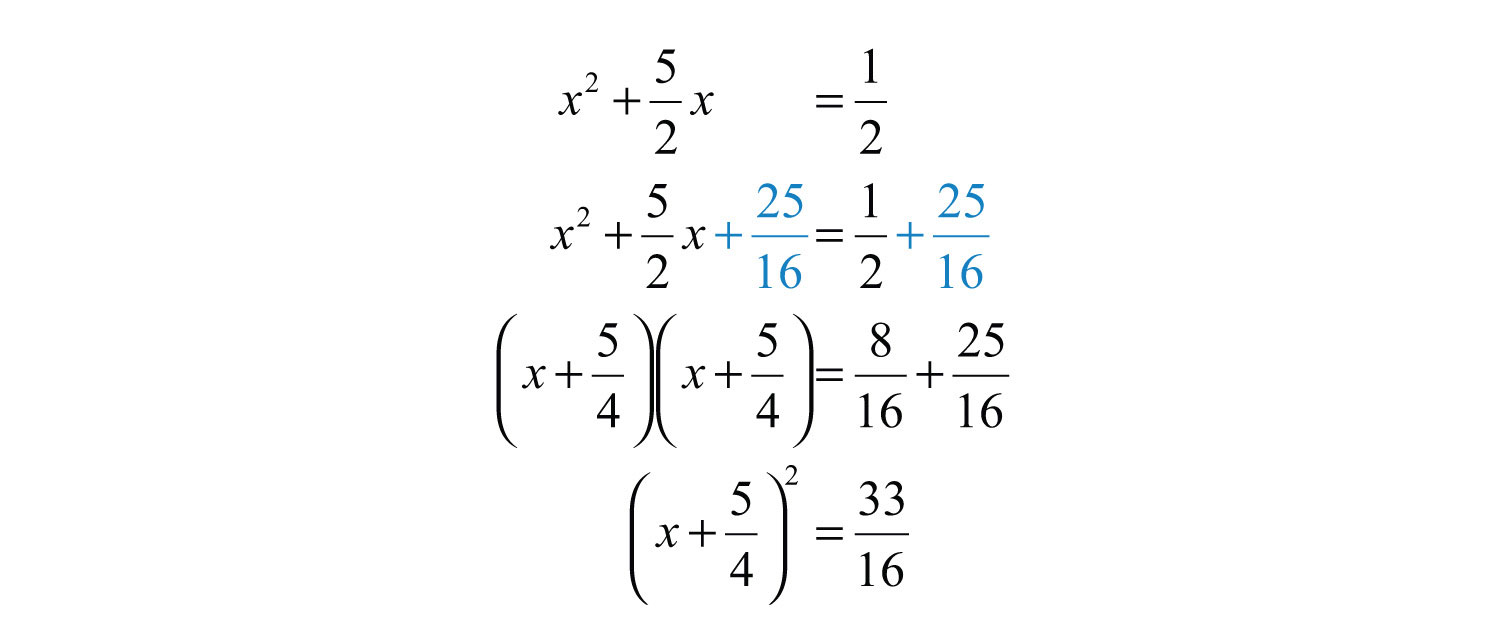
Next, solve by extracting roots.

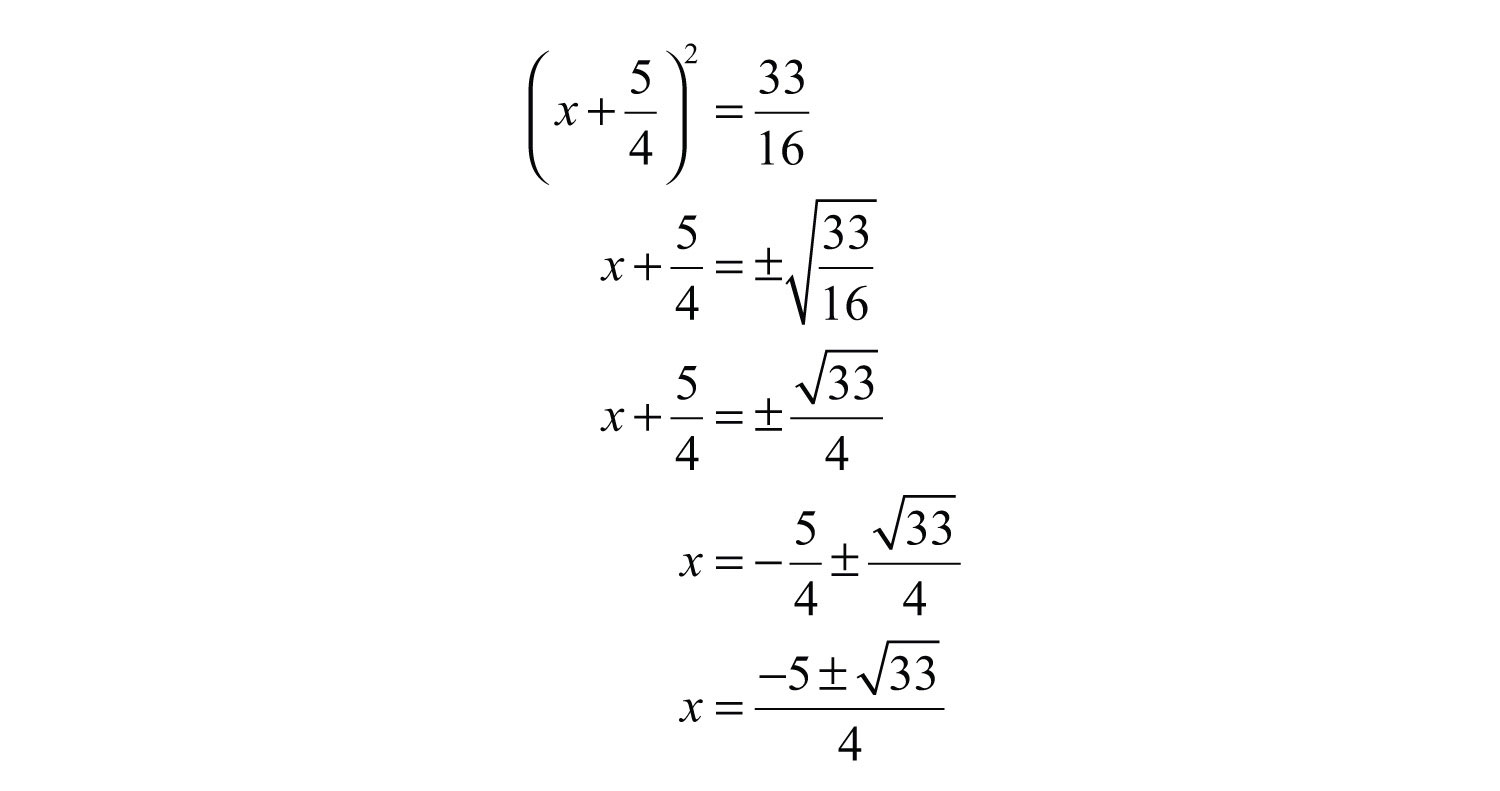
Answer: The solutions are $\frac{- 5 \pm \sqrt{33}}{4}$ .

Try this! Solve: $2 x^{2} - 2 x - 3 = 0$ .

Answer: $x = \frac{1 \pm \sqrt{7}}{2}$

Video Solution

(click to see video)

Key Takeaways

Solve any quadratic equation by completing the square.
You can apply the square root property to solve an equation if you can first convert the equation to the form ${(x - p)}^{2} = q$ .
To complete the square, first make sure the equation is in the form $x^{2} + b x = c$ . Then add the value ${(\frac{b}{2})}^{2}$ to both sides and factor.
The process for completing the square always works, but it may lead to some tedious calculations with fractions. This is the case when the middle term, b, is not divisible by 2.

Topic Exercises

Part A: Completing the Square

Complete the square.

1. $x^{2} + 6 x + ? = {(x + ?)}^{2}$

2. $x^{2} + 8 x + ? = {(x + ?)}^{2}$

3. $x^{2} - 2 x + ? = {(x - ?)}^{2}$

4. $x^{2} - 4 x + ? = {(x - ?)}^{2}$

5. $x^{2} + 7 x + ? = {(x + ?)}^{2}$

6. $x^{2} + 3 x + ? = {(x + ?)}^{2}$

7. $x^{2} + \frac{2}{3} x + ? = {(x + ?)}^{2}$

8. $x^{2} + \frac{4}{5} x + ? = {(x + ?)}^{2}$

9. $x^{2} + \frac{3}{4} x + ? = {(x + ?)}^{2}$

10. $x^{2} + \frac{5}{3} x + ? = {(x + ?)}^{2}$

Solve by factoring and then solve by completing the square. Check answers.

11. $x^{2} + 2 x - 8 = 0$

12. $x^{2} - 8 x + 15 = 0$

13. $y^{2} + 2 y - 24 = 0$

14. $y^{2} - 12 y + 11 = 0$

15. $t^{2} + 3 t - 28 = 0$

16. $t^{2} - 7 t + 10 = 0$

17. $2 x^{2} + 3 x - 2 = 0$

18. $3 x^{2} - x - 2 = 0$

19. $2 y^{2} - y - 1 = 0$

20. $2 y^{2} + 7 y - 4 = 0$

Solve by completing the square.

21. $x^{2} + 6 x - 1 = 0$

22. $x^{2} + 8 x + 10 = 0$

23. $x^{2} - 2 x - 7 = 0$

24. $x^{2} - 6 x - 3 = 0$

25. $x^{2} - 2 x + 4 = 0$

26. $x^{2} - 4 x + 9 = 0$

27. $t^{2} + 10 t - 75 = 0$

28. $t^{2} + 12 t - 108 = 0$

29. $x^{2} - 4 x - 1 = 15$

30. $x^{2} - 12 x + 8 = - 10$

31. $y^{2} - 20 y = - 25$

32. $y^{2} + 18 y = - 53$

33. $x^{2} - 0.6 x - 0.27 = 0$

34. $x^{2} - 1.6 x - 0.8 = 0$

35. $x^{2} - \frac{2}{3} x - \frac{1}{3} = 0$

36. $x^{2} - \frac{4}{5} x - \frac{1}{5} = 0$

37. $x^{2} + x - 1 = 0$

38. $x^{2} + x - 3 = 0$

39. $y^{2} + 3 y - 2 = 0$

40. $y^{2} + 5 y - 3 = 0$

41. $x^{2} + 3 x + 5 = 0$

42. $x^{2} + x + 1 = 0$

43. $x^{2} - 7 x + \frac{11}{2} = 0$

44. $x^{2} - 9 x + \frac{3}{2} = 0$

45. $t^{2} - \frac{1}{2} t - 1 = 0$

46. $t^{2} - \frac{1}{3} t - 2 = 0$

47. $x^{2} - 1.7 x - 0.0875 = 0$

48. $x^{2} + 3.3 x - 1.2775 = 0$

49. $4 x^{2} - 8 x - 1 = 0$

50. $2 x^{2} - 4 x - 3 = 0$

51. $3 x^{2} + 6 x + 1 = 0$

52. $5 x^{2} + 10 x + 2 = 0$

53. $3 x^{2} + 2 x - 3 = 0$

54. $5 x^{2} + 2 x - 5 = 0$

55. $4 x^{2} - 12 x - 15 = 0$

56. $2 x^{2} + 4 x - 43 = 0$

57. $2 x^{2} - 4 x + 10 = 0$

58. $6 x^{2} - 24 x + 42 = 0$

59. $2 x^{2} - x - 2 = 0$

60. $2 x^{2} + 3 x - 1 = 0$

61. $3 x^{2} + 2 x - 2 = 0$

62. $3 x^{2} - x - 1 = 0$

63. $x (x + 1) - 11 (x - 2) = 0$

64. $(x + 1) (x + 7) - 4 (3 x + 2) = 0$

65. $y^{2} = (2 y + 3) (y - 1) - 2 (y - 1)$

66. $(2 y + 5) (y - 5) - y (y - 8) = - 24$

67. ${(t + 2)}^{2} = 3 (3 t + 1)$

68. $(3 t + 2) (t - 4) - (t - 8) = 1 - 10 t$

Solve by completing the square and round off the solutions to the nearest hundredth.

69. ${(2 x - 1)}^{2} = 2 x$

70. ${(3 x - 2)}^{2} = 5 - 15 x$

71. $(2 x + 1) (3 x + 1) = 9 x + 4$

72. $(3 x + 1) (4 x - 1) = 17 x - 4$

73. $9 x (x - 1) - 2 (2 x - 1) = - 4 x$

74. ${(6 x + 1)}^{2} - 6 (6 x + 1) = 0$

Part B: Discussion Board

75. Research and discuss the Hindu method for completing the square.

76. Explain why the technique for completing the square described in this section requires that the leading coefficient be equal to 1.

Answers

1: $x^{2} + 6 x + 9 = {(x + 3)}^{2}$

3: $x^{2} - 2 x + 1 = {(x - 1)}^{2}$

5: $x^{2} + 7 x + \frac{49}{4} = {(x + \frac{7}{2})}^{2}$

7: $x^{2} + \frac{2}{3} x + \frac{1}{9} = {(x + \frac{1}{3})}^{2}$

9: $x^{2} + \frac{3}{4} x + \frac{9}{64} = {(x + \frac{3}{8})}^{2}$

11: −4, 2

13: −6, 4

15: −7, 4

17: 1/2, −2

19: −1/2, 1

21: $- 3 \pm \sqrt{10}$

23: $1 \pm 2 \sqrt{2}$

25: No real solution

27: −15, 5

29: $2 \pm 2 \sqrt{5}$

31: $10 \pm 5 \sqrt{3}$

33: −0.3, 0.9

35: −1/3, 1

37: $\frac{- 1 \pm \sqrt{5}}{2}$

39: $\frac{- 3 \pm \sqrt{17}}{2}$

41: No real solution

43: $\frac{7 \pm 3 \sqrt{3}}{2}$

45: $\frac{1 \pm \sqrt{17}}{4}$

47: −0.05, 1.75

49: $\frac{2 \pm \sqrt{5}}{2}$

51: $\frac{- 3 \pm \sqrt{6}}{3}$

53: $\frac{- 1 \pm \sqrt{10}}{3}$

55: $\frac{3 \pm 2 \sqrt{6}}{2}$

57: No real solution

59: $\frac{1 \pm \sqrt{17}}{4}$

61: $\frac{- 1 \pm \sqrt{7}}{3}$

63: $5 \pm \sqrt{3}$

65: $\frac{1 \pm \sqrt{5}}{2}$

67: $\frac{5 \pm \sqrt{21}}{2}$

69: 0.19, 1.31

71: −0.45, 1.12

73: 0.33, 0.67