This is “Multiplying and Dividing Radical Expressions”, section 8.4 from the book Beginning Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
8.4 Multiplying and Dividing Radical Expressions
Learning Objectives
- Multiply radical expressions.
- Divide radical expressions.
- Rationalize the denominator.
Multiplying Radical Expressions
When multiplying radical expressions with the same index, we use the product rule for radicals. If a and b represent positive real numbers,
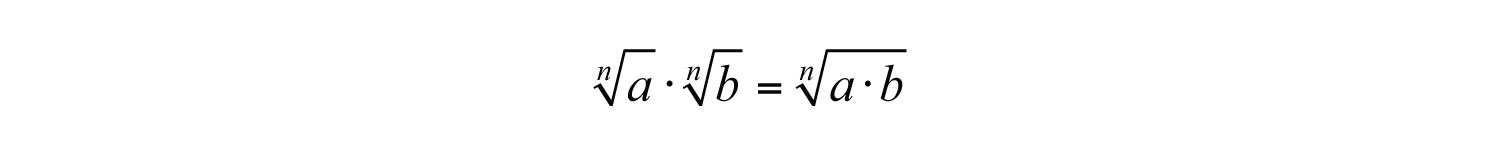
Example 1: Multiply: .
Solution: This problem is a product of two square roots. Apply the product rule for radicals and then simplify.
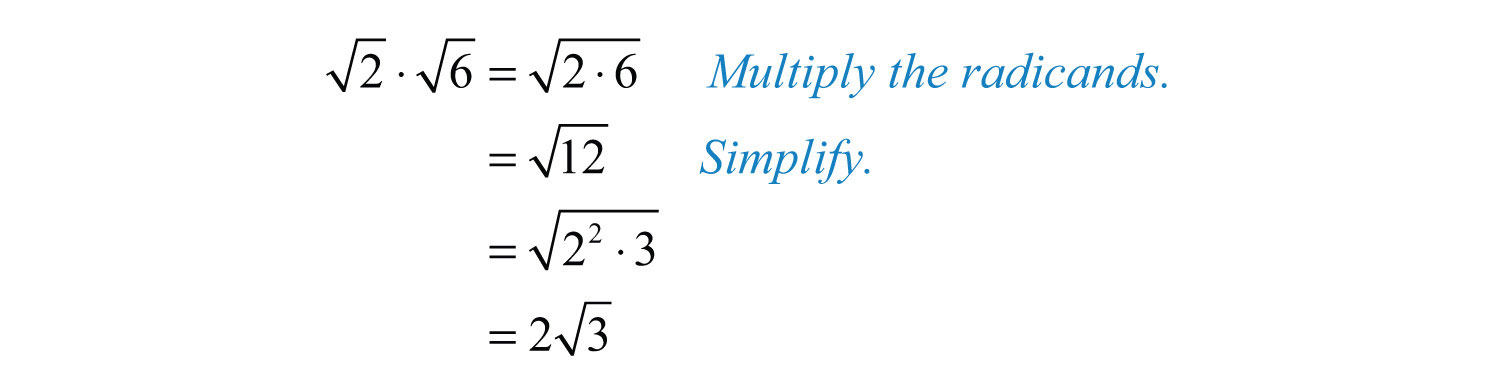
Answer:
Example 2: Multiply: .
Solution: This problem is a product of cube roots. Apply the product rule for radicals and then simplify.
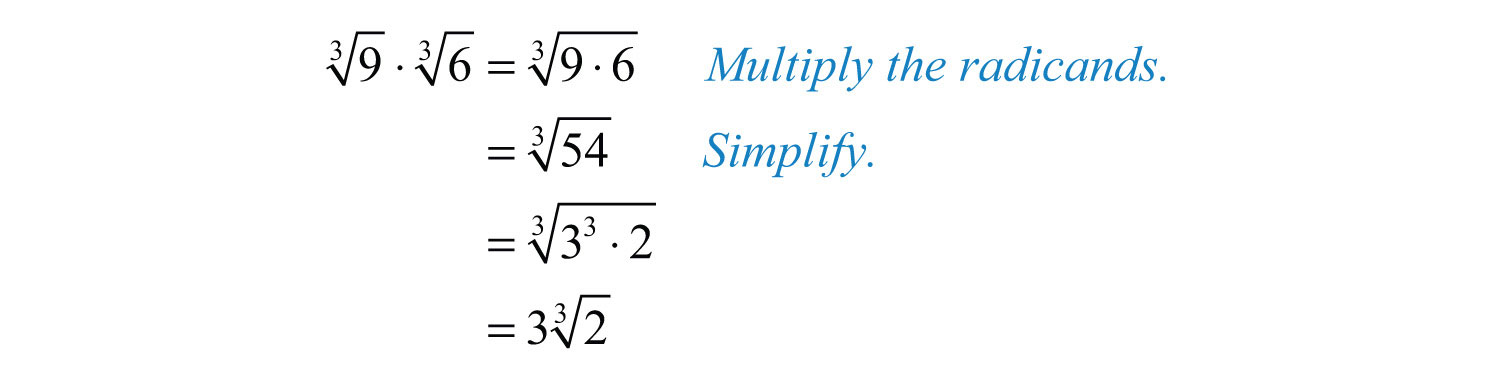
Answer:
Often there will be coefficients in front of the radicals.
Example 3: Multiply: .
Solution: Using the product rule for radicals and the fact that multiplication is commutative, we can multiply the coefficients and the radicands as follows.
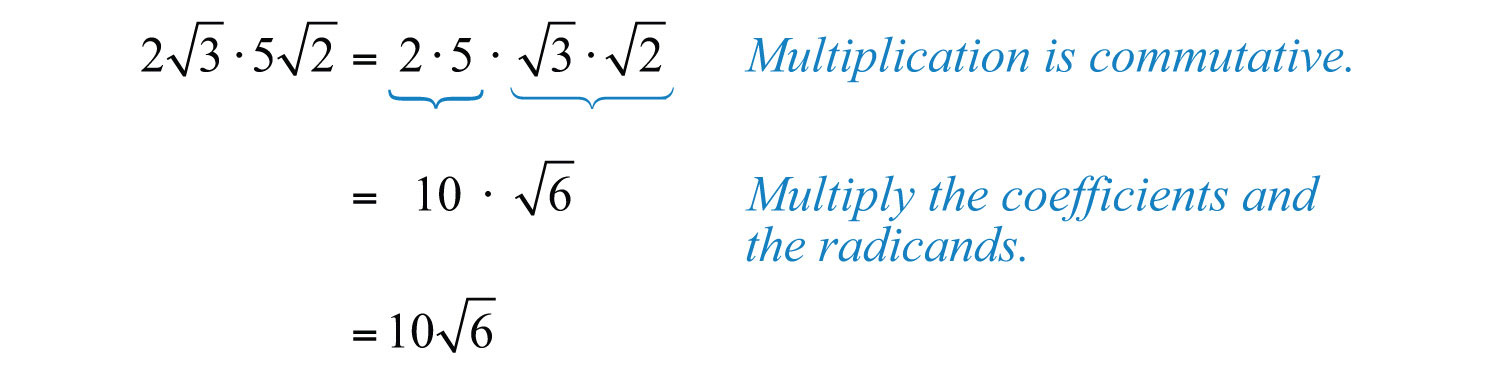
Typically, the first step involving the application of the commutative property is not shown.
Answer:
Example 4: Multiply: .
Solution:
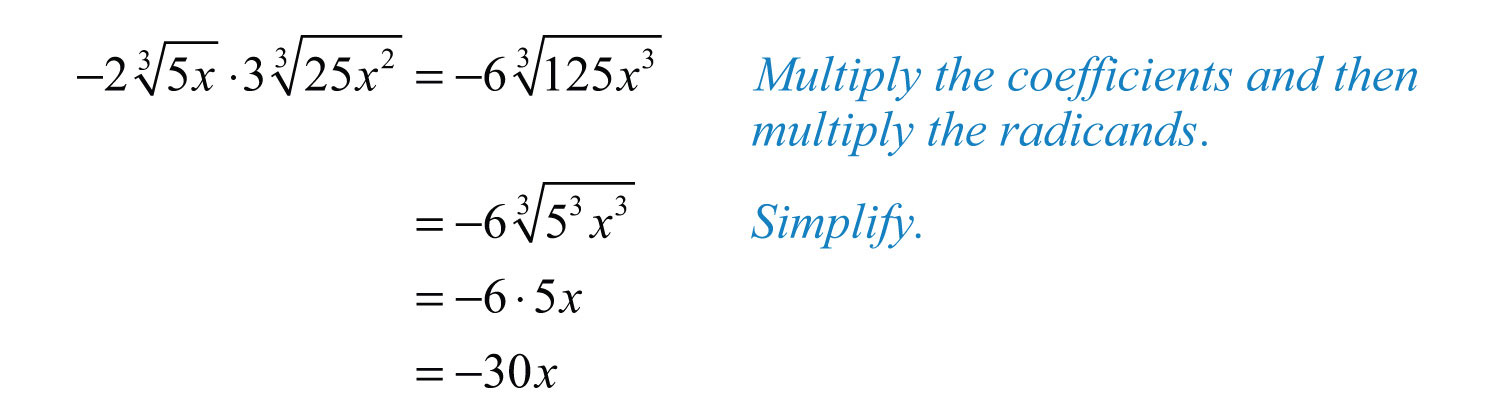
Answer:
Use the distributive property when multiplying rational expressions with more than one term.
Example 5: Multiply: .
Solution: Apply the distributive property and multiply each term by .
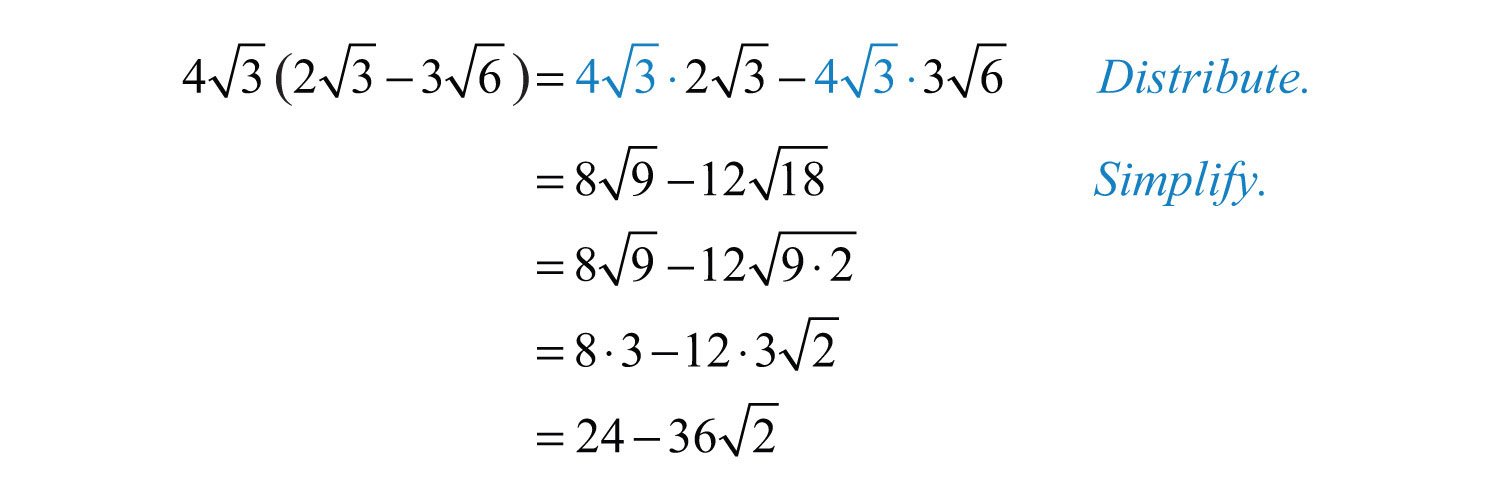
Answer:
Example 6: Multiply: .
Solution: Apply the distributive property and then simplify the result.
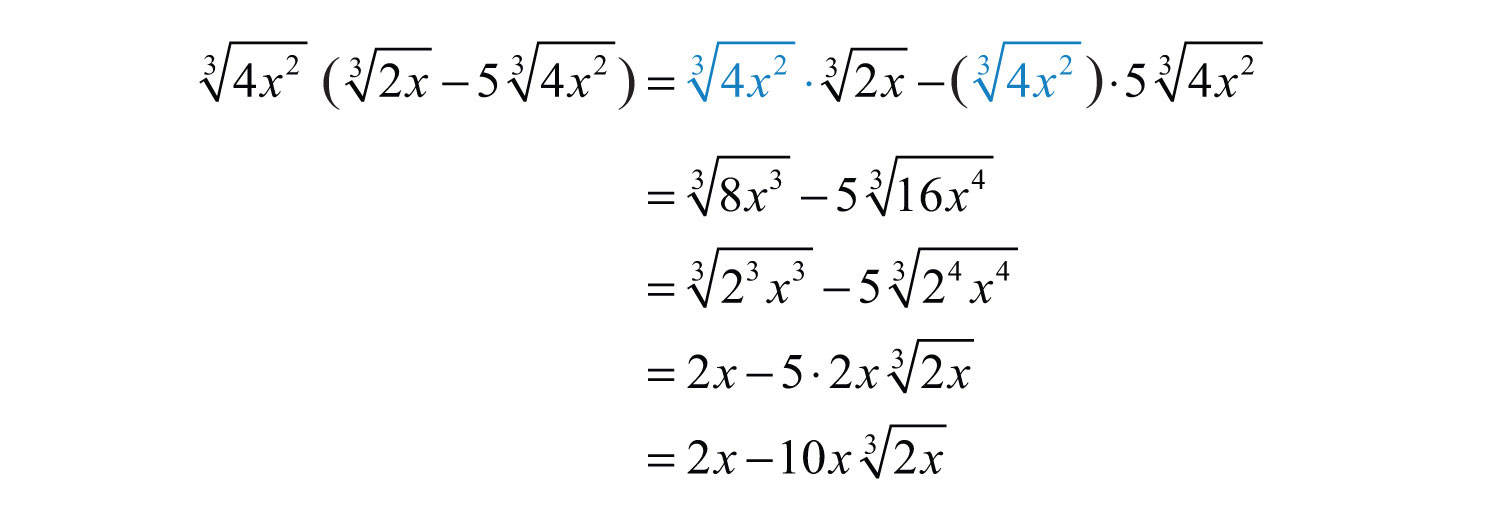
Answer:
The process for multiplying radical expressions with multiple terms is the same process used when multiplying polynomials. Apply the distributive property, simplify each radical, and then combine like terms.
Example 7: Multiply: .
Solution: Begin by applying the distributive property.
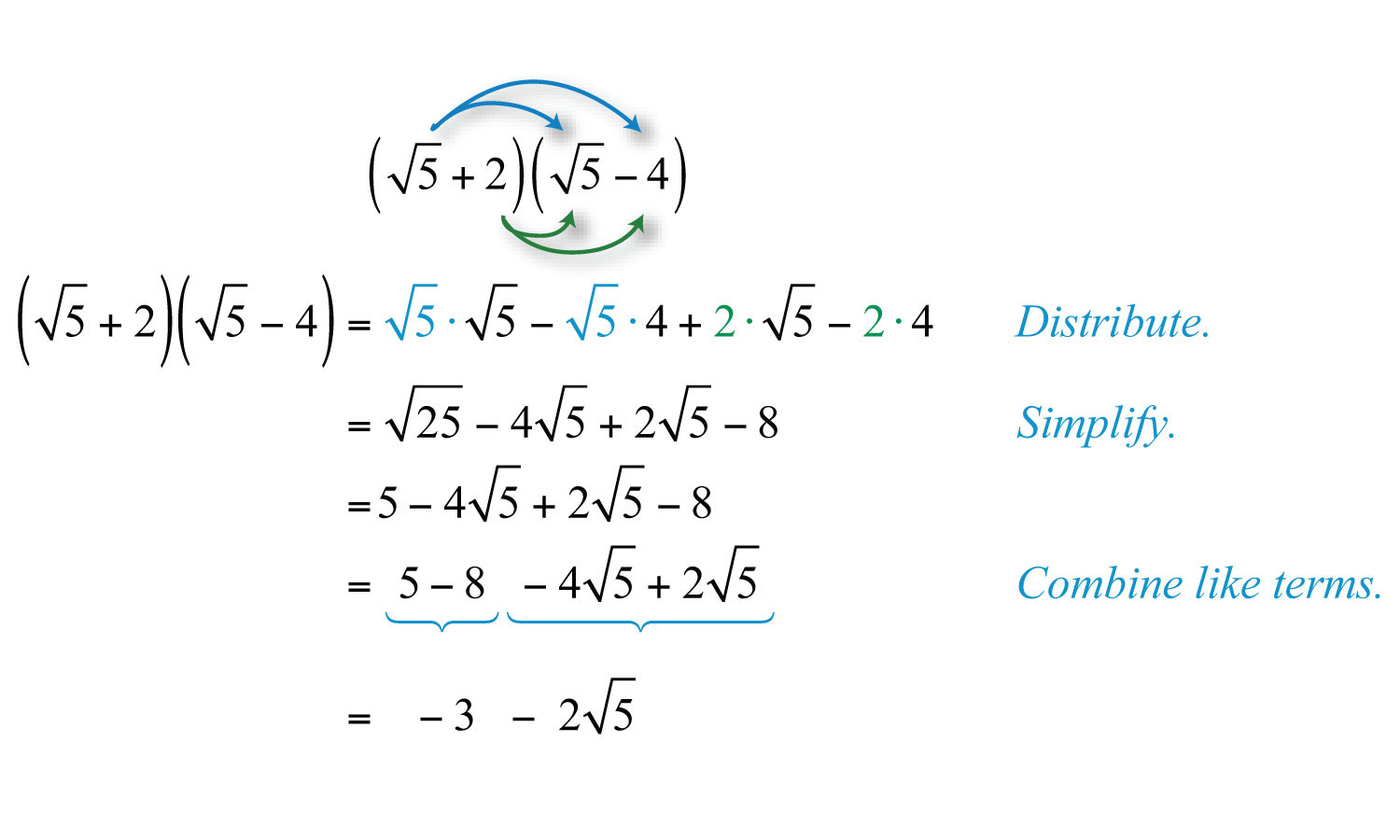
Answer:
Example 8: Multiply: .
Solution:
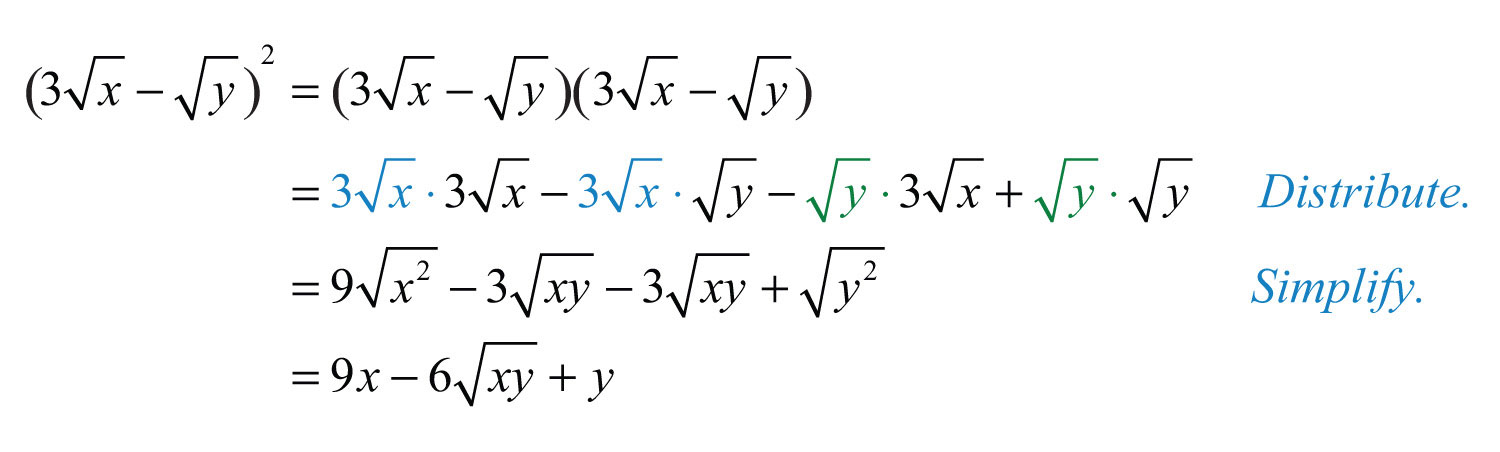
Answer:
Try this! Multiply: .
Answer:
Video Solution
(click to see video)The expressions and are called conjugatesThe factors and are conjugates.. When multiplying conjugates, the sum of the products of the inner and outer terms results in 0.
Example 9: Multiply: .
Solution: Apply the distributive property and then combine like terms.
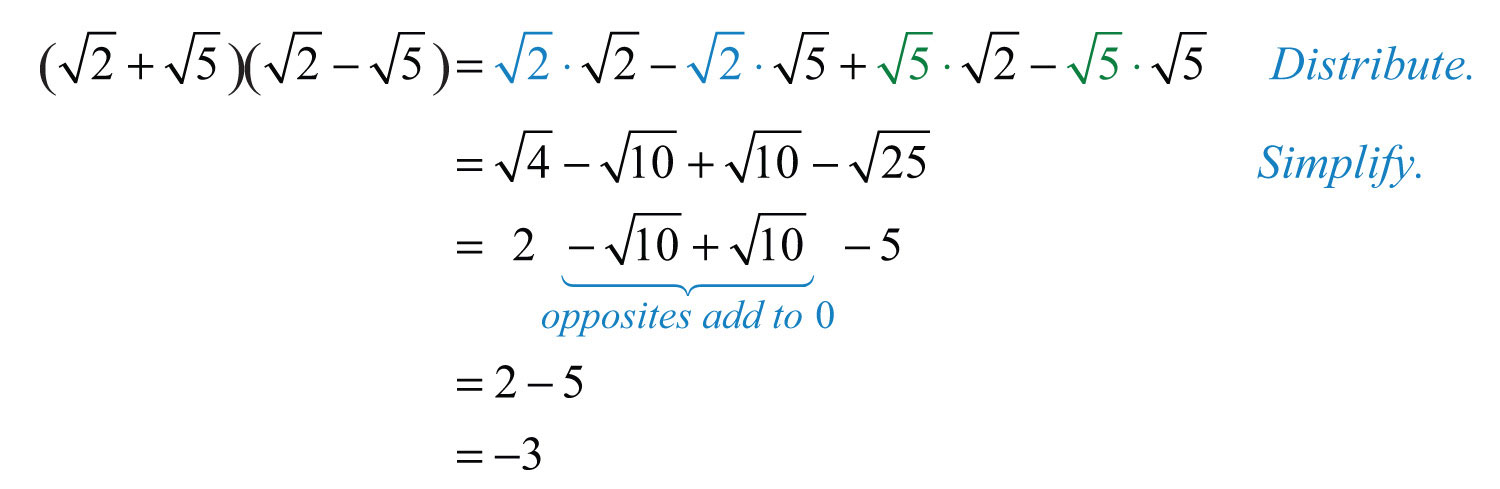
Answer: −3
It is important to note that when multiplying conjugate radical expressions, we obtain a rational expression. This is true in general and is often used in our study of algebra.
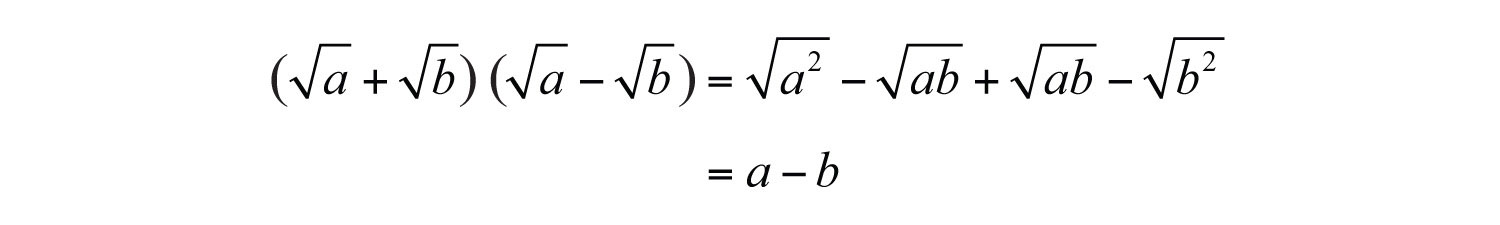
Therefore, for nonnegative real numbers a and b, we have the following property:
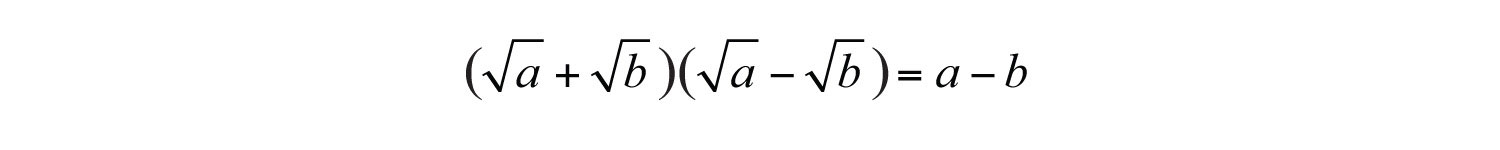
Dividing Radical Expressions (Rationalizing the Denominator)
To divide radical expressions with the same index, we use the quotient rule for radicals. If a and b represent nonnegative numbers, where , then we have
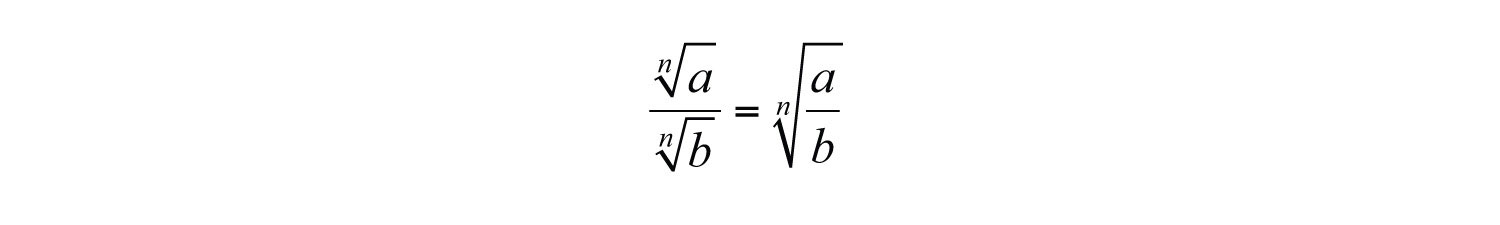
Example 10: Divide: .
Solution: In this case, we can see that 10 and 80 have common factors. If we apply the quotient rule for radicals and write it as a single square root, we will be able to reduce the fractional radicand.

Answer:
Example 11: Divide: .
Solution:
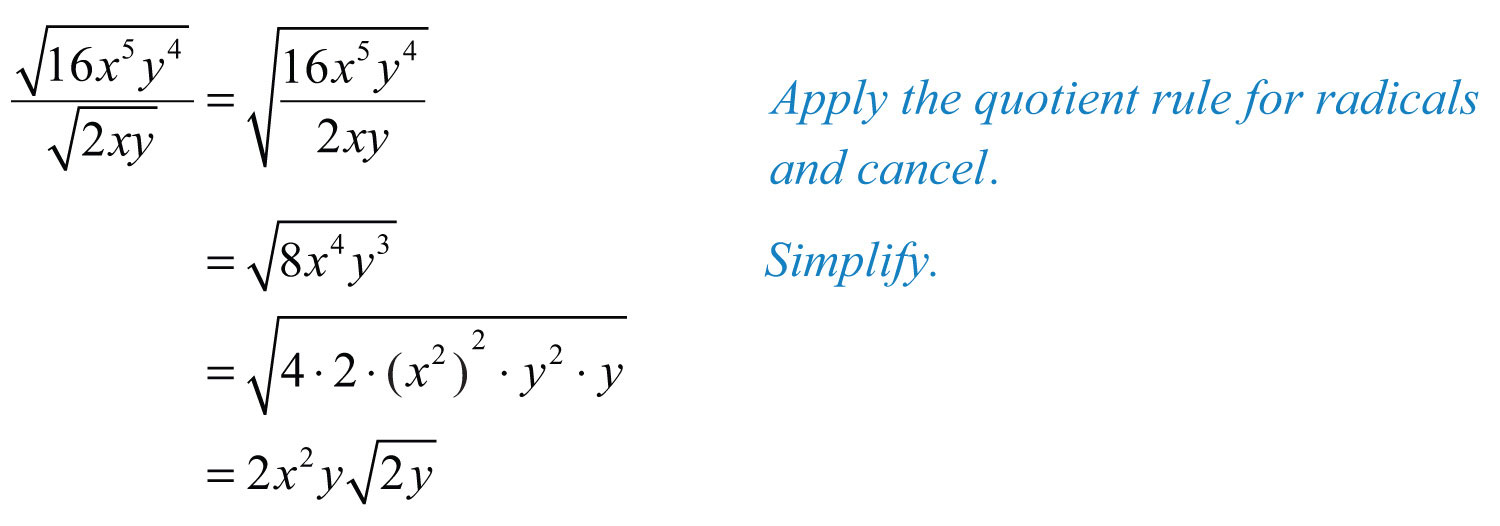
Answer:
Example 12: Divide: .
Solution:

Answer:
When the divisor of a radical expression contains a radical, it is a common practice to find an equivalent expression where the denominator is a rational number. Finding such an equivalent expression is called rationalizing the denominatorThe process of determining an equivalent radical expression with a rational denominator..

To do this, multiply the fraction by a special form of 1 so that the radicand in the denominator can be written with a power that matches the index. After doing this, simplify and eliminate the radical in the denominator. For example,
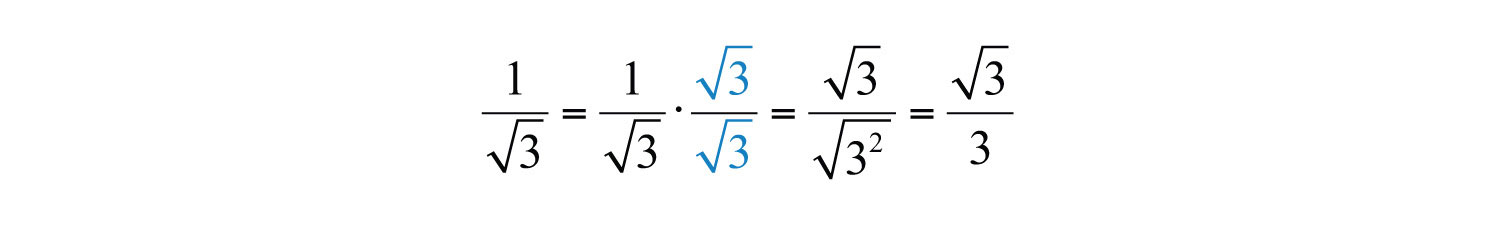
Remember, to obtain an equivalent expression, you must multiply the numerator and denominator by the exact same nonzero factor.
Example 13: Rationalize the denominator: .
Solution: The goal is to find an equivalent expression without a radical in the denominator. In this example, multiply by 1 in the form .

Answer:
Example 14: Rationalize the denominator: .
Solution: The radicand in the denominator determines the factors that you need to use to rationalize it. In this example, multiply by 1 in the form .
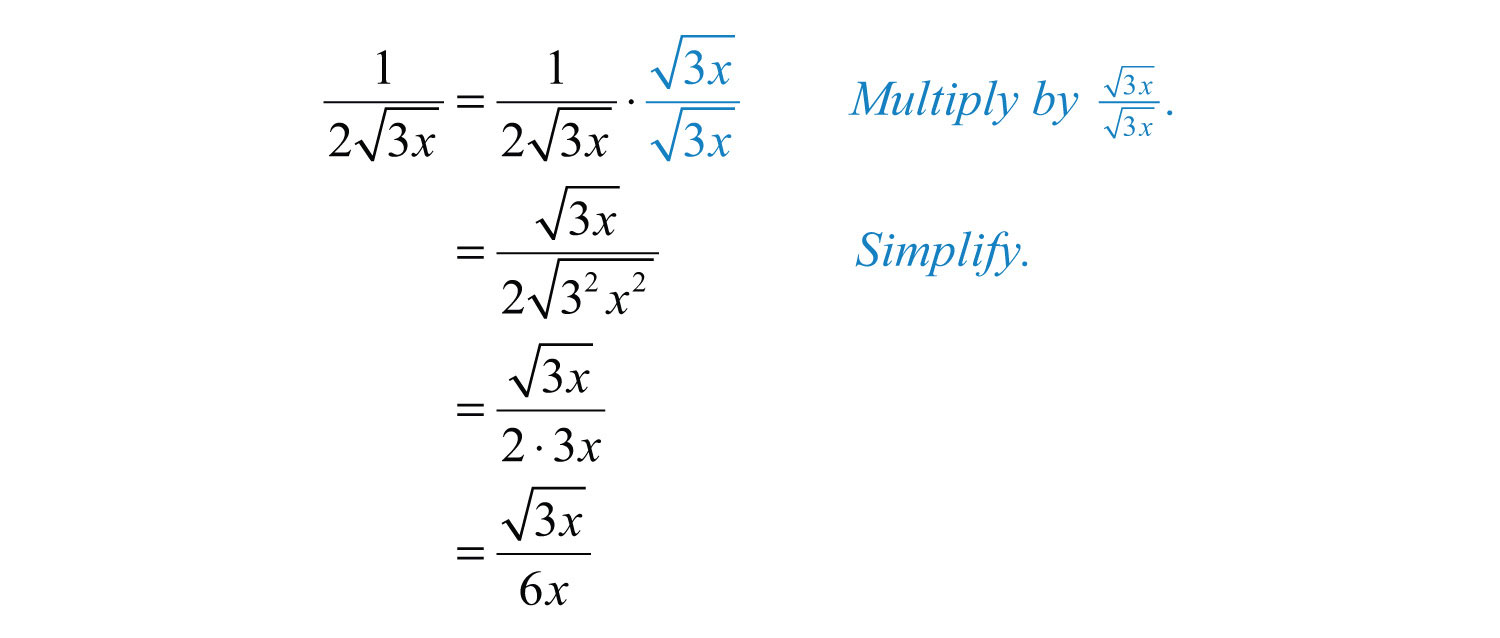
Answer:
Typically, we will find the need to reduce, or cancel, after rationalizing the denominator.
Example 15: Rationalize the denominator: .
Solution: In this example, we will multiply by 1 in the form .
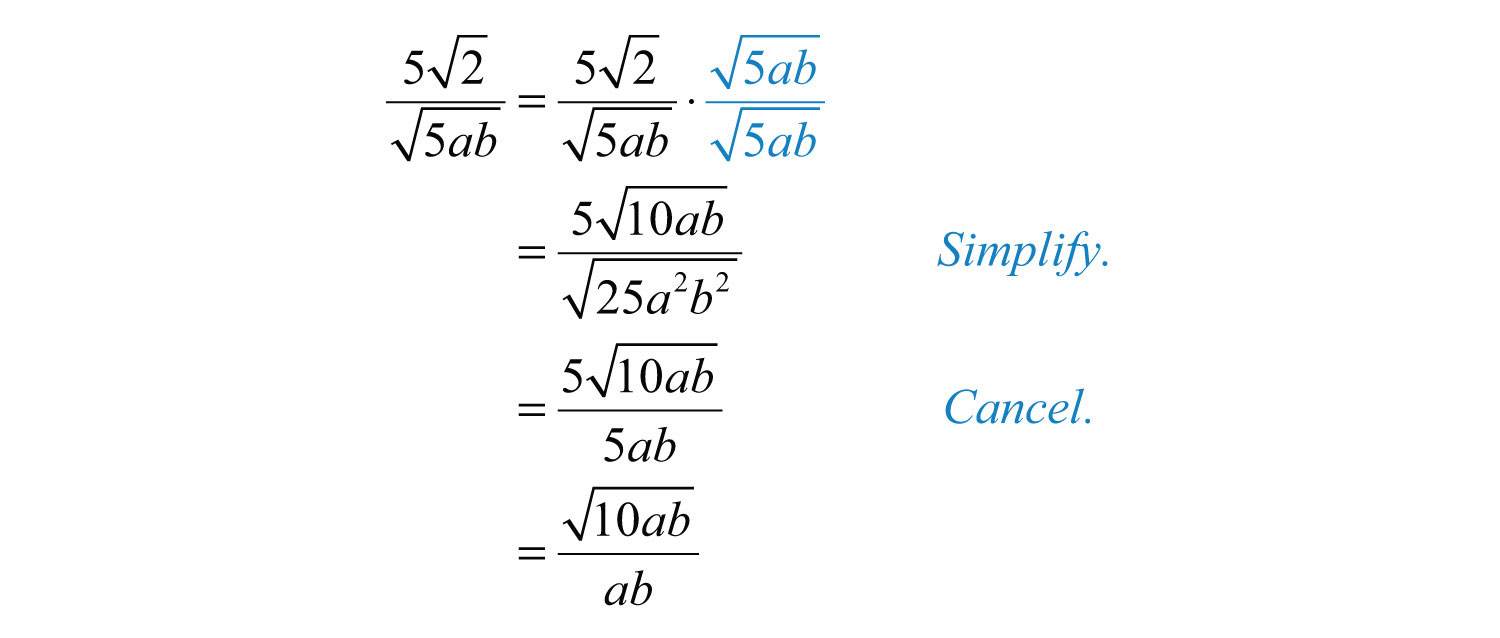
Notice that a and b do not cancel in this example. Do not cancel factors inside a radical with those that are outside.
Answer:
Try this! Rationalize the denominator: .
Answer:
Video Solution
(click to see video)Up to this point, we have seen that multiplying a numerator and a denominator by a square root with the exact same radicand results in a rational denominator. In general, this is true only when the denominator contains a square root. However, this is not the case for a cube root. For example,
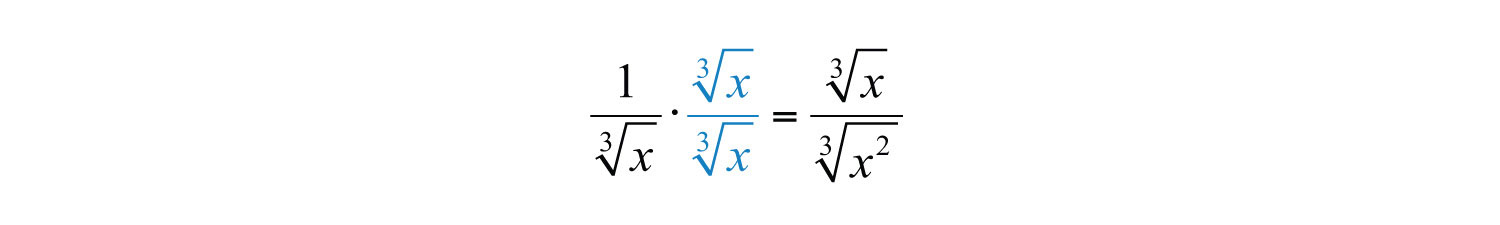
Note that multiplying by the same factor in the denominator does not rationalize it. In this case, if we multiply by 1 in the form of , then we can write the radicand in the denominator as a power of 3. Simplifying the result then yields a rationalized denominator. For example,
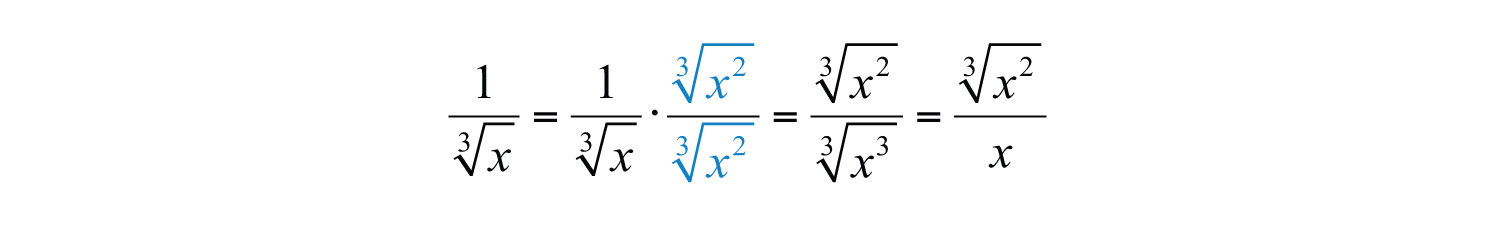
Therefore, to rationalize the denominator of radical expressions with one radical term in the denominator, begin by factoring the radicand of the denominator. The factors of this radicand and the index determine what we should multiply by. Multiply numerator and denominator by the nth root of factors that produce nth powers of all the factors in the radicand of the denominator.
Example 16: Rationalize the denominator: .
Solution: The radical in the denominator is equivalent to . To rationalize the denominator, it should be . To obtain this, we need one more factor of 5. Therefore, multiply by 1 in the form of .
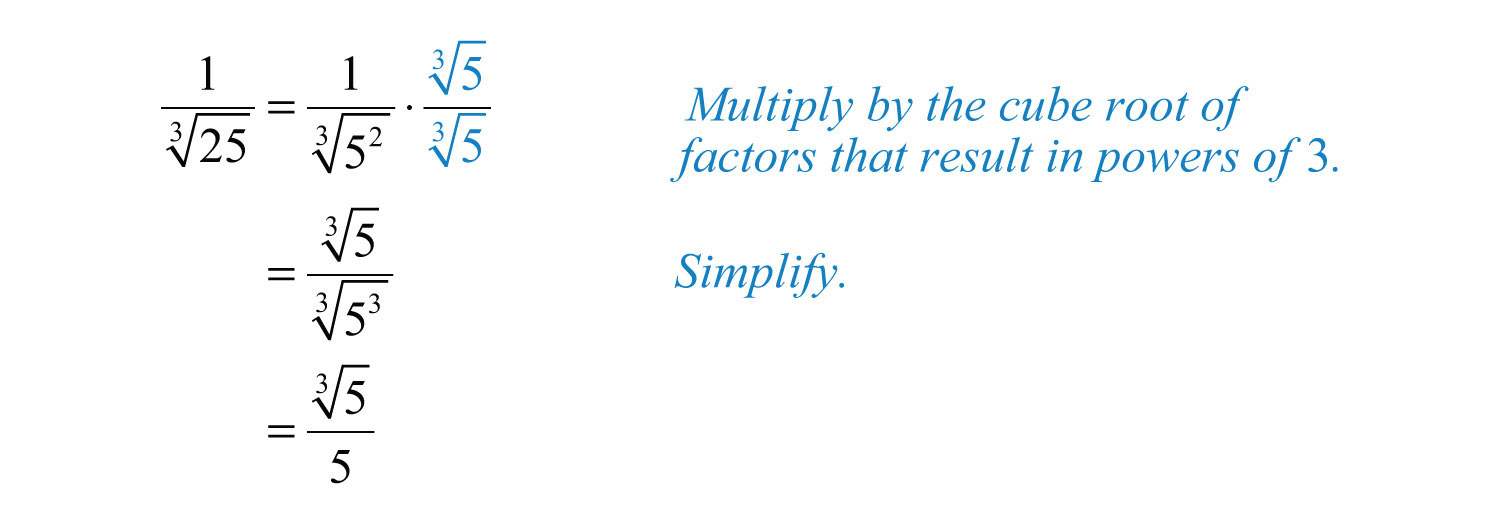
Answer:
Example 17: Rationalize the denominator: .
Solution: In this example, we will multiply by 1 in the form .

Answer:
Example 18: Rationalize the denominator: .
Solution: In this example, we will multiply by 1 in the form .
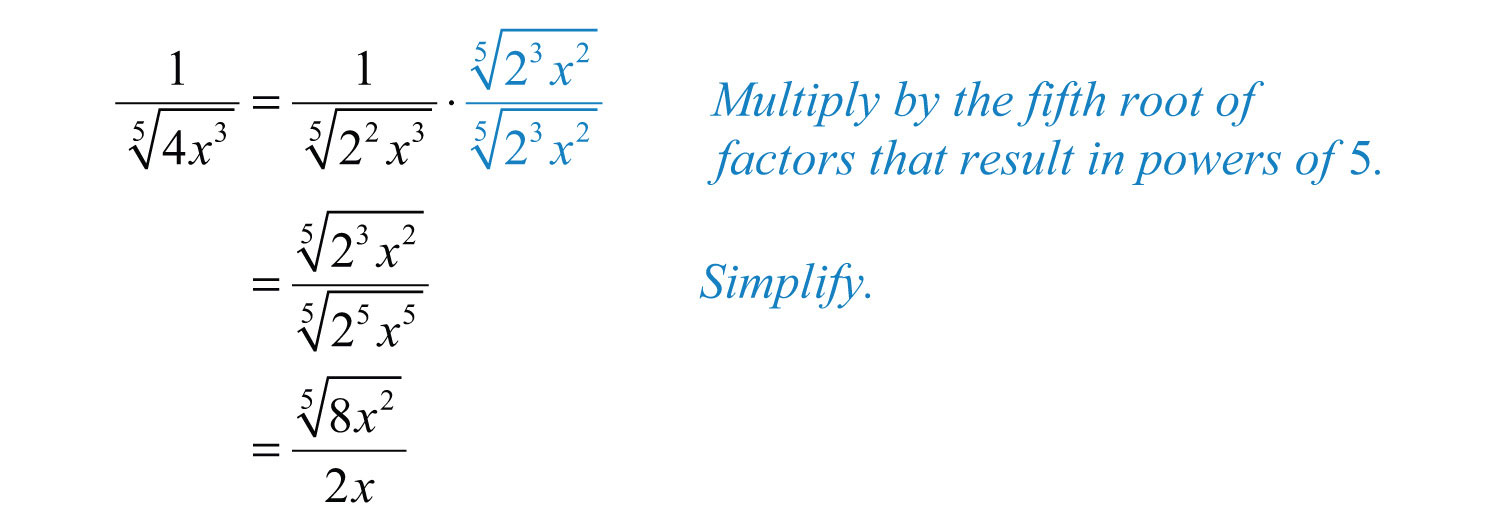
Answer:
When two terms involving square roots appear in the denominator, we can rationalize it using a very special technique. This technique involves multiplying the numerator and the denominator of the fraction by the conjugate of the denominator. Recall that multiplying a radical expression by its conjugate produces a rational number.
Example 19: Rationalize the denominator: .
Solution: In this example, the conjugate of the denominator is . Therefore, multiply by 1 in the form .
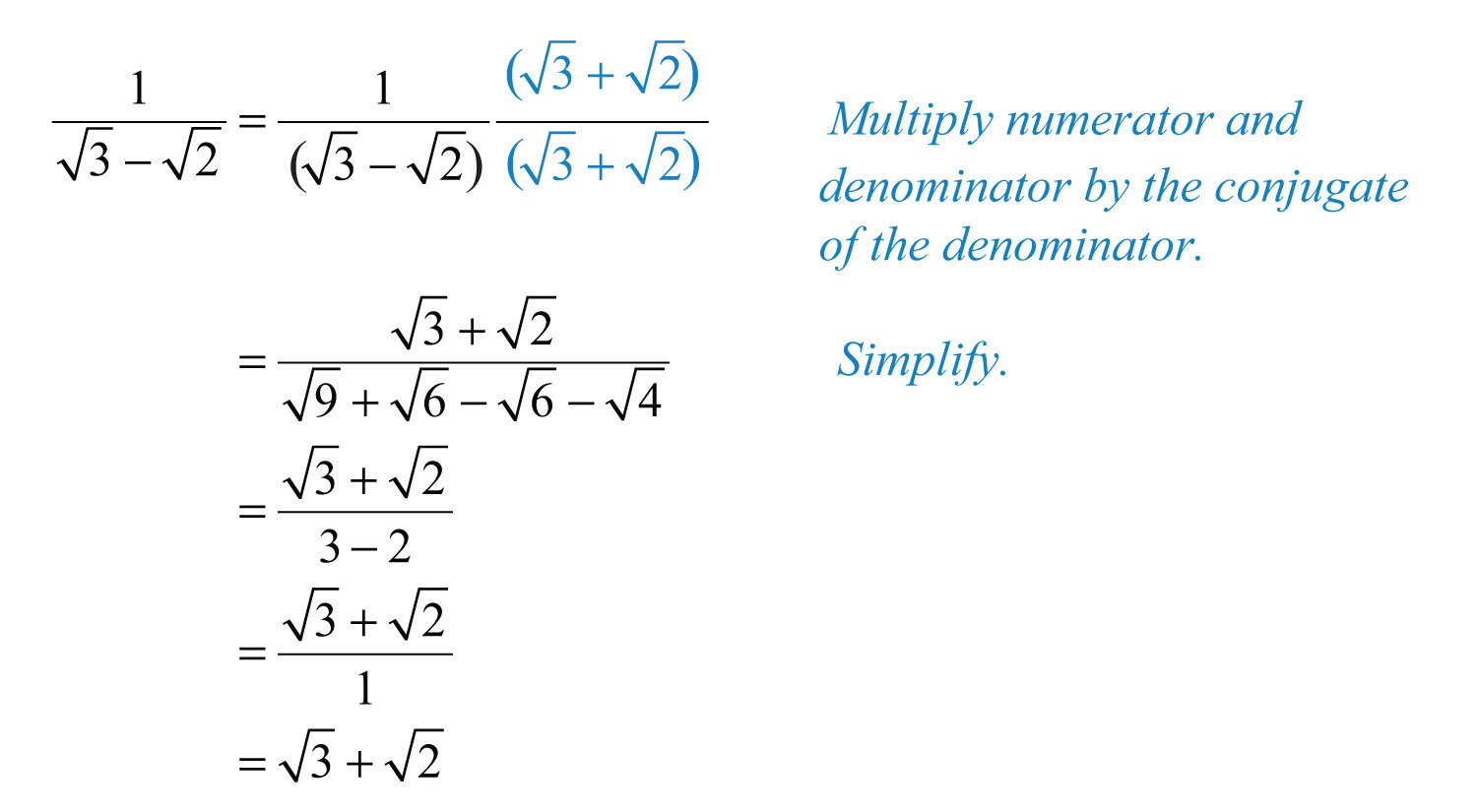
Answer:
Notice that the terms involving the square root in the denominator are eliminated by multiplying by the conjugate. We can use the property to expedite the process of multiplying the expressions in the denominator.
Example 20: Rationalize the denominator: .
Solution: Multiply by 1 in the form .

Answer:
Example 21: Rationalize the denominator: .
Solution: In this example, we will multiply by 1 in the form .
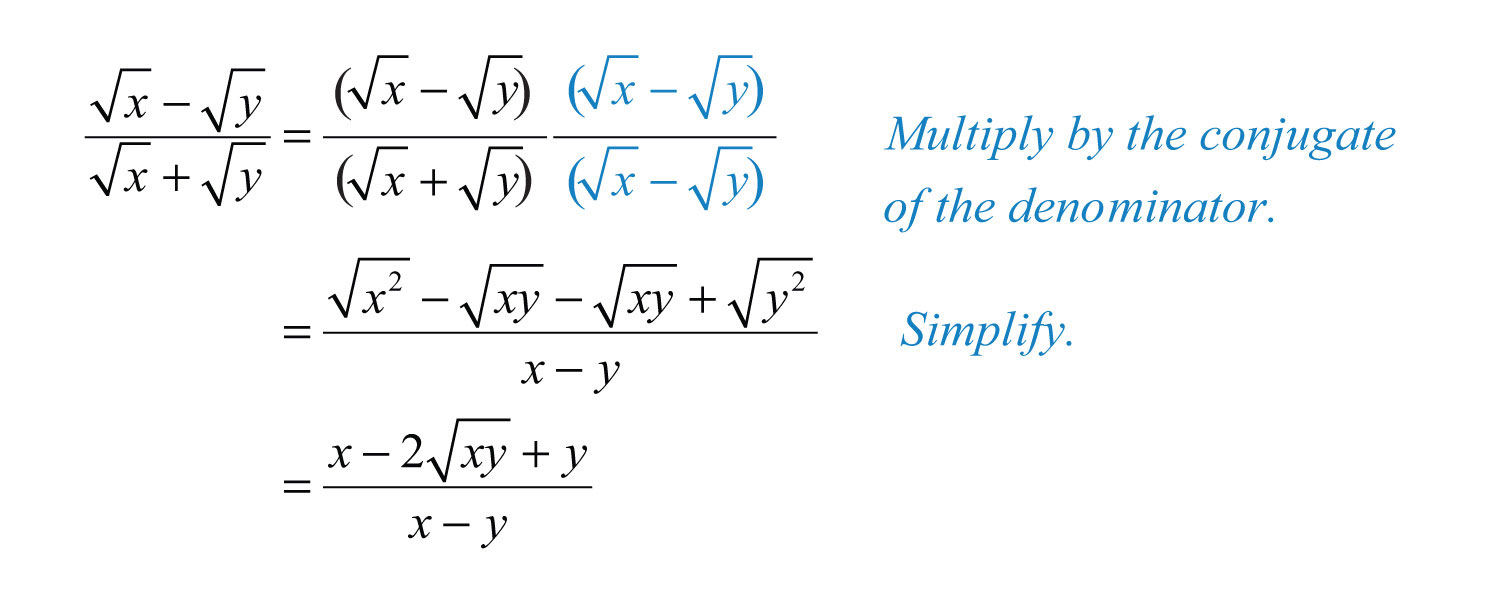
Answer:
Try this! Rationalize the denominator: .
Answer:
Video Solution
(click to see video)Key Takeaways
- To multiply two single-term radical expressions, multiply the coefficients and multiply the radicands. If possible, simplify the result.
- Apply the distributive property when multiplying radical expressions with multiple terms. Then simplify and combine all like radicals.
- Multiplying a two-term radical expression involving square roots by its conjugate results in a rational expression.
- It is common practice to write radical expressions without radicals in the denominator. The process of finding such an equivalent expression is called rationalizing the denominator.
- If an expression has one term in the denominator involving a radical, then rationalize it by multiplying numerator and denominator by the nth root of factors of the radicand so that their powers equal the index.
- If a radical expression has two terms in the denominator involving square roots, then rationalize it by multiplying the numerator and denominator by its conjugate.
Topic Exercises
Part A: Multiplying Radical Expressions
Multiply. (Assume all variables are nonnegative.)
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51. What are the perimeter and area of a rectangle with length of centimeters and width of centimeters?
52. What are the perimeter and area of a rectangle with length of centimeters and width of centimeters?
53. If the base of a triangle measures meters and the height measures meters, then what is the area?
54. If the base of a triangle measures meters and the height measures meters, then what is the area?
Part B: Dividing Radical Expressions
Divide.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
Rationalize the denominator.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
99.
100.
101.
102.
103.
104.
105.
106.
Part C: Discussion
107. Research and discuss some of the reasons why it is a common practice to rationalize the denominator.
108. Explain in your own words how to rationalize the denominator.
Answers
1:
3:
5: 7
7:
9: 20
11:
13:
15:
17: 5
19:
21:
23: 16
25:
27:
29:
31:
33:
35:
37:
39:
41:
43:
45:
47: 10
49:
51: Perimeter: centimeters; area: square centimeters
53: 18 square meters
55: 5
57:
59:
61:
63:
65:
67:
69:
71:
73:
75:
77:
79:
81:
83:
85:
87:
89:
91:
93:
95:
97:
99:
101:
103:
105:




