This is “Radicals”, section 8.1 from the book Beginning Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
8.1 Radicals
Learning Objectives
- Find square roots.
- Find cube roots.
- Find nth roots.
- Simplify expressions using the product and quotient rules for radicals.
Square Roots
The square rootThe number that, when multiplied by itself, yields the original number. of a number is that number that when multiplied by itself yields the original number. For example, 4 is a square root of 16, because . Since , we can say that −4 is a square root of 16 as well. Every positive real number has two square roots, one positive and one negative. For this reason, we use the radical sign to denote the principal (nonnegative) square rootThe positive square root of a real number, denoted with the symbol . and a negative sign in front of the radical to denote the negative square root.

Zero is the only real number with one square root.
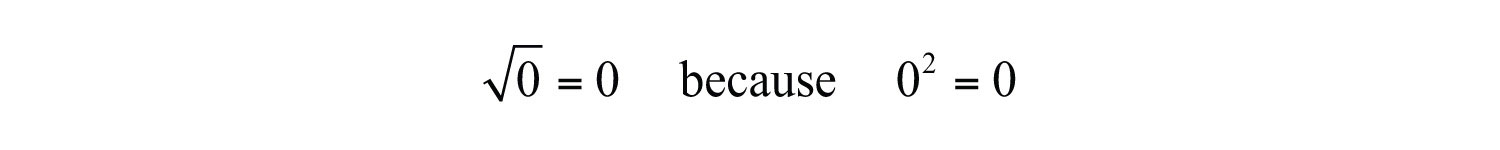
If the radicandThe expression a within a radical sign, ., the number inside the radical sign, is nonnegative and can be factored as the square of another nonnegative number, then the square root of the number is apparent. In this case, we have the following property:
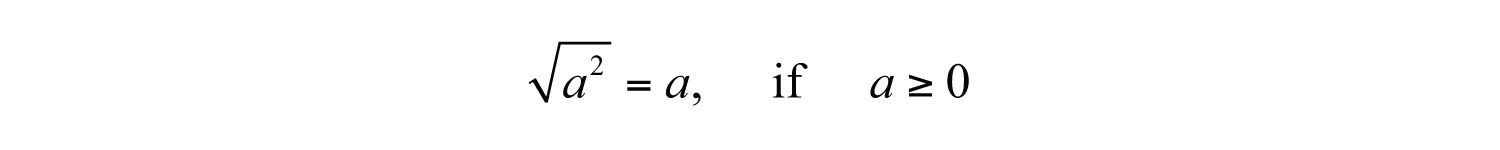
Example 1: Find the square root.
a.
b.
c.
d.
Solution:
a.
b.
c.
d.
Example 2: Find the negative square root.
a.
b.
Solution:
a.
b.
The radicand may not always be a perfect square. If a positive integer is not a perfect square, then its square root will be irrational. For example, is an irrational number and can be approximated on most calculators using the square root button.
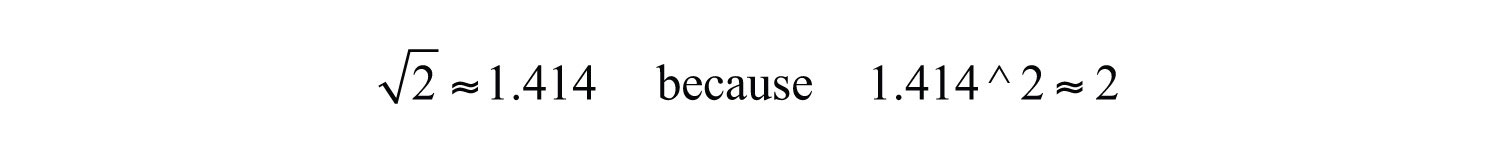
Next, consider the square root of a negative number. To determine the square root of −9, you must find a number that when squared results in −9:
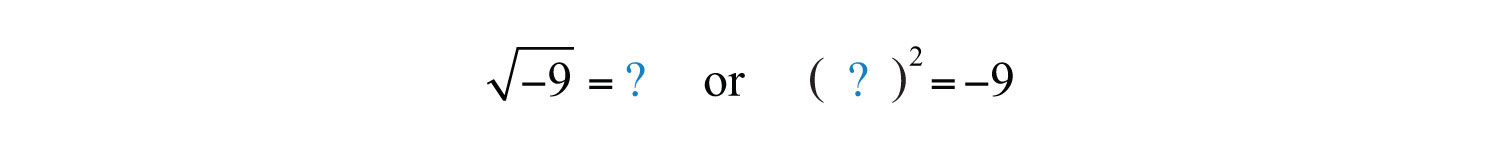
However, any real number squared always results in a positive number:
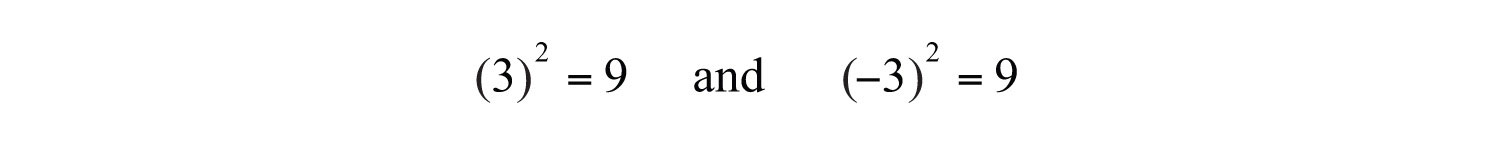
The square root of a negative number is currently left undefined. For now, we will state that is not a real a number.
Cube Roots
The cube rootThe number that, when used as a factor with itself three times, yields the original number; it is denoted with the symbol . of a number is that number that when multiplied by itself three times yields the original number. Furthermore, we denote a cube root using the symbol , where 3 is called the indexThe positive integer n in the notation that is used to indicate an nth root.. For example,
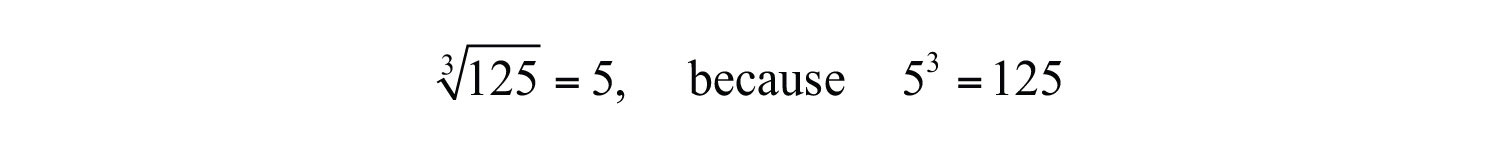
The product of three equal factors will be positive if the factor is positive and negative if the factor is negative. For this reason, any real number will have only one real cube root. Hence the technicalities associated with the principal root do not apply. For example,
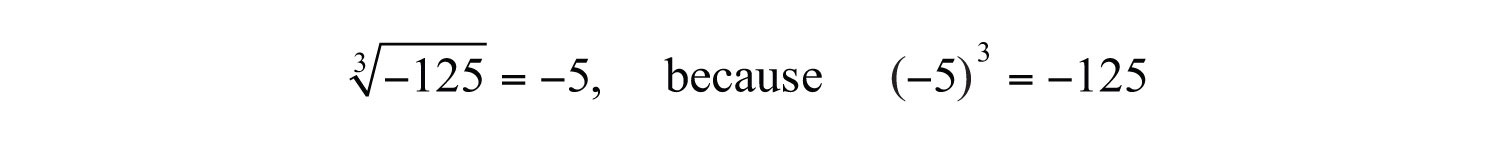
In general, given any real number a, we have the following property:
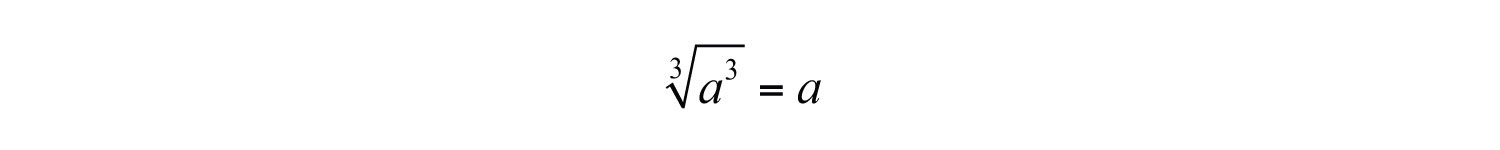
When simplifying cube roots, look for factors that are perfect cubes.
Example 3: Find the cube root.
a.
b.
c.
d.
Solution:
a.
b.
c.
d.
Example 4: Find the cube root.
a.
b.
c.
Solution:
a.
b.
c.
It may be the case that the radicand is not a perfect cube. If an integer is not a perfect cube, then its cube root will be irrational. For example, is an irrational number which can be approximated on most calculators using the root button. Depending on the calculator, we typically type in the index prior to pushing the button and then the radicand as follows:
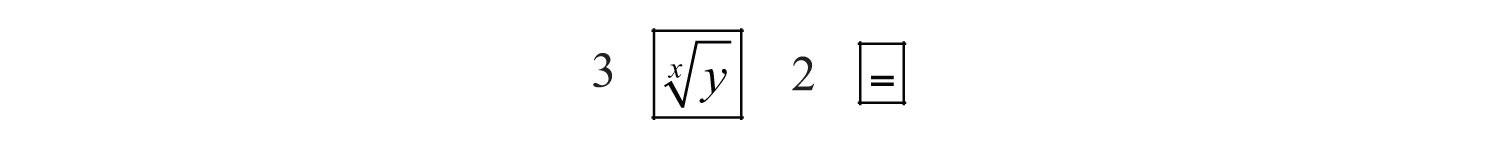
Therefore, we have
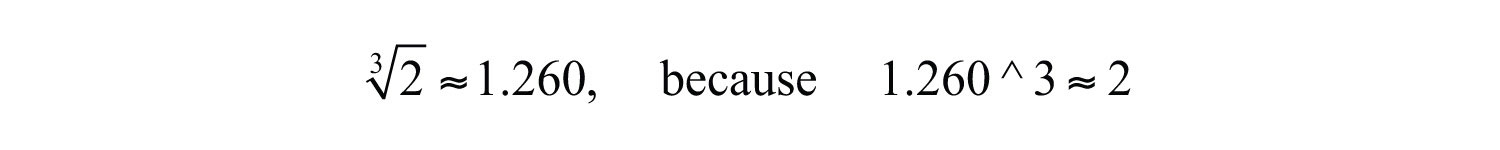
nth Roots
For any integer , we define the nth rootThe number that, when raised to the nth power, yields the original number. of a positive real number as that number that when raised to the nth power yields the original number. Given any nonnegative real number a, we have the following property:
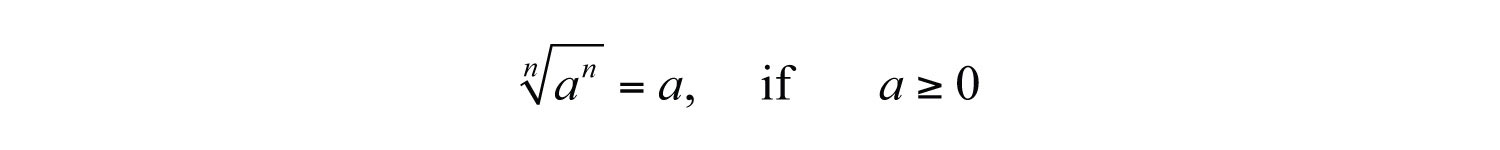
Here is called the index and is called the radicand. Furthermore, we can refer to the entire expression as a radicalUsed when referring to an expression of the form .. When the index is an integer greater than 3, we say “fourth root”, “fifth root”, and so on. The nth root of any number is apparent if we can write the radicand with an exponent equal to the index.
Example 5: Find the nth root.
a.
b.
c.
d.
Solution:
a.
b.
c.
d.
If the index is , then the radical indicates a square root and it is customary to write the radical without the index, as illustrated below:
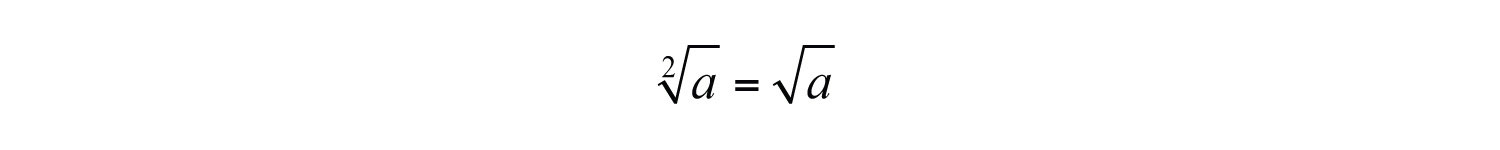
We have already taken care to define the principal square root of a number. At this point, we extend this idea to nth roots when n is even. For example, 3 is a fourth root of 81, because . And since , we can say that −3 is a fourth root of 81 as well. Hence we use the radical sign to denote the principal (nonnegative) nth rootThe positive nth root when n is even. when n is even. In this case, for any real number a, we use the following property:

For example,
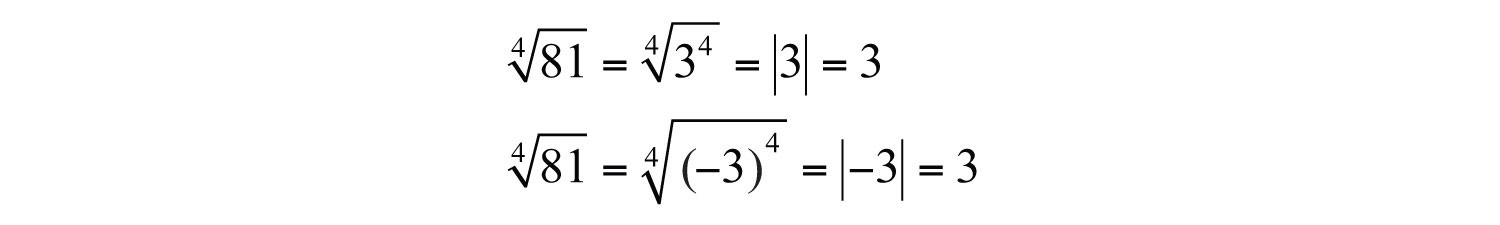
The negative nth root, when n is even, will be denoted using a negative sign in front of the radical .
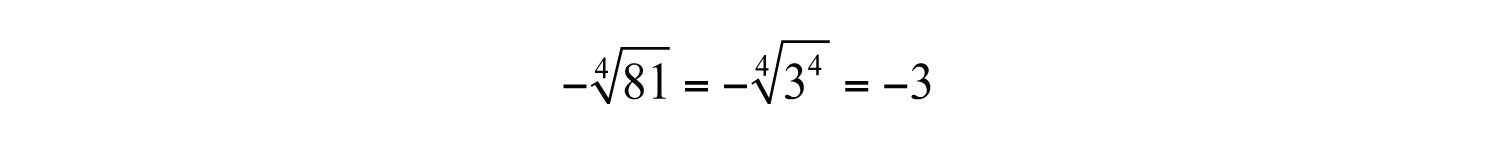
We have seen that the square root of a negative number is not real because any real number, when squared, will result in a positive number. In fact, a similar problem arises for any even index:
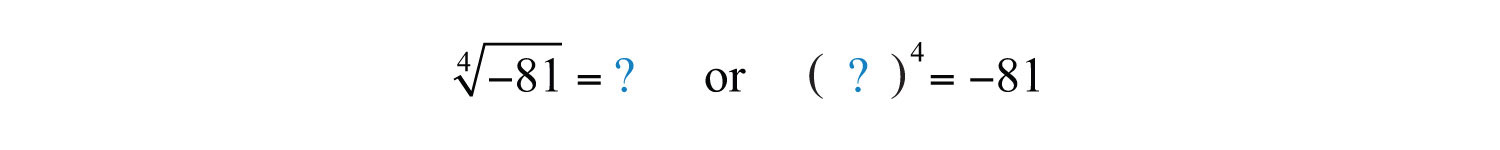
Here the fourth root of −81 is not a real number because the fourth power of any real number is always positive.

Example 6: Simplify.
a.
b.
Solution:
a. The radicand is negative and the index is even. Therefore, there is no real number that when raised to the fourth power is −16.

b. Here the radicand is positive. Furthermore, , and we can simplify as follows:
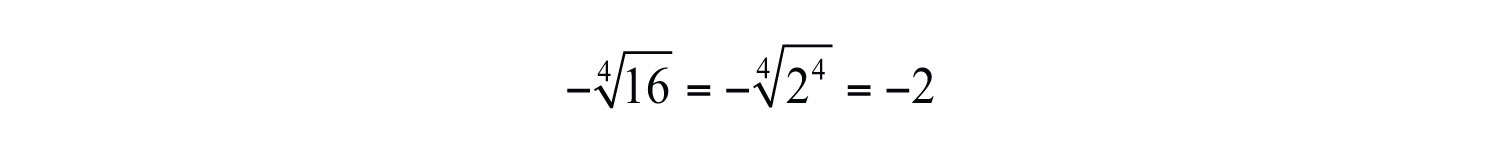
When n is odd, the same problems do not occur. The product of an odd number of positive factors is positive and the product of an odd number of negative factors is negative. Hence when the index n is odd, there is only one real nth root for any real number a. And we have the following property:

Example 7: Find the nth root.
a.
b.
Solution:
a.
b.
Try this! Find the fourth root: .
Answer: 5
Video Solution
(click to see video)Summary: When n is odd, the nth root is positive or negative depending on the sign of the radicand.
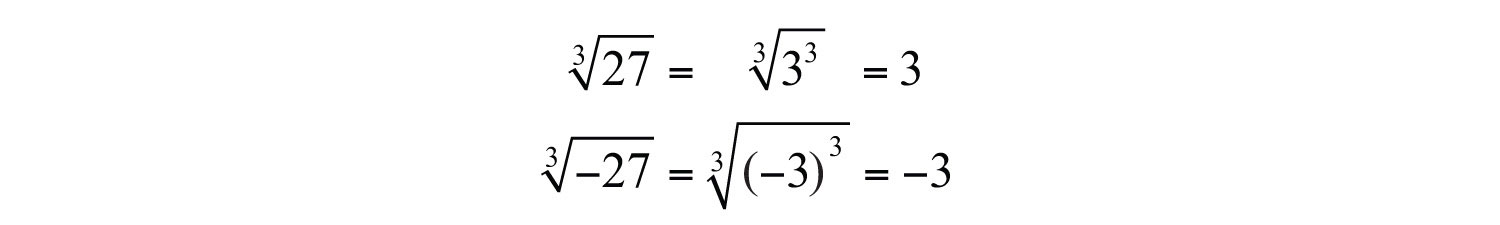
When n is even, the nth root is positive or not real depending on the sign of the radicand.
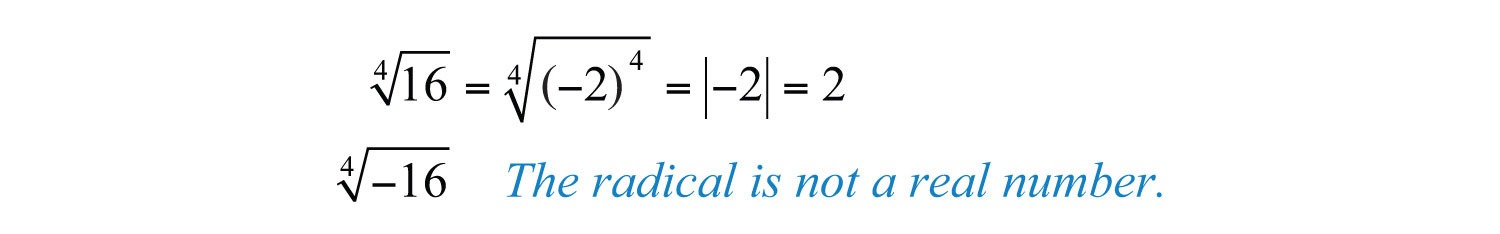
Simplifying Using the Product and Quotient Rule for Radicals
It will not always be the case that the radicand is a perfect power of the given index. If not, we use the following two properties to simplify them. If a and b represent positive real numbers, then we have
Product rule for radicals, where a and b represent positive real numbers.: |
|
Quotient rule for radicals, where a and b represent positive real numbers.: |
A radical is simplifiedA radical where the radicand does not consist of any factor that can be written as a perfect power of the index. if it does not contain any factor that can be written as a perfect power of the index.
Example 8: Simplify: .
Solution: Here 12 can be written as 4 ⋅ 3, where 4 is a perfect square.

We can verify our answer on a calculator:
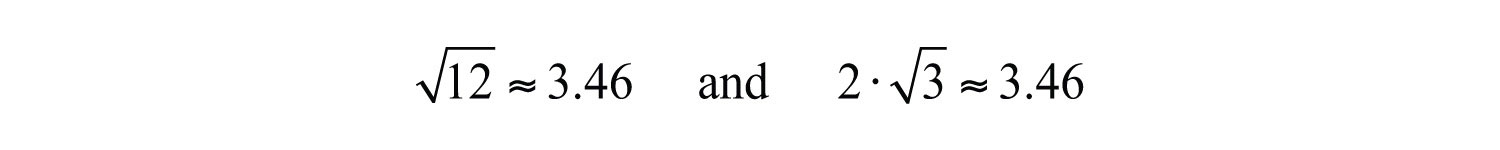
Also, it is worth noting that
Answer:
Example 9: Simplify: .
Solution: Begin by finding the largest perfect square factor of 135.
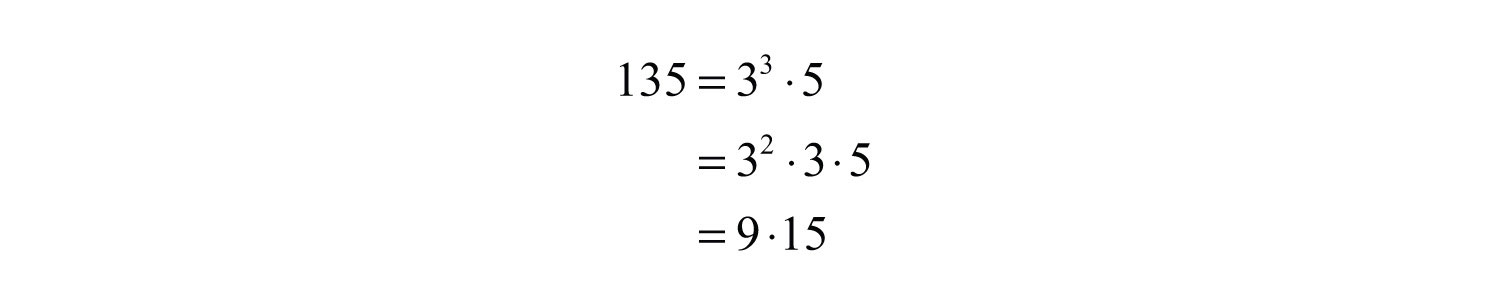
Therefore,

Answer:
Example 10: Simplify: .
Solution: Begin by finding the prime factorizations of both 50 and 121. This will enable us to easily determine the largest perfect square factors.
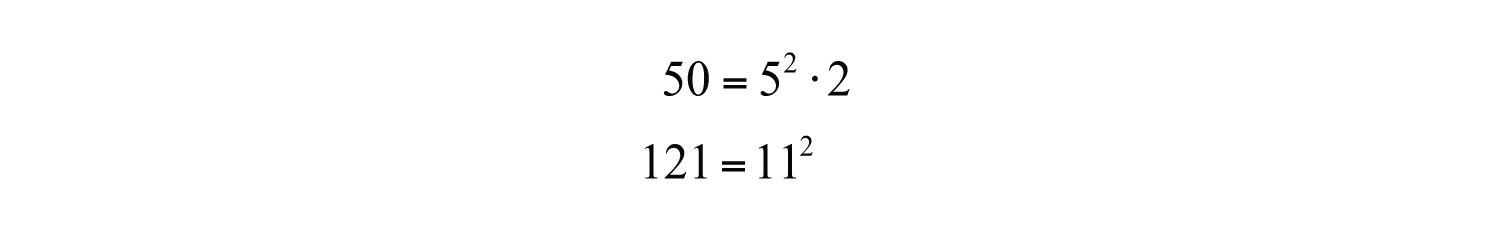
Therefore,
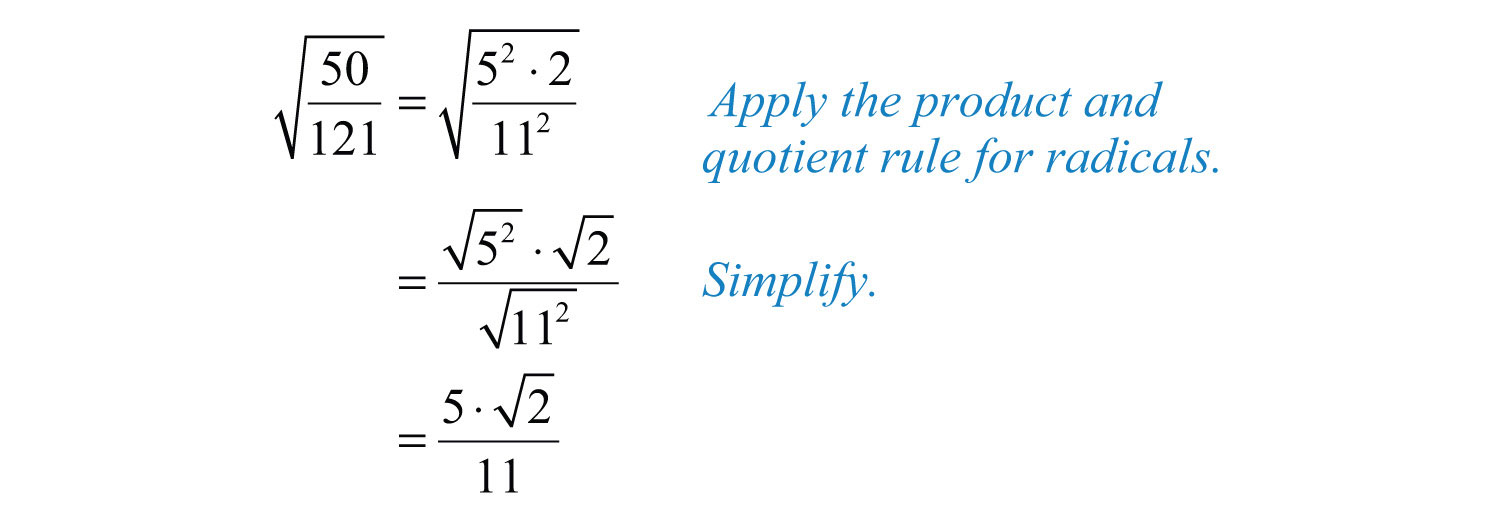
Answer:
Example 11: Simplify: .
Solution: Use the prime factorization of 162 to find the largest perfect cube factor:
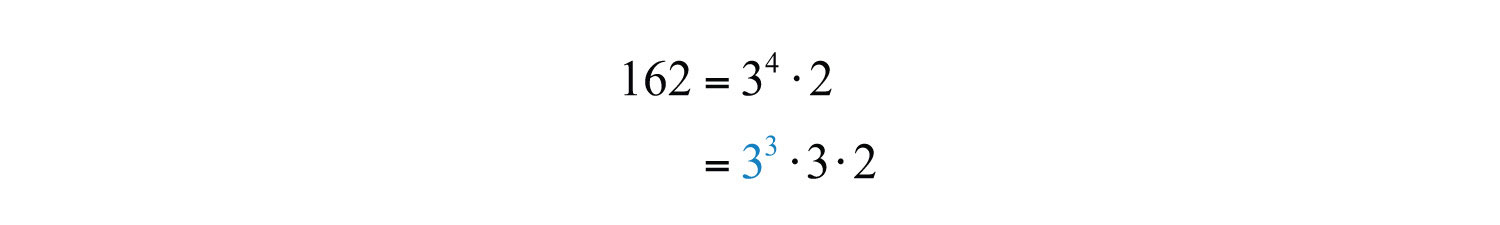
Replace the radicand with this factorization and then apply the product rule for radicals.

We can verify our answer on a calculator.
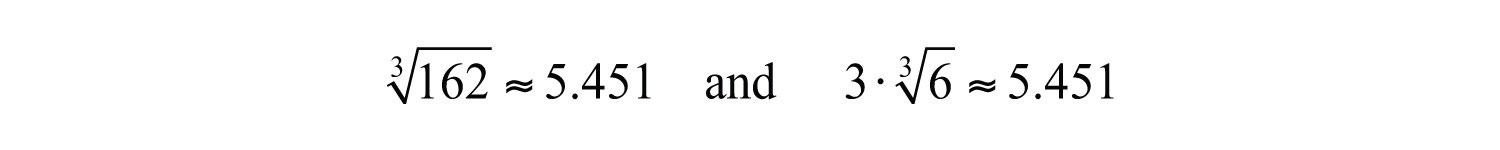
Answer:
Try this! Simplify: .
Answer:
Video Solution
(click to see video)
Example 12: Simplify: .
Solution: Here we note that the index is odd and the radicand is negative; hence the result will be negative. We can factor the radicand as follows:
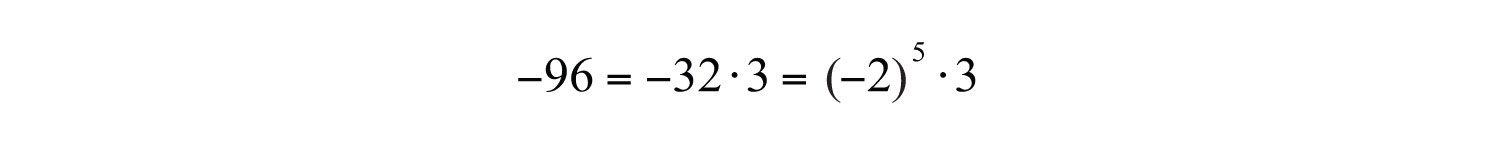
Then simplify:

Answer:
Example 13: Simplify: .
Solution: In this case, consider the equivalent fraction with in the numerator and then simplify.

Answer: −1/2
Try this! Simplify .
Answer:
Video Solution
(click to see video)Key Takeaways
- The square root of a number is that number that when multiplied by itself yields the original number. When the radicand a is positive, . When the radicand is negative, the result is not a real number.
- The cube root of a number is that number that when used as a factor with itself three times yields the original number. The cube root may be positive or negative depending on the sign of the radicand. Therefore, for any real number a, we have the property .
- When working with nth roots, n determines the definition that applies. We use when n is odd and when n is even. When n is even, the negative nth root is denoted with a negative sign in front of the radical sign.
- To simplify square roots, look for the largest perfect square factor of the radicand and then apply the product or quotient rule for radicals.
- To simplify cube roots, look for the largest perfect cube factor of the radicand and then apply the product or quotient rule for radicals.
- To simplify nth roots, look for the factors that have a power that is equal to the index n and then apply the product or quotient rule for radicals. Typically, the process is streamlined if you work with the prime factorization of the radicand.
Topic Exercises
Part A: Radicals
Simplify.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
Part B: Simplifying Radicals
Simplify.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
99.
100.
Simplify. Give the exact answer and the approximate answer rounded to the nearest hundredth.
101.
102.
103.
104.
105.
106.
107.
108.
109.
110.
111.
112.
Rewrite the following as a radical expression with coefficient 1.
113.
114.
115.
116.
117.
118.
119.
120.
121. The formula for the area A of a square is . If the area is 18 square units, then what is the length of each side?
122. Calculate the length of a side of a square with an area of 60 square centimeters.
123. The formula for the volume V of a cube is . If the volume of a cube is 112 cubic units, then what is the length of each side?
124. Calculate the length of a side of a cube with a volume of 54 cubic centimeters.
Part C: Discussion Board
125. Explain why there are two square roots for any nonzero real number.
126. Explain why there is only one cube root for any real number.
127. What is the square root of 1, and what is the cube root of 1? Explain why.
128. Explain why is not a real number and why is a real number.
Answers
1: 9
3: 8
5: 0
7: 0.5
9: 1.1
11: 1/2
13: 5/4
15: Not a real number
17: −6
19: −10
21: 3
23: 4
25: 1/2
27: 2/3
29: 0.1
31: −1
33: −3
35: −1/2
37: −2/3
39: 3
41: 2
43: 2
45: 3
47: −2
49: −2
51: Not a real number
53: 15
55: −50
57: Not a real number
59: 15
61: 6
63: −14
65: 60
67:
69:
71:
73:
75:
77:
79:
81:
83:
85:
87:
89:
91:
93:
95:
97:
99:
101:
103:
105:
107:
109:
111:
113:
115:
117:
119:
121: units
123: units




