This is “Solving Rational Equations”, section 7.5 from the book Beginning Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
7.5 Solving Rational Equations
Learning Objectives
- Solve rational equations.
- Solve literal equations, or formulas, involving rational expressions.
Solving Rational Equations
A rational equationAn equation containing at least one rational expression. is an equation containing at least one rational expression. Rational expressions typically contain a variable in the denominator. For this reason, we will take care to ensure that the denominator is not 0 by making note of restrictions and checking our solutions.
Solve rational equations by clearing the fractions by multiplying both sides of the equation by the least common denominator (LCD).
Example 1: Solve: .
Solution: We first make a note that and then multiply both sides by the LCD, 3x:

Check your answer by substituting 12 for x to see if you obtain a true statement.

Answer: The solution is 12.
After multiplying both sides of the previous example by the LCD, we were left with a linear equation to solve. This is not always the case; sometimes we will be left with a quadratic equation.
Example 2: Solve: .
Solution: In this example, there are two restrictions, and . Begin by multiplying both sides by the LCD, .
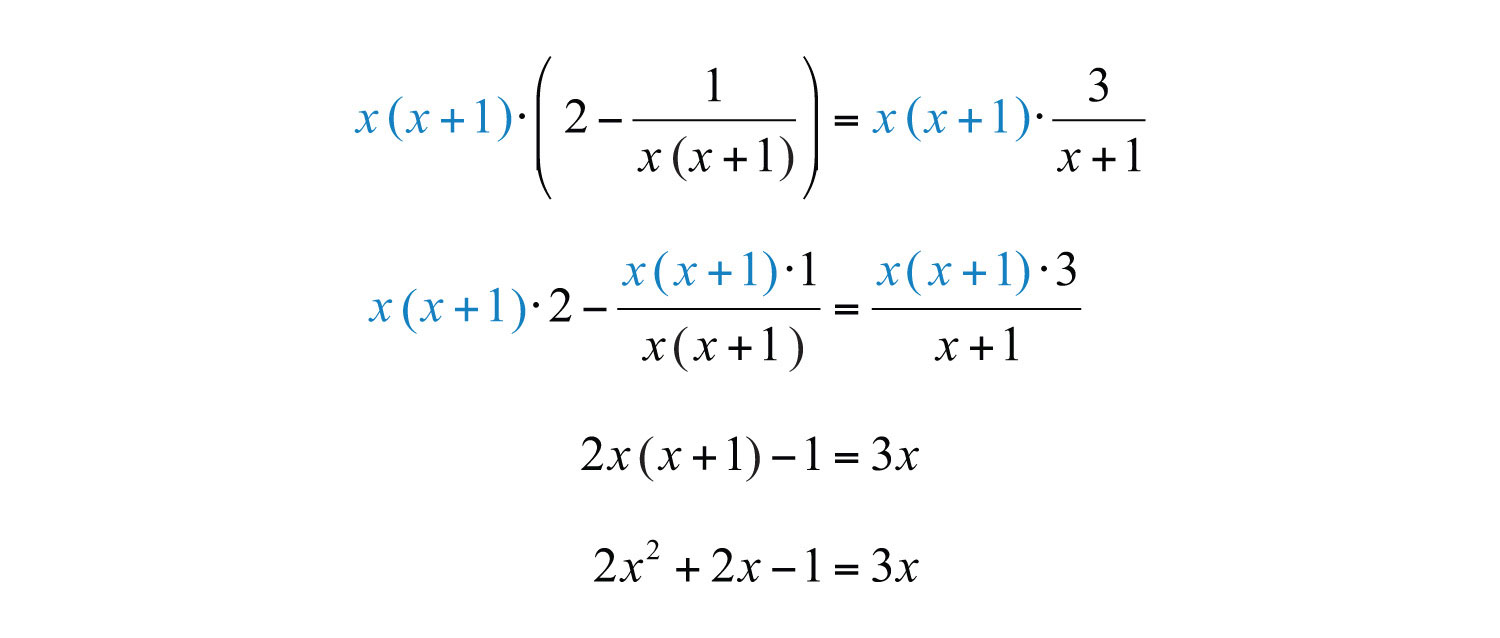
After distributing and dividing out the common factors, a quadratic equation remains. To solve it, rewrite it in standard form, factor, and then set each factor equal to 0.
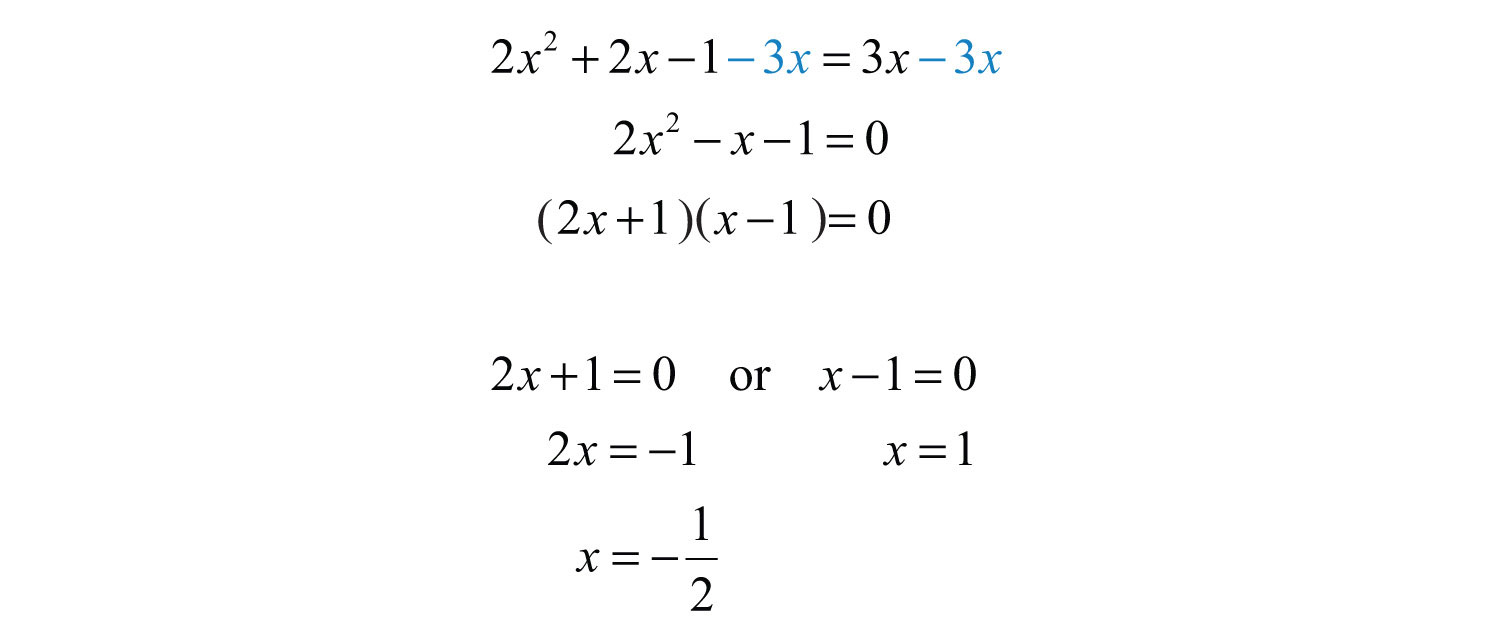
Check to see if these values solve the original equation.

Answer: The solutions are −1/2 and 1.
Up to this point, all of the possible solutions have solved the original equation. However, this may not always be the case. Multiplying both sides of an equation by variable factors may lead to extraneous solutionsA solution that does not solve the original equation., which are solutions that do not solve the original equation. A complete list of steps for solving a rational equation is outlined in the following example.
Example 3: Solve: .
Solution:
Step 1: Factor all denominators and determine the LCD.
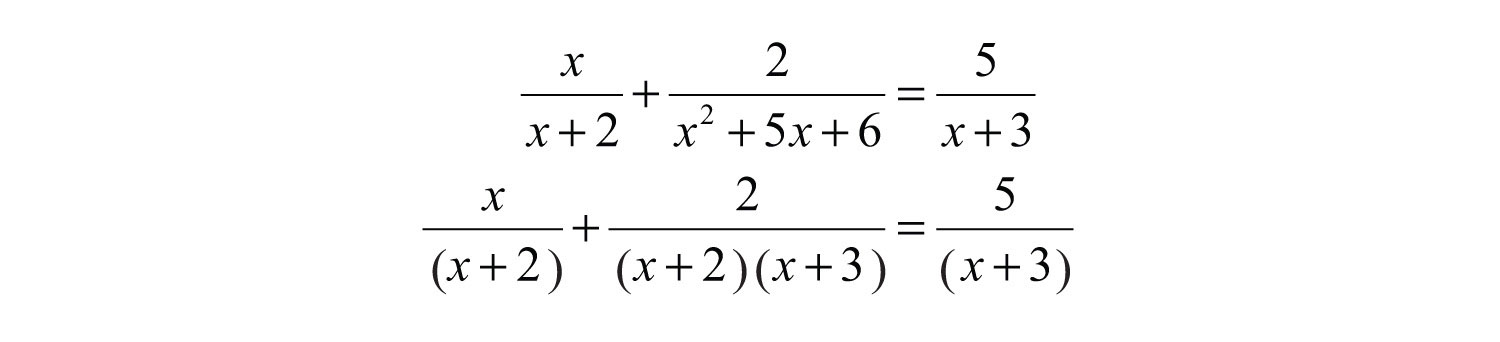
The .
Step 2: Identify the restrictions. In this case, they are and .
Step 3: Multiply both sides of the equation by the LCD. Distribute carefully and then simplify.
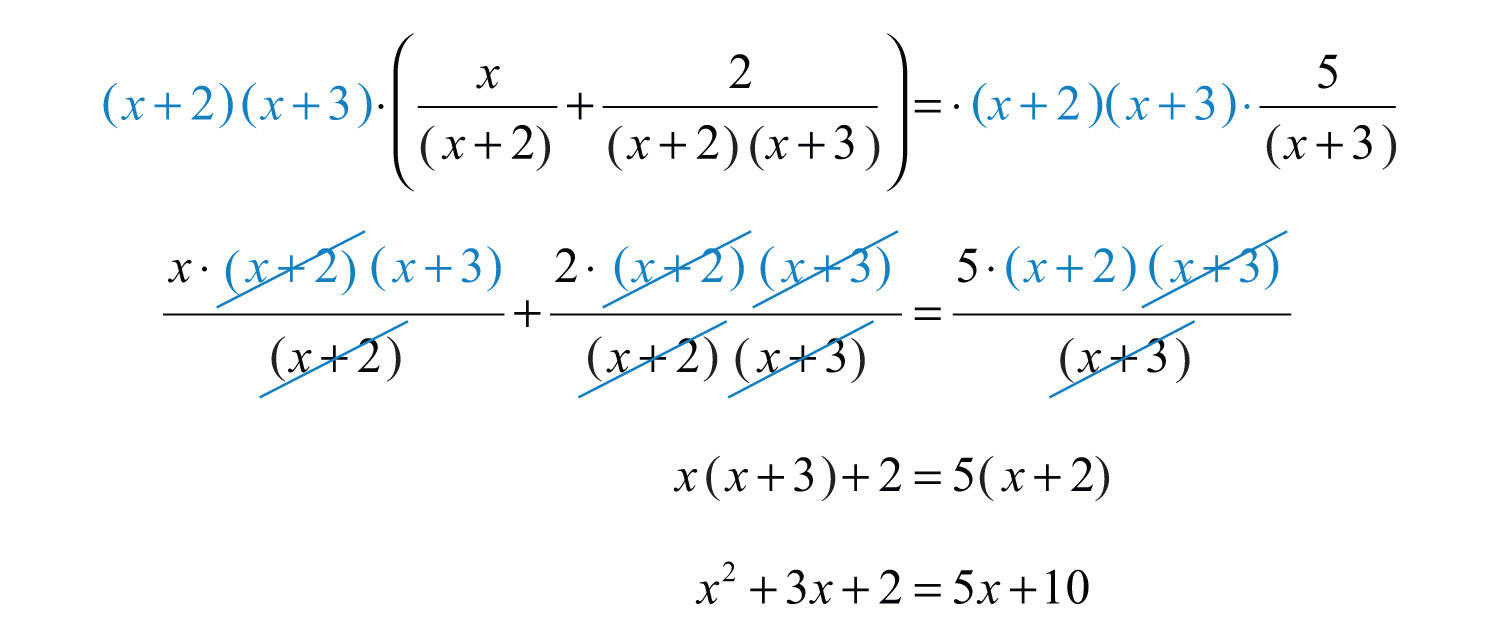
Step 4: Solve the resulting equation. Here the result is a quadratic equation. Rewrite it in standard form, factor, and then set each factor equal to 0.
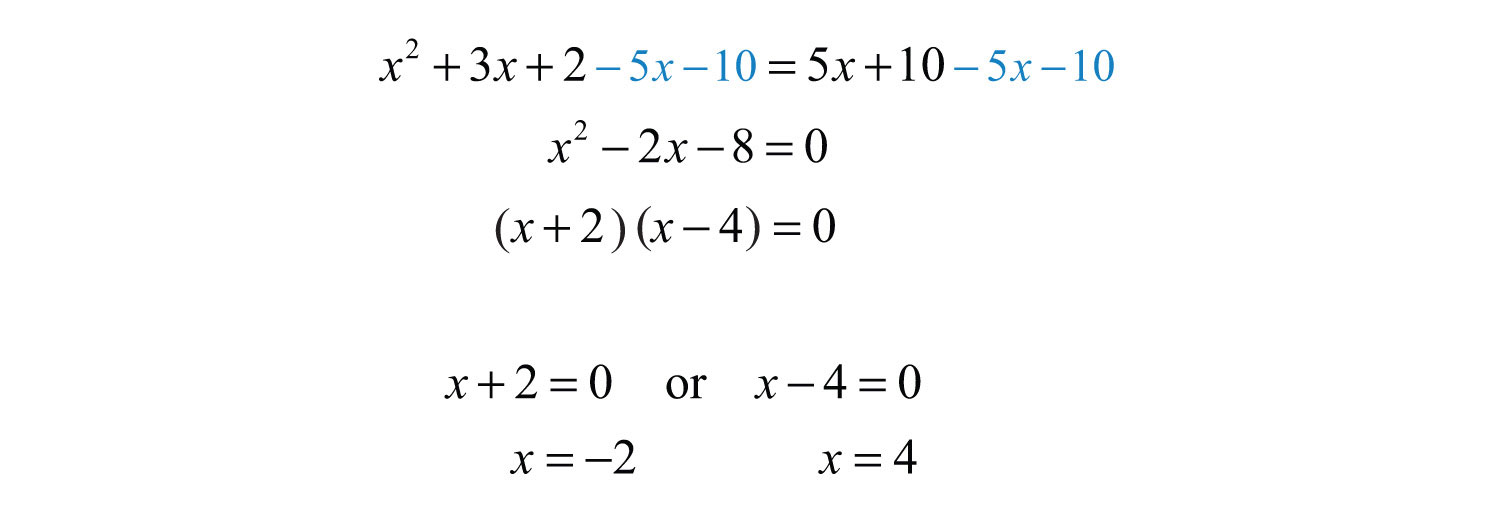
Step 5: Check for extraneous solutions. Always substitute into the original equation, or the factored equivalent. In this case, choose the factored equivalent to check:

Here −2 is an extraneous solution and is not included in the solution set. It is important to note that −2 is a restriction.
Answer: The solution is 4.
If this process produces a solution that happens to be a restriction, then disregard it as an extraneous solution.
Try this! Solve: .
Answer: −3
Video Solution
(click to see video)Sometimes all potential solutions are extraneous, in which case we say that there is no solution to the original equation. In the next two examples, we demonstrate two ways in which a rational equation can have no solutions.
Example 4: Solve: .
Solution: To identify the LCD, first factor the denominators.
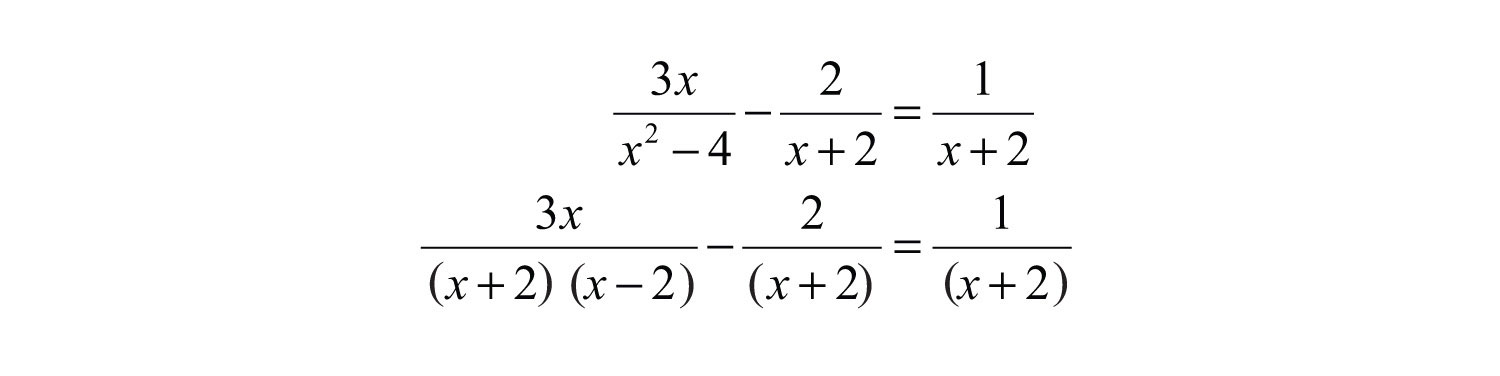
Multiply both sides by the least common denonominator (LCD), , distributing carefully.
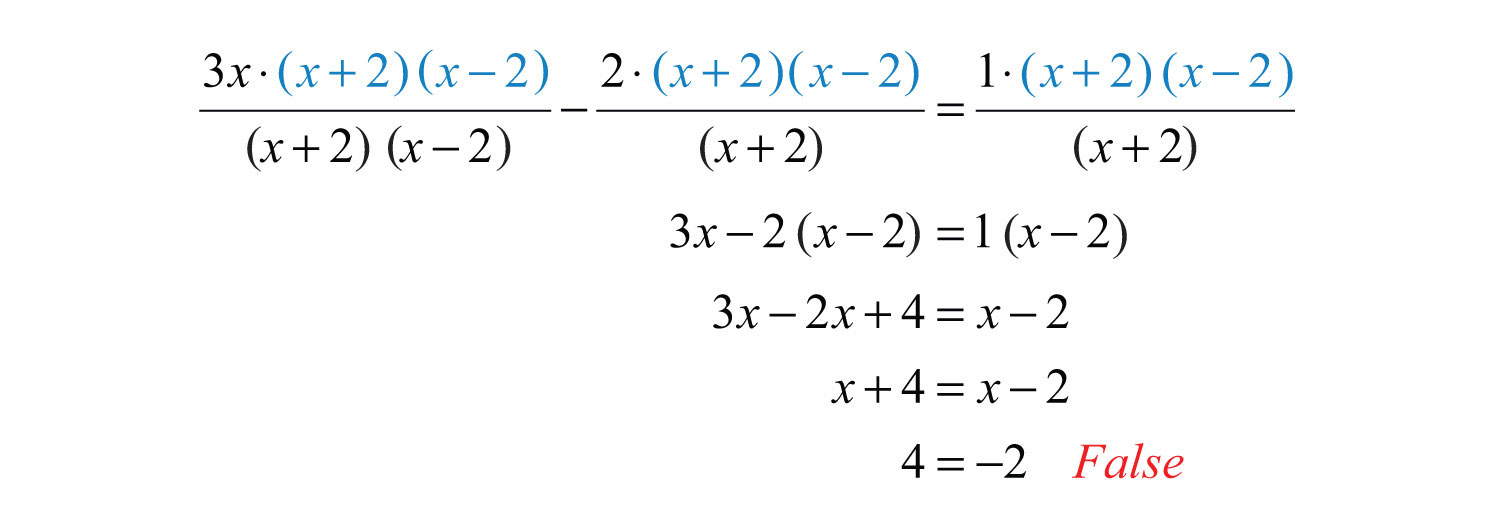
The equation is a contradiction and thus has no solution.
Answer: No solution,
Example 5: Solve: .
Solution: First, factor the denominators.
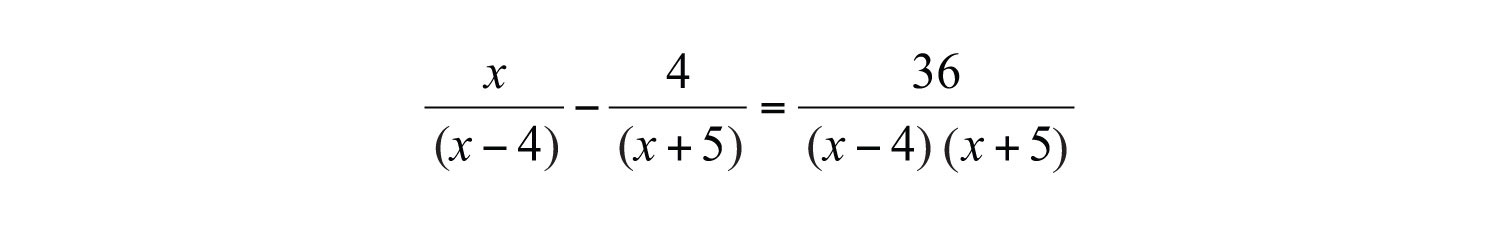
Take note that the restrictions are and . To clear the fractions, multiply by the LCD, .
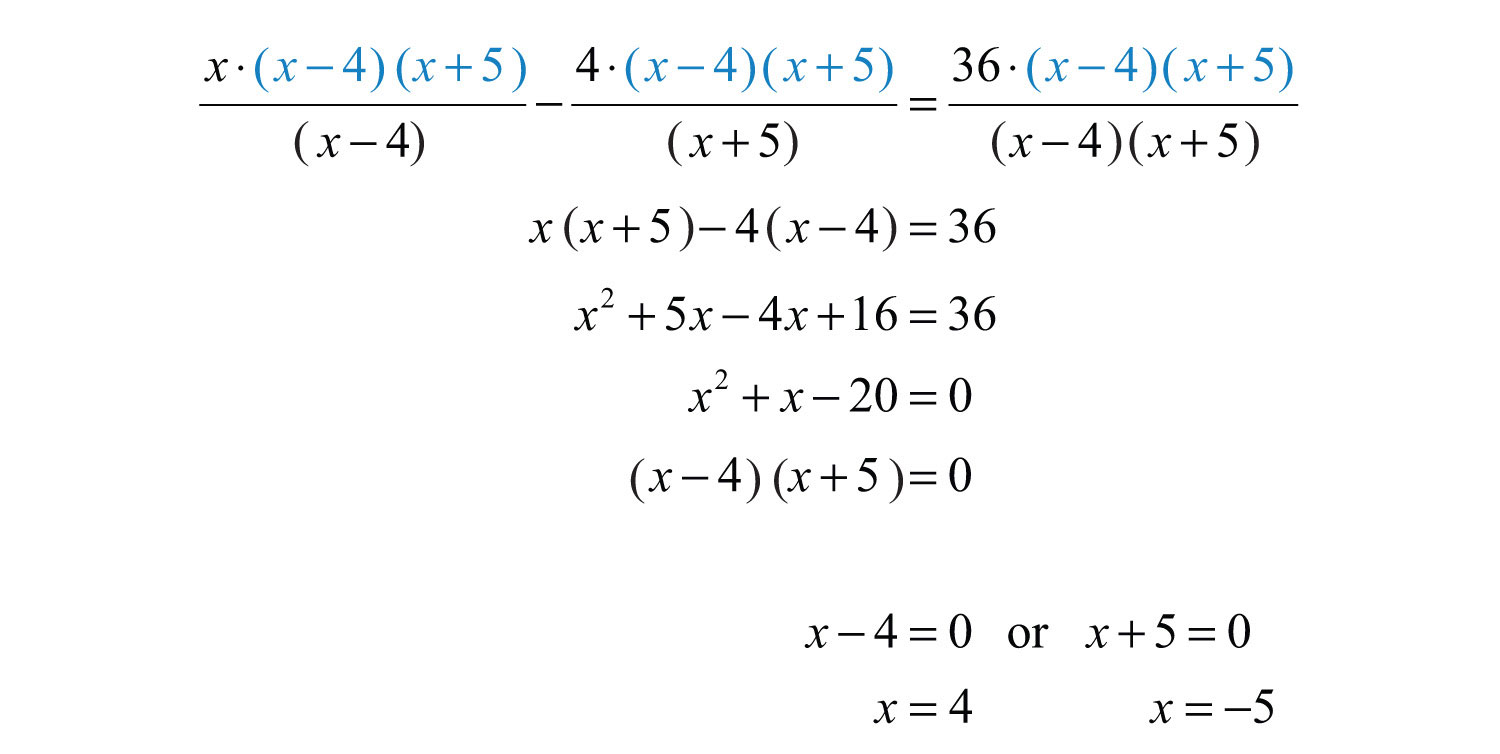
Both of these values are restrictions of the original equation; hence both are extraneous.
Answer: No solution,
Try this! Solve: .
Answer:
Video Solution
(click to see video)It is important to point out that this technique for clearing algebraic fractions only works for equations. Do not try to clear algebraic fractions when simplifying expressions. As a reminder, we have

Expressions are to be simplified and equations are to be solved. If we multiply the expression by the LCD, , we obtain another expression that is not equivalent.
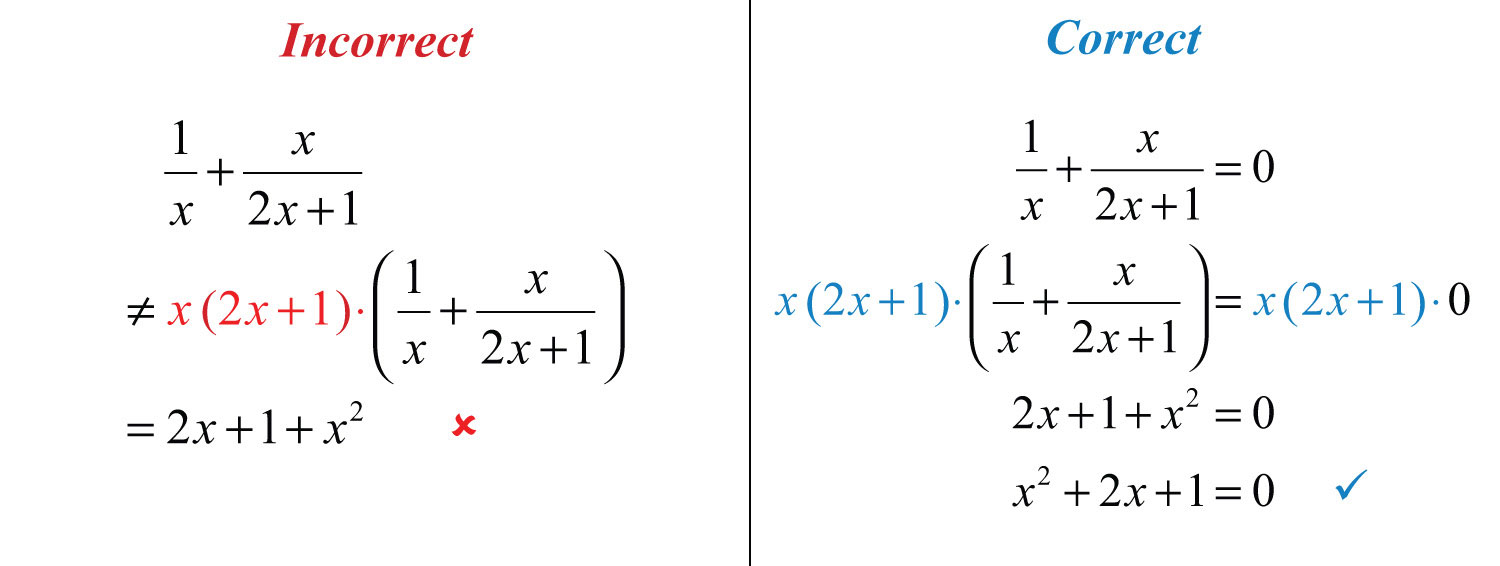
Literal Equations
Literal equations, or formulas, are often rational equations. Hence the techniques described in this section can be used to solve for particular variables. Assume that all variable expressions in the denominator are nonzero.
Example 6: Solve for x: .
Solution: The goal is to isolate x. Assuming that y is nonzero, multiply both sides by y and then add 5 to both sides.

Answer:
Example 7: Solve for c: .
Solution: In this example, the goal is to isolate c. We begin by multiplying both sides by the LCD, , distributing carefully.
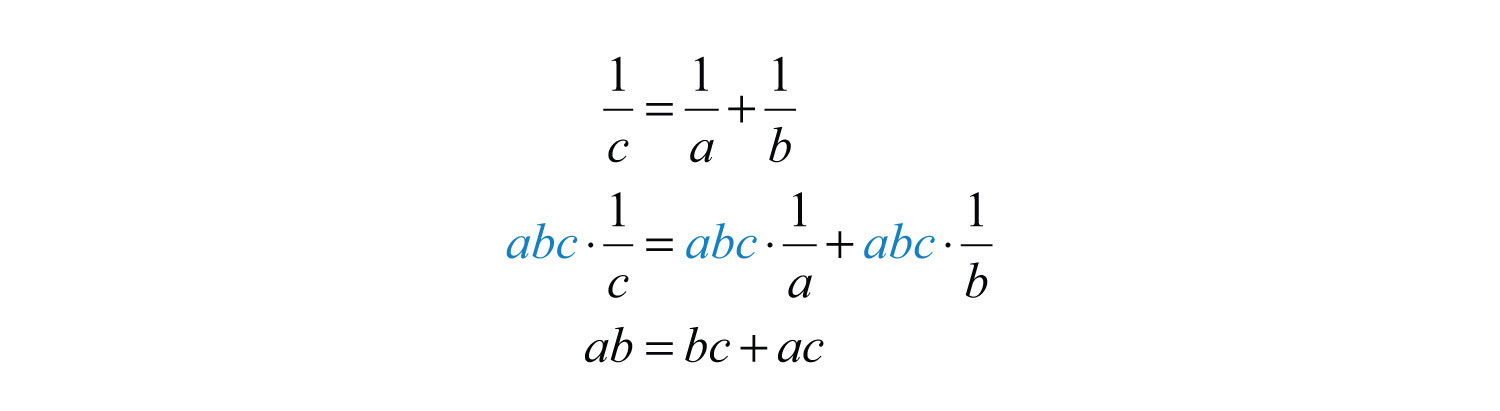
On the right side of the equation, factor out c.
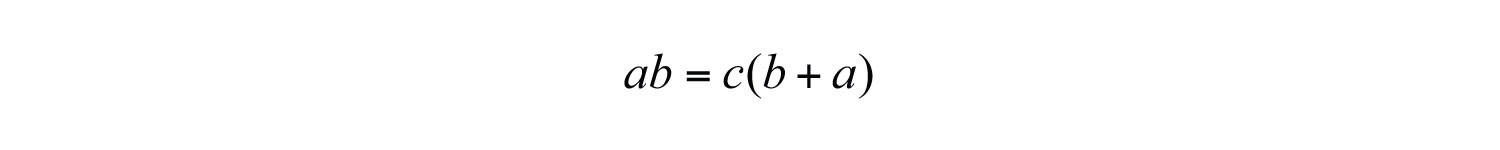
Next, divide both sides of the equation by the quantity .
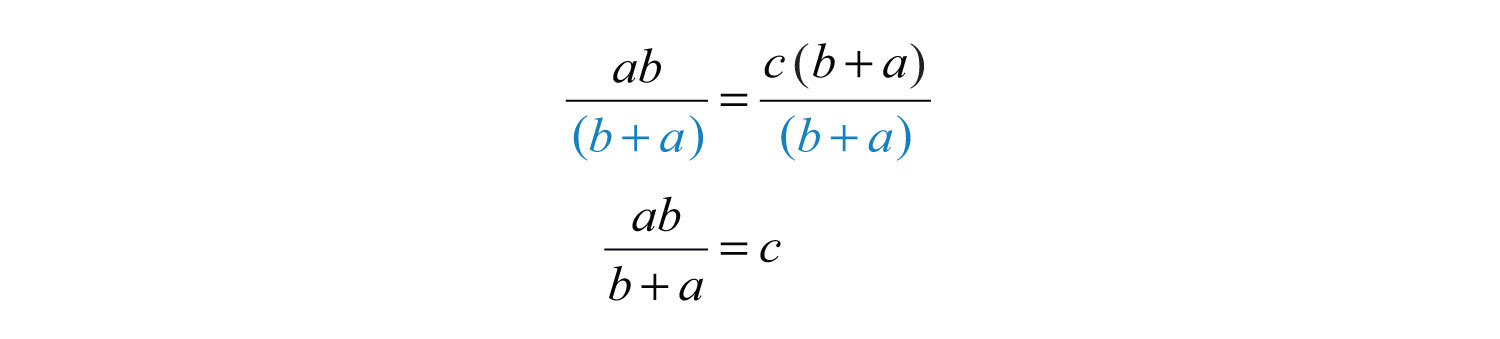
Answer:
Try this! Solve for y: .
Answer:
Video Solution
(click to see video)Key Takeaways
- Begin solving rational equations by multiplying both sides by the LCD. The resulting equivalent equation can be solved using the techniques learned up to this point.
- Multiplying both sides of a rational equation by a variable expression introduces the possibility of extraneous solutions. Therefore, we must check the solutions against the set of restrictions. If a solution is a restriction, then it is not part of the domain and is extraneous.
- When multiplying both sides of an equation by an expression, distribute carefully and multiply each term by that expression.
- If all of the resulting solutions are extraneous, then the original equation has no solutions.
Topic Exercises
Part A: Rational Equations
Solve.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
Part B: Literal Equations
Solve for the indicated variable.
65. Solve for r: .
66. Solve for b: .
67. Solve for P: .
68. Solve for : .
69. Solve for c: .
70. Solve for y: .
71. Solve for w: .
72. Solve for t: .
73. Solve for m: .
74. Solve for S: .
75. Solve for x: .
76. Solve for x: .
77. Solve for R: .
78. Solve for : .
Part C: Discussion Board
79. Explain why multiplying both sides of an equation by the LCD sometimes produces extraneous solutions.
80. Explain the connection between the technique of cross multiplication and multiplying both sides of a rational equation by the LCD.
81. Explain how we can tell the difference between a rational expression and a rational equation. How do we treat them differently?
Answers
1: −8/3
3: −1
5: −2/5
7: 5/2
9: −3
11: −6, 6
13: −4, 6
15: −1
17: −6, 8
19: −4, 6
21: −7, 4
23:
25:
27: −39
29: 4/3, 3/2
31: −1/3
33: −1/2, 1/2
35: 2/5
37:
39: −1/2
41:
43: −7
45: 5
47: −1
49:
51: −4
53: 5/3
55:
57: 1/2
59: −6, 4
61: 10
63: 1/3
65:
67:
69:
71:
73:
75:
77:




