This is “Simplifying Rational Expressions”, section 7.1 from the book Beginning Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
7.1 Simplifying Rational Expressions
Learning Objectives
- Determine the restrictions to the domain of a rational expression.
- Simplify rational expressions.
- Simplify expressions with opposite binomial factors.
- Simplify and evaluate rational functions.
Rational Expressions, Evaluating, and Restrictions
A rational number, or fraction , is a real number defined as a quotient of two integers a and b, where . Similarly, we define a rational expressionThe quotient of two polynomials P and Q, where Q ≠ 0., or algebraic fractionTerm used when referring to a rational expression. , as the quotient of two polynomials P and Q, where . Some examples of rational expressions follow:
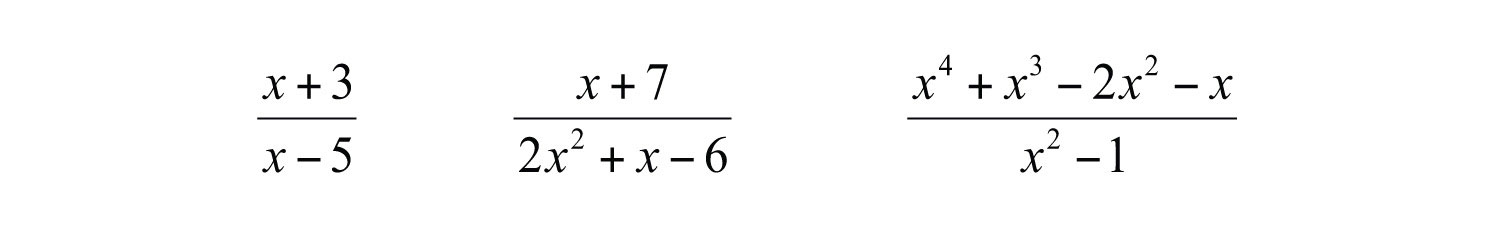
The example consists of linear expressions in both the numerator and denominator. Because the denominator contains a variable, this expression is not defined for all values of x.
Example 1: Evaluate for the set of x-values {−3, 4, 5}.
Solution: Substitute the values in for x.
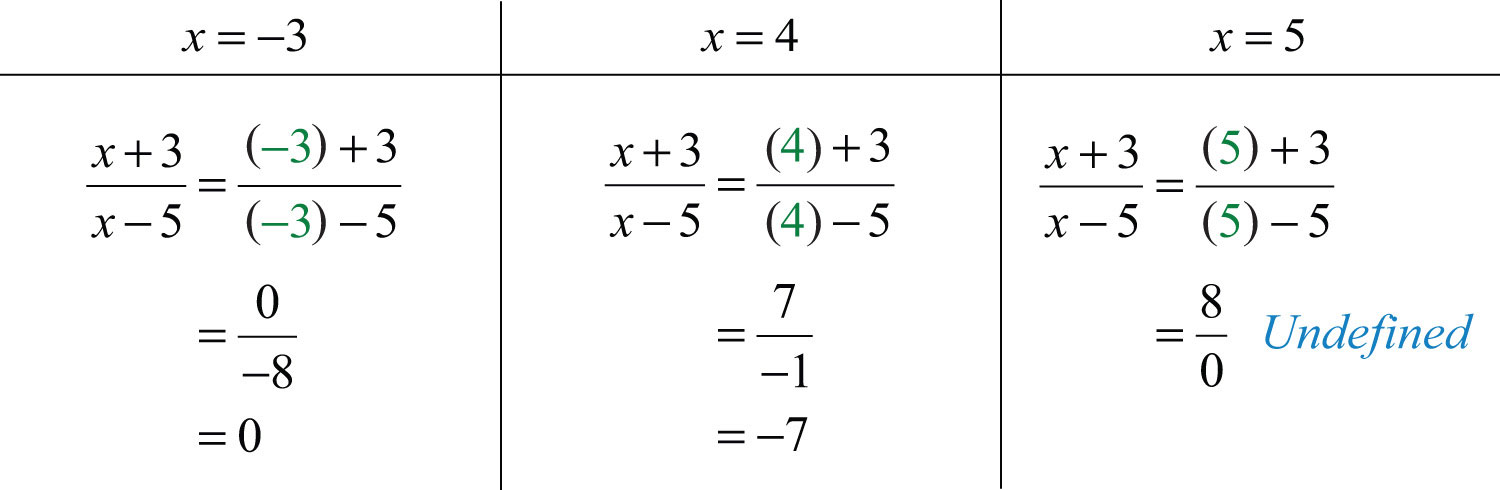
Answer: When , the value of the rational expression is 0; when , the value of the rational expression is −7; and when , the value of the rational expression is undefined.
This example illustrates that variables are restricted to values that do not make the denominator equal to 0. The domain of a rational expressionThe set of real numbers for which the rational expression is defined. is the set of real numbers for which it is defined, and restrictionsThe set of real numbers for which a rational expression is not defined. are the real numbers for which the expression is not defined. We often express the domain of a rational expression in terms of its restrictions.
Example 2: Find the domain of the following: .
Solution: In this example, the numerator is a linear expression and the denominator is a quadratic expression. If we factor the denominator, then we will obtain an equivalent expression.
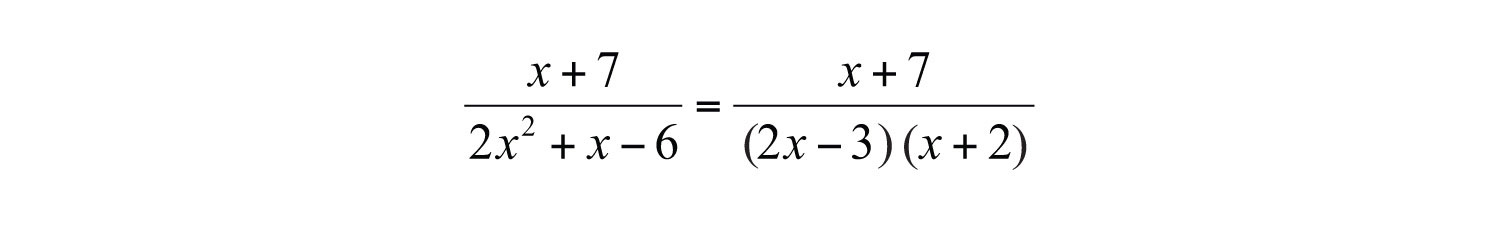
Because rational expressions are undefined when the denominator is 0, we wish to find the values for x that make it 0. To do this, apply the zero-product property. Set each factor in the denominator equal to 0 and solve.
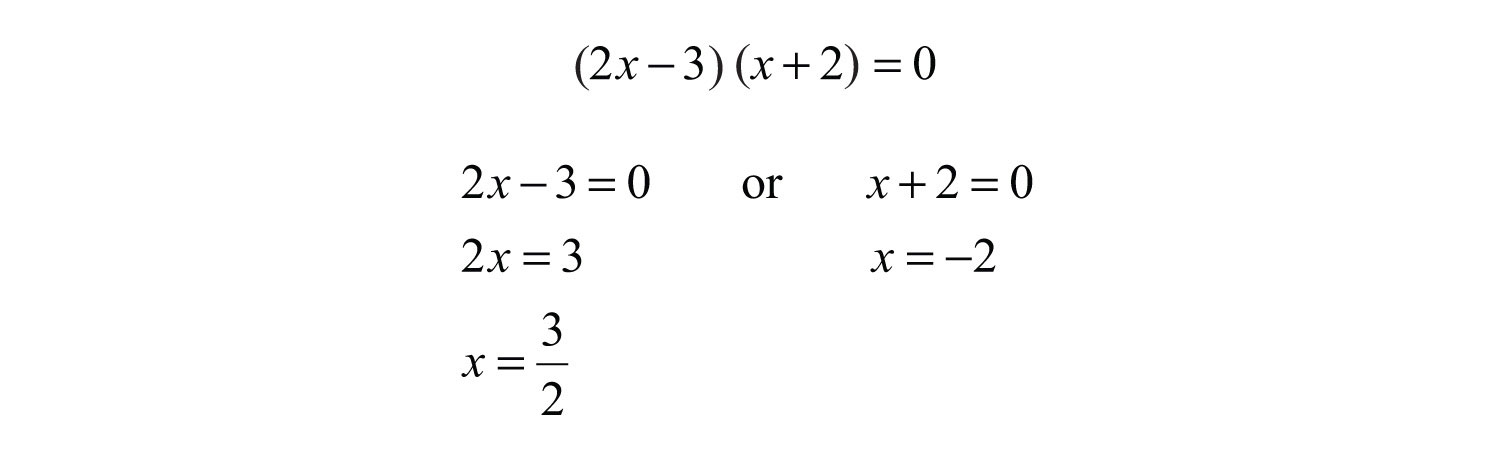
We conclude that the original expression is defined for any real number except 3/2 and −2. These two values are the restrictions to the domain.
It is important to note that −7 is not a restriction to the domain because the expression is defined as 0 when the numerator is 0.
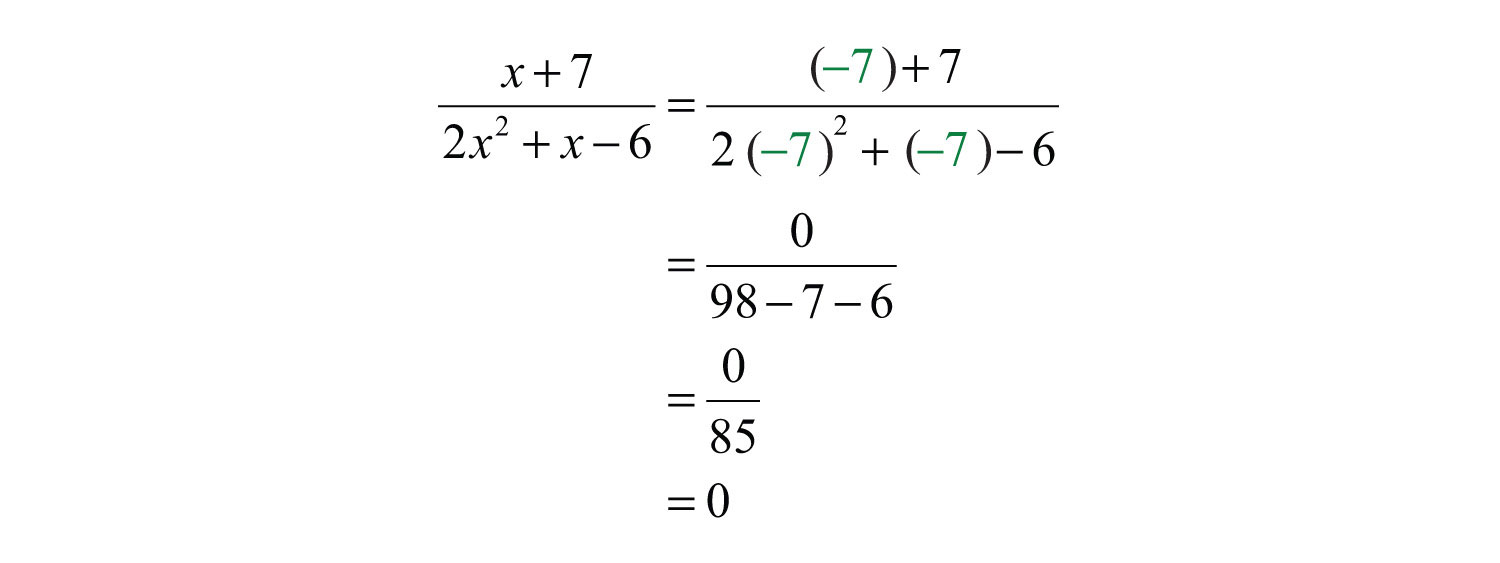
Answer: The domain consists of any real number x, where and .
We can express the domain of the previous example using notation as follows:
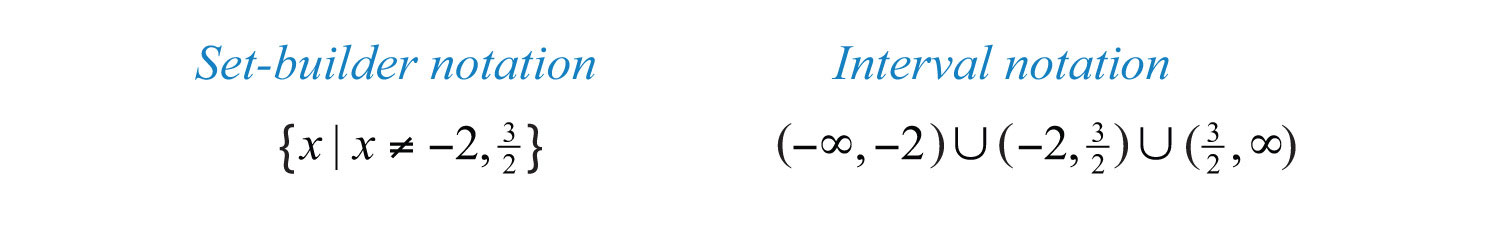
The restrictions to the domain of a rational expression are determined by the denominator. Ignore the numerator when finding those restrictions.
Example 3: Determine the domain: .
Solution: To find the restrictions to the domain, set the denominator equal to 0 and solve:
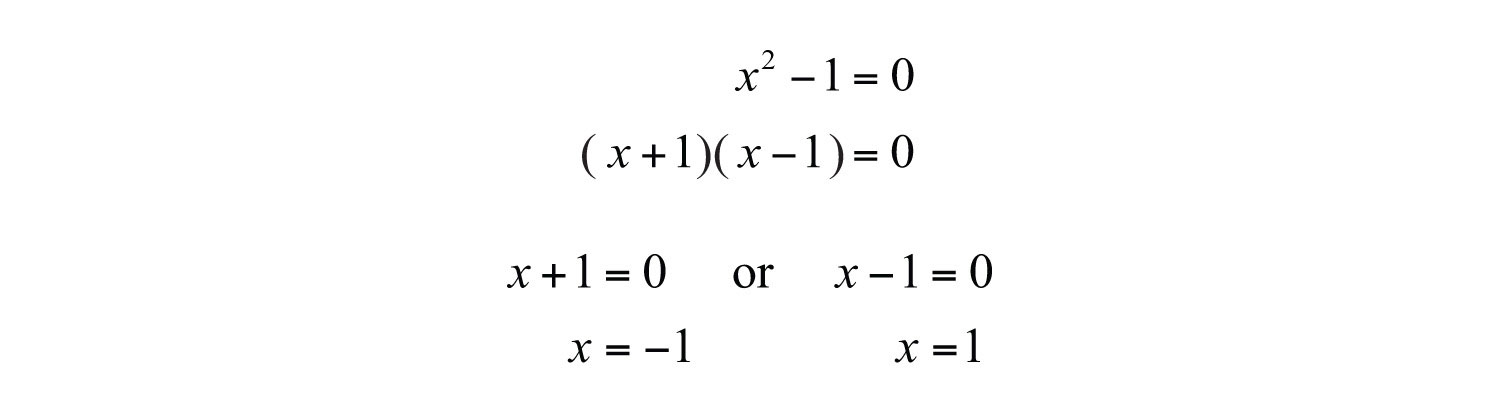
These two values cause the denominator to be 0. Hence they are restricted from the domain.
Answer: The domain consists of any real number x, where .
Example 4: Determine the domain: .
Solution: There is no variable in the denominator and thus no restriction to the domain.
Answer: The domain consists of all real numbers, R.
Simplifying Rational Expressions
When simplifying fractions, look for common factors that cancel. For example,
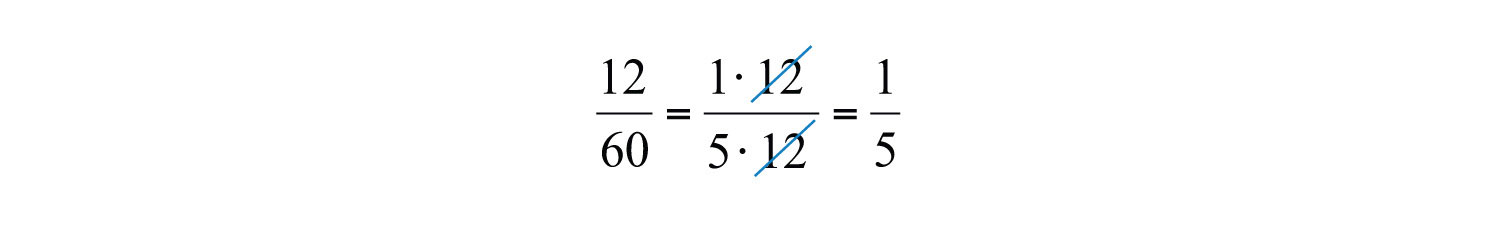
We say that the fraction 12/60 is equivalent to 1/5. Fractions are in simplest form if the numerator and denominator share no common factor other than 1. Similarly, when working with rational expressions, look for factors to cancel. For example,
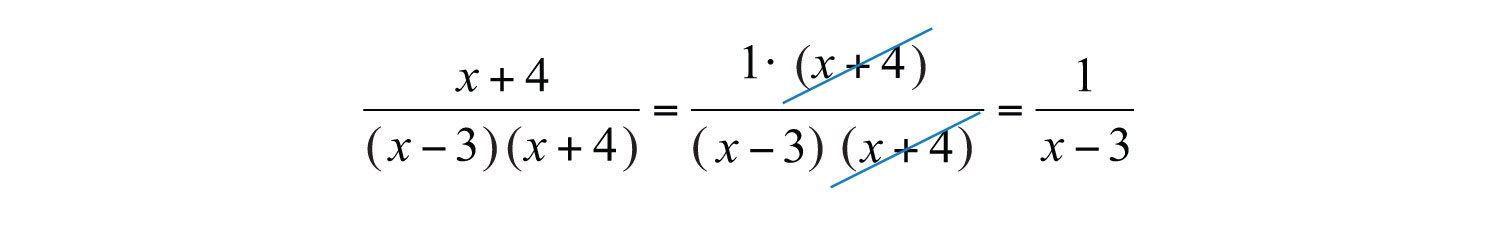
The resulting rational expression is equivalent if it shares the same domain. Therefore, we must make note of the restrictions and write
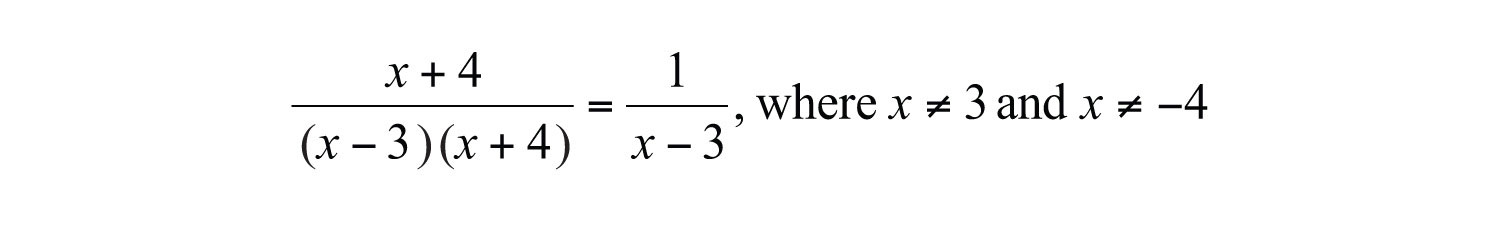
In words, is equivalent to , if and . We can verify this by choosing a few values with which to evaluate both expressions to see if the results are the same. Here we choose and evaluate as follows:
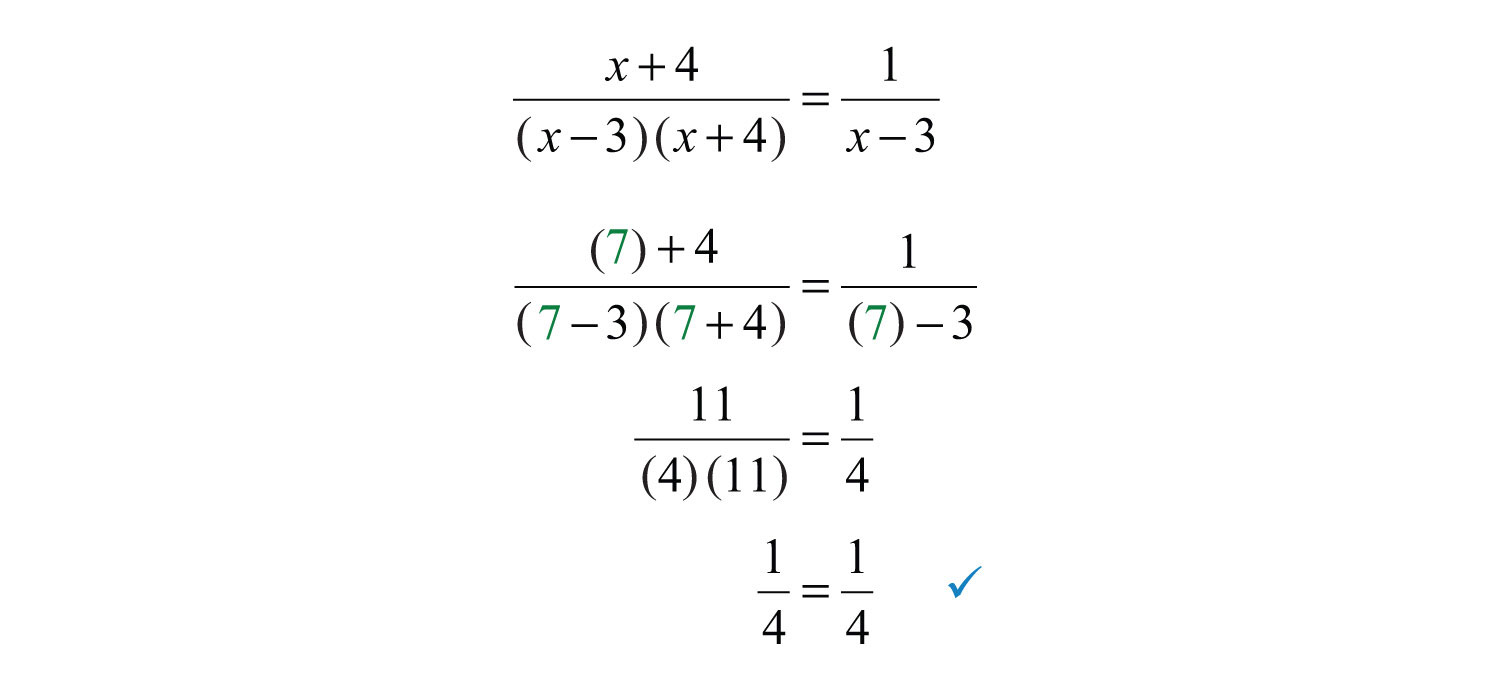
It is important to state the restrictions before simplifying rational expressions because the simplified expression may be defined for restrictions of the original. In this case, the expressions are not equivalent. Here −4 is defined for the simplified equivalent but not for the original, as illustrated below:
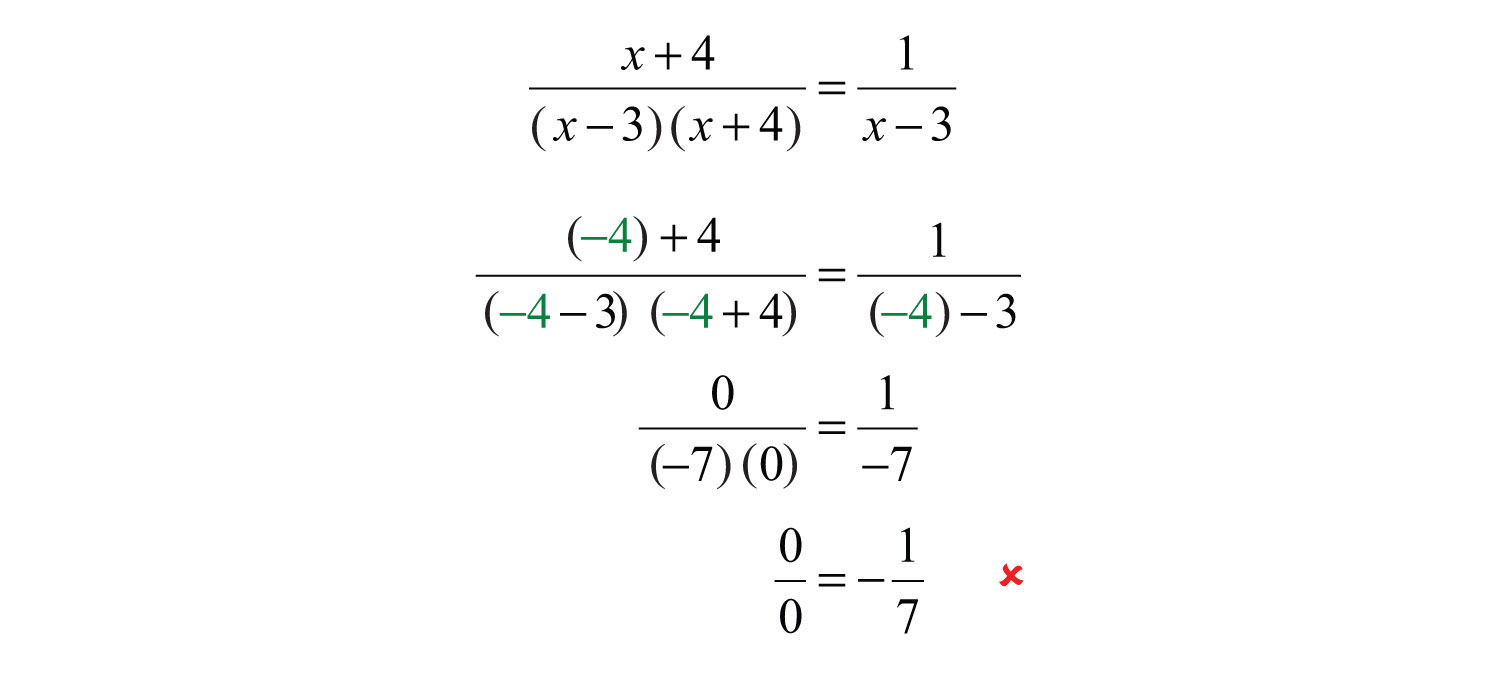
Example 5: Simplify and state the restriction: .
Solution: In this example, the expression is undefined when x is 0.
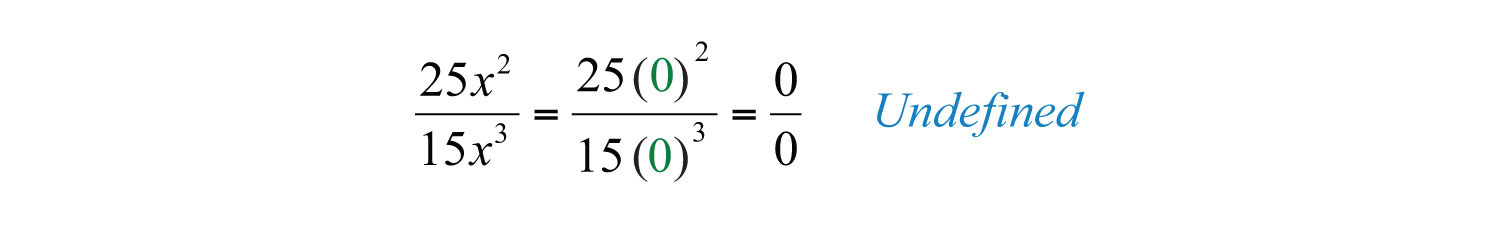
Therefore, the domain consists of all real numbers x, where . With this understanding, we can cancel common factors.
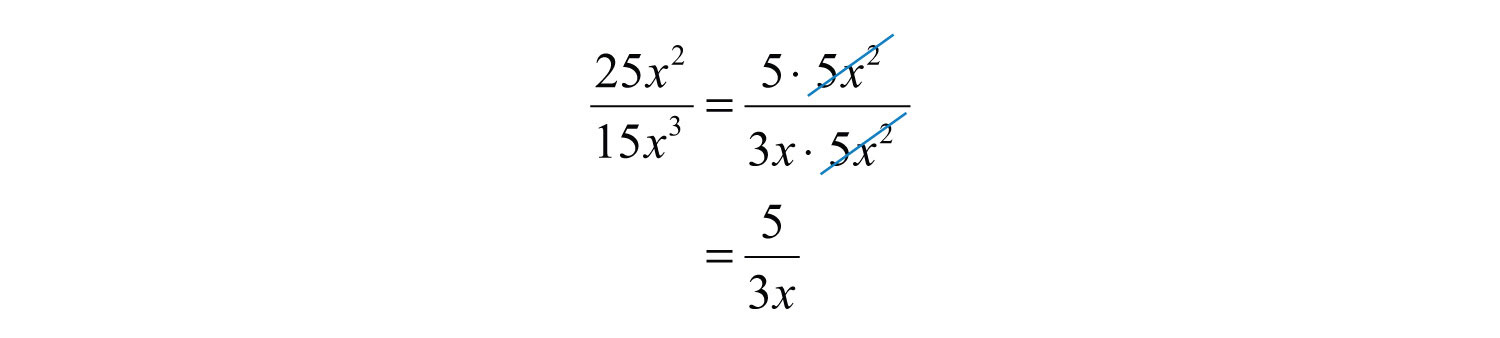
Answer: , where
Example 6: State the restrictions and simplify: .
Solution: To determine the restrictions, set the denominator equal to 0 and solve.
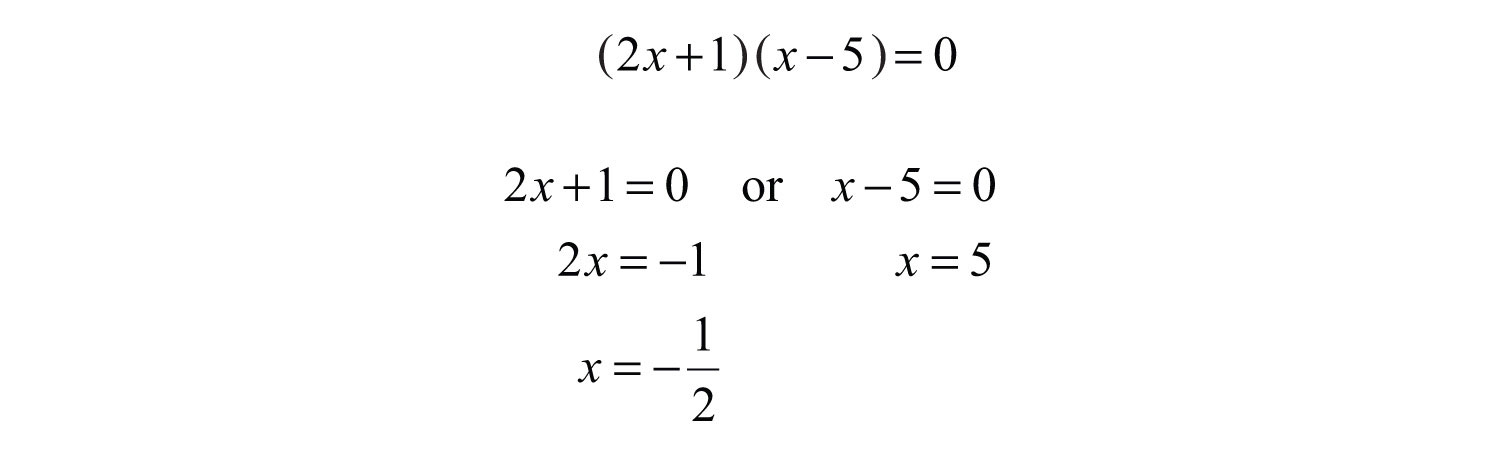
The domain consists of all real numbers except for −1/2 and 5. Next, we find an equivalent expression by canceling common factors.
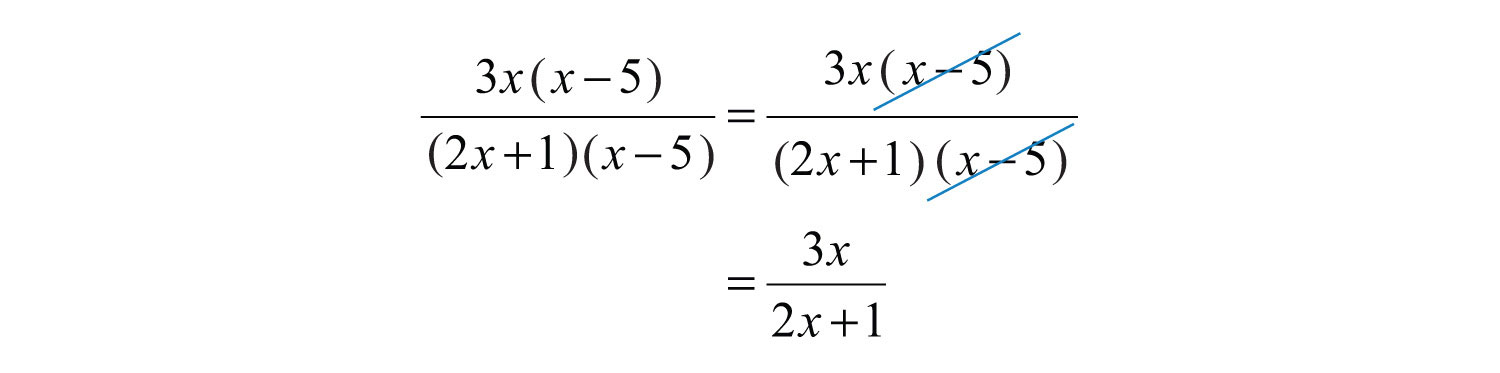
Answer: , where and
Typically, rational expressions are not given in factored form. If this is the case, factor first and then cancel. The steps are outlined in the following example.
Example 7: State the restrictions and simplify: .
Solution:
Step 1: Completely factor the numerator and denominator.
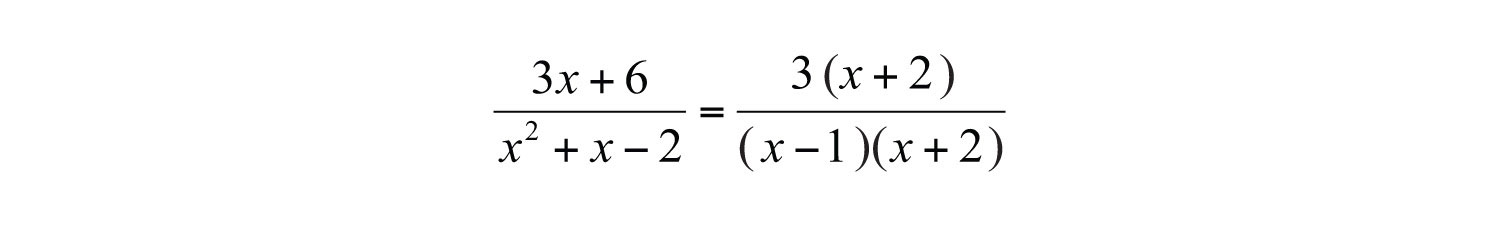
Step 2: Determine the restrictions to the domain. To do this, set the denominator equal to 0 and solve.
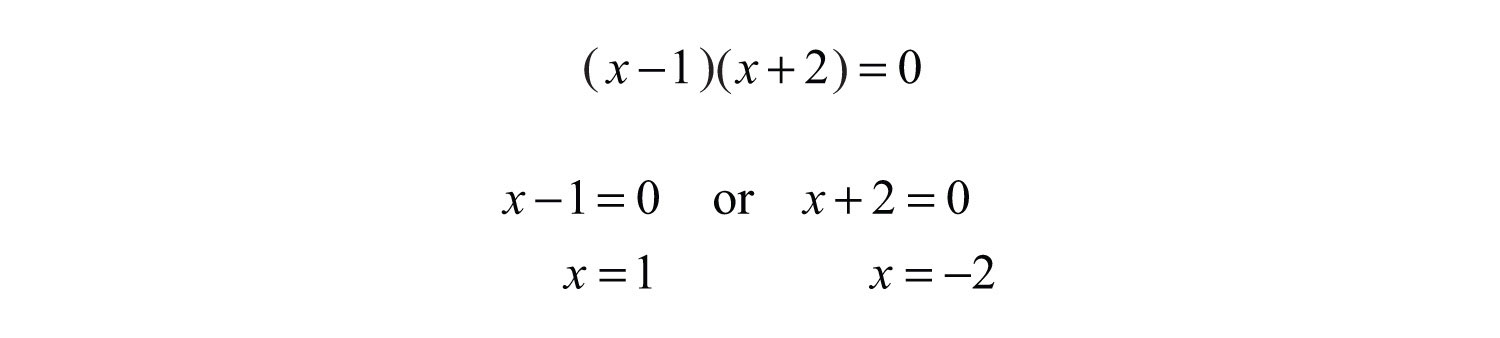
The domain consists of all real numbers except −2 and 1.
Step 3: Cancel common factors, if any.
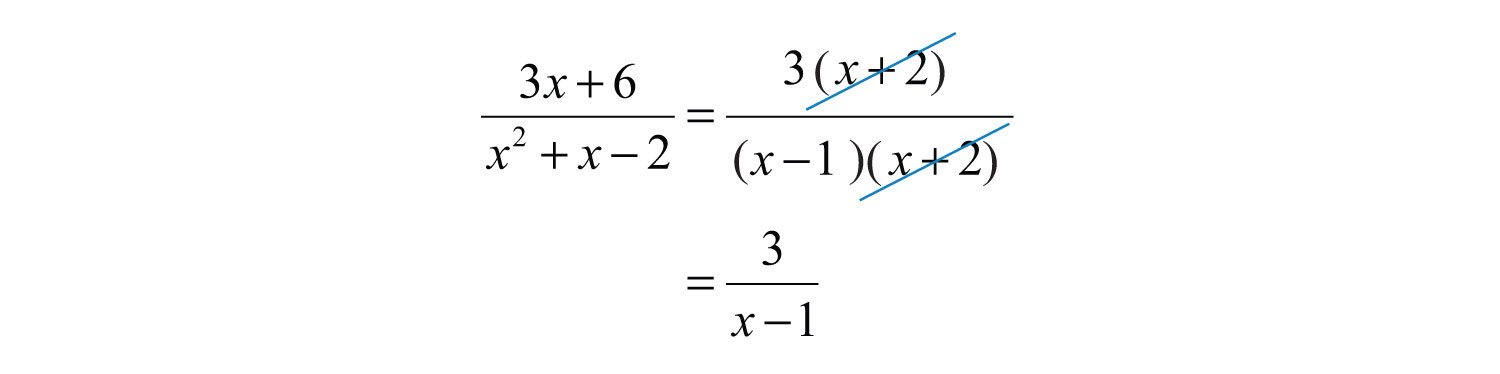
Answer: , where and
Example 8: State the restrictions and simplify: .
Solution: First, factor the numerator and denominator.
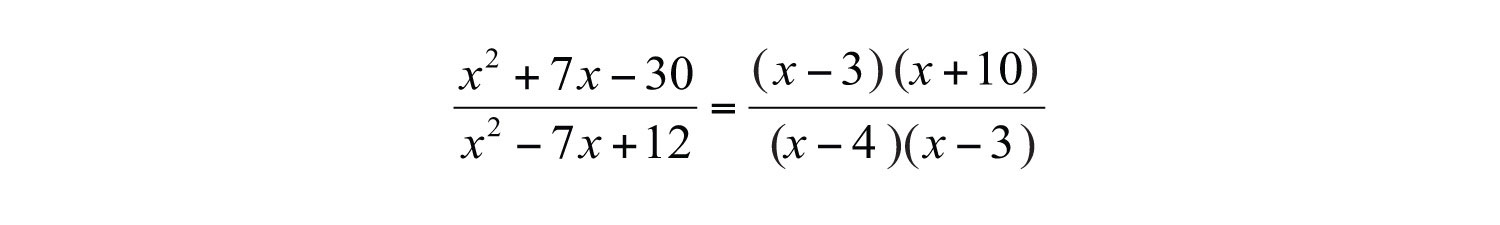
Any value of x that results in a value of 0 in the denominator is a restriction. By inspection, we determine that the domain consists of all real numbers except 4 and 3. Next, cancel common factors.
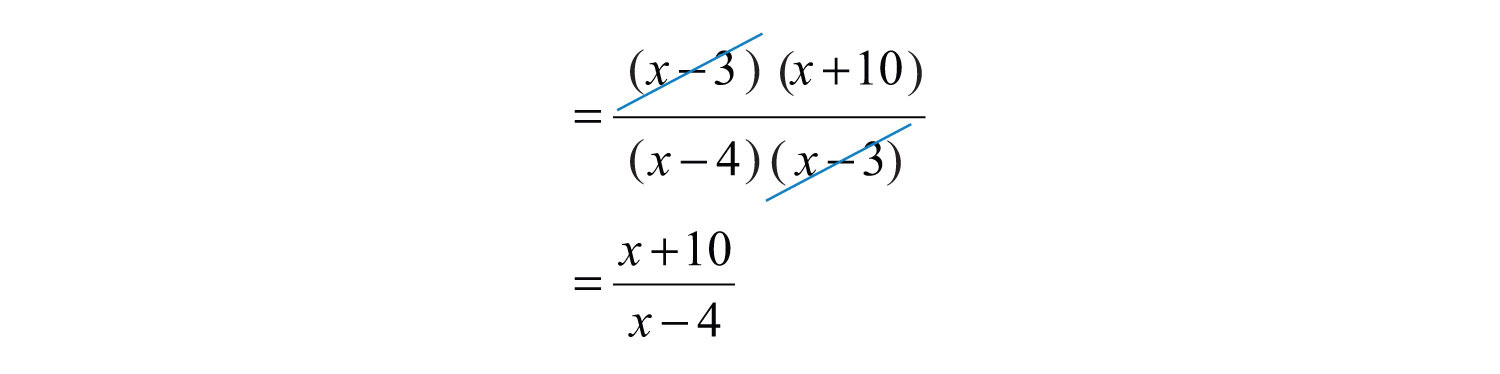
Answer: , where and
It is important to remember that we can only cancel factors of a product. A common mistake is to cancel terms. For example,
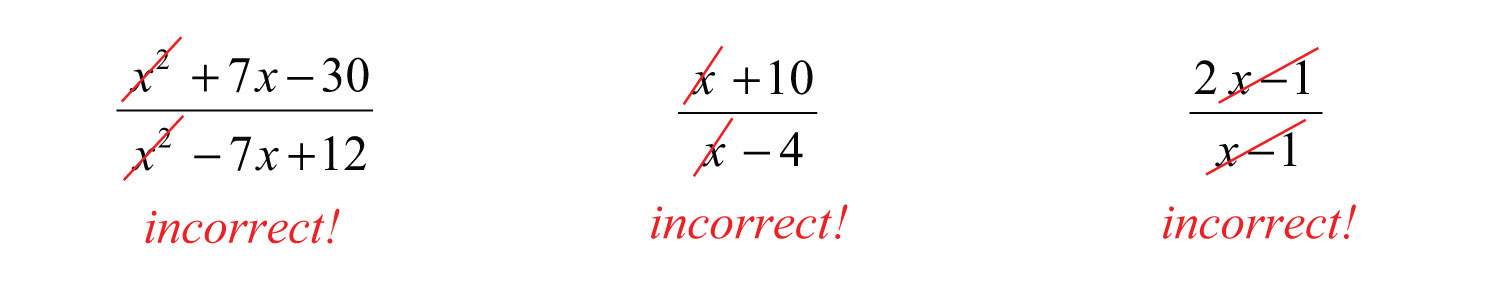
Try this! State the restrictions and simplify: .
Answer: , where and
Video Solution
(click to see video)In some examples, we will make a broad assumption that the denominator is nonzero. When we make that assumption, we do not need to determine the restrictions.
Example 9: Simplify: . (Assume all denominators are nonzero.)
Solution: Factor the numerator by grouping. Factor the denominator using the formula for a difference of squares.
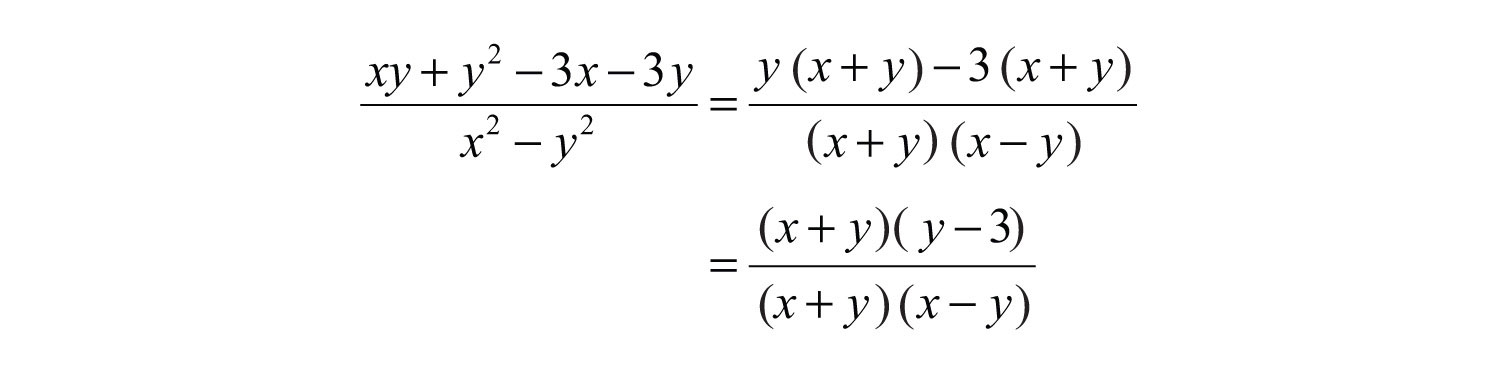
Next, cancel common factors.
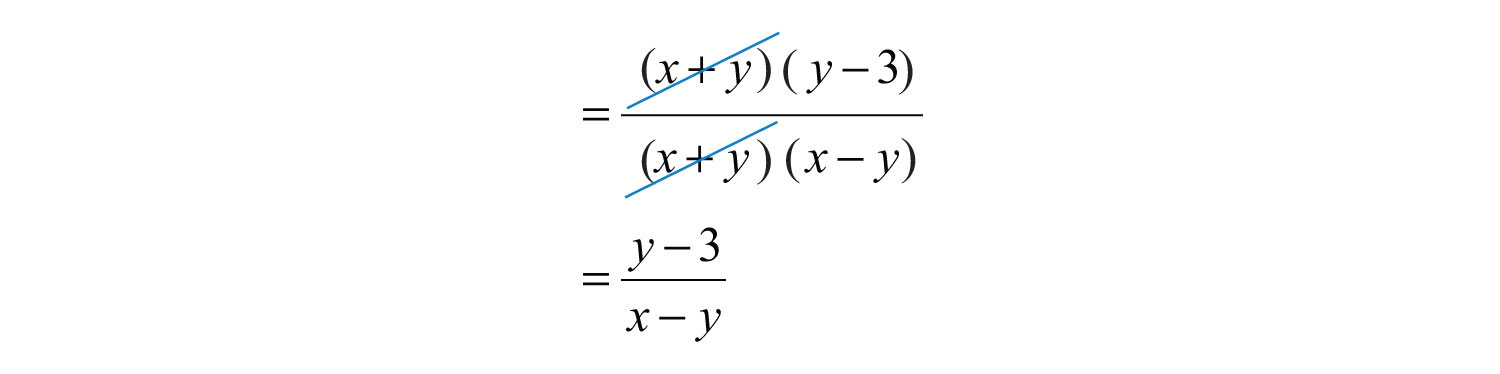
Answer:
Opposite Binomial Factors
Recall that the opposite of the real number a is −a. Similarly, we can define the opposite of a polynomial P to be −P. We first consider the opposite of the binomial :
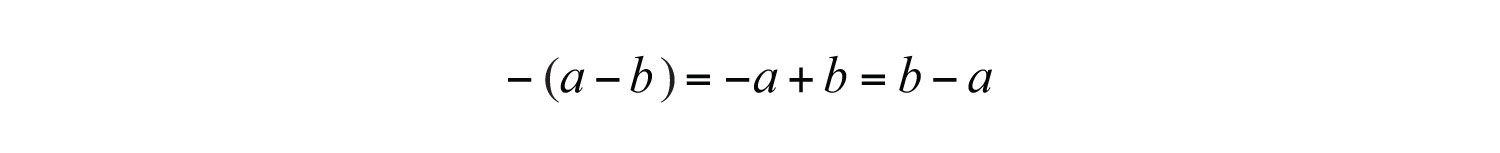
This leads us to the opposite binomial propertyIf given a binomial , then the opposite is .:
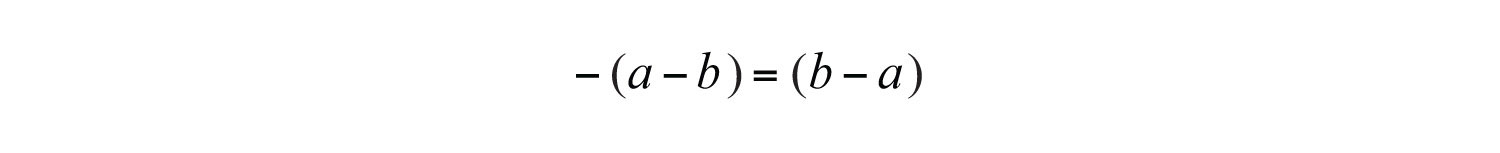
This is equivalent to factoring out a –1.
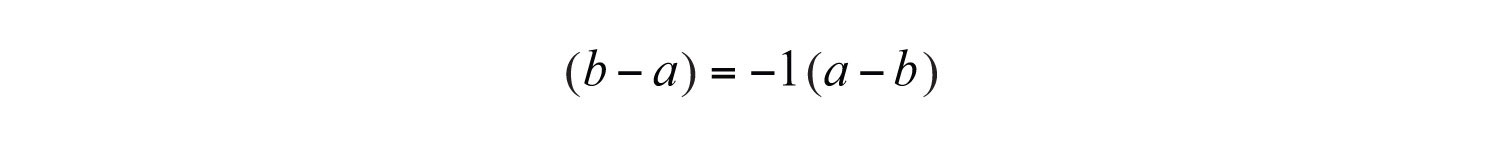
If , then we can divide both sides by and obtain the following:
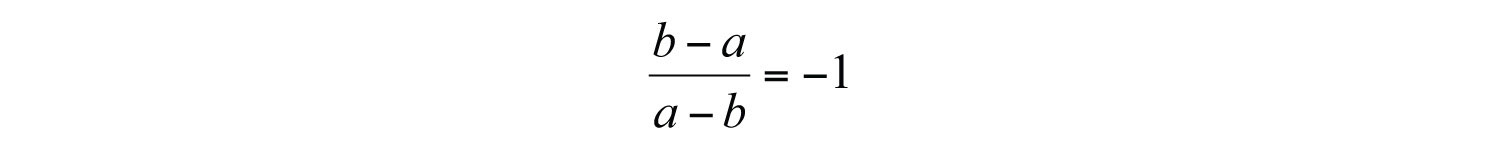
Example 10: State the restrictions and simplify: .
Solution: By inspection, we can see that the denominator is 0 if . Therefore, 3 is the restriction to the domain. Apply the opposite binomial property to the numerator and then cancel.
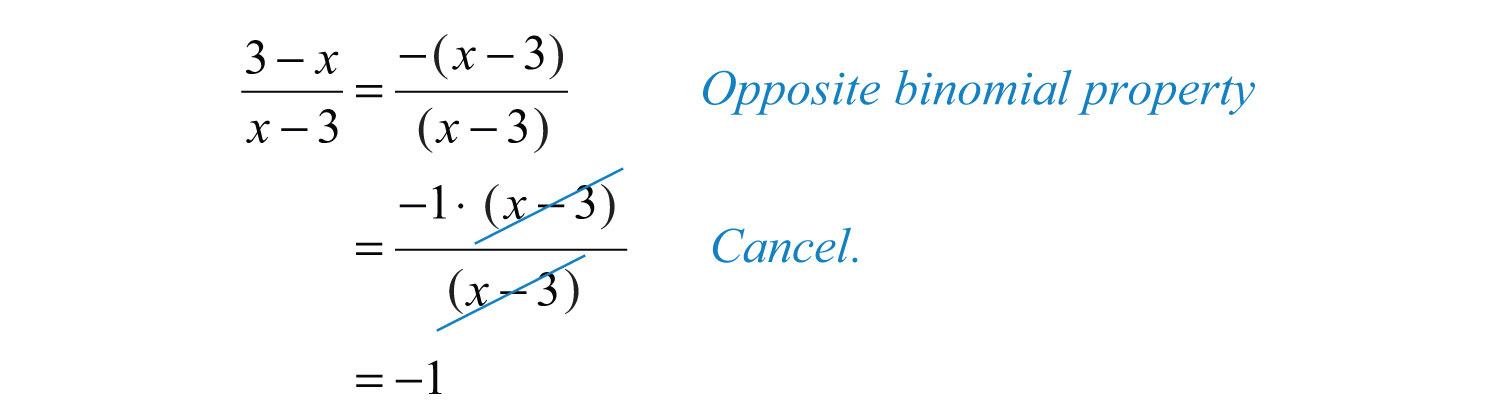
Answer: , where
Since addition is commutative, we have
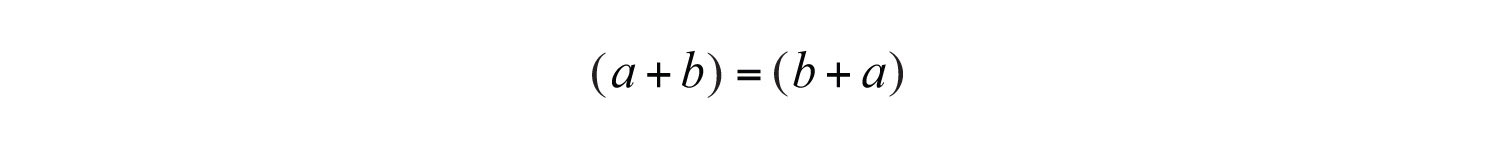
or
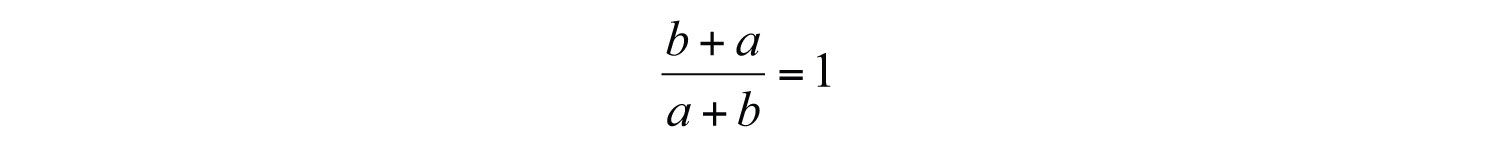
Take care not to confuse this with the opposite binomial property. Also, it is important to recall that
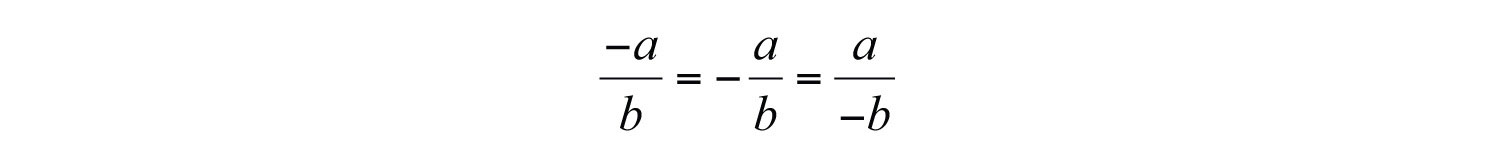
In other words, show a negative fraction by placing the negative sign in the numerator, in front of the fraction bar, or in the denominator. Generally, negative denominators are avoided.
Example 11: Simplify and state the restrictions: .
Solution: Begin by factoring the numerator and denominator.

Answer: , where and
Try this! Simplify and state the restrictions: .
Answer: , where
Video Solution
(click to see video)Rational Functions
Rational functions have the form
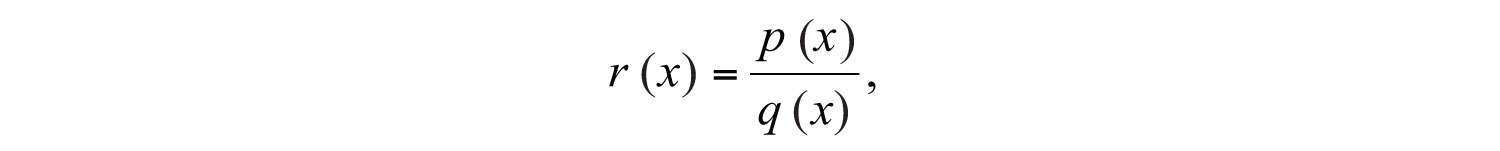
where and are polynomials and . The domain of a rational function consists of all real numbers x such that the denominator .
Example 12:
a. Simplify: .
b. State the domain.
c. Calculate .
Solution:
a. To simplify the rational function, first factor and then cancel.
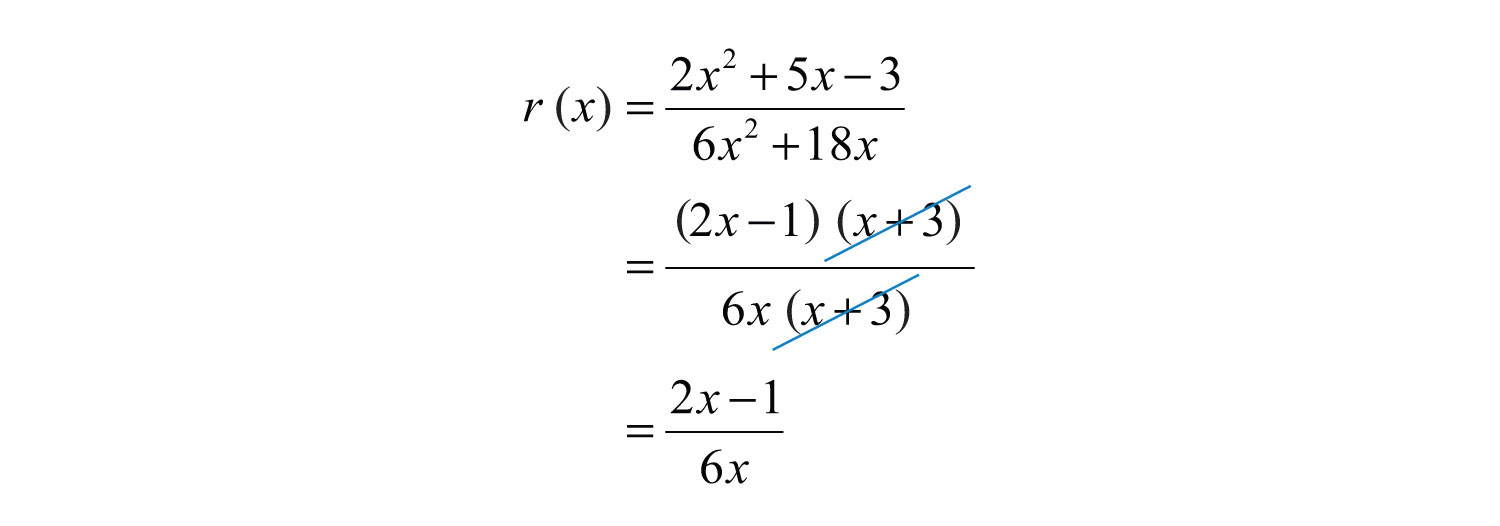
b. To determine the restrictions, set the denominator of the original function equal to 0 and solve.
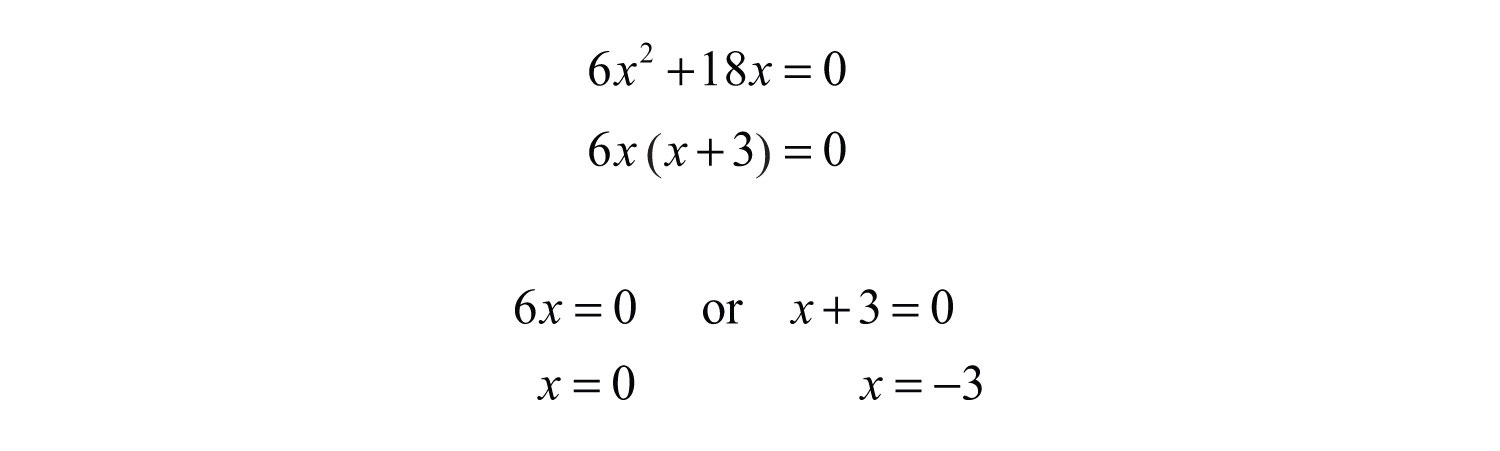
The domain consists of all real numbers x, where and .
c. Since −2 is not a restriction, substitute it for the variable x using the simplified form.
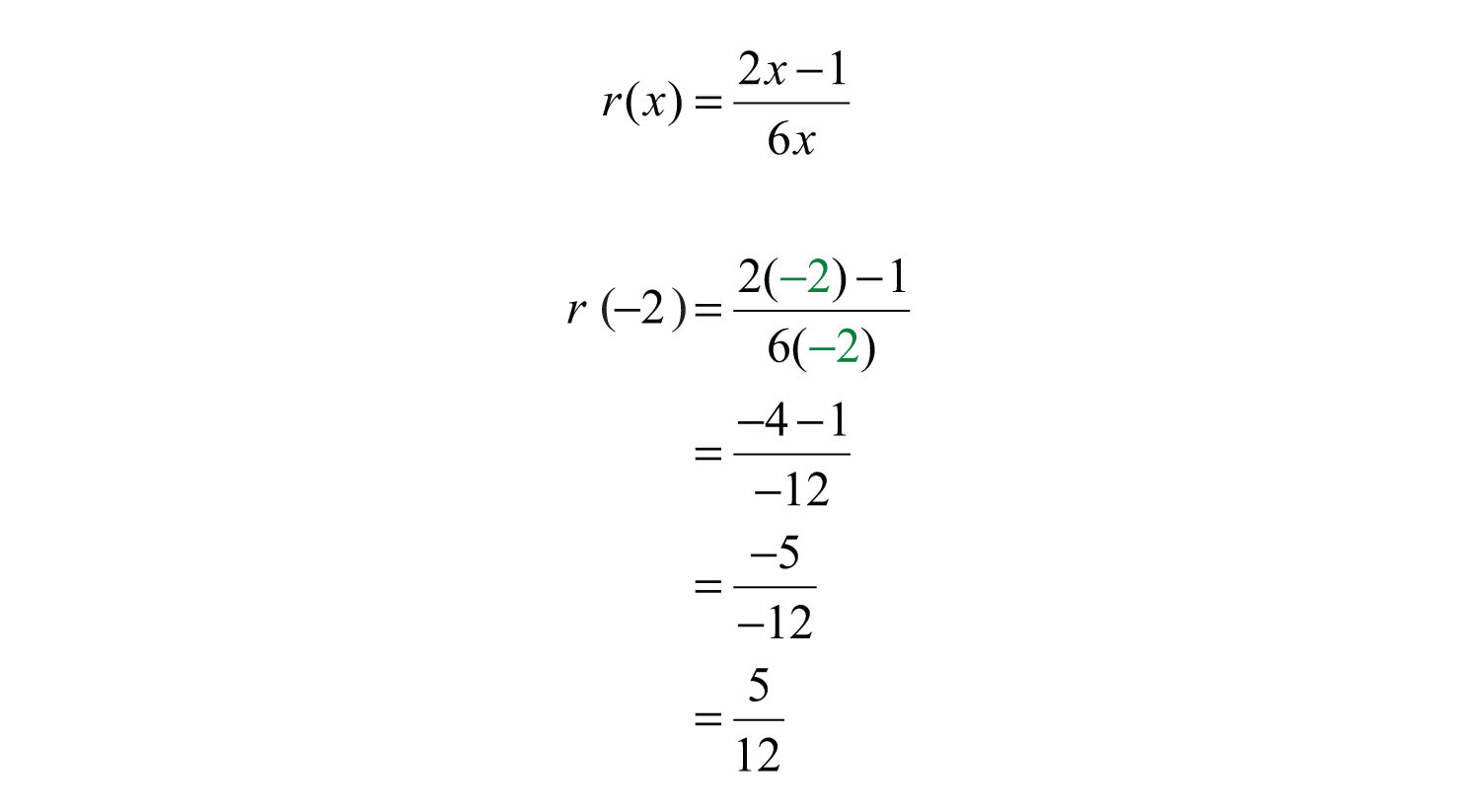
Answers:
a.
b. The domain is all real numbers except 0 and −3.
c.
If a cost functionA function that represents the cost of producing a certain number of units. represents the cost of producing x units, then the average costThe total cost divided by the number of units produced, which can be represented by , where is a cost function. is the cost divided by the number of units produced.
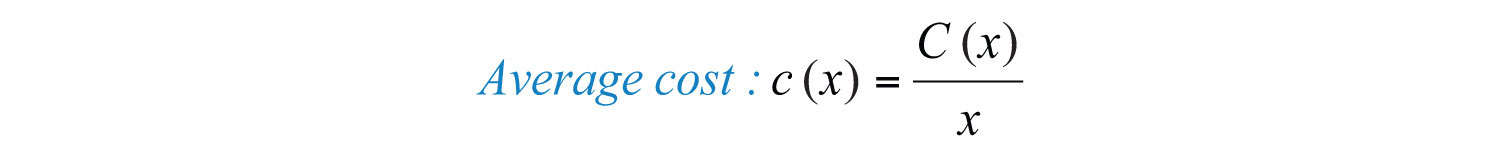
Example 13: The cost in dollars of producing t-shirts with a company logo is given by , where x represents the number of shirts produced. Determine the average cost of producing
a. 40 t-shirts
b. 250 t-shirts
c. 1,000 t-shirts
Solution: Set up a function representing the average cost.
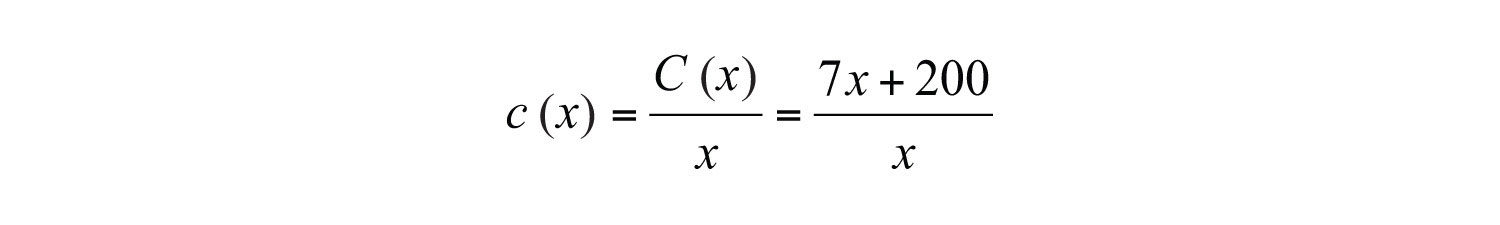
Next, calculate , , and .
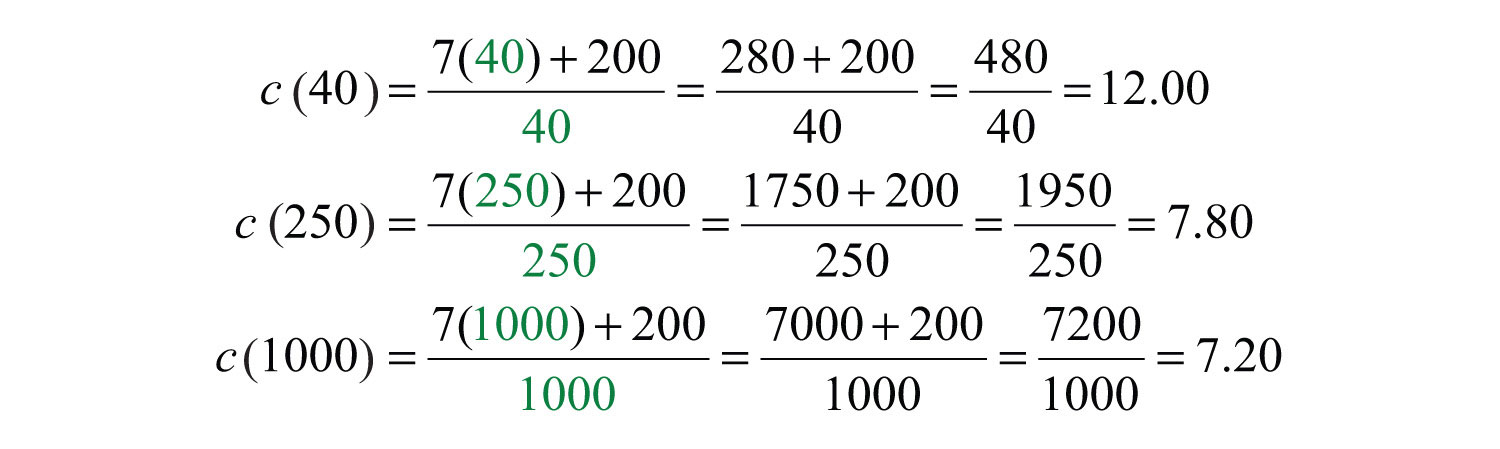
Answers:
a. If 40 t-shirts are produced, then the average cost per t-shirt is $12.00.
b. If 250 t-shirts are produced, then the average cost per t-shirt is $7.80.
c. If 1,000 t-shirts are produced, then the average cost per t-shirt is $7.20.
Key Takeaways
- Rational expressions usually are not defined for all real numbers. The real numbers that give a value of 0 in the denominator are not part of the domain. These values are called restrictions.
- Simplifying rational expressions is similar to simplifying fractions. First, factor the numerator and denominator and then cancel the common factors. Rational expressions are simplified if there are no common factors other than 1 in the numerator and the denominator.
- Simplified rational expressions are equivalent for values in the domain of the original expression. Be sure to state the restrictions if the denominators are not assumed to be nonzero.
- Use the opposite binomial property to cancel binomial factors that involve subtraction. Use to replace factors that will then cancel. Do not confuse this with factors that involve addition, such as .
Topic Exercises
Part A: Rational Expressions
Evaluate for the given set of x-values.
1. ; {−1, 0, 1}
2. ; {−1, 0, 1}
3. ; {−10, −9, 0}
4. ; {−6, 0, 5}
5. ; {0, 1/2, 2}
6. ; {0, 1/3, 7}
7. ; {−3, 0, 3}
8. ; {−5, −4, 5}
9. Fill in the following chart:
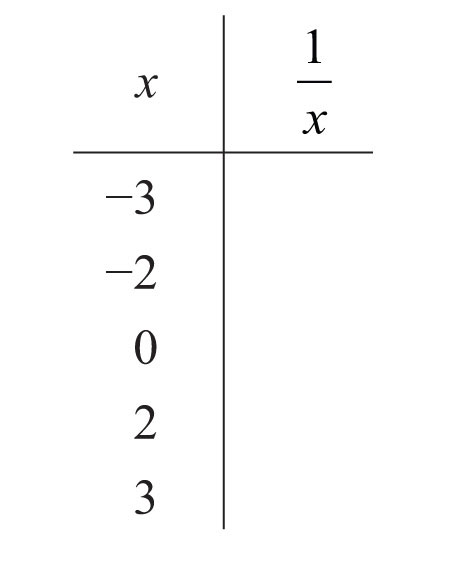
10. Fill in the following chart:
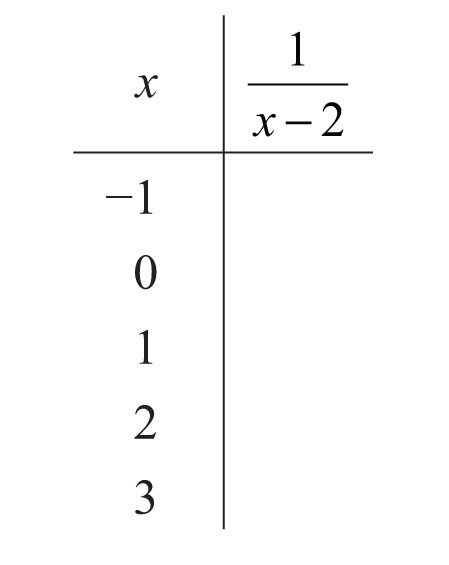
11. Fill in the following chart:
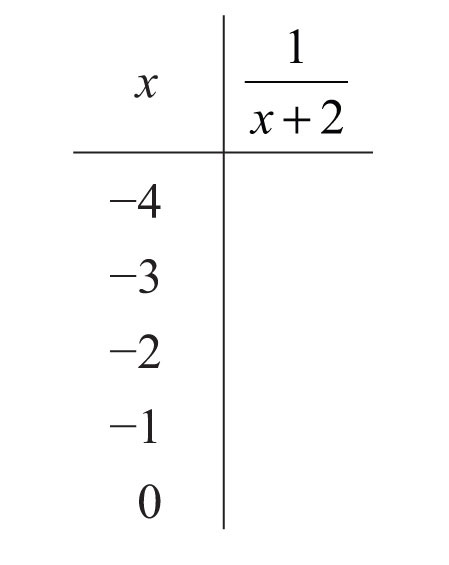
12. Fill in the following chart:
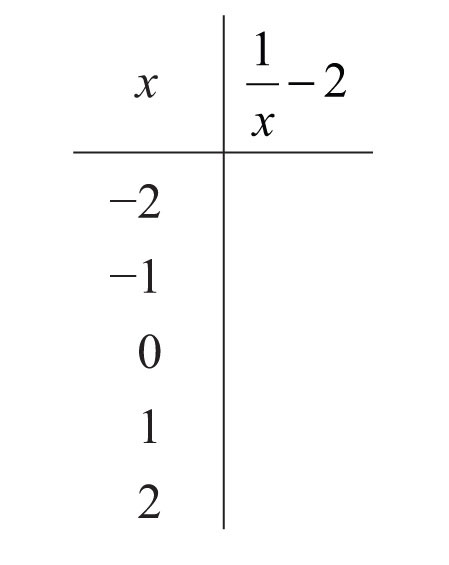
An object’s weight depends on its height above the surface of earth. If an object weighs 120 pounds on the surface of earth, then its weight in pounds, W, x miles above the surface is approximated by the formula
For each problem below, approximate the weight of a 120-pound object at the given height above the surface of earth. (1 mile = 5,280 feet)
13. 100 miles
14. 1,000 miles
15. 44,350 feet
16. 90,000 feet
The price to earnings ratio (P/E) is a metric used to compare the valuations of similar publicly traded companies. The P/E ratio is calculated using the stock price and the earnings per share (EPS) over the previous 12‑month period as follows:
If each share of a company stock is priced at $22.40, then calculate the P/E ratio given the following values for the earnings per share.
17. $1.40
18. $1.21
19. What happens to the P/E ratio when earnings decrease?
20. What happens to the P/E ratio when earnings increase?
State the restrictions to the domain.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
Part B: Simplifying Rational Expressions
State the restrictions and then simplify.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
Part C: Simplifying Rational Expressions with Opposite Binomial Factors
State the restrictions and then simplify.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
Simplify. (Assume all denominators are nonzero.)
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
Part D: Rational Functions
Calculate the following.
85. ; , ,
86. ; , ,
87. ; , ,
88. ; , ,
89. ; , ,
90. ; , ,
State the restrictions to the domain and then simplify.
91.
92.
93.
94.
95.
96.
97. The cost in dollars of producing coffee mugs with a company logo is given by , where x represents the number of mugs produced. Calculate the average cost of producing 100 mugs and the average cost of producing 500 mugs.
98. The cost in dollars of renting a moving truck for the day is given by , where x represents the number of miles driven. Calculate the average cost per mile if the truck is driven 250 miles in one day.
99. The cost in dollars of producing sweat shirts with a custom design on the back is given by , where x represents the number of sweat shirts produced. Calculate the average cost of producing 150 custom sweat shirts.
100. The cost in dollars of producing a custom injected molded part is given by , where x represents the number of parts produced. Calculate the average cost of producing 1,000 custom parts.
Part E: Discussion Board
101. Explain why and illustrate this fact by substituting some numbers for the variables.
102. Explain why and illustrate this fact by substituting some numbers for the variables.
103. Explain why we cannot cancel x in the expression .
Answers
1: −5, undefined, 5
3: −1, undefined, 1/9
5: 0, undefined, 0
7: Undefined, −5/9, undefined
9:

11:
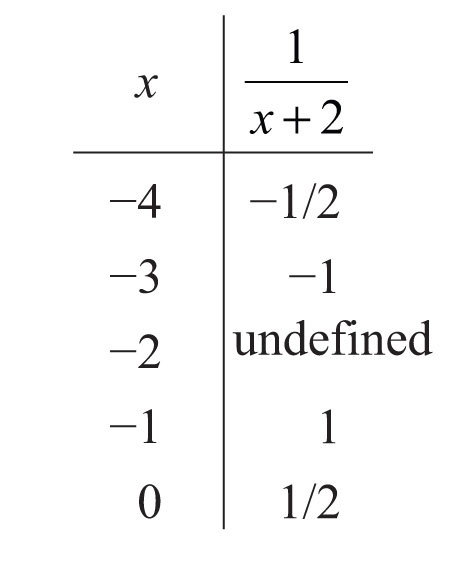
13: 114 pounds
15: 119.5 pounds
17: 16
19: The P/E ratio increases.
21:
23:
25:
27: and
29:
31: , , and
33: and
35: ;
37: ;
39: ;
41: ;
43: ;
45: ;
47: ;
49: ;
51: ;
53: ;
55: −1;
57: 1;
59: ;
61: ;
63: ;
65: ;
67: ;
69: ; none
71: ;
73:
75:
77:
79:
81:
83:
85: , ,
87: , undefined,
89: , ,
91: ;
93: ;
95: ;
97: The average cost of producing 100 mugs is $1.40 per mug. The average cost of producing 500 mugs is $1.08 per mug.
99: $12.50




