This is “Factoring Special Binomials”, section 6.4 from the book Beginning Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
6.4 Factoring Special Binomials
Learning Objectives
- Factor binomials that are differences of squares.
- Factor binomials that are sums and differences of cubes.
Difference of Squares
A binomial is a polynomial with two terms. We begin with our first special binomial called difference of squares where a and b represent algebraic expressions.:
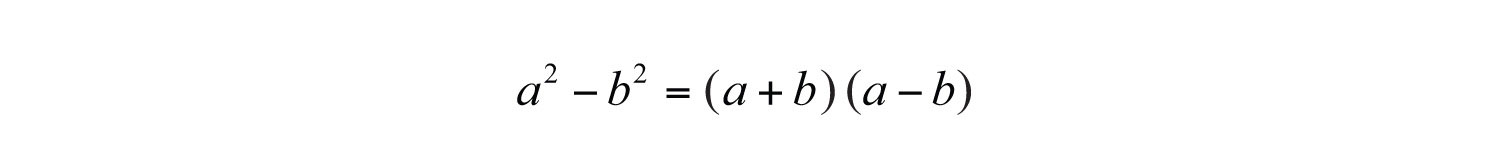
To verify the above formula, multiply:

We use this formula to factor certain special binomials.
Example 1: Factor: .
Solution:
Step 1: Identify the binomial as difference of squares and determine the square factors of each term.
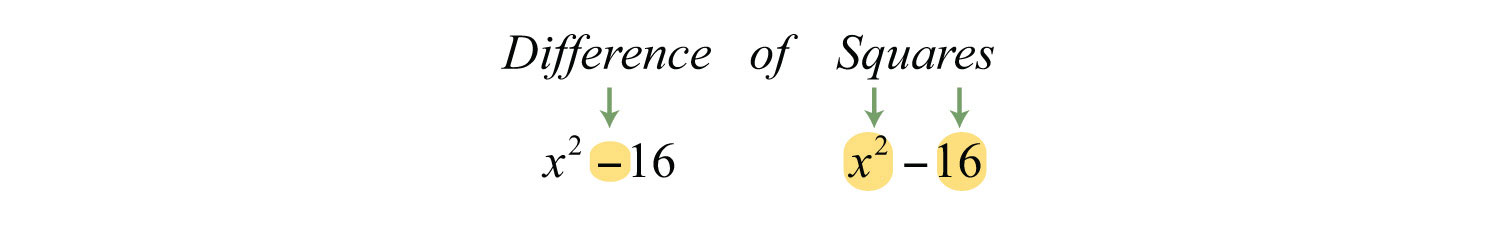
Here we can write
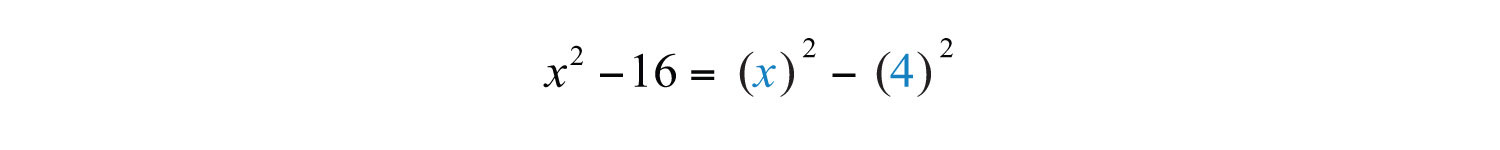
The terms are squares of x and 4. Hence and .
Step 2: Substitute into the difference of squares formula.
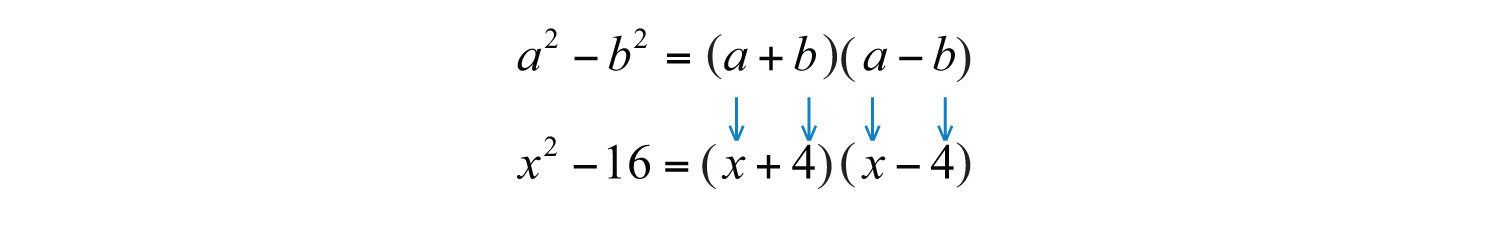
Step 3: Multiply to check. This step is optional.
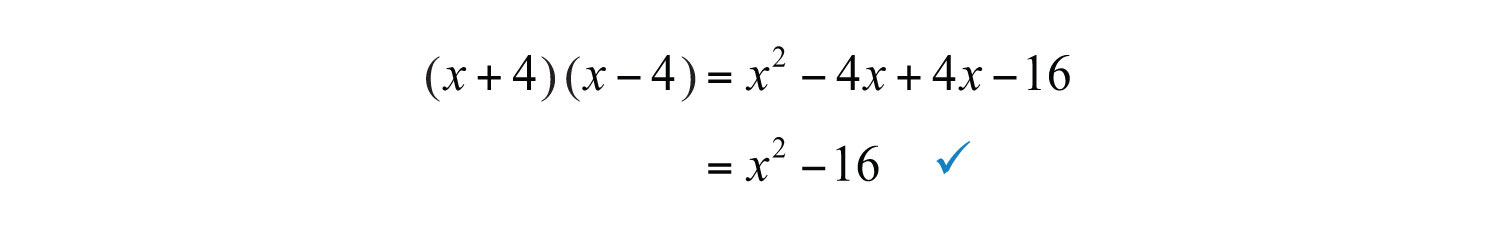
Answer:
It is worth taking some extra time at this point to review all of the squares of integers from 1 to 12.

Recognizing these perfect square integers helps speed the factoring process.
Example 2: Factor: .
Solution: The subtraction indicates that this is a difference. Furthermore, we recognize that the terms are squares.
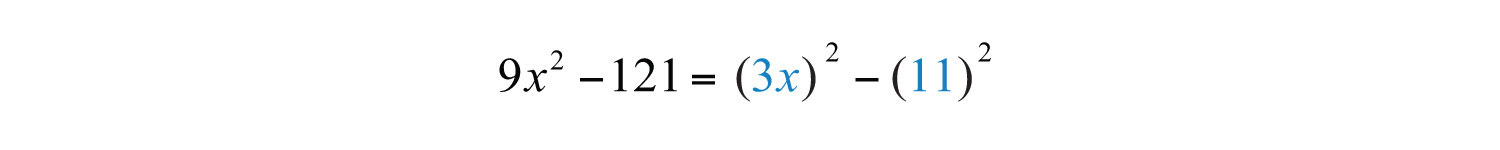
In this case, and . Substitute into the formula for difference of squares.
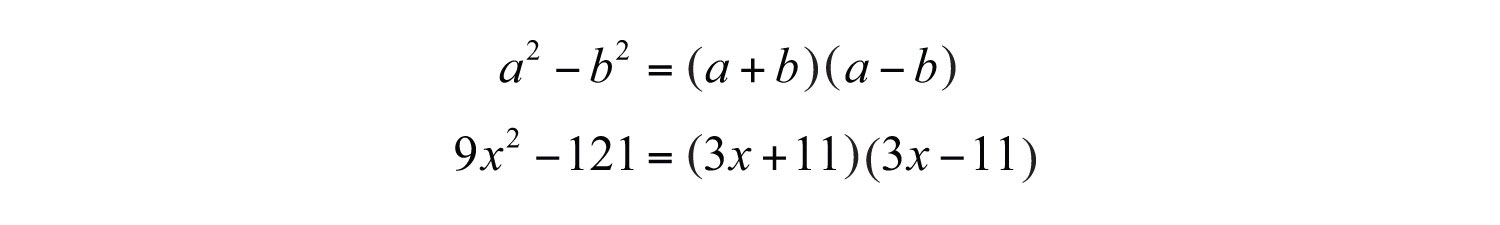
Answer:
It may be the case that the terms of the binomial have a common factor. If so, it will be difficult to identify the perfect squares until we first factor out the GCF.
Example 3: Factor: .
Solution: The terms are not perfect squares. However, notice that they do have a common factor. First, factor out the GCF, 3.
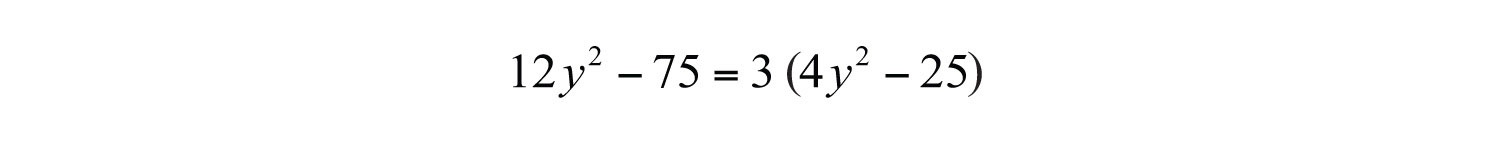
The resulting binomial factor is a difference of squares with and .

Answer:
Example 4: Factor: .
Solution: Here we have a binomial with two variables and recognize that it is a difference of squares.
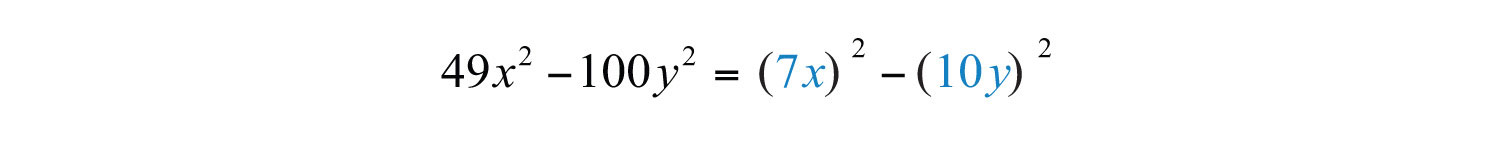
Therefore, and . Substitute into the formula for difference of squares.
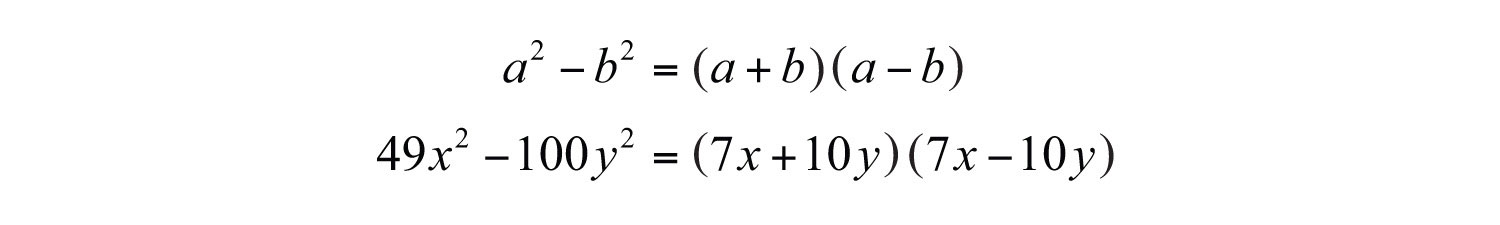
Answer:
Try this! Factor: .
Answer:
Video Solution
(click to see video)Given any real number b, a polynomial of the form is prime. Furthermore, the sum of squares does not have a general factored equivalent. does not have a general factored equivalent. Care should be taken not to confuse this with a perfect square trinomial:
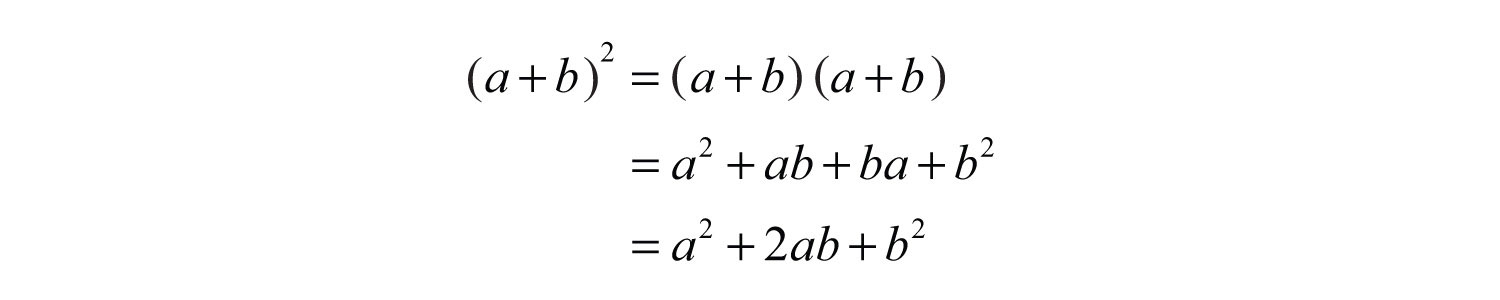
Therefore,
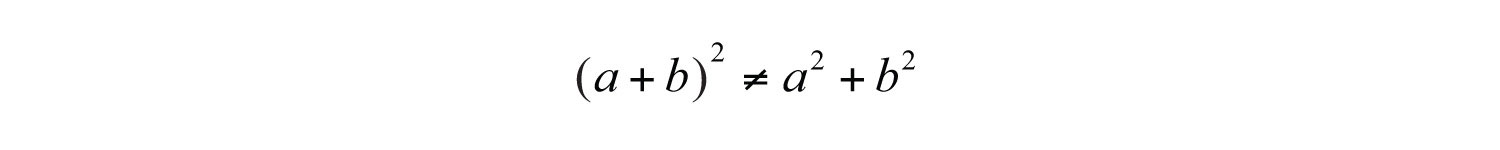
When the degree of the special binomial is greater than two, we may need to apply the difference of squares formula multiple times. A polynomial is completely factored when none of the factors can be factored any further.
Example 5: Factor completely: .
Solution: First, identify what is being squared:
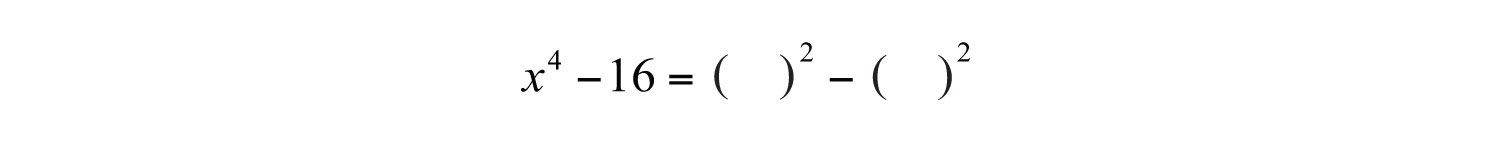
To do this, recall the power rule for exponents, . When exponents are raised to a power, multiply them. With this in mind, determine that and write
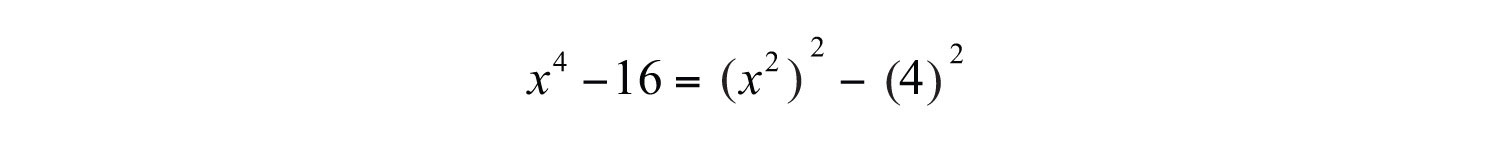
Therefore, and . Substitute into the formula for difference of squares.
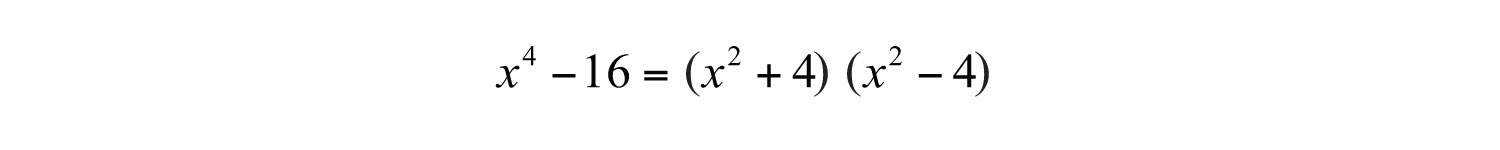
At this point, notice that the factor is itself a difference of two squares and thus can be further factored using and . The factor is a sum of squares, which cannot be factored using real numbers.
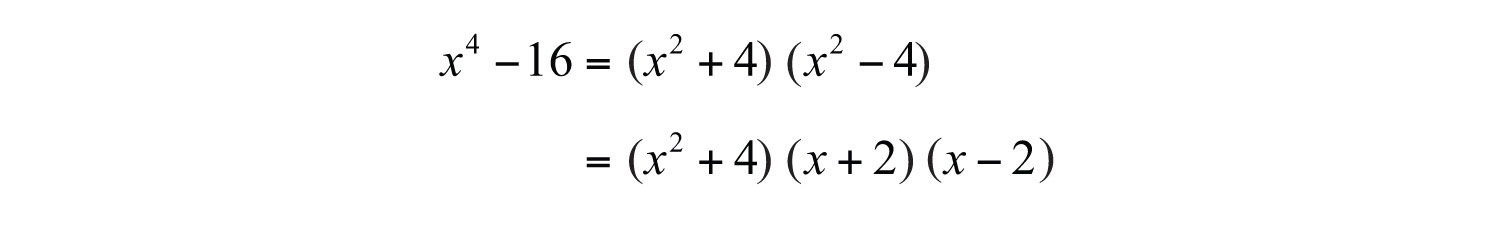
Answer:
Try this! Factor completely: .
Answer:
Video Solution
(click to see video)Sum and Difference of Cubes
Two other special binomials of interest are the sum where a and b represent algebraic expressions. and difference of cubes where a and b represent algebraic expressions.:
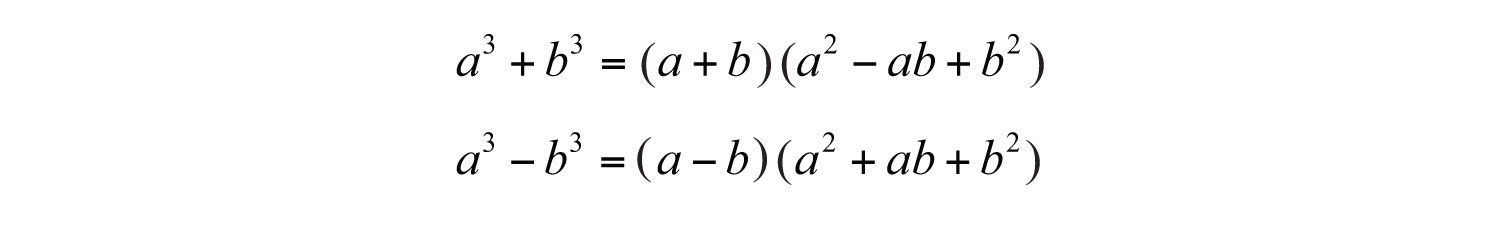
We can verify these formulas by multiplying:
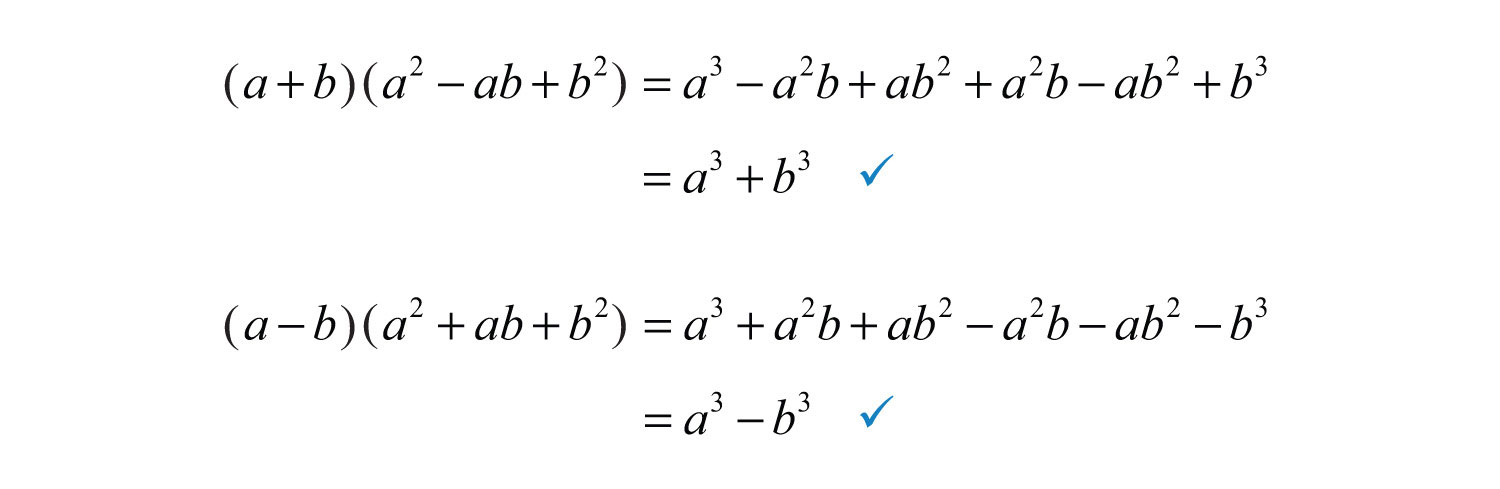
The process for factoring the sum and difference of cubes is very similar to that for the difference of squares. We first identify a and b and then substitute into the appropriate formula. The separate formulas for sum and difference of cubes allow us to always choose a and b to be positive.
Example 6: Factor: .
Solution: The plus sign and the fact that the terms are cubes indicate to us that this is a sum of cubes.
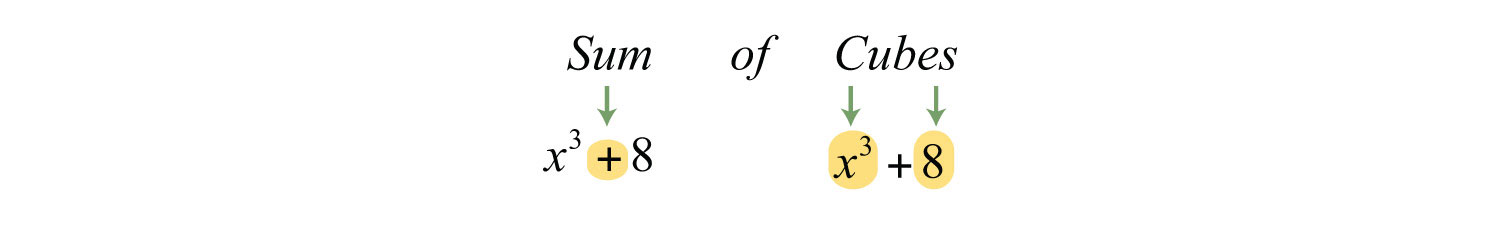
Next, identify what is being cubed.
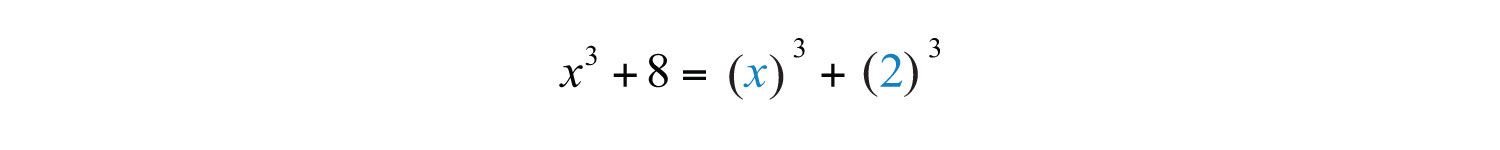
In this case, and . Substitute into the sum of cubes formula.
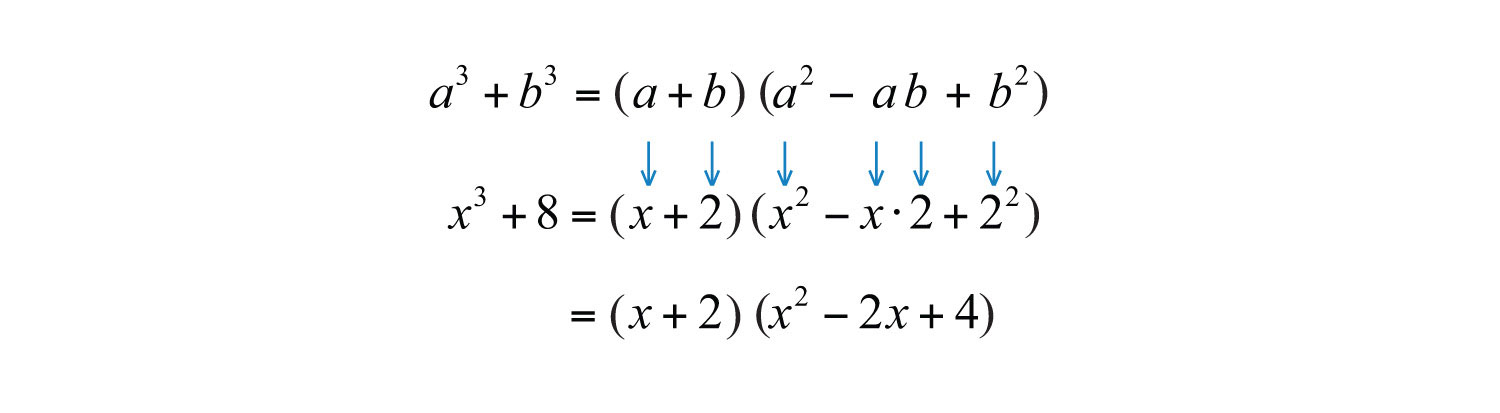
The resulting trinomial is prime and the factoring is complete. We can check this factorization by multiplying.
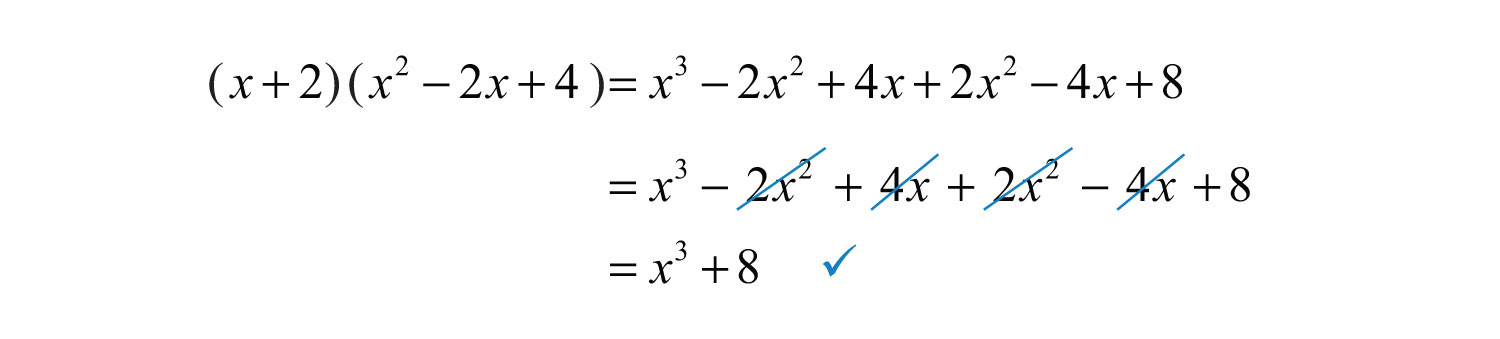
Answer:
It is helpful to review the perfect cubes of integers from 1 to 12. This will aid you in identifying sums and differences of cubes.

Example 7: Factor: .
Solution: In this case, we have a difference of cubes.
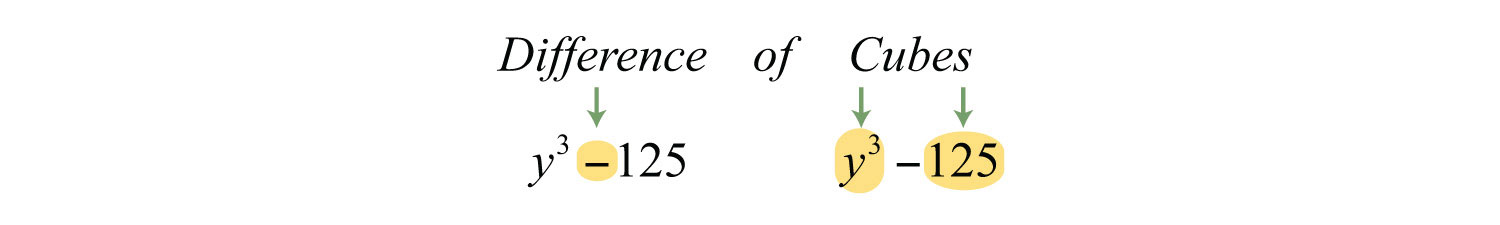
We can write
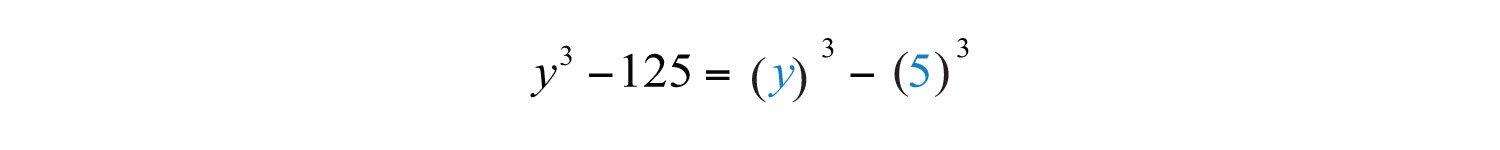
Substitute and into the formula for difference of cubes.
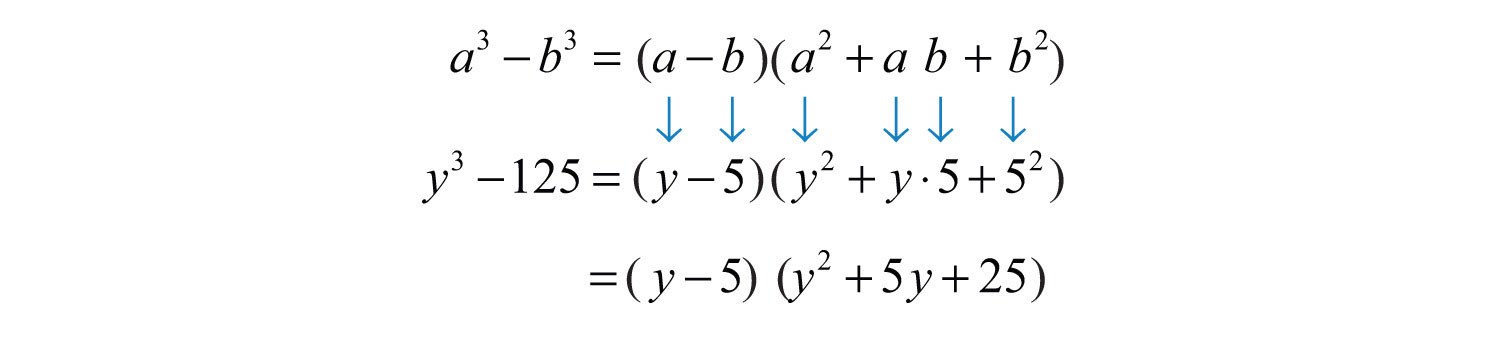
Answer:
Always look for common factors when factoring. If the terms of the binomial have a GCF other than 1, then factor that out first.
Example 8: Factor: .
Solution: Begin by factoring out the GCF .
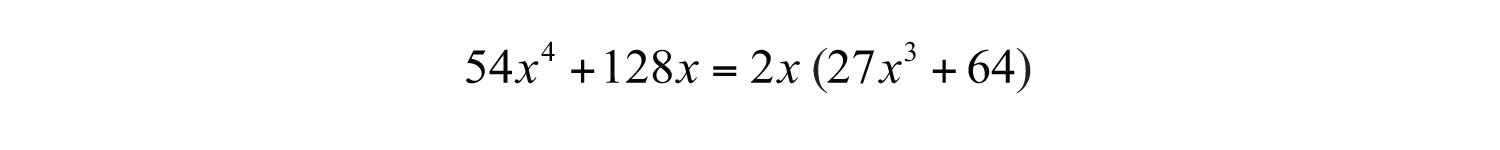
The resulting binomial factor is a sum of cubes, where and .

Answer:
Example 9: Factor: .
Solution: This binomial is a difference of cubes with two variables. Identify what is being cubed.
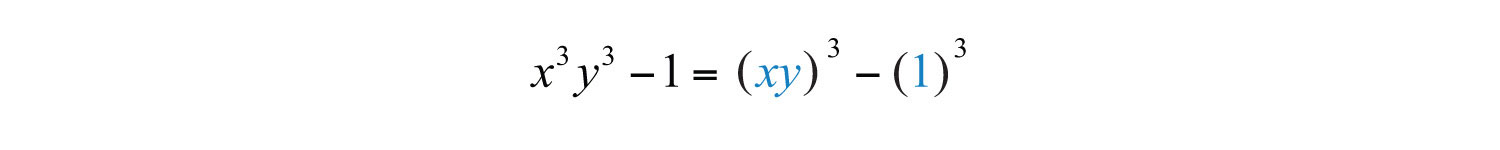
Here and . Substitute into the appropriate formula and simplify.
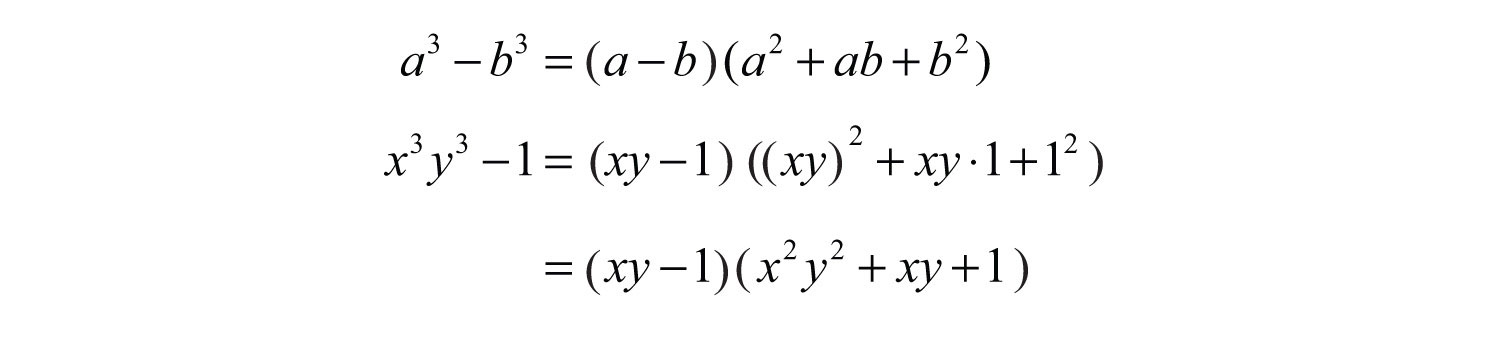
Answer:
Try this! Factor: .
Answer:
Video Solution
(click to see video)When factoring, always look for resulting factors to factor further.
Example 10: Factor completely: .
Solution: When confronted with a binomial that is both a difference of squares and cubes, as this is, make it a rule to factor using difference of squares first.
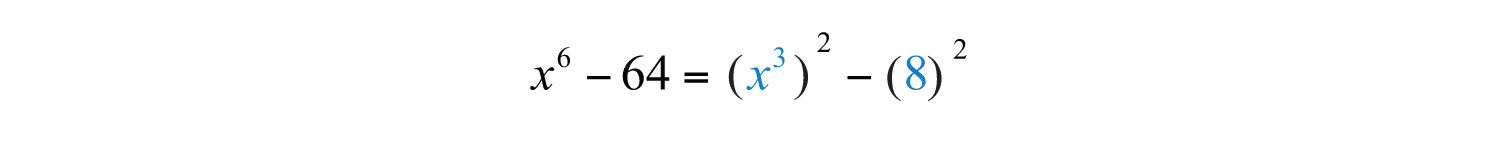
Therefore, and . Substitute into the difference of squares formula.
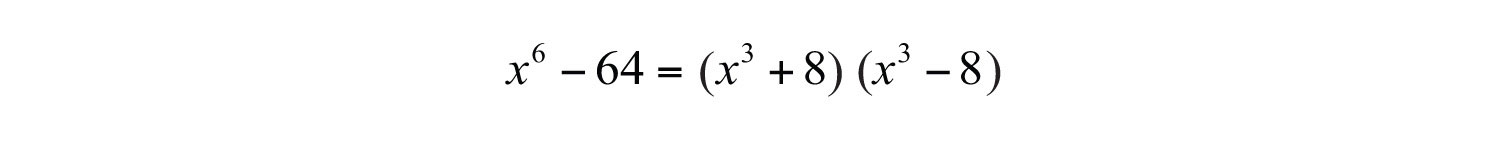
The resulting two binomial factors are a sum and a difference of cubes. Each can be factored further.
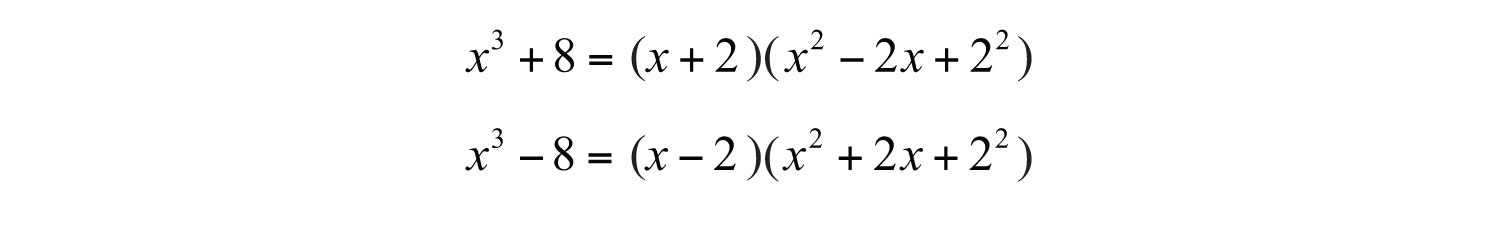
Therefore, we have
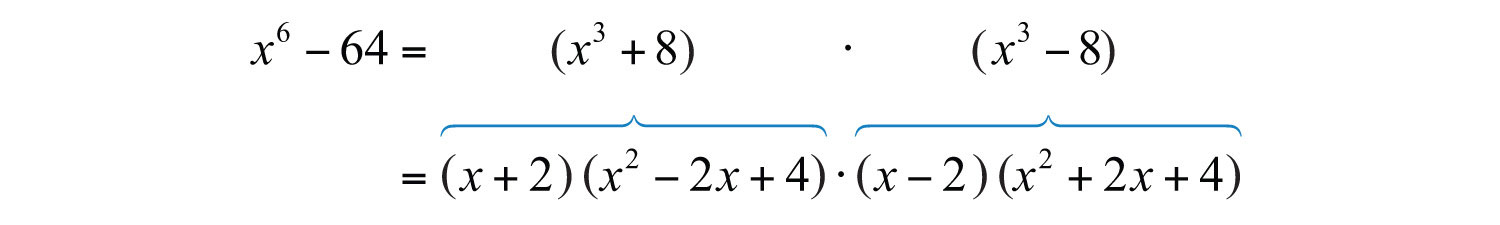
The trinomial factors are prime and the expression is completely factored.
Answer:
As an exercise, factor the previous example as a difference of cubes first and then compare the results. Why do you think we make it a rule to factor using difference of squares first?
Try this! Factor: .
Answer:
Video Solution
(click to see video)Key Takeaways
- When factoring special binomials, the first step is to identify it as a sum or difference. Once we identify the binomial, we then determine the values of a and b and substitute into the appropriate formula.
- The formulas for all of the special binomials should be memorized. In addition, to help facilitate the identification of special binomials, memorize the squares and cubes of integers up to at least 12.
- If a binomial is both a difference of squares and cubes, then first factor it as a difference of squares.
Topic Exercises
Part A: Difference of Squares
Factor completely.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51. The height of a projectile dropped from a 64-foot tower is given by the function , where t represents the time in seconds after it is dropped. Rewrite this function in factored form. (Hint: Factor out −16 first.)
52. The height of a projectile dropped from a 36-foot tower is given by the function , where t represents the time in seconds after it is dropped. Rewrite this function in factored form.
Part B: Sum and Difference of Cubes
Factor completely.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
Part C: Discussion Board Topics
95. If a binomial falls into both categories, difference of squares and difference of cubes, which would be best to factor it as, and why? Create an example that illustrates this situation and factor it using both formulas.
96. What can be said about the degrees of the factors of a polynomial? Give an example.
97. Make up your own difference of squares factoring exercise and provide the answer. Explain how you solved it.
98. Make up your own sum or difference of cubes factoring exercise and provide the answer. Explain how you solved it.
Answers
1:
3:
5: Prime
7:
9:
11:
13:
15:
17:
19:
21:
23:
25:
27:
29:
31:
33:
35:
37:
39:
41:
43:
45:
47:
49:
51:
53:
55:
57:
59:
61:
63:
65:
67:
69:
71: Prime
73:
75:
77:
79:
81:
83:
85:
87:
89:
91:
93:




