This is “Finding Linear Equations”, section 3.5 from the book Beginning Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
3.5 Finding Linear Equations
Learning Objectives
- Given a graph, identify the slope and y-intercept.
- Find the equation of the line using the slope and y-intercept.
- Find the equation of the line using point-slope form.
Finding Equations Using Slope-Intercept Form
Given the algebraic equation of a line, we are able to graph it in a number of ways. In this section, we will be given a geometric description of a line and be asked to find the algebraic equation. Finding the equation of a line can be accomplished in a number of ways, the first of which makes use of slope-intercept form, . If we know the slope, m, and the y-intercept, (0, b), we can construct the equation.
Example 1: Find the equation of a line with slope and y-intercept (0, 1).
Solution: The given y-intercept implies that . Substitute the slope m and the y-value of the y-intercept b into the equation .
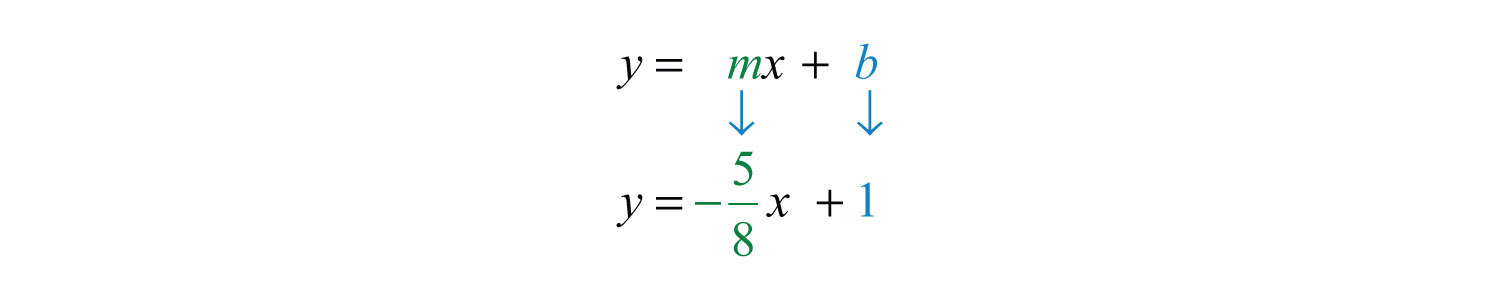
Answer:
Finding a linear equation is very straightforward if the slope and y-intercept are given. This is certainly not always the case; however, the example demonstrates that the algebraic equation of a line depends on these two pieces of information. If the graph is given, then we can often read it to determine the y-intercept and slope.
Example 2: Find the equation of the line given the graph:
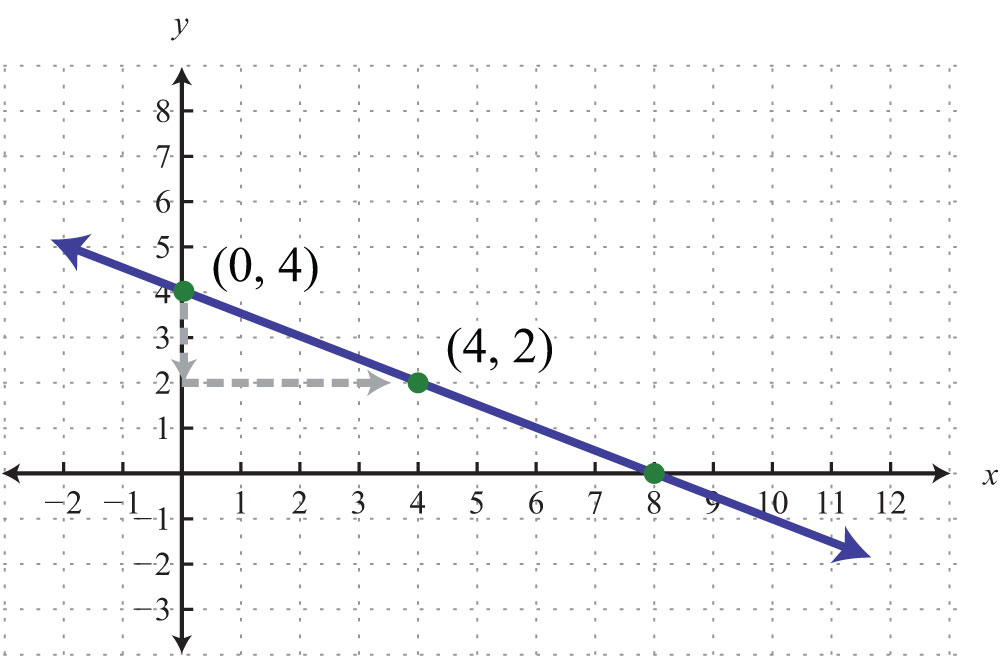
Solution: By reading the graph, we can see that the y-intercept is (0, 4), and thus
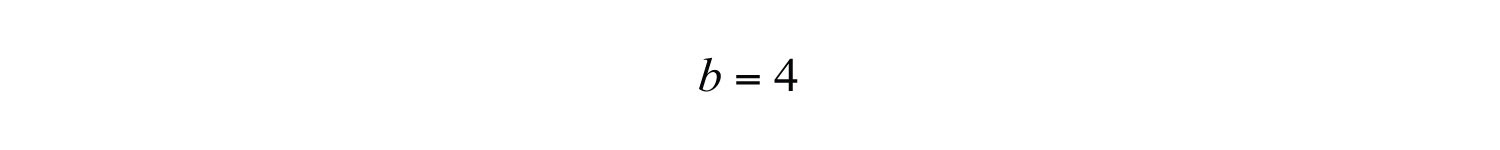
Furthermore, from the points (0, 4) to (4, 2), we can see that the rise is −2 units and the run is 4 units.
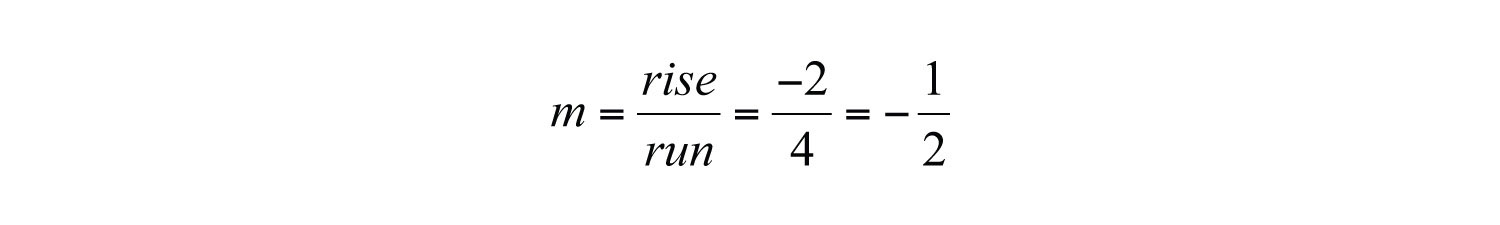
Now substitute m and b into slope-intercept form:
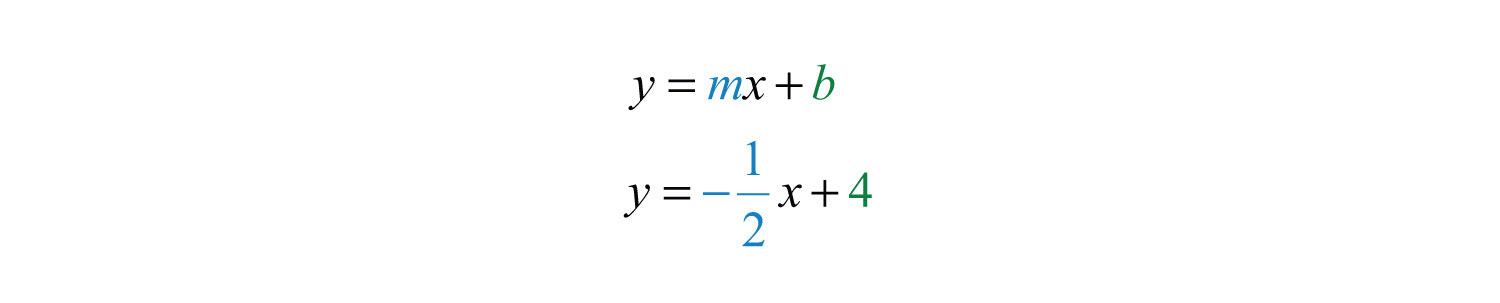
Answer:
Often the y-intercept and slope will not be given or are not easily discernible from the graph. For this reason, we will develop some algebraic techniques that allow us to calculate these quantities.
Example 3: Find the equation of the line with slope passing through (−6, 3).
Solution: Begin by substituting the given slope into slope-intercept form.
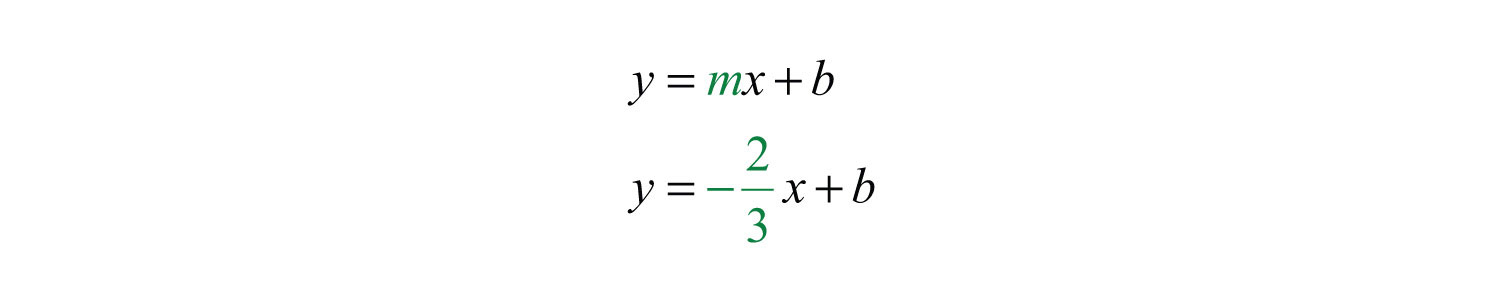
For the ordered pair (−6, 3) to be a solution, it must solve the equation. Therefore, we can use it to find b. Substitute the appropriate x- and y-values as follows:
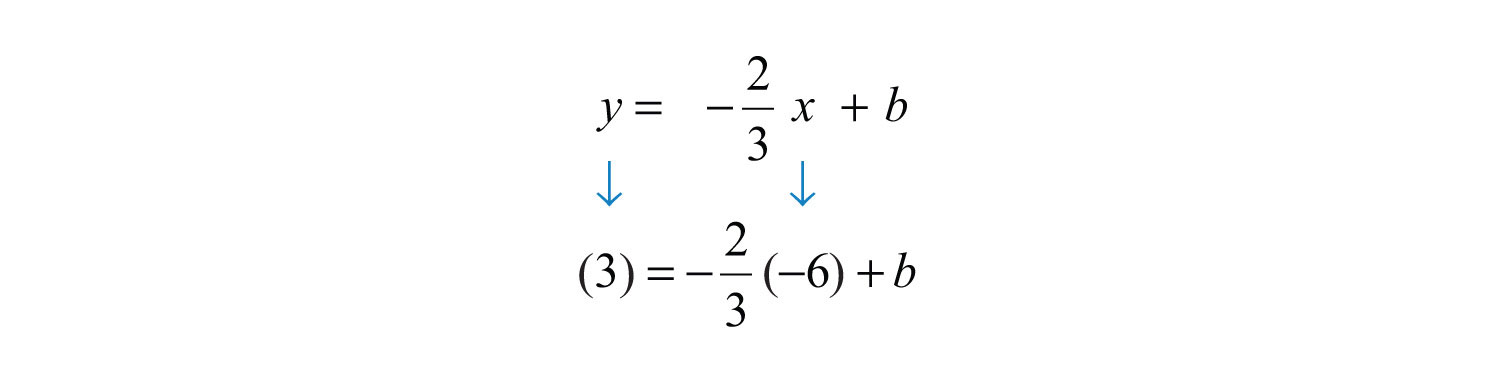
After substituting the appropriate values, solve for the only remaining variable, b.
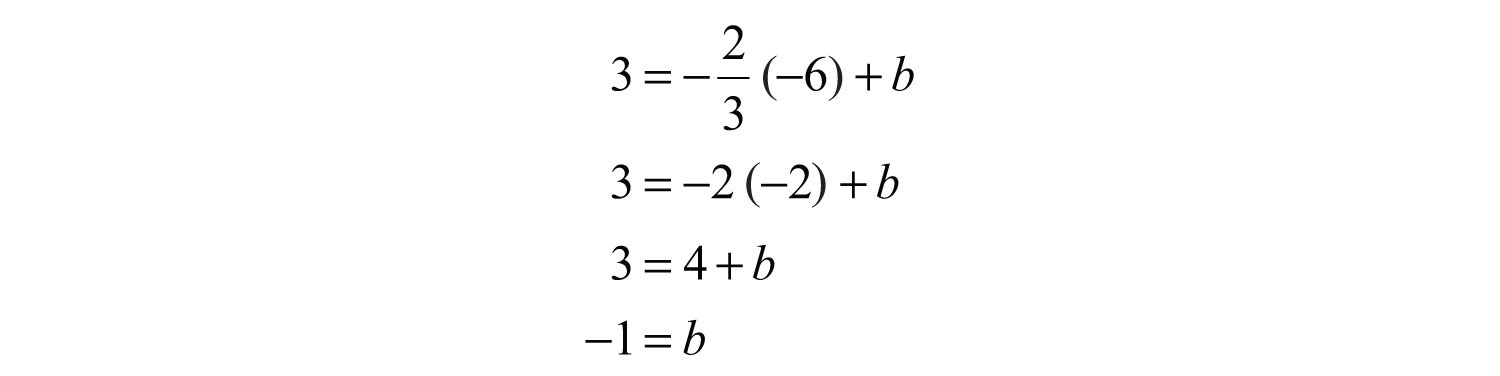
Once we have b, we can then complete the equation:
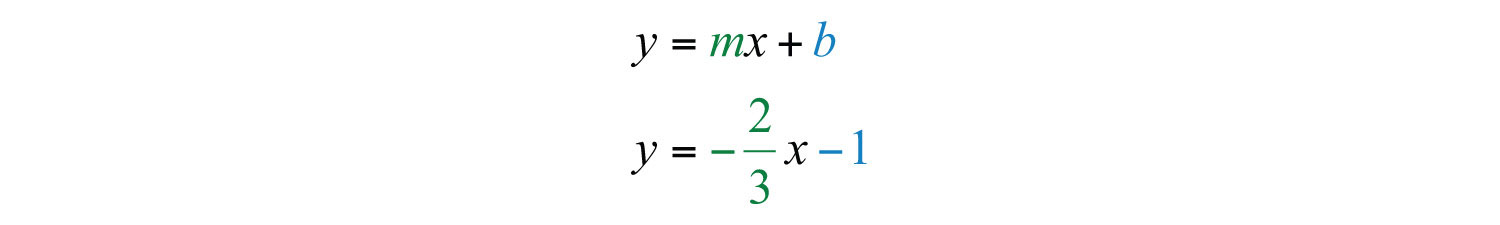
As a check, verify that (−6, 3) solves this linear equation as follows:
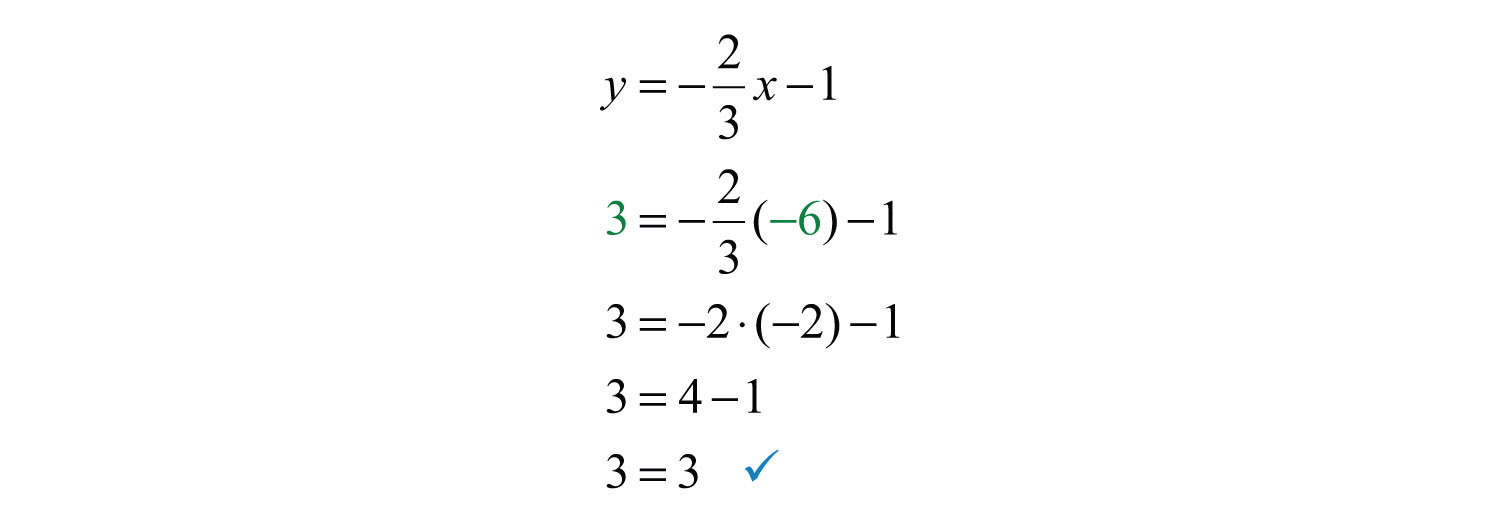
Answer:
Example 4: Find the equation of the line given the graph:
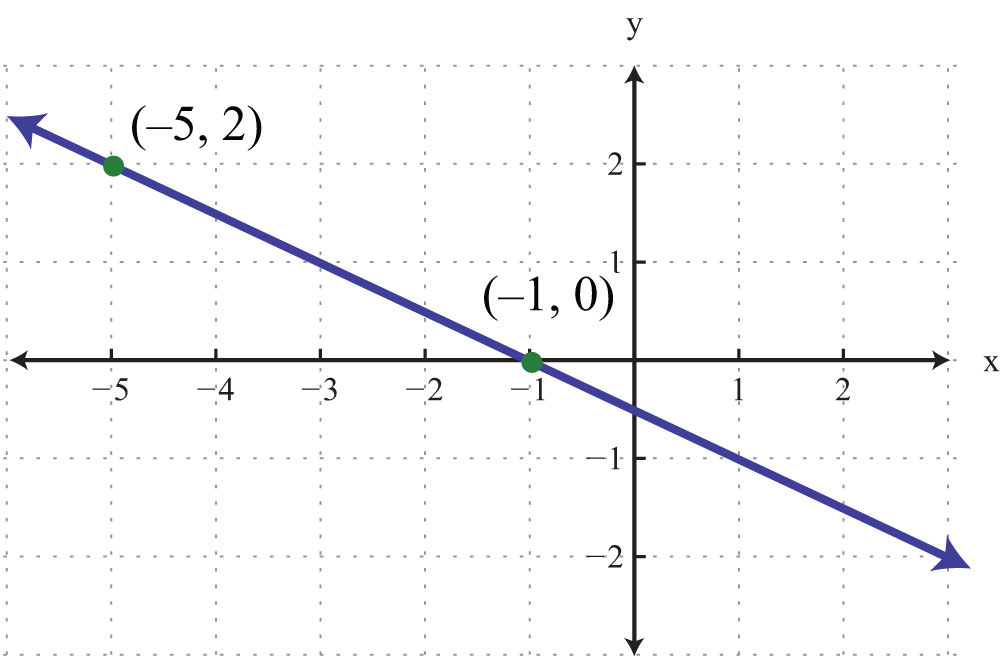
Solution: Use the graph to determine the slope. From the points (−5, 2) to (−1, 0), we can see that the rise between the points is −2 units and the run is 4 units. Therefore, we calculate the slope as follows:
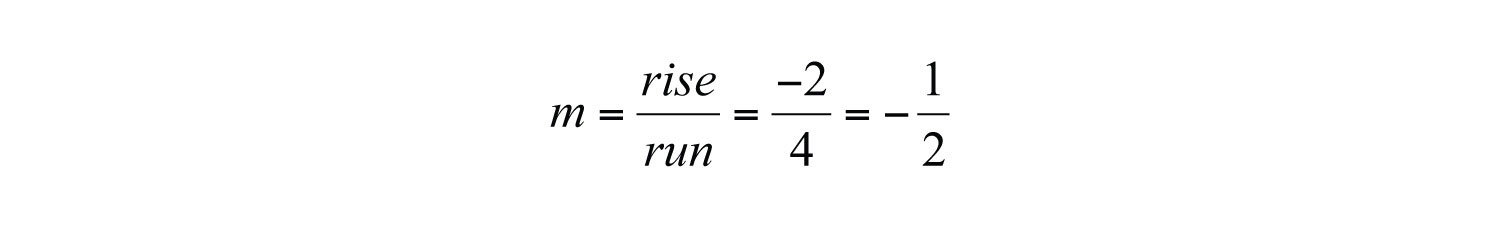
Substitute the slope into slope-intercept form.
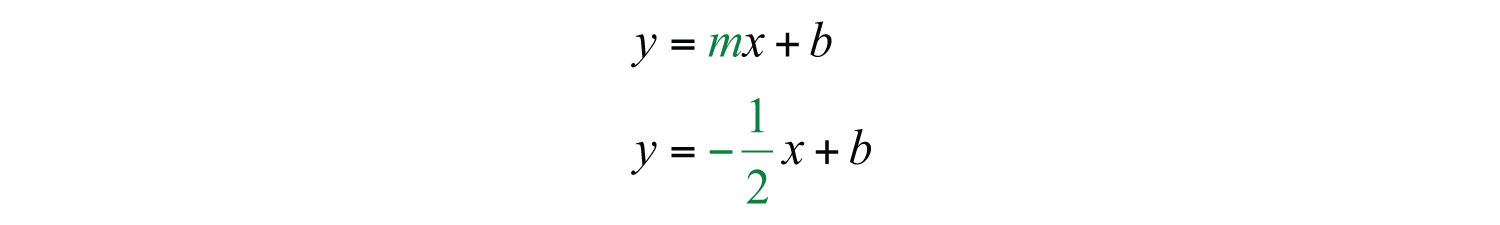
Now substitute the coordinates of one of the given points to find b. It does not matter which one you choose. Here choose (−1, 0):
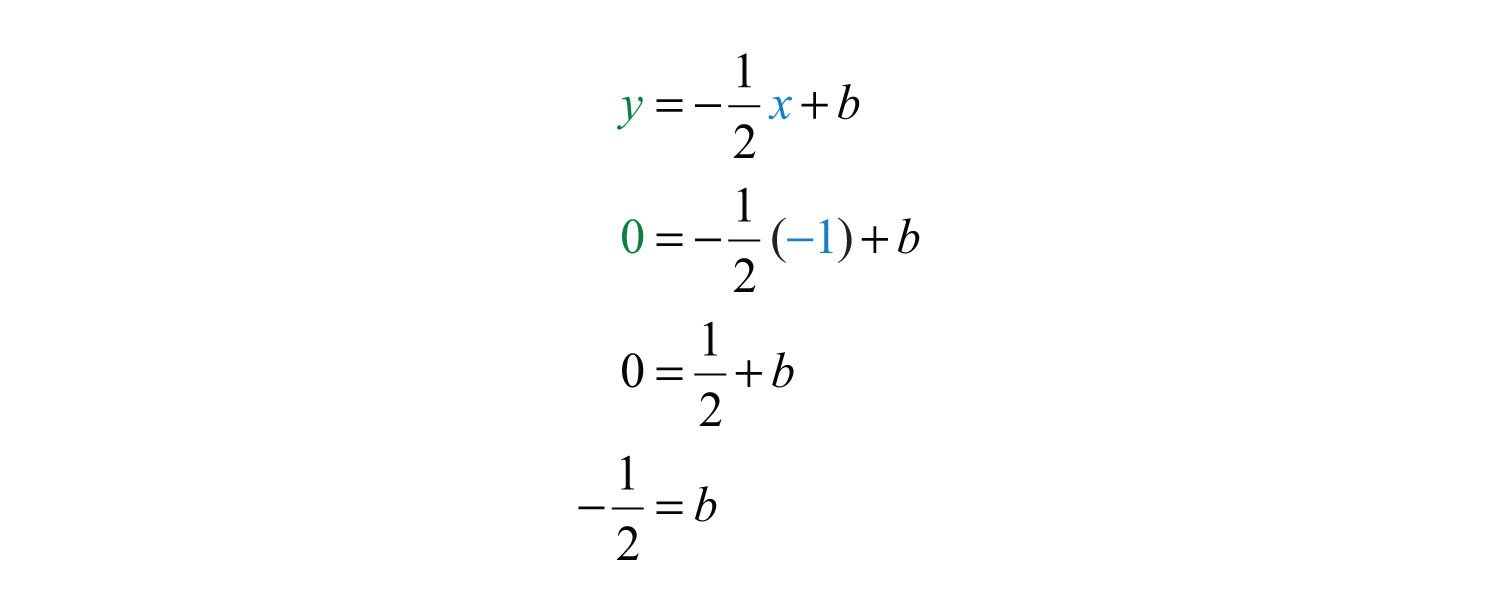
Next, put it all together.
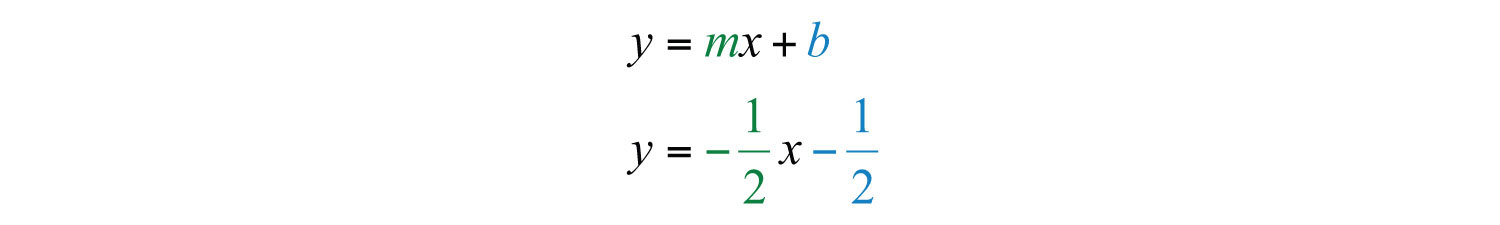
Answer:
As an exercise, substitute the coordinates of the point (−5, 2) to see that b will turn out to be the same value. In fact, you can substitute any ordered pair solution of the line to find b. We next outline an algebraic technique for finding the equation of a nonvertical line passing through two given points.
Example 5: Find the equation of the line passing through (−4, −2) and (1, 3).
Solution: When finding a linear equation using slope-intercept form , the goal is to find m and then b.
Step 1: Find the slope m. In this case, given two points, use the slope formula.
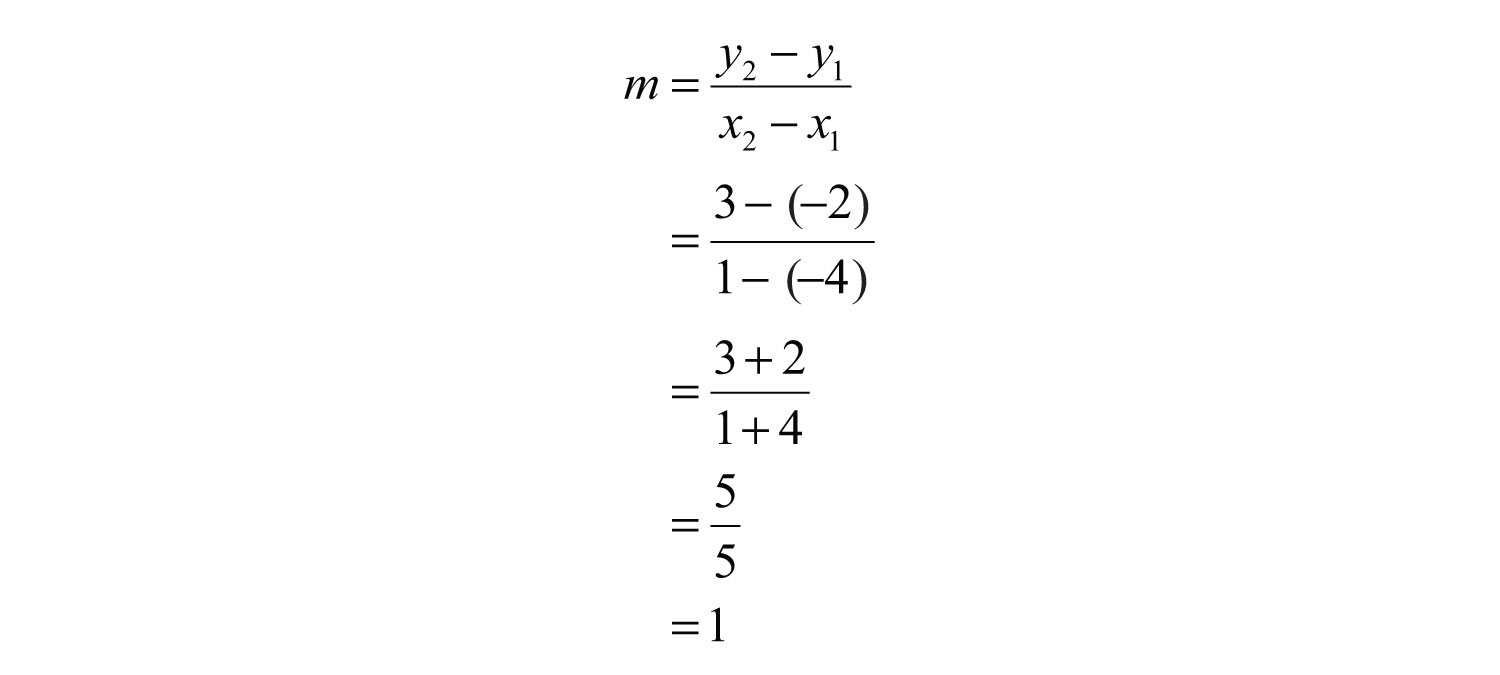
Substitute into slope-intercept form.
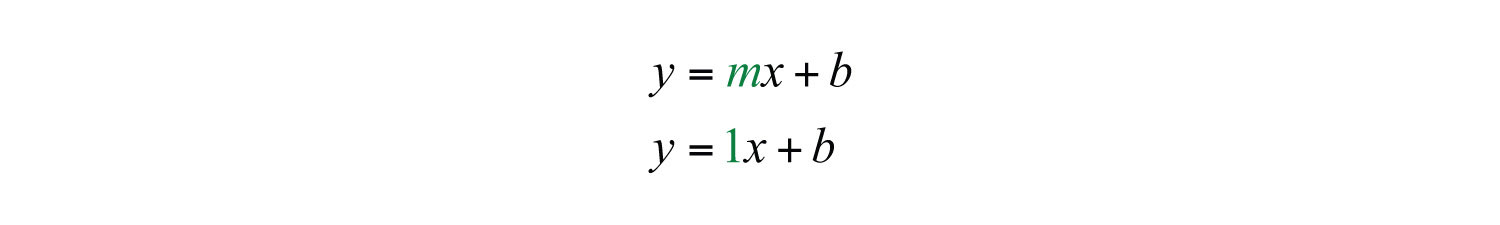
Step 2: Find b. To do this, substitute the coordinates of any given ordered pair solution. Use (1, 3):
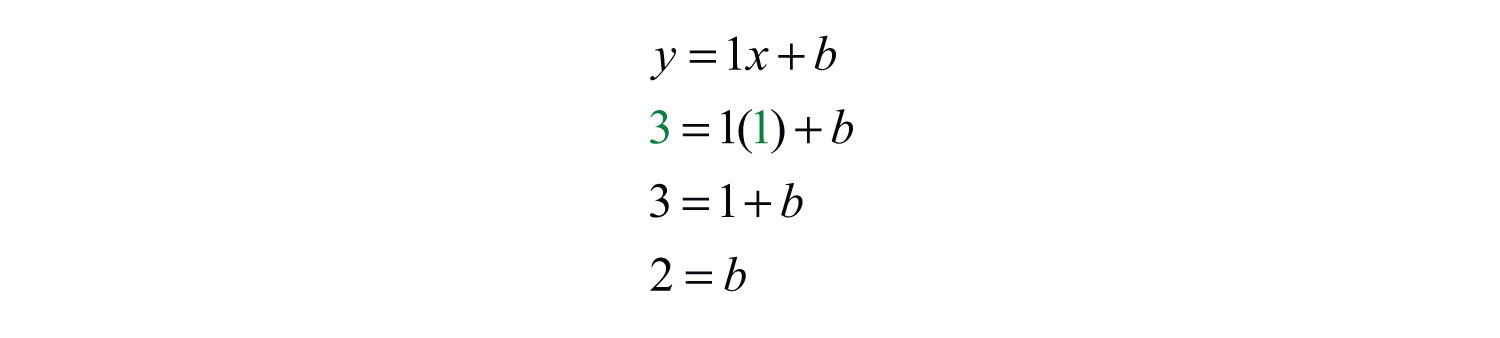
Step 3: Finish building the equation by substituting in the value for b. In this case, we use .
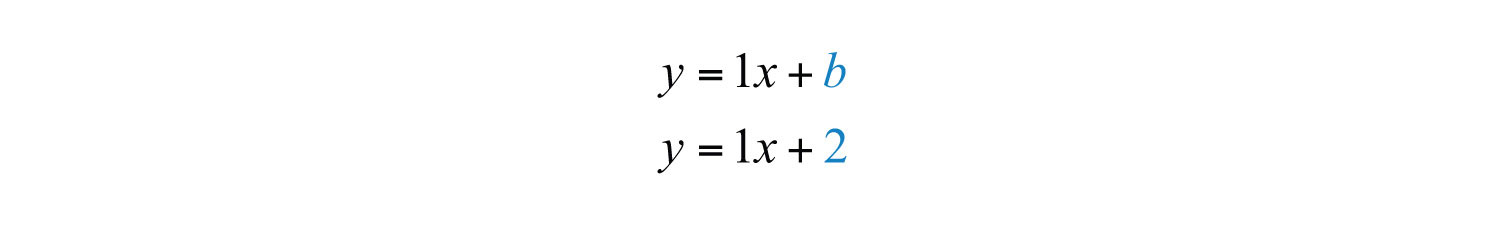
Answer:
These three steps outline the process for finding the equation of any nonvertical line in slope-intercept form. This is a completely algebraic method, but always keep in mind the geometry behind the technique.

Note that the line has a y-intercept at (0, 2), with slope .
Example 6: Find the equation of the line passing through (−1, 3) and (5, 1).
Solution: First, find m, the slope. Given two points, use the slope formula as follows:
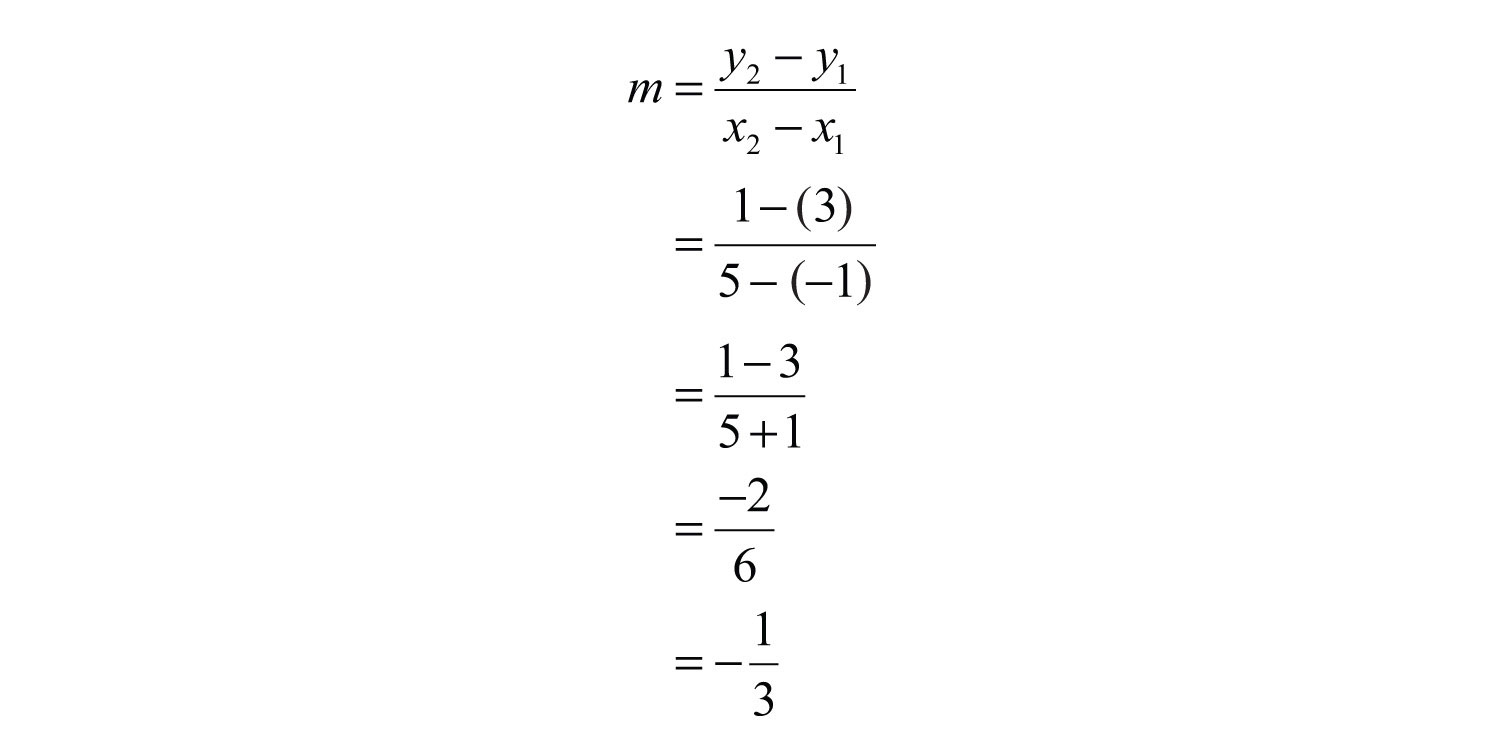
Substitute into slope-intercept form.
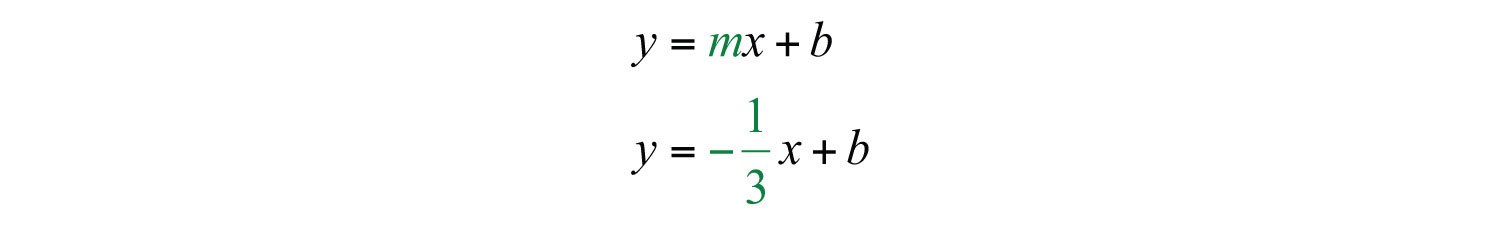
Next, find b. Substitute the coordinates of the point (−1, 3).
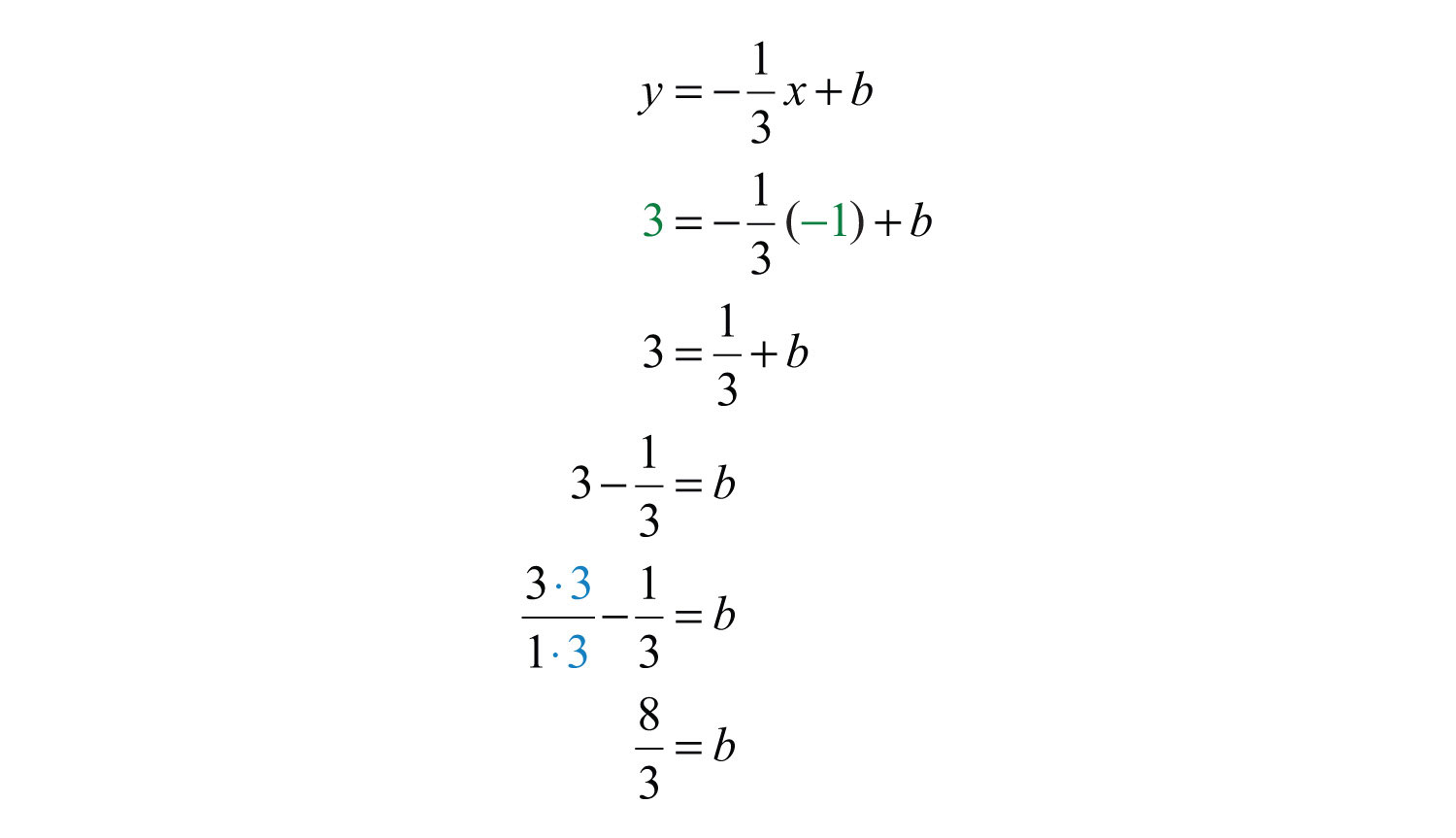
Finally, substitute into the equation.
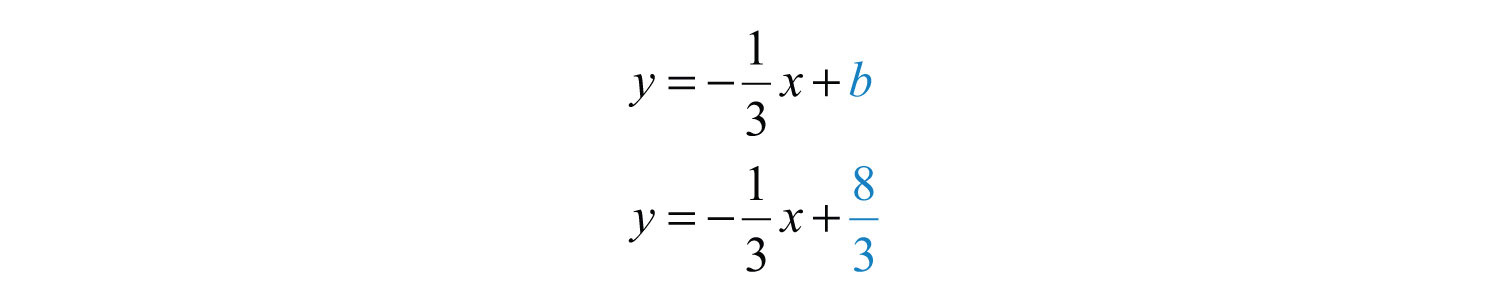
Answer:
Try this! Find the equation of the line passing through (−3, 4) and (6, −2).
Answer:
Video Solution
(click to see video)Finding Equations Using a Point and the Slope
Given any point on a line and its slope, we can find the equation of that line. Begin by applying the slope formula with a given point and a variable point .

The equation is called the point-slope form of a lineAny nonvertical line can be written in the form , where m is the slope and is any point on the line.. Any nonvertical linear equation can be written in this form. It is useful for finding the equation of a line given the slope and any ordered pair solution.
Example 7: Find the equation of the line with slope passing through (4, −1).
Solution: Use point-slope form, where and .
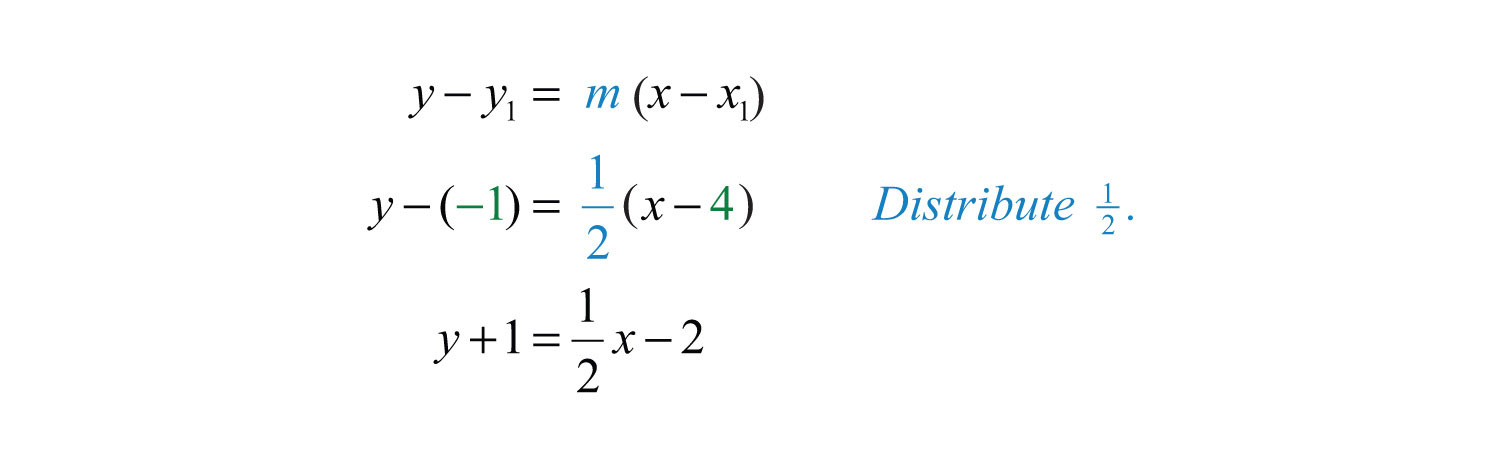
At this point, we must choose to present the equation of our line in either standard form or slope-intercept form.

In this textbook, we will present our lines in slope-intercept form. This facilitates future graphing.
Answer:
Example 8: Find the equation of the line passing through (−5, 3) with slope .
Solution: Substitute (−5, 3) and into point-slope form.
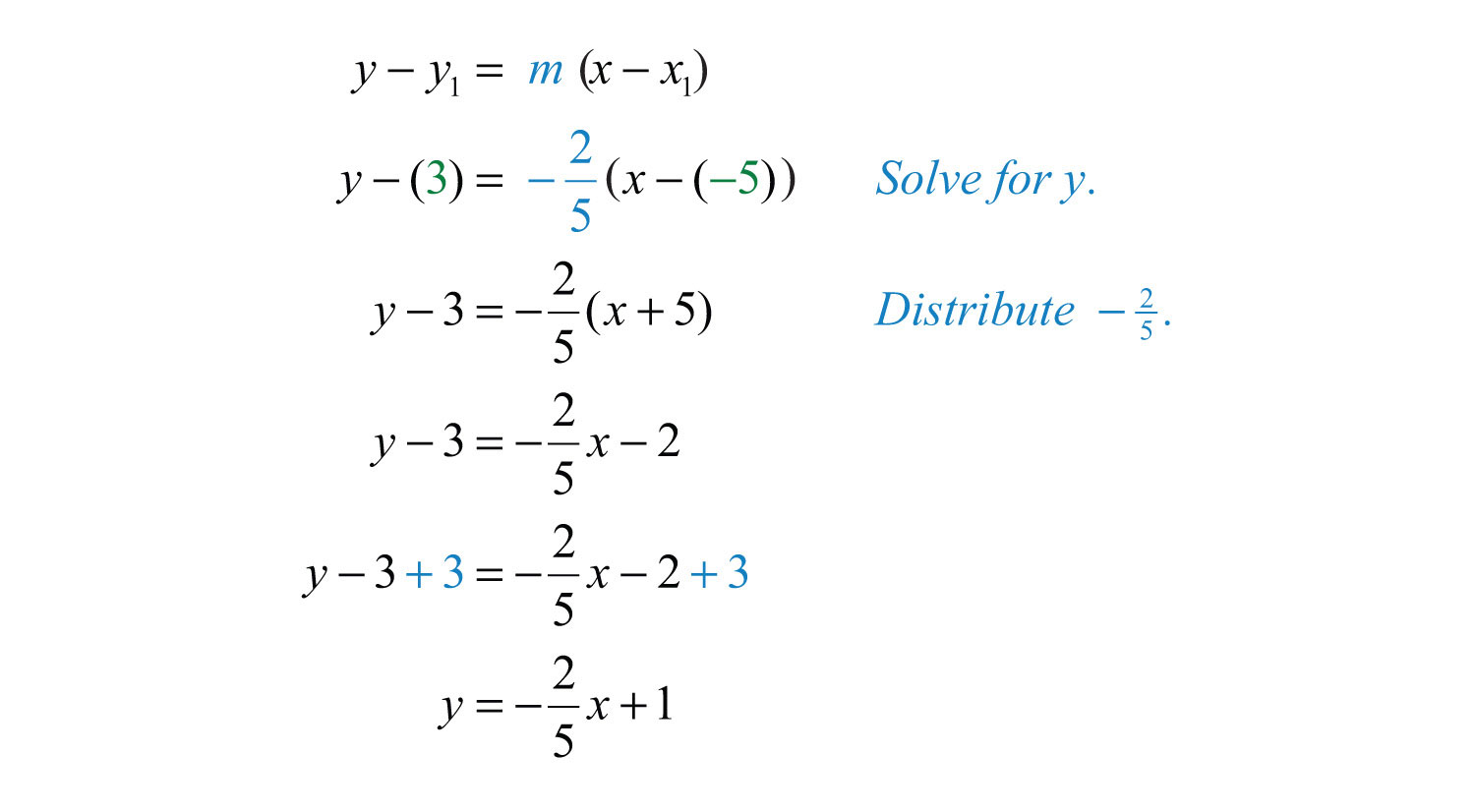
Answer:
It is always important to understand what is occurring geometrically. Compare the answer for the last example to the corresponding graph below.
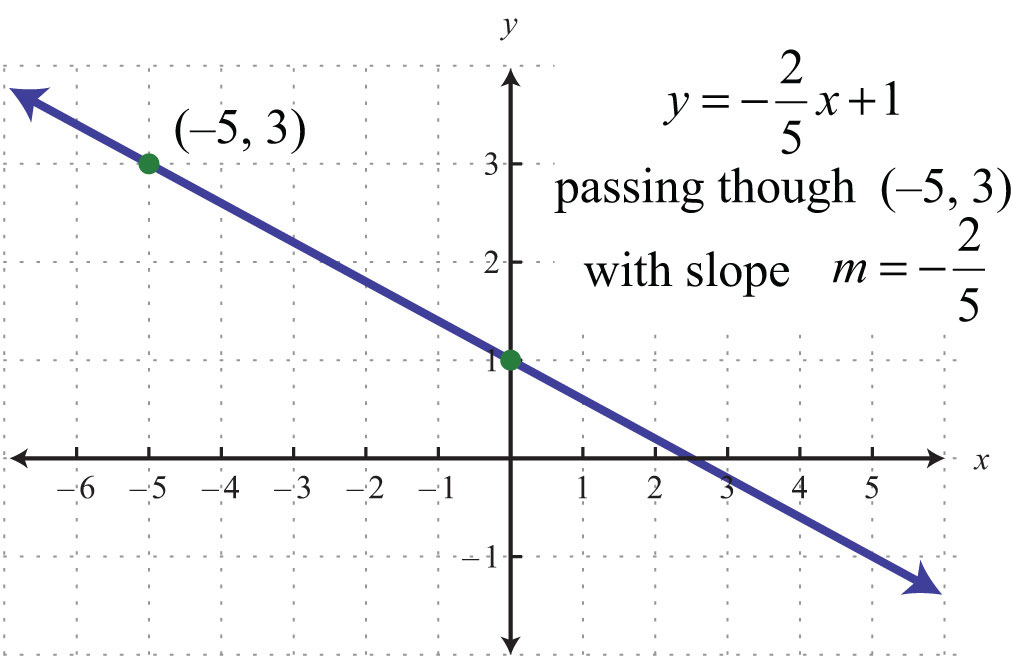
The geometric understanding is important because you will often be given graphs from which you will need to determine a point on the line and the slope.
Example 9: Find an equation of the given graph:

Solution: Between the points (1, 1) to (3, 0), we can see that the rise is −1 unit and the run is 2 units. The slope of the line is . Use this and the point (3, 0) to find the equation as follows:
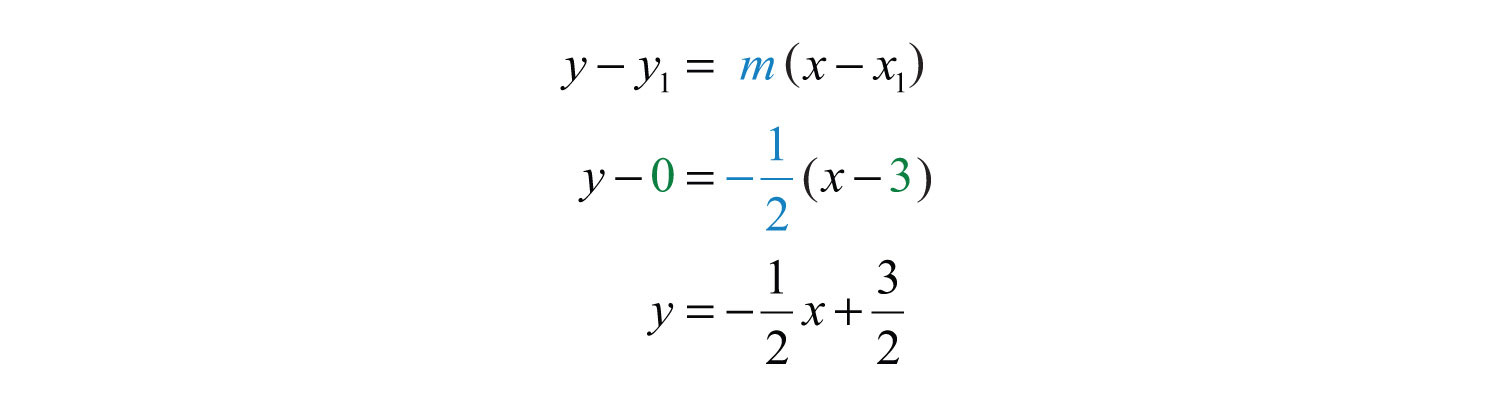
Answer:
Example 10: Find the equation of the line passing through (−1, 1) and (7, −1).
Solution: Begin by calculating the slope using the slope formula.
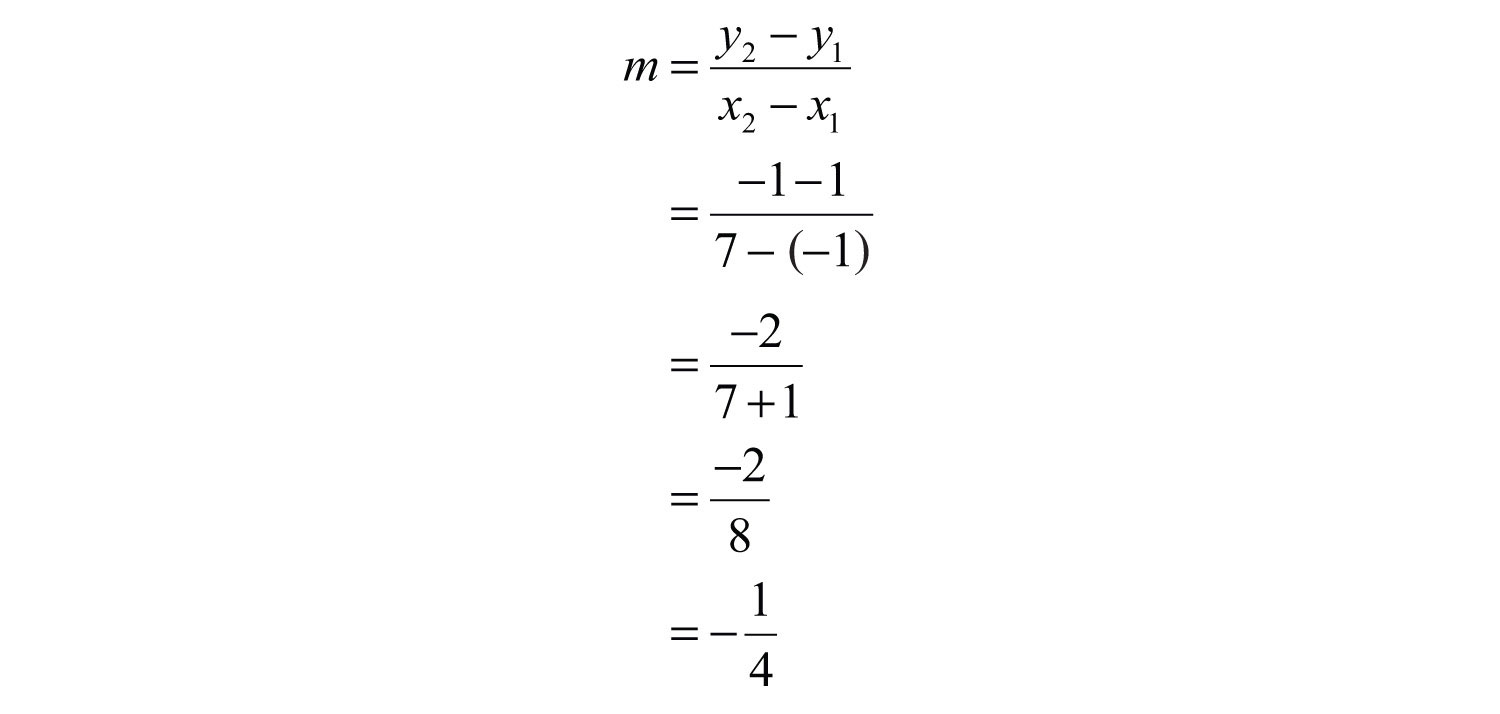
Next, substitute into point-slope form using one of the given points; it does not matter which point is used. Use and the point (−1, 1).
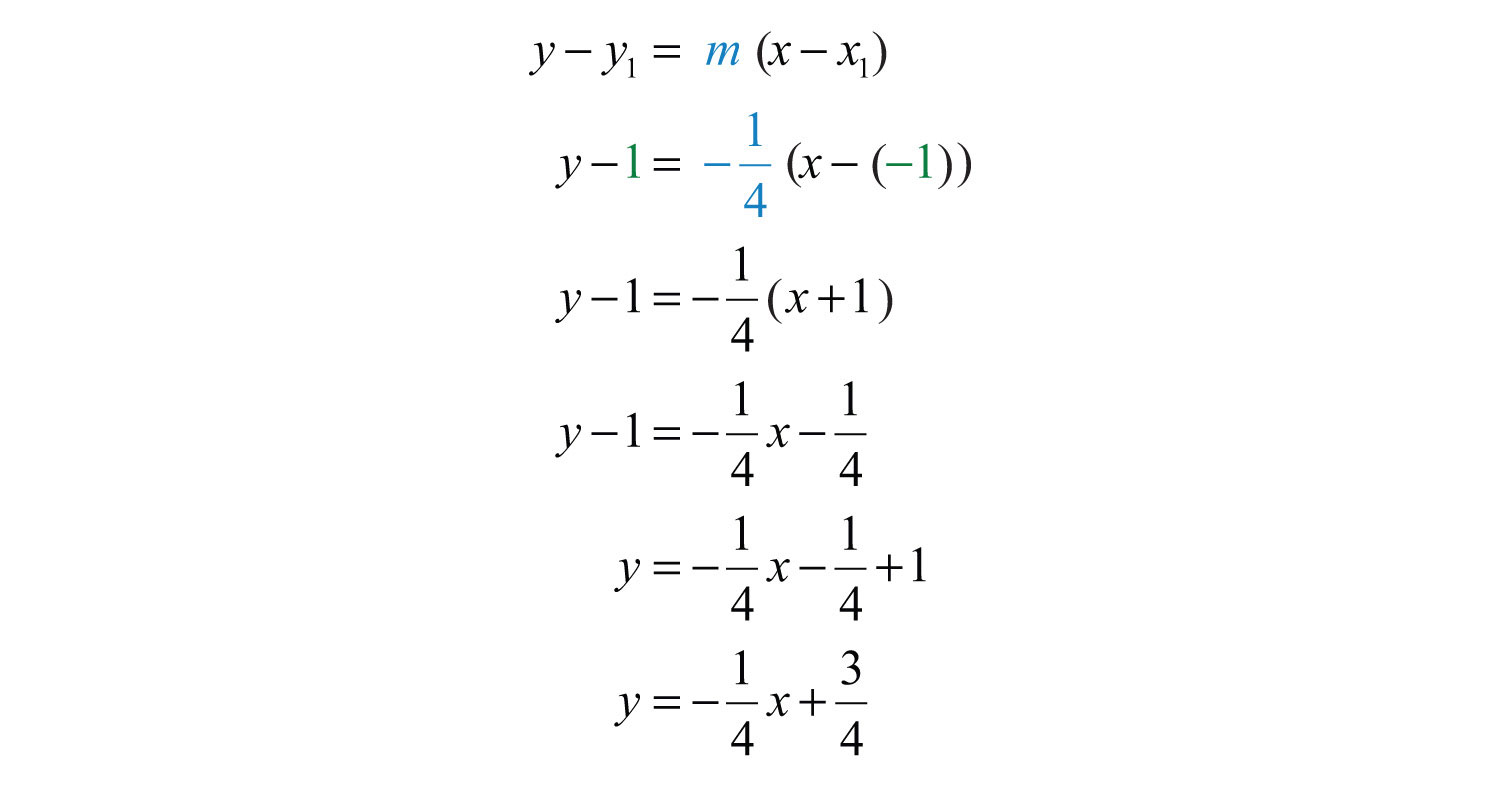
Answer:
Try this! Find the equation of the line passing through (4, −5) and (−4, 1).
Answer:
Video Solution
(click to see video)Key Takeaways
- Given the graph of a line, you can determine the equation in two ways, using slope-intercept form, , or point-slope form, .
- The slope and one point on the line is all that is needed to write the equation of a line.
- All nonvertical lines are completely determined by their y-intercept and slope.
- If the slope and y-intercept can be determined, then it is best to use slope-intercept form to write the equation.
- If the slope and a point on the line can be determined, then it is best to use point-slope form to write the equation.
Topic Exercises
Part A: Slope-Intercept Form
Determine the slope and y-intercept.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
Part B: Finding Equations in Slope-Intercept Form
Given the slope and y-intercept, determine the equation of the line.
13. m = 1/2; (0, 5)
14. m = 4; (0, −1)
15. m = −2/3; (0, −4)
16. m = −3; (0, 9)
17. m = 0; (0, −1)
18. m = 5; (0, 0)
Given the graph, find the equation in slope-intercept form.
19.
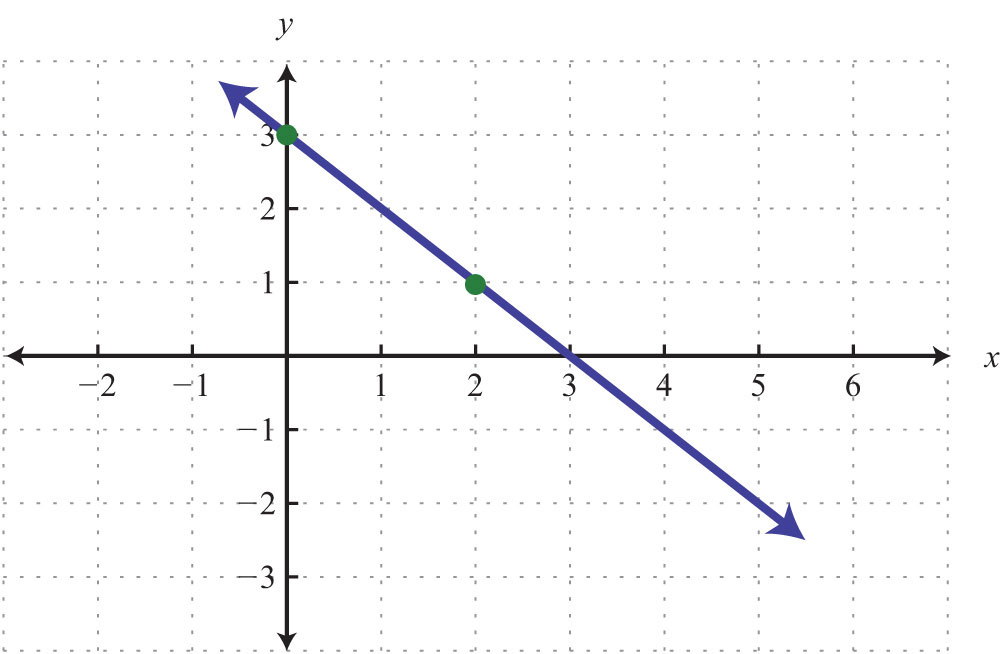
20.
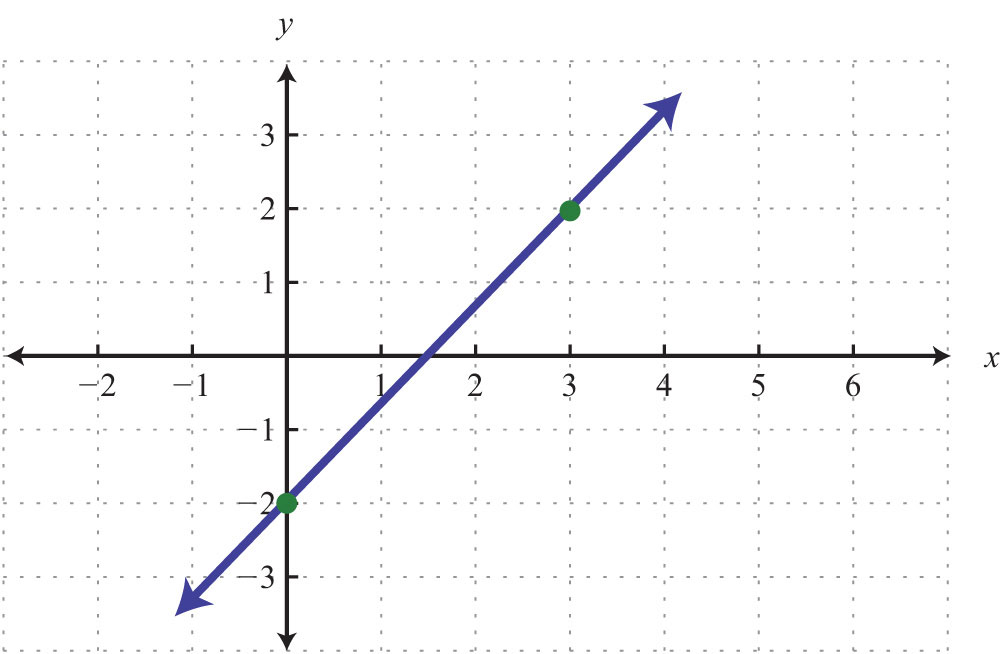
21.
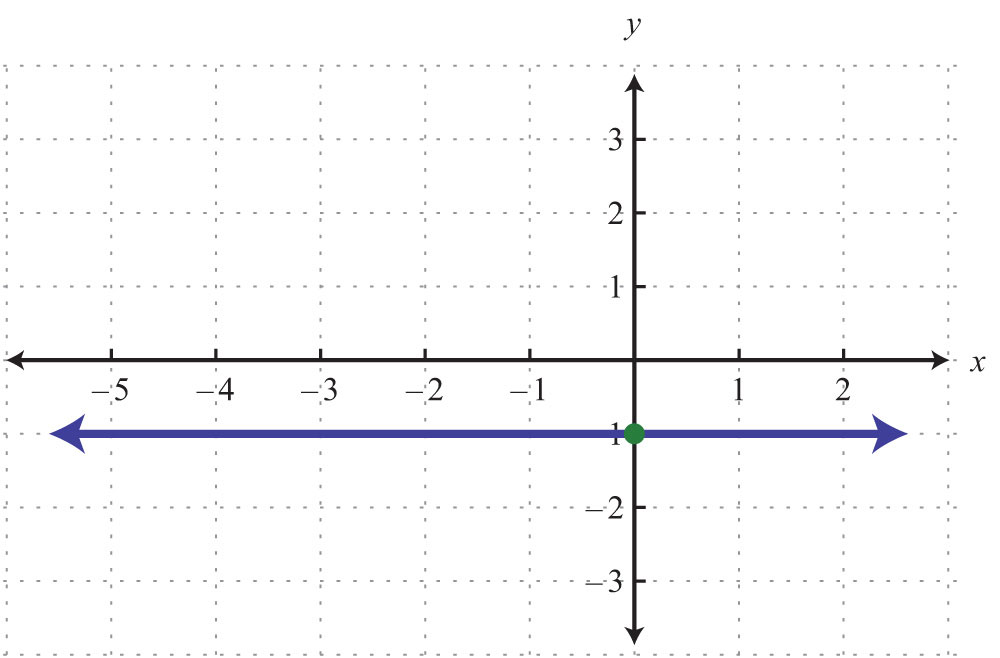
22.
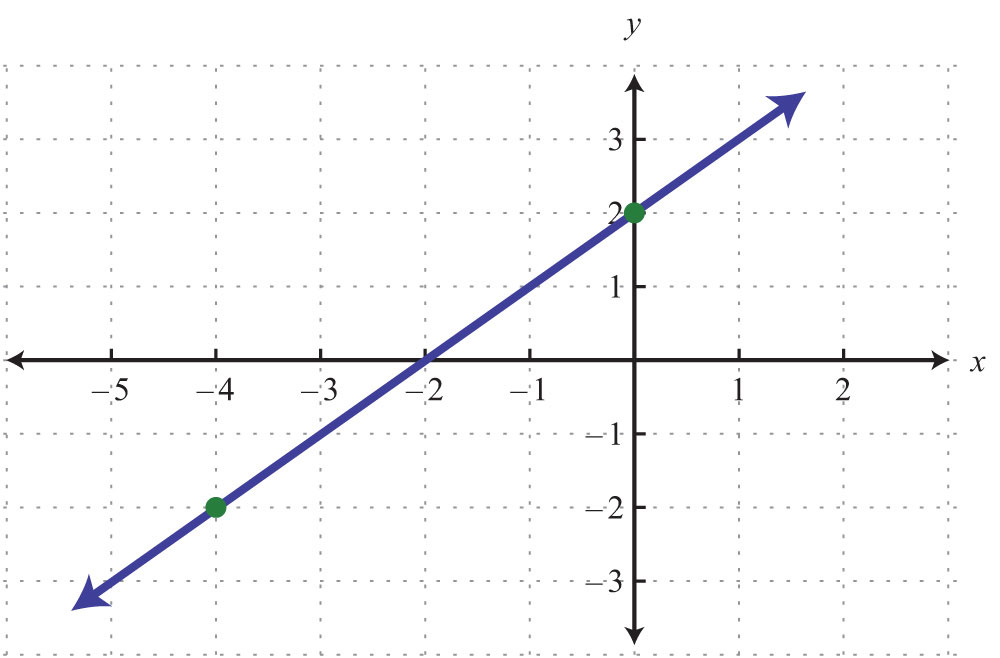
23.
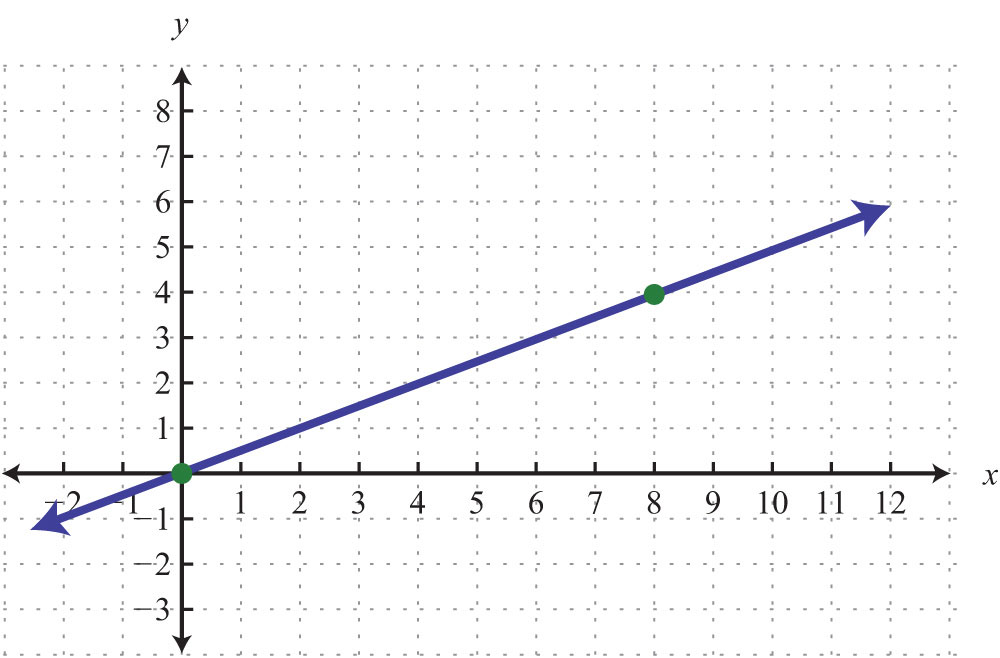
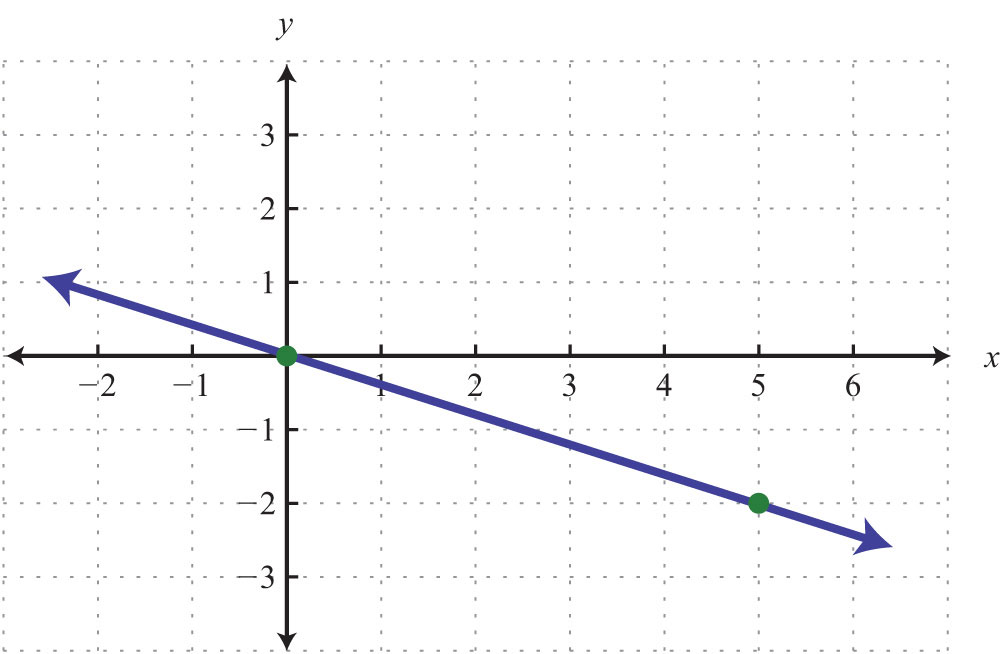
24.
Find the equation, given the slope and a point.
25. m = 2/3; (−9, 2)
26. m = −1/5; (5, −5)
27. m = 0; (−4, 3)
28. m = 3; (−2, 1)
29. m = −5; (−2, 8)
30. m = −4; (1/2, −3/2)
31. m = −1/2; (3, 2)
32. m = 3/4; (1/3, 5/4)
33. m = 0; (3, 0)
34. m undefined; (3, 0)
Given two points, find the equation of the line.
35. (−6, 6), (2, 2)
36. (−10, −3), (5, 0)
37. (0, 1/2), (1/2, −1)
38. (1/3, 1/3), (2/3, 1)
39. (3, −4), (−6, −7)
40. (−5, 2), (3, 2)
41. (−6, 4), (−6, −3)
42. (−4, −4), (−1, −1)
43. (3, −3), (−5, 5)
44. (0, 8), (−4, 0)
Part C: Equations Using Point-Slope Form
Find the equation, given the slope and a point.
45. m = 1/2; (4, 3)
46. m = −1/3; (9, −2)
47. m = 6; (1, −5)
48. m = −10; (1, −20)
49. m = −3; (2, 3)
50. m = 2/3; (−3, −5)
51. m = −3/4; (−8, 3)
52. m = 5; (1/5, −3)
53. m = −3; (−1/9, 2)
54. m = 0; (4, −6)
55. m = 0; (−5, 10)
56. m = 5/8; (4, 3)
57. m = −3/5; (−2, −1)
58. m = 1/4; (12, −2)
59. m = 1; (0, 0)
60. m = −3/4; (0, 0)
Given the graph, use the point-slope formula to find the equation.
61.
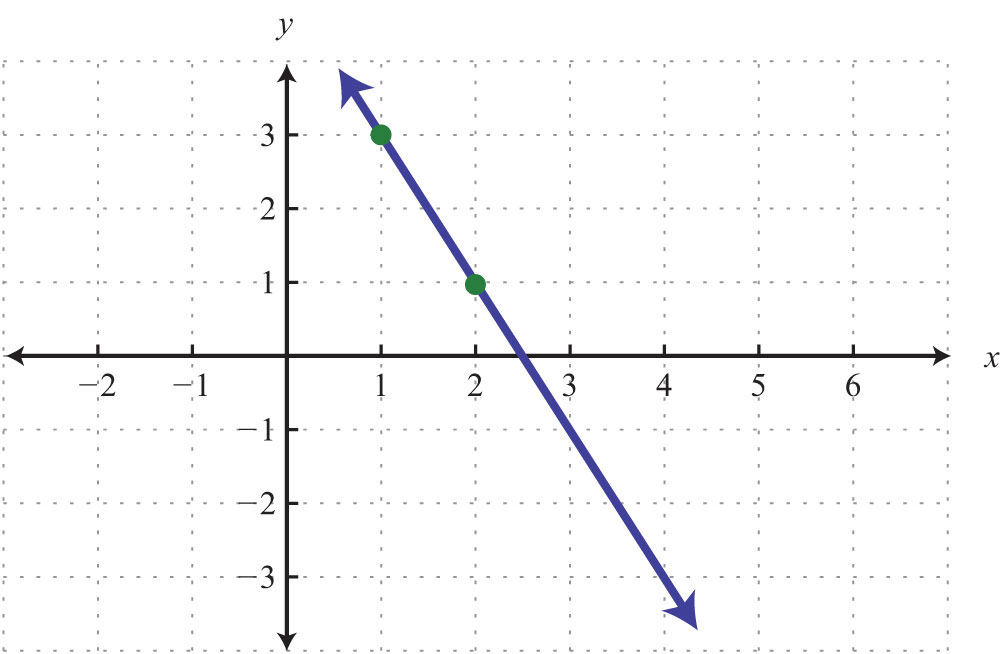
62.
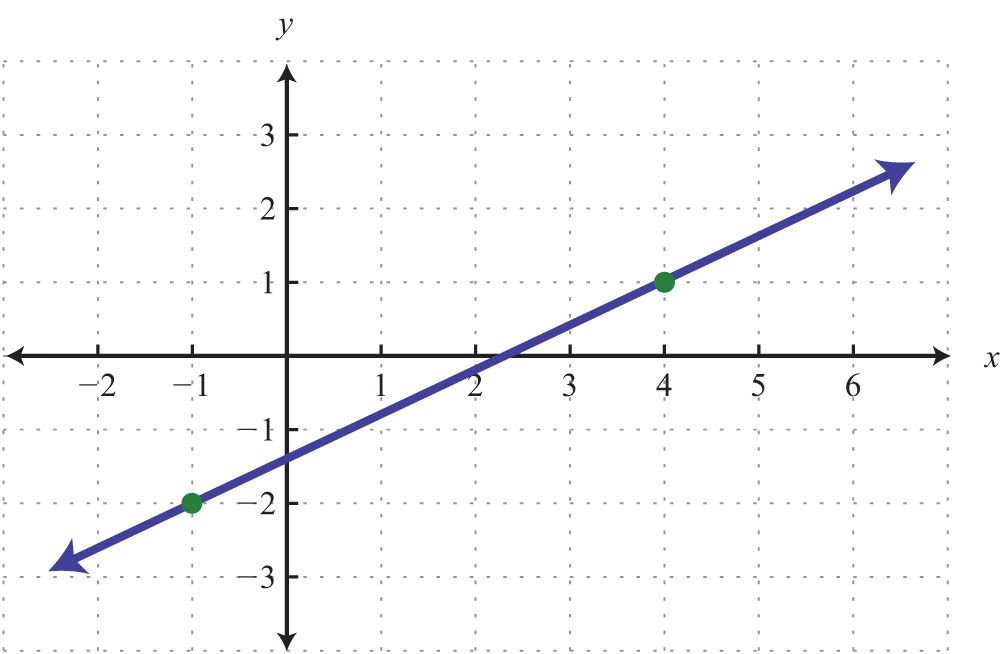
63.
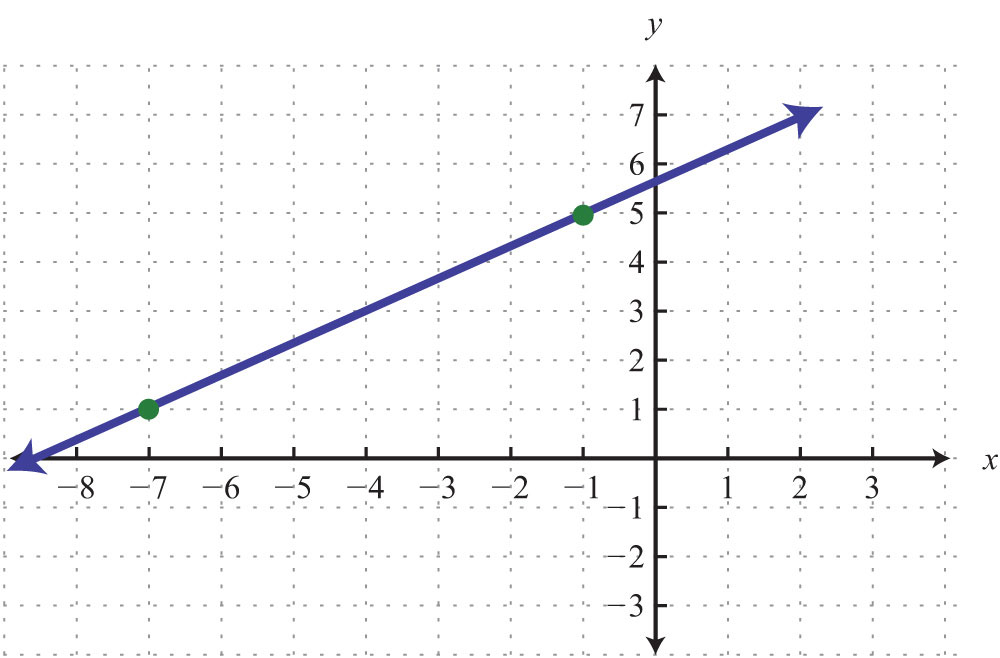
64.
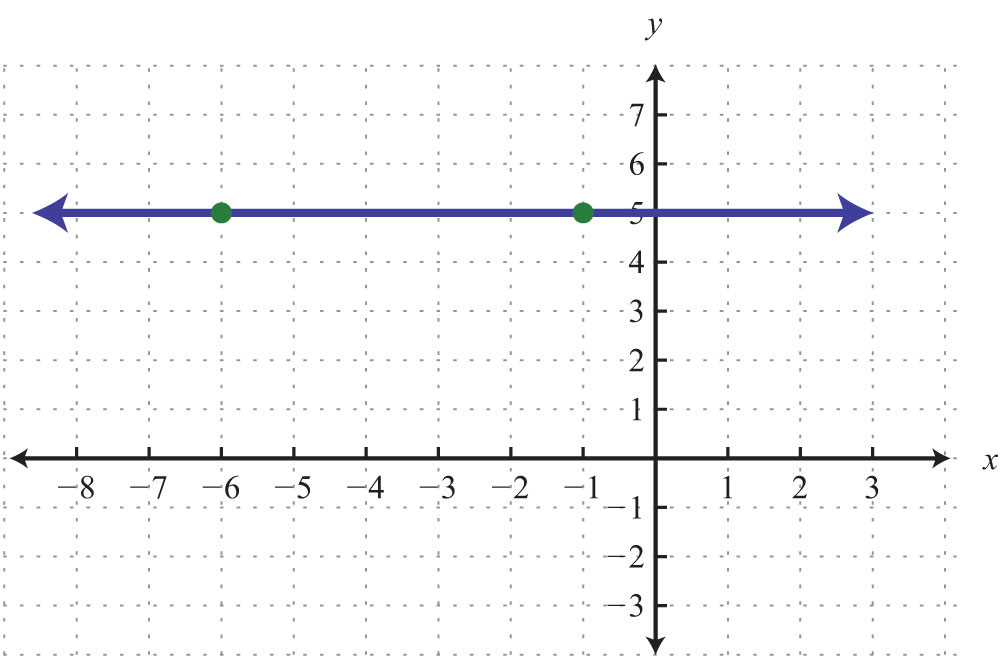
65.
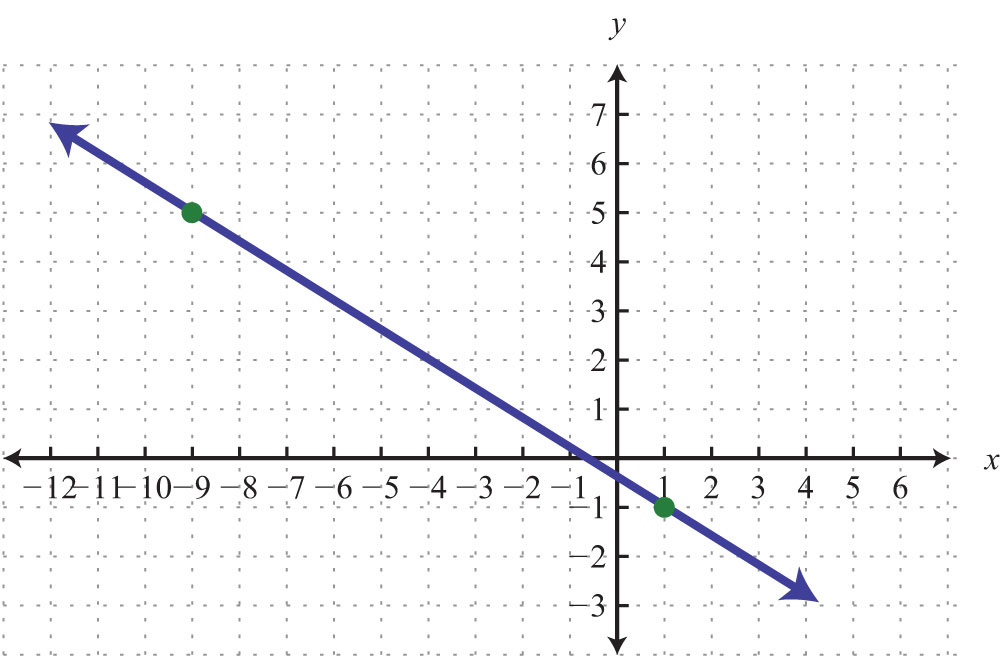
66.
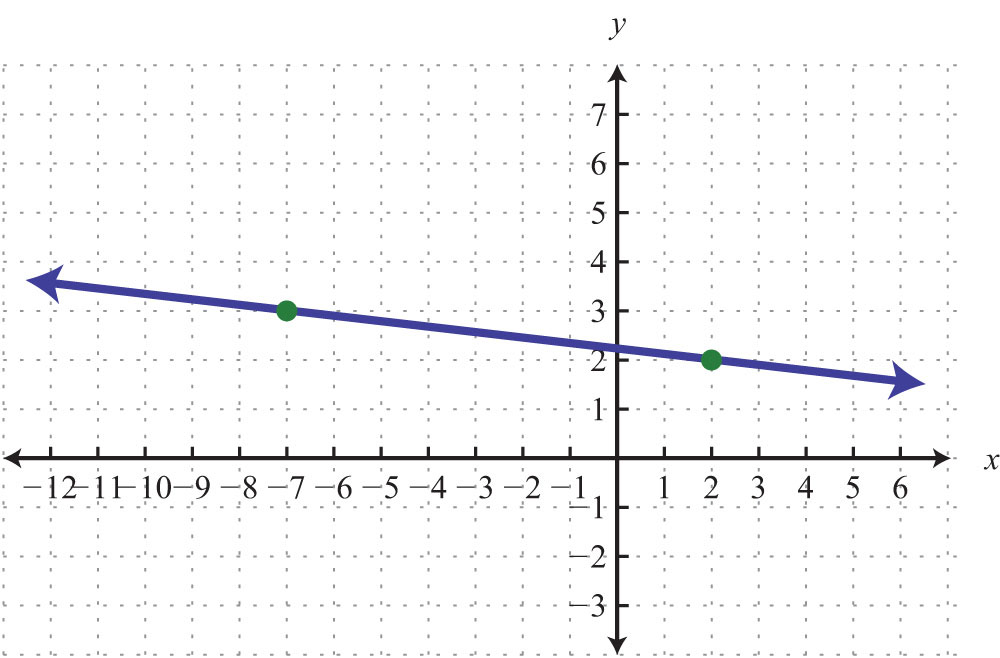
Use the point-slope formula to find the equation of the line passing through the two points.
67. (−4, 0), (0, 5)
68. (−1, 2), (0, 3)
69. (−3, −2), (3, 2)
70. (3, −1), (2, −3)
71. (−2, 4), (2, −4)
72. (−5, −2), (5, 2)
73. (−3, −1), (3, 3)
74. (1, 5), (0, 5)
75. (1, 2), (2, 4)
76. (6, 3), (2, −3)
77. (10, −3), (5, −4)
78. (−3, 3), (−1, 12)
79. (4/5, −1/3), (−1/5, 2/3)
80. (5/3, 1/3), (−10/3, −5/3)
81. (3, −1/4), (4, −1/2)
82. (0, 0), (−5, 1)
83. (2, −4), (0, 0)
84. (3, 5), (3, −2)
85. (−4, 7), (−1, 7)
86. (−8, 0), (6, 0)
Part D: Applications
87. Joe has been keeping track of his cellular phone bills for the last two months. The bill for the first month was $38.00 for 100 minutes of usage. The bill for the second month was $45.50 for 150 minutes of usage. Find a linear equation that gives the total monthly bill based on the minutes of usage.
88. A company in its first year of business produced 150 training manuals for a total cost of $2,350. The following year, the company produced 50 more manuals at a cost of $1,450. Use this information to find a linear equation that gives the total cost of producing training manuals from the number of manuals produced.
89. A corn farmer in California was able to produce 154 bushels of corn per acre 2 years after starting his operation. Currently, after 7 years of operation, he has increased his yield to 164 bushels per acre. Use this information to write a linear equation that gives the total yield per acre based on the number of years of operation, and use it to predict the yield for next year.
90. A Webmaster has noticed that the number of registered users has been steadily increasing since beginning an advertising campaign. Before starting to advertise, he had 1,200 registered users, and after 3 months of advertising he now has 1,590 registered users. Use this data to write a linear equation that gives the total number of registered users, given the number of months after starting to advertise. Use the equation to predict the number of users 7 months into the advertising campaign.
91. A car purchased new cost $22,000 and was sold 10 years later for $7,000. Write a linear equation that gives the value of the car in terms of its age in years.
92. An antique clock was purchased in 1985 for $1,500 and sold at auction in 1997 for $5,700. Determine a linear equation that models the value of the clock in terms of years since 1985.
Part E: Discussion Board Topics
93. Discuss the merits and drawbacks of point-slope form and y-intercept form.
94. Research and discuss linear depreciation. In a linear depreciation model, what do the slope and y-intercept represent?
Answers
1: m = 5/3; (0, −6)
3: m = 1; (0, −5)
5: m = 4/5; (0, −3)
7: m = 0; (0, 3)
9: m = 3/5; (0, 3)
11: m = 4/15; (0, 1/2)
13:
15:
17:
19:
21:
23:
25:
27:
29:
31:
33:
35:
37:
39:
41:
43:
45:
47:
49:
51:
53:
55:
57:
59:
61:
63:
65:
67:
69:
71:
73:
75:
77:
79:
81:
83:
85:
87:
89: ; 166 bushels
91:




