This is “Real Numbers and Their Operations”, chapter 1 from the book Beginning Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
Chapter 1 Real Numbers and Their Operations
1.1 Real Numbers and the Number Line
Learning Objectives
- Construct a number line and graph points on it.
- Use a number line to determine the order of real numbers.
- Determine the opposite of a real number.
- Determine the absolute value of a real number.
Definitions
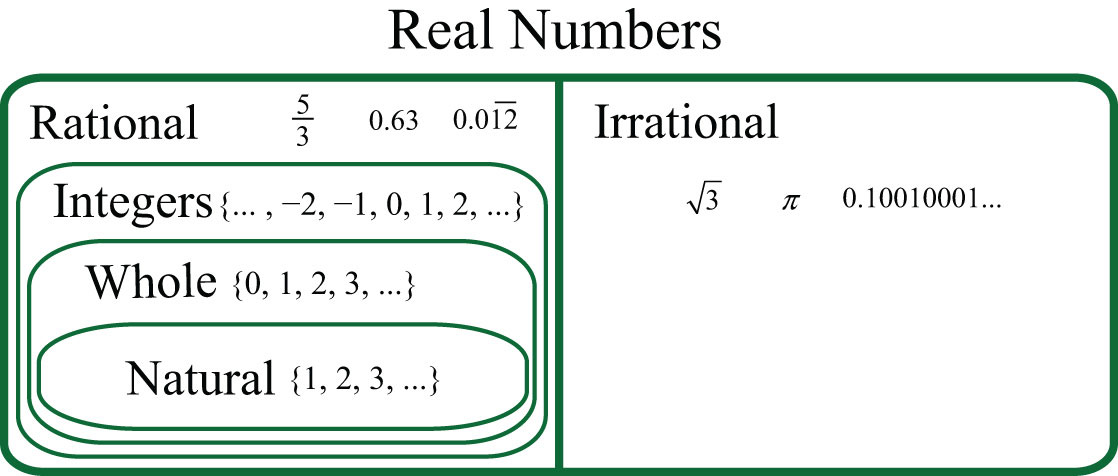
A setAny collection of objects. is a collection of objects, typically grouped within braces { }, where each object is called an elementAn object within a set.. For example, {red, green, blue} is a set of colors. A subsetA set consisting of elements that belong to a given set. is a set consisting of elements that belong to a given set. For example, {green, blue} is a subset of the color set above. A set with no elements is called the empty setA subset with no elements, denoted or { }. and has its own special notation, { } or ∅.
When studying mathematics, we focus on special sets of numbers. The set of natural (or counting) numbersThe set of counting numbers {1, 2, 3, 4, 5, …}., denoted N, is
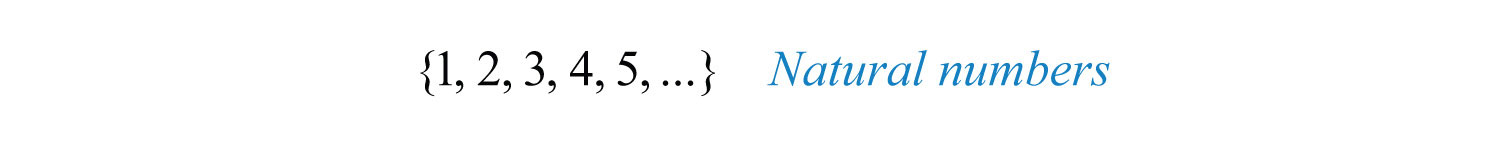
The three periods (…) is called an ellipsis and indicates that the numbers continue without bound. The set of whole numbersThe set of natural numbers combined with zero {0, 1, 2, 3, 4, 5, …}., denoted , is the set of natural numbers combined with zero.
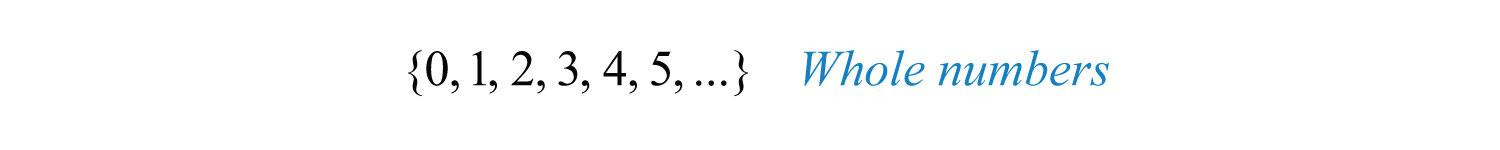
The set of integersThe set of positive and negative whole numbers combined with zero {…, −3, −2, −1, 0, 1, 2, 3, …}., denoted Z, consists of both positive and negative whole numbers, as well as zero.
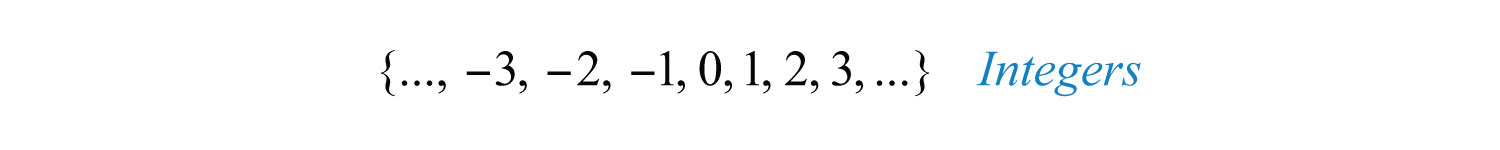
Notice that the sets of natural and whole numbers are both subsets of the set of integers.
Rational numbersNumbers of the form , where a and b are integers and b is nonzero., denoted Q, are defined as any number of the form , where a and b are integers and b is nonzero. Decimals that repeat or terminate are rational. For example,
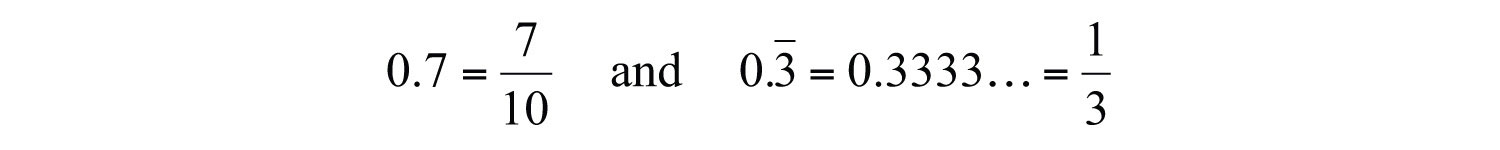
The set of integers is a subset of the set of rational numbers because every integer can be expressed as a ratio of the integer and 1. In other words, any integer can be written over 1 and can be considered a rational number. For example,
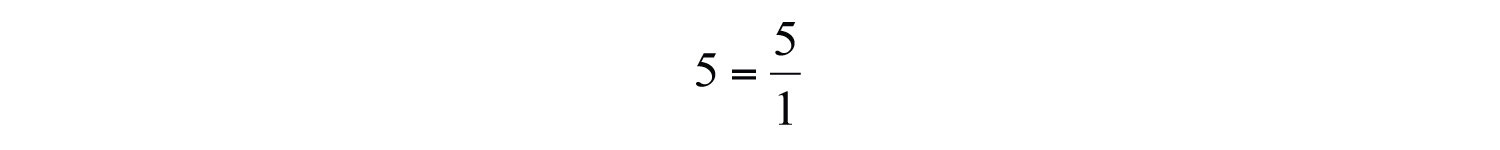
Irrational numbersNumbers that cannot be written as a ratio of two integers. are defined as any number that cannot be written as a ratio of two integers. Nonterminating decimals that do not repeat are irrational. For example,
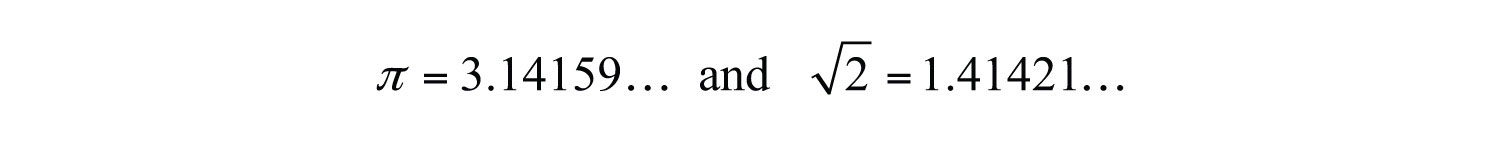
The set of real numbersThe set of all rational and irrational numbers., denoted R, is defined as the set of all rational numbers combined with the set of all irrational numbers. Therefore, all the numbers defined so far are subsets of the set of real numbers. In summary,
Number Line
A real number lineA line that allows us to visually represent real numbers by associating them with points on the line., or simply number line, allows us to visually display real numbers by associating them with unique points on a line. The real number associated with a point is called a coordinateThe real number associated with a point on a number line.. A point on the real number line that is associated with a coordinate is called its graphA point on the number line associated with a coordinate..
To construct a number line, draw a horizontal line with arrows on both ends to indicate that it continues without bound. Next, choose any point to represent the number zero; this point is called the originThe point on the number line that represtents zero..
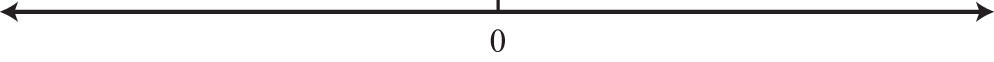
Mark off consistent lengths on both sides of the origin and label each tick mark to define the scale. Positive real numbers lie to the right of the origin and negative real numbers lie to the left. The number zero (0) is neither positive nor negative. Typically, each tick represents one unit.
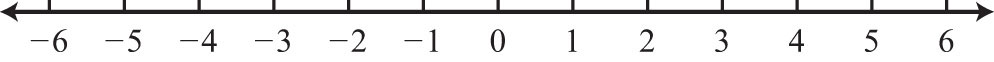
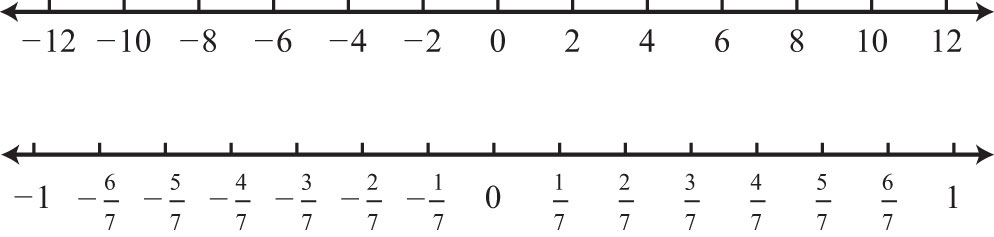
As illustrated below, the scale need not always be one unit. In the first number line, each tick mark represents two units. In the second, each tick mark represents .
The graph of each real number is shown as a dot at the appropriate point on the number line. A partial graph of the set of integers Z follows:

Example 1: Graph the following set of real numbers: .
Solution: Graph the numbers on a number line with a scale where each tick mark represents unit.

Ordering Real Numbers
When comparing real numbers on a number line, the larger number will always lie to the right of the smaller one. It is clear that 15 is greater than 5, but it may not be so clear to see that −1 is greater than −5 until we graph each number on a number line.

We use symbols to help us efficiently communicate relationships between numbers on the number line. The symbols used to describe an equality relationshipExpress equality with the symbol =. If two quantities are not equal, use the symbol . between numbers follow:
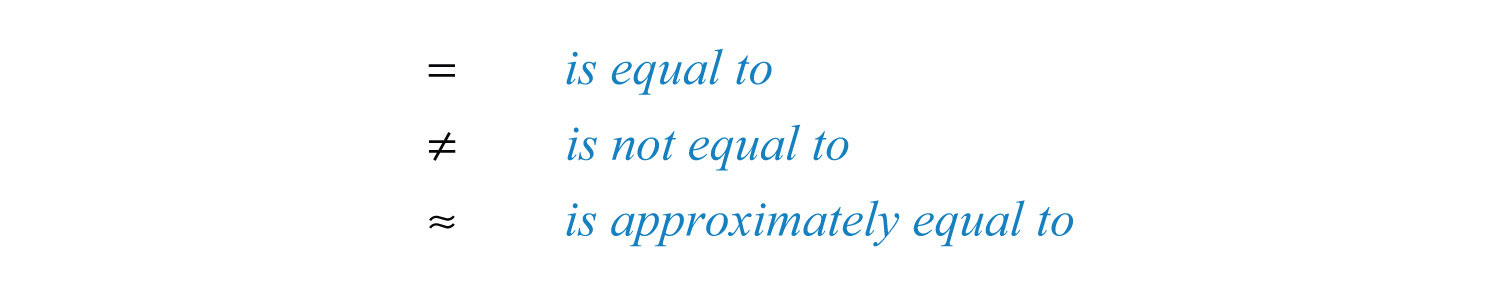
These symbols are used and interpreted in the following manner:

We next define symbols that denote an order relationship between real numbers.
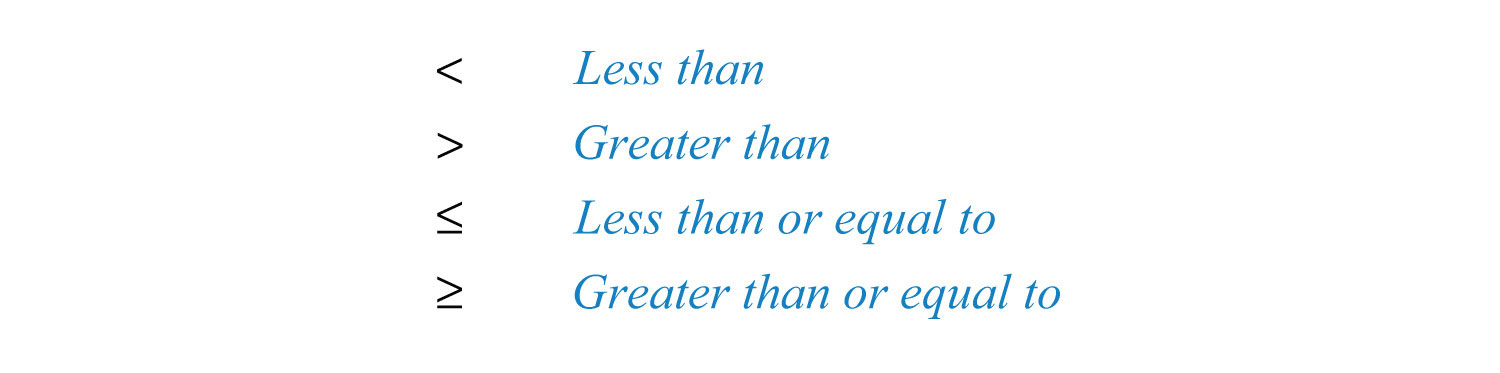
These symbols allow us to compare two numbers. For example,

Since the graph of −120 is to the left of the graph of –10 on the number line, that number is less than −10. We could write an equivalent statement as follows:
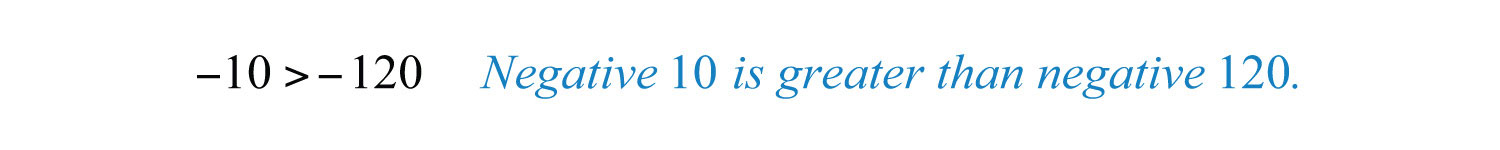
Similarly, since the graph of zero is to the right of the graph of any negative number on the number line, zero is greater than any negative number.

The symbols < and > are used to denote strict inequalitiesExpress ordering relationships using the symbol < for “less than” and > for “greater than.”, and the symbols and are used to denote inclusive inequalitiesUse the symbol to express quantities that are “less than or equal to” and for quantities that are “greater than or equal to” each other.. In some situations, more than one symbol can be correctly applied. For example, the following two statements are both true:
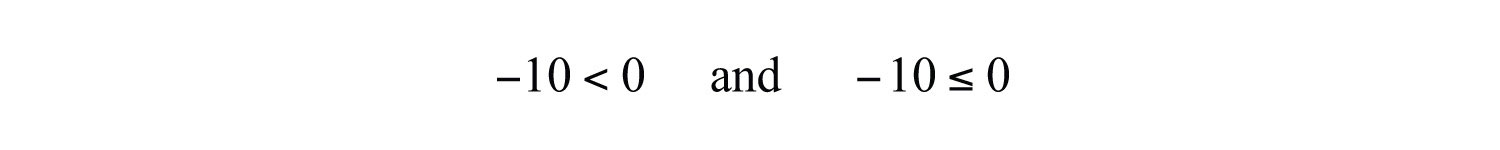
In addition, the “or equal to” component of an inclusive inequality allows us to correctly write the following:
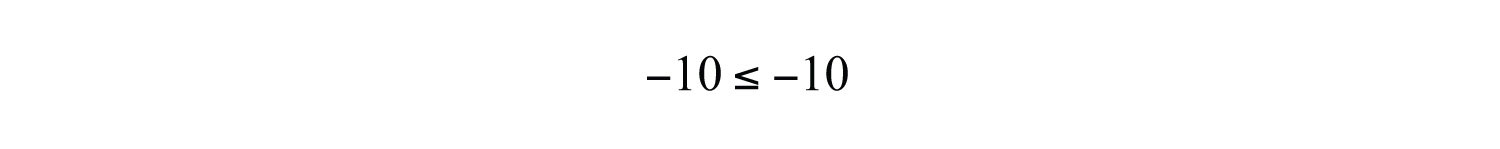
The logical use of the word “or” requires that only one of the conditions need be true: the “less than” or the “equal to.”
Example 2: Fill in the blank with <, =, or >: −2 ____ −12.
Solution: Use > because the graph of −2 is to the right of the graph of −12 on a number line. Therefore, −2 > −12, which reads “negative two is greater than negative twelve.”
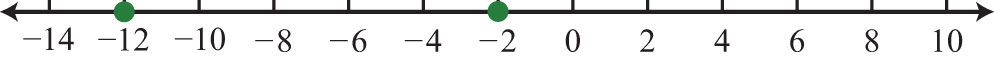
Answer: −2 > −12
In this text, we will often point out the equivalent notation used to express mathematical quantities electronically using the standard symbols available on a keyboard. We begin with the equivalent textual notation for inequalities:
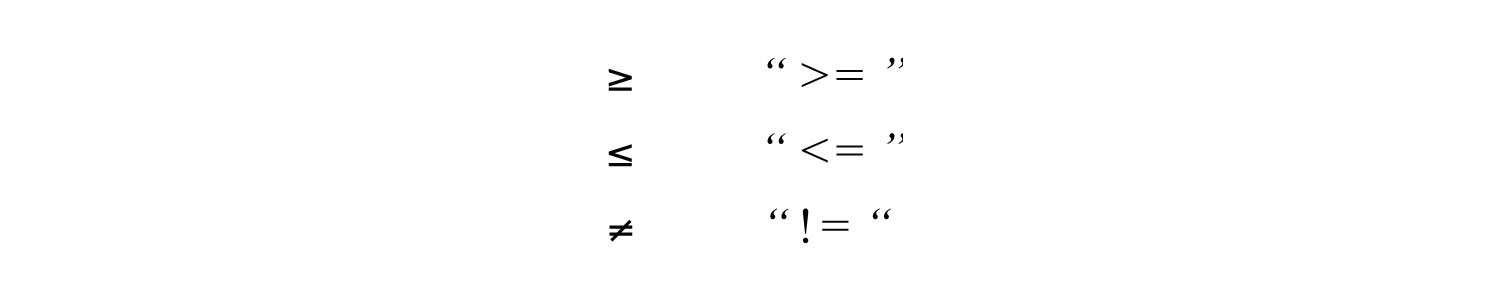
Many calculators, computer algebra systems, and programming languages use this notation.
Opposites
The oppositeReal numbers whose graphs are on opposite sides of the origin with the same distance to the origin. of any real number a is −a. Opposite real numbers are the same distance from the origin on a number line, but their graphs lie on opposite sides of the origin and the numbers have opposite signs.
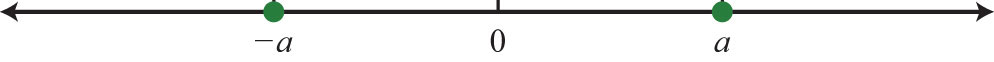
For example, we say that the opposite of 10 is −10.
Next, consider the opposite of a negative number. Given the integer −7, the integer the same distance from the origin and with the opposite sign is +7, or just 7.

Therefore, we say that the opposite of −7 is −(−7) = 7. This idea leads to what is often referred to as the double-negative propertyThe opposite of a negative number is positive: −(−a) = a.. For any real number a,
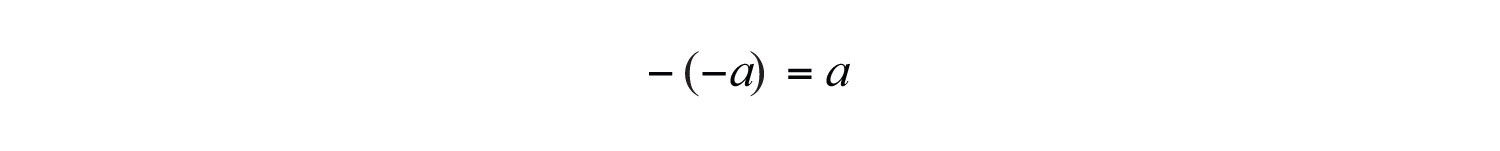
Example 3: What is the opposite of ?
Solution: Here we apply the double-negative property.
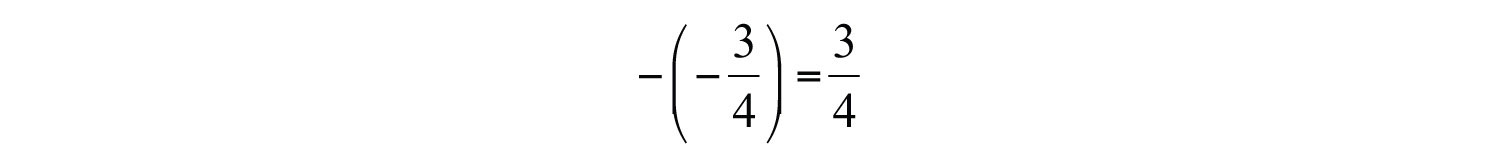
Answer:
Example 4: Simplify: .
Solution: Start with the innermost parentheses by finding the opposite of +4.
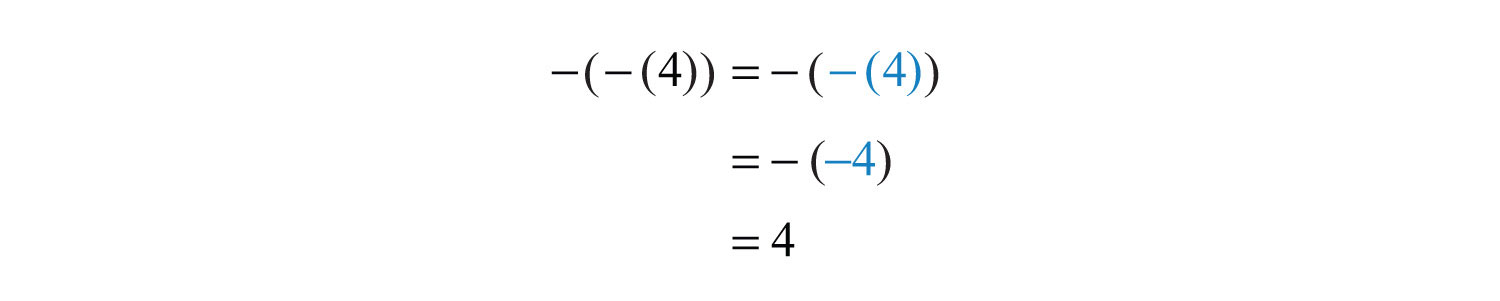
Answer: 4
Example 5: Simplify: .
Solution: Apply the double-negative property starting with the innermost parentheses.
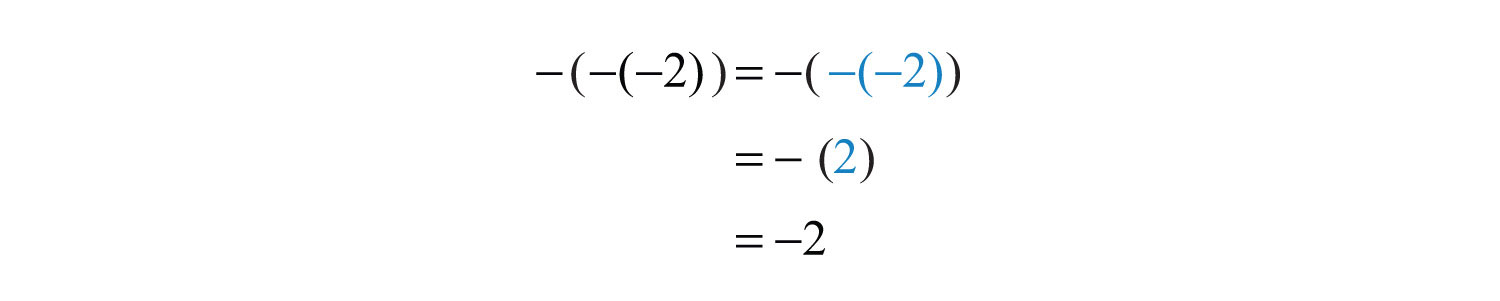
Answer: −2
Tip
If there is an even number of consecutive negative signs, then the result is positive. If there is an odd number of consecutive negative signs, then the result is negative.
Try this! Simplify: .
Answer: −5
Video Solution
(click to see video)Absolute Value
The absolute valueThe absolute value of a number is the distance from the graph of the number to zero on a number line. of a real number a, denoted , is defined as the distance between zero (the origin) and the graph of that real number on the number line. Since it is a distance, it is always positive. For example,
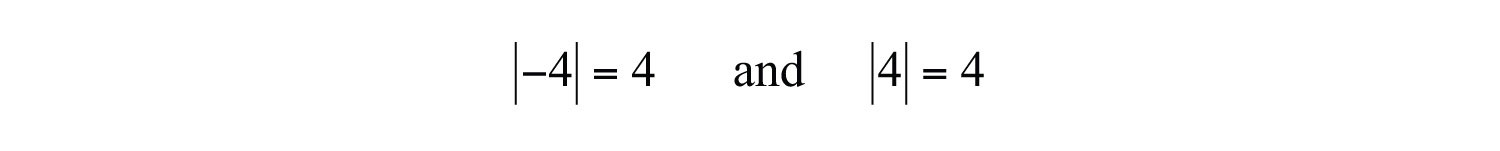
Both 4 and −4 are four units from the origin, as illustrated below:

Example 6: Simplify:
a.
b.
Solution: Both −12 and 12 are twelve units from the origin on a number line. Therefore,
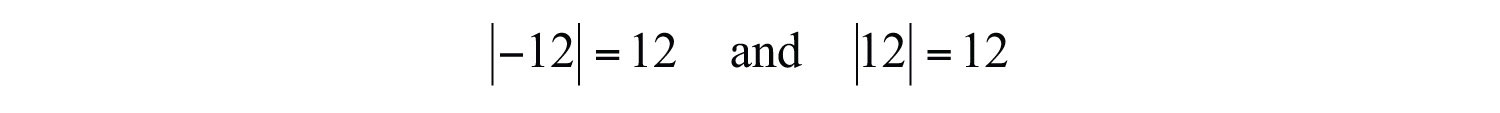
Answers: a. 12; b. 12
Also, it is worth noting that
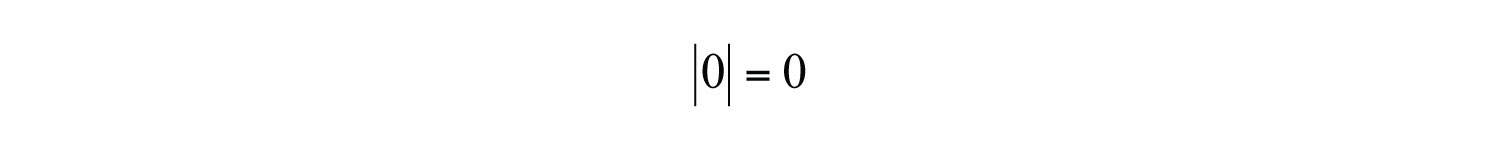
The absolute value can be expressed textually using the notation abs(a). We often encounter negative absolute values, such as or −abs(3). Notice that the negative sign is in front of the absolute value symbol. In this case, work the absolute value first and then find the opposite of the result.
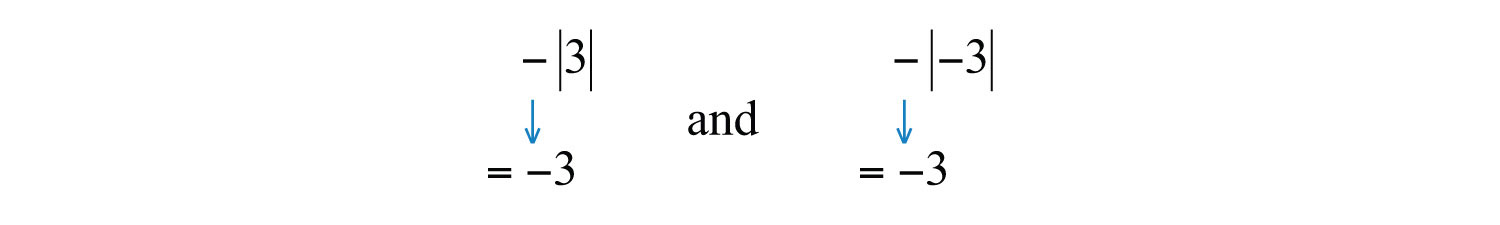
Try not to confuse this with the double-negative property, which states that .
Example 7: Simplify: .
Solution: First, find the opposite of −7 inside the absolute value. Then find the opposite of the result.
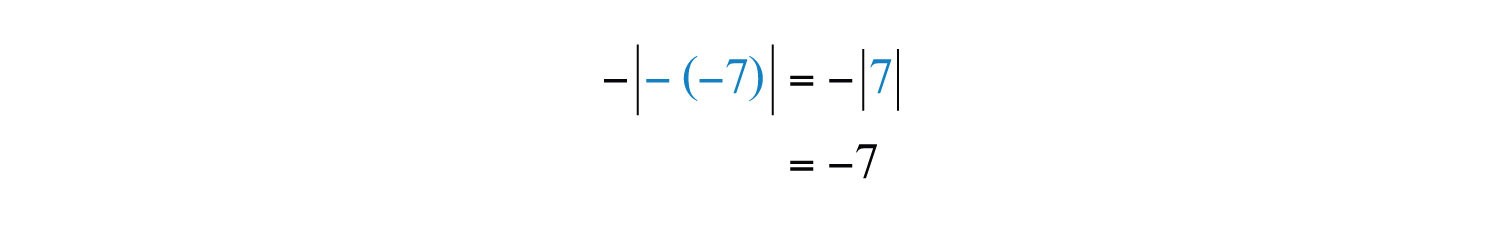
Answer: −7
At this point, we can determine what real numbers have a particular absolute value. For example,
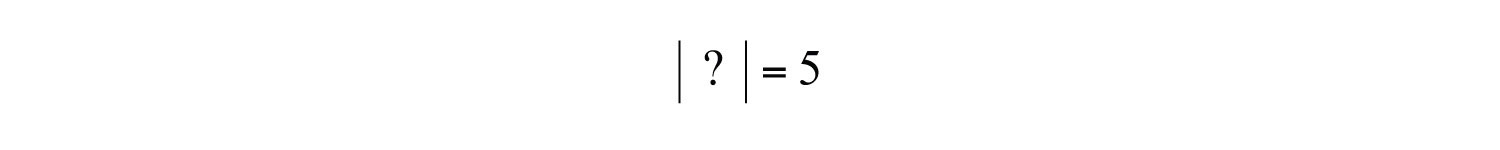
Think of a real number whose distance to the origin is 5 units. There are two solutions: the distance to the right of the origin and the distance to the left of the origin, namely, . The symbol (±) is read “plus or minus” and indicates that there are two answers, one positive and one negative.
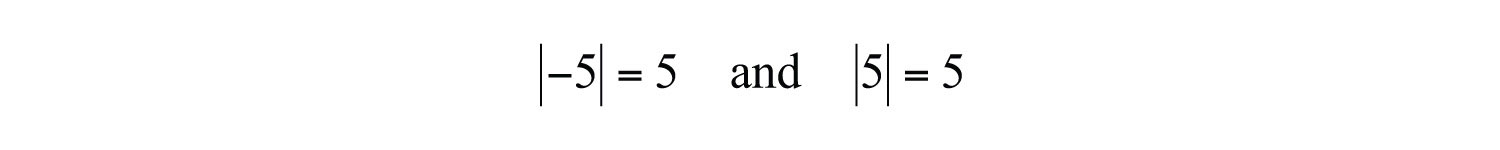
Now consider the following:
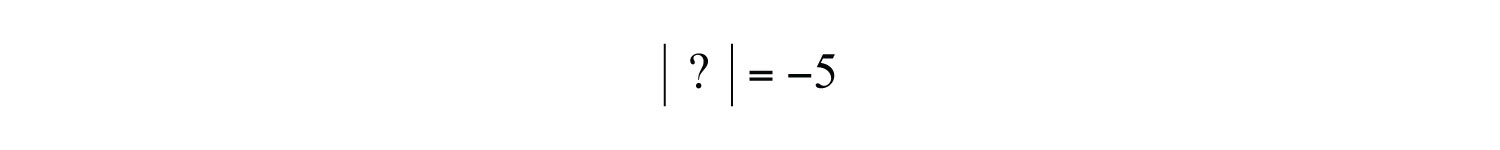
Here we wish to find a value for which the distance to the origin is negative. Since negative distance is not defined, this equation has no solution. If an equation has no solution, we say the solution is the empty set: Ø.
Key Takeaways
- Any real number can be associated with a point on a line.
- Create a number line by first identifying the origin and marking off a scale appropriate for the given problem.
- Negative numbers lie to the left of the origin and positive numbers lie to the right.
- Smaller numbers always lie to the left of larger numbers on the number line.
- The opposite of a positive number is negative and the opposite of a negative number is positive.
- The absolute value of any real number is always positive because it is defined to be the distance from zero (the origin) on a number line.
- The absolute value of zero is zero.
Topic Exercises
Part A: Real Numbers
Use set notation to list the described elements.
1. The hours on a clock.
2. The days of the week.
3. The first ten whole numbers.
4. The first ten natural numbers.
5. The first five positive even integers.
6. The first five positive odd integers.
Determine whether the following real numbers are integers, rational, or irrational.
7.
8. −3
9. 4.5
10. −5
11.
12.
13.
14.
15.
16.
17. −7
18. 3.14
19.
20. 1.33
21. 0
22. 8,675,309
True or false.
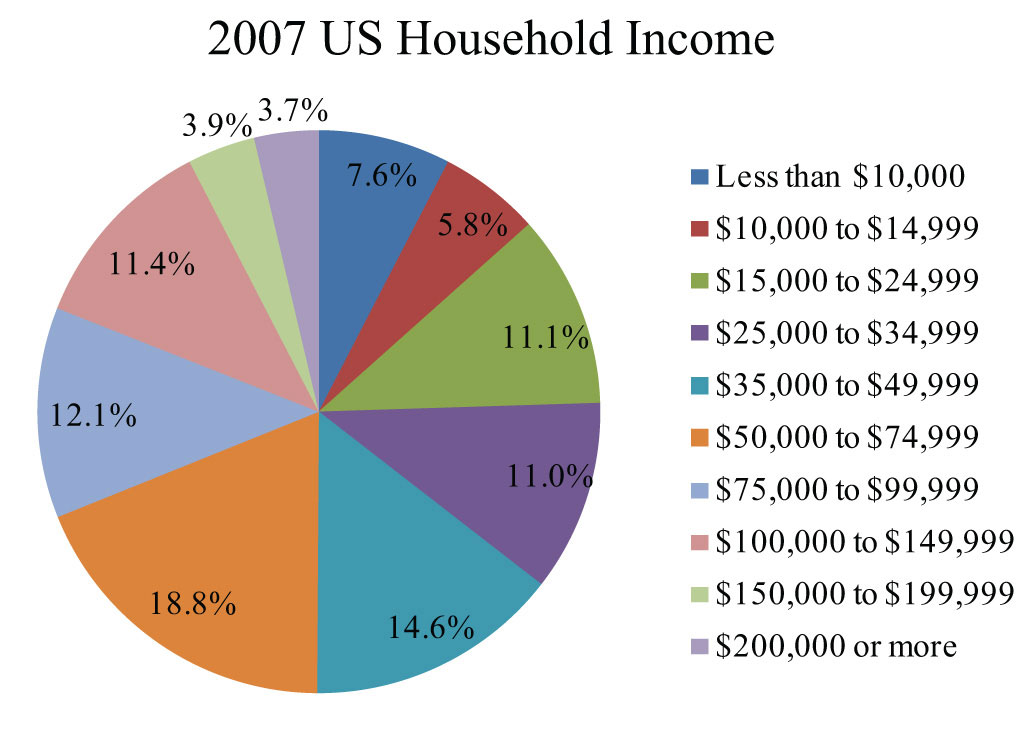
23. All integers are rational numbers.
24. All integers are whole numbers.
25. All rational numbers are whole numbers.
26. Some irrational numbers are rational.
27. All terminating decimal numbers are rational.
28. All irrational numbers are real.
Part B: Real Number Line
Choose an appropriate scale and graph the following sets of real numbers on a number line.
29. {−3, 0 3}
30. {−2, 2, 4, 6, 8, 10}
31.
32.
33.
34.
35.
36. {−2.5, −1.5, 0, 1, 2.5}
37. {0, 0.3, 0.6, 0.9, 1.2}
38. {−10, 30, 50}
39. {−6, 0, 3, 9, 12}
40. {−15, −9, 0, 9, 15}
Part C: Ordering Real Numbers
Fill in the blank with <, =, or >.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
True or false.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61. List three integers less than −5.
62. List three integers greater than −10.
63. List three rational numbers less than zero.
64. List three rational numbers greater than zero.
65. List three integers between −20 and −5.
66. List three rational numbers between 0 and 1.
Translate each statement into an English sentence.
67.
68.
69.
70.
71.
72.
Translate the following into a mathematical statement.
73. Negative seven is less than zero.
74. Twenty-four is not equal to ten.
75. Zero is greater than or equal to negative one.
76. Four is greater than or equal to negative twenty-one.
77. Negative two is equal to negative two.
78. Negative two thousand is less than negative one thousand.
Part D: Opposites
Simplify.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90. What is the opposite of
91. What is the opposite of ?
92. What is the opposite −0.01?
93. Is the opposite of −12 smaller or larger than −11?
94. Is the opposite of 7 smaller or larger than −6?
Fill in the blank with <, =, or >.
95.
96.
97.
98.
99.
100.
Part E: Absolute Value
Simplify.
101.
102.
103.
104.
105.
106.
107.
108.
109.
110.
111.
112.
113.
114.
115.
116.
117.
118.
119.
120.
121. abs(6)
122. abs(−7)
123. −abs(5)
124. −abs(−19)
125. − (−abs(9))
126. −abs(−(−12))
Determine the unknown.
127.
128.
129.
130.
131.
132.
133.
134.
Fill in the blank with <, , or >.
135.
136.
137.
138.
139.
140.
Part F: Discussion Board Topics
141. Research and discuss the history of the number zero.
142. Research and discuss the various numbering systems throughout history.
143. Research and discuss the definition and history of .
144. Research the history of irrational numbers. Who is credited with proving that the square root of 2 is irrational and what happened to him?
145. Research and discuss the history of absolute value.
146. Discuss the “just make it positive” definition of absolute value.
Answers
1: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
3: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
5: {2, 4, 6, 8, 10}
7: Rational
9: Rational
11: Rational
13: Irrational
15: Irrational
17: Integer, Rational
19: Rational
21: Integer, Rational
23: True
25: False
27: True
29:

31:

33:

35:

37:

39:

41: <
43: >
45: >
47: <
49: =
51: True
53: False
55: True
57: True
59: True
61: −10, −7, −6 (answers may vary)
63: −1, −2/3, −1/3 (answers may vary)
65: −15, −10, −7 (answers may vary)
67: Ten is less than twenty.
69: Negative four is not equal to zero.
71: Zero is equal to zero.
73:
75:
77:
79: 9
81: −10
83: −5
85: 1
87: 1
89: 11
91:
93: Larger
95: <
97: >
99: <
101: 20
103: 33
105: 2/5
107: 0
109: −12
111: −20
113: −7
115: 8/9
117: −3
119: 45
121: 6
123: −5
125: 9
127:
129: 0
131: Ø, No solution
133:
135: >
137: <
139: <
1.2 Adding and Subtracting Integers
Learning Objectives
- Add and subtract signed integers.
- Translate English sentences involving addition and subtraction into mathematical statements.
- Calculate the distance between two numbers on a number line.
Addition and Subtraction (+, −)
Visualize adding 3 + 2 on the number line by moving from zero three units to the right then another two units to the right, as illustrated below:

The illustration shows that 3 + 2 = 5. Similarly, visualize adding two negative numbers (−3) + (−2) by first moving from the origin three units to the left and then moving another two units to the left.

In this example, the illustration shows (−3) + (−2) = −5, which leads to the following two properties of real numbers.
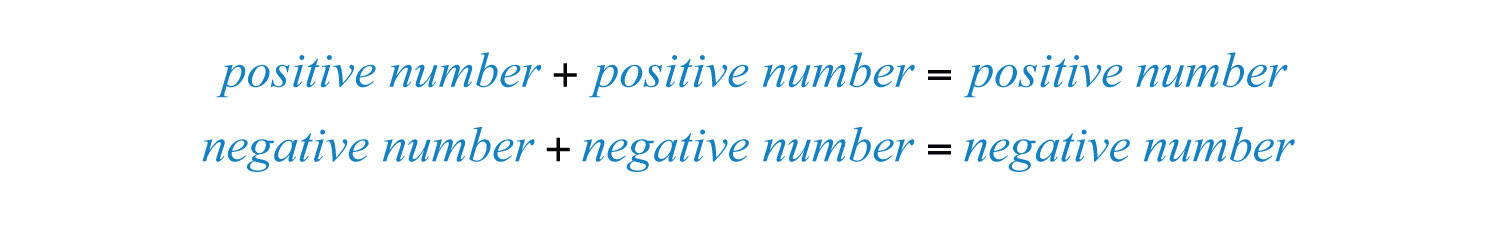
Next, we will explore addition of numbers with unlike signs. To add 3 + (−7), first move from the origin three units to the right, then move seven units to the left as shown:

In this case, we can see that adding a negative number is equivalent to subtraction:
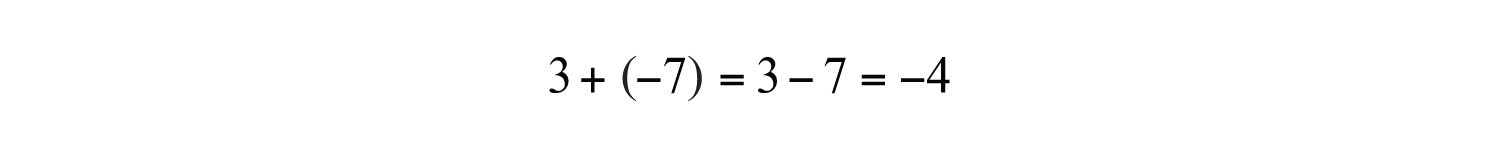
It is tempting to say that a positive number plus a negative number is negative, but that is not always true: . The result of adding numbers with unlike signs may be positive or negative. The sign of the result is the same as the sign of the number with the greatest distance from the origin. For example, the following results depend on the sign of the number 12 because it is farther from zero than 5:
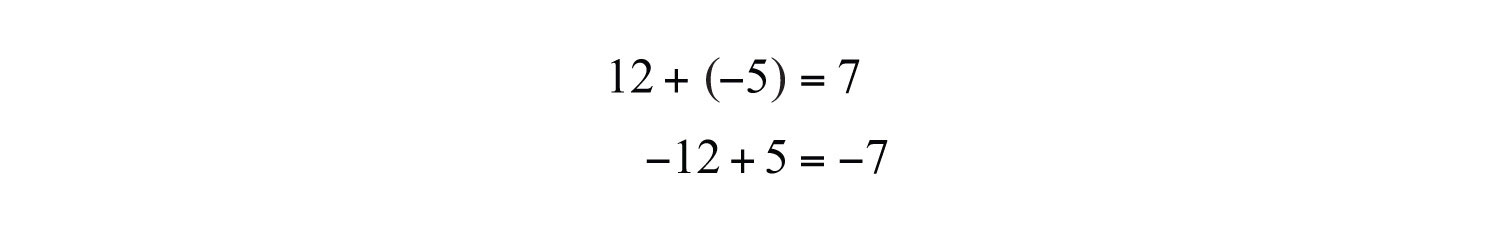
Example 1: Simplify: .
Solution: Here −25 is the greater distance from the origin. Therefore, the result is negative.
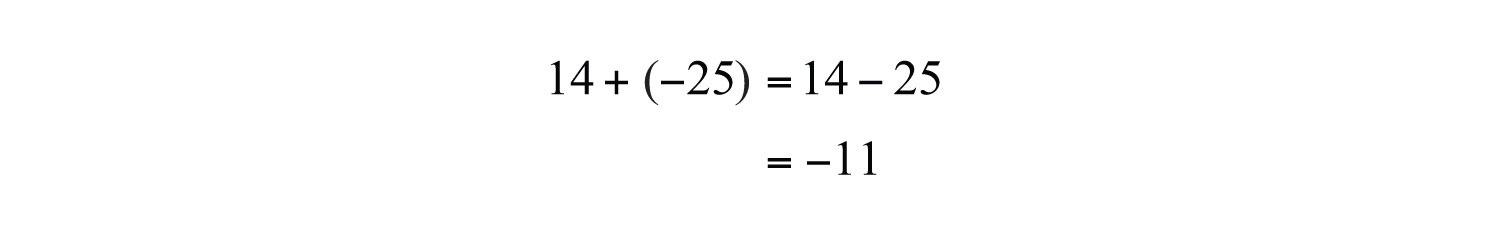
Answer: −11
Given any real numbers a, b, and c, we have the following properties of addition:
Additive identity propertyGiven any real number a, : |
|
Additive inverse propertyGiven any real number a, : |
|
Associative propertyGiven real numbers a, b and c, .: |
|
Commutative propertyGiven real numbers a and b, .: |
Example 2: Simplify:
a.
b.
Solution:
a. Adding zero to any real number results in the same real number.
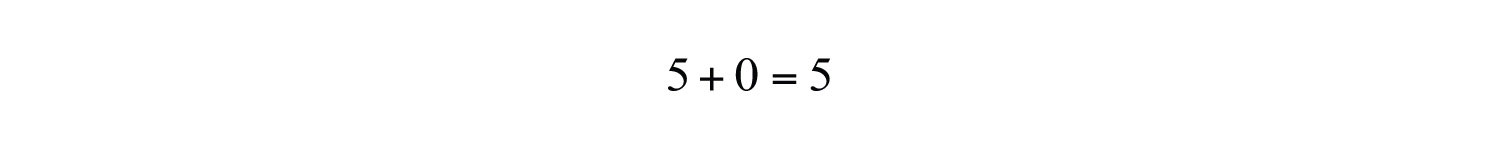
b. Adding opposites results in zero.
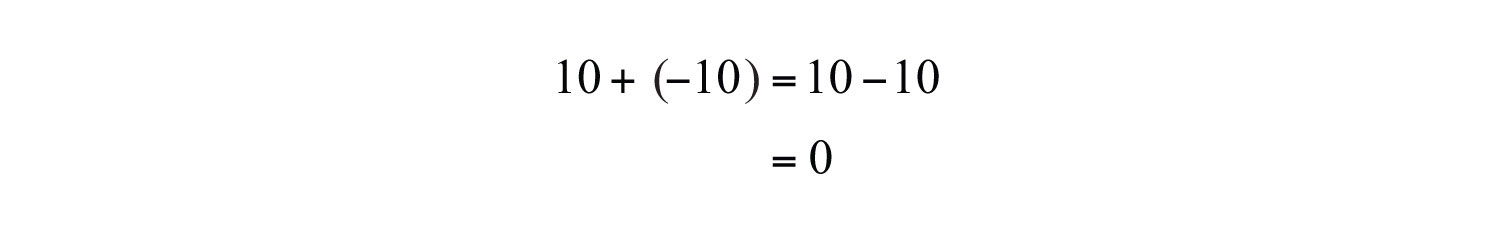
Answers: a. 5; b. 0
Example 3: Simplify:
a.
b.
Solution: Parentheses group the operations that are to be performed first.
a.
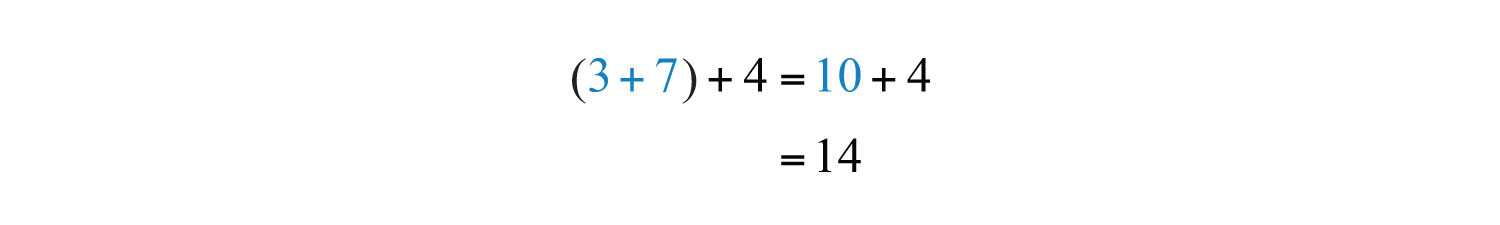
b.
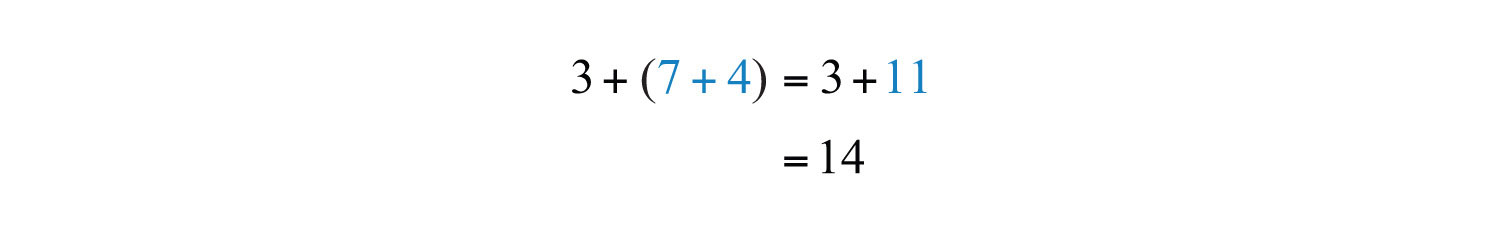
These two examples both result in 14: changing the grouping of the numbers does not change the result.
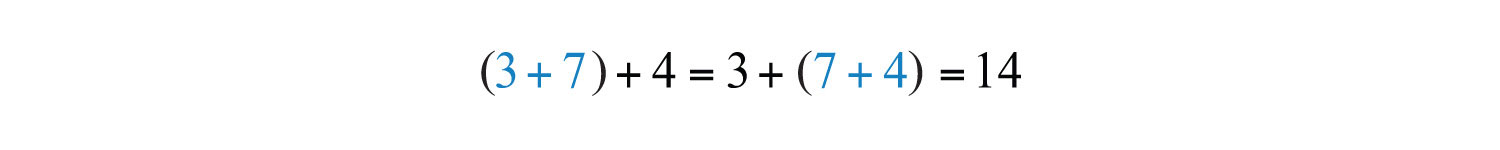
Answers: a. 14; b. 14
At this point, we highlight the fact that addition is commutative: the order in which we add does not matter and yields the same result.
On the other hand, subtraction is not commutative.
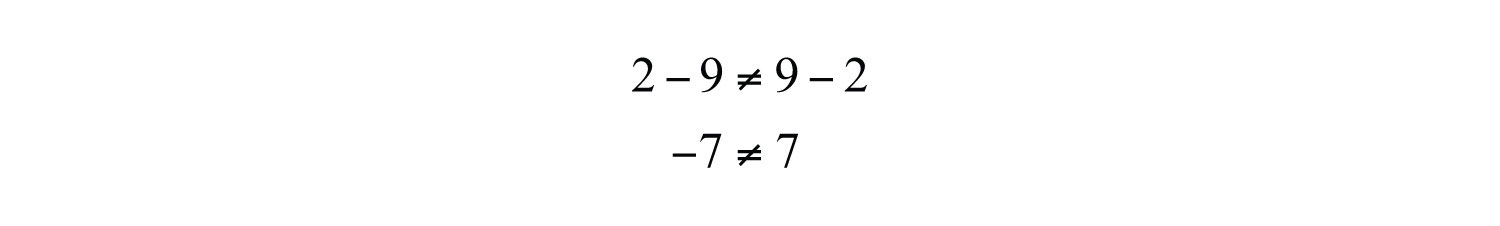
We will use these properties, along with the double-negative property for real numbers, to perform more involved sequential operations. To simplify things, we will make it a general rule to first replace all sequential operations with either addition or subtraction and then perform each operation in order from left to right.
Example 4: Simplify: .
Solution: Replace the sequential operations and then perform them from left to right.
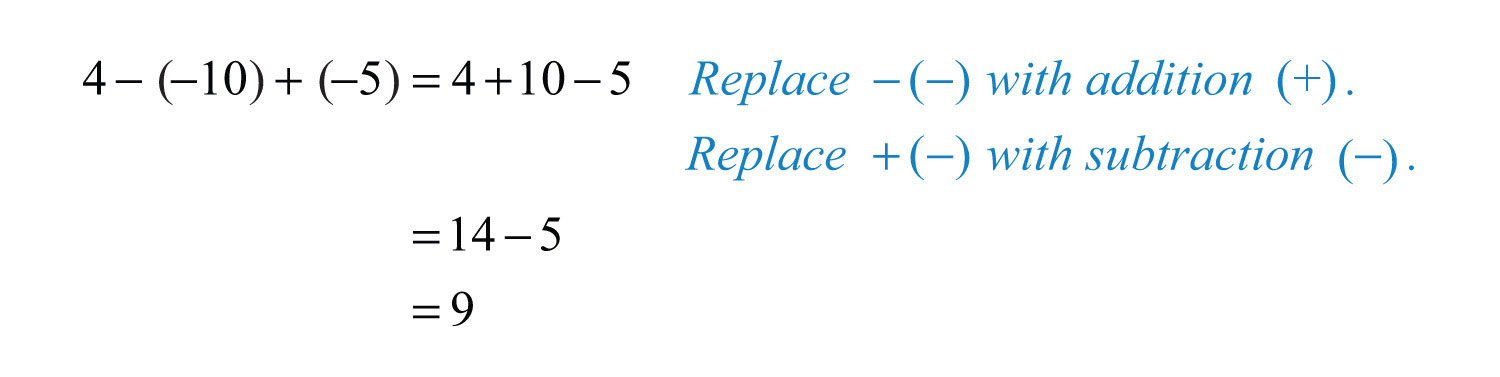
Answer: 9
Example 5: Simplify: .
Solution:
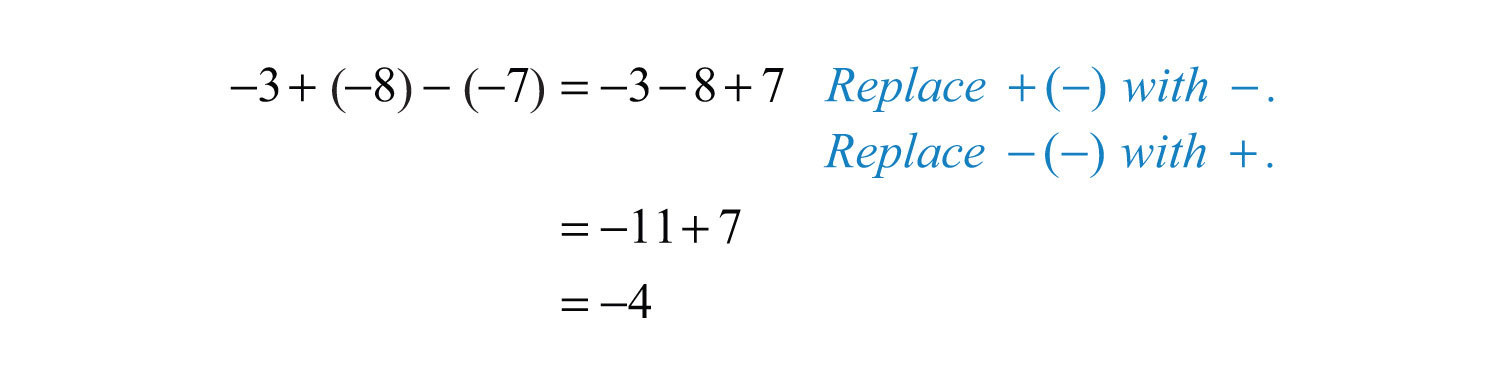
Answer: −4
Try this! Simplify: .
Answer: 15
Video Solution
(click to see video)Often we find the need to translate English sentences involving addition and subtraction to mathematical statements. Listed below are some key words that translate to the given operation.
| Key Words | Operation |
|---|---|
| Sum, increased by, more than, plus, added to, total | + |
| Difference, decreased by, subtracted from, less, minus | − |
Example 6: What is the difference of 7 and −3?
Solution: The key word “difference” implies that we should subtract the numbers.
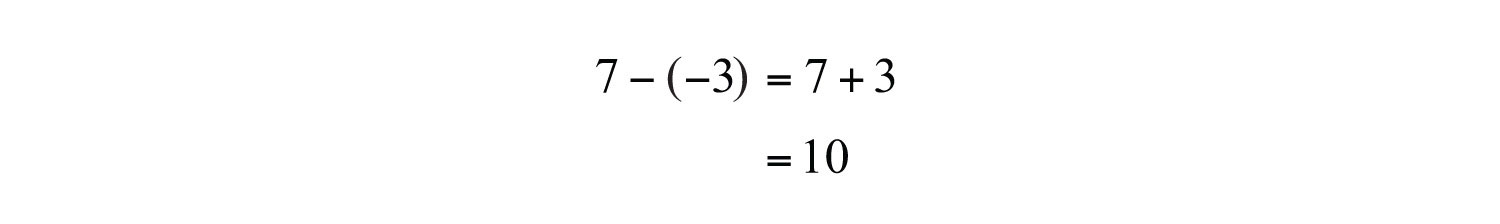
Answer: The difference of 7 and −3 is 10.
Example 7: What is the sum of the first five positive integers?
Solution: The initial key word to focus on is “sum”; this means that we will be adding the five numbers. The first five positive integers are {1, 2, 3, 4, 5}. Recall that 0 is neither positive nor negative.
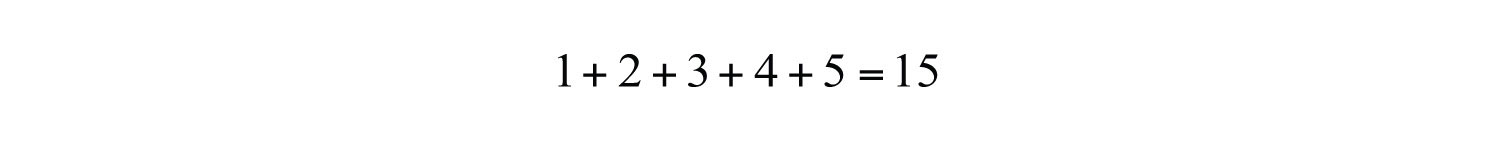
Answer: The sum of the first five positive integers is 15.
Example 8: What is 10 subtracted from the sum of 8 and 6?
Solution: We know that subtraction is not commutative; therefore, we must take care to subtract in the correct order. First, add 8 and 6 and then subtract 10 as follows:
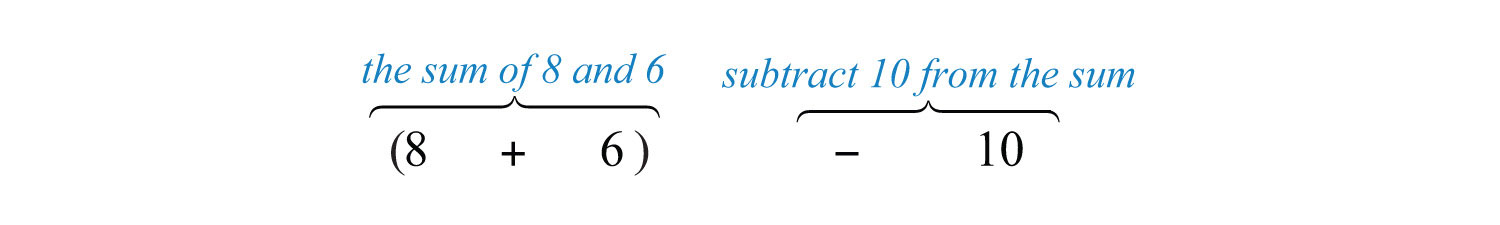
It is important to notice that the phrase “10 subtracted from” does not translate to a mathematical statement in the order it appears. In other words, would be an incorrect translation and leads to an incorrect answer. After translating the sentence, perform the operations.
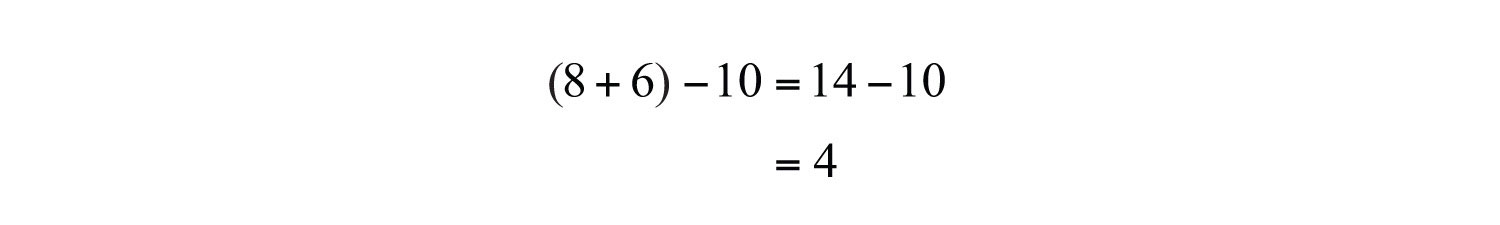
Answer: Ten subtracted from the sum of 8 and 6 is 4.
Distance on a Number Line
One application of the absolute value is to find the distance between any two points on a number line. For real numbers a and b, the distance formula for a number lineThe distance between any two real numbers a and b on a number line can be calculated using the formula . is given as,
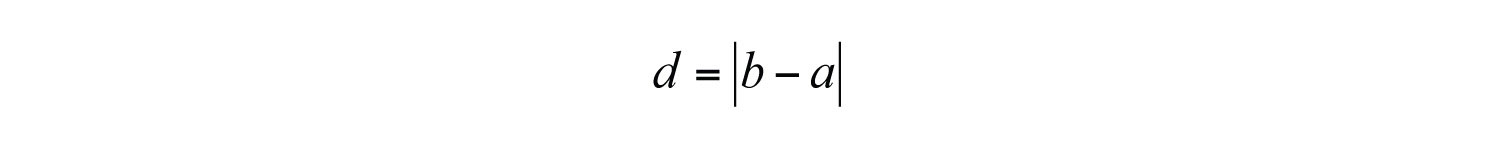
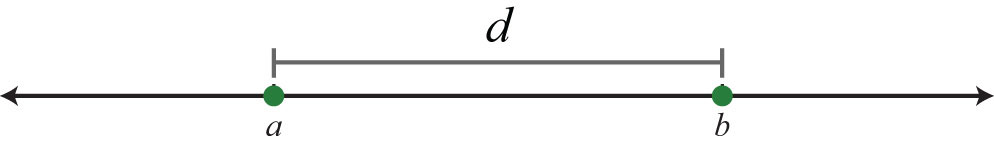
Example 9: Determine the distance between 2 and 7 on a number line.
Solution: On the graph we see that the distance between the two given integers is 5 units.

Using the distance formula we obtain the same result.
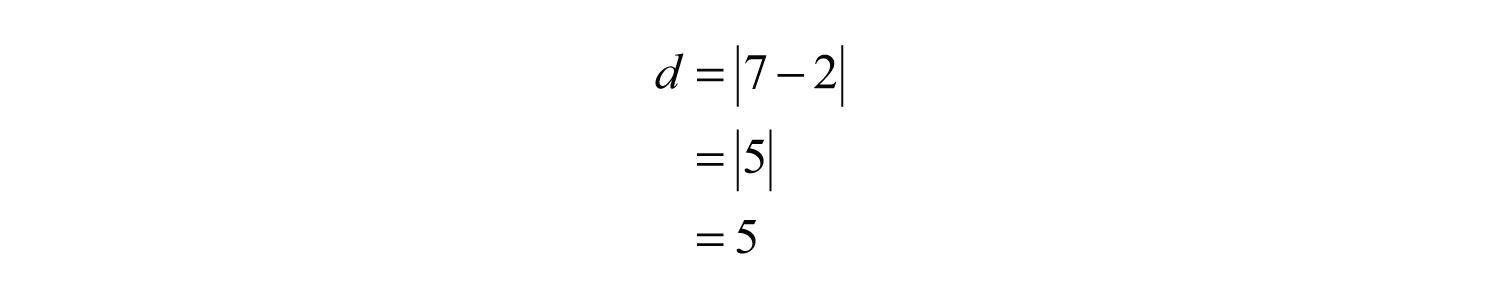
Answer: 5 units
Example 10: Determine the distance between −4 and 7 on a number line.
Solution: Use the distance formula for a number line , where and .
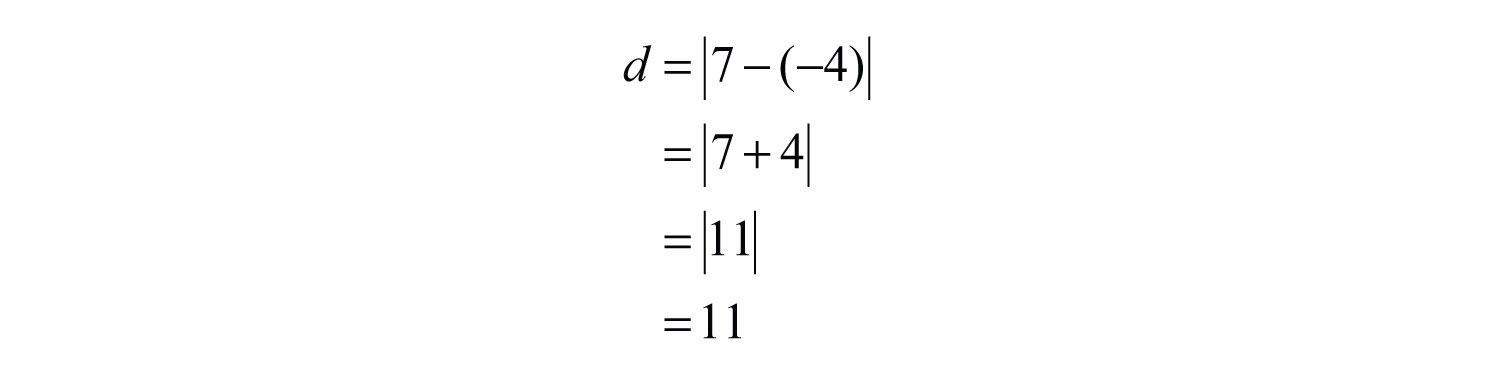
Answer: 11 units
It turns out that it does not matter which points are used for a and b; the absolute value always ensures a positive result.
| Using a = −4 and b = 7 | Using a = 7 and b = −4 |
|---|---|
Try this! Determine the distance between −12 and −9 on the number line.
Answer: 3
Video Solution
(click to see video)Key Takeaways
- A positive number added to a positive number is positive. A negative number added to a negative number is negative.
- The sign of a positive number added to a negative number is the same as the sign of the number with the greatest distance from the origin.
- Addition is commutative and subtraction is not.
- When simplifying, it is a best practice to first replace sequential operations and then work the operations of addition and subtraction from left to right.
- The distance between any two numbers on a number line is the absolute value of their difference. In other words, given any real numbers a and b, use the formula to calculate the distance d between them.
Topic Exercises
Part A: Addition and Subtraction
Add and subtract.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
Translate each sentence to a mathematical statement and then simplify.
23. Find the sum of 3, 7, and −8.
24. Find the sum of −12, −5, and 7.
25. Determine the sum of the first ten positive integers.
26. Determine the sum of the integers in the set {−2, −1, 0, 1, 2}.
27. Find the difference of 10 and 6.
28. Find the difference of 10 and −6.
29. Find the difference of −16 and −5.
30. Find the difference of −19 and 7.
31. Subtract 12 from 10.
32. Subtract −10 from −20.
33. Subtract 5 from −31.
34. Subtract −3 from 27.
35. Two less than 8.
36. Five less than −10.
37. Subtract 8 from the sum of 4 and 7.
38. Subtract −5 from the sum of 10 and −3.
39. Subtract 2 from the difference of 8 and 5.
40. Subtract 6 from the difference of −1 and 7.
41. Mandy made a $200 deposit into her checking account on Tuesday. She then wrote 4 checks for $50.00, $125.00, $60.00, and $45.00. How much more than her deposit did she spend?
42. The quarterback ran the ball three times in last Sunday’s football game. He gained 7 yards on one run but lost 3 yards and 8 yards on the other two. What was his total yardage running for the game?
43. The revenue for a local photographer for the month is $1,200. His costs include a studio rental of $600, props costing $105, materials fees of $135, and a make-up artist who charges $120. What is his total profit for the month?
44. An airplane flying at 30,000 feet lost 2,500 feet in altitude and then rose 1,200 feet. What is the new altitude of the plane?
45. The temperature was 22° at 6:00 p.m. and dropped 26° by midnight. What was the temperature at midnight?
46. A nurse has 30 milliliters of saline solution but needs 75 milliliters of the solution. How much more does she need?
47. The width of a rectangle is 2 inches less than its length. If the length measures 16 inches, determine the width.
48. The base of a triangle is 3 feet shorter than its height. If the height measures 5 feet, find the length of the base.
Part B: Distance on a Number Line
Find the distance between the given numbers on a number line.
49. −3 and 12
50. 8 and −13
51. −25 and −10
52. −100 and −130
53. −7 and −20
54. 0 and −33
55. −10 and 10
56. −36 and 36
57. The coldest temperature on earth, −129°F, was recorded in 1983 at Vostok Station, Antarctica. The hottest temperature on earth, 136°F, was recorded in 1922 at Al ’Aziziyah, Libya. Calculate earth’s temperature range.
58. The daily high temperature was recorded as 91°F and the low was recorded as 63°F. What was the temperature range for the day?
59. A student earned 67 points on his lowest test and 87 points on his best. Calculate his test score range.
60. On a busy day, a certain website may have 12,500 hits. On a slow day, it may have as few as 750 hits. Calculate the range of the number of hits.
Part C: Discussion Board Topics
61. Share an example of adding signed numbers in a real-world application.
62. Demonstrate the associative property of addition with any three real numbers.
63. Show that subtraction is not commutative.
Answers
1: 6
3: −26
5: −38
7: −14
9: 1
11: −10
13: −1
15: 0
17: 1
19: −2
21: 29
23: 2
25: 55
27: 4
29: −11
31: −2
33: −36
35: 6
37: 3
39: 1
41: $80
43: $240
45: −4°
47: 14 inches
49: 15 units
51: 15 units
53: 13 units
55: 20 units
57: 265°F
59: 20 points
1.3 Multiplying and Dividing Integers
Learning Objectives
- Multiply and divide signed integers.
- Translate English sentences involving multiplication and division into mathematical statements.
- Determine the prime factorization of composite numbers.
- Interpret the results of quotients involving zero.
Multiplication and Division
We begin with a review of what it means to multiply and divide signed numbers. The result of multiplying real numbers is called the productThe result of multiplying. and the result of dividing is called the quotientThe result after dividing.. Recall that multiplication is equivalent to adding:
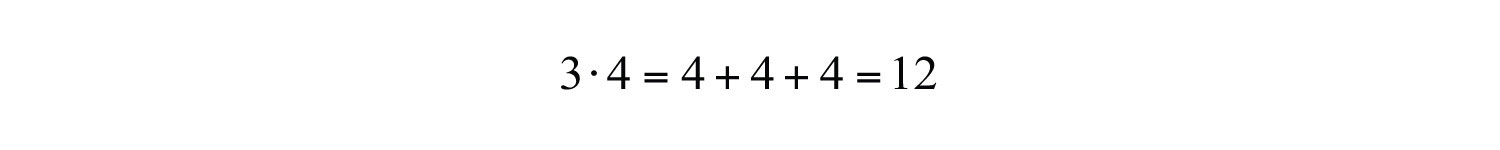
Clearly, the product of two positive numbers is positive. Similarly, the product of a positive number and negative number can be written as shown:
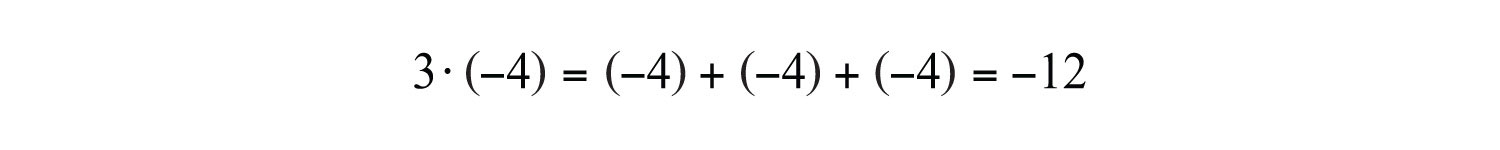
We see that the product of a positive number and a negative number is negative. Next, explore the results of multiplying two negative numbers. Consider the products in the following illustration and try to identify the pattern:

This shows that the product of two negative numbers is positive. To summarize,
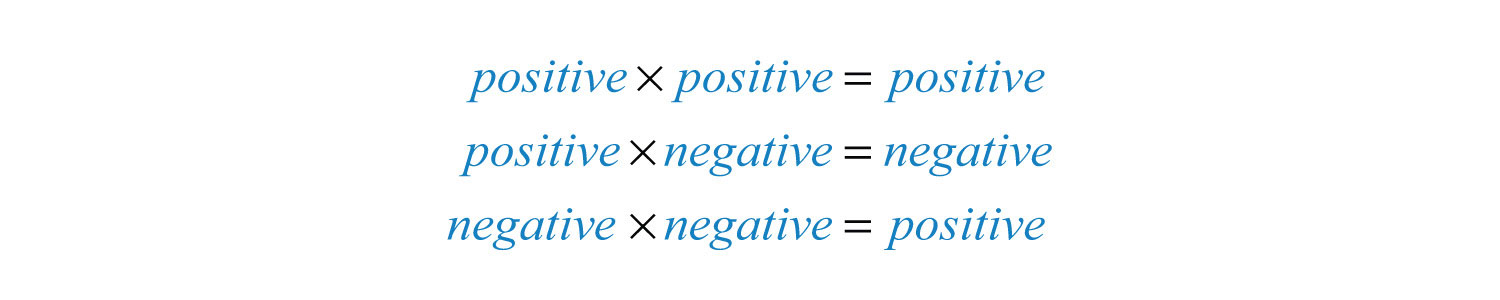
The rules for division are the same because division can always be rewritten as multiplication:
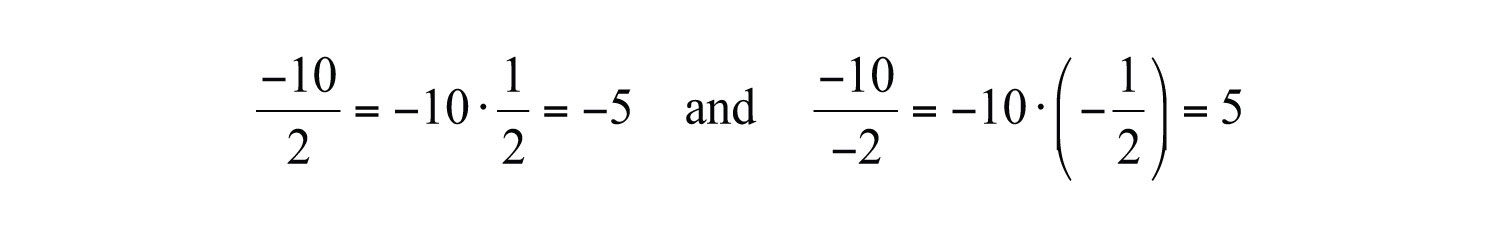
The rules for multiplication and division should not be confused with the fact that the sum of two negative numbers is negative.
Example 1: Simplify:
a.
b.
Solution: Here we add and multiply the same two negative numbers.
a. The result of adding two negative numbers is negative.
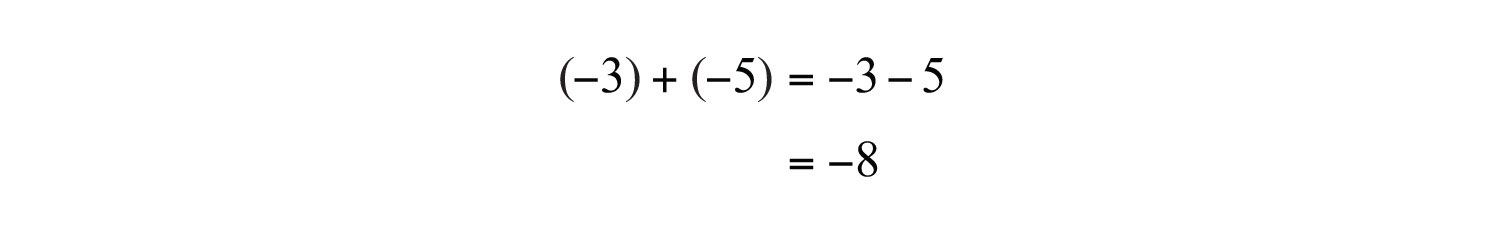
b. The result of multiplying two negative numbers is positive.
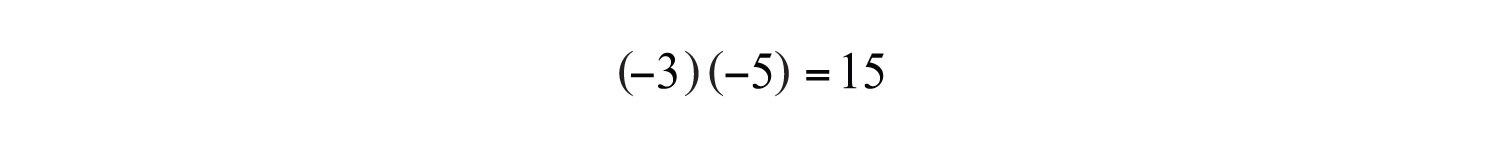
Answers: a. −8; b. 15
Given any real numbers a, b, and c, we have the following properties of multiplication:
Zero factor propertyGiven any real number a, : |
|
Multiplicative identity propertyGiven any real number a, : |
|
Associative propertyGiven any real numbers a, b, and c, : |
|
Commutative propertyGiven any real numbers a and b, : |
Example 2: Simplify:
a.
b.
Solution:
a. Multiplying by zero results in zero.
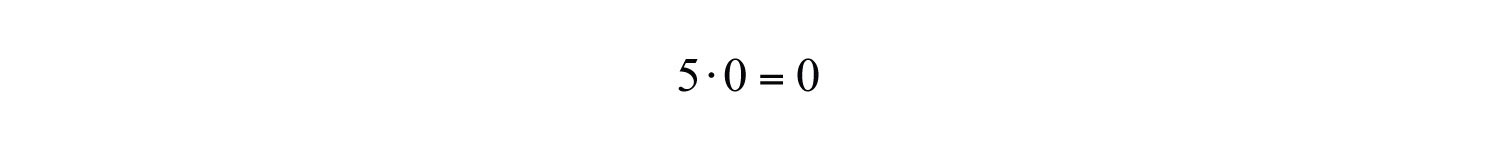
b. Multiplying any real number by one results in the same real number.
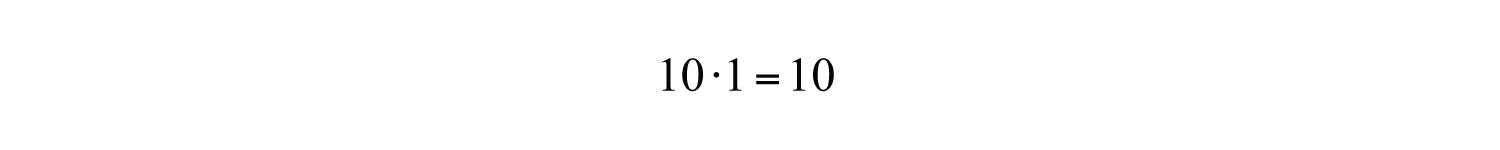
Answers: a. 0; b. 10
Example 3: Simplify:
a.
b.
Solution:
a.
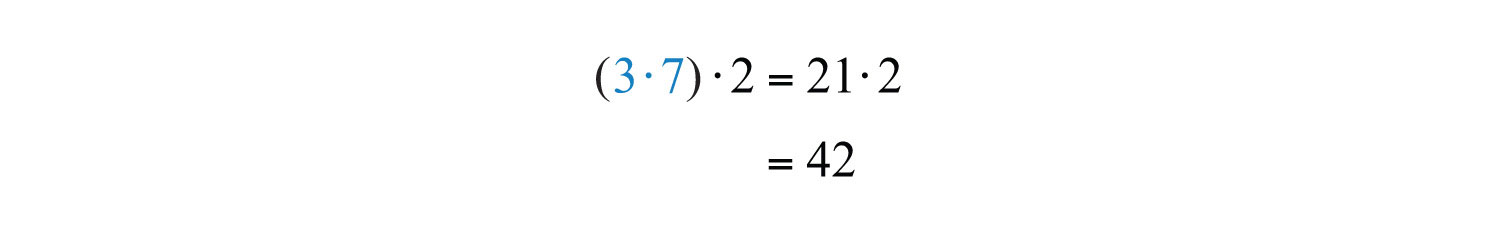
b.
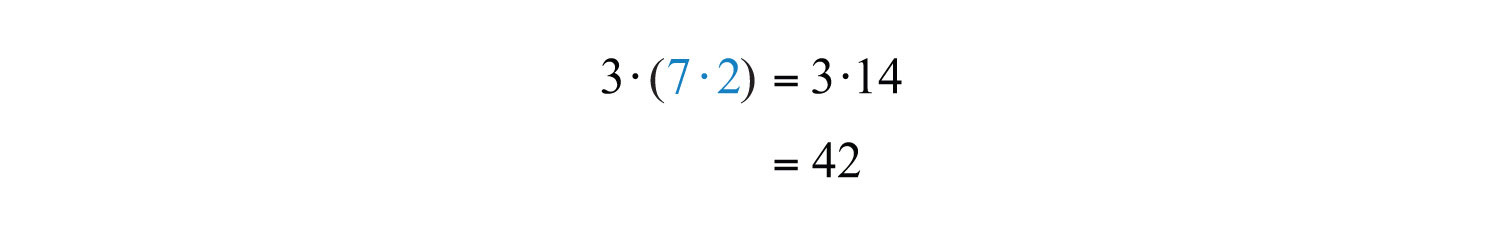
The value of each expression is 42. Changing the grouping of the numbers does not change the result.
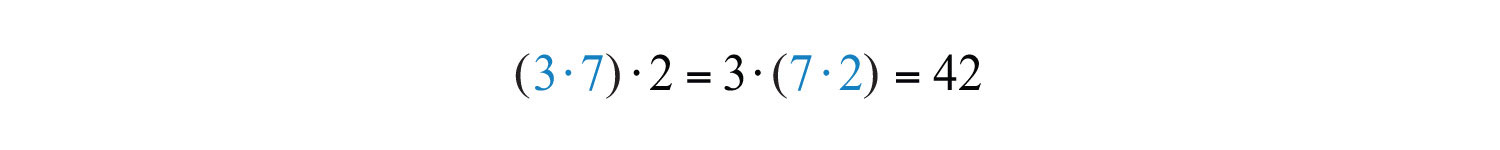
Answers: a. 42; b. 42
At this point, we highlight that multiplication is commutative: the order in which we multiply does not matter and yields the same result.
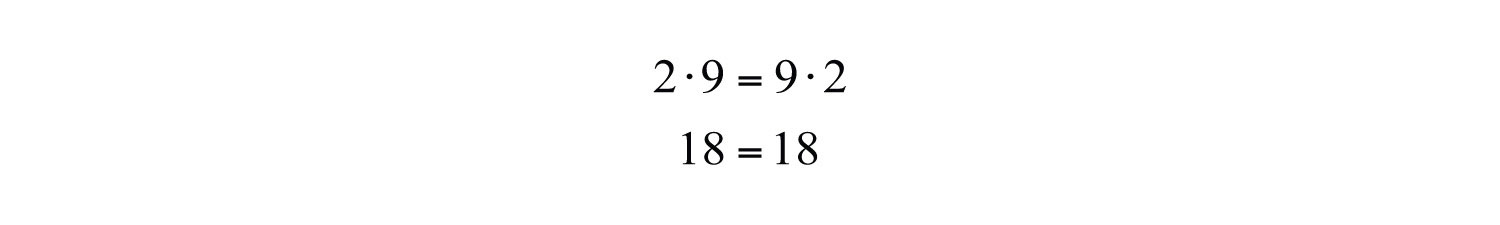
On the other hand, division is not commutative.
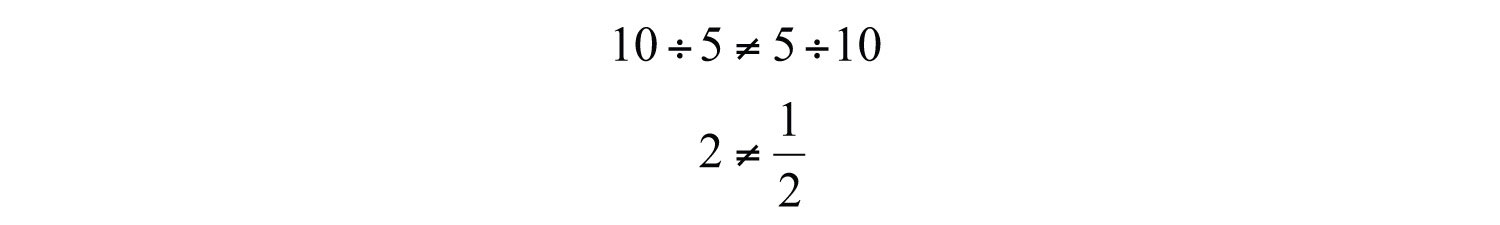
Use these properties to perform sequential operations involving multiplication and division. When doing so, it is important to perform these operations in order from left to right.
Example 4: Simplify: .
Solution: Multiply two numbers at a time as follows:
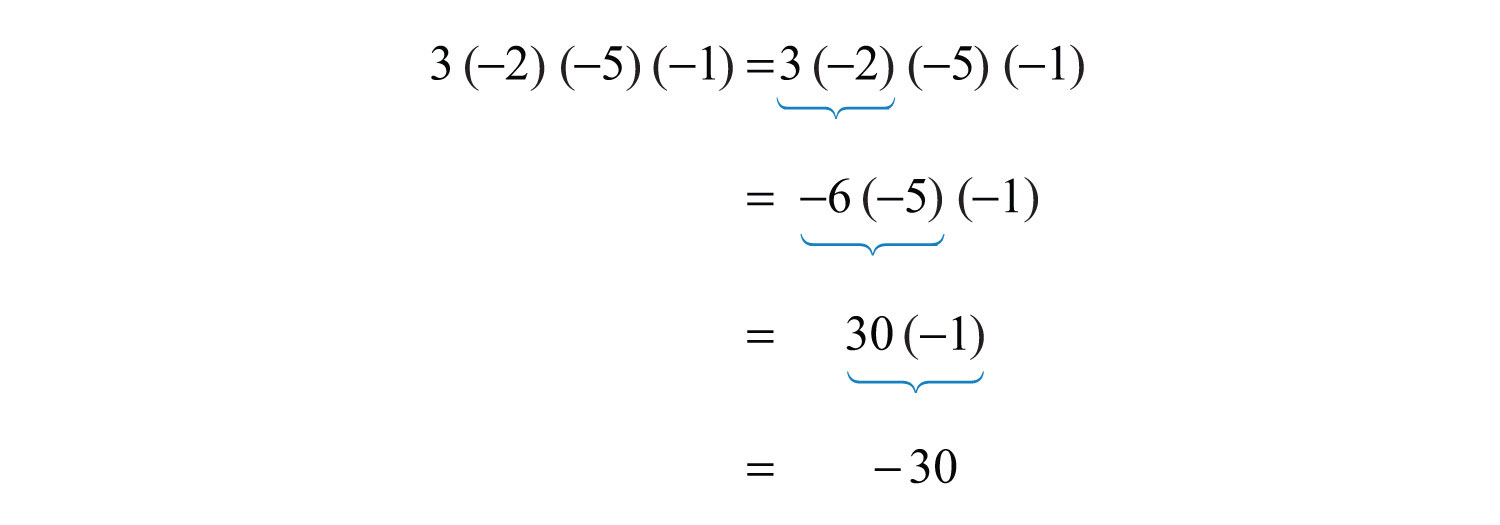
Answer: −30
Because multiplication is commutative, the order in which we multiply does not affect the final answer. When sequential operations involve multiplication and division, order does matter; hence we must work the operations from left to right to obtain a correct result.
Example 5: Simplify: .
Solution: Perform the division first; otherwise, the result will be incorrect.

Answer: 25
Notice that the order in which we multiply and divide does affect the final result. Therefore, it is important to perform the operations of multiplication and division as they appear from left to right.
Example 6: Simplify: .
Solution: Work the operations one at a time from left to right.
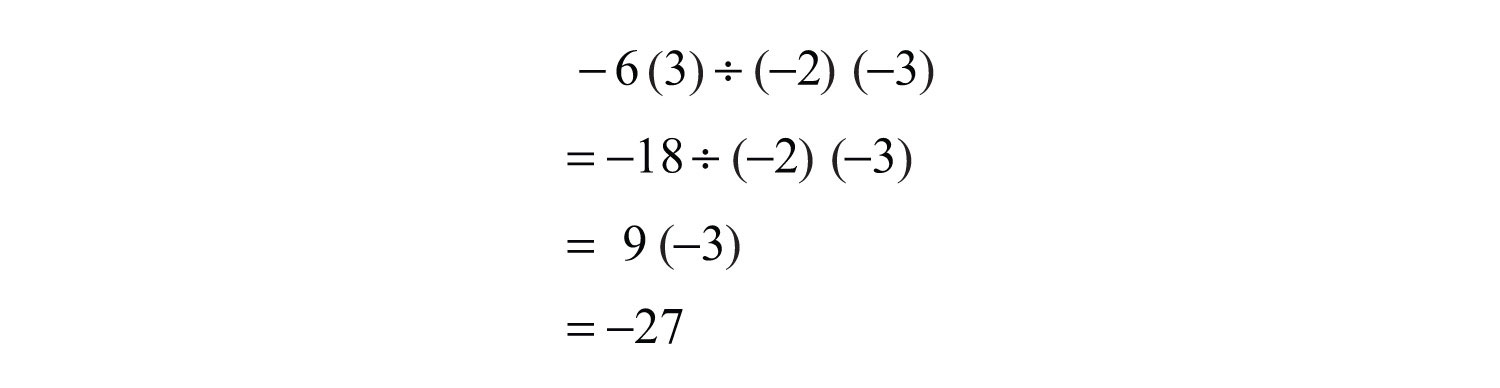
Try this! Simplify: .
Answer: 6
Video Solution
(click to see video)Within text-based applications, the symbol used for multiplication is the asteriskThe symbol (*) that indicates multiplication within text-based applications. (*) and the symbol used for division is the forward slash (/).
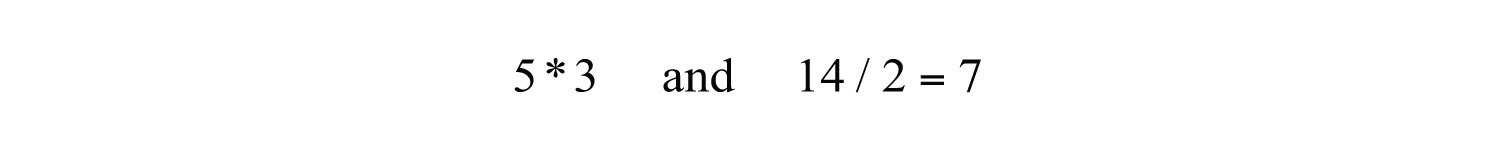
The set of even integersIntegers that are divisible by two or are multiples of two. is the set of all integers that are evenly divisible by 2. We can also obtain the set of even integers by multiplying each integer by 2.
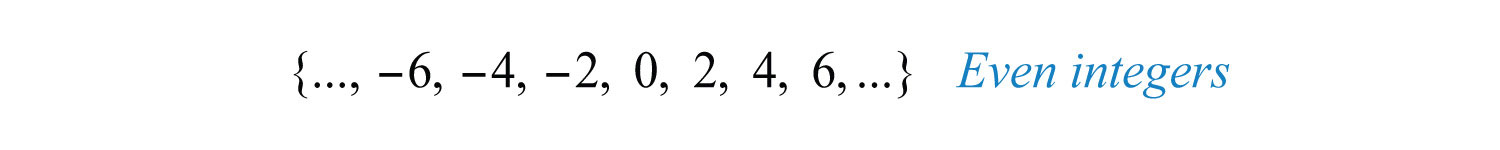
The set of odd integersIntegers that are not divisible by 2. is the set of all integers that are not evenly divisible by 2.
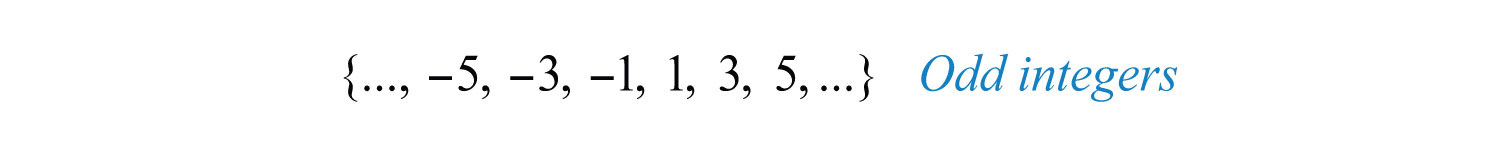
A prime numberIntegers greater than 1 that are divisible only by 1 and itself. is an integer greater than 1 that is divisible only by 1 and itself. The smallest prime number is 2 and the rest are necessarily odd.
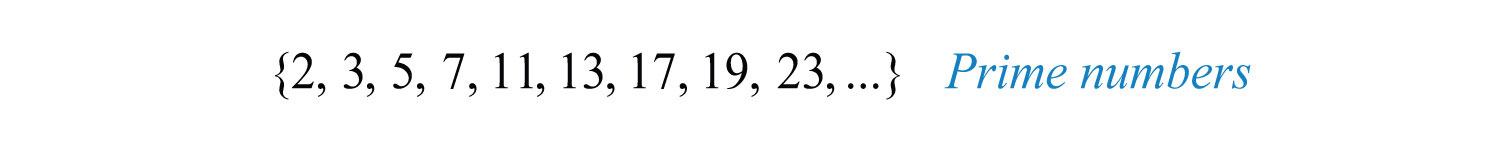
Any integer greater than 1 that is not prime is called a composite numberIntegers greater than 1 that are not prime. and can be written as a product of primes. When a composite number, such as 30, is written as a product, , we say that is a factorizationAny combination of factors, multiplied together, resulting in the product. of 30 and that 2 and 15 are factorsAny of the numbers or expressions that form a product.. Note that factors divide the number evenly. We can continue to write composite factors as products until only a product of primes remains.
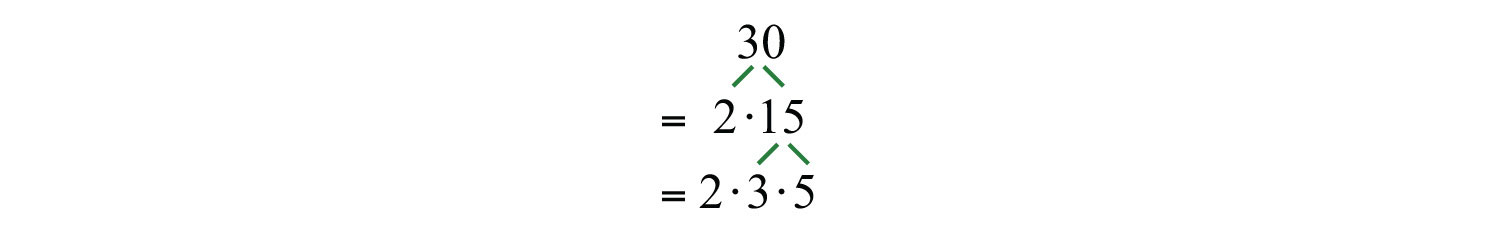
The prime factorizationThe unique factorization of a natural number written as a product of primes. of 30 is .
Example 7: Determine the prime factorization of 70.
Solution: Begin by writing 70 as a product with 2 as a factor. Then express any composite factor as a product of prime numbers.
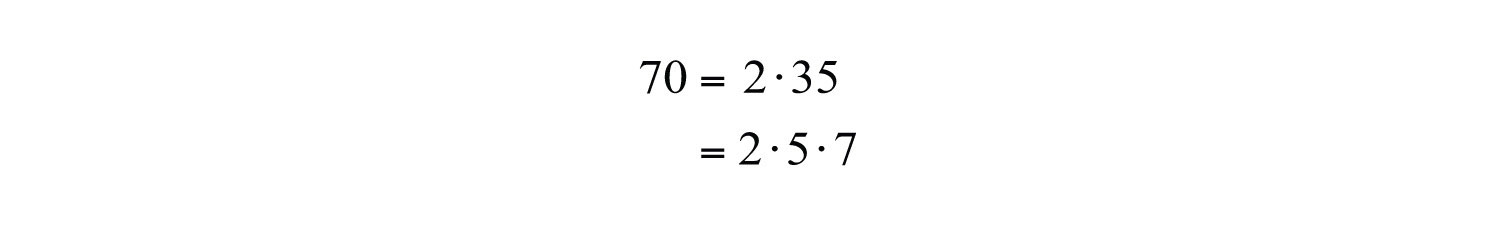
Since the prime factorization is unique, it does not matter how we choose to initially factor the number because the end result is the same.
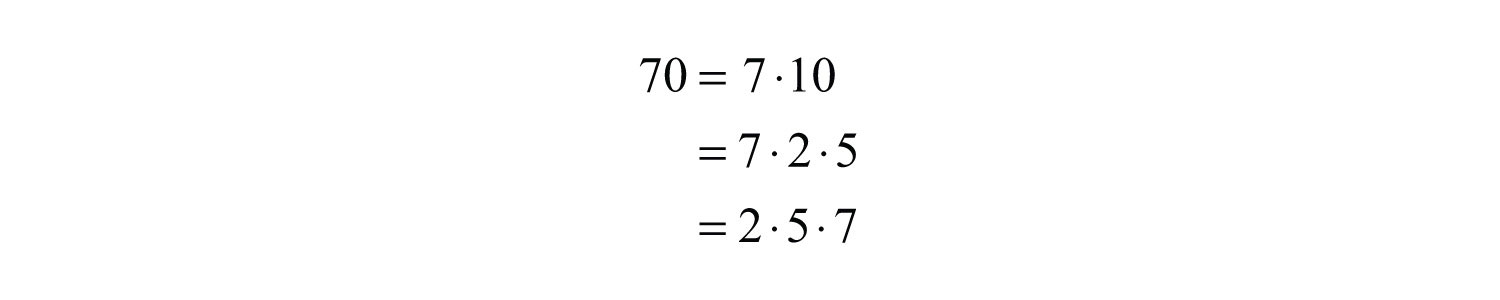
Answer: The prime factorization of 70 is .
Some tests (called divisibility tests) useful for finding prime factors of composite numbers follow:
- If the integer is even, then 2 is a factor.
- If the sum of the digits is evenly divisible by 3, then 3 is a factor.
- If the last digit is a 5 or 0, then 5 is a factor.
Often we find the need to translate English sentences that include multiplication and division terms to mathematical statements. Listed below are some key words that translate to the given operation.
| Key Words | Operation |
|---|---|
Product, multiplied by, of, times |
* or |
Quotient, divided by, ratio, per |
/ or |
Example 8: Calculate the quotient of 20 and −10.
Solution: The key word “quotient” implies that we should divide.
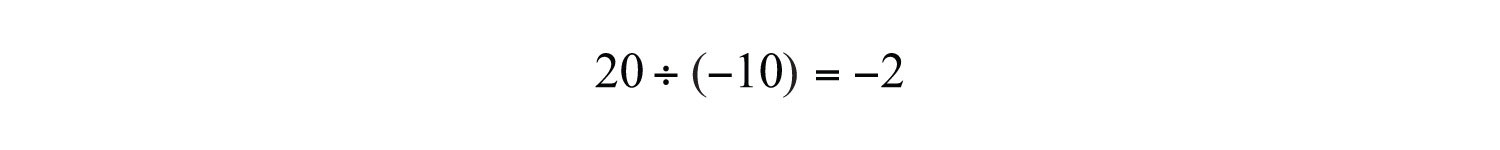
Answer: The quotient of 20 and −10 is −2.
Example 9: What is the product of the first three positive even integers?
Solution: The first three positive even integers are {2, 4, 6} and the key word “product” implies that we should multiply.
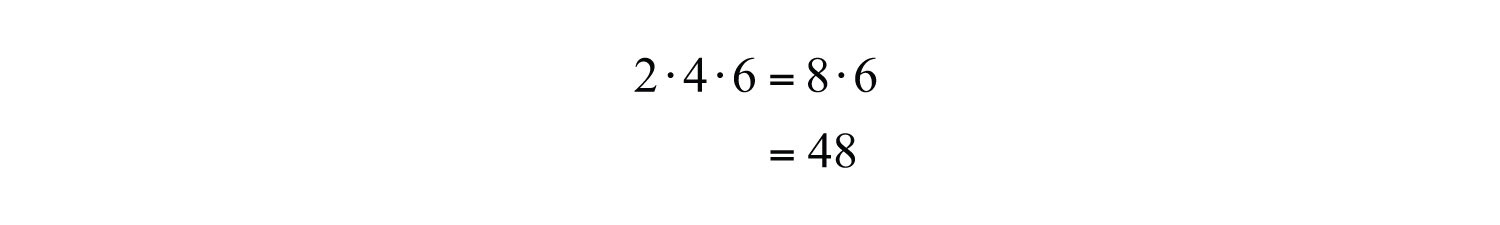
Answer: The product of the first three positive even integers is 48.
Example 10: Joe is able to drive 342 miles on 18 gallons of gasoline. How many miles per gallon of gas is this?
Solution: The key word “per” indicates that we must divide the number of miles driven by the number of gallons used:

Answer: Joe gets 19 miles per gallon from his vehicle.
In everyday life, we often wish to use a single value that typifies a set of values. One way to do this is to use what is called the arithmetic meanA numerical value that typifies a set of numbers. It is calculated by adding up the numbers in the set and dividing by the number of elements in the set. or averageUsed in reference to the arithmetic mean.. To calculate an average, divide the sum of the values in the set by the number of values in that set.
Example 11: A student earns 75, 86, and 94 on his first three exams. What is the student’s test average?
Solution: Add the scores and divide the sum by 3.
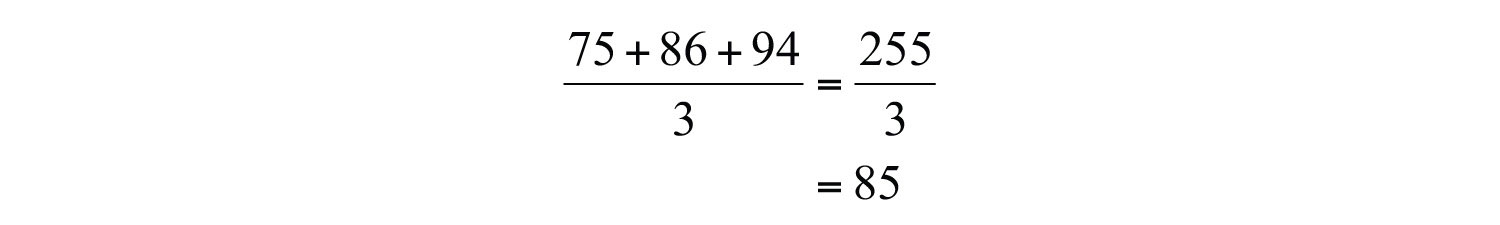
Answer: The student’s test average is 85.
Zero and Division
Recall the relationship between multiplication and division:

In this case, the dividendThe numerator of a quotient. 12 is evenly divided by the divisorThe denominator of a quotient. 6 to obtain the quotient, 2. It is true in general that if we multiply the divisor by the quotient we obtain the dividend. Now consider the case where the dividend is zero and the divisor is nonzero:
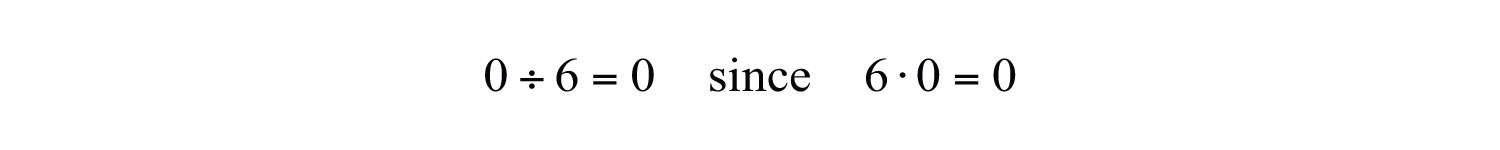
This demonstrates that zero divided by any nonzero real number must be zero. Now consider a nonzero number divided by zero:
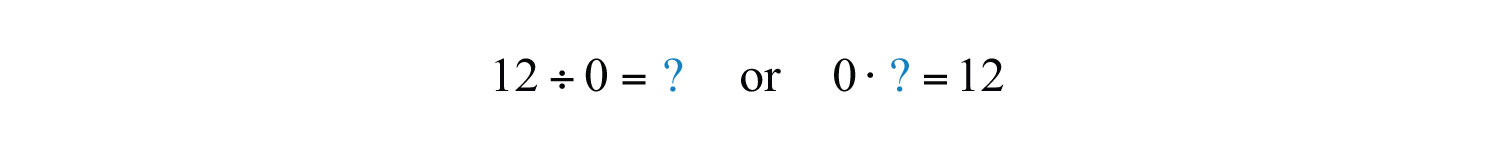
The zero-factor property of multiplication states that any real number times 0 is 0. We conclude that there is no real number such that and thus, the quotient is left undefinedA quotient such as , which is left without meaning and is not assigned an interpretation.. Try on a calculator. What does it say? For our purposes, we will simply write “undefined.”
To summarize, given any real number , then
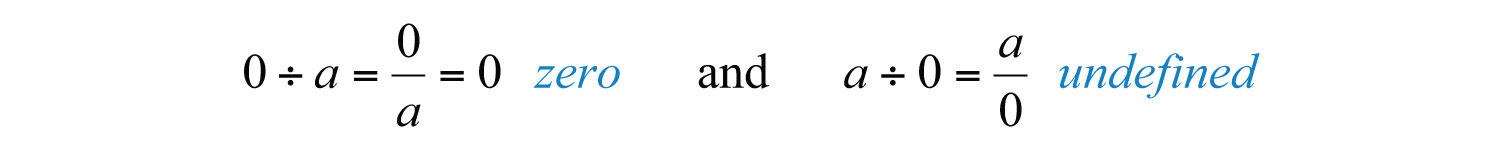
We are left to consider the case where the dividend and divisor are both zero.
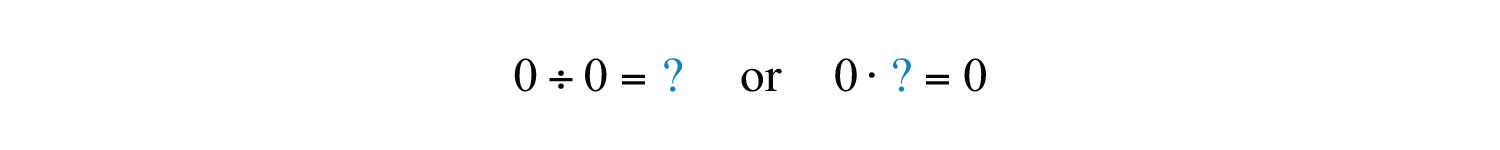
Here any real number seems to work. For example, and . Therefore, the quotient is uncertain or indeterminateA quotient such as , which is a quantity that is uncertain or ambiguous..

In this course, we state that is undefined.
Key Takeaways
- A positive number multiplied by a negative number is negative. A negative number multiplied by a negative number is positive.
- Multiplication is commutative and division is not.
- When simplifying, work the operations of multiplication and division in order from left to right.
- Even integers are numbers that are evenly divisible by 2 or multiples of 2, and all other integers are odd.
- A prime number is an integer greater than 1 that is divisible only by 1 and itself.
- Composite numbers are integers greater than 1 that are not prime. Composite numbers can be written uniquely as a product of primes.
- The prime factorization of a composite number is found by continuing to divide it into factors until only a product of primes remains.
- To calculate an average of a set of numbers, divide the sum of the values in the set by the number of values in the set.
- Zero divided by any nonzero number is zero. Any number divided by zero is undefined.
Topic Exercises
Part A: Multiplication and Division
Multiply and divide.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14. 6*(−3)/(−9)
15. 20/(−5)*2
16. −50/2*5
17. Determine the product of 11 and −3.
18. Determine the product of −7 and −22.
19. Find the product of 5 and −12.
20. Find the quotient of negative twenty-five and five.
21. Determine the quotient of −36 and 3.
22. Determine the quotient of 26 and −13.
23. Calculate the product of 3 and −8 divided by −2.
24. Calculate the product of −1 and −3 divided by 3.
25. Determine the product of the first three positive even integers.
26. Determine the product of the first three positive odd integers.
Determine the prime factorization of the following integers.
27. 105
28. 78
29. 138
30. 154
31. 165
32. 330
Calculate the average of the numbers in each of the following sets.
33. {50, 60, 70}
34. {9, 12, 30}
35. {3, 9, 12, 30, 36}
36. {72, 84, 69, 71}
37. The first four positive even integers.
38. The first four positive odd integers.
The distance traveled D is equal to the average rate r times the time traveled t at that rate: . Determine the distance traveled given the rate and the time.
39. 60 miles per hour for 3 hours
40. 55 miles per hour for 3 hours
41. 15 miles per hour for 5 hours
42. 75 feet per second for 5 seconds
43. 60 kilometers per hour for 10 hours
44. 60 meters per second for 30 seconds
45. A student club ran a fund-raiser in the quad selling hot dogs. The students sold 122 hot dog meals for $3.00 each. Their costs included $50.00 for the hot dogs and buns, $25.00 for individually wrapped packages of chips, and $35.00 for the sodas. What was their profit?
46. A 230-pound man loses 4 pounds each week for 8 weeks. How much does he weigh at the end of 8 weeks?
47. Mary found that she was able to drive 264 miles on 12 gallons of gas. How many miles per gallon does her car get?
48. After filling his car with gasoline, Bill noted that his odometer reading was 45,346 miles. After using his car for a week, he filled up his tank with 14 gallons of gas and noted that his odometer read 45,724 miles. In that week, how many miles per gallon did Bill’s car get?
Part B: Zero and Division with Mixed Practice
Perform the operations.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62. 0/(−3*8*5)
63. (−4*3)/(2*(−3))
64. −16/(−2*2)*3
65. −44/11*2
66. −5*3/(−15)
67. 4*3*2/6
68. −6*7/( −2)
69. During 5 consecutive winter days, the daily lows were −7°, −3°, 0°, −5°, and −10°. Calculate the average low temperature.
70. On a very cold day the temperature was recorded every 4 hours with the following results: −16°, −10°, 2°, 6°, −5°, and −13°. Determine the average temperature.
71. A student earns 9, 8, 10, 7, and 6 points on the first 5 chemistry quizzes. What is her quiz average?
72. A website tracked hits on its homepage over the Thanksgiving holiday. The number of hits for each day from Thursday to Sunday was 12,250; 4,400; 7,750; and 10,200, respectively. What was the average number of hits per day over the holiday period?
Part C: Discussion Board Topics
73. Demonstrate the associative property of multiplication with any three real numbers.
74. Show that division is not commutative.
75. Discuss the importance of working multiplication and division operations from left to right. Make up an example where order does matter and share the solution.
76. Discuss division involving 0. With examples, explain why the result is sometimes 0 and why it is sometimes undefined.
77. Research and discuss the fundamental theorem of arithmetic.
78. Research and discuss other divisibility tests. Provide an example for each test.
79. The arithmetic mean is one way to typify a set of values. Research other methods used to typify a set of values.
Answers
1: −35
3: 72
5: 0
7: 1
9: −4
11: −9
13: 15
15: −8
17: −33
19: −60
21: −12
23: 12
25: 48
27:
29:
31:
33: 60
35: 18
37: 5
39: 180 miles
41: 75 miles
43: 600 kilometers
45: $256.00
47: 22 miles per gallon
49: 0
51: Undefined
53: 0
55: −26
57: 1
59: 1
61: 48
63: 2
65: −8
67: 4
69: −5°
71: 8 points
1.4 Fractions
Learning Objectives
- Reduce a fraction to lowest terms.
- Multiply and divide fractions.
- Add and subtract fractions.
Reducing
A fractionA rational number written as a quotient of two integers: , where b is nonzero. is a real number written as a quotient, or ratioRelationship between two numbers or quantities usually expressed as a quotient., of two integers a and b, where .

The integer above the fraction bar is called the numeratorThe number above the fraction bar. and the integer below is called the denominatorThe number below the fraction bar.. The numerator is often called the “part” and the denominator is often called the “whole.” Equivalent fractionsTwo equal fractions expressed using different numerators and denominators. are two equal ratios expressed using different numerators and denominators. For example,
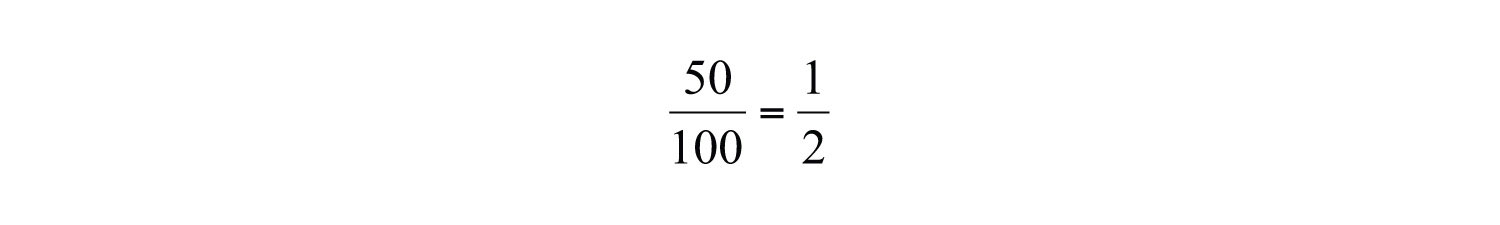
Fifty parts out of 100 is the same ratio as 1 part out of 2 and represents the same real number. Consider the following factorizations of 50 and 100:
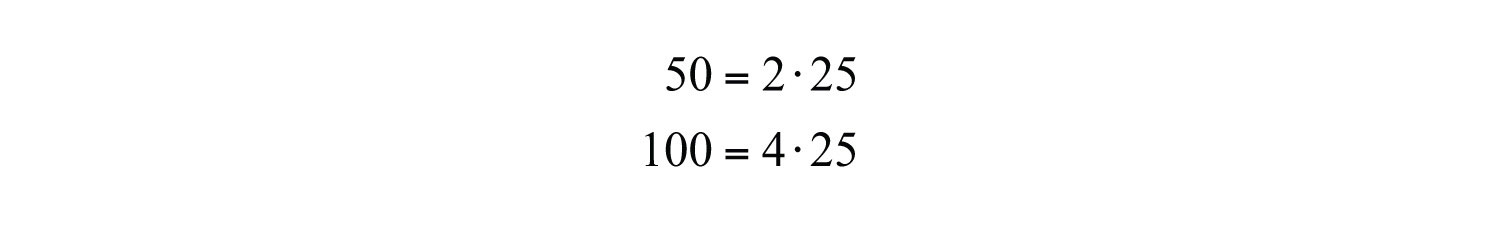
The numbers 50 and 100 share the factor 25. A shared factor is called a common factorA factor that is shared by more than one real number.. We can rewrite the ratio as follows:
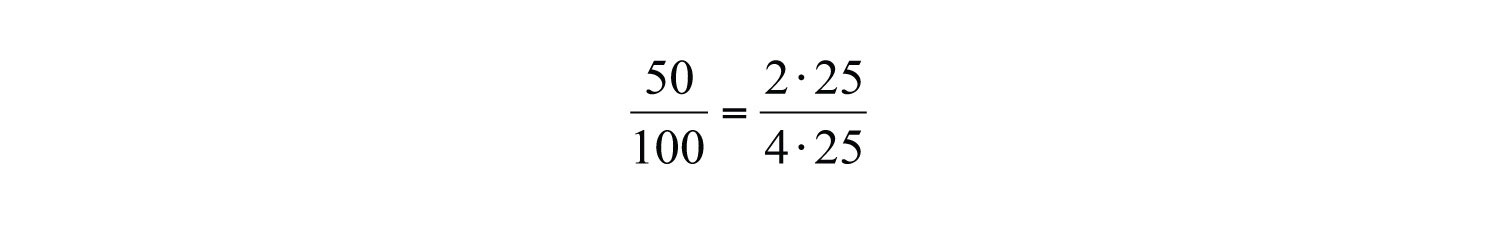
Making use of the multiplicative identity property and the fact that , we have
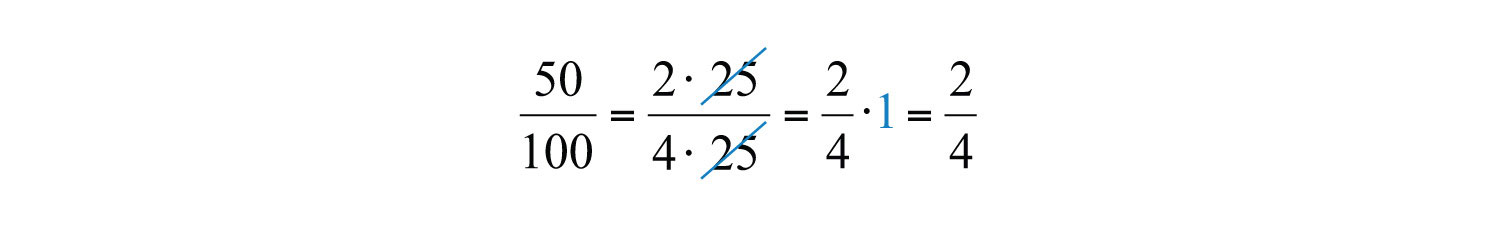
Dividing and replacing this factor with a 1 is called cancelingThe process of dividing out common factors in the numerator and the denominator.. Together, these basic steps for finding equivalent fractions define the process of reducingThe process of finding equivalent fractions by dividing the numerator and the denominator by common factors.. Since factors divide their product evenly, we achieve the same result by dividing both the numerator and denominator by 25 as follows:
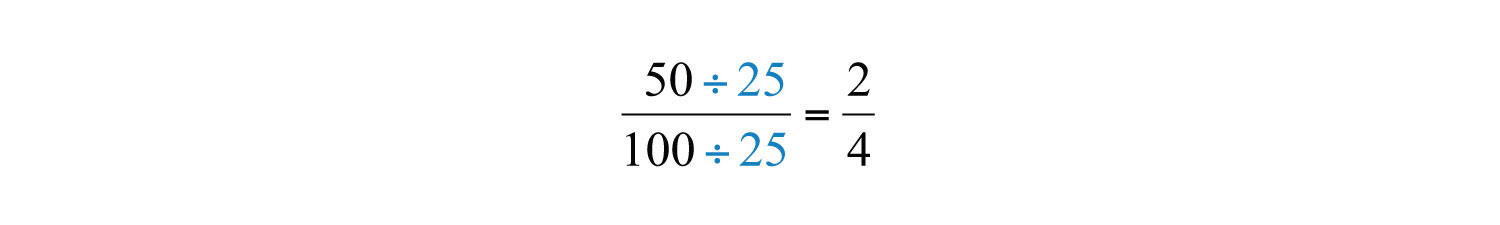
Finding equivalent fractions where the numerator and denominator have no common factor other than 1 is called reducing to lowest termsFinding equivalent fractions where the numerator and the denominator share no common integer factor other than 1.. When learning how to reduce to lowest terms, it is helpful to first rewrite the numerator and denominator as a product of primes and then cancel. For example,
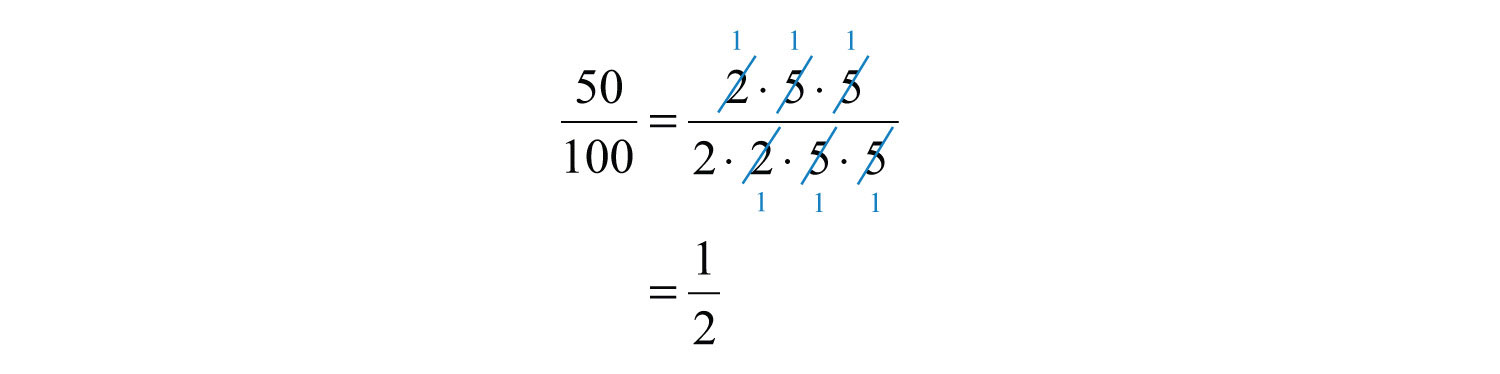
We achieve the same result by dividing the numerator and denominator by the greatest common factor (GCF)The largest shared factor of any number of integers.. The GCF is the largest number that divides both the numerator and denominator evenly. One way to find the GCF of 50 and 100 is to list all the factors of each and identify the largest number that appears in both lists. Remember, each number is also a factor of itself.
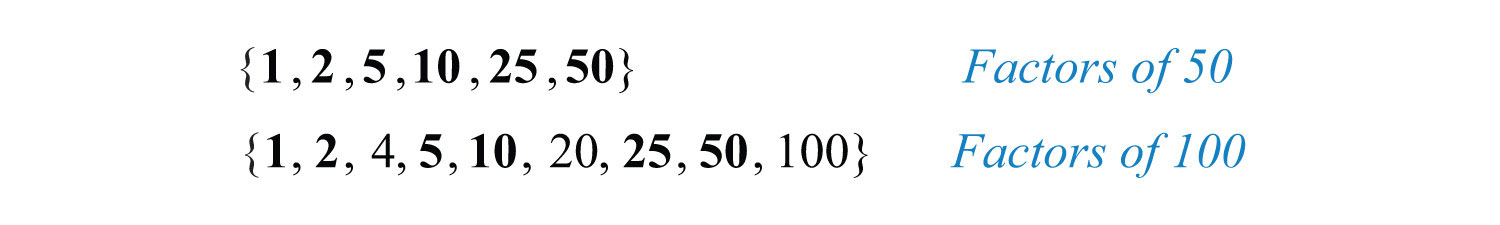
Common factors are listed in bold, and we see that the greatest common factor is 50. We use the following notation to indicate the GCF of two numbers: GCF(50, 100) = 50. After determining the GCF, reduce by dividing both the numerator and the denominator as follows:
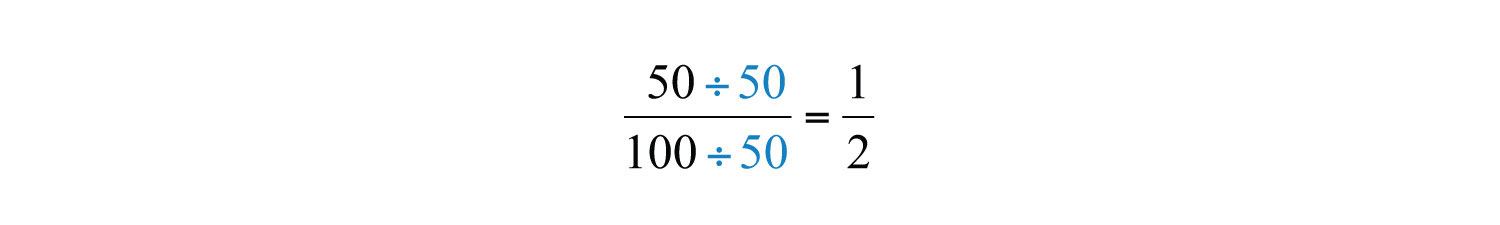
Example 1: Reduce to lowest terms: .
Solution: Rewrite the numerator and denominator as a product of primes and then cancel.
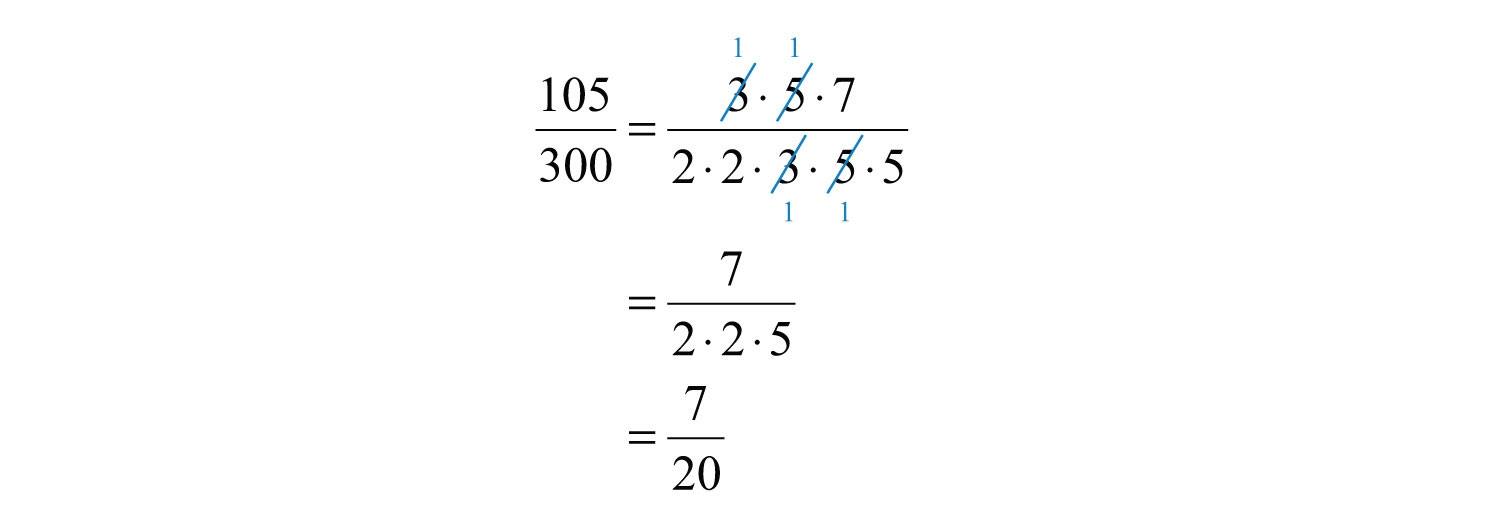
Alternatively, we achieve the same result if we divide both the numerator and denominator by the GCF(105, 300). A quick way to find the GCF of the two numbers requires us to first write each as a product of primes. The GCF is the product of all the common prime factors.
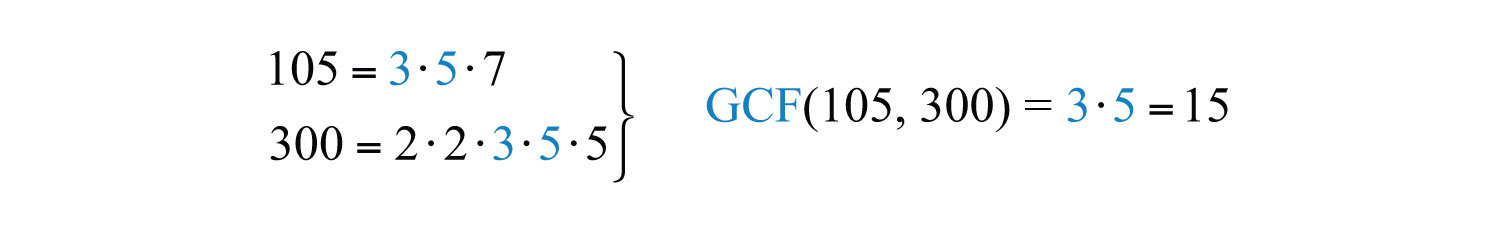
In this case, the common prime factors are 3 and 5 and the greatest common factor of 105 and 300 is 15.
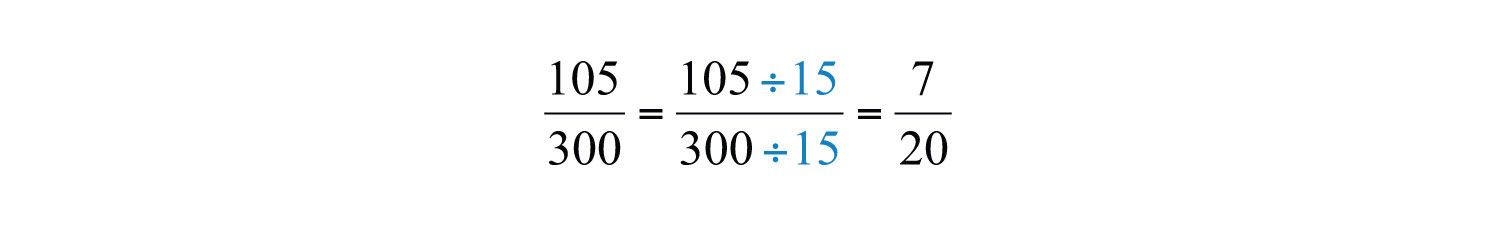
Answer:
Try this! Reduce to lowest terms: .
Answer:
Video Solution
(click to see video)An improper fractionA fraction where the numerator is larger than the denominator. is one where the numerator is larger than the denominator. A mixed numberA number that represents the sum of a whole number and a fraction. is a number that represents the sum of a whole number and a fraction. For example, is a mixed number that represents the sum . Use long division to convert an improper fraction to a mixed number; the remainder is the numerator of the fractional part.
Example 2: Write as a mixed number.
Solution: Notice that 5 divides into 23 four times with a remainder of 3.
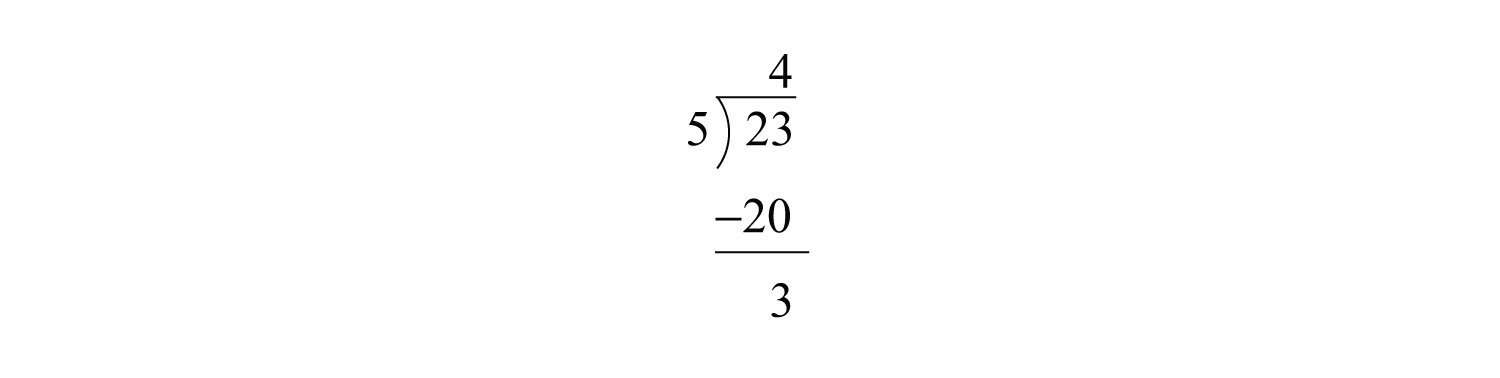
We then can write
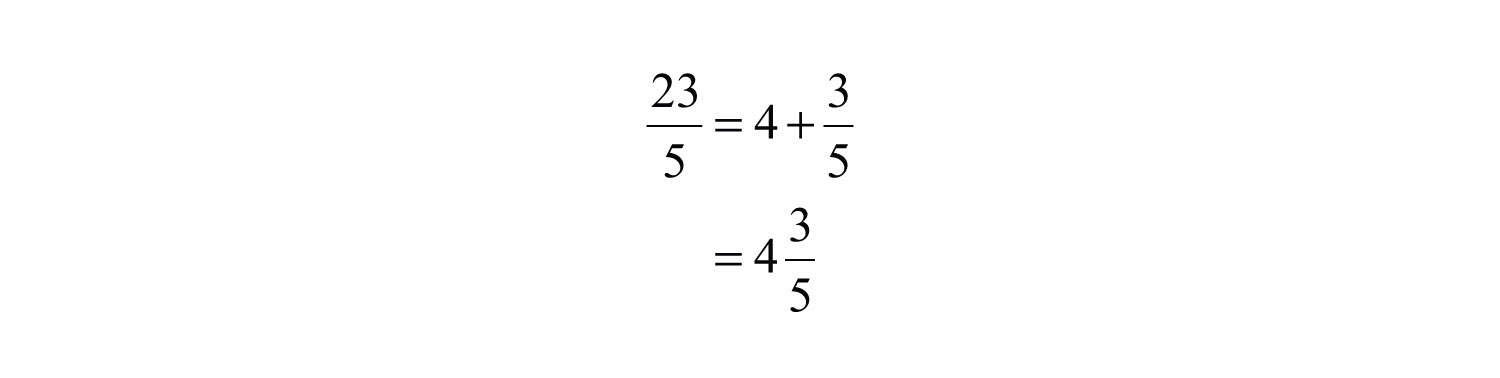
Note that the denominator of the fractional part of the mixed number remains the same as the denominator of the original fraction.
Answer:
To convert mixed numbers to improper fractions, multiply the whole number by the denominator and then add the numerator; write this result over the original denominator.
Example 3: Write as an improper fraction.
Solution: Obtain the numerator by multiplying 7 times 3 and then add 5.
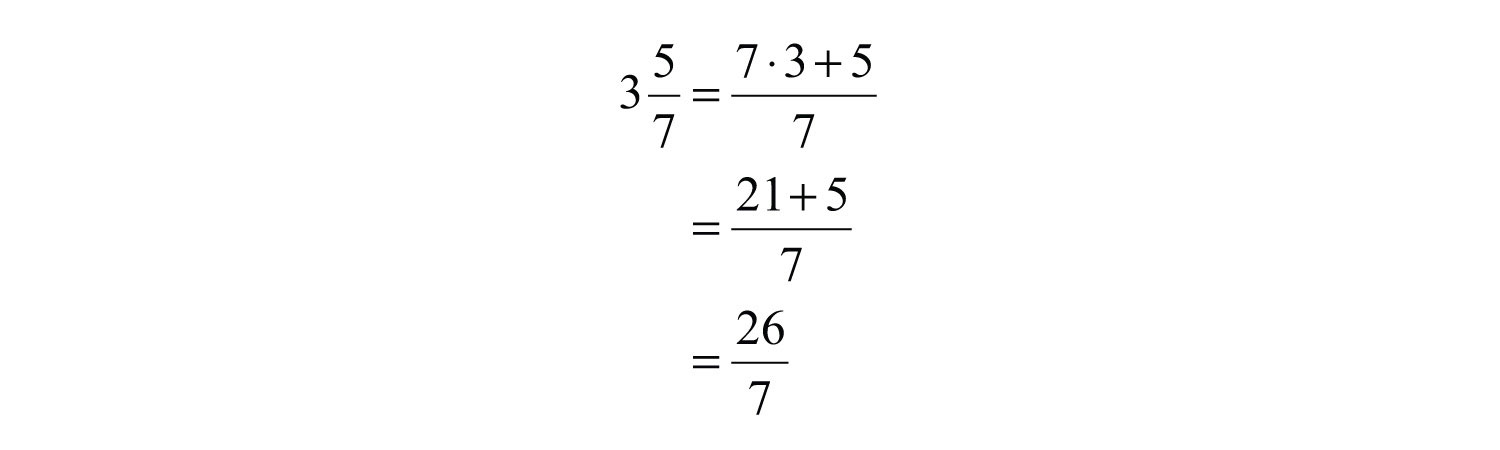
Answer:
It is important to note that converting to a mixed number is not part of the reducing process. We consider improper fractions, such as , to be reduced to lowest terms. In algebra it is often preferable to work with improper fractions, although in some applications, mixed numbers are more appropriate.
Try this! Convert to an improper fraction.
Answer:
Video Solution
(click to see video)Multiplying and Dividing Fractions
In this section, assume that a, b, c, and d are all nonzero integers. The product of two fractions is the fraction formed by the product of the numerators and the product of the denominators. In other words, to multiply fractions, multiply the numerators and multiply the denominators:
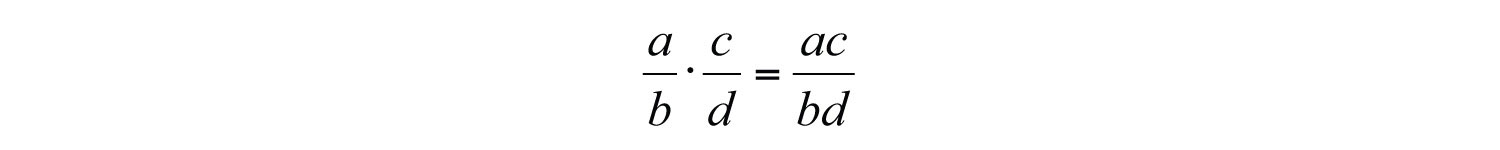
Example 4: Multiply: .
Solution: Multiply the numerators and multiply the denominators.
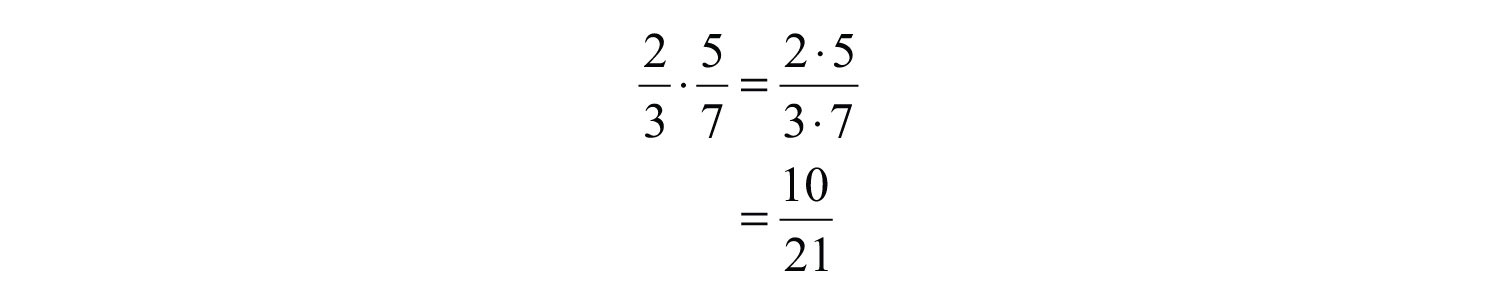
Answer:
Example 5: Multiply: .
Solution: Recall that the product of a positive number and a negative number is negative.
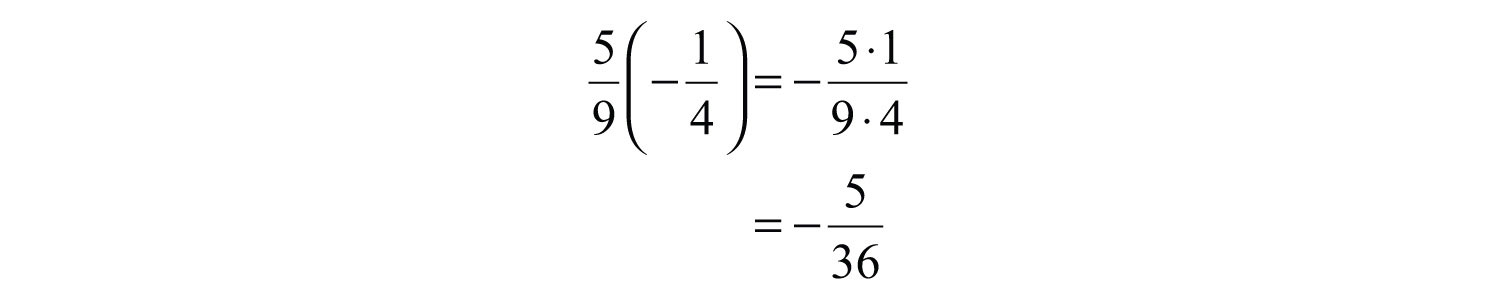
Answer:
Example 6: Multiply: .
Solution: Begin by converting to an improper fraction.

In this example, we noticed that we could reduce before we multiplied the numerators and the denominators. Reducing in this way is called cross cancelingCancelling common factors in the numerator and the denominator of fractions before multiplying., and can save time when multiplying fractions.
Answer:
Two real numbers whose product is 1 are called reciprocalsThe reciprocal of a nonzero number n is 1/n.. Therefore, and are reciprocals because . For example,
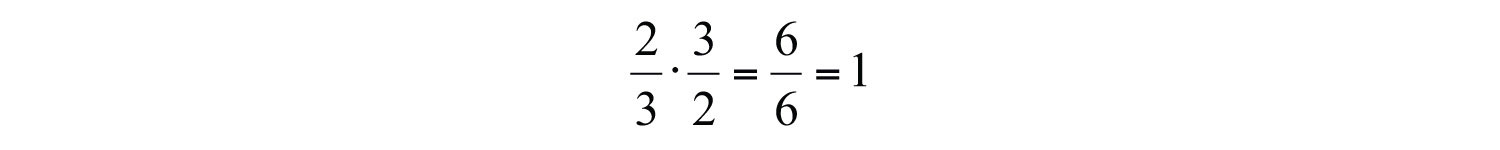
Because their product is 1, and are reciprocals. Some other reciprocals are listed below:
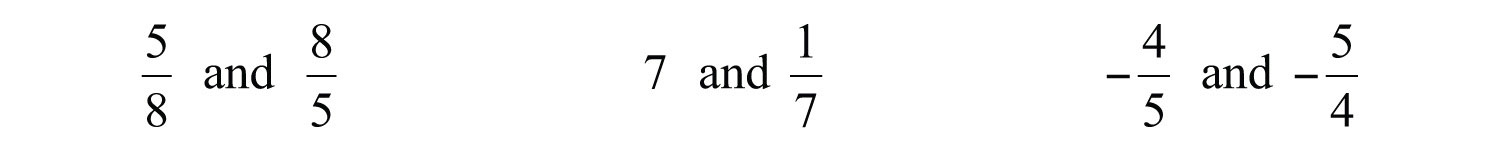
This definition is important because dividing fractions requires that you multiply the dividend by the reciprocal of the divisor.
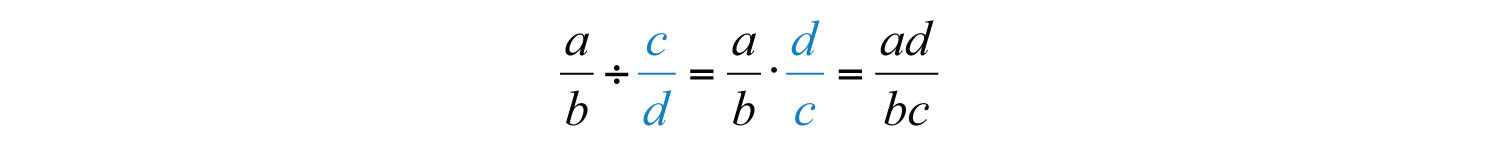
Example 7: Divide: .
Solution: Multiply by the reciprocal of .
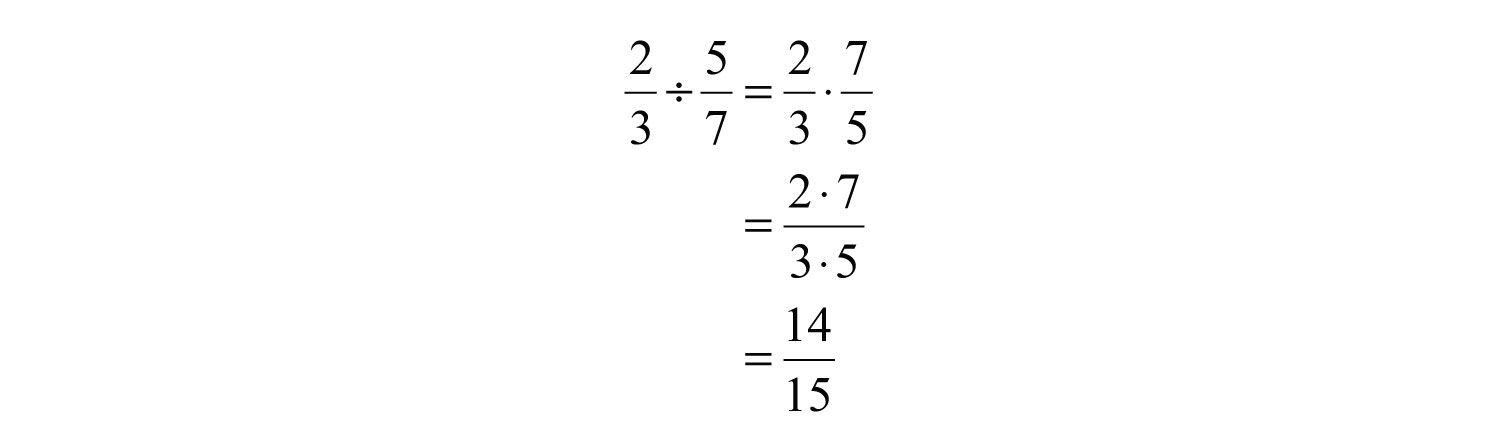
Answer:
You also need to be aware of other forms of notation that indicate division: / and —. For example,
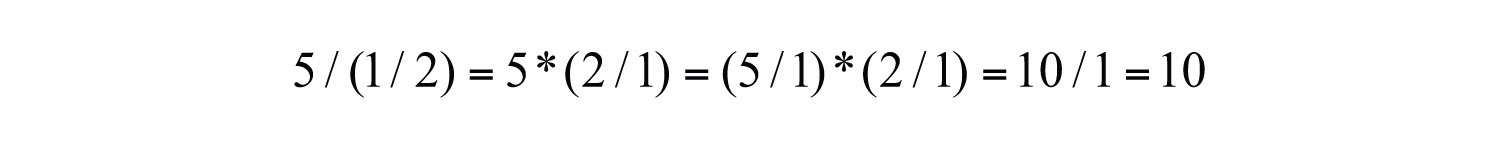
Or
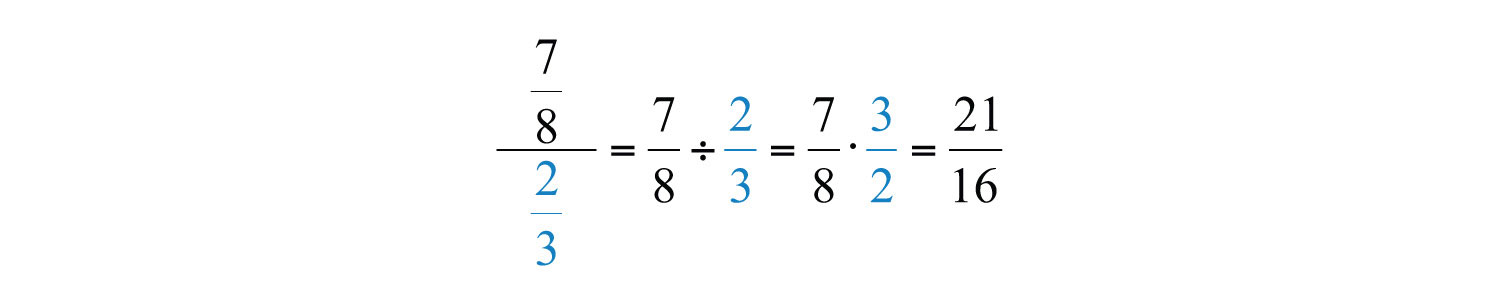
The latter is an example of a complex fractionA fraction where the numerator or denominator consists of one or more fractions., which is a fraction whose numerator, denominator, or both are fractions.
Note
Students often ask why dividing is equivalent to multiplying by the reciprocal of the divisor. A mathematical explanation comes from the fact that the product of reciprocals is 1. If we apply the multiplicative identity property and multiply numerator and denominator by the reciprocal of the denominator, then we obtain the following:
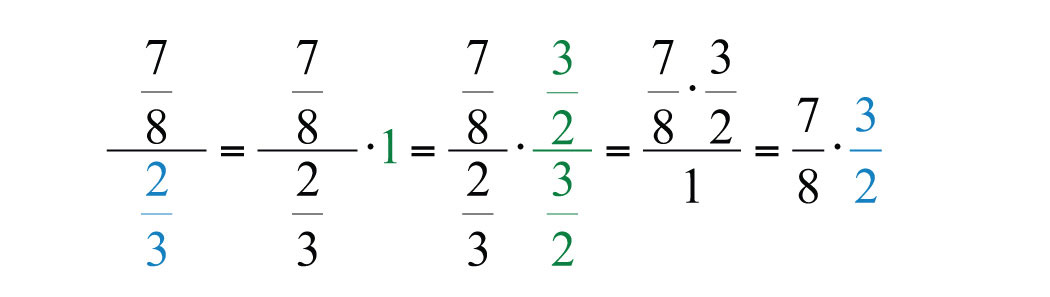
Before multiplying, look for common factors to cancel; this eliminates the need to reduce the end result.
Example 8: Divide: .
Solution:
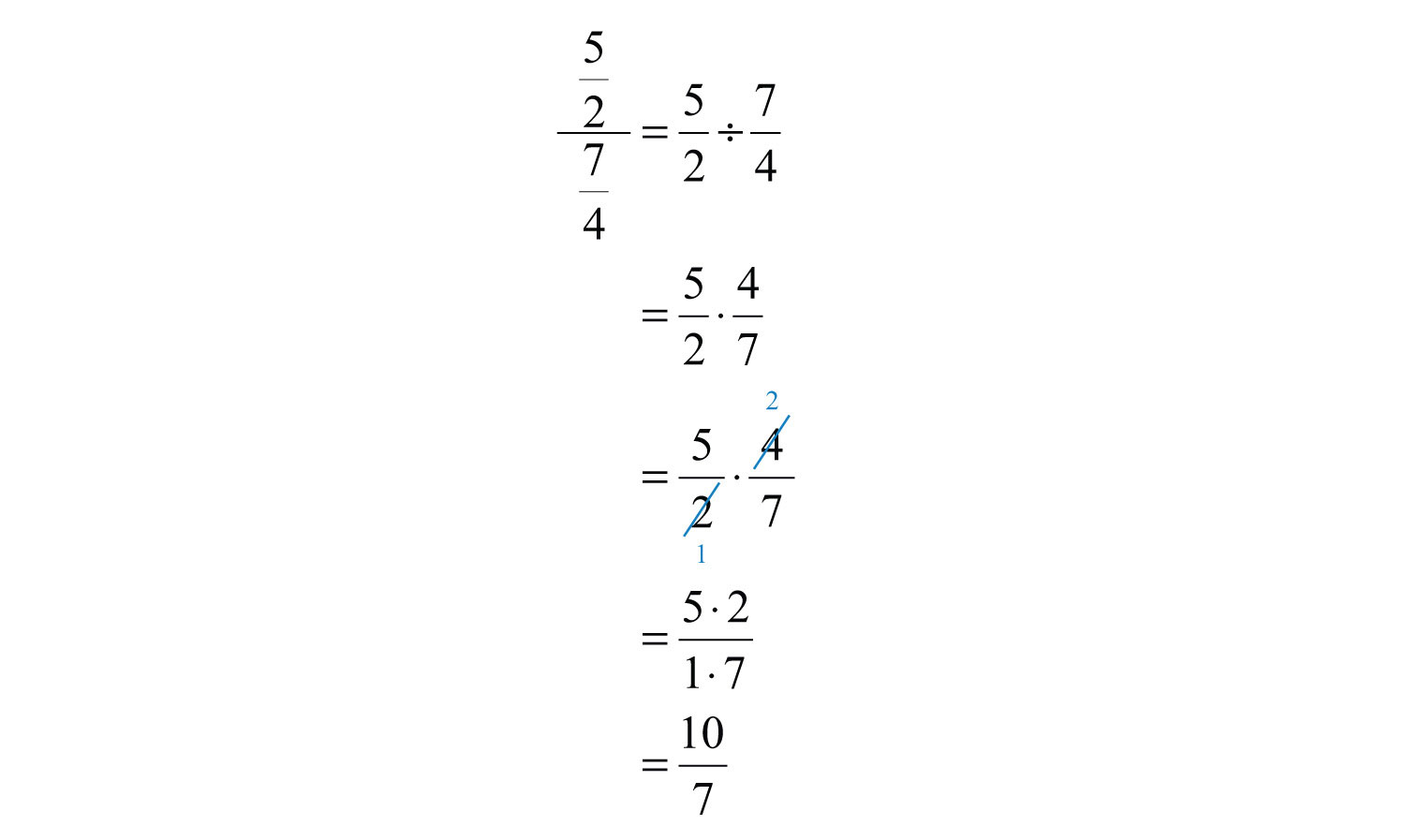
Answer:
When dividing by an integer, it is helpful to rewrite it as a fraction over 1.
Example 9: Divide: .
Solution: Rewrite 6 as and multiply by its reciprocal.
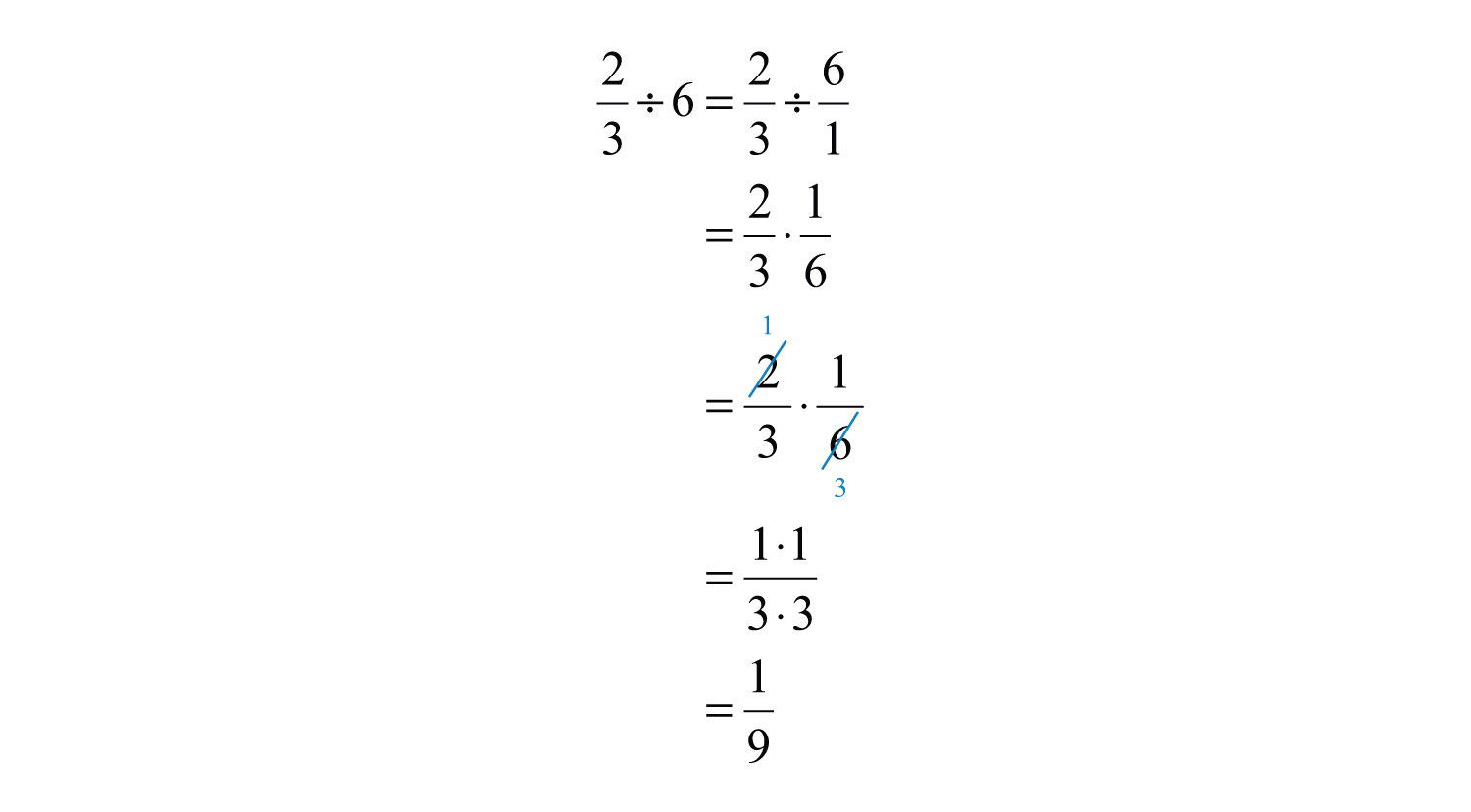
Answer:
Also, note that we only cancel when working with multiplication. Rewrite any division problem as a product before canceling.
Try this! Divide: .
Answer:
Video Solution
(click to see video)Adding and Subtracting Fractions
Negative fractions are indicated with the negative sign in front of the fraction bar, in the numerator, or in the denominator. All such forms are equivalent and interchangeable.
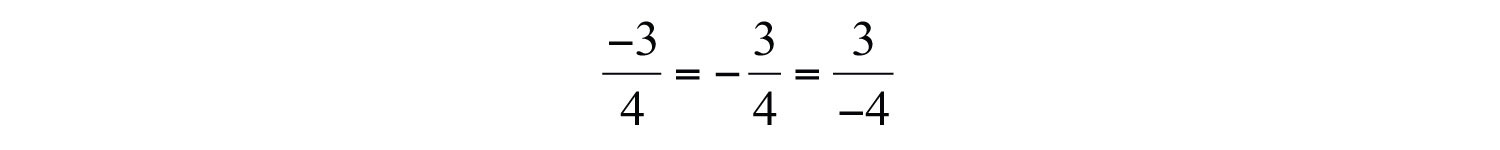
Adding or subtracting fractions requires a common denominatorA denominator that is shared by more than one fraction.. In this section, assume the common denominator c is a nonzero integer.
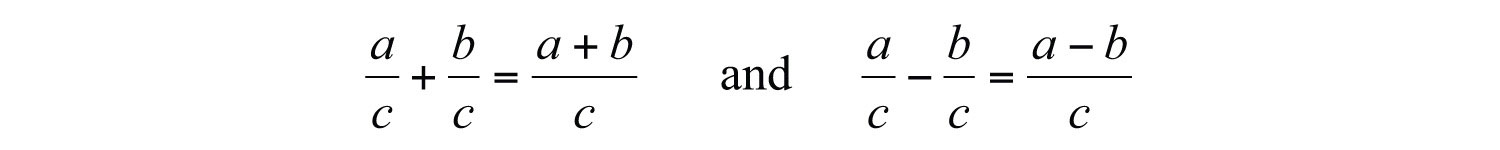
It is good practice to use positive common denominators by expressing negative fractions with negative numerators. In short, avoid negative denominators.
Example 10: Subtract: .
Solution: The two fractions have a common denominator 15. Therefore, subtract the numerators and write the result over the common denominator:

Answer:
Most problems that you are likely to encounter will have unlike denominatorsDenominators of fractions that are not the same.. In this case, first find equivalent fractions with a common denominator before adding or subtracting the numerators. One way to obtain equivalent fractions is to divide the numerator and the denominator by the same number. We now review a technique for finding equivalent fractions by multiplying the numerator and the denominator by the same number. It should be clear that 5/5 is equal to 1 and that 1 multiplied times any number is that number:
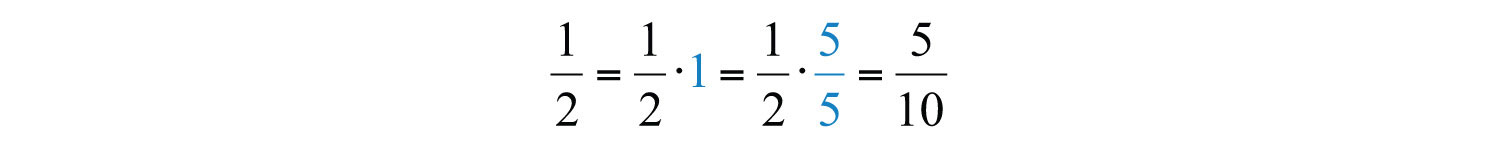
We have equivalent fractions . Use this idea to find equivalent fractions with a common denominator to add or subtract fractions. The steps are outlined in the following example.
Example 11: Subtract: .
Solution:
Step 1: Determine a common denominator. To do this, use the least common multiple (LCM)The smallest number that is evenly divisible by a set of numbers. of the given denominators. The LCM of 15 and 10 is indicated by LCM(15, 10). Try to think of the smallest number that both denominators divide into evenly. List the multiples of each number:

Common multiples are listed in bold, and the least common multiple is 30.
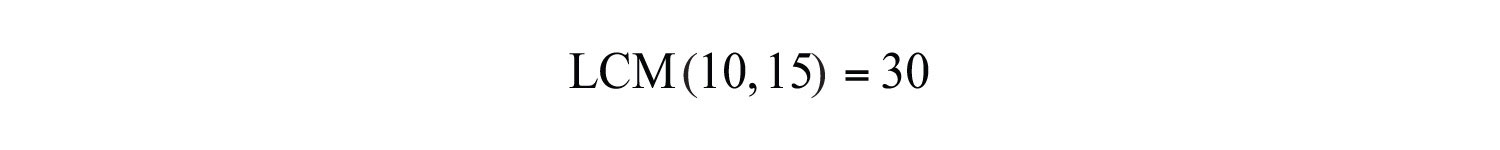
Step 2: Multiply the numerator and the denominator of each fraction by values that result in equivalent fractions with the determined common denominator.
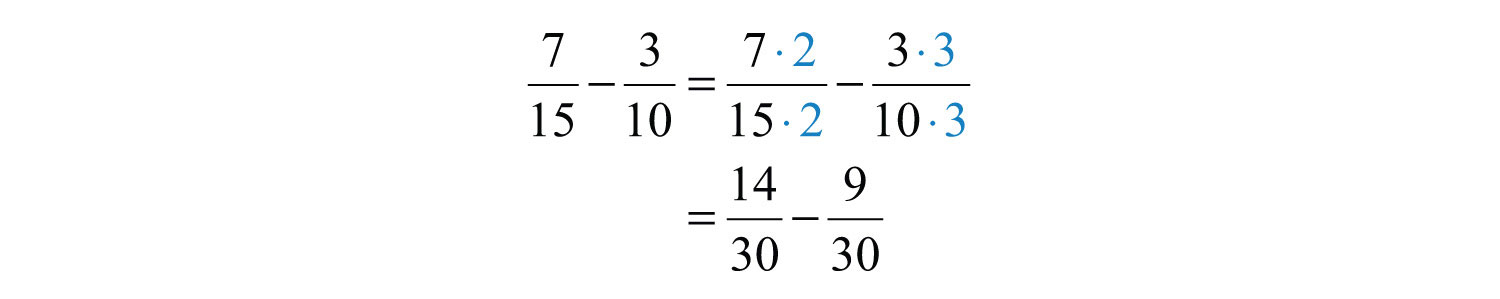
Step 3: Add or subtract the numerators, write the result over the common denominator and then reduce if possible.
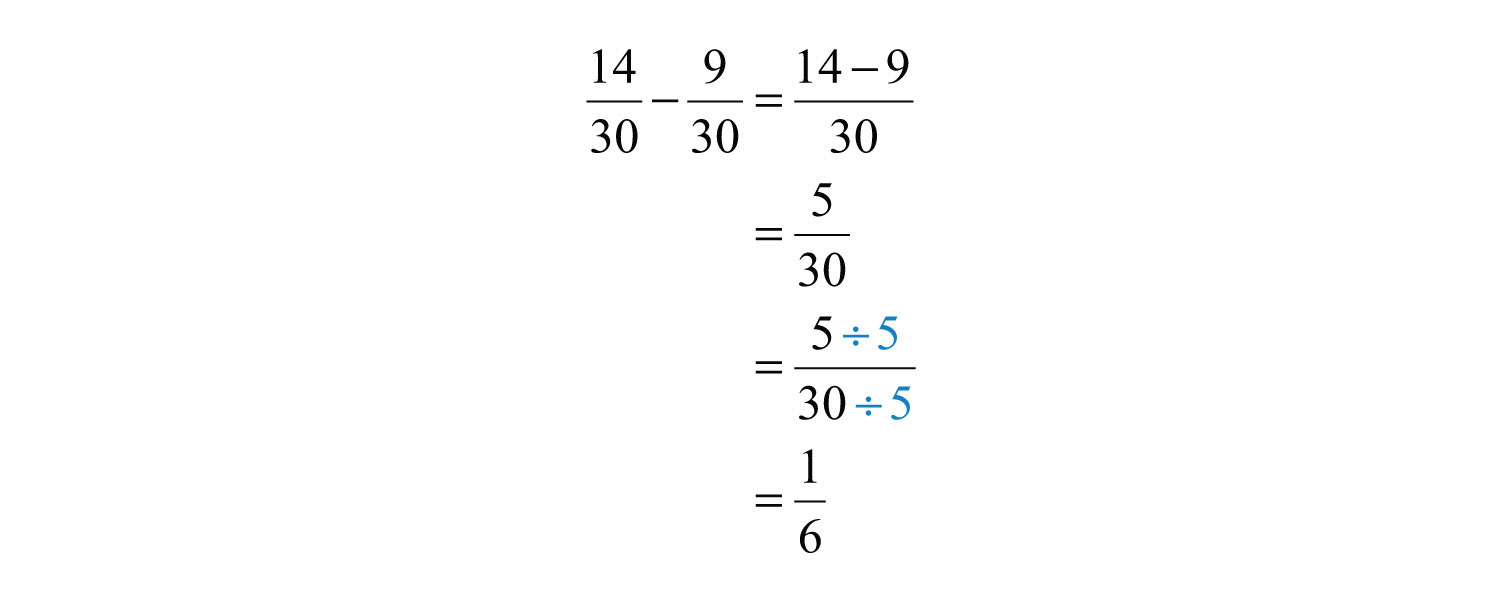
Answer:
The least common multiple of the denominators is called the least common denominator (LCD)The least common multiple of a set of denominators.. Finding the LCD is often the difficult step. It is worth finding because if any common multiple other than the least is used, then there will be more steps involved when reducing.
Example 12: Add: .
Solution: First, determine that the LCM(10, 18) is 90 and then find equivalent fractions with 90 as the denominator.
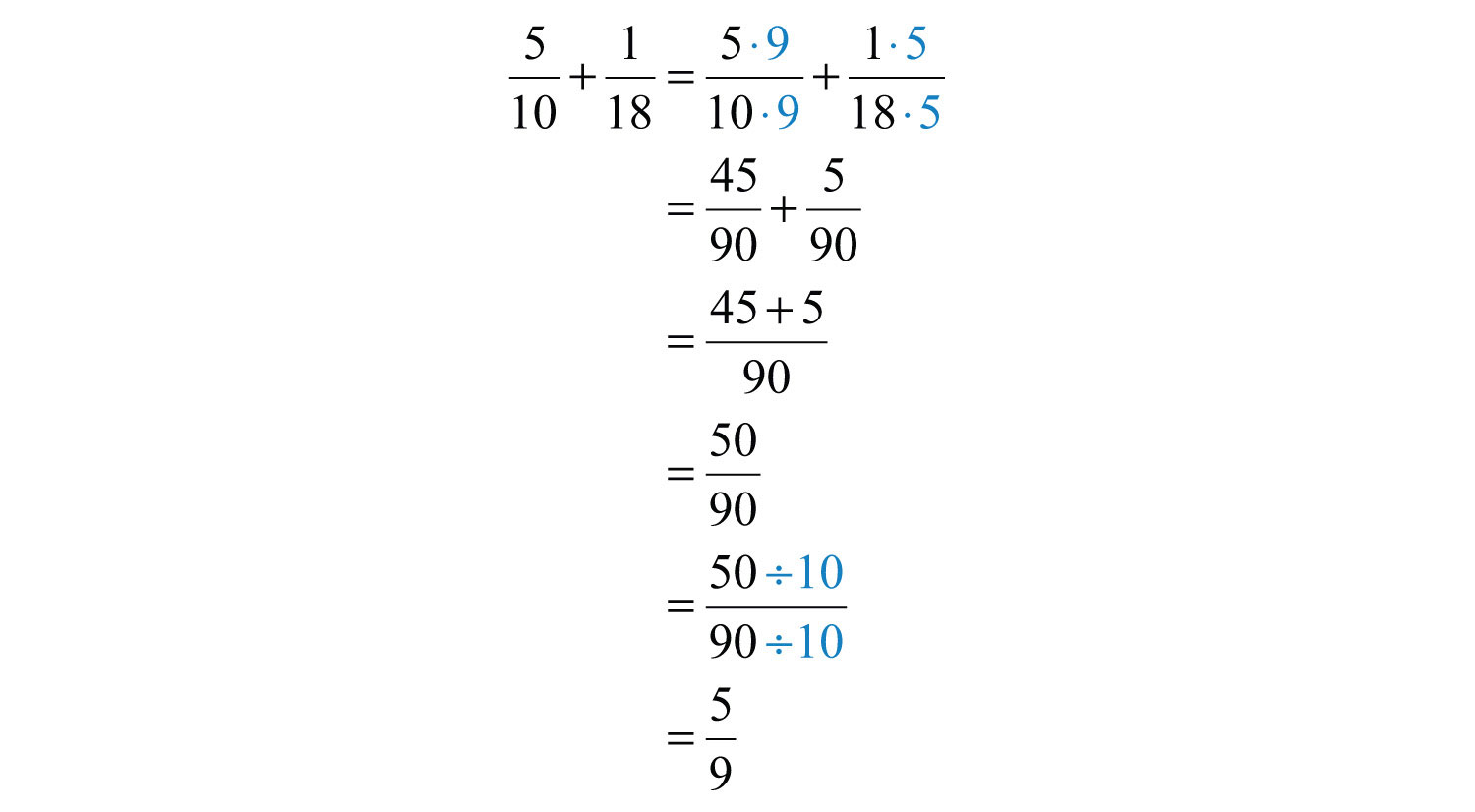
Answer:
Try this! Add: .
Answer:
Video Solution
(click to see video)
Example 13: Simplify: .
Solution: Begin by converting to an improper fraction.

Answer:
In general, it is preferable to work with improper fractions. However, when the original problem involves mixed numbers, if appropriate, present your answers as mixed numbers. Also, mixed numbers are often preferred when working with numbers on a number line and with real-world applications.
Try this! Subtract: .
Answer:
Video Solution
(click to see video)
Example 14: How many inch thick paperback books can be stacked to fit on a shelf that is feet in height?
Solution: First, determine the height of the shelf in inches. To do this, use the fact that there are 12 inches in 1 foot and multiply as follows:
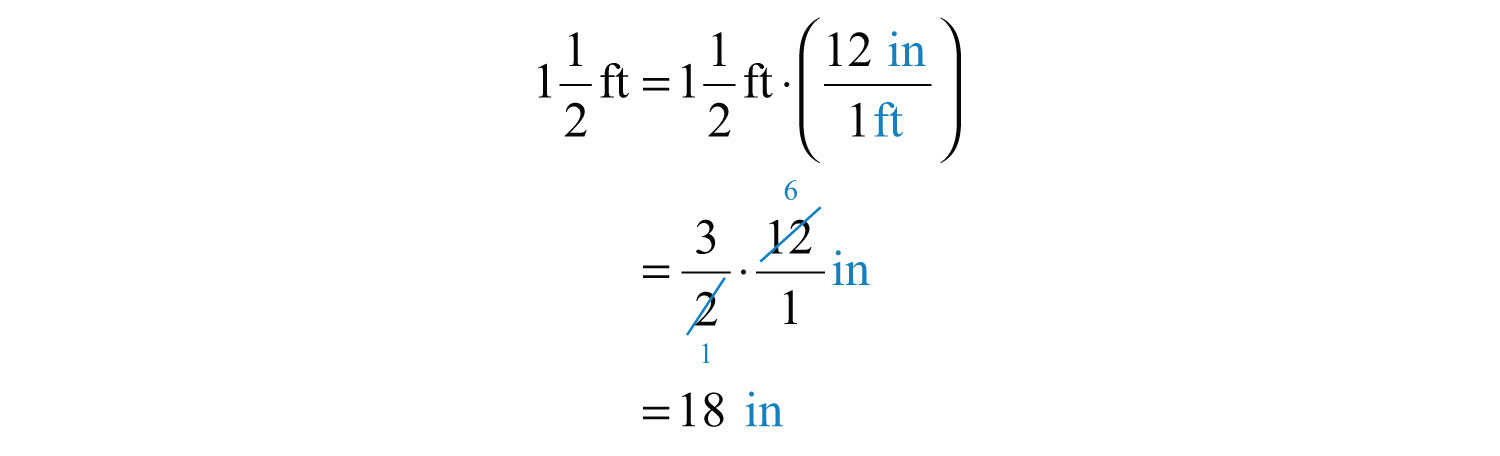
Next, determine how many notebooks will fit by dividing the height of the shelf by the thickness of each book.
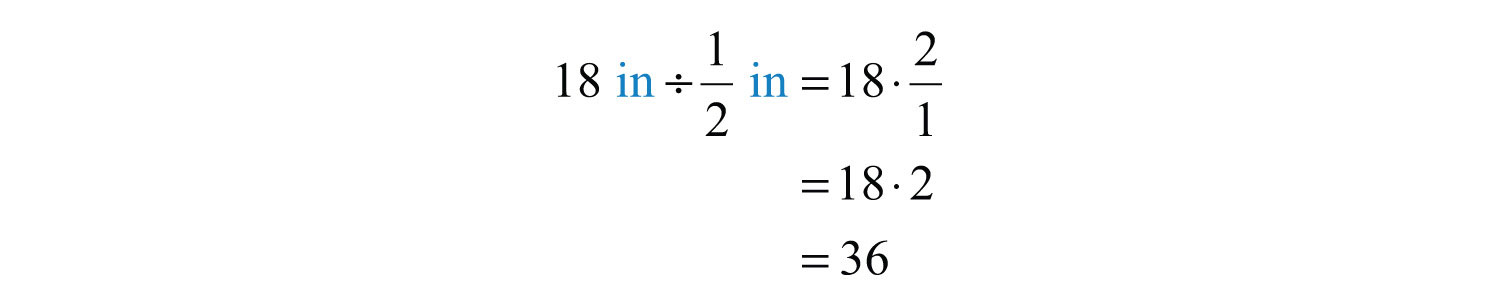
Answer: 36 books can be stacked on the shelf.
Key Takeaways
- Fractions are not unique; there are many ways to express the same ratio. Find equivalent fractions by multiplying or dividing the numerator and the denominator by the same real number.
- Equivalent fractions in lowest terms are generally preferred. It is a good practice to always reduce.
- In algebra, improper fractions are generally preferred. However, in real-life applications, mixed number equivalents are often preferred. We may present answers as improper fractions unless the original question contains mixed numbers, or it is an answer to a real-world or geometric application.
- Multiplying fractions does not require a common denominator; multiply the numerators and multiply the denominators to obtain the product. It is a best practice to cancel any common factors in the numerator and the denominator before multiplying.
- Reciprocals are rational numbers whose product is equal to 1. Given a fraction , its reciprocal is .
- Divide fractions by multiplying the dividend by the reciprocal of the divisor. In other words, multiply the numerator by the reciprocal of the denominator.
- Rewrite any division problem as a product before canceling.
- Adding or subtracting fractions requires a common denominator. When the denominators of any number of fractions are the same, simply add or subtract the numerators and write the result over the common denominator.
- Before adding or subtracting fractions, ensure that the denominators are the same by finding equivalent fractions with a common denominator. Multiply the numerator and the denominator of each fraction by the appropriate value to find the equivalent fractions.
- Typically, it is best to convert all mixed numbers to improper fractions before beginning the process of adding, subtracting, multiplying, or dividing.
Topic Exercises
Part A: Working with Fractions
Reduce each fraction to lowest terms.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
Rewrite as an improper fraction.
16.
17.
18.
19.
20.
21.
22.
23.
Rewrite as a mixed number.
24.
25.
26.
27.
28.
29.
30.
Part B: Multiplying and Dividing
Multiply and reduce to lowest terms.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
Determine the reciprocal of the following numbers.
51.
52.
53.
54.
55.
56.
57.
58.
Divide and reduce to lowest terms.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
Part C: Adding and Subtracting Fractions
Add or subtract and reduce to lowest terms.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
Part D: Mixed Exercises
Perform the operations. Reduce answers to lowest terms.
99.
100.
101.
102.
103.
104.
105.
106.
107. What is the product of and ?
108. What is the product of and ?
109. What is the quotient of and ?
110. What is the quotient of and 32?
111. Subtract from the sum of and .
112. Subtract from the sum of and .
113. What is the total width when 3 boards, each with a width of inches, are glued together?
114. The precipitation in inches for a particular 3-day weekend was published as inches on Friday, inches on Saturday, and inches on Sunday. Calculate the total precipitation over this period.
115. A board that is feet long is to be cut into 7 pieces of equal length. What is length of each piece?
116. How many inch thick notebooks can be stacked into a box that is 2 feet high?
117. In a mathematics class of 44 students, one-quarter of the students signed up for a special Saturday study session. How many students signed up?
118. Determine the length of fencing needed to enclose a rectangular pen with dimensions feet by feet.
119. Each lap around the track measures mile. How many laps are required to complete a mile run?
120. A retiree earned a pension that consists of three-fourths of his regular monthly salary. If his regular monthly salary was $5,200, then what monthly payment can the retiree expect from the pension plan?
Part E: Discussion Board Topics
121. Does 0 have a reciprocal? Explain.
122. Explain the difference between the LCM and the GCF. Give an example.
123. Explain the difference between the LCM and LCD.
124. Why is it necessary to find an LCD in order to add or subtract fractions?
125. Explain how to determine which fraction is larger, or .
Answers
1: 1/6
3: 3/7
5: 11/21
7: 9/2
9: 3
11: 14/5
13: 1/3
15: 3/4
17: 5/2
19: 3/2
21: 7/4
23: −7/4
25:
27:
29:
31: 10/21
33: 1/6
35: 7/2
37: 3/4
39:
41: −15/22
43: 27/50
45: 3/8
47: 1/42
49: 1
51: 2
53: −3/2
55: 1/10
57: 3/7
59: 3/4
61: −25/32
63: 1
65: 40/3
67: 9/25
69: 25/2
71:
73:
75: 3/5
77: 4/5
79:
81: 5/6
83: −7/4
85: 1/6
87: 32/105
89:
91: 1
93: 29/30
95:
97: 19/24
99: 4
101: 2/15
103: 9/28
105: 1/10
107: 1/12
109: 1/15
111: 5
113: inches
115: feet
117: 11 students
119: 10 laps
1.5 Review of Decimals and Percents
Learning Objectives
- Convert fractions to decimals and back.
- Perform operations with decimals.
- Round off decimals to a given place.
- Define a percent.
- Convert percents to decimals and back.
- Convert fractions to percents and back.
Decimals
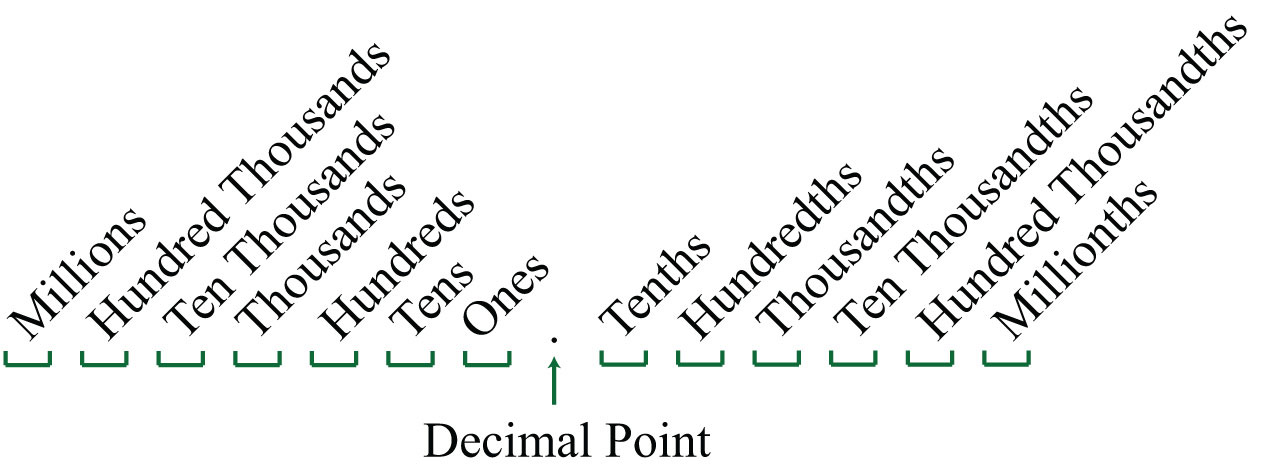
In this section, we provide a brief review of the decimal system. A real number in decimal form, a decimalA real number expressed using the decimal system. consists of a decimal point, digits (0 through 9) to the left of the decimal point representing the whole number part, and digits to the right of the decimal point representing the fractional part. The digits represent powers of 10 as shown in the set {…, 1,000, 100, 10, 1, 1/10, 1/100, 1/1,000, …} according to the following diagram:
For example, the decimal 538.3 can be written in the following expanded form:
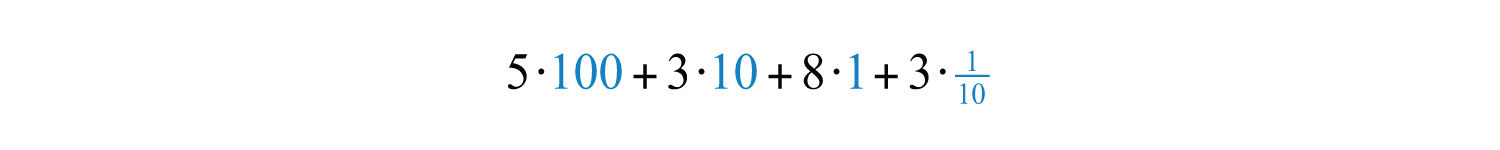
After simplifying, we obtain the mixed number . Use this process to convert decimals to mixed numbers.
Example 1: Write as a mixed number: 32.15.
Solution: In this example, 32 is the whole part and the decimal ends in the hundredths place. Therefore, the fractional part will be 15/100, and we can write
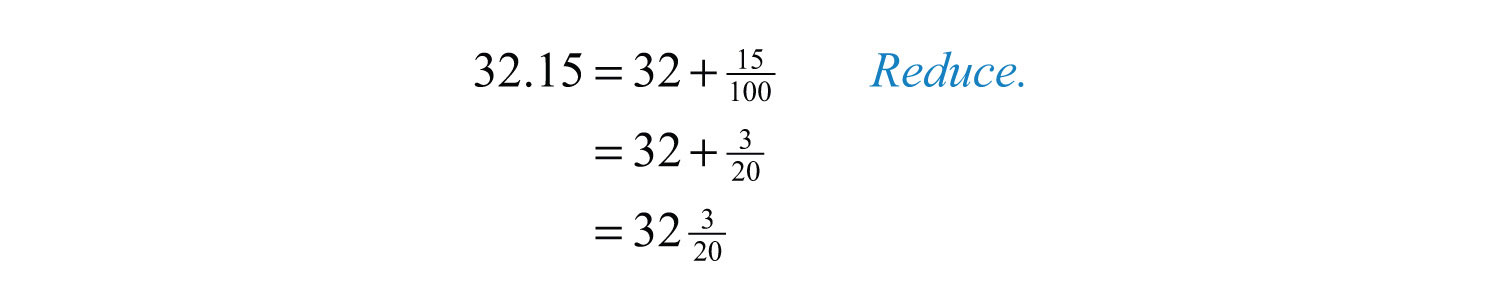
Answer:
To convert fractions to decimal equivalents, divide.
Example 2: Write as a decimal: .
Solution: Use long division to convert to a decimal.
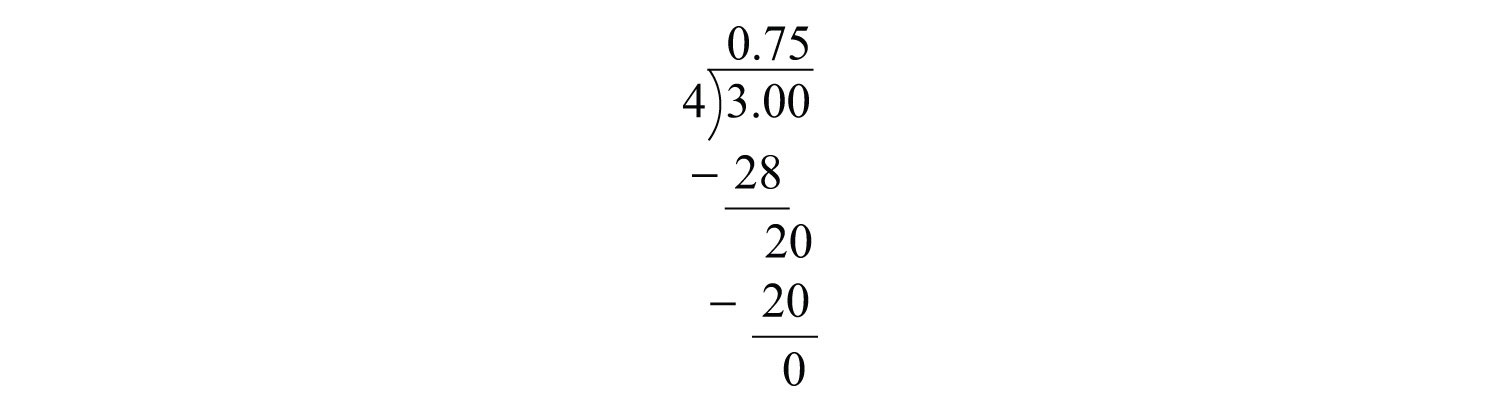
Answer:
If the division never ends, then use a bar over the repeating digit (or block of digits) to indicate a repeating decimal.
Example 3: Write as a decimal: .
Solution: Use long division to convert the fractional part to a decimal and then add the whole part.

At this point, we can see that the long division will continue to repeat. When this is the case, use a bar over the repeating digit to indicate that it continues forever:
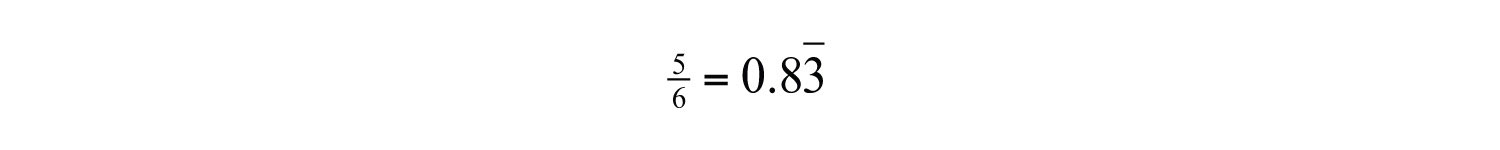
Then write
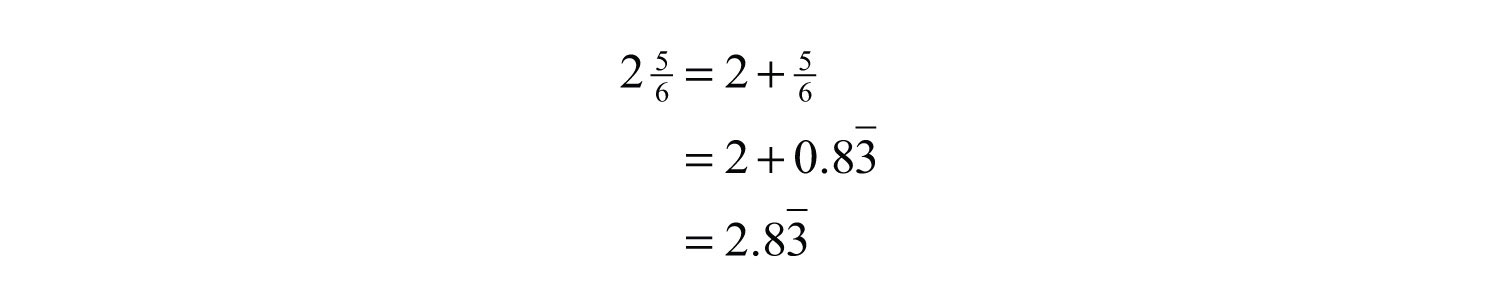
Answer:
To add or subtract decimals, align them vertically with the decimal point and add corresponding place values. Recall that sometimes you need to borrow from or carry over to the adjoining column (regrouping).
Example 4: Subtract: .
Solution: Note that trailing zeros to the right of the decimal point do not change the value of the decimal, 23.25 = 23.250. In this case, you need to borrow from the tenths place (regroup) to subtract the digits in the hundredths place.
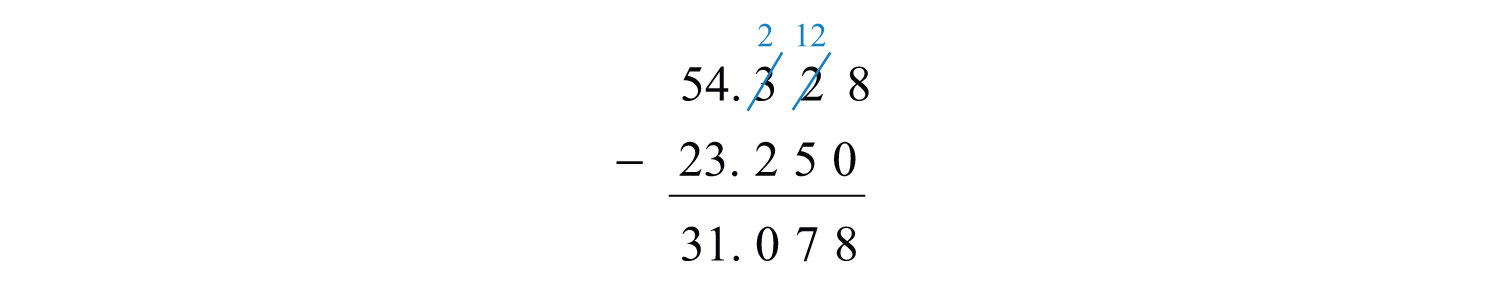
Answer: 31.078
Multiply decimals the same way you multiply whole numbers. The number of decimal places in the product will be the sum of the decimal places found in each of the factors.
Example 5: Multiply: .
Solution: The total number of decimal places of the two factors is 2 + 1 = 3. Therefore, the result has 3 decimal places.

Answer: 39.664
When dividing decimals, move the decimal points of both the dividend and the divisor so that the divisor is a whole number. Remember to move the decimal the same number of places for both the dividend and divisor.
Example 6: Divide: .
Solution: Move the decimal point to turn the divisor into a whole number: 624. Move the decimal points of both the divisor and dividend two places to the right.

Next, divide.
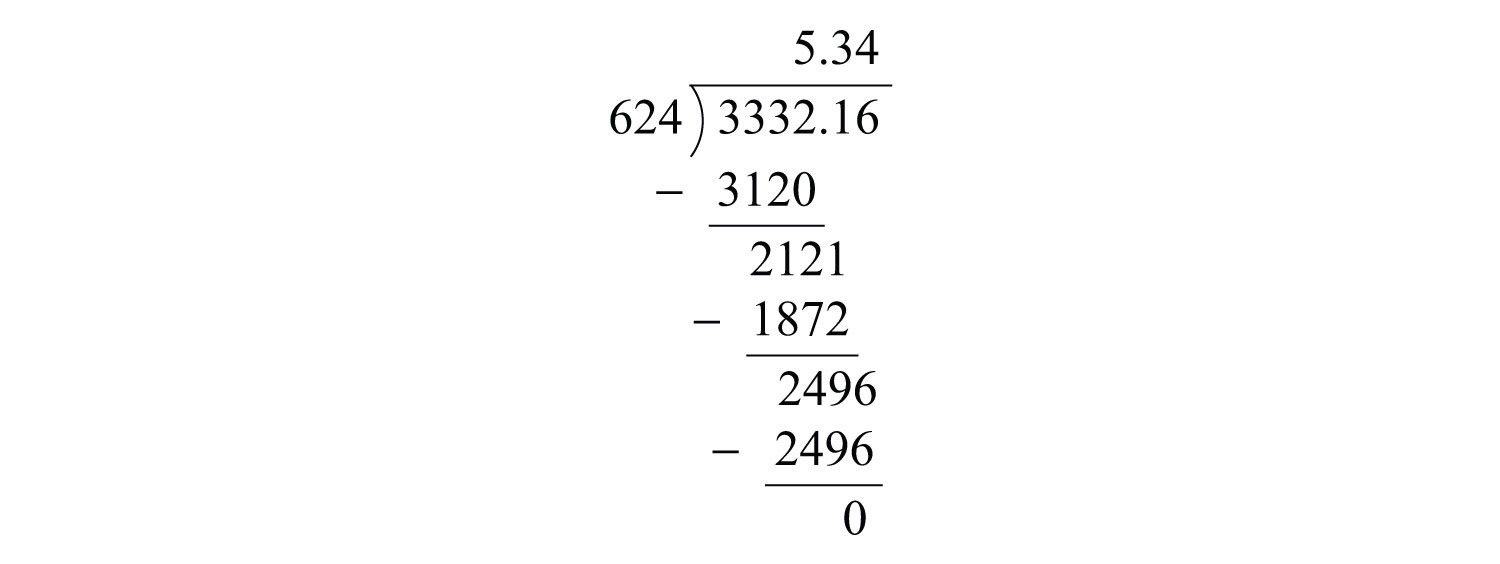
Answer: 5.34
It is often necessary to round offA means of approximating decimals with a specified number of significant digits. decimals to a specified number of decimal places. Rounding off allows us to approximate decimals with fewer significant digits. To do this, look at the digit to the right of the specified place value.
- If the digit to the right of the specified place is 4 or less, then leave the specified digit unchanged and drop all subsequent digits.
- If the digit to the right of the specified place is 5 or greater, then increase the value of the digit in the specified place by 1 and drop all subsequent digits.
Recall that decimals with trailing zeros to the right of the decimal point can be dropped. For example, round 5.635457 to the nearest thousandth:

Round the same number 5.635457 to the nearest hundredth:

After rounding off, be sure to use the appropriate notation ( ) to indicate that the number is now an approximation. When working with US currency, we typically round off to two decimal places, or the nearest hundredth.
Example 7: Calculate and round off to the nearest hundredth.
a. 1/3 of $10.25.
b. 1/4 of $10.25.
Solution: In this context, the key word “of” indicates that we should multiply.
a. Multiplying by is equivalent to dividing by 3.
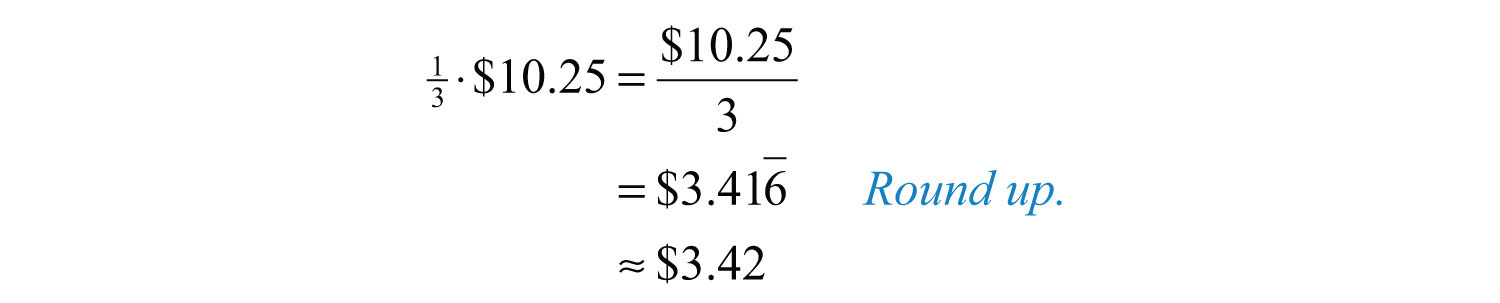
b. Multiplying by is equivalent to dividing by 4.
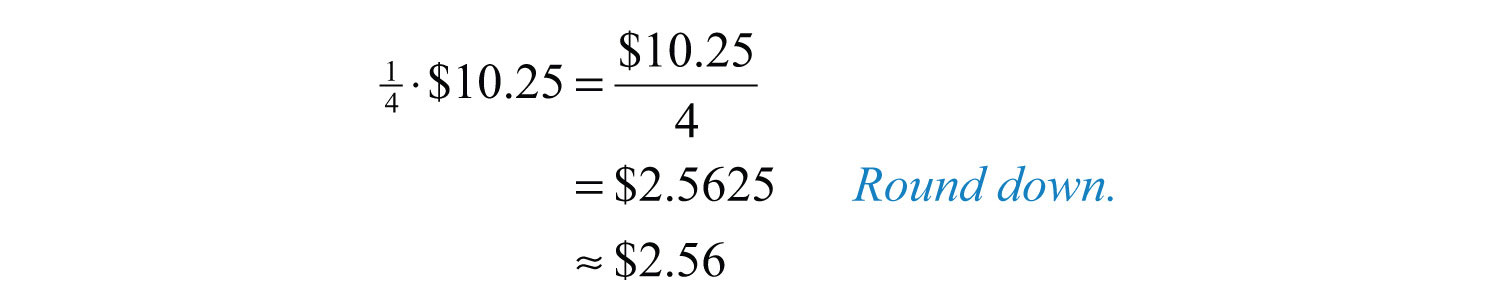
Answers: a. $3.42; b. $2.56
Definition of Percent
A percentA representation of a number as part of 100: . is a representation of a number as a part of one hundred. The word “percent” can be written “per cent” which means “per 100” or “/100.” We use the symbol ( % ) to denote a percentage:
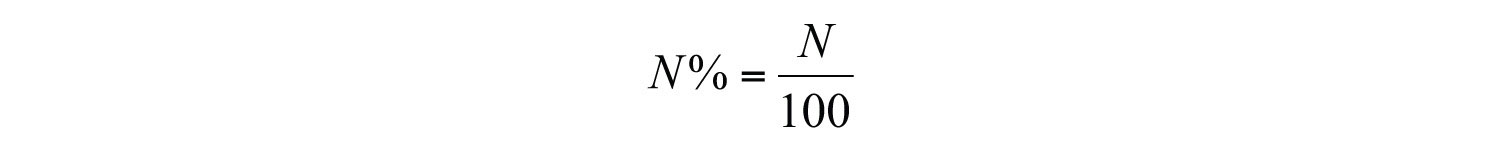
For example,
Percents are an important part of our everyday life and show up often in our study of algebra. Percents can be visualized using a pie chartA circular graph divided into sectors whose area is proportional to the relative size of the ratio of the part to the total. (or circle graph), where each sector gives a visual representation of a percentage of the whole. For example, the following pie chart shows the percentage of students in certain age categories of all US community colleges.
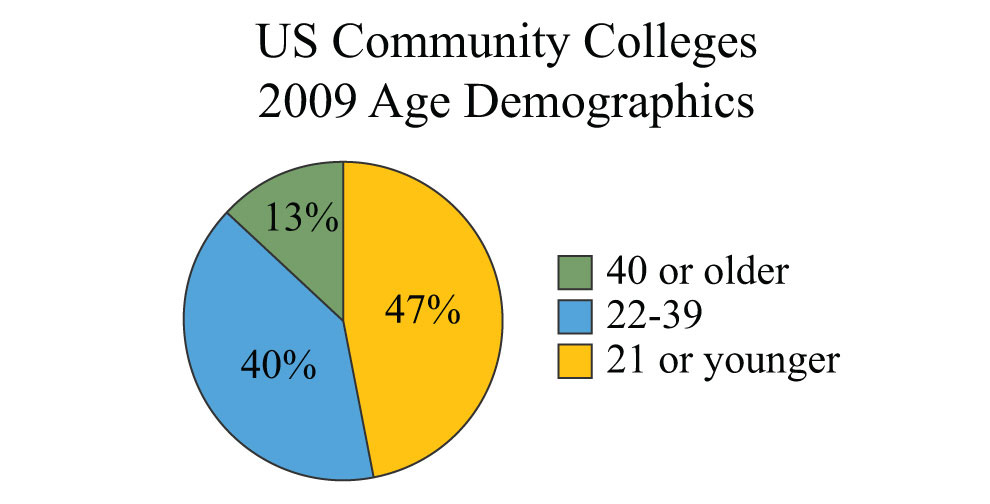
Source: American Association of Community Colleges.
Each sector is proportional to the size of the part out of the whole. The sum of the percentages presented in a pie chart must be 100%. To work with percentages effectively, you have to know how to convert percents to decimals or fractions and back again.
Percents to Decimals
Applying the definition of percent, you see that . The same result can be obtained by moving the decimal two places to the left. To convert percents to decimals, either apply the definition or move the decimal two places to the left.
Example 8: Convert to a decimal: 152%.
Solution: Treat and move the decimal two places to the left.
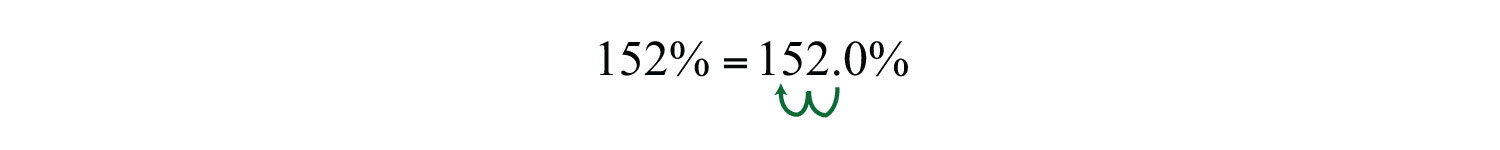
Answer: 1.52
Example 9: Convert to a decimal: .
Solution: First, write the decimal percent equivalent,
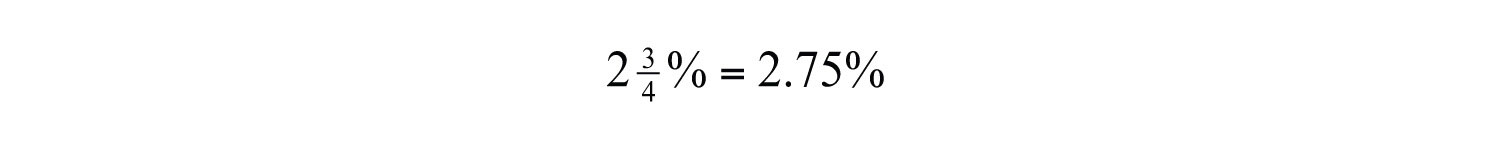
Next, move the decimal two places to the left,

At this point, fill in the tenths place with a zero.
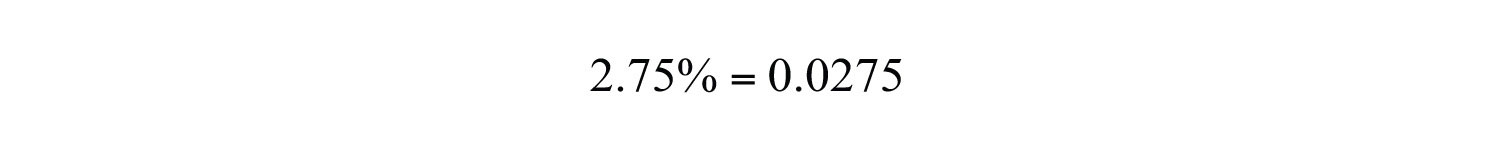
Answer: 0.0275
Try this! Convert to a decimal: 215%.
Answer: 2.15
Video Solution
(click to see video)Decimals and Fractions to Percents
To convert a decimal to a percent, convert the decimal to a fraction of 100 and apply the definition of percent, or equivalently, move the decimal to the right two places and add a percent sign.
Example 10: Convert 0.23 to a percent.
Solution: First, convert the decimal to a fraction of 100 and apply the definition.
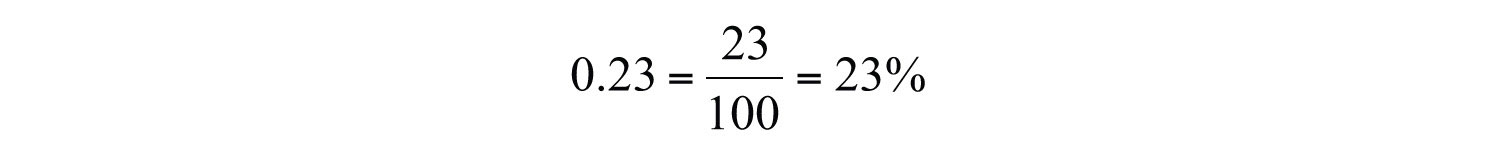
You can achieve the same result by moving the decimal two places to the right and adding a percent sign.
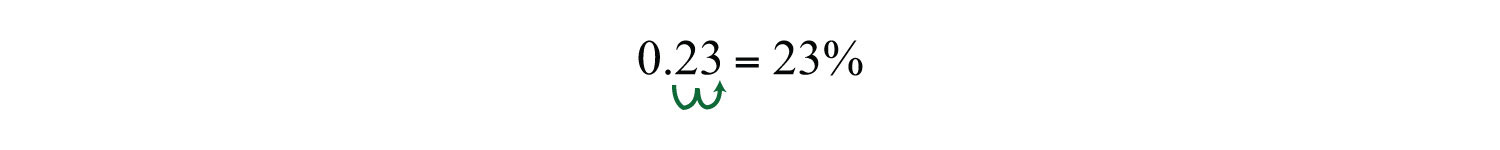
Answer: 23%.
Alternatively, you can multiply by 1 in the form of 100%.
Example 11: Convert 2.35 to a percent.
Solution: Recall that 1 = 100%.
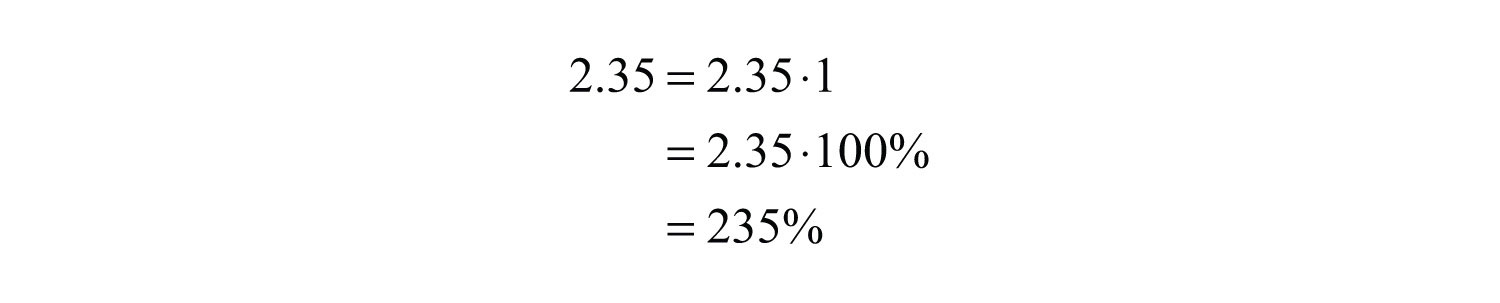
You can achieve the same result by moving the decimal two places to the right and adding a percent sign.
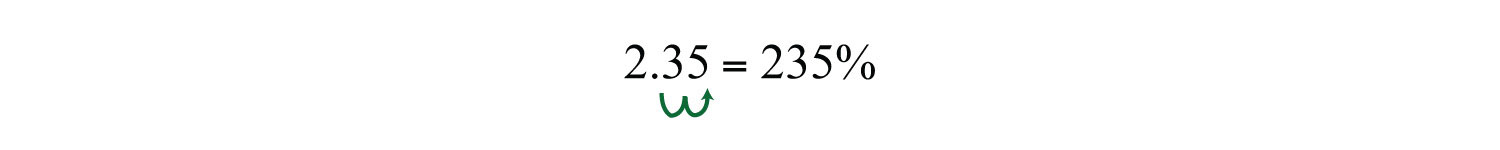
Answer: 235%
Example 12: Convert to a percent.
Solution:
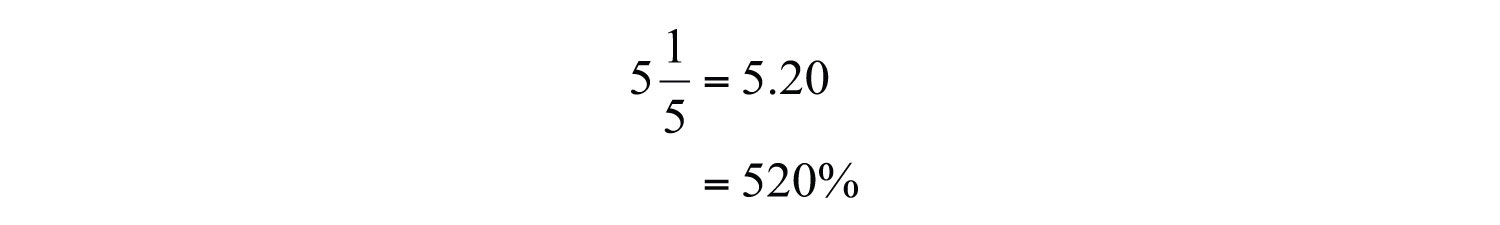
Answer: 520%
Sometimes we can use the definition of percent and find an equivalent fraction with a denominator of 100.
Example 13: Convert to a percent.
Solution: Notice that the denominator 25 is a factor of 100. Use the definition of percent by finding an equivalent fraction with 100 in the denominator.
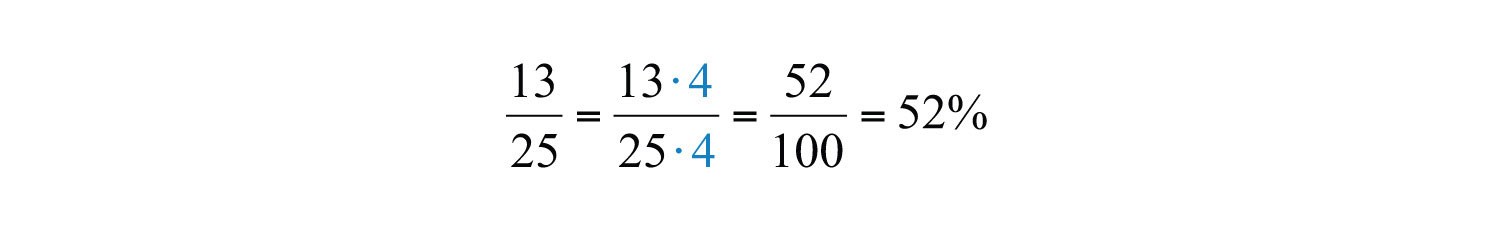
Answer: 52%
This is a very specialized technique because 100 may not be a multiple of the denominator.
Example 14: Convert to a percent.
Solution: Notice that the denominator 3 is not a factor of 100. In this case, it is best to multiply by 1 in the form of 100%.
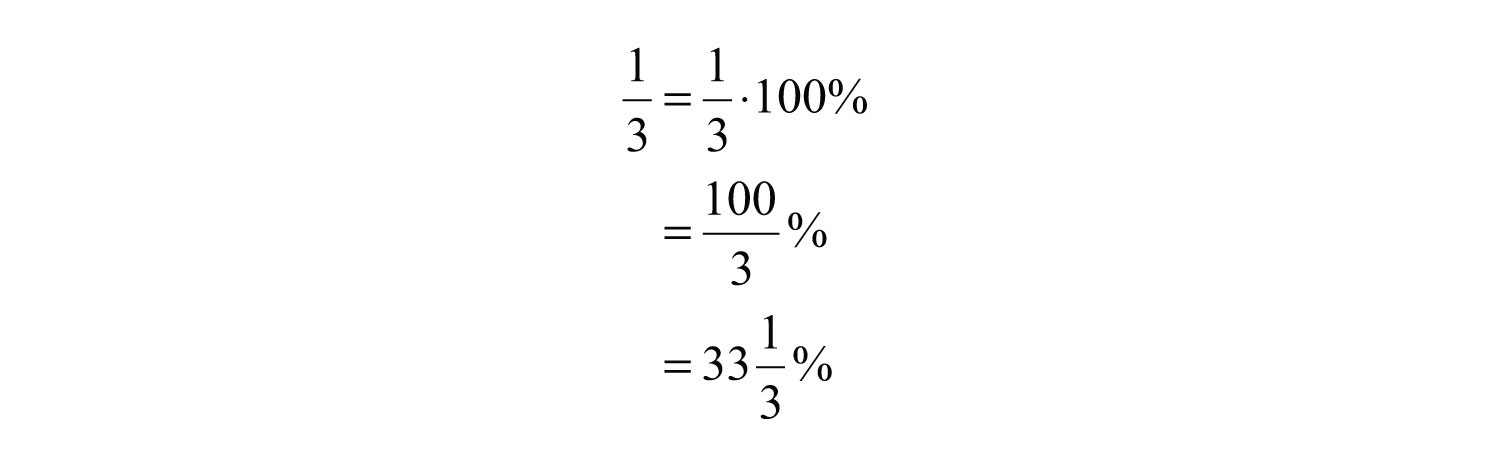
Answer:
Try this! Convert to a percent: .
Answer:
Video Solution
(click to see video)Percents to Fractions
When converting percents to fractions, apply the definition of percent and then reduce.
Example 15: Convert to a fraction: .
Solution:

Answer:
Applying the definition of percent is equivalent to removing the percent sign and multiplying by .
Example 16: Convert to a fraction: .
Solution: First, convert to an improper fraction and then apply the definition of percent.
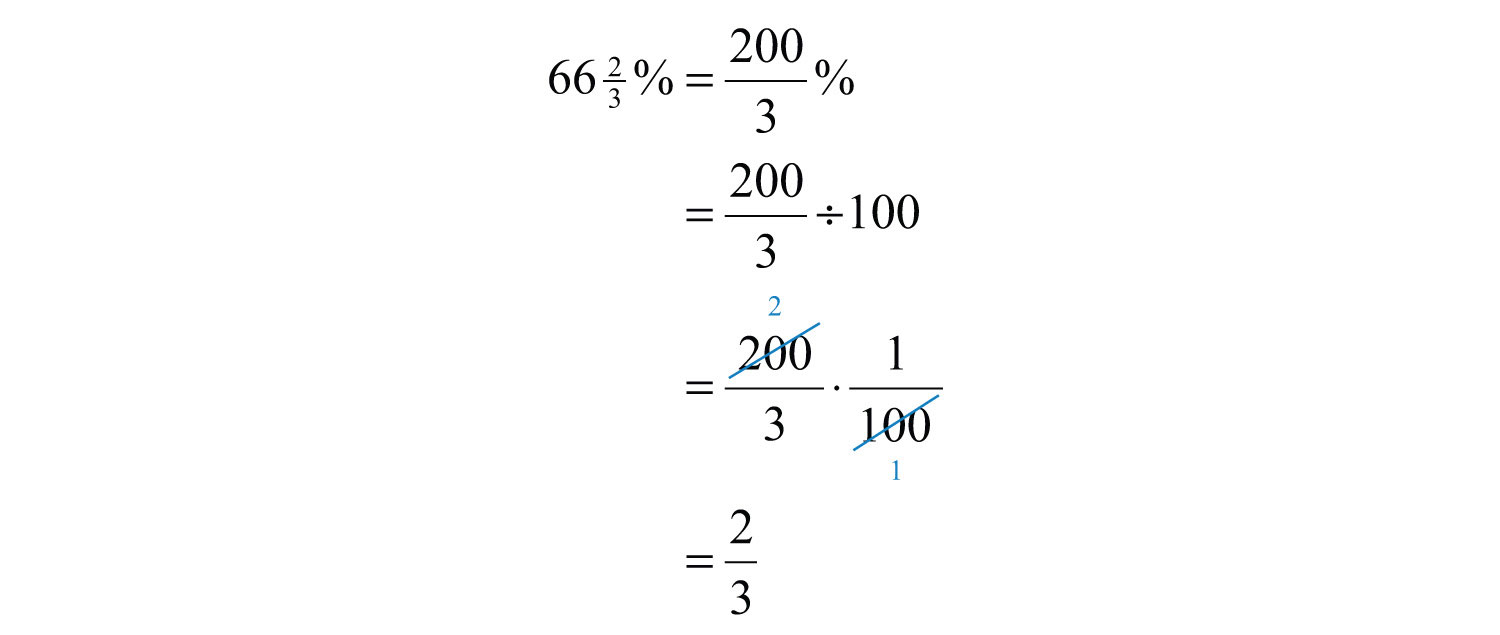
Answer:
Try this! Convert to a fraction: .
Answer:
Video Solution
(click to see video)
Example 17: Using the given pie chart, calculate the total number of students that were 21 years old or younger if the total US community college enrollment in 2009 was 11.7 million.
Solution: From the pie chart we can determine that 47% of the total 11.7 million students were 21 years old or younger.
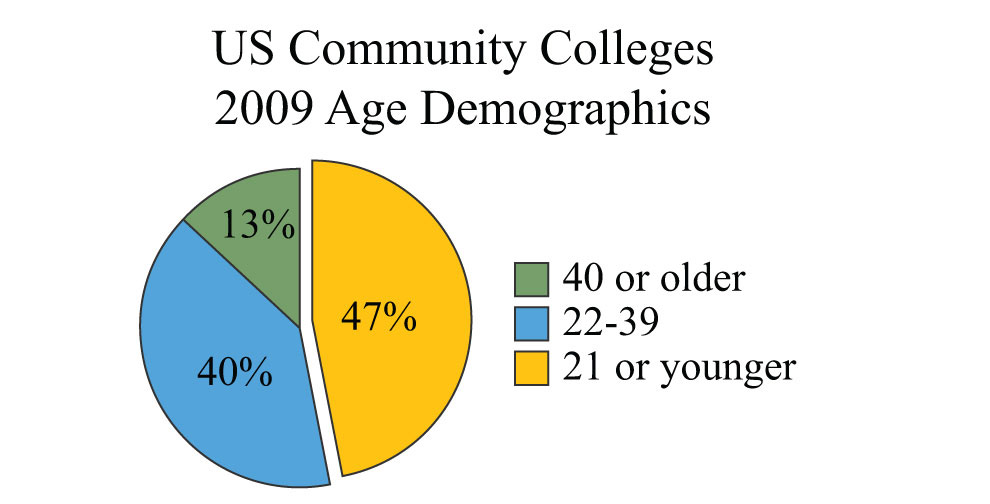
Source: American Association of Community Colleges.
Convert 47% to a decimal and multiply as indicated by the key word “of.”
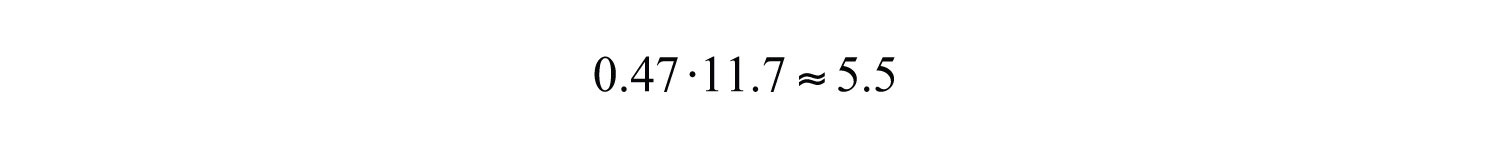
Answer: In 2009, approximately 5.5 million students enrolled in US community colleges were 21 years old or younger.
Key Takeaways
- To convert a decimal to a mixed number, add the appropriate fractional part indicated by the digits to the right of the decimal point to the whole part indicated by the digits to the left of the decimal point and reduce if necessary.
- To convert a mixed number to a decimal, convert the fractional part of the mixed number to a decimal using long division and then add it to the whole number part.
- To add or subtract decimals, align them vertically with the decimal point and add corresponding place values.
- To multiply decimals, multiply as usual for whole numbers and count the number of decimal places of each factor. The number of decimal places in the product will be the sum of the decimal places found in each of the factors.
- To divide decimals, move the decimal in both the divisor and dividend until the divisor is a whole number and then divide as usual.
- When rounding off decimals, look to the digit to the right of the specified place value. If the digit to the right is 4 or less, round down by leaving the specified digit unchanged and dropping all subsequent digits. If the digit to the right is 5 or more, round up by increasing the specified digit by one and dropping all subsequent digits.
- A percent represents a number as part of 100: .
- To convert a percent to a decimal, apply the definition of percent and write that number divided by 100. This is equivalent to moving the decimal two places to the left.
- To convert a percent to a fraction, apply the definition of percent and then reduce.
- To convert a decimal or fraction to a percent, multiply by 1 in the form of 100%. This is equivalent to moving the decimal two places to the right and adding a percent sign.
- Pie charts are circular graphs where each sector is proportional to the size of the part out of the whole. The sum of the percentages must total 100%.
Topic Exercises
Part A: Decimals
Write as a mixed number.
1. 45.8
2. 15.4
3. 1.82
4. 2.55
5. 4.72
6. 3.14
Write as a decimal.
7.
8.
9.
10.
11.
12.
13.
14.
Perform the operations. Round dollar amounts to the nearest hundredth.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27. Find of $20.00.
28. Find of $33.26.
29. Find of $15.25.
30. Find of $15.50.
31. A gymnast scores 8.8 on the vault, 9.3 on the uneven bars, 9.1 on the balance beam, and 9.8 on the floor exercise. What is her overall average?
32. To calculate a batting average, divide the player’s number of hits by the total number of at-bats and round off the result to three decimal places. If a player has 62 hits in 195 at-bats, then what is his batting average?
Part B: Percents to Decimals
Convert each percent to its decimal equivalent.
33. 43%
34. 25%
35. 33%
36. 100%
37. 150%
38. 215%
39.
40.
41.
42.
43.
44.
45. 1.75%
46.
47. 0%
48. 1%
49.
50.
51. Convert one-half of one percent to a decimal.
52. Convert three-quarter percent to a decimal.
53. What is 20% of zero?
54. What is 50% of one hundred?
55. What is 150% of 100?
56. What is 20% of $20.00?
57. What is 112% of $210?
58. What is of $1,200?
59. If the bill at a restaurant comes to $32.50, what is the amount of a 15% tip?
60. Calculate the total cost, including a 20% tip, of a meal totaling $37.50.
61. If an item costs $45.25, then what is the total after adding 8.25% for tax?
62. If an item costs $36.95, then what is the total after adding 9¼% tax?
63. A retail outlet is offering 15% off the original $29.99 price of branded sweaters. What is the price after the discount?
64. A solar technology distribution company expects a 12% increase in first quarter sales as a result of a recently implemented rebate program. If the first quarter sales last year totaled $350,000, then what are the sales projections for the first quarter of this year?
65. If a local mayor of a town with a population of 40,000 people enjoys a 72% favorable rating in the polls, then how many people view the mayor unfavorably?
66. If a person earning $3,200 per month spends 32% of his monthly income on housing, then how much does he spend on housing each month?
Part C: Decimals and Fractions to Percents
Convert the following decimals and fractions to percents.
67. 0.67
68. 0.98
69. 1.30
70. 2.25
71.
72.
73.
74.
75.
76.
77.
78.
79. 0.0023
80. 0.000005
81. 20
82. 100
Part D: Percents to Fractions
Use the definition of percent to convert to fractions.
83. 20%
84. 80%
85. 57%
86. 97%
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
99. 0.7%
100. 0.05%
101. 1.2%
102. 12.5%
The course grade weighting for a traditional mathematics course with 1,200 total points is shown in the pie chart below. Use the chart to answer the following questions.
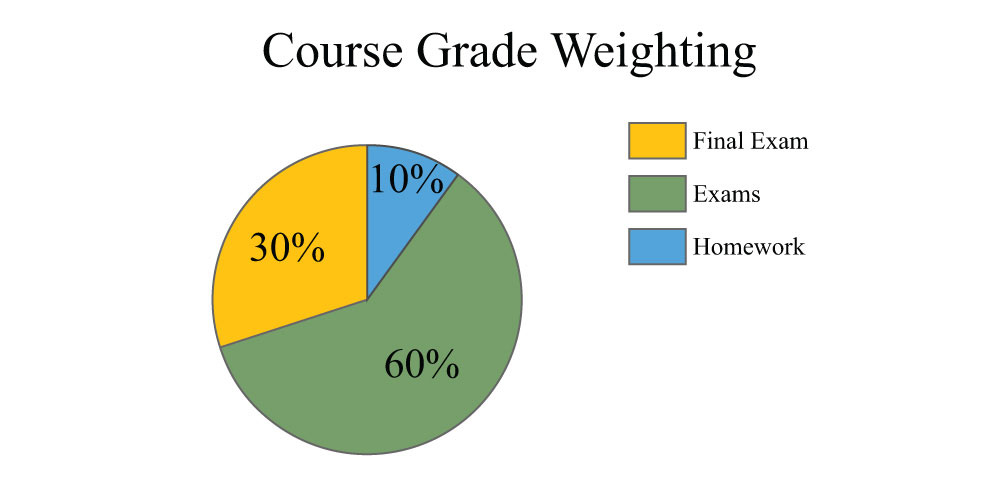
103. How many points will the final exam be worth?
104. How many points will the homework be worth?
105. How many points will each of the four regular exams be worth?
106. How many 10-point homework assignments can be assigned?
A website had 12,000 unique users in the fall of 2009. Answer the questions based on the pie chart below depicting total Web browser usage.
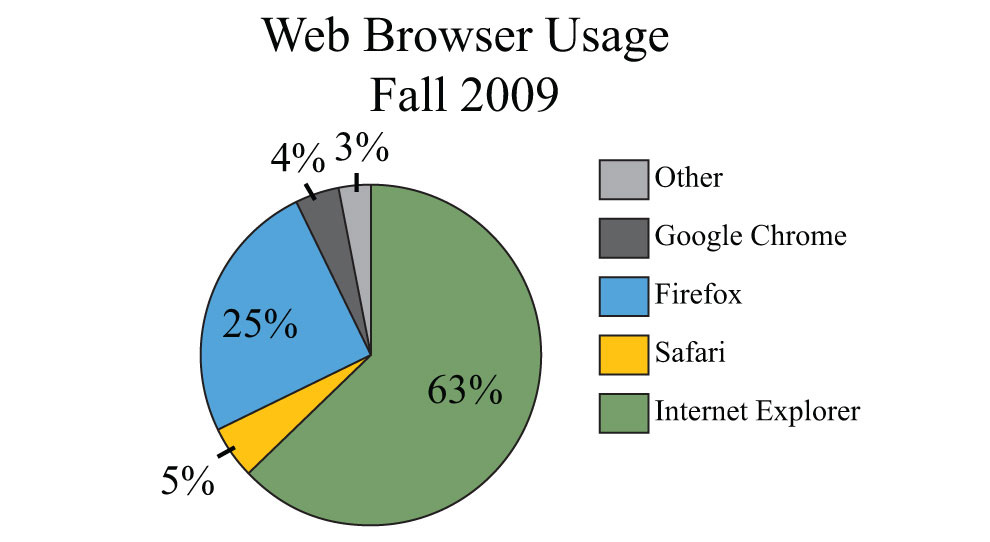
107. How many users used the Firefox Web browser?
108. How many users used a browser other than Internet Explorer?
109. How many users used either Firefox or Internet Explorer?
110. How many users used Google Chrome or Safari?
The 2009 employment status of 11.7 million full-time community college students is given in the following pie chart. Use the chart to answer the following questions. Round off each answer to the nearest hundredth.
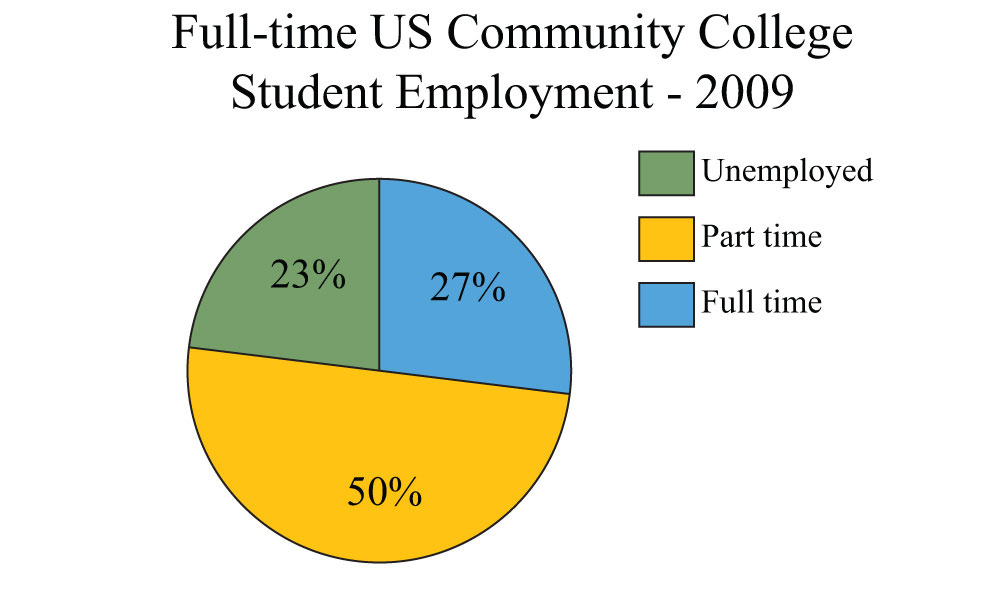
Source: American Association of Community Colleges.
111. How many full-time students were employed full time?
112. How many full-time students were employed part time?
113. How many full-time students were unemployed or employed part time?
114. How many full-time students also worked part time or full time?
The pie chart below depicts all US households categorized by income. The total number of households in 2007 was about 111,600,000. Use the chart to answer the following questions.
Source: US Census Bureau.
115. How many households reported an income from $50,000 to $74,999?
116. How many households reported an income from $75,000 to $99,999?
117. How many households reported an income of $100,000 or more?
118. How many households reported an income of less than $25,000?
Part E: Discussion Board Topics
119. The decimal system is considered a base-10 numeral system. Explain why. What other numeral systems are in use today?
120. Research and discuss the history of the symbol %.
121. Research and discuss simple interest and how it is calculated. Make up an example and share the solution.
122. Discuss methods for calculating tax and total bills.
123. Research and discuss the history of the pie chart.
124. Research and discuss the idea of a weighted average.
Answers
1:
3:
5:
7: 2.8
9: 3.125
11: 0.375
13:
15: 8.94
17: 53.451
19: 75.638
21: 0.6765
23: 7.23
25: 40.6
27: $3.33
29: $10.17
31: 9.25
33: 0.43
35: 0.33
37: 1.5
39: 0.005
41: 0.015
43: 0.00025
45: 0.0175
47: 0
49: 0.0305
51: 0.005
53: 0
55: 150
57: $235.20
59: $4.88
61: $48.98
63: $25.49
65: 11,200 people
67: 67%
69: 130%
71: 57%
73: 20%
75: 312.5%
77: 34%
79: 0.23%
81: 2,000%
83:
85:
87:
89:
91: 4
93: 1
95:
97:
99:
101:
103: 360 points
105: 180 points
107: 3,000 users
109: 10,560 users
111: 3.16 million
113: 8.54 million
115: 20,980,800 households
117: 21,204,000 households
1.6 Exponents and Square Roots
Learning Objectives
- Interpret exponential notation with positive integer exponents.
- Calculate the nth power of a real number.
- Calculate the exact and approximate value of the square root of a real number.
Exponential Notation and Positive Integer Exponents
If a number is repeated as a factor numerous times, then we can write the product in a more compact form using exponential notationThe compact notation used when a factor is repeated multiple times.. For example,
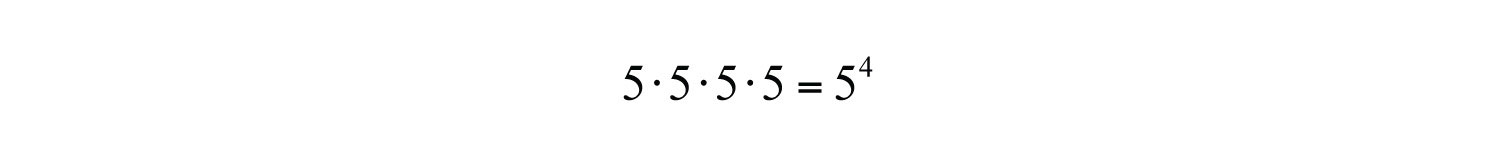
The baseThe factor a in the exponential notation . is the factor, and the positive integer exponentThe positive integer n in the exponential notation that indicates the number of times the base is used as a factor. indicates the number of times the base is repeated as a factor. In the above example, the base is 5 and the exponent is 4. In general, if a is the base that is repeated as a factor n times, then
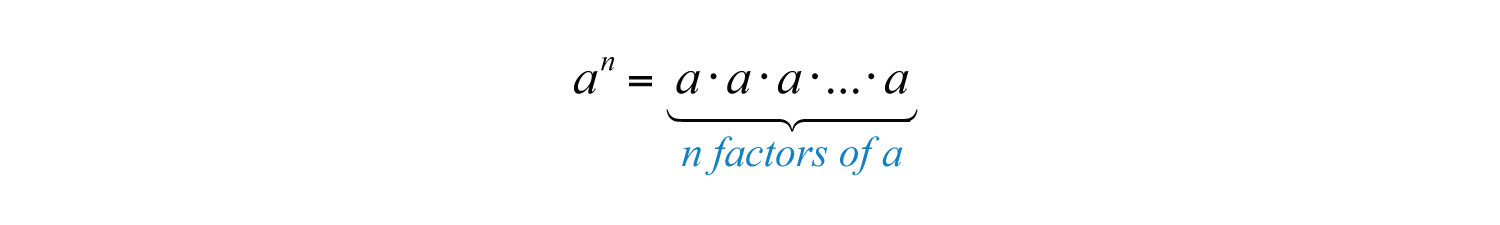
When the exponent is 2, we call the result a squareThe result when the exponent of any real number is 2.. For example,
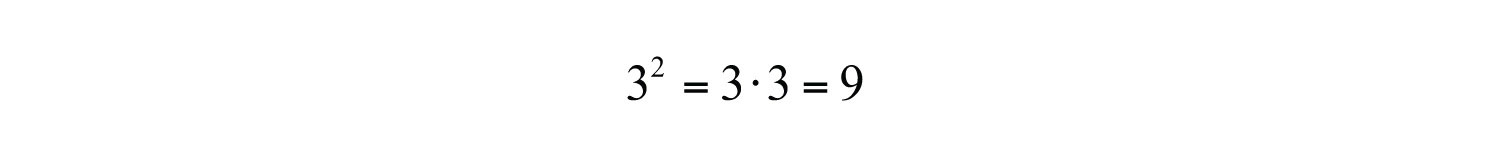
The number 3 is the base and the integer 2 is the exponent. The notation can be read two ways: “three squared” or “3 raised to the second power.” The base can be any real number.
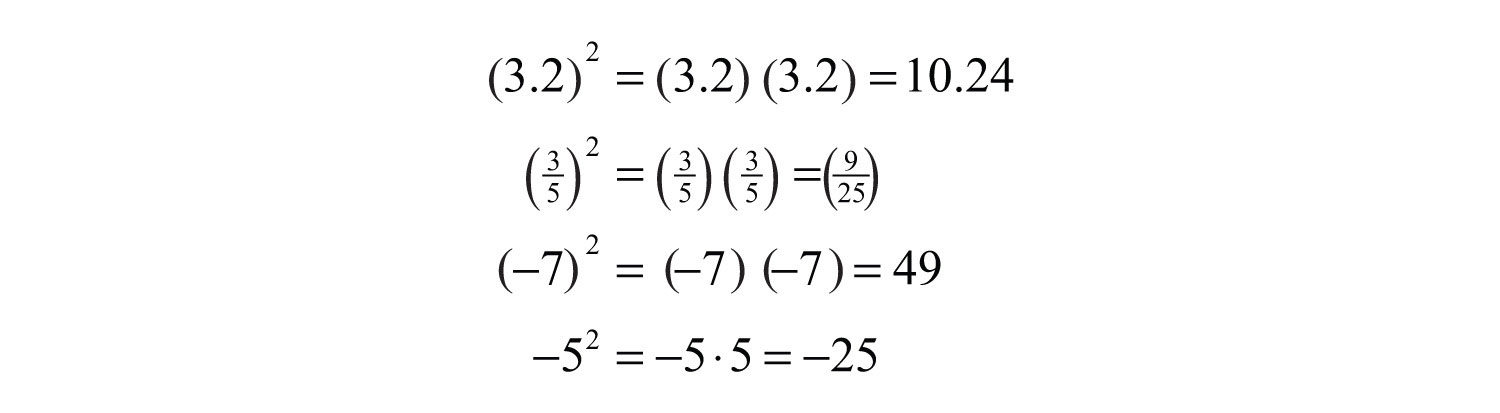
It is important to study the difference between the ways the last two examples are calculated. In the example , the base is −7 as indicated by the parentheses. In the example , the base is 5, not −5, so only the 5 is squared and the result remains negative. To illustrate this, write
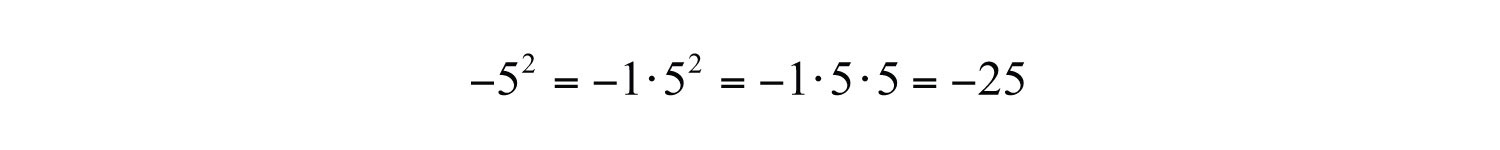
This subtle distinction is very important because it determines the sign of the result.
The textual notation for exponents is usually denoted using the caretThe symbol ^ that indicates exponents on many calculators, . (^) symbol as follows:
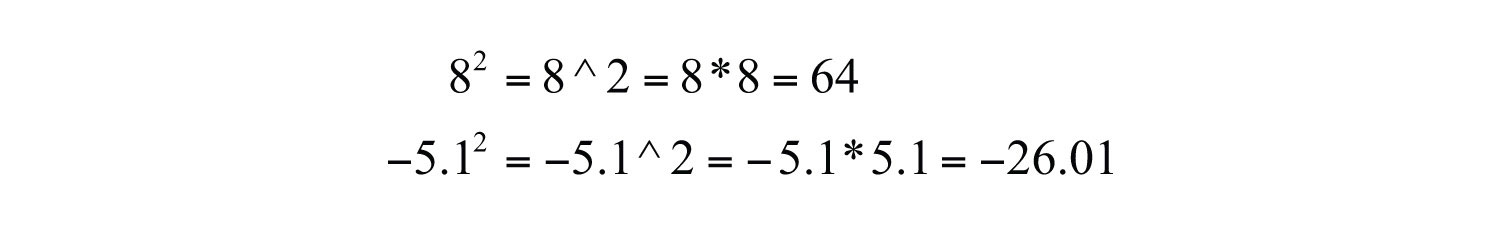
The square of an integer is called a perfect squareThe result of squaring an integer.. The ability to recognize perfect squares is useful in our study of algebra. The squares of the integers from 1 to 15 should be memorized. A partial list of perfect squares follows:
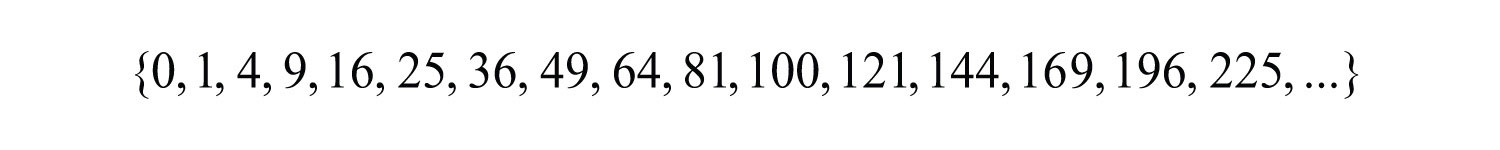
Try this! Simplify .
Answer: 144
Video Solution
(click to see video)When the exponent is 3 we call the result a cubeThe result when the exponent of any real number is 3.. For example,
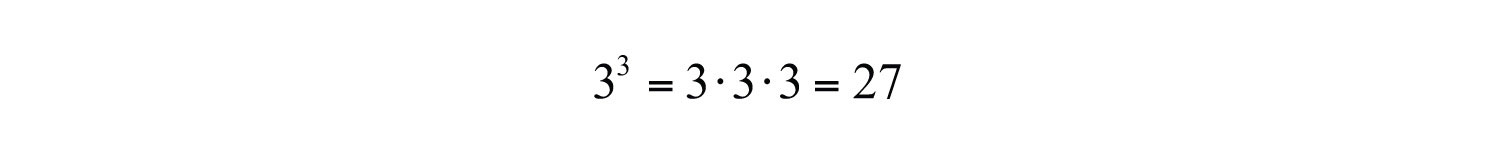
The notation can be read two ways: “three cubed” or “3 raised to the third power.” As before, the base can be any real number.
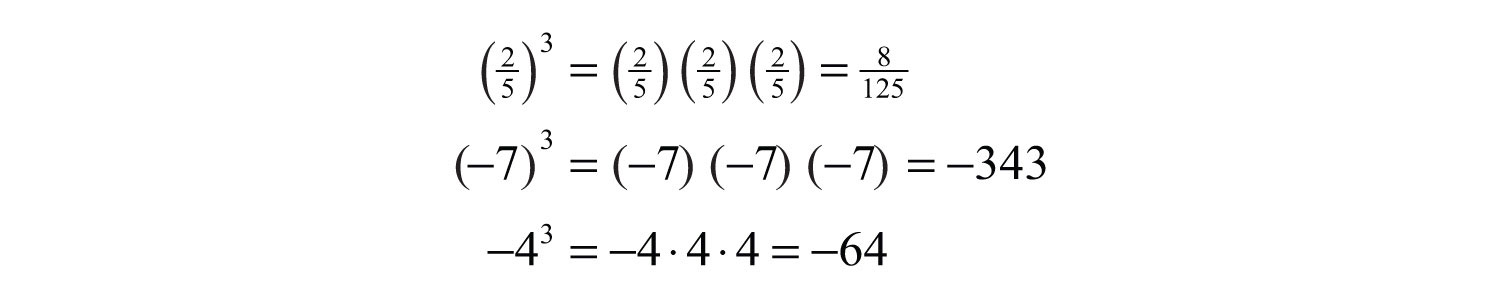
Note that the result of cubing a negative number is negative. The cube of an integer is called a perfect cubeThe result of cubing an integer.. The ability to recognize perfect cubes is useful in our study of algebra. The cubes of the integers from 1 to 10 should be memorized. A partial list of perfect cubes follows:
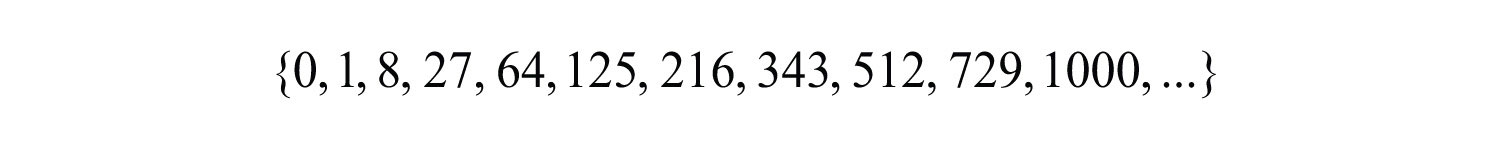
Try this! Simplify .
Answer: −8
Video Solution
(click to see video)If the exponent is greater than 3, then the notation is read “a raised to the nth power.”
Notice that the result of a negative base with an even exponent is positive. The result of a negative base with an odd exponent is negative. These facts are often confused when negative numbers are involved. Study the following four examples carefully:
| The base is (−2) | The base is 2 |
|---|---|
The parentheses indicate that the negative number is to be used as the base.
Example 1: Calculate:
a.
b.
Solution: The base is for both problems.
a. Use the base as a factor three times.
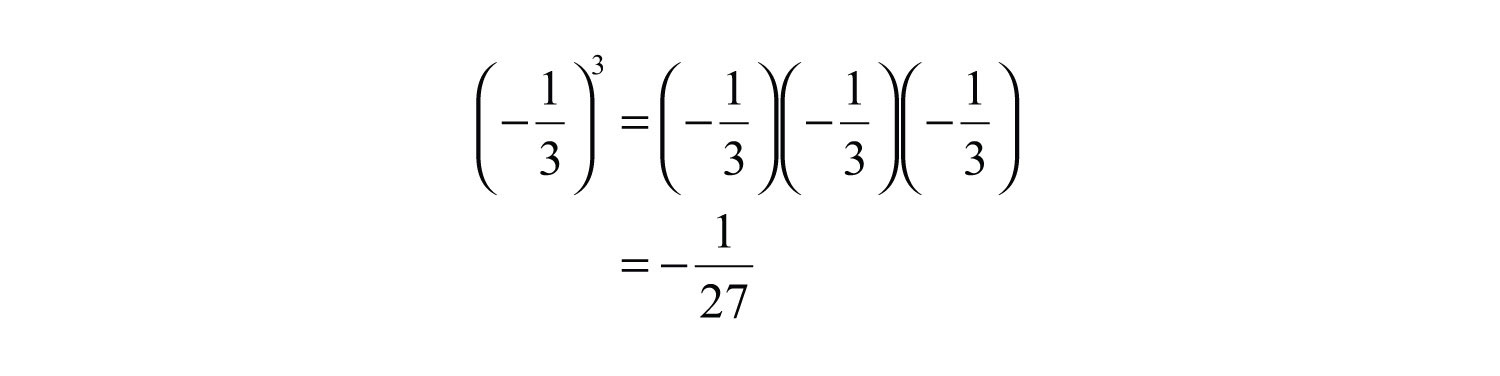
b. Use the base as a factor four times.
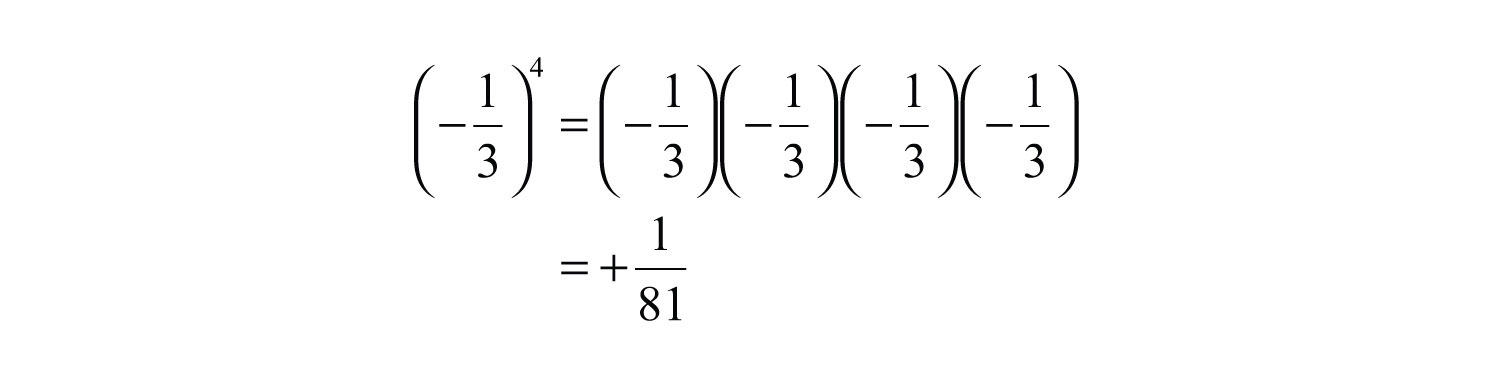
Answers: a. ; b.
Try this! Simplify: and .
Answers: and
Video Solution
(click to see video)Square Root of a Real Number
Think of finding the square rootThe number that, when multiplied by itself, yields the original number. of a number as the inverse of squaring a number. In other words, to determine the square root of 25 the question is, “What number squared equals 25?” Actually, there are two answers to this question, 5 and −5.
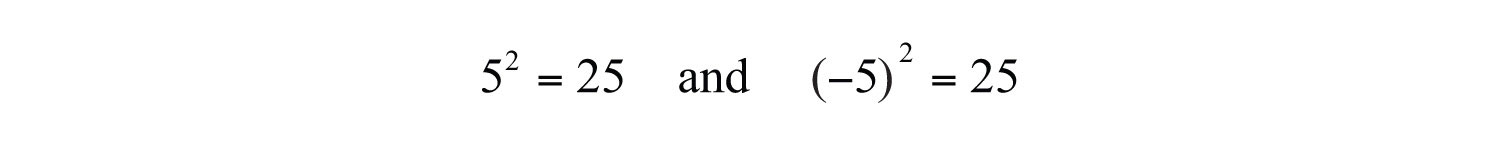
When asked for the square root of a number, we implicitly mean the principal (nonnegative) square rootThe non-negative square root.. Therefore we have,
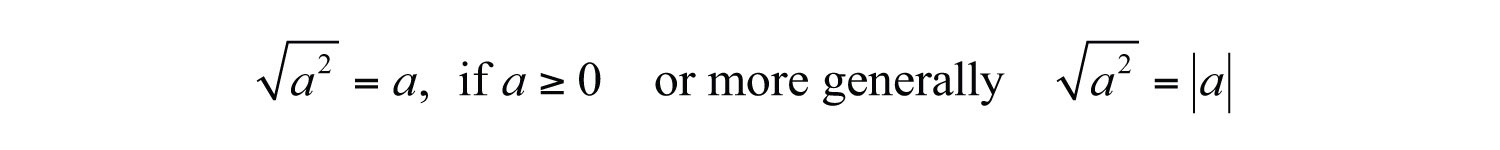
As an example, , which is read “square root of 25 equals 5.” The symbol √ is called the radical signThe symbol √ used to denote a square root. and 25 is called the radicandThe expression a within a radical sign, .. The alternative textual notation for square roots follows:
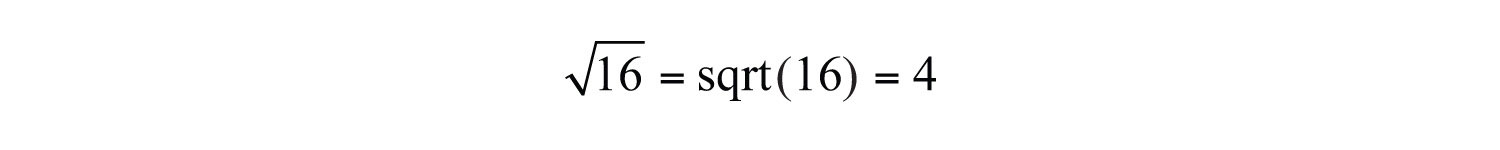
It is also worthwhile to note that
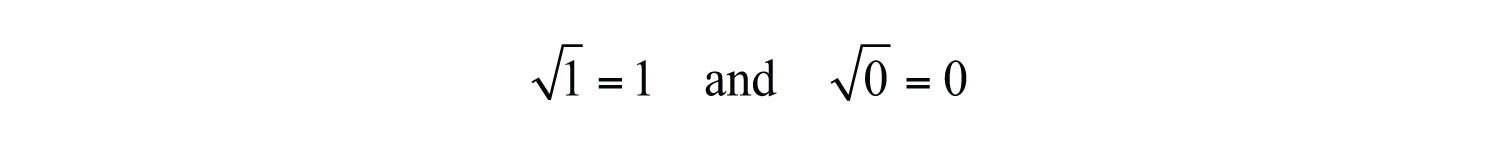
This is the case because and .
Example 2: Simplify: .
Solution: 10,000 is a perfect square because .
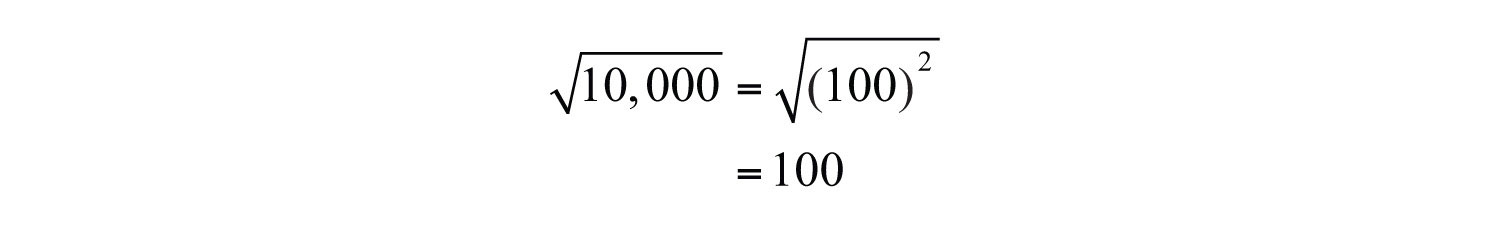
Answer: 100
Example 3: Simplify: .
Solution: Here we notice that is a square because .
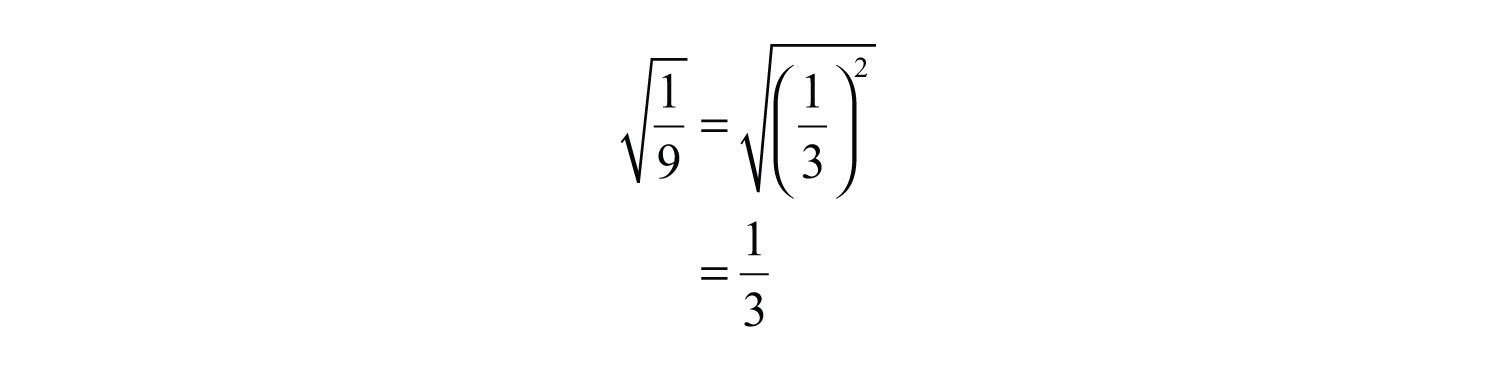
Answer:
Given a and b as positive real numbers, use the following property to simplify square roots whose radicands are not squares:
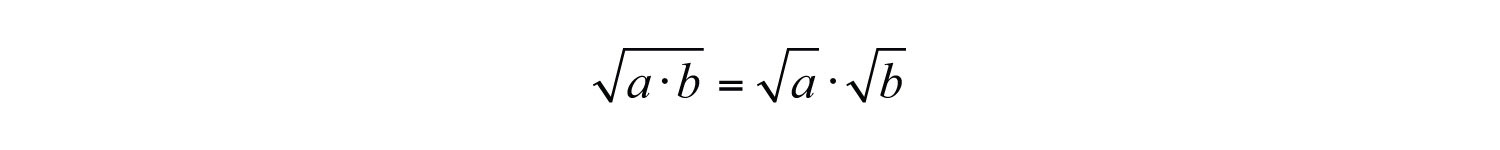
The idea is to identify the largest square factor of the radicand and then apply the property shown above. As an example, to simplify notice that 8 is not a perfect square. However, and thus has a perfect square factor other than 1. Apply the property as follows:
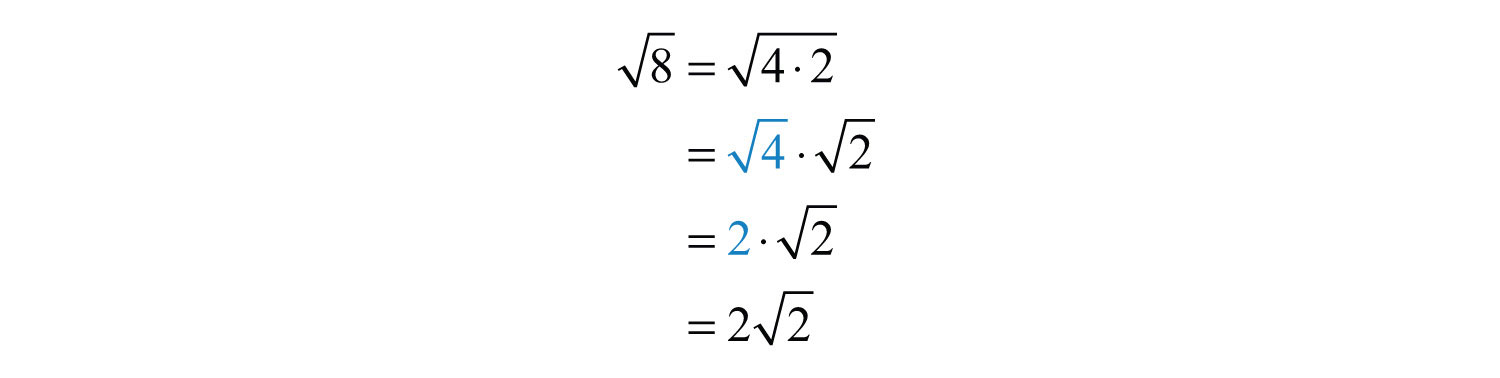
Here is a simplified irrational number. You are often asked to find an approximate answer rounded off to a certain decimal place. In that case, use a calculator to find the decimal approximation using either the original problem or the simplified equivalent.
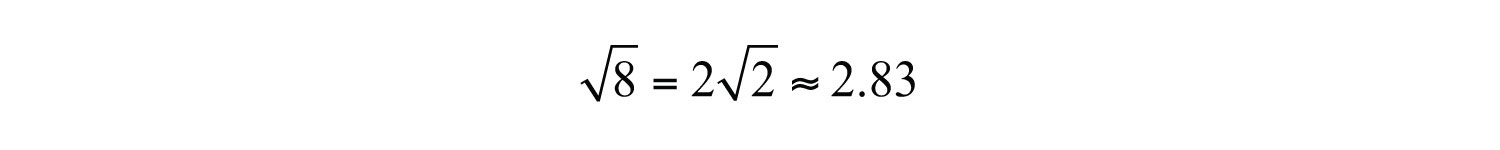
On a calculator, try 2.83^2. What do you expect? Why is the answer not what you would expect?
It is important to mention that the radicand must be positive. For example, is undefined since there is no real number that when squared is negative. Try taking the square root of a negative number on your calculator. What does it say? Note: taking the square root of a negative number is defined later in the course.
Example 4: Simplify and give an approximate answer rounded to the nearest hundredth: .
Solution: The radicand 75 can be factored as 25 ⋅ 3 where the factor 25 is a perfect square.
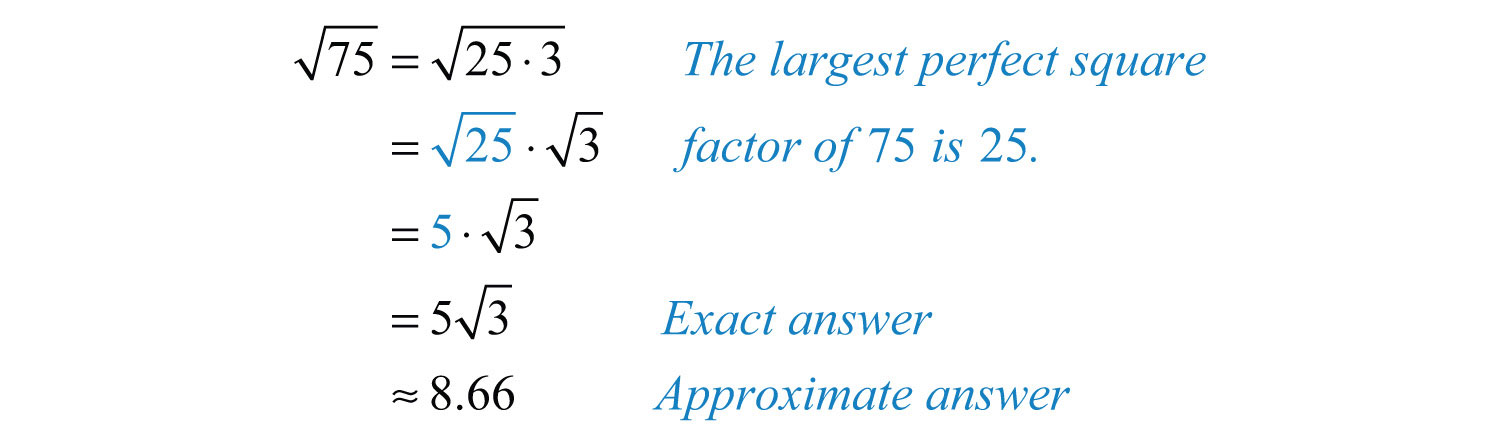
Answer:
As a check, calculate and on a calculator and verify that the both results are approximately 8.66.
Example 5: Simplify: .
Solution:
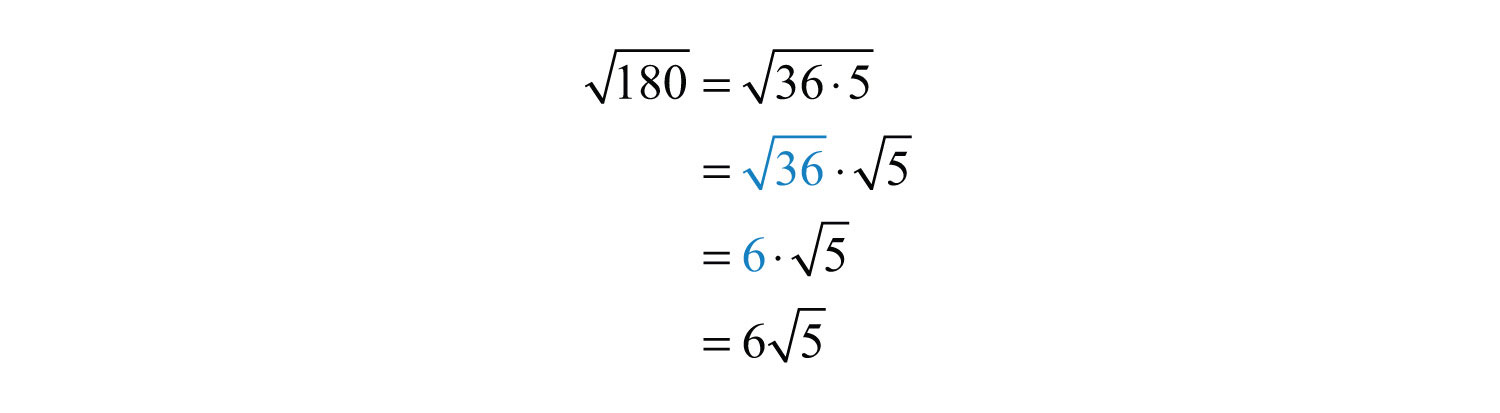
Since the question did not ask for an approximate answer, we present the exact answer.
Answer:
Example 5: Simplify: .
Solution:
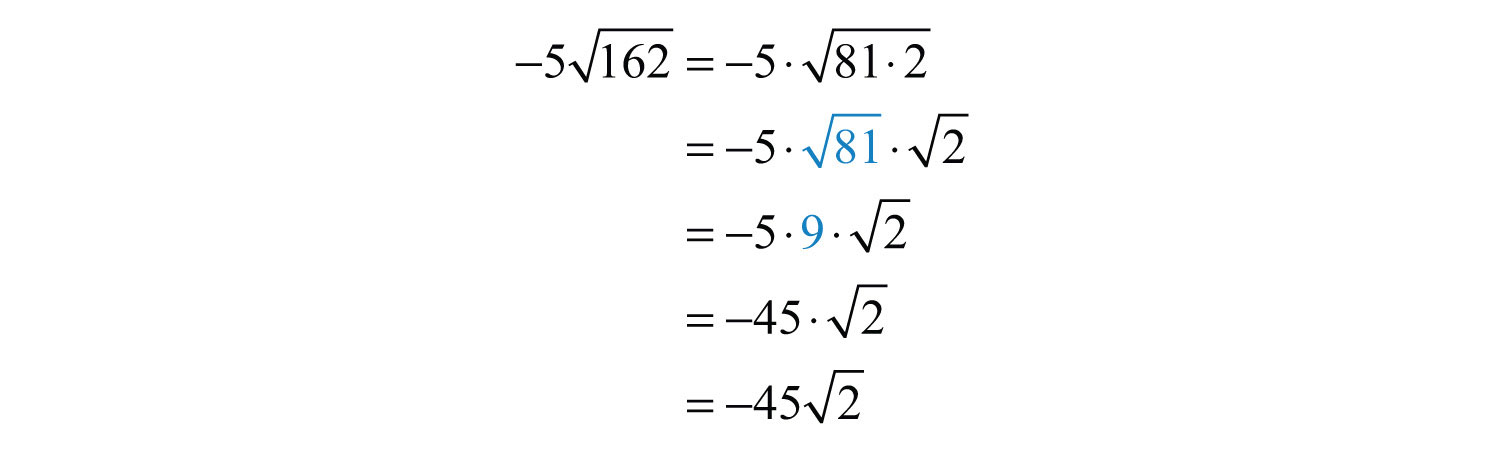
Answer:
Try this! Simplify and give an approximate answer rounded to the nearest hundredth: .
Answer:
Video Solution
(click to see video)Figure 1.1 Pythagoras

Source: Detail of The School of Athens by Raffaello Sanzio, 1509, from http://commons.wikimedia.org/wiki/File:Sanzio_01_Pythagoras.jpg.
A right triangleA triangle with an angle that measures 90°. is a triangle where one of the angles measures 90°. The side opposite the right angle is the longest side, called the hypotenuseThe longest side of a right triangle, it will always be the side opposite the right angle., and the other two sides are called legsThe sides of a right triangle that are not the hypotenuse.. Numerous real-world applications involve this geometric figure. The Pythagorean theoremGiven any right triangle with legs measuring a and b units and hypotenuse measuring c units, then . states that given any right triangle with legs measuring a and b units, the square of the measure of the hypotenuse c is equal to the sum of the squares of the measures of the legs: . In other words, the hypotenuse of any right triangle is equal to the square root of the sum of the squares of its legs.
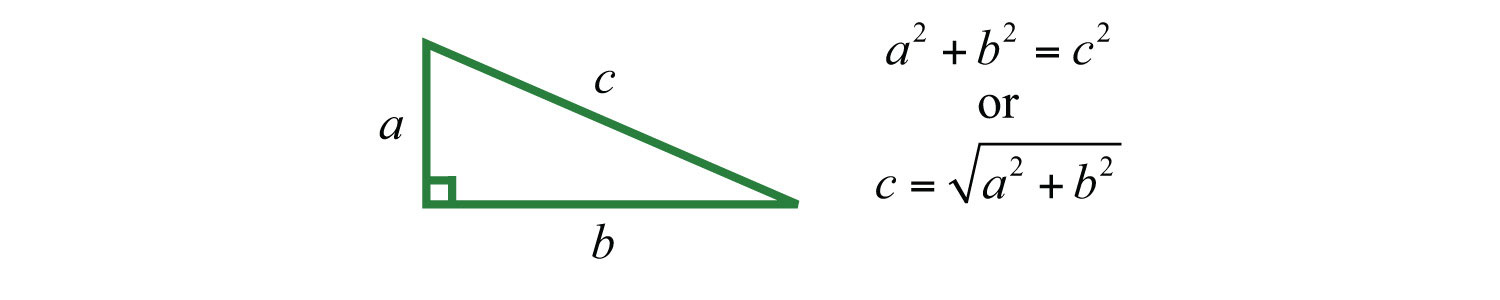
Example 6: If the two legs of a right triangle measure 3 units and 4 units, then find the length of the hypotenuse.
Solution: Given the lengths of the legs of a right triangle, use the formula to find the length of the hypotenuse.

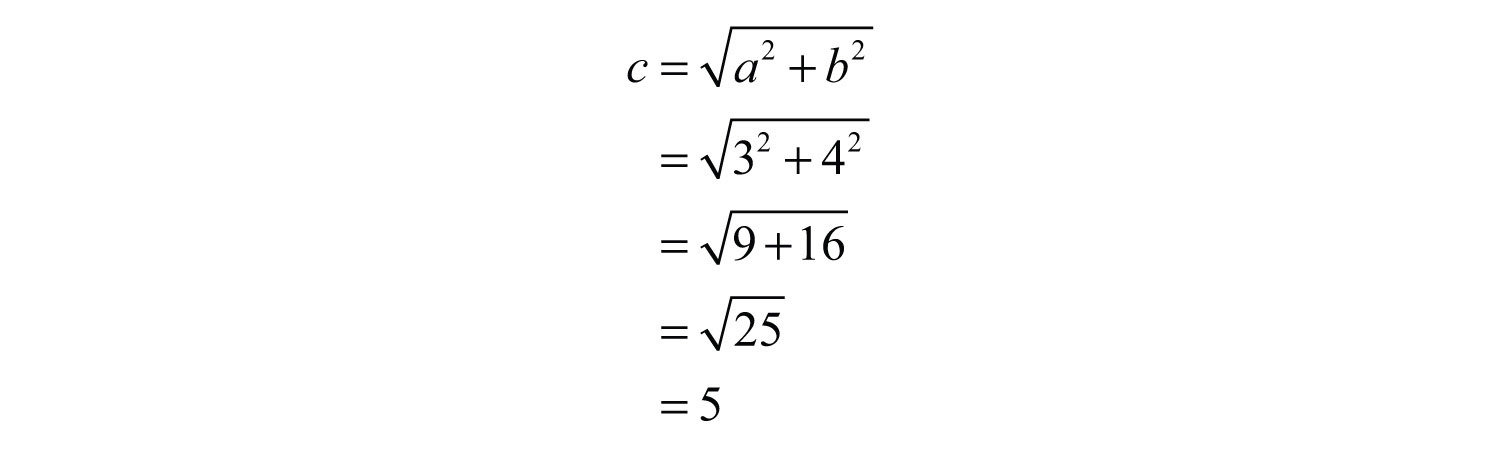
Answer: c = 5 units
When finding the hypotenuse of a right triangle using the Pythagorean theorem, the radicand is not always a perfect square.
Example 7: If the two legs of a right triangle measure 2 units and 6 units, find the length of the hypotenuse.
Solution:
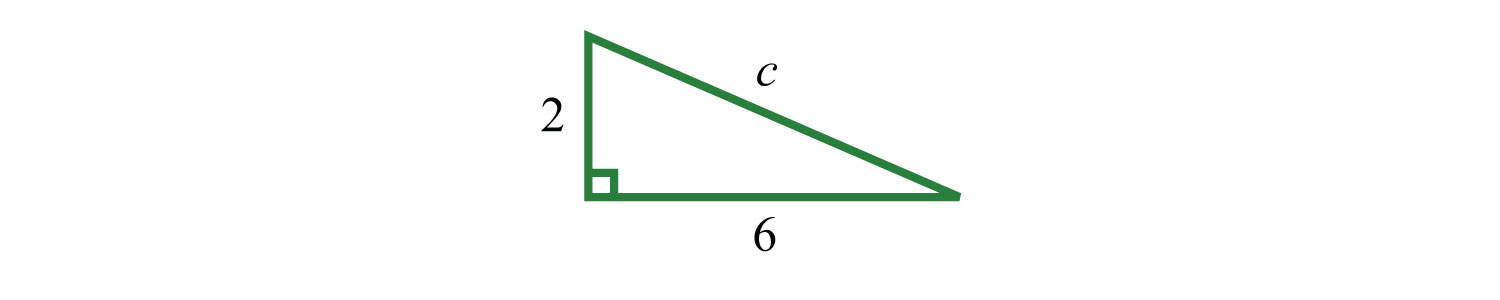
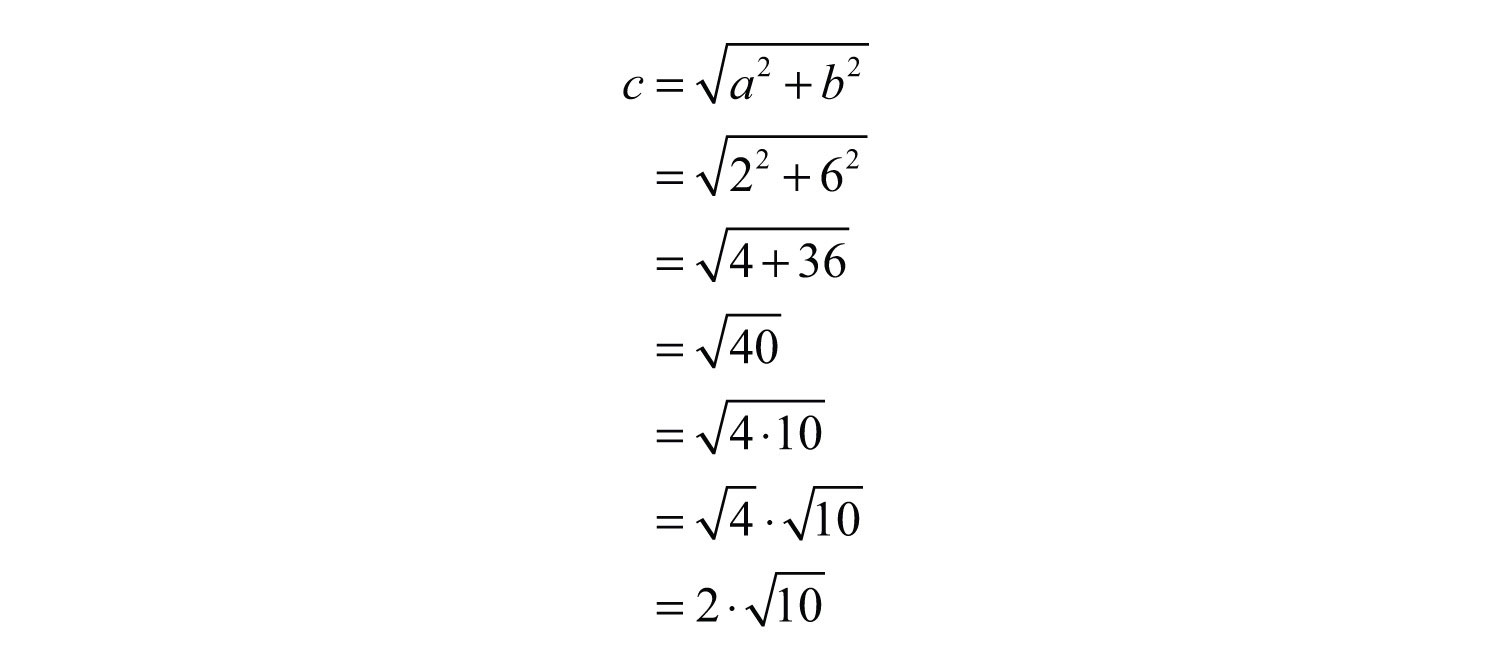
Answer: units
Key Takeaways
- When using exponential notation , the base a is used as a factor n times.
- When the exponent is 2, the result is called a square. When the exponent is 3, the result is called a cube.
- Memorize the squares of the integers up to 15 and the cubes of the integers up to 10. They will be used often as you progress in your study of algebra.
- When negative numbers are involved, take care to associate the exponent with the correct base. Parentheses group a negative number raised to some power.
- A negative base raised to an even power is positive.
- A negative base raised to an odd power is negative.
- The square root of a number is a number that when squared results in the original number. The principal square root is the positive square root.
- Simplify a square root by looking for the largest perfect square factor of the radicand. Once a perfect square is found, apply the property , where a and b are nonnegative, and simplify.
- Check simplified square roots by calculating approximations of the answer using both the original problem and the simplified answer on a calculator to verify that the results are the same.
- Find the length of the hypotenuse of any right triangle given the lengths of the legs using the Pythagorean theorem.
Topic Exercises
Part A: Square of a Number
Simplify.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13. 0.5^2
14. 1.25^2
15. (−2.6)^2
16. −(−5.1)^2
17.
18.
If s is the length of the side of a square, then the area is given by .
19. Determine the area of a square given that a side measures 5 inches.
20. Determine the area of a square given that a side measures 2.3 feet.
21. List all the squares of the integers 0 through 15.
22. List all the squares of the integers from −15 to 0.
23. List the squares of all the rational numbers in the set .
24. List the squares of all the rational numbers in the set .
Part B: Integer Exponents
Simplify.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45. List all the cubes of the integers −5 through 5.
46. List all the cubes of the integers from −10 to 0.
47. List all the cubes of the rational numbers in the set .
48. List all the cubes of the rational numbers in the set .
Part C: Square Root of a Number
Determine the exact answer in simplified form.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
Approximate the following to the nearest hundredth.
79.
80.
81.
82.
83.
84.
85.
86.
87. sqrt(79)
88. sqrt(54)
89. −sqrt(162)
90. −sqrt(86)
91. If the two legs of a right triangle measure 6 units and 8 units, then find the length of the hypotenuse.
92. If the two legs of a right triangle measure 5 units and 12 units, then find the length of the hypotenuse.
93. If the two legs of a right triangle measure 9 units and 12 units, then find the length of the hypotenuse.
94. If the two legs of a right triangle measure units and 2 units, then find the length of the hypotenuse.
95. If the two legs of a right triangle both measure 1 unit, then find the length of the hypotenuse.
96. If the two legs of a right triangle measure 1 unit and 5 units, then find the length of the hypotenuse.
97. If the two legs of a right triangle measure 2 units and 4 units, then find the length of the hypotenuse.
98. If the two legs of a right triangle measure 3 units and 9 units, then find the length of the hypotenuse.
Part D: Discussion Board Topics
99. Why is the result of an exponent of 2 called a square? Why is the result of an exponent of 3 called a cube?
100. Research and discuss the history of the Pythagorean theorem.
101. Research and discuss the history of the square root.
102. Discuss the importance of the principal square root.
Answers
1: 100
3: 81
5: 121
7: 0
9: −64
11: 1/4
13: .25
15: 6.76
17:
19: 25 square inches
21: {0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225}
23: {0, 1/9, 4/9, 1, 16/9, 25/9, 4}
25: 125
27: 1
29: −1
31: −343
33: 27
35: 1
37: −216
39: 1
41:
43:
45: {−125, −64, −27, −8, −1, 0, 1, 8, 27, 64, 125}
47:
49: 11
51: 10
53: −5
55:
57:
59:
61:
63:
65: 0.8
67: 30
69: 2
71: Not real
73: 12
75: −12
77:
79: 1.41
81: 3.16
83: 3.46
85: −13.42
87: 8.89
89: −12.73
91: 10 units
93: 15 units
95: units
97: units
1.7 Order of Operations
Learning Objectives
- Identify and work with grouping symbols.
- Understand the order of operations.
- Simplify using the order of operations.
Grouping Symbols
In a computation where more than one operation is involved, grouping symbols help tell us which operations to perform first. The grouping symbolsParentheses, brackets, braces, and the fraction bar are the common symbols used to group expressions and mathematical operations within a computation. commonly used in algebra are

All of the above grouping symbols, as well as absolute value, have the same order of precedence. Perform operations inside the innermost grouping symbol or absolute value first.
Example 1: Simplify: .
Solution: Perform the operations within the parentheses first. In this case, first subtract 12 from 4.
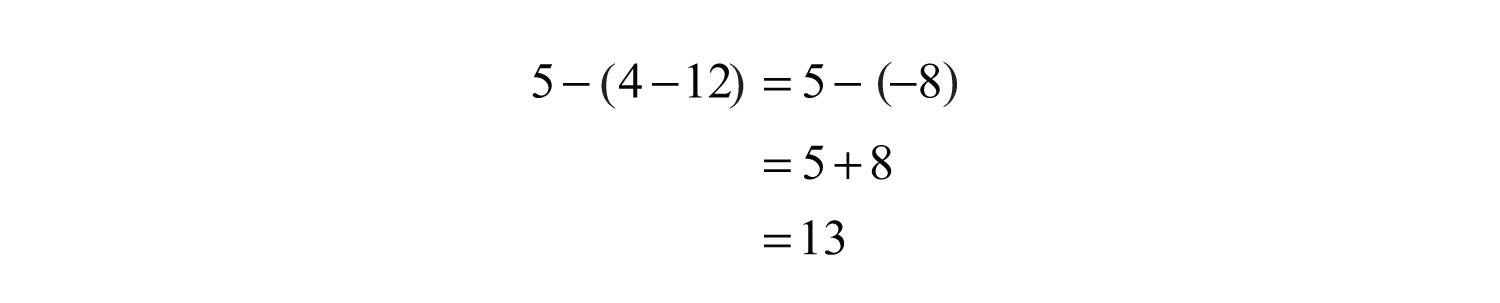
Answer: 13
Example 2: Simplify: .
Solution:
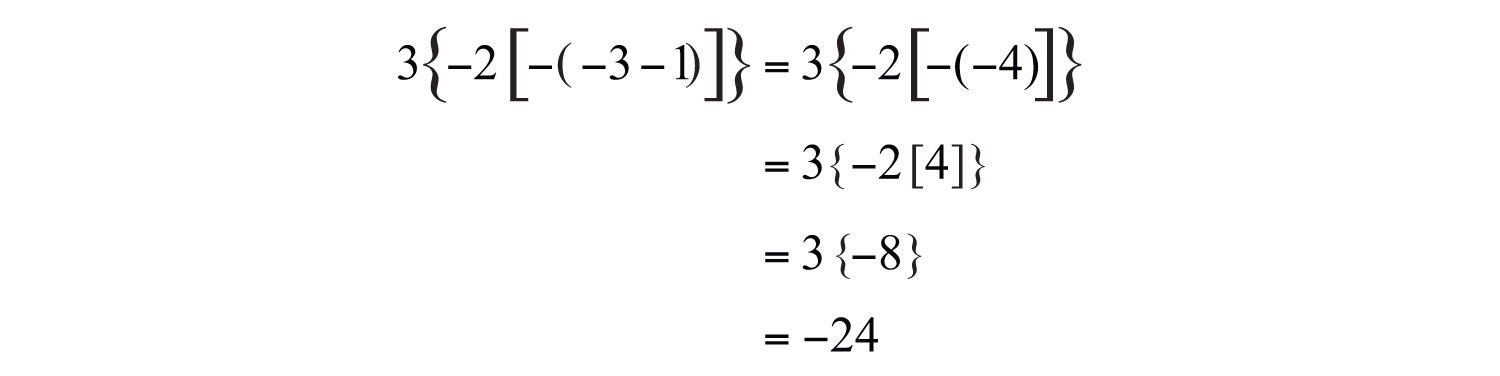
Answer: −24
Example 3: Simplify: .
Solution: The fraction bar groups the numerator and denominator. They should be simplified separately.
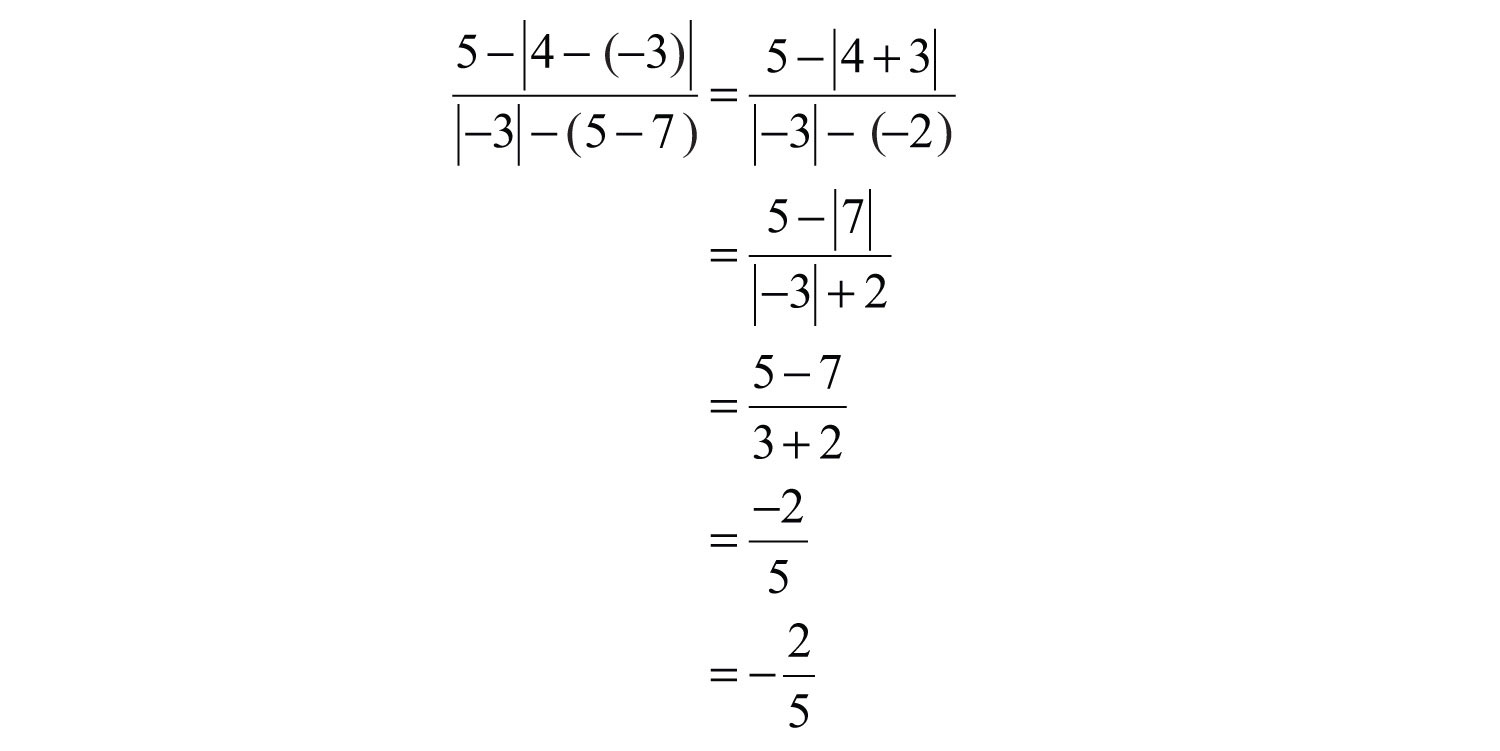
Answer:
Try this! Simplify: .
Answer: 15
Video Solution
(click to see video)Order of Operations
When several operations are to be applied within a calculation, we must follow a specific orderTo ensure a single correct result, perform mathematical operations in a specific order. to ensure a single correct result.
- Perform all calculations within the innermost parentheses or grouping symbols.
- Evaluate all exponents.
- Perform multiplication and division operations from left to right.
- Finally, perform all remaining addition and subtraction operations from left to right.
Caution: Note that multiplication and division operations must be worked from left to right.
Example 4: Simplify: .
Solution: First, evaluate and then perform multiplication and division as they appear from left to right.
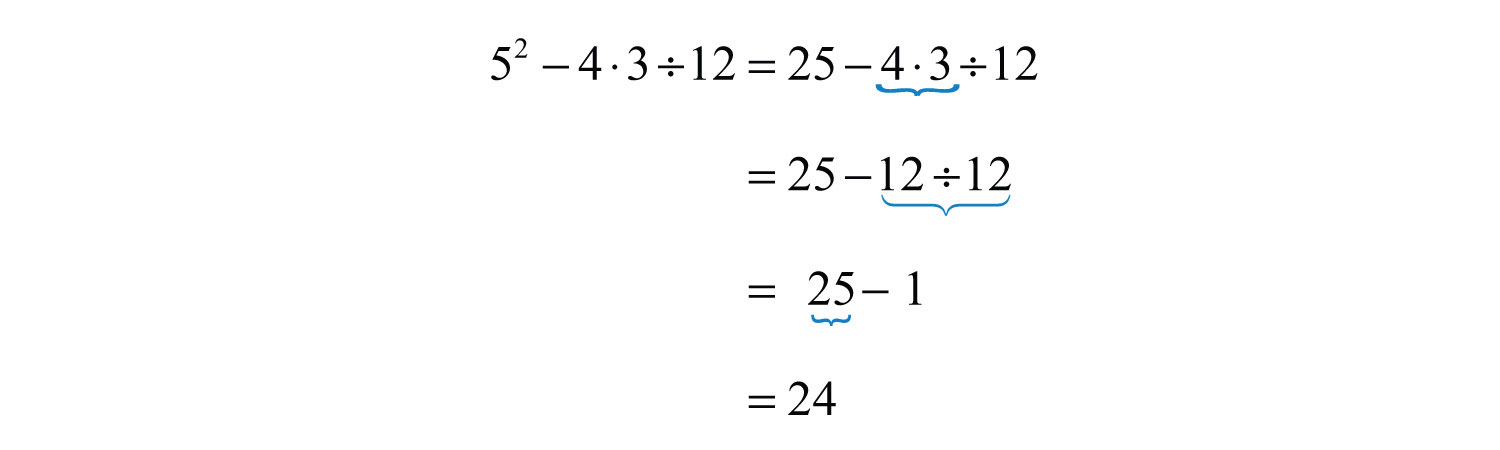
Answer: 24
Because multiplication and division operations should be worked from left to right, it is sometimes correct to perform division before multiplication.
Example 5: Simplify: .
Solution: Begin by evaluating the exponent, .
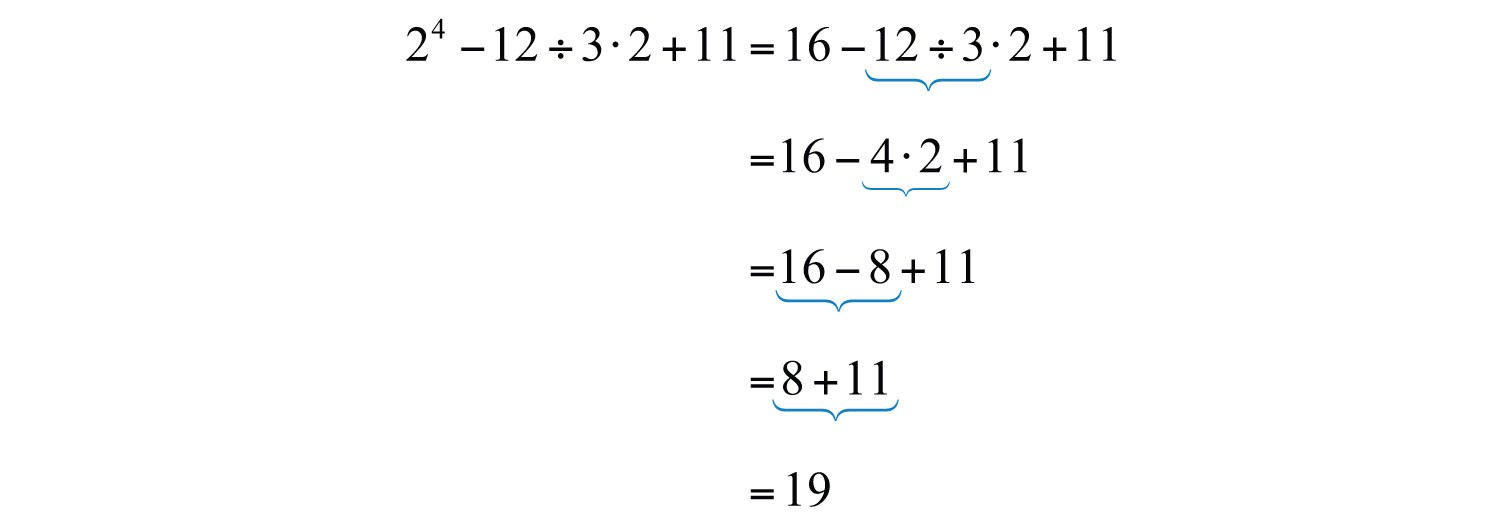
Multiplying first leads to an incorrect result.

Answer: 19
Example 6: Simplify: .
Solution: Take care to correctly identify the base when squaring.
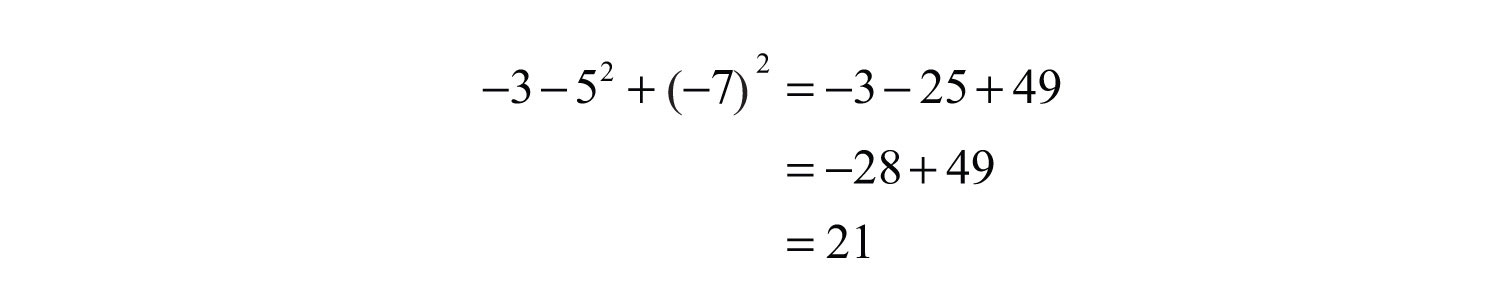
Answer: 21
Example 7: Simplify: .
Solution: It is tempting to first subtract 5 − 3, but this will lead to an incorrect result. The order of operations requires us to simplify within the brackets first.
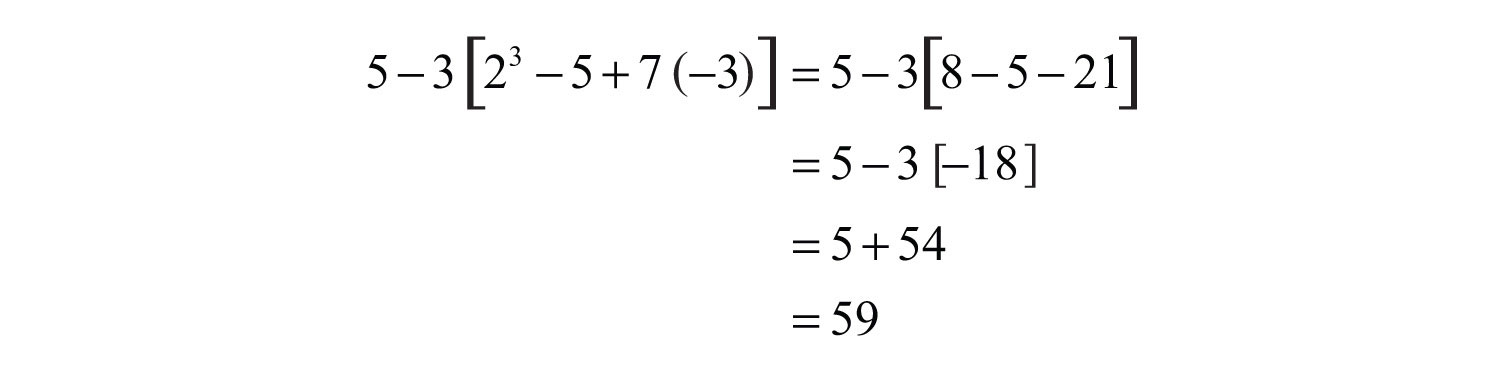
Subtracting 5 − 3 first leads to an incorrect result.
Answer: 59
Example 8: Simplify: .
Solution: Perform the operations within the innermost parentheses first.
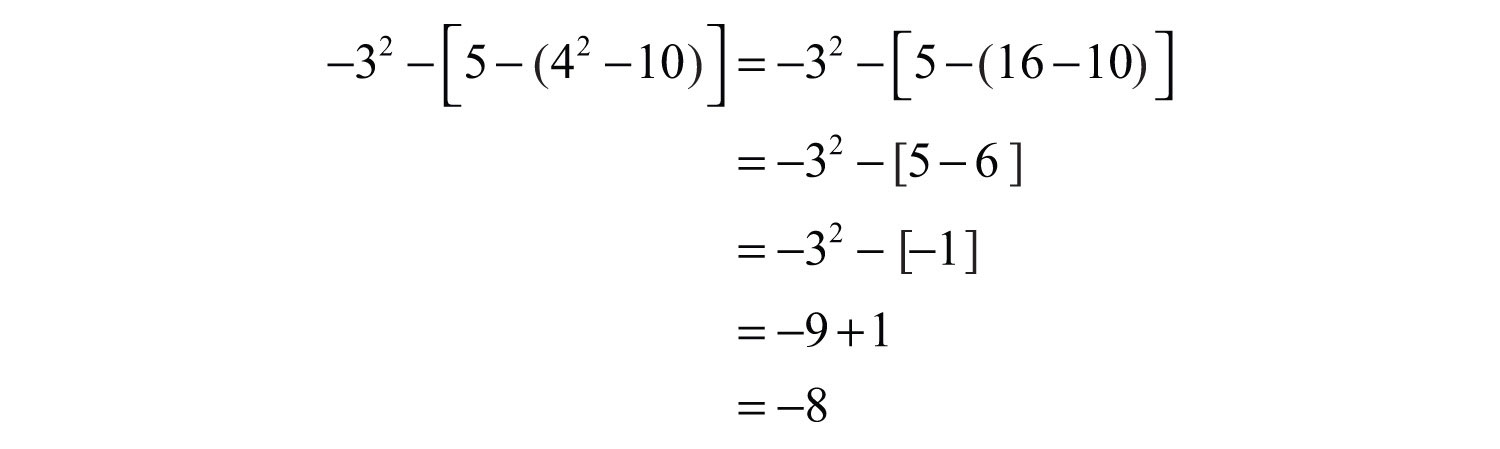
Answer: −8
Example 9: Simplify: .
Solution:
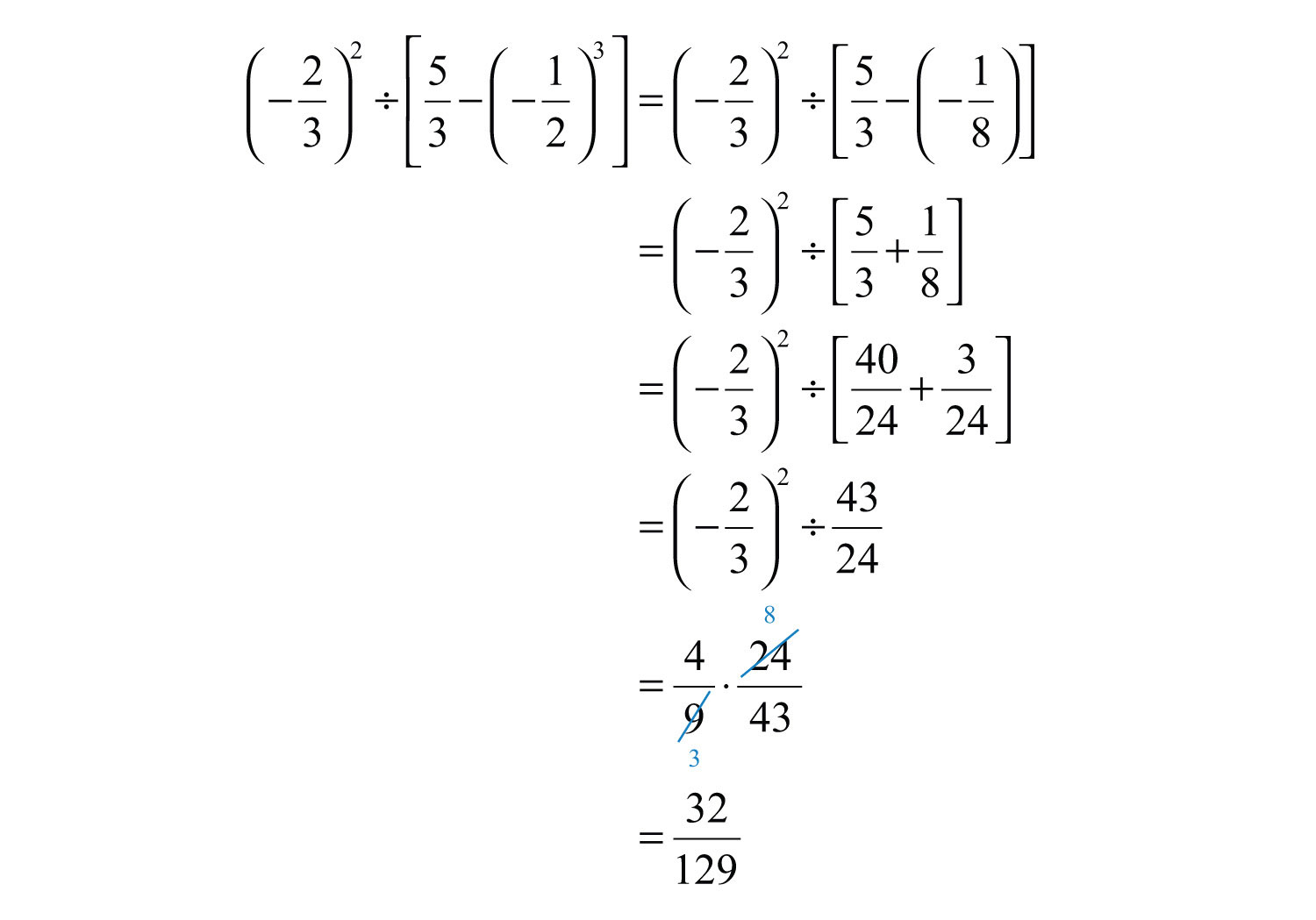
Answer:
We are less likely to make a mistake if we work one operation at a time. Some problems may involve an absolute value, in which case we assign it the same order of precedence as parentheses.
Example 10: Simplify: .
Solution: We begin by evaluating the absolute value and then the exponent .
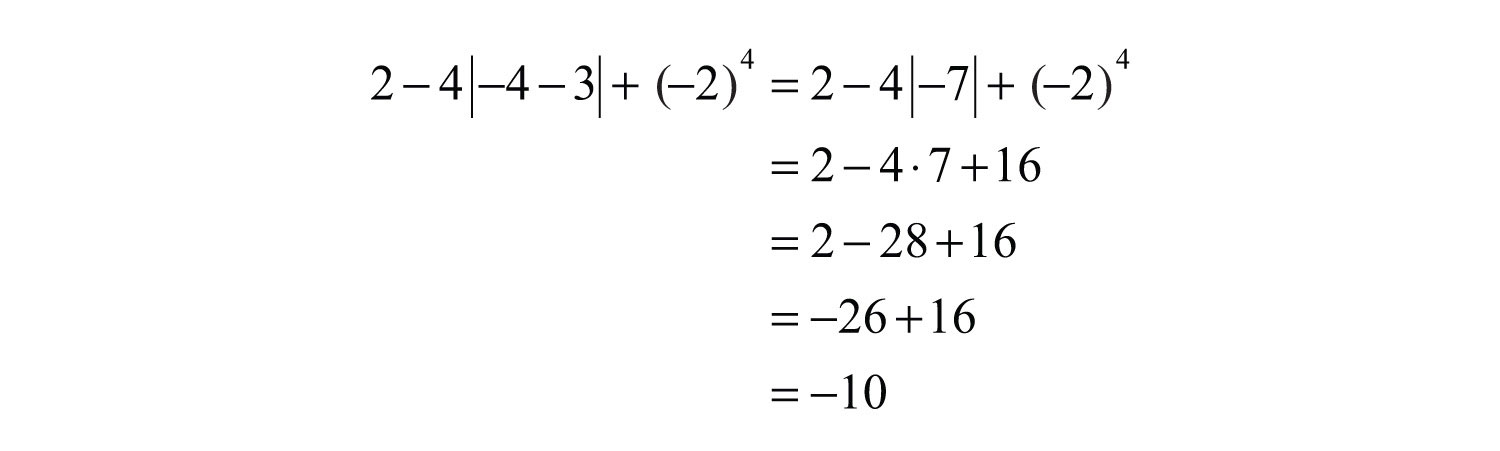
Answer: −10
Try this! Simplify: .
Answer: 13
Video Solution
(click to see video)Key Takeaways
- Grouping symbols indicate which operations to perform first. We usually group mathematical operations with parentheses, brackets, braces, and the fraction bar. We also group operations within absolute values. All groupings have the same order of precedence: the operations within the innermost grouping are performed first.
-
When applying operations within a calculation, follow the order of operations to ensure a single correct result.
- Address innermost parentheses or groupings first.
- Simplify all exponents.
- Perform multiplication and division operations from left to right.
- Finally, perform addition and subtraction operations from left to right.
- It is important to highlight the fact that multiplication and division operations should be applied as they appear from left to right. It is a common mistake to always perform multiplication before division, which, as we have seen, in some cases produces incorrect results.
Topic Exercises
Part A: Order of Operations
Simplify.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51. Mary purchased 14 bottles of water at $0.75 per bottle, 4 pounds of assorted candy at $3.50 per pound, and 16 packages of microwave popcorn costing $0.50 each for her party. What was her total bill?
52. Joe bought four 8-foot 2-by-4 boards for $24.00. How much did he spend per linear foot?
53. Margaret bought two cases of soda at the local discount store for $23.52. If each case contained 24 bottles, how much did she spend per bottle?
54. Billy earns $12.00 per hour and “time and a half” for every hour he works over 40 hours a week. What is his pay for 47 hours of work this week?
55. Audry bought 4 bags of marbles each containing 15 assorted marbles. If she wishes to divide them up evenly between her 3 children, how many will each child receive?
56. Mark and Janet carpooled home from college for the Thanksgiving holiday. They shared the driving, but Mark drove twice as far as Janet. If Janet drove 135 miles, then how many miles was the entire trip?
Part B: Order of Operations with Absolute Values
Simplify.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
Find the distance between the given numbers on a number line.
77. and
78. and
79. and
80. and
81. −0.5 and 8.3
82. 10.7 and −2.8
83. and
84. and
Part C: Discussion Board Topics
85. Convert various examples in this section to equivalent expressions using text-based symbols.
86. What is PEMDAS and what is it missing?
87. Discuss the importance of proper grouping and give some examples.
88. Experiment with the order of operations on a calculator and share your results.
Answers
1: −22
3: −42
5: 4
7:
9: 7.24
11: −11
13: 6
15: −5
17: 0
19: 20
21: −75
23: 29
25: −33
27: −10
29: 67.22
31: −124
33:
35:
37:
39:
41: 50
43: −17
45:
47:
49: −1
51: $32.50
53: $0.49
55: 20 marbles
57: 13
59: −8
61: 18
63: −9
65: 6
67: −27
69: 8
71: 1
73:
75: −63
77: unit
79: unit
81: 8.8 units
83: units
1.8 Review Exercises and Sample Exam
Review Exercises
Real Numbers and the Number Line
Choose an appropriate scale and graph the following sets of real numbers on a number line.
1. {−4, 0, 4}
2. {−30, 10, 40}
3. {−12, −3, 9}
4. {−10, 8, 10}
Fill in the blank with <, , or >.
5.
6.
7.
8.
9.
10.
Determine the unknown.
11.
12.
13.
14.
Translate the following into a mathematical statement.
15. Negative eight is less than or equal to zero.
16. Seventy-eight is not equal to twelve.
17. Negative nine is greater than negative ten.
18. Zero is equal to zero.
Adding and Subtracting Integers
Simplify.
19.
20.
21.
22.
23.
24.
25.
26.
Find the distance between the given numbers on a number line.
27. −8 and 14
28. −35 and −6
29. What is 2 less than 17?
30. What is 3 less than −20?
31. Subtract 30 from the sum of 8 and 12.
32. Subtract 7 from the difference of −5 and 7.
33. An airplane flying at 22,000 feet descended 8,500 feet and then ascended 5,000 feet. What is the new altitude of the airplane?
34. The width of a rectangle is 5 inches less than its length. If the length measures 22 inches, then determine the width.
Multiplying and Dividing Integers
Simplify.
35.
36.
37.
38.
39.
40.
41. Find the product of −6 and 9.
42. Find the quotient of −54 and −3.
43. James was able to drive 234 miles on 9 gallons of gasoline. How many miles per gallon did he get?
44. If a bus travels at an average speed of 54 miles per hour for 3 hours, then how far does the bus travel?
Fractions
Reduce each fraction to lowest terms.
45.
46.
47. Convert to a mixed number: .
48. Convert to an improper fraction: .
Simplify.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61. Subtract from the sum of and .
62. Subtract from the difference of and .
63. If a bus travels at an average speed of 54 miles per hour for hours, then how far does the bus travel?
64. Determine the length of fencing needed to enclose a rectangular pen with dimensions feet by feet.
Decimals and Percents
65. Write as a mixed number: 5.32.
66. Write as a decimal: .
Perform the operations.
67.
68.
69.
70.
Convert to a decimal.
71.
72.
73.
74.
Convert to a percent.
75. 0.055
76. 1.75
77.
78.
79. Mary purchased 3 boxes of t-shirts for a total of $126. If each box contains 24 t-shirts, then what is the cost of each t-shirt?
80. A retail outlet is offering 12% off the original $39.99 price of tennis shoes. What is the price after the discount?
81. If an item costs $129.99, then what is the total after adding sales tax?
82. It is estimated that 8.3% of the total student population carpools to campus each day. If there are 13,000 students, then estimate the number of students that carpool to campus.
Exponents and Square Roots
Simplify.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
99.
100.
101.
102.
103. Calculate the area of a square with sides measuring 3 centimeters. ()
104. Calculate the volume of a cube with sides measuring 3 centimeters. ()
105. Determine the length of the diagonal of a square with sides measuring 3 centimeters.
106. Determine the length of the diagonal of a rectangle with dimensions 2 inches by 4 inches.
Order of Operations
Simplify.
107.
108.
109.
110.
111.
112.
113.
114.
115.
116.
117.
118.
Find the distance between the given numbers on a number line.
119. −14 and 22
120. −42 and −2
121. and
122. and
Sample Exam
1. List three integers greater than −10.
2. Determine the unknown(s): .
3. Fill in the blank with <, =, or >: .
4. Convert to a fraction: .
5. Convert to a percent: .
6. Reduce: .
Calculate the following.
7. a. ; b. ; c.
8. a. ; b. ; c.
9. a. ; b. ; c.
Simplify.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22. Subtract 2 from the sum of 8 and −10.
23. Subtract 10 from the product of 8 and −10.
24. A student earns 9, 8, 10, 7, and 8 points on the first 5 chemistry quizzes. What is her quiz average?
25. An foot plank is cut into 5 pieces of equal length. What is the length of each piece?
Review Exercises Answers
1:

3:
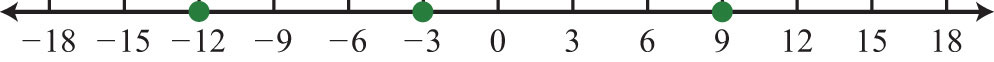
5: >
7: <
9: >
11: ±2
13: Ø, No Solution
15:
17:
19: 5
21: −16
23: 9
25: −6
27: 22 units
29: 15
31: −10
33: 18,500 feet
35: 4
37: 36
39: Undefined
41: −54
43: 26 miles per gallon
45:
47:
49:
51:
53:
55: 1
57:
59:
61:
63: 126 miles
65:
67: 8.222
69: 21.6999
71: 0.072
73: 1.47
75: 5.5%
77: 90%
79: $1.75
81: $139.41
83: 64
85: −16
87: 4/81
89: 27
91:
93: −16
95: 7
97: 10
99:
101:
103: 9 square centimeters
105: centimeters
107: −59
109: −22
111: 31
113: 3
115: 5
117: −12
119: 36 units
121: units
Sample Exam Answers
1: {−5, 0, 5} (answers may vary)
3: <
5: 275%
7:a. 49; b. −49; c. −49
9:a. 10; b. −10; c. −10
11:
13: 48
15:
17: 20
19: 10
21:
23: −90
25: feet




