This is “Exponents and Square Roots”, section 1.6 from the book Beginning Algebra (v. 1.0). For details on it (including licensing), click here.
For more information on the source of this book, or why it is available for free, please see the project's home page. You can browse or download additional books there. To download a .zip file containing this book to use offline, simply click here.
1.6 Exponents and Square Roots
Learning Objectives
- Interpret exponential notation with positive integer exponents.
- Calculate the nth power of a real number.
- Calculate the exact and approximate value of the square root of a real number.
Exponential Notation and Positive Integer Exponents
If a number is repeated as a factor numerous times, then we can write the product in a more compact form using exponential notationThe compact notation used when a factor is repeated multiple times.. For example,
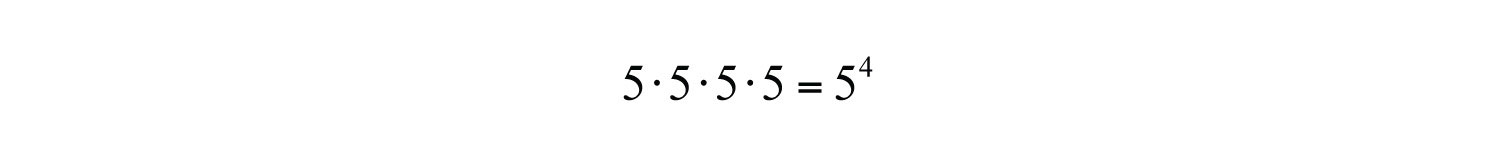
The baseThe factor a in the exponential notation . is the factor, and the positive integer exponentThe positive integer n in the exponential notation that indicates the number of times the base is used as a factor. indicates the number of times the base is repeated as a factor. In the above example, the base is 5 and the exponent is 4. In general, if a is the base that is repeated as a factor n times, then
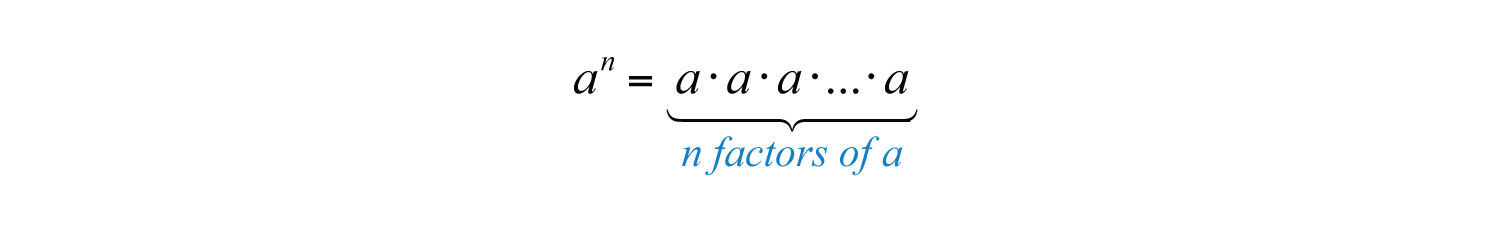
When the exponent is 2, we call the result a squareThe result when the exponent of any real number is 2.. For example,
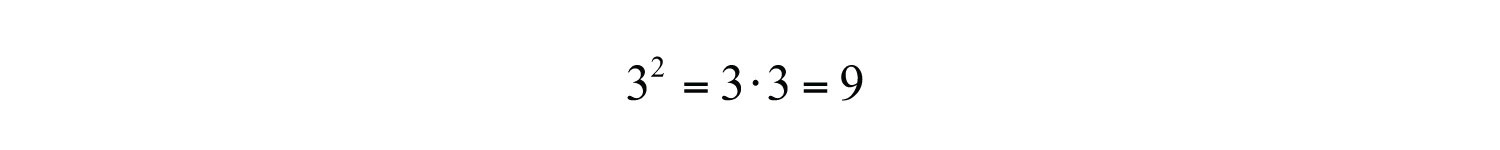
The number 3 is the base and the integer 2 is the exponent. The notation can be read two ways: “three squared” or “3 raised to the second power.” The base can be any real number.
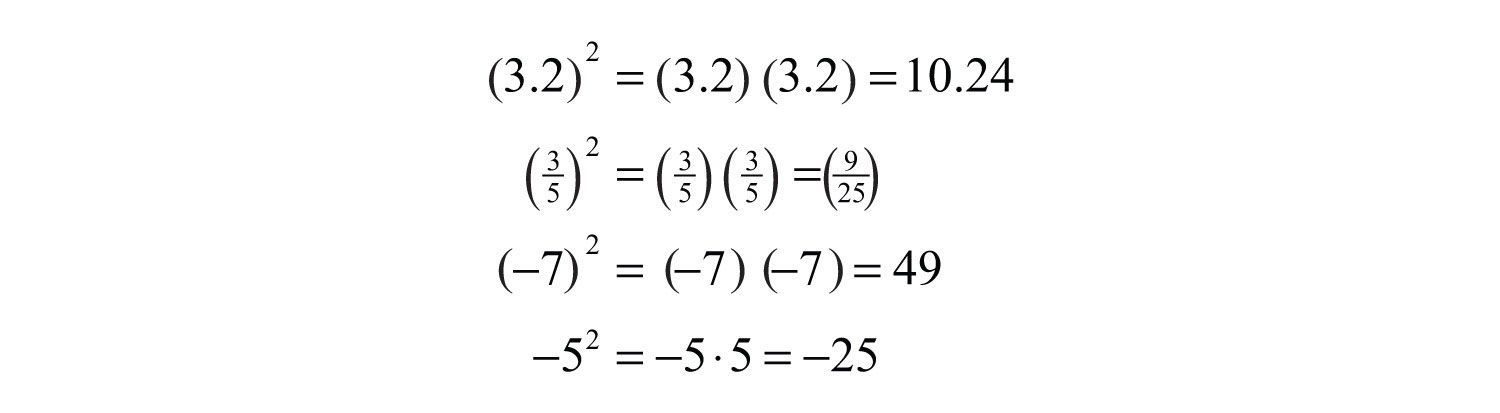
It is important to study the difference between the ways the last two examples are calculated. In the example , the base is −7 as indicated by the parentheses. In the example , the base is 5, not −5, so only the 5 is squared and the result remains negative. To illustrate this, write
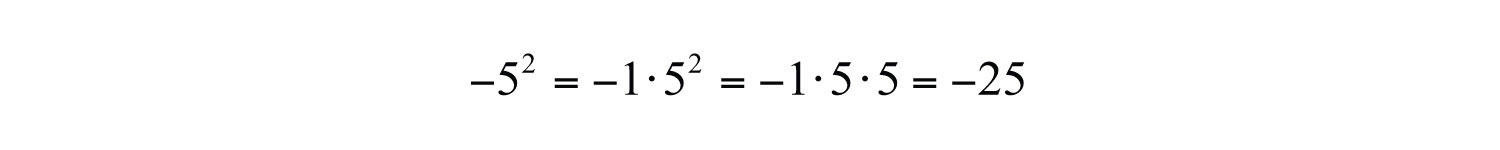
This subtle distinction is very important because it determines the sign of the result.
The textual notation for exponents is usually denoted using the caretThe symbol ^ that indicates exponents on many calculators, . (^) symbol as follows:
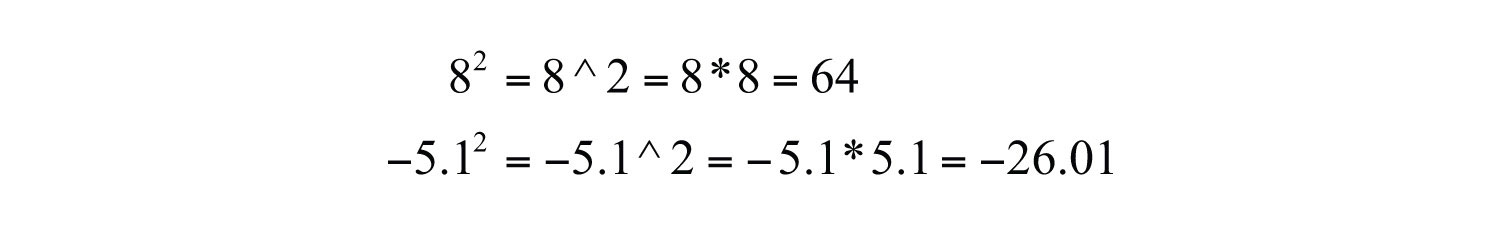
The square of an integer is called a perfect squareThe result of squaring an integer.. The ability to recognize perfect squares is useful in our study of algebra. The squares of the integers from 1 to 15 should be memorized. A partial list of perfect squares follows:
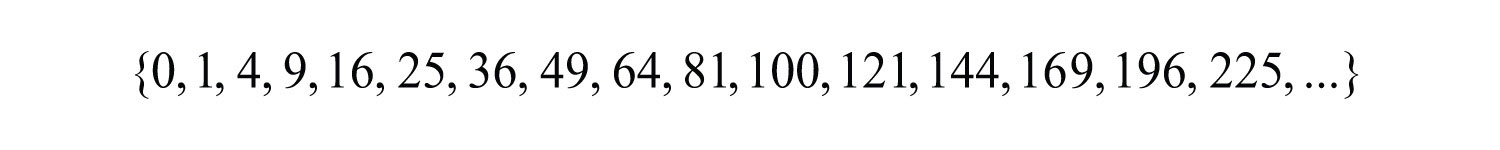
Try this! Simplify .
Answer: 144
Video Solution
(click to see video)When the exponent is 3 we call the result a cubeThe result when the exponent of any real number is 3.. For example,
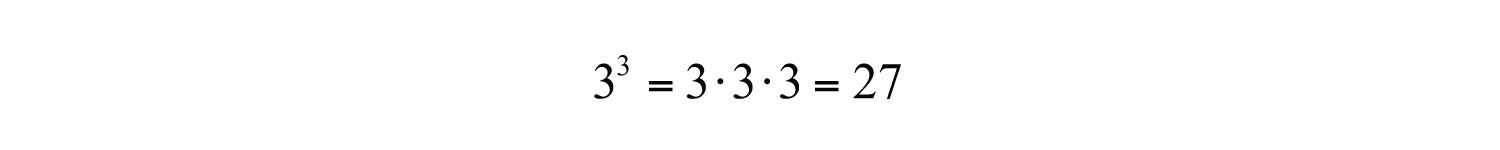
The notation can be read two ways: “three cubed” or “3 raised to the third power.” As before, the base can be any real number.
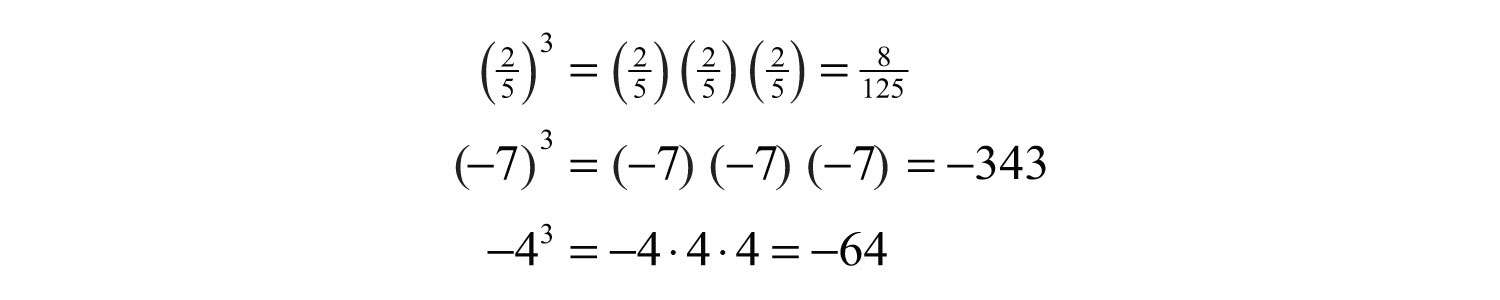
Note that the result of cubing a negative number is negative. The cube of an integer is called a perfect cubeThe result of cubing an integer.. The ability to recognize perfect cubes is useful in our study of algebra. The cubes of the integers from 1 to 10 should be memorized. A partial list of perfect cubes follows:
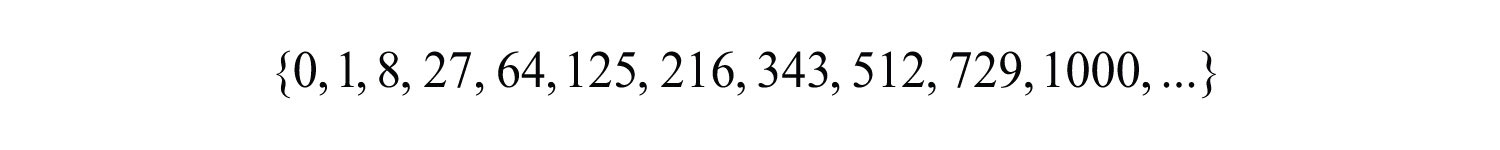
Try this! Simplify .
Answer: −8
Video Solution
(click to see video)If the exponent is greater than 3, then the notation is read “a raised to the nth power.”
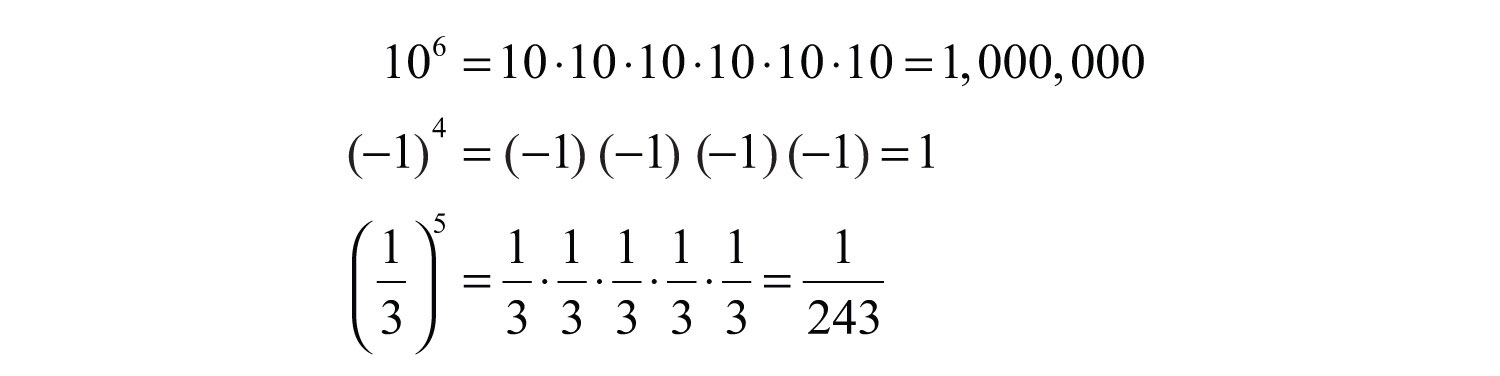
Notice that the result of a negative base with an even exponent is positive. The result of a negative base with an odd exponent is negative. These facts are often confused when negative numbers are involved. Study the following four examples carefully:
| The base is (−2) | The base is 2 |
|---|---|
The parentheses indicate that the negative number is to be used as the base.
Example 1: Calculate:
a.
b.
Solution: The base is for both problems.
a. Use the base as a factor three times.
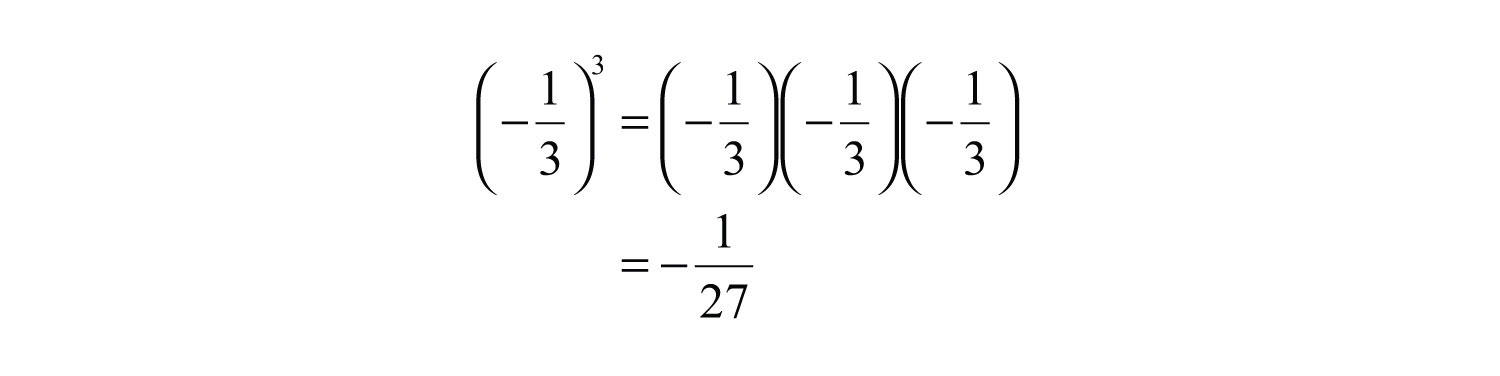
b. Use the base as a factor four times.
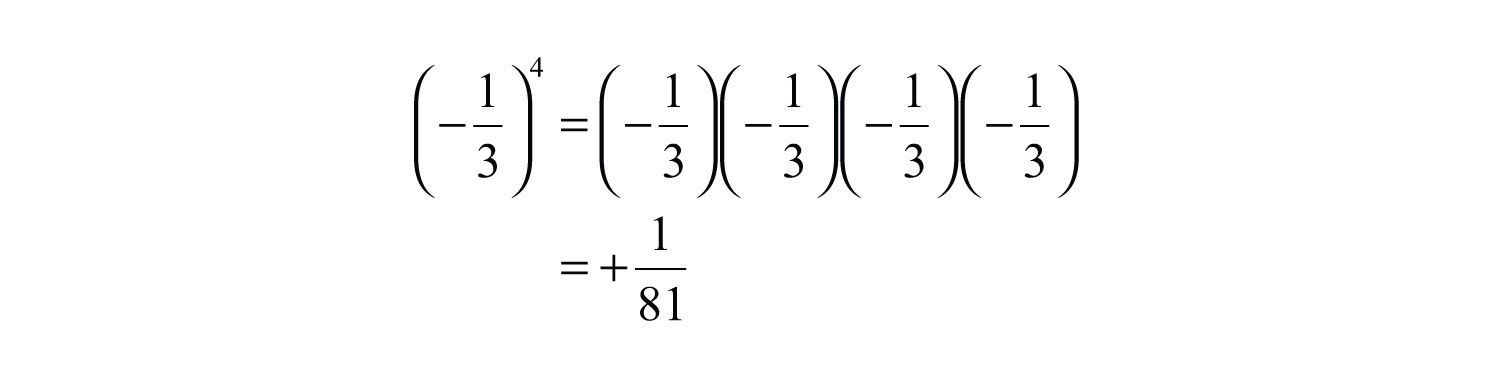
Answers: a. ; b.
Try this! Simplify: and .
Answers: and
Video Solution
(click to see video)Square Root of a Real Number
Think of finding the square rootThe number that, when multiplied by itself, yields the original number. of a number as the inverse of squaring a number. In other words, to determine the square root of 25 the question is, “What number squared equals 25?” Actually, there are two answers to this question, 5 and −5.
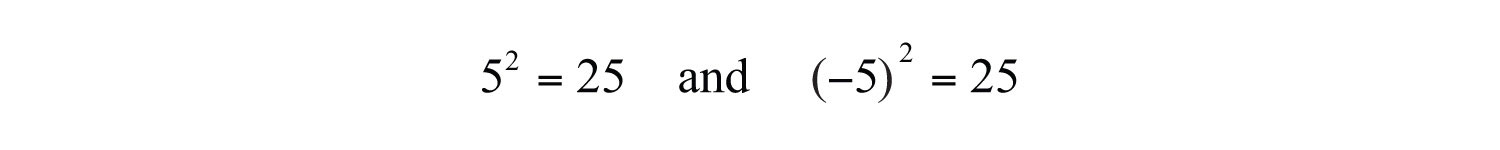
When asked for the square root of a number, we implicitly mean the principal (nonnegative) square rootThe non-negative square root.. Therefore we have,
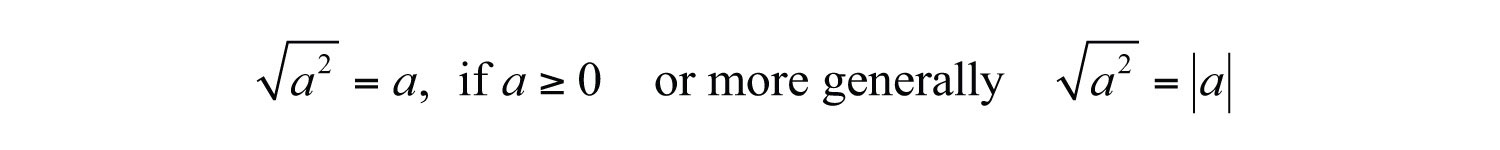
As an example, , which is read “square root of 25 equals 5.” The symbol √ is called the radical signThe symbol √ used to denote a square root. and 25 is called the radicandThe expression a within a radical sign, .. The alternative textual notation for square roots follows:
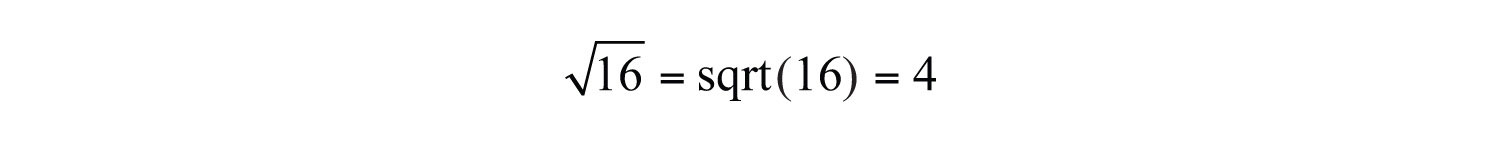
It is also worthwhile to note that
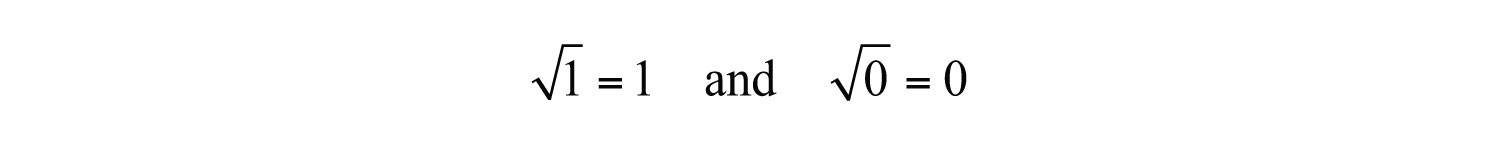
This is the case because and .
Example 2: Simplify: .
Solution: 10,000 is a perfect square because .
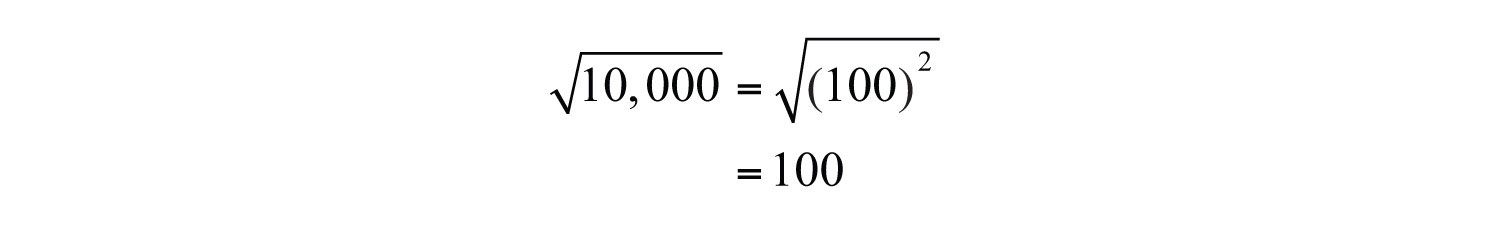
Answer: 100
Example 3: Simplify: .
Solution: Here we notice that is a square because .
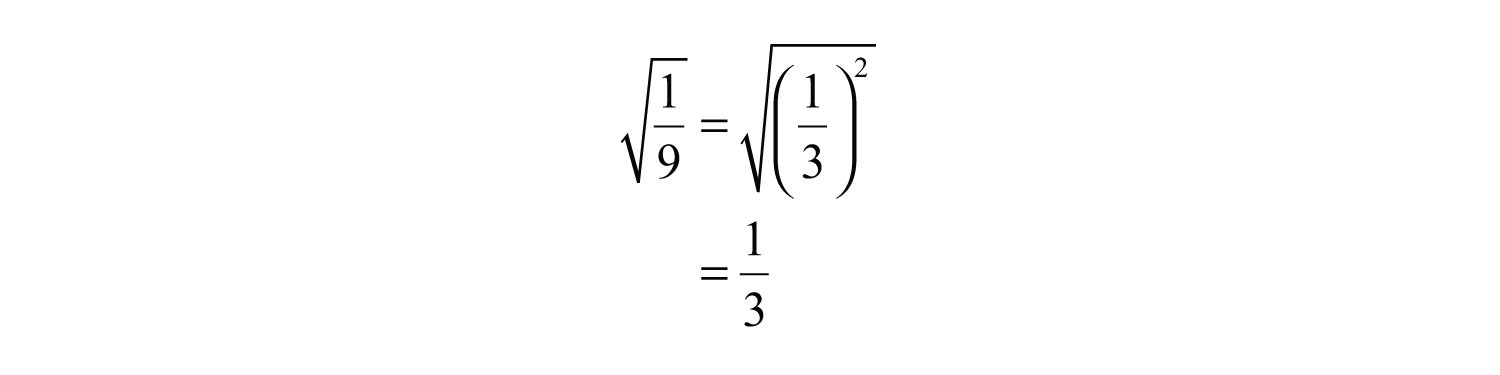
Answer:
Given a and b as positive real numbers, use the following property to simplify square roots whose radicands are not squares:
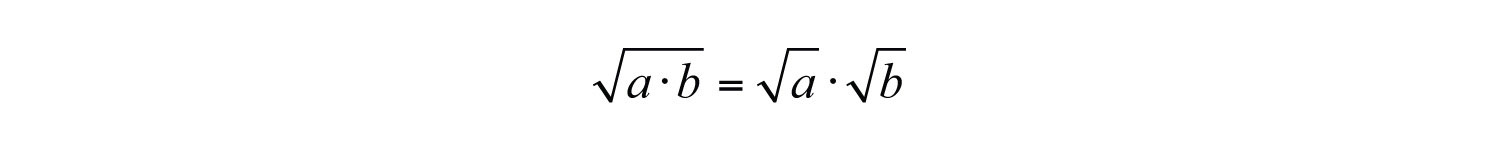
The idea is to identify the largest square factor of the radicand and then apply the property shown above. As an example, to simplify notice that 8 is not a perfect square. However, and thus has a perfect square factor other than 1. Apply the property as follows:
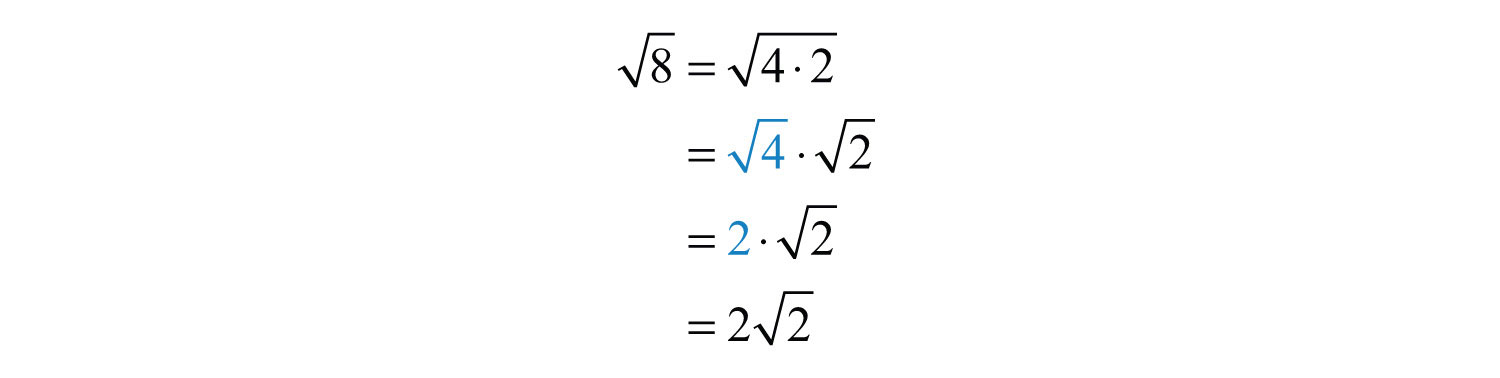
Here is a simplified irrational number. You are often asked to find an approximate answer rounded off to a certain decimal place. In that case, use a calculator to find the decimal approximation using either the original problem or the simplified equivalent.
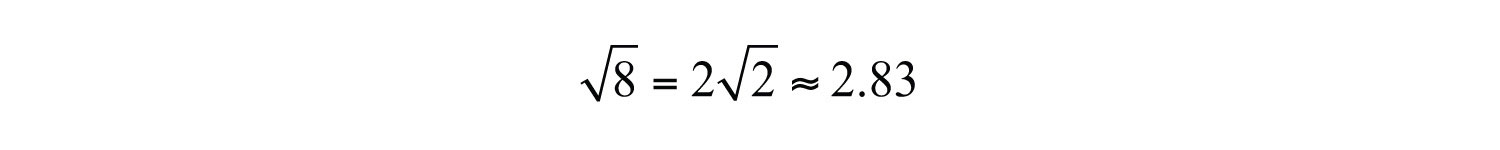
On a calculator, try 2.83^2. What do you expect? Why is the answer not what you would expect?
It is important to mention that the radicand must be positive. For example, is undefined since there is no real number that when squared is negative. Try taking the square root of a negative number on your calculator. What does it say? Note: taking the square root of a negative number is defined later in the course.
Example 4: Simplify and give an approximate answer rounded to the nearest hundredth: .
Solution: The radicand 75 can be factored as 25 ⋅ 3 where the factor 25 is a perfect square.
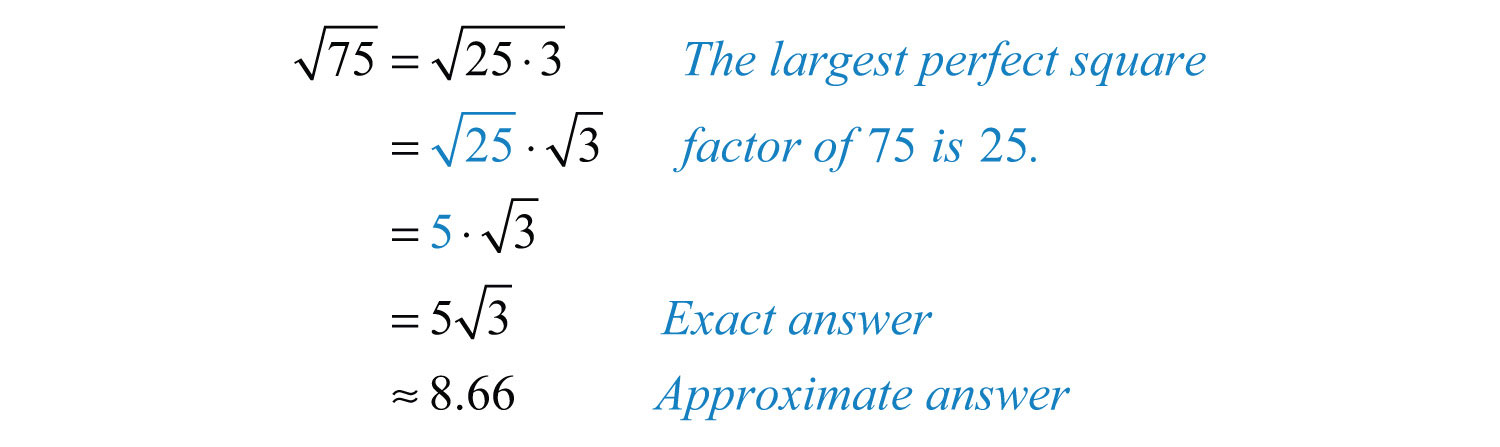
Answer:
As a check, calculate and on a calculator and verify that the both results are approximately 8.66.
Example 5: Simplify: .
Solution:
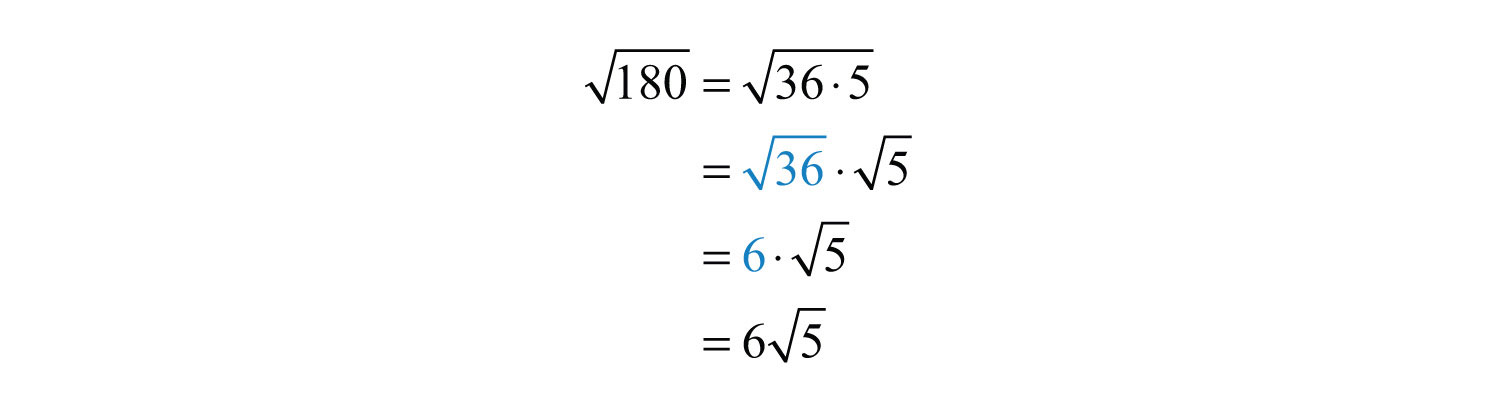
Since the question did not ask for an approximate answer, we present the exact answer.
Answer:
Example 5: Simplify: .
Solution:
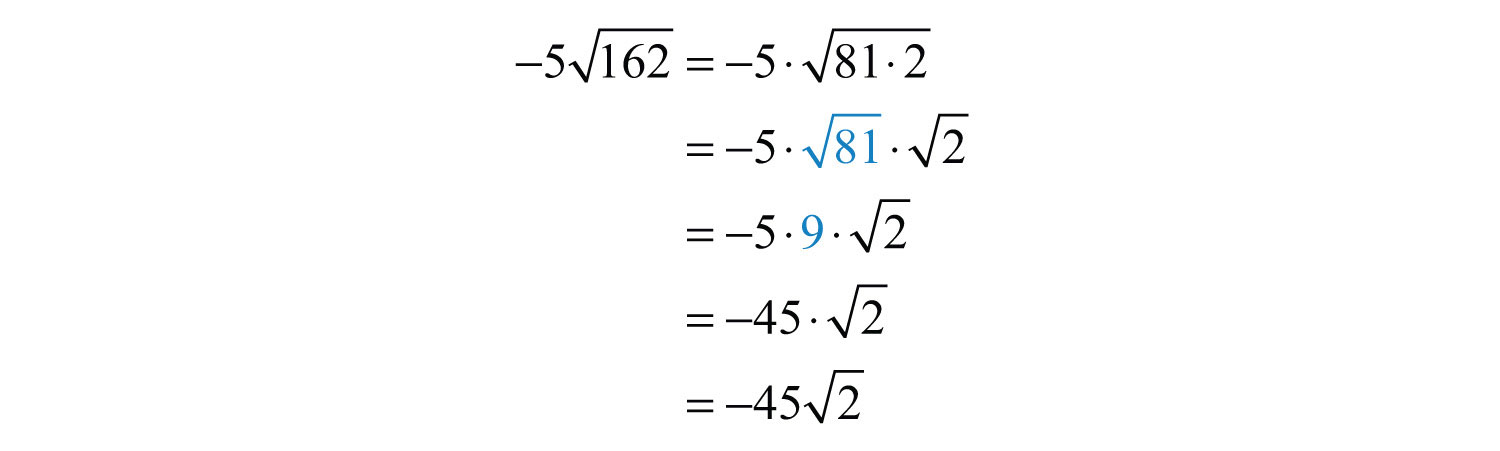
Answer:
Try this! Simplify and give an approximate answer rounded to the nearest hundredth: .
Answer:
Video Solution
(click to see video)Figure 1.1 Pythagoras

Source: Detail of The School of Athens by Raffaello Sanzio, 1509, from http://commons.wikimedia.org/wiki/File:Sanzio_01_Pythagoras.jpg.
A right triangleA triangle with an angle that measures 90°. is a triangle where one of the angles measures 90°. The side opposite the right angle is the longest side, called the hypotenuseThe longest side of a right triangle, it will always be the side opposite the right angle., and the other two sides are called legsThe sides of a right triangle that are not the hypotenuse.. Numerous real-world applications involve this geometric figure. The Pythagorean theoremGiven any right triangle with legs measuring a and b units and hypotenuse measuring c units, then . states that given any right triangle with legs measuring a and b units, the square of the measure of the hypotenuse c is equal to the sum of the squares of the measures of the legs: . In other words, the hypotenuse of any right triangle is equal to the square root of the sum of the squares of its legs.
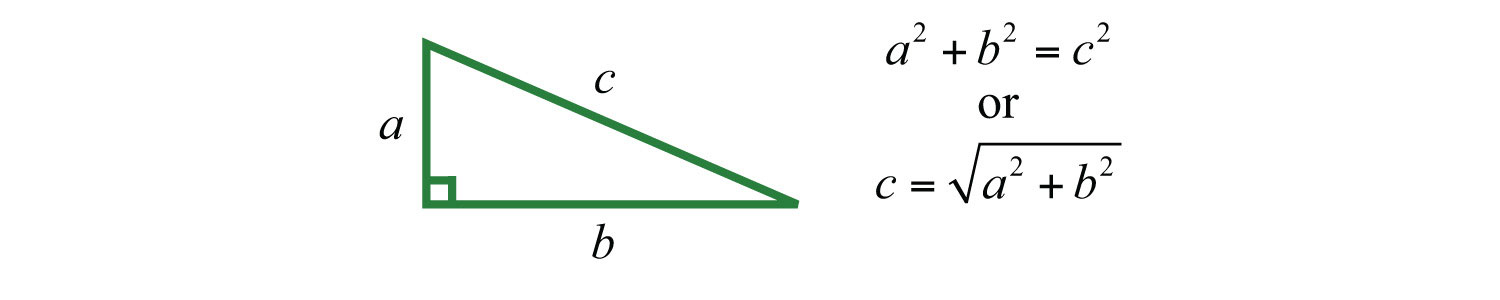
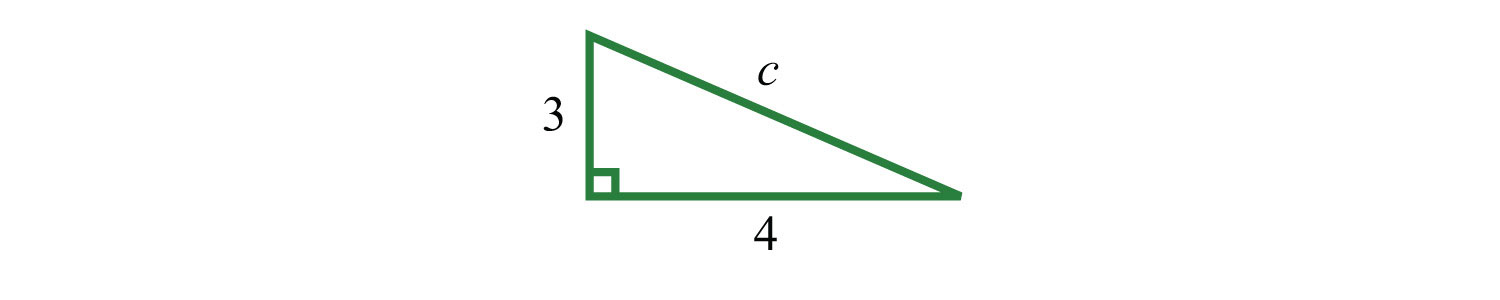
Example 6: If the two legs of a right triangle measure 3 units and 4 units, then find the length of the hypotenuse.
Solution: Given the lengths of the legs of a right triangle, use the formula to find the length of the hypotenuse.
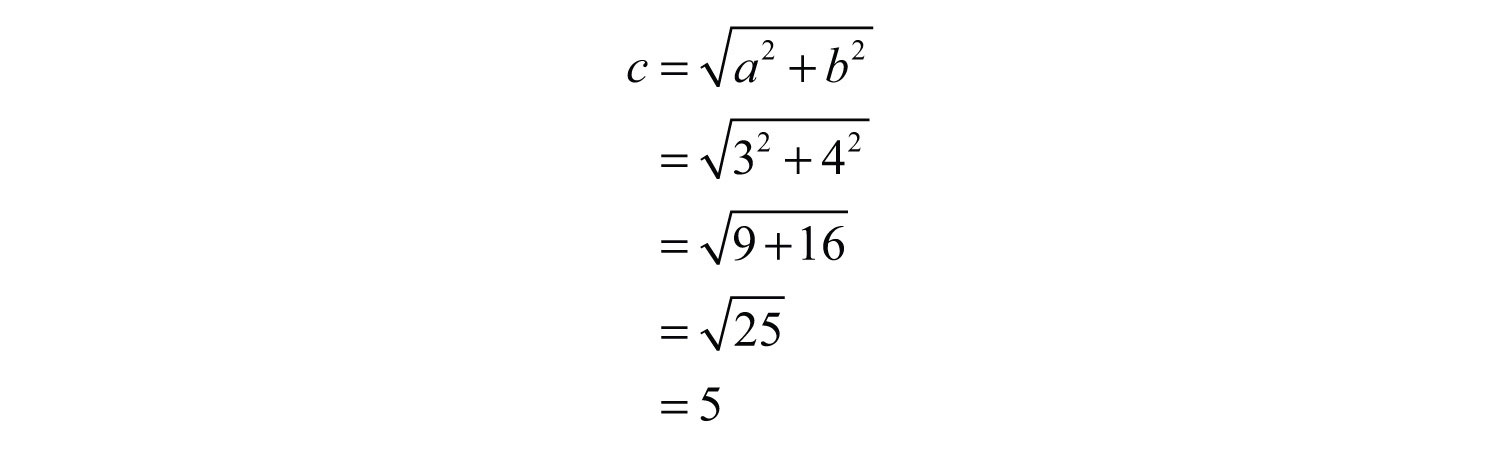
Answer: c = 5 units
When finding the hypotenuse of a right triangle using the Pythagorean theorem, the radicand is not always a perfect square.
Example 7: If the two legs of a right triangle measure 2 units and 6 units, find the length of the hypotenuse.
Solution:
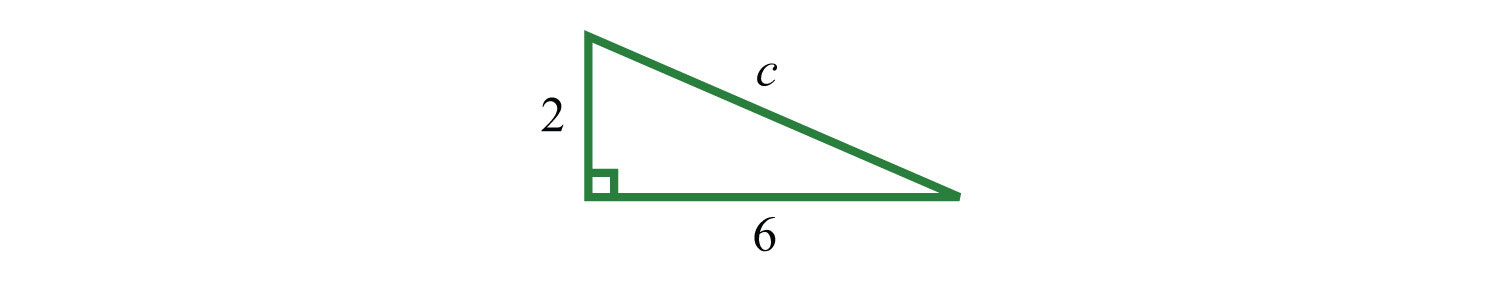
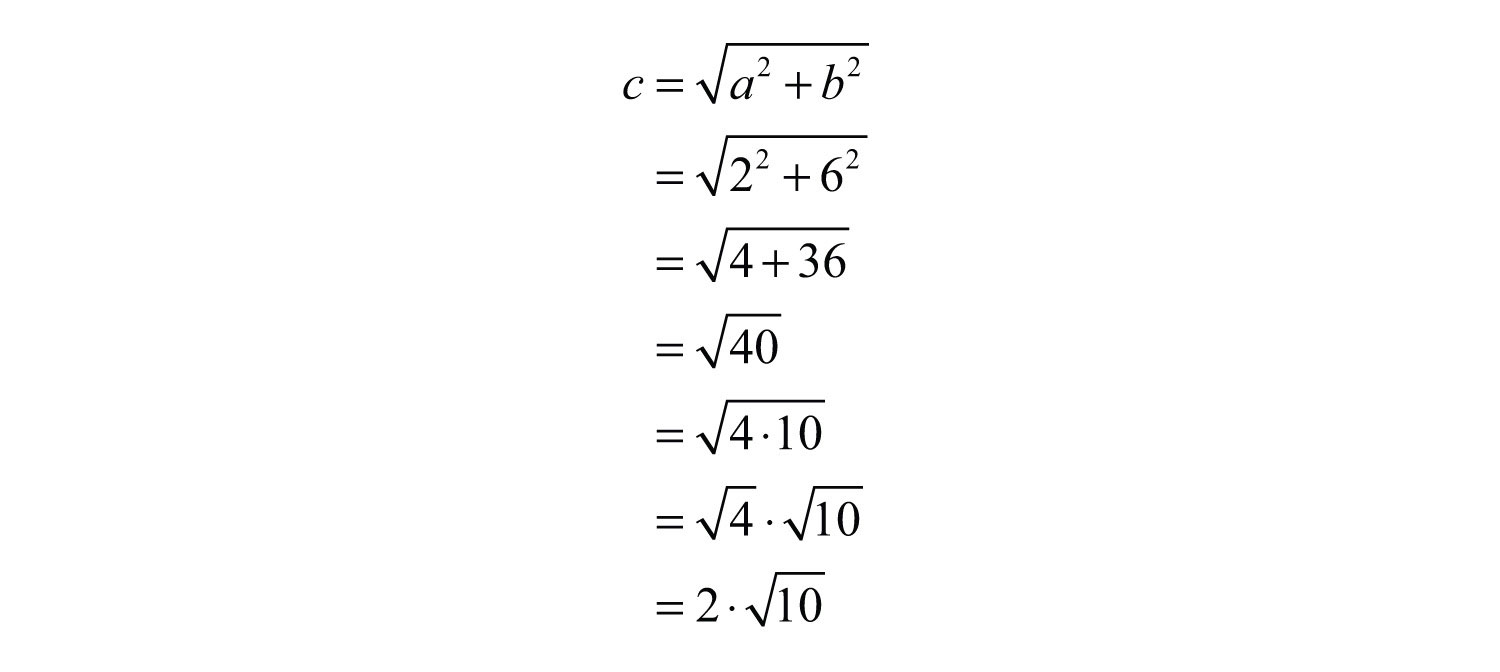
Answer: units
Key Takeaways
- When using exponential notation , the base a is used as a factor n times.
- When the exponent is 2, the result is called a square. When the exponent is 3, the result is called a cube.
- Memorize the squares of the integers up to 15 and the cubes of the integers up to 10. They will be used often as you progress in your study of algebra.
- When negative numbers are involved, take care to associate the exponent with the correct base. Parentheses group a negative number raised to some power.
- A negative base raised to an even power is positive.
- A negative base raised to an odd power is negative.
- The square root of a number is a number that when squared results in the original number. The principal square root is the positive square root.
- Simplify a square root by looking for the largest perfect square factor of the radicand. Once a perfect square is found, apply the property , where a and b are nonnegative, and simplify.
- Check simplified square roots by calculating approximations of the answer using both the original problem and the simplified answer on a calculator to verify that the results are the same.
- Find the length of the hypotenuse of any right triangle given the lengths of the legs using the Pythagorean theorem.
Topic Exercises
Part A: Square of a Number
Simplify.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13. 0.5^2
14. 1.25^2
15. (−2.6)^2
16. −(−5.1)^2
17.
18.
If s is the length of the side of a square, then the area is given by .
19. Determine the area of a square given that a side measures 5 inches.
20. Determine the area of a square given that a side measures 2.3 feet.
21. List all the squares of the integers 0 through 15.
22. List all the squares of the integers from −15 to 0.
23. List the squares of all the rational numbers in the set .
24. List the squares of all the rational numbers in the set .
Part B: Integer Exponents
Simplify.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45. List all the cubes of the integers −5 through 5.
46. List all the cubes of the integers from −10 to 0.
47. List all the cubes of the rational numbers in the set .
48. List all the cubes of the rational numbers in the set .
Part C: Square Root of a Number
Determine the exact answer in simplified form.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
Approximate the following to the nearest hundredth.
79.
80.
81.
82.
83.
84.
85.
86.
87. sqrt(79)
88. sqrt(54)
89. −sqrt(162)
90. −sqrt(86)
91. If the two legs of a right triangle measure 6 units and 8 units, then find the length of the hypotenuse.
92. If the two legs of a right triangle measure 5 units and 12 units, then find the length of the hypotenuse.
93. If the two legs of a right triangle measure 9 units and 12 units, then find the length of the hypotenuse.
94. If the two legs of a right triangle measure units and 2 units, then find the length of the hypotenuse.
95. If the two legs of a right triangle both measure 1 unit, then find the length of the hypotenuse.
96. If the two legs of a right triangle measure 1 unit and 5 units, then find the length of the hypotenuse.
97. If the two legs of a right triangle measure 2 units and 4 units, then find the length of the hypotenuse.
98. If the two legs of a right triangle measure 3 units and 9 units, then find the length of the hypotenuse.
Part D: Discussion Board Topics
99. Why is the result of an exponent of 2 called a square? Why is the result of an exponent of 3 called a cube?
100. Research and discuss the history of the Pythagorean theorem.
101. Research and discuss the history of the square root.
102. Discuss the importance of the principal square root.
Answers
1: 100
3: 81
5: 121
7: 0
9: −64
11: 1/4
13: .25
15: 6.76
17:
19: 25 square inches
21: {0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225}
23: {0, 1/9, 4/9, 1, 16/9, 25/9, 4}
25: 125
27: 1
29: −1
31: −343
33: 27
35: 1
37: −216
39: 1
41:
43:
45: {−125, −64, −27, −8, −1, 0, 1, 8, 27, 64, 125}
47:
49: 11
51: 10
53: −5
55:
57:
59:
61:
63:
65: 0.8
67: 30
69: 2
71: Not real
73: 12
75: −12
77:
79: 1.41
81: 3.16
83: 3.46
85: −13.42
87: 8.89
89: −12.73
91: 10 units
93: 15 units
95: units
97: units




